Simultaneous ground-state cooling of two mechanical modes of a levitated nanoparticle

Abstract

The quantum ground state of a massive mechanical system is a stepping stone for investigating macroscopic quantum states and building high fidelity sensors. With the recent achievement of ground-state cooling of a single motional mode, levitated nanoparticles have entered the quantum domain. To overcome detrimental cross-coupling and decoherence effects, quantum control needs to be expanded to more system dimensions, but the effect of a decoupled dark mode has so far hindered cavity-based ground-state cooling of multiple mechanical modes. Here, we demonstrate two-dimensional ground-state cooling of an optically levitated nanoparticle. Utilizing coherent scattering into an optical cavity mode, we reduce the occupation numbers of two separate centre-of-mass modes to 0.83 and 0.81, respectively. By controlling the frequency separation and the cavity coupling strengths of the nanoparticle’s mechanical modes, we show the transition from 1D to 2D ground-state cooling. This 2D control lays the foundations for quantum-limited orbital angular momentum states for rotation sensing and, combined with ground-state cooling along the third motional axis shown previously, may allow full 3D ground-state cooling of a massive object.

Main

Testing the limits of quantum mechanics as the system size approaches macroscopic scales is one of the grand fundamental and engineering challenges in modern physics^1,2,3,4. Levitated systems are ideal testbeds for exploring macroscopic quantum physics due to the dynamical and full control over their trapping potential^5,6,7,8,9. The motional ground state is the stepping stone for the preparation of quantum states that are delocalized over scales larger than the zero-point motion. Recently, the ground state of the centre-of-mass (COM) motion of a levitated nanoparticle has been reached along a single direction, using both passive feedback via an optical cavity^10,11 as well as active measurement-based feedback^12,13,14.

Even though ground-state cooling is typically necessary for preparing macroscopic quantum states, it is not sufficient, as these states are susceptible to decoherence^5,6,7,8,9. Cross-coupling between a hot and the ground-state cooled COM mode provides a decoherence channel for the ground-state cooled target mode. Cooling of the hot mode would mitigate this cross-coupling decoherence. Additionally, a second ground-state cooled mode (ancilla mode) would be a powerful tool to understand, or even compensate, decoherence effects that influence both ground-state cooled modes. As an example, common dephasing sources (for example, trap frequency noise¹⁵) could be measured in the ancilla mode and then be counteracted in the target mode.

In our levitated particle setup, we achieve simultaneous ground-state cooling of two mechanical modes. We circumvent the key obstacle preventing multimode ground-state cooling in optomechanical systems^16,17, namely the effect of the dark mode^18,19,20,21. The dark hybrid mode is decoupled from the cavity and thus inhibits the efficient cooling of its constituent mechanical modes when they are strongly interacting. We use the unique tunability of levitated systems and adjust the frequency difference between the involved mechanical modes to be larger than the optomechanical coupling rate^18,22. Under this constraint, we optimize the optomechanical coupling strength for efficient cooling by coherent scattering^23,24.

Experimental setup

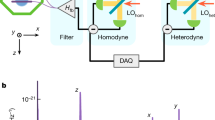
A sketch of our optomechanical system is shown in Fig. 1a. Additional information can be found in the Methods. We detect and cool the COM mechanical modes of a single spherical SiO₂ nanoparticle of nominal diameter 143 ± 6 nm and mass 3.4 ± 0.4 fg. The nanoparticle is levitated in high vacuum (pressure of (5 ± 4) × 10⁻⁹ mbar) using optical tweezers at a wavelength of 1,550.0 ± 0.5 nm (frequency ω₀) with optical power of 1.20 ± 0.08 W, focused by a high numerical aperture (NA, 0.75) lens. The polarization at the focus is defined by the tilt angle θ between the major axis of the polarization ellipse and the cavity axis and by the degree of ellipticity. We choose the polarization by tuning a set of waveplates, compensating for the birefringence of our vacuum window and trapping lens. The nanoparticle’s reference frame is defined by the tweezers’ propagation (z) and polarization (x) axes, as well as the axis orthogonal to the two (y). Strong focusing of the linearly polarized optical tweezers results in non-degenerate, bare mechanical frequencies of the COM motion of Ω_x,y,z/2π = 224 ± 2, 268 ± 2, 80 ± 1 kHz. The asymmetric cavity consists of two mirrors with different transmission separated by 6.4 ± 0.1 mm, resulting in a linewidth of κ/2π = 330 ± 9 kHz. The nanoparticle scatters light into the cavity, which leaks through the higher transmission mirror, is combined with a local oscillator (ω_LO/2π = ω₀/2π + 1.5 MHz) and then split equally onto a balanced photodetector. Heterodyne spectra are calculated as power spectral densities (PSDs) of the balanced photodetector voltage.

Fig. 1: Cooling and detection by coherent scattering.

a, A schematic of the cavity-coupled levitated nanoparticle. The cavity enhances anti-Stokes (blue arrow) over Stokes (red arrow) scattering, leading to cooling of the nanoparticle’s mechanical modes. The scattered light at ω₀ ± Ω_x,y,z leaks through the high transmission mirror, and interferes with a strong local oscillator at ω_LO in a heterodyne detection scheme. The optical tweezers’ propagation direction and its polarization define the z and x axis, respectively. The polarization vector is tilted by an angle θ with respect to the cavity axis. b, A schematic heterodyne power spectral density ($S^{\mathrm{het}}_{\mathrm{vv}}$) of the levitated nanoparticle without the cavity (grey) and filtered by a cavity (black). Six Lorentzian sidebands around the central carrier contain the information of the nanoparticle’s three COM modes. The Stokes (anti-Stokes) amplitudes are proportional to $\bar{n}_j+1$ ($\bar{n}_j$), which we use for sideband thermometry. The cavity transfer function (dashed blue line) is detuned by Δ from the tweezers’ frequency and enhances the anti-Stokes processes, leading to cooling of the mechanical modes.

Cooling to 2D ground state

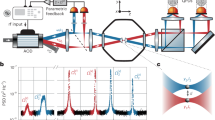
Our two-mode ground-state cooling experiment relies on coherent scattering^25,26,27, referring to light being scattered off a polarizable particle and populating an optical cavity. This method has attracted interest as, compared with other cavity cooling schemes, it offers larger optomechanical coupling strengths and reduced phase noise heating²⁴. Here, we exploit coherent scattering for coupling two motional modes of a single nanoparticle to an optical cavity mode^23,24,28,29. A harmonically trapped nanoparticle scatters light elastically (Rayleigh) and inelastically (Raman). The Raman processes lead to sidebands in the scattered light spectrum. Figure 1b shows a schematic of the resulting heterodyne spectrum, which illustrates the cooling mechanism of coherent scattering. The positive and negative frequencies correspond to the destruction and creation of a phonon, which are denoted by anti-Stokes and Stokes scattering, respectively. The grey line represents the spectrum of the mechanical oscillations without cavity. We introduce an optical cavity (dashed blue line is the intensity transfer function), whose resonance frequency ω_c is detuned by Δ = ω_c − ω₀. As we choose Δ ≈ (Ω_x + Ω_y)/2, the cavity enhances anti-Stokes relative to Stokes scattering in the spectrum (black line), which reduces the occupation numbers ${\bar{n}}_{j}$ (j = x, y) of the COM modes. The asymmetry between Stokes and anti-Stokes peaks is additionally influenced by the fact that their scattering rates are proportional to ${\bar{n}}_{j}+1$ and ${\bar{n}}_{j}$, respectively. Taking into account the cavity transfer function, we use the measured asymmetry in the PSDs to extract ${\bar{n}}_{x,y}$ through a technique called sideband thermometry^24,30 (Methods). Figure 2a shows the measured heterodyne PSDs normalized to shot noise level. The PSDs contain Stokes and anti-Stokes sidebands of both transversal modes (x and y), simultaneously coupled to the cavity at θ = 0.25π, for different cavity detunings Δ. The cooling by coherent scattering becomes more efficient as Δ approaches (Ω_x + Ω_y)/2, which results in a smaller amplitude and broader width of the sidebands. For each detuning and each COM mode, we fit Lorentzians (lines) of equal widths but independent amplitudes to the Stokes and anti-Stokes sidebands. The asymmetries that we use for sideband thermometry are then given by the ratio of anti-Stokes to Stokes amplitudes. Figure 2b shows the extracted occupation numbers as a function of the cavity detuning. The shaded areas represent simulations based on coupling strengths g_j and heating rates Γ_j which we extract (Methods) from our data to be g_x/2π = 14.1 ± 2.7 kHz, g_y/2π = 15.4 ± 1.9 kHz, Γ_x/2π = 1.0 ± 0.4 kHz and Γ_y/2π = 1.0 ± 0.4 kHz. We infer the heating rates to be limited by photon recoil (Methods), as they are in good agreement with values calculated from system parameters. For Δ/2π = 232 kHz close to (Ω_x + Ω_y)/2, we reach occupation numbers of ${\bar{n}}_{x}=0.83\pm 0.10$ and ${\bar{n}}_{y}=0.81\pm 0.12$, cooling the COM motion into its two-dimensional (2D) quantum ground state.

Fig. 2: Two-mode ground-state cooling.

a, Heterodyne PSDs of Stokes and anti-Stokes sidebands of x and y modes for different cavity detunings Δ. From Lorentzian fits (lines), the thermal occupation numbers are extracted via sideband thermometry. b, Occupation numbers (calculated from fits in a with colours matching the detunings) for x and y modes as functions of cavity detuning. For Δ/2π = 232 kHz, close to the optimal value (Ω_x + Ω_y)/2 for simultaneous cooling, both occupation numbers are cooled below 1 (dashed grey line). Error bars correspond to one s.d. of the fitted asymmetries and the cavity parameters Δ and κ around the calculated occupation numbers. Shaded areas show theoretical estimations of n_x (upper) and n_y (lower, overlap is darker) based on coupling and heating rates and their uncertainties extracted from the measured PSDs.

Transition from 2D to 1D ground-state cooling

We explore the robustness of our cooling scheme to changes of the coupling rates by changing the polarization angle θ of the trapping light. The linearized optomechanical coupling strengths g_x,y for linear polarization have the form ${g}_{x}\propto \cos \theta$ and ${g}_{y}\propto \sin \theta$ (ref. ²⁸). Figure 3a–d displays anti-Stokes sidebands of x and y modes for different θ at Δ/2π = 246 ± 8 kHz. By tuning θ from 0.25π to 0.5π, we observe the transition from 2D to 1D ground-state cooling. Close to θ = 0.5π, the shrinking/rising peak amplitudes indicate the motion along y/x being cooled more/less efficiently owing to larger/smaller coupling strength g_y/g_x. Note that, at θ = 0.5π, the x motion is still imprinted in the spectrum of the cavity field and remains cooled. We attribute this to imperfections in the polarization state and in the angular alignment between the optical axes of the trap and cavity. Additionally, small shifts in the frequencies Ω_j for different θ are caused by power drifts of the optical tweezers on the 5% level. The phonon occupations extracted from sideband thermometry ${\bar{n}}_{x,y}$ are displayed in Fig. 3e. The simulations (shaded areas; Methods) show the increasing and decreasing occupation numbers of the x and y mode, respectively, in agreement with the data. This result is well aligned with the predicted decrease (increase) of ${g}_{x}\propto \cos \theta$ (${g}_{y}\propto \sin \theta$) as θ is increased from 0.25π to 0.5π. Experimentally, we find robust two-mode ground-state cooling at θ = 0.25π and 0.33π. Furthermore, we observe our lowest single-mode phonon occupation of ${\bar{n}}_{y}=0.46\pm 0.05$ paired with a high phonon occupation of ${\bar{n}}_{x}=14\pm 12$ at θ = 0.5π.

Fig. 3: Polarization dependence of two-mode cooling.

a–d, Anti-Stokes sidebands of x and y modes and Lorentzian fits (lines) for different polarization angle θ of 0.25π (a), 0.33π (b), 0.42π (c) and 0.50π (d). In a, both modes have similar coupling strengths. In d, optimal y axis cooling is achieved. e, Occupation numbers of x and y modes (colours matching a–d) separate for θ > 0.25π, transitioning from 2D to 1D cooling. Error bars correspond to one s.d. of the fitted asymmetries and the cavity parameters Δ and κ around the calculated occupation numbers. Shaded areas mark theoretical predictions based on extracted coupling strengths.

Limits of 2D sideband cooling and thermometry

To efficiently cool two COM modes (x, y) of a levitated nanoparticle, several conditions must be met. First, the optical cavity must simultaneously resolve the anti-Stokes sidebands of the x and y modes, that is ∣Ω_y − Ω_x∣ ≲ κ ≲ Ω_y, Ω_x. Further, the system needs to be in the weak coupling regime ∣g_j∣ ≪ κ, to prevent hybridization of the cavity and mechanical modes, which hinders efficient cooling³¹. Finally, Ω_x and Ω_y must be sufficiently separated. The x and y modes are cooled by the cavity via a collective bright mechanical mode, while the orthogonal dark mechanical mode is only sympathetically cooled when coupling to the bright mode²². For near-degenerate Ω_x and Ω_y, the dark mode decouples, and this inhibits cooling of its constituent x and y modes (Methods). The condition ∣Ω_y − Ω_x∣ ≳ ∣g_j∣ is thus necessary for 2D ground-state cooling^18,22 (see Methods for details).

The unique in situ tunability of levitated systems allows us to observe the effect of the dark mode decoupling on ${\bar{n}}_{x,y}$. For a highly focused beam, the shape of the focus spot and thus the resulting trap frequencies are dependent on the incoming polarization³². We change Ω_x,y by tuning the ellipticity of the trapping beam polarization while keeping θ = 0.25π and Δ/2π = 257 ± 11 kHz. Comparing Fig. 4a and b, we observe that Ω_x and Ω_y approach each other as the polarization changes from linear to elliptical. In Fig. 4b, both modes heat up to ${\bar{n}}_{x}=2.0\pm 0.4$ and ${\bar{n}}_{y}=2.8\pm 0.8$ as weak coupling of the dark mode inhibits cooling. As we polarize the tweezers circularly for Fig. 4c, x and y peaks merge and we are unable to extract individual occupation numbers by conventional sideband thermometry.

Fig. 4: Limits of 2D sideband cooling.

a–c, Anti-Stokes sidebands of x and y modes for linear (a), elliptical (b) and circular (c) ellipticity in the trap’s polarization. The separation between peaks Ω_y − Ω_x decreases with increasing ellipticity. In b, cross-coupling increases the occupation numbers to ${\bar{n}}_{x}=2.1\pm 0.4$ and ${\bar{n}}_{y}=2.8\pm 0.8$. Circular polarization causes degenerate peaks in c. d,e, The relative error of x (d) and y (e) occupation extracted by sideband thermometry versus the real phonon number. Parameter pairs of measurements in Figs. 2 and 3b–d as well as b and c are marked by points. The dark mode decoupling prevents efficient cooling for Ω_y − Ω_x < (g_x + g_y)/2 (black line), and sideband thermometry becomes impossible for degenerate peaks (white area).

We further theoretically test the validity of extracting phonon numbers by sideband thermometry using a full quantum model²⁸ (Methods). We first calculate the true phonon occupation ${\bar{n}}_{j}^{{{{\rm{model}}}}}$ for j = x, y. Then, using the same model, we calculate PSDs of the heterodyne detection and perform sideband thermometry on them to extract ${\bar{n}}_{j}$. We define the systematic error $\updelta {\bar{n}}_{j}=| ({\bar{n}}_{j}^{{{{\rm{model}}}}}-{\bar{n}}_{j})/{\bar{n}}_{j}^{{{{\rm{model}}}}}|$ and show the result in Fig. 4d,e. Mostly we find that ${\bar{n}}_{j}$ underestimates ${\bar{n}}_{j}^{{{{\rm{model}}}}}$. In the weak coupling regime and for well-separated COM mode frequencies, $\updelta {\bar{n}}_{j}$ is negligible. For stronger coupling and constant mode spacing, hybridization between optical and mechanical modes becomes more impactful and $\updelta {\bar{n}}_{j}$ increases. At constant coupling rate, the error also increases as the mechanical frequencies approach degeneracy and the effect of the dark mode gains importance. We cannot perform 2D sideband thermometry for degenerate peaks, which occurs at small mode spacing and large coupling strength (Fig. 4d,e white areas). Finally we display the estimated errors for all measurements presented in Figs. 2–4. These errors of our sideband thermometry method are marginal, for Fig. 2 only about 1%, which confirms that we have achieved two-mode ground-state cooling.

Conclusions

We have simultaneously prepared two out of three COM modes of a levitated particle in their ground state with residual occupation numbers of ${\bar{n}}_{x}=0.83$ and ${\bar{n}}_{y}=0.81$. With respect to the optical axis of the tweezers, our cooling scheme controls the transversal degrees of freedom, resulting in two important implications.

First, together with the demonstrated ground-state cooling along the tweezers’ axis^12,13,14, 3D COM quantum control is within experimental reach. Demonstrating 3D ground-state cooling would be an important step towards full control of large systems at the quantum limit.

Second, control over transversal COM motion implies control of the orbital angular momentum along the tweezers’ axis, given by ${\hat{L}}_{z}=\hat{x}{\hat{p}}_{y}-\hat{y}{\hat{p}}_{x}$, where $(\hat{x},\hat{y})$ and $({\hat{p}}_{x},{\hat{p}}_{y})$ are the transverse position and momentum vector operator, respectively. As the particle’s transversal motion is in a thermal state, the variance of the corresponding angular momentum is given by $\langle {\hat{L}}_{z}^{2}\rangle /{\hslash }^{2}=({\bar{n}}_{x}+1/2)({\bar{n}}_{y}+1/2)({\varOmega }_{x}/{\varOmega }_{y}+{\varOmega }_{y}/{\varOmega }_{x})-1/2$. With our occupation numbers and trap frequencies, we find $\sqrt{\langle {\hat{L}}_{z}^{2}\rangle }\approx 1.7\,\hslash$. We have therefore prepared our system close to an angular momentum eigenstate along z ($\langle {\hat{L}}_{z}^{2}\rangle =0$) with $\langle {\hat{L}}_{z}\rangle =0$. This opens the door to realizing protocols combining 2D ground-state cooling with coherently pumped orbital angular momentum³³ to stabilize a state with large orbital angular momentum $\langle {\hat{L}}_{z}\rangle \gg \hslash$ and quantum-limited variance. Those minimally fluctuating high orbital angular momentum states (‘quantum orbits’) would be promising not only for fundamental studies of low-noise and massive high angular momentum states but also for becoming building blocks of a gyroscope with quantum-limited performance.

Methods

Setup

A detailed view of the experimental setup is shown in Extended Data Figs. 1 and 2. To keep our cavity free of contaminants and at vacuum conditions (below 10⁻² mbar) at all times, we load nanoparticles (SiO₂-F-L3205-23, 143 ± 6 nm nominal diameter; microParticles GmbH) in a separate loading chamber (not drawn in Extended Data Fig. 1) using a nebulizer (Omron). The loading tweezers are mounted on a movable arm, and its light is frequency shifted by acousto-optic modulator (AOM)3 by 80 MHz to avoid interference. After loading, we seal and evacuate the loading chamber to 1 × 10⁻² mbar and move the loading tweezers into the cavity chamber. We use two photodetectors and the loading tweezers’ nanopositioner (SmarAct GmbH) to align the focal points of loading and science tweezers. Initially, we measure the intensity of light passing by the particle on PD_BR to roughly align the two foci, while the science tweezers are still turned off. Afterwards, we gradually increase the power of the science tweezers and measure the light coupling into the fibre of the loading tweezers and shining on PD_L. Eventually, we turn down and up the power in the trapping and science tweezers, respectively, to transfer the nanoparticle to the science tweezers. Thereafter, the science chamber is sealed off and pumped down to 5 × 10⁻⁹ mbar by using a combination of a turbomolecular pump and an ion-getter pump.

The cavity with linewidth κ/2π = 330 kHz, finesse ${{{\mathcal{F}}}}=70\,{{{\rm{k}}}}$ and focal spot waist w_c = 48 ± 5 μm is built from a low and high finesse mirror (specified finesse of coatings of 37k and 126k) with a radius of curvature of 10 mm and cavity length of L = 6.4 mm. The absorption A and transmission T of the low (high) finesse coatings are 4 and 79 ppm (5 and 20 ppm), respectively. We lock the cavity to the TEM₁₀ mode of the cavity to avoid interference with light scattered off the particle into the TEM₀₀ mode. The necessary frequency shift ω₁₀ − ω₀₀ of approximately 8 GHz is generated by AOM1 and electro-optic modulator (EOM)1 to obtain the lock beam sent into the cavity. We define the cavity detuning Δ = ω_c − ω₀ with respect to the cavity resonance frequency ω_c of the TEM₀₀ mode. The backscattered light is collected on a photodiode (PD_PDH) to generate the error signal for a Pound–Drever–Hall lock³⁴ of the cavity length. The small sidebands necessary for the error signal are generated by EOM2 at 23 MHz.

Detuning calibration

To perform accurate sideband thermometry, we need to compensate for the effect of cavity filtering of the motional sidebands. For a known detuning Δ and linewidth κ, we can readily calculate the cavity-induced asymmetry at a mode frequency Ω_j by assuming a Lorentzian filter function³⁵:

$${A}_{j}^{({{{\rm{cav}}}})}=\frac{{\kappa }^{2}+4{\left(\varDelta +{\varOmega }_{j}\right)}^{2}}{{\kappa }^{2}+4{\left(\varDelta -{\varOmega }_{j}\right)}^{2}}.$$

In our experiments, the particle scatters light into the TEM₀₀ of the optical cavity, while the cavity is locked to the TEM₁₀ mode. The difference of the two TEM mode frequencies is very sensitive to drifts of the cavity length between experiments. Thus, we need to calibrate the detuning of the cavity with respect to the science tweezers. As a particle-independent measure, we temporarily send a calibration laser through the cavity before performing cooling experiments. This laser has sidebands modulated by an electro-optic modulator (EOM3) at 300 kHz and higher harmonics, which are filtered by the detuned cavity and then detected in our heterodyne scheme (Extended Data Fig. 3a). We extract the asymmetry of these three sidebands and the z-peak of the particle motion while tuning the cavity lock frequency with EOM1. In Extended Data Fig. 3b, we fit the Lorentzian cavity filter function to the measured sideband asymmetry to extract the linewidth and calibrate the detuning Δ. The linewidth agrees with an independent measurement of κ/2π = 330 kHz. The s.d. values for Δ in Fig. 2b are below 3 kHz, and therefore the error bars are smaller than the markers.

Sideband thermometry

For extracting the phonon occupation from measured heterodyne signals, we rely on the different scaling of Stokes and anti-Stokes scattering processes. As the latter requires the presence of a phonon, its scattering rate scales with the average phonon number n, while the Stokes scattering rate scales with n + 1. This leads to an asymmetry of the anti-Stokes and Stokes sidebands dependent on the occupation number:

$${A}_{j}^{(n)}=\frac{{\bar{n}}_{j}}{{\bar{n}}_{j}+1}.$$

The total asymmetry of the PSD at the frequency Ω_j

$${A}_{j}=\frac{{S}_{vv}({\varDelta }_{{{{\rm{lo}}}}}+{\varOmega }_{j})}{{S}_{vv}({\varDelta }_{{{{\rm{lo}}}}}-{\varOmega }_{j})}={A}_{j}^{(n)}{A}_{j}^{({{{\rm{cav}}}})}$$

is the product of the thermal asymmetry ${A}_{j}^{(n)}$ and the cavity/induced asymmetry ${A}_{j}^{{{{\rm{(cav)}}}}}$. Given both, we can calculate the average occupation number

$${\bar{n}}_{j}=\frac{{A}_{j}}{{A}_{j}^{({{{\rm{cav}}}})}-{A}_{j}}.$$

To access the thermal asymmetry, we assume a Lorentzian shape of the motional sidebands

$${S}_{jj}(\varOmega )\approx \frac{{a}_{j}}{2\uppi }\frac{\frac{{\gamma }_{j}}{2}}{{\left(\varOmega -{\varOmega }_{j}\right)}^{2}+{\left(\frac{{\gamma }_{j}}{2}\right)}^{2}},$$

with amplitude a_j, width γ_j and centre frequency Ω_j. Our fitting function

$$F={S}_{xx,({{{\rm{AS}}}})}+{S}_{xx,({{{\rm{S}}}})}+{S}_{yy,({{{\rm{AS}}}})}+{S}_{yy,({{{\rm{S}}}})}+{S}_{{{{\rm{SN}}}}}$$

lets us extract four values for a_j, γ_j and Ω_j, one for each Stokes and anti-Stokes sideband of mode j = x, y, and gives ${A}_{j}^{(n)}={a}_{j,{{{\rm{AS}}}}}/{a}_{j,S}$. We require γ_j,AS = γ_j,S and Ω_j,AS = −Ω_j,S. The shot noise level ${S}_{{{{\rm{SN}}}}}$ is extracted for each PSD in a region far away from any spectral features to account for small drifts in the local oscillator power. We normalize all spectra to the shot noise level. For the error bars, we propagate the s.d. of the fitted amplitudes a_j and the cavity parameters Δ and κ.

Quantum model

The Hamiltonian describing coherent scattering is²⁸

$$\frac{{\hat{{{{{H}}}}}}_{{{{\rm{CS}}}}}}{\hbar }=\varDelta {\hat{a}}^{{\dagger} }\hat{a}+\mathop{\sum}\limits_{j=x,y,z}{\varOmega }_{j}{\hat{b}}_{j}^{{\dagger} }{\hat{b}}_{j}-\mathop{\sum}\limits_{j=x,y,z}({g}_{j}{\hat{a}}^{{\dagger} }+\,{{\mbox{h.c.}}}\,)({\hat{b}}_{j}^{{\dagger} }+\hat{{b}_{j}}),$$

with $\hat{a}$ (${\hat{a}}^{{\dagger} }$) being the photon annihilation (creation) operator, ${\hat{b}}_{j}$ (${\hat{b}}_{j}^{{\dagger} }$) the phonon annihilation (creation) operator along motional axis j = x, y, z, and h.c. the Hermitian conjugate. This interaction allows to cool the COM motion along all three axes, as has been demonstrated experimentally^36,37. The linearized optomechanical coupling strengths g_j for linear polarization are given by

$$\left[\begin{array}{c}{g}_{x}\\ {g}_{y}\\ {g}_{z}\end{array}\right]=-\frac{{G}_{0}}{2}\left[\begin{array}{c}{k}_{{{{\rm{c}}}}}{x}_{{{{\rm{zpf}}}}}\sin \phi \cos \theta \\ {k}_{{{{\rm{c}}}}}{y}_{{{{\rm{zpf}}}}}\sin \phi \sin \theta \\ -\mathrm{i}{k}_{{{{\rm{t}}}}}{z}_{{{{\rm{zpf}}}}}\cos \phi \end{array}\right]$$

(1)

with k_c = 2π/λ_c the cavity wavevector, $[{x}_{{{{\rm{zpf}}}}},{y}_{{{{\rm{zpf}}}}},{z}_{{{{\rm{zpf}}}}}]=\sqrt{\frac{\hslash }{2\hspace{2.22144pt}m\hspace{2.22144pt}{\varOmega }_{x,y,z}}}$ the zero-point fluctuations (zpf) along each axis and ϕ = 2πy₀/λ_c, with y₀ being the particle position along the cavity axis and y₀ = λ_c/4 corresponding to an intensity minimum of the cavity standing wave. The rate ${G}_{0}=\alpha {E}_{0}\sqrt{\frac{{\omega }_{{{{\rm{c}}}}}}{2\hbar {\epsilon }_{0}{V}_{{{{\rm{c}}}}}}}{\mathbf{e}}_{x}\cdot {\mathbf{e}}_{\alpha }$ contains the particle polarizability $\alpha =4\uppi {\epsilon }_{0}{R}^{3}\frac{{n}_{{{{\rm{r}}}}}^{2}-1}{{n}_{{{{\rm{r}}}}}^{2}+2}$ (with n_r the refractive index of the particle, R its radius and ϵ₀ the vacuum permittivity), the trap electric field amplitude ${E}_{0}=\sqrt{\frac{4P}{\uppi {\epsilon }_{0}c{{{{\rm{w}}}}}_{{{{{x}}}}}{{{{{w}}}}}_{{{{{y}}}}}}}$ with w_x,y the trap waists at the focus, and the cavity parameters, namely the mode volume ${V}_{{{{\rm{c}}}}}=\uppi {{{{\rm{w}}}}}_{{{{\rm{c}}}}}^{2}{L}_{{{{\rm{c}}}}}/4$, the cavity waist w_c, the cavity length L_c, the frequency ω_c = 2πc/λ_c and the unit vector along the cavity axis ${\mathbf{e}}_{\alpha}$. Note that the vector dot product ${\mathbf{e}}_{x}\cdot {\mathbf{e}}_{\alpha }$ introduces an additional dependence on the trap polarization angle $\propto \cos \theta$, which hinders the possibility of coupling solely the x motional mode to the cavity.

The quantum state of the cavity–nanoparticle system is given by its density matrix $\hat{\rho }$, which obeys the dynamical equation²⁸

$$\begin{array}{l}\frac{{\mathrm{d}}}{{\mathrm{d}}t}\hat{\rho }=-\frac{{\mathrm{i}}}{\hbar }\left[{\hat{H}}_{{{{\rm{CS}}}}},\hat{\rho }\right]\,+\,\kappa \left[\hat{a}\hat{\rho }{\hat{a}}^{{\dagger} }-\{{\hat{a}}^{{\dagger} }\hat{a},\hat{\rho }\}/2\right]\\ \qquad \quad -\mathop{\sum}\limits_{j=x,y,z}\frac{{\varGamma }_{j}}{2}\left[{\hat{b}}_{j}+{\hat{b}}_{j}^{{\dagger} },\left[{\hat{b}}_{j}+{\hat{b}}_{j}^{{\dagger} },\hat{\rho }\right]\right]\\ \qquad \quad +\,\frac{\gamma }{4}\mathop{\sum}\limits_{j=x,y,z}\left[{\hat{b}}_{j}+{\hat{b}}_{j}^{{\dagger} },\left\{{\hat{b}}_{j}^{{\dagger} }-{\hat{b}}_{j},\hat{\rho }\right\}\right],\end{array}$$

(2)

where {・} denotes the anticommutator, γ is the friction rate due to gas damping and the heating rates ${\varGamma }_{j}={\varGamma }_{j}^{({\mathrm{r}})}+{\varGamma }_{j}^{({\mathrm{g}})}$ contain a contribution from gas molecules

$${\varGamma }_{j}^{({\mathrm{g}})}=\gamma \frac{{k}_{\mathrm{B}}T}{\hbar {\varOmega }_{j}}$$

(3)

and a contribution from laser recoil heating

$$\left[\begin{array}{c}{\varGamma }_{x}^{(r)}\\ {\varGamma }_{y}^{(r)}\\ {\varGamma }_{z}^{(r)}\end{array}\right]=\frac{\pi }{15\hbar {\epsilon }_{0}}{\left(\frac{\alpha {E}_{0}}{2\uppi }\right)}^{2}{k}_{0}^{5}\left[\begin{array}{c}{x}_{{{{\rm{zpf}}}}}^{2}\\ 2{y}_{{{{\rm{zpf}}}}}^{2}\\ 7{z}_{{{{\rm{zpf}}}}}^{2}\end{array}\right].$$

(4)

To obtain analytical expressions, we simplify the model by making two assumptions. First, friction due to gas molecules is negligible, which at the pressures used for this work can be checked to be a good approximation^28,38. This amounts to neglecting the friction term in the master equation, namely the last line in equation (2). Note that the associated heating rate ${\varGamma }_{j}^{({\mathrm{g}})}\gg \gamma$ is not neglected. Second, the particle equilibrium position is at the intensity minimum of the cavity mode (ϕ = π/2). This is the case for all measurements in this work within an accuracy of 1 nm. At this position, the couplings g_x,y are simultaneously maximized while the z mode becomes uncoupled. Under these approximations, the system is reduced to a three-mode system including only the cavity mode and the x and y motional modes, whose steady-state properties can be computed analytically (see below).

Within this three-mode approximation, we can explain the dark-mode effect. The Hamiltonian can be cast in the form

$$\frac{{\hat{{{{{H}}}}}}_{{{{\rm{CS}}}}}}{\hslash }=\varDelta {\hat{a}}^{{\dagger} }\hat{a}+\mathop{\sum}\limits_{j=\pm }{\omega }_{j}{\hat{B}}_{j}^{{\dagger} }{\hat{B}}_{j}+{G}_{\pm }\left({\hat{B}}_{+}^{{\dagger} }{\hat{B}}_{-}+\,{{\mbox{h.c.}}}\right)-({g}_{t}{\hat{a}}^{{\dagger} }+\,{{\mbox{h.c.}}})({\hat{B}}_{+}^{{\dagger} }+{\hat{B}}_{+}).$$

(5)

Here, we have changed basis in the x–y subspace to define two collective mechanical modes, namely the bright and dark modes

$${\hat{B}}_{+}\equiv \frac{{g}_{x}{\hat{b}}_{x}+{g}_{y}{\hat{b}}_{y}}{{g}_{\mathrm{t}}},\quad {\hat{B}}_{-}\equiv \frac{{g}_{y}{\hat{b}}_{x}-{g}_{x}{\hat{b}}_{y}}{{g}_{\mathrm{t}}},$$

(6)

with the total coupling rate ${g}_{\mathrm{t}}=\sqrt{{g}_{x}^{2}+{g}_{y}^{2}}$. The corresponding mechanical frequencies of bright and dark mode read

$${\omega }_{+}=\frac{{\varOmega }_{x}{g}_{x}^{2}+{\varOmega }_{y}{g}_{y}^{2}}{{g}_{\mathrm{t}}^{2}},\quad {\omega }_{-}=\frac{{\varOmega }_{x}{g}_{y}^{2}+{\varOmega }_{y}{g}_{x}^{2}}{{g}_{\mathrm{t}}^{2}}.$$

(7)

According to the Hamiltonian in equation (5), the cavity couples directly only to the bright mode and can thus only cool this mode. The dark mode can be only sympathetically cooled through its coupling to the bright mode, which has a rate

$${G}_{\pm }=\frac{{g}_{x}{g}_{y}}{{g}_{\mathrm{t}}^{2}}({\varOmega }_{x}-{\varOmega }_{y}).$$

(8)

In the optimal 2D cooling configuration, Γ_x ≈ Γ_y ≡ Γ and g_x ≈ g_y ≡ g, so that the above rates simplify to ${g}_{\mathrm{t}}\approx \sqrt{2}| g|$ and G_± ≈ (Ω_x − Ω_y)/2. For 2D ground-state mechanical cooling, both the bright and dark states must be cooled at a rate higher than their respective heating rate. For the bright state, this reduces to the standard optomechanical condition $\frac{8{g}^{2}}{\kappa } > \varGamma$. As the dark state is cooled by the bright state and not by the cavity, for the dark state the condition reads

$$\frac{4{G}_{\pm }^{2}}{(8{g}^{2}/\kappa )}=\frac{\kappa {({\omega }_{x}-{\omega }_{y})}^{2}}{8{g}^{2}} > \varGamma .$$

(9)

Combining both conditions, we arrive to the inequality

$$\sqrt{\frac{\varGamma \kappa }{8}} < g < | {\omega }_{x}-{\omega }_{y}| \sqrt{\kappa /(8\varGamma )},$$

(10)

which defines a ‘Goldilocks zone’ for 2D cooling³⁹. In particular, if the mechanical modes are close to degeneracy, the cooling of the dark mode is not efficient enough for it to reach the ground state. This in turn limits the steady-state occupations of the original modes x and y, which are now limited by the thermal dark-mode occupation, $\langle {\hat{b}}_{x,y}^{{\dagger} }{\hat{b}}_{x,y}\rangle \sim \langle {\hat{b}}_{-}^{{\dagger} }{\hat{b}}_{-}\,\rangle$. Note that, in typical coherent scattering experiments, $\sqrt{\kappa /8\varGamma }$ is on the order of 1–10, so that the the right-hand side of the Goldilocks condition reduces to the condition ∣ω_x − ω_y∣ ≳ ∣g∣ given in the main text.

Extracting coupling and heating rates

Within the two above assumptions (negligible friction and z motion uncoupled), the heterodyne power spectral density can be analytically calculated. The heterodyne PSD, after subtraction of the noise floor and normalization to it, can be written as⁴⁰

$${S}_{{{{\rm{het}}}}}(\omega )=\kappa \left[{S}_{{{{\rm{c}}}}}({\delta }_{{{{\rm{LO}}}}}-\omega )+{S}_{{{{\rm{c}}}}}(\omega +{\delta }_{{{{\rm{LO}}}}})\right]$$

(11)

with δ_LO = ω_LO − ω₀. It is expressed in terms of the cavity PSD

$${S}_{{\mathrm{c}}}(\omega )=\int\nolimits_{-\infty }^{\infty }\frac{{\mathrm{d}}s}{2\pi }{{\mathrm{e}}}^{-{\mathrm{i}}\omega s}{\langle {\hat{a}}^{{\dagger} }(0)\hat{a}(s)\rangle }_{{{{\rm{ss}}}}},$$

(12)

where the subscript ‘ss’ indicates the steady state. We compute the two-time correlator using the quantum regression theorem²⁸, obtaining the following analytical expression:

$$\begin{array}{l}{S}_{{{{\rm{c}}}}}(\omega )= \frac{\begin{array}{l}16\left[4{g}_{x}^{4}\kappa {\varOmega }_{x}^{2}{\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)}^{2}\right.\\ +\,{g}_{x}^{2}{\varOmega }_{x}\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)\left[{\varGamma }_{x}{\varOmega }_{x}\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)\left(4{(\varDelta -\omega )}^{2}+{\kappa }^{2}\right)\right.\\ +\,\left.8{g}_{y}^{2}\kappa {\varOmega }_{y}\left({\omega }^{2}-{\varOmega }_{x}^{2}\right)\right]\\ +\,\left.{g}_{y}^{2}{\varOmega }_{y}^{2}{\left({\omega }^{2}-{\varOmega }_{x}^{2}\right)}^{2}\left({\varGamma }_{y}\left(4{(\varDelta -\omega )}^{2}+{\kappa }^{2}\right)+4{g}_{y}^{2}\kappa \right)\right]\end{array}}{\begin{array}{l}\uppi \left[\left[4{\varDelta }^{2}\left({\omega }^{2}-{\varOmega }_{x}^{2}\right)\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)\right.\right.\\ +\,16\varDelta \left({g}_{x}^{2}{\varOmega }_{x}\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)+{g}_{y}^{2}{\varOmega }_{y}\left({\omega }^{2}-{\varOmega }_{x}^{2}\right)\right)\\ +\,{\left.\left({\kappa }^{2}-4{\omega }^{2}\right)\left({\omega }^{2}-{\varOmega }_{x}^{2}\right)\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)\right]}^{2}\\ +\left.16{\kappa }^{2}{\omega }^{2}{\left({\omega }^{2}-{\varOmega }_{x}^{2}\right)}^{2}{\left({\omega }^{2}-{\varOmega }_{y}^{2}\right)}^{2}\right].\end{array}}\end{array}$$

(13)

To extract from our data the experimental values for g_x,y and Γ_x,y, we fit equation (11) to our time traces while setting κ and Δ to the values from our calibration.

Calculated heating rates

Using equations (3) and (4), we calculate the heating rates of x and y motion using the parameters given in the main text and T = 300 K, n_r = 1.439, w_x = 1.023 μm, w_y = 0.856 μm and γ = 4,812 Hz × p_gas,mbar, with p_gas,mbar the gas pressure in mbar. At p_gas,mbar = 5 × 10⁻⁹, we obtain ${\varGamma }_{x}^{({\mathrm{g}})}=2\uppi \times 0.053\,{{{\rm{kHz}}}}$, ${\varGamma }_{y}^{({\mathrm{g}})}=2\uppi \times 0.045\,{{{\rm{kHz}}}}$, ${\varGamma }_{x}^{({\mathrm{r}})}=2\uppi \times 0.825\,{{{\rm{kHz}}}}$ and ${\varGamma }_{y}^{({\mathrm{r}})}=2\uppi \times 1.379\,{{{\rm{kHz}}}}$. The total heating rate is thus dominated by photon recoil, ${\varGamma }_{x,y}^{({\mathrm{g}})}\ll {\varGamma }_{x,y}^{({\mathrm{r}})}$ and ${\varGamma }_{x,y}^{({\mathrm{r}})}$ agrees with the values extracted from our measured PSDs. We heavily suppress heating due to phase noise, as we position the particle in the cavity node and use an ultra-low phase noise laser source⁴¹. Note that the stated pressure reading of p_gas = 5 × 10⁻⁹ mbar is measured close to the ion-getter pump. The actual pressure at the position of the nanoparticle could be larger. ${\varGamma }_{x,y}^{({\mathrm{g}})}$ becomes comparable to ${\varGamma }_{x,y}^{({\mathrm{r}})}$ at p_gas,mbar ≈ 10⁻⁷, suggesting that the gas pressure near the nanoparticle is lower than this value.

Error in sideband thermometry

The effects of optical–mechanical mode hybridization and the decoupling of the dark mode modify the spectra measured through the cavity. As conventional sideband thermometry does not take these effects into account when estimating occupation numbers, the method is affected by a systematic error. To obtain this error, we theoretically calculate the occupation ${\bar{n}}_{j}$ estimated via sideband thermometry by numerically computing the maxima of equation (13) and compensating for the cavity asymmetry as detailed above. We then compare this result with the exact phonon occupations ${\bar{n}}_{j}^{{{{\rm{model}}}}}=\langle {\hat{b}}_{j}^{{\dagger} }{\hat{b}}_{j}\rangle$ within our approximations (negligible friction and z motion uncoupled). For the results in Fig. 4d,e, we fix Δ = 2π × 240 kHz, g_x = g_y = g, Ω_x = Δ − δ and Ω_y = Δ + δ, and sweep over the parameters δ and g. At each point (that is, for each value of Ω_x,y), the corresponding heating rates Γ_j are calculated from equations (3) and (4).