Introduction

Industrial and natural fluids detract from Newton's viscosity law because their viscosity does not correlate with deformation rate. These fluids are recognized as non-Newtonian fluids (NNF). They are further subdivided into numerous classes. There are some notorious classes of NNF, whose shear rate is not independent of flow direction. Shear rate-dependent viscosity fluids are subdivided further Herschel–Bulkley, Casson fluids, Bingham fluids, Carreau-Yasuda fluid, Carreau fluids and power-law fluid1,2,3,4,5,6. Minakov et al.7 described the findings of a practical assessment of the nanofluids (NF) flow incorporating nano particulates of various metals and oxides. Al-Mubaddel et al.8 has utilized the rheological model to predict the energy and mass transfer via hybrid NF fluid subjected to a magnetic field. The findings revealed that the transport of species in a power-law fluid is influenced by the opposite trends of chemical reactions. Using a power law fluid model, Cheng9 studied the energy and mass transmission. A porous, parallel plate microreactor with NN working fluid was inspected by Javidi et al.10 with the transfer of heat and mass, as well as thermodynamic irreversibility. The results show that Microreactor thermodynamic irreversibility is shown to be affected by wall thickness and thermal variance. Chavaraddi et al.11 examined the thermal properties of a passive conducting fluid in a bounded domain subjected to external effects. The results exposed that a power-law fluid stabilize the system while an electric field or magnetic field destabilizes the interface. Alsallami et al.12 develop an Maxwell nanofluid flow with arrhenius activation energy over a rotating disk. The dynamics of a bubble confined within an elastic solid in a non-Newtonian power-law fluid are investigated by Arefmanesh et al.13. The numerical examination of 2D non-Newtonian power-law fluids through a circular cylinder is presented by Bilal et al.14. The conclusions show that the system's frequency and apparent viscosity have a significant impact on the VIV of the cylinder's properties. Elattar et al.15 studied the power-law fluid flows past over a porous slender stretching surface. Some recent contributions have been made by many researchers towards power-law fluid flow through porous enlarging surface16,17,18,19.

Heat and mass transfer are utilized in a wide range of industries, including heating and air conditioning, energy systems, cars, steam-electric power production, disease detection and electronic device cooling20,21,22,23,24. Ordinary fluid, on the other hand, is unable to meet this requirement of heat transition. As a result, the incorporation of NPs in the base fluid is very suggestive. Nanofluids have gotten a lot of attention in the previous decade, especially in heat transfer enhancement and renewable energy. Nanofluids are used in ocean power plants, thermodynamics, solar collectors, hydropower rotors, geothermal heat exchangers and wind turbines25,26,27,28,29,30. Jia et al.31 described a realistic approach for synthesizing cell membrane (CM)-coated iron oxide nanoclusters as a nanocarrier for anticancer medicine Iron oxide nanoparticles were used by Schwaminger et al.32 to design novel flotation process approaches that took use of their particular features. An alkaline coprecipitation procedure was used to create magnetic nanoparticles with a basic crystal structure of 9 nm, which were subsequently coated with sulfate. A study conducted by Bilal et al.33 considered the impacts of Hall current on the flow of carbon nanotubes and iron ferrite hybrid nanoliquids along the surface of a spinning disc.

The C–C bond makes CNTs in base fluid more effective than other nanocomposite forms. The desired outcome can be obtained by covalent or non-covalent manipulation of CNT nanofluid34,35,36. Ferrofluid flow across an endless, impermeable disc was analyzed by Tassaddiq et al.37. They found that the combination of CNTs and Fe2O3 nanoparticles significantly increases the transfer of energy and mass. CNT + Fe2O3/H2O has a stronger impact on carrier fluid thermophysical parameters than magnetic ferrite nanoparticles. Bilal et al.38 scrutinized the cumulative upshots of electro- and magneto-hydrodynamics on the flow of water-based hybrid nanofluids over two collateral sheets in a two-collateral sheet arrangement Ullah et al.39 numerically investigated an unstable squeezed flow of a HNF comprising CNTs and CuO, as well as a nanofluid containing CNTs. In an experimental context, Alharbi et al.40 calculated the upshot of particle and energy concentration on the dynamic of hybrid nanoliquid. The results show that by increasing the number of nanoparticles, the viscosity increases up to 168 percent. Ullah et al.41 investigated how a hybrid nanofluid flow on the outside of a revolving disc could improve mass and heat conduction. They observed that hybrid nanofluids are more successful at transporting heat than regular nanofluids42,43,44,45,46. discuss the further uses, synthesis, utilization, and structural characteristics of magnetic nanomaterials and carbon nanotubes.

It has been revealed that fluids with shear rate-dependent viscosity can return to their thermal equilibrium state as a result of the thermal relaxation time features of the fluids47,48. Heat and mass transmission through convective Maxwell nanoliquid across an extending sheet was studied by Sui et al.49 using the Cattaneo–Christov (CC) double-diffusion model. The results show that this viscoelastic relaxation framework system predicts relaxation timings transport properties. The CC theory is used by Hafeez et al.50 instead of traditional Fourier's and Fick's laws to investigate the energy propagation in the fluid. Manjunatha et al.51 and Naveen et al.52 inspected the energy and mass transportation mechanisms caused by a chemical reaction, thermophoresis effect and Brownian motion in a stream of viscous nanocomposites submitted to a curvy stretched surface. Madhukesh et al.53 considered CC double diffusion models to investigate 3D Prandtl liquid flow. Similar studies related to the proposed model can be found in refs54,55.

The literature revealed that no investigation on the argumentation of energy transmission in a power-law fluid due to the combined dispersion of Cu and Graphene nanoparticles has been found. The motive of the research is to develop a computational model using copper and Graphene nanoparticles in the carrier fluid ethylene glycol, to magnify the energy communication rate and boost the competence and ability of thermal energy transference for a variety of biological and commercial purposes. Furthermore, the PCM procedure has been used to tackle the modeled equations of the proposed model.

Mathematical formulation

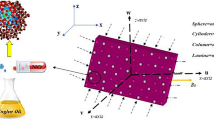
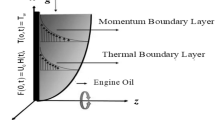
We considered a 2D HNF flow over a stretchable moving surface with fixed temperature \(T_{w}\) with velocity \(V_{w} = ax\hat{i} + by\hat{j}\), the sheet surface is moving. The non- Newtonian hybrid nanofluid fluid, flow over the surface, obeys the power-law rheological model. Figure 1 revealed the physical mechanism of the fluid flow over a moving permeable surface. The energy transport mechanism is supposed to be augmented with the dispersion of nanoparticles Copper and Graphene. The wall of sheet is moving with 2D velocity, but as a result the heat transfer and of fluid flow will be 3D. The basic equation, which regulates the fluid flow and energy transport mechanism are as follow27,56,57:

Figure 1
figure 1

Hybrid nanofluid flow over a moving permeable surface.

Full size image

Continuity equation

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}} = 0,$$
(1)

Momentum equation along x-axis

$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + w\frac{\partial u}{{\partial z}} = \frac{{k_{1} }}{{\rho_{hnf} }}\frac{\partial }{\partial z}\left( {\left| {\frac{\partial u}{{\partial z}}} \right|^{n - 1} \frac{\partial u}{{\partial z}}} \right) - \left( {\frac{{\sigma_{hnf} B_{0}^{2} }}{{\rho_{hnf} }}(u - v)} \right) - \frac{{\upsilon_{hnf} }}{{K^{*} }}u - \frac{1}{{\rho_{hnf} }}Fu^{2} ,$$
(2)

Momentum equation along y-axis

$$u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + w\frac{\partial v}{{\partial z}} = \frac{{k_{1} }}{{\rho_{hnf} }}\frac{\partial }{\partial z}\left( {\left| {\frac{\partial u}{{\partial z}}} \right|^{n - 1} \frac{\partial v}{{\partial z}}} \right) - \left( {\frac{{\sigma_{hnf} B_{0}^{2} }}{{\rho_{hnf} }}(u + v)} \right) - \frac{{\upsilon_{hnf} }}{{K^{*} }}v - \frac{1}{{\rho_{hnf} }}Fv^{2} ,$$
(3)

Energy equation

$$\begin{aligned} u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} + w\frac{\partial T}{{\partial z}} &+ \lambda_{1} \left( \begin{gathered} u^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + w^{2} \frac{{\partial^{2} T}}{{\partial z^{2} }} + v^{2} \frac{{\partial^{2} T}}{{\partial y^{2} }} + 2vw\frac{{\partial^{2} T}}{\partial y\partial z} + 2uv\frac{{\partial^{2} T}}{\partial x\partial y} + 2uw\frac{{\partial^{2} T}}{\partial x\partial z} \hfill \\ + \left( {u\frac{\partial u}{{\partial x}} + w\frac{\partial u}{{\partial z}} + v\frac{\partial u}{{\partial y}}} \right)\frac{\partial T}{{\partial x}} - \frac{{Q_{0} }}{{(\rho C_{p} )_{hnf} }}\left( {u\frac{\partial T}{{\partial x}} + w\frac{\partial T}{{\partial z}} + v\frac{\partial T}{{\partial y}}} \right) \hfill \\ + \left( {u\frac{\partial v}{{\partial x}} + w\frac{\partial v}{{\partial z}} + v\frac{\partial v}{{\partial y}}} \right)\frac{\partial T}{{\partial y}} + \left( {u\frac{\partial w}{{\partial x}} + w\frac{\partial w}{{\partial z}} + v\frac{\partial w}{{\partial y}}} \right)\frac{\partial T}{{\partial z}} \hfill \\ \end{gathered} \right) \\ &\quad = \frac{{k_{hnf} }}{{(\rho C_{p} )_{hnf} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} (T - T_{\infty } )}}{{(\rho C_{p} )_{hnf} }}. \\ \end{aligned}$$
(4)
$$\left. \begin{gathered} u = ax = U_{w} ,\,\,\,\,\,v = by = V_{w} ,\,\,\,\,T - T_{w} = 0,\,\,\,\,w\, = 0\,\,\,\,\,{\text{as}}\,\,\,\,z = 0,\, \hfill \\ u \to 0,\,\,\,\,\,\,v \to 0,\,\,\,\,T \to T_{\infty } \,\,\,\,\,{\text{as}}\,\,\,\,\,z \to \infty . \hfill \\ \end{gathered} \right\}$$
(5)

here \(U_{w}\) and \(V_{w}\) represents that the surface is stretching along both x-axis and y-axis directions.

Similarity transformation

The similarity variables are defined as59:

$$\begin{gathered} \,u = axf^{\prime } (\eta ),\,\,\,w = - a\left( {\frac{{ba^{n - 2} }}{{\rho_{f} }}} \right)^{{\frac{1}{n + 1}}} \left( {\frac{2n}{{n + 1}}f(\eta ) + \frac{1 - n}{{1 + n}}\eta f^{\prime}(\eta ) + g(\eta )} \right)x^{{\frac{n - 1}{{n + 1}}}} ,\,\,\,v = ybg^{\prime } (\eta ),\,\, \hfill \\ \,\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\,\,\eta = z\left( {\frac{{ba^{n - 2} }}{{\rho_{f} }}} \right)^{{\frac{1}{n + 1}}} x^{{\frac{1 - n}{{1 + n}}}} \hfill \\ \end{gathered}$$
(6)

Incorporating Eq. (6) into Eqs. (1–4), we get:

$$\begin{aligned} & \left( {\left| {f^{\prime \prime } } \right|^{n - 1} f^{\prime } } \right)^{\prime } - \left( {1 - \varphi_{2} } \right)\left( {\left( {1 - \varphi_{1} } \right) + \varphi_{1} \frac{{\rho_{s1} }}{{\rho_{f} }}} \right) + \varphi_{2} \frac{{\rho_{s2} }}{{\rho_{f} }}\left[ {Frf^{\prime 2} + \left( {\frac{2n}{{n + 1}}f + g} \right)f^{\prime \prime } } \right] \\ & \quad - \;(1 - \varphi_{1} )^{2.5} (1 - \varphi_{2} )^{2.5} \frac{{\sigma_{hnf} }}{{\sigma_{f} }}M^{2} (\lambda f^{\prime } - g^{\prime } ) = 0, \\ \end{aligned}$$
(7)
$$\begin{aligned} & \left( {\left| {f^{\prime \prime } } \right|^{n - 1} g^{\prime \prime } } \right)^{\prime } - (1 - \varphi_{2} )\left[ {(1 - \varphi_{1} ) + \varphi_{1} \frac{{\rho_{s1} }}{{\rho_{f} }}} \right] + \varphi_{2} \frac{{\rho_{s2} }}{{\rho_{f} }}\left[ {Frg^{\prime 2} + \left( {\frac{2n}{{n + 1}}f + g} \right)g^{\prime \prime } } \right] \\ & - (1 - \varphi_{1} )^{2.5} (1 - \varphi_{2} )^{2.5} \frac{{\sigma_{hnf} }}{{\sigma_{f} }}M^{2} (2\lambda g^{\prime } ) = 0, \\ \end{aligned}$$
(8)
$$\begin{aligned} & \theta^{\prime \prime } + \frac{{k_{f} (\rho C_{p} )_{hnf} }}{{k_{hnf} (\rho C_{p} )_{f} }}\left[ {Pr\left( {\frac{2n}{{n + 1}}} \right)f\theta^{\prime } + Prg\theta } \right] + \frac{{k_{f} }}{{k_{hnf} }}h_{s} \left( {\frac{2n}{{n + 1}}} \right)Pr\theta \\ & \quad - \;\frac{{k_{f} (\rho C_{p} )_{hnf} }}{{k_{hnf} (\rho C_{p} )_{f} }}Pr\lambda_{E} \left\{ {\left( {\frac{2n}{{n + 1}}f + g} \right)\left( {\frac{2n}{{n + 1}}f^{\prime } + g^{\prime } } \right)\theta^{\prime } \left( {\frac{2n}{{n + 1}}f + g} \right)^{2} \theta^{\prime \prime } + h_{s} Pr\left( {\frac{2n}{{n + 1}}f + g} \right)\theta^{\prime } } \right\} = 0. \\ \end{aligned}$$
(9)

Incorporating \(\wp_{1} ,\,\,\,\wp_{2} ,\,\,\,\wp_{3}\) in Eqs. (7–9) for simplification purpose, where \(\wp_{1} ,\,\,\,\wp_{2} ,\,\,\,\wp_{3}\) are defined as:

$$\wp_{1} = \left( {1 - \varphi_{2} } \right)\left( {\left( {1 - \varphi_{1} } \right) + \varphi_{1} \frac{{\rho_{s1} }}{{\rho_{f} }}} \right) + \varphi_{2} \frac{{\rho_{s2} }}{{\rho_{f} }},\,\,\,\wp_{2} = \left( {1 - \varphi_{1} } \right)^{2.5} \left( {1 - \varphi_{2} } \right)^{2.5} \frac{{\sigma_{hnf} }}{{\sigma_{f} }},\,\,\,\wp_{3} = \frac{{k_{f} (\rho C_{p} )_{hnf} }}{{k_{hnf} (\rho C_{p} )_{f} }}.$$

we get

$$\left( {\left| {f^{\prime \prime } } \right|^{n - 1} f^{\prime \prime } } \right)^{\prime } - \wp_{1} \left( {Frf^{\prime 2} + \left( {\frac{2n}{{n + 1}}f + g} \right)f^{\prime \prime } } \right) - \wp_{2} M^{2} \left( {\lambda f^{\prime } - g^{\prime } } \right) = 0,$$
(10)
$$\left( {\left| {f^{\prime \prime } } \right|^{n - 1} g^{\prime \prime } } \right)^{\prime } - \wp_{1} \left( {Frg^{\prime 2} + \left( {\frac{2n}{{n + 1}}f + g} \right)g^{\prime \prime } } \right) - \wp_{2} M^{2} \left( {2\lambda g^{\prime } } \right) = 0,$$
(11)
$$\left. \begin{aligned} & \theta^{\prime \prime } + \wp_{3} \left( {Pr\left( {\frac{2n}{{n + 1}}} \right)f\theta^{\prime \prime } + Pr\theta g} \right) + \frac{{k_{f} }}{{k_{hnf} }}h_{s} \left( {\frac{2n}{{n + 1}}} \right)Pr\theta - \wp_{3} Pr\lambda_{E} \\ & \left\{ {\left( {\frac{2n}{{n + 1}}f + g} \right)\left( {\frac{2n}{{n + 1}}f^{\prime } + g^{\prime } } \right)\theta^{\prime}\left( {\frac{2n}{{n + 1}}f + g} \right)^{2} \theta^{\prime \prime } + h_{s} Pr\left( {\frac{2n}{{n + 1}}f + g} \right)\theta^{\prime } } \right\} = 0. \\ \end{aligned} \right\}$$
(12)

The boundary conditions are given below:

$$\left. \begin{gathered} f(0) = 0,\,\,\,f^{\prime } (0) = \,g^{\prime } (0) = 1,\,\,g(0) = 0,\,\,\,\,\theta (0) = 1 \hfill \\ f(\infty ) = 0,\,\,\,\,g(\infty ) = 0,\,\,\,\,\,\theta (\infty ) = 0. \hfill \\ \end{gathered} \right\}$$
(13)

here \(M^{2} = \frac{{2\sigma_{f} B_{0}^{2} }}{{a\rho_{f} }}\) is the Hartmann number, \(h_{s} = \frac{Q}{{a(C_{p} )_{f} \rho_{f} }}\) is the heat generation term, \(\lambda_{E} = \frac{{a\lambda_{1} }}{x}\) is the thermal relaxation constraint, \(Re = \frac{{x^{n} (U_{w} )^{2 - n} \rho_{f} }}{{k_{f} }}\) is the Reynolds number, \(Pr = \frac{{(C_{p} )\rho_{f} ax^{2} {\text{Re}}^{{\frac{2}{n + 1}}} }}{{k_{f} }}\) is the Prandtl number and \(Fr = \frac{{xC_{b} }}{{\sqrt {K^{*} } }}\) is the Darcy Forchhemier number. where, \(s_{1}\) and \(s_{2}\) represent the Copper and Graphene nanoparticles respectively.

The skin friction expressed as:

$$\frac{1}{2}C_{f} (Re)^{{\frac{1}{n + 1}}} = \frac{{\left| {f^{\prime \prime } (0)} \right|^{n} }}{{(1 - \varphi_{1} )^{2.5} (1 - \varphi_{2} )^{2.5} }},\,\,\frac{1}{2}C_{g} (Re)^{{\frac{1}{n + 1}}} = \frac{{\left| {f^{\prime \prime } (0)} \right|^{n - 1} g^{\prime \prime } (0)}}{{(1 - \varphi_{1} )^{2.5} (1 - \varphi_{2} )^{2.5} }}.$$
(14)

The heat transfer rate can be stated as:

$$Nu = \frac{{xq_{w} }}{{K_{f} (T_{w} - T_{\infty } )}},\,\,\,q_{w} = \left. { - k_{hnf} \frac{\partial T}{{\partial z}}} \right|_{{{\text{at}}\,\,{\text{wall}}}} ,\,\,\,({\text{Re}} )^{0.5} Nu = \frac{{k_{hnf} }}{{k_{f} }}\theta^{\prime}(0).$$
(15)

Numerical solution

The main steps, while dealing with PCM method are60,61,62,63:

Step 1 Converting the system of BVP to the ODEs

$$\left. \begin{gathered} \hbar_{1} (\eta ) = f(\eta ),\,\,\hbar_{2} (\eta ) = f^{\prime } (\eta ),\,\,\,\hbar_{3} (\eta ) = g(\eta ),\,\, \hfill \\ \hbar_{4} (\eta ) = g^{\prime } (\eta ),\,\,\hbar_{5} (\eta ) = \theta (\eta ),\,\,\hbar_{6} (\eta ) = \theta^{\prime } (\eta ).\, \hfill \\ \end{gathered} \right\}$$
(16)

By putting Eq. (16) in Eq. (10–13), we get:

$$\left( {\left| {\hbar^{\prime }_{2} } \right|^{n - 1} \hbar^{\prime }_{2} } \right)^{\prime } - \wp_{1} \left( {Fr\hbar_{2}^{2} + \left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right)\hbar^{\prime }_{2} } \right) - \wp_{2} M^{2} \left( {\lambda \hbar_{2} - \hbar_{4} } \right) = 0,$$
(17)
$$\left( {\left| {\hbar^{\prime}_{2} } \right|^{n - 1} \hbar^{\prime}_{4} } \right)^{\prime } - \left( {\wp_{1} Fr\hbar_{4}^{{}} + 2\lambda \wp_{2} M^{2} } \right)\hbar_{4} - \wp_{1} \left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right)\hbar^{\prime}_{4} = 0,$$
(18)
$$\begin{aligned} & \hbar^{\prime }_{6} - \wp_{3} Pr\lambda_{E} \left\{ \begin{gathered} \wp_{3} Pr\left( {\frac{2n}{{n + 1}}} \right)\hbar_{1} + \left( {\hbar_{1} \frac{2n}{{n + 1}} + \hbar_{3} } \right)\left( {\frac{2n}{{n + 1}}\hbar_{2} + \hbar_{4} } \right) \hfill \\ \left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right)^{2} \hbar^{\prime }_{6} + h_{s} Pr\left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right) \hfill \\ \end{gathered} \right\}\hbar_{6} \\ & + \wp_{3} Pr\hbar_{5} \hbar_{3} + \frac{{k_{f} }}{{k_{hnf} }}h_{s} \left( {\frac{2n}{{n + 1}}} \right)Pr\hbar_{5} = 0. \\ \end{aligned}$$
(19)

the boundary conditions are:

$$\left. \begin{gathered} \hbar_{1} (0) = \hbar_{3} (0) = 0,\,\,\,\hbar_{2} (0) = \,\hbar_{4} (0) = 1,\,\,\hbar_{5} (0) = 1 \hfill \\ \hbar_{1} (\infty ) = \hbar_{3} (\infty ) = 0,\,\,\,\,\,\hbar_{5} (\infty ) = 0. \hfill \\ \end{gathered} \right\}$$
(20)

Step 2 Introducing the embedding parameter p in Eqs. (17–19):

$$\left( {\left| {\hbar^{\prime }_{2} } \right|^{n - 1} \hbar^{\prime }_{2} } \right)^{\prime } - \left( {\wp_{1} Fr\hbar_{2}^{{}} + \wp_{2} M^{2} \lambda } \right)(\hbar_{2} - 1)p + \wp_{2} M^{2} \hbar_{4} - \wp_{1} \left( {\hbar_{1} \frac{2n}{{n + 1}} + \hbar_{3} } \right)\hbar^{\prime }_{2} = 0,$$
(21)
$$\left( {\left| {\hbar^{\prime }_{2} } \right|^{n - 1} \hbar^{\prime }_{4} } \right)^{\prime } - \left( {\wp_{1} Fr\hbar_{4}^{{}} + 2\lambda \wp_{2} M^{2} } \right)(\hbar_{4} - 1)p - \wp_{1} \left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right)\hbar^{\prime }_{4} = 0,$$
(22)
$$\begin{gathered} \hbar^{\prime}_{6} - \wp_{3} Pr\lambda_{E} \left\{ \begin{gathered} \wp_{3} Pr\left( {\frac{2n}{{n + 1}}} \right)\hbar_{1} + \left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right)\left( {\frac{2n}{{n + 1}}\hbar_{2} + \hbar_{4} } \right) \hfill \\ \left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right)^{2} \hbar^{\prime}_{6} + h_{s} Pr\left( {\frac{2n}{{n + 1}}\hbar_{1} + \hbar_{3} } \right) \hfill \\ \end{gathered} \right\}(\hbar_{6} - 1)p + \hfill \\ \wp_{3} Pr\hbar_{5} \hbar_{3} + \frac{{k_{f} }}{{k_{hnf} }}h_{s} \left( {\frac{2n}{{n + 1}}} \right)Pr\hbar_{5} = 0. \hfill \\ \end{gathered}$$
(23)

Step 3 Differentiating by parameter ’p’

$$V^{\prime } = \rlap{--} \Delta V + R,$$
(24)

where \(\rlap{--} \Delta\) is the coefficient matrix.

$$V = \frac{{d\hbar_{i} }}{d\tau }$$
(25)

where i = 1, 2,…11.

Step 4 Apply the Cauchy Principal

$$V = aU + W,$$
(26)

where W and U are the indefinite vector functions.

$$U^{\prime } = aU,$$
(27)
$$W^{\prime } = \rlap{--} \Delta W + R,$$
(28)

Using Eq. (26) in Eq. (24), we get

$$(aU + W)^{\prime } = \rlap{--} \Delta (aU + W) + R,$$
(29)

Step 5 Solving the Cauchy problems

$$\frac{{U^{i + 1} - U^{i} }}{\Delta \eta } = \rlap{--} \Delta U^{i + 1} ,\,\,\,\,\frac{{W^{i + 1} - W^{i} }}{\Delta \eta } = \rlap{--} \Delta W^{i + 1} .$$
(30)

Finally, we get:

$$U^{i + 1} = (I - \Delta \rlap{--} \Delta \eta )^{ - 1} U^{i} ,\,\,\,\,\,\,\,\,W^{i + 1} = (I - \Delta \rlap{--} \Delta \eta )^{ - 1} (W^{i} + \Delta \eta R).$$
(31)

Results and discussion

This section explains the physical mechanism behind each result, which is shown in the Figures and Table.

Figures 2, 3, 4 and 5 revealed the conduct of velocity contour \(f^{\prime } \left( \eta \right)\) versus the variation of nanoparticles volume friction \(\phi\), Darcy Forchhemier term Fr, magnetic term M and parameter n (for \(n = 1,\) the fluid behave as Newtonian, while at \(n > 1,\) the shear thicking phenomena occur) respectively. Figure 2 reported that the axial velocity outline boosts with the addition of hybrid NPs in EG. Physically, the specific heat capacity of ethylene glycol is greater than copper and graphene NPs, so the addition of nanoparticles declines its thermal absorbing capability, as a result, the fluid velocity enhances. Figure 3 signifies that the axial velocity \(f^{\prime } \left( \eta \right)\) reduces with the flourishing Darcy effect. Figure 4 manifested that the fluid velocity lessens with the rising effect of the magnetic field, because the resistive force, which is generated due to magnetic force contests the fluid flow. The fluid velocity declines under the consequences of parameter n as shown in Fig. 5.

Figure 2
figure 2

Velocity \(f^{\prime } \left( \eta \right)\) outlines versus the effect of nanoparticles volume friction \(\phi\).

Full size image
Figure 3
figure 3

Velocity \(f^{\prime } \left( \eta \right)\) outlines versus the effect of Darcy Forchhemier term Fr.

Full size image
Figure 4
figure 4

Velocity \(f^{\prime}\left( \eta \right)\) outlines versus the effect of magnetic term M.

Full size image
Figure 5
figure 5

Velocity \(f^{\prime } \left( \eta \right)\) outlines versus the effect of parameter n.

Full size image

Figures 6 and 7 illustrated that the velocity field in radial direction \(g^{\prime } \left( \eta \right)\) diminishes with the growing values of magnetic effect and parameter n respectively. The Lorentz force formed due to magnetic term variation opposes the flow field, which costs in the lessening of the radial velocity field. Similarly, the increment of parameter n also reduces the momentum boundary layer as presented in Fig. 7.

Figure 6
figure 6

Velocity \(g^{\prime } \left( \eta \right)\) outlines versus the effect of magnetic term M.

Full size image
Figure 7
figure 7

Velocity \(g^{\prime } \left( \eta \right)\) outlines versus the effect of parameter n.

Full size image

Figures 8, 9, 10 and 11 revealed the presentation of energy contour against the flourishing trend of nanoparticulate volume friction \(\phi\), parameter n, versus thermal Deborah number \(\lambda_{E}\) and heat generation term \(h_{s}\) respectively. Figure 8 elaborated that the variation of nanomaterials in the base fluid significantly magnifies its thermal conduction, which is more effective for industrial uses. The thermal conductivity of nanoparticles is greater than the ethylene glycol, that’s why its addition boosts the thermal property of the carrier fluid. Figure 9 demonstrated that the energy profile declines with the upshot of parameter n. Figure 10 and 11 display that the thermal energy outline decreases with the upshot of thermal Deborah number \(\lambda_{E}\) while enhancing with the variation of heat source term hs. The heat source term augments the internal energy of the fluid, which encourages the fluid energy profile to enhance.

Figure 8
figure 8

Energy \(\theta \left( \eta \right)\) outlines versus the effect of nanoparticle volume friction \(\phi\).

Full size image
Figure 9
figure 9

Energy \(\theta \left( \eta \right)\) outlines versus the effect of parameter n.

Full size image
Figure 10
figure 10

Energy \(\theta \left( \eta \right)\) outlines versus the effect of thermal Deborah number \(\lambda_{E}\).

Full size image
Figure 11
figure 11

Energy \(\theta \left( \eta \right)\) outlines versus the effect of heat generation term \(h_{s}\).

Full size image

Table 1 reported the experimental values of nanoparticulate \(\left( {\phi_{1} = \phi_{C} ,\,\,\phi_{2} = \phi_{Cu} } \right)\) and base fluid (ethylene glycol). Table 2 show the comparative analysis between nanofluid and hybrid nanofluid for skin friction along x \(\left( { - ({\text{Re}} )^{{ - \frac{1}{2}}} C_{f} } \right)\) and y \(\left( { - ({\text{Re}} )^{{ - \frac{1}{2}}} C_{g} } \right)\) direction and Nusselt number \(\left( { - ({\text{Re}} )^{{ - \frac{1}{2}}} C_{Nu} } \right).\) It revealed that the energy conduction of hybrid nanofluid as compared to nanofluid is greater. The heat source and thermal Deborah number enhance the skin friction and Nusselt number remarkably. Table 3 shows the comparative evaluation of the published results with the current outcomes for skin friction and Nusselt number. It can be seen that the present results show closed adjustment with the existing literature, which ensure the validity of the results and proposed technique.

Table 1 The experimental values of base fluid (ethylene glycol) and nano particulates (copper and graphene58.
Full size table
Table 2 Statistical outcomes for physical quantities, such as skin friction \(\left( { - (Re)^{{ - \frac{1}{2}}} C_{f} ,\,\, - (Re)^{{ - \frac{1}{2}}} C_{g} } \right)\) and Nusselt number \(\left( { - (Re)^{{ - \frac{1}{2}}} C_{Nu} } \right)\) in case of both nanofluid and hybrid nanofluid.
Full size table
Table 3 Comparative assessment of published results with the current outcomes.
Full size table

Conclusion

The three-dimensional Darcy Forchhemier hybrid nanofluid flow has been studied under the impact of heat generation and magnetic field over a two-dimensionally stretchable moving permeable surface. The phenomena are characterized as a nonlinear system of PDEs. The solution has been obtained through the PCM procedure. The key findings are:

  • The accumulation of copper and graphene nanoparticulate to the base fluid ethylene glycol significantly improves velocity and heat conduction rate over a stretching surface.

  • The axial velocity contour boosts with the addition of hybrid NPs in EG while reducing with the flourishing Darcy and magnetic effect.

  • The variation of magnetic effect and parameter n diminishes the velocity field towards the radial direction \(g^{\prime } \left( \eta \right)\).

  • The thermal energy profile decreases with the effect of thermal Deborah number and parameter n. while enhancing with the variation of heat source term.

  • As compared to the nanofluid (copper or graphene), hybrid nanofluid (copper + graphene) has a greater tendency for thermal energy conduction.

  • The rising influence of heat source enhances the skin friction, while declines the Nusselt number.

  • The effect of magnetic force also boosts the skin friction, while declines the Nusselt number.