Introduction

Designing, investigating, and understanding the optomechanical interaction plays a key role in tailoring the light-matter interaction and hence for testing quantum mechanics1,2,3,4. In addition, optomechanics is also the basis for detection schemes with extreme sensitivity used in gravitational wave detection5, mechanical sensing6 as well as the creation of mechanical quantum states7,8. This potential triggered a multitude of realizations of optomechanical systems4,9 including systems based on superconducting circuits, which define the field of nano-electromechanics10,11,12,13,14,15,16. Here, the photonic cavity is implemented as a microwave resonator and the electromechanical interaction is typically realized using a mechanically compliant capacitance, which transfers a mechanical displacement into a change of the resonance frequency of the microwave circuit10,11,12,13,14,17. It was proposed early on that inductive coupling schemes can allow for higher coupling rates than capacitive ones18,19,20,21.

SQUID tunable microwave resonators can be designed to realize qubits or effective two-level systems22,23. In this context, electromechanical interactions have also been studied15,24,25,26,27 enabling large optomechanical couplings with the potential to realize quantum interference of massive objects’ trajectories28. In addition, they provide a route to implement even more complex coupled quantum systems, which, e.g., allow to create photon–phonon entanglement, phonon Fock state generation, and three partite entanglement29,30,31. However, these systems employ the effective two-level character and hence go beyond the traditional optomechanical system.

Only recently, an electromechanical coupling on-par with capacitive approaches was demonstrated by using an inductive coupling scheme based on a lumped-element microwave resonator and a mechanically compliant Josephson inductance32. By design, the linear inductance of the resonator was chosen much larger than the Josephson inductance, limiting the coupling strength in favor of tolerating large photon numbers. Complementary, it was shown that a distributed resonator with an embedded Josephson inductance allows to design arbitrarily large nonlinearities and can be used to realize two-level systems33.

Here, we present such an inductive coupling scheme based on a Josephson nonlinearity integrated into a coplanar waveguide resonator (CPW). For this device, we find a magnetic field tunable electromechanical vacuum coupling of up to 1.62 kHz. Moreover, we find a proportionality factor of 3.1 MHz T−1, between the coupling rate and the applied magnetic field, exceeding the one reported in ref. 32 by a factor of 120. In addition, the high coupling rate allows us to detect the mechanical motion with probe powers of 2.7 fW corresponding to an occupation of the microwave resonator with only a few photons. Hence, our device concept is naturally compatible with quantum microwave sources, which typically offer only a limited output power, and quantum-limited amplifiers with low saturation powers. These benefits make the device class ideally suited to act as a building block for the realization of inductively coupled devices integrated in more complex quantum circuits. Our results represent a significant step toward reaching the single-photon strong-coupling regime in electromechanics, allowing the investigation of quantum mechanical effects such as single-photon single-phonon blockade4,34, the creation of mechanical quantum states35, and the generation of non-classical light36.

Results and discussion

Circuit concept and fabrication

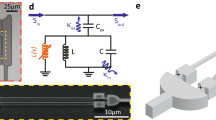
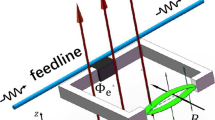
The nano-electromechanical device discussed here is based on a λ/4 superconducting CPW resonator which is shunted to ground at one of its ends via a direct-current superconducting quantum interference device (dc-SQUID) (cf. Fig. 1). As the SQUID acts as a flux-dependent inductance, the resonance frequency of the microwave circuit becomes flux sensitive. In addition, the SQUID loop is partly suspended and contains two nanomechanical string oscillators. Any displacement x of the strings translates into a change of the magnetic flux Φ threading the SQUID loop and, in turn, into the microwave resonance frequency ωc. The mechanically induced frequency shift can be described by the electromechanical interaction Hamiltonian \({\hat{H}}_{{\rm{int}}}=\hslash {g}_{0}{\hat{a}}^{\dagger }\hat{a}({\hat{b}}^{\dagger }+\hat{b})\), where \(\hat{a}\) (\(\hat{b}\)) are the ladder operators of the microwave resonator (mechanical oscillator). The electromechanical coupling constant18,19,21,37

$${g}_{0}=\frac{\partial {\omega }_{{\rm{c}}}}{\partial \Phi }\delta \Phi =\frac{\partial {\omega }_{{\rm{c}}}}{\partial \Phi }\gamma {B}_{{\rm{ext}}}l{x}_{{\rm{zpm}}},$$
(1)

scales with the length l of the string, the zero-point displacement \({x}_{{\rm{zpm}}}=\sqrt{\hslash /2{m}_{{\rm{eff}}}{\Omega }_{{\rm{m}}}}\), and the mode-shape γ of the mechanical resonator. Note, that g0 is tunable as the applied magnetic field Bext and the flux to resonance frequency transfer function ∂ωc/∂Φ, which we call in the following flux responsivity, can be controlled in situ.

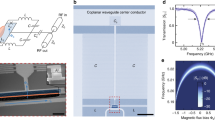
Fig. 1: Sample schematic and device images.
figure 1

Panel a shows a schematic of the device. The superconducting λ/4-coplanar microwave resonator is coupled capacitively with a coupling rate κext to a microwave transmission line acting as feed-line, where Sin and Sout denote the microwave input and output signal. A dc-SQUID with two freely suspended arms, which are separated by w, shunts the resonator to ground on the other end. The resonance frequency is tunable by varying the flux through the SQUID loop, e.g., by adjusting the external magnetic field Bext. In addition, the freely suspended SQUID arms (strings) modulate the SQUID inductance with the mechanical frequency via a change in the area of the SQUID loop and hereby realize the electromechanical coupling. In total, we expect the presence of four mechanical modes (one in- and one out-of-plane for each of the two strings) in our device. In our experiments, we focus only on one of them as sketched in panel (a). Panel b shows a microscope image of the aluminum resonator with the SQUID located at one end fabricated using a lift-off process. Panel c shows a tilted scanning electron microscope (SEM) image of a similar partly suspended SQUID structure. Note that the strings investigated in this work have dimensions of 20 μm × 110 nm × 200 nm.

Full size image

We fabricate the electromechanical system as an all-aluminum superconducting circuit using electron beam lithography, double-layer shadow evaporation, and reactive ion etching (cf. Fig. 1 and Supplementary Note 3  for details). The SQUID contains two freely suspended mechanical string oscillators as well as the two Josephson junctions. Each string has a length l = 20 μm, a width w = 200 nm, and a thickness t = 110 nm, corresponding to an effective mass of meff = 0.6 pg (all parameters of the device are summarized in Table 1). During the device fabrication, we anneal the entire chip at 350 ∘C resulting in tensile stressed aluminum strings with mechanical resonance frequencies Ωm ≃ 6.3 MHz at millikelvin temperatures. Thus, we obtain a zero-point fluctuation of xzpm = 47 fm. The microwave resonator is coupled capacitively at one of its ends to a microwave CPW feed-line, enabling the microwave spectroscopy of the device. The other end, is shunted to ground via the SQUID. In this way, we obtain a flux-tunable resonator with large flux responsivity ∂ωc/∂Φ, which is essential for the realization of a large electromechanical coupling strength.

Table 1 Summary of all sample parameters.
Full size table

Microwave resonator characterization

We start the characterization of the microwave circuit by performing microwave transmission measurements as shown in Fig. 2 (see Supplementary Note 1 B for details). Figure 2a shows the data as a function of the applied flux Φ, where the resonator appears as an absorption signature in dark blue. Figure 2b, c shows transmission data for two selected flux bias. For a quantitative analysis of the evolution of the microwave resonance frequency ωc, we locate the transmission minimum for each flux bias and plot ωc as well as ∂ωc/∂Φ versus the applied flux in Fig. 2d, e. We find that ∂ωc/∂Φ reaches values of up to 10 GHz/Φ0, underlining the performance of this coupling scheme. In addition, the ωc(Φ) dependence allows us to extract the single-junction critical current of the SQUID, Ic = 0.44 μA, and the minimum Josephson inductance, LJ = 0.36 nH, at ∂ωc/∂Φ = 0 (see Supplementary Note 2). Recording transmission data for selected flux bias points with higher frequency resolution (as shown in Fig. 2b, c) allows to determine the external coupling rate κext between the resonator and the feed-line as well as the internal loss rate κint of the microwave circuit. At ∂ωc/∂Φ = 0, we find a total linewidth of κ/2π = (κint + κext)/2π = 2.5 MHz. Figure 2f shows κext and κint as a function of the flux responsivity. While κext remains nearly constant, κint increases for large ∂ωc/∂Φ, which is attributed to the increased sensitivity of the circuit to flux noise. However, even at the bias point K, the device remains in the resolved sideband regime (Ωm > κ).

Fig. 2: Flux tuning of the microwave resonator.
figure 2

Panel a shows the calibrated microwave transmission as a function of the normalized applied magnetic flux. The tunable resonator exhibits a maximum frequency of 7.45 GHz and remains visible down to  ≈6.7 GHz. Around 7.3 GHz, we find a parasitic resonance, which we avoid in our experiments. In addition, we perform a detailed analysis of the electromechanical coupling rate at the operation points indicated. Panels b and c display the transmission data at points D and K as well as a fit, which allows to quantify the internal and external loss rates of the microwave resonator. Panel d displays the evolution of the microwave resonance frequency as function of the flux bias. The flux to resonance frequency transfer function ∂ωc/∂Φ is computed from this data and shown in panel (e), demonstrating responsivities exceeding 10 GHz/Φ0. To judge whether the device operates in the resolved sideband regime, we analyse the transmission data for all operation points and extract the internal and external loss rates as depicted in panel (f). While the external coupling rate is rather constant, the internal loss rate increases with increasing responsivity ∂ωc/∂Φ.

Full size image

Quantification of the electromechanical readout performance

Next, we investigate the mechanical properties including the electromechanical coupling rate. For this experiment, we probe the microwave sideband fluctuations originating from the interaction of the incident probe tone with the mechanics. The probe tone is set to a blue sideband configuration (ωp = ωc + Ωm) to enable a sensitive detection of the scattered photons4. The resulting signal is down-converted with ωp. Figure 3a shows the voltage power spectral density SUU(Ω) detected using a spectrum analyzer (cf.  Supplementary Note 1) for a temperature of 185 mK, when the microwave resonator is biased to working point K at ωc/2π = 6.887 GHz with Bext = −470 μT. We find a mechanical signature with a resonance frequency Ωm/2π = 6.34311 MHz and a full-width at half-maximum linewidth of Γm/2π = 33.6 Hz. In addition, we modulate the frequency of the incident microwave probe tone resulting in a calibration peak visible in panel a at ~−2 kHz. Similar to refs. 12,38, the comparison of the calibration tone amplitude \({S}_{{\rm{UU}}}({\Omega }_{{\rm{mod}}})\) with the mechanical response SUU(Ωm)Γm/2 allows us to quantify the electromechanical coupling rate g0. Due to the specific detection scheme used for this experiment, we need to account for an additional factor \({\mathcal{Y}}\), which relates the transfer function of the mechanical motion to the transmission function of the calibration tone (refer to Supplementary Note 4  for details). From this data, we obtain g0/2π = (1.62 ± 0.12) kHz. This value exceeds the highest coupling rate of 280 Hz17 achieved for capacitive coupling by a factor of 5.8 and corresponds to a single-photon cooperativity C0 of about 0.1. This large coupling strength allows us to use ultra-low probe powers for the detection of the mechanical sidebands. In fact, we use a probe power corresponding to an average photon number of \({\bar{n}}_{{\rm{r}}}=1.6\) in the microwave resonator for the spectrum shown in Fig. 3a. At this power level, we suppress back-action induced heating of the mechanical mode. In particular, for the parameters used in our experiment, we estimate an electromechanically induced damping rate of ∣Γem = −2.6 Hz∣ ≪ Γm, resulting in an increase in the thermal phonon occupation by 4%4, as we probe with a cooperativity of C ≃ C0 ≃ 0.1. This contribution is already accounted for in the stated value of g0 (for details see Supplementary Note 5). The background of SUU(Ω) shows the experimental imprecision noise \({S}_{{\rm{UU}}}^{{\rm{imp}}}\) of the experiment, which is presently limited by the performance of the cryogenic microwave amplifier used as the first amplification stage.

Fig. 3: Thermal mechanical displacement noise.
figure 3

Panel a shows the voltage noise spectral density SUU of the down-converted microwave spectroscopy tone. At Ωm/2π = 6.34311 MHz, we observe the mechanical signature with a peak amplitude of SUU(Ωm) = 1.26 μV2 Hz−1 and a linewidth of Γm/(2π) = 33.6 Hz. In this experiment, we configure the microwave spectroscopy tone to the blue sideband configuration (ωp = ωc + Ωm) to efficiently detect the Stokes field within the bandwidth of the resonator. However, we suppress back-action induced heating by using an ultra-weak probe tone corresponding to an average photon number of \({\bar{n}}_{{\rm{r}}}=1.6\) in the microwave resonator. The sharp peak at (Ω − Ωm)/2π ≈ −2 kHz with an amplitude of \({S}_{{\rm{UU}}}({\Omega }_{{\rm{mod}}})=2.56\ \upmu {{\rm{V}}}^{2}\ {{\rm{Hz}}}^{-1}\) stems from the phase modulation of the microwave spectroscopy tone (ϕ0 = 3.94 × 10−4). Combining the information of the mechanical signature and the calibration peak, we find an electromechanical vacuum coupling of g0/2π = (1.62 ± 0.12) kHz. We further show the mechanical displacement density \({S}_{{\rm{xx}}}^{\det }\) in panel (b) for T = 126 mK (blue), 186 mK (green), and 232 mK (red dots) including the Lorentzian fits to the data (solid lines). The peak area scales as expected with temperature via the mechanical linewidth. All spectra are recorded with the same averaging. Panel c shows the spectral force sensitivity \({S}_{{\rm{FF}}}^{\det }\) at T = 126  mK for the microwave probe powers as indicated. On-resonance, we reach sub-attonewton force sensitivities even for these ultra-low microwave probe powers.

Full size image

Our calibration technique allows us to express SUU(Ω) as the mechanical displacement spectrum Sxx(Ω) (see Supplementary Note 4). Figure 3b displays these spectra for various temperatures. We observe the expected increase in the phonon number with temperature in the form of an enlarged peak area. This manifests itself as an enhancement of the linewidth Γm with temperature (cf. Supplementary Information, Fig. S10a). This behavior has been observed for aluminum nano-strings and is attributed to the reduced dimensionality (1D) of the phonon mode39. In addition, we find a non-monotonic dependence of the imprecision noise floor on the environmental temperature. This behavior correlates with the temperature-dependent quality factor of the microwave resonator, which decreases above 185 mK. We speculate that this observation is connected to its population with thermal microwave photons, the presence of quasiparticles, and the motion of flux vortices (for details see Supplementary Note 4B).

The detected displacement power spectral density Sxx directly relates to the force sensitivity \({S}_{{\rm{FF}}}^{\det }\) via \({S}_{{\rm{FF}}}^{\det }=2{S}_{{\rm{xx}}}(\Omega )/| \chi {| }^{2}\)40 with the mechanical susceptibility \(\chi ={[{m}_{{\rm{eff}}}({\Omega }^{2}-{\Omega }_{{\rm{m}}}^{2}-i{\Gamma }_{{\rm{m}}}\Omega )]}^{-1}\) (cf. Supplementary Note 6). For T = 126 mK, we find an on-resonance force sensitivity of \({({S}_{{\rm{FF}}}^{\det })}^{1/2}=\,\text{0.70}\) aN Hz−1/2 (0.98 aN Hz−1/2) for a probe tone power of 5.3 fW (2.7 fW) corresponding to \({\bar{n}}_{{\rm{r}}}=1.7\) (0.86) photons. Here, the large electromechanical coupling rate (cf. Fig. 3c) allows to operate the device at much lower power compared to capacitive electromechanical devices having demonstrated 0.54 aN Hz−1/2 at probe powers of 1 pW40.

Tuning of the vacuum coupling strength

Next, we investigate the scaling of the electromechanical coupling strength with the applied magnetic field Bext and the flux responsivity ∂ωc/∂Φ, cf. Eq. (1). To this end, we excite the mechanical motion using an oscillatory mechanical force provided by piezo actuators resulting in a controlled oscillating displacement of the nano-strings. Under these conditions, the displacement amplitude is much larger compared to the thermal noise-driven measurements and hence much easier to detect (details are found in Supplementary Note 7). Figure 4a shows the measured resonance frequency shift of the microwave resonator δωc for various flux responsivities using a coherent excitation force at an approximately constant magnetic field of Bext ≈ −440 μT. As the frequency shift δωc is proportional to the product (∂ωc/∂Φ)δΦ, we observe a large δωc for large flux responsivity ∂ωc/∂Φ. Figure 4b summarizes the coupling rates derived from the peak amplitudes presented in Fig. 4a (dark green triangles) as well as the results of further experiments with a lower piezo actuator drive power (light green triangles) and links them to displacement noise measurements of g0 (red cross). The data corroborate the predicted linear scaling of the electromechanical coupling with the flux responsivity of up to 10 GHz/Φ0.

Fig. 4: Scaling of the electromechanical coupling rate at T = 126 mK.
figure 4

Panel a shows the mechanically driven resonator shift δωc close to Ωm for a coherent mechanical drive at angular frequency Ω generated by a piezo actuator for the various operation points labeled in Fig. 2. The external static magnetic field is set to Bext ≈ −440 μT. At magnetic field bias points (e.g., C, D) with low flux responsivity, almost no mechanical signature is observed, in contrast to those points (E to H) with large flux responsivity. Panel b displays the electromechanical coupling rate g0 deduced from the response in panel (a). The derived values are plotted versus the flux responsivity for low (light green triangles) and high piezo drive amplitudes (dark green triangles), and are linked to the thermal displacement measurements (red cross). This data confirms the linear scaling of the electromechanical coupling strength with ∂ωc/∂Φ. In panel c, we plot the coupling rate g0 obtained both from driven (green) and thermal displacement measurements (red) versus the applied magnetic field Bext for a fixed flux responsivity of ∂(ωc/2π)/∂Φ = 6.6 GHz/Φ0. In the given experimental configuration, the external field sets the working point of the microwave resonator. As flux jumps occurred during the experiments the recorded driven measurements could not be performed at identical field bias as the thermal ones. The error bars on the data in panels (b) and (c) include the standard error originating from the model-fit to the data and errors originating from the calibration. If not shown, error bars are smaller than the symbol size.

Full size image

In a similar fashion, we measure the electromechanical response as a function of the applied magnetic field for a fixed flux responsivity of ∂(ωc/2π)/∂Φ = 6.6 GHz/Φ0 (bias point K) and present the data in Fig. 4c. Again, we link these data points to the thermal displacement measurements (red circles) and corroborate the linear scaling with Bext.

From Fig. 4c, we extract a scaling factor of (3.13 ± 0.20) MHz T−1 for the electromechanical coupling with respect to the applied magnetic field Bext. This value exceeds those of previous reports by two orders of magnitude32 and represents an important figure of merit as it allows one to estimate g0 at the given physical parameters of the device. For example, for the 70 nm thin aluminum film, we expect an in-plane critical field of 130 mT41 which extrapolates to g0/2π = 410 kHz. This coupling rate does not yet satisfy the single-photon strong coupling condition. However, improved microwave decoherence rates of up to 400 kHz as reported for superconducting quantum circuits42 in combination with an optimized critical current Ic of the SQUID will allow to reach the strong-coupling regime (see Supplementary Note 9). Nevertheless, ground-state cooling for \({\bar{n}}_{{\rm{r}}}=1\) is expected to be within reach for this device using moderate fields of Bext = 20 mT applied in parallel to the superconducting layer. Overall, we find an improvement of the vacuum coupling strength by a factor of 7 in comparison to previous inductive coupling schemes32.

Finally, Eq. (1) includes a mode-shape factor γ. With our experimental parameters outlined so far, we find γ = 0.99, which is in good agreement with previous findings16,32.

Besides electromechanically induced transparency (EMIT), which can be used to measure g0 given quantitative knowledge of the photon number12,32,43,44,45, one can utilize the signature of a modification of the microwave resonator absorption lineshape, using the strong binding condition δωc > Ωm46 to confirm g0. Given our parameters (see Table 1), we use the second strategy. Here, a large amplitude coherent oscillation of the displacement is excited by a coherent mechanical drive causing the characteristic pattern of the microwave resonator absorption lineshape. When combined with the nonlinear response of the string-oscillator, we can quantify the displacement and hence g0. Corresponding data (shown in Supplementary Information, Fig. S12) corroborates the coupling strengths determined via thermal displacement noise (data analysis is presented in Supplementary Note 8).

Conclusions

In summary, we present a device implementing an inductive electromechanical coupling scheme based on a superconducting coplanar waveguide resonator and a dc-SQUID operating in the resolved sideband regime. We demonstrate an electromechanical coupling rate of 1.62 kHz, exceeding values of capacitive coupling schemes by almost an order of magnitude. This high coupling rate enables an ultra-high force sensitivity of 0.70 aN Hz−1/2 at an ultra-low microwave readout power of 5.4 fW, making this device a very promising low-power force sensor. In addition, the maximum electromechanical coupling of 1.62 kHz in combination with the investigated tuning of the electromechanical coupling indicates that this coupling strategy has the potential to reach the single-photon strong-coupling regime of electromechanics. Moreover, the tunability of the coupling provides the access to new features of electromechanical systems such as state amplification and readout techniques using the resonator as a parametric amplifier.

During the review process, we became aware of similar works by refs. 47,48.

Methods

Calibration of the electromechanical coupling via thermal motion

For the determination of the electromechanical coupling constant, we use a scheme similar to the calibration tone technique discussed by Gorodetsky et al. in ref. 38. In particular, we use the microwave detection scheme where the frequency modulates the microwave source to generate the calibration tone. We down-convert the signal coming from the dilution fridge with an unmodulated local oscillator and perform a spectrum analysis of the down-converted signal. This results in the spectra shown in Fig. 3a. Via this scheme, the vacuum coupling strength is determined by

$${g}_{0}^{2}=\frac{1}{2{n}_{{\rm{m}}}}\frac{{\Omega }_{{\rm{m}}}^{2}{\phi }_{0}^{2}}{2}\frac{{\Gamma }_{{\rm{m}}}}{4}\frac{1}{{\mathcal{Y}}}\frac{1}{{\rm{ENBW}}}\frac{{S}_{{\rm{UU}}}({\Omega }_{{\rm{m}}})}{{S}_{{\rm{UU}}}({\Omega }_{{\rm{mod}}})}.$$
(2)

This is derived in full detail in Supplementary Note 4 

Determination of the resonator transfer function

For a quantitative analysis of Eq. (2), we need to obtain information about the transfer functions \({\mathcal{Y}}\) involved as well. For our case, we find the transfer function depending in general on the microwave resonator characteristics and the employed probe tone configuration

$${\mathcal{Y}}\approx \frac{16{\eta }^{2}{\kappa }^{2}{\Omega }_{{\rm{m}}}^{2}}{\left(4{\Delta }^{2}+{\kappa }^{2}\right)\left(4{(\Delta -{\Omega }_{{\rm{m}}})}^{2}+{(1-2\eta )}^{2}{\kappa }^{2}\right)},$$
(3)

as we derive in more detail in Supplementary Note 4A.

Scaling of the electromechanical coupling

Due to the nature of the inductive coupling, the electromechanical coupling rate is flux tunable (see Eq. (1)). Thus, we expect a linear scaling of the electromechanical coupling rate with ∂ωc/∂Φ and Bext. As discussed in the main text, one option to explore the scaling of g0 are thermal displacement noise experiments. Alternatively, and more time efficiently, one can measure the frequency shift of the microwave resonator for a fixed mechanical excitation amplitude. In this experiment, the signal amplitudes are significantly larger resulting in a faster data acquisition. In detail, we use a piezo actuator mounted on the outside of the sample enclosure to excite the nanostring. The piezo actuator is addressed using a fixed excitation voltage. As the displacement strength is independent of ∂ωc/∂Φ and Bext, the piezo actuator induces a displacement of constant amplitude. Thus, the recorded frequency shift δωc is determined only by the coupling strength, without the need for a calibration of the piezo susceptibility. If a quantification of the vacuum coupling strength is desired, the extracted frequency shift has to be calibrated independently. For that purpose, we use the spectroscopy of the nanostring’s thermal motion.