Field-induced quantum critical point in the itinerant antiferromagnet Ti₃Cu₄

Abstract

New phases of matter emerge at the edge of magnetic instabilities, which can occur in materials with moments that are localized, itinerant or intermediate between these extremes. In local moment systems, such as heavy fermions, the magnetism can be tuned towards a zero-temperature transition at a quantum critical point (QCP) via pressure, chemical doping, and, rarely, magnetic field. By contrast, in itinerant moment systems, QCPs are more rare, and they are induced by pressure or doping; there are no known examples of field induced transitions. This means that no universal behaviour has been established across the whole itinerant-to-local moment range—a substantial gap in our knowledge of quantum criticality. Here we report an itinerant antiferromagnet, Ti₃Cu₄, that can be tuned to a QCP by a small magnetic field. We see signatures of quantum criticality and the associated non-Fermi liquid behaviour in thermodynamic and transport measurements, while band structure calculations point to an orbital-selective, spin density wave ground state, a consequence of the square net structural motif in Ti₃Cu₄. Ti₃Cu₄ thus provides a platform for the comparison and generalisation of quantum critical behaviour across the whole spectrum of magnetism.

Introduction

Quantum critical points (QCPs) emerge upon the continuous (second order) suppression of magnetic order to zero temperature via non-thermal tuning parameters such as doping, pressure or magnetic field. The interplay of magnetism, electron correlations, and quantum critical fluctuations in the vicinity of quantum phase transitions (QPTs) has been linked to novel emergent physics like unconventional superconductivity^1,2,3,4, non-Fermi liquid (NFL) behavior^5,6,7,8, and heavy fermion behavior^9,10,11.

Even though QPTs have been induced by pressure and doping in numerous systems, including local and itinerant magnetic compounds, these tuning parameters present experimental challenges: the former often requires experimentally difficult high pressure values to suppress the transition to T = 0, while the latter results in convoluted effects of disorder and quantum criticality, often difficult to resolve separately. Magnetic field appears as an advantageous tuning parameter to study quantum criticality¹², although there are much fewer experimental observations of field-induced QCPs. Field induced quantum criticality has been reported in the heavy-fermions YbRh₂Si₂^13,14,15, YbAgGe¹⁶, CePdAl¹⁷, CeCoIn₅¹⁸, CeAuSb₂¹⁹, YbPtIn²⁰, CePtIn₄²¹, Bose-Einstein condensates (BECs) in quantum magnets²², or the metamagnets with either f electrons as in CeRu₂Si₂²³ and UCoAl²⁴, or d electrons in Sr₃Ru₂O₇^25,26,27,28. No universal behavior can so far be established across the whole itinerant-to-local moment range^{11,29,30,31,32}, in large because of the complexities associated with local moments hybridizing with conduction electrons. It thus seems advantageous to study purely itinerant magnets, i.e., magnetic systems with no partially filled electronic shells. While the only known such itinerant magnets ZrZn₂^33,34, Sc_3.1In^35,36, and TiAu^37,38, have been tuned to QCPs by doping, the lack of experimental observation of field-induced QCPs in the extreme limit of itinerant moments is likely a reflection of the larger magnetic energy scales associated with d-electron systems compared to their f-electron counterparts. Furthermore, the magnetism in Cr, the prototypical spin-density wave (SDW) system, can be suppressed to a QCP with doping^39,40 or pressure⁴¹, but magnetic field has little or no effect on the ordering temperature⁴². On the other hand, Sr₃Ru₂O₇^25,26,27,28, a paramagnet in zero magnetic field, can be tuned to a quantum critical end point, where a line of first-order itinerant metamagnetic transitions terminates at T = 0, motivating further theories of first-order metamagnetic itinerant quantum criticality^31,32. Thus the experimental realization of a field-induced second-order QPT in a purely itinerant magnetic system has until now remained elusive.

Here we report evidence of itinerant antiferromagnetism (AFM) in metallic Ti₃Cu₄, where Ti and Cu have empty or filled d shells, and therefore neither carry a local moment. The Néel temperature T_N = 11.3 K is continuously suppressed to zero at a magnetic field-induced QCP at a critical field H_c = 4.87 T. Concurrently, the magnetic Grüneisen ratio ${{{\Gamma }}}_{H}\,=\,\frac{1}{T}{\left.\frac{\partial T}{\partial H}\right|}_{S}$ diverges as H → H_c and T → 0, with a sign change and divergence in T at H = H_c, accompanied by a NFL-FL crossover. The continuous suppression of the magnetic order to T = 0 by magnetic field, together with the divergence of thermodynamic properties (such as the magnetic Grüneisen ratio) are the benchmarks for identifying QPTs. Ti₃Cu₄ provides a unique platform to study a field-induced QCP at a low field scale for a d-electron itinerant magnet, and without the complexities of the interplay between local and itinerant moments.

Results and discussion

Crystal structure

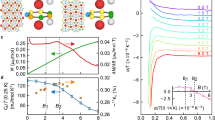
Flux-grown single crystals of Ti₃Cu₄ form as flat plates, with typical dimensions of 2 mm × 2 mm × 0.5 mm (Fig. 1). Ti₃Cu₄ crystallizes in the tetragonal I4/mmm space group⁴³. The crystal growth and structural characterization details are given in the Methods. X-ray diffraction measurements with the beam incident on the as-grown surface reveal a series of sharp (00l) Bragg reflections shown in Fig. 1a, consistent with the I4/mmm symmetry. This layered structure shown in Fig. 1b contains two different crystallographic sites for both Cu (light and dark red) and Ti (light and dark blue). Alternating layers of Ti are arranged in buckled (Ti1) and square (Ti2) nets, separated by staggered buckled nets of Cu. The connectivity of the Ti2 atoms in Ti₃Cu₄ is likely responsible for its remarkable electronic and magnetic properties, as discussed in the Electronic structure subsection.

Fig. 1: Antiferromagnetic order in Ti₃Cu₄.

a X-ray diffraction pattern of single crystalline Ti₃Cu₄ with the beam incident on the as grown surface showing a series of (00l) Bragg reflections. b The tetragonal crystal structure of Ti₃Cu₄, composed of alternating layers of Ti (blue) and Cu (red), with two unique crystallographic sites for each, indicated by the dark and light shading. c The temperature dependent magnetization scaled by field M/H (left axis, filled circles) measured with an applied field H = 0.1 T parallel to the ab plane, shows a cusp at the Néel temperature T_N = 11.3 K. The inverse susceptibility H/ΔM (right axis, open circles) is fit with a Curie-Weiss-like equation (black line) which gives a paramagentic moment μ_PM = 1.0 μ_B per formula unit (F.U.) and Weiss-like temperature T^* = 19.4 K. d Temperature dependent resistivity ρ with current i∥ab showing a sharp decrease at T_N. (inset) A typical single crystal of Ti₃Cu₄ with the grid lines spaced 1mm apart. e The heat capacity scaled by temperature C_p/T (left axis) exhibits a peak at T_N. The non-magnetic contribution was fit to a polynomial (black line). The calculated entropy S_mag (right axis) saturates at just 0.8% of $R\ln 2$. f The H → 0 magnetic susceptibility χ(T) derived from the field dependent derivative of magnetization discussed in Supplementary Note 1, showing an AFM cusp with H∥ab (red symbols), while χ(T) plateaus for H∥c (grey symbols). g Zoomed in resistivity showing the anomaly at 11.3 K that coincides with the anomalies in susceptibility and heat capacity at T_N (dashed line).

Antiferromagnetic order

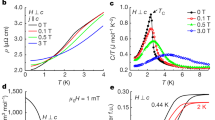
The DC magnetic susceptibility M(T)/H for H = 0.1 T (Fig. 1c, full symbols, left axis), shows Curie-Weiss-like temperature dependence, with no irreversibility in the field-cooled (FC) and zero-field-cooled (ZFC) data. Throughout the paper, only ZFC data is shown for clarity. Indeed, the inverse susceptibility H/ΔM is linear in T down to ~20 K (Fig. 1c, open symbols, right axis), where ΔM = M − M₀ corresponds to the magnetization after a small temperature-independent Pauli term, M₀ = 4.5 × 10⁻⁴ emu(mol_F.U.)⁻¹, has been subtracted. In the same temperature range, the zero field, H = 0, resistivity ρ(T) measurements (Fig. 1d) reveal the metallic character of Ti₃Cu₄; ρ(T) decreases monotonically with decreasing temperature, T, before a drop at the lowest temperatures. Together, these two measurements provide preliminary indication of itinerant moment magnetism in Ti₃Cu₄, which will be more convincingly demonstrated once the nature of the low temperature phase transition is established.

The low temperature thermodynamic and transport data show that a phase transition in Ti₃Cu₄ occurs around 11 K (Fig. 1e-g), first revealed by the small peak in the specific heat scaled by temperature C_p/T (symbols, Fig. 1e, left axis). While such a transition could have a structural component, this is ruled out by single crystal elastic neutron scattering measurements (discussed in the Experimental determination of the magnetic propogation vector subsection) that show no detectable change to the crystal structure down to 5 K. The antiferromagnetic order at T_N = 11.3 K is confirmed by the H = 0 susceptibility χ(T) and electrical resistivity ρ(T) (Fig. 1f,g). Anisotropic χ(T) data (determined from low H magnetization isotherms M(H), detailed in Supplementary Note 1) reveal a peak at T_N for H∥ab (red symbols, Fig. 1f), and a nearly temperature-independent plateau below T_N for H∥c (grey symbols, Fig. 1f). In a local moment picture, such magnetic anisotropy would be consistent with an AFM ordered state; the susceptibility peaks at T_N when the field is parallel to the direction of the ordered moments. The implication for the itinerant AFM order in Ti₃Cu₄ is that the moments are likely oriented within the ab plane, consistent with the neutron scattering experiments discussed in the Experimental determination of the magnetic propogation vector subsection. Upon cooling through T_N, a drop in resistivity signals loss of spin-disorder scattering (full symbols, Fig. 1g), with a peak in the resistivity derivative dρ/dT, coincident with the peak in C_p/T and susceptibility derivative d(χT)/dT (for a detailed comparison see Supplementary Note 2 and Supplementary Fig. 2)^44,45.

Evidence for bulk magnetism

Muon spin relaxation (μSR) measurements were performed, in order to confirm that the magnetic order at T_N = 11.3 K in Ti₃Cu₄ is intrinsic, and not arising from a small impurity phase. Several representative muon decay asymmetry spectra P(t) are plotted in Fig. 2a. A small H = 10 Oe field was applied to decouple any relaxation due to nuclear dipoles. From 12 to 20 K, P(t) is temperature independent and exhibits slow relaxation, consistent with a paramagnetic state. Upon cooling through T_N = 11.3 K, there is a sharp increase in the relaxation at early times. Within the magnetically ordered state, P(t) takes a characteristic Kubo-Toyabe form⁴⁶ with a minimum at early times followed by a recovery to 1/3 of the initial asymmetry. The solid lines in Fig. 2a are fits to P(t) of the following form:

$$P(t)= \; (1-{f}_{mag})\cdot {e}^{-at}\\ + {f}_{mag}\left(\frac{1}{3}+\frac{2}{3}\cdot (1-{\sigma }^{2}{t}^{2}-\lambda t)\cdot {e}^{-\frac{{\sigma }^{2}{t}^{2}}{2}-\lambda t}\right)\cdot {e}^{-bt}.$$

(1)

Muons that land in the non-magnetic fraction of the sample, 1 − f_mag, experience a weak temperature-independent exponential relaxation. The magnetic fraction of the sample, f_mag, is well-described by a combined Kubo-Toyabe function, where the Gaussian relaxation is given by σ and the Lorentzian relaxation by λ. The dynamics in the 1/3 tail are phenomenologically captured by the inclusion of an exponential relaxation. The temperature dependence of the fitted parameters, f_mag, σ, and λ, are presented in Fig. 2b, where each is observed to sharply increase below T_N = 11.3 K. At the lowest temperatures, f_mag (full circles, left axis) is close to 100%, confirming that the magnetsim in Ti₃Cu₄ is an intrinsic bulk property. The static nature of the magnetic order is confirmed through longitudinal field μSR measurements, where the relaxation is significantly decoupled by fields as small as H = 50 Oe and fully decoupled by a field of H = 500 Oe (open triangles, Fig. 2a).

Fig. 2: Bulk magnetism in Ti₃Cu₄ from muon spin relaxation.

a Representative muon decay asymmetry for Ti₃Cu₄ in an applied magnetic field H = 10 Oe for various temperatures (filled triangles) as well as at T = 2 K and H = 500 Oe (open triangles) with fits to Eqn. 1 (solid lines), showing the onset of static magnetic order. b The temperature dependence of the fit parameters: the magnetic volume fraction, f_mag (red circles, left axis), and the Gaussian, σ (filled diamonds), and Lorentzian, λ (open diamonds), relaxation rates. Error bars, where indicated, represent one standard deviation.

Experimental determination of the magnetic propogation vector

With μSR measurements confirming the intrinsic magnetism, we performed single crystal elastic neutron scattering measurements to investigate the nature of the magnetically ordered state in Ti₃Cu₄. Measurements above (T = 20 K) and below T_N (T = 5 K) reveal the formation of magnetic Bragg peaks on several high symmetry positions, including (100) and (001), as shown in the rocking curve scans in Fig. 3a, b (for all measured reflections see Supplementary Fig. 4). The double peak that appears for (001) and the other reflections with a non-zero l component are not intrinsic, but rather the result of two closely aligned grains. The intensity of the (100) and (001) Bragg peaks (measured both on warming and cooling) as a function of temperature is presented in Fig. 3c, confirming that the onset of magnetic order occurs at T_N = 11.3 K without measurable hysteresis. While the (001) and (100) Bragg peaks were measured in different sample geometries, and therefore their intensities cannot be directly compared, it is nonetheless evident that (001) is significantly more intense than (100), indicative of ordered moments that lie in the ab-plane, consistent with the low field susceptibility.

Fig. 3: Elastic neutron scattering.

Rocking curve measurements on the (a) (100) and (b) (001) positions at temperatures T = 20 and 5 K reveal the formation of magnetic Bragg peaks. Solid lines are fits to a Gaussian lineshape. Note that the maximum divergence in the orthogonal direction for the rocking curves was of order 0.02%. c An order parameter, constructed by measuring the intensity of the (001) and (100) Bragg peaks as a function of temperature, confirms that the magnetic order onsets at the Néel temperature T_N = 11.3 K. d The periodicity (red arrows) of the magnetic order as determined by symmetry analysis for Ti2 at the 2b Wyckoff site (blue spheres) in the I4/mmm space group. Error bars, where indicated, represent one standard deviation.

The commensurate positions where magnetic Bragg peaks form in Ti₃Cu₄ are not allowed by the body-centered selection rules (h + k + l = 2n) for the I4/mmm structure and therefore no nuclear Bragg peaks are observed on these positions. We can index these magnetic Bragg reflections with a propagation vector of k = (001). We proceed by assuming that, as indicated by the density functional theory (DFT) calculations discussed in the Electronic structure subsection, the magnetism in Ti₃Cu₄ originates from the conduction bands of the Ti atoms which occupy the 2b Wyckoff site (Ti2). It should be emphasized that the neutron data cannot independently distinguish which of the atomic sites in Ti₃Cu₄ is responsible for the magnetism. There are two symmetry-allowed irreducible representations for the 2b Wyckoff site with a k = (001) propagation vector within the I4/mmm space group: Γ₃ (c-axis antiferromagnet) and Γ₉ (ab-plane antiferromagnet). While both of these magnetic structures produce Bragg peaks at (100), only Γ₉ yields intense reflections at (001) and (003), consistent with our experiment. The periodicity of this structure is shown in Fig. 3d, consistent with a transverse commensurate spin density wave (SDW) order. Linear combinations of the two basis vectors that make up Γ₉ allow a continuous rotation within the ab-plane. We note that we cannot determine the exact moment orientation in an unpolarized neutron experiment. The magnitude of the ordered moment, which was estimated by comparing the intensity of the nuclear and magnetic reflections in the (h0l) plane measurements and assuming a Ti³⁺ magnetic form factor, is 0.17(5) μ_B. The result is in good agreement with the high field magnetization data discussed in the next subsection Evidence for itinerant magnetism.

Evidence for itinerant magnetism

With the bulk antiferromagnetic magnetic order below T_N firmly established, we turn to further evidence of itinerant moment magnetism in Ti₃Cu₄. Recalling the linear inverse susceptibility of Ti₃Cu₄ (Fig. 1c), we recognize it as a signature of either local or itinerant moment magnetism, albeit with very different origins. For the former case, mean field theory predicts $\chi (T) \sim \frac{{\mu }_{PM}^{2}}{(T-\theta)}$, where μ_PM is the paramagnetic moment, and θ is a measure of the inter-atomic moment coupling. For the latter case, Moriya’s theory of spin fluctuations^{47,48,49,50,51,52} predicts $\chi (T) \sim \frac{I}{(T-{T}^{* })}$, where I is a measure of the intra-atomic coupling. In Ti₃Cu₄, the slope and intercept of the linear fit to H/ΔM between 50 and 300 K (solid line, Fig. 1c) yield a paramagnetic moment μ_PM = 1.0 μ_B per F.U. and T^* = 19.4 K, respectively, where T^* is analogous to the Weiss temperature in local moment systems. The positive T^* is consistent with ferromagnetic in-plane interactions characteristic of the Γ₉ magnetic structure, where the c direction coupling is AFM.

While the linear inverse susceptibility alone is not enough to indicate itinerant moments in Ti₃Cu₄, the paramagnetic moment μ_PM is too small to be explained by a local moment scenario, in which the smallest possible unscreened moment would be 1.73 μ_B per F.U. corresponding to S = 1/2 at the Ti2 site (all other sites in this structure have higher multiplicities and would therefore produce even larger magnetic moments per F.U.).

The magnetic entropy S_mag (estimated from the grey area under the C_p/T peak in Fig. 1e) falls in line with the same conclusion: S_mag (thin line, right axis in Fig. 1e) reaches only ~1% R ln 2 up to 16 K (above T_N). Such a small entropy release is consistent with small moment ordering, likely even smaller than that in the itinerant antiferromagnet TiAu³⁷ where S_mag was close to 3% $R\ln 2$. This indicates that the paramagnetic moment in Ti₃Cu₄ is best explained as originating from itinerant spin fluctuations, a scenario corroborated below by our ab initio calculations in the Electronic structure subsection.

Another empirical signature of itinerant moment magnetism is a divergent Rhodes-Wohlfarth ratio q_c/q_s > > 1, where q_c and q_s correspond to the number of magnetic carriers above and below the ordering temperature⁵³. Experimentally, q_c is extracted from the paramagnetic moment μ_PM determined from high temperature fits of the inverse magnetic susceptibility:

$${\mu }_{PM}^{2}={q}_{c}({q}_{c}+2){\mu }_{B}^{2},\,{{\mbox{or}}}\,{q}_{c} \sim 0.4,$$

(2)

and q_s is determined from the low temperature (ordered) moment μ_ord

$${\mu }_{ord}={q}_{s}{\mu }_{B},$$

(3)

The Rhodes-Wohlfarth ratio q_c/q_s close to unity corresponds to the local moment scenario, while an increase in q_c/q_s with lower ordering temperature indicates an increased degree of itinerancy⁵³. Magnetization measurements M(H) for Ti₃Cu₄ (Fig. 4) point to a small μ_7T ~ 0.25μ_B, while single crystal neutron measurements indicate that the ordered moment μ_ord is even smaller, 0.17(5)μ_B. These values result in a large q_c/q_s ≈ 2.4, reinforcing the itinerant magnetism picture in Ti₃Cu₄.

Fig. 4: Field dependence of the magnetization in Ti₃Cu₄.

Field dependent magnetization M(H) isotherms in units of μ_B per formula unit (F.U.) measured at temperatures T = 50 K (yellow, open squares), and T = 4 K (yellow, solid squares). Lines were fit above and below the metamagnetic transition near 4 T (black, dashed lines). The intersection gives the critical field H_C = 4.3 T at 4K.

Electronic structure

In order to glean insight into the nature of the magnetic order, and in particular the small value of the ordered moment, we performed first principles calculations based on DFT. The calculations reveal a Fermi surface consisting of four sheets centered around the Γ point, and a small pocket around the X point (Fig. 5a–c). The analysis of the orbital-projected band structure (so-called “fat bands”) in Fig. 5d shows that the main contribution to the nested Fermi surface sheet in Fig. 5a comes from the ${d}_{{x}^{2}-{y}^{2}}$ orbital on the Ti2 atom, whereas the partial contributions from the other orbitals and from Ti1 atoms are much smaller, as demonstrated by the projected density of states (DOS) in Fig. 5e. The reason for this orbital selectivity appears to be connected to the square net geometry of the Ti2 layer, where the ${d}_{{x}^{2}-{y}^{2}}$ orbital lies along the Ti2-Ti2 bonds, reminiscent of the cuprates⁵⁴.

Fig. 5: Electronic structure from density functional theory calculation.

a, b and c Fermi sheets constituting the Fermi surface (FS) of Ti₃Cu₄. Panel (a) displays the FS originating from the ${d}_{{x}^{2}-{y}^{2}}$ orbital of Ti2, which contributes most to the density of states (DOS) at the Fermi level. The arrows indicate possible nesting wavevectors of the FS. d Band structure near the Fermi level of Ti₃Cu₄. The width of the red line is proportional to the projection onto the ${d}_{{x}^{2}-{y}^{2}}$ orbital of Ti2. e, f Projected density of states (PDOS) in the paramagnetic (PM) and spin-density wave (SDW) phase, respectively, with the red line indicating the contribution of Ti2 ${d}_{{x}^{2}-{y}^{2}}$ orbital. The blue lines indicate the partial density of states of the other Ti2 d-orbitals, which are comparatively negligible at the Fermi level.

The calculations performed in the magnetically ordered phase, with the experimentally determined wavevector k = (001) show that the DOS gets depleted around the chemical potential (Fig. 5f), and that the sharp DOS peak present in the PM phase (Fig. 5e) is split into two peaks separated by about 0.5 eV, with a pseudogap in between. This peak separation, due to the internal staggered magnetic field, is quantitatively consistent with the DFT-predicted ordered moment of 0.25 μ_B per Ti2 ion. Interestingly, the calculations show zero ordered moment on the buckled Ti1 layer. The reason is that the center of mass of the Ti1 ${d}_{{x}^{2}-{y}^{2}}$ band lies far below the Fermi level (close to −1 eV) due to greater hybridization with the d_xz and d_yz orbitals within the buckled layer, thus unable to participate in the formation of the magnetic order on the Ti1 sites.

The above analysis, combined with the smallness of the magnetic moment on the Ti2 ion, clearly indicates the itinerant nature of the magnetism in Ti₃Cu₄. Of note, the Fermi sheets in Fig. 5a–c appear to be nested, suggesting that an SDW order is likely to be realized with wavevectors along either k₁∥(100) (brown arrow in panel a) or k₂∥(110) (blue arrow). However, the neutron diffraction instead shows an out-of-plane wavevector k = (001). In order to elucidate this puzzling behaviour, we performed a series of ab initio calculations with various ordering wavevectors detailed in Supplementary Note 3. Supplementary Fig. 6 shows that the candidate SDW states with various commensurate wavevectors along (100) and (110) are all higher in energy than that of the experimentally observed k = (001) state, with one notable exception: the noncollinear $(\frac{1}{8}\,0\,0)$ state is predicted to lie slightly (about 1 meV per F.U.) lower in energy. This energy difference is however within the error bars of the DFT calculation and is therefore not significant. We conclude that the nested nature of the Fermi surfaces allows for several candidate SDW states very close in energy. We therefore rely on the neutron diffraction study to deduce the ordered state with the wavevector k = (001).

Continuous suppression of the Néel temperature by magnetic field

We return to the field-induced transition in Ti₃Cu₄. Increasing magnetic field continuously suppresses T_N as seen in M(H), M(T)/H, C_p, and ρ(T) measurements for both H∥ab and H∥c. A field H_c ~ 4.87 T suppresses the magnetic order all the way to zero temperature, as shown in the T − H phase diagram in Fig. 6 (details of the determination of the phase boundary can be found in Supplementary Note 2), raising the possibility of a field-induced QCP in Ti₃Cu₄. Down to 0.5 K, the transition is continuous, with no apparent hysteresis. The log-log T − H plot around H_C is linear (inset, Fig. 6), such that the phase boundary in the vicinity of H_C can be described by an exponential behavior T$\propto {\left|H-{H}_{C}\right|}^{\delta }$, with H_C = 4.87 ± 0.005 and δ = 2/3. This corresponds to the expected Hertz-Millis exponent for a 3D AFM^6,29,30 or Bose-Einstein condensation of magnons^55,56,57.

Fig. 6: Temperature–magnetic field phase diagram for Ti₃Cu₄.

The Néel temperature T_N, below which Ti₃Cu₄ is an itinerant antiferromagnet (IAFM), were determined from the temperature dependent derivative of magnetization multiplied by temperature d(MT)/dT (red circles), isothermal magnetization M(H) (yellow squares), heat capacity scaled by temperature C_p/T (blue diamonds), and temperature dependent derivative of the resistivity dρ/dT (black squares). Examples of the data used to construct the phase diagram are shown in Supplementary Fig. 3. Closed and open symbols denote measurements with H∥c and H∥ab, respectively. The IAFM order is fully suppressed for applied magnetic fields above H_C = 4.87 T, and the contour plot maps the resistivity (ρ) exponent n from fits of ρ = ρ₀ + A_nTⁿ, exhibiting a crossover from non-Fermi liquid behavior (NFL) (n < 2) to a Fermi liquid (FL) region n = 2 as the quantum critical point (QCP) is crossed in the field direction at the lowest measured temperatures. The grey hashed regions correspond to temperatures not accessed by our ρ(T) experiments. (inset) A log-log plot of T_N vs. ∣H − H_C∣ (yellow squares), with the black line corresponding to the fit of T_N ∝ ∣H − H_C∣^δ, yielding H_C = 4.87 ± 0.005 T and δ = 2/3.

Divergence of the magnetic Grüneisen ratio

Thermodynamic measurements provide convincing evidence of field-induced quantum criticality^27,58,59. We therefore turn to the magnetic Grüneisen ratio Γ_H defined as⁶⁰

$${{{\Gamma }}}_{H}=-\frac{{(\partial M/\partial T)}_{H}}{{C}_{H}}=-\frac{{\left(\partial S/\partial H\right)}_{T}}{T{\left(\partial S/\partial T\right)}_{H}}=\frac{1}{T}{\left.\frac{\partial T}{\partial H}\right|}_{S},$$

(4)

which measures the slope of the isentropes of the magnetic phase boundary in the T − H plane⁶¹. Across a classical phase transition, Γ_H is expected to be finite and temperature-independent⁶⁰. Near a QCP, an entropy ridge is expected to form where the system is maximally undecided between the ordered state and the disordered state (for dH > 0, ${\left(\partial S/\partial H\right)}_{T}\, > \,0$ when H < H_c and ${\left(\partial S/\partial H\right)}_{T}\, < \,0$ when H > H_c), which is reflected by a sign change of Γ_H at the QCP⁶¹. Furthermore, in the low-temperature limit, the singularities in S and T cancel out in Eq. (4), leaving only singularities associated with H⁶⁰. Zhu et al. showed that Γ_H scales as $\frac{1}{H-{H}_{c}}$ as T → 0 and ${{{\Gamma }}}_{H} \sim \frac{1}{{T}^{1/\nu z}}$ at H = H_c⁶⁰. Here ν is the exponent of the correlation length and z is the dynamical critical exponent. Together, the sign change of Γ_H at H_c and the scaling relations are definitive proof of a field induced QCP^60,61,62.

We obtain Γ_H by measuring the magneto-caloric effect (MCE) (∂T/∂H) under quasi-adiabatic conditions (S ~ constant for a duration smaller than it takes for the thermometer to relax). In Fig. 7a, we plot MCE, i.e. the temperature change driven by ramping the magnetic field H across H_C from 3.5 T to 5.5 T at various bath temperatures 0.25 K < T_B < 1.00 K for H∥c. Upon increasing H from below H_c, T decreases, such that ∂T/∂H < 0. Since C_H is a positive quantity, the sign of ∂T/∂H is always opposite to the sign of ∂S/∂H. Consequently, the decrease in T during the field upsweep indicates an increase in magnetic entropy (∂S/∂H > 0). Near H_C, there is a sudden increase in T, indicating a sudden reduction of the magnetic entropy. Subsequently, T decreases again due to the measurement apparatus relaxing back to T_B. To confirm that the decrease in T above H_C is indeed related to the measurement apparatus relaxation and not intrinsic to the sample, we measured the MCE sweeping H down from 5.5 T to 3.5 T (Fig. 7b, dashed line). Upon decreasing H above H_C, T decreases indicating an increase in magnetic entropy as the QCP is approached. The sudden increase in T reflects a decrease in magnetic entropy as H crosses H_c. Upon further decreasing H, the temperature again relaxes towards T_B before increasing due to a reduction of magnetic entropy as the distance from H_c is increased.

Fig. 7: Divergence of the Grüneisen ratio at the critical field.

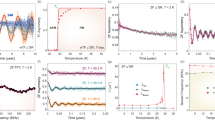
a Magneto-caloric effect (MCE) measurements for magnetic fields H∥c and dH > 0 measured at various bath temperatures T_B. Data are offset by arbitrary values for clarity, where the red lines indicated a zero change in temperature ΔT, and the scale bar on the right gives the absolute change in temperature. b A zoom in of the T_B = 0.35 K MCE data measured with dH > 0 (solid line) and dH < 0 (dashed line). c The field-dependent magnetic Grüneisen ratio (${{{\Gamma }}}_{H}\,=\,\frac{1}{{T}_{B}}\frac{{{\Delta }}T}{{{\Delta }}H}$) diverges as H approaches the critical field H_C. The pink solid line is a guide to the eye and is proportional to $\frac{1}{H-{H}_{c}}$, while the vertical pink dashed line denotes H_C. d The temperature dependence of the magnetic Grüneisen ratio at selected fields below H_C (red squares and pink circles), at H_C (light green triangles), and above H_C (dark green diamonds). At H = H_C, the magnetic Grüneisen ratio diverges as T^−b (solid black line).

Figure 7c shows Γ_H(H) at selected T_B, approximated as ${{{\Gamma }}}_{H}\,\approx \,\frac{1}{{T}_{B}}\frac{{{\Delta }}T}{{{\Delta }}H}$. Though we cannot reliably extract the exponents due to the quasi-adiabatic nature of our experiments, as T → 0 it is apparent that Γ_H diverges as ${(H-{H}_{c})}^{-1}$, as illustrated by the pink solid line. Furthermore, Γ_H(T) (Fig. 7d) switches signs across H_C and diverges as T^−b (black solid line) for H = H_C. While the quasi-adiabiatic conditions render the exponents’ determination uncertain, the MCE power law divergence is unambiguous: assuming constant heat loss, the exponent may vary, but such a scenario cannot cause a divergence. For a classical phase transition, the Grüneisen ratio is a constant, and therefore the divergence must come from the QCP.

Together, the sign change of Γ_H across H_C and the divergences at Γ_H(H, T → 0) and Γ_H(H = H_C, T) provide ample evidence for a field induced QCP at H_C = 4.87  T^60,61.

Non-fermi liquid to Fermi liquid crossover

Now turning to the electrical transport, we note that QCPs are often (albeit not always) accompanied by non-Fermi liquid (NFL) behavior, with a NFL-FL crossover convergent at the QCP. Signatures of the NFL behavior are revealed by the resistivity analysis ρ = ρ₀ + A_nTⁿ, where the T − H dependence of the exponent n is represented by the contour plot in Fig. 6 for H∥c. A subset of the ρ(T) data and fits to ρ = ρ₀ + A_nTⁿ can be found in Supplementary Fig. 7. At high temperatures in the paramagnetic state, ρ(T) varies sub-linearly with temperature, i.e., n < 1. In other itinerant systems, similar behavior has been attributed to the conduction electrons being scattered by spin fluctuations of the d-band electrons^63,64. Just below T_N, n → 1  before crossing over to n → 2 at the lowest measured T, for H → 0. Above the QCP (H > H_C) as the temperature is lowered (Fig. 6 and Supplementary Fig. 7), n crosses over to n ≈ 1 at intermediate temperatures, and to 2 on further cooling, signaling a FL regime at the lowest temperatures. Resitivity measured down to T = 50 mK for H ≥ H_c, shown in Fig. 8a as ρ(T) and in Fig. 8b–d as ρ vs. Tⁿ, demonstrate unambiguously a crossover from NFL (n < 2) to FL behavior (n = 2) as H moves away from H_c. Closest to H_c (Fig. 8b), the exponent n = 1.3 is registered over nearly two decades in T from 50 mK to ~3 K. Similarly, NFL (n = 1.7, Fig. 8c) or FL (n = 2, Fig. 8d) behavior occurs over two decades in temperature as the field increases up to 10 T.

Fig. 8: Evidence for non-Fermi liquid behavior in Ti₃Cu₄.

a Temperature dependent resistivity ρ measured for temperatures 50 mK < T < 14 K for applied magnetic fields H greater or equal to the critical field H_c (closed symbols). Solid lines are fits to the lowest temperature data to the equation ρ = ρ₀ + ATⁿ, where n = 1.3 (non-Fermi liquid), 1.7 (intermediate) and 2 (Fermi liquid), for H = 4.9 T, 6 T, and 10 T, respectively. ρ(T) data (symbols) are plotted against Tⁿ for (b) n = 1.3 and H = 4.9 T, (c) n = 1.7 and H = 6 T, and (d) n = 1.7 and H = 10 T. The pink lines are fits that show a single power corresponding to n describe the resistivity for well over a decade in T for all fields. e Heat capacity scaled by temperature C_p/T on a semi-log T scale from 0.3 K < T < 1.5 K for fields 0 T < H < 8 T. A non-Fermi liquid divergence is seen near H_c ~ 4.9 T.

Beyond transport, thermodynamic measurements reinforce the NFL behavior with the divergence of the low T specific heat (Fig. 8e). For metals, at low T, the electronic contribution to the specific heat is expected to dominate and the temperature dependence varies as T^m, where m = 1 for a FL, and m > 1 is often associated with NFL behavior due to quantum fluctuations^6,7. Figure 8e shows C_p/T plotted on a semi-log scale for 0.3 K ≤ T ≤ 1.5 K at various fields 0 ≤ H ≤ 8 T. For H = 0, the data plateau towards the lowest temperature T = 0.3 K, as expected for a FL. A power-law divergence (m > 1) develops at H = 4.5 T and persists beyond H_c up to H = 8 T, with the steepest divergence close to H_c (black squares). Supplementary Fig. 8 shows evidence for a Schottky anomaly at the lowest temperatures. C_p/T increases on cooling starting at higher T as H is increased. However, for temperatures beyond those where the Schottky contribution is largest (T > 0.3 K, Fig. 8e), the specific heat does not follow the trend expected from Schottky anomaly (no increase in T as H increases). The divergence in C_p/T is therefore ascribed to NFL behavior, consistent with the transport measurements.

Discussion

Ti₃Cu₄ is an itinerant antiferromagnet for which the ordering temperature can be suppressed towards T = 0 with a modest field, resulting in a field induced QCP. This is therefore not only an example of an itinerant magnet with no magnetic elements, one of very few known to date, but also the first known (to the best of our knowledge) such compound with a field-induced QCP. Typically, itinerant antiferromagnetism is associated with a strongly nested Fermi surface, where the nesting wavevector dictates the magnetic wavevector. Such a mechanism applies to the prototypical itinerant antiferromagnet or SDW system, elemental Cr⁴². While the calculated Fermi surface for Ti₃Cu₄ appears nested in the ab plane (Fig. 5a–c), the experimental propagation wavevector points in the out-of-plane direction (Fig. 3). An added conundrum is that the Fermi level lies on a sharp van-Hove singularity in the density of states (Fig. 5e), which is often associated with itinerant ferromagnetism. A similar scenario was found in TiAu³⁷, and it was later established that a new mechanism of mirrored van-Hove singularities in the Fermi surface, separated by the experimentally determined magnetic wavevector, lie at the origin of the itinerant antiferromagnetism^65,66. Further efforts are required to elucidate the origin of the magnetism in Ti₃Cu₄.

From a quantum criticality perspective, Ti₃Cu₄ represents a system without 4f electrons and is therefore free of the complication of f-d electron hybridization in the quantum critical regime. Since Fermi surface instabilities lie at the heart of itinerant magnetism, it is intuitive to understand how the effects of pressure or chemical doping may alter the Fermi surface, and in turn, the resulting magnetism or quantum criticality. However, it is less clear what the role of magnetic field is in tuning magnetism towards a QCP. Compared to f-electron systems, d-electron systems, have much larger energy scales associated with the magnetism which is reflected in their ordering temperatures (T_ord): T_ord ~0.1–5 K in the former, and 10–100’s of K in the latter. Ti₃Cu₄ (T_N = 11.3 K) is unique in that the energy scale is seemingly small (a magnetic field of H_c = 4.87 T can completely suppress the magnetism) compared to TiAu (T_N = 26 K)³⁷ or Cr (T_N = 311 K)⁴² where magnetic fields have little effect on the magnetic ordering temperature. Ti₃Cu₄ therefore provides a model platform to study the of role magnetic fields as a tuning parameter for itinerant magnetic quantum criticality. It will be specifically informative to compare and contrast future studies when either chemical doping or pressure are used as the non-thermal control parameter. For example, doping Cr with V suppresses the magnetic order ending in a QCP^40,67, while Re and Ru^68,69,70,71 suppress the magnetism resulting in a superconducting state which may be unconventional⁷².

Conclusion

In conclusion, Ti₃Cu₄ is an itinerant AFM with no magnetic elements: T_N = 11.3 K and μ_ord = 0.17μ_B per F.U. The magnetic state is remarkably fragile for a transition metal magnetic system, and can be suppressed to T = 0 with a small applied field H_C = 4.87 T, resulting in a field-induced QCP. Measurements of the magnetic Grüneisen ratio provide strong evidence for the quantum criticality, reinforced by the accompanied NFL-FL crossover revealed by the resistivity and heat capacity measurements. Ti₃Cu₄ can serve as as a platform for comparison and potentially generalization of the quantum critical behavior over the entire spectrum of magnetic moments from local to itinerant. In future studies, it will be important to understand the effects of pressure, chemical substitution, and disorder in Ti₃Cu₄, all of which are currently underway.

Methods

Crystal growth

Ti₃Cu₄ was grown using a self flux method with a starting composition of Ti_0.33Cu_0.67. The constituent elements were arc melted and placed in a Ta crucible and sealed under partial argon pressure in a quartz ampoule. After the initial heating to 950^∘C over 6 hours, a first step of fast cooling to 935 °C was followed by slow cooling to 895 °C over 62 hours, where the crystals were separated from the excess flux by spinning in a centrifuge.

Single-crystal X-ray diffraction

Single-crystal X-ray diffraction data on a Ti₃Cu₄ crystal were collected at 100(2) K with the use of a Bruker APEX2⁷³ kappa diffractometer equipped with graphite-monochromized MoK_α radiation (λ = 0.71073 Å). The data collection strategy was optimized with the use of the algorithm COSMO in the APEX2 package as a series of ω and ϕ scans. Scans of 0.5${}^{\underline{{{{{{{{\rm{o}}}}}}}}}}$ at 6 s/frame were used. The detector to crystal distance was 40 mm. The collection of intensity data as well as cell refinement and data reduction were carried out with the use of the program APEX2. The structure of Ti₃Cu₄ was initially solved and refined with the use of the SHELX-14 algorithms of the SHELXTL program package⁷⁴. Face indexed absorption, incident beam, and decay corrections of the substructure were performed with the use of the program SADABS⁷⁵. The program STRUCTURE TIDY⁷⁶ in PLATON⁷⁷ was used to standardize the atomic positions of the substructure. Furthermore, powder diffraction was done using a Bruker x- ray diffractometer with Cu K_α radiation. Powder and single crystal x-ray diffraction confirm the reported crystal structure for Ti₃Cu₄⁴³, apart from signs of mechanical stresses and possible minute (<5%) Ta inclusions (non-magnetic). However, these do not affect the results of the current study on the magnetic properties of Ti₃Cu₄.

Magnetization and resistivity measurements

DC magnetization measurements were performed in a Quantum Design (QD) magnetic property measurement system from T = 1.8 K–300 K. The same system was used with a helium 3 insert for measurements from T = 0.5 K–1.8 K. Magnetization measurements up to H = 30 T were carried out with an extraction magnetometer in a capacitor-powered pulsed magnet at the NHMFL pulsed field facility. The ac electrical resistivity measurements were made in a QD physical properties measurement system (PPMS) with a standard four-point probe technique for temperatures 2–300 K and magnetic field from 0–14 T. Measurements down to 50 mK were made in the same instrument equipped with a dilution refridgerator.

Magneto-caloric effect measurements

Quasi-adiabatic magneto-caloric effect (MCE) measurements between 0.25 K < T < 1 K were carried out in a QD PPMS equiped with a dilution refrigerator using the heat capacity option to ensure a quasi-adiabatic environment. The thermometer of a heat capacity puck with no sample mounted was calibrated as a function of field and temperature at several fields ranging from 0 < H < 14 T. From this procedure, a calibration map was extablished for the thermometer resistance R, temperature T, and magnetic field H. The sample was then mounted and cooled using the heat capacity option to ensure that the sample temperature was at equilibrium with the bath temperature. H was then swept at a rate of 105 Oe/s between 3.5 and 5.5 T and R of the heat capacity thermometer was measured. Using the calibration map, the measured R was converted to temperature, from which the MCE values were derived.

Muon spin relaxation measurements

Muon spin relaxation (μSR) measurements were performed on a mosaic of single crystals at the M20 surface muon channel at TRIUMF. The crystals were mounted on a low background sample holder with aluminum backed Mylar tape with their crystallographic c-axis parallel to the incident muon beam. Measurements were performed in the LAMPF spectrometer between 2 and 20 K in both longitudinal field geometry and in a weak (H = 30 G) transverse field. In this experiment, the total initial asymmetry, A₀, was determined by fitting the asymmetry spectra at high temperatures, in the weakly relaxing paramagnetic regime, giving A₀ = 0.220. Here we present the normalized muon polarization, P(t) = A(t)/A₀. Measurements were collected with the muon spins parallel to their momentum, such that the muons are implanted with their spins pointing along the c-axis, and also in spin-rotated mode, such that the muons are implanted with their spins lying within the crystals’ ab-plane. No significant anisotropy was detected. The muon decay asymmetry spectra were fitted with a least squares minimization protocol using the muSRfit software package.

Elastic neutron scattering measurements

Single crystal elastic neutron scattering measurements were performed on the E_i = 14.5 meV fixed-incident energy triple axis spectrometer HB-1A at the High Flux Isotope Reactor, Oak Ridge National Laboratory. This experiment was performed with standard collimation settings (40’ − 40’ − 40’ − 80’), and the energy resolution at the elastic line was ~1 meV (full-width half-maximum). Adhesive was used to attach a 70 mg single crystal of Ti₃Cu₄ onto an aluminum plate. Measurements were performed in both the (hk0) and the (h0l) scattering planes. The crystal was oriented prior to the experiment at the CG-1B neutron alignment station. Measurements were performed at temperatures between 5 K and 20 K using a closed-cycle refrigerator. The magnetic symmetry analysis was performed with SARAh⁷⁸ and Rietveld refinements were carried out using FullProf⁷⁹.

Density functional theory calculations

We performed Density Functional Theory (DFT) based calculations using the full-potential WIEN2K⁸⁰ and pseudo-potential ABINIT⁸¹ packages, with the generalized gradient approximation (GGA) used to account for the exchange-correlation interactions⁸². The band structure, density of states and Fermi surfaces were computed with the full-potential WIEN2K code, whereas ABINIT was used to perform large supercell calculations to accommodate various spin-density wave (SDW) orders. We ensured that both codes produced similar results at the level of the primitive unit cell. The polyhedron integration method was used to calculate the electronic density of states (DOS).