Spatial pattern of lake evaporation increases under global warming linked to regional hydroclimate change

Abstract

Lakes are critical natural resources that are vulnerable to climate change. In a warmer climate, lake evaporation is projected to increase globally, but with substantial variation between regions. Here, based on ensemble projections of climate and lake models and an attribution method, we show that future lake evaporation increase is strongly modulated by regional hydroclimate change. Specifically, a drying hydroclimate will amplify evaporation increase by enlarging surface vapor pressure deficit and reducing cloud shortwave reflection. Future lake evaporation increase is amplified in tropical America, the Mediterranean and Southeast China with drier future hydroclimates, and dampened in high latitudes and the Tibetan Plateau with wetter future hydroclimates. Such spatially coupled changes in lake evaporation and hydroclimate have important implications on regional lake water balance and volume change, which can aggravate water scarcity and flood risks.

Introduction

Lakes hold ~87% of Earth’s surface liquid freshwater¹ and provide critical resources to support the ecosystem and human society^2,3. A warmer climate will affect many aspects of lakes and one of the most concerning changes is the enhanced lake evaporation (LakeE)^{4,5,6,7,8,9,10}. Under global warming, the global LakeE is projected to increase by ~4% per degree of the global-mean surface warming¹⁰ (4% K⁻¹). This increase is much greater than the ~2% K⁻¹ increase of the global ocean evaporation^11,12,13,14 which is constrained by atmospheric energy demand, and the ~1% K⁻¹ increase of the global land evaporation (estimated based on Refs. ^15,16) which is limited by water availability and stomatal conductance.

While lake evaporation is projected to increase ubiquitously around the globe under global warming, the magnitude of the increase varies strongly across different regions¹⁰. This spatial pattern of the LakeE increase is important for regional lake changes, yet its formation has not been well understood. Previous studies have applied the Priestley–Taylor (PT)¹⁷ equation to interpret the LakeE increase, highlighting the effect of warmer temperature that allocates more energy into evaporation and the contribution of increased atmospheric radiative flux into lakes¹⁰. However, by using a constant factor to account for the effect of the near-surface dryness, the PT equation omits potential contribution of the changing dryness under global warming¹⁸. Furthermore, it remains unclear what drives the regional changes in the atmospheric radiative flux. Both the changes in the near-surface dryness and in the atmospheric radiative flux may be regulated by regional hydroclimate change, suggesting overlooked effects of regional hydroclimate change on future LakeE increase.

In the absence of water inflow changes, the amplified evaporative loss will reduce lake volumes and downgrade lake functions. However, as climate change profoundly affects regional hydroclimate^19,20,21,22, water inflow can change substantially at regional scales, offsetting or reinforcing the effect of the amplified LakeE. The responses of lake volumes to climate change remain elusive, despite a few observational studies indicating trends in specific regions^23,24 and modeling studies projecting changes of specific lakes^{25,26,27,28,29}. The potential links between regional hydroclimate change and the LakeE increase will have important implications on future lake volume changes.

In this study, we reveal the overlooked role of regional hydroclimate change in shaping the spatial pattern of future lake evaporation increase and illustrate the implication of this connection on regional lake volume changes. First, we illustrate a spatial correlation between amplified LakeE increase and regional hydroclimatic drying, based on ensemble projections of climate and lake models. Then, we reveal that regional drying effectively enhances the LakeE through combined energetic and aerodynamic effects, based on a reformulated Penman equation that explicitly considers the effect of the near-surface dryness and untangles the atmospheric radiative flux. Finally, we illustrate the implications of the spatially coupled changes in lake evaporation and hydroclimate on regional lake water balance and volume changes.

Results

Spatially correlated future changes in hydroclimate and lake evaporation

The responses of regional hydroclimate to global warming are projected by an ensemble of global climate models in Phase 5 of the Coupled Model Intercomparison Project (CMIP5)³⁰. The lake responses are simulated offline by the Community Land Model (CLM)³¹, with lake geometry prescribed according to the lake area and depth databases^32,33 and driving atmospheric forcings obtained from the global climate model (Methods). Both the Representative Concentration Pathway 8.5 (RCP8.5) and 4.5 (RCP4.5) warming scenarios are considered and the responses to global warming are estimated from the differences between the historical (1971–2000) and future (2071–2100) periods. The results presented in the main text are based on the RCP8.5 projection but consistent results are found for RCP4.5. The lake simulations by CLM are corroborated by two other lake models (ALBM³⁴ and VIC^35,36) from the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP)³⁷.

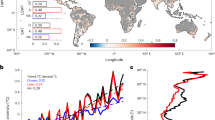
As shown in Figs. 1a and 1c respectively, the projected future changes in lake evaporation and hydroclimate (indicated by the land precipitation minus evaporation, P – E) are spatially correlated. The LakeE increase is largest in tropical America, the Mediterranean and Southeast China that are associated with a drier hydroclimate in the future, and less substantial in high latitudes and the Tibetan Plateau that are associated with a wetter hydroclimate in the future. The regionally averaged changes in lake evaporation and land P – E are summarized in Fig. 1b, d, respectively. In tropical America, the LakeE is projected to increase by 328 mm y⁻¹ while the land P – E will decrease by 50 mm y⁻¹. In high latitudes, the LakeE is projected to increase by 75 mm y⁻¹ while the land P – E will increase by 72 mm y⁻¹. This spatial correlation between changes in lake evaporation and hydroclimate is consistently seen under the RCP4.5 warming scenario (Fig. S1); in simulations of two other lake models (Fig. S2); and from other hydroclimate indicators such as runoff and soil moisture (Fig. S3).

Fig. 1: Spatially coupled future changes in lake evaporation and hydroclimate and the implication on regional lake volume changes.

a Spatial pattern of future changes in lake evaporation based on the CLM projection (under RCP8.5; 2071–2100 minus 1971–2000). b Future changes in lake evaporation averaged over tropical America (12°S–9°N; 70°W–50°W and 10°N–20°N; 105°W-85°W), the Mediterranean (35°N–47°N; 10°W–40°E), Southeast China (20°N–35°N; 110°E–125°E), Great Lakes (41°N–49°N; 92°W–77°W), Tibetan Plateau (28°N–36°N; 75°E–95°E), and high latitudes (poleward of 60°N). c Spatial pattern of future changes in the land P-E based on the mean projection of 22 CMIP5 models. d Future changes in the land P-E averaged over the six regions. The mean and standard deviation of the ensemble projection are shown in the bar plot. e Qualitative prediction of future lake volume changes based on P-E’s over land and lake. f Fraction changes in the lake and land P-E’s averaged over the six regions. The regions with a drier future hydroclimate, i.e., tropical America, the Mediterranean and Southeast China, are denoted by the black rectangles.

The spatial correlation between drier (wetter) future hydroclimate and amplified (dampened) LakeE increase suggests potential causality between them. Regional hydroclimate change may affect the LakeE through its influences on the near-surface dryness and atmospheric radiative flux. To examine such links, we attribute the spatially varying LakeE increase to changes in hydroclimate-related variables based on a reformulated Penman equation derived below.

A longwave-untangled Penman equation

The standard Penmen equation³⁸ estimates evaporation over open water (E) as

$${L}_{v}E=\frac{\varDelta }{\varDelta +\gamma }({R}_{n}-G)+\frac{\gamma }{\varDelta +\gamma }\kappa {e}^{\ast }(1-RH),$$

(1)

where L_v is the latent heat of vaporization, e^* is the near-surface saturation vapor pressure, $\varDelta \equiv \frac{\partial {e}^{\ast }}{\partial T}=\frac{{L}_{v}{e}^{\ast }}{{R}_{v}{T}^{2}}$ measures the sensitivity of e^* to temperature, γ is the psychometric constant, $\kappa \equiv \frac{\rho {C}_{p}}{\gamma {r}_{a}}$, r_a is the aerodynamic resistance, T and RH are the near-surface air temperature and relative humidity, R_n is the net surface radiation, and G is the ground heat flux. The first term in the RHS represents the potential evaporation under saturated air and the second term represents the effect of the near-surface dryness. Following ref. ¹⁴, the Penman evaporation can be rewritten as,

$${L}_{v}E=f[{R}_{n}-G+\xi (1-RH)],$$

(2)

where $f\equiv \frac{\varDelta }{\varDelta \;+\;\gamma }$ is the energy allocation factor (${\varDelta}{:}{\gamma}$ measures the ratio between latent and sensible heat flux under saturated air) and $\xi =\frac{{R}_{v}{T}^{2}}{{L}_{v}}k\gamma$ scales the RH effect. By using an empirical constant α_e (≈1.3) to account for the RH effect, the PT equation¹⁷ estimates ${L}_{v}E={\alpha }_{e}f({R}_{n}-G)$. Ref. ¹⁰ has used the PT equation to understand the lake evaporation increase while Ref. ¹⁴ has used the Penman equation to understand the ocean evaporation increase.

In both the Penman and PT equations, the evaporation changes are partially attributed to changes in the net surface radiation R_n, which equals the net shortwave input SW_n minus the net outgoing longwave radiation LW_n. Future changes in SW_n can be interpreted from changes in the incoming shortwave flux SW_in and lake albedo. For longwave radiation, the outgoing and incoming fluxes are not proportional. It is difficult to directly understand the regional changes in LW_n as both the outgoing and incoming fluxes are large and will increase with warming. In contrast to SW_in which can be considered as an independent atmospheric forcing, the incoming longwave radiation LW_in depends strongly on the lake state due to the coupling between the surface and air temperatures. To facilitate a clearer understanding of the longwave effect, we reformulate the net outgoing longwave radiation as the sum of two smaller terms,

$$L{W}_{n}={{\epsilon }}_{s}\sigma {T}_{s}^{4}-{{\epsilon }}_{s}{\epsilon }\sigma {T}^{4}\cong 4{{\epsilon }}_{s}\sigma {T}^{3}({T}_{s}-T)+{{\epsilon }}_{s}\sigma {T}^{4}(1-{\epsilon }),$$

(3)

where T_s is the lake surface temperature, T is the near-surface air temperature, $\sigma$ is Stefan-Boltzmann constant, ${{\epsilon }}_{s}$ = 0.97 is the constant lake emissivity and ${\epsilon }$ is the effective near-surface air emissivity. The term $4{{\epsilon }}_{s}\sigma {T}^{3}({T}_{s}-T)$ represents the effect of the temperature difference between the surface and air while the term ${{\epsilon }}_{s}\sigma {T}^{4}(1-{\epsilon })$ arises from the fact that the effective near-surface air emissivity is less than 1.

The term $4{{\epsilon }}_{s}\sigma {T}^{3}({T}_{s}-T)$ is analogous to the sensible heat flux $k\gamma ({T}_{s}-T)$, emitting energy from lakes at a rate proportional to T_s – T. By incorporating this LW_n decomposition, we derive a longwave-untangled version of the Penman equation (Eq. 2) as,

$${L}_{v}E=f[S{W}_{n}-{{\epsilon }}_{s}\sigma {T}^{4}(1-{\epsilon })-G+\xi (1-RH)].$$

(4)

Here, $f\equiv \frac{\varDelta }{\varDelta \,+\,\gamma \,+\,u}$ is the updated energy allocation factor, $\xi =\frac{{R}_{v}{T}^{2}}{{L}_{v}}k(\gamma +u)$ is the updated RH-effect scaling factor, and the parameter $u\equiv \frac{4{{\epsilon }}_{s}\sigma {T}^{3}}{\kappa }$ represents the effect of $4{{\epsilon }}_{s}\sigma {T}^{3}({T}_{s}-T)$. Essentially, the parameter u accounts for the dependency of LW_n on T_s – T ($u\equiv \frac{\partial L{W}_{n}}{k\partial ({T}_{s}-T)}$), analogous to γ for the sensible heat flux ($\gamma \equiv \frac{\partial SH}{k\partial ({T}_{s}-T)}$) and $\varDelta$ for the latent heat flux ($\varDelta \equiv \frac{\partial {L}_{v}E}{k\partial ({T}_{s}-T)}$). With the dependency of LW_n on T_s – T separated and represented by the parameter u, the longwave effect can be cleanly understood from changes in the air emissivity ${\epsilon }$. In Methods, we provide a complete derivation of the LP equation and further elaborate its advantages.

Attribution of the spatially varying LakeE changes

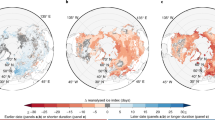
With input parameters obtained from the CLM simulation (Methods), the LP equation well reproduces the spatial patterns of the simulated LakeE climatology (Fig. S4) and the response to global warming (Fig. 2a, b). The pattern correlation r and root mean square error RMSE are r = 0.998 and RMSE = 30.6 mm y⁻¹ for the climatology and r = 0.996 and RMSE = 10.8 mm y⁻¹ for future changes. The precision of the LP equation is similar to the standard Penman equation and higher than the PT equation (Fig. S4). We then use the LP equation to attribute future LakeE changes to changes of individual parameters. Specifically, the contribution of each parameter is estimated as the change in the LP evaporation after switching the parameter values from those in the historical climate to those in the future climate (Methods). The contributions of the following factors are highlighted (Fig. 2c–j).

Fig. 2: Understanding the spatially varying lake evaporation increase based on the longwave-untangled Penman (LP) equation.

a Spatial pattern of the lake evaporation increase projected by CLM (δE). b Spatial pattern of the lake evaporation increase estimated by the LP equation ($\delta {E}^{LP}$). c, e, g, i Changes in the annual-mean air temperature (δT), emissivity ($\delta {\epsilon }$), relative humidity (δRH) and incoming shortwave radiation (δSW_in). d, f, h, j Contributions of individual factors to the lake evaporation changes according to the LP equation.

First, the LP equation reaffirms the effect of the larger energy allocation factor due to warmer temperature^10,14 (Fig. 2c, d). As the temperature increases, $\varDelta$ increases exponentially ($\frac{dln\varDelta }{dT}=\frac{{L}_{v}}{{R}_{v}{T}^{2}}-\frac{2}{T}\cong \,$5.8% K⁻¹), while u increases slowly ($\frac{dlnu}{dT}\cong \frac{3}{T}\cong \,$1% K⁻¹) and γ does not change. This means latent heat flux becomes much more efficient at releasing energy than sensible and longwave fluxes. As a result, more energy is released through evaporation, with the energy allocation factor $f\equiv \frac{\varDelta }{\varDelta +\gamma +u}$ increasing with warming at a rate of $\frac{dlnf}{dT}\cong (1-f)\frac{dln\varDelta }{dT}\cong$ 2–6% K⁻¹ (equivalent to Eq. 15 in Ref. ¹⁴). $\frac{dlnf}{dT}$ depends on temperature and is larger in cold temperatures (Fig. S5). The LakeE increase from the warming-induced larger $f\,,E\frac{dlnf}{dT}\delta T$, is partially offset by the effect of the warming-induced larger longwave radiance, $-f{{\epsilon }}_{s}\sigma (1-{\epsilon })\delta {T}^{4}$ (the second term in RHS of Eq. 4). Overall, the warmer temperature contributes to substantial increases in lake evaporation around the globe (Fig. 2d).

Second, the LP equation reveals an important contribution from the increasing air emissivity ${\epsilon }$ (Fig. 2e, f). Under global warming, the atmosphere will become more opaque to longwave radiation due to increased concentrations of carbon dioxide and water vapor. This leads to lower effective emission level (higher effective emission temperature) and equivalently increased ${\epsilon }$ at the global scale. At regional scales, the ${\epsilon }$ increase is regulated by changes in humidity and clouds, which are further linked to regional changes in temperature and relative humidity (Fig. S6). ${\epsilon }$ increases more substantially in high latitudes with enhanced warming and wetter/cloudier hydroclimate, and less substantially in drying regions with reduced humidity and clouds. Despite the notable regional pattern of $\delta {\epsilon }$, the resultant LakeE increase, $\delta {E}_{{\epsilon }}^{LP}=f\sigma {T}^{4}\,\delta {\epsilon }$, is rather smooth, as f and T are smallest in high latitudes where $\delta {\epsilon }$ is largest (Fig. 2f).

Neither the warmer temperature nor the increased air emissivity explains the amplified LakeE increase over the drying regions. It turns out that the spatial pattern of future LakeE changes is strongly modulated by regional changes in surface relative humidity (RH) and incoming shortwave radiation (SW_in). Over future drying regions such as tropical America, the Mediterranean and Southeast China, RH will decrease by more than 0.04 (Fig. 2g) and SW_in will increase by more than 10 W m⁻² (Fig. 2i). According to the LP equation, a reduced RH will increase the LakeE by enhancing the surface vapor pressure deficit ($\delta {E}_{RH}^{LP}=-f\xi \delta RH$) and an increased SW_in will increase the LakeE by feeding more energy into lakes ($\delta {E}_{S{W}_{I}}^{LP}=f(1-Alb)\delta S{W}_{in}$). Together, the decreased RH and the increased SW_in substantially enhance the LakeE over the drying regions (Fig. 2h, j). In contrast, over regions with increased future $P-E$ such as high latitudes and Tibetan Plateau, the RH barely decreases and the SW_in decreases by ~5 W m⁻². As a result, the LakeE increase from the RH decrease is insignificant and the decreased SW_in partially offsets the LakeE increase induced by other factors. Together, the effects of $\delta RH$ and $\delta S{W}_{in}$ lead to a ~150 mm y⁻¹ difference in the LakeE increase between the drying and wetting regions (Fig. 2h, j).

In high latitudes and Tibetan Plateau, future LakeE increase is contributed by changes in lake albedo and ground heat flux. As lake ice melts under warming, lake albedo decreases so that lakes absorb more solar radiation and evaporate more (Fig. S7). As the seasonal cycle of lake temperature weakens under warming, the seasonal ground heat flux G (positive in the warm season and negative in the cold season) is reduced. This shifts more energy to the evaporative warm season and increases the annual mean LakeE (Fig. S8).

The contributions of individual factors to the LakeE increase are summarized for different regions and compared with those for the global ocean (Fig. 3). Over future drying regions, the LakeE increases at a rate of ~6.3% K⁻¹ (with respect to regional surface warming), which translates to a 25% or an equivalent 295 mm y⁻¹ increase from the historical (1971–2000) to the future (2071–2100) period (Fig. 3a). The decreased RH and increased SW_in together contribute to more than half of this increase. In high latitudes and Tibetan Plateau, the LakeE increases by ~3.86% K⁻¹, which translates to a 23.5% or an equivalent 76 mm y⁻¹ increase (Fig. 3b). The contributions from RH and SW_in are negligible or even negative while the reduced albedo and the weakened seasonal G jointly contribute to one-third of this increase. At the global scale, the LakeE increases by ~4% K⁻¹. The effects of the warmer temperature and increased air emissivity dominate while other factors contribute positively (Fig. 3c). The 4% K⁻¹ increase of the global lake evaporation is two times of the ~2% K⁻¹ increase of the global ocean evaporation (Fig. 3d). In contrast to lakes, the ocean will experience increased relative humidity³⁹, reduced surface solar radiation and large positive heat uptake⁴⁰ under global warming. All these changes lower the increasing rate of ocean evaporation from 3% K⁻¹, as set by the warmer temperature and increased air emissivity, to the projected 2% K⁻¹ (Fig. 3d).

Fig. 3: Drivers of evaporation increase in different regions.

a Lakes over the drying regions including tropical America, the Mediterranean and Southeast China. b Lakes over the climatologically cold regions including high latitudes and Tibetan Plateau. c Global Lakes. d Global Ocean. $dlnE/dT$ computes the fractional increase in evaporation with respect to regional surface warming. The black bars show the lake and ocean evaporation increases simulated by models. The gray bars show the evaporation increase estimated by the LP equation. The color bars show the contributions of individual factors.

The collective effect of regional hydroclimate change on the LakeE increase

Future changes in surface relative humidity RH (Fig. 2g) and incoming shortwave flux SW_in (Fig. 2i) are spatially correlated at r = 0.74 (Fig. 4a). This spatial correlation arises from the effect of hydroclimatic drying on SW_in. Specifically, regional drying enhances SW_in through the cloud radiative effect (Fig. 4c) and to a lesser extent through the clear-sky changes (Fig. 4d). With reduced moist convection over the drying regions, cloud fraction decreases substantially (Fig. 4e). This leads to less cloud reflection of solar insolation and thus more shortwave radiation received by lakes (Fig. 4c). For the clear-sky part, while more solar radiation is absorbed by the increased atmospheric water vapor at the global scale, the clear-sky SW_I increases slightly over the Mediterranean and Southeast China (Fig. 4d). In these regions, the water vapor increases less substantially due to regional drying and the aerosol optical depth decreases due to reduced emission in the future (Fig. 4f). Both factors increase the regional clear-sky SW_in.

Fig. 4: The collective effect of regional hydroclimate change on lake evaporation through coupled changes in surface relative humidity and incoming shortwave radiation.

a Scatterplot between future changes in surface relative humidity (δRH) and incoming shortwave radiation (δSW_in). b Scatterplot between δRH and $\delta {E}_{RH+S{W}_{in}}^{LP}$, i.e., the combined evaporation changes due to δRH and δSW_in estimated by the LP equation. c Changes in the cloud shortwave effect. d Changes in the clear-sky incoming shortwave radiation. e Changes the cloud fraction. f Changes in the aerosol optical depth (contours; levels at 0.05, 0.1,0.2, 0.4) and column-integrated water vapor content. The cloud fraction and the integrated vapor content have been normalized (denoted by the hat symbol) by solar insolation at the top of the atmosphere.

According to the scatterplot between $\delta RH$ and $\delta S{W}_{in}$ (Fig. 4a), a 1% decrease in relative humidity corresponds to a ~3 W m⁻² increase in the incoming solar radiation, that is $\eta \!=-\frac{\partial S{W}_{in}}{\partial RH}\cong 3$ W m⁻² %⁻¹. The collective effect, through both $\delta RH$ and $\delta S{W}_{in}$, of hydroclimatic drying on lake evaporation is then estimated as ${L}_{v}\delta {E}_{Dry}={L}_{v}\delta {E}_{RH}^{LP}+{L}_{v}\delta {E}_{S{W}_{in}}^{LP}\!=\!-f\xi \delta RH+f(1-Alb)\frac{\partial S{W}_{in}}{\partial RH}\delta RH=-f[\xi +(1-Alb)\eta ]\delta RH.$ Using approximate average values of $f\!=\!0.45$, $\xi \!=\!3$ W m⁻² %⁻¹ and $Alb=0.2$ leads to $\delta {E}_{Dry}[mm\,{y}^{-1}]\cong 30\delta RH\,[ \% ].$ That is, a 1% decrease in relative humidity implies a 30 mm y⁻¹ increase in lake evaporation. This estimate is consistent with the slope of the scatterplot between the simulated $\delta RH$ and the LP-estimated $\delta E$ from ${{{{{\rm{\delta }}}}}}RH$ and ${{{{{\rm{\delta }}}}}}S{W}_{in}$ (Fig. 4b).

Implications of spatially coupled changes in lake evaporation and hydroclimate on lake volume changes

The water budget of a lake^41,42 is maintained by the precipitation minus evaporation over the lake surface area, ${A}_{lake}{(P-E)}_{lake}$, and the net water inflow into lakes through runoff, streams and ground seepage, $flow$. Global warming will affect both ${(P-E)}_{lake}$ and $flow$, thereby modifying the lake water budget. The change in the net water inflow can be linked to the change in the net water gain over the lake catchment, that is,

$$\delta flow=\,\alpha {A}_{c}\delta {(P-E)}_{land},$$

(5)

where A_c is the area of the lake catchment and α measures the proportion ($0\le \alpha \le 1$) of ${A}_{c}\delta {(P-E)}_{land}$ that drains into the net water inflow. As shown in Fig. S3, future changes in the runoff are indeed positively correlated with $\delta {(P-E)}_{land}$.

In response to these warming-induced changes, lake volume will adjust for a new water budget balance as

$${A}_{lake}\delta {(P-E)}_{lake}+\alpha {A}_{c}\delta {(P-E)}_{land}-\beta \delta V=0.\,$$

(6)

Here, β measures the negative feedback on the water budget due to the changes in lake volume ($\beta \; > \; 0$), i.e., an increased lake volume will suppress water inflow and increase evaporative loss, with elevated water level (higher hydraulic head), expanded surface area and/or enhanced surface winds.

Hence, the lake volume changes are linked to changes in$\,{(P-E)}_{lake}$ and ${(P-E)}_{land}$ as,

$$\delta V=\frac{\delta {(P-E)}_{lake}+\alpha \frac{{A}_{c}}{{A}_{lake}}\delta {(P-E)}_{land}}{\beta }.$$

(7)

Given both α and β are positive, one can make qualitative predictions of regional lake volume changes if $\delta {(P-E)}_{lake}$ and $\delta {(P-E)}_{land}$ are of the same sign. Such qualitative prediction does not rely on the exact values of α and β, that is, the detailed characteristics of the lake watershed.

With spatially coupled future changes in lake evaporation and hydroclimate, ${(P-E)}_{lake}$ and ${(P-E)}_{land}$ are projected to change in the same direction over many regions. We have categorized the potential lake volume changes into five groups according to the fractional changes in $P-E$ over lakes ($P{E}_{lake}={\frac{\delta (P-E)}{|P-E|}}_{lake}$) and over land ($P{E}_{lnad}={\frac{\delta (P-E)}{|P-E|}}_{land}$) (Fig. 1e, f). In tropical America and the Mediterranean, the drier future hydroclimate concurrently reduces precipitation and amplifies the LakeE increase, so that both ${(P-E)}_{lake}$ and ${(P-E)}_{land}$ decrease substantially ($P{E}_{lake}$ and $P{E}_{land}$ are both smaller than −0.1), suggesting decreased lake volumes over these regions. In high latitudes and Tibetan Plateau, the wetter future hydroclimate increases precipitation and dampens the LakeE increase, so that both ${(P-E)}_{lake}$ and ${(P-E)}_{land}$ increase substantially ($P{E}_{lake}$ and $P{E}_{land}$ are both larger than 0.1), suggesting increased lake volumes over these regions. In central North America including the Great Lakes, $P{E}_{lake}$ and $P{E}_{land}$ are not both smaller than −0.1 but their sum is smaller than −0.15, indicating that lake volumes will likely decrease but with some uncertainty. In maritime continents and India, $P{E}_{lake}$ and $P{E}_{land}$ are not both larger than 0.1 but their sum is larger than 0.15, indicating that lake volumes will likely increase. In regions where $|P{E}_{lake}+P{E}_{land}|$ is less than 0.1, lake volume changes are considered as highly uncertain.

Discussion

Based on an attribution method of longwave-untangled Penman equation and ensemble projections of climate and lake models, we present an improved understanding of the spatially varying lake evaporation increase under global warming and illustrate the implications on regional lake volume changes. At the global scale, the larger energy allocation and the larger effective atmospheric longwave emissivity contribute substantially to the lake evaporation increase. At regional scales, the lake evaporation increase is strongly modulated by hydroclimate change. Specifically, a drier future hydroclimate amplifies the lake evaporation increase by enlarging surface vapor pressure deficit with reduced relative humidity and by enhancing surface solar radiation with reduced clouds. As regional hydroclimate change concurrently affects precipitation and lake evaporation, $P-E$’s over the lake and over the land change substantially in the same direction in many regions. Based on the lake water budget, this implies lake expansion in wetting regions including high latitudes and the Tibetan Plateau but lake shrinkage in drying regions including tropical America, the Mediterranean and Southeast China. Such lake volume responses may further aggravate the impacts of regional hydroclimate change, as the shrinking lakes in the drying regions can exacerbate the water scarcity while the expanding lakes in the wetting regions will become less capable of buffering flood risks. To prevent such crises, significant actions in lake protection and management are needed.

Our study has focused on the effect of global warming on lakes. The effects of potential changes in land use, water consumption and hydraulic engineering are not investigated. Our qualitative prediction of lake volumes highlights regions where we have confidence and regions where future lake volume changes are deemed uncertain due to opposite changes in ${(P-E)}_{lake}$ and ${(P-E)}_{land}$. It remains challenging to quantitatively predict future lake volume changes, due to the lack of detailed information about regional lake watersheds and lack of numerical models that represent detailed lake dynamics and interactions with the environment. Water level changes of specific lakes have been projected based on observation-guided water budget analysis, indicating potential water level drop for Great Lakes²⁸ and substantial drying for the largest freshwater⁴³ and salt⁴⁴ lakes in the Mediterranean, which are consistent with our qualitative prediction shown in Fig. 1e, f. The projected lake changes under global warming may have already emerged in observations, which feature drying lakes in the Mediterranean^44,45 and expanding lakes in Tibetan Plateau⁴⁶.

The increasing rate of lake evaporation with warming can be consistently understood from changes in the surface temperature disequilibrium T_s − T. In the absence of changes in T_s − T, lake evaporation will increase at a rate of $\frac{dln{e}^{\ast }}{dT}\cong$ 6.5% K⁻¹. However, as evaporation becomes more efficient at releasing energy under warming, T_s − T must decrease to satisfy the surface energy balance¹⁴ (Fig. S9). Mathematically, this can be understood from Eq. S6 in which the exponentially increased $\varDelta$ reduces T_s − T. Due to the presence of γ and u, however, the decreasing rate of T_s − T is smaller than the exponential rate. Therefore, evaporation will still increase but at a rate much less than 6.5% K⁻¹. Other factors, such as the increased incoming solar radiation and air emissivity, further modulate the decreasing rate of T_s − T. Our results highlight the key differences between lakes and ocean that lead to their distinct evaporation increases. While the lake evaporation increase is amplified by the reduced relative humidity and increased shortwave radiation, the ocean evaporation increase is muted by the increased relative humidity and reduced shortwave radiation.

Methods

Global climate models

The responses of regional hydroclimate to global warming are projected by 22 global climate models (Table S1) from the Coupled Model Intercomparison Project Phase 5 (CMIP5)³⁰. Both the RCP8.5 and RCP4.5 warming scenarios are considered. Future changes are estimated as the difference between the historical period (1971–2000) and the future period (2071–2100). The analyses use the monthly outputs of the precipitation, surface latent flux, soil moisture, runoff, atmospheric specific humidity, cloud fraction, surface clear-sky and total-sky solar radiation and aerosol optical depth.

Lake models

The Community Land Model³¹ (CLM, version 5) is used for projecting the lake responses to global warming. In CLM, the land surface heterogeneity at the subgrid level is represented by land tiles (e.g., glacier, urban, agricultural, vegetation and lake). For each grid point, the lake area fraction is prescribed according to the Global Lake and Wetland Database³² and the lake depth is estimated from the global gridded dataset of lake coverage and depth designed for numerical weather prediction and climate modelling³³. The lake is simulated by the Lake, Ice, Snow, and Sediment Simulator (LISSS)^47,48, which includes substantial improvements from the lake code⁴⁹ used in CLM versions 2 through 4. LISSS is a one-dimensional, thermodynamic lake model. It has realistic representations of surface fluxes, snow and ice phenology, and sediment heat exchange. Heat diffusion within the water column includes eddy diffusion, wind-driven mixing, buoyant convection, molecular conduction. The overall diffusivity is enhanced for large lakes, considering the mixing of three-dimensional circulations. Since the lake depth is prescribed, potential feedbacks from the changing lake water level are not presented in LISSS. The overall performance of LISSS has been tested against observations in ref. ⁴⁸, and the simulated lake evaporation has been validated against observations in ref. ¹⁰. More details about CLM5 and LISSS can be found in the online technical note (https://escomp.github.io/ctsm-docs/versions/release-clm5.0/html/tech_note/index.html).

The CLM is driven by atmospheric forcings of the incoming (downward) solar and longwave radiation, the atmospheric temperature, humidity, pressure and winds, obtained from the coupled run of the Community Earth System Model. To be consistent with the GCM simulations, the lake responses to global warming are estimated as the differences between the historical period (1971–2000) and the future period (2071–2100). Both the RCP8.5 and RCP4.5 warming scenarios are considered.

The CLM results are further corroborated by projections of two other lake models: the Arctic Lake Biogeochemistry Model³⁴ (ALBM) and the Variable Infiltration Capacity Model (VIC). The outputs of these two lake models are obtained from phase 2b of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Lake simulations are driven by three different atmospheric driving forcings, from GFDL-ESM2M, HadGEM2-ES, and MIROC5, under the warming scenario of RCP8.5.

The longwave-untangled Penman equation: derivation, advantages and application

Evaporation over lakes is a function of the surface vapor pressure deficit,

$${L}_{v}E=\frac{\rho {C}_{p}}{\gamma {r}_{a}}({e}_{s}^*-e),$$

(S1)

where L_v is the latent heat of vaporization, $\rho$ and C_p are the density and specific heat of air, ${e}_{s}^*$ and e are the surface saturation and near-surface vapor pressure, γ is the psychometric constant, and r_a is the aerodynamic resistance. By linearizing the Clausius–Clapeyron relation, lake evaporation can be rewritten as a function of the temperature (T) and relative humidity (RH) differences between the surface and the near-surface,

$${L}_{v}E=\kappa ({e}_{s}^*-e)=\kappa \varDelta ({T}_{s}-T)+\kappa {e}{\ast }(1-RH),\,$$

(S2)

where $\varDelta \equiv \frac{\partial {e}{\ast }}{\partial T}=\frac{{L}_{v}{e}{\ast }}{{R}_{v}{T}^{2}}$ measures the slope of the $T-{e}{\ast }$ curve and $\kappa \equiv \frac{\rho {C}_{p}}{\gamma {r}_{a}}.$

Given the sensible heat flux $SH=\kappa \gamma ({T}_{s}-T)$ and the surface energy balance ${L}_{v}E+SH={R}_{n}-G$, Penman resolves T_s − T and subsequently evaporation as,

$${T}_{s}-T=\frac{{R}_{n}-G-\kappa {e}{\ast }(1-RH)}{\varDelta +\gamma },$$

(S3)

and

$${L}_{v}E=\frac{\varDelta }{\varDelta +\gamma }({R}_{n}-G)+\frac{\gamma }{\varDelta +\gamma }\kappa {e}{\ast }(1-RH),\,$$

(S4)

where R_n is the net surface radiation and G is the ground heat flux.

The incoming longwave flux is given by $L{W}_{in}=\,{\epsilon }\sigma {T}^{4}$ where $\sigma$ is Stefan–Boltzmann constant and ${\epsilon }$ is the effective near-surface air emissivity. The outgoing longwave flux is the sum of the radiation emitted by the lake surface and the reflection of the incoming flux. Since the longwave reflectivity of a surface equals one minus its emissivity ${{\epsilon }}_{s}$, the outgoing longwave flux is given by $L{W}_{out}=\,{{\epsilon }}_{s}\sigma {T}_{s}^{4}+(1-{{\epsilon }}_{s}){\epsilon }\sigma {T}^{4}$. To facilitate a clear understanding of the longwave, we decompose the net surface longwave radiation into a T_s − T-dependent term and an emissivity-related term, that is,

$$L{W}_{n}=L{W}_{out}-L{W}_{in}={{\epsilon }}_{s}\sigma {T}_{s}^{4}-{{\epsilon }}_{s}{\epsilon }\sigma {T}^{4}\cong 4{{\epsilon }}_{s}\sigma {T}^{3}({T}_{s}-T)+{{\epsilon }}_{s}(1-{\epsilon })\sigma {T}^{4}.$$

(S5)

By moving all the (T_s − T)-dependent terms in ${L}_{v}E$, SH and LW_n to the one side of the equation, we solve T_s − T and consequently evaporation. This leads to a longwave-untangled Penman (LP) equation as,

$${T}_{s}-T=\frac{S{W}_{n}-{{\epsilon }}_{s}\sigma {T}^{4}-G-\kappa {e}^*(1-RH)}{\varDelta +\gamma +u},$$

(S6)

and

$${L}_{v}E=\frac{\varDelta }{\varDelta +\gamma +u}(S{W}_{n}-{{\epsilon }}_{s}\sigma {T}^{4}(1-{\epsilon })-G)+\frac{\gamma +u}{\varDelta +\gamma +u}\kappa {e}^*(1-RH),$$

(S7)

where $u=\frac{4{{\epsilon }}_{s}\sigma {T}^{3}}{\kappa }$ represents the dependency of the net longwave radiation on T_s – T ($u\equiv \frac{\partial L{W}_{n}}{k\partial ({T}_{s}-T)}$), similar to $\varDelta$ and γ for latent and sensible heat fluxes ($\varDelta \equiv \frac{\partial LE}{k\partial ({T}_{s}-T)}$, $\gamma \equiv \frac{\partial SH}{k\partial ({T}_{s}-T)}$). The energetic term distributes the received energy to the latent, sensible, and longwave fluxes, according to their relative weights defined by $\varDelta$, γ, and u. The net shortwave input is given by $S{W}_{n}=(1-Alb)S{W}_{in}$ where SW_in is the incoming shortwave flux. Eq. S7 can be further rewritten as Eq. 4 by putting the energy allocation factor $f=\frac{\varDelta }{\varDelta +\gamma +u}$ before all the terms.

The LP equation has two advantages compared to the standard Penman equation. First, it provides a clear understanding of the longwave effect. LW_n is reformulated from the difference of two large terms to the sum of the small terms. The effect of $4{{\epsilon }}_{s}\sigma {T}^{3}({T}_{s}-T)$ is nicely represented by the parameter u and the convoluted longwave effect is reduced to changes in the air emissivity, which can be satisfactorily explained at regional scales. Second, by separating the dependency of LW_n on T_s – T and representing it by the parameter u, the LP equation allows a cleaner interpretation of future changes in T_s – T and consequently E. In the standard Penman equation, future changes in T_s – T are partially attributed to the net longwave radiation, which itself depends on T_s – T. This can lead to convolved arguments as follows. On one hand, a reduced T_s – T would reduce the net outgoing longwave radiation and consequently increase evaporation. On the other hand, the bulk transfer formula states that a reduced T_s – T will decrease evaporation. Such convolved arguments are resolved in the LP equation.

For application, the LP equation estimates evaporation based on the inputs of air temperature T, relative humidity RH, incoming shortwave radiation SW_in, air emissivity $\varepsilon$, lake albedo $Alb$, ground heat flux G, and surface wind speed U. The air emissivity is diagnosed as $\varepsilon =L{W}_{in}/\sigma {T}^{4}$. The lake albedo is diagnosed as $Alb=S{W}_{out}/S{W}_{in}$. The aerodynamic resistance is computed from the surface wind speed as ${r}_{a}=1.1\times {10}^{-3}(1+U)$, which best fits the CLM simulation results. When estimating the contribution of a particular parameter to the LakeE increase, its values in the LP equation are changed from those in historical climate (1971–2000) to those in future climate (2071–2100) while other parameters are unchanged. That is, the contribution of the parameter A is estimated as

$$\delta {E}_{A}^{LP}={E}^{LP}({A}_{future},{B}_{historical},{C}_{historical},\ldots \!\!)-\,{E}^{LP}({A}_{historical},{B}_{historical},{C}_{historical},\ldots \!\!)$$