Abstract
Standardised mortality-linked securities are easier to analyse and more conducive to the development of liquidity. However, when a pension plan relies on standardised instruments to hedge its longevity risk exposure, it is inevitably subject to various forms of basis risk. In this paper, we use an economic pricing method to study the impact of population basis risk, that is, the risk due to the mismatch in the populations of the exposure and the hedge, on prices of mortality-linked securities. The pricing method we consider is highly transparent, allowing us to understand how population basis risk affects the demand and supply of a mortality-linked security. We apply the method to a hypothetical longevity bond, using real mortality data from different populations. Our illustrations show that, interestingly, population basis risk can affect the price of a mortality-linked security in different directions, depending on the properties of the populations involved.
Similar content being viewed by others
Introduction
Pension plans and annuity providers are subject to the threat of longevity risk. One way to mitigate the risk is to trade mortality-linked securities in capital markets. Some investors including hedge funds are interested in acquiring an exposure to longevity risk, because mortality-linked securities have a very low correlation to virtually every other asset class. In recent years, we have seen many trades of mortality-linked securities between pension plans and investment banks. It is estimated that the potential size of the longevity securities market exceeds US$2 trillion in the United Kingdom alone, and exceeds US$25 trillion worldwide.Footnote 1
While hedgers may prefer bespoke securities that are based on the hedger's own mortality experience, investors and intermediaries prefer standardised instruments that are linked to broad population mortality indexes. This is because standardised securities are easier to analyse and more conducive to the development of liquidity. Standardisation has been a goal of various participants in the longevity risk market. In 2010, the Life and Longevity Markets Association (LLMA) was established to promote the development of a liquid traded market in longevity- and mortality-related risk. Part of the LLMA's work is to develop standardised longevity indexes, upon which securities with a secondary market can be written.
However, when a pension plan relies on standardised instruments to hedge its longevity risk exposure, it is inevitably subject to various forms of basis risk. In this paper, we focus on population basis risk, that is, the risk due to the mismatch in the populations of the exposure and the hedge.Footnote 2 According to Coughlan,Footnote 3 the lack of knowledge in population basis risk is a major challenge to market development. Research work on population basis risk is therefore very helpful for the development of the longevity risk market.
The problem of population basis risk has recently been considered by some academics, including Cairns et al.,Footnote 4 Coughlan et al.,Footnote 5 Dowd et al. Footnote 6 and Li and Hardy.Footnote 7 Their studies focus mainly on the measurement of basis risk, but have made no attempt to investigate how population basis risk may affect the trade and hence the price of a mortality-linked security. This paper fills this gap by extending the economic pricing method introduced by Zhou et al. Footnote 8 so that it can be applied in the presence of population basis risk. Given the proposed extension, practitioners can readily estimate the time-zero price of a standardised mortality-linked security, such as the mortality forwards sold by JP Morgan and the longevity bond jointly announced by the European Investment Bank and BNP Paribas. More importantly, practitioners can understand how the price of a security would change if different populations are involved in the trade.
Besides prices, we also investigate the impact of population basis risk on the behaviour of hedgers and investors in the longevity risk market. For a deeper understanding of population basis risk, we delve into its fundamental components:
-
1
the difference in the magnitude of mortality rates between the two populations involved in the pricing framework;
-
2
the volatility of the mortality-linked cash flows associated with the hedger's liability relative to that associated with the security being priced;
-
3
the (imperfect) correlation between the mortality-linked cash flows associated with the hedger's liability and the security being priced.
We shall examine the influence of these three components of population basis risk on the trading of mortality-linked securities.
Hedging is another focus of this paper. Using our proposed method, a practitioner can easily construct a static longevity hedge with standardised instruments, provided that his/her objective is to maximise his/her expected utility at some future time. We shall investigate how such a hedging strategy would depend on the properties of the populations involved in the trade. Using a two-population mortality model, we shall also study the effectiveness of hedging strategies formed by our method.
We illustrate our proposed method with a hypothetical mortality-linked security. The security, which is similar to the longevity bond jointly announced by the European Investment Bank and BNP Paribas in 2004, is designed to help pension funds and annuity providers hedge their exposures to longevity risk. The illustrations are based on mortality data from the U.K. male population and two of its sub-populations, the Scottish male population and U.K. male insured lives.
The rest of this paper is organised as follows. In the second section, we present an economic pricing method that is applicable to a situation when population basis risk exists. In the third section, we describe the two-population mortality model for use with the proposed pricing method. In the fourth section, we illustrate the effect of population basis risk on security prices, static hedging strategies and the behaviour of the counterparties involved. In the last section, we conclude the paper with several suggestions for further research.
The tâtonnement pricing process
Background
In a parallel study, Zhou et al. 8 introduced an economic approach for pricing mortality-linked securities. This new pricing method is developed from an idea called tâtonnement, which was first proposed by WalrasFootnote 9 to model trades in an exchange economy. The pricing process models the trade between two economic agents, one of which is subject to some mortality or longevity risk. The agent with the risk exposure hedges its risk by trading a mortality-linked security with the other agent, who participates in the trade for earning a risk premium. It is assumed that, given a price, both agents would maximise their expected terminal utilities by altering their demand or supply of the security. The price of the security is adjusted iteratively to match the supply and demand, and finally, the estimated price is the price at which the demand and supply are equal, that is, the market clears.
This new pricing method models the actual trade between the hedger and investor. It is therefore more transparent relative to standard no-arbitrage approaches, in which the price of a security is estimated by extrapolating prices of other similar securities available in the market. On top of the estimated price, the economic pricing method provides us with a pair of demand and supply curves, from which we can infer the quantity of a mortality-linked security to be traded in equilibrium. Another appealing feature is that, as opposed to no arbitrage approaches, it does not require the market prices of other mortality-linked securities as input. This can spare us from the problems associated with the lack of market price data.
It is assumed in Zhou et al. 8 that the population of individuals associated with the hedger's risk exposure is identical to that associated with the security being priced. This simple set-up is appropriate for pricing bespoke securities, such as the longevity swap agreed between Babcock International and Crédit Suisse in 2009. However, it is not adequate for valuing standardised mortality-linked instruments, which are based on broad population mortality indexes rather than the hedger's own mortality experience.
We herein introduce a tâtonnement process for pricing mortality-linked securities when population basis risk exists. In the rest of this section, we will first present the generalised pricing process, and then we provide two methods for solving the tâtonnement equilibrium. The first method solves the exact equilibrium price numerically, while the second method calculates an approximate equilibrium price by an analytic formula, which is based on some assumptions on the contingent cash flows.
The set-up
Suppose that Agent A has life contingent liabilities that are due at times 1, 2, …, T. The amount due at time t is f t (Q t L), which is a deterministic function of Q t L, where Q t L=(q 1 L, …, q t L) is a vector of mortality indexes up to and including time t. The index q t L contains information about the mortality of the population associated with Agent A's liability over the period of t−1 to t. At time 0, the values of q t L for t0 are not known and are governed by an underlying stochastic process.
To mitigate its exposure to mortality or longevity risk, Agent A sells (or purchases) a mortality-linked security maturing at time T. At time t, the security makes a payout of g t (Q t H), which is deterministic function of Q t H, where Q t H=(q 1 H, …, q t H) is a vector of mortality indexes up to and including time t. The index q t H contains information about the mortality of the population associated with the security over the period of t−1 to t. We emphasise that, due to population basis risk, q t H and q t L are not necessarily the same.
Agent B is an investor who trades the mortality-linked security with Agent A, in order to earn a risk premium. At time t, Agent B receives (or pays) an amount of g t (Q t H) per unit of the mortality-linked security purchased (or sold).
We let θ A and θ B respectively be the quantity that Agents A and B are willing to trade at given price P. Both θ A and θ B are functions of P, but we suppress the argument P for brevity. Here, a positive quantity means that the agent purchases the security, while a negative quantity means the agent sells the security.
We assume that the wealth of each agent can only be invested in either the mortality-linked security or a bank account which yields a continuously compounded risk-free interest rate of r per annum. We allow a negative wealth, which means that the agent borrows money from a bank account and pays an interest rate of r to the bank. Other than the bank account, the mortality-linked security and the life contingent liability, there is no source of income or payout. We assume r=3 per cent in our numerical illustrations.
Let W t A and W t B be the time-t wealth of Agents A and B, respectively. For Agent A, the terminal wealth W T A can be calculated recursively as follows:

where W 1 A=(W 0 A−θ A P)e r+θ A g 1(Q 1 H)−f 1(Q 1 L) and W 0 A is a constant. Similarly, for Agent B, the terminal wealth W T B can be calculated as follows:

where W 1 B=(W 0 B−θ B P)e r+θ B g 1(Q 1 H) and W 0 B is a constant.
We denote the utility functions for Agents A and B by U A and U B, respectively. We assume that, at time 0, each agent trades a quantity that maximizes its expected terminal utility. Using the notation defined above, the objectives of the two agents can be formulated as follows:


In the pricing process, the price P is adjusted until the market has reached equilibrium, that is, θ A+θ B=0. We use P * to denote the resulting tâtonnement equilibrium price.
We assume an exponential utility function, U(x)=1−e −kx, for each agent. In the utility function, parameter k is the absolute risk aversion for all wealth levels. A larger k means that the agent is more conservative and risk averse. In a study of an insurer's optimal premium strategy, Emms and HabermanFootnote 10 assume k=1.0 for an insurer. We also assume in our numerical illustrations that Agent A, which is likely to be an insurer or a pension plan provider, has an absolute risk aversion of k A=1.0. It is reasonable to assume that Agent A is more conservative than Agent B, because Agent A wants to hedge away its mortality or longevity risk exposure while Agent B is willing to take the risk in return of a risk premium. In our numerical examples, the assumed value of k for Agent B is k B=0.5.
The numerical results, of course, depend on the risk aversion parameters. When the investor (Agent B) is less risk-adverse, he/she is willing to take more mortality or longevity risk exposure. If Agent B is the buyer, then the demand and hence the price of the security will rise. Zhou et al. 8 sensitivity tested the absolute risk aversion parameters. They found that the resulting tâtonnement equilibrium depends on the absolute values of k A and k B, rather than the difference k A−k B only.
When exponential utility functions are used, the initial wealth of each agent has no effect on the estimated price and the quantity traded in the tâtonnement equilibrium. This property, which is proved in Zhou et al.,8 facilitates optimisation. Further, in our set-up, an agent's wealth might become negative in some future time. A negative wealth is permitted when exponential utility functions are assumed.
Power utility functions are sometimes considered more realistic, because they imply a decreasing absolute risk aversion. However, to work with power utility functions, we require assumed values of W 0 A and W 0 B. Also, power utility functions do not permit a negative wealth.
Solving by a numerical procedure
We now present a numerical procedure that aims to find the exact solution to the tâtonnement equilibrium. Beginning with P 0, the initial guess of the equilibrium price P *, we calculate the values of θ A and θ B at which the expected utilities of the agents are maximised. The expected utilities are calculated with 10,000 simulated mortality paths. We then adjust the estimate of the equilibrium price iteratively using the following equation:

where γ is a positive real constant, until ∣θ A+θ B∣ is less than the tolerance level of 10−6.
Solving by an approximate analytic formula
Alternatively, if we were to impose some assumptions on the contingent cash flows involved in the wealth processes, we can solve for the tâtonnement equilibrium analytically.
Let v L and v H respectively be the accumulated values of the life contingent liabilities and the payouts from one unit of the mortality-linked security at a future time T. Both v L and v H are positive real numbers.
We can obtain an analytical formula for the tâtonnement equilibrium price if we assume that (v H , v L )′ follows a bivariate normal distribution with mean vector (μ H , μ L )′ and variance-covariance matrix

where −1⩽ρ⩽1 is the correlation coefficient between the random variables v H and v L . Under this assumption, at a given price P, Agent A will trade

units of the security, while Agent B will trade

units of the security. A proof of the results above is provided in Appendix A.
In the tâtonnement equilibrium, we have θ A+θ B=0. Substituting θ A and θ B into this equation, we obtain the following expression for the tâtonnement equilibrium price P *:

To evaluate θ A, θ B, and P *, we need the parameters in the bivariate normal distribution which (v H , v L )′ follows. To estimate these parameters, we first simulate 10,000 values of (v H , v L )′ using the assumed mortality model. We then take the sample mean vector and the sample variance-covariance matrix of the simulated values as estimates of (μ H , μ L )′ and Σ, respectively.
The analytic solution requires a rather restrictive assumption on (v H , v L )′, but, as we will demonstrate in the section entitled ‘An illustration’, it allows us to understand the impact of population basis risk on the tâtonnement equilibrium more easily.
Modeling mortality dynamics
Data
Recall that the generalised pricing process involves two populations; one is associated with the hedger's exposure and the other is linked directly to the security being priced. To illustrate the pricing process, we consider the following two pairs of populations:
-
1
U.K. male population and Scottish male population.
-
2
U.K. male population and the population of U.K. male insured lives (thereafter called the CMI population for brevity).
In both pairs, the second population is a subset of the first one. We believe that such an arrangement would maximise the resemblance of our illustrations to actual trades, because, for example, in forming a longevity hedge with a standardised instrument, a U.K. pension plan would naturally choose one that is linked to the national population of the U.K., if that is available.
The data (death and exposure counts) for the two national populations are obtained from the Human Mortality Database,Footnote 11 while that of the insured lives are provided by the CMI Bureau of the Institute and Faculty of Actuaries. For all three populations, we consider a sample period of 1947 to 2005 and a sample age range of 60 to 89. Hence, the estimated models cover 88 years of birth (1858 to 1945).
In Figure 1 we compare the mortality of the two subpopulations with that of the U.K. population. We observe that the mortality of Scottish males is higher than that of U.K. males, while the mortality of CMI males is the opposite. It is not surprising that the CMI population has a lighter mortality, as people who are willing and able to buy insurance are generally wealthier and healthier. In the section entitled ‘An illustration’, we will demonstrate that the difference in the magnitude of mortality rates between the populations involved in the trade would have an effect on the tâtonnement equilibrium.
A joint mortality model
For two reasons, we should use a joint mortality model rather than two independent mortality models. First, using two independent mortality models is likely to result in an increasing divergence in life expectancy in the long run, counter to the expected and observed trend towards convergence.Footnote 12 Second, given that the populations involved in the trade are related, the use of two independent models will overstate the underlying population basis risk. This may lead us to overestimate the agents’ reaction to population basis risk, and consequently misestimate the tâtonnement equilibrium.
In this paper, we implement the generalised pricing process with the two-population age-period-cohort model proposed by Cairns et al. 4 This joint model is built from two classical age-period-cohort models, one for each population. Each period and cohort index in the model is assumed to follow a discrete-time stochastic process. The complete model specification is provided in Appendix B.
We acknowledge the shortcomings of the age-period-cohort structure. Previous studies based on single-population models have shown empirically that using age-period and age-cohort interaction terms may give a better fit to historical data. However, as of this writing, the model we use is the only two-population mortality model that incorporates cohort effects. We have not seen any two-population model with both age-period and age-cohort interaction terms, possibly because of the additional challenge of ensuring that the resulting mortality projections do not diverge over the long run.
From the parameter estimates, we can calculate the volatilities of the year-on-year innovations for the period and cohort effects associated with each of the three populations. The results, which we summarise in Table 1, indicate that Scottish males have the most volatile period effect index, while CMI males have the most volatile cohort effect index. As we will see in the section entitled ‘An illustration’, the knowledge on the sources of volatility can help us better understand the tâtonnement equilibria formed with different pairs of populations.
From the joint model, we can simulate mortality paths. The simulated mortality paths enable us to evaluate expressions (1) and (2) in the numerical procedure for solving the tâtonnement equilibrium. They also allow us to calculate the sample mean and sample variance-covariance matrix for (v H , v L )′ in the approximate analytic formula for the tâtonnement equilibrium price. The procedure for simulating mortality paths is detailed in Appendix C.
An illustration
Specification of the security
In this section, we illustrate the generalised tâtonnement pricing process with a hypothetical security. The security we consider is a 25-year annuity bond (a bond without principal repayment), which is similar to the longevity bond jointly announced by the European Investment Bank and BNP Paribas in November 2004.
The coupon payments are linked to the realised mortality rates of individuals in the reference population who are aged 65 at time 0 (the beginning of year 2006). They can be specified by using the notation defined in the sub-section entitled ‘The set-up’ Specifically, we set the mortality index q t H to the time-t value of the central death rate for the cohort of individuals. Let Q t H=(q 1 H, …, q t H) be the vector of mortality indexes up to and including time t. The coupon payment at time t=1, 2, …, 25 is given by g t (Q t H)=Π i=1 t(1−q i H), which is the (approximate) realised survival rate to time t.Footnote 13
If the realised survival rates are larger than expected, then pension payments, on the whole, will last longer, which means larger pension liabilities. Therefore, a pension plan wishing to hedge longevity risk may purchase the longevity bond, which will pay out to the pension plan, at time t=1, 2, …, 25, an amount that increases with the realized survival rate to offset the correspondingly higher value of pension liabilities.
In the absence of credit risk, the cash flows involved are simple to specify (see Figure 2). The investor makes an initial payment of US$P (i.e., the issue price) and receives in return an annual mortality-dependent payment of g t (Q t H) in each year t for 25 years.
The trade
We assume that the longevity bond is sold by Agent B, which could possibly be an investment bank attempting to earn a longevity risk premium. The bond is sold to Agent A, a pension plan provider having an exposure to longevity risk.
We assume that Agent A is forced to pay each of its pensioners an amount of US$0.01 at the end of each year. The payment to a pensioner ceases when the pensioner dies or reaches age 90, whichever occurs earlier. At time 0 (the beginning of year 2006), the plan contains 1000 pensioners, who are distributed over the age range of 65 to 89. The age distribution of the pensioners is shown in Figure 3. For simplicity, we assume that the plan is closed, that is, there are no new entrants to the plan.
It is obvious that Agent A's financial obligation is linked to the mortality of its pensioners. In particular, it is linked to an index q t L, which contains the realised death rates of 25 cohorts of pensioners (with years of birth ranging from 1916 to 1940) at time t. We permit population basis risk in our pricing process so that q t L and q t H are not necessarily associated with the same population.
If q t L and q t H are positively correlated, then an increase in the pension liability will be accompanied with an increase in the coupon payments from the longevity bond. Hence, by purchasing the bond, Agent A can reduce its risk exposure.
As mentioned earlier, our illustrations are based on two different pairs of populations. Each pair is composed of U.K. males and one of its subpopulation, which is either Scottish males or CMI males. For each pair of populations, the following three cases are examined:
-
Case 1: Both the pension liability and the longevity bond are linked to the mortality of U.K. males.Footnote 14 There is no basis risk involved in this case.
-
Case 2: The bond is linked to the mortality of U.K. males, while the pension liability is linked to subpopulation. Basis risk is involved in this case.
-
Case 3: Both the pension liability and the longevity bond are linked to the mortality of the subpopulation. There is no basis risk involved in this case.
U.K. and Scottish males
Let us suppose here that the subpopulation is Scottish males. For each of the three cases, we calculate the exact tâtonnement equilibrium price of the longevity bond by using the algorithm presented in the sub-section entitled ‘Solving by a numerical procedure’. The estimated prices are displayed in Table 2. Also shown in Table 2 are the quantities traded in each case.
To know how the prices are formed, we need to examine the demand and supply curves, which can be derived by evaluating expressions (1) and (2) at different price levels.
The upper panel of Figure 4 depicts the demand and supply curves for Cases 1 and 2. The supply curves for both cases are the same, but the demand curve shifts downwards when the population to which the pension liability is linked is changed from U.K. males to Scottish males. This leads to a reduction in the price of the security.
The lower panel of Figure 4 depicts the demand and supply curves for Cases 2 and 3. As we change the population to which the longevity bond is linked, the demand curve shifts downwards, but the supply curve shifts upwards. This results in a reduction in the price of the security.
What constitutes the shifts in the supply and demand curves? The analytic formulas in the sub-section entitled ‘Solving by an approximate analytic formula’ may help us answer this question. In the current application, Agent B is the supplier, so we have θ B⩽0 and hence θ A⩾0. Using Eqs. (3) and (4), at a price P, the (approximate) demand of the security from Agent A is

while the (approximate) supply of the security from Agent B is

We observe that both ∣θ A∣ and ∣θ B∣ are linear functions of the price P when they are greater than zero. Their slopes and intercepts are related to parameters μ H , σ H , σ L , and ρ. The effects of these parameters on the supply and demand of the security are summarised in Table 3. In the table, ‘↑’ means an increase, ‘↓’ means a decrease, and ‘−’ means there is no change.
The relations are rather intuitive. First, consider the supply, ∣θ B∣, from Agent B. Recall that v H is the accumulated value of the payouts from the longevity bond at maturity, and that μ H is its expectation. Therefore, the difference Pe rT−μ H is the reward to Agent B for accepting a longevity risk exposure. As a result, when μ H increases, the reward to Agent B is smaller, and hence it will supply less. On the other hand, when σ H increases, the longevity bond becomes more risky. If the reward is held constant, then Agent B must supply less.
Next, we consider the demand, ∣θ A∣, from Agent A. It is quite obvious that Agent A will demand more if its pension liability is more volatile (i.e., σ L is larger). It will also demand more if less compensation to Agent B is needed (i.e., μ H is higher). Moreover, the demand from Agent A is dependent on ρ, which is a positive number in this application. When ρ increases (becomes closer to one), the bond becomes a more effective hedging instrument, and therefore Agent A will demand more. Finally, Agent A will demand less when σ H is large relative to σ L , as in this situation fewer units of the bond will be needed for the same amount of risk reduction.
In Table 2 we show the estimates μ H , σ H , σ L , and ρ when the pension liability and the longevity bond are linked to the mortality of either U.K. or Scottish males.
Recall that the longevity bond is related only to the cohort born in 1940 and that the pension liability is related only to cohorts born between 1916 and 1940. These years of birth are covered by the data sample, so when we project v H and v L , future values of the cohort indexes are not required. Consequently, the values of σ H and σ L depend entirely on the variability in the period indexes. As the period index for Scottish males is more volatile (see Table 1), the value of σ H in Case 3 is higher than that in Cases 1 and 2, and the value of σ L in Cases 2 and 3 is higher than that in Case 1.
Recall also that the payouts from the longevity bond are proportional to the realised survival rates. Since Scottish males have heavier mortality than U.K. males (see Figure 1), the value of μ H in Case 3 is smaller than that in Cases 1 and 2.
Finally, ρ is the lowest (closest to zero) in Case 2, since in this case the longevity bond and the pension liability are linked to different populations.
Using Eq. (5), the approximate prices in Cases 1, 2 and 3 are 13.1372, 13.1219 and 12.3683, respectively. They are quite close to the corresponding prices obtained by the numerical procedure that aims to find exact prices, indicating that the bivariate normal approximation is reasonable.
Now, let us revisit the supply and demand curves in Figure 4. The supply curves for Cases 1 and 2 are the same, as μ H and σ H remains unchanged when we alter the population to which the pension liability is linked. Nevertheless, the change in the hedger's population would lead to an increase in σ L and a decrease in ρ. These changes, according to Table 3, have offsetting effects on the demand. In this example, the effect of ρ outweighs that of σ L , and therefore the demand curve shifts downwards.
Similar arguments can explain the shifts in the curves when we move from Case 2 to Case 3. As the bond's reference population is changed from U.K. males to Scottish males, μ H decreases, σ H increases, and ρ increases. According to Table 3, a lower μ H and a higher σ H have opposite effects on the supply. In this example, the effect of μ H is more significant and therefore the supply curve shifts upwards. On the other hand, the changes in μ H and σ H will exert pressure on the demand. Although a higher ρ will bring the demand up, its effect is not as great as the combined effect of μ H and σ H . Overall, the demand curve shifts downwards.
If the hedger's objective is to maximise its expected utility at a certain future time, then the quantity traded in the tâtonnement equilibrium can be regarded as the corresponding static hedging strategy. From Table 2 we observe that, in the presence of population basis risk, the hedger tends to use fewer longevity bonds to statically hedge its risk exposure.
We also evaluate the effectiveness of this static hedging strategy over a horizon of 25 years. The measure we use is the reduction in the variance of Agent A's terminal wealth, that is, the wealth at t=25.Footnote 15 From Table 2 we observe that the static hedge is fairly effective, even though it is composed of one single instrument only. In Cases 1 and 3, more than 80 per cent of the variance is elimiated. In Case 2, the population basis risk involved brings down the hedge effectiveness to about 75 per cent.Footnote 16
U.K. and CMI males
In this subsection, we repeat the same analysis by assuming that the subpopulation is CMI males. Again we use the algorithm in the sub-section entitled ‘Solving by a numerical procedure’ to solve for the tâtonnement equilibrium in each case. The results are summarised in Table 4.
The upper panel of Figure 5 shows the demand and supply curves for Cases 1 and 2. The supply curves for both cases are the same, but the demand curve shifts downwards when the population to which the pension liability is linked is changed from U.K. males to CMI males. This leads to a reduction in the price of the security. Note that the reduction is more dramatic than that observed in the previous example.
The lower panel of Figure 5 shows the demand and supply curves for Cases 2 and 3. As we change the population to which the longevity bond is linked, the demand curve shifts upwards, while the supply curve shifts downwards. This results in an increase in the price of the security. It is noteworthy that the changes here are exactly opposite to the corresponding changes in the previous example.
Again we use the analytic formulas in the sub-section entitled ‘Solving by an approximate analytic formula’ to explain the changes. In Table 4 we show the estimates μ H , σ H , σ L , and ρ when the pension liability and the longevity bond are linked to the mortality of either U.K. or CMI males.
As the period index for CMI males is less volatile (see Table 1), the value of σ H in Case 3 is smaller than that in Cases 1 and 2, and the value of σ L in Cases 2 and 3 is smaller than that in Case 1. Also, since CMI males have lighter mortality than U.K. males (see Figure 1), the value of μ H in Case 3 is higher than that in Cases 1 and 2. Further, the difference between the hedger's population and the bond's reference population makes ρ in Case 2 the lowest (closest to zero) among the three cases.
Using Eq. (5), the approximate prices in Cases 1, 2 and 3 are 13.1372, 12.9945 and 14.5909, respectively. By comparing them with the corresponding values in Table 4, we find that the bivariate normal approximation is also reasonable in this example.
With the information above, the explanation to the changes becomes straightforward. First, let us focus on Cases 1 and 2. As all parameters in Eq. (7) are unaffected, there is no change to the supply curve. However, the change in the hedger's population will reduce σ L and ρ. Both reductions will exert pressure on the demand, causing the demand curve to shift downwards.
Next, we focus on Cases 2 and 3. As the bond's reference population is changed from U.K. males to CMI males, μ H increases, σ H decreases, and ρ increases. According to Table 3, these changes will all lead to a higher demand, bringing the demand curve up. On the other hand, the changes in μ H and σ H have opposite effects on the supply. In this example, the effect of μ H is more significant, and therefore the supply curve shifts downwards.
As in the previous example, when population basis risk exists (Case 2), the hedger uses fewer longevity bonds to statically hedge its risk exposure, and the effectiveness of the hedge becomes lower.
Concluding remarks
In this paper, we proposed an economic pricing method that is applicable when population basis risk exists. The proposed method has a wide range of applications. First, with our method, practitioners can easily price standardised mortality-linked securities, such as the mortality bonds issued by Swiss Reinsurance and the mortality forwards sold by JP Morgan. Second, practitioners can use our method to examine how the demand and supply of a mortality-linked security would change if different populations were involved in the trade. Finally, practitioners can easily develop a static longevity hedge using our method. The effectiveness of the hedge can also be evaluated straightforwardly.
From the solution to the tâtonnement pricing process, we can conclude that, on top of correlations, the magnitude and volatility of mortality rates play a critical role in determining the impact of population basis risk on security prices. As these factors are different among different pairs of populations, the effect of the risk varies. Our illustrations have shown empirically that, interestingly, population basis risk can affect the price of a mortality-linked security in different directions, depending on the properties of the populations involved.
It might be difficult to conduct a similar analysis with a no-arbitrage approach. Technically speaking, we could construct a risk-adjusted two-population mortality model by introducing a market price of risk to each stochastic factor in the model. However, in today's market where market price data are very limited, it is difficult, if not impossible, to estimate that many market prices of risk. Even if we have such a model, a no-arbitrage approach does not give us information such as demand and supply, which would help us better understand how population basis risk and its components are involved in the pricing process.
One reason for using standardised instruments is that they potentially have better liquidity. In our presentation, liquidity was not given much attention, as we assumed that the agents will hold their positions until the security matures. This assumption can be relaxed by employing a sequential decision process, which is detailed in Zhou et al. 8 This extension allows both agents to unwind their positions at discrete time points before maturity. However, as decisions (optimisations) are made at multiple time points, this extension demands significantly more computational resources, adding an extra challenge in the pricing process.
The calculations in this paper assume that there is no small sample risk (or sampling risk), that is, the risk that the realised mortality experience is different from the true mortality rate. Small sample risk is diversifiable, so it does not matter much for a large population, say one with more than 100,000 lives. However, for smaller populations, the risk may be significant. In future research, we may incorporate small sample risk by treating the hedger's population as a random survivorship group, and by modelling the number of deaths in the population with a death process, possibly a Poisson or binomial.
Recently, there has been a wave of research work on mortality modelling for two related populations. Other than the model we considered, Dowd et al. 6 proposed a gravity model of mortality rates for two populations, and Zhou et al. Footnote 17 introduced a two-population mortality model with jump effects. In future research, it is warranted to perform serious validation work, similar to the recent contributions by Cairns et al. Footnote 18 and Dowd et al.,Footnote 19 for various two-population mortality models, and revisit our pricing framework using the model with the highest ranking.
Another possible avenue of future research is to extend the two-population age-period-cohort model we considered. It would be interesting to develop an extension that can handle more than two populations simultaneously. Such an extension would have a wide range of applications, including the modeling of a trade involving more than two counterparties, each of which is associated with a different population.
Notes
Source: The Life and Longevity Markets Association ( www.llma.org ).
Basis risk can arise from other sources, for example, the mismatch in the timing of cash flows. According to Coughlan et al. (2011), population basis risk can be further divided into four categories: (1) the mismatch in mortality rates between males and females (the gender basis); (2) the mismatch between mortality at different ages (the age basis); (3) the mismatch between national mortality and the mortality of a particular subpopulation (the subpopulation basis); (4) the mismatch between mortality in different countries (the country basis). In our numerical illustrations, we focus on the subpopulation basis.
see, e.g., Li and Lee (2005).
It is approximate because it is based on central death rates rather than death probabilities.
By saying the pension liability is linked to a certain population, we mean that the realised mortality rates for members in the pension plan and individuals in that population are the same.
The terminal wealth is the accumulated value of the initial wealth and all subsequent net cash flows over the hedging horizon. In some other studies, for example, Li and Hardy (2011), the evaluation of hedge effectiveness is based on the present value of the cash flows instead.
Coughlan et al. (2011) and Li and Hardy (2011) also use hypothetical pension plans to analyse the effectiveness of longevity hedges. Li and Hardy (2011) obtain a hedge effectiveness of 81.61 per cent using a portfolio of four mortality forwards, while Coughlan et al. (2011) obtain a hedge effectiveness of 82.4 per cent using a ten-year deferred annuity swap. However, because different hedging instruments and pension plans are used, the hedging results from our study are not directly comparable with those from Coughlan et al. (2011) and Li and Hardy (2011).
References
Cairns, A.J.G., Blake, D., Dowd, K., Coughlan, G.D., Epstein, D., Ong, A. and Balevich, I. (2009) ‘A quantitative comparison of stochastic mortality models using data from England and Wales and the United States’, North American Actuarial Journal 13 (1): 1–35.
Cairns, A.J.G., Blake, D., Dowd, K., Coughlan, G.D. and Khalaf-Allah, M. (2011) ‘Bayesian stochastic mortality modelling for two populations’, ASTIN Bulletin 41: 29–59.
Coughlan, G.D. (2010) ‘Life and longevity markets association: The development of a longevity and mortality trading market’, Presentation at the Sixth International Longevity Risk and Capital Markets Solutions Conference, Sydney, Australia. Available at http://www.longevity-risk.org/Presentations/Coughlan_LLMA.pdf.
Coughlan, G.D., Khalaf-Allah, M., Ye, Y., Kumar, S., Cairns, A.J.G., Blake, D. and Dowd, K. (2011) ‘Longevity hedging 101: A framework for longevity basis risk analysis and hedge effectiveness’, North American Actuarial Journal, 15: 150–176.
Dowd, K., Cairns, A.J.G., Blake, D., Coughlan, G.D., Epstein, D. and Khalaf-Allah, M. (2011) ‘A gravity model of mortality rates for two related populations’, North American Actuarial Journal 15: 334–356.
Dowd, K., Cairns, A.J.G., Blake, D., Coughlan, G.D., Epstein, D. and Khalaf-Allah, M. (2010a) ‘Evaluating the goodness of fit of stochastic mortality models’, Insurance: Mathematics and Economics 47 (3): 255–265.
Dowd, K., Cairns, A.J.G., Blake, D., Coughlan, G.D., Epstein, D. and Khalaf-Allah, M. (2010b) ‘Backtesting stochastic mortality models: An ex-post evaluation of multi-period-ahead density forecasts’, North American Actuarial Journal 14: 281–298.
Emms, P. and Haberman, S. (2009) ‘Optimal management of an insurer's exposure in a competitive general insurance market’, North American Actuarial Journal 13 (1): 77–105.
Human Mortality Database (2010) University of California, Berkeley (U.S.), and Max Planck Institute of Demographic Research (Germany). Available at www.mortality.org or www.humanmortality.de (data downloaded on 1 July 2010).
Li, N. and Lee, R. (2005) ‘Coherent mortality forecasts for a group of population: An extension of the Lee-Carter method’, Demography 42: 575–594.
Li, J.S.-H. and Hardy, M.R. (2011) ‘Measuring basis risk in longevity hedges’, North American Actuarial Journal 15: 177–200.
Walras, L. (1874) Élements d’économie politique pure, Lausanne: Corbaz.
Zhou, R., Li, J.S.-H. and Tan, K.S. (2010) Economic pricing of mortality-linked securities: A tâtonnement approach, WatRISQ Working Paper. Available at http://www.watrisq.uwaterloo.ca/.
Zhou, R., Li, J.S.-H. and Tan, K.S. (2011) ‘A two-population mortality model with transitory jump effects’, Paper presented at the Seventh Longevity Risk and Capital Markets Solutions Conference, Frankfurt, Germany.
Acknowledgements
The authors acknowledge the financial support from the Natural Science and Engineering Research Council of Canada and the MOE Project of Key Research Institute of Humanities and Social Sciences at Universities (11JJD790004), as well as the U.K. insured lives mortality data from the Faculty and Institute of Actuaries. The authors would also like to thank Professor Andrew Cairns and other participants at the Sixth International Longevity Risk and Capital Markets Solutions Conference for their stimulating discussions.
Author information
Authors and Affiliations
Appendices
Appendix A
A proof of equations (3) and (4)
When exponential utility functions are assumed, the initial wealths have no effect on the tâtonnement equilibrium. So, we may set W T A=W T B=0 without loss of generality. In this case, the terminal wealths for Agents A and B can be expressed as W T A=−v L +θ A(v H −Pe rT) and W T B=θ B(v H −Pe rT), respectively.
Assuming that (v H , v L )′ follows the bivariate normal distribution specified in the sub-section entitled ‘Solving by an approximate analytic formula’, the terminal wealths W T A and W T B are normally distributed. Specifically,


where N(μ, σ 2) denotes a normal distribution with mean μ and variance σ 2.
For Agent A, the value of θ A given a price P is

In the above, the third step follows from the moment generating function for a normal distribution. Similarly, for Agent B, the value of θ A given a price P is

Appendix B
The two-population mortality model
The two-population mortality model proposed by Cairns et al. (2011) is built from two classical age-period-cohort models, one for each population:

where m x,t (i) is the central death rate at age x and in year t for population i, and n a is a constant which equals the total number of ages in the sample age range. In the model, the base age-pattern of mortality for population i is characterised by an age-specific parameter β x (i). For each population, the variation of mortality over time is captured by two indexes: a period effect index κ t (i) and a cohort effect index γ t−x (i). Note that t−x is the year of birth for an individual who is aged x in year t. Projections of future mortality can be made by extrapolating the indexes.
In both models we are estimating, population 1 refers to U.K. male population. This larger population is assumed to have a dominant effect on the mortality improvements for populations 1 and 2. Following Cairns et al.,4 we model κ t (1) using a random walk with drift,

where μ κ is a constant, and model γ t−x (1) using a second order autoregressive model with a deterministic trend,

where c=t−x, and μ γ , φ γ,1, φ γ,2, and δ γ are constants.
The indexes for population 2 may deviate from those for population 1. However, to ensure that the resulting forecasts are biologically reasonable, there is a need to avoid a divergence of mortality between the two populations over time. The conditions for non-divergence are:
-
1
Δ κ (t)=κ t (1)−κ t (2) is mean-reverting;
-
2
Δ γ (c)=γ c (1)−γ c (2) is mean-reverting.
Following Cairns et al.,4 we model Δ κ (t) and Δ γ (c) with an AR(1) process and an AR(2) process, respectively. That is,

and

where  ,
,  ,
,  ,
,  , and
, and  are constants. These two time-series processes are stationary, ensuring that both Δ
κ
(t) and Δ
γ
(c) will revert to their long-term means.
are constants. These two time-series processes are stationary, ensuring that both Δ
κ
(t) and Δ
γ
(c) will revert to their long-term means.
Other than mean-reversions, as indicated in the empirical results of Coughlan et al.,5 we might also expect to see some correlations between the year-on-year changes in both the period and cohort effects. For instance, a flu epidemic may have similar effects on populations 1 and 2. To incorporate these potential correlations, we treat both  and
and  as zero-mean bivariate normal random vectors, with variance-covariance matrices V
κ
and V
γ
, respectively.
as zero-mean bivariate normal random vectors, with variance-covariance matrices V
κ
and V
γ
, respectively.
The model is fitted in two stages. In the first stage, we estimate the parameters β x (i), κ t (i) and γ t−x (i) for i=1, 2, t=1947, …, 2005 and x=60, …, 89 by the method of maximum likelihood. The maximisation can be accomplished by an iterative Newton-Raphson method, in which parameters are updated one at a time. We acknowledge that the age-period-cohort model has an identifiability problem. To stipulate parameter uniqueness, three constraints are needed for each population. The constraints used here are the same as those used by Cairns et al. 18 (p. 8). They are applied at the end of each iteration of the Newton-Raphson algorithm.
In the second stage, we estimate the time-series processes for κ t (1), γ t−x (1), Δ κ (t) and Δ γ (c). We first fit the processes as if κ t (1) is independent of Δ κ (t) and γ (1)(c) is independent of Δ γ (c). This would give estimates of all parameters in the time-series processes, except the variance-covariance matrices V κ and V γ . We then estimate V κ with the sample variance-covariance matrix for the residuals in fitting κ t and Δ κ (t). Similarly, we estimate V γ with the sample variance-covariance matrix for the residuals in fitting γ c and Δ γ (c).
Appendix C
A procedure for simulating mortality paths
A naïve way to simulate mortality paths for the three populations is to first simulate from the mortality model for U.K. and Scottish males, and then simulate from the mortality model for U.K. and CMI males. However, this method would produce two different collections of sample paths for U.K. males. The inconsistency would create two (slightly) different supply (or demand) curves for a security, even though all pricing parameters remain unchanged.
To ensure a consistent collection of mortality paths is produced for U.K. males, we use the following procedure to conduct the necessary simulations:
-
1
generate 10,000 sample paths for Z κ (t) on the basis of its marginal distribution, N(0, V κ (1, 1));
-
2
generate 10,000 sample paths for Z γ (c) on the basis of its marginal distribution, N(0, V γ (1, 1));
-
3
based on the simulated values of Z κ (t) and Z γ (c) in Steps 1 and 2, obtain 10,000 sample mortality paths for U.K. males;
-
4
for each value of Z κ (t) in Step 1, find the distribution of
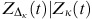 for Scottish males, and simulate a value of
for Scottish males, and simulate a value of  from the conditional distribution;
from the conditional distribution; -
5
for each value of Z γ (c) in Step 2, find the distribution of
 for Scottish males, and simulate a value of
for Scottish males, and simulate a value of  from the conditional distribution;
from the conditional distribution; -
6
based on the 10,000 simulated paths of Z κ (t),
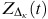 , Z
γ
(c), and
, Z
γ
(c), and 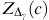 , obtain 10,000 sample mortality paths for Scottish males;
, obtain 10,000 sample mortality paths for Scottish males; -
7
repeat Steps 4 to 6 for CMI males to obtain 10,000 sample paths for CMI males.
It can be shown easily that when  follows a bivariate normal distribution with a zero mean vector and a variance-covariance matrix of V
κ
, we have
follows a bivariate normal distribution with a zero mean vector and a variance-covariance matrix of V
κ
, we have

where det(v) denotes the determinant of a matrix v. Similarly, we have

Rights and permissions
About this article
Cite this article
Zhou, R., Li, JH. & Tan, K. Economic Pricing of Mortality-linked Securities in the Presence of Population Basis Risk. Geneva Pap Risk Insur Issues Pract 36, 544–566 (2011). https://doi.org/10.1057/gpp.2011.21
Published:
Issue Date:
DOI: https://doi.org/10.1057/gpp.2011.21










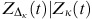 for Scottish males, and simulate a value of
for Scottish males, and simulate a value of  from the conditional distribution;
from the conditional distribution; for Scottish males, and simulate a value of
for Scottish males, and simulate a value of  from the conditional distribution;
from the conditional distribution;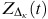 , Z
γ
(c), and
, Z
γ
(c), and 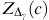 , obtain 10,000 sample mortality paths for Scottish males;
, obtain 10,000 sample mortality paths for Scottish males;