A DIRECT METHOD TO DETERMINE THE PARALLEL MEAN FREE PATH OF SOLAR ENERGETIC PARTICLES WITH ADIABATIC FOCUSING

The propagation of cosmic rays in interplanetary space is one of the fundamental problems of astrophysics and heliophysics. It is the basic knowledge needed to study space weather. To study the modulation of cosmic rays and the transport of solar energetic particles (SEPs), a focused transport equation was obtained (Parker 1963, 1965; Roelof 1969; Ng & Reames 1994). It is very difficult to solve the focused transport equation analytically; consequently, numerical methods are usually adopted (e.g., Ng & Wong 1979; Schlüter 1985; Ruffolo 1991; Zhang et al. 2009; Dröge & Kartavykh 2009; He et al. 2011; Qin et al. 2011). To study the transport of charged energetic particles, we must understand their diffusion mechanism. The diffusion of cosmic rays in the direction parallel to a mean magnetic field plays an important role in the transport processes (Jokipii 1966). Therefore, the parallel transport of charged energetic particles has been extensively studied (e.g., Dröge 2000; Teufel & Schlickeiser 2002, 2003; Shalchi & Schlickeiser 2005; Shalchi et al. 2006; He & Qin 2011; He et al. 2011). The parallel mean free path λ_{∥, 0} without adiabatic focusing is related to the pitch-angle diffusion coefficient D_μμ (Jokipii 1966; Hasselmann & Wibberenz 1968; Earl 1974) as

$$\begin{equation} \lambda _{\parallel,0}=\frac{3v}{8}\int _{-1}^{+1}\frac{(1-\mu ^{2})^{2}}{D_{\mu \mu }}d\mu, \end{equation} \tag{ 1 }$$

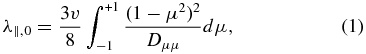
and the radial mean free path can be defined as

$$\begin{equation} \lambda _{r,0}=\lambda _{\parallel,0}\cos ^{2}\psi, \end{equation} \tag{ 2 }$$

where ψ is the angle between the local magnetic field direction and the radial direction. In the equation above, cos ²ψ can be written as (Ng & Gleeson 1971)

$$\begin{equation} \cos ^{2}\psi =V^2/(V^2+\Omega ^2r^2\sin ^2\theta), \end{equation} \tag{ 3 }$$

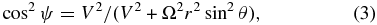
where V is the solar wind speed, Ω is the angular rotation velocity of the Sun, and r and θ are the coordinates of the heliocentric spherical polar coordinate system (r, θ, ϕ), i.e., r is the radial distance from the center of the Sun, and θ is the colatitude, which is measured from the rotation axis of the Sun.

The parallel mean free path of SEPs, which is determined by the physical properties of SEPs as well as those of solar wind, is a very important parameter in space physics to study the transport of charged energetic particles in the heliosphere, especially for space weather prediction. To accurately obtain the parallel mean free path of SEPs for a solar event, one usually has to fit time profiles of both flux and anisotropy between spacecraft observations and numerical simulations of SEPs' transport processes through interplanetary space (e.g., Beeck et al. 1987; Kallenrode 1993; Dröge & Kartavykh 2009). This method can be called a simulation method. However, a reasonably good fitting usually requires a number of simulations that demand a large amount of calculation resources, so they are time-consuming even with modern supercomputers. Alternatively, He & Qin (2011) provided an analytical method to quickly estimate the parallel mean free path of SEPs for impulsive SEP events by fitting the anisotropy time profiles between spacecraft observations with the approximate analytical formula

$$\begin{equation} A(t)\approx 3\mu _{0}e^{-vt/3\lambda _{\parallel }}. \end{equation} \tag{ 4 }$$

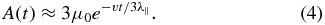
Usually, for example, in space weather practice, we usually need to quickly estimate the parallel mean free path of SEPs to predict their transport process and space-time evolution before they arrive at the spacecraft or enter Earth's orbit and damage the electronic components on satellites and risk the health of the astronauts working in space, and therefore it is necessary to find a direct way to determine the parallel mean free path of SEPs.

In the solar system, the mean magnetic field is not constant, and this spatially varying mean magnetic field causes the adiabatic focusing effect of charged particles (Roelof 1969; Earl 1976; Bieber & Burger 1990; Ruffolo 1995; Bieber et al. 2002; Schlickeiser & Shalchi 2008). This effect will be taken into account when we investigate the parallel diffusion coefficient of SEPs from the focused transport equation, especially in the inner heliosphere scenario, since that is where the nonuniformity of the mean magnetic field structure may be important. Recently, Shalchi (2011) presented an analytical description for the parallel diffusion coefficient with adiabatic focusing. It is possible to develop a direct analytical formula of the parallel mean free path of SEPs with adiabatic focusing as a function of parameters concerning the physical properties of SEPs and solar wind.

In this paper, we provide a direct analytical method to determine the parallel mean free path of SEPs with adiabatic focusing. Based on this direct method, we present the inherent relations between the parallel mean free path and various parameters concerning the physical properties of SEPs and solar wind. Comparisons of parallel mean free paths with and without adiabatic focusing are also presented. We will first provide an analytical description, as a function of spatial position and solar wind speed, of adiabatic focusing length for spatial variations of the mean Parker interplanetary magnetic field. In Section 3, we present a direct analytical method for obtaining the parallel mean free path of SEPs with adiabatic focusing. Based on the direct method, Section 4 discusses the inherent relations between the parallel mean free path and various parameters concerning the physical properties of SEPs and solar wind. A summary of our results will be provided in Section 5.

In the heliosphere, the mean magnetic field is not constant; rather, it is spatially varying. Therefore, the adiabatic focusing effect for SEPs is generated. To investigate the parallel diffusion of cosmic rays with adiabatic focusing, Shalchi (2011) used the Fokker–Planck equation,

$$\begin{eqnarray} \frac{\partial f}{\partial t}+\mu v\frac{\partial f}{\partial z}+\frac{v}{2L}(1-\mu ^2)\frac{\partial f}{\partial \mu }&=&\frac{\partial }{\partial \mu }\left(D_{\mu \mu }\frac{\partial f}{\partial \mu }\right)\nonumber\\ &&+D_{\perp }\left(\frac{\partial ^{2} f}{\partial x^{2}}+\frac{\partial ^{2} f}{\partial y^{2}}\right).\quad \end{eqnarray} \tag{ 5 }$$

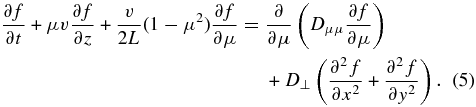
In Equation (5), z is the coordinate along the mean magnetic field line, μ is the particle pitch-angle cosine, t is the time, v is the particle velocity, D_μμ is the pitch-angle diffusion coefficient, D_⊥ is the perpendicular diffusion coefficient, and L is the adiabatic focusing length and is defined by

$$\begin{equation} \frac{1}{L(z)}=-\frac{1}{B(z)}\frac{\partial B}{\partial z}, \end{equation} \tag{ 6 }$$

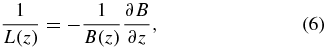
where B is the average magnetic field with direction z.

In this work, we consider the Archimedean spiral magnetic field model originally suggested by Parker (1958). Some properties of the Parker magnetic field model have been verified by observations (e.g., Smith et al. 1986; Forsyth et al. 1996). The Parker spiral magnetic field model can be written as

$$\begin{equation} B_{r}=\frac{B_{0}}{r^{2}}, \end{equation} \tag{ 7 }$$

$$\begin{equation} B_{\theta }=0, \end{equation} \tag{ 8 }$$

and

$$\begin{equation} B_{\phi }=-\frac{B_{0}\Omega \sin \theta }{rV}. \end{equation} \tag{ 9 }$$

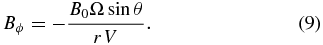
Here V is the solar wind speed, Ω is the angular rotation velocity of the Sun, and r and θ are the coordinates of the heliocentric spherical polar coordinate system (r, θ, ϕ). The magnetic field magnitude can easily be given as

$$\begin{equation} B(z)=\frac{B_{0}}{r^{2}}\sqrt{\frac{V^{2}+\Omega ^{2}r^{2}\sin ^{2}\theta }{V^{2}}}. \end{equation} \tag{ 10 }$$

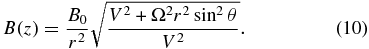
The spatial variation of the magnetic field magnitude along direction z could be derived as

$$\begin{eqnarray} \tsty\frac{\partial B}{\partial z}&=&\frac{\frac{\partial B}{\partial r}}{\frac{\partial z}{\partial r}} \nonumber \\ &=&\frac{\frac{-B_{0}(2V^{2}+\Omega ^2r^2\sin ^2\theta)}{Vr^{3}\sqrt{V^{2}+\Omega ^2r^2\sin ^2\theta }}}{\frac{V}{2}\left(\frac{V^{2}+2\Omega ^2r^2\sin ^2\theta }{V^{2}\sqrt{V^{2}+\Omega ^2r^2\sin ^2\theta }}+\frac{\Omega r\sin \theta +\sqrt{V^{2}+\Omega ^2r^2\sin ^2\theta }}{V^{2}+\Omega ^2r^2\sin ^2\theta +\Omega r\sin \theta \sqrt{V^{2}+\Omega ^2r^2\sin ^2\theta }}\right)} \nonumber \\ &=&\tsty\frac{-B_{0}(2V^{2}+\Omega ^2r^2\sin ^2\theta)}{r^{3}(V^{2}+\Omega ^2r^2\sin ^2\theta)}. \end{eqnarray} \tag{ 11 }$$

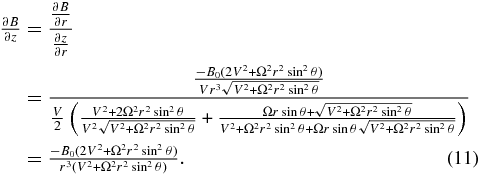
By combining Equation (11) with Equations (6) and (10), we can derive the analytical description of adiabatic focusing length as

$$\begin{equation} L(z)=\frac{r(V^{2}+\Omega ^2r^2\sin ^2\theta)^{3/2}}{V(2V^{2}+\Omega ^2r^2\sin ^2\theta)}, \end{equation} \tag{ 12 }$$

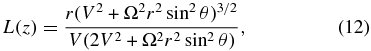
which is a function of the spatial position and the solar wind speed. By using Equation (12), we can calculate the adiabatic focusing length of the heliospheric magnetic field at any location and with any solar wind speed throughout the interplanetary space.

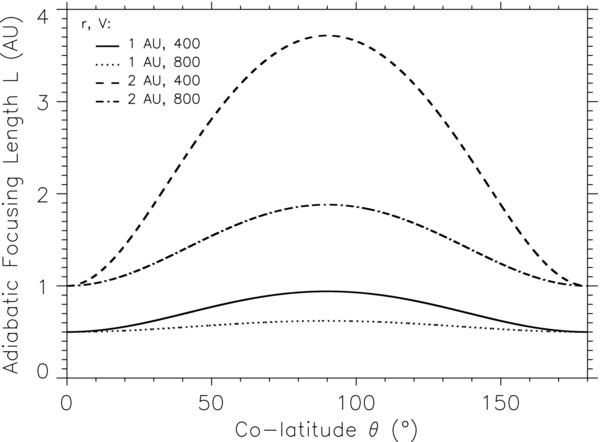
Figure 1 shows the adiabatic focusing length's radial distance (r) dependence with different colatitudes θ, which are measured from the rotation axis of the Sun and solar wind speeds V in km s⁻¹. For every case in Figure 1, we can see that the adiabatic focusing length monotonously increases with radial distance. In addition, in the inner heliosphere, i.e., when r ≲ 1 AU, the adiabatic focusing length is very short. This indicates that the adiabatic focusing effect is very important near the Sun. In the outer heliosphere, e.g., when r = 10 AU, the adiabatic focusing length is very long, which means that the adiabatic focusing effect is not significant far away from the Sun.

Zoom In Zoom Out Reset image size

Figure 2 displays the dependence of adiabatic focusing length on colatitude θ with different radial distances r and solar wind speeds V in km s⁻¹. In Figure 2, we can see that the adiabatic focusing length increases with the colatitude until θ = 90° where it peaks, and then it decreases with the colatitude θ. Therefore, this means that the adiabatic focusing effect near the solar equatorial plane is relatively weak for every case with different conditions of radial distance r and solar wind speed V.

Zoom In Zoom Out Reset image size

Figure 3 depicts the adiabatic focusing length's solar wind speed (V) dependence with different radial distances r and colatitudes θ. As we can see in Figure 3, the adiabatic focusing length monotonously decreases for every case with the solar wind speed V. Therefore, the significance of the adiabatic focusing effect increases with increasing solar wind speed.

Zoom In Zoom Out Reset image size

Shalchi (2011) used an isotropic form of the pitch-angle diffusion coefficient as (Shalchi et al. 2009)

$$\begin{equation} D_{\mu \mu }=D_{{\rm iso}}(1-\mu ^{2}), \end{equation} \tag{ 13 }$$

where D_iso can be written as

$$\begin{equation} D_{{\rm iso}}=\frac{\pi }{q}C(q)\frac{v}{l_{{\rm slab}}}R^{q-2}\left(\frac{\delta B}{B}\right)^{q+1}. \end{equation} \tag{ 14 }$$

In Equation (14), q is the inertial range spectral index, C(q) is the normalization function, v is the particle velocity, l_slab is the slab bend-over scale, R is the dimensionless rigidity of particles, δB is the strength of the turbulent magnetic field, and B is the strength of the mean magnetic field. C(q) could be written as

$$\begin{equation} C(q)=\frac{\Gamma \left(\frac{q}{2}\right)}{2\sqrt{\pi }\Gamma \left(\frac{q}{2}-\frac{1}{2}\right)}, \end{equation} \tag{ 15 }$$

and R may be expressed by the unperturbed Larmor radius R_L of the particle and the slab bend-over scale as

$$\begin{equation} R=\frac{R_{L}}{l_{{\rm slab}}}. \end{equation} \tag{ 16 }$$

For Equation (5), with the isotropic form of the pitch-angle diffusion coefficient (13), Shalchi (2011) derived an exact formula for the parallel mean free path with the adiabatic focusing effect as

$$\begin{equation} \lambda _{\parallel }=\frac{3L^{3}}{\lambda _{\parallel,0}^{2}}\left[\frac{\lambda _{\parallel,0}}{L}-\tanh \left(\frac{\lambda _{\parallel,0}}{L}\right)\right]. \end{equation} \tag{ 17 }$$

In Equation (17), a constant adiabatic focusing length L was assumed. In reality, however, the spatial dependence of the adiabatic focusing length should be specified as Equation (12). By combining Equation (1) with Equation (13), we can easily derive

$$\begin{equation} \lambda _{\parallel,0}=\frac{v}{2D_{{\rm iso}}}. \end{equation} \tag{ 18 }$$

In the heliosphere, by combining Equation (17) with Equations (12) and (18), we can obtain the parallel mean free path of SEPs with adiabatic focusing for SEP events. This method can be called a direct method. When using this method, we only need some observable parameters concerning the physical properties of SEPs and solar wind. Therefore, we can quickly determine the parallel mean free path of SEPs without adopting the time-consuming numerical simulations of the particle transport processes.

For an arbitrary pitch-angle diffusion coefficient and weak focusing, Shalchi (2011) provided an approximate formula of the parallel mean free path of SEPs with adiabatic focusing, which has second-order precision in the focusing strength

$$\begin{equation} \lambda _{\parallel }=\lambda _{\parallel,0}+\frac{l^{2}\lambda _{\parallel,0}}{L^{2}}+\frac{6}{L^{2}}\int _{-1}^{+1}\mu \left[\frac{1}{3}F^{3}(\mu)-lF^{2}(\mu)\right]d\mu, \end{equation} \tag{ 19 }$$

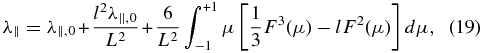
where F(μ) is

$$\begin{equation} F(\mu)=\frac{v}{4}\int _{-1}^{\mu }\frac{1-\nu ^{2}}{D_{\nu \nu }}d\nu \end{equation} \tag{ 20 }$$

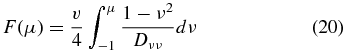
and l is

$$\begin{equation} l=F(\mu =1)=\frac{v}{4}\int _{-1}^{+1}\frac{1-\nu ^{2}}{D_{\nu \nu }}d\nu. \end{equation} \tag{ 21 }$$

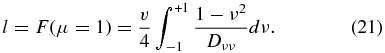
For a specific form of D_μμ, by combining Equation (19) with Equations (1), (12), (20), and (21), we can approximately calculate the parallel mean free path of SEPs with weak adiabatic focusing for an arbitrary pitch-angle diffusion coefficient. As an example, Shalchi (2011) considered the quasilinear (QLT; Jokipii 1966) form of the pitch-angle diffusion coefficient as

$$\begin{equation} D_{\mu \mu }=D_{{\rm QLT}}(1-\mu ^{2})|\mu |^{q-1} \end{equation} \tag{ 22 }$$

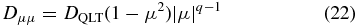
with

$$\begin{equation} D_{{\rm QLT}}=\pi C(q)\frac{v}{l_{{\rm slab}}}R^{q-2}\left(\frac{\delta B}{B}\right)^{2}, \end{equation} \tag{ 23 }$$

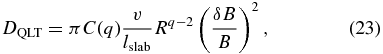
where the parameters used are explained in the text after Equation (14). For Equation (5), with the QLT form of the pitch-angle diffusion coefficient (22), Shalchi (2011) deduced a formula for the parallel mean free path with adiabatic focusing as

$$\begin{equation} \lambda _{\parallel }=\lambda _{\parallel,0}-\frac{2(5-2q)(4-q)^{2}\lambda _{\parallel,0}^{3}}{27(8-3q)L^{2}}. \end{equation} \tag{ 24 }$$

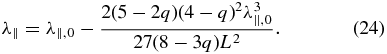
By combining Equation (1) with Equation (22), we can derive

$$\begin{equation} \lambda _{\parallel,0}=\frac{3v}{2D_{{\rm QLT}}(2-q)(4-q)}. \end{equation} \tag{ 25 }$$

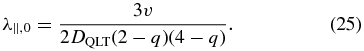
By combining Equation (24) with Equations (12) and (25), we can approximately estimate the parallel mean free path of SEPs with weak adiabatic focusing for the QLT form of the pitch-angle diffusion coefficient.

In the following section, some applications of the direct method will be presented. We will visualize the results of the parallel mean free path with adiabatic focusing for both isotropic and QLT forms of the pitch-angle diffusion coefficient. For comparison, we will also visualize the parallel mean free path without adiabatic focusing for each case.

In the following figures, the solid and dotted lines indicate the parallel mean free paths of SEPs with and without adiabatic focusing, respectively, for the isotropic form of the pitch-angle diffusion coefficient. The dashed and dash-dotted curves indicate the parallel mean free paths of SEPs with and without adiabatic focusing, respectively, for the QLT form of the pitch-angle diffusion coefficient. In addition, we typically use the inertial range spectral index q = 5/3 that corresponds to the value suggested by Kolmogorov (1941) in pitch-angle diffusion coefficients. In this work, we present the results of the parallel mean free path of protons.

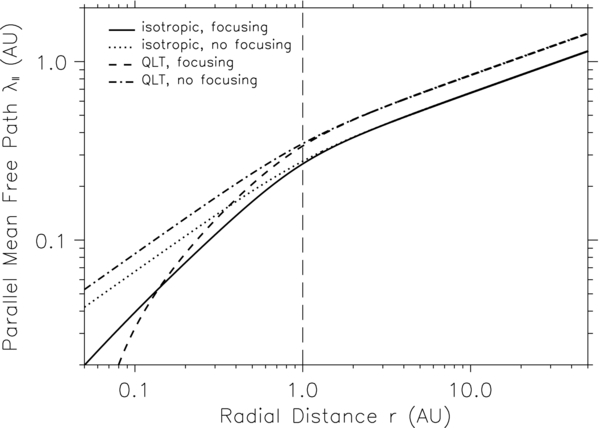
Figure 4 shows the parallel mean free path of SEPs as a function of the radial distance from the center of the Sun in the heliosphere. We typically set the colatitude θ = 90°, the solar wind speed V = 400 km s⁻¹, the turbulence strength δB/B = 0.4, and the slab bend-over scale l_slab = 0.03 AU for 50 MeV protons. In Figure 4, we can see that the parallel mean free path for each case increases with increasing radial distance through the entire range from 0.05 to 50 AU. The difference between parallel mean free paths with and without adiabatic focusing is significant for both isotropic and QLT forms of the pitch-angle diffusion coefficient in the inner heliosphere, i.e., when radial distance r ≲ 1 AU. The parallel mean free path without adiabatic focusing is larger than that with adiabatic focusing for both isotropic and QLT forms of the pitch-angle diffusion coefficient. However, this difference decreases with increasing radial distance. When r  ≳  1 AU, the difference is negligible. In addition, with the same physical conditions, the parallel mean free path obtained with the QLT form of the pitch-angle diffusion coefficient is larger than that obtained with the isotropic form.

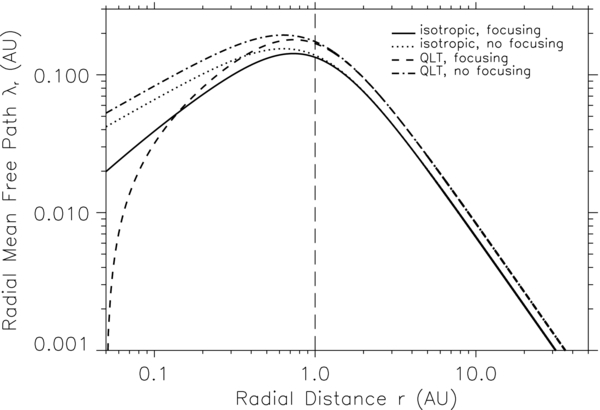
Zoom In Zoom Out Reset image size

The radial dependence of the radial mean free path is a very interesting topic in the community, and it was usually modeled by a power law λ_r(r) ∼ r^b in previous investigations of the transport of SEPs through interplanetary space. Figure 5 displays the radial mean free path of SEPs as a function of the radial distance from the center of the Sun. The physical parameters we set are the same as Figure 4. When radial distance r ≲ 1 AU, we can see that the scenario in Figure 5 is similar to that in Figure 4. However, when r ≳ 1 AU, the radial mean free path either with or without adiabatic focusing decreases with increasing radial distance for both isotropic and QLT forms of the pitch-angle diffusion coefficient. For the QLT form of the pitch-angle diffusion coefficient, the radial mean free path with adiabatic focusing is significantly reduced near the Sun, i.e., when the radial distance r ∼ 0.05 AU in the figure. Generally speaking, the results of the radial dependence of the parallel and radial mean free paths presented in Figures 4 and 5, respectively, are consistent with the results from observations in previous studies (e.g., Zwickl & Webber 1977; Hamilton 1977; Goeman & Webber 1983; Beeck et al. 1987).

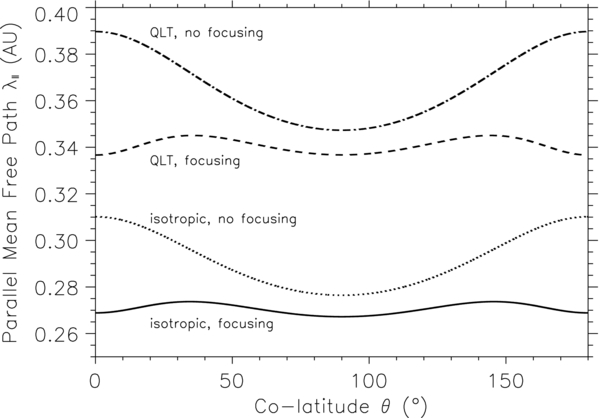
Zoom In Zoom Out Reset image size

Figure 6 depicts the parallel mean free path of SEPs as a function of the colatitude θ. We typically set the radial distance r = 1 AU, the solar wind speed V = 400 km s⁻¹, the turbulence strength δB/B = 0.4, and the slab bend-over scale l_slab = 0.03 AU for 50 MeV protons. For both isotropic and QLT forms of the pitch-angle diffusion coefficient, we can see that the parallel mean free path without adiabatic focusing is larger than that with adiabatic focusing across the entire range from 0 to 180°. The parallel mean free path obtained with the QLT form of the pitch-angle diffusion coefficient is larger than that obtained with the isotropic form. Additionally, for both isotropic and QLT forms, the parallel mean free path without adiabatic focusing decreases with the colatitude until θ = 90° where it minimizes and then increases with the colatitude θ. However, the parallel mean free path with adiabatic focusing does not vary significantly with the colatitude θ for both isotropic and QLT forms of the pitch-angle diffusion coefficient.

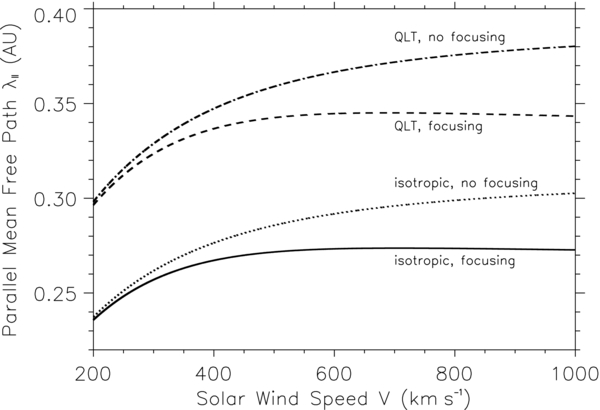
Zoom In Zoom Out Reset image size

Figure 7 presents the parallel mean free path of SEPs as a function of the solar wind speed. We typically set the radial distance r = 1 AU, the colatitude θ = 90°, the turbulence strength δB/B = 0.4, and the slab bend-over scale l_slab = 0.03 AU for 50 MeV protons. For both isotropic and QLT forms of the pitch-angle diffusion coefficient, we can see that the parallel mean free path without adiabatic focusing is larger than that with adiabatic focusing across the entire range from 200 to 1000 km s⁻¹. With increasing solar wind speed, the difference increases between parallel mean free paths with and without adiabatic focusing. This indicates that the adiabatic focusing effect is more considerable when SEPs transport in the solar wind with higher speed. In addition, the parallel mean free path obtained with the QLT form of the pitch-angle diffusion coefficient is larger than that obtained with the isotropic form.

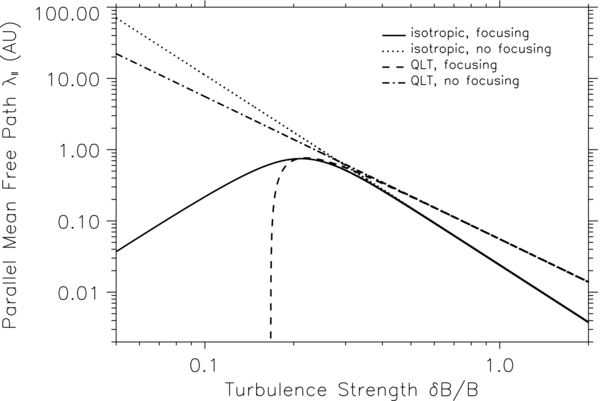
Zoom In Zoom Out Reset image size

Figure 8 shows the parallel mean free path of SEPs as a function of the magnetic field turbulence strength δB/B. We typically set the radial distance r = 1 AU, the colatitude θ = 90°, the solar wind speed V = 400 km s⁻¹, and the slab bend-over scale l_slab = 0.03 AU for 50 MeV protons. In Figure 8, when δB/B ≲ 0.3 for both isotropic and QLT forms of the pitch-angle diffusion coefficient, we can see that the parallel mean free path without adiabatic focusing is much larger than that with adiabatic focusing; in addition, the parallel mean free path obtained with the isotropic form of the pitch-angle diffusion coefficient is larger than that obtained with the QLT form. However, when δB/B ≳ 0.3, there is basically no difference between parallel mean free paths with and without adiabatic focusing, and the parallel mean free path obtained with the QLT form of the pitch-angle diffusion coefficient is larger than that obtained with the isotropic form. Across the entire range of turbulence strength δB/B from 0.05 to 2, the parallel mean free path without adiabatic focusing monotonously decreases from tens of AUs with increasing turbulence strength, while the parallel mean free path with adiabatic focusing increases with the turbulence strength until δB/B ≈ 0.21, where it peaks at about 1 AU and then decreases with the turbulence strength δB/B.

Zoom In Zoom Out Reset image size

Figure 9 displays the parallel mean free path of SEPs as a function of the slab bend-over scale l_slab. We typically set the radial distance r = 1 AU, the colatitude θ = 90°, the solar wind speed V = 400 km s⁻¹, and the turbulence strength δB/B = 0.4 for 50 MeV protons. With the exception of the case with adiabatic focusing for the QLT form of the pitch-angle diffusion coefficient, we can see that the parallel mean free path for each case monotonously increases with increasing slab bend-over scale across the entire range from 0 to 0.5 AU. Additionally, the parallel mean free path without adiabatic focusing is larger than that with adiabatic focusing for both isotropic and QLT forms of the pitch-angle diffusion coefficient. Moreover, note that when the slab bend-over scale l_slab > 0.41 AU, the parallel mean free path with adiabatic focusing for the QLT form of the pitch-angle diffusion coefficient is negative. The reason for this problem may be that Equation (24) is used for weak focusing and only has second-order precision in the focusing strength.

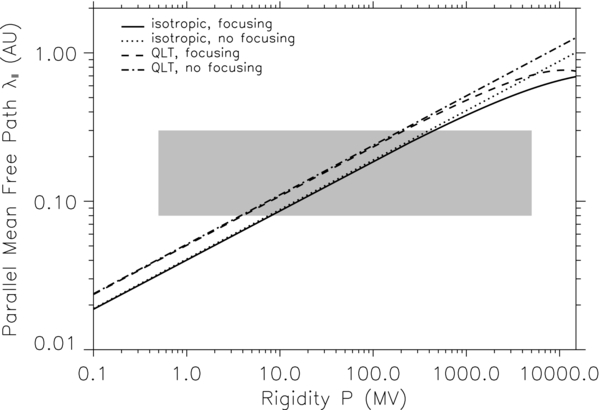
Zoom In Zoom Out Reset image size

The rigidity dependence of the parallel mean free path of SEPs is a very significant topic in the community, and it was investigated by a number of authors (e.g., Palmer 1982; Bieber et al. 1994; Giacalone 1998). Figure 10 depicts the parallel mean free path of SEPs as a function of particle rigidity. We typically set the radial distance r = 1 AU, the colatitude θ = 90°, the solar wind speed V = 400 km s⁻¹, the turbulence strength δB/B = 0.4, and the slab bend-over scale l_slab = 0.03 AU. The gray horizontal shading area in Figure 10 denotes the observational consensus for the parallel mean free path, which was first characterized by Palmer (1982). The Palmer consensus extends from 0.08 to 0.3 AU and covers a rigidity range of 0.5–5000 MV. As one can see, for both isotropic and QLT forms of the pitch-angle diffusion coefficient, the parallel mean free path either with or without adiabatic focusing monotonously increases with increasing particle rigidity across the entire range from 0.1 to 15, 000 MV, which agrees well with the results of Bieber et al. (1994). The parallel mean free path obtained with the QLT form of the pitch-angle diffusion coefficient is larger than that obtained with the isotropic form. For both isotropic and QLT forms of the pitch-angle diffusion coefficient, the difference between parallel mean free paths with and without adiabatic focusing increases with particle rigidity. Specifically, when particle rigidity P ≲ 200 MV, the difference between parallel mean free paths with and without adiabatic focusing is negligible; when particle rigidity P ≳ 200 MV, the difference increases gradually with particle rigidity. This indicates that for the SEPs with higher energy, the adiabatic focusing effect is more important in their transport processes through interplanetary space. Note that the parallel mean free paths presented in Figure 10 remain in or near the Palmer consensus band.

Zoom In Zoom Out Reset image size

The parallel mean free path of SEPs, which is determined by physical properties of SEPs as well as those of solar wind, is a very important physical parameter in space weather. To accurately estimate the parallel mean free path of SEPs for a solar event, one usually must use a so-called simulation method, i.e., fitting time profiles of both flux and anisotropy from spacecraft observations to simulations of the transport processes of SEPs. However, as we know, such fittings and simulations are time consuming, even with modern supercomputers. In space weather practice, we usually need to obtain a quick approximation of the parallel mean free path of SEPs. Therefore, it is quite necessary to provide an efficient method to quickly estimate the parallel mean free path of SEPs. He & Qin (2011) presented an analytical method by fitting the anisotropy time profiles between spacecraft observations and the approximate analytical formula as Equation (4) to quickly estimate the parallel mean free path of SEPs for impulsive SEP events. Basically, however, this method can determine the parallel mean free path of SEPs only when the anisotropy time profile has been observed by spacecraft, i.e., after the SEPs arrive at the spacecraft. This limitation would be an obstacle in space weather forecasting since we usually need to quickly estimate the parallel mean free path of SEPs after they have been produced from the surface of the Sun to predict their transport process and space-time evolution before they arrive at the spacecraft or enter Earth's orbit.

Based on the results of Shalchi (2011), we provide a so-called direct method in this paper to quickly determine the parallel mean free path of SEPs with adiabatic focusing. This method uses a direct analytical formula as a function of the physical parameters corresponding to realistic properties of SEPs and solar wind. Therefore, the method is reliable from a theoretical point of view and is computationally tractable with a simple mathematical form. So, in space weather practice, we could use the direct method to quickly estimate the parallel mean free path of SEPs with adiabatic focusing for both impulsive and gradual SEP events. Additionally, we apply the direct method in the present paper to investigate the inherent relations between the parallel mean free path of SEPs and the physical properties of SEPs as well as those of solar wind. Comparisons of the parallel mean free paths of SEPs with and without adiabatic focusing are also presented. The main conclusions of our results in this paper are as follows:

• 1.  
  By using realistic physical parameters concerning the properties of SEPs and solar wind as inputs other than fitting time profiles of flux or anisotropy, the direct method presented in this work can easily be applied to quickly determine the parallel mean free path of SEPs with adiabatic focusing for both impulsive and gradual SEP events.
• 2.  
  The rigidity dependence of the parallel mean free path of SEPs obtained with the direct method for typical physical parameters agrees well with the Palmer consensus band and the results of Bieber et al. (1994).
• 3.  
  In the inner heliosphere, i.e., when the radial distance r ≲ 1 AU, especially near the Sun, the adiabatic focusing effect plays a very important role in the transport processes of SEPs in interplanetary space. However, in the outer heliosphere, the significance of the adiabatic focusing effect is largely reduced.
• 4.  
  Generally, with the same physical conditions, the parallel mean free path obtained with the QLT form of the pitch-angle diffusion coefficient is larger than that obtained with the isotropic form of the pitch-angle diffusion coefficient.
• 5.  
  For the isotropic form of the pitch-angle diffusion coefficient, the parallel mean free path of SEPs is always a positive value; however, the parallel mean free path for the QLT form of the pitch-angle diffusion coefficient can be a negative value, which is difficult to understand since the parallel mean free path is defined as a positive parameter. The reason for this difference may be that Equation (17) is an exact formula for both weak and strong adiabatic focusing; however, Equations (19) and (24) are only used for weak focusing, and have up to second-order precision in the focusing strength (Shalchi 2011). Therefore, Equation (17) is preferred.
• 6.  
  As demonstrated in the present paper, the parallel or radial mean free path of SEPs depends on the physical properties of SEPs as well as those of interplanetary conditions such as solar wind and the turbulent magnetic field. To more accurately simulate the transport processes of SEPs throughout interplanetary space, it is suggested to adopt the spatially dependent parallel or radial mean free path with adiabatic focusing presented in this paper.

The direct method to determine the parallel mean free path of SEPs provided in the present paper is a reliable and useful tool in practice, especially for space weather forecasting. In the future, we will use this new direct method in space weather research to quickly determine the parallel mean free path of SEPs with adiabatic focusing and try to use it to investigate the transport processes of SEPs through interplanetary space for both impulsive and gradual SEP events.

We were supported in part by the National Important Basic Research Project under grant 2011CB811405, the National Natural Science Foundation of China under grant NNSFC 41131066, the China Postdoctoral Science Foundation under grant 2011M500381, and the Key Laboratory of Random Complex Structures and Data Science, CAS.