THE ENERGY DEPENDENCE OF GRB MINIMUM VARIABILITY TIMESCALES

, , and

Published 2015 September 28 • © 2015. The American Astronomical Society. All rights reserved.
, , Citation V. Zach Golkhou et al 2015 ApJ 811 93 DOI 10.1088/0004-637X/811/2/93

Download Article PDF

Article metrics

1929 Total downloads

Share this article

Author e-mails

vgolkhou@asu.edu

natbutler@asu.edu

olittlej@asu.edu

Author affiliations

1 School of Earth and Space Exploration, Arizona State University, Tempe, AZ 85287, USA; vgolkhou@asu.edu, natbutler@asu.edu, olittlej@asu.edu

2 Cosmology Initiative, Arizona State University, Tempe, AZ 85287, USA

Dates

  1. Received 2015 January 20
  2. Accepted 2015 June 2
  3. Published
Keywords

gamma-ray burst: general; gamma-rays: general; methods: statistical

Journal RSS
Create or edit your corridor alerts

What are corridors?opens in new tab

0004-637X/811/2/93

ABSTRACT

We constrain the minimum variability timescales for 938 gamma-ray bursts (GRBs) observed by the Fermi/Gamma-ray Burst Monitor instrument prior to 2012 July 11. The tightest constraints on progenitor radii derived from these timescales are obtained from light curves in the hardest energy channel. In the softer bands—or from measurements of the same GRBs in the hard X-rays from Swift—we show that variability timescales tend to be a factor of two to three longer. Applying a survival analysis to account for detections and upper limits, we find median minimum timescale in the rest frame for long-duration and short-duration GRBs of 45 and 10 ms, respectively. Less than 10% of GRBs show evidence for variability on timescales below 2 ms. These shortest timescales require Lorentz factors 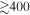$\gtrsim 400$ and imply typical emission radii 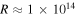$R\approx 1\times {10}^{14}$ cm for long-duration GRBs and 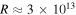$R\approx 3\times {10}^{13}$ cm for short-duration GRBs. We discuss implications for the GRB fireball model and investigate whether or not GRB minimum timescales evolve with cosmic time.

Export citation and abstract BibTeX RIS

Previous article in issue
Next article in issue

1. INTRODUCTION

Gamma-ray bursts (GRBs) are the most luminous explosions in the universe, originating at cosmological distances and releasing $\sim {10}^{51}$ erg over timescales of seconds to tens of seconds. The gargantuan energy release is accompanied by a very rapid and stochastic temporal variability in the gamma-ray emission. The Swift (Gehrels et al. 2004) and Fermi Space Telescopes (Meegan et al. 2009) have deepened immensely our understanding of these cosmological beacons (e.g., Gehrels & Razzaque 2013).

The pulses observed in prompt GRB light curves often have a Fast Rising Exponential Decay profile (Norris et al. 1996). The time profiles can have a broad morphological diversity in both the number and duration of these pulses. In the external shock model for GRBs, shells of material produced by the GRB impact material in the circumburst medium (e.g., Rees & Meszaros 1992). Unless the circumburst medium is highly clumped (Fenimore et al. 1999), this process tends to produce a smooth GRB light curve in contrast to the rapid temporal variability observed in many GRBs. Under the internal shock mechanism (Rees & Meszaros 1994), a variable central engine emits a relativistic outflow comprised of multiple shells with different Lorentz factors, Γ. As faster shells collide with slower shells, kinetic energy is converted to radiation, and multiple shell collisions can lead to a complex GRB light curve (e.g., Rees & Meszaros 1994).

Traditional duration measures such as ${T}_{90}$ (Kouveliotou et al. 1993), which describes the time during which the central 90% of prompt gamma-ray counts are received, only describe bulk emission properties of the burst. Such a duration does not capture information concerning individual collisions between shells. Instead, detailed temporal analyses that probe variability over a function of timescales are required.

A variety of time series analyses have previously been used to explore the rich properties of prompt GRB light curves. These include structure function (SF) analyses (Hook et al. 1994; Trevese et al. 1994; Cristiani et al. 1996; Aretxaga et al. 1997), autocorrelation function analyses (Link et al. 1993; Fenimore et al. 1995; in't Zand & Fenimore 1996; Borgonovo 2004; Chatterjee et al. 2012), and Fourier power spectral density analyses (Beloborodov et al. 2000; Chang 2001; Abdo et al. 2010; Guidorzi et al. 2012; Dichiara et al. 2013). Compared to power spectral analyses, the SF approach is less dependent on the time sampling (Paltani 1999). In Golkhou & Butler (2014, hereafter Paper I), we developed and applied a fast (i.e., linear) and robust SF estimator, based on non-decimated Haar wavelets, to measure the minimum variability timescale, ${\rm{\Delta }}{t}_{\mathrm{min}}$, of Swift GRBs. We used the first-order SF of light curves as measured by the Swift Burst Alert Telescope (BAT; Barthelmy et al. 2005) to infer the shortest timescale at which a GRB exhibit uncorrelated temporal variability.

One limitation of the work presented in Paper I is that we only consider the variability timescale using light curves measured over the narrow 15–350 keV energy band of Swift/BAT. A fixed and narrow energy band in the observer frame would probe different regions of the intrinsic GRB spectra because GRBs are known to occur over a wide range of redshifts (see, e.g., Salvaterra et al. 2009; Tanvir et al. 2009; Cucchiara et al. 2011; Jakobsson et al. 2012). Previous studies have shown that GRB pulses vary in duration as a function of energy, with harder energy channels having a lower observed duration (Fenimore et al. 1995; Norris et al. 1996). Working at higher energies—where pulses are narrower—also has the potential to provide tighter limits on variability timescales.

We wish to use the broad Fermi Gamma-ray Burst Monitor (GBM; Meegan et al. 2009) energy coverage to overcome this limitation and to effectively standardize a measure of the minimum variability timescale by studying the energy evolution and/or evaluating the minimum timescale in a fixed rest-frame bandpass. Broad energy coverage can potentially also allow us to disentangle the role the ejecta velocity plays in relating radius to minimum timescale and to understand how minimum timescales measured for different instruments should be compared (see, e.g., Sonbas et al. 2014). Also, it is important to note that the GBM provides very fine time resolution (2 μs) event mode data for the full GRB and not just the first 1–2 s as was the case for BATSE (e.g., Walker et al. 2000).

In the discussion below, we begin with a brief application and summary of the method outlined in detail in Paper I. We then investigate how ${\rm{\Delta }}{t}_{\mathrm{min}}$ depends on energy for a large sample of Fermi/GBM GRBs (Section 3.1). We compare ${\rm{\Delta }}{t}_{\mathrm{min}}$ estimates from Swift and Fermi for bursts detected in common to demonstrate stability and accuracy of error estimates (Section 3.2). We then use spectral hardness to standardize the ${\rm{\Delta }}{t}_{\mathrm{min}}$ estimate (Section 3.4) and conclude by deriving constraints on the sample Lorentz factors and emission radii (Section 3.5) and by investigating potential evolution of ${\rm{\Delta }}{t}_{\mathrm{min}}$ with cosmic time (Section 3.6).

2. DATA

We consider 949 GRBs published in the second Fermi/GBM GRB catalog (von Kienlin et al. 2014), spanning the first four years of the Fermi mission (between 2008 July 14 and 2012 July 11, inclusive). Event lists for 942 of these bursts were downloaded from the online Fermi/GBM burst catalog.3

We analyze the Fermi/GBM Time-Tagged Event data for each of the 12 sodium iodide scintillators. We only consider those detectors in which each GRB was brightest, as listed in column 2 of Table 7 in von Kienlin et al. (2014). Typically, this entails using event lists for three detectors for each GRB. Following MacLachlan et al. (2013), we extract 200 μs binned light curves in the full (8–1000 KeV) energy range. We also extract light curves in four energy channels of an equal logarithmic width (8–26, 26–89, 89–299, and 299–1000 keV). These channels are referred to as channels 1–4 below.

To remove background counts from the Fermi/GBM we employ a two-pass procedure. Using the estimates of ${T}_{90}$ from Table 7 of von Kienlin et al. (2014), we bin each light curve at a resolution of ${T}_{90}/100$ and fit a linear background model. The background is initially determined considering two regions of each light curve, both ${T}_{90}$ in length, occurring immediately before and after the identified period of burst emission. Using the background-subtracted light curve, we then estimated ${T}_{100}$ by accumulating a further 5% of the ${T}_{90}$ interval counts outward from both the beginning and end of ${T}_{90}$. The second pass at fitting a linear background is then conducted, masking out all bins included in the total ${T}_{100}$ region. This second background fit is then scaled to subtract the predicted background counts in the fine time resolution light curve. Our analysis—which identifies variations on timescales short compared to the overall burst durations—does not require the fitting of background models more complex than linear.

We analyze the background-subtracted burst counts in the full ${T}_{100}$ region following the procedure outlined in Paper I. One change is made to the algorithm to optimize for the detection of signal variations on short timescales: instead of re-binning the 200 μs light curve to a fixed signal-to-noise ratio (S/N) per bin, we weight the unbinned light curve by the denoised (following Kolaczyk 1997) signal. This zeros out portions of the light curve containing no signal and permits use of the full ${T}_{100}$ region without adversely affecting our ability to identify variations on much shorter timescales.

For 109 bursts in the second Fermi/GBM GRB catalog that also have Swift high-energy prompt coverage, the Swift/BAT data were obtained from the Swift Archive.4 Using calibration files from the 2008 December 17 BAT data release, we construct 100 μs light curves in the full 15–350 keV BAT energy range. We use the standard Swift software tools: bateconvert, batmaskwtevt, and batbinevt. Further details regarding the extraction of the Swift/BAT light curves can be found in Paper I.

3. DISCUSSION AND RESULTS

In Paper I, we demonstrate the power of a novel, wavelet-based method—the Haar-SF (denoted ${\sigma }_{X,{\rm{\Delta }}t}$)—to robustly extract the shortest variability timescale of GRBs detected by Swift/BAT. In this work, we implement our technique on GRBs detected by the Fermi/GBM instrument, which is sensitive to a much broader range of energies. We obtain constraints on the minimum variability timescales for 938 of 949 GRBs reported in the second Fermi/GBM GRB catalog (von Kienlin et al. 2014). Of these, we are able to confirm the presence of a linear rise phase (see Section 3.1) in the Haar-SF on short timescales for 528 GRBs. We quote upper limit values for the remainder. Most (421) of the bursts in this sub-sample are long-duration (${T}_{90}\gt 3$ s) GRBs. In this sub-sample, 24 GRBs have a measured redshift, z. The temporal specifications of all 938 GRBs discussed here are determined using fully automatic software and are presented in the extended table provided as supplementary material in this paper.

3.1. Studying the Energy-dependence of Δtmin

It has been recognized for decades (e.g., Fenimore et al. 1995; Norris et al. 1996) that a defining feature of GRB emission is a narrowing of pulse profiles observed in increasingly higher-energy bands. As a result, durations measured by different instruments can be different (e.g., Virgili et al. 2012). Durations also appear to depend on redshift, perhaps as a result of the dependence on bandpass: recently, Zhang et al. (2013) have found evidence that ${T}_{90}$ duration—when z is known and used to evaluate the GRB duration in a fixed rest-frame energy band—may correlate linearly with redshift as is expected from cosmological time dilation. This result is quite sensitive to the particular choice of binning in the analysis (see Littlejohns & Butler 2014). Here, we seek to understand whether or not our measure of the shortest duration in GRBs is also highly dependent upon the observed energy band, and on the instrument detecting the GRB, in particular.

The prompt GBM gamma-ray light curve for GRB 110721A, split into four energy bands, and our derived ${\sigma }_{X,{\rm{\Delta }}t}$ curve for each channel are shown in Figure 1. There is a clear evolution in ${\rm{\Delta }}{t}_{\mathrm{min}}$ with bandpass, decreasing from the softest to the hardest energy band. To guide the eye, several lines of constant ${\sigma }_{X,{\rm{\Delta }}t}\propto {\rm{\Delta }}t$ are also plotted. The expected Poisson level (i.e., measurement error) has been subtracted away, leaving only the flux variation expected for each channel.

Figure 1.

Figure 1. Top panel: Fermi/GBM light curves of the GRB 110721A split into four different energy bands. Bottom panel: the Haar wavelet scaleogram ${\sigma }_{X,{\rm{\Delta }}t}$, rescaled for plotting purposes, corresponding to each channel vs. timescale ${\rm{\Delta }}t$ for GRB 110721A. We derive minimum timescales (marked with green circles)—0.56 ± 0.09, 0.28 ± 0.05, 0.24 ± 0.04, and 0.22 ± 0.04 s for channels 1, 2, 3, and 4, respectively—which increase in lower-energy bands. In the top panel, the inset displays the pulse rise with finer time binning, with dashed lines dropped onto the x-axis to demark the derived ${\rm{\Delta }}{t}_{\mathrm{min}}$ values for each channel.

Download figure:

Standard image High-resolution image

Briefly, we review here how our ${\rm{\Delta }}{t}_{\mathrm{min}}$ is identified. A general feature observed in our GRB scaleograms, provided there is sufficient S/N, is a linear rise phase relative to the Poisson noise. Poisson noise sets a floor on the shortest measurable timescale (denoted ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$, with ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}\approx 0.1$ s for channels 2 and 3 in Figure 1, bottom). Unlike previous studies by other authors (Walker et al. 2000; Bhat 2013; MacLachlan et al. 2013), we do not implicate the shortest observable timescale as ${\rm{\Delta }}{t}_{\mathrm{min}}$. Instead, we recognize that pulses can be temporally smooth on short timescales. The departure from this smoothness creates a break in the scaleogram, and this in turn defines our timescale ${\rm{\Delta }}{t}_{\mathrm{min}}$ for temporally unsmooth variability. Naturally, this timescale also corresponds to a length scale, which must be reconciled with GRB progenitor models (Section 3.5).

We now focus on the softest energy band of GRB 110721A, denoting the light curve as $X(t)$. Although there is excess signal present on timescales as short as ${\rm{\Delta }}t=0.4$ s (Figure 1—channel 1), these timescales correspond to a region of the plot where the first-order SF rises linearly in timescale, ${\sigma }_{X,{\rm{\Delta }}t}\equiv {\left\langle{| X(t+{\rm{\Delta }}t)-X(t)| }^{2}\right\rangle}_{t}^{1/2}\propto {\rm{\Delta }}t$. (Here, ${\left\langle\langle ,.,\rangle \right\rangle}_{t}$ denotes an average over time t.) We interpret this linear rise as an indication that the GRB exhibits temporally smooth variations on these timescales (i.e., $X(t+{\rm{\Delta }}t)\approx X(t)+X^{\prime} (t){\rm{\Delta }}t$), while changing to exhibit temporally unsmooth variations on longer timescales. The ${\sigma }_{X,{\rm{\Delta }}t}$ points deviate significantly from the ${\sigma }_{X,{\rm{\Delta }}t}\propto {\rm{\Delta }}t$ curve at ${\rm{\Delta }}{t}_{\mathrm{min}}=0.56\pm 0.09$ s. This is the timescale of interest, describing the minimum variability time for uncorrelated variations in the GRB. This timescale is associated with the initial rise of the GRB in this channel, as can be seen from the Figure 1 inset.

The value for ${\rm{\Delta }}{t}_{\mathrm{min}}$ is found by fitting a broken power law to the ${\sigma }_{X,{\rm{\Delta }}t}$ data points below the peak, assuming that ${\sigma }_{X,{\rm{\Delta }}t}$ initially rises linearly with ${\rm{\Delta }}t$ (see also Paper I) until flattening at ${\rm{\Delta }}{t}_{\mathrm{min}}$. Uncertainties quoted here and below for ${\rm{\Delta }}{t}_{\mathrm{min}}$ are determined by direct propagation of errors and correspond to 1σ confidence. If the lower limit on ${\rm{\Delta }}{t}_{\mathrm{min}}$ falls below the lowest measurable timescale (i.e., ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$), we report only the 1σ upper limit for ${\rm{\Delta }}{t}_{\mathrm{min}}$.

For this particular burst, ${\rm{\Delta }}{t}_{\mathrm{min}}$ evolves from the hardest energy band to the softest energy band as one might expect: the softest energy band of a burst has a longer minimum variability timescale compared to the hardest energy band of that burst. On timescales longer than ${\rm{\Delta }}{t}_{\mathrm{min}}$, ${\sigma }_{X,{\rm{\Delta }}t}$ is flatter than ${\sigma }_{X,{\rm{\Delta }}t}\propto {\rm{\Delta }}t$, indicating the presence of temporally variable structure on these timescales. On a timescale of about 6 s, ${\sigma }_{X,{\rm{\Delta }}t}$ begins turning over as we reach the timescales (tens of seconds) describing the overall emission envelope. We are not concerned here with those longer timescale structures, although we do note that ${\sigma }_{X,{\rm{\Delta }}t}$ provides a rich, aggregate description of this temporal activity.

In order to characterize and measure the average ${\rm{\Delta }}{t}_{\mathrm{min}}$ for the Fermi sample as a function of spectral energy band, we utilize the Kaplan–Meier (KM; Kaplan & Meier 1958; see also Feigelson & Nelson 1985) survival analysis. This is necessary because many bursts only permit upper limit measurements of ${\rm{\Delta }}{t}_{\mathrm{min}}$. Figure 2 summarizes how the minimum variability timescale varies with energy band. The KM cumulative plots—including the shaded 1σ error region—for each bandpass and the full (all channels combined) Fermi/GBM energy range are shown in the top panel. The sample 50th percentiles (i.e., medians) and the lowest 10th percentiles (shown with the dotted lines in the top panel of Figure 2) are plotted in the bottom panel. Table 1 summarizes the corresponding values. Since the KM cumulative estimation curve of channel 4 does not cross the 10% limit line, there is no value reported in Table 1 for this case. The reported values clearly show the tendency of increasing ${\rm{\Delta }}{t}_{\mathrm{min}}$ with decreasing energy band. Because we tend to find a clear association between ${\rm{\Delta }}{t}_{\mathrm{min}}$ and the rise time of the shortest GRB pulse (see also Paper I), this confirms that GRB pulse structures are narrower at higher energy and that understanding this effect is important for understanding any implications drawn from ${\rm{\Delta }}{t}_{\mathrm{min}}$.

Figure 2.

Figure 2. Top panel: the KM cumulative estimation curve of all long-duration GRBs in the Fermi sample for each energy band including the shaded 1σ region around each bandpass. The dotted lines show the 50th percentile and the lowest 10th percentile for each bandpass. The location of the of measured ${\rm{\Delta }}{t}_{\mathrm{min}}$ values (top ticks) and upper limits (bottom ticks of the same color) are shown in the sub-panel. Bottom panel: the KM median estimation of ${\rm{\Delta }}{t}_{\mathrm{min}}$ vs. energy band and the lowest 10th percentile of ${\rm{\Delta }}{t}_{\mathrm{min}}$ values vs. energy band, including error bars. Note: since the KM cumulative estimation curve of channel 4 does not cross the 10% line, we plot an upper limit.

Download figure:

Standard image High-resolution image

Table 1.  The Kaplan–Meier Median and 10th Percentile Timescales for Long-duration GRBs

Band ${\rm{\Delta }}{t}_{\mathrm{min}}^{50\%}$ ${\rm{\Delta }}{t}_{\mathrm{min}}^{10\%}$ Number Number
(keV) (ms) (ms) Detected Upper Limit
8–26 540 ± 67 25 ± 8 395 307
26–89 260 ± 26 ${4}_{-2}^{+4}$ 431 319
89–299 ${150}_{-18}^{+23}$ ${2}_{-1}^{+2}$ 413 335
299–1000 ${72}_{-21}^{+24}$ ⋯ 156 278
8–1000 130 ± 18 ${2}_{-1}^{+5}$ 421 334

Download table as:  ASCIITypeset image

The KM median values of ${\rm{\Delta }}{t}_{\mathrm{min}}$ versus energy band are well fitted by a line ${\rm{\Delta }}{t}_{\mathrm{min}}^{50\%}=0.20{(E/89\;\mathrm{keV})}^{-0.53\pm 0.06}$ s (with reduced ${\chi }^{2}=0.64$). The derived power-law index here is in agreement with the power-law index of the relationship found for the average pulse width of peaks as a function of energy (Fenimore et al. 1995; and also from Norris et al. 1996). The KM estimation of the lowest 10% of ${\rm{\Delta }}{t}_{\mathrm{min}}$ values versus the energy band can also be fitted by a power law, with a steeper index, ${\rm{\Delta }}{t}_{\mathrm{min}}^{10\%}=0.01{(E/48\;\mathrm{keV})}^{-0.97\pm 0.20}$ s (with reduced ${\chi }^{2}=1.4$). The steeper index indicates that rare GRBs, which tend to be bright and spectrally hard GRBs, allow for tighter constraints on minimum timescales. This shifts the typical minimum timescales to smaller values as compared to those found for the bulk of the population. We explore the minimum timescale dependence on S/N and spectral hardness below for individual GRBs.

3.2. Consistency in the Joint Fermi/GBM and Swift/BAT Sample

In Paper I, we studied the robustness of our minimum timescales extracted for simulated bursts as the S/N is varied. It was demonstrated that the shapes of the ${\sigma }_{X,{\rm{\Delta }}t}$ curves are highly stable as the S/N is strongly decreased (by a factor of ten), but the determination of the true ${\rm{\Delta }}{t}_{\mathrm{min}}$ can be challenging. This is because GRBs tend to show evidence for temporally smooth variation between timescales of non-smooth variability (e.g., pulse rise times)—which become harder to measure as S/N is decreased—and the longer timescales associated with non-smooth variability (e.g., the full duration of the pulse). The sample of bursts detected jointly by both Swift/BAT and Fermi/GBM provides a rich data set to study this behavior. In addition to allowing us to verify consistency in the ${\rm{\Delta }}{t}_{\mathrm{min}}$ estimates for bursts with similar S/N values, we can also directly observe (in many cases) the reliability of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for different S/N values.

Figure 3 captures the variety of scaleograms produced for bursts detected by both the Swift/BAT and Fermi/GBM instruments. Here, we utilize the 15–350 keV energy range for both Swift/BAT and Fermi/GBM, and we align the light curves and extract counts over the same time intervals for each burst. Although the instruments do not have identical effective area curves in these ranges, choosing the same energy range should minimize differences due to energy band (discussed in more detail in Section 3.4 below).

Figure 3.

Figure 3. Gallery of Haar scaleograms ${\sigma }_{X,{\rm{\Delta }}t}$, representing a variety of possible structure functions calculated for Fermi/GBM and Swift/BAT (both: 15–350 keV) with a different level of sensitivity for detection of various GRBs. The left, middle, and right panels correspond to GRB 110213A, GRB 080916A, and GRB 120119A, respectively. The first and second rows show the structure functions retrieved from the GRBs light curves detected by Fermi/GBM and Swift/BAT, respectively. The third row shows the light curves in the ${T}_{100}$ duration region. In each of these, the red dashed lines represent a passage from the temporally smooth (${\sigma }_{X,{\rm{\Delta }}t}\propto {\rm{\Delta }}t$) region to a flatter region, and the red circle marks the extracted minimum variability timescale, ${\rm{\Delta }}{t}_{\mathrm{min}}$, after which the light curves transition to a temporally unsmooth behavior. Triangles denote $3\sigma $ upper limits.

Download figure:

Standard image High-resolution image

In the case of GRB 110213A (left panels), Fermi/GBM captured the higher sensitivity burst light curve. Oppositely in the case of GRB 080916A (middle panels), Swift/BAT captured a higher S/N light curve. The S/N level can be gauged from the light curves and taken directly from the ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ values, with high S/N translating directly to lower ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$. There are many bursts (e.g., GRB 120119A, right panels) in the joint Fermi/GBM and Swift/BAT sample that correspond to closely similar S/N values and for which the resulting scaleograms are almost identical. We note that minimum timescales based simply on ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ (e.g., Walker et al. 2000) directly track the noise floor level. This is also the case for ${t}_{\beta }$, calculated according to the prescription of MacLachlan et al. (2013). In the most extreme examples (i.e., GRBs 090519A and 101011A), the ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ values differ by approximately an order of magnitude, and the ${t}_{\beta }$ values differ by approximately a factor of five, while the ${\rm{\Delta }}{t}_{\mathrm{min}}$ values are consistent (Table 2). Our method distinguishes between the minimum detectable timescale and the true minimum timescale in a more robust (although not perfect, as we discuss more below) fashion.

Table 2.  GRB Minimum Timescales

Trigger ID GRB Name ${\rm{\Delta }}{t}_{\mathrm{min}}$ ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ ${T}_{90}$ ${T}_{100}^{\mathrm{start}}$ ${T}_{100}^{\mathrm{stop}}$ ${\sigma }_{X,{t}_{\mathrm{min}}}$ ${\sigma }_{X,{t}_{{\rm{S}}/{\rm{N}}}}$ z
    (s) (s) (s) (s) (s)      
080714086 080714B 0.821 ± 0.223 0.522 ± 0.045 5.376 ± 2.360 −3.437 7.283 0.90 0.57 ⋯
080714425 080714C 1.984 ± 1.040 1.241 ± 0.108 40.192 ± 1.145 −22.987 55.766 0.64 0.40 ⋯
080714745 080714A 1.384 ± 0.143 0.620 ± 0.054 59.649 ± 11.276 −29.747 88.936 0.74 0.33 ⋯
080715950 080715A $\lt 0.101$ 0.011 ± 0.001 7.872 ± 0.272 −2.203 11.867 0.90 0.20 ⋯
080717543 080717A 0.568 ± 0.194 0.369 ± 0.032 36.609 ± 2.985 −23.414 49.420 0.53 0.34 ⋯
080719529 080719A 1.990 ± 0.830 1.241 ± 0.108 16.128 ± 17.887 −12.339 19.739 0.64 0.40 ⋯
080723557 080723B 0.040 ± 0.017 0.027 ± 0.002 58.369 ± 1.985 −0.180 89.694 0.22 0.15 ⋯

Note. Redshift values marked with $\star $ are taken from http://www.mpe.mpg.de/~jcg/grbgen.html.

Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.

Download table as:  DataTypeset image

Figure 4 displays a scatter plot of ${\rm{\Delta }}{t}_{\mathrm{min}}$ determined for Swift/BAT versus Fermi/GBM. A line fit through the data points (blue curve with shaded gray 90% confidence region) is consistent with the dotted line representing equality. The best-fit line has a normalization $=\;1.13\pm 0.13$ and a slope $=\;0.99\pm 0.02$. For this fit, the reduced ${\chi }^{2}=2.86$ (for 42 degrees of freedom) and is dominated by a small number of outliers. The fraction of bursts not consistent with the fit, both below and above the line are 12% and 15%, respectively. The close consistency of this line with the unit line demonstrates that our method is robust and that our error bars, calculated by direct error propagation, are likely to be accurate.

Figure 4.

Figure 4.  ${\rm{\Delta }}{t}_{\mathrm{min}}$ for the sample of joint Fermi/GBM and Swift/BAT bursts. The red and blue histograms correspond to the short- and long-duration GRBs, respectively. The arrows show the upper limit burst cases. The black dotted line represents equality. The relative size of the circles is scaled with the absolute value of the log of the ratio of flux variation at the shortest observable variability timescale ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$, providing a measure of whether each satellite samples the same (small circles) or very different (large circles) regions of the scaleogram at the inferred ${\rm{\Delta }}{t}_{\mathrm{min}}$. The color bar can be used to identify which instrument generated the higher ${\sigma }_{X,{\rm{\Delta }}t}$.

Download figure:

Standard image High-resolution image

We do note, however, that the ${\rm{\Delta }}{t}_{\mathrm{min}}$ values calculated for Swift versus Fermi do exhibit small, systematic differences. On average, bursts detected by Swift (in the same energy band) tend to have 13% longer ${\rm{\Delta }}{t}_{\mathrm{min}}$ values as compared to Fermi. Histograms showing the spread in the overall populations are also drawn along the axes in Figure 4.

To study the origin of the outliers to the fit in Figure 4, we scale the relative size of the circles with the absolute value of the log of the ratio of flux variation at the shortest observable variability timescale ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$. This is intended to provide an indication of whether each satellite sampled the same (small circles) or very different (large circles) regions of the scaleogram at the inferred ${\rm{\Delta }}{t}_{\mathrm{min}}$. The color bar can be used to identify which instrument generated the higher ${\sigma }_{X,{\rm{\Delta }}t}$.

In general, we find that once the $\mathrm{log}({\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}})$ ratios exceed 0.5 dex (corresponding to 0.5 dex in $\mathrm{log}({\rm{S}}/{\rm{N}})$ or roughly a factor of 10 in flux) the more sensitive satellite tends to yield a lower measurement of ${\rm{\Delta }}{t}_{\mathrm{min}}$. This is consistent with our findings from Paper I. Given that such variation is not known a priori in this case (because the light curves are not based on a simulation), the tendency to detect lower ${\rm{\Delta }}{t}_{\mathrm{min}}$ when possible suggests a fractal nature of the phenomenon. Care must be taken in interpreting GRB minimum timescales because the phenomenology suggests these could always be limits on the true minimum timescales. However, we do note the important feature of the scaleograms: hidden (i.e., low S/N) minimum timescales will always correspond to smaller variations in the fractional flux levels. In this sense, a perfect accounting of the minimum timescales may not be necessary because very short minimum timescales tend to represent fractionally tiny (or alternatively very rare) episodes in the GRB emission.

3.3. Distribution of Δtmin Values for Fermi/GBM

Figure 5 (left) shows histograms for the Fermi GRBs permitting measurement of and also upper limits on ${\rm{\Delta }}{t}_{\mathrm{min}}$. The two distributions have consistent mean values. The middle and right panels of Figure 5 show the KM cumulative histograms in the observer and source frames, respectively. The dotted lines correspond to the minimum timescale of the lowest 10% and 50% (median) of short- and long-duration bursts.

Figure 5.

Figure 5. Left panel: the histograms of ${\rm{\Delta }}{t}_{\mathrm{min}}$ with measurements (blue) and for GRBs allowing for upper limits only (red). Middle and right panels: the cumulative histograms of bursts in the observer and source frames, respectively. The KM estimation curve with $1\sigma $ error region around the curve is shown in these panels. The dotted lines correspond to the minimum timescale of the lowest 10% and 50% of bursts, shown for the short- and long-duration GRBs, separately. Sub-panels show the locations of detections and upper limits, as in Figure 2. For long-duration (short-duration) GRBs, we have 421 (107) measurements and 334 (76) upper limits in the observer frame and 24 (3) measurements and 18 (1) upper limits in the source frame.

Download figure:

Standard image High-resolution image

We find a median minimum timescale for long-duration (short-duration) GRBs in the observer frame of 134 ms (18 ms). In the source frame, we find a median minimum timescale for long-duration (short-duration) GRBs of 45 ms (10 ms). It is interesting that these numbers are a factor of 3–10 smaller than those we found for Swift in Paper I. The largest differences, in the case of short-duration GRBs, are attributable to the increased number of well-detected short-duration GRBs by Fermi. As we discuss below (Section 3.4), ${\rm{\Delta }}{t}_{\mathrm{min}}$ also appears to vary by a factor of $\approx 3$ depending on the burst hardness. The Fermi sample is studied using the full energy range, and the sample appears to be spectrally harder than the Swift sample overall.

We also report ${\rm{\Delta }}{t}_{\mathrm{min}}$ of the most exotic GRBs in Fermi sample—the lowest 10th percentile of bursts with the shortest ${\rm{\Delta }}{t}_{\mathrm{min}}$. The 10th percentile ${\rm{\Delta }}{t}_{\mathrm{min}}$ values for long-duration (short-duration) GRBs in the observer frame are found to be 2.2 ms (1.9 ms). In the source frame, we find 2.9 ms (2.4 ms). These numbers are consistent with the findings in Paper I that millisecond variability appears to be rare in GRBs.

From Figure 5, we find that the ${\rm{\Delta }}{t}_{\mathrm{min}}$ distribution of long-duration GRBs is displaced from that of short-duration GRBs ($16\sigma $, t-test $17\sigma $, log-rank test; Mantel 1966). The log-rank test includes the upper limits, unlike the t-test. This finding is consistent with the results presented in Paper I for Swift. This discrepancy is still present in the source frame ($2.3\sigma $, t-test and $3.4\sigma $, log-rank test), unlike in Paper I where the distribution centers appeared to be consistent. The Swift small sample of short-duration GRBs with known z is likely the main reason for the observed degeneracy. The significant observer frame discrepancy is likely driven by the fact that short-duration GRBs tend to be detected only at low redshift, unlike long-duration GRBs that span a broad range of redshifts. Examining the dispersion in $\mathrm{log}({\rm{\Delta }}{t}_{\mathrm{min}})$ values, we see no strong evidence for dissimilar values for the long- and short-duration samples ($\lt 1.3\sigma $, F-test). This finding is also fully consistent with the results presented in Paper I, where it was also found (using a sample of Swift GRBs) that the two histograms are quite broad and very similar in dispersion.

Figure 6 displays our minimum variability timescale, ${\rm{\Delta }}{t}_{\mathrm{min}}$, versus the GRB duration, ${T}_{90}$. The short- and long-duration GRBs are shown with diamond and circle symbols, respectively. In this plot, the relative size of symbols is proportional to the ratio between minimum variability and S/N timescale (${\rm{\Delta }}{t}_{\mathrm{min}}/{\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$). As described above, ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ represents the first statistically significant timescale in the Haar wavelet scaleogram. The color of the points in Figure 6 corresponds to the flux variation level, ${\sigma }_{X,{\rm{\Delta }}t}$, at ${\rm{\Delta }}{t}_{\mathrm{min}}$. A curved black line is also plotted to show a typical value for the minimum observable time (${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$) versus ${T}_{90}$. Values for ${T}_{90}$ are taken from Table 7 of von Kienlin et al. (2014).

Figure 6.

Figure 6. GRB minimum timescale, ${\rm{\Delta }}{t}_{\mathrm{min}}$, plotted vs. the GRB ${T}_{90}$ duration. Circles (diamonds) represent long-duration (short-duration) GRBs. The point colors represent the flux variation level (${\sigma }_{X,{\rm{\Delta }}{t}_{\mathrm{min}}}$) at ${\rm{\Delta }}{t}_{\mathrm{min}}$. Also plotted as a curved line is the typical minimum observable timescale, ${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$, as a function of ${T}_{90}$. The symbol sizes are proportional to the ratio of ${\rm{\Delta }}{t}_{\mathrm{min}}/{\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ for each GRB. The dashed line shows the equality line.

Download figure:

Standard image High-resolution image

We first note from the colors in Figure 6 that GRBs with ${\rm{\Delta }}{t}_{\mathrm{min}}$ close to ${T}_{90}$ tend to have flux variations of the order of unity. These are bursts with simple, single-pulse time profiles. As can be seen from the range of point sizes in Figure 6, most are not simply low S/N events where fine time structure cannot be observed. Also, we see that there are GRBs with both high and low S/N that have complex time series (${\rm{\Delta }}{t}_{\mathrm{min}}\ll {T}_{90}$). Based on the point sizes, the short-timescale variations have higher ratio of ${\rm{\Delta }}{t}_{\mathrm{min}}/{\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$ for the short-duration GRBs of the similar ${\rm{\Delta }}{t}_{\mathrm{min}}$ in comparison with that of the long-duration GRBs. Short-duration GRBs tend to have a higher ${\sigma }_{X,{\rm{\Delta }}t}$ for the similar value of ${\rm{\Delta }}{t}_{\mathrm{min}}$ compared with the long-duration GRBs.

These findings are all consistent with the similar results explained in Paper I, although here we have a better ratio of short-duration GRBs to long-duration GRBs.

From a Kendall's τ test (Kendall 1938), we find only marginal evidence that ${\rm{\Delta }}{t}_{\mathrm{min}}$ and ${T}_{90}$ are correlated (${\tau }_{k}=0.33$, $11\sigma $ above zero). The ${\rm{\Delta }}{t}_{\mathrm{min}}$ values in Figure 6 are bound from above by ${T}_{90}$, and they do not strongly correlate with ${T}_{90}$ within the allowed region of the plot. In Paper I, we studied this relation for the entire sample of Swift GRBs and found only marginal evidence that ${\rm{\Delta }}{t}_{\mathrm{min}}$ and ${T}_{90}$ are correlated (${\tau }_{k}=0.38$, $1.5\sigma $). Even when we utilized the robust duration estimate ${T}_{{\rm{R}}45}$ (Reichart et al. 2001) in place of ${T}_{90}$, no significant correlation was found (${\tau }_{k}=0.6$, $2.4\sigma $). If we perform a truncated Kendall's τ test that only compares GRBs above one another's threshold (Lloyd-Ronning & Petrosian 2002), the correlation strength drops precipitously (${\tau }_{k}=0.06$, $1.4\sigma $). We, therefore, believe there is no strong evidence supporting a real correlation between ${\rm{\Delta }}{t}_{\mathrm{min}}$ and ${T}_{90}$.

3.4. The Dependence of ${\rm{\Delta }}{t}_{{min}}$ on Spectral Hardness

We investigate here how a burst's spectral hardness impacts its minimum variability timescale. We define the hardness ratio (HR) as the total counts in the hard composite channel (89–1000 keV, our combined channels 3 and 4) divided by the total counts in the soft composite channel (8–89 keV, our channels 1 and 2). We plot in Figure 7 (top panel) the ratio of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for these two composite channels against the HR of the two corresponding bandpasses. GRBs with harder spectra tend to have a lower ${\rm{\Delta }}{t}_{\mathrm{min}}$ ratio, by as much as a factor of $\approx 3$, for both short- and long-duration GRBs. This relationship can be captured using a best-fitted linear model through all the bursts, shown in Figure 7 (top panel), with slope $=-0.34\pm 0.04$.

Figure 7.

Figure 7. Top panel: the ratio of minimum variability timescale for channels $3+4$ and channels $1+2$, plotted against hardness ratio for the corresponding composite channels. Middle and bottom panels: the ratio of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for channels $1+2$ and channel 4 over full energy band, separately plotted against hardness ratio. The best-fitted linear model through the bursts including the shaded $1\sigma $ error region is also shown in each panel.

Download figure:

Standard image High-resolution image

The change in minimum timescale with hardness can be understood from the effects of relativistic beaming on emission instantaneously emitted in the rest frame by a moving shell (e.g., Fenimore et al. 1996; Ryde & Petrosian 2002; Kocevski et al. 2003). If the material on the line of sight has a Doppler factor ${\rm{\Gamma }}(1-\beta )$, propagating with a speed $v=\beta c$ and Lorentz factor Γ, material above or below the line of sight at angle θ will have a Doppler factor ${\rm{\Gamma }}(1-\beta \mathrm{cos}(\theta ))\approx (1+{({\rm{\Gamma }}\theta )}^{2})/2{\rm{\Gamma }}$, larger by a factor of $1+{({\rm{\Gamma }}\theta )}^{2}$. The off-axis emission will also arrive later, at a time $t-{t}_{{\rm{e}}}=R/c(1-\mathrm{cos}(\theta ))$, where R is the emission radius, after the start of the emission at te. If we assume $R=2{{\rm{\Gamma }}}^{2}{{ct}}_{{\rm{e}}}$, then the Doppler factor increases in time in the observer frame as $t/{t}_{{\rm{e}}}$. As a result, the photon flux observed at fixed energy E will decrease as higher and higher rest-frame-energy photons reach the bandpass, as ${(t/{t}_{{\rm{e}}})}^{\alpha -2}$. Here, α is the photon index and the power of two arises from relativistic beaming.

Thus, we expect that impulsive releases of energy in the rest frame will be smoothed over—in a fashion that is stronger at low energy ($\alpha \approx -1$) as compared to high energy (above ${E}_{\mathrm{peak}}$, $\alpha \lesssim -2$)—as viewed in the observer frame. The degree of smoothing expected above ${E}_{\mathrm{peak}}$ is a factor of two to three less than the smoothing expected at observer frame energies below ${E}_{\mathrm{peak}}$. This effect naturally explains the decreasing minimum timescale we observe with increasing spectral bandpass, and it suggests that the tightest constraints on minimum timescale should be obtained from the highest available instrument bandpass. It should also be sufficient to confirm that ${E}_{\mathrm{pk}}$ is below, or perhaps within, a given bandpass.

Figure 7 (middle panel) shows the ratio of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for the soft composite channel over the full energy band against the HR. This plot shows how ${\rm{\Delta }}{t}_{\mathrm{min}}$ is approximately the same in each bandpass until the HR goes beyond roughly its median value. The bursts in this plot are well fitted by a line with slope $=\;0.12\pm 0.02$.

The ratio of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for the hardest channel (#4) over the full energy band against the HR is shown in Figure 7 (bottom panel). Here, the best-fit line (slope $=-0.02\pm 0.09$) is consistent with being flat: the minimum timescales appear to be independent of this HR for all but perhaps the hardest handful of Fermi GRBs. We conclude that utilizing the full Fermi/GBM bandpass—which yields ${\rm{\Delta }}{t}_{\mathrm{min}}$ constraints consistent with those derived from the soft energy channel for soft GRBs and also ${\rm{\Delta }}{t}_{\mathrm{min}}$ constraints consistent with those derived from the hard energy channel for hard GRBs—is an acceptable procedure for determining the tightest constraints on ${\rm{\Delta }}{t}_{\mathrm{min}}$.

3.5. Constraints on the Size of the Central Engine

The minimum timescale provides an upper limit on the size of the GRB emission region, in turn providing hints on the nature of the GRB progenitor and potentially shedding light on the nature of emission mechanism. In Paper I, we summarized how an association of a minimum timescale with a physical size is not unique because the observed timescales also depend strongly on the emitting surface velocity.

The minimum Lorentz factor Γ can be estimated from the compactness argument (Lithwick & Sari 2001). If we assume a spectrum with photon index $\alpha =-2$ (see Ackermann et al. 2013, Figure 25)—typical for GRB spectra above the pair-production limit and also appropriate for the range of energies that dominate the luminosity (near the $\nu {F}_{\nu }$ spectral peak)—we find

Equation (1)

where L is the gamma-ray luminosity. If we regard ${\rm{\Delta }}{t}_{\mathrm{min}}$ as corresponding to the bolometric emission, it is most natural to use the full Fermi/GBM bandpass for its estimation rather than a fixed rest-frame bandpass. It could be argued that corrections should also be made to account for spectral hardness, based perhaps on the assumption that GRBs have a single, fixed rest-frame hardness—an unlikely possibility—modulated only by the Lorentz factor. However, based on the analysis in Section 3.4 above, any corrections would be small.

Utilizing our ${\rm{\Delta }}{t}_{\mathrm{min}}$ estimates and limits for the full Fermi/GBM bandpass, we find that 50% of Fermi GRBs must have ${\rm{\Gamma }}\gt 190$. In the case of the most energetic events, 10% of Fermi GRBs require ${\rm{\Gamma }}\gt 410$. To calculate these fractions for short-duration bursts without measured redshift, we follow D'Avanzo et al. (2014) in assigning an average $z=0.85$. For long-duration GRBs lacking redshift, we assign the average $z=2.18$.

Similarly, for some maximally allowed ${{\rm{\Gamma }}}_{\mathrm{max}}$, compactness limits the emission radius to be greater than

Equation (2)

This minimum bound on the radius can be compared to the maximum bound on the radius established by the temporal variability:

Equation (3)

Here, we conservatively take ${{\rm{\Gamma }}}_{\mathrm{max}}\sim 1200$ from Racusin et al. (2011).

If emission were to occur at the minimum allowable radius, ${R}_{\mathrm{min}}$, it would correspond to variability timescales as short as ${\rm{\Delta }}t={R}_{\mathrm{min}}/(2c{{\rm{\Gamma }}}_{\mathrm{max}}^{2})\lesssim 1$ μs. Because such timescales are not observed, a more realistic bound on the minimum emission radius is ${R}_{{\rm{c}}}=2c{{\rm{\Gamma }}}_{\mathrm{min}}^{2}{\rm{\Delta }}{t}_{\mathrm{min}}/(1+z)$ or

Equation (4)

Figure 8 shows the emission radius, Rc, for all the bursts with measured ${\rm{\Delta }}{t}_{\mathrm{min}}$ in Fermi/GBM sample versus rest-frame ${T}_{90}$. The shaded region shows the interval between the ${R}_{\mathrm{min}}$ and ${R}_{\mathrm{max}}$. The interpretation of Rc as a characteristic minimum radius for the emission is described further in Section 4.

Figure 8.

Figure 8. Characteristic emission radii Rc (Equation (4)) plotted vs. rest-frame ${T}_{90}$ for the Fermi/GBM bursts. The shaded region shows the interval between the minimum and maximum emission radii allowed. The bursts with known z and assigned z are denoted with filled and unfilled circles, respectively. The short- and long-duration GRBs are denoted with red and blue colors, respectively.

Download figure:

Standard image High-resolution image

The short-duration GRBs have a KM mean ${R}_{{\rm{c}}}=3.3\times {10}^{13}$ cm. This is about four times smaller than the KM mean ${R}_{{\rm{c}}}=1.3\times {10}^{14}$ cm for long-duration GRBs. While this represents a statistically significant separation ($18\sigma $, t-test), it is substantially less than the factor of approximately 20 separation between the mean ${T}_{90}$ durations (Figure 8; also Kouveliotou et al. 1993). In contrast to the findings of Barnacka & Loeb (2014)—where the emission radius was argued to simply scale with the ${T}_{90}$ duration—we find a broader overlap in the populations.

3.6. Evolution of ${\rm{\Delta }}{t}_{{min}}$ with z

Because GRBs are present over a very broad redshift range, the signature of time dilation—and perhaps of any evolution in GRB time structure with redshift—should be present in GRB time series. Finding the signature of time dilation in GRBs has remained elusive (Norris et al. 1994; Kocevski & Petrosian 2013; but see, e.g., Zhang et al. 2013). In our previous attempt described in Paper I, we utilized Swift GRBs and demonstrated a correlation between ${\rm{\Delta }}{t}_{\mathrm{min}}$ and redshift, marginally stronger than expected simply from time dilation. We discussed how this excess correlation strength was possibly due to the utilization of a fixed observer frame bandpass instead of a fixed rest-frame bandpass in the analysis. For Fermi/GBM, the broad instrument energy range permits analysis in a fixed rest-frame bandpass.

We identify 46 Fermi GRBs, including 4 short-duration GRBs, with measured redshifts. Light curves are extracted in the rest-frame 89–299 keV band and analyzed. In Figure 9, we plot ${\rm{\Delta }}{t}_{\mathrm{min}}/(1+z)$ versus $1+z$ for the long-duration GRBs. Redshift values are taken from Butler et al. (2007, 2010 and references therein), Butler (2013), and this webpage.5 The blue circles in Figure 9 correspond to the KM mean values of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for sets of 7–10 bursts, grouped by redshift intervals. The unbinned data are plotted in the background for the entire sample and for those with measured ${\rm{\Delta }}{t}_{\mathrm{min}}$ using unfilled and filled circles, respectively. We find that the binned data can be well fitted by a line ${\rm{\Delta }}{t}_{\mathrm{min}}/(1+z)\sim 140{((1+z)/2.8)}^{0.5\pm 1.0}$ ms, suggesting a possible increase in timescale with z but also consistent the prediction of simple time dilation (dotted line).

Figure 9.

Figure 9. Minimum variability timescale in the rest-frame 89–299 keV energy band vs. redshift, z. The blue circles show the KM mean values of ${\rm{\Delta }}{t}_{\mathrm{min}}$ for groups of 7–10 bursts of similar redshift. The shaded region represents the $1\sigma $ confidence interval for the fitted red line. The dotted black line shows the expected evolution due to simple cosmological time dilation, namely, ${\rm{\Delta }}{t}_{\mathrm{min}}\sim 1+z$. The faint blue circles show all GRBs with measured ${\rm{\Delta }}{t}_{\mathrm{min}}$ and known z, and the unfilled circles show GRBs with upper limit values for ${\rm{\Delta }}{t}_{\mathrm{min}}$.

Download figure:

Standard image High-resolution image

4. CONCLUSIONS

Using a technique based on Haar wavelets, previously developed in Paper I, we studied the temporal properties of a large sample of GRB gamma-ray prompt-emission light curves captured by the GBM instrument on board Fermi prior to 2012 July 11. We analyzed the time histories in four energy bands. While the derived values for ${\rm{\Delta }}{t}_{\mathrm{min}}$ are highly dependent upon bandpass, we find that the use of the full energy band allows for the tightest constraints on the size of the emission region. In principle, the highest-energy bandpass should yield the tightest constraint (Section 3.4). However, S/N in the highest-energy channels is often low; the full energy bandpass allows for increased S/N while maintaining a consistent ${\rm{\Delta }}{t}_{\mathrm{min}}$ estimate.

Applying our technique to the joint Fermi/GBM and Swift/BAT sample, we find close consistency in the minimum timescales derived for each instrument. However, as suggested by simulations in Paper I—and observed for a handful of bursts of widely varying in S/N in Section 3.2—${\rm{\Delta }}{t}_{\mathrm{min}}$ values below the measurement limit (${\rm{\Delta }}{t}_{{\rm{S}}/{\rm{N}}}$) can be present. It is thus important to consider our ${\rm{\Delta }}{t}_{\mathrm{min}}$ values as defined given the observed data, with the possibility of improved limits given better data. We urge caution, in particular, in interpreting minimum timescales determined using hard X-ray data (e.g., Swift/BAT). Minimum timescale estimates using the full Fermi/GBM bandpass are a factor of two to three times more constraining than those determined from Fermi/GBM data in a Swift/BAT bandpass.

Considering measurements and limits, we find a median minimum variability timescale in the observer frame of 134 ms (long-duration; 18 ms for short-duration GRBs). In the source frame, for a smaller sample of 33 GRBs, we find a median timescale of 45 ms (long-duration; 10 ms for short-duration GRBs). This finding validates our previous results in Paper I, confirming that millisecond variability appears to be rare in GRBs. In the most extreme examples, 10% of the long-duration GRB sample yields evidence for 2.2 ms variability (1.9 ms for short-duration GRBs). In the source frame, we find similar numbers, 2.9 ms for long-duration GRBs and 2.4 ms for short-duration GRBs. Even if we are restricted to the 67 GRBs within minimum detectable timescales ${t}_{{\rm{S}}/{\rm{N}}}\lt 10$ ms, only 10% of the brightest and/or most impulsive GRBs show evidence for variability on timescales below 4.2 ms in the observer frame.

4.1. Constraints on the Fireball Model

In the "external shock" model (e.g., Rees & Meszaros 1992), gamma-rays are produced as the GRB sweeps up and excites clouds in the external medium. The extracted ${\rm{\Delta }}{t}_{\mathrm{min}}$ can circumscribe the size scale of the impacted cloud along the line of sight. For a thin shell (e.g., Mészáros 2006), the gamma-ray radiation will start when the relativistic shell hits the inner boundary of the cloud with the peak flux produced as the shell reaches the densest region or center of the cloud. The size scale of the impacted cloud is limited by $2{{\rm{\Gamma }}}^{2}c\;{\rm{\Delta }}{t}_{\mathrm{min}}$ since the shock is moving near light speed (Fenimore et al. 1996). For the smallest ${\rm{\Delta }}{t}_{\mathrm{min}}$ found at ∼1 ms, and assuming ${\rm{\Gamma }}\lt 1000$, the cloud size must be smaller than 4 AU.

If the angular size of an impacted cloud as viewed from the GRB central engine is Θ, the minimum variability timescales is constrained to be $\delta {\rm{\Theta }}\;{\rm{\Gamma }}\lt {\rm{\Delta }}{t}_{\mathrm{min}}/2{T}_{\mathrm{rise}}$ (Paper I). Here, ${T}_{\mathrm{rise}}$ denotes the overall time to reach the maximum gamma-ray flux. The fraction of the emitting shell that becomes active is expected to be of the order of $0.1{\rm{\Delta }}{t}_{\mathrm{min}}/2{T}_{\mathrm{rise}}$ (Fenimore et al. 1999). For the bursts in the Fermi sample with a typical minimum variability timescale ${\rm{\Delta }}{t}_{\mathrm{min}}\sim {T}_{\mathrm{rise}}$, there is no need to consider a highly clumped external medium, and the external shock scenario is viable.

However, there are many bursts (e.g., Figure 6) that do exhibit ${\rm{\Delta }}{t}_{\mathrm{min}}/{T}_{\mathrm{rise}}\ll 1$. If this variability results from a clumped external medium, then a significant fraction of the energy from the GRB must escape without interacting and producing gamma-rays. Early X-ray afterglow observations (e.g., Nousek et al. 2006), on the other hand, demonstrate the need for a high (order of unity) efficiency in tapping the kinetic energy of the flow to produce gamma-rays. Thus, external shocks likely cannot explain the finest timescale variability.

In the "internal shock" scenario (e.g., Rees & Meszaros 1994), the relativistic expanding outflow released from a central engine is assumed to be variable, consisting of multiple shells of different Γ. The dispersion in Γ is related to the observed variability of the light curve, as ${\rm{\Delta }}{\rm{\Gamma }}/{\rm{\Gamma }}\approx 1/2\;({\rm{\Delta }}{t}_{\mathrm{min}}/{T}_{\mathrm{rise}})$ (Paper I), with many of the Fermi light curves requiring ${\rm{\Delta }}{\rm{\Gamma }}\approx {\rm{\Gamma }}$. Efficient production of gamma-rays also requires ${\rm{\Delta }}{\rm{\Gamma }}\approx {\rm{\Gamma }}$ (Piran 1999; Kobayashi & Sari 2001). It is, therefore, natural to assume that some of the gamma-ray emission is released with the minimum possible Lorentz factor ${{\rm{\Gamma }}}_{\mathrm{min}}\approx 200$ (Section 3.5) allowed from compactness considerations. As a result, considering variability at the few millisecond level, some GRBs must emit at radii of the order of ${R}_{{\rm{c}}}\approx 2{{\rm{\Gamma }}}_{\mathrm{min}}^{2}c\;{\rm{\Delta }}{t}_{\mathrm{min}}\approx {10}^{13}$ cm (Equation (4); Figure 8). This is also the extent to which minimum variability timescales can limit the size of the progenitor.

We find that long-duration GRBs appear to have typical emission radii, ${R}_{{\rm{c}}}\approx 1.3\times {10}^{14}$ cm, while short-duration GRBs have four times smaller typical emission radii, ${R}_{{\rm{c}}}\approx 3.3\times {10}^{13}$ cm. There is large scatter in the inferred radii of each population, and the distributions appear to strongly overlap. It is unclear whether the dichotomy in short- and long-duration GRB ${T}_{90}$ durations maps cleanly to a similar dichotomy in the size of the emission regions.

Finally, we note that our minimum timescales appear to correlate with redshift in a fashion consistent with cosmological time dilation. Correcting for this, we find no significant evidence that ${\rm{\Delta }}{t}_{\mathrm{min}}/(1+z)$ evolves with redshift. This may be partly because the number of Fermi GRBs with measured redshifts is low (e.g., as compared to Swift; Paper I). Future increases in the sample size will surely allow for tighter constraints on minimum emission radii, Lorentz factors, and progenitor dimensions as well as allowing us to better understand whether any of these quantities vary with cosmic time.

Footnotes

Please wait… references are loading.
10.1088/0004-637X/811/2/93