Abstract
A complete scalar classification for dark Sharma–Tasso–Olver's (STO's) equations is derived by requiring the existence of higher order differential polynomial symmetries. There are some free parameters for every class of dark STO systems, thus some special equations including symmetry equation and dual symmetry equation are obtained by selecting a free parameter. Furthermore, the recursion operators of STO equation and dark STO systems are constructed by a direct assumption method.
Export citation and abstract BibTeX RIS
Analogous to the concept of dark matter and dark energy in cosmologists, Kupershmidt proposed the concept of dark equation in nonlinear equations and investigated linear extensions of dynamical systems in general.[1] These dark equations are similar in spirit to what one obtains when linearizing a given system, or studies how an external linear wave interacts with a particular solution of a given system. According to the definition of a dark equation, it is interesting to give a complete classification for a given integrable model.
The basic idea of dark equations is as follows: given two commuting dynamical systems X and Y,

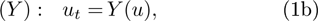
find/classify all their linear extensions  and
and  of the form
of the form
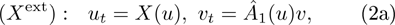

which still commute, v is a vector, and  are matrix linear differential operators dependent only upon u, not v.
are matrix linear differential operators dependent only upon u, not v.
According to commutativity
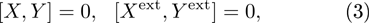
dark equations (i.e., linear extension equation) are obtained.
In fact, the linear extensions  and
and  can be regarded as some kinds of integrable coupling. Integrable coupling with different nonlinear equations have been explored by many researchers. For example, Qiao investigated various nonlinear constrained and restricted systems and the algebra-geometric solutions of integrable nonlinear evolution equations by constructing a generalized r-matrix structure of finite dimensional systems.[2] Magri suggested a method of analysis of the infinite-dimensional Hamiltonian equations, which avoids the introduction of the Bäcklund transformation or the use of the Lax equation.[3]
can be regarded as some kinds of integrable coupling. Integrable coupling with different nonlinear equations have been explored by many researchers. For example, Qiao investigated various nonlinear constrained and restricted systems and the algebra-geometric solutions of integrable nonlinear evolution equations by constructing a generalized r-matrix structure of finite dimensional systems.[2] Magri suggested a method of analysis of the infinite-dimensional Hamiltonian equations, which avoids the introduction of the Bäcklund transformation or the use of the Lax equation.[3]
Through the definition of dark equation (2), the dark KdV equations and the dark MKdV equation have been classified by Kupershmidt in 2001[1] and by Xiong et al. in 2017.[4] With regard to the MKdV equation, there are some other kinds of integrable extensions such as the complex MKdV equation with self-consistent sources,[5] a supersymmetric second MKdV equation.[6] In this work, we try to give out a complete classification of dark equations of the Sharma–Tasso–Olver (STO) equation[7,8]
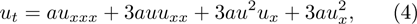
where  is a constant. Many physicists and mathematicians have paid attention to the STO equation in recent years because it is an important equation in mathematical physics. Wang et al. examined the soliton fission and fusion thoroughly by means of the Hirota bilinear method and the Bäcklund transformation method.[9] The generalized Kaup–Newell-type hierarchy of nonlinear evolution equations is explicitly related to the STO equation.[10] In Ref. [11], some exact solutions of the STO equation are given by implying a generalized tanh function method for approximating some solutions which have been known. Huang and Cai obtained the analytic solution of the STO equation by the homotopy analysis method.[12] By applying the fermionization approach, three simple super-symmetric extensions of the STO equation are obtained.[13]
is a constant. Many physicists and mathematicians have paid attention to the STO equation in recent years because it is an important equation in mathematical physics. Wang et al. examined the soliton fission and fusion thoroughly by means of the Hirota bilinear method and the Bäcklund transformation method.[9] The generalized Kaup–Newell-type hierarchy of nonlinear evolution equations is explicitly related to the STO equation.[10] In Ref. [11], some exact solutions of the STO equation are given by implying a generalized tanh function method for approximating some solutions which have been known. Huang and Cai obtained the analytic solution of the STO equation by the homotopy analysis method.[12] By applying the fermionization approach, three simple super-symmetric extensions of the STO equation are obtained.[13]
As we all know, symmetry analysis plays an important role in nonlinear mathematical physics.[14–19] Thanks to the Lie group method, a complete scalar classification for dark STO's equations is derived by requiring the existence of higher order differential polynomial symmetries. The dark equation may be integrable because of not only its linearity but also the existence of higher order symmetries, which usually implies the possible existence of infinitely many higher order symmetries. To guarantee the existence of infinitely many higher order symmetries, it is enough to find a recursion operator or a master symmetry. In this study, the recursion operators of the dark STO equations have been derived.
In fact, Kupershmidt's definition on dark equations means that both the original model Eq. (1a) and its extension Eq. (2a) are integrable under the meaning that they possess higher order symmetries Eq. (1b) and Eq. (2b), respectively.
For the STO equation (4), its symmetry equation reads
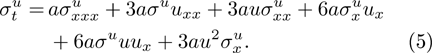
It is known that
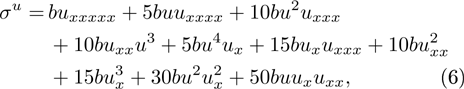
is a fifth order symmetry of the STO equation, where  and
and  are arbitrary constants.
are arbitrary constants.
Inspired by the main idea in Ref. [1] and based on the theory of high order symmetry, we look for the linear scalar homogeneous extensions of the STO equation (4) with the form
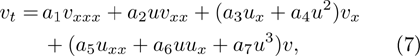
and its fifth order symmetry
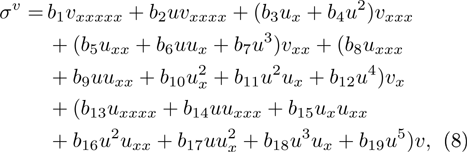
under the condition that the field u possesses unchanged symmetry Eq. (6).
The combination of Eqs. (4) and (7) is called the dark STO system (the one component integrable coupling system).
The only thing we need to carry out is to select out all independent versions of Eq. (7) by fixing  ,
,  with requiring σv satisfies the following symmetry equation
with requiring σv satisfies the following symmetry equation
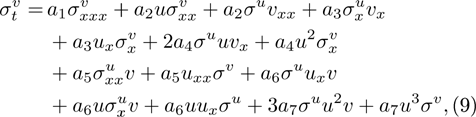
while σu is given by Eq. (6). Substituting Eqs. (4) and (6)–(8) into Eq. (9) yields the 58 determining equations for 26 constants,  and
and  . For simplification, we do not list them here.
. For simplification, we do not list them here.
After the tedious calculations, we can find 15 sets of solutions and only 9 of them are independent. Thus nine classes of independent dark STO models are obtained. Here we just list the extended equations for the scalar field v and its related fifth order symmetry σv.
Class 1:

where a, b, c and d are arbitrary constants. This equation is a decomposed equation.
Class 2:
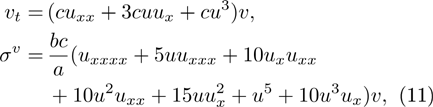
where a, b and c are arbitrary constants.
Class 3:
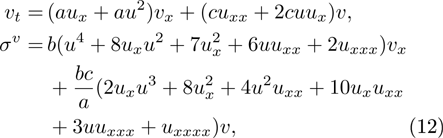
where a, b and c are arbitrary constants.
Class 4:

where a, b and c are arbitrary constants.
The special c = 3a case
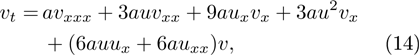
which is the dual equation of class 5 special case.
Class 5:
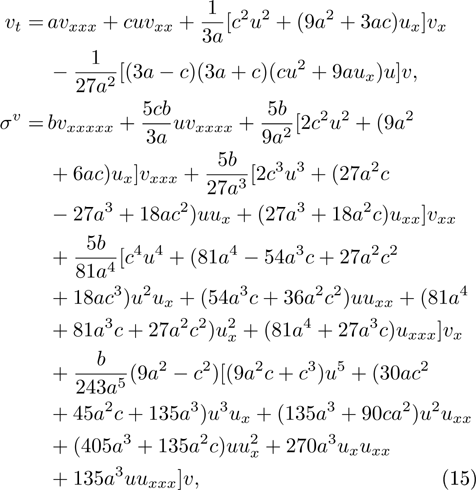
where a, b and c are arbitrary constants.
The special c = 3a case
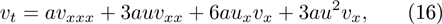
which is the dual equation of class 4 special case Eq. (14).
Class 6:
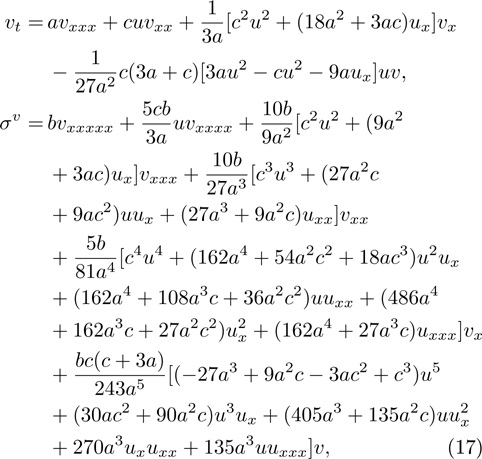
where a, b and c are arbitrary constants.
class 7:
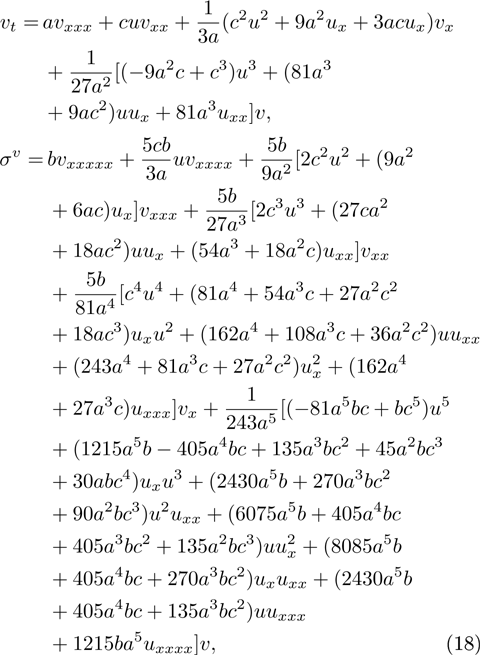
where a, b and c are arbitrary constants.
The special c = 3a case
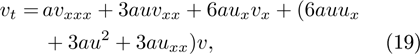
is the symmetry equation (5) of the STO equation.
Class 8:
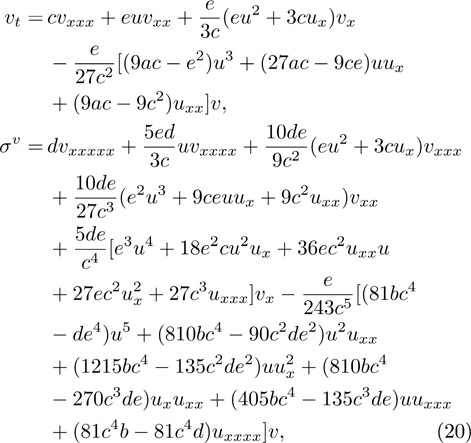
where a, b, c, d and e are arbitrary constants.
The special c = a and e = 3a case
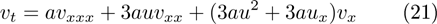
is the dual of the symmetry equation (19) of the STO equation.
Class 9:
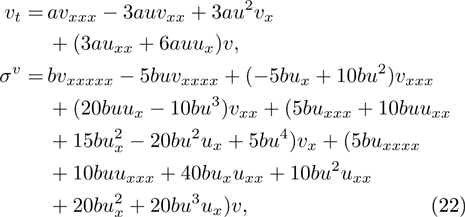
where a, b and c are arbitrary constants.
Usually, the existence of higher order symmetries may imply the possibility of the infinitely many symmetries. However, to guarantee the existence of infinitely many higher order symmetries, it is necessary to find a recursion operator such that infinitely many higher order symmetries can be obtained systematically. In the following, we try to construct the recursion operators of dark STO equations.
Based on the Lax representation, some researchers utilize eigenvalue equation for the squared eigenfunctions of the Lax operator to construct recursion operator.[20–24] Cao and Qiao constructed recursion operator using a pair of Lenard's operators,[25–29] while others[30–33] used Hamiltonian operators to realize it. Moreover, a simple effective method[34] for constructing the recursion operator has been proposed when the Lax representation is given. However, for the dark equations, the corresponding Lax representations are unknown. Here on the basis of the known symmetries, the recursion operators of dark equations are directly constructed by an assumption method.
Take class 8 Eqs. (4) and (20) as an example, the first order symmetry is
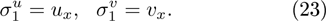
The third order symmetry is
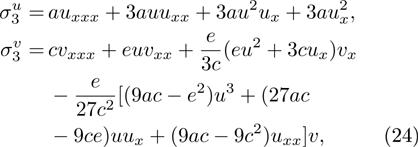
and fifth order symmetry is
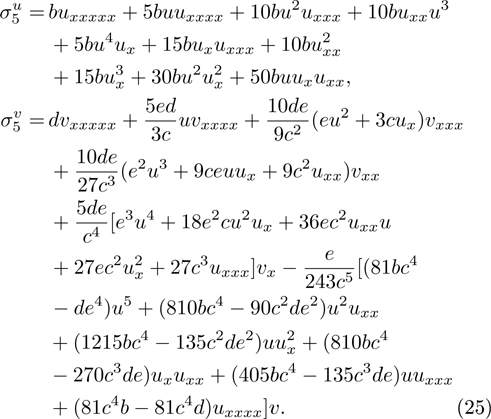
By virtue of these symmetries and properties of dark STO equations, we assume that the strong symmetry  is of the form
is of the form
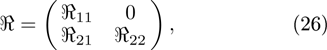
where
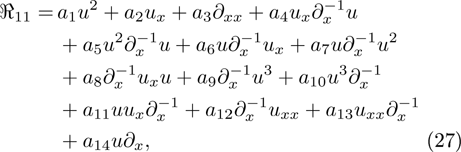
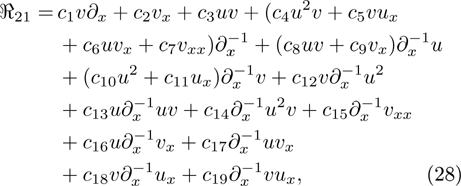
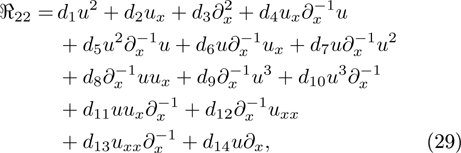
and  ,
,  and
and  are arbitrary constants.
are arbitrary constants.
According to the definition of strong symmetry, we have
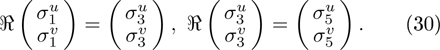
After the tedious calculation with Maple, we obtain
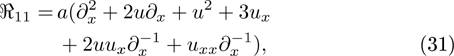
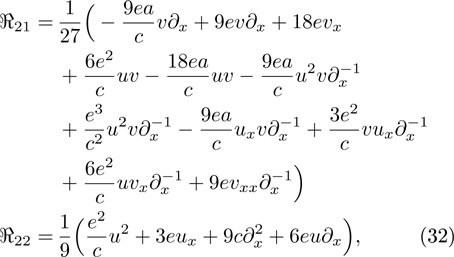
with the constraint  , and
, and  is just a recursion operator of the STO equation.
is just a recursion operator of the STO equation.
In fact, the operator Eq. (26) along with Eqs. (31) and (32) can also be proven to be a strong symmetry operator of Eqs. (4) and (20) by the following definition of strong symmetry operator.
An operator-valued function  will be called a strong symmetry[35,36] for the evolution equation
will be called a strong symmetry[35,36] for the evolution equation  if
if
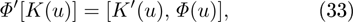
where ![$[{K}^{{\prime} },{{\varPhi }}]=[{K}^{{\prime} }\circ {{\varPhi }}-{{\varPhi }}\circ {K}^{{\prime} }]$](https://content.cld.iop.org/journals/0256-307X/35/1/010201/revision1/cpl_35_1_010201_ieqn21.gif) and
and ![${K}^{{\prime} }(u)[\varphi ]=\tfrac{\partial }{\partial \varepsilon }K(u+\varepsilon \varphi ){| }_{\varepsilon =0}$](https://content.cld.iop.org/journals/0256-307X/35/1/010201/revision1/cpl_35_1_010201_ieqn22.gif) .
.
Here we only take the STO equation (4) as an example. When  and
and  is taken as Eq. (31), we have
is taken as Eq. (31), we have
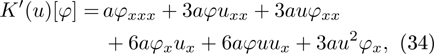
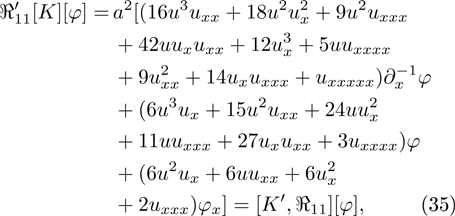
thus  is a strong symmetry operator of the STO equation. By symbolic computation with Maple, the strong symmetry properties of operators given by Eq. (26) along with Eq. (32) for Eq. (20) are proved in the same way as above and we omit cumbersome details here.
is a strong symmetry operator of the STO equation. By symbolic computation with Maple, the strong symmetry properties of operators given by Eq. (26) along with Eq. (32) for Eq. (20) are proved in the same way as above and we omit cumbersome details here.
In the same way, the recursion operators of other dark STO equations are derived and listed in Table 1. However, we do not find recursion operators of classes 1, 4, 6, 9 by the above method.
Table 1. Recursion operators of dark STO equations.
| Class 2 |
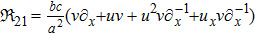
|
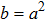
|
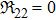
|
||
| Class 3 |
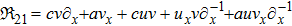
|
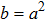
|
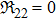
|
||
| Class 5 |
![${{\mathfrak{R}}}_{21}=a[(2{{uv}}_{x}-{v}_{{xx}}){\partial }_{x}^{-1}-{\partial }_{x}^{-1}{v}_{{xx}}+2{\partial }_{x}^{-1}{{uv}}_{x}]$](https://content.cld.iop.org/journals/0256-307X/35/1/010201/revision1/cpl_35_1_010201_ieqn32.gif)
|
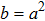 , , 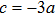
|
![${{\mathfrak{R}}}_{22}=a[{\partial }_{x}^{2}+{u}^{2}+{u}_{x}+2{\partial }_{x}^{-1}{{uu}}_{x}-{\partial }_{x}^{-1}{u}_{{xx}}-2u{\partial }_{x}]$](https://content.cld.iop.org/journals/0256-307X/35/1/010201/revision1/cpl_35_1_010201_ieqn35.gif)
|
||
| Class 7 |
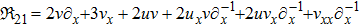
|
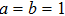 , , 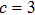
|
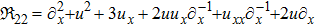
|
In summary, a complete classification of the dark STO systems with scalar extension has been given. The results show that there are nine classes of dark STO equations, which are all integrable coupling systems meaning that they possess higher order symmetries. Every class of the dark STO equation possesses some free parameters. From these dark STO systems, symmetric and dual symmetric equations for the STO equation are obtained by selecting free parameters. Furthermore, the recursion operators of five classes of dark STO equations are explicitly given by a direct assumption method.
The methods presented here for constructing dark equations and corresponding recursion operators can also be applied to other nonlinear equations. In addition, the explicit solutions of the generalized dark equations will be produced through some valid methods, such as symmetry reduction method, Hirota bilinear method, and Darboux transformation. The above topics will be discussed in our future work.
Footnotes
- *
Supported by the National Natural Science Foundation of China under Grant Nos 11775121, 11775116 and 11435005, the Ningbo Natural Science Foundation of China under Grant No 2015A610159, and the K. C. Wong Magna Fund in Ningbo University.
