High-order harmonic generation with μJ laser pulses at high repetition rates

High-order harmonic generation (HHG) in gases makes it possible to produce extreme ultraviolet (XUV) pulses on the femtosecond or even attosecond timescale that is of interest for a broad range of experiments in different fields of physics and chemistry [1, 2]. Since the generation itself requires intensities in the range of 10¹⁴ W cm⁻², high-power laser systems are normally used to drive this highly nonlinear light conversion process. Due to average power limitations, the repetition rate of such laser systems is usually low, i.e. less than a few kHz. However, many experiments would benefit greatly from a higher repetition rate, in the 100 kHz or even MHz range. In particular, there are a number of applications where ultrashort XUV pulses at high repetition rates are required without demanding a very high photon flux or XUV photon energies that could only be generated in very high harmonic orders.

This work was mainly motivated by the application of time-resolved photoelectron spectroscopy for studies of ultrafast dynamics in solids and at solid surfaces. In the last two decades, the use of visible or near-ultraviolet femtosecond pump and probe pulses in the so-called two-photon photoemission (2PPE) has enabled many novel experiments, probing the ultrashort lifetime of electronic excitations in metals and at metal surfaces [3–7], the dynamics of adsorbate motion [8], electron localization and solvation at surfaces [9, 10], charge-transfer processes at molecular interfaces [11], coherently controlled electron currents [12], phase transitions and other ultrafast processes in solids [13]. These types of experiments can benefit from higher probe photon energies for a variety of reasons. First of all, the dynamics of holes, in addition to that of electrons, become more easily accessible [14]. Second, the range of detectable electron momenta can cover the complete surface Brillouin zone [15]. Last but not the least, variable photon energies allow—like in ultraviolet photoelectron spectroscopy (UPS) with synchrotron radiation—the suppression or enhancement of selected states due to energy-dependent photoemission cross-sections [16]. Unlike in time-resolved core-level spectroscopy employing high-harmonic sources [17], photon energies in excess of 40 eV are usually not required or even desirable. The signal-to-noise ratio, however, greatly benefits from high repetition rates since the number of emitted electrons per pulse has to be limited in order to avoid space charge effects. This is also important for time-resolved photoelectron microscopy studies [18, 19], where the spatial resolution of an photoelectron emission microscope could be combined with the temporal resolution of attosecond pulses. A high-repetition-rate high-harmonic source would, e.g., allow the investigation of surface plasmons on attosecond timescales with a high signal-to-noise ratio [20].

A high repetition rate to improve statistics, while keeping the number of events per pulse at a very low level is also required for all kinds of coincidence measurements where more than one detected particle needs to be linked to the same excitation event. Typical examples are experiments where electrons and ions or ionized molecules are detected using a reaction microscope [21, 22] or experiments on correlated two-electron emission from solids [23]. A further application is the generation of frequency combs in the XUV range for high-resolution spectroscopy [24, 25]. Since the line spacing of a frequency comb is inversely proportional to the repetition rate, a high repetition rate allows a mode spacing in the comb that is large enough for high-resolution spectroscopy. A promising approach would be Fourier-transform spectroscopy in the XUV regime [26].

To date, a few groups reported the generation of high-order harmonics at repetition rates above a few tens of kHz [24, 27–31, 33, 34]. In order to reach the high intensities required for the HHG process using pulses with a few μJ energy, three different schemes have been applied. In the first one, the amplified laser is focused using either a mirror or an achromatic lens with short focal length (free focus geometry) [27]. In the second scheme, a high-finesse optical resonator that contains the nonlinear interaction medium is used. Intra-cavity enhancement enables the generation of XUV pulses at the high repetition rate of the seed laser oscillator. The generation geometry in this scheme is typically very similar to the free focus geometry. This technique suffers, however, from the difficulty of extracting the generated pulses [35]. A third scheme utilizes the local field enhancement induced by resonant plasmons within a metallic nanostructure [28, 36]. This interesting method has been experimentally demonstrated but not applied yet in a reproducible manner.

In this work, we investigate HHG under tight focusing conditions using a free focus geometry. In section 2, we analyse the macroscopic effects in HHG by introducing a generalized phase-matching model valid for all the focal length³. We further specify the conditions needed for efficient generation using a tight focus geometry. In section 3, we show results of an experiment with a 100 kHz laser system and pulse energies of only 6 μJ. Spectrally narrow and spatially confined high-order harmonics are generated even under non-phase-matched conditions.

2.1. Brief summary of macroscopic phase effects

The properties of a harmonic signal depend both on the single-atom response as well as on macroscopic effects such as phase matching and the generation geometry. From a single-atom point of view, the HHG process can be described by a semi-classical three-step model [37, 38]: the electron wave packet leaves the atom via tunnelling being accelerated by the external laser field and recombines with its ion, emitting a burst of XUV radiation. Two different kinds of electron trajectories can be identified. Reflecting the duration of the excursion in the continuum they are called 'short' and 'long'. Both trajectories contribute with different phases to the harmonic emission and are therefore affecting the macroscopic conditions differently [39]. In general, the single-atom response does not directly depend on macroscopic parameters. On the other hand, macroscopic effects play an essential role for HHG with low driving pulse energies since a tight focus geometry is typically required under these conditions. We therefore concentrate here on macroscopic effects.

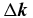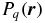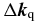The yield S_q of harmonic order q depends on the wave vector mismatch $\Delta {\bm k}$ between the laser-induced polarization $P_q({\bm r})$ at the frequency qω and the generated field. In the HHG process, $\Delta {\bm k}$ consists of four different terms: the wave vector mismatch due to the intensity-dependent single-atom dipole phase [40], $\Delta {\bm k}_{\rm q}$; the geometrical wave vector mismatch due to focusing, 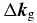$\Delta {\bm k}_{\rm g}$; and the difference in wave vectors at frequencies ω and qω [41], due to dispersion in the neutral medium, $\Delta {\bm k}_{\rm n}$, and due to free electrons, $\Delta {\bm k}_{\rm p}$. We neglect non-adiabatic phase-matching effects relevant for few cycle laser pulses as investigated in [42] as well as a possible reshaping of the fundamental laser pulse envelope. In order to generate the harmonic signal fully phase matched, the four contributions have to compensate each other for all radial (r) and longitudinal (z) positions within the nonlinear medium, for all times t. Since the emission from all atoms has to add up constructively along the propagation axis in order to maximize the harmonic yield of a collimated beam, we consider in the following only the longitudinal component of the wave vectors Δk_z = ∂Δφ/∂z, where Δφ is the corresponding phase mismatch⁴:

$$\begin{eqnarray} &&\fl 0 = \Delta { k}_{\rm z} (r,z,t) =\underbrace{\Delta { k}_{\rm q}}_{\stackrel{\ssty {<}0\; {\rm for }\; z <0}{\ssty {>} 0 \; {\rm for } \; z > 0}} + \underbrace{\Delta { k}_{\rm g}}_{\quad < 0 \quad } + \underbrace{\Delta { k}_{\rm n}}_{\quad > 0 \quad } + \underbrace{\Delta { k}_{\rm p}}_{\quad < 0\quad }.\nonumber\\ \end{eqnarray} \tag{ 1 }$$

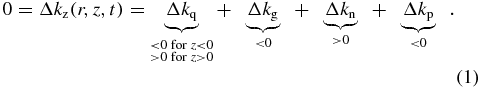
Here, z < 0 (z > 0) denotes the condition where the nonlinear medium is placed before (behind) the focus. The first and last terms on the right-hand side depend on both time and spatial coordinates, whereas the second and third terms can be treated as constant in time, depending only on the position in the nonlinear medium. The first term can be well approximated as Δk_q = −α_q∂I/∂z, where I is the laser intensity [40]. The proportionality constant α_q is positive; it is small for the short trajectories and large for the long trajectories [40, 43]. In order to achieve phase matching at the focus (Δk_q ≈ 0), the neutral dispersion has to compensate the negative plasma dispersion as well as the geometrical Gouy phase term Δk_g. With increasing distance to the focus, Δk_g as well as ∂(Δk_g)/∂z decreases. This makes it easier to compensate for Δk_g and leads to a larger phase-matched generation volume. For z > 0, the dipole phase contributes as an additional positive term [40] that leads typically to better phase-matching conditions for the short trajectory behind the focus [39]. For the long trajectory, Δk_q contributes as a dominant positive term behind the focus but leads to strongly time-dependent phase-matching conditions [44].

2.2. Phase matching at short confocal parameters

At a given focusing geometry, phase matching can be typically achieved by adjusting the gas pressure p and laser pulse energy E_f. Providing that the intensity is low enough to ensure that the negative plasma dispersion does not dominate the positive contributions in (1), phase matching occurs at a certain pressure p_match called phase-matching pressure [45]. Driving the HHG process at high repetition rates and therefore with low pulse energies requires typically a tight focus geometry. In order to understand how the macroscopic parameters have to be chosen in order to achieve phase matching under such conditions, we analyse the scaling of the relevant parameters with the focal length f and pulse energy. We thereby refer to the focal length as a scaling parameter, considering a fixed beam diameter D before focusing instead of the more general confocal parameter b. Throughout this paper, we use Gaussian optics, where b and f are related through 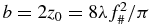$b = 2 z_0 = 8\lambda f_{ \#}^2/\pi$, where z₀ is the Rayleigh range and 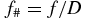$f_{\#} = f/D$ is the f-number of the focused beam with the central wavelength λ.

As f decreases, the wave vector mismatch due to the Gouy phase Δk_g increases rapidly since it scales as Δk_g∝1/f² at the focus. Consequently, it seems to prevent a phase-matched generation. It is, however, possible to obtain identical phase-matching conditions at long or short focal lengths if E_f and p are scaled appropriately with f. This can be seen by modifying (1). The wave vector mismatch due to dispersion can be rewritten as Δk_{n, p} = p · ∂(Δk_{n, p})/∂p, the partial derivatives being independent on pressure. Considering the scaling of Δk_g with the focal length, we can treat (Δk_g · f²) as independent of f. At the focus where Δk_q vanishes and at an intensity sufficient to generate harmonics, but such that |Δk_n| ⩾ |Δk_p|, we obtain

$$\begin{equation} \frac{(\Delta k_{{\rm g}} \cdot f^2)}{f^2} + p_{\rm match}\left[ \frac{\partial (\Delta k_{{\rm n}})}{\partial p} + \frac{\partial (\Delta k_{{\rm p}})}{\partial p} \right] = 0, \end{equation} \tag{ 2 }$$

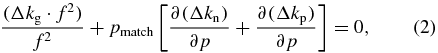
for p = p_match. p_match is proportional to 1/f², provided we scale the pulse energy appropriately in order to maintain the intensity distribution within the interaction volume. For a Gaussian laser pulse with the pulse length τ, the peak intensity in the focus is given by

$$\begin{equation} I_0 = \frac{\pi }{2\tau \lambda ^2}\frac{E_{\rm f}}{f_{\#}^2}. \end{equation} \tag{ 3 }$$

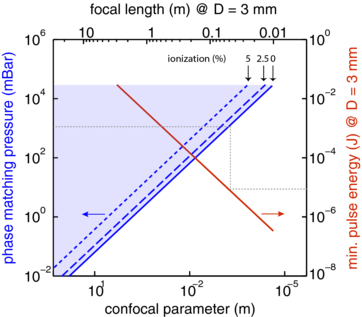
Scaling E_f as f² ensures a constant focus intensity, and consequently, a constant degree of ionization. Figure 1 illustrates this scaling for the generation of harmonic 21 in argon at the focus. The phase-matching pressure is represented as a function of focal length, for different degrees of ionization. The dispersion data for the 21st harmonic were taken from [46]. In general, the negative dispersion due to free electrons and the Gouy phase shift can be compensated by the neutral dispersion as long as the free electron dispersion does not exceed the dispersion in the neutral gas. Depending on the gas, this happens typically at an ionization level of a few per cent. For |Δk_n| ⩾ |Δk_p|, an increased ionization level leads to a higher phase-matching pressure. Under conditions where higher ionization levels are reached, phase matching can still be reached in the leading edge of the laser pulse.

Zoom In Zoom Out Reset image size

We also show in figure 1, the minimum pulse energy E_f required to reach an intensity of 1.5 × 10¹⁴ W cm⁻² assuming a pulse length of 45 fs. Using a laser pulse with for instance 10 μJ pulse energy, a focal length of approximately 6 cm is needed for a Gaussian beam with 3 mm diameter before focusing. Under these conditions, with a degree of ionization less than 1%, a pressure of approximately 1 bar is necessary in order to achieve phase matching.

The above argumentation considers the phase-matching situation at the focus. More generally, it is possible to express phase-matching conditions that are independent of focal length within a generating volume. We consider the generation volume with the length L_max and radial diameter D_max in which the laser intensity I exceeds the threshold intensity I_t to generate a certain harmonic order q, i.e. such that qℏω ⩽ I_p + 3.17U_p(I), where I_p is the ionization potential and U_p the ponderomotive energy. I_t is therefore given by

$$\begin{equation} I_{\rm t}(q) = \frac{2 m \omega ^2 c_0 \varepsilon _0}{e^2} \frac{(q\hbar \omega - I_{\rm p})}{3.17}, \end{equation} \tag{ 4 }$$

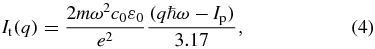
where m, c₀, ε₀ and e denote electron mass, speed of light, dielectric constant and electron charge, respectively. Assuming Gaussian optics, it is straightforward to derive the following relations:

$$\begin{equation} L_{\rm max} = \frac{8\lambda }{\pi } f_{\#}^2 \sqrt{\left.\frac{I_0}{I_{\rm t}}\right.-1}, \end{equation} \tag{ 5 }$$

$$\begin{equation} D_{\rm max} = \frac{\lambda }{\pi } f_{\#} \sqrt{8 \ln \left( \frac{I_0}{I_{\rm t}}\right)}. \end{equation} \tag{ 6 }$$

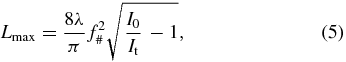
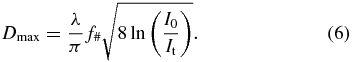
Equations (5) and (6) show that the length of the generation volume scales as L_max∝f² and its radial diameter as D_max∝f. Scaling the driving pulse energy as E_f∝f² leads to a constant intensity distribution within the considered volume. Since the longitudinal dimension of this volume scales with f², Δk_q follows the same scaling law. Therefore, equation (2) can be generalized to z ≠ 0, by including a term (Δk_q · f²).

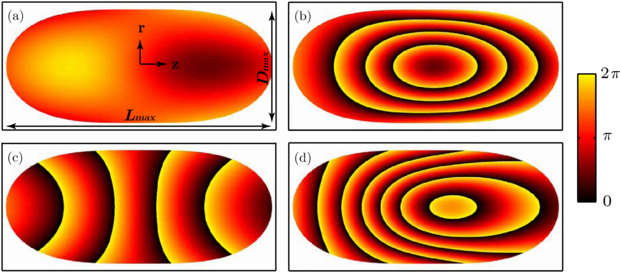
In figure 2, we show a generalized phase-matching map valid for all the focal lengths. In contrast to previous work [47, 48], where the degree of phase matching was represented graphically via the coherence length L_coh = π/Δk over which the harmonic field can be built up constructively, we plot simply Δφ modulo 2π as a function of r and z centred at the focus and in time (t = 0) at the maximum of the fundamental laser pulse envelope. The dipole phase is calculated within the approximation of classical trajectories in order to define the proportionality constants α_q. For q = 17, as considered in figure 2, α₁₇ = 2.4 × 10⁻¹³ cm² W⁻¹ for the long and approximately zero for the short trajectory. For higher harmonic orders, α_q increases for the short trajectory, being, however, significantly smaller than for the long trajectory. While the dipole phase as well as the Gouy phase can be calculated directly as a function of r and z, the dispersion terms are calculated via integration of $\Delta {\bm k}_{\rm n}$ and $\Delta {\bm k}_{\rm p}$ along the propagation axis. In figure 2(a), the phase-matching condition is approximately optimized for the short trajectory for two areas before and behind the focus, indicated by an almost constant value of Δφ. 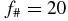For $f_{\#} = 20$ and 10 μJ pulse energy (the same example as above), the corresponding phase-matching pressure is 600 mbar. A slightly higher pressure would lead to optimized conditions at the focus which would correspond to the situation in figure 1. For the same conditions, Δφ varies strongly for the long trajectory, as shown in figure 2(b).

Zoom In Zoom Out Reset image size

In figures 2(c) and (d), we show the situation where the dispersion terms are negligibly small which is typically the case when the gas pressure is too low. Under these conditions, the geometrical phase leads to strong phase modulations along z, which results in a reduced signal strength for the short trajectory. The spatial and temporal properties of the generated harmonic beam are, however, not significantly affected by a longitudinal phase mismatch. Spatial phase and intensity modulations in the far-field typically arise due to radial phase modulations in the generation volume, which lead to a distorted wave front, whereas temporal modulations occur if the phase-matching situation is time dependent. Since only small phase modulations occur in the radial direction the emitted beam is spatially well confined even under these non-phase-matched generation conditions. Additionally, only weak temporal variations of the phase mismatch can be expected for the short trajectory. The typical phase-matching problem at short focal lengths does limit the overall efficiency but still allows for a high beam quality. In contrast, strong spatial intensity modulations are expected for the long trajectory due to a strong radial variation of Δφ. Furthermore, the strongly intensity-dependent dipole phase leads to temporal phase variations that can lead to complicated temporal and spectral structures [32].

Aside from phase matching, we have to consider absorption effects within the generation volume. Increasing the pressure up to the phase-matching pressure would typically lead to conditions where the absorption length (L_abs = 1/σρ, where ρ is the gas density and σ is the ionization cross section) is significantly shorter than the medium length L_med. Following the argumentation in [49], the optimum is reached for L_coh > 5L_abs and L_med > 3L_abs. In order to avoid re-absorption of the emitted XUV photons behind the generation volume, L_med should not exceed L_max. Therefore, we obtain

$$\begin{equation} L_{\rm max} > L_{\rm med} > 3 L_{\rm abs}. \end{equation} \tag{ 7 }$$

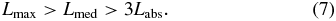
Although the theoretical considerations above show that in principle, the same phase-matching conditions can be reached with long as well as with short focal lengths so that (7) can be fulfilled, technical constraints typically set the limits at tight focus geometries. At focal lengths of a few centimeter, the gas medium has to be confined to a size below 1 mm, while allowing a pressure of a few bar. For p ≪ p_match (7) cannot be fulfilled. Since the amount of contributing atoms within the generation volume as well as L_coh is very small under these conditions, this leads to a dramatically reduced HHG signal. As explained above, this should, however, not deteriorate the spatial and temporal coherence properties for the short-trajectory emission significantly.

Furthermore, it is very important to minimize the ionization level when generating high-order harmonics under tight focusing conditions in order to keep the phase-matching pressure as low as possible. A possible way to achieve such a situation, while still reaching high harmonic orders would be to use longer driving wavelengths in the μm range [50].

2.3. Geometrical scaling

Aside from a possible influence due to phase matching, the geometrical scaling of the generation volume limits the generated photon flux at short focal lengths. A general expression can be formulated by considering the number of atoms n contributing to the harmonic emission [51]. n can be expressed as a product of the pressure p and the maximum dimensions of the nonlinear medium: n∝pL_maxD²_max. According to the above argumentation, we have to scale p as ∝1/f² in order to maintain the phase-matching conditions. Considering further the scaling relations for L_max and D_max, we obtain n∝f². Since E_f has to be scaled in the same way in order to maintain the intensity, the amount of fundamental pulse energy per contributing atom is independent of focal length. For a certain phase-matching situation, we therefore achieve a conversion efficiency η_q = E_h/E_f, which is independent of f. Consequently, the harmonic pulse energy E_h follows the same scaling relation as E_f and we obtain

$$\begin{equation} E _{\rm h} \propto f^2 . \end{equation} \tag{ 8 }$$

This equation is valid not only for a phase-matched generation but in general for all phase-matching conditions as long as the generation parameters are scaled appropriately. This implies a sufficiently long medium or a scaling of the medium length with L_max and therefore as L_med∝f². All relevant scaling relations are summarized in table 1, showing f, as well as E_f, as a scaling parameter.

Table 1. Scaling relations: a scaling of the given experimental parameters f, E_f, p and L_med with f or E_f, as shown on the left side of the table, causes the scaling behaviour of L_max, D_max, n, E_h and n_q shown on the right side.

Scaling parameter	f	Ef	p	Lmed	Lmax	Dmax	n	Eh	ηq
f	–	f2	1/f2	f2	f2	f	f2	f2	Const.
Ef	$\sqrt{E_{\rm f}}$	–	1/Ef	Ef	Ef	$\sqrt{E_{\rm f}}$	Ef	Ef	Const.

In contrast to possible phase-matching problems that can, in principle, be solved even at a short focal length, the geometrical scaling relations described above set a general limit for the harmonic yield. Due to a geometrical scaling of the interaction volume, the laser pulse energy that can be up-converted into high harmonic radiation scales quadratically with focal length. This indicates that the focal length should always be chosen as long as possible when a high XUV photon flux is required. At short focal lengths, technical constraints typically limit the pressure to values well below p_match. This leads to a reduced signal due to a deteriorated phase-matching situation and a reduced number of contributing atoms. For many applications, however, the photon flux is not a limitation. Instead, good coherence as well as good spatial and spectral properties are often more important and can be achieved easily even at short focal lengths.

The average power of current femtosecond laser systems is typically limited to a few watts. Therefore, a high repetition rate is always linked to a low-pulse energy. Consequently, a short focal length is necessary to generate high-order harmonics at high repetition rates in order to reach the intensities required for the generation process.

An overview of the experimental setup is shown in figure 3. The laser system used in our experiments delivers pulses up to 7 μJ with a pulse duration of 45 fs full-width at half-maximum, centred at 800 nm. It is based on a commercial system from Coherent Inc., consisting of a titanium–sapphire oscillator (Mira) and a regenerative amplifier (Rega). The latter is continuously pumped by a 10 W neodym:yttrium–vanadium solid-state laser (VERDI-V10). The repetition rate of the amplifier can be adjusted between 10 and 250 kHz. For the HHG experiments, a repetition rate of 100 kHz was chosen. For higher repetition rates, the pulse energy starts to decrease considerably. By replacing the standard stretcher and compressor unit, the system was changed to down chirped pulse amplification (DPA) operation [52]. The employed Grism stretcher [53, 54] stretches the incoming laser pulses by a factor of around 350 to a pulse length of several picoseconds, introducing a negative chirp of around −400 000 fs². The amplified laser pulses are then re-compressed by passing a SF6 glass block of 25 cm length six times. By using this amplification scheme, the compressor transmission could be increased to above 90%, while avoiding the introduction of pulse front distortions due to a misaligned compressor. This leads to a significantly better beam quality and a 30% higher pulse energy after compression. Furthermore, a Grism-based stretcher allows for a precise chirp compensation up to the third order [54]. Even large additional dispersion due to dispersive elements in the beam path behind the compressor can easily be compensated.

Zoom In Zoom Out Reset image size

The linear polarized amplified laser pulses are focused with an achromatic lens (f = 60 mm) into the interaction gas. The gas is supplied by a thin nozzle, consisting of a stainless steel tube with an inner diameter of 90 μm. In the experiment, two different kinds of nozzle geometries were used. The laser was focused either through two 50 μm holes into the nozzle (configuration A) or directly in front of the open nozzle (configuration B). The nozzle was mounted on a three-dimensional translation stage for precise positioning within the focus. A camera was used to image the nozzle on axis through a dielectric mirror. This is important since the laser beam has to be adjusted with a precision of 10 μm relative to the nozzle.

The emitted harmonics pass a pinhole (0.5 mm diameter) used for differential pumping and located directly behind the interaction volume. A 200 nm thick aluminium foil is used to block the fundamental beam, while transmitting the harmonics. A concave XUV grating (Hitachi, Grating 001-0639, 600 l mm⁻¹) is used for spectral imaging onto a microchannel plate (MCP) assembly in the horizontal plane. In the vertical plane, the grating reflects the harmonics without any refocusing, allowing us to image spectral and spatial profiles simultaneously.

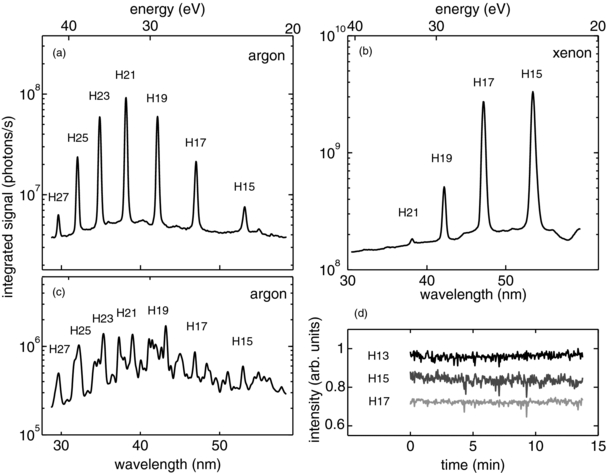
Typical harmonic spectra generated in argon and xenon are shown in figures 4(a) and (b). In both spectra, we observe the typical comb structure of high contrast peaks occurring at odd multiples of the driving laser frequency. The vertical axis displays the estimated spatially integrated photon flux per harmonic order. The calibration was done by extrapolating single-photon counts at low intensities taking into account the efficiency of the grating and the MCP as well as the transmission through the filter. We achieve a photon flux of up to 10⁸ in argon and 3 × 10⁹ photons s⁻¹ in xenon. This is comparable to the photon flux used in [15] for time-resolved 2PPE, where, however, a high-power 3 kHz system was employed. The spectra were recorded when the gas cell was placed approximately 200 μm behind the focus. Under these conditions, a dominant contribution from the short trajectory can be expected [39]. As typical for the short trajectory, the harmonics appear spatially well confined (approximately 30 mrad divergence) and spectrally narrow (approximately 250 meV at harmonic 21) even though we cannot assume a phase-matched generation due to a pressure well below the calculated phase-matching pressure. This is in good agreement with our theoretical considerations as presented above (see figure 2(c)).

Zoom In Zoom Out Reset image size

At the focus, phase matching for the short trajectory is worse but it improves considerably for the long trajectory. This can be seen when comparing the longitudinal phase variations close to and behind the focus in figures 2(c) and (d). In the experiment, we observe a weaker, more divergent and spectrally broadened signal at the focus that we interpret as due to a dominant contribution from the long trajectory. The spectral and spatial characteristics can be explained as due to the dipole phase that varies strongly in time and in space within the generation volume. A strong variation of the dipole phase in radial direction across the focus leads to a divergent beam and intensity modulations in the spatial profile. The phase variation in time leads to a spectral splitting of the individual harmonic lines [32]. A strong temporal intensity modulation can therefore be expected under these conditions. We observe these phenomena for argon as well as for xenon. In accordance with previous results [27] and due to a lower ionization potential, the harmonics generated in xenon are characterized by a higher yield and a less pronounced plateau extension. However, no further qualitative differences have been observed.

In figure 4(c), the temporal stability of the harmonic signal generated in argon is shown. As in a typical application where integration times in the order of 1 s are common, the spectrally and spatially integrated signal was time averaged over 0.5 s. We then compute a RMS deviation of only 2.5%.

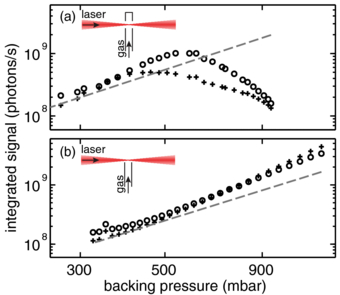
We have further investigated the influence of different target sizes and geometries. A pressure-dependent signal measured with two different gas nozzles is shown in figure 5. The conditions here are similar to those shown in figure 4(b). In configuration A (figure 5(a)), where the laser beam passes through the nozzle, the gas flow is directed along the beam axis. In configuration B (figure 5(b)), where the beam is focused directly in front of the open nozzle, the gas flow occurs perpendicular to the beam axis. Although we expect a higher gas density in the generation volume in configuration A, the highest yield was measured with configuration B. We interpret this result as follows: due to the gas flow geometry, the gas medium in configuration A extends far behind the generation volume. Absorption of the generated harmonics leads to a dropping signal at higher pressures. In configuration B, no absorption effects are visible.

Zoom In Zoom Out Reset image size

In both configurations, a signal that increases more than quadratically with pressure can be observed. Measuring the harmonic yield as a function of the pressure gives direct information about the phase-matching conditions. In general, a quadratic growth indicates that the phase-matching situation does not change with increasing pressure, which is typically the case at low pressure conditions well below the phase-matching pressure. A super quadratic growth indicates improving phase-matching conditions [45]. The opposite behaviour can be expected if phase matching deteriorates or if absorption starts to play a role. Following this argumentation, a clear indication for an improving phase-matching situation is visible in figure (5). A comparison with our simulations suggests that the phase-matching pressure needed in our experimental conditions lies in the range of 1 bar, while gas flow estimations yield a pressure of 50 mbar in the interaction volume at 800 mbar backing pressure. At 50 mbar, L_abs is smaller than 1 mm for harmonics 15 and 17, supporting our interpretation for an absorption limited signal in configuration A. Assuming that the intensity is below the critical limit where plasma dispersion would prevent phase matching, the harmonic yield could be increased dramatically and phase matching could be achieved by increasing the pressure in the interaction volume. Using the classical cut-off law, the peak intensity in our experimental conditions was estimated to approximately 1.5 × 10¹⁴ W cm⁻². At this intensity, the estimated ionization level at the peak of the pulse is below 1% (estimated with a modified Ammosov–Delone–Krainov model using the correction factors introduced in [48]), and therefore, a phase-matched generation should be possible.

While absorption sets the limit in configuration A, the limit in B is simply given by the pressure in the vacuum chamber (the chamber was pumped using a 500 l s⁻¹ turbomolecular pump) that has to be limited to avoid a damage of the MCP detector. As expected for a higher refractive index, the phase-matching conditions improve faster with increasing pressure for the 15th harmonic than for the 17th. Furthermore, the absorption limit sets in earlier for harmonic 15 due to a shorter absorption length. Both effects are clearly visible in figure 5. In both configurations, the highest yield was measured with the smallest gas nozzle. The reason is a relatively short coherence length well below the length of the gas volume due to a gas pressure well below the phase-matching pressure.

In conclusion, we have systematically analysed the generation of high-order harmonics for different focusing geometries. A generalized macroscopic model allows us to specify the conditions for the efficient generation of high-order harmonics using tight focus geometries. We identify a simple geometrical scaling for the maximum harmonic yield as a function of focal length and pulse energy. Scaling the focal length with $\sqrt{E_{\rm f}}$, the medium length with E_f and the pressure as 1/E_f allows for the generation of high-order harmonics with the same phase-matching conditions and the same conversion efficiency. Considering the situation where the average laser power does not depend on the repetition rate, this implies a repetition rate-independent average power for the generated XUV beam.

Using a 100 kHz laser system, we generate high-order harmonics in argon and xenon with a laser pulse energy of only a few μJ. Measuring the harmonic spectral and spatial profiles at different focus positions allows us to identify contributions from different trajectories. We show experimentally and theoretically that our harmonics are not generated phase matched. A phase-matched generation could, however, be expected at much higher gas densities. Nevertheless, spatially well-confined, spectrally narrow harmonics are generated with a photon flux up to 3 × 10⁹ photons s⁻¹ (conversion efficiency 10⁻⁸) into one harmonic order, which is sufficient for a typical photoemission experiment. The efficiency is comparable to the value reported in [31] where the authors claim a phase-matched generation. In contrast, we show that we achieve similar results under non-phase matched conditions, which implies the possibility of increasing the efficiency (and the photon flux) considerably, by using smaller gas volumes at higher densities.

Our results clearly show that the generation of high-order harmonics is possible even with relatively low pulse energies, which opens the way for high-repetition-rate attosecond XUV sources. We show further that there are no fundamental differences between HHG with high-energy laser pulses and the generation with μJ pulses. With the currently available laser systems, this implies the possibility for the generation of single attosecond pulses at MHz repetition rates.

This research was supported by the Deutsche Forschungsgemeinschaft through HO 2295/1-2 and GRK 790, the European Research Council (ALMA), the Marie Curie Training Network ATTOFEL, the Knut and Alice Wallenberg foundation and the Swedish Research Council.