Abstract
In this work, a model is developed to continuously predict homogeneous and inhomogeneous swelling behavior of pH/temperature sensitive PNIPAM hydrogels. Employing the model, homogeneous swelling of the pH/temperature sensitive hydrogel is investigated for free and biaxial constrained swelling cases. Comparing the model results with the experimental data available in the literature, the validity of the model is confirmed. The model is then employed to investigate inhomogeneous swelling of a spherical shell on a hard core both analytically and numerically for pH or temperature variations. In this regard, numerical tools are developed via preparing a user defined subroutine in ABAQUS software. Then, the complicated problem of contact between the hydrogel shell and a micro-channel with rigid walls is also investigated. Considering the results, we can say that the model is applicable for solving engineering boundary value problem of pH/temperature sensitive hydrogels.
Export citation and abstract BibTeX RIS
1. Introduction
Smart hydrogels consist of covalently cross-linked networks which are capable of responding to the environmental conditions through the swelling phenomenon. The major reaction of the network against the environmental conditions is change in the swelling amount. Some of the effective parameters in the amount of swelling are temperature [1–3], pH [4, 5], mechanical load [6, 7], ionic and salt concentration [8], light [9, 10] and electric field [11, 12]. Due to this interesting behavior, these materials have found novel applications in tissue engineering and drug delivery systems [13], sensors and actuators [14–18], microfluidics and micro-valves [19, 20]. In most of applications, a constitutive model is required to describe the hydrogel response under complicated thermo-chemo-mechanical conditions.
The coupled nonlinear field theory of hydrogels has attracted a great deal of interest, especially in recent years [4, 6, 8, 21–26]. A basic work in this field is that of Hong et al [23] in which a constitutive model was presented for neutral hydrogels. This work provided a framework for other researcher study in this field. On the other hand, in line with their previous work, Hong et al [27] developed a FEM tools for modeling the swelling behavior of neutral hydrogels, successfully. Following these pioneering works, the behavior of the neutral hydrogels was studied by other researcher. The coupled thermo-mechanical behavior of the temperature-sensitive hydrogels has been investigated in recent years. Ji et al [28] developed a constitutive model in the scope of finite-strain kinematics for thermally induced volume transitions in stimulus–responsive hydrogels. Employing a biphasic approach, Birgersson et al [29] presented a model for transient deformation of a neutral hydrogel due to the temperature gradient. Chester and Anand [30] introduced a large deformation constitutive model for the coupled thermo-mechanical behavior of thermally responsive elastomeric gels. Validating with the experimental data, Cai and Suo [31] established a constitutive model for the temperature sensitive poly-(N-isopropylacrylamide) hydrogel (PNIPAM hydrogel). However, in the vicinity of the phase-transition temperature, multiple-solutions and snap-through instability was observed. Following Cai and Suo [31], Mazaheri et al [32] presented a modified model for the PNIPAM hydrogel which eliminates the instability and successfully implemented the modified model in inhomogeneous swelling problems [20].
Furthermore, complicated behavior of the pH-sensitive hydrogels has been studied in recent years [4, 5, 33, 34]. Marcombe et al [4] developed a model for the pH-sensitive hydrogels at the equilibrium state. They successfully employed electro-neutrality assumption for the hydrogel network and the external solution. Comparing to the experimental results, they validated their model. Implementing the model in the finite element framework, they discussed on some examples. Also, Kurnia et al [35] studied the behavior of pH-sensitive hydrogels and presented the solution for the swelling behavior of a cylinder made of the pH-sensitive hydrogel. They employed conservation laws for mass, momentum and ion, and validated the results with the available experimental data. Li et al [36] investigated the constitutive modeling of polyelectrolyte gels and verified the model using a polyacrylamide-co-acrylic acid hydrogel. They utilized the Gent model for capturing the non-Gaussian chain effect and validated the model through comparing with the experiments. Following Marcombe et al [4], Yan et al [34] developed a field theory for the behavior of a network of polyampholytic pH-sensitive hydrogel. They studied the influence of pH, salt concentration, geometric constraint and the effects of the electrical double layer on the swelling properties.
In this work following Guo and Gao [37] and Mazaheri et al [32], we develop a field theory for the swelling behavior of the pH/temperature-responsive carboxymethyl chitosan/poly(N-isopropylacrylamide)semi-IPN hydrogels. We consider this material as a PNIPAM hydrogel with some acidic groups attached to it. The interaction parameter of the network is assumed to be a function of both the temperature and polymer volume fraction as reported for the PNIPAM hydrogels by Afroze et al [38]. Also, we employ the electro-neutrality assumption for the electric charge distribution. The presented model is validated with the experimental results available in the literature. It is noteworthy to mention that the multiple-solutions and instability problems in the vicinity of PTT are also avoided.
The paper is organized as follows. Firstly, the model is explained in detail and governing formulations are presented in section 2. Thereafter, homogeneous swelling of the pH/temperature sensitive hydrogels is investigated in section 3.1. In section 3.1.1, a comprehensive study on the free swelling problem is presented and the model is validated comparing to the experimental data reported by Guo and Gao [37]. As another example of the homogeneous deformation, the biaxial constrained swelling problem of the hydrogel is studied in section 3.1.2. Then, the inhomogeneous swelling of the spherical hydrogel shells on a fixed rigid core is analytically studied for pH/temperature sensitive hydrogel and the results are presented in section 3.2.1. Also, numerical implementation of the presented model in ABAQUS is performed. With the aid of this numerical tool, considering the contact effects, the inhomogeneous swelling of the spherical hydrogel shells on a fixed rigid core is investigated in section 3.2.2. Finally, we present a summary and draw conclusions in section 4.
2. Model description
In this paper, the pH/temperature sensitive hydrogel network is composed of polymeric chains bearing acidic groups  Immersing in an aqueous solution, the network imbibes the solution and swells. Due to existence of ions in the solutions and acidic groups on the network, the swelling of the network is affected by the external solutions conditions, specially its pH and ionic strength. Also, due to existence of semi-NIPAM chain in the network, the network is capable of responding to the temperature changes. A schematics draw of this material structure beside the external solution is shown in figure 1.
Immersing in an aqueous solution, the network imbibes the solution and swells. Due to existence of ions in the solutions and acidic groups on the network, the swelling of the network is affected by the external solutions conditions, specially its pH and ionic strength. Also, due to existence of semi-NIPAM chain in the network, the network is capable of responding to the temperature changes. A schematics draw of this material structure beside the external solution is shown in figure 1.
Figure 1. Schematics draw for structure of a pH/temperature sensitive hydrogel beside the external solution with salt contents. Due to pH changes  groups dissociate into
groups dissociate into 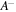 and
and 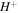 .
.
Download figure:
Standard image High-resolution imageDiffusion of the external solvent molecules and ions through the hydrogel, results in deformation in the network. Considering an element of the network in the reference (dry) and current (deformed) states, the coordinates are denoted by vectors 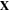 and
and 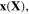 respectively. Employing the Lagrangian approach, the current coordinate,
respectively. Employing the Lagrangian approach, the current coordinate,  is a function of its reference one which describes the network deformation. In terms of
is a function of its reference one which describes the network deformation. In terms of  the deformation gradient tensor,
the deformation gradient tensor, 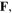 and consequently, the right Cauchy-Green deformation tensor,
and consequently, the right Cauchy-Green deformation tensor, 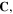 can be defined as:
can be defined as:
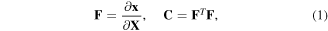
where the superscript 'T' denotes the transpose of the tensor. The region occupied by the network in the references state and its boundary are denoted by  and
and  respectively. As shown in figure 1, in the equilibrium state, the external solution is composed of four species, i.e. solvent molecules, counter-ion, co-ion and hydrogen ion which their number in the external solution are
respectively. As shown in figure 1, in the equilibrium state, the external solution is composed of four species, i.e. solvent molecules, counter-ion, co-ion and hydrogen ion which their number in the external solution are 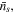
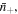
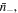 and
and 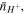 respectively. Assuming small variations in the species numbers, the change in the free energy of the external solution at a specified temperature,
respectively. Assuming small variations in the species numbers, the change in the free energy of the external solution at a specified temperature,  is:
is:

where 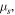

 and
and 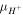 are electro-chemical potential of the related species, respectively and
are electro-chemical potential of the related species, respectively and  denotes the variational operator. Also, neglecting body forces, the amount of potential energy change in the network due to the mechanical force is equal to
denotes the variational operator. Also, neglecting body forces, the amount of potential energy change in the network due to the mechanical force is equal to  where
where 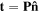 is the traction force on the boundary of the network.
is the traction force on the boundary of the network. 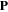 and
and 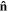 are the nominal stress tensor and the boundary unit normal vector, respectively. The change in the free energy of the network is equal to
are the nominal stress tensor and the boundary unit normal vector, respectively. The change in the free energy of the network is equal to  in which
in which 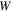 is the free energy density of the network expressed in the reference state. Considering both the hydrogel and the external solution as a system, the condition of the equilibrium is [4]:
is the free energy density of the network expressed in the reference state. Considering both the hydrogel and the external solution as a system, the condition of the equilibrium is [4]:
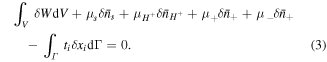
On account of conservation of any species in the system, we may write:
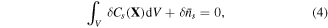
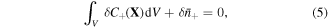

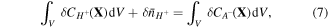
where  is nominal concentration of species
is nominal concentration of species 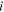 in the network and is related to the true concentration,
in the network and is related to the true concentration,  via
via 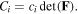 Also, employing the electro-neutrality both in the network and the external solution we arrive at:
Also, employing the electro-neutrality both in the network and the external solution we arrive at:
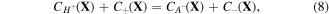

Substituting (4)–(9) in (3), we attain a variational statement for the free energy change of the system as:
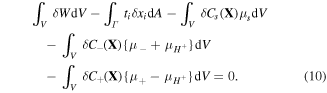
During the acidic dissociation, the number of the fixed acidic groups on the network remains constant and only the hydrogen ions can freely move between the external solution and the network. Thus, we have [4]:
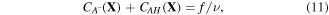
where 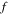 and
and 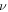 are number of the acidic groups attached to the network per monomer and volume of a monomer, respectively. It is concluded from (8) and (11) that both the
are number of the acidic groups attached to the network per monomer and volume of a monomer, respectively. It is concluded from (8) and (11) that both the  and
and 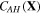 are not independent variables and can be stated in terms of
are not independent variables and can be stated in terms of 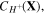
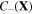 and
and  Thus, considering the free energy function as
Thus, considering the free energy function as 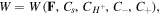 its variation statement is calculated as
its variation statement is calculated as 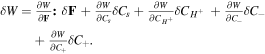 Now, considering the free energy variation and employing divergence theorem for the second term of (10), we arrive at:
Now, considering the free energy variation and employing divergence theorem for the second term of (10), we arrive at:
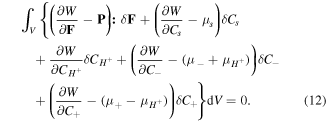
Therefore, following the standard arguments, the constitutive laws for the network are expressed as:
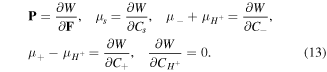
Neglecting the volume of the other species in the network due to their low concentration, the change in the volume of the network originates from the fluid molecules diffusion through the network. Thus, we have [23]:
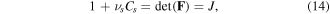
where 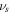 and
and 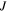 are the volume of a molecule of the fluid and deformation gradient determinant, respectively. To implement this constraint on the system, employing the Lagrange method, we should modify the free energy as
are the volume of a molecule of the fluid and deformation gradient determinant, respectively. To implement this constraint on the system, employing the Lagrange method, we should modify the free energy as 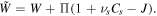 In terms of the modified free energy density, the constitutive laws for the nominal stress and chemical potential of solvent molecules are recalculated as:
In terms of the modified free energy density, the constitutive laws for the nominal stress and chemical potential of solvent molecules are recalculated as:

where 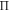 is the Lagrange multiplier and its elimination from (15) results in:
is the Lagrange multiplier and its elimination from (15) results in:
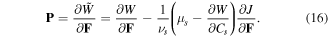
Considering a small density of crosslinking for the hydrogel, we assume an additive decomposition of the free energy density in the form of (see e.g., [4, 23, 27, 30, 31, 39] among others):
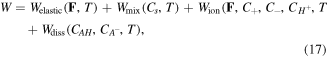
where 
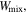
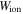 and
and  are the free energy density due to the elastic deformation, mixing between the solvent and the network chain, mixing of ions and dissociation of the acidic groups, respectively. We use a neo-Hookean model to describe the elastic deformation of the network where it is expressed in terms of the deformation as:
are the free energy density due to the elastic deformation, mixing between the solvent and the network chain, mixing of ions and dissociation of the acidic groups, respectively. We use a neo-Hookean model to describe the elastic deformation of the network where it is expressed in terms of the deformation as:
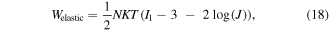
in which  and
and 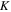 are density of the polymer chains in the reference state and Boltzmann constant, respectively. In addition,
are density of the polymer chains in the reference state and Boltzmann constant, respectively. In addition, 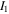 is the first invariant of
is the first invariant of 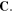 Also, based on the Florry–Huggins theory, the mixing part of the free energy density is [40, 41]:
Also, based on the Florry–Huggins theory, the mixing part of the free energy density is [40, 41]:
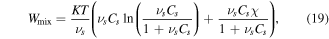
where 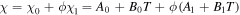 is the interaction parameter of the network assumed to be a function of the temperature and the polymer volume fraction,
is the interaction parameter of the network assumed to be a function of the temperature and the polymer volume fraction, 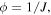 for the temperature sensitive PNIPAM hydrogel. In addition,
for the temperature sensitive PNIPAM hydrogel. In addition, 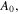

 and
and 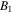 are material parameters adopted for the experiments reported by Afroze et al [38]. In light of the swelling constraint, (14), we rewrite (19) as:
are material parameters adopted for the experiments reported by Afroze et al [38]. In light of the swelling constraint, (14), we rewrite (19) as:
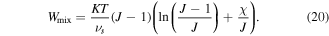
However, as discussed by Mazaheri et al [32] this part of the free energy density encounters a numerical instability in the vicinity of phase transition temperature due to multiple solution problems. It is worth to mention that some techniques such as Riks methods can be used to overcome this instability however, this is computationally expensive in a numerical scheme [27, 42]. To avoid such numerical difficulties, we should modify the mixing energy statement so that the instability is removed while the model accuracy is preserved. To this end the method presented by Mazaheri et al [32] is utilized. This instability is eliminated via polynomial expanding of the ill-posed logarithmic term as [32]:
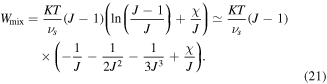
Employing this free energy, a stable model is developed which is capable of predicting the transition behavior of the hydrogel for temperature changes. As a results, we can use this model in the inhomogeneous problems without encountering any inherent instability of the model with a lower computational cost. Considering a low concentration of the ions, the change in the free energy density of the system due to the ions mixing is entropic and expressed as [4]:

where 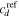 is a reference concentration for the species
is a reference concentration for the species 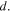 Also, the free energy change of the acidic dissociation which originates from the entropy change due to mixing and enthalpy change for the acidic dissociation, is stated as [4]:
Also, the free energy change of the acidic dissociation which originates from the entropy change due to mixing and enthalpy change for the acidic dissociation, is stated as [4]:
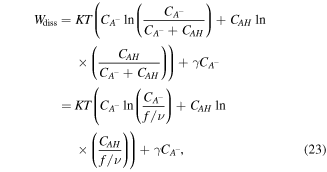
where 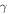 is the enthalpy change due to the dissociation of one acidic group. Employing the defined free energy density and constitutive laws, we arrive at:
is the enthalpy change due to the dissociation of one acidic group. Employing the defined free energy density and constitutive laws, we arrive at:
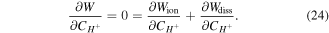
Keeping in mind that both  and
and  are not independent, through applying the chain rule in (24), we have:
are not independent, through applying the chain rule in (24), we have:

Now, based on (13), the chemical potential of the co-ion is:
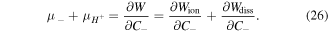
Substituting (25) in (26) and after some mathematical manipulation we obtain:
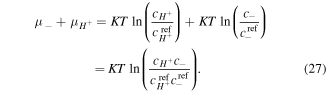
Similarly, for the chemical potential of counter-ion we deduce:
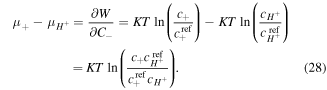
Assuming the dilute solution, the chemical potential of species  in the solution is [8]:
in the solution is [8]:
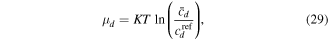
in which  is the true concentration for the species
is the true concentration for the species  Substituting (29) in (27) and (28) yields:
Substituting (29) in (27) and (28) yields:
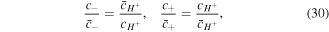
which are well-known equations named the Donnan equations. Based on (30), it is concluded that the co-ion and counter-ion true concentrations in the network are dependent on the true concentration of the hydrogen ion in the network and external solution conditions. Thus, once the external solution conditions and hydrogen ion concentration in network are known, dependent values of the co-ion and counter-ion true concentrations in the network are determined.
The acidic dissociation obeys a relation as below:
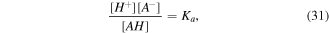
where ![$[i]$](https://content.cld.iop.org/journals/0964-1726/25/8/085034/revision1/smsaa2748ieqn68.gif) represents the molarity of species
represents the molarity of species  in the network which is equal to
in the network which is equal to ![${c}_{i}=[i]{N}_{A}$](https://content.cld.iop.org/journals/0964-1726/25/8/085034/revision1/smsaa2748ieqn70.gif) while
while  is the Avogadro number. Now, substituting (8) and (11) in (31) and expressing the concentration in the current state we arrive at:
is the Avogadro number. Now, substituting (8) and (11) in (31) and expressing the concentration in the current state we arrive at:
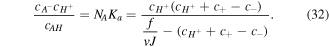
Also, replacing (30) in (32) results in a cubic equation for 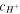 as below:
as below:
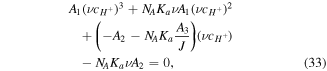
where the coefficients  are:
are:
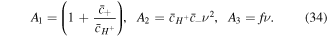
As concluded from Donnan equations, the co-ion and counter-ion concentrations in the network are dependent on the  which could be determined from (33) and are functions of the deformation due to presence of
which could be determined from (33) and are functions of the deformation due to presence of  in the coefficient of this cubic equation. Thus, all variables can be expressed as functions of the deformation field and external solution concentrations. It is assumed that the external solution is large enough so that the salt concentration and pH are assumed to be constant during the deformation of the hydrogel network. The hydrogen ion concentration in the external solution is calculated as:
in the coefficient of this cubic equation. Thus, all variables can be expressed as functions of the deformation field and external solution concentrations. It is assumed that the external solution is large enough so that the salt concentration and pH are assumed to be constant during the deformation of the hydrogel network. The hydrogen ion concentration in the external solution is calculated as: ![${\bar{c}}_{{H}^{+}}={N}_{A}[{H}^{+}]={N}_{A}{10}^{-\overline{pH}}.$](https://content.cld.iop.org/journals/0964-1726/25/8/085034/revision1/smsaa2748ieqn76.gif) Also, having the counter-ion concentration in the external solution, the related co-ion concentration can be computed from the electro-neutrality assumption as:
Also, having the counter-ion concentration in the external solution, the related co-ion concentration can be computed from the electro-neutrality assumption as:  Now, having the external concentration, the hydrogen ion, the co-ion and the counter-ion concentrations in the hydrogel network can be determined from the Donnan equation (30) and the cubic equation of (33). Thus, the complicated multi-field swelling problem is reduced to a deformation field problem. In order to investigate the deformation field, a statement for the stress is necessary. In this paper, we use the nominal stress determined from the constitutive laws. After some simplifications we have:
Now, having the external concentration, the hydrogen ion, the co-ion and the counter-ion concentrations in the hydrogel network can be determined from the Donnan equation (30) and the cubic equation of (33). Thus, the complicated multi-field swelling problem is reduced to a deformation field problem. In order to investigate the deformation field, a statement for the stress is necessary. In this paper, we use the nominal stress determined from the constitutive laws. After some simplifications we have:

where  It is worth to mention that in this work we present a constitutive model for pH and temperature sensitive hydrogels. To account for the pH sensitivity, we employ the well-known model of Marcombe et al [4]. But to capture the temperature sensitive behavior of the model, we implement the mixing parameter function in the free energy to model the temperature sensitivity. Also, to achieve a stable behavior of the model especially in the vicinity of the phase transition temperature, the mixing function is modified. Thus, the model is capable of simulating the behavior of the pH and temperature sensitive hydrogels.
It is worth to mention that in this work we present a constitutive model for pH and temperature sensitive hydrogels. To account for the pH sensitivity, we employ the well-known model of Marcombe et al [4]. But to capture the temperature sensitive behavior of the model, we implement the mixing parameter function in the free energy to model the temperature sensitivity. Also, to achieve a stable behavior of the model especially in the vicinity of the phase transition temperature, the mixing function is modified. Thus, the model is capable of simulating the behavior of the pH and temperature sensitive hydrogels.
3. Results and discussion
In this section, the proposed model is employed to investigate some bench-mark problems involving homogeneous and/or inhomogeneous swelling of the pH/temperature sensitive hydrogels. The material parameters of the network are adopted for experiments available in the literature and shown in table 1. Based on the other works [4, 23, 37], we assume that 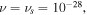
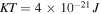 and
and 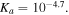 Firstly in section 3.1, some homogeneous examples are solved and the results are compared to the experimental data available in the literature to show the validity of the model. Then in section 3.2, inhomogeneous swelling of the hydrogel is studied for a spherical shell of the pH/temperature sensitive hydrogel on a hard core for variation of the both pH and temperature. This problem is solved both analytically and numerically. To solve boundary value problems the proposed model is implemented in the finite element framework through producing a user defined subroutine in ABAQUS software.
Firstly in section 3.1, some homogeneous examples are solved and the results are compared to the experimental data available in the literature to show the validity of the model. Then in section 3.2, inhomogeneous swelling of the hydrogel is studied for a spherical shell of the pH/temperature sensitive hydrogel on a hard core for variation of the both pH and temperature. This problem is solved both analytically and numerically. To solve boundary value problems the proposed model is implemented in the finite element framework through producing a user defined subroutine in ABAQUS software.
Table 1. Material parameters for the network [38].

|
|
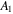
|

|
|---|---|---|---|
| −12.947 | 0.044 96 K−1 | 17.92 | −0.0569 K−1 |
3.1. Homogeneous deformations
3.1.1. Free swelling
In this section, we investigate the free swelling of pH/temperature sensitive hydrogels to validate the model with the experimental results available in the literature. Due to the homogenous deformation in the free swelling problem, we have:

where 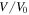 is the swelling ratio defined as the ratio of the current volume
is the swelling ratio defined as the ratio of the current volume 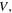 to its value at the dry state,
to its value at the dry state, 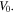 In the free swelling problem, the network experiences a free-stress state. Thus, to determine the equilibrium state for the free swelling state, equating the stress equation, namely (35), to zero, the value of swelling ratio at the equilibrium is identified and the results are shown in figure 2 for both the temperature and pH variations. For comparison we present the results of the free swelling of the neutral PNIPAM hydrogel where
In the free swelling problem, the network experiences a free-stress state. Thus, to determine the equilibrium state for the free swelling state, equating the stress equation, namely (35), to zero, the value of swelling ratio at the equilibrium is identified and the results are shown in figure 2 for both the temperature and pH variations. For comparison we present the results of the free swelling of the neutral PNIPAM hydrogel where 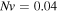 and
and 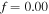 in figure 2(a). As depicted in this figure, the neutral PNIPAM has no sensitivity to the pH variation but in contrary is sensitive to the temperature variation. In figures 2(b) and (c), the results are shown for
in figure 2(a). As depicted in this figure, the neutral PNIPAM has no sensitivity to the pH variation but in contrary is sensitive to the temperature variation. In figures 2(b) and (c), the results are shown for 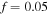 and
and  respectively, while
respectively, while 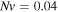 and the salt molarity is
and the salt molarity is  for both cases. The results demonstrate that increasing the acidic group density on the network, makes it more sensitive to the pH variations. To investigate the effect of salt concentration, the free swelling results are presented for the external solutions with salt molarity of
for both cases. The results demonstrate that increasing the acidic group density on the network, makes it more sensitive to the pH variations. To investigate the effect of salt concentration, the free swelling results are presented for the external solutions with salt molarity of 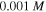 and
and  in figures 2(b) and (d), respectively, in which
in figures 2(b) and (d), respectively, in which  and
and  As observed from figures 2(b) and (d), the swelling ratio decreases by increase in the molarity of the external solution due to the diffusion of more ions in the network space and consequently, repulsion of some solvent molecules from the network.
As observed from figures 2(b) and (d), the swelling ratio decreases by increase in the molarity of the external solution due to the diffusion of more ions in the network space and consequently, repulsion of some solvent molecules from the network.
Figure 2. The free swelling results for the neutral PNIPAM hydrogels and the pH/temperature sensitive PNIPAM hydrogels with different values of cross linking density 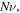 acid group number
acid group number  and salt molarity M. The related values these parameters are shown in the bottom of each figure. The sensitivity of the model to both pH and emperature variations is depicted in this figure.
and salt molarity M. The related values these parameters are shown in the bottom of each figure. The sensitivity of the model to both pH and emperature variations is depicted in this figure.
Download figure:
Standard image High-resolution imageTo study the effect of the crosslinking density, namely 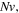 the relevant results are shown for
the relevant results are shown for 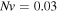 and
and  in figures 2(e) and (f), respectively, where the salt molarity and acidic group density are constant and equal to
in figures 2(e) and (f), respectively, where the salt molarity and acidic group density are constant and equal to  and
and 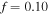 for both cases. As illustrated in figures 2(b), (e) and (f), the network is more sensitive to pH/temperature for the smaller values of
for both cases. As illustrated in figures 2(b), (e) and (f), the network is more sensitive to pH/temperature for the smaller values of 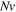 and larger volume change is observed due to the less resistance of the network against deformation. As depicted in all parts of figure 2, the swelling ratio decreases as the temperature increases due to PNIPAM content of the network. But, increasing the pH value results in a decrease in the hydrogen ion and, as a result, more acidic groups are going to be dissociated and consequently more hydrophilic regions are developed and the chains are stretched due to electrical repulsion of the negative dissociated acidic groups. Thereupon, more fluid molecules are absorbed in the network and larger amounts of the volume change are observed. The attained results are in agreement with the experimental data available in the literature [37].
and larger volume change is observed due to the less resistance of the network against deformation. As depicted in all parts of figure 2, the swelling ratio decreases as the temperature increases due to PNIPAM content of the network. But, increasing the pH value results in a decrease in the hydrogen ion and, as a result, more acidic groups are going to be dissociated and consequently more hydrophilic regions are developed and the chains are stretched due to electrical repulsion of the negative dissociated acidic groups. Thereupon, more fluid molecules are absorbed in the network and larger amounts of the volume change are observed. The attained results are in agreement with the experimental data available in the literature [37].
To validate the model with the experimental data, we consider the experiments reported by Guo and Gao [37]. But the required parameters have not been reported in the mentioned reference. Thus, we should fit the values of 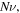
 and the external solution molarity for the experiments. First, we determine the value of
and the external solution molarity for the experiments. First, we determine the value of 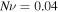 for the swelling behavior of neutral PNIPAM when
for the swelling behavior of neutral PNIPAM when  Then,
Then,  and the external solution molarity should be found through fitting for pH values of 2.1 and 7.4 as reported by Guo and Gao [37]. The fitted value of the external solution molarity that is kept constant in all experiments is equal to
and the external solution molarity should be found through fitting for pH values of 2.1 and 7.4 as reported by Guo and Gao [37]. The fitted value of the external solution molarity that is kept constant in all experiments is equal to  The value of
The value of  which should be fitted for every experimental data set, is computed as
which should be fitted for every experimental data set, is computed as 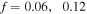 and
and 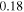 for the best-fit.
for the best-fit.
As shown in figure 3, the presented model predicts qualitatively, the swelling behavior of the pH/temperature sensitive hydrogel. Also, below the phase transition temperature, a good agreement is observed between the present work results with those of the experiments. As one may see from this figure, at the small values of pH, the network is not that sensitive to the acidic group density due to the large amount of hydrogen ion in the external solution which prevents from the acidic groups dissociation. Thus, the acidic group density has almost no effect on the swelling behavior of the network as predicted by the model and confirmed by the experiments. But, for the larger values of pH, scarcity of the hydrogen ion results in the acidic group dissociation and the larger values of swelling ratio. This phenomenon is more prominent for larger amounts of the acidic group density as shown in figure 3(a). In this case, a network with more amounts of the acidic groups produces more hydrogen ions which results in more fluid uptake in the network and consequently more swelling. As depicted in figure 3, the presented model can predict the pH/temperature behavior qualitatively both in the small and large values of pH. Also, the model is capable of predicting the hydrogel behavior for the temperature changes.
Figure 3. Comparison between the presented model results and the experiment (EXP) reported by Guo and Gao [37], (a) for pH = 7.4 and (b) for pH = 2.1. For these results, the fitted values of the material parameter and salt concentration are  and
and 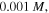 respectively. Also, the value of
respectively. Also, the value of  is determined from curve fitting as shown in figures.
is determined from curve fitting as shown in figures.
Download figure:
Standard image High-resolution image3.1.2. Biaxial constrained swelling
As investigated by many researchers, the swelling of a hydrogel layer on a hard sub-layer is studied in this section. The hydrogel layer is assumed to be in the biaxial constrained conditions due to its small thickness. The pre-stretches of the hydrogel layer in two constrained directions are fixed and equal to 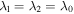 where
where 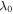 is the equilibrium stretch at a reference point in which the hydrogel has a stress-free state. Also, the stretch in the direction normal to the constrained plane is
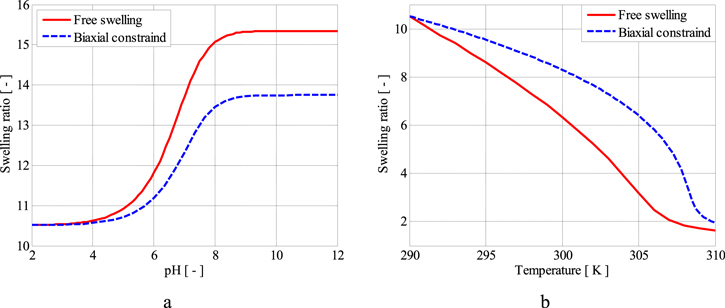
is the equilibrium stretch at a reference point in which the hydrogel has a stress-free state. Also, the stretch in the direction normal to the constrained plane is 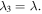 Substituting the pre-stretch in the stress expression and equating it to zero, the value of swelling ratio at the equilibrium is calculated. The equilibrium point of the hydrogel is found in terms of the pH and temperature changes and shown in figures 4(a) and (b), respectively, in which the free swelling results are available for comparison. The material parameters are selected as
Substituting the pre-stretch in the stress expression and equating it to zero, the value of swelling ratio at the equilibrium is calculated. The equilibrium point of the hydrogel is found in terms of the pH and temperature changes and shown in figures 4(a) and (b), respectively, in which the free swelling results are available for comparison. The material parameters are selected as  and
and  where the external solution molarity is
where the external solution molarity is 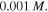 We assume the reference point with pH = 2 and T = 290 K and as a result, the corresponding value of
We assume the reference point with pH = 2 and T = 290 K and as a result, the corresponding value of 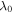 is obtained as 2.190. As depicted in figure 4(a), increasing the pH value leads to increase in the swelling ratio for both the free swelling and biaxial constrained cases. But, for the biaxial constrained the swelling ratio is smaller than the free swelling case due to presence of a constraint that prevents the hydrogel from swelling. The effect of increasing the temperature is shown in figure 4(b). As illustrated in this figure, increasing the temperature results in reduction in volume of the hydrogel both for the free and biaxial constrained swelling. However, the amount of volume reduction is larger for the free swelling state due to absence of any constraint against shrinkage of the network. Thus, despite of figure 4(a) results, for increasing the temperature from the reference point, the swelling ratio for the biaxial constrained swelling is larger than the free swelling case due to preventing the hydrogel from shrinking.
is obtained as 2.190. As depicted in figure 4(a), increasing the pH value leads to increase in the swelling ratio for both the free swelling and biaxial constrained cases. But, for the biaxial constrained the swelling ratio is smaller than the free swelling case due to presence of a constraint that prevents the hydrogel from swelling. The effect of increasing the temperature is shown in figure 4(b). As illustrated in this figure, increasing the temperature results in reduction in volume of the hydrogel both for the free and biaxial constrained swelling. However, the amount of volume reduction is larger for the free swelling state due to absence of any constraint against shrinkage of the network. Thus, despite of figure 4(a) results, for increasing the temperature from the reference point, the swelling ratio for the biaxial constrained swelling is larger than the free swelling case due to preventing the hydrogel from shrinking.
Figure 4. Comparison between the free and biaxial constrained swelling of the pH/temperature sensitive hydrogel from a reference point of pH = 2 and T = 290 K for variation of, (a) pH and, (b) temperature.
Download figure:
Standard image High-resolution image3.2. Inhomogeneous deformations
In this paper, a modified version of mixing part of the free energy is used and as a result, a continuous model is developed which is numerically stable and can be implemented for solving inhomogeneous swelling problems [32]. To show the capability of the model in the inhomogeneous swelling, we present the solution of the inhomogeneous swelling of a pH/temperature sensitive hydrogel spherical shell on a rigid core. The hard core constrains the hydrogel shell swelling in its inner radius which results in the inhomogeneous deformation of the shell. Analytical and numerical solutions are derived and compared. Thereafter, the numerical framework which is validated with the analytical results is employed to simulate the complicated contact problem of the mentioned hydrogel shell with a flat channel.
3.2.1. Analytical solution
Motivated from Zhao et al [43], a bench-mark problem in the hydrogel inhomogeneous swelling is a spherical shell on a hard core whose volume changes due to the environmental conditions, e.g. pH and temperature changes. The schematic draw of this problem is shown in figure 5 in which the shell is shown at a stress-free state (reference state). In figure 5, 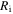 and
and 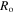 are inner and outer radii of the spherical shell in the stress-free state, respectively.
are inner and outer radii of the spherical shell in the stress-free state, respectively.
Figure 5. Schematic draw of the spherical hydrogel shell on a hard core inserted in a channel with rigid flat walls.
Download figure:
Standard image High-resolution imageFor the spherical shell, all field variables are functions of  which is the radius of an element in the stress-free state. All energy statements are recast with respect to the reference state through substituting
which is the radius of an element in the stress-free state. All energy statements are recast with respect to the reference state through substituting 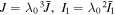 in the free energy statements in which
in the free energy statements in which 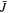 and
and 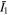 are corresponding values of
are corresponding values of 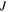 and
and 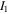 with respect to this state. The temperature and pH at the stress-free state are 290 K and 2, respectively. So, the corresponding value of
with respect to this state. The temperature and pH at the stress-free state are 290 K and 2, respectively. So, the corresponding value of  is obtained as 2.190. Due to the symmetry, the equilibrium equation in the radial direction is:
is obtained as 2.190. Due to the symmetry, the equilibrium equation in the radial direction is:
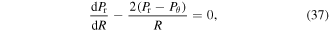
where Pr and Pθ are the nominal radial and hoop stresses, respectively. These stress components are obtained from the free energy expressions as:
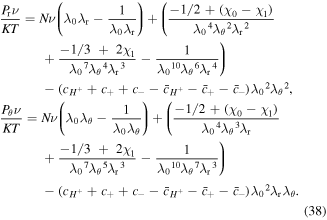
Also, the stretch components in terms of the current element radius are:

in which 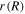 is the radius of the element of the hydrogel in the current state. Substituting (38) and (39) in (37), a differential equation in terms of
is the radius of the element of the hydrogel in the current state. Substituting (38) and (39) in (37), a differential equation in terms of 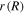 and
and 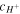 is obtained, and accompanying (33), a system of two nonlinear equations established. One method of dealing with this problem is elimination of
is obtained, and accompanying (33), a system of two nonlinear equations established. One method of dealing with this problem is elimination of  from the two equations and solving the problem for the displacement field
from the two equations and solving the problem for the displacement field  The relevant boundary conditions for this problem are then expressed as:
The relevant boundary conditions for this problem are then expressed as:
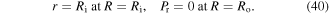
The material parameters are selected as 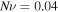 and
and 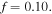 Also, the external solution molarity is
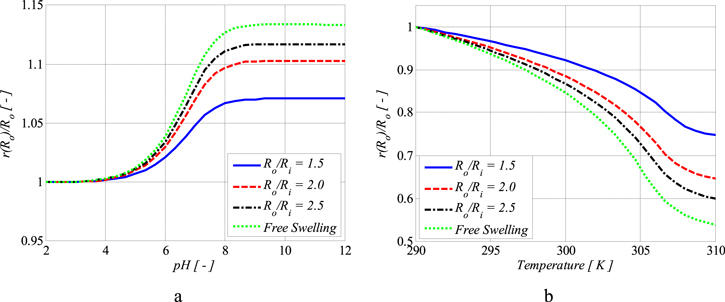
Also, the external solution molarity is 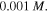 To solve the present boundary value problem, a finite difference technique with Richardson extrapolation is used [44]. The calculated results as depicted in figure 6, are reported for different values of thickness ratio, namely
To solve the present boundary value problem, a finite difference technique with Richardson extrapolation is used [44]. The calculated results as depicted in figure 6, are reported for different values of thickness ratio, namely 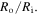 The normalized outer radius of the hydrogel shell is plotted versus the pH and temperature in figures 6(a) and (b), respectively. The normalized outer radius is defined as ratio of the current outer radius of the hydrogel shell
The normalized outer radius of the hydrogel shell is plotted versus the pH and temperature in figures 6(a) and (b), respectively. The normalized outer radius is defined as ratio of the current outer radius of the hydrogel shell 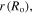 to its value at the reference point
to its value at the reference point 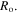 As shown in figure 6(a) increasing the pH results in an increase in the normalized outer radius. As the thickness ratio increases, the added material in the outer radius experiences a low level of confinement and as a result, can swell more freely with increase in pH. Therefore, increasing the thickness ratio, the behavior of the shell approaches to the free swelling state as understood from figure 6(a). The effect of temperature increase is also illustrated in figure 6(b) in which the hydrogel experiences shrinkage due to an increase in the temperature. In contrast to figures 6(a), in (b) the normalized outer radius is larger for smaller values of the thickness ratio. Again, the behavior of the shell approaches to the free swelling state as the thickness ratio increases.
As shown in figure 6(a) increasing the pH results in an increase in the normalized outer radius. As the thickness ratio increases, the added material in the outer radius experiences a low level of confinement and as a result, can swell more freely with increase in pH. Therefore, increasing the thickness ratio, the behavior of the shell approaches to the free swelling state as understood from figure 6(a). The effect of temperature increase is also illustrated in figure 6(b) in which the hydrogel experiences shrinkage due to an increase in the temperature. In contrast to figures 6(a), in (b) the normalized outer radius is larger for smaller values of the thickness ratio. Again, the behavior of the shell approaches to the free swelling state as the thickness ratio increases.
Figure 6. Analytical results for the inhomogeneous swelling of a spherical shell on a rigid pillar at different pH and temperatures.
Download figure:
Standard image High-resolution image3.2.2. Numerical implementation
In the last section, the model is successfully used for solving an inhomogeneous swelling problem. Implementing the constitutive models of smart hydrogels as UHYPER in ABAQUS is popular in the literature because of the vast facilities of ABAQUS for FEM simulations [4, 43, 45]. Following other researchers, the proposed model is implemented in an ABAQUS user subroutine, namely UHYPER, to obtain a numerical tool for solving more complicated boundary value problems. To show the capability of the numerical scheme, inhomogeneous swelling of a hydrogel shell on a rigid pillar with boundary conditions identical to the analytical solution, presented in the previous section, is solved and the results are compared in figure 7 for  The material parameters and the external solution molarity are the same as those of the analytical solution presented in section 3.2.1. As shown in figure 7, the numerical and analytical results are in excellent agreement and the validity of the FEM solution is successfully checked.
The material parameters and the external solution molarity are the same as those of the analytical solution presented in section 3.2.1. As shown in figure 7, the numerical and analytical results are in excellent agreement and the validity of the FEM solution is successfully checked.
Figure 7. Comparison between the analytical and the numerical solution of inhomogeneous swelling of a pH/temperature sensitive hydrogel shell on a rigid pillar for (a) pH and (b) temperature variations.
Download figure:
Standard image High-resolution imageIn addition, for 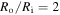 we solve inhomogeneous swelling of a hydrogel shell on a rigid pillar which may experience a contact with rigid flat walls of a channel as shown in figure 5. The half-width of the channel,
we solve inhomogeneous swelling of a hydrogel shell on a rigid pillar which may experience a contact with rigid flat walls of a channel as shown in figure 5. The half-width of the channel, 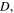 is selected such that
is selected such that 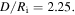 Due to the symmetry, simulations are carried out for a quarter of the real spherical shell and the results are shown in figure 8.
Due to the symmetry, simulations are carried out for a quarter of the real spherical shell and the results are shown in figure 8.
Figure 8. deformation contours of the spherical pH/temperature sensitive hydrogel at various conditions. Columns from left to right show the contours at 290 K, 300 K and 310 K, respectively. Rows top-down show the contours at pH equal to 2, 5, 7 and 10, respectively.
Download figure:
Standard image High-resolution imageIn this figure the columns from left to right show the results at temperatures 290 K, 300 K and 310 K, respectively and also, the top-down rows are the results for pH values of 2, 5, 7 and 10, respectively. The material parameters, the stress-free condition and the external solution molarity are identical to the previous numerical problem. The inner radius of the hydrogel shell is constrained to the rigid pillar while the outer radius of the shell experiences a contact with the walls. Thus, this problem contains a complicated coupling between the temperature changes, pH changes, large deformations and a mechanical contact. As shown in figure 8, a temperature decrease or a pH increase may result in contact between the shell and the flat walls. For example when pH = 10, the shell is initially in contact with the wall at T = 290 K. Any increase in the temperature or decrease in pH lead to shrinkage of the shell and as a result they are not in contact anymore as observed at T = 300 K and T = 310 K. For the case that no contact occurs at the low temperature, an increase in the channel opening eventuates from increasing in the temperature or decreasing in pH. These observations are reasonable and the validated numerical scheme derived in this section can be employed to simulate boundary value problems for the swelling of the pH/temperature sensitive hydrogels.
4. Summary and conclusions
In this work the equilibrium behavior of the pH/temperature sensitive PNIPAM hydrogel was studied and a model was presented with a good agreement with the experimental results available in the literature. The free and biaxial constrained swelling of the pH/temperature sensitive hydrogel was investigated and some parameter studies were performed. One of the main advantageous of the presented model was its continuity especially against the temperature variations which makes it appropriate for implementing in the inhomogeneous swelling problems whether analytically or numerically. Thereafter, the inhomogeneous swelling of a spherical shell on a hard core was analytically studied and the results were presented for various thicknesses of the shell. Also, the model was implemented in ABAQUS via a user subroutine UHYPER. Then, the inhomogeneous swelling of a spherical shell on a hard core, with boundary conditions identical to the analytical one, was solved and the validity of the numerical results was successfully confirmed. Finally, the numerical simulation of the complicated problem of contact between the hydrogel shell and a channel with rigid walls due to the pH or temperature variations was performed with reasonable results. Based on the results, it is concluded that the presented model is suitable for predicting the behavior of pH/temperature hydrogels and has the capability for implementing in the homogeneous and inhomogeneous problems.
Acknowledgments
The second author is grateful for the research support of the Iran National Science Foundation (INSF).