Abstract
Ultra-short extreme ultraviolet pulses from the free-electron laser FLASH are characterized using terahertz-field driven streaking. Measurements at different ultra-short extreme ultraviolet wavelengths and pulse durations as well as numerical simulations were performed to explore the application range and accuracy of the method. For the simulation of streaking, a standard classical approach is used which is compared to quantum mechanical theory, based on strong field approximation. Various factors limiting the temporal resolution of the presented terahertz streaking setup are investigated and discussed. Special attention is paid to the cases of very short (∼10 fs) and long (up to ∼350 fs) pulses.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Free-electron lasers (FELs) working in the extreme ultraviolet (XUV) and x-ray region deliver unrivalled intense pulses of fs-duration [1–6]. They allow the investigation of basic light–matter interactions at high photon intensities such as multiphoton ionization of atoms and molecules. The most promising application of the XUV FELs is the investigation of the time evolution of electronic processes by applying pump-probe techniques. For the realization of this method it is crucial to know the temporal characteristics of the XUV pulses delivered by the FEL such as arrival time, pulse duration and—at best—the temporal shape of the pulses.
Most FELs in the XUV and x-ray range operate in the self-amplified spontaneous emission (SASE) regime relying on stochastic processes, resulting in pulses varying on a shot-to-shot basis [7, 8]. Each pulse is composed of independent, temporally coherent spikes, with the duration of these spikes ranging from hundreds of attoseconds to tens of femtoseconds depending on the wavelength and coherence length of the FEL process. The stochastic nature of the FEL radiation leads to large shot-to-shot fluctuations in the temporal characteristics of the pulses. Most of the known temporal characterization methods are based on averaging over many pulses [9], which strongly limits the accuracy of the pump-probe experiments. The necessity to know the duration and temporal profile of each individual pulse stimulated the development of different methods that are suitable for single-shot temporal characterization. Besides terahertz (THz) streaking, there are mainly three different techniques available: (1)—the observation of optical properties changes in solid thin films upon XUV pumping (e.g. [10, 11]). This method however only works within a very limited dynamic range in the XUV and it is questionable how the method can be scaled to the MHz high-repetition rate of FLASH. (2) A different approach investigates the temporal profile modulation of the electron bunch during the XUV/x-ray creation process using a radiofrequency transverse deflector device [12]. It has been shown that these measurements can provide photon pulse durations with very high temporal resolution, however, currently cannot be scaled to the burst mode structure of FLASH. (3) A similar approach using an optical replica of the electron bunch modulation ('optical afterburner') [13] is potentially also able to deliver single-shot pulse duration information but has so far not been demonstrated experimentally.
THz streaking [14–19] on the other hand can overcome these limits and has the potential to deliver single-shot pulse duration information basically wavelength independent and over a large dynamic range (in pulse duration and FEL energy). It can be operated with repetition rates up to several hundred kHz (potentially even MHz). In addition, it can provide arrival time information of the FEL pulse with respect to the laser driving THz generation for each single pulse with an accuracy well below 10 fs [18]. Due to its wide working range the concept can not only be used at soft x-ray FEL like FLASH, but also at hard x-ray FELs [17, 20].
Recently a THz-field driven streaking setup has been installed at FLASH1 [18] delivering photon pulse duration as well as arrival time information for each individual XUV pulse. In this paper, we report on measurements performed with this streaking setup and theoretical simulations devoted to the investigation of its accuracy and limitations. Previous THz streaking experiments [14, 15, 17, 19] have been performed at fixed FEL settings where the average XUV wavelength, pulse duration and pulse energy were essentially stable. Here, for the first time, a comprehensive collection of measurements recorded at various FEL parameters governing the pulse duration are presented. From shortest possible FLASH SASE pulses in the sub 10 fs range (single longitudinal mode) with only few μJ of pulse energy to intense >100 μJ pulses containing a large number of longitudinal modes extending to pulse durations >300 fs (FWHM) have been investigated.
The paper structure is as follows: the next section is devoted to the theoretical description of the streaking process which is used in the simulations and the reconstruction of the temporal profiles from the electron time-of-flight (eTOF) measurements. In section 3 the experimental setup at FLASH1 is briefly described providing necessary information about the parameters of the XUV and the THz fields. In subsection 3.2 the analysis of the possible error sources as well as limitations of the described streaking setup is given. Section 4 presents experimental results for different XUV pulse durations and various parameters of the THz field. Finally, we conclude in section 5.
2. Theoretical background
2.1. Streaking principle. Classical description
We consider the photoionization of an atom by a short (femtosecond) XUV pulse in the presence of a co-propagating THz radiation field. Both fields are linearly polarized in the same direction. In the scope of the current paper, we assume a single-cycle THz pulse with duration much longer than that of the XUV pulse [15]. The XUV pulse produces a distribution of photoelectrons via ionization that carries the temporal information of the ionizing XUV pulse. The kinetic energy of the photoelectrons is modified by the interaction with the THz electric field, and their final energy is determined by the instant THz-field vector potential at the moment of ionization. Thus, the temporal structure of the electron wave packet is mapped onto the kinetic energy distribution of the photoelectrons.
Classically, one can write the final energy W of photoelectrons emitted at the instant of time t as (atomic units (a.u.) are used in this section unless otherwise indicated)

where W0 is the initial energy of the ejected electron without THz field,  is its final linear momentum directed at angle θ to the polarization direction of both pulses, and
is its final linear momentum directed at angle θ to the polarization direction of both pulses, and  is the THz-field vector potential, with ETHz(t') being the THz electric field. Note that the THz field is weak and the quadratic term in equation (1) can be ignored. One can further simplify the THz field-induced photoelectron energy modulation to
is the THz-field vector potential, with ETHz(t') being the THz electric field. Note that the THz field is weak and the quadratic term in equation (1) can be ignored. One can further simplify the THz field-induced photoelectron energy modulation to  by assuming θ = 0 (detecting only electrons along the polarization direction). Thus, the shift of the kinetic energy peaks provides the arrival time of the XUV pulse.
by assuming θ = 0 (detecting only electrons along the polarization direction). Thus, the shift of the kinetic energy peaks provides the arrival time of the XUV pulse.
The relation between the time interval δt and the energy interval δ(ΔWstreak) is as follows:
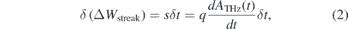
where s is the so-called streaking speed. As a first approximation, the value s may be set to be a constant proportional to the derivative of the vector potential at the center of the slope. The pulse duration τXUV can thus be extracted from the broadening of the photoelectron spectrum due to the presence of the THz field. For a Fourier limited Gauss-shaped peak the following equations apply:
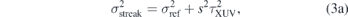
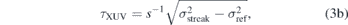
with σstreak and σref being the widths of the peak with and without the THz field, respectively.
If the XUV pulse has a linear chirp, e.g.  where
where  is the envelope and ω is the center frequency of the XUV field, equation (3a) becomes
is the envelope and ω is the center frequency of the XUV field, equation (3a) becomes  which may be used for experimental determination of the chirp [14, 19, 21].
which may be used for experimental determination of the chirp [14, 19, 21].
As the THz pulse is focused the phase of the THz field changes continually along the propagation direction. This effect, often called Gouy phase, changes the phase by 180° across the Raleigh range. Thus, electrons generated at different positions within the interaction region are accelerated by a slightly different THz field and therefore experience a different energy modulation. This leads to an additional broadening σGouy of the photoelectron line independent of the XUV pulse duration [21]. The broadening can, at least approximately, be determined from the THz focusing geometry and the acceptance volume from which the electrons are collected. This Gouy phase broadening has to be subtracted from the actually measured width:

2.2. Quantum mechanical simulation
A more accurate description of the streaking process can be achieved by a quantum mechanical approach. For calculations of the double differential cross section of the photoionization (in energy and angle), the strong field approximation (SFA) can be used [22] since it is valid for medium strong streaking fields and relatively fast electrons (kinetic energies of more than 1 a.u. (27.2 eV)). Realization of the SFA in the context of streaking was discussed in references [23–26]. Within this approximation, pulse duration, temporal profile, kinetic energy, target gas, streaking field and strength can be independently varied to study the role of each parameter in the streaking process. As a result, the simulation provides the energy and angular resolved double differential cross sections for the streaked photoelectrons. Several examples will be discussed later.
The SFA approach, however, is computationally rather demanding limiting its applicability in fast (on-line) shot-to-shot analysis of experimental spectra. The description of the process can be significantly simplified within a quasi-classical approach using the stationary phase method as suggested in [24, 25]. Recently, a very simple and fast method of FEL pulse retrieval from the THz streaking spectrum has been suggested in reference [26]. The method is based on SFA and uses the stationary phase approximation. As shown in reference [26] the double differential cross section (DDCS) for XUV ionization in the presence of the THz field can be presented as:

where the last factor is the common DDCS of photoionization of the l0 shell of the atom by the XUV pulse alone which can be presented in a standard form:
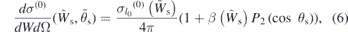
here  and
and  are the cross-section and anisotropy parameter for the photoionization of the l0 shell of the atom by the XUV pulse alone, P2(x)is the second Legendre polynomial. The energy
are the cross-section and anisotropy parameter for the photoionization of the l0 shell of the atom by the XUV pulse alone, P2(x)is the second Legendre polynomial. The energy  and angle
and angle  are defined as:
are defined as:
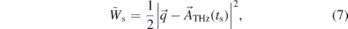
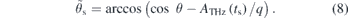
They have the meaning of the electron energy and emission angle before entering the THz field. The stationary point ts (the time of ionization providing the final energy (W = q2/2) is given by the equation:
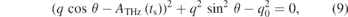
with  and W0 being the initial energy of the photoelectrons.
and W0 being the initial energy of the photoelectrons.
Equation (9) has two solutions  . The experiment implies that the momenta q0 and q involved are substantially larger than the magnitude of the vector potential of the THz field ATHz. Thus, if one considers the case cos θ > 0, the solution with the plus sign should be chosen while the solution with the minus sign should be chosen for cos θ < 0. If only complex roots ts of equation (9) exist, for computation of the SFA amplitude the saddle point method should be used instead of the stationary phase method. The saddle point method allows one to obtain the Airy function representation for the SFA amplitude which exponentially decreases with increase of the absolute value of the imaginary part of ts. For the present problem this case is not relevant.
. The experiment implies that the momenta q0 and q involved are substantially larger than the magnitude of the vector potential of the THz field ATHz. Thus, if one considers the case cos θ > 0, the solution with the plus sign should be chosen while the solution with the minus sign should be chosen for cos θ < 0. If only complex roots ts of equation (9) exist, for computation of the SFA amplitude the saddle point method should be used instead of the stationary phase method. The saddle point method allows one to obtain the Airy function representation for the SFA amplitude which exponentially decreases with increase of the absolute value of the imaginary part of ts. For the present problem this case is not relevant.
The expression (5) can be directly used to retrieve the temporal XUV pulse profile from a measured electron energy spectrum:

The retrieval strategy is the following: for each energy W = q2/2, angle θ and a given time-dependence of the THz vector potential ATHz(t), the emission moment ts is found from the relation (9). Then the energy  and angle
and angle  are calculated according to equations (7) and (8), respectively. Finally using equation (10) the XUV pulse is evaluated, provided the cross section dσ0/dWdΩ is known.
are calculated according to equations (7) and (8), respectively. Finally using equation (10) the XUV pulse is evaluated, provided the cross section dσ0/dWdΩ is known.
Since expression (10) is algebraic, the pulse retrieval is as fast as using the classical expression (1) with linear approximation of the vector-potential. The former expression (10) has the advantage that it can be used for any shape of the vector potential and therefore is suitable also for comparatively long XUV pulses. The only limitation is that the THz vector potential must be a monotonous function in time during the XUV pulse duration.
3. Experiment
3.1. THz-streaking setup and data acquisition
The experiments were performed at the plane grating (PG) monochromator beamline [27, 28] of the free-electron laser in Hamburg (FLASH) [1]. The PG beamline was operated in the so-called parallel configuration. This configuration enables the utilization of the 0th diffraction order (at the PG0 beamline branch) for experiments or diagnostics (THz streaking in our case) while the dispersed radiation is simultaneously used to measure the XUV FEL spectrum with high resolution.
Various settings of the accelerator were used to test the applicability of the streaking diagnostic over a wide range of FEL parameters. The FEL was operated in single bunch mode at 10 Hz, with electron bunch charges altered from 0.08 nC up to 0.44 nC, leading to different XUV pulse durations from ∼10 fs to ∼350 fs (FWHM) as well as to XUV pulse energies ranging between only a few μJ at 7 nm to >100 μJ per pulse at 20 nm.
An 80 fs, 800 nm, 6.5 mJ, 10 Hz Ti:Sapphire laser [29] with a sub 10 fs synchronization to the optical master oscillator [30] was used to generate single-cycle THz streaking pulses based on pulse front tilt optical rectification in a lithium niobate (LiNbO3) crystal [31]. The obtained THz pulse energy was on the order of 15 μJ leading to a THz field strength up to 300 kV cm−1 (see figure 3 in [18]). A detailed description of the experimental setup and the working principle can be found in reference [18]. In brief, the XUV pulses are focused into a noble gas target (see figure 1) and create photoelectrons via ionization. The XUV focus size is chosen to be sufficiently smaller (∼300 μm diameter (FWHM)) as compared to the THz focus size of 2.1 mm (FWHM). A Ce:YAG screen and fast photodiode were used to find the coarse spatial and temporal overlap between the XUV and THz pulses [32].
Figure 1. (a) Geometry of the THz streaking setup used at the PG0 beamline of FLASH. (b) THz streaking principle. Photoelectrons are emitted from free (noble gas) atoms ionized by short XUV pulses in the presence of a strong linearly polarized THz field, thus modifying the momentum component of the photoelectrons. (c) Mapping of the temporal information to the kinetic energy distribution from the THz vector potential (streaking trace).
Download figure:
Standard image High-resolution imageNeon was chosen as the target gas providing the 2p and 2s photoelectron spectral lines in the energy range of interest. The electron binding energies are 21.7 eV (2p) and 48.5 eV (2s), respectively [33]. At the FEL wavelength of 6.8 nm (182.3 eV), two single, well separated spectral lines with kinetic energies of 160.6 eV and 133.8 eV were measured. At 20 nm (62.0 eV) XUV wavelength the photoelectron kinetic energies are 40.3 eV and 13.5 eV, respectively.
As will be shown below, the range of XUV pulse durations from 30 fs < τXUV < 150 fs can be evaluated for XUV wavelengths up to about 30 nm. For longer wavelengths, pulse durations of 30 fs approach the few-mode operation and have to be treated more carefully. Furthermore, the photoelectron kinetic energy gets smaller, thus making it increasingly more difficult to reach sufficient streaking strength (see equation (2)). Nevertheless, pulse duration measurements using a similar setup have been successfully measured at 34 nm seeded VUV radiation [19].
The mapping between the streaked kinetic photoelectron energy and the time is given by  . The right-hand side of this equation is usually called 'streaking trace' and provides the maximum energy shift of photoelectrons for a given THz field. By fitting the linear part of the vector potential we can evaluate the streaking speed 's' which relates the energy shift and emission time [14, 21].
. The right-hand side of this equation is usually called 'streaking trace' and provides the maximum energy shift of photoelectrons for a given THz field. By fitting the linear part of the vector potential we can evaluate the streaking speed 's' which relates the energy shift and emission time [14, 21].
3.2. Possible sources of errors and limitations
One of the main challenges of pulse duration diagnostics is the determination of measurement error bars. There are several different sources of inaccuracy that have already been discussed in [14–16, 34]. Here we summarize the factors that limit the accuracy and the temporal resolution of THz streaking in general. In section 4 we focus on the specific influence of the error sources for the different pulse duration ranges and provide experimental results from FLASH.
3.2.1. Spectral fluctuations of the SASE FEL pulse
As follows from equation (2) the shorter the XUV pulses are, the smaller the broadening induced by the streaking for a certain THz field is. Ultimately, for the shortest pulses available at FLASH the broadening approaches the spectral width fluctuations caused by the SASE process (see e.g. figure 6). In addition, for short pulses only a few or eventually one spectral mode is present [35]. Thus, the spectral distribution changes significantly from shot to shot while the influence of the broadening due to streaking is decreasing, leading to a more challenging data analysis. For this work it is mandatory to use the information of reference spectra from each XUV pulse measured either by a second eTOF [14] or by an XUV spectrometer. In the present case, the XUV spectral distribution is measured for each FEL pulse simultaneously to the THz streaking by the PG monochromator beamline operating in spectrometer mode [27]. These spectra can then be used to provide the reference energy width on a single-shot basis with significantly higher resolution as compared to an eTOF [27]. In order to crosscheck the approach, a set of un-streaked photoelectron spectra were recorded and the determined width of these eTOF spectra were found to correlate well with the spectral width determined by the XUV spectrometer. Since the few-spectral-mode substructure is also visible in the eTOF spectra an analysis based on a single-peak Gaussian approximation has severe limitations and the analysis has to be adapted individually for each pulse as has been shown in [14, 15].
An alternative way to cope with the spectral fluctuations of the SASE pulses is the utilization of Auger emission processes. Here the SASE pulses eject an inner shell electron of noble gas atoms. The excited ions will later decay via the emission of Auger electrons. The energy of the Auger electrons only depends on the involved atomic states and is independent of the energy of the ionizing photons. The spectral width of the Auger electrons is determined by the lifetime of the excited state and is typically about 100 meV or smaller [36]. Thus, the spectra of the Auger electrons are extremely narrow and stable as compared to direct photoelectron spectra at SASE FELs. The measured temporal distribution of the Auger-electron wave-packets is a convolution of the temporal profile of the ionizing light pulse and the exponential Auger decay. The XUV pulse duration can be extracted from the streak-measurements by a simple deconvolution. The Auger lifetimes are usually well known and typically lie in the range of a few femtoseconds. Therefore they do not pose a severe limit for the target pulse duration range.
3.2.2. Gouy phase broadening
The THz phase shift before and after the focus leads to an additional broadening of the eTOF signal resulting in a longer retrieved XUV pulse. Our eTOF spectrometer has a ∼0.5 mm FWHM acceptance range [18]. In table 1 we present the Gouy broadening calculated for our THz source [18] for different acceptance volumes, source size (horizontal length) and interaction point position regarding the THz focus. In order to reduce the Gouy phase induced broadening, one can either move the interaction point away from the THz focus position or minimize the interaction volume. The latter could be achieved by using a more narrow gas target and a restricted eTOF acceptance range.
Table 1. Broadening of the streaking signal in fs (FWHM) calculated for 300 kV cm−1 THz field and different horizontal positions (along the FEL propagation) of the eTOF with respect to the THz focus and for different acceptance volumes-source size (horizontal length) of the eTOF [18].
| eTOF position | Source | Phase | Gouy broadening |
|---|---|---|---|
| (mm) | size (mm) | (rad) | FWHM (fs) |
| 0 | 0.25 | 0.023 | 6.2 |
| 0 | 0.5 | 0.047 | 13 |
| 0 | 0.75 | 0.071 | 19 |
| 6 | 0.25 | 0.017 | 4.7 |
| 6 | 0.5 | 0.033 | 10 |
| 6 | 0.75 | 0.053 | 14 |
3.2.3. eTOF spectrometer resolution, acceptance angle and signal to noise ratio (SNR)
The energy resolution of the used eTOF (Kaesdorf ETF11) is approximately 1% of the initial electron kinetic energy similar to the photon energy bandwidth of the XUV pulse. Thus, in the case of 7 nm XUV wavelength, the un-streaked peak width is on the order of 1.0–1.5 eV. It should be noted that for a given eTOF spectrometer, the temporal resolution can be improved either by applying a more intense THz field or by streaking more energetic photoelectrons.
Nevertheless, the increased energy resolution usually leads to a reduced collection efficiency, and it is challenging to achieve high energy resolution and high collection efficiency simultaneously. The single-shot streaked photoelectron signal has to be intense enough to determine the streaking for each single XUV pulse, i.e. to collect a sufficient number of electrons per pulse while avoiding unwanted spectral broadening due to space charge resulting from too many ions created in the FEL focal volume [37]. By increasing the target gas pressure until a significant broadening of the un-streaked photo-line was observed, we could determine that a total number of collected electrons in the range of few hundred per XUV pulse does not lead to significant space charge broadening. Considering the 45° collection angle this corresponds to a total number of a few ten thousand electrons within the FEL focus volume.
The collected electrons are distributed by the time-of-flight principle of the spectrometer to a certain time interval which is typically few times longer than the signal produced by a single electron (1.2 ns (FWHM) for the used setup).
Thus the recorded amplitude of an eTOF trace at a certain point is typically composed of a few tens of electrons only.
The finite number of electrons contributing to the signal leads to a statistical uncertainty of the signal shape [21]. In the case of a Gaussian distribution the uncertainty due to the Poisson statistics can be easily calculated. For n electrons contributing to the amplitude of the photoelectron signal, the uncertainty of the amplitude is given by Poisson statistics: √n. Thus the uncertainty range for the normalized amplitude is 1 ± 1/√n as shown in figures 5, 7 and 9.
A simulation of the streaked eTOF signal dependence on the acceptance angle was performed to verify the additional broadening due to the rather large acceptance angle of the used eTOF spectrometer. Using equation (5) the DDCS was calculated for the model case of six 5 fs XUV pulses in three pairs spaced by 200 fs and each of the pairs separated by a 15 fs interval. The calculation was performed for neon 2p ionization at an XUV wavelength of 6.8 nm (electron energy 160 eV) in a THz field of 250 kV cm−1. As shown in figure 2(a) the strongest effect of the streaking field is for electrons moving along the polarization direction (theta = 0 degrees).
Figure 2. SFA simulation according to equation (5). The 2D figure shows the double differential cross-section simulated for the neon 2p ionization (at an incident photon energy of 182 eV/6.8 nm) using three pairs of 5 fs (FWHM) XUV pulses which are spaced by 15 fs while the pairs are 200 fs separated. A 250 kV cm−1 streaking field was chosen. The middle pair was set at the zero crossing of the vector potential. The streaking field acts strongest at 0 degrees (electrons emitted parallel to the THz polarization) and its effect is decreasing for higher angles. In the angular range of ±22.5 degrees for the used spectrometer there is already a certain change visible in the angular distribution. The lineouts (b) and (c) show the integrated photoelectron signal for the angular acceptance of ±22.5 degrees (red) and for the reference signal taking only the emission at 0 degrees into account—(blue). Two cases are shown: for a THz field of (b) 150 kV cm−1 and (c) 250 kV cm−1. While there is a significant difference in the resolution for the temporally shifted peaks (∼190 eV), the difference between the large acceptance angle and the reference is almost negligible for the streaked signals at the zero crossing of the vector potential (∼160 eV). One can also see the better resolution at 250 kV cm−1 compared to 150 kV cm−1.
Download figure:
Standard image High-resolution imageFor electrons moving perpendicular to the THz field (90 degrees) there is practically no energy shift. It is interesting to note that the photoelectron lines do not cross the initial photoelectron energy of 160 eV but the electrons not emitted at the zero crossing of the streaking trace end up with less kinetic energy at 90 degrees than the un-streaked electrons. In equation (1) there are two terms depending on the field  and
and  . The term
. The term  is typically very small and can be neglected, however, it causes the asymmetric shift at 90 degrees.
is typically very small and can be neglected, however, it causes the asymmetric shift at 90 degrees.
The angular distribution at the zero crossing of the THz vector potential has almost no angular dependence. Therefore, a larger acceptance angle does not limit the resolution significantly. On the other hand, at streaking positions outside the zero crossing (yielding an energetic shift at 0 degrees), a significant effect of the acceptance angle can be observed (see figures 2(b) and (c)).
In our case, the acceptance angle of 45 degrees (full solid angle) shows only an additional broadening of <1 fs at the zero crossing of the vector potential and <5 fs measured 200 fs away from the crossing. Reducing the field to 150 kV cm−1, the two pulses located 200 fs away from the crossing cannot be resolved anymore showing the importance of the correct setting of the relative timing between XUV and THz fields.
3.2.4. Influence of the non-linearities of the THz vector potential
Usually the analysis of the streaking spectra is performed assuming a linear slope in the THz vector potential (constant streaking speed). However, the vector potential is non-linear and the streaking speed depends on the arrival time. For very short pulses and for arrival times close to the zero-crossing of the THz field vector potential the difference is negligible. Nevertheless, for longer pulses this difference may be considerable. We investigated the influence of the non-linear ramp by retrieving Gaussian streaked XUV pulses using equation (10) for different pulse durations. The results are shown in figure 3. When the pulses are almost as long as the range of the vector potential slope, the non-linearity is reflected as a change in the shape of the pulse as well as a small shift in the arrival time.
Figure 3. XUV pulse retrieval simulations using equation (10). Figure 3(a) shows three streaked Gaussian pulses of different XUV durations in the energy domain (with a central energy of 68 eV). The lower panel figure 3(b) displays the corresponding retrieved XUV pulses. The dashed lines denote the linear (L) reconstruction of the pulse (assuming a linear behavior of the main slope of the vector potential); the solid lines denote the reconstruction of the same streaked pulse but using equation (10) (NL) with a measured THz potential (streaking trace). The streaking trace is shown in black dots. For pulses <150 fs, the reconstruction gives a Gaussian-like pulse. As the pulse duration increases, the shape of the THz vector potential has a greater influence, leading to a considerable change in the shape of the XUV pulse.
Download figure:
Standard image High-resolution image3.2.5. SASE induced error sources
Another source of uncertainty results from radiation properties of the SASE pulse itself. Measurements of the electron phase space and the spectral width of the XUV radiation give strong hints that the SASE radiation can be chirped due to the influence of space charge and radio frequency (RF) slopes [38–41]. The energy chirp results in an SASE pulse whose leading part has a slightly different average wavelength as compared to the trailing part. This leads to different measured pulse durations depending on the relative sign of the THz streaking field and the chirp as explained e.g. in [21]. To estimate the influence of the effect, one can compare the pulse durations retrieved from the positive and negative THz slopes (compare streaking trace shown in figure 1(c), if only one eTOF is used. For two eTOFs facing each other see [14, 21]) the chirp can be derived for each measured XUV pulse.
4. Measurements and discussion
4.1. Streaking in the 'standard' XUV pulse range (30 fs < τXUV < 150 fs)
Before focusing on the limits of the method, we have investigated the 'standard' pulse duration regime of FLASH. Note that the error sources discussed above are in a tolerable range and the pulse duration can be determined rather accurately. A detailed investigation of the pulse duration fluctuations and their correlations to other pulse parameters such as pulse energy and spectral distribution was discussed in [42]. For this pulse duration region the influence of the different error sources is comparatively small.
Figure 4 shows the single-shot pulse duration with the unavoidable and expected fluctuations due to the SASE process pointing again on the need to provide a single-shot diagnostic for SASE based FELs.
Figure 4. (a) Single-shot pulse duration measurements shown for three thousand FLASH pulses. The red line indicates the mean value of ∼102 fs FWHM. The error bars of each measured pulse duration (not shown in the plot) is ±20% including all different contributions discussed in the text. (b) Histogram of pulse durations.
Download figure:
Standard image High-resolution image4.1.1. Reference spectra-SASE fluctuations
For the used experimental setup, the streaked photoelectron spectra are significantly broadened as compared to the un-streaked ones (figures 5 and 6(b)). We therefore can simplify the analysis by recording the averaged un-streaked reference spectral width by blocking the THz beam every few minutes.
Figure 5. Streaked (red) and un-streaked (blue) photoelectron spectra of ∼60 fs (FWHM) XUV FEL pulses are shown (thick lines) including the 1/σ error bars (shaded area) caused by the Poisson statistics due to the limited number (about 80–100 electrons in the peak) of electrons in the spectrum. The streaking speed s was 0.05 eV fs−1. FEL photon energy was 70.2 eV (wavelength 17.6 nm). Streaked spectrum for Ne 2p was taken at the 0-crossing of the THz-vector potential.
Download figure:
Standard image High-resolution imageFigure 6. Upper row: XUV spectra for different pulse duration settings. Column (a): represents the case τXUV < 30 fs; (b): 30 fs < τXUV < 150 fs; (c): τXUV > 150 fs. Green, blue and red lines are examples of single-shot spectra measured with the PG spectrometer. Black curves represent the average spectra. One can clearly see the different number of spectral spikes/modes for the different settings. The lower row shows the corresponding histograms for the eTOF spectral width (FWHM in eV) for streaked and un-streaked (reference) spectra. While for the long pulse duration (column (c)) the width fluctuations of the reference (un-streaked) spectra is negligible, for the short pulses (column (a)) there is a significant overlap showing the need of a careful consideration of the reference pulses.
Download figure:
Standard image High-resolution imageSince the eTOF resolution is not good enough to resolve the temporal sub-structure in the streaked spectrum, we used a Gaussian fit to determine the line width (FWHM) of both streaked and un-streaked spectra. In order to get an estimate of the error introduced by taking the averaged reference, the resulting XUV pulse duration was calculated by using the smaller and larger FWHM values of the reference spectrum width histogram. The widths of the reference spectra histogram shown in figure 6(b) is 0.9 ± 0.1 eV which leads (using equation (3b)) to an uncertainty of <1% for determination of the pulse duration and therefore negligible.
4.1.2. Gouy phase broadening
The influence of the Gouy phase was taken into account for the THz beam shape around the interaction point (see also figure 4 in reference [18]). According to table 1, the Gouy broadening is (13 ± 2 fs) for the THz focus position and ∼0.5 mm source size (horizontal length). The uncertainty in the Gouy broadening stems from the not precisely known source size. Due to the quadratic dependence, the influence on the acquired pulse duration is rather small (see equation (3)) and the uncertainty in the knowledge of the Gouy phase leads to an error of <5%.
4.1.3. eTOF spectrometer resolution, acceptance angle and signal to noise ratio (SNR)
As shown in figure 2 the broadening by a larger angular acceptance is (at the zero crossing of the vector potential) only a few fs and thus leads, in the considered pulse duration range, to an error of less than 5%.
The photoelectron peak width/shape has an uncertainty due to the limited number of electrons in a shot (∼200–500 electrons). The finite number of electrons contributing to the signal, leads to a statistical uncertainty of the signal shape. The statistical error of the width determination together with the Gaussian fitting leads to an uncertainty of 10%–25% as illustrated in figure 5. Typically, the eTOF resolution in combination with counting statistics shows an error that is too large for a detailed analysis of the pulse shape. Thus, only the pulse duration is analyzed. However, for longer pulses some information about the rough overall pulse structure can be determined as shown in section 4.2.
4.1.4. Influence of the non-linearities of the THz vector potential
In the considered pulse duration range, the SASE pulses consist of several sub pulses which cannot be resolved by the current eTOF spectrometer, thus we only apply a Gaussian fit. As shown in figure 3 the influence of the non-linear THz field is only a few percent and thus for the standard analysis, the linear approach (equation (4)) can be applied.
4.1.5. SASE induced error sources
Potentially, a strong energy chirp in the electron bunch generating the XUV pulse, can lead to a corresponding frequency chirp of the XUV pulse which is not detectable on a single shot basis with the present setup due to the given statistical uncertainty. However, the average amount of frequency chirp was determined by comparing the average streaking width on the positive and negative vector potential slope, similar to how it was done in reference [19]. Interestingly, we did not find an indication of chirp (larger than the error bars) for the whole large range of measured FEL parameters.
In summary, for pulse durations in the range 30 fs < τXUV < 150 fs we can state a typical uncertainty of ±20% for the determination of the single-shot pulse duration.
4.2. Exploring the upper limit: 'long' (τXUV > 150 fs) XUV pulses
For pulses that cover a significant fraction of the streaking slope, the THz streaking induced broadening is so large that the XUV pulse shape deviates from the initial Gaussian shape and shows a convolution of the reference line shape with the actual XUV pulse shape (see figure 6(c)). In this case, we can determine not only a value (FWHM) for the pulse duration but reconstruct the pulse shape of the individual XUV pulses, making a deconvolution of streaked and reference spectra using the non-linear equation (10) (see figure 7). Note, that here the influence of the various error sources is different as compared to the standard streaking case (section 4.1).
Figure 7. Reconstruction of the XUV pulse shape for pulses that are almost as long as the ramp of the THz vector potential. Red and green curves represent two examples of measured eTOF spectra with a pulse duration of ∼350fs (FWHM). The error envelope takes into account the statistical uncertainty. The dotted line represents the THz streaking trace. The streaking speed s was ∼0.043 eV fs−1.
Download figure:
Standard image High-resolution image4.2.1. Reference spectra-SASE fluctuations
One can see from figure 6(c) that the width distribution of the reference spectra (no THz) and of the actual streaked spectra are sufficiently well separated. Thus, the SASE fluctuations show almost no contribution to the pulse duration uncertainties (<0.1%).
4.2.2. Gouy phase broadening
Gouy correction leads to <1% change of the pulse duration and does not have to be considered.
4.2.3. eTOF spectrometer resolution, acceptance angle and signal to noise ratio (SNR)
The maximum streaking field strength has to be adjusted to provide sufficient streaking strength to clearly broaden the photoelectron peaks in comparison to the reference width. This allows one to determine the actual XUV pulse shape, while keeping the signal level still large enough within the time bins of the eTOF signal. If the streaked photoelectron line is broadened too much, there are only few electrons per time bin left leading to a large Poisson uncertainty and thus a large error in the determination of the pulse shape.
We found that 30–40 electrons contributing to the maximum signal are sufficient to reduce the error for the signal amplitude to <20%. Figure 7 shows the retrieved XUV pulses including the statistical error bands.
4.2.4. Influence of the non-linearities of the THz vector potential
The reconstruction of the XUV pulse shape from the measured photoelectron distribution needs to take the measured vector potential into account if the pulses cover large parts of the slope. The XUV pulses were reconstructed using equation (10), taking the quantum mechanical nature of the interaction into account. In addition, the acceptance angle of the eTOF was included in the simulation. The differences in pulse reconstruction between the linear and nonlinear approaches are in the same range as the statistical errors (see figures 3 and 7).
4.2.5. SASE induced error sources
Using only one eTOF, no single-shot information about the chirp can be acquired. Unfortunately, the comparison of the pulse durations acquired from the positive and negative slope as shown in [19] is not applicable here since the XUV pulses are too long to be properly be measured by the 'shorter' side slope (see figure 1(c)).
4.3. Exploring the lower limit: 'short' (τXUV < 30 fs) XUV pulses
Up to date, higher frequency streaking fields in the infrared or near infrared ranges have been applied to measure XUV pulses down to attosecond pulse duration [43–45]. Shorter wavelength streaking fields usually provide more intense streaking strength while restricting the temporal window of the measurement. Thus, one has to be sure that both temporal jitter and the pulse duration are shorter than the streaking slope.
THz generation based on lithium niobate (LiNbO3), centered around 0.6 THz with a field strength of ∼300 kV cm−1 (maximum achieved streaking speed s of ∼0.11 eV fs−1 in the THz focus), is ideally suited for the main working range of FLASH, providing XUV pulse durations of ∼30 fs to ∼150 fs (FWHM). The achievable streaking speed is rather low (as compared to e.g. IR streaking) and thus the ability to measure few fs pulse duration is rather poor. Nevertheless, we want to explore the resolution limit for measuring short pulse durations with the present setup.
In order to experimentally test the limits of the presented technique, we employed a new option of FLASH to produce sub 10 fs pulses [35]. As FLASH operates in the SASE mode, the generated XUV pulses consist of a stochastically fluctuating sequence of sub spikes [7, 40, 46]. Thus, the shortest pulse that can be generated by an SASE FEL without additional beam modulation is a single spike [35, 47]. Each temporal spike has a duration of roughly the coherence time τc. For the experimental wavelength of 6.8 nm, the coherence time is about 6 fs (FWHM) [35, 47]. Reference [35] provides a detailed description of how to achieve single mode operation at FLASH by using a dedicated photocathode laser with an about ten times shorter pulse duration as compared to the standard laser used. This configuration produces low charge electron bunches (∼80 pC) that can be compressed to below 30 fs (FWHM) leading, in the nonlinear amplification process, to sub 10 fs XUV pulses. This results in strongly fluctuating XUV pulses with average pulse energies of about 1 μJ. Measurements of the XUV spectral distribution show that about 50% of the produced XUV pulses have only one single spectral spike. In the following section we present a detailed analysis of the error sources in pulse duration determination for such single spike short pulses.
4.3.1. Spectral fluctuations of the SASE pulse
Looking at figure 6(a) one notes that the width distributions of the reference spectra (no THz) and of the streaked spectra are partially overlapping. Thus, without a precise knowledge of the individual reference pulses the analysis is strongly limited.
In order to test the resolution of the streaking setup, we used the option of recording a high resolution XUV spectrum for each FEL pulse and a streaked electron spectrum simultaneously. To make sure that only the shortest XUV pulses are analyzed, we selected in a first step the XUV pulses showing only one single spectral peak and thus only one temporal spike. The spectral width of the single spike still varies in width by ±15% due to SASE fluctuations. The Fourier limit of the narrowest spikes was calculated to be below 5 fs (FWHM). To determine the resolution of the streaking setup, a selection of single spike pulses has been used while in general few spike pulses require iterative reconstruction algorithms to determine the most likely pulse duration shape [14, 48, 49].
Here, we also want to emphasize that there is an alternative approach which can be used to determine the small differences between streaked and un-streaked spectra for ultrashort pulses without the need of precise knowledge of the actual reference XUV-spectrum. If Auger lines are used for streaking, the analysis is independent of energy fluctuations of the incident XUV pulse. Any energetic shift of the streaked lines can directly be ascribed to a shift of the arrival time. In the present case, krypton MNN-Auger electrons emitted after ionization of the Kr 3d shell have been investigated. Figure 8 shows streaked and un-streaked Auger spectra. The Auger spectrum consists of several narrow lines. The line width is determined by the resolution of the electron spectrometer which was ∼1 eV. The THz field shifts and broadens the spectra. The shift is proportional to the THz-vector potential at the instance of ionization and thus a measure for the chosen XUV/THz arrival time.
Figure 8. Measured Kr MNN-Auger spectra with (green) and without (blue) THz field.
Download figure:
Standard image High-resolution imageTo determine the shortest XUV pulse durations within this approach we have again chosen XUV shots with only single modes in the simultaneously measured XUV-spectra. After averaging 50 spectra with the same relative XUV/THz arrival time, the widths of the streaked and un-streaked spectral lines were fitted by four Gaussian functions. After the deconvolution of the streaked and un-streaked spectra as in equation (3b) an FWHM duration of the Auger-electron emission of 10–15 fs has been determined whereby the streaking speed s was 0.05 eV fs−1.
For Auger electrons the emission rate is not proportional to the XUV intensity profile but consists of a convolution of the XUV intensity distribution with the exponential Auger decay rate. In case of krypton the lifetime of the M-shell vacancy is 7.9 fs [50]. Plotted in figure 9 are calculated electron emission rates for direct photo- (blue) and krypton MNN-Auger-electrons (orange) ionized by an XUV pulse with Gaussian envelope and 10 fs FWHM duration. The FWHM width of the Auger emission is 15 fs and thus significantly larger than the XUV pulse duration.
Figure 9. Calculated photo- (blue) and Auger- (orange) electron emission rates assuming a Gaussian intensity distribution of the ionizing XUV pulse with an FWHM duration of 10 fs and a 7.9 fs Auger lifetime.
Download figure:
Standard image High-resolution imageHowever, since the Auger-lifetime is well known it is possible to reconstruct the XUV pulse duration from the measured Auger emission rates. The here observed FWHM Auger emission widths of 10–15 fs correspond to XUV pulse durations of 5–10 fs which is in good agreement with the values inferred from spectral analysis and photoelectron streaking.
4.3.2. Gouy phase broadening
For the short XUV pulses, the Gouy broadening is on the order of the pulse duration and thus of uttermost importance. Here the uncertainty of the knowledge of the Gouy phase has a severe impact on the error bars of the retrieved XUV pulse. In order to reduce the Gouy phase induced broadening, we moved the interaction point (eTOF spectrometer and gas source) out of the THz focus by ∼6 mm. The corresponding effective broadening is on the order of 10 fs (see table 1).
4.3.3. eTOF spectrometer resolution, acceptance angle and signal to noise ratio (SNR)
To determine the small differences between the streaked and un-streaked spectra the Poisson statistics is very important to be considered. In order to keep the signals below the space charge limit, the signal amplitude of the individual pulses was on the order of 100–200 electrons leading to the contribution of about 40–80 electrons in the peak of the signal. Figure 10(a) shows the rather large error bars (>15%) for a single shot spectrum (red: streaked, blue: reference). As one can see, the reference and streaked confidence bands overlap. Thus, for single-shot spectra the uncertainty of the pulse duration measurement is on the order of 100% due to counting statistics.
Figure 10. Streaked (red) and un-streaked (blue) photoelectron spectra are shown (thick lines) including the 1/σ error bars (shaded area) caused by the Poisson statistics due to the limited number of electrons in the spectrum. (a) A single-shot spectra for an XUV pulse containing single spectral spike (wavelength 6.8 nm). (b) The average over ten streaked and ten reference pulses from similar single spectral spike pulses. The streaking speed s was 0.09 eV fs−1.
Download figure:
Standard image High-resolution imageHaving the set of sorted data as described above we can average 10 spectra leading to a ∼3 times smaller error due to Poisson statistics. The confidence bands shrink to a level that the pulse duration can be determined with <50% error.
For ultra-short pulses the angular acceptance of the eTOF spectrometer has to be taken into account as well. Figure 2 shows that only spectra measured at the zero-crossing of the vector potential are not affected for eTOF spectrometers having a large collection angle, while additional broadening is observed for delay times far away from the zero-crossing. Indeed, after correcting for the different eTOF resolutions at different kinetic energies and streaking strength, we see a slight trend of broader spectra as the delay is moved away from the zero-crossing. The effect is however within the error bars.
4.3.4. Influence of the non-linearity of the vector potential
Since the streaking for ultrashort pulses uses only a small fraction of the streaking slope, the linear approximation of the streaking slope is sufficient.
4.3.5. SASE chirp
For the present setup the resolution is not good enough to tell anything about the chirp of singles-spike XUV SASE pulses.
In summary, the main limiting factors of the present streaking setup at the short pulse limit are the counting statistics and the uncertainty in the knowledge of the Gouy phase broadening. Summarizing the errors discussed above we can state that a measured pulse duration for the single-shot single spectral spike SASE pulses (at 6.8 nm) relying on the streaking data is  . Using the Fourier limit derived from the spectral information as additional constrain (the lower bound is more confined), we can state for a single shot measurement
. Using the Fourier limit derived from the spectral information as additional constrain (the lower bound is more confined), we can state for a single shot measurement  . By averaging pulses with similar XUV spectra we can reduce the pulse duration value and the error range to
. By averaging pulses with similar XUV spectra we can reduce the pulse duration value and the error range to  [35].
[35].
5. Conclusion
Terahertz-field-driven streaking is a powerful tool for measuring the duration and (to a certain extent) time-structure of ultra-short XUV pulses on a single-shot basis. We investigated the applicability of the method by using the large parameter range of FLASH delivering pulse durations from ∼10 fs to ∼350 fs at different XUV wavelengths.
We show that the streaking technique relying on laser based THz generation in LiNbO3, yielding a field strength of 300 kV cm−1, is ideally suited to measure the pulse duration in the range of 30 fs to 150 fs with an overall precision of typically ±20%. The individual error contributions are discussed in detail. In addition, for the precise analysis of the spectra and the simulation of the influence of different parameters, the theoretical description of the streaking process based on quantum mechanical principles is presented. Here, a novel approximation of the common SFA approach allows the fast reconstruction of XUV pulses from measured photoelectron spectra including the angular distribution of the photoelectrons as well as the nonlinear vector potential of the streaking field.
To determine the limits of the method we explored the long pulse limit where the XUV pulses extend over essentially the whole streaking slope, as well as sub-10 fs pulses to determine the resolution limit. In the present setup, pulse durations down to about 20 fs can be measured reliably while for even shorter pulses higher streaking fields are required. In principle, this can be achieved using higher THz frequencies [20] or even using IR radiation [45]. However, in this range the jitter between THz (IR) and XUV easily becomes larger than the streaking slope and new methods have to be applied [48].
Acknowledgments
We want to acknowledge the work of the scientific and technical team at FLASH. NMK acknowledges the hospitality and financial support from DESY and from the theory group in cooperation with the SQS research group of the European XFEL (Hamburg). KW and MD acknowledge support by the SFB925-A1. UF and AD acknowledge support by the excellence cluster 'The Hamburg Center for Ultrafast Imaging—Structure, Dynamics and Control of Matter at the Atomic Scale' (DFG)—EXC 1074 project ID 194651731. SW acknowledges support by the DFG Forschergruppe FOR 1789.










