Abstract
We propose a scheme to generate steady-state bipartite and tripartite entanglement in the cavity magnomechanical system, which consists of a microwave (MW) cavity field, three magnons, and a phonon mode. The three magnons are coupled to the MW cavity via the magnetic dipole interaction, and one of them is also coupled to the phonon mode through the magnetostrictive force. By utilizing the nonlinearity of the magnetostrictive force and the cavity-magnon interaction, the three magnons become mutually entangled, and the steady-state of the system displays a genuine tripartite entanglement. We found that there are optimum parameters, including the detunings and the cavity-magnon coupling, which lead to maximum entanglement. Moreover, the entanglement is robust against thermal effects.
Export citation and abstract BibTeX RIS
1. Introduction
The collective excitations of spins known as magnons in ferrimagnetic materials such as the yttrium-iron-garnet (YIG) spheres, have attracted the attention of researchers in recent years owing to their high spin density and low damping rate. The magnon mode in the YIG sphere can strongly couple to the microwave (MW) cavity photons, resulting in cavity-polaritons [1–4], which provide a potentially useful framework for magnon-based information processing, including the remote manipulation of spin current [5], the magnon dark modes and gradient memory [6] and bistability [7].
Another exciting option is to couple the magnons to the phonons [8, 9] or superconducting qubits [10–12] in order to transform magnon-cavity systems into hybrid systems. In particular, the cavity magnomechanical (CMM) system [8] consists of an MW cavity and a YIG sphere where the magnon mode in the YIG sphere couple simultaneously to the MW cavity and phonon modes through the magnetic dipole interaction and magnetostrictive force (which plays the role of the radiation pressure in optomechanics (OM) systems), respectively. Compared to the OM systems [13–19], the CMM systems benefit from more flexibility and lower loss, which offers a potential vision for implementing quantum information theory and macroscopic quantum effects. Among these effects, quantum entanglement is a primary physical resource for quantum information processing. It is an essential part of a wide variety of fields of study that include quantum dense coding [20], quantum key distribution [21], quantum teleportation [22], and quantum cryptography [23].
In the CMM system, Li et al have utilized the nonlinearity of magnetostrictive interaction to investigate various interesting quantum effects. They have demonstrated the generation of bipartite entanglements and even a genuine tripartite photon-magnon-phonon entanglement [24], which is the most significant feature of this system. Additionally, they have also demonstrated squeezing of the MW fields [25] and entangled two magnons by coupling two YIG to a single MW cavity and activating the magnomechanical interaction [26]. In the same vein, other researchers have investigated other phenomena. For instance, we may cite the generation of stationary entanglement between two MW fields by using magnetostrictive interaction [27–29] and the entanglement of two phonon modes of two YIG by utilizing the nonlinearity of the magnetostriction [30]. Interestingly enough, other nonlinearities have been used in the CMM systems [31], such as the nonlinearity of a flux-driven Josephson parametric amplifier to generate squeezed states of magnon and phonon modes [32] and entanglement of two magnon modes [33–37]. Additionally, the nonlinearity of the Kerr effect was utilized to enhance the entanglement between two magnons [38] and squeeze the state of magnon mode to enhance the entanglement [39]. Recently, the nonlinearity of the optical parametric amplifier has been utilized to improve entanglement in the CMM system [40, 41], entangle two cavity modes, and squeeze the magnon mode [42]. Moreover, a coherent feedback loop has been also employed to significantly improve entanglement in the CMM system [43].
Here, we present a model for a CMM system which involves a MW cavity field, three magnon modes and a phonon mode. Specifically, we show that by using the nonlinearity of the magnetostrictive interaction activated in one YIG sphere, it is possible to generate, both the bipartite entanglement between distinct magnon-mode subsystems and also a genuine tripartite entanglement. Furthermore, by choosing the appropriate experimental parameters in our simulations, we show that the entanglement is robust to the thermal influences. In our scheme, the entanglement results from the combination of the cavity-magnon beam-splitter interaction and the nonlinearity of magnetostrictive force, which can be enhanced by driving the YIG sphere using a laser.
This paper is organized as follows: In section 2, we introduce our system and its Hamiltonian. In section 3, we give the quantum Langevin equations (QLEs) and investigate the dynamical equation for the covariance matrix (CM), i.e. the steady-state solution of QLEs, we also give the definition of bipartite and tripartite entanglements. Section 4 is devoted to the examination of the feasibility of the system. In section 5, we present and discuss our numerical results. Finally, our conclusions are presented in section 6.
2. The model and Hamiltonian
We propose in figure 1(a) hybrid CMM system which contains five modes: a MW cavity mode (a), the three magnon modes (m1, m2 and m3), and a mechanical mode (b). The MW cavity field and the three magnon modes interact through the magnetic dipole interaction. Due to the high spin density of the YIG spheres, this coupling can be very strong [1, 2, 9]. In addition, the magnetostrictive force mediates the coupling between the magnon and the phonon modes of the YIG-1 sphere. In particular, the variation of magnetization inside the YIG-1 caused by the magnon excitation leads to the deformation of its geometry structure and yields the magnon1-phonon coupling [24]. Furthermore, since the dimensions of the YIG spheres are considerably smaller than the wavelength of the MW field, the influence of radiation pressure can be considered negligible [24]. The Hamiltonian of the system with respect to the magnon drive frequency ωd reads:
Figure 1. Schematic diagram of three YIG spheres positioned close to the maximum magnetic fields of the MW cavity and at the same time in a uniform bias magnetic field, which is responsible for the photon-magnon coupling. In addition, the YIG-1 sphere is directly driven by a MW source to turn on the magnetostrictive interaction and get the coupling magnon1-phonon. The bias magnetic field, the drive magnetic field, and the magnetic field of the MW cavity are applied along the z-axis, y-axis and x-axis, respectively.
Download figure:
Standard image High-resolution image
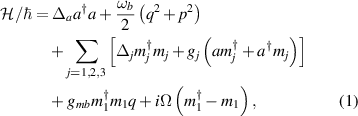
where  /a and
/a and  /mj
being the creation/annihilation operators of the cavity mode and jth magnon mode, respectively, with the corresponding frequencies ωa
and ωj
, fulfilling the commutation relation
/mj
being the creation/annihilation operators of the cavity mode and jth magnon mode, respectively, with the corresponding frequencies ωa
and ωj
, fulfilling the commutation relation ![$ [O,O^{\dagger}] = 1 $](https://content.cld.iop.org/journals/0953-4075/56/11/115401/revision3/bacce11ieqn3.gif) (
( ). p and q are dimensionless momentum and position quadratures of the mechanical mode with corresponding frequency ωb
, fulfilling the commutation relation
). p and q are dimensionless momentum and position quadratures of the mechanical mode with corresponding frequency ωb
, fulfilling the commutation relation ![$ [q,p] = i $](https://content.cld.iop.org/journals/0953-4075/56/11/115401/revision3/bacce11ieqn5.gif) . In addition,
. In addition,  and
and  are the detunings, respectively, of the cavity mode and the jth magnon mode defined from the driven field. By altering the external bias magnetic field (H), the frequency of magnon modes can be adjusted over a wide range via
are the detunings, respectively, of the cavity mode and the jth magnon mode defined from the driven field. By altering the external bias magnetic field (H), the frequency of magnon modes can be adjusted over a wide range via  with
with  GHz T−1 being the gyromagnetic ratio. gj
denotes the coupling force between the cavity mode and the jth magnon mode, which corresponds to the strong coupling regime when gj
is greater than the decay rates of the cavity (κa
) and the jth magnon (κj
) modes, i.e.
GHz T−1 being the gyromagnetic ratio. gj
denotes the coupling force between the cavity mode and the jth magnon mode, which corresponds to the strong coupling regime when gj
is greater than the decay rates of the cavity (κa
) and the jth magnon (κj
) modes, i.e.  [1–3]. In addition, gmb
denotes the magnomechanical coupling strength which is generally small, but it can be increased by applying a powerful MW field to excite the magnon mode, which can be realized for example by using a small loop antenna at the end of a superconducting MW line to drive the YIG sphere [7, 27, 44]. The Rabi frequency
[1–3]. In addition, gmb
denotes the magnomechanical coupling strength which is generally small, but it can be increased by applying a powerful MW field to excite the magnon mode, which can be realized for example by using a small loop antenna at the end of a superconducting MW line to drive the YIG sphere [7, 27, 44]. The Rabi frequency  [24] represents the coupling strength between the magnon mode and its driving magnetic field with amplitude B0 and frequency ωd
, where
[24] represents the coupling strength between the magnon mode and its driving magnetic field with amplitude B0 and frequency ωd
, where  is the total spin number with the spin density
is the total spin number with the spin density 
 and V the volume of the sphere [24]. It is worth noting here that the bosonic operators
and V the volume of the sphere [24]. It is worth noting here that the bosonic operators  and mj
are derived under the assumption of low-lying excitations, i.e.
and mj
are derived under the assumption of low-lying excitations, i.e.  , where
, where  is the spin number of the ground-state Fe3+ ion in the YIG sphere [24].
is the spin number of the ground-state Fe3+ ion in the YIG sphere [24].
3. Quantum dynamics and magnons entanglement
In this section, we derive the dissipative dynamics of our system described by the following set of QLEs:
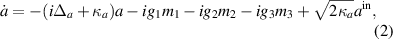
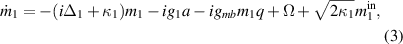
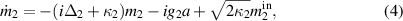
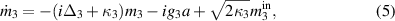

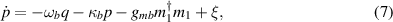
where κb
is the mechanical dissipation rate, while  and
and  denote the input noise operators for the cavity and the jth magnon modes, respectively. These operators have a mean of zero and are associated with the following correlation functions [45]:
denote the input noise operators for the cavity and the jth magnon modes, respectively. These operators have a mean of zero and are associated with the following correlation functions [45]:

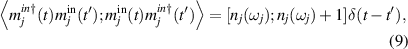
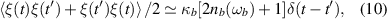
where the correlation function of the Langevin force operator ξ has been taken into account for the mechanical Brownian motion under the Markovian approximation, which is valid for a large mechanical quality factor, i.e.  [46, 47].
[46, 47]. ![$ n_{O}(\omega _{O}) = [\exp (\frac{\hbar \omega _{O}}{k_\mathrm{B}T})-1]^{-1} $](https://content.cld.iop.org/journals/0953-4075/56/11/115401/revision3/bacce11ieqn21.gif) (
( ) being the equilibrium mean thermal photon, jth magnon, and phonon numbers, with
) being the equilibrium mean thermal photon, jth magnon, and phonon numbers, with  is the Boltzmann constant and T is the environmental temperature.
is the Boltzmann constant and T is the environmental temperature.
Since the first magnon mode (m1) is strongly driven, its steady-state amplitude is much larger than one, i.e.  . This large amplitude of the first magnon mode leads to significant amplitudes of the cavity, magnon 2, and magnon 3 modes, respectively, due to the beam-splitter interaction between the magnons and the cavity mode, which implies that the amplitudes of
. This large amplitude of the first magnon mode leads to significant amplitudes of the cavity, magnon 2, and magnon 3 modes, respectively, due to the beam-splitter interaction between the magnons and the cavity mode, which implies that the amplitudes of  . As a result, the QLEs (2)–(7) can be linearized using the standard linearization technique. This involves expressing each Heisenberg operator as a sum of its classical average and a fluctuation operator with zero mean, i.e.
. As a result, the QLEs (2)–(7) can be linearized using the standard linearization technique. This involves expressing each Heisenberg operator as a sum of its classical average and a fluctuation operator with zero mean, i.e.  (
( ), and neglecting higher-order fluctuations. After linearization, two types of linearized QLEs are obtained for the classical averages and fluctuation operators. The solutions for the first type of equations are:
), and neglecting higher-order fluctuations. After linearization, two types of linearized QLEs are obtained for the classical averages and fluctuation operators. The solutions for the first type of equations are:
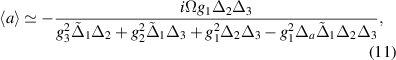
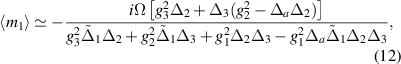
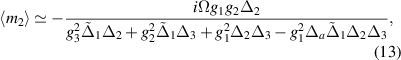
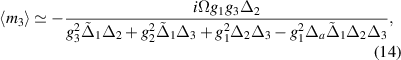
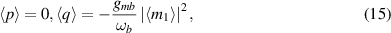
where the above expressions are reached within the condition that  (
( ) and
) and  represents the effective detuning of the first magnon mode, which takes into account the frequency shift brought on by the interaction between magnon1 and mechanical mode.
represents the effective detuning of the first magnon mode, which takes into account the frequency shift brought on by the interaction between magnon1 and mechanical mode.
Alternatively, the linearized QLEs can be represented in quadrature form as:
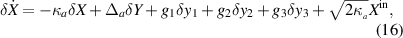
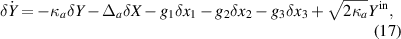
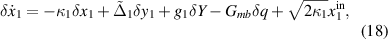
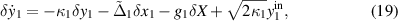
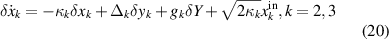


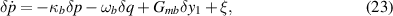
in which we have characterized the quadrature fluctuations defined as:  .
.  is the effective magnomechanical coupling strength. In addition, the aforementioned linearized QLEs (16)–(23) can be expressed in the following compact matrix form:
is the effective magnomechanical coupling strength. In addition, the aforementioned linearized QLEs (16)–(23) can be expressed in the following compact matrix form:
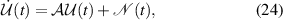
with 
![$\delta y_{3}(t), \delta q(t), \delta p(t)] $](https://content.cld.iop.org/journals/0953-4075/56/11/115401/revision3/bacce11ieqn34.gif) and
and 




 ,
,
![$\sqrt{2\kappa _{3}}y_{3}^{\mathrm{in}}(t), 0, \xi(t)]$](https://content.cld.iop.org/journals/0953-4075/56/11/115401/revision3/bacce11ieqn41.gif) are the vectors for quantum fluctuations and noise, respectively, and the matrix
are the vectors for quantum fluctuations and noise, respectively, and the matrix  reads:
reads:
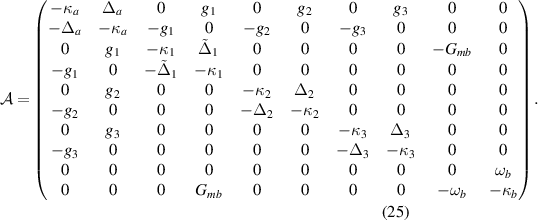
Since we are working with linearized versions of the QLEs and all noises are Gaussian, the quantum fluctuation steady-state of the system is a continuous variable Gaussian state with five modes. This state can be described by a  CM whose elements are defined by
CM whose elements are defined by  for
for  .
.
To derive the steady-state CM  , we can solve the following Lyapunov equation, as guaranteed by the negativity of the real parts of the eigenvalues of the matrix
, we can solve the following Lyapunov equation, as guaranteed by the negativity of the real parts of the eigenvalues of the matrix  [48]:
[48]:
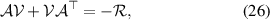
where  is the diffusion matrix of elements:
is the diffusion matrix of elements:  (
( ) and given by:
) and given by: 



 .
.
After obtaining the CM  , the bipartite entanglement between the different magnons and cavity mode, can be quantified using the logarithmic negativity EN
[49], which is defined as:
, the bipartite entanglement between the different magnons and cavity mode, can be quantified using the logarithmic negativity EN
[49], which is defined as:
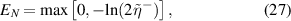
where  is the smallest symplectic eigenvalue of the partial transpose CM
is the smallest symplectic eigenvalue of the partial transpose CM  .
.  (with σ2 is the y-Pauli matrix) is the symplectic matrix,
(with σ2 is the y-Pauli matrix) is the symplectic matrix,  is the matrix that performs the partial transposition at the level of the CMs and
is the matrix that performs the partial transposition at the level of the CMs and  is the
is the  CM of the two interested subsystems, which derived by deleting the uninteresting mode's rows and columns in
CM of the two interested subsystems, which derived by deleting the uninteresting mode's rows and columns in  . In this CMM system, the presence of bipartite entanglement is reflected by the nonzero of the logarithmic negativity, i.e.
. In this CMM system, the presence of bipartite entanglement is reflected by the nonzero of the logarithmic negativity, i.e.  .
.
Next, we investigate the tripartite entanglement  (
( ) as measured by the residual contangle, which is given by [24, 38, 49, 50]:
) as measured by the residual contangle, which is given by [24, 38, 49, 50]:

where the indices i, j, and k refer to three modes a, m1, and m2, or to m1, m2, and m3, respectively.  represents the contangle between subsystems u and v. In this context, subsystem v may consist of one or two modes. The contangle is a proper entanglement monotone defined as the squared logarithmic negativity [49, 50], i.e.
represents the contangle between subsystems u and v. In this context, subsystem v may consist of one or two modes. The contangle is a proper entanglement monotone defined as the squared logarithmic negativity [49, 50], i.e.  . The logarithmic negativity of one mode with respect to that of two modes
. The logarithmic negativity of one mode with respect to that of two modes  is defined as follows:
is defined as follows:

similar to the logarithmic negativity for bipartite entanglement (27),  is the smallest symplectic eigenvalue of the
is the smallest symplectic eigenvalue of the  CM
CM  and
and  being the symplectic matrix. Here
being the symplectic matrix. Here  is the
is the  CM describing the three interesting modes which can be obtained by deleting the uninteresting mode's rows and columns in
CM describing the three interesting modes which can be obtained by deleting the uninteresting mode's rows and columns in  .
.  ,
,  and
and  are partial transposition matrices at the level of the CM
are partial transposition matrices at the level of the CM  . Furthermore, the residue contangle fulfills the monogamy of quantum entanglement, that is,
. Furthermore, the residue contangle fulfills the monogamy of quantum entanglement, that is,  , i.e.
, i.e.  , which is similar to the monogamy inequality for a three-qubit cases established by Coffman et al in [51]. A bona fide minimum residual cotangle
, which is similar to the monogamy inequality for a three-qubit cases established by Coffman et al in [51]. A bona fide minimum residual cotangle  provides a genuine measure of tripartite entanglement for Gaussian states, which is given by:
provides a genuine measure of tripartite entanglement for Gaussian states, which is given by:
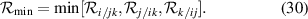
This relation ensures the invariance of tripartite entanglement under any permutation of the three modes. A nonzero minimal residual contangle  indicates that the three modes are genuinely entangled.
indicates that the three modes are genuinely entangled.
4. Feasibility of the model
Let's evaluate the feasibility of our proposed scheme by utilizing experimentally feasible parameters taken from [24]. The parameters are as follows:  MHz,
MHz,  Hz,
Hz,  GHz,
GHz,  MHz, T = 10 mK,
MHz, T = 10 mK,  MHz and
MHz and  MHz.
MHz.
On one hand, we made the assumption of a low-lying excitation for which the numerical results are applicable, i.e. when the magnon excitation numbers satisfy  [24]. According to references [24, 26, 30], in our simulation, we used YIG spheres with a diameter of 250
[24]. According to references [24, 26, 30], in our simulation, we used YIG spheres with a diameter of 250  , containing
, containing  spins, and
spins, and  Hz, corresponding to a Rabi frequency
Hz, corresponding to a Rabi frequency  Hz. Additionally,
Hz. Additionally,  , so
, so  , which is holds. Similarly,
, which is holds. Similarly,  and
and  are also satisfied for the parameters used in this manuscript because
are also satisfied for the parameters used in this manuscript because  .
.
On the other hand, if a strong pump is utilized to drive the magnon mode, it can introduce the Kerr nonlinear term  into the Hamiltonian [7, 52], where the value of the Kerr coefficient K is determined by the volume of the YIG sphere and is inversely proportional to it. For a YIG sphere with a diameter of 250
into the Hamiltonian [7, 52], where the value of the Kerr coefficient K is determined by the volume of the YIG sphere and is inversely proportional to it. For a YIG sphere with a diameter of 250  [24], the Kerr coefficient K is estimated to be approximately
[24], the Kerr coefficient K is estimated to be approximately  Hz [24]. The Kerr effect can be considered negligible only if the condition
Hz [24]. The Kerr effect can be considered negligible only if the condition  is well satisfied. The parameters used in our simulations lead to
is well satisfied. The parameters used in our simulations lead to  Hz
Hz 
 Hz. Therefore, we can conclude that the Kerr nonlinearity can be neglected in our scheme.
Hz. Therefore, we can conclude that the Kerr nonlinearity can be neglected in our scheme.
5. Results and discussion
In this section, we will explore the results of the study regarding the entanglement between different magnons and cavity mode, including bipartite and tripartite entanglement.
In figures 2(a) and (b), we present the bipartite entanglements, namely (a) cavity-magnon1  and (b) magnon1-phonon
and (b) magnon1-phonon  , as a functions of the normalized detunings
, as a functions of the normalized detunings  and
and  . It is important to mention that all results in this paper are in steady-state, which has been verified by ensuring that the real parts of the eigenvalues of the matrix
. It is important to mention that all results in this paper are in steady-state, which has been verified by ensuring that the real parts of the eigenvalues of the matrix  are negative (see appendix). It can be seen from figure 2(a) that there is a specific set of detunings, centered around
are negative (see appendix). It can be seen from figure 2(a) that there is a specific set of detunings, centered around  and
and  , where the magnon1 and cavity modes are in resonance with the two mechanical sidebands. This detunings implies strong entanglement between the magnon1 and cavity modes. Furthermore, applying a strong red-detuned driving field to the magnon1 mode results in the cooling of the hot mechanical mode b (which is a necessary step in preparing quantum states), as shown in [24]. At the same time, this activates the magnomechanical parametric down-conversion interaction and generates significant magnomechanical entanglement
, where the magnon1 and cavity modes are in resonance with the two mechanical sidebands. This detunings implies strong entanglement between the magnon1 and cavity modes. Furthermore, applying a strong red-detuned driving field to the magnon1 mode results in the cooling of the hot mechanical mode b (which is a necessary step in preparing quantum states), as shown in [24]. At the same time, this activates the magnomechanical parametric down-conversion interaction and generates significant magnomechanical entanglement  due to the strong coupling Gmb
(see figure 2(b)) [24]. This results in partial transfer of entanglement to the cavity-magnon1 subsystem, meaning that both the cavity and magnon1 mode become entangled, as evidenced by a positive value of
due to the strong coupling Gmb
(see figure 2(b)) [24]. This results in partial transfer of entanglement to the cavity-magnon1 subsystem, meaning that both the cavity and magnon1 mode become entangled, as evidenced by a positive value of  , and the same effect is observed for the cavity-phonon subsystem [24]. This entanglement transfer is more pronounced when the cavity detuning is approximately
, and the same effect is observed for the cavity-phonon subsystem [24]. This entanglement transfer is more pronounced when the cavity detuning is approximately  (see figure 2(a)). On the other hand, we plot in figure 2(c)
(see figure 2(a)). On the other hand, we plot in figure 2(c)  versus
versus  and
and  . As can be seen from figure 2(c), when
. As can be seen from figure 2(c), when  , we note that the bipartite entanglement
, we note that the bipartite entanglement  , which is natural due to the fact that the linear cavity-magnon beam splitter interaction generally generates zero entanglement, and only the nonlinearity of the magnetostrictive force is responsible for generating the squeezing and entanglement in the CMM system [24, 32]. We also note that strong entanglement is generated when the two couplings are of the same magnitude, i.e.
, which is natural due to the fact that the linear cavity-magnon beam splitter interaction generally generates zero entanglement, and only the nonlinearity of the magnetostrictive force is responsible for generating the squeezing and entanglement in the CMM system [24, 32]. We also note that strong entanglement is generated when the two couplings are of the same magnitude, i.e.  .
.
Figure 2. Density plot of (a)  , (b)
, (b)  as a function of the detunings
as a function of the detunings  and
and  . (c)
. (c)  as a function of
as a function of  and
and  . We take
. We take  in (c) and
in (c) and  in all cases.
in all cases.
Download figure:
Standard image High-resolution imageFigure 3 presents the bipartite cavity-magnon2 entanglement ( ) as a function of (a)
) as a function of (a)  and
and  , (b)
, (b)  and
and  , and (c)
, and (c)  and
and  . Figures 3(a) and (b) show that there are optimal detunings for the cavity and magnon modes that lead to strong entanglement between the magnon2 and cavity modes. These detunings are given as
. Figures 3(a) and (b) show that there are optimal detunings for the cavity and magnon modes that lead to strong entanglement between the magnon2 and cavity modes. These detunings are given as  (i.e. when the cavity mode resonates with the driving field),
(i.e. when the cavity mode resonates with the driving field),  , and
, and  . This entanglement is achieved through a combination of nonlinear magnetostrictive interaction and linear beam splitter interaction, as well as carefully chosen detunings for each mode. The nonlinearity of the magnetostrictive interaction is essential for creating entangled states that cannot be achieved using linear interaction alone (see figure 2), while the linear interaction enhances the entanglement and allows for efficient information transfer between the cavity and jth magnon subsystems. Furthermore, figure 3(c) shows that there are also optimal couplings that lead to significant entanglement between the magnon2 and cavity modes when
. This entanglement is achieved through a combination of nonlinear magnetostrictive interaction and linear beam splitter interaction, as well as carefully chosen detunings for each mode. The nonlinearity of the magnetostrictive interaction is essential for creating entangled states that cannot be achieved using linear interaction alone (see figure 2), while the linear interaction enhances the entanglement and allows for efficient information transfer between the cavity and jth magnon subsystems. Furthermore, figure 3(c) shows that there are also optimal couplings that lead to significant entanglement between the magnon2 and cavity modes when  and
and  . It is worth mentioning that similar optimal conditions for strong entanglement between the cavity and magnon3 modes can be also obtained by interchanging the roles of m2 and m3 in the analysis. However, to keep the discussion concise, we have not explored this scenario in detail here.
. It is worth mentioning that similar optimal conditions for strong entanglement between the cavity and magnon3 modes can be also obtained by interchanging the roles of m2 and m3 in the analysis. However, to keep the discussion concise, we have not explored this scenario in detail here.
Figure 3. Density plot of  as a function of the detunings (a)
as a function of the detunings (a)  and
and  , (b)
, (b)  and
and  . (c)
. (c)  as a function of
as a function of  and
and  . We take
. We take  and
and  in (a) and (b).
in (a) and (b).  in (a) and (c),
in (a) and (c),  in (b) and (c), and
in (b) and (c), and  in all cases.
in all cases.
Download figure:
Standard image High-resolution imageIn order to examine the entanglement between the three magnon modes, we have presented bipartite entanglement  in figure 4 and analyzed it against (a)
in figure 4 and analyzed it against (a)  and
and  , (b)
, (b)  and
and  and (c)
and (c)  and
and  . Based on figures 4(a) and (b), we can conclude that the maximum entanglement
. Based on figures 4(a) and (b), we can conclude that the maximum entanglement  can be achieved when the cavity and magnon2 modes are approximately resonant with the red sideband, i.e.
can be achieved when the cavity and magnon2 modes are approximately resonant with the red sideband, i.e.  , while the magnon m3 and m1 modes are approximately resonant with the blue sideband of the mechanical mode, i.e.
, while the magnon m3 and m1 modes are approximately resonant with the blue sideband of the mechanical mode, i.e.  . This entanglement is possible due to the magnon-cavity interaction between the three magnon and cavity modes, which is partially transferred from the cavity-magnon1 subsystem to the cavity-magnon2 and cavity-magnon3 subsystems. It is worth mentioning that a similar scenario can be seen in achieving strong entanglement between two MW cavities using the magnetostrictive interaction as reported in [27], where the MW 1 must be resonant with the red sideband, and the MW 2 must be resonant with the blue sideband, and vice versa. Additionally, figure 4(c) demonstrates that there is an optimal coupling g2 for achieving strong entanglement when g2 is of the same order as g3, i.e.
. This entanglement is possible due to the magnon-cavity interaction between the three magnon and cavity modes, which is partially transferred from the cavity-magnon1 subsystem to the cavity-magnon2 and cavity-magnon3 subsystems. It is worth mentioning that a similar scenario can be seen in achieving strong entanglement between two MW cavities using the magnetostrictive interaction as reported in [27], where the MW 1 must be resonant with the red sideband, and the MW 2 must be resonant with the blue sideband, and vice versa. Additionally, figure 4(c) demonstrates that there is an optimal coupling g2 for achieving strong entanglement when g2 is of the same order as g3, i.e.  . It is important to note that the same situation can occur for the bipartite entanglement
. It is important to note that the same situation can occur for the bipartite entanglement  when interchanging the roles of m2 and m3, but we have not discussed it here for the sake of brevity.
when interchanging the roles of m2 and m3, but we have not discussed it here for the sake of brevity.
Figure 4. Density plot of  versus (a)
versus (a)  and
and  , (b)
, (b)  and
and  , (c)
, (c)  and the ratio of
and the ratio of  . We take
. We take  in (a) and (c).
in (a) and (c).  and
and  in all cases.
in all cases.
Download figure:
Standard image High-resolution imageIn figure 5, we display the bipartite entanglement  between two indirectly coupled magnon modes as a function of three different parameters: (a) the ratios of
between two indirectly coupled magnon modes as a function of three different parameters: (a) the ratios of  and
and  , (b) the ratios of
, (b) the ratios of  and
and  , and (c) the ratio of coupling rates
, and (c) the ratio of coupling rates  and
and  . Figures 5(a) and (b) show that strong entanglement occurs under the same detuning conditions as those illustrated in figure 4, precisely when
. Figures 5(a) and (b) show that strong entanglement occurs under the same detuning conditions as those illustrated in figure 4, precisely when  and
and  for
for  and
and  . We note here that when
. We note here that when  and
and  , the optimal detunings are
, the optimal detunings are  and
and  . Finally, figure 5(c) investigates the optimal values of the coupling rates g2 and g3, revealing that the magnon mode resonating with the red (blue) mechanical sideband should have a reduced (increased) coupling rate compared to the other magnon mode. For instance,
. Finally, figure 5(c) investigates the optimal values of the coupling rates g2 and g3, revealing that the magnon mode resonating with the red (blue) mechanical sideband should have a reduced (increased) coupling rate compared to the other magnon mode. For instance,  and
and  are optimal to achieve strong entanglement between the two magnons as shown in figure 5(c).
are optimal to achieve strong entanglement between the two magnons as shown in figure 5(c).
Figure 5. Density plot of  versus (a)
versus (a)  and
and  , (b)
, (b)  and
and  , (c) the ratio of
, (c) the ratio of  and
and  . We take
. We take  in (a) and (c).
in (a) and (c).  and
and  in (a) and (b), and
in (a) and (b), and  in (b) and (c).
in (b) and (c).
Download figure:
Standard image High-resolution imageTo test the robustness of entanglement between bipartite subsystems against environmental temperature, we plotted three measures of entanglement, namely  ,
,  , and
, and  , against T in figure 6. We used the optimal parameters for each subsystem from figures 3–5 and considered two cases:
, against T in figure 6. We used the optimal parameters for each subsystem from figures 3–5 and considered two cases:  (dashed line) and
(dashed line) and  (solid line). Figure 6 reveals that all the subsystems are most robust when the damping rates of the magnon1 and magnon2 modes are low. Additionally,
(solid line). Figure 6 reveals that all the subsystems are most robust when the damping rates of the magnon1 and magnon2 modes are low. Additionally,  is more temperature-resistant than
is more temperature-resistant than  and
and  . Specifically, for
. Specifically, for  (
( ),
),  at
at  mK (
mK ( mK),
mK),  at
at  mK (
mK ( mK), and
mK), and  at
at  mK (
mK ( mK). Thus, the damping rate of the magnon1 and magnon2 modes can also be used to control entanglement in this system. Furthermore, the entanglement decreases with increasing temperature due to the decoherence effect. Note that the highest temperature observed here is higher than the temperature obtained in [26] and lower than the temperature of 250 mK recently observed in [28] using two indirectly coupled MW fields.
mK). Thus, the damping rate of the magnon1 and magnon2 modes can also be used to control entanglement in this system. Furthermore, the entanglement decreases with increasing temperature due to the decoherence effect. Note that the highest temperature observed here is higher than the temperature obtained in [26] and lower than the temperature of 250 mK recently observed in [28] using two indirectly coupled MW fields.
Figure 6. Plot of (a)  , (b)
, (b)  and (c)
and (c)  versus the temperature T for
versus the temperature T for  (dashed line) and
(dashed line) and  (solid line). We take optimal parameters obtained in figures 3–5 for (a), (b) and (c), respectively.
(solid line). We take optimal parameters obtained in figures 3–5 for (a), (b) and (c), respectively.
Download figure:
Standard image High-resolution imageIn addition to the generation of bipartite entanglement between the different magnon modes, it is also possible to generate genuine tripartite entanglement in the system by exploiting the nonlinearity of the magnetostrictive interaction, as illustrated by the nonzero minimum residual contangle  in figures 7 and 8. In figure 7 we present the tripartite cavity-magnon1-magnon2 entanglement as a function of
in figures 7 and 8. In figure 7 we present the tripartite cavity-magnon1-magnon2 entanglement as a function of  and temperature T for the optimal parameters obtained in figure 3. As can be seen from figure 7, the system exhibits a genuine tripartite entanglement against the detuning
and temperature T for the optimal parameters obtained in figure 3. As can be seen from figure 7, the system exhibits a genuine tripartite entanglement against the detuning  and the tripartite entanglement survives up to the temperature of 160 mK. It is worth mentioning again that similar results for tripartite cavity-magnon1-magnon3 entanglement can be obtained by interchanging the roles of m2 and m3 in the analysis. However, to keep the discussion concise, we have not explored this scenario in detail here.
and the tripartite entanglement survives up to the temperature of 160 mK. It is worth mentioning again that similar results for tripartite cavity-magnon1-magnon3 entanglement can be obtained by interchanging the roles of m2 and m3 in the analysis. However, to keep the discussion concise, we have not explored this scenario in detail here.
Figure 7. A genuine tripartite cavity-magnon1-magnon2 entanglement  as a functions of (a) detuning
as a functions of (a) detuning  and (b) the temperature T for
and (b) the temperature T for  ,
,  ,
,  ,
,  and
and  in all cases.
in all cases.  in (b).
in (b).
Download figure:
Standard image High-resolution imageFigure 8. A genuine tripartite magnon1-magnon2-magnon3 entanglement  as a functions of detuning
as a functions of detuning  [panels (a) and (b)] and the temperature T [panels (c) and (d)]. The optimal parameters obtained from figures 4 and 5 are used in panels (a) and (b), and panels (c) and (d), respectively.
[panels (a) and (b)] and the temperature T [panels (c) and (d)]. The optimal parameters obtained from figures 4 and 5 are used in panels (a) and (b), and panels (c) and (d), respectively.
Download figure:
Standard image High-resolution imageOn the other hand we plot in figure 8 the tripartite magnon1-magnon2-magnon3 entanglement as a function of  [panels (a) and (b)] and temperature T [panels (c) and (d)]. We used the optimal parameters obtained from figures 4, and 5 in [panels (a) and (c)] and [panels (b) and (d)], respectively. We can see from figures 8(a) and (b) that in both cases, the system exhibits genuine tripartite entanglement against the detuning
[panels (a) and (b)] and temperature T [panels (c) and (d)]. We used the optimal parameters obtained from figures 4, and 5 in [panels (a) and (c)] and [panels (b) and (d)], respectively. We can see from figures 8(a) and (b) that in both cases, the system exhibits genuine tripartite entanglement against the detuning  . Furthermore, the tripartite entanglement shows robustness against the temperature T: the best robustness highlighted when we use the optimum parameters used to achieve strong entanglement between magnon2 and magnon3. In fact,
. Furthermore, the tripartite entanglement shows robustness against the temperature T: the best robustness highlighted when we use the optimum parameters used to achieve strong entanglement between magnon2 and magnon3. In fact,  for
for  mK [panel (c)] and
mK [panel (c)] and  mK [panel (d)].
mK [panel (d)].
Before concluding this section, and following references [24, 26, 30], we will discuss the experimental implementation. The verification of the generated bipartite or tripartite entanglement can be achieved through measurements of the corresponding CMs [54, 55]. The cavity field quadratures can be directly measured by homodyning the cavity output, and the state of the three magnons can be indirectly measured by homodyning the cavity output of a probe field introduced into the system [24, 26, 30]. In addition, an extra optical cavity can be employed to couple the YIG-1 sphere, enabling the measurement of mechanical quadratures [24, 30, 56].
6. Conclusions
We studied a CMM system consisting of an MW cavity field, three magnons and a phonon mode, where the three magnon modes in the YIG spheres interact with the MW cavity field through the magnetic dipole interaction, and one of them additionally interacts with the phonon mode of the YIG sphere through the magnetostrictive interaction. By selecting experimentally reachable parameters and fully exploiting the aforementioned nonlinearity of the magnetostrictive force and the linear cavity-magnon (beam-splitter) interaction, we have shown that the three magnons become mutually entangled, and the steady-state of the system displays a genuine tripartite entanglement, where the entanglement is resistant to the environmental temperature. Furthermore, our findings show that to have a strong bipartite magnon-magnon entanglement, the magnon that resonates with the red (blue) mechanical sideband must have a reduced (increased) coupling rate compared to the other magnon mode. Due to the macroscopic scale of the YIG spheres ( -diameter), our system exhibits macroscopic quantum states that are useful for investigating quantum/classical transitions, as well as testing decoherence theory. Therefore, research involving the creation of macroscopic entangled states may benefit from this work.
-diameter), our system exhibits macroscopic quantum states that are useful for investigating quantum/classical transitions, as well as testing decoherence theory. Therefore, research involving the creation of macroscopic entangled states may benefit from this work.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix: Stability
The stability of strongly magnomechanical systems is a challenging issue that requires careful analysis. Here, we will focus on the stability of our particular system. Specifically, for our system to be stable, all the eigenvalues of the drift matrix  should have negative real parts. If the real part of any eigenvalue changes sign, the system becomes unstable. We can employ the Routh-Hurwitz criterion [53] to gain a more comprehensive comprehension of the range of parameters where stability takes place. As the process of calculating eigenvalues through analytical methods is complex, we have chosen to utilize a numerical method to address this issue.
should have negative real parts. If the real part of any eigenvalue changes sign, the system becomes unstable. We can employ the Routh-Hurwitz criterion [53] to gain a more comprehensive comprehension of the range of parameters where stability takes place. As the process of calculating eigenvalues through analytical methods is complex, we have chosen to utilize a numerical method to address this issue.
In figure 9, we present the maximum real parts of the eigenvalues of  , denoted as
, denoted as  , plotted against the normalized detunings. We define
, plotted against the normalized detunings. We define  as
as ![$\lambda_{\max} = \max[\text{real}(\lambda_{\mathcal{A}})]$](https://content.cld.iop.org/journals/0953-4075/56/11/115401/revision3/bacce11ieqn258.gif) with
with  . It is important to note that if
. It is important to note that if  , the system will become unstable. However, according to figure 9, it is clear that the system remains stable for the given parameters as the maximum eigenvalue
, the system will become unstable. However, according to figure 9, it is clear that the system remains stable for the given parameters as the maximum eigenvalue  remains negative.
remains negative.
Figure 9. The real part of the maximum eigenvalues of the drift matrix  as a function of detunings
as a function of detunings  and
and  . In panels (a), (b) and (c) we use the optimal parameters obtained for each bipartite entanglement from figures 3, 4, and 5, respectively.
. In panels (a), (b) and (c) we use the optimal parameters obtained for each bipartite entanglement from figures 3, 4, and 5, respectively.
Download figure:
Standard image High-resolution imageThus, the stability conditions are satisfied by all numerical parameters used in this manuscript, leading to the conclusion that the selected working regime is stable.










