Abstract
The promising technological material Eu0.1Bi0.9VO4, has been studied for the first time at room-temperature under high-pressure, up to 24.9 GPa, by means of in situ angle dispersive powder x-ray diffraction (XRD). The compound undergoes two phase transitions at 1.9 and 16.1 GPa. The first transition is from the monoclinic fergusonite-type structure (space group I2/a) to a tetragonal scheelite-type structure (space group I41/a), being a ferroelastic-paraelastic transformation similar to that previously reported for isomorphic pristine BiVO4. The second phase transition is first-order in nature. The scheelite-type and the second high-pressure phase coexist in a wide pressure range. A monoclinic structure (space group P21/n) is proposed for the second high-pressure phase. Both transitions are reversible upon decompression. Details of the different crystal structures are reported. All the three observed structures are composed of network of VO4 tetrahedra and BiO8 (or EuO8 due to the substitution of Bi by Eu) dodecahedra. The room-temperature P–V equation of state and axial anisotropic compressibilities of the fergusonite and scheelite polymorphs are also given. In particular, the isothermal compressibility tensor for the monoclinic fergusonite phase has been calculated.
Export citation and abstract BibTeX RIS
Introduction
BiVO4 and AxBi1−xVO4 solid solutions are materials of interest for many technological applications. The current interest comes mainly because of their uses in photocatalytic devices [1–3], near-infrared to visible upconversion [4], and luminescent phosphors [5]. Specially, EuxBi1−xVO4 solid solutions have been gaining popularity for applications in lighting and display materials, mainly because of their stability, brightness and durability compared to other materials [6, 7]. For the applications listed above, knowledge of the electronic band gap is fundamental requirement. The electronic band structure is intimately related to the crystal structure of EuxBi1−xVO4 [8, 9], which can be affected by the content of europium [10], changing from the different polymorphs of BiVO4 [11] to the zircon-type structure of EuVO4 [12].
Another interest on EuxBi1−xVO4 solutions is their high-pressure (HP) behaviour. Since the seminal study of Hazen and Mariathasan [13] multiple HP studies have been reported on BiVO4, which are mainly focussed on the ferroelastic-paraelastic transition found at 1.4 GPa. This compound has been broadly studied under HP for more than three decades. Recently, a second transition has been reported at 15.7 GPa by Raman spectroscopy measurements, but the crystal structure of the new HP phase remains unknown [14]. HP x-ray diffraction (XRD) studies have been reported on related vanadates [15–17] leading to the discovery and characterization of new polymorphs, but no similar studies have been carried out on EuxBi1−xVO4 solutions to the best of our knowledge. It is known that small changes in the composition of oxides affect their structural stability and compressibility [18, 19]. Thus, XRD studies on EuxBi1−xVO4 are needed in order to characterize its HP behaviour and the possible existence of phase transitions. Part of the information from these studies (such as linear compressibilities and bulk modulus) could also be relevant for the development of technological applications.
The aim of this work is to study the HP structural properties of Eu0.1Bi0.9VO4 up to 24.9 GPa. We have decided to study this composition because it has been reported to optimize photoluminescence from EuxBi1−xVO4 [20]. Our results have allowed us to accurately determine the structural sequence and the crystal structure of the ambient-pressure and two HP polymorphs. We have also determined the compressibility of different phases, including a room-temperature equation of state and the isothermal compressibility tensor of the ambient pressure monoclinic fergusonite-type polymorph.
Experimental details
Polycrystalline sample of Eu0.1Bi0.9VO4 was synthesized by solid-state reaction of appropriate amounts of high-purity Bi2O3 (Alfa Aesar 99.9%), Eu2O3 (Alfa Aesar 99.9%) and V2O5 (Aldrich 99.6%) which were pre-heated at 425 K for 24 h. to remove the moisture and organic impurities. The mixture of oxides was ground with an agate mortar and pestle and subsequently pelletized by cold pressing. The pellets were heated at 800 °C for 24 h. and cooled to room temperature. The obtained compound was characterized by powder XRD and energy-dispersive spectroscopy (EDAX). A single phase with the fergusonite-type structure was confirmed and the composition was established to be Eu0.1Bi0.9VO4. Details of the ambient-pressure crystal structure are given in the next section. Notice that secondary phases were not detected in the synthesized sample.
Eu0.1Bi0.9VO4 was studied under compression up to 24.9 GPa by means of powder XRD. Experiments were carried out using 16:3:1 methanol-ethanol-water mixture as pressure-transmitting medium (PTM) which guarantee quasi-hydrostatic conditions up to 10 GPa [21, 22]. Angle-dispersive x-ray diffraction (ADXRD) experiments were carried out using a diamond-anvil cell (DAC) with diamond culets of 500 µm. A hardened stainless steel gasket pre-indented to the thickness of 50 µm with a hole of 200 µm diameter in the center served as pressure chamber. Fine grounded Eu0.1Bi0.9VO4 powder was loaded so as to avoid sample bridging between diamonds [23]. Pressure was determined using the ruby scale with an accuracy of 0.05 GPa [24]. Experiments were carried out at the MSPD beam-line of ALBA synchrotron [25] using a monochromatic beam of wavelength 0.4246 Å which was focused down to a 20 µm × 20 µm (FWHM) spot. A Rayonix CCD detector was used to collect XRD patterns. The sample-detector distance (240 mm) and the beam center position were calibrated using FIT2D [26] and LaB6 as standard reference under the same experimental conditions than the sample. Structural analysis was performed with PowderCell [27] and GSAS [28].
Results and discussion
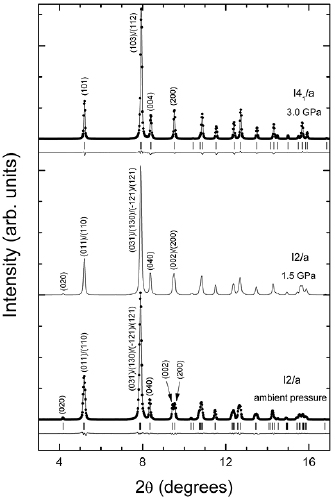
Figure 1 shows powder XRD patterns measured at ambient conditions and a few selected pressures up to 3 GPa. The results at ambient pressure correspond to the fergusonite-type structure (space group I2/a), which is isostructural to one of the polymorphs of BiVO4 [13]. The small residuals and low Rietveld quality factors (see table 1) undoubtedly assign this structure to the sample investigated in the present studies. In the Rietveld refinement we fit the unit-cell parameters and atomic positions. The occupancy factors were constrained to the values determined from EDAX measurements (and are given in table 1) and the overall displacement factors were fixed to 0.5 Å2 [29]. Good refinements are obtained by assuming that Eu substitute Bi in the crystal structure. The complete structural information is given in table 1. Unit-cell parameters and atomic positions are comparable with those reported for the same polymorph of BiVO4 [13, 30]. The crystal structure of Eu0.1Bi0.9VO4 is shown in figure 2. It consists of irregular dodecahedra in which Bi (Eu) are coordinated by eight oxygen atoms sharing corners with adjacent VO4 tetrahedral units. Each tetrahedron has two short and two long V–O distances; 1.7282(7) and 1.7611(7) Å; and the Bi(Eu) bond lengths range from 2.3329(9) Å to 2.6662(9) Å; being the distortion index of the bond length 0.0567 and the effective coordination number 6.86 [31].
Table 1. Crystal structure information of fergusonite-type Eu0.1Bi0.9VO4 at ambient pressure. Fit indicators of the Rietveld refinement (Rp and Rwp) and occupation factors (SOF) are also given.
| Space group: I2/a, a = 5.1083(4) Å, b = 11.7181(9) Å, c = 5.1988(4) Å, and β = 90.51(5)°. Rp = 7.34% and Rwp = 13.19% | |||||
|---|---|---|---|---|---|
| Atom | Site | x | y | z | SOF |
| Bi | 4e | 0.25 | 0.6338(6) | 0 | 0.9 |
| Eu | 4e | 0.25 | 0.6338(6) | 0 | 0.1 |
| V | 4e | 0.25 | 0.1322(4) | 0 | 1 |
| O1 | 8f | 0.5086(9) | 0.2097(9) | 0.1462(9) | 1 |
| O2 | 8f | 0.3740(9) | 0.4488(9) | 0.2569(9) | 1 |
Figure 1. XRD patterns at ambient pressure, 1.5 and 3 GPa. At ambient pressure and 3 GPa the experiments are shown with symbols and the refinements and residuals with solid lines. Ticks indicate the position of Bragg peaks. A few of them have been labelled. The structure are described by their spaces groups I2/a (fergusonite) and I41/a (scheelite).
Download figure:
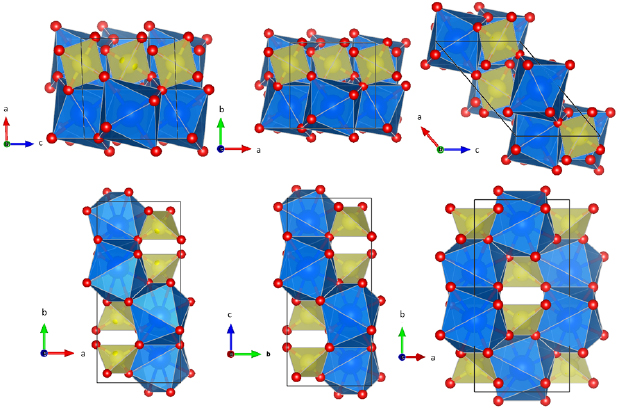
Standard image High-resolution imageFigure 2. Crystal structures of the fergusonite (left), scheelite (center), and HP monoclinic (right) phases. Large, medium and small spheres represent the Bi(Eu), V and O atoms respectively. Polyhedral units are also displayed. The unit-cells are shown with solid lines. Note the changes of unit-cell vectors described in the text.
Download figure:
Standard image High-resolution imageThe diffraction patterns measured up to 1.9 GPa can be explained by the fergusonite structure. This is illustrated in figure 1 by the XRD pattern measured at 1.5 GPa. As pressure increase the values of the unit-cell parameters a and c becomes gradually equal and the β angle gradually approaches 90°. We found that at 1.9 GPa, β angle is equal to 90° and a = 5.1305(4) Å, b = 11.6323(9) Å, and c = 5.1355(4) Å; i.e. the structure can be described as pseudo-tetragonal. The gradual pressure-induced symmetry increase of the crystal structure can be clearly noticed in figure 1 by the pressure evolution of Bragg peaks (2 0 0) and (0 0 2).
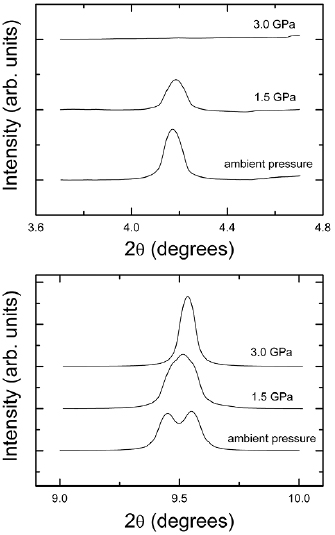
Upon further compression subtle qualitative changes occur in the XRD pattern. One of them is the disappearance of Bragg peak (0 2 0) and the other one is decrease of width of all peaks corresponding to multiplets. In figure 3 we show a zoom of the pressure evolution of peak (0 2 0)—see top panel—and the doublet (2 0 0)/(0 0 2)—see bottom panel—to illustrate the described changes. They are typical of the fergusonite-scheelite transition observed in BiVO4 [13]. Evidence supporting that this is a second-order transition from a ferroelastic to a paraelastic state [14] will be provided when discussing the pressure dependence of unit-cell parameters. Based upon the fact that at 1.9 GPa the structure can be considered as pseudo-tetragonal we will assume this as the transition pressure.
Figure 3. (Top) zoom of the (0 2 0) peak of fergusonite illustrating that it disappears at 3 GPa. (Bottom) zoom of the (2 0 0) and (0 0 2) Bragg peaks of fergusonite showing how they gradually merge and finally become a single peak at 3 GPa.
Download figure:
Standard image High-resolution imageThe XRD pattern measured at 3 GPa can be accurately refined assuming a tetragonal scheelite-type structure (space group I41/a). As can be seen in figure 1, the residuals, obtained assuming the scheelite structure are small. In addition, the goodness-of-fit parameters (see table 2) support a good quality refinement [32]. The details of the obtained crystal structure at 3 GPa are given in table 2. The tetragonal scheelite structure is a symmetrized version of fergusonite [13]. Before detailed discussions about the fergusonite-scheelite transition, it has to be noted here that there is cyclic rotation of axes in the settings normally used in the literature to describe fergusonite and scheelite (which we used in this work). The axes rotation from fergusonite to scheelite is given by the matrix  . Consequently, the long axis of fergusonite, the unique b-axis, becomes the c-axis of scheelite. This can be seen in figure 2 where the crystal structures are represented. The scheelite structure, similar to the fergusonite structure, is composed of framework of chains of corner-linked VO4 tetrahedra and Bi(Eu)O8 dodecahedra.
. Consequently, the long axis of fergusonite, the unique b-axis, becomes the c-axis of scheelite. This can be seen in figure 2 where the crystal structures are represented. The scheelite structure, similar to the fergusonite structure, is composed of framework of chains of corner-linked VO4 tetrahedra and Bi(Eu)O8 dodecahedra.
Table 2. Crystal structure information of scheelite-type Eu0.1Bi0.9VO4 at 3 GPa. Fit indicators of the Rietveld refinement (Rp and Rwp) and SOF are also given.
| Space group: I41/a, a = 5.1144(4) Å, and c = 11.5822(9) Å. Rp = 5.48% and Rwp = 9.33% | |||||
|---|---|---|---|---|---|
| Atom | Site | x | y | z | SOF |
| Bi | 4b | 0 | 0.25 | 0.625 | 0.9 |
| Eu | 4b | 0 | 0.25 | 0.625 | 0.1 |
| V | 4a | 0 | 0.25 | 0.125 | 1 |
| O | 16f | 0.2520(9) | 0.1080(9) | 0.0460(9) | 1 |
The transformation from fergusonite to scheelite not only implies the transformation of the unit-cell from monoclinic to tetragonal but the progressive movement of the atoms. Both Bi(Eu) and V atoms move along the long axis, the movement of both cations is similar in magnitude (compare the atomic positions in tables 1 and 2). The displacement of O atoms is more important going to positions that make the coordination polyhedral more regular. In the HP tetragonal structure, the V–O distance in the regular VO4 tetrahedron is 1.7395(7) Å and the Bi(Eu)O8 dedecahedron has only two different Bi(Eu)–O distances, being 2.4615(9) and 2.4080(9) Å. As a consequence, the distortion index of the bond length is reduced to 0.0110 and the effective coordination number increased to 7.97.
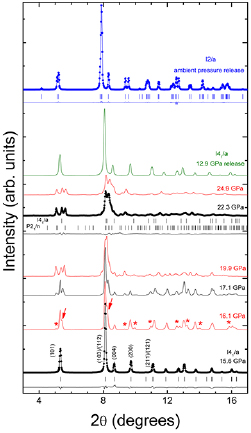
Upon further compression, the XRD patterns can be undoubtedly assigned to the scheelite structure up to 15.6. This is illustrated in figure 4 by the lowest trace that shows the Rietveld refinement of the XRD experiment measured at 15.6 GPa for which the small residuals are shown. The quality of the fit is similar to the one obtained at 3 GPa (shown in figure 1). When increasing pressure to 16.1 GPa a new phase appears, as can be seen in figure 4, by the appearance of several additional peaks, which are indicated by arrows and asterisks in the figure. Upon further compression, the intensity of the new peaks is gradually enhanced, while the peaks of scheelite are reduced in intensity. However, the two phases coexist from 16.1 GPa up to 24.9 GPa. Scheelite remains as a minority phase with the (1 0 1) peak being detectable up to 24.9 GPa. All these facts can be understood as the onset of a phase transition at 16.1 GPa with the second HP phase and scheelite coexisting up to the highest pressure reached in our experiments. The transition pressure is the same as that previously reported for scheelite-type BiVO4 [14]. In order to explain the crystal structure of the new HP phase we considered several structures of related ternary oxides which, based on crystal chemistry arguments can be considered as good candidate structures [33]. However, none of these structures, including zircon [34], pucherite [35], monazite [36], SbPO4-type [36], barite [37], post-barite [37], CaSeO4-type [38], BaWO4-II-type [39], AgMnO4-type [40], anhydrite [41], and the several orthorhombic post-scheelite structures proposed in the literature [42], could explain observed diffraction patterns of second high pressure phase.
Figure 4. Selection of XRD patterns from 15.6 to 24.9 GPa. The bottom trace corresponds to the scheelite structure. Experiment (dots), Rietveld refinement and residuals (solid lines) are shown. Ticks indicate the positions of Bragg peaks. Some of them are labelled. Asterisks and arrows at 16.1 GPa show new peaks associated to the onset of the phase transition. For the experiment at 22.3 GPa we show the Le Bail refinement (considering two phases) and the residuals. The positions of reflexions of each phase are indicated. The top trace show the XRD pattern measured after decompression, which can be assigned to the fergusonite structure. The trace just below it shows a XRD pattern measured for scheelite under pressure release at 12.9 GPa. Different colours are just used to facilitate the identification of different XRD patterns.
Download figure:
Standard image High-resolution imageAfter this conclusion we followed a different strategy to find a possible crystal structure of the post-scheelite phase. There are ternary oxides where the HP structure has been found by means of structural transformation via group-subgroup relations [43]. This hypothesis is reasonable in our case because all the new peaks appear on the sides of the peaks of scheelite. Consequently, we made a Baernighausen tree of structures [44]. In this procedure, starting from a higher-symmetry crystal structure more complicated structures are derived with the help of group-subgroup relationships. By exploring the different branches of this tree we found a monoclinic structure described by space group P21/n which could explain our results beyond 15.6 GPa. This structure is obtained by means of a translationgleiche transformation from I41/a to I2/a and a subsequent klassengleiche transformation to P21/n. The obtained atomic positions for this structure are given in table 3. By considering this structure coexisting with scheelite we have been able to reproduce the results after the phase transition. To illustrate it, we show in figure 4 the results of a Le Bail refinement. We did not perform a Rietveld refinement because the large number of atomic position to be determined, the texturing effects present after the transition (in spite of the 6° rocking of the DAC), and certain influence of non-hydrostaticity preclude it.
Table 3. Crystal structure information of the proposed monoclinic HP polymorph of Eu0.1Bi0.9VO4 at 22.3 GPa. Fit indicators of the Rietveld refinement (Rp and Rwp) and SOF are also given.
| Space group: P21/n, a = 6.9915(4) Å, b = 10.7665(9) Å, c = 4.7215(3) Å, and β = 130.26(9)º. Rp = 11.72% and Rwp = 16.38% | |||||
|---|---|---|---|---|---|
| Atom | Site | x | y | z | SOF |
| Bi | 4e | 0 | 0.625 | 0.25 | 0.9 |
| Eu | 4e | 0 | 0.625 | 0.25 | 0.1 |
| V | 4e | 0 | 0.125 | 0.25 | 1 |
| O1 | 4e | 0.748 | 0.046 | 0.856 | 1 |
| O2 | 4e | 0.252 | 0.046 | 0.644 | 1 |
| O3 | 4e | 0.358 | 0.296 | 0.856 | 1 |
| O4 | 4e | 0.642 | 0.296 | 0.644 | 1 |
The unit-cell parameters obtained at 22.3 GPa are given in table 3. The volume of the post-scheelite phase is 0.3% smaller than the volume determined for scheelite at the same pressure. This and the phase coexistence of the two structures in large pressure range suggest that the transition is a first-order being affected by the kinetic hindrance [45]. The monoclinic post-scheelite structure is shown in figure 2. Notice that the axes of fergusonite and post-scheelite (P21/n) are related via the transformation matrix  . The new structure is composed of the same kind of tetrahedral and dodecahedral units as the other two structures of Eu0.1Bi0.9VO4. It can be considered as a distortion of the scheelite structure. In particular, if in the monoclinic HP structure (space group P21/n) the angle b is 135° and a =
. The new structure is composed of the same kind of tetrahedral and dodecahedral units as the other two structures of Eu0.1Bi0.9VO4. It can be considered as a distortion of the scheelite structure. In particular, if in the monoclinic HP structure (space group P21/n) the angle b is 135° and a =  , it becomes a tetragonal scheelite structure. Notice that the new monoclinic structure has a primitive unit-cell, in contrast with the two other, which are body-centered. In addition, all the three structures have an inversion center of symmetry. We would also like to remark that the new HP structure here proposed as post-scheelite structure (space group P21/n) is described by the same space group than monazite [36], AgMnO4-type [39], and BaWO4-III-type [42]; however, the unit-cell parameters are very different. Indeed, as we mentioned above, none of these three structures can explain the observed XRD patterns for the new HP phase. It should be noted here, that the structure reported in table 3 for the post-scheelite phase of Eu0.1Bi0.9VO4 is isostructural to the post-scheelite HP phase proposed by Misinini et al for LiYF4 [46] (described by them using a different setting P21/c). In particular, such a phase can explain the doubling of modes observed in BiVO4 at 15.7 GPa. Therefore, the proposed HP structure is a good model for testing the post-scheelite structures found by Raman spectroscopy in BiVO4 [14]. Confirmation of it should come from future single-crystal XRD studies, as done for the HP phases of PbCrO4 and LaPO4 [47, 48].
, it becomes a tetragonal scheelite structure. Notice that the new monoclinic structure has a primitive unit-cell, in contrast with the two other, which are body-centered. In addition, all the three structures have an inversion center of symmetry. We would also like to remark that the new HP structure here proposed as post-scheelite structure (space group P21/n) is described by the same space group than monazite [36], AgMnO4-type [39], and BaWO4-III-type [42]; however, the unit-cell parameters are very different. Indeed, as we mentioned above, none of these three structures can explain the observed XRD patterns for the new HP phase. It should be noted here, that the structure reported in table 3 for the post-scheelite phase of Eu0.1Bi0.9VO4 is isostructural to the post-scheelite HP phase proposed by Misinini et al for LiYF4 [46] (described by them using a different setting P21/c). In particular, such a phase can explain the doubling of modes observed in BiVO4 at 15.7 GPa. Therefore, the proposed HP structure is a good model for testing the post-scheelite structures found by Raman spectroscopy in BiVO4 [14]. Confirmation of it should come from future single-crystal XRD studies, as done for the HP phases of PbCrO4 and LaPO4 [47, 48].
On pressure release we observed that both phase transitions are reversible. For the second transition we observed peaks that can be assigned to the post-scheelite phase down to 13.9 GPa. A single-phase scheelite XRD pattern was recovered at 12.9 GPa (see figure 4). Therefore, the hysteresis of the transition is 3.2 GPa, which is in agreement to the first-order character previously assigned to the transition. Upon further pressure decrease we observed the scheelite phase up to 2.5 GPa. In the next decompression step the pressure was 1.6 GPa and the fergusonite phase was recovered. Therefore, there was no hysteresis as expected for the second-order character of the fergusonite-scheelite transition. In figure 4, we show the XRD pattern recovered at ambient conditions, which can be undoubtedly assigned to the fergusonite structure as supported by the Rietveld refinement shown in the figure. Notice the reappearance of the (0 2 0) peak of fergusonite around 2θ = 4° and the clear splitting of (2 0 0) and (0 0 2) peaks near 2θ = 9.3°. Before starting the discussion of the compressibility of Eu0.1Bi0.9VO4, we would like to mention that in our experiment we did not find any evidence of a possible decomposition of the compound in the constituent oxides as observed in zircon-type NdVO4 and EuVO4 [11, 15].
From the analysis of XRD patterns we have extracted the unit-cell parameters of different structures as a function of pressure. The results are reported in figure 5. For the sake of accuracy, we only include results for the pressure points where there is no phase coexistence (P ⩽ 15.6 GPa). Results from compression and decompression measurements are included in the figure. Results from the second HP phase are not included in the figure because the phase coexists with scheelite in the pressure range covered by our studies. It can be seen that the compression of fergusonite-type Eu0.1Bi0.9VO4 is anisotropic. The b and c lattice parameters decrease with pressure and the a lattice parameter increases with pressure. The β angle rapidly decreases becoming 90° at 1.9 GPa, and a and c gradually merges to the same value. Since the fergusonite structure is monoclinic, its compressibility can be described by means of the eigenvalues and eigenvectors of the isothermal compressibility tensor [49]. In our case, we have obtained them using PASCAL [50]. Their values are reported in table 4. According to it, the major compression direction corresponds to the b-axis. In the plane perpendicular to it, there is a main compression direction that makes 128.4° angle to the a-axis (from a to c) and a main expansion direction which makes 60.4° angle with the main compression direction. The obtained eigenvalues of the compressibility indicate that most of the crystal compression over the pressure range 0–1.9 GPa, is being accommodated along the b-axis. Note that the sum of the three eigenvalues gives the volume compressibility, which in our case is 8.8(9) × 10−3 GPa−1, which corresponds to a bulk modulus of 113(12) GPa. In case of the scheelite structure, the compression is also non-isotropic. In this polymorph, the most compressible axis is c (with a linear compressibility of 2.4(5) × 10−3 GPa−1) and the less compressible direction is a (with a linear compressibility of 1.8(5) × 10−3 GPa−1). Remembering that the c-axis of scheelite correspond to the b-axis of fergusonite, one can see that the direction of main compression is not affected by the phase transition, which is consistent with the similarity between both structures, which share the same polyhedral framework.
Table 4. Eigenvalues, λi, and eigenvectors, eνi, for the isothermal compressibility tensor coefficients of fergusonite-type BiVO4.
| λ1 = 6.7(9) 10−3 GPa−1 | eν1 = (0, 1, 0) |
| λ2 = 4.6(6) 10−3 GPa−1 | eν2 = (−0.6213, 0, 0.7835) |
| λ3 = −2.5(6) 10−3 GPa−1 | eν3 = (−0.9983, 0, −0.1523) |
Figure 5. Pressure dependence of the unit-cell parameters and volume. Black circles are from compression experiments and red diamonds from decompression experiments. Solid and empty symbols stand for the fergusonite and scheelite phases respectively. The evolution of the fergusonite β angle is displayed in the inset. For the unit-cell volume the calculated EOS is shown with a solid line.
Download figure:
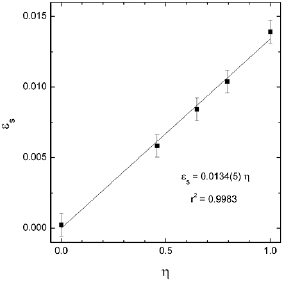
Standard image High-resolution imageFrom the pressure dependence of the unit-cell parameters of the fergusonite and scheelite polymorphs, the spontaneous strain (εs) of the fergusonite structure can be obtained as a function of pressure using the definition given by Aizu [51, 52]. This parameter is useful to confirm the second-order nature of the phase transition. In such a case, it should have a linear dependence with a Landau order parameter, which can be defined as  , where P is the pressure and PT the transition pressure [51]. In our case, we assumed PT = 1.9 GPa. The obtained results for εs versus η are shown in figure 6 confirming that the condition required by a second-order transition is fulfilled; being the fergusonite-scheelite transition of Eu0.1Bi0.9VO4 analogous to the same transition of BiVO4 [13, 14].
, where P is the pressure and PT the transition pressure [51]. In our case, we assumed PT = 1.9 GPa. The obtained results for εs versus η are shown in figure 6 confirming that the condition required by a second-order transition is fulfilled; being the fergusonite-scheelite transition of Eu0.1Bi0.9VO4 analogous to the same transition of BiVO4 [13, 14].
Figure 6. Correlation between the spontaneous strain εs and the Landau order parameter η Symbols are the calculated values. The solid line is a linear fit which is shown in the plot together with the r2 of the fit.
Download figure:
Standard image High-resolution imageTo conclude the discussion of the results, we will focus now on the pressure dependence of the unit-cell volume. The results are shown in figure 5. The pressure dependence of the volume of both the fergusonite and scheelite structure is smooth (no discontinuity at the phase transition as expected for a second-order transition) and can be well fitted using a third order Birch–Murnaghan (BM) equation of state (EOS) [53] using the EosFit7 software [54]. The results are shown in the figure (solid line) being the fit to the experimental results quite good. We have obtained the ambient pressure bulk modulus B0 = 105(2) GPa, its pressure derivative  = 5.8(3), and the zero-pressure unit-cell volume V0 = 311.5(1) Å3. The implied value of the second pressure derivative of the bulk is
= 5.8(3), and the zero-pressure unit-cell volume V0 = 311.5(1) Å3. The implied value of the second pressure derivative of the bulk is  = 0.085(9) GPa−1 [55]. The value of the bulk modulus is comparable with the value obtained from the isothermal compressibility tensor of the fergusonite phase. Both values are also comparable to the results from recent density-functional theory calculations carried out for BiVO4, B0 = 111 GPa [56]. Theoretical reported values for the bulk modulus for different polymorphs of BiVO4 range from 103 to 132 GPa [57]. Interestingly, both calculations and our experiments do not see the compressibility change reported by Hazen et al [13] at the fergusonite-scheelite transition in BiVO4. This fact has led these authors to underestimate the compressibility of the scheelite phase. On the other hand, when compared with other AVO4 vanadates [10], the bulk modulus of Eu0.1Bi0.9VO4 is found to be one of the smallest except for InVO4 and FeVO4 which are highly compressible (B0 = 69 and 76 GPa respectively) [58, 59]. This is because the last two compounds have a very open structure which has large empty space between the InO6 (FeO6) octahedra and VO4 tetrahedra that comprises the crystalline framework. Finally, Eu0.1Bi0.9VO4 has a similar bulk modulus than monazite-type BiPO4 (B0 = 99–117 GPa) [60] and BiSbO4 (B0 = 109–149 GPa) [61], but its resistance to compression is smaller than in BiNbO4 (B0 = 185 GPa) [62]. The incompressibility of the last compound is due to the fact that the average distance of Bi–O bonds (2.3624 Å) is 6% smaller than in BiVO4 and BiPO4. This makes the coordination polyhedron of Bi (the one that dominates compressibility [10]) less compressible than in other bismuth ternary oxides and thus the whole structure is more incompressible.
= 0.085(9) GPa−1 [55]. The value of the bulk modulus is comparable with the value obtained from the isothermal compressibility tensor of the fergusonite phase. Both values are also comparable to the results from recent density-functional theory calculations carried out for BiVO4, B0 = 111 GPa [56]. Theoretical reported values for the bulk modulus for different polymorphs of BiVO4 range from 103 to 132 GPa [57]. Interestingly, both calculations and our experiments do not see the compressibility change reported by Hazen et al [13] at the fergusonite-scheelite transition in BiVO4. This fact has led these authors to underestimate the compressibility of the scheelite phase. On the other hand, when compared with other AVO4 vanadates [10], the bulk modulus of Eu0.1Bi0.9VO4 is found to be one of the smallest except for InVO4 and FeVO4 which are highly compressible (B0 = 69 and 76 GPa respectively) [58, 59]. This is because the last two compounds have a very open structure which has large empty space between the InO6 (FeO6) octahedra and VO4 tetrahedra that comprises the crystalline framework. Finally, Eu0.1Bi0.9VO4 has a similar bulk modulus than monazite-type BiPO4 (B0 = 99–117 GPa) [60] and BiSbO4 (B0 = 109–149 GPa) [61], but its resistance to compression is smaller than in BiNbO4 (B0 = 185 GPa) [62]. The incompressibility of the last compound is due to the fact that the average distance of Bi–O bonds (2.3624 Å) is 6% smaller than in BiVO4 and BiPO4. This makes the coordination polyhedron of Bi (the one that dominates compressibility [10]) less compressible than in other bismuth ternary oxides and thus the whole structure is more incompressible.
Conclusions
High-pressure room-temperature angle-dispersive powder XRD experiments on Eu0.1Bi0.9VO4 were performed up to ≈25 GPa. A fergusonite-scheelite transition has been found at 1.9 GPa. Details of both crystal structures are reported. In addition, a new phase, observed at 16.1 GPa, remains stable up to 25 GPa. This HP phase is proposed to be monoclinic and belong to the space group P21/n. The two observed transitions are reversible. The first transition has been characterized as a second-order transformation and the second transition as a first-order transformation. The pressure dependence of the unit cell parameters and the equations of state of different phases are reported. In the case of monoclinic fergusonite structure the isothermal compressibility tensor has been calculated.
Acknowledgments
This work was supported by the Spanish Ministry of Science, Innovation and Universities under Grant MAT2016-75586-C4-1-P and by Generalitat Valenciana under Grant Prometeo/2018/123 (EFIMAT). The authors thank ALBA synchrotron for providing beam-time for the XRD experiments (Project no. 2016081779).