Numerical modelling of dynamic resistance in high-temperature superconducting coated-conductor wires

The 2D infinitely long numerical model, shown in figure 1, is based on the H-formulation [10–16], where the governing equations are derived from Maxwell's equations: Faraday's law (1) and Ampere's law (2).

$$\begin{eqnarray}&&{\rm{\nabla }}\times {\boldsymbol{E}}+\frac{{\rm{d}}{\boldsymbol{B}}}{{\rm{d}}t}={\rm{\nabla }}\times {\boldsymbol{E}}+\frac{{\rm{d}}({{\mu }}_{0}{{\mu }}_{r}{\boldsymbol{H}})}{{\rm{d}}t}=0,\end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray}&&{\boldsymbol{\nabla }}\times {\boldsymbol{H}}={\boldsymbol{J}},\end{eqnarray} \tag{ 2 }$$

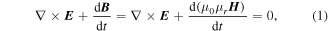
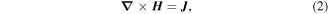
where H = [H_x, H_y] represents the components of the magnetic field strength, J = [J_z] represents the current density and E = [E_z] represents the electric field. μ₀ is the permeability of free space, and for the superconducting layer and surrounding sub-domain (simply assumed to be air), the relative permeability is simply μ_r = 1. Only the superconducting layer of the wire is modelled, assuming that eddy current losses within the wire architecture (e.g., substrate, stabiliser layers) is negligible: a reasonable assumption for the wire at power frequencies (∼50/60 Hz) [17, 18]. Since the substrate of the wire under investigation is non-magnetic, consideration of any ferromagnetic losses, and indeed the influence of a magnetic substrate on the superconducting properties, is also unnecessary. Isothermal conditions are assumed and a constant temperature, T = 77 K; hence, no thermal model is included.

Zoom In Zoom Out Reset image size

It is assumed that electric field E_z is parallel to the current density J_z and the electrical properties of the superconductor are modelled by the E–J power law [19, 20] in (3).

$$\begin{eqnarray}&&{\boldsymbol{E}}=\frac{{E}_{0}}{{J}_{{\rm{c}}}(B,{\theta })}| \frac{J}{{J}_{{\rm{c}}}(B,{\theta })}{| }^{n-1}{\boldsymbol{J}},\end{eqnarray} \tag{ 3 }$$

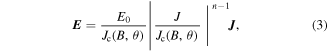
where E₀ is the characteristic electric field, 1 μV cm⁻¹, B is magnitude of the local magnetic flux density and θ is the angular direction of that field as defined in figure 1.

Traditionally, the relationship between the critical current density J_c(B, θ) and the critical current I_c(B, θ) is given by (4), where S is the cross-sectional area of the superconducting layer. However, this direct approach does not include self-field effects, i.e., B refers to the external applied field, rather than the local magnetic flux density in (3). This can introduce numerical errors when the applied field is comparable to the self-field. Since, in this paper, the applied fields are 100 mT or less, the self-field is taken into account when calculating J_c(B, θ) based on the technique presented in [21], and using the example model files available at [22], which obtains J_c(B, θ) based on the local magnetic flux density, rather than the external applied field using (4). The width of the tape is 4 mm and the thickness of the superconducting layer is 1 μm; however, the homogenisation technique presented in [23, 24] is used to improve the computational speed of the model without compromising accuracy, and the thickness of the superconducting layer in the model is artificially expanded to 100 μm.

$$\begin{eqnarray}&&{J}_{{\rm{c}}}(B,{\theta })=\frac{{I}_{{\rm{c}}}(B,{\theta })}{S}.\end{eqnarray} \tag{ 4 }$$

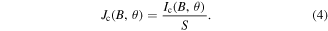
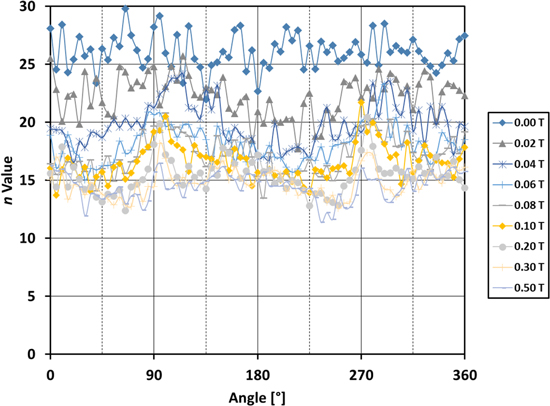
Experimentally measured values of I_c(B, θ) (from which J_c(B, θ) is calculated as described above) and n(B, θ) were used in the H-formulation model. This data was obtained at 77 K in magnetic fields up to 0.5 T, from a short sample of the same SuperPower SCS4050-AP wire as used in our dynamic resistance experiments. The experimental values, shown in figures 2 and 3, respectively, are input into the model using a two-variable, direct interpolation [25, 26], which is significantly faster than data fitting methods, yet without compromising accuracy. The measured, self-field critical current, I_c0, of the wire at 77 K is 107.5 A. In figure 3, there is some scatter in the calculated n-values after fitting equation (3) to the experimental data, most noticeable for the 0 T data where a scatter of n ± 2–3 is observed. The n-value fit is sensitive to the curvature of the experimental data above J_c, a regime where the experimental data is also vulnerable to the influence of resistive heating. However, at higher fields, this scatter is substantially depressed and the systematic 'double-peak' in the n-value is clear, following the measured I_c data in figure 2.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

A mapped mesh (200 x-elements along the width, 10 y-elements along the thickness, and a linear element distribution with an element ratio of 3 between the central elements and the edge and top/bottom surface elements) is used in the superconducting layer to decrease the number of mesh elements [27], while still retaining enough mesh elements at the top and bottom of the wire to accurately simulate the current density associated with the DC current, and a free triangular mesh is used in the surrounding sub-domain. Linear, curl-conforming elements are employed for the entire model. For the non-superconducting sub-domain surrounding the superconducting layer, a linear Ohm's law is considered, E = ρJ, where ρ = 1 Ω m is a specific, high constant resistivity.

An integral constraint is applied to the superconducting layer to represent the DC transport current flowing in the superconducting tape. A transport current, I, through the cross-section S of the tape is therefore described by (5).

$$\begin{eqnarray}&&I=\displaystyle \int {\boldsymbol{J}}\cdot {\rm{d}}{\boldsymbol{S}}={I}_{{\rm{a}}{\rm{p}}{\rm{p}}}(t),\end{eqnarray} \tag{ 5 }$$

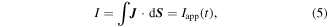
where I_app(t) is a ramp function of ramp rate 10 A s⁻¹ that is then held at its final value, I_DC, which is defined by the ratio of I_DC/I_c. In this paper, the cases for I_DC/I_c = 0.3, 0.5, 0.7 and 0.9 are examined, where I_c = 107.5 A as defined earlier.

Once the appropriate I_DC/I_c value is reached, AC magnetic fields up to 100 mT in amplitude are applied in 5 mT increments by setting appropriate boundary conditions for H_x, H_y [28]: the instantaneous external AC magnetic field applied to the wire at frequency f is B_a(t) = B_app·sin(2πft), and H_a,x, H_a,y are the Cartesian components of H_a = B_a/μ₀, as shown in figure 1. As such both θ = 0° and θ = 180° are perpendicular to the plane of the wire, but point in opposite directions, i.e., into top surface and substrate side of the wire, respectively.

The calculation of the total AC loss (J m⁻¹/cycle) includes separate contributions from the magnetisation loss, Q_mag, and the dynamic resistance, Q_dyn, and in the 2D infinitely long model of the superconducting tape, this can be expressed as (6).

$$\begin{eqnarray}&&{\rm{T}}{\rm{o}}{\rm{t}}{\rm{a}}{\rm{l}}\,{\rm{A}}{\rm{C}}\,{\rm{l}}{\rm{o}}{\rm{s}}{\rm{s}}\,({\rm{J}}/{\rm{c}}{\rm{y}}{\rm{c}}{\rm{l}}{\rm{e}}/{\rm{m}})=\displaystyle {\int }_{0}^{T}\displaystyle \int {\boldsymbol{E}}\cdot {\boldsymbol{J}}{\rm{d}}S\,{\rm{d}}t\,=\,{Q}_{{\rm{m}}{\rm{a}}{\rm{g}}}+\,{Q}_{{\rm{d}}{\rm{y}}{\rm{n}}},\end{eqnarray} \tag{ 6 }$$

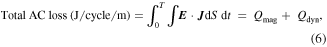
where T is the period of one cycle. When computing this value, we have taken the integral result between 0.5 T and 1.5 T, as this period does not include the transient, first half-cycle, where the superconductor is magnetised from its 'virgin' state [29].

In order to calculate the dynamic resistance, the average electric field across the entire conductor cross-section is firstly obtained using (7). The instantaneous dynamic resistance and associated power loss can then be obtained from (8) and (9), respectively, and the dynamic resistance loss, Q_dyn, can be calculated from (10). Finally, the dynamic resistance, R_dyn, in units of (Ω m⁻¹/cycle) can be found using (11).

$$\begin{eqnarray}&&{E}_{{\rm{a}}{\rm{v}}{\rm{e}}}(t)=\displaystyle \frac{\displaystyle {\int }_{S}{\boldsymbol{E}}(t)\cdot {\rm{d}}{\boldsymbol{S}}}{S},\end{eqnarray} \tag{ 7 }$$

$$\begin{eqnarray}&&{R}_{{\rm{d}}{\rm{y}}{\rm{n}}}(t)=\displaystyle \frac{{{E}}_{{\rm{a}}{\rm{v}}{\rm{e}}}(t)}{I(t)}=\displaystyle \frac{{{E}}_{{\rm{a}}{\rm{v}}{\rm{e}}}(t)}{{I}_{{\rm{d}}{\rm{c}}}},\end{eqnarray} \tag{ 8 }$$

$$\begin{eqnarray}&&{P}_{{\rm{d}}{\rm{y}}{\rm{n}}}(t)={I}^{2}(t){R}_{{\rm{d}}{\rm{y}}{\rm{n}}}(t)={I}_{{\rm{d}}{\rm{c}}}^{2}{R}_{{\rm{d}}{\rm{y}}{\rm{n}}}(t),\end{eqnarray} \tag{ 9 }$$

$$\begin{eqnarray}&&{Q}_{{\rm{d}}{\rm{y}}{\rm{n}}}\,({\rm{J}}\,{{\rm{m}}}^{-1}/{\rm{c}}{\rm{y}}{\rm{c}}{\rm{l}}{\rm{e}})=\displaystyle {\int }_{0}^{T}{I}_{{\rm{d}}{\rm{c}}}^{2}{R}_{{\rm{d}}{\rm{y}}{\rm{n}}}(t)\cdot {\rm{d}}t={I}_{{\rm{d}}{\rm{c}}}^{2}\displaystyle {\int }_{0}^{T}{R}_{{\rm{d}}{\rm{y}}{\rm{n}}}(t)\cdot {\rm{d}}t,\end{eqnarray} \tag{ 10 }$$

$$\begin{eqnarray}&&{R}_{{\rm{d}}{\rm{y}}{\rm{n}}}\,({\rm{\Omega }}\,{{\rm{m}}}^{-1}/{\rm{c}}{\rm{y}}{\rm{c}}{\rm{l}}{\rm{e}})={Q}_{{\rm{d}}{\rm{y}}{\rm{n}}}/{I}_{{\rm{d}}{\rm{c}}}^{2}.\end{eqnarray} \tag{ 11 }$$

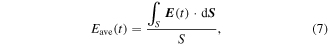
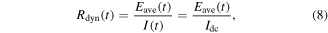
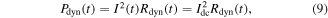
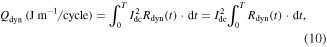
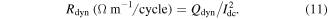
This approach removes ambiguity in defining the geometric boundaries between the transport and magnetisation currents throughout the AC cycle, and hence differs from previous analytical and finite-element approaches, which have considered dynamic resistance to arise only from current flowing in the central region of the wire [30–32].

A detailed description of the experimental procedure for the dynamic resistance measurements can be found in [33]. An AC magnetic field was applied by a copper-wound electro-magnet that can generate up to 100 mT peak magnetic field at frequencies up to 112.5 Hz [34]. The sample can be rotated inside the magnet, and the field angle, θ, can thus be varied. A DC power supply was used to supply a DC transport current of up to 300 A to the SuperPower sample. Two voltage taps were soldered on the edges of the sample, and the leads were arranged in a spiral loop to minimise induced AC pick-up from the external magnetic field [35]. The distance between the voltage taps in these experiments was 5 cm and the time-averaged DC voltage across the voltage taps was measured using a Keithley 2182 nano-voltmeter.

2.1.1. Total AC loss

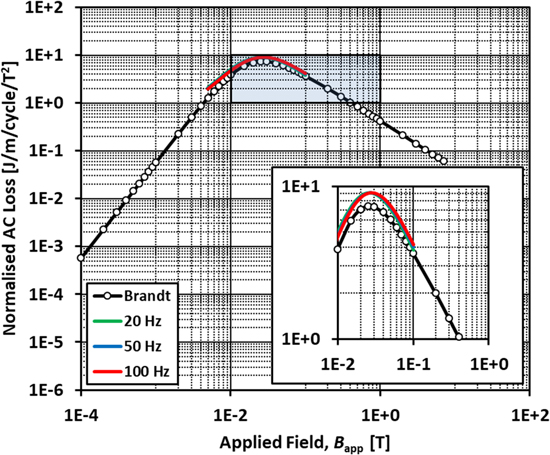
Firstly, the magnetisation AC loss of the wire is calculated for the case where the DC transport current is zero and an external AC magnetic field is applied perpendicular to the plane of the wire, i.e., θ = 0°. Figure 4 shows the calculated magnetisation AC loss, normalised by ∣B_app∣² (where B_app = μ₀H_app), of the wire for magnetic fields up to 100 mT and for frequencies of 20, 50 and 100 Hz, as calculated by the numerical model and compared with Brandt's analytical equation [36]. It is shown that the numerical model calculation is slightly higher than the analytical result due to our use of measured, real J_c(B) characteristics, rather than the constant J_c approximation used in the Brandt equation. There is also a slight frequency dependence of the simulation result, which is commonly observed when using time-dependent models based on the E–J power law [37–40]. The impact of this on the dynamic resistance calculations is discussed later in the paper. Despite these minor discrepancies, values calculated using equation (6) are broadly consistent with the Brandt expression, thus validating our numerical model. This also gives a base case to compare subsequent total AC loss calculations in which a DC transport current gives rise to loss components from both magnetisation loss and dynamic resistance.

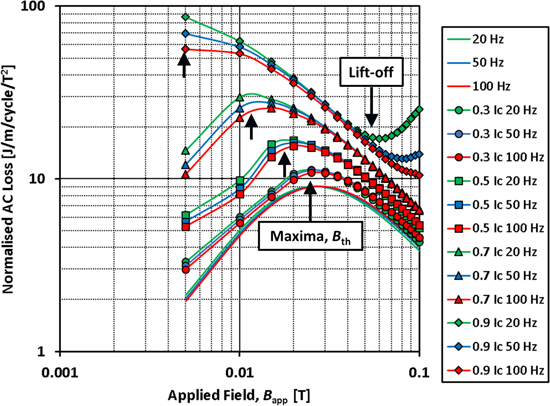
Zoom In Zoom Out Reset image size

The maxima of the normalised magnetisation AC loss in figure 4 correspond to the effective penetration field of the wire, as it denotes the point at which the shielding current capacity is effectively saturated [30]. For values of I_DC > 0, the maxima shift due to the superposition of the transport current and shielding (magnetisation) currents, with the effective penetration field decreasing with increasing values of I_DC. This is shown clearly in figure 5. As in the zero current case, these maxima similarly correspond to the threshold field, B_th, above which where there is no longer a shielded region inside the wire and hence dynamic resistance occurs. For the case I_DC/I_c = 0.9, there are also minima turning points, such that for fields above these points, the normalised total AC loss begins to increase again. This relates to the emergence of an additional flux-flow resistance term that arises once the total driven transport current exceeds the field-dependent I_c of the wire [30]. In the following section, the relationship of these maxima and minima present in the total AC loss curves and the particular characteristics of the dynamic resistance curves are explained in more detail.

Zoom In Zoom Out Reset image size

2.1.2. Dynamic resistance

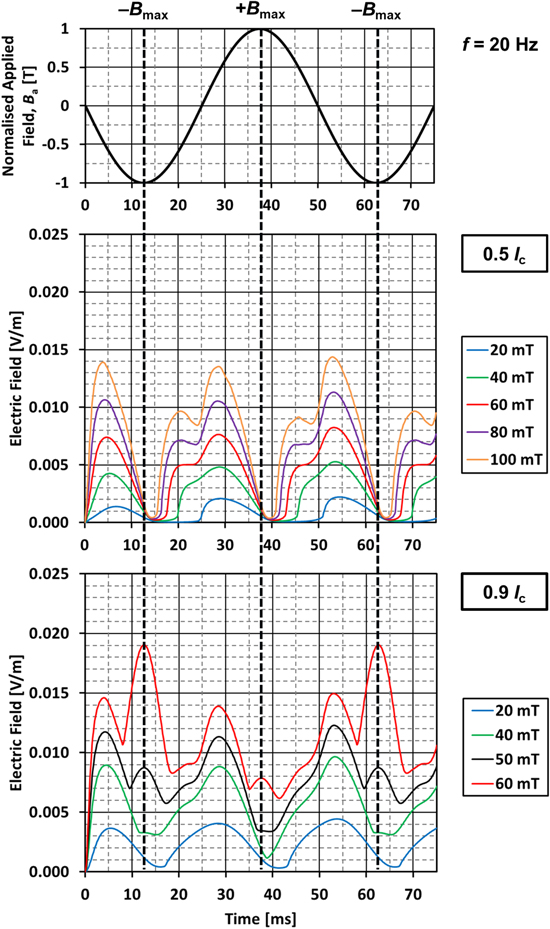
In this section, the dynamic resistance is calculated using the numerical model based on (7)–(11). Figure 6 shows the calculated average electric field, using (7), across the cross-section of the wire for 0.5I_c under perpendicular external AC magnetic fields with ∣B_app∣ = 20, 40, 60, 80 and 100 mT (middle); and 0.9 I_c for ∣B_app∣ = 20, 40, 50 and 60 mT (bottom). The data from such waveforms can then be transformed using (8)–(11) to calculate the dynamic resistance in (Ω m⁻¹/cycle). Interestingly, figure 6 shows that dynamic resistance is incurred when d∣B_a(t)∣/dt is largest, i.e., in the region around B_a(t) = 0. In contrast, flux-flow resistance manifests itself as a spike in the voltage when d∣B_a(t)∣/dt is lowest, i.e., at the maxima and minima of the applied field, ±B_max. Additionally, there is some noticeable asymmetry of the voltage between positive and negative half-cycles of the applied field. This is related to the angular dependence of the superconducting properties of the wire (see figures 2 and 3), which differs slightly depending on whether the field is oriented towards the top surface (θ = 0°) or bottom surface (substrate side; θ = 180°). For the wire studied here (for fields up to 100 mT), we see that J_c(B, θ = 180°) tends to be slightly lower than J_c(B, θ = 0°).

Zoom In Zoom Out Reset image size

Figure 7 shows a comparison of the calculated dynamic resistance per cycle with the experimental results for I_DC/I_c = (a) 0.3, (b) 0.5, (c) 0.7 and (d) 0.9 under applied perpendicular magnetic fields up to 100 mT (in 5 mT increments). The numerical results are calculated for frequencies of 20, 50 and 100 Hz whilst the experimental results correspond to frequencies of 26.62, 65.44 and 112.5 Hz. In figure 7(d), the calculated results using the analytical equations presented in [30] are also included (closed symbols), which takes into account the flux-flow resistance term that arises once the total driven transport current exceeds the field-dependent I_c of the wire. This effect gives rise to a nonlinear 'lift-off' from the constant value of dR_dyn/d∣B_app∣ observed at lower fields. The modelling results show excellent qualitative agreement with the experimental results and very good quantitative agreement, especially with respect to B_th (the threshold field above which R_dyn is generated) and the slope of R_dyn. Three important points to make are: (a) the calculated values exhibit a small frequency dependence of the slope, dR_dyn/d∣B_app∣, due to the use of the E–J power law (as described earlier with reference to the AC loss results shown in figures 4 and 5); (b) isothermal conditions are assumed with a constant temperature, T = 77 K, so this ignores any temperature increase that might occur due to heat dissipation (in particular when the J_c of the wire is exceeded resulting in the 'lift-off' regime); and (c) the wire is assumed to have uniform properties across the entire cross-section (and along the length, which is a necessary condition for the 2D infinitely long approximation). Real wires do not entirely meet this criteria, and this can influence the DC and AC properties of an HTS coated-conductor wire [31, 41, 42]. In principle such information could also be implemented in the model to improve the modelling assumptions, as shown in [40]. Nevertheless, the numerical model developed here now provides a useful and flexible tool to predict the characteristics of dynamic resistance generated in any HTS coated-conductor wire for which the relevant geometric and superconducting properties are known, as well as more complicated arrangements of such wires, such as multiple-wire stacks [43], cables and so on.

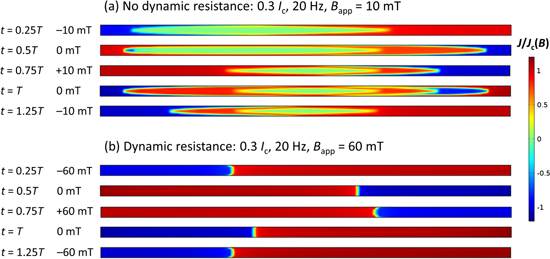
Zoom In Zoom Out Reset image size

In figure 5, the AC loss maxima are indicated for each DC transport current case. These correspond to the threshold field, B_th, below which it is energetically favourable for the central region of the wire to be shielded from changes in the applied field [30]. When B_th is exceeded, dynamic resistance is incurred and increases linearly with ∣B_app∣. Using the numerical model, it is easy to visualise this effect, through mapping the current density distribution within the wire cross-section for different regimes under a perpendicular external AC magnetic field. Figure 8 shows the calculated current density distribution, normalised by J_c(B) (where B is the local magnetic flux density), for the simple DC transport current cases (in the absence of an applied AC field) at the time when the ramped current reaches its final value, I_DC/I_c. Figure 9 then shows the normalised, calculated current density distribution, which arises under a perpendicular external AC magnetic field when I_DC = 0.3I_c, for ∣B_app∣ = 10 mT (figure 9(a)) and 60 mT (figure 9(b)). The distributions are shown at the positive and negative peaks of the applied field, as well as the zero-crossing (f = 20 Hz). Figure 9(a) corresponds to R_dyn = 0 in figure 7(a), and shows the superposition of the transport current and magnetisation currents (with respect to figure 8). It clearly shows a shielded central region that does not experience a change in applied field, and for which J = 0. In contrast, figure 9(b) shows the situation when the central region is no longer shielded throughout the entire cycle, such that J ≥ J_c at all points within the wire, except for a very thin boundary region in which the current reverses direction. The result in this case is that a net flow of flux crosses the DC current-carrying region [4], leading to the development of R_dyn.

Zoom In Zoom Out Reset image size

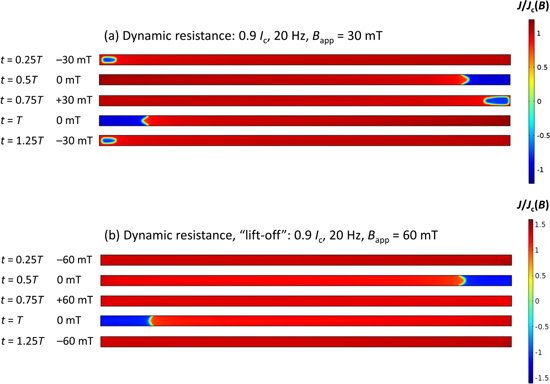
Zoom In Zoom Out Reset image size

In contrast, figure 10 shows the normalised current density distribution, J/J_c(B) when I_DC = 0.9I_c for ∣B_app∣ = 30 mT (figure 10(a)) and 60 mT (figure 10(b)). As before, the distributions are shown at the positive and negative peaks of the applied field, as well as the zero-crossing (f = 20 Hz). The top figure corresponds to the linear regime (no shielded region and ±J_c current-carrying regions). The bottom figure corresponds to the 'lift-off' regime (see figure 7(d)), where there exists an additional flux-flow resistance term because the total driven transport current exceeds the field-dependent I_c of the wire. This 'lift-off' also results in the minima observed in the calculated total AC loss (see figure 5) and the development of a 'spike' in the calculated average electric field (see figure 6) around the peak of ∣B_app∣, which is in clear contrast to figure 6 (middle), where the average electric field is close to zero around the peak of ∣B_app∣.

Zoom In Zoom Out Reset image size

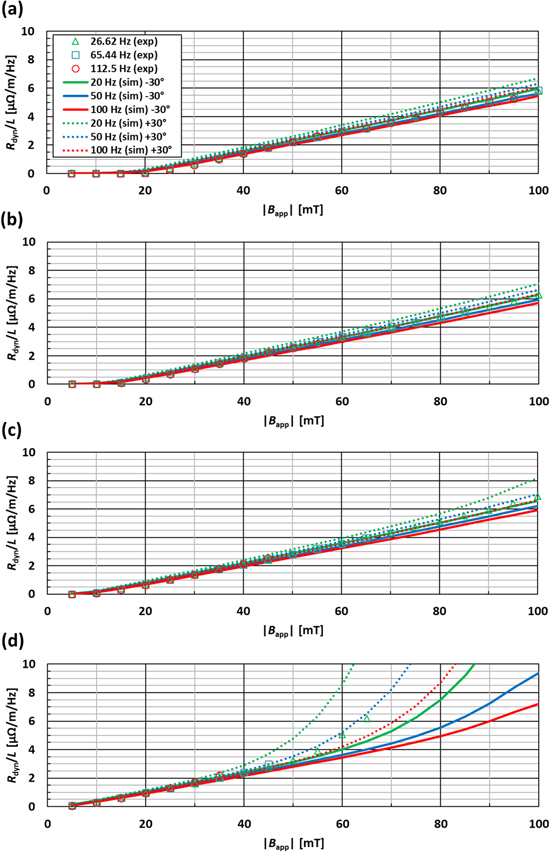
The flexibility of the numerical model and the inclusion of the full angular dependence of the superconducting properties of the wire allows us to simulate the angular dependence of the dynamic resistance over the full range of applied field angles. Recent experimental measurements on a similar wire presented in [31] have shown that the dynamic resistance is dominated by the perpendicular magnetic field component, with negligible contribution from the parallel component. Figure 11 shows a comparison of the calculated dynamic resistance and experimental results for I_DC/I_c = (a) 0.3, (b) 0.5, (c) 0.7 and (d) 0.9 for magnetic fields up to 100 mT (in 5 mT increments and f = 20 Hz (simulation) and 26.62 Hz (experiment)) applied perpendicularly and at angles of θ = −30° and −60°. These results are plotted as a function of the amplitude of the perpendicular component of the applied magnetic field, B_app,⊥ = B_app · cos(θ). This clearly shows that the dynamic resistance is dominated by the perpendicular component of the applied magnetic field, with some subtle differences: for θ = −60°, the slope dR_dyn/d∣B_app,⊥∣ is slightly higher and 'lift-off' occurs at a lower value of ∣B_app,⊥∣.

Zoom In Zoom Out Reset image size

To explain these subtle differences and to obtain a complete picture of the dynamic resistance of the wire, figure 12 shows a comparison of the angular dependence of the calculated dynamic resistance and experimental results for I_DC/I_c = (a) 0.3, (b) 0.5, (c) 0.7 and (d) 0.9 for magnetic fields up to 100 mT (in 5 mT increments) applied at an angle of θ = ±30°, and figure 13 shows the same plots, but for an applied field angle of θ = ±60°. The numerical results are calculated for frequencies of 20, 50 and 100 Hz and the experimental results correspond to frequencies of 26.62, 65.44 and 112.5 Hz. The modelling results show excellent qualitative agreement with the experimental results and very good quantitative agreement, with the same comments to be made with respect to the observed quantitative discrepancies, i.e., a small frequency dependence due to the E–J power law.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The results clearly show the influence of the asymmetric angular dependence of J_c and n on the dynamic resistance. Figures 12 and 13 show that positive (dotted lines) and negative (solid lines) field angles result in different slopes of R_dyn in the linear regime and a different onset of 'lift-off' behaviour (for I = 0.9I_c). These asymmetric effects are caused by the different values of J_c and n at +∣θ∣ and −∣θ∣ respectively. For example, and referring back to figure 2, the J_c of the wire at θ = +30° (and θ = +210° for the negative half-cycle of the applied field) is comparatively lower than at θ = −30° (i.e., at θ = +150° and +330° in figure 2). Hence, the slope of R_dyn is higher for θ = +30°, and the 'lift-off' criteria is satisfied at a lower value of ∣B_app∣. The same is true for the ±60° results shown in figure 12.

In summary, the dynamic resistance in an HTS coated-conductor wire can be mostly determined by the perpendicular field component with subtle differences determined by the angular dependence of the superconducting properties of the wire, which can be included in detail within the numerical modelling framework.

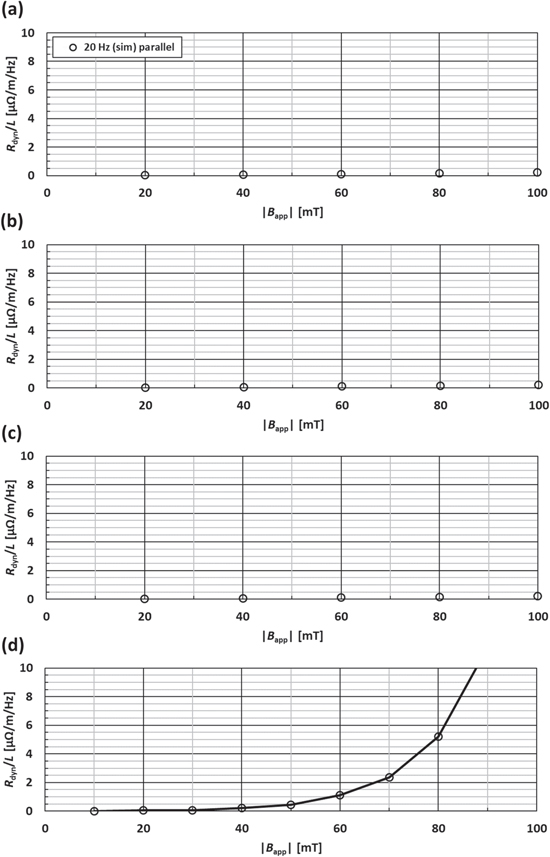
Finally, in this section, the dynamic resistance in parallel applied magnetic fields (at an angle θ = ±90°) is simulated using the same numerical framework. Figure 14 shows the calculated dynamic resistance for I_DC/I_c = (a) 0.3, (b) 0.5, (c) 0.7 and (d) 0.9 for parallel magnetic fields up to 100 mT (in 20 mT increments for (a)–(c) and 10 mT increments for (d), and f = 20 Hz). There is negligible dynamic resistance generated until the total driven transport current exceeds I_c of the wire (in this case, when I_DC/I_c = 0.9 and ∣B_app∣ is about 40 mT or higher), resulting in the 'lift-off' regime explained earlier. This provides further evidence that the dynamic resistance in an HTS coated-conductor wire is determined mostly by the perpendicular component of the applied magnetic field and agrees with experimental measurements presented in [31]. This is in direct contrast with BSCCO wires [4, 44]. From the viewpoint of practical applications, it is therefore the perpendicular component of any external, time-varying magnetic field that is of most interest, having a dominant impact on the generated dynamic resistance.

Zoom In Zoom Out Reset image size