Abstract
In-field angular pinning performances at different temperatures have been analysed on chemical solution deposited (CSD) YBa2Cu3O7−x (YBCO) pristine films and nanocomposites. We show that with this analysis we are able to quantify the vortex pinning strength and energies, associated with different kinds of natural and artificial pinning defects, acting as efficient pinning centres at different regions of the H–T phase diagram. A good quantification of the variety of pinning defects active at different temperatures and magnetic fields provides a unique tool to design the best vortex pinning landscape under different operating conditions. We have found that by artificially introducing a unique defect in the YBCO matrix, the stacking faults, we are able to modify three different contributions to vortex pinning (isotropic-strong, anisotropic-strong, and isotropic-weak). The isotropic-strong contribution, widely studied in CSD YBCO nanocomposites, is associated with nanostrained regions induced at the partial dislocations surrounding the stacking faults. Moreover, the stacking fault itself acts as a planar defect which provides a very effective anisotropic-strong pinning at H//ab. Finally, the large presence of Cu–O cluster vacancies found in the stacking faults have been revealed as a source of isotropic-weak pinning sites, very active at low temperatures and high fields.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The fabrication of nanostructured YBa2Cu3O7−x (YBCO) thin films by the incorporation of nanosized oxide secondary phases as artificial pinning centres (APC) has been shown to strongly enhance their performance, ensuring great potential for use in a broad number of power applications [1–5]. The final nanostructure of YBCO nanocomposites and thus their pinning landscape deeply differs depending on many different parameters such as the growing technique, the growth conditions (temperature, growing rate, atmosphere, and substrate), the chemistry of the secondary phase artificially included, and their amount, among others. All these parameters will have a direct influence on the shape (nanorods, nanoparticles, nanoplatelets), size, distribution, and orientation of secondary phases. Moreover, the APC will generate and/or interact with natural defects of many types, appearing at different growth stages. Figure 1(a) shows a schematic representation of typical defects observed in YBCO films. Some of them, such as misoriented grains, high angle grain boundaries, or porosity, are detrimental to the superconducting properties and must be avoided. However, many others, with nanometric size (illustrated in pink), can act as very active pinning centres of different dimensionalities, thus determining the final pinning landscape. In all the cases, one also has to consider the nanostrain associated with the presence of defects.
Figure 1. Schematic representation of (a) different defects present in YBCO films and nanocomposites. The pink regions represent the nanosized regions able to act as pinning centres. The dimensionality of the pinning centres (0D, 1D, 2D, or 3D) is also indicated (b) and (c) shows the growth of a nanocomposite with simultaneous and sequential nucleation of secondary phases and the YBCO matrix, respectively.
Download figure:
Standard image High-resolution imageIn particular, by using in situ growth techniques such as pulsed laser deposition (PLD), chemical vapour deposition (CVD), or hybrid liquid phase epitaxy (HLPE) simultaneous nucleation and growth of the YBCO and epitaxial nanoscale secondary phases occur. In this case, secondary phases form self-assembled nanostructures, such as columnar nanorods along the c-axis, with coherent or semi-coherent interphases with the YBCO matrix (figure 1(b)) [6–9].
Artificial vortex pinning centres induced in these systems are mostly ascribed to self-assembled secondary phases and the associated interfacial strain [10]. By tuning the growth conditions and the nature of the artificial columnar nanoinclusions one obtains either continuous or interrupted nanocolumns going straight or splayed through the film. Moreover, other defects such as plates along the a–b planes, intergrowths (extra Y or CuO2 planes) or anti-phase boundaries can be generated, giving rise to very complex pinning landscapes [3, 9, 11, 12].
On the other hand, in YBCO films grown by chemical solution deposition (CSD) techniques, artificial nanosized secondary phases are formed in a precursor film with a deferred sequential nucleation and growth of the YBCO matrix. In this case, nanosized secondary phases (nanoparticles) remain trapped during the YBCO growth and they lay mainly randomly oriented within the film (figure 1(c)) [13–16]. The presence of random nanoparticles during the YBCO growth induces a high density of stacking faults (double or triple CuO chain layers) in the film as a mechanism to relax the incoherent interfaces. Very efficient artificially induced isotropic core pinning in CSD nanocomposites is attributed to Cooper pair suppression nanostrained regions surrounding the stacking faults in the form of partial dislocations [16, 17].
In this work, we have performed an extensive investigation by comparing the critical current density behaviour of CSD YBCO pristine films and nanocomposites with the objective of distinguishing and separating the different kinds of artificial defects induced by the presence of randomly oriented nanoparticles. We have studied the effectivity of APC, interacting with natural intrinsic defects, and analysed their cooperative/competitive role in the final pinning behaviour. Analysis of the angular dependent critical current density curves at different magnetic fields and temperatures has provided us with a detailed picture of the vortex pinning landscape generated in CSD nanocomposites. We are able to sort out the weight of isotropic and anisotropic pinning contributions, as well as distinguish weak from strong pinning effects, their efficiency, and characteristic pinning energies at different regions of the H–T phase diagram.
2. Sample description and experimental details
We have evaluated the pinning performance of a set of 250 nm thick YBCO pristine film compared with nanocomposites with different nanoparticles, BaZrO3 (BZO), Ba2YTaO6 (BYTO), Y2O3 (YO), ZrO2 (ZO), and mixed compositions, deposited by spin-coating and grown by CSD following the trifluoroacetate route [16, 18, 19]. We have also included an 800 nm thick nanocomposite grown by inkjet printing [20]. Two different approaches have been followed to form the nanocomposites, the spontaneous segregation of secondary phases (SS-nanocomposites [16, 19] or preformed nanoparticles (PN-nanocomposites)) [21, 22]. In the first case, metal–organic salts are added to the YBCO precursor solution, which spontaneously segregate in the form of the desired nanoparticles during the growth process of obtaining the final nanocomposite film. This methodology allows controlling the amount and nature of the secondary phase introduced, although the size, density, and distribution of nanoparticles cannot be adjusted, since it is a spontaneous segregation. A good option to tune the size and density of nanoparticles is to use a colloidal solution with preformed colloidal stable nanoparticles [21, 22]. The nature, number, and size of nanoparticles, together with the nanocomposite processing conditions has enabled us to control the planar intergrowths scenario and the nanostrained regions associated with the surrounding partial dislocations [16, 19, 23]. In particular, the value of the nanostrain, which determines the isotropic-strong pinning contribution, can be increased with the volume of the secondary phase if the nanoparticle size is preserved [16]. However, we observed that above a certain concentration, nanoparticles tend to aggregate reducing the current cross section and thus strongly reducing the self-field Jc (see figure 2(a)) [19]. Two different routes have been identified as good options to enlarge the volume fraction of nanoparticles without segregation. One option is to use mixed spontaneous segregated nanocomposites with the combination of different phases. Figure 2(a) shows that by combining BZO and YO we could enhance the self-field from Jc < 2 MA cm−2 (obtained in pure 15% BZO and 15% BYTO spontaneously segregated nanocomposites (SS-15BZO and SS-15BYTO)) to 3 MA cm−2 in a mixed 10% BZO–5% YO (SS-10BZO-5YO). The other route is to use non-reactive preformed BZO nanoparticles where up to 25 mol% of the secondary phase has been introduced with a very high self-field Jc ∼ 4 MA cm−2 and no decrease of Tc. This option is especially interesting since, as mentioned above, it allows good control of nanoparticle size and density and it can be easily transferred to inkjet printing deposition of CSD thick films [20]. In this work, we analyse two films with preformed nanoparticles, a 250 nm YBCO with 13% M ZrO2 (PN-13ZO) and a 800 nm thick YBCO with 20% M BZO (PN-20BZO).
Figure 2. (a) Self-field Jc values obtained at 77 K for SS-nanocomposites with BZO (closed circles), BYTO (open circles), mixed SS-10BZO5YO (star), and PN-nanocomposites with BZO (squares)) as a function of the amount of nanoparticles added. (b) Temperature dependence of H* measured at H//c (closed symbols) and H//ab (open symbols), for a pristine sample (black squares), and two nanocomposites, SS-8BYTO (orange stars), mixed SS-10BZO5YO (blue circles).
Download figure:
Standard image High-resolution imageTransport properties were measured using a four-probe configuration in 10–30 μm patterned tracks by a physical property measurement system (PPMS, quantum design). A voltage criterion of 5 μV cm−1 was used to obtain the critical current values. Angular dependent current density curves at different magnetic fields and temperatures, Jc (θ, H, T), were obtained for fields ranging from μ0H = 0–9 T at different current field orientations, θ = 0°–90° (with θ = 0° for H//c and 90° for H//ab) and temperatures ranging from 5–85 K, providing a detailed picture of the pinning effects. The microstructure of the YBCO films and nanocomposites was analysed by performing scanning transmission electron microscopy (STEM) studies with an FEI Titan low base system equipped with a CESCOR probe aberration corrector, a monochromator, and a XFEG electron gun operated at 200 KV.
3. Results and discussion
3.1. Magnetic field dependence of Jc
The influence of APC on the pinning performance has been studied by analysing the magnetic field dependence of the critical current density for H//c and H//ab, at different temperatures. Figure 3 shows the data obtained for a pristine YBCO film compared with two SS-nanocomposites with 8% BYTO (SS-8BYTO) and mixed 10% BZO–5%YO (SS-10BZO5YO).
Figure 3. Magnetic field dependence of the critical current density at different temperatures indicated in the graphs (77, 50, 25, and 5 K) for a pristine sample (black squares), SS-8BYTO (orange stars), and mixed SS-10BZO5YO (blue circles), for H///c (closed symbols) and H//ab (open symbols).
Download figure:
Standard image High-resolution imageA typical characteristic feature of the Jc(H) curves of CSD nanocomposites is the extension of the low field plateau (associated with single vortex pinning) up to higher fields, producing a smoother Jc(H) performance [24]. In general, in a Jc(H) log–log plot one defines a crossover field, H*, that defines the transition from a single vortex pinning regime (plateau in Jc(H)) to a collective pinning behaviour (Jc decreasing with H). Figure 2(b) shows the temperature dependence of H* (determined at 90% of self-field Jc) obtained for the different samples analysed at H//c and H//ab. Note that for both nanocomposites H* is extended to higher fields in the whole temperature range evaluated. The shift in H* indicates that the APC induced are able to preserve the single vortex pinning regime up to higher fields. It is also observed that the best pinning landscape to extend H* is the one generated in the mixed SS-10BZO5YO nanocomposite. The nanostructure of these three different samples, evaluated through high angle annular dark field (HAADF) STEM images, is shown in figure 4. The dark horizontal stripes in the images correspond to Y124 intergrowths (stacking faults).
Figure 4. HAADF-STEM cross-sections for a (a) pristine YBCO film, (b) SS-8BYTO, and (c) SS-10BZO5YO.
Download figure:
Standard image High-resolution imageThe amount and length of intergrowths is highly dependent on the sample considered. The intergrowth density (and thus the nanostrain associated) is clearly enhanced in both nanocomposites which can be straightly correlated with the H* shift to higher fields [19, 22–24]. Nanostrain values go from 0.05%–0.1% in pristine films and to 0.2%–0.3% in nanocomposites [16, 23]. The particular values obtained for the three samples shown in figure 4 are 0.1%, 0.19%, and 0.25% for pristine YBCO, SS-8BYTO, and mixed SS-10BZO5YO, respectively. The best performances are observed for the mixed SS-10BZO5YO pinning landscape which shows a large amount of very short stacking faults (much shorter than those observed for SS-8BYTO) which are the ones that generate the higher nanostrained regions within the matrix [19].
By comparing the different Jc(H) dependencies shown in figure 3 we observe that at high temperature (77 K) and the H//c extra pinning force provided by the artificial defects is mainly effective at low and intermediate fields (0.03–4 T). At this temperature, the Jc(H) curves for the nanocomposites cross the one obtained for the pristine sample at ∼6 T. The crossing is explained by the fact that the main pinning defects acting at high temperatures and H//c in the pristine sample are the twin boundaries (TBs) [25]. In the case of nanocomposites, the large amount of intergrowths induced in the matrix interact with them breaking the TB coherence along the c-axis [26, 27] and thus reducing their pinning efficiency at high temperatures. Figure 7(d) shows a high-resolution TEM image with TB domains depicted as green and brown colours were the broken coherence can be clearly observed. The identification of different domains has been performed by considering the different arrangement of Cu atoms in the double Cu–O chains when viewed along the 〈100〉 and 〈010〉 zone axes [26, 27]. Thus, the sample with a large amount of stacking faults (mixed nanocomposite) is the one with less coherent TB plains, showing the lower irreversibility line at 77 K. Fine-tuning of the specific stacking fault density and length may be performed in order to obtain large H* values while preserving the irreversibility line at H//c at high temperature, as obtained in [15]. It is important to remark that although TB planes with no vertical coherence are not very effective pinning centres at high temperatures (close to the irreversibility line) they preclude vortex channelling at low temperature, thus avoiding the Jc minima observed in current/field configurations where channelling effects may induce fast vortex motion [26, 27]. At lower temperatures (below 50 K) pinning in both nanocomposites is enhanced for the entire magnetic field range evaluated in H//c and H//ab, opening the way for ultra-high field applications at low temperatures. It is also observed that the value of the self-field is very similar for all samples at 77 K and 50 K, whereas it is largely enhanced at lower temperatures (25 K and 5 K) in the mixed nanocomposite.
With the aim of disentangling the pinning sites responsible for the Jc performances obtained, we have evaluated the contribution of different type of defects (isotropic-weak, isotropic-strong, and anisotropic-strong) at different regions of the H–T phase diagram. Although interaction between different pinning centres occurs, in general a direct summation of contributions is able to account for most relevant pinning behaviour [28].
3.2. Strength and energy scale of different pinning contributions
Isotropic pinning sites (those whose pinning length does not depend on the magnetic field orientation) can be separated from anisotropic pinning centres (correlated along a certain field direction) by using the Blatter scaling approach [18, 28, 29] on a series of Jc(θ, H, T) curves plotted as a function of the effective magnetic field, Heff,

were θ is the angle between the magnetic field and the c-axis and γ is the anisotropy parameter. Based on the temperature dependence of Jc, flux pinning can be categorized as strong or weak. It has been shown that Jc(T) decays exponentially with T for weak pinning (equation (2)) [30], and with T2 for strong pinning (equation (3)) [31].
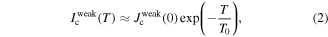
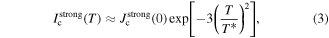
where Jcweak(0) and Jcstrong(0) are the contributions to Jc at 0 K of weak and strong pinning defects, respectively, in the absence of creep, thus they are proportional to the density of defects. T0 and T* are the characteristic pinning energies of the different weak and strong defects, respectively, and thus they account for the effectiveness of their pinning potential in relation with KT. The above equations can be linked to evaluate, separate, and quantify the isotropic-weak, isotropic-strong and anisotropic-strong pinning contributions to Jc, at different temperatures and magnetic fields [28, 32, 33].
Figure 5(a) shows the values of T0 and T* obtained by fitting equations (2) and (3) for different magnetic fields at H//c, for a pristine film and the two nanocomposites. The same analysis was performed to obtain the values at H//ab giving similar results. Coloured bands show the dispersion of T0 and T* values obtained by measuring a large set of pristine and nanocomposite films both at H//c and H//ab. Note that, regardless the sample considered, we obtain very similar values of T* and T0 for each contribution, with a general trend of decreasing of the pinning energy with increasing of the magnetic field. This can be understood since all samples have the same nature of defects and each one presents a typical reduction of vortex pinning due to thermal activation, though the amount of each defect is particular to each sample, as we will discuss in the following. It should be noted, however, that the largest dispersion in the energy values is obtained for the anisotropic pinning contribution. In this case, lower T* values at high fields are obtained for the mixed nanocomposite (T* ∼ 60–70 K) in accordance with a lower irreversibility line observed at high temperatures (see figure 3(a)). This reduction, as discussed in the previous section, can be associated with the loss of coherence of the TBs due to the large density of stacking faults. In figure 5(b) we have plotted the normalized temperature dependence of each contribution considering their characteristic pinning energies T* ∼ 100 K for anisotropic-strong, T* ∼ 70 K for isotropic-strong. and T0 ∼ 10 K for isotropic-weak. We observe that due to the fast temperature decay of isotropic-weak pinning, this contribution is only relevant at low temperatures (<40 K). Isotropic-strong pinning, with an intermediate Jc(T) dependence is relevant at intermediate temperatures. The large values of T* obtained for the anisotropic-strong pinning contribution make it active up to high temperatures, being the one with the largest irreversibility field. It is important to remark that besides the thermal activation of each contribution, what does differ from sample to sample is the concentration of defects, and thus the value of Jc at 0 K. For instance, randomly oriented nanoparticles in CSD nanocomposites will strongly enlarge the Jc(0) isotropic-strong contribution associated with the nanostrained regions. Moreover, the presence of a large density of stacking faults, interacting with the intrinsic defect structure, may also change the other two contributions. In the next section, we analyze the pinning contributions to Jc at 0 K for the two SS-nanocomposites analyzed above (SS-8BYTO and SS-10BZO5YO), compared with a pristine YBCO film in order to correlate their different microstructures (shown in figure 4) with the strength of pinning centres at different regions of the H–T phase diagram.
Figure 5. (a) T0 and T* parameters obtained by fitting equation (2) for isotropic-weak pinning centres and equation (3) for isotropic-strong and anisotropic-strong pinning centres, at different magnetic fields applied H//c, for a pristine YBCO film (closed symbols), SS-8BYTO nanocomposite (half-closed symbols), and a mixed SS-10BZO5YO nanocomposite (open symbols). (b) Temperature dependence of different pinning centres considering their characteristic average vortex pinning energies.
Download figure:
Standard image High-resolution image3.3. Role of pinning centres at 0 K, Jc(0)
Figure 6 shows the magnetic field dependence of Jc(0) obtained for isotropic-weak, isotropic-strong determined at H//c, and anisotropic-strong at H//ab (associated with intrinsic pinning and intergrowths) and H//c (mainly correlated to the TBs) for a pristine YBCO film and the two SS-nanocomposites analysed in section 3.1.
Figure 6. (a) Isotropic-weak (b) isotropic-strong, and (c) anisotropic-strong (open symbols for H//ab and closed symbols for H//c) pinning contributions to Jc at 0 K, obtained by fitting equations (2) and (3) at different applied magnetic fields, for the pristine YBCO film (black squares), SS-8BYTO (orange stars), and SS-10BZO-5YO (blue circles).
Download figure:
Standard image High-resolution imageAs expected, an important increase in the Jc(0) contribution associated with the isotropic-strong defects is obtained for both nanocomposites (figure 6(b)). As discussed above, nanostrained regions induced due to the presence of a large density of dislocations surrounding the stacking faults act as very effective isotropic-strong pinning centres. This contribution is especially enhanced at the low and intermediate fields though it also remains higher than that of the pristine film for the high fields. Moreover, for the mixed nanocomposite, with a landscape of a large density of short stacking faults, an important increase of the Jc(0) contribution associated with isotropic-weak defects is also observed (figure 6(a)). In general, the isotropic-weak pinning contribution is ascribed to point defects (oxygen vacancies, atomic inclusions). In the case of the YBCO films with a large concentration of stacking faults, a huge density of complex point-like defects made up of ferromagnetic clusters including two Cu vacancies decorated by three O vacancies, embedded in particular extra Cu–O chains, were detected [34, 35].
Figure 7 shows high-resolution STEM images of highly strained films with a large amount of YBCO stacking faults, at different magnifications. Note that the double Cu chain exhibits an irregular contrast associated with missing atoms within the chain. These atomic vacancies have been identified as Cu–O clusters formed by two Cu vacancies decorated by three oxygen vacancies [34]. A large amount of low intensity columns with Cu–O cluster vacancies are identified within the stacking faults observed in figure 7(a) (some of them indicated by yellow circles). We are convinced that these defects, and the associated distortions of a few nanometres in the YBCO matrix [35] may act as very effective isotropic-weak pinning sites since the enhancement of this contribution is particularly observed in films with a very high density of stacking faults. Cu–O cluster vacancies are present in all the YBCO films containing stacking faults. However, not all the stacking fault scenarios produce a clear enrichment of this kind of point defect compared with a standard YBCO sample. Our results indicate that the best pinning landscape to improve the isotropic-weak pinning contribution is that with a large density of short stacking faults (obtained for the mixed nanocomposite). In this case, the increase of Jc(0) shows a very soft magnetic field dependence, within the range explored, suggesting a high density of this kind of point defect, as illustrated in the STEM images.
Figure 7. High-resolution HAADF-TEM cross section images of (a)–(c) 10% BZO YBCO SS-nanocomposite with a large density of stacking faults, at different magnifications, and several Cu–O vacancies indicated. (d) Twin boundary domains in a highly distorted region of a 10% BYBCO YBCO SS-nanocomposite. Green and brown coloured regions mark different twin domains, corresponding to [100] and [010] YBCO zone axes, respectively. Dashed-vertical lines mark the limit of the twin domains. The inset shows a close-up view of a TB.
Download figure:
Standard image High-resolution imageRegarding anisotropic-strong pinning contributions, we find a large enhancement of Jc(0) at H//ab for the mixed nanocomposite, very effective up to high magnetic fields (open symbols in figure 6(c)). The enhancement is directly associated with the large density of stacking faults that act as very effective anisotropic pinning centres at H//ab. The contribution of Jc(0) at H//c, principally associated with the TBs, present the minority contribution at 0 K and remains mainly unchanged in all three samples (closed symbols in figure 6(c)). As we discussed in the previous sections, the reduction of the TB vertical coherence due to the presence of stacking faults (figure 7(d)) outcome with a decrease in the pinning efficiency at high temperatures (in the presence of high thermal activations) [26, 27]. However, at low temperatures the Jc(0) contribution stays unaffected (or even is slightly increased in the case of the mixed SS-nanocomposite).
In summary, we can conclude that the large density of stacking faults induced, due to the presence of nanoparticles, generate concomitant defects within the films able to modify the three pinning contributions. The strain associated dislocations surrounding the stacking faults act as an isotropic-strong defect, Cu–O cluster vacancies identified within the double Cu chain may act as isotropic-weak pinning centres. and the stacking fault itself increases the anisotropic-strong pinning contribution at H//ab.
3.4. Temperature dependence of Jc
Let us now consider the influence of various types of pinning centres on the temperature dependence of the critical current density. The whole analysis of the Jc(0) associated with each pinning contribution and their characteristic pinning energies allows us to evaluate and quantify the dominant pinning centres active at different regions of the H–T phase diagram which will determine the final Jc(T) dependence at different fields and orientations. Figure 8(a) plots log Jc versus T2 measured for a pristine film and the mixed nanocomposite sample at 1 T H//c. The dashed lines show linear fits to the curves characteristic of strong pinning, according to equation (3).
Figure 8. (a) Log Jc versus T2 at 1 T, H//c measured for a pristine YBCO film and SS-10BZO5YO nanocomposite. (b) and (c) show the temperature dependence of the weight of isotropic-strong, isotropic-weak, and anisotropic-strong critical current density contributions obtained by fitting equations (2) and (3) to the curves shown in (a) for the pristine film and nanocomposite, respectively.
Download figure:
Standard image High-resolution imageDeviation of the linear fits are observed at low temperatures (where the isotropic-weak pinning contribution plays an important role) and at high temperatures when approaching the irreversibility line. The weights of different pinning contributions obtained for the different samples are shown in figures 8(b) and (c). We observe that all contributions (isotropic-strong, isotropic-weak, and anisotropic-strong) play a role in the case of the pristine sample. Isotropic-weak and isotropic-strong contributions are similar at low temperatures (5 K) whereas the anisotropic contribution, associated with the TBs, start to be relevant in comparison with the other defects at high temperatures (60–90 K). Contrary to the nanocomposite, the isotropic-strong contribution, associated with the nanostrain, is strongly enhanced in the whole temperature range, completely dominates the pinning performance. Although in this case pinning is mainly dominated by the isotropic-strong contribution; if we compare the absolute value of the other two contributions with the ones obtained for the pristine sample, we observe a clear enhancement of the isotropic-weak contribution while the anisotropic-strong contribution remains at the same values (being completely negligible compared with the other contributions). Consistent with this analysis the Jc versus T2 dependence plotted in figure 8(a), associated with strong pinning defects, is well fitted down to very low temperatures for the nanocomposite.
We next discuss the same study performed at H//c and high magnetic fields (9 T) (figure 9). We observe that the isotropic-weak contribution is the most relevant at low temperatures for both samples, being higher than the isotropic-strong contribution, especially in the case of the pristine sample.
Figure 9. (a) Log Jc versus T2 at 9 T, H//c measured for a pristine YBCO film and SS-10BZO5YO nanocomposite. (b) and (c) show the temperature dependence of the weights of the isotropic-strong, isotropic-weak, and anisotropic-strong critical current density contributions obtained by fitting equations (2) and (3) to the curves shown in (a) for the pristine film and nanocomposite, respectively.
Download figure:
Standard image High-resolution imageThe improvement of Jc for the nanocomposite at low temperature in comparison with the pristine film (a factor of 5 at 5 K) is mainly associated with the extensive contribution of both the isotropic-strong and isotropic-weak pinning centres. As shown in figure 6(a) the Jc(0) value associated with isotropic-weak pinning overcomes the one associated with isotropic-strong defects at high fields, evidencing the high density of point defects in the sample. The contribution of weak pinning at low temperatures and high fields is clearly observed in the Jc versus T2 fittings shown in figure 9(a) where Jc goes above the linear fits up to ∼20 K. The Jc(T) curves for the two measured samples at 9 T merge at high temperatures, where anisotropic-strong defects start to dominate the phase diagram. Finally, the same analysis performed at 9 T H//ab is shown in figure 10.
Figure 10. (a) Log Jc versus T2 at 9 T, H//ab measured for a pristine YBCO film and SS-10BZO5YO nanocomposite. (b) and (c) shows the temperature dependence of the weight of isotropic-strong, isotropic-weak, and anisotropic-strong critical current density contributions obtained by fitting equations (2) and (3) to the curves shown in (a) for the pristine film and nanocomposite, respectively.
Download figure:
Standard image High-resolution imageIn this case, the fittings associated with the strong pinning can be performed down to 5 K in agreement with a dominant component of the anisotropic-strong contribution, associated with intrinsic pinning and planar intergrowths. As observed in figures 10(a) and (b), this contribution completely determines the pinning performance in the pristine film and it is very relevant for the nanocomposite (with a high density of intergrowths), although it competes with the isotropic-strong contribution, strongly enhanced due to the presence of nanostrain. Note that for the pristine sample Jc values go above the fit at high temperatures, which may indicate a region dominated by different kind of correlated defects (stacking faults and intrinsic pinning).
3.5. Pinning landscape disentanglement
The analysis performed enable us to evaluate the whole magnetic field/temperature evolution of the different pinning defects in an H–T landscape. Figure 11 shows the Jc contributions obtained for the three samples analysed at different temperatures and fields for H//c.
Figure 11. H–T phase diagram obtained at H//c showing the evolution of different pinning contributions to Jc for a pristine YBCO film, SS-8BYTO nanocomposite, and SS-10BZO5YO nanocomposite.
Download figure:
Standard image High-resolution imageAs has been discussed throughout the whole analysis, the contribution of isotropic-weak defects is very relevant at low temperatures with the best Jc performances observed for the mixed nanocomposite showing a large enhancement of this contribution at both low and high fields. At these temperatures, one also has to consider the isotropic-strong contribution, which directly competes with the isotropic-weak contribution with similar weights. At intermediate temperatures, the weak pinning contribution disappears and the critical current density in the nanocomposites is mainly determined by isotropic-strong pinning centres. In this case, the mixed nanocomposite shows better performances at low fields where the enhancement associated with isotropic-strong defects is much higher than the one obtained for the BYTO nanocomposite. At higher fields, both nanocomposites show the same isotropic-strong contribution. Finally, at high temperatures the anisotropic-strong pinning centres, with larger pinning energy values play an important role in the Jc contribution, at high fields. The pristine sample, with much higher pinning energies associated with the correlated TB, defects shows the best pinning performance.
As an example of the valuable insights that one can get from the analysis of the different pinning contributions, we compare the Ic(T) dependence of different samples, at 9 T H//c (figure 12).
Figure 12. (a) Ic(T) dependence obtained at 9 T and H//c for different 250 nm YBCO pristine and nanocomposite films, including SS and PN nanocomposites. An PN nanocomposite film with a thickness of 800 nm (thick) is also included. (b) Weak and strong contributions to Ic(0) for the samples shown in (a). Dashed line is to guide the eye.
Download figure:
Standard image High-resolution imageFigure 12(a) shows the data measured for a set of 250 nm thick samples, a pristine YBCO film, the two SS-nanocomposites analysed in the previous sections, and PN-13ZO. We have also included an 800 nm thick PN-nanocomposite (PN-20BZO (thick)). One can clearly see from the graph that the Ic(T) performance strongly changes from sample to sample with very different values of Ic(9 T, 5 K). According to the analysis performed in the previous sections, we know that at this particular field and temperature the main contributions to Jc are the isotropic-weak and the isotropic-strong pinning centres. Thus, in order to simplify the analysis we fit the Ic(T) curves shown in figure 12(a) with two contributions, weak and strong, according to equations (2) and (3), respectively. Figure 12(b) shows the Ic(0) weak (open symbols) and strong (closed symbols) fitting values obtained. We observe that the strong contribution increases almost linearly with the amount of nanoparticles. It is important to remark however that the two thin nanocomposites with the best performances at 5 K, 9 T (mixed SS-10BZO10YO and PN-13ZO) are the ones with a large amount of nanoparticles that preserve a good balance between the weak and strong pinning centres. The SS-8BYTO nanocomposite shows a lack of weak defects linked with a lower value of Ic(9 T, 5 K). Regarding the PN-20BZO (thick) nanocomposite, we observe an increase in the strong Ic component while the weak remains nearly unchanged. It is clear that the pinning landscape obtained in this case follows the trend of thin films regarding the strong contribution and according to the percentage of nanoparticles used, but further tuning should be done to increase the weak pinning contribution. The analysis reported here will help us follow the evolution of different pinning contributions during growth process optimization and thus provides a good tool for designing the desired pinning landscape.
4. Conclusions
We have shown that the strength of different kinds of vortex pinning centres can be tailored through the introduction of nanoparticles in CSD grown YBCO thin films. A full analysis of Jc(θ, H, T) has enabled us to sort out and quantify the pinning strength and energies associated with different pinning centres (isotropic-strong, isotropic-weak, and anisotropic-strong) in different CSD nanocomposites. A clear correlation between nanostructure and properties has been established. In particular, we observe that nanocomposites having the best superconducting performances, with a large density of stacking faults, show (i) a strong increase of the isotropic-strong contribution, associated with nanostrained regions, especially effective at intermediate fields and temperatures, (ii) an enhancement of the isotropic-weak contribution, effective at low temperatures (<20 K) at any field, related to Cu–O cluster vacancies appearing at the intergrowths, and (iii) an additional improvement in Jc at H//ab, associated with the large presence of intergrowths that enhance the anisotropic-strong contribution in this magnetic field orientation. The knowledge acquired in this study has enabled us to identify the most effective pinning centres at different H–T regions, and magnetic field orientations for laboratory-scale nanocomposites, that may be transferred to the production of thicker films and longer lengths. We have shown that the presence of stacking faults induces other defects in the matrix (dislocations, Cu–O cluster vacancies) relevant for the three pinning contributions thus revealing stacking faults as a key defect to be promoted in YBCO nanocomposites.
Acknowledgments
We would like to acknowledge S Ricard, N Chamorro, and J Ros for the preformed nanoparticle preparation. We acknowledge financial support from the Spanish Ministry of Economy and Competitiveness through the 'Severo Ochoa' Programme for Centres of Excellence in R&D (SEV-2015-0496), and the COACHSUPENERGY project (MAT2014-51778-C2-1-R, co-financed by the European Regional Development Fund). We also thank the European Union for its support under the EUROTAPES project (FP7-NMP-Large-2011-280432), ULTRASUPERTAPE project (ERC-2014-ADG-669504), and COST Action NANOCOHYBRI (CA16218), and from the Catalan Government under 2014-SGR-753 and Xarmae.












