Abstract
We report that β-InSe endowed with external strain realizes a novel three dimensional topological insulator (TI) by ab initio calculations. We predicate that the promising topological non-trivial state can be observed in an accessible temperature regime in β-InSe for its large spin–orbital band gap up to 121 meV. Specifically, unlike in previous literature where the band inversion (BI) in TIs is induced using heavy elements that have strong spin–orbital coupling (SOC), we provide a remarkable blueprint for stabilizing BI solely by mechanical deformation so that β-InSe could display BI even without considering SOC. Nevertheless, SOC is still needed to create a band gap at the crossing point by breaking the incompatibility symmetry of the inverted bands.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY Introduction and background. Topological insulators are becoming one of the most studied classes of novel materials due to their great potential for applications ranging from spintronics to quantum computers.
Main results. In this paper, we apply fully relativistic first principles calculations to predicate that layered semiconductor β-InSe can be transformed into topological insulators by strain engineering. Consequently, different from previous literature on topological insulators where band inversion in topological insulators is induced by using heavy elements that have strong spin–orbital coupling, we propose viewng the formation of topologically nontrivial states from a new perspective: band inversion can be induced only by strain due to the modification of electron hybridizations, even without considering spin–orbital coupling. The latter, however, is indispensable for introducing a gap at the crossing points of the inverted bands. Emphasis of the role of strain for the formation of a three-dimensional topological insulator is essential from the application point of view. While it is not convenient to tune the spin–orbital coupling by modifying the composition of the sample, strain is an efficient tool to alter the band topology.
Wider implications. Our work provides a fascinating guiding principle for tuning the topological order by other controllable external parameters instead of the immutable intrinsic spin–orbital coupling.
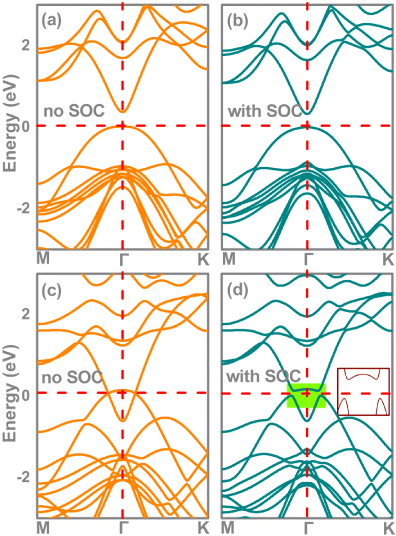
 Figure. Band structures of β-InSe, with the upper row corresponding to unstrained β-InSe (a) without and (b) with spin–orbital coupling; and the lower row corresponding to strained β-InSe (6%) (c) without and (d) with spin–orbital coupling.
Figure. Band structures of β-InSe, with the upper row corresponding to unstrained β-InSe (a) without and (b) with spin–orbital coupling; and the lower row corresponding to strained β-InSe (6%) (c) without and (d) with spin–orbital coupling.
1. Introduction
Recently, the subject of time-reversal-invariant topological insulators (TIs) has attracted great interest in condensed matter physics due to their novel quantum state based on the quantum spin Hall effect and hence the potential application in quantum computation and spintronics [1–6]. Typical TIs differ from normal insulators in that they exhibit gapless boundary states inside a bulk energy gap. These materials support an odd number of surface states with linear dispersion, which can be viewed as a sea of massless Dirac cones, with a single Dirac cone being the simplest case. The conducting surface states in TIs are protected by time-reversal symmetry and are immune to scattering by non-magnetic impurities, thus opening new ways for backscattering-free transport. The existence of an odd number of Dirac cones on the surface is ensured by the Z2 topological invariant of the bulk [7–9]. In TIs, the TI properties can be understood from a simple mechanism of band inversion (BI) caused by the spin–orbital coupling (SOC). Such inversion must occur at the time-reversal-invariant momentum (TRIM) points of the Brillouin zone [7, 10, 11]. The guiding principle to identify TIs is that the conduction and valence bands have the opposite parity, and a BI occurs when the strength of some parameter, say SOC, is tuned [12]. The family of known TIs has grown steadily in recent years; the search for new TIs is under way [13–18]. For example, in a recent study, it was proposed that Pb-based ternary chalcogenides PbnBi2Sen+3 and PbnSb2Ten+3 could be new candidates for TIs [19]. In another work, Kim et al and Sa et al predicted the structure-related topological insulating behavior in Ge2Sb2Te5 alloys [3, 20]. Another class is thallium-based ternary III–V–VI2 chalcogenides, which were proposed theoretically [21, 22] and then verified experimentally [23–25]. Nearly all new reported TIs are relatively uncommonly materials; however, a few TIs which could be fully integrated in the current electronic technology have been reported thus far.
Indium selenide (InSe) and other III–VI layered semiconductors have received extensive attention due to the unusual nature of the electronic interaction and also because of their applications in solar energy conversion, nonlinear optics, terahertz generation and memory devices [26–31]. At a more fundamental level, the band structure of InSe presents some specific features that are related to the strong anisotropy of its electronic structure [28]. InSe presents an anisotropic crystalline structure with layers formed by two deformed sublayers of hexagonal symmetry held together by strong covalent bonds. The weaker bonding between the layers is of the van der Waals type and leads to the existence of different polytypes. Among them, the β-type lattice is the most studied structure [26–31]. The space symmetry group of β-InSe is D6h. This structure consists of covalently bonded Se–In–In–Se tetra-layer sheets (figure 1(a)), with the sheets held to each other by van der Waals forces.
Figure 1. (a) Top and (b) side views of the crystal structure of the β-InSe. (c) The Brillouin zone of the honeycomb lattice; eight TRIM points are denoted by the red stars. (d) Three-dimensional band structures around the Γ points calculated for the β-InSe with strain (ε = 1.4%).
Download figure:
Standard image High-resolution imageIn this work, we theoretically demonstrate that β-InSe could enter into a topologically non-trivial state at a reasonable biaxial lattice expansion. Specifically, different from the current accepted view that the BI in three dimensional TIs is induced by heavy elements that have strong SOC, we demonstrate that the BI in β-InSe could be created solely by external strain, even without considering the SOC. SOC plays a vital role in creating a gap at the crossing points originating from the BI; for example, at 6% strain, the SOC yields a gap on the order of 121 meV, which approaches room temperature. These properties offer interesting alternatives for engineering devices for spintronics, ultra-low-dissipation electronics and quantum information processing.
2. Calculation methods
In this study, the first-principles calculations are based on the density functional theory (DFT) in conjunction with projector augmented wave potentials, which is implemented in the Vienna ab initio simulation package [32, 33]. For the exchange–correlation functional, the generalized gradient approximations (GGA) [34] of Perdew–Burke–Ernzerhof [35] are used. Pseudopotentials with 4s24p2 and 5s25p1 valence electron configurations, respectively, for Se and In atoms are used. The experimental lattice parameters of β-InSe: a = b = 4.050 Å, c = 16.930 Å are used for the calculations [36]. Strain is simulated by variating a for a constant cell volume. The isotropic strain is defined as ε = Δa/a, where the lattice constant of the strained unit cell is equal to Δa + a. A unit cell is used for all the calculations; test calculations with a supercell ensure that unit cell calculations are sufficient. The Brillouin zone is represented by a Monkhorst–Pack special k-point mesh [37] of 13 × 13 × 3, both geometry optimizations and the static total energy calculations. The relaxation convergences for ions and electrons are 1 × 10–5 and 1 × 10–6 eV, respectively. A cutoff energy of 450 eV is used for the plane wave expansion of the wave function to converge the relevant quantities. The positions of all the atoms in the supercell are fully relaxed. The electron spin–orbit interaction is introduced with time-reversal inversion SOC calculations [38]. Although the post-DFT calculations [39, 40] may provide relative precise electronic structures, previous theoretical studies [3–5, 11, 16] on TIs have confirmed that the GGA method is valuable to investigate the electronic structures of TIs. In addition, almost all of the previous theoretical studies [3–5, 11, 16] on TIs were based on the GGA method. Thus, for a convenient comparison with previous works, all calculations in this work are also performed using the same method.
3. Results and discussion
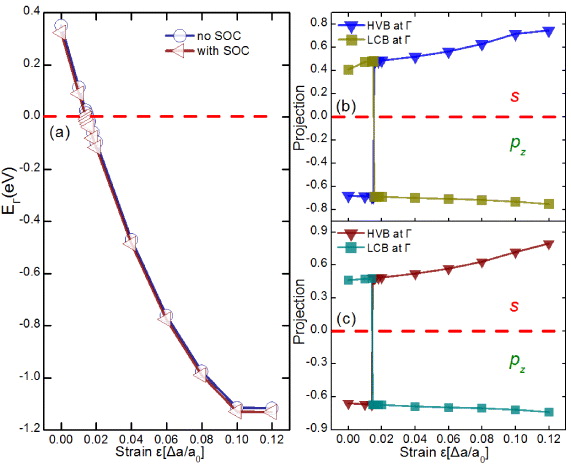
The band structures without and with SOC for β-InSe without strain are plotted in figures 2(a) and (b). They show that β-InSe is a narrowed band gap semiconductor with a direct band gap at the Γ point without SOC. The conduction band minimum (CBM) at the Γ point is dominated by Se s, Se pz and In s states; the valence band maximum (VBM) at the Γ point mainly consists of Se pz states. By introducing SOC, the band structure of β-InSe displays a very small change; no BI characterizations of the CBM and VBM were observed. Note that there are two ways to change the band order [11, 41]: (i) if the SOC strength is increased, the necessary BI could occur; (ii) besides varying the SOC strength, which is an intrinsic property of the material and is hard to modulate, the band order can also be changed by varying the coupling potentials. Increasing the strain can lead to a decrease of the coupling potentials, which could reduce the energy difference, Ek = Ecb − Evb, between the conduction band, Ecb, and the valence band, Evb, at the TRIM points. At a sufficiently large mechanical deformation, even materials with relatively weaker SOC could display BI. In what follows, we apply strain ranging from 0 to 12% to examine the effect of strain on the band properties of β-InSe. The corresponding band energy difference EΓ (Ek calculated at the Γ ∈ TRIM points), is illustrated in figure 3(a). It is seen that with increasing strain, the CBM lowers in energy, thus resulting in a significant decrease of the energy gap EΓ. Remarkably, in passing from a critical strain of 1.4%, EΓ is rapidly quenched to zero and then is incremental with negative values; two bands with Γ3+ and Γ4− symmetries around the Fermi level are inverted, which thus indicates BI characterizations. The three-dimensional band structure of β-InSe under this critical strain point is shown in figure 1(d). From this figure, we can clearly see that the BI characterization appears at the Γ point yielded by the lowering of the lowest unoccupied band at the Γ point. The argument can be confirmed by the direct calculation of the protections of the lowest-conduction band (LCB) and the highest-valence band (HVB) of β-InSe at the Γ point versus the strain variation. The corresponding results are plotted in figure 3(c). Knowing that the positive and negative values correspond to s and pz states, respectively, one can rapidly find that, below the critical strain of 1.4%, the main projections of the LCB and the HVB of β-InSe at the Γ point are predominated by the s and pz orbitals, respectively. When the strain passes from the critical point, the main projections of the LCB and the HVB of β-InSe at the Γ point are a contribution from the pz and s orbitals, respectively, meaning that BI at the Γ point takes place upon the critical strain point. Taking β-InSe with ε = 6% as an example, as shown in figure 2(d), an insulating phase with a band gap of 121 meV is established. Further calculations reveal that it is indeed a fully gapped insulator. Thus it can be concluded that the β-InSe could transform from an ordinary semiconductor to a TI by engineering strain. Furthermore, the gap magnitude is significantly larger than kBT (about 26 meV) at room temperature, suggesting that the TI character could be supported at room temperature. This gap with SOC is very close to the newly discovered actinide TIs [42].
Figure 2. Band structures of β-InSe, with the upper row corresponding to unstrained β-InSe (a) without SOC and (b) with SOC; the lower row corresponds to band-inverted β-InSe (ε = 6%) (c) without SOC and (d) with SOC. The horizontal dashed red lines indicate the Fermi level. The inset in (d) is a magnified view near the Fermi level.
Download figure:
Standard image High-resolution imageFigure 3. (a) The energy gap EΓ with and without SOC under different strain conditions. (b) The main projection of the LCB and the HVB at Γ point without SOC under different strain conditions. (c) The main projection of the LCB and the HVB at Γ point with SOC under different strain conditions. The positive and negative values in (b) and (c) correspond to s and pz states, respectively.
Download figure:
Standard image High-resolution imageIt is known that the most general and direct approach to understand a TI with inversion symmetry is to analyze the Z2 topological invariants ν0;(ν1ν2ν3). One can interpret non-zero topological invariants as an obstruction to make the wave functions smoothly defined over half of the entire Brillouin zone under a certain gauge of the time-reversal constraint. According to the Z2 classification, Z2 = 0 means a trivial band topology while Z2 = 1 characterizes a non-trivial band topology. Since all the investigated configurations possess inversion symmetry, a parity analysis can be used to identify the Z2 topological invariants ν0;(ν1ν2ν3). As shown in figure 1(c), there are eight time-invariant points in the Brillouin zone, but only four points (Γ, Z, M and L) are inequivalent. Here, following the method proposed by Fu and Kane [7], we calculate the product of the parities of the Bloch wavefunction for the filled bands at all TRIM points in the Brillouin zone. As figure 1(c) illustrates, eight TRIM points are labeled as Γ, Z, M1,2,3 and L1,2,3. The product of parity eigenvalues of the valence band at TRIM point, δi, is −1 if an odd number of BIs occur at the corresponding TRIM point; while δi is +1 if an even number of BIs occur at the corresponding TRIM point. From our calculation, we find that at the Γ point, the parity of one occupied band changes after BI induced by strain, whereas the parity remains unchanged for all occupied bands at the other momenta Z, M1,2,3 and L1,2,3. Therefore, the strained β-InSe with BI has δΓ = −1 and δZ = δ1,2,3 = δ1,2,3 = + 1 . Whereas, for unstrained β-InSe, the parity remains unchanged for occupied bands at the all momenta Γ, Z, M1,2,3 and L1,2,3. Consequently, the unstrained β-InSe without BI has δΓ = δZ = δ1,2,3 = δ1,2,3 = + 1 . The topological indexes ν0, ν1, ν2 and ν3 of Z2 ν0;(ν1ν2ν3) are established by
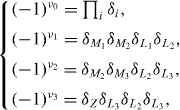
In other words, ν0 corresponds to all eight TRIM points, while ν1, ν2 and ν3 correspond to four TRIM points belonging to the parallelepiped constructed by these eight TRIM points. Before BI, the calculated Z2 topological invariants ν0;(ν1ν2ν3) are 0;(000), indicating a topologically trivial feature. After BI, the calculated Z2 topological invariants ν0;(ν1ν2ν3) are 1;(000), which confirms the topological non-trivial state.
From previous studies [11, 12], the likelihood of incorporating BI in materials is determined by their SOC strength, it follows that it is more probable to find the TIs among heavier compounds (with stronger SOC). Alternatively, they have proven that if the system is not a TI under equilibrium conditions, it can be made so by applying appropriate strain. Yet, they have also demonstrated that BI in materials would not occur even with sufficient mechanical deformation if it were not for the protection received from the SOC. It is quite a paradox that this holds for all the TIs. Now a question arises: since the driving force for the BI is taken for granted to be SOC according to the existing literature, what is the role related to strain in this procedure? To answer this question, we investigate the evolution of the energy level near the Fermi level at Γ point without SOC as a function of strains for β-InSe; the corresponding results are presented in figure 3(a). It is seen that with the increasing strain, the energy difference EΓ decreases and finally becomes zero at ε = 1.5%. Most excitingly, by further increasing the strains, two bands with Γ3+ and Γ4− symmetries around the Fermi level are inverted. Then the value of EΓ is incremental with the increasing strain, indicating that strain will result in the anti-crossing band behavior (as addressed in figure 2(c)), which changes the sign of the parity at Γ point at a strain higher than ε = 1.5%. It is also noted from figure 3(b), at below critical strain ε = 1.5%, that the main projections of the LCB and the HVB of β-InSe at the Γ point are occupied by the s and pz orbitals, respectively; vice versa, at above critical strain ε = 1.5%, those are the contribution from the pz and s orbitals, respectively. Herein, in contrast to previous studies, BI characterization at the Γ point could be realized by mechanical deformation solely, even without SOC. With the advancement in experimental techniques, we expect that the corresponding experiments will soon be carried out. The experimental data available can then be compared with our interesting theoretical prediction.
Now, since the strain is known to support BI characterization in β-InSe, to explore the role of SOC we focus here on the contrast between the results with and without SOC. As figure 3(a) displays, the difference between the values of energy gap EΓ with and without SOC under different strain conditions are less than 23 and 16 meV for β-InSe at below and above the strain ε = 4%, respectively. By comparing with the absolute value of the energy gap EΓ, these values of the differences are negligible. These results are in good agreement with those addressed in figures 3(b) and (c). Figures 3(b) and (c) display that the critical BI points without and with SOC are slightly different, except the critical point with SOC is smaller than that without SOC in strain by 0.1%. Quite naturally, it seems that the role of SOC in this proceeding can be ignored. To further uncover the effect of SOC, we additionally compare the bands around the Fermi level with and without SOC. As mentioned above, the changes of band structures by introducing SOC before the BI can be ignored. Here, we focus on introducing SOC after BI and take β-InSe with ε = 6% as an example. In figure 2(c), the band structure of β-InSe with ε = 6% is calculated without SOC. It follows that β-InSe with ε = 6% is semimetal with the band crossing at the Fermi level along the Γ–M and Γ–K directions if SOC is omitted. By breaking it, i.e. inclusion of SOC, the band gap could be opened at the Fermi level at the crossing points, leading to a typical dip in the band structure for β-InSe with ε = 6%. By comparing the two figure parts, one can rapidly obtain that any gap opening at the crossing points must originate from the SOC. It thus can be concluded that although the SOC does not exchange the characteristics of VBM and CBM and the corresponding role of SOC in previous literatures can be replaced by strain, the SOC being there to support gap opening at the crossing points of the inverted bands is indispensable for realizing the topologically non-trivial taste of the β-InSe.
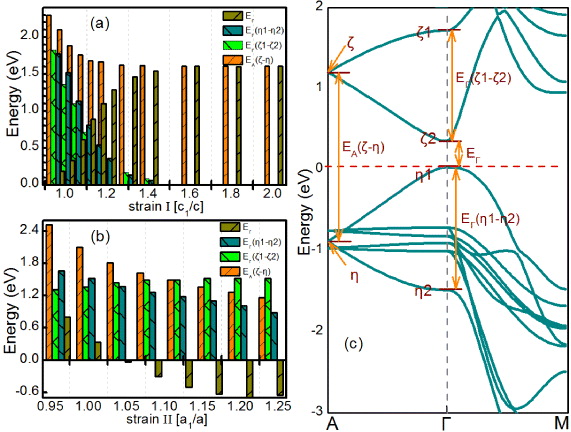
Based on the discussion above, the variation of the BI characterization as a function of strain is the result of a significant change of EΓ induced by mechanical deformation. To understand this result more precisely, let us examine the electronic band structure of β-InSe in detail (figure 4(c)). The direct gap occurs between the bands ζ2 and η1 at Γ point of the Brillouin zone. On the other hand, the maximum of band ζ2 and minimum of band η1 are located at point A and degenerate with ζ1 and η2 into bands ζ and η, respectively; they form a large gap at point A (EA(ζ − η), as denoted in figure 4(c). From the projection analysis, these bands are derived from the s-states and pz-states. In detail, the valence bands η, η1 and η2 are predominantly derived from the Se pz orbitals; while the conduction bands ζ, ζ1 and ζ2 originate from mostly Se s and In s orbitals with weak contribution of the Se pz orbitals. Notice that the bands (ζ1, ζ2) and (η1, η2) are split from the bands ζ and η, respectively, whereas the last two remain degenerate at point A. After this splitting, the energy levels close to Fermi energy turn out to be bands ζ2 and η1. In this case, the energy gap EΓ is related to bands ζ, ζ1, ζ2, η, η1 and η2, i.e. EA(ζ − η), EΓ(ζ1 − ζ2) and EΓ(η1 − η2) (as labeled in figure 4(c)). As figure 4(c) denotes, EA(ζ − η), EΓ(ζ1 − ζ2) and EΓ(η1 − η2) are related to bands (ζ, η), (ζ1, ζ2) and (η1, η2) respectively; combined with the projection analysis, the formation of EA(ζ − η), EΓ(ζ1 − ζ2) and EΓ(η1 − η2) is determined by the s-pz, s–s and pz–pz interactions, respectively. However, we stress that detecting whether these interactions are intraslab or interslab interactions is challenging. To further uncover the mechanism of this strain induced topological insulting behavior, we consider two types of lattice expansion. In the first case, strain is simulated by the variation of the lattice along the c-axis for constant a and the slab thickness (denoted as strain I, as illustrated in figure 4(a)). For the second case, we consider the biaxial lattice expansion, where the crystal structure is expanded in the ab plane and fixed in the c-axis (denoted as strain II, as illustrated in figure 4(b)). These situations are more about academic interest rather than for practical applications. As figure 4(a) addresses, on application of strain I, EΓ(ζ1 − ζ2) and EΓ(η1 − η2) decrease monotonically and dramatically in energy down to zero. On the other hand, with increasing strain I, the interslab interaction between adjacent slabs (i.e., a weak van der Waals interaction) is substantially quenched due to the remarkable decrease of the distance between the two slabs. Evidently, the EΓ(ζ1 − ζ2) and EΓ(η1 − η2) are determined by the interslab s–s and pz–pz interactions. It is also concluded that the band splitting (ζ–ζ1 and ζ2, η–η1 and η2) arises from the effect of interslab coupling. However, EA(ζ − η) is almost independent of strain. Furthermore, the interslab interaction cannot induce large variations of EΓ and thus the BI could not occur. Thus the change of the interslab interaction can nevertheless induce the topological phase transition. We explicitly confirm these conclusions in the strain II situation, to which we now turn. As figure 4(b) illustrates, the EΓ(ζ1 − ζ2) and EΓ(η1 − η2) are found to be almost unaltered with strain, except for a slight change. That is because, with increasing strain II, the interslab interaction between adjacent slabs is almost insusceptible, while the intraslab interaction is weakened. It is important to note that, different from strain I situation, strain II reduces the values of EA(ζ − η) significantly. In this case, the EA(ζ − η) is related to the intraslab s–pz interactions. Additionally, as displayed in figure 4(b), with increasing strain II, the EΓ is rapidly quenched to zero and then is incremental with negative values, meaning an obvious BI characterization. It is therefore worth highlighting that the BI originates predominately from strain II with a weak contribution of strain I. With this result in hand, one can then establish that the topological insulting nature of β-InSe can be tuned effortlessly by external control parameters, such as the electric field. This can be achieved by growing β-InSe on the top of a piezoelectric substrate, whose lattice can then be changed by applying an electric field.
Figure 4. (a), (b) The energy difference labeled in (c) versus different strain conditions. For (a), strain I is simulated by varying c for constant a and the slab thickness. For (b), strain II is simulated by varying a for constant c. (c) Band structure of β-InSe without SOC. The horizontal dashed red lines indicate the Fermi level.
Download figure:
Standard image High-resolution image4. Conclusion
In conclusion, we have explored the strain tuning of topological band order in β-InSe by DFT calculations. We have predicated that β-InSe is a promising TI candidate for its large energy gap up to 121 meV. These results are confirmed by the direct calculations of the topological Z2 invariants. In particular, unlike previous literature, only strain is capable of stabilizing a robust BI in β-InSe even without considering SOC. However, SOC is indispensable for breaking the incompatibility symmetry of the inverted bands to yield a band gap at the crossing points. Additionally, our detailed calculations have shown that the BI originates predominately from strain II, with a weak contribution of strain I. Our work provides a fascinating guiding principle for tuning the topological order by other controllable external parameters instead of the immutable intrinsic SOC. All of these make β-InSe cornucopias of fundamental interest with promising applications.
Acknowledgment
This work is supported by the National Basic Research Program of China (973 program, 2013CB632401), the National Science foundation of China under grant number 11174180 and the Fund for Doctoral Program of National Education 20120131110066, the Natural Science Foundation of Shandong Province under grant number ZR2011AM009 and the Ministry of Education Academic Award for Postgraduates. We also thank the National Supercomputer Center in Jinan for providing high performance computation.