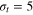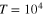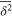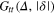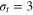Abstract
Based on extensive Brownian dynamics simulations we study the thermal motion of a tracer bead in a cross-linked, flexible gel in the limit when the tracer particle size is comparable to or even larger than the equilibrium mesh size of the gel. The analysis of long individual trajectories of the tracer demonstrates the existence of pronounced transient anomalous diffusion. From the time averaged mean squared displacement and the time averaged van Hove correlation functions we elucidate the many-body origin of the non-Brownian tracer bead dynamics. Our results shed new light onto the ongoing debate over the physical origin of steric tracer interactions with structured environments.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Modern single particle tracking technology [1] unveils the non-Brownian stochastic motion of submicron tracers or fluorescently labelled macromolecules in a variety of complex liquids. Anomalous diffusion of the form 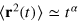 with
with 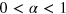 [2] was observed in the cytoplasm and membrane [3–5] of living biological cells, as well as in dense polymer or protein solutions [6]. Causes for the observed subdiffusion may be the crowded state of the environment [7] or sticking effects between the tracer and the environment [8]. Another important origin for anomalous diffusion is the subtle interaction between the tracer particle and the dynamic confines of a structured, gel-like environment with a well defined mesh size [9].
[2] was observed in the cytoplasm and membrane [3–5] of living biological cells, as well as in dense polymer or protein solutions [6]. Causes for the observed subdiffusion may be the crowded state of the environment [7] or sticking effects between the tracer and the environment [8]. Another important origin for anomalous diffusion is the subtle interaction between the tracer particle and the dynamic confines of a structured, gel-like environment with a well defined mesh size [9].
Mesh-like, structured environments are a defining property in various systems: biological cells are equipped with a characteristic mechanical network consisting of actin and other bio-filaments through which submicron particles diffuse or are actively transported [10]. Inside eukaryotic nuclei, biomolecules diffuse through the complex chromatin network [11]. Particles in a biofilm move through a flexible, porous bacterial matrix [12], and in cellular tissues the intercellular space is filled with a mesh-like extracellular matrix [13]. In novel clinical diagnosis tools pathogens diffuse in a hydrogel [14].
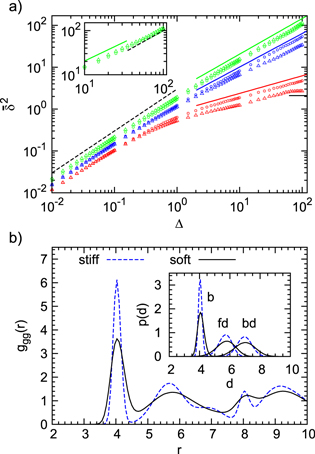
How do particles diffuse through a flexible, fluctuating mesh such as a hydrogel? When the particles are much smaller or larger than the typical mesh size, they diffuse normally or are fully immobilized [9]. We here consider the physically interesting case when the size of the particle is comparable to the typical mesh size (figure 1). From extensive Brownian dynamics simulations we elucidate the micro- and mesoscopic principles behind the complex tracer dynamics. The time averaged mean squared displacement (TAMSD) and the van Hove cross-correlation function (TAHCF) demonstrate the occurrence of significant tracer subdiffusion (figure 2(a)) and cooperative mesh fluctuations, allowing relatively large particles to move in the gel albeit at massively reduced diffusivity.
Figure 1. Schematic of the tracer particle (red) in a network of gel beads (green) connected by Morse springs (gray sticks). For the parameters used in this study, the tracer bead size σt
is comparable to the mesh size of the gel, spanning the diameters 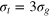 (equalling the equilibrium distance in between the surfaces of the two gel beads of diameter σg
along one of the nearest-neighbour bonds),
(equalling the equilibrium distance in between the surfaces of the two gel beads of diameter σg
along one of the nearest-neighbour bonds), 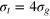 (just short of the face diagonal of a unit cell of the gel subtracted by σg
,
(just short of the face diagonal of a unit cell of the gel subtracted by σg
, 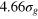 ), and
), and 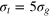 (short of the body diagonal subtracted by σg
,
(short of the body diagonal subtracted by σg
, 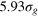 ). In all cases, our analysis shows that the tracer beads of all sizes achieve diffusion through the elastic gel.
). In all cases, our analysis shows that the tracer beads of all sizes achieve diffusion through the elastic gel.
Download figure:
Standard image High-resolution imageFigure 2. (a) TAMSD for tracers of diameter 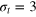 , 4, 5 (top to bottom) versus lag time Δ, and
, 4, 5 (top to bottom) versus lag time Δ, and  (circles) and
(circles) and 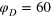 (triangles). Intermediate-asymptotics
(triangles). Intermediate-asymptotics  (full lines) shown for
(full lines) shown for 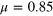 , 0.8, and 0.4, for increasing tracer size. Dashed and full black lines denote a linear scaling and a plateau. Each curve is a time average over
, 0.8, and 0.4, for increasing tracer size. Dashed and full black lines denote a linear scaling and a plateau. Each curve is a time average over 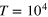 and additional average over 10 independent realizations. Inset: magnification of the last decade of Δ in the case of
and additional average over 10 independent realizations. Inset: magnification of the last decade of Δ in the case of  . The transition from the subdiffusive
. The transition from the subdiffusive 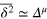 (greenline) to diffusive
(greenline) to diffusive  (dashed black line) regime is nicely visible. (b) Gel correlation ggg
(r) for
(dashed black line) regime is nicely visible. (b) Gel correlation ggg
(r) for  (blue dashed) and
(blue dashed) and 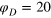 (full black). Inset: distribution of bond length (b), face diagonal (fd), and body diagonal (bd) for both stiffnesses.
(full black). Inset: distribution of bond length (b), face diagonal (fd), and body diagonal (bd) for both stiffnesses.
Download figure:
Standard image High-resolution imageThe tracer motion in a flexible mesh can be viewed as a convolution of the Brownian self-dynamics of the tracer and the thermal agitation of the interacting gel particles. Important ingredients characteristic for the tracer-gel system are the steric obstruction of the tracer by the mesh [15], tracer-gel interactions [16], and the elastic response of the network itself [17]. In an effective continuum view, these features translate into the local viscoelasticity [18], which is probed in microrheology experiments [19]. In this picture, memory effects in the dynamics cause an anomalous frequency dependence of the generalized friction coefficient and hence, expressed in terms of the generalized Langevin equation, an anomalous diffusion of the tracer. Remarkably, distinct anomalous tracer diffusion was found in numerous experiments [9, 16, 20–22] and simulations [23]. To explain this non-Brownian dynamics in the gel two scenarios are typically invoked: (i) trapping of the tracer due to attractive tracer-gel interactions, that effect transient binding to the gel network [16, 20, 24, 25], such that the tracer intermittently follows the gelʼs Rouse dynamics [20] or remains transiently immobilized [24]. (ii) Sterical hindrance within a fractal organization of the accessible volume [9, 16, 21–23, 26]. In these approaches the gel is represented by impenetrable beads (static [23] or dynamic [26]) on a lattice. In static networks simulations showed that isolated, randomly positioned beads effect non-transient subdiffusion, whereas tracer diffusion in the presence of local bead clusters in the form of randomly distributed, condensed cubes is only transiently anomalous [23]. The debate on the dominant mechanism in real gels remains open [16]. Notably, both of the above mechanisms are only explained on a heuristic level and a better physical understanding is needed.
2. Model
While lattice representations of gels are a computationally efficient approach for the modelling of tracer diffusion [23, 26], they suffer from the severe localization of the gel despite its exposure to a thermostat. Moreover, static gels introduce spurious artifacts in the tracer dynamics, as quenched configurational disorder of obstacles introduces a persistent memory in the motion of a Brownian particle at all obstacle densities [27]. As shown here, the tracer motion is inherently related to collective soft modes of local expansion and contraction of the thermalized mesh. Such modes cannot be appropriately captured in lattice models, calling for more realistic models with fully coupled, many-body tracer-gel dynamics.
We consider a gel of  connected beads with a simple cubic unit cell and a freely diffusing tracer bead (figure 1). Tracer and gel beads are impenetrable via the repulsive part of the Lennard-Jones potential. Nearest neighbour gel beads are connected via Morse springs. The size a of the unit cell, the equilibrium centre-to-centre distance between nearest neighbours beads, is 4 times the gel bead diameter σg
, and the gel density is
connected beads with a simple cubic unit cell and a freely diffusing tracer bead (figure 1). Tracer and gel beads are impenetrable via the repulsive part of the Lennard-Jones potential. Nearest neighbour gel beads are connected via Morse springs. The size a of the unit cell, the equilibrium centre-to-centre distance between nearest neighbours beads, is 4 times the gel bead diameter σg
, and the gel density is  . We use three tracer bead diameters,
. We use three tracer bead diameters, 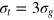 , 4σg
and 5σg
. The average face and body diagonals (fd and bd) of the unit cell are then equal to
, 4σg
and 5σg
. The average face and body diagonals (fd and bd) of the unit cell are then equal to 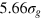 and 6.93σg
. Thus, the smallest tracer comfortably passes through a static mesh, while the middle size is already similar to the value
and 6.93σg
. Thus, the smallest tracer comfortably passes through a static mesh, while the middle size is already similar to the value 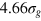 (
(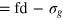 ). The largest bead still fits the unit cell as set by
). The largest bead still fits the unit cell as set by 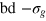 . However, it can no longer pass through the static mesh. We express distances in units of σg
, energy in units of thermal energy
. However, it can no longer pass through the static mesh. We express distances in units of σg
, energy in units of thermal energy  and time in units of
and time in units of 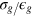 , where
, where  g
is the energy scale of the repulsive LJ potential. The tracers' diffusion coefficient is given by the Stokes–Einstein relation, and the gel stiffness is set by the width
g
is the energy scale of the repulsive LJ potential. The tracers' diffusion coefficient is given by the Stokes–Einstein relation, and the gel stiffness is set by the width 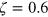 and depth
and depth 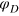 of the Morse potential. We consider two depths resulting after shifting due to the cut-off in the potential minima at
of the Morse potential. We consider two depths resulting after shifting due to the cut-off in the potential minima at 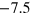 and
and 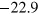
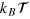 . The two values represent a moderately soft and a rather stiff gel (see figure 2(b)). The dynamics of both tracer and gel beads are governed by overdamped Langevin equations with Gaussian white noise. After extensive equilibration we simulate trajectories of length
. The two values represent a moderately soft and a rather stiff gel (see figure 2(b)). The dynamics of both tracer and gel beads are governed by overdamped Langevin equations with Gaussian white noise. After extensive equilibration we simulate trajectories of length 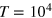 . More details on the model and simulations are found in the appendix.
. More details on the model and simulations are found in the appendix.
3. Analysis of the tracer dynamics
The gel–gel position correlation
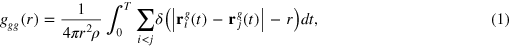
see figure 2(b), confirms the simple cubic structure of the gel: the first three peaks correspond to a, fd and bd, where the latter is not clearly observed in the softer gel due to the more pronounced thermal fluctuations. The length fd is smeared out over the interval 4–7 causing a larger effective gel bead size. Comparing the structural features of the gel in the presence and absence of the tracer we see no appreciable difference, indicating a large effective tracer dilution, that is, the length-scale of deformation is small compared to size of the system.
We use the TAMSD at lag time Δ over a trajectory of length T,
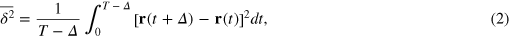
to characterize the tracer dynamics. For a wide parameter range 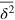 exhibits a distinct transient subdiffusion regime between the initial free diffusion and asymptotic long time diffusion (figure 2(a))5
, in agreement with similar simulations [28]. The stiffness only affects the values of the short and long time diffusivities and the time window of the intermediate-asymptotic subdiffusion regime (circles and triangles of same colour in figure 2(a)).
exhibits a distinct transient subdiffusion regime between the initial free diffusion and asymptotic long time diffusion (figure 2(a))5
, in agreement with similar simulations [28]. The stiffness only affects the values of the short and long time diffusivities and the time window of the intermediate-asymptotic subdiffusion regime (circles and triangles of same colour in figure 2(a)).
Evidently a pronounced subdiffusive power-law regime  emerges for
emerges for  , and the anomalous diffusion exponent μ delicately depends on the tracer size but, remarkably, is almost independent of the gel stiffness, except for a terminal scaling for the largest tracer which completely localizes within the unit cell. Intuitively, a smaller tracer, which comfortably passes through a unit cell surface in a static gel, diffuses faster in a stiffer gel due to the smaller effective size (smaller fluctuations around the equilibrium position) of the gel beads. Clearly, as the tracer diameter reaches 4 the situation is reversed: now the effective size of the gel beads prevents an unobstructed passage of the tracer and larger gel fluctuations allow passage events. We stress that
, and the anomalous diffusion exponent μ delicately depends on the tracer size but, remarkably, is almost independent of the gel stiffness, except for a terminal scaling for the largest tracer which completely localizes within the unit cell. Intuitively, a smaller tracer, which comfortably passes through a unit cell surface in a static gel, diffuses faster in a stiffer gel due to the smaller effective size (smaller fluctuations around the equilibrium position) of the gel beads. Clearly, as the tracer diameter reaches 4 the situation is reversed: now the effective size of the gel beads prevents an unobstructed passage of the tracer and larger gel fluctuations allow passage events. We stress that 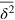 is a weighted average of squared relative displacements along the trajectory. Hence,
is a weighted average of squared relative displacements along the trajectory. Hence, 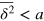 does not necessarily mean that the tracer remains localized within the same unit cell.
does not necessarily mean that the tracer remains localized within the same unit cell.
To gain a deeper understanding we study the TAHCF
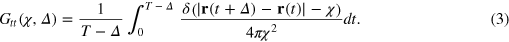
where 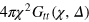 is the probability density to find the tracer at time
is the probability density to find the tracer at time 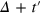 at a distance between χ and
at a distance between χ and 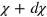 from its position at time
from its position at time 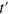 , averaged over all instantaneous positions along the trajectory. The usual ensemble van Hove self correlation function (HCF) measures position correlations at time t with the initial position at time t = 0 over an ensemble of independent realizations. The TAHCF measures correlations between positions at different times along the same trajectory (similar to the difference between the MSD and the TAMSD)6
. A broad or multimodal HCF denotes an inherently heterogeneous tracer population, while the same features in the TAHCF reveal temporally heterogeneous dynamics. The TAHCF can be thought of as a distributional analysis of single particle traces.
, averaged over all instantaneous positions along the trajectory. The usual ensemble van Hove self correlation function (HCF) measures position correlations at time t with the initial position at time t = 0 over an ensemble of independent realizations. The TAHCF measures correlations between positions at different times along the same trajectory (similar to the difference between the MSD and the TAMSD)6
. A broad or multimodal HCF denotes an inherently heterogeneous tracer population, while the same features in the TAHCF reveal temporally heterogeneous dynamics. The TAHCF can be thought of as a distributional analysis of single particle traces.
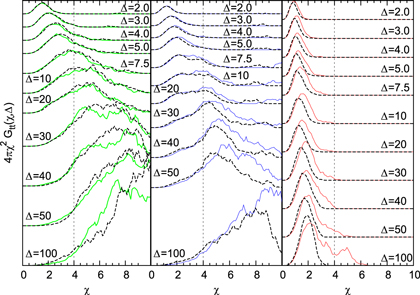
Figure 3 shows the results of  . Strikingly, for
. Strikingly, for 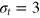 and 4 already at time lags
and 4 already at time lags 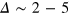 , where the relative displacement along the trajectory is mostly
, where the relative displacement along the trajectory is mostly 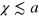 , we find that the tracer is occasionally displaced over several a and hence visits several new cells. Thus, while it spends most of the time fluctuating within the confines of a cell it occasionally ventures into new cells. The stiffness of the gel does not affect the qualitative dynamics beyond the fact that transport is more efficient in stiffer gels if the tracer is small enough and vice versa for larger tracer size. The largest tracer, which can only escape a cell at an extreme gel fluctuation, occasionally visits other cells at a much later point
, we find that the tracer is occasionally displaced over several a and hence visits several new cells. Thus, while it spends most of the time fluctuating within the confines of a cell it occasionally ventures into new cells. The stiffness of the gel does not affect the qualitative dynamics beyond the fact that transport is more efficient in stiffer gels if the tracer is small enough and vice versa for larger tracer size. The largest tracer, which can only escape a cell at an extreme gel fluctuation, occasionally visits other cells at a much later point 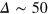 and only for the softer gel. The stiffer gel does not allow sufficiently large fluctuations on the observed time scale and the tracer remains localised in the same cell, fluctuating around its mean position (figure 3 right panel). Possibly, an escape may occur at longer time scales. How can we reconcile the intermediate anomalous scaling for all tracer sizes with the different statistics of relative displacements?
and only for the softer gel. The stiffer gel does not allow sufficiently large fluctuations on the observed time scale and the tracer remains localised in the same cell, fluctuating around its mean position (figure 3 right panel). Possibly, an escape may occur at longer time scales. How can we reconcile the intermediate anomalous scaling for all tracer sizes with the different statistics of relative displacements?
Figure 3.
 for tracer sizes
for tracer sizes 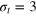 (left),
(left), 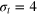 (middle),
(middle),  (right). Black dashed lines represent the stiffer gel. Each curve is a time average over
(right). Black dashed lines represent the stiffer gel. Each curve is a time average over  with additional average over 10 independent realizations.
with additional average over 10 independent realizations.
Download figure:
Standard image High-resolution image4. Collective gel-tracer dynamics
The escape from a mesh cell is slow on time scales of the anomalous diffusion regime, effecting a local violation of the central limit theorem in this regime. What is the microscopic mechanism? Are the tracerʼs cell-to-cell passages simply governed by an averaged obstruction effect and thus decoupled from the gel dynamics, or by many-body tracer-gel interactions? We address this question via the tracer-gel TAHCF
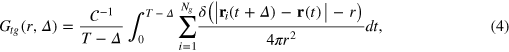
where the sum i includes all gel beads of coordinate 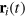 and
and 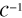 normalizes the probability density to observe a gel bead infinitely far away from the initial tracer position to unity at any lag time, i.e. it corresponds to the ratio of the uncorrected correlator and the number density ρ of beads.
normalizes the probability density to observe a gel bead infinitely far away from the initial tracer position to unity at any lag time, i.e. it corresponds to the ratio of the uncorrected correlator and the number density ρ of beads. 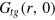 is the static gel-tracer pair correlation function. Equation (4) effectively measures the memory loss of the environment of the instantaneous tracer location and thus reflects the dynamic correlations of the gel beads and the tracer. As
is the static gel-tracer pair correlation function. Equation (4) effectively measures the memory loss of the environment of the instantaneous tracer location and thus reflects the dynamic correlations of the gel beads and the tracer. As 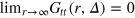 while
while 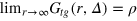 , we omit the prefactor
, we omit the prefactor  to more clearly observe the relative motions of the gel beads. As for the self-part, the meaning of
to more clearly observe the relative motions of the gel beads. As for the self-part, the meaning of 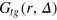 differs from the ensemble picture. The present weighted average along the tracer trajectory integrates out all effects of the tracer motion such that
differs from the ensemble picture. The present weighted average along the tracer trajectory integrates out all effects of the tracer motion such that 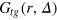 truly measures relative motions of gel beads. We expect that the instantaneous tracer position is dominated by statistically likely configurations and 'transition states' (locations within a cell face) have a smaller statistical weight. Gel beads should thus be found at characteristic distances from the tracer.
truly measures relative motions of gel beads. We expect that the instantaneous tracer position is dominated by statistically likely configurations and 'transition states' (locations within a cell face) have a smaller statistical weight. Gel beads should thus be found at characteristic distances from the tracer.
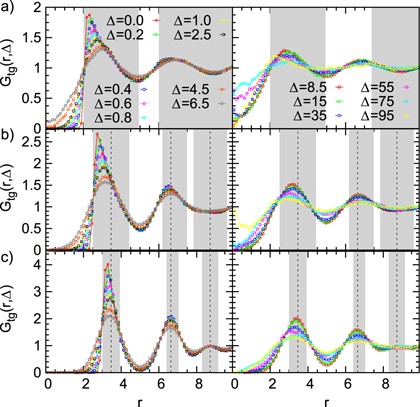
Figure 4 shows results for 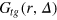 for different tracer sizes. The first peak corresponding to nearest gel beads shows a high initial correlation due to frequent collisions. Entropic effects smear out the peaks around their mean (we typically expect to find gel beads in the shaded areas if the tracer is moved along the bd up to contact with a bead). Since the gel structure on average is well defined the tracer mostly moves along 'paths of free volume' while constantly colliding with gel beads, resembling hopping transport [29]. According to figure 4, for
for different tracer sizes. The first peak corresponding to nearest gel beads shows a high initial correlation due to frequent collisions. Entropic effects smear out the peaks around their mean (we typically expect to find gel beads in the shaded areas if the tracer is moved along the bd up to contact with a bead). Since the gel structure on average is well defined the tracer mostly moves along 'paths of free volume' while constantly colliding with gel beads, resembling hopping transport [29]. According to figure 4, for 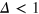 gel beads diffuse rather freely, effecting the broadening of the main peak, which also becomes more symmetric. Similar trends hold for the second peak corresponding to next-nearest neighbours. On time scales
gel beads diffuse rather freely, effecting the broadening of the main peak, which also becomes more symmetric. Similar trends hold for the second peak corresponding to next-nearest neighbours. On time scales 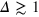 , for small and intermediate tracer sizes some of the nearest gel beads exhibit excursions towards
, for small and intermediate tracer sizes some of the nearest gel beads exhibit excursions towards  made possible by exceeding tracer fluctuations within a cell. Concurrently, below
made possible by exceeding tracer fluctuations within a cell. Concurrently, below 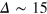 , the peak positions of the nearest and next-nearest neighbours drift towards a larger r, indicating cooperative tracer-cage fluctuations. At these time scales the inter-peak distance remains constant, suggesting that bond lengths are maintained near their equilibrium values and cage fluctuations are in fact mediated by collective displacements. Strikingly, on time scales
, the peak positions of the nearest and next-nearest neighbours drift towards a larger r, indicating cooperative tracer-cage fluctuations. At these time scales the inter-peak distance remains constant, suggesting that bond lengths are maintained near their equilibrium values and cage fluctuations are in fact mediated by collective displacements. Strikingly, on time scales  (and up to 75 for
(and up to 75 for 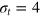 ) both peaks simultaneously move towards smaller r while the value at
) both peaks simultaneously move towards smaller r while the value at 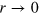 simultaneously increases, indicating cell compression. At even longer Δ, the first and second peak move towards smaller and larger r, indicating that the tracer particle escaped the cell7
. We stress that
simultaneously increases, indicating cell compression. At even longer Δ, the first and second peak move towards smaller and larger r, indicating that the tracer particle escaped the cell7
. We stress that 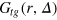 is a weighted average over escape and blocking events, such that it is natural to expect that the result will contain a progressively smaller contribution of escaped configurations as the tracer size grows. This is exactly what is observed here. Moreover, as the tracer size grows the magnitude of fluctuations decreases, indicating that the tracer locally stiffens the network8
. The same qualitative features are also observed for the stiffer gel with the sole exception that for the largest tracer the position of the second peak does not move at all while the position of the first peak still oscillates at long times. This suggests localized fluctuations within the same cell, in agreement with the results for
is a weighted average over escape and blocking events, such that it is natural to expect that the result will contain a progressively smaller contribution of escaped configurations as the tracer size grows. This is exactly what is observed here. Moreover, as the tracer size grows the magnitude of fluctuations decreases, indicating that the tracer locally stiffens the network8
. The same qualitative features are also observed for the stiffer gel with the sole exception that for the largest tracer the position of the second peak does not move at all while the position of the first peak still oscillates at long times. This suggests localized fluctuations within the same cell, in agreement with the results for 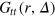 . As shown in figure 5, due to the higher gel stiffness the peaks are more pronounced, as expected. A distinct feature is indeed the strong localization of the largest tracer due to the fact that the gel stiffness is too large to allow sufficient cage-opening fluctuations needed for a particle to escape a cell on the investigated time scale.
. As shown in figure 5, due to the higher gel stiffness the peaks are more pronounced, as expected. A distinct feature is indeed the strong localization of the largest tracer due to the fact that the gel stiffness is too large to allow sufficient cage-opening fluctuations needed for a particle to escape a cell on the investigated time scale.
Figure 4. TAHCF for different tracer sizes and lag times, for 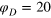 and (a)
and (a) 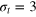 , (b)
, (b) 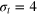 , and (c)
, and (c) 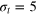 . For clarity the plots are divided into two panels for different Δ. Dashed lines denote the positions of vertices for a static gel if the tracer sits in the centre of a cell. In the shaded areas we would find the vertices if the tracer is displaced diagonally up to the point of contact with a gel bead. Corresponding results for
. For clarity the plots are divided into two panels for different Δ. Dashed lines denote the positions of vertices for a static gel if the tracer sits in the centre of a cell. In the shaded areas we would find the vertices if the tracer is displaced diagonally up to the point of contact with a gel bead. Corresponding results for 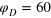 are shown in figure 5. Each curve represents a time average over
are shown in figure 5. Each curve represents a time average over  and 10 independent realizations.
and 10 independent realizations.
Download figure:
Standard image High-resolution imageFigure 5. TAHCF for different tracer sizes at various lag times for 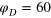 : (a)
: (a)  , (b)
, (b)  , and (c)
, and (c)  . For visual convenience the curves were divided in two panels according to Δ. The dashed lines denote the positions of vertices for a static gel if the tracer sits in the centre of a cell. We would find the vertices in the shaded areas if the tracer is displaced diagonally up to the point of contact with a gel bead. Note the different scales of TAHCF.
. For visual convenience the curves were divided in two panels according to Δ. The dashed lines denote the positions of vertices for a static gel if the tracer sits in the centre of a cell. We would find the vertices in the shaded areas if the tracer is displaced diagonally up to the point of contact with a gel bead. Note the different scales of TAHCF.
Download figure:
Standard image High-resolution image5. Discussion
To rationalize these observations, we note that the gel-bond fluctuations are much faster than the cell-to-cell tracer motion. Hence, it is reasonable to assume that the gel is locally equilibrated corresponding to a free energy minimum, i.e. gel beads are on average at equilibrium bond-distance concurrent with extensive mutual fluctuations of nearby bead pairs9 . In such a case larger local rearrangements in the gel necessarily have to be collective, otherwise they would be thermodynamically penalised. However, such collective fluctuation events demand many-body correlations and thus come at an entropic cost and are thereby statistically less probable. Hence, correlated fluctuations of gel bead positions on the many-body level may effect the slow cage-opening dynamics and thereby the transient subdiffusion of tracers with size comparable to the mesh size.
These results enable us to draw a full physical picture for the emergence of transient anomalous diffusion in flexible gels. For tracer sizes comparable to the gel mesh the probability of collision with the gel is very high. The rate-determining step is the cell-to-cell passage of a tracer, demanding cage opening fluctuations, which were shown to be collective. Open cage states are thus entropic bottlenecks and cause slow tracer motion on intermediate time scales and violation of the central limit theorem. A finite characteristic escape time 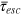 , albeit large, restores normal diffusion at long time scales with an effective diffusion coefficient
, albeit large, restores normal diffusion at long time scales with an effective diffusion coefficient 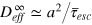 . Tracers considerably larger then the mesh size are expected to be completely localized in a cell, as seen in experiment [9]. At this point, a few remarks are in order. First, on a time scale on which correlations of the gel bead positions have all died out, the model gel system behaves as an array of ordered static beads and the gel does not exhibit any features of glassy dynamics. This is not necessarily the case in real gels [32]. Second, even though hydrodynamic interactions are believed to be effectively screened in such a dense system [33], direct solvent effects might nevertheless become important.
. Tracers considerably larger then the mesh size are expected to be completely localized in a cell, as seen in experiment [9]. At this point, a few remarks are in order. First, on a time scale on which correlations of the gel bead positions have all died out, the model gel system behaves as an array of ordered static beads and the gel does not exhibit any features of glassy dynamics. This is not necessarily the case in real gels [32]. Second, even though hydrodynamic interactions are believed to be effectively screened in such a dense system [33], direct solvent effects might nevertheless become important.
To conclude, extensive Brownian dynamics simulations of tracer particles in a flexible, thermally agitated gel in conjunction with a single trajectory analysis of the tracer dynamics and many-body correlations demonstrate that the distinct transient subdiffusion, frequently observed in experiments and simulations, is effected by the collective fluctuations of both the tracer and the vicinal gel beads. On the scale of the typical escape time of the tracer from a unit cell the dynamics of nearby gel beads turns out to be appreciably correlated. We here obtained compelling evidence identifying the physical origin of the anomalous diffusion, namely, collective fluctuations in the entangled tracer-gel dynamics representing an entropic bottleneck and thereby slowing down the tracer dynamics. This physical insight obtained from the time average van Hove correlation functions provides a significantly improved understanding of the elusive problem of tracer-gel interaction in the experimentally important limit when the tracer size is comparable to the typical mesh size. On a continuum level, these findings translate into the viscoelastic properties of the gel and thus establish a link with the insight obtained from microrheology [19]. We are confident that these results will inspire new experimental and theoretical investigations of tracer motion in structured matrices.
Acknowledgements
The authors thank A Cherstvy for stimulating discussions. AG acknowledges funding through an Alexander von Humboldt Fellowship. RM acknowledges funding from the Academy of Finland (FiDiPro scheme). The authors thank the National Institute of Chemistry, Slovenia for access to computing facilities. Financial support from the German Ministry for Education and Research is also acknowledged.
: Appendix
We consider a gel of  connected beads forming a simple cubic lattice with periodic boundary conditions and a freely diffusing tracer bead. The gel beads are allowed to move off-lattice in continuous space. Each gel bead interacts with other gel beads as well as with the tracer with the repulsive part of the shifted Lennard-Jones (LJ) potential
connected beads forming a simple cubic lattice with periodic boundary conditions and a freely diffusing tracer bead. The gel beads are allowed to move off-lattice in continuous space. Each gel bead interacts with other gel beads as well as with the tracer with the repulsive part of the shifted Lennard-Jones (LJ) potential
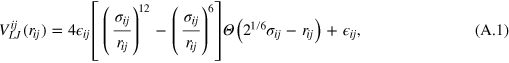
where we use a two-index notation for compactness. In expression (A.1) i and j for a specific pairwise interaction take on the values t for the tracer particle and g for gel beads. 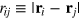 is the physical separation between i and j. Using combining rules,
is the physical separation between i and j. Using combining rules,  are the separations at zero unshifted potential, i.e. σii
is the diameter of species i (σg
or σt
in the notation of the main text).
are the separations at zero unshifted potential, i.e. σii
is the diameter of species i (σg
or σt
in the notation of the main text).  ij (with
ij (with 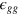 equalling
equalling  g
used in the main text) sets the respective energy scales, and
g
used in the main text) sets the respective energy scales, and 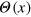 is the step function. Each gel bead is additionally connected with its six nearest neighbours with a Morse potential (figure A.1)
is the step function. Each gel bead is additionally connected with its six nearest neighbours with a Morse potential (figure A.1)
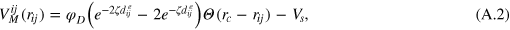
where 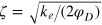 determines the width of the potential.
determines the width of the potential. 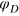 is the potential depth and thus sets the energy scale, ke
is the force constant at the potential minimum, and
is the potential depth and thus sets the energy scale, ke
is the force constant at the potential minimum, and 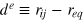 , and req
is the equilibrium separation. rc
is a cutoff distance (taken here as 1.4a) and
, and req
is the equilibrium separation. rc
is a cutoff distance (taken here as 1.4a) and  . In general, ζ controls the width of the potential well. The inclusion of LJ repulsion in Morse-bound neighbours is necessary to prevent potential overlaps caused by rare, but still possible, exceedingly large thermal fluctuations where the Morse potential might not be sufficiently stiff.
. In general, ζ controls the width of the potential well. The inclusion of LJ repulsion in Morse-bound neighbours is necessary to prevent potential overlaps caused by rare, but still possible, exceedingly large thermal fluctuations where the Morse potential might not be sufficiently stiff.
Figure A.1. The two Morse potentials used in the simulations. See text for details.
Download figure:
Standard image High-resolution imageThe particle positions are governed by the overdamped Langevin equations

where Di
is the diffusion coefficient of the tracer or gel beads,  , and
, and

is the force exerted on particle i by particle j, and equals the sum of the negative gradients of the Lennard-Jones potential (A.1) and the Morse potential (A.2), respectively.  is a delta-correlated Gaussian noise with zero mean and component-wise variance
is a delta-correlated Gaussian noise with zero mean and component-wise variance

Since hydrodynamic interactions are screened in dense systems [33] we neglect them in our model. We use dimensionless units and express distances in units of the gel bead diameter σg
, energies in units of β−1 and diffusivities in units of 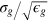 , thus fixing the time unit
, thus fixing the time unit 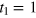 . We take
. We take 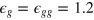 and
and 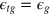 . We choose
. We choose  , which also fixes the gel unit cell size
, which also fixes the gel unit cell size 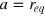 . Finally, we consider various sizes σt
of the tracer particle,
. Finally, we consider various sizes σt
of the tracer particle,  and spring stiffness ke
. While we performed simulations using a wide span of different parameters we here focus on two representative cases and fix
and spring stiffness ke
. While we performed simulations using a wide span of different parameters we here focus on two representative cases and fix 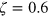 and use
and use 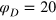 to describe the softer gel, and
to describe the softer gel, and 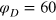 to describe the stiffer gel. The value of
to describe the stiffer gel. The value of  g
is essentially irrelevant as long as it is not too big, because it only affects the softness of the gel-tracer collision. Moreover, after testing for several values we choose
g
is essentially irrelevant as long as it is not too big, because it only affects the softness of the gel-tracer collision. Moreover, after testing for several values we choose 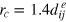 for the cutoff of the Morse potential. A further increase of this cutoff does not affect the results, but naturally makes the simulation slower. The obtained shifted potentials are shown in figure A.1. Such a choice of Morse parameters represents a well structured gel (see figure 2(b)), with roughly 5% of bonds dissociated on average. The resulting effective stiffness of the gels is best seen from the fluctuations of the unit cell parameters (figure 2(b)). These cases in fact suffice to demonstrate the qualitative physical picture of transient subdiffusion.
for the cutoff of the Morse potential. A further increase of this cutoff does not affect the results, but naturally makes the simulation slower. The obtained shifted potentials are shown in figure A.1. Such a choice of Morse parameters represents a well structured gel (see figure 2(b)), with roughly 5% of bonds dissociated on average. The resulting effective stiffness of the gels is best seen from the fluctuations of the unit cell parameters (figure 2(b)). These cases in fact suffice to demonstrate the qualitative physical picture of transient subdiffusion.
The scale of the free tracer diffusivity is set by the Stokes–Einstein relation, 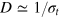 . The Langevin equations are solved with the Euler method with integration step 10−4 under periodic boundary conditions. A small integration step is needed because of the high collision frequency in cases where the tracer is comparable to the mesh size. The initial configuration is chosen randomly to be slightly displaced from the energetically minimal configuration, not allowing significant overlap nor significant bond stretching. After extensive equilibration time of 102, trajectories of length 104 are simulated and analyzed. The overall time to simulate and analyze a single trajectory of length
. The Langevin equations are solved with the Euler method with integration step 10−4 under periodic boundary conditions. A small integration step is needed because of the high collision frequency in cases where the tracer is comparable to the mesh size. The initial configuration is chosen randomly to be slightly displaced from the energetically minimal configuration, not allowing significant overlap nor significant bond stretching. After extensive equilibration time of 102, trajectories of length 104 are simulated and analyzed. The overall time to simulate and analyze a single trajectory of length 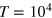 was 5–6 weeks of single-CPU time on a computer cluster, and our study thus reaches the current computational limit.
was 5–6 weeks of single-CPU time on a computer cluster, and our study thus reaches the current computational limit.
Footnotes
- 5
For
 terminal normal diffusion is reached approximately at
terminal normal diffusion is reached approximately at  while in the case of
while in the case of  a clear crossover to linear scaling was not observed after averaging over a trajectory of length
a clear crossover to linear scaling was not observed after averaging over a trajectory of length  . For
. For  the results become progressively noisier due to deteriorating statistics in the time average.
the results become progressively noisier due to deteriorating statistics in the time average. - 6
In fact,
 is the second moment of
is the second moment of  .
. - 7
For
 we even observe a recoil at
we even observe a recoil at  , suggesting that as the particle leaves the cell the originally innermost gel beads are entropically pulled back as they have changed their topological position with respect to the tracer. Moreover, the peaks at
, suggesting that as the particle leaves the cell the originally innermost gel beads are entropically pulled back as they have changed their topological position with respect to the tracer. Moreover, the peaks at  are a consequence of the fact that the spherical volume element diverges.
are a consequence of the fact that the spherical volume element diverges. - 8
This is similar to the effect of fillers in rubber networks [30].
- 9
A similar situation is encountered in hydrogen-bond dynamics in water around a hydrophobic particle; see [31].