Abstract
Within the established theoretical framework of quantum mechanics, interference always occurs between pairs of paths through an interferometer. Higher order interferences with multiple constituents are excluded by Born's rule and can only exist in generalized probabilistic theories. Thus, high-precision experiments searching for such higher order interferences are a powerful method to distinguish between quantum mechanics and more general theories. Here, we perform such a test in an optical multi-path interferometer, which avoids crucial systematic errors, has access to the entire phase space and is more stable than previous experiments. Our results are in accordance with quantum mechanics and rule out the existence of higher order interference terms in optical interferometry to an extent that is more than four orders of magnitude smaller than the expected pairwise interference, refining previous bounds by two orders of magnitude.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
Since arising almost a century ago, quantum mechanics has long become an established paradigm for the description of nature on a submicroscopic scale. It is at the basis of an enormous variety of present and potential future applications [1], such as quantum communication [2, 3], quantum computation [4–6] and protocols like entanglement swapping [7] or teleportation [8]. However, all these applications ultimately rely on interference and entanglement, which can be alternatively explained by theories sharing only some fundamental features with quantum mechanics, such as the superposition principle or probabilistic predictions for outcomes, and yet differing from it in other aspects [9–12]. In order to distinguish between quantum theory and such alternatives, one needs to design dedicated experiments. The situation may be compared with the time before the first Bell test experiments had been performed. Until then, one could explain all quantum mechanical phenomena with a local hidden variable theory. It was required, to first state Bell's theorem [13], and then to perform dedicated experiments with space-like separated laboratories to exclude the alternative. Only last year all experimental loopholes were finally closed [14–17]. Similarly to Bell, Leggett and Garg developed an analogous inequality for correlations among measurements performed on a system at different times [18]. If this inequality is violated, the time evolution of a system cannot be understood classically. Also recently the Leggett-Garg inequality was violated with neutrino oscillations by more than 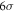 [19]. Another example is the experiment that distinguishes between quaternion and complex (standard) quantum theory [20, 21]. In this work, we focus on an experimental test capable of discerning between quantum mechanics and its generalizations exhibiting higher order interference [22].
[19]. Another example is the experiment that distinguishes between quaternion and complex (standard) quantum theory [20, 21]. In this work, we focus on an experimental test capable of discerning between quantum mechanics and its generalizations exhibiting higher order interference [22].
The probabilistic nature of quantum theory is stated by Born's rule [23], i.e. that the probability density 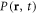 for an observation of a quantum object at a certain time t and a certain position
for an observation of a quantum object at a certain time t and a certain position 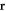 is given by the absolute square of its wavefunction
is given by the absolute square of its wavefunction  :
:
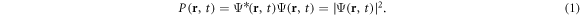
As a consequence of Born's rule and quantum superposition, interference can take place even for single particles [24]. For concreteness, consider an interferometer with multiple non-overlapping paths 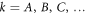 which superpose in some output port to the final wavefunction
which superpose in some output port to the final wavefunction 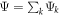 . Equation (1) implies:
. Equation (1) implies:
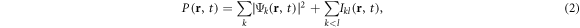
with pairwise (first-order) interference terms 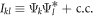 , depending on the relative phase between the two paths k and l. Thus, one obtains interference terms that always originate from pairings of paths, but no higher order interferences involving more than two paths at once.
, depending on the relative phase between the two paths k and l. Thus, one obtains interference terms that always originate from pairings of paths, but no higher order interferences involving more than two paths at once.
In this vein, one can use the presence or absence of higher-order interferences as an experimental probe of the current framework of quantum mechanics. First developed by Sorkin in the context of a measure theory on spacetime [25], one can define a hierarchy of interference terms. In a three-path interferometer with individually blockable paths 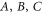 , we define PABC as the probability to find a particle in the output port of the interferometer if all paths are open, PAB for only paths A and B being open, etc. The so-called second-order interference term
, we define PABC as the probability to find a particle in the output port of the interferometer if all paths are open, PAB for only paths A and B being open, etc. The so-called second-order interference term
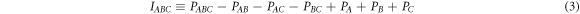
should be zero, independent of the individual phases and amplitudes in each interferometer arm, due to equation (2). Conversely, a significant deviation from 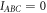 would indicate the existence of higher-order interferences and contradict conventional quantum theory. Note that the definition (3) accounts for deviations from the standard theory in a model-independent way.
would indicate the existence of higher-order interferences and contradict conventional quantum theory. Note that the definition (3) accounts for deviations from the standard theory in a model-independent way.
In any experiment with discrete particles, the probability P will be proportional to the detected particle flux p. Therefore, a directly measurable quantity
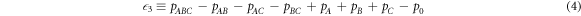
can be defined [26]. In this expression, for example, pAB is the detected particle flux at the output when only paths A and B are open. The background term p0 gives the measured signal when all paths are blocked, accounting for detector dark current/dark counts. For a better comparison of the results with the expected behavior, one can introduce the normalized quantity 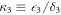 measuring the ratio of hypothetical second-order interference to the sum of the expected first-order interference,
measuring the ratio of hypothetical second-order interference to the sum of the expected first-order interference, 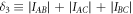 , with
, with 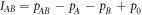 being the first-order interference between A and B. For interferometers with more than three paths, the higher (third, fourth,...)-order interference terms (
being the first-order interference between A and B. For interferometers with more than three paths, the higher (third, fourth,...)-order interference terms (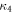 ,
, 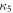 ,...), which of course are also zero in standard quantum theory, can be defined accordingly.
,...), which of course are also zero in standard quantum theory, can be defined accordingly.
Different Sorkin experiments have been realized previously to obtain an upper bound on the modulus of the second-order interference term. These experiments were implemented in optics [27–29] as well as via nuclear magnetic resonance (NMR) in molecules [30], and by using a single spin in diamonds delivering results [31] which were all in accordance with the expectation  . The NMR experiment provided the hitherto tightest constraint with
. The NMR experiment provided the hitherto tightest constraint with 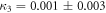 .
.
As is the case for any such null-test experiment, the tightness of the bound and, thereby, the strength of any conclusions to be drawn about the foundations of the theory depend on the measurement uncertainties. In previous optical 3-path interferometers, the precision was mostly limited by the phase stability of the interferometer, while the accuracy suffered from detector nonlinearities [29]. In this work, we present a greatly improved multi-path experiment, namely a stabilized 5-path interferometer, with which we are not only able to tighten the bound on second-order interference by two orders of magnitude, but also measure third and fourth-order interference terms. The 5-path interferometer has the additional advantage of permitting the acquisition of more statistics for the second- and third-order interference term since it consists of ten 3-path interferometers and five 4-path interferometers. It was recently shown that near-field effects in slit-based measurements, where the relevant dimensions are just one or two orders of magnitude larger than the wavelength λ, can lead to so-called non-classical paths associated with apparent higher-order interference and, therefore, bias the experiment [32, 33]. In our interferometer this effect is negligibly small, which eliminates this bias. The systematic error of detector nonlinearities is also taken into account for the first time in this type of experiment by separate detector calibration and full quantum state tomography of the produced 5-dimensional qudit state.
We were able to perform measurements in three different regimes: classical (with coherent laser light), semi-classical (thermal single photons) and quantum (heralded single photons). A measurement in the classical regime is basically a test of Poynting's theorem (energy conservation in the electromagnetic field), whereas a measurement in the quantum regime is a test against higher order interferences. As recently suggested there should exist correspondences between the classical electromagnetic field and the quantum field [34], therefore a violation of Born's rule should directly imply a deviation from Poynting's theorem and vice versa. By performing the measurements in those different regimes and comparing the results it is possible to test these correspondences. If there were deviations from one but not from the other regime, then this would be a strong evidence for yet unknown behavior in the transition between the macroscopic and the quantum world.
The optical 5-path interferometer
A schematic drawing of our setup can be seen in figure 1. For the measurements in the classical regime (C) we used a continuous-wave single frequency laser at 808 nm power-stabilized to 1 mW with relative fluctuations smaller than 0.1% over the complete measurement time of several days by using a liquid crystal noise eater (Thorlabs LCC3112). We used a single photon source to perform measurements in the semi-classical (SC) and quantum regimes (Q). Photon pairs at 808 nm are produced via type-II spontaneous parametric down conversion (SPDC) in a 10 mm long periodically poled potassium titanyl phosphate (ppKTP) crystal, which is pumped by a blue laser (404 nm). The orthogonally polarized photons are separated by a polarizing beam splitter (PBS). We collect  single photons per second in each of the outputs in single mode fibers and we get 105 pairs per second at 4 mW pump power. One of the photons serves as a heralding photon, whereas the other is sent through our multi-path interferometer. Therefore, we have two possibilities to conduct the measurement with single photons: either free running, where all photons transmitted through the interferometer are counted (yielding a thermal photon number distribution) in the semi-classical regime or conditioned, where only photons are counted if there is a heralding photon (producing a sub-Poissonian distribution) [35] in the quantum regime. All light sources were linearly polarized.
single photons per second in each of the outputs in single mode fibers and we get 105 pairs per second at 4 mW pump power. One of the photons serves as a heralding photon, whereas the other is sent through our multi-path interferometer. Therefore, we have two possibilities to conduct the measurement with single photons: either free running, where all photons transmitted through the interferometer are counted (yielding a thermal photon number distribution) in the semi-classical regime or conditioned, where only photons are counted if there is a heralding photon (producing a sub-Poissonian distribution) [35] in the quantum regime. All light sources were linearly polarized.
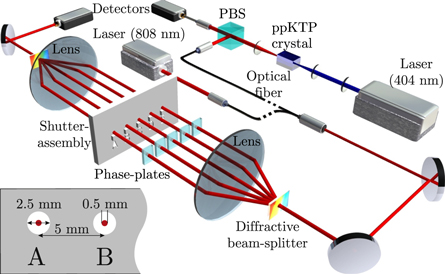
Figure 1. Experimental setup. The light source is either given by a power stabilized laser or single photons (both at 808 nm) produced via SPDC in a ppKTP crystal pumped by a blue laser. The interferometer consists of two diffractive beamsplitters and two lenses. Shutters and phase plates in each of the paths allow independent manipulation. The inset shows the dimensions and separations of the shutters and the 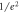 intensity diameters of the beams.
intensity diameters of the beams.
Download figure:
Standard image High-resolution imageThe interferometer is a Mach-Zehnder-type 5-path interferometer consisting of a diffractive beam splitter (a diffractive optical element—Holoeye DE 263—modulating the incident light via a micro-relief surface) which creates five almost equally powerful beams, collimated by a lens (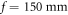 ). A shutter assembly serves to block or unblock each of the five beams individually, phase plates (glass plates with a thickness of 0.15 mm and anti-reflection coated for 808 nm) mounted on motorized rotation stages in all of the five beams allow us to set the phase of each path independently. We are able to achieve an absolute repeatability of 0.005°, which corresponds to
). A shutter assembly serves to block or unblock each of the five beams individually, phase plates (glass plates with a thickness of 0.15 mm and anti-reflection coated for 808 nm) mounted on motorized rotation stages in all of the five beams allow us to set the phase of each path independently. We are able to achieve an absolute repeatability of 0.005°, which corresponds to 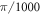 in phase. A second lens (
in phase. A second lens (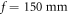 ) overlaps the five beams on a second grating at the end of the interferometer before the resulting beam is sent onto a detector. The interferometer is designed in
) overlaps the five beams on a second grating at the end of the interferometer before the resulting beam is sent onto a detector. The interferometer is designed in 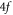 -configuration and the individual beams are separated by 5 mm, therefore the overall dimensions are
-configuration and the individual beams are separated by 5 mm, therefore the overall dimensions are 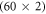 cm2. For detecting single photons we used SPCM-AQRH-12-FC single photon counting modules from Perkin Elmer followed by a quTAU time-to-digital converter from qutools GmbH. This system has a deadtime of
cm2. For detecting single photons we used SPCM-AQRH-12-FC single photon counting modules from Perkin Elmer followed by a quTAU time-to-digital converter from qutools GmbH. This system has a deadtime of 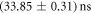 and
and  dark counts per second. The laser radiation is detected by a Physimetron A139-001 photoreceiver based on a Si-photodiode (Hamamatsu S2386-18K) and a 1 MVA−1 transimpedance amplifier, read out by an Agilent 34410A multimeter. This detection system has a low maximum nonlinearity of less than 35 ppm [36]. One measurement set consists of the
dark counts per second. The laser radiation is detected by a Physimetron A139-001 photoreceiver based on a Si-photodiode (Hamamatsu S2386-18K) and a 1 MVA−1 transimpedance amplifier, read out by an Agilent 34410A multimeter. This detection system has a low maximum nonlinearity of less than 35 ppm [36]. One measurement set consists of the 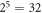 different possible open/closed combinations of the five paths. These 32 combinations were measured in random order to reduce the influence of any memory effects of the detectors and of drifts of the sources. To obtain data with comprehensive statistics we recorded several thousand measurement sets within a total measurement time of several days. The whole interferometer is shielded against air motion and stray light as well as passively and actively temperature stabilized with a PI controller (Wavelength Electronics HTC1500) and heating mats to a root-mean-square fluctuation <0.02 K in 24 h (The temperature was monitored with a PT1000 resistance thermometer). Additionally, the phases are actively stabilized by optimizing the phase-plate position after 100 measurement cycles towards maximally constructive interference of all two-path combinations. This point in phase space was chosen for convenience of alignment and because small phase changes lead only in second order to deviations in output power. This results in good phase stability over the whole measurement time. By comparing the fluctuations and drifts of the single-path power with the multi-path powers (see figures 4 and 5 of the supplementary material [37]), which have the same order of magnitude, we found that phase uncertainty plays a minor role compared to power noise from the light source.
different possible open/closed combinations of the five paths. These 32 combinations were measured in random order to reduce the influence of any memory effects of the detectors and of drifts of the sources. To obtain data with comprehensive statistics we recorded several thousand measurement sets within a total measurement time of several days. The whole interferometer is shielded against air motion and stray light as well as passively and actively temperature stabilized with a PI controller (Wavelength Electronics HTC1500) and heating mats to a root-mean-square fluctuation <0.02 K in 24 h (The temperature was monitored with a PT1000 resistance thermometer). Additionally, the phases are actively stabilized by optimizing the phase-plate position after 100 measurement cycles towards maximally constructive interference of all two-path combinations. This point in phase space was chosen for convenience of alignment and because small phase changes lead only in second order to deviations in output power. This results in good phase stability over the whole measurement time. By comparing the fluctuations and drifts of the single-path power with the multi-path powers (see figures 4 and 5 of the supplementary material [37]), which have the same order of magnitude, we found that phase uncertainty plays a minor role compared to power noise from the light source.
The resulting average powers of the different path combinations can be seen in figure 2 for the measurement with the power stabilized laser [37] (The measured powers over the whole measurement time for laser and single photons can be found in the supplementary material). We filtered the data for extreme outliers (resulting from shutter failure) according to Grubbs' test for outliers (with a significance level of 99%) [38, 39]. After that the largest relative standard deviation of the various classical signals is 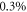 for 5618 measurement sets recorded within 68 h. For the semi-classical (quantum) single photon measurement with 1912 measurement sets the largest standard deviation was measured to be
for 5618 measurement sets recorded within 68 h. For the semi-classical (quantum) single photon measurement with 1912 measurement sets the largest standard deviation was measured to be 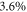 (
(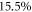 ) over a measurement time of 88 h. These higher values result mainly from shot noise.
) over a measurement time of 88 h. These higher values result mainly from shot noise.
Figure 2. Mean values of the measured powers for the different path-combinations with classical light. Extreme outliers have already been removed.
Download figure:
Standard image High-resolution imageDue to the anti-correlation between the numerator  and the denominator δ in the definition of κ, a bias towards positive values can arise from random fluctuations in the data when calculating κ for every shutter cycle and averaging over the data sets. However, calculating the averages of numerator and denominator in the definition of κ separately,
and the denominator δ in the definition of κ, a bias towards positive values can arise from random fluctuations in the data when calculating κ for every shutter cycle and averaging over the data sets. However, calculating the averages of numerator and denominator in the definition of κ separately,
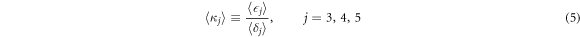
eliminates their correlations and yields an unbiased estimator of the higher-order interference terms. Indeed, one can show that error sources, which typically occur in interference experiments, such as power fluctuations of the photon source, countrate fluctuations of the detectors (Poissonian photon counting uncertainties), detector/electronic noise, coherent phase fluctuations as well as incoherence, have no systematic effect on the measurement outcome [40].
For each of the measured 32-tuples we calculate 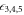 and
and 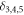 . Examples of histogram plots of the measured ensemble of
. Examples of histogram plots of the measured ensemble of 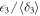 ,
, 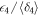 and
and 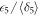 in the three different regimes are shown in figure 3 [48]. After averaging across all possible path combinations one obtains the mean values and associated uncertainties presented in table 1.
in the three different regimes are shown in figure 3 [48]. After averaging across all possible path combinations one obtains the mean values and associated uncertainties presented in table 1.
Figure 3. Histograms of 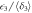 values in the (a) classical, (b) semiclassical and (c) quantum regime for the 3-path subset
values in the (a) classical, (b) semiclassical and (c) quantum regime for the 3-path subset 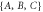 . Histograms of
. Histograms of 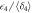 values in the (d) classical, (e) semiclassical and (f) quantum regime for the 4-path subset
values in the (d) classical, (e) semiclassical and (f) quantum regime for the 4-path subset 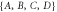 . Histograms of
. Histograms of 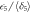 values in the (g) classical, (h) semiclassical and (i) quantum regime in the 5-path interferometer. The blue line is a Gaussian fit to the distribution of the data and the mean value is indicated by the vertical black line, whose width corresponds to the standard error of the mean (one standard deviation).
values in the (g) classical, (h) semiclassical and (i) quantum regime in the 5-path interferometer. The blue line is a Gaussian fit to the distribution of the data and the mean value is indicated by the vertical black line, whose width corresponds to the standard error of the mean (one standard deviation).
Download figure:
Standard image High-resolution imageFigure 4. The density matrix ρ of the 5-dimensional qudit state in our interferometer, with 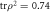 .
.
Download figure:
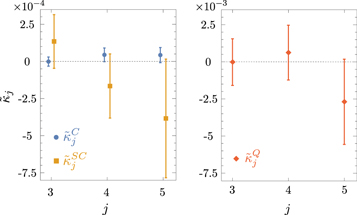
Standard image High-resolution imageFigure 5. Final result.  gives the difference between the experimentally measured
gives the difference between the experimentally measured 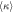 and the value expected from detector nonlinearities
and the value expected from detector nonlinearities 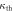 for the measurements in the three regimes. The order of
for the measurements in the three regimes. The order of  increases along the horizontal axis and the error bars indicate one standard deviation.
increases along the horizontal axis and the error bars indicate one standard deviation.
Download figure:
Standard image High-resolution imageTable 1. Mean values of the measured higher-order interferences and their standard errors in the classical, semi-classical and quantum regimes.
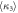
|
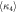
|
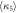
|
|
|---|---|---|---|
classical 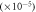
|
9.7 ± 0.1 | 2.7 ± 0.2 | 0.3 ± 0.3 |
semi-classical (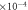 ) ) |
−9.9 ± 1.8 | −5.1 ± 2.1 | −3.8 ± 3.9 |
quantum 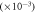
|
−1.1 ± 1.6 | 0.3 ± 1.8 | −2.6 ± 2.9 |
Analysis of systematic errors
Due to the macroscopic separation of the paths and beam width in our interferometer, exceeding λ by 3 to 4 orders of magnitude (see inset in figure 1), the effect of non-classical paths [32, 33] is of negligible influence. Specifically, one can bound the bias to 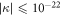 by making the worst case assumption that all light, which is not passing through the apertures is diffracted into any of the other interferometer modes. Instead, the main systematic uncertainty in our experimental configuration arises from the nonlinearity of the detectors. Real detectors usually have a nonlinear response function, which means that the recorded value (voltage, photon counts,...) is not linear in the incident power or photon flux, but biased differently for different optical powers. This biases the value of κ, as we measure light powers varying over more than one order of magnitude. Here, the bias arises mainly due to nonlinearities in the electronics of our photoreceiver and due to deadtime in the single photon detector. To take this error into account it is useful to fully characterize our 5-path interferometer, which can be described as a 5-dimensional qudit state. Therefore, we additionally performed complete quantum state tomography [41, 42]. The density matrix ρ was numerically reconstructed from single- and two-path measurements with defined phases via direct reconstruction. The phases are calibrated via scanning the classical two-path laser interference. We used the direct reconstruction instead of a maximum likelihood estimation to avoid systematic deviations in the state reconstruction, which have recently been shown to arise due to the constraint of physicality in maximum likelihood estimates [43]. The real and imaginary parts of the resulting density matrix are shown in figure 4. We calculated
by making the worst case assumption that all light, which is not passing through the apertures is diffracted into any of the other interferometer modes. Instead, the main systematic uncertainty in our experimental configuration arises from the nonlinearity of the detectors. Real detectors usually have a nonlinear response function, which means that the recorded value (voltage, photon counts,...) is not linear in the incident power or photon flux, but biased differently for different optical powers. This biases the value of κ, as we measure light powers varying over more than one order of magnitude. Here, the bias arises mainly due to nonlinearities in the electronics of our photoreceiver and due to deadtime in the single photon detector. To take this error into account it is useful to fully characterize our 5-path interferometer, which can be described as a 5-dimensional qudit state. Therefore, we additionally performed complete quantum state tomography [41, 42]. The density matrix ρ was numerically reconstructed from single- and two-path measurements with defined phases via direct reconstruction. The phases are calibrated via scanning the classical two-path laser interference. We used the direct reconstruction instead of a maximum likelihood estimation to avoid systematic deviations in the state reconstruction, which have recently been shown to arise due to the constraint of physicality in maximum likelihood estimates [43]. The real and imaginary parts of the resulting density matrix are shown in figure 4. We calculated 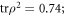 the deviation from 1 (a pure state with no which-path information) can be attributed to an imperfect overlap of the five beams at the second beamsplitter. While this degree of coherence in the interferometer must be determined for an accurate prediction of the influence of the nonlinearities, its actual value has no systematic impact on the Sorkin experiment. The effect of the nonlinearity on the reconstruction is negligible for two reasons: the ratio of the photon fluxes for the different measurement settings is much smaller than in the measurements contributing to the evaluation of κ. More importantly, deviations in the density matrix do not produce a systematic effect on the expected higher-order interference, as
the deviation from 1 (a pure state with no which-path information) can be attributed to an imperfect overlap of the five beams at the second beamsplitter. While this degree of coherence in the interferometer must be determined for an accurate prediction of the influence of the nonlinearities, its actual value has no systematic impact on the Sorkin experiment. The effect of the nonlinearity on the reconstruction is negligible for two reasons: the ratio of the photon fluxes for the different measurement settings is much smaller than in the measurements contributing to the evaluation of κ. More importantly, deviations in the density matrix do not produce a systematic effect on the expected higher-order interference, as  holds for all states in quantum theory.
holds for all states in quantum theory.
From the density matrix it is possible to calculate the expected powers for the different settings of the shutters in the Sorkin experiment. We found good accordance with our measurement data [44], suggesting that the tomography produces an accurate description of the interferometer. The nonlinearities of both detectors were characterized in separate experiments [36]. Applying them to the powers/count rates predicted from the density matrix yields small corrections of these powers (relative change 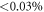 for the laser powers and
for the laser powers and 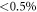 for the unheralded single photon rates).
for the unheralded single photon rates).
One can then calculate the apparent higher-order interferences 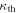 , which would be expected in the Sorkin measurements, from the density matrix and the nonlinear correction (see table 2). Note that in case of the heralded single photon data, we did not calculate an explicit prediction for because the nonlinearity model is quite involved in this case. Instead we used the model to correct the raw experimental data, in order to obtain [45].
, which would be expected in the Sorkin measurements, from the density matrix and the nonlinear correction (see table 2). Note that in case of the heralded single photon data, we did not calculate an explicit prediction for because the nonlinearity model is quite involved in this case. Instead we used the model to correct the raw experimental data, in order to obtain [45].
Table 2.
Predicted values 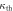 of the higher-order interferences and their standard errors in the classical and semi-classical regimes.
of the higher-order interferences and their standard errors in the classical and semi-classical regimes.
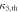
|
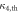
|
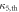
|
|
|---|---|---|---|
classical 
|
9.7 ± 3.1 | −1.6 ± 4.1 | 3.9 ± 5.1 |
semi-classical (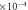 ) ) |
−11.2 ± 0.1 | −3.5 ± 0.1 | 0.0 ± 0.8 |
The differences between the experimentally measured higher-order interferences and the expected values due to the nonlinearities 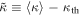 give corrected higher-order interferences as the final results, which can be found in table 3. A final summary of all the different values is presented in figure 5. One finds that all these values are within one standard deviation of the expected zero value.
give corrected higher-order interferences as the final results, which can be found in table 3. A final summary of all the different values is presented in figure 5. One finds that all these values are within one standard deviation of the expected zero value.
Table 3.
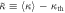 is the nonlinearity-corrected higher-order interference for all measurement regimes. All these values are within one standard deviation of the expected zero value.
is the nonlinearity-corrected higher-order interference for all measurement regimes. All these values are within one standard deviation of the expected zero value.

|

|
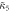
|
|
|---|---|---|---|
classical 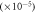
|
0.0 ± 3.1 | 4.3 ± 4.4 | 4.2 ± 5.1 |
semi-classical (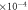 ) ) |
1.3 ± 1.8 | −1.6 ± 2.1 | −3.8 ± 4.0 |
quantum 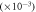
|
0.0 ± 1.6 | 0.6 ± 1.8 | −2.7 ± 2.9 |
Conclusion
The optical 5-path interferometer presented in this work permitted us to experimentally confine the allowed domain of second order interference to an uncertainty of 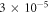 in the classical light regime. This is two orders of magnitude tighter than the bounds obtained from the most precise experiments in any system to date. The uncertainties in the semi-classical and quantum regimes of
in the classical light regime. This is two orders of magnitude tighter than the bounds obtained from the most precise experiments in any system to date. The uncertainties in the semi-classical and quantum regimes of 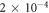 and
and 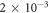 , respectively, are also much lower than what has been reported before [26, 29]. This new level of precision has been reached by a range of technical improvements over previous interferometers including power stabilization, phase stabilization and increased throughput as well as a judicious analysis of detector nonlinearities, which are the dominant origin of systematic error. Furthermore, we have performed the first measurement of third- and fourth-order interference terms, with similarly small uncertainties. So far, all our experimental results showed no significant higher-order interferences and no violation of the correspondence principle between classical electromagnetic and quantum field and therefore fully agree with the conventional theory. The dominant sources of imprecision in our setup are the uncertainties in determining the detector nonlinearities as well as shot noise in the single photon regime. In order to tighten the bound on higher-order interference further, highly linear detection systems and brighter single photon sources or higher detection efficiency will be required. A tighter experimental bound will aid the development of new theories or constrain free parameters of existing ones. In particular, knowledge of the various higher-order terms should permit discriminating between different models for generalized theories, such as coefficients in nonlinear extensions of Born's rule [9], the theory of density cubes [10] and quartic quantum theory [11]. For example, the bounds on
, respectively, are also much lower than what has been reported before [26, 29]. This new level of precision has been reached by a range of technical improvements over previous interferometers including power stabilization, phase stabilization and increased throughput as well as a judicious analysis of detector nonlinearities, which are the dominant origin of systematic error. Furthermore, we have performed the first measurement of third- and fourth-order interference terms, with similarly small uncertainties. So far, all our experimental results showed no significant higher-order interferences and no violation of the correspondence principle between classical electromagnetic and quantum field and therefore fully agree with the conventional theory. The dominant sources of imprecision in our setup are the uncertainties in determining the detector nonlinearities as well as shot noise in the single photon regime. In order to tighten the bound on higher-order interference further, highly linear detection systems and brighter single photon sources or higher detection efficiency will be required. A tighter experimental bound will aid the development of new theories or constrain free parameters of existing ones. In particular, knowledge of the various higher-order terms should permit discriminating between different models for generalized theories, such as coefficients in nonlinear extensions of Born's rule [9], the theory of density cubes [10] and quartic quantum theory [11]. For example, the bounds on 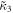 translate directly to bounds on the magnitude of off-diagonal elements in the theory of density cubes [10]. All these alternative theories contain quantum theory as a subset similarly as quantum theory contains classical theory as a subset. The mechanism by which theories exhibiting higher-order interferences reduce to standard quantum theory is called hyper-decoherence [11, 12]. This mechanism would be analogous to the process of decoherence, which induces the quantum-to-classical transition. Our experiment also places a bound on the hyper-decoherence time of the potential extensions of quantum theory with second-, third- and fourth- order interference. Such post-quantum theories are not only interesting from the foundational point of view; they are also under investigation for their applicability towards quantum computation [46, 47].
translate directly to bounds on the magnitude of off-diagonal elements in the theory of density cubes [10]. All these alternative theories contain quantum theory as a subset similarly as quantum theory contains classical theory as a subset. The mechanism by which theories exhibiting higher-order interferences reduce to standard quantum theory is called hyper-decoherence [11, 12]. This mechanism would be analogous to the process of decoherence, which induces the quantum-to-classical transition. Our experiment also places a bound on the hyper-decoherence time of the potential extensions of quantum theory with second-, third- and fourth- order interference. Such post-quantum theories are not only interesting from the foundational point of view; they are also under investigation for their applicability towards quantum computation [46, 47].
Acknowledgments
This work was supported by the Austrian Science Fund (FWF) through projects I-2562, M-1849, P-24621, and F-40 (FoQuS), the European Research Council (ERC) project 257531 (EnSeNa), the Quantum Information Science program of the Canadian Institute for Advanced Research (CIFAR), and by the Foundational Questions Institute (FQXi) through Grant 2011-02814.