Abstract
We show that, under certain circumstances, an optical field in a two-mode squeezed vacuum (TMSV) state can propagate through a lossy atomic medium without degradation or evolution. Moreover, the losses give rise to that state when a different state is initially injected into the medium. Such a situation emerges in a Λ-type atomic system, in which both optical transitions are driven by strong laser fields that are two-photon resonant with the respective signal modes. Then the interactions of the two signal modes with the ground-state atomic coherence interfere destructively, thereby ensuring the preservation of the TMSV with a particular squeezing parameter. This mechanism permits unified interpretation of recent experimental results and predicts new phenomena.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
It has been known since first years of quantum optics that nonclassical properties of optical states, such as squeezing, antibunching, and entanglement, are vulnerable to attenuation [1]. Propagating through an attenuator (a lossy channel), the quantum features of an optical state are shared with the environment, and lost when the environment is traced over. Hence it has been a long standing effort to minimize the amount of losses in the preparation and manipulation of these states in order to enhance their utility for quantum information processing [2], quantum metrology [3], and other applications.
In this paper, we challenge this paradigm, showing a family of nonclassical, entangled states of light that not only propagate through an attenuating medium without being affected by losses, but, moreover, are created thanks to these losses. That is, any other state, after entering and propagating through this medium, is converted into a state from this family. We call these states optical dark (OD) states, in analogy to the dark states of atoms which do not absorb light in spite of it being in resonance with the atomic transition.
Similarly to the atomic dark state, the OD state arises in Λ-shaped atomic systems. The two ground states are coupled to each other in a Raman-like manner by two pairs of fields. In each pair, one field is quantum and the other is a strong laser (figure 1(a)). In this way, the quantum fields directly interact with the atomic ground states: absorption of a photon in mode 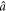 transfers a photon from level
transfers a photon from level  to level
to level  , whereas mode
, whereas mode 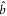 has the opposite effect. When both modes are populated with photons, these processes occur in superposition. Moreover, if the state of these modes is two-mode squeezed vacuum (TMSV) with a certain squeezing parameter (determined by the ratio of the effective coupling constants between the optical modes and matter), the two processes interfere destructively, thereby effectively precluding the interaction of the atomic and optical states. Then, even if the ground state coherence experiences decay, this OD state will propagate through a gas of such atoms without any loss or evolution.
has the opposite effect. When both modes are populated with photons, these processes occur in superposition. Moreover, if the state of these modes is two-mode squeezed vacuum (TMSV) with a certain squeezing parameter (determined by the ratio of the effective coupling constants between the optical modes and matter), the two processes interfere destructively, thereby effectively precluding the interaction of the atomic and optical states. Then, even if the ground state coherence experiences decay, this OD state will propagate through a gas of such atoms without any loss or evolution.
Figure 1. (a) The atomic level scheme. The two quantum modes 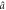 and
and 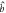 , in which the OD state is present, are in two-photon resonance with the strong classical fields Ωa and Ωb, respectively. (b) Generating the two-mode squeezed OD state
, in which the OD state is present, are in two-photon resonance with the strong classical fields Ωa and Ωb, respectively. (b) Generating the two-mode squeezed OD state 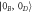 from vacuum input
from vacuum input 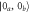 in two atomic samples. Left: scheme of the experiment and energy level diagrams. The coupling constants and the populations of the two samples are exchanged with respect to the two ground states. Right: exchange of entanglement among the optical modes and atomic coherences. Red circles symbolize the Bogoliubov transformation that relate the pairs of optical modes
in two atomic samples. Left: scheme of the experiment and energy level diagrams. The coupling constants and the populations of the two samples are exchanged with respect to the two ground states. Right: exchange of entanglement among the optical modes and atomic coherences. Red circles symbolize the Bogoliubov transformation that relate the pairs of optical modes  and
and 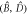 . Shading marks the modes that are in the vacuum state, infinity symbols denote the TMSV state. Top: at the entrance of the first sample, the atomic ensembles and the physical modes
. Shading marks the modes that are in the vacuum state, infinity symbols denote the TMSV state. Top: at the entrance of the first sample, the atomic ensembles and the physical modes 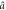 and
and 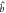 are in their ground states, which means that the Bogoliubov modes
are in their ground states, which means that the Bogoliubov modes 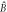 and
and 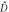 are TMSV entangled as per equation (7). Center: the interaction in the first sample swaps the optical Bogoliubov mode
are TMSV entangled as per equation (7). Center: the interaction in the first sample swaps the optical Bogoliubov mode 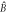 and the atomic coherence
and the atomic coherence 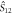 . Bottom: in the second sample, the contents of
. Bottom: in the second sample, the contents of 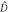 and
and  are swapped. Now the atomic samples are TMSV entangled while the Bogoliubov modes are in the vacuum state, which means that the physical light modes are in the TMSV state as well according to equation (5).
are swapped. Now the atomic samples are TMSV entangled while the Bogoliubov modes are in the vacuum state, which means that the physical light modes are in the TMSV state as well according to equation (5).
Download figure:
Standard image High-resolution imageThe physics of the phenomena studied here are closely related to those of [4, 5], where entanglement of two macroscopic atomic ensembles has been driven created by dissipative phenomena. In fact, it is the same processes that generate the entangled states of both light and atoms, as we show below.
We emphasize the difference between the OD-state setting studied here and the four-wave mixing regime which is known to produce two-mode squeezing in a system similar to that of figure 1(a). In four-wave mixing, the Raman population transfer between the ground states is eliminated by either working away from the two-photon resonance [6–8], or by means of electromagnetically-induced transparency [9]. In this case, the atomic state is decoupled from the evolution, resulting in the usual two-mode squeezing Hamiltonian, which leads to exponential growth of squeezing as the field is propagating through the sample (albeit with fragility to losses). We, in contrast, work under the conditions of two-photon resonance, so both quantum fields, taken individually, experience significant Raman absorption or amplification. In this regime, the squeezing is not amplified with the propagation. It stays constant, but any other state of the two-mode field asymptotically approaches the OD state thanks to that Raman interaction.
Our results furthermore differ from the recent work on environment-induced spatial entanglement of a single photon [10, 11]. In that work, the transformation is of linear optical nature, so the dissipatively generated entangled state between polarization and transverse profile of the light is not pure and cannot be produced without initial nonclassicality of the input state.
Finally, we stress the difference between the physics studied here and that of electromagnetically-induced transparency in multilevel atoms [12, 13]. In the latter, the control fields couple to one ground level of a 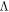 -system, and the signal fields to the other, and the medium is transparent to any signal state of the normal mode. In the present work, the control and signal fields couple to both ground levels, which results in the medium being transparent only to OD states.
-system, and the signal fields to the other, and the medium is transparent to any signal state of the normal mode. In the present work, the control and signal fields couple to both ground levels, which results in the medium being transparent only to OD states.
2. Concept
We limit our analysis to one dimension and assume that the light fields propagate along z direction. The atomic ensemble has the length L and linear atomic density n0 = N/L , where N is the total number of atoms. The atoms, initially prepared in the state 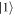 , are described by slowly-varying collective coherence operators
, are described by slowly-varying collective coherence operators 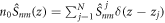 with the commutation relation
with the commutation relation ![${n}_{0}\left[{\hat{S}}_{{nm}}(z^{\prime} ),{\hat{S}}_{{mn}}(z^{\prime\prime} )\right]=\delta (z^{\prime} -z^{\prime\prime} )\left\{{\hat{S}}_{{nn}}(z^{\prime} )-{\hat{S}}_{{mm}}(z^{\prime} )\right\}$](https://content.cld.iop.org/journals/1367-2630/22/1/013014/revision3/njpab5facieqn22.gif) , where
, where 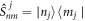 for the jth atom.
for the jth atom.
The two quantum fields, which we call signal and idler, are described by annihilation operators  and
and 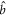 , whose commutation relation is
, whose commutation relation is ![$[\hat{a}(z),{\hat{a}}^{\dagger }(z^{\prime} )]=[\hat{b}(z),{\hat{b}}^{\dagger }(z^{\prime} )]=\delta (z-z^{\prime} )$](https://content.cld.iop.org/journals/1367-2630/22/1/013014/revision3/njpab5facieqn26.gif) . The Rabi frequencies of the corresponding control fields are Ωa and Ωb, respectively.
. The Rabi frequencies of the corresponding control fields are Ωa and Ωb, respectively.
The interaction Hamiltonian in the rotating-wave approximation is then [14, 15]:

where g31 and g32 are photon-atom coupling constants for the corresponding optical transitions [16], ωa,b and 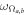 are the carrier frequencies of the quantum and control fields, respectively. We assume the phase matching condition to hold, so the relative phase of the atomic and optical operators stays constant throughout the sample.
are the carrier frequencies of the quantum and control fields, respectively. We assume the phase matching condition to hold, so the relative phase of the atomic and optical operators stays constant throughout the sample.
If the signal and control fields are far detuned for the respective atomic transitions (i.e. Δa,b ≫ γ3, Ωa,b, where γ3 is the spontaneous decay rate from the excited level 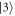 ), we can adiabatically eliminate level
), we can adiabatically eliminate level 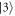 , arriving at the following effective interaction Hamiltonian:
, arriving at the following effective interaction Hamiltonian:
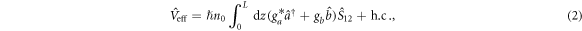
where  and
and  are the effective coupling constants of the signal and idler modes with the spin wave (we specialize to the case
are the effective coupling constants of the signal and idler modes with the spin wave (we specialize to the case 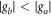 ). Equation (2) is valid if the respective control and quantum field pairs are in a two-photon resonance with the ground states that are ac Stark shifted by the control fields, which we assume to be the case. Another important assumption is that the overwhelming majority of the atomic population is in state
). Equation (2) is valid if the respective control and quantum field pairs are in a two-photon resonance with the ground states that are ac Stark shifted by the control fields, which we assume to be the case. Another important assumption is that the overwhelming majority of the atomic population is in state  , which is valid on time scales that are small compared to the inverse optical pumping rate associated with the control field Ωb:
, which is valid on time scales that are small compared to the inverse optical pumping rate associated with the control field Ωb: 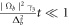 , provided that the signal and idler fields are sufficiently weak. In this case,
, provided that the signal and idler fields are sufficiently weak. In this case, ![${n}_{0}[{\hat{S}}_{12}(z^{\prime} ),{\hat{S}}_{21}(z^{\prime\prime} )]\approx \delta (z^{\prime} -z^{\prime\prime} )$](https://content.cld.iop.org/journals/1367-2630/22/1/013014/revision3/njpab5facieqn35.gif) the Hilbert space associated with the atomic ground state coherence becomes isomorphic to that of the harmonic oscillator under the Holstein–Primakoff transformation [17].
the Hilbert space associated with the atomic ground state coherence becomes isomorphic to that of the harmonic oscillator under the Holstein–Primakoff transformation [17].
To demonstrate the OD state, we perform a Bogoliubov transformation of the signal and idler modes according to
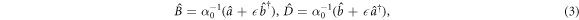
where  and
and  = gb/ga (hereafter we assume the phase convention for
= gb/ga (hereafter we assume the phase convention for 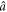 and
and 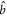 to be chosen such that ga and gb are real and positive). For
to be chosen such that ga and gb are real and positive). For  < 1 the Hamiltonian (2) is transformed into
< 1 the Hamiltonian (2) is transformed into
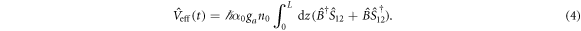
We see that the field in the 'dark' mode 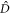 , no matter what state it is in, is decoupled from the interaction (
, no matter what state it is in, is decoupled from the interaction (![$[\hat{D},{\hat{V}}_{\mathrm{eff}}]=0$](https://content.cld.iop.org/journals/1367-2630/22/1/013014/revision3/njpab5facieqn40.gif) ). The atomic system is coupled only to the 'bright' mode
). The atomic system is coupled only to the 'bright' mode 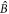 . If the atomic coherence experiences relaxation, this beam-splitter-like coupling will result in absorption, so the bright mode will gradually decay into its ground state
. If the atomic coherence experiences relaxation, this beam-splitter-like coupling will result in absorption, so the bright mode will gradually decay into its ground state 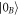 . If the bright mode is initially prepared in that state, it will propagate through the atomic sample without evolution, akin to a conventional optical mode in the vacuum state propagating through an ensemble of resonant atoms. Therefore any state of the form
. If the bright mode is initially prepared in that state, it will propagate through the atomic sample without evolution, akin to a conventional optical mode in the vacuum state propagating through an ensemble of resonant atoms. Therefore any state of the form 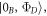 with arbitrary
with arbitrary 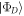 , is an OD state (hereafter, the states in the Bogolubov (dark-bright) basis are denoted by indices B and D, while a and b indices correspond to the 'physical' modes). This state, combined with the collective atomic state
, is an OD state (hereafter, the states in the Bogolubov (dark-bright) basis are denoted by indices B and D, while a and b indices correspond to the 'physical' modes). This state, combined with the collective atomic state 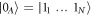 , is an eigenvector of the interaction Hamiltonian (2) with eigenvalue 0.
, is an eigenvector of the interaction Hamiltonian (2) with eigenvalue 0.
3. Ground OD state
Of particular interest among the OD states is the vacuum state 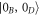 of modes
of modes 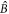 and
and 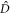 . Because the original modes (
. Because the original modes (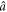 ,
, 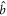 ) are related to (
) are related to (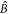 ,
, 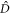 ) via the Bogoliubov transformation, the state
) via the Bogoliubov transformation, the state 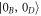 in the eigenbasis of (
in the eigenbasis of (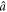 ,
, 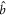 ) is a TMSV:
) is a TMSV:
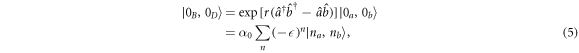
where  is the squeezing parameter and
is the squeezing parameter and  denotes number states. This state is characterized by the mean photon numbers
denotes number states. This state is characterized by the mean photon numbers  and the position/momentum quadrature correlation are found as variances of the sum or difference of the operators averaged over state (5):
and the position/momentum quadrature correlation are found as variances of the sum or difference of the operators averaged over state (5):
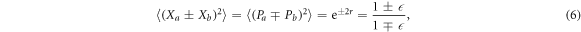
with  = r = 0 corresponding to the standard quantum limit [18]. Canonical position and momentum operators are defined, e.g. for mode
= r = 0 corresponding to the standard quantum limit [18]. Canonical position and momentum operators are defined, e.g. for mode 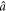 , as
, as 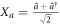 and
and 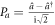 . The squeezing becomes infinite in theory for
. The squeezing becomes infinite in theory for  → 1.
→ 1.
State (5) coincides with the vacuum state 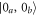 if
if  = 0. This case corresponds to the idler control field being absent, so in accordance with interaction (4) the signal field can experience Raman absorption, decaying into the vacuum state while propagating through the sample. On the other hand, for
= 0. This case corresponds to the idler control field being absent, so in accordance with interaction (4) the signal field can experience Raman absorption, decaying into the vacuum state while propagating through the sample. On the other hand, for 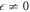 , the physical vacuum is not an OD state. To see this, we notice that this state is two-mode squeezed in the basis of the Bogoliubov bright and dark modes:
, the physical vacuum is not an OD state. To see this, we notice that this state is two-mode squeezed in the basis of the Bogoliubov bright and dark modes:
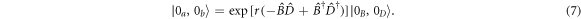
Suppose this state is injected into our atomic sample. In the dark-bright basis, the light-field evolution is accompanied by the absorption of the bright mode by the atoms and its decay into the state 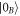 . But in the physical basis, remarkably, this process corresponds to the emission of photons into both modes
. But in the physical basis, remarkably, this process corresponds to the emission of photons into both modes 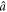 and
and 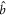 due to four-wave mixing. Due to the dissipation of the entanglement between the bright and dark modes, the state of mode
due to four-wave mixing. Due to the dissipation of the entanglement between the bright and dark modes, the state of mode 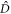 becomes thermal:
becomes thermal:
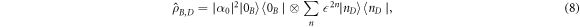
State (8), albeit unpure, is two-mode squeezed in the basis of modes 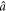 and
and 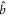 :
:

This squeezing can be experimentally observed by performing a homodyne measurement on the signal and idler modes upon exiting the sample.
The fact that an entangled state remains unchanged while propagating through an absorbing medium, while the vacuum state loses its purity and becomes entangled, is highly counterintuitive. We explain this by observing that the interaction of the light with the environment occurs via the bright mode  . The pair of modes
. The pair of modes 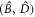 therefore defines the decoherence-preferred basis. States that are entangled in this basis do decohere. However, because this basis is itself entangled in terms of the physical modes
therefore defines the decoherence-preferred basis. States that are entangled in this basis do decohere. However, because this basis is itself entangled in terms of the physical modes 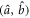 , this decoherence presents itself as growth of entanglement of the latter modes.
, this decoherence presents itself as growth of entanglement of the latter modes.
We reiterate that the state (8) is not pure. The product of uncertainties given by equation (9) exceeds the minimum-uncertainty limit and the sum and difference quadrature squeezing can be reduced by no more than a factor of 2 with respect to the standard quantum limit. However, we can obtain pure TMSV from this state by the following process.
We send the optical modes through an additional, similar atomic sample (figure 1(b)) with the atomic population prepared in state 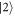 . In addition, we invert the ratio
. In addition, we invert the ratio  , which is equivalent to exchanging the values of the coupling constants ga and gb on the atomic transitions. This is done by adjusting the amplitudes and phases of the Rabi frequencies Ωa and Ωb. In this case the effective Hamiltonian is
, which is equivalent to exchanging the values of the coupling constants ga and gb on the atomic transitions. This is done by adjusting the amplitudes and phases of the Rabi frequencies Ωa and Ωb. In this case the effective Hamiltonian is
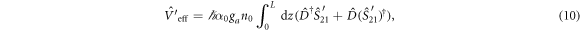
where the primes mark the second sample. Now mode 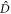 becomes bright and experiences absorption, while mode
becomes bright and experiences absorption, while mode 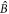 is dark and does not evolve. Since, after the first sample, mode
is dark and does not evolve. Since, after the first sample, mode 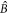 is already in the vacuum state (8), propagation through the second optically deep sample will yield the pure double-vacuum state (5) of modes
is already in the vacuum state (8), propagation through the second optically deep sample will yield the pure double-vacuum state (5) of modes 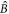 and
and  , whose position and momentum correlations (6) comply with the minimum-uncertainty limit (figures 2(a), (b)).
, whose position and momentum correlations (6) comply with the minimum-uncertainty limit (figures 2(a), (b)).
Figure 2. (a) Development of entanglement of the optical modes as they propagate through the two samples for the vacuum input 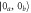 and
and  = 0.5. (a) Bogoliubov
= 0.5. (a) Bogoliubov 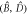 modes; (b) Physical modes
modes; (b) Physical modes 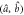 . The variances of the individual position quadratures as well as their sum and difference are displayed. At the entrance of the first sample, the Bogoliubov modes are in the TMSV state. Between the samples, the state is mixed and described by equations (8) and (9). After the second sample, the Bogoliubov modes are in the vacuum state, and the physical modes are in TMSV described by equations (5) and (6). (c) Photon number of the signal mode propagating through an atomic sample with a longitudinal inhomogeneous broadening of the ground state transition according to ω21(z) = ω21(0) + β (Z − L/2), where β is gradient constant. The optical depth normalized by the inhomogeneous broadening is κγ12/β = 5.
. The variances of the individual position quadratures as well as their sum and difference are displayed. At the entrance of the first sample, the Bogoliubov modes are in the TMSV state. Between the samples, the state is mixed and described by equations (8) and (9). After the second sample, the Bogoliubov modes are in the vacuum state, and the physical modes are in TMSV described by equations (5) and (6). (c) Photon number of the signal mode propagating through an atomic sample with a longitudinal inhomogeneous broadening of the ground state transition according to ω21(z) = ω21(0) + β (Z − L/2), where β is gradient constant. The optical depth normalized by the inhomogeneous broadening is κγ12/β = 5.
Download figure:
Standard image High-resolution imageWe see, remarkably, that a pure entangled two mode state (5) can be not only preserved, but also generated through a dissipative (absorptive) process. The decay constant of the atomic coherence determined by the spontaneous emission processes from level  is derived in supplementary materials.
is derived in supplementary materials.
In addition to robustness to losses, our technique permits easy control of the squeezing parameter r( ) by adjusting the strengths of the control fields. Potential detrimental factors such as nonlinearities caused by a finite population in level
) by adjusting the strengths of the control fields. Potential detrimental factors such as nonlinearities caused by a finite population in level  can be suppressed by reducing the interaction time and working at sufficiently large one-photon detunings.
can be suppressed by reducing the interaction time and working at sufficiently large one-photon detunings.
4. OD states and quantum optical memory
The beam-splitter form of coupling defined by the Hamiltonian (4) in an optically deep medium leads to the swapping of the states between the optical mode  and the atomic coherence
and the atomic coherence  , which is the basis of many quantum optical memory protocols [16, 19]. Similarly, the interaction (10) that takes place in the second sample will swap the contents between
, which is the basis of many quantum optical memory protocols [16, 19]. Similarly, the interaction (10) that takes place in the second sample will swap the contents between 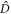 and
and 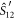 . So far, we assumed the atomic spin state to dissipate after this swap due to the ground state decoherence. However, an interesting interpretation arises if we include the atomic state into our analysis, which is justified if its dissipation is sufficiently slow.
. So far, we assumed the atomic spin state to dissipate after this swap due to the ground state decoherence. However, an interesting interpretation arises if we include the atomic state into our analysis, which is justified if its dissipation is sufficiently slow.
If the state entering the first sample is physical vacuum 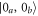 , modes
, modes 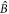 and
and 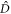 are in the TMSV state (7). When the light propagates through the atoms, this entanglement will be swapped to the first and second samples, as shown in the right panel of figure 1(b). At the same time, modes
are in the TMSV state (7). When the light propagates through the atoms, this entanglement will be swapped to the first and second samples, as shown in the right panel of figure 1(b). At the same time, modes 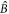 and
and 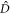 will now take over the vacuum from the initial atomic states, thereby bringing the signal and idler modes
will now take over the vacuum from the initial atomic states, thereby bringing the signal and idler modes 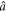 and
and 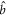 into the TMSV state according to equation (5). In this way, both the atomic and optical states will become entangled, at the same time remaining in states that are separable from each other.
into the TMSV state according to equation (5). In this way, both the atomic and optical states will become entangled, at the same time remaining in states that are separable from each other.
These phenomena, in our understanding, offer alternative physical intuition behind the recent experiments on entanglement generated by dissipation [4, 5] and producing the TMSV state of light [20]. In these experiments, the two samples are atomic cesium vapor cells, with the roles of levels  played by the magnetic states
played by the magnetic states 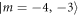 of the ground level 6S1/2, F = 4 in one of the samples, and
of the ground level 6S1/2, F = 4 in one of the samples, and 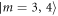 in the other one. Such a configuration automatically ensures the inversion of the coupling constants ga and gb between the two samples.
in the other one. Such a configuration automatically ensures the inversion of the coupling constants ga and gb between the two samples.
5. Propagation of OD states
To explicitly show that OD state is preserved in an ensemble with incoherent decay, we study the evolution of the modes by taking into account the effective Hamiltonian (10) with the free Hamiltonians of atoms, dark and bright fields, we have the following Heisenberg–Langevin equations:

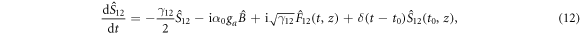
where γ12 is the ground state coherence decay constant,  are the Langevin forces with the correlation functions
are the Langevin forces with the correlation functions 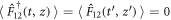 ,
, 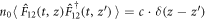 . In the Supplementary, we derive the contribution to this decoherence associated with the interaction of the ground state coherence with the bath of quantum modes that are not collinear with the pump.
. In the Supplementary, we derive the contribution to this decoherence associated with the interaction of the ground state coherence with the bath of quantum modes that are not collinear with the pump.
A general solution to equation (12) can be found similarly to [21]. Using the Fourier transformation 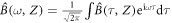 in the co-moving reference frame τ = t−z/c, Z = z and parameterizing the Raman absorption index via
in the co-moving reference frame τ = t−z/c, Z = z and parameterizing the Raman absorption index via
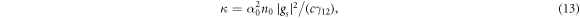
we arrive at
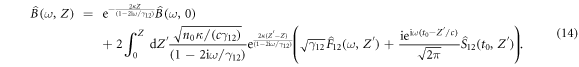
Mode 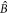 exhibits usual Beer's absorption and tends to the vacuum state
exhibits usual Beer's absorption and tends to the vacuum state 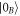 in the limit of infinite optical depth (figure 2(a)). Solution (14) allows us to write a closed form expression for the behavior of the position and momentum quadratures of mode
in the limit of infinite optical depth (figure 2(a)). Solution (14) allows us to write a closed form expression for the behavior of the position and momentum quadratures of mode 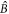 as it propagates through the sample. For example, if the initial state is
as it propagates through the sample. For example, if the initial state is 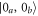 , the transformation (14) together with the delta-correlation of Langevin forces allows us to calculate the respective variance quadrature (figure 2(b)):
, the transformation (14) together with the delta-correlation of Langevin forces allows us to calculate the respective variance quadrature (figure 2(b)):
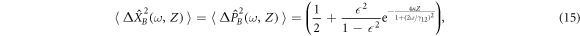
by taking into account 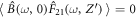 ,
, 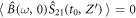 ,
, 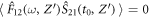 , and the absence of initial atomic coherence at
, and the absence of initial atomic coherence at  . We see that the quadrature variance of the bright field evolves to the value of
. We see that the quadrature variance of the bright field evolves to the value of  , which is characteristic of the vacuum state.
, which is characteristic of the vacuum state.
Equations (13) and (14) illuminate the role of the ground state homogeneous width γ12 in the process studied. On the one hand, it determines the spectral width of the Raman absorption line. On the other hand, the optical depth κZ is inversely proportional to γ12, meaning that a medium with more ground state decoherence would require a longer sample to achieve high optical depth.
It is interesting to analyze the emergence of OD states in the context of gradient echo memory setting [22, 23], in which the frequency of the ground state transition varies along the sample. Figure 2(c) shows the number of photons in the signal mode as it propagates through the sample. When the fields enter the atomic sample, the two-photon detuning for each pair of control and quantum fields is significant, so a four-wave mixing process develops, leading to amplification. At the center of the sample, with the onset of two-photon resonance, the bright mode is absorbed; its optical state becomes vacuum 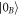 .
.
Curiously, with further propagation, this state remains unchanged in spite of the reemergence of the two-photon detuning. This can be intuitively explained as follows. In the presence of two-photon detuning δ12(Z), the Hamiltonian (4) acquires an additional position-dependent term 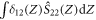 [24]. When this detuning is significant, it dominates the light-atom interaction and results in the evolution of the dark field according to the phase shift
[24]. When this detuning is significant, it dominates the light-atom interaction and results in the evolution of the dark field according to the phase shift 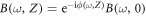 with
with 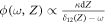 . In the Schrödinger picture, this phase shift corresponds to the evolution operator
. In the Schrödinger picture, this phase shift corresponds to the evolution operator 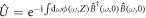 . If the bright mode is in the vacuum state, this operator equals identity, so no evolution is present.
. If the bright mode is in the vacuum state, this operator equals identity, so no evolution is present.
6. Discussion and outlook
The OD state formalism proposed here introduces a unified theoretical framework for a whole range of recent theoretical and experimental studies of different quantum systems of various nature. In addition to the aforementioned application to light-atom interfacing [4, 5, 20], this mechanism can be used to interpret the emergence of entangled states of the collective spin and the mechanical motion of an atomic cloud interacting with a dissipative common cavity mode [25–27]. Similar physics occurs in optomechanics, where two cavity modes are weakly coupled with a single mechanical oscillator [28, 29]. By proper choice of the detunings of the driving optical fields (e.g. one field being blue-detuned with respect to the first cavity mode the other is red with respect to the second), one can obtain an interaction of the form (2), which can again be treated by introducing the dark and bright modes of the cavities.
In this work, we concentrated on the regime of  < 1, which describes a beam-splitter-like interaction (4). The special case
< 1, which describes a beam-splitter-like interaction (4). The special case  = 1 results in the so-called quantum mechanics free subsystem [30], providing a way to evade quantum-measurement backaction [31]. For the case of gb > ga, a transformation analogous to equation (3) can be applied, resulting in the interaction of the parametric form
= 1 results in the so-called quantum mechanics free subsystem [30], providing a way to evade quantum-measurement backaction [31]. For the case of gb > ga, a transformation analogous to equation (3) can be applied, resulting in the interaction of the parametric form 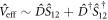 . The associated physics will be studied elsewhere.
. The associated physics will be studied elsewhere.
Acknowledgments
We thank E Polzik for illuminating discussions. The reported study was funded by Russian Foundation for Basic Research according to the research project 17-52-560009.





