Abstract
We introduce a class of parity-time symmetric elastodynamic metamaterials (Ed-MetaMater) whose Hermitian counterpart exhibits unfolding (fractal) spectral symmetries. Our study reveals a scale-free formation of exceptional points in those Ed-MetaMaters whose density is dictated by the fractal dimension of their Hermitian spectra. We demonstrate this scale-free EP-formation in a quasi-periodic Aubry-Harper Ed-MetaMater, a geometric H-tree-fractal Ed-MetaMater, and an aperiodic Fibonacci Ed-MetaMater—each having a specific fractal spectrum—using finite element models and establish a universal route for EP-formation via a coupled mode theory model with controllable fractal spectrum. This universality may enable the rational design of novel Ed-MetaMater for hypersensitive sensing and elastic wave control.
Export citation and abstract BibTeX RIS
1. Introduction
Distinct from common geometric symmetries of phononic crystals and metamaterials, the parity-time (PT)-symmetric materials [1–5] utilize hidden symmetries that are encoded in the governing dynamical equations and are consequences of judicious spatially-distributed attenuation and amplification mechanisms. The PT-symmetric systems have been shown to exhibit novel transport phenomena in various application domains such as optics [6–10], microwaves and radiofrequency waves [11–14], and acoustics [4, 15–20]. Unidirectional invisibility [17, 18], shadow-free sensing [16], asymmetric switching [4, 12], and non-reciprocal transport [21, 22] are some of those exotic wave phenomena that have been demonstrated both theoretically and experimentally. On the other hand, very few works have been focused on the implementation of PT-symmetry in the realm of elastodynamics concerning the elastic wave dynamics in solids [5, 23].
A PT-symmetric elastodynamic metamaterial (Ed-MetaMater) has recently been realized by embedding a gain and a lossy mechanical resonators in an elastic medium that facilitates coupling between them [5]. When the intensity of the equal gain and loss and/or the elastic coupling strength between the two resonators of such an Ed-MetaMater are varied, a branch-point singularity forms where the eigenvalues as well as the corresponding eigenmodes of the system coalesce. Such degeneracy is known as an exceptional point (EP) and it is the most intriguing feature of PT-symmetric systems: it signifies a transition from a parameter domain where the eigenfrequencies are real and the corresponding eigenmodes of the system respect the PT-symmetry (exact PT-symmetric phase) to a domain where the eigenfrequencies are complex conjugate pairs and the normal modes violate the PT-symmetry (broken PT-symmetric phase) [24, 25]. The EPs can also be realized in a more general class of non-Hermitian systems with differential loss and without any gain [26, 27]. However, in the absence of gain, the signal quality may be affected when the overall damping in the structure is very high. In the vicinity of an EP, the degenerate eigenfrequencies can be expanded in a fractional (Puiseux–Newton) power series whose importance in sensing applications has been recognized only recently [28–31]. The EP degeneracies have so far been implemented using coupled resonators in zero (e.g. pair of coupled resonators) or one-dimensional geometries (e.g. one-dimensional arrays of coupled resonators). Developing methods that allow the implementation of EPs in more complex geometries will provide exciting opportunities to engineer mechanical wave dynamics.
The quasi-periodic, aperiodic, and geometric fractal architectures offer new ways of engineering metamaterials across multiple length scales and response time scales because of their intriguing frequency spectrum demonstrating unfolding (fractal) symmetries [15, 32–36]. For example, figure 1 shows the response of an Aubry-Harper Ed-MetaMater in which the resonance modes emerge in a self-similar manner as the generation of the Ed-MetaMater is increased from 9 to 11 (figure 1(b)). The embodiment of fractality in PT-symmetric metamaterials offers the potential to create numerous EPs in a scale-free fashion similar to the scale-free nature of their fractal frequency spectra. Here, we introduce PT-symmetric Ed-MetaMaters with fractal frequency spectra and establish a universal route for the emergence of EPs in those metamaterials. We describe the mechanisms of the emerging EPs induced by the elastodynamic interactions in three classes of such PT-symmetric Ed-MetaMater with fractal spectrum—a quasi-periodic (incommensurate) Ed-MetaMater inspired by the Aubry-Harper model [37–43], a geometric fractal Ed-MetaMater made of H-shaped motifs [44], and an aperiodic Ed-MetaMater that follows Fibonacci substitutional rule [45, 46]. The universal scale-free nature of the EP formation and its connection to the fractal dimension of the frequency spectrum of the underlying Hermitian Ed-MetaMater are established using a coupled-mode-theory (CMT) modeling.
Figure 1. (a) Illustration of a generation-7 (Gen-7) Aubry-Harper Ed-MetaMater; red/blue represents energy gain/loss. For the right half (blue) of the Ed-MetaMater, 8 vertical beams (length: 6 cm; radius: 0.5 cm) are coupled by a horizontal rod with the beam positions given by xs
= sa + R sin(sθ), where 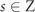 is the rod index, a (5 cm) is the distance between the centers of neighboring projection circles, and R (2 cm < a/2) is the radius of the circle. The left half of the Ed-MetaMater (red) is a mirror reflection of the right one. The metamaterial is made of aluminum (Young's modulus: 68.9 GPa, Poisson's ratio: 0.33, density: 2700 kg m−3) to which the gain/loss is introduced by structural anti-damping/damping. (b) Self-similarity of the modes as the generation is increased from Gen-9 to Gen-11.
is the rod index, a (5 cm) is the distance between the centers of neighboring projection circles, and R (2 cm < a/2) is the radius of the circle. The left half of the Ed-MetaMater (red) is a mirror reflection of the right one. The metamaterial is made of aluminum (Young's modulus: 68.9 GPa, Poisson's ratio: 0.33, density: 2700 kg m−3) to which the gain/loss is introduced by structural anti-damping/damping. (b) Self-similarity of the modes as the generation is increased from Gen-9 to Gen-11.
Download figure:
Standard image High-resolution image2. Method: finite element modeling
We used a commercial finite element platform, Abaqus Simulia, to computationally model the steady-state dynamics of the Ed-MetaMater. The material properties of aluminum (Young's modulus: 68.9 GPa, Poisson's ratio: 0.33, density: 2700 kg m−3) is assumed for all components of the Ed-MetaMater which are modeled with cylindrical beam elements. The modal response convergence has been tested for different element sizes and types and twenty 3-node quadratic Timoshenko beam elements (Abaqus Simulia: B32) in each segment of the structure has been chosen. The P-symmetric Ed-MetaMater is harmonically excited using a prescribed axial displacement at the left end of the horizontal coupling rod generating a longitudinal wave in the rod, and the corresponding sinusoidal axial reaction force at its fixed-right-end is measured, simulating a steady-state elastic wave dynamics in the metamaterial. The PT-symmetry is created by introducing equal amount of energy amplification and attenuation at each P-symmetric part of the Ed-MetaMater, characterized by an amplification/attenuation rate. These gain/loss mechanisms have been modeled by introducing a structural anti-damping/damping coefficient in Abaqus Simulia with its magnitude varying from γ = 0.001 to 1. We also used another commercial finite element platform, COMSOL Multiphysics, to perform eigenfrequency analyses to examine the eigenmodes of EP pairs in both exact and broken phases (figures 2(b)–(d)). In this model, quadratic Timoshenko beam elements have been used and the ends of the coupling rod on either side has been fixed-constrained to respect P-symmetry. The response consistency between Abaqus Simulia and COMSOL Multiphysics has also been verified. It is noteworthy that these implicit dynamic simulations of fractal elastodynamic systems with PT-symmetry require significant computational time.
Figure 2. (a) The formation of a typical EP (inset shows a log–log plot of the frequency difference ΔEP vs 1 − γ/γEP near the EP). The red line has a slope of 0.5 shows the square-root characteristic. (b)–(d) The displacement fields u (x) of the eigenmodes corresponding to (b) the exact phase, (c) EP, and (d) broken phase (the upper and lower figures show the real and imaginary parts of the displacement field and red/blue represents mode-1/mode-2).
Download figure:
Standard image High-resolution image3. Results
3.1. PT-symmetric quasi-periodic Aubry-Harper Ed-MetaMater
The finite element model of the quasi-periodic Aubry-Harper Ed-MetaMater (figure 1(a)) is generated by several vertical beams (length: 6 cm; radius: 0.5 cm) coupled by a horizontal rod with the beam positions given by xs
= sa + R sin(sθ), where 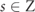 is the rod index, a (5 cm) is the distance between the centers of neighboring projection circles, and R (2 cm < a/2) is the radius of the circle. When the projection parameter θ ∈ (0, 1) is an irrational number, the period of the impedance profile of the structure is incommensurate with the lattice period. To this end, we use the ratio of two adjacent numbers in a Fibonacci sequence for θ = p/q, so that the impedance profile of the structure becomes commensurate with the lattice of rods with period q, defining the generation of this Ed-MetaMater (e.g. 7th generation (Gen-7) corresponds to θ = 5/8, which is composed of the 6th and 7th numbers in Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, ...). The incommensurate limit associated with a truly quasi-periodic structure is investigated via a scaling procedure and it is reached when q → ∞.
is the rod index, a (5 cm) is the distance between the centers of neighboring projection circles, and R (2 cm < a/2) is the radius of the circle. When the projection parameter θ ∈ (0, 1) is an irrational number, the period of the impedance profile of the structure is incommensurate with the lattice period. To this end, we use the ratio of two adjacent numbers in a Fibonacci sequence for θ = p/q, so that the impedance profile of the structure becomes commensurate with the lattice of rods with period q, defining the generation of this Ed-MetaMater (e.g. 7th generation (Gen-7) corresponds to θ = 5/8, which is composed of the 6th and 7th numbers in Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, ...). The incommensurate limit associated with a truly quasi-periodic structure is investigated via a scaling procedure and it is reached when q → ∞.
The P-symmetric (γ = 0) Aubry-Harper Ed-MetaMater is harmonically excited (0–25 kHz) using a prescribed axial displacement at the left end of the horizontal coupling rod generating a longitudinal wave in the rod, and the corresponding sinusoidal axial reaction force at its fixed-right-end is measured, simulating a steady-state elastic wave dynamics in the metamaterial. The fractal dimension D of its frequency spectra (see figure S1 in supplementary material (https://stacks.iop.org/NJP/23/063079/mmedia)) is calculated using the correlation-dimension method [47] and found to be D = 0.83 ± 0.02 (see figure S2 in supplementary material) (a standard box-counting method results in the same D—albeit the correlation-dimension method converges faster to the value of D). We also find that the D of the P-symmetric Ed-MetaMater is the same as that of the corresponding Ed-MetaMater without being coupled to its mirror image. The D remains the same even in the PT-symmetric case—albeit in this case, it refers only to the real part of the frequencies. This robustness of the D of the real part of frequency spectrum against P or PT-symmetries was checked for all the systems we studied.
The PT-symmetry is created by introducing at each P-symmetric part of the Ed-MetaMater equal amount of energy gain and loss (−/+γ), characterized by an amplification/attenuation rate γ. When γ is increased, several pairs of modes interact and coalesce to form a cascade of EPs at different critical values {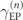 } and a square-root behavior typical of order-two EPs can be observed near the EP. An example of a typical EP in Gen-10 PT-symmetric Aubry-Harper Ed-MetaMater is shown in figure 2. At a critical gain/loss intensity γEP = 0.00251, the eigenvalues (figure 2(a)) and the corresponding eigenmodes (figure 2(c)) coalesce to form an EP. The square-root behavior typical of order-two EPs can be observed in the inset of figure 2(a); ΔEP is the frequency difference between the corresponding mode pairs. The eigenmode components of the vector
u
(xs
) in (figure 2(b)–(d)) describe the displacement field of the transverse tip-deflections of the cross beams at xs
. While in our computation we evaluate the complex displacement fields, the physically relevant information is their amplitude and the phase difference between the components of the mode. We expect that for γ ⩽ γEP
(exact PT-symmetric phase) these eigenmodes are also eigenmodes of the PT-operator, i.e. the complex field remains invariant under the combined parity (xs
→ x−s
) and time (i → −i) operations (figures 2(b) and (c)). In contrast, for γ > γEP (broken PT-symmetric phase) the modes are not any more eigenmodes of the PT-operator. They are rather mapped to one another once the joint PT-operation is applied (figure 2(d)).
} and a square-root behavior typical of order-two EPs can be observed near the EP. An example of a typical EP in Gen-10 PT-symmetric Aubry-Harper Ed-MetaMater is shown in figure 2. At a critical gain/loss intensity γEP = 0.00251, the eigenvalues (figure 2(a)) and the corresponding eigenmodes (figure 2(c)) coalesce to form an EP. The square-root behavior typical of order-two EPs can be observed in the inset of figure 2(a); ΔEP is the frequency difference between the corresponding mode pairs. The eigenmode components of the vector
u
(xs
) in (figure 2(b)–(d)) describe the displacement field of the transverse tip-deflections of the cross beams at xs
. While in our computation we evaluate the complex displacement fields, the physically relevant information is their amplitude and the phase difference between the components of the mode. We expect that for γ ⩽ γEP
(exact PT-symmetric phase) these eigenmodes are also eigenmodes of the PT-operator, i.e. the complex field remains invariant under the combined parity (xs
→ x−s
) and time (i → −i) operations (figures 2(b) and (c)). In contrast, for γ > γEP (broken PT-symmetric phase) the modes are not any more eigenmodes of the PT-operator. They are rather mapped to one another once the joint PT-operation is applied (figure 2(d)).
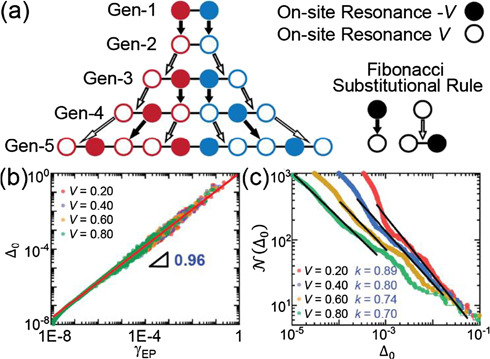
To further estimate the non-Hermitian perturbation strength γ that enforces an EP degeneracy for a specific pair of modes, we plot γEP vs Δ0 for each EP found in the spectrum. Here,  is the frequency difference between the corresponding mode pairs when γ = 0. All EPs (<25 kHz) in a Gen-10 PT-symmetric Aubry-Harper Ed-MetaMater are shown in figure 3(a). Their linear relation demonstrates the intimate relation between the initial (i.e. when γ = 0) frequency split of these two interacting modes Δ0 and the critical gain/loss intensity γEP which coalesce those modes to form an EP. In other words, the non-Hermitian perturbation strength γEP that is needed for enforcing a degeneracy between an EP-pair must be of the same order as the frequency split of those modes in the P-symmetric Ed-MetaMater. Therefore, a statistical analysis of γEP reduces to the statistical description of these Δ0, which are associated with the specific mode pairs that eventually form EPs. The latter is easier to evaluate numerically since it does not require a high-resolution parametric evaluation of the modes—as opposed to the precise determination of γEP.
is the frequency difference between the corresponding mode pairs when γ = 0. All EPs (<25 kHz) in a Gen-10 PT-symmetric Aubry-Harper Ed-MetaMater are shown in figure 3(a). Their linear relation demonstrates the intimate relation between the initial (i.e. when γ = 0) frequency split of these two interacting modes Δ0 and the critical gain/loss intensity γEP which coalesce those modes to form an EP. In other words, the non-Hermitian perturbation strength γEP that is needed for enforcing a degeneracy between an EP-pair must be of the same order as the frequency split of those modes in the P-symmetric Ed-MetaMater. Therefore, a statistical analysis of γEP reduces to the statistical description of these Δ0, which are associated with the specific mode pairs that eventually form EPs. The latter is easier to evaluate numerically since it does not require a high-resolution parametric evaluation of the modes—as opposed to the precise determination of γEP.
Figure 3. The EPs in PT-symmetric Gen-10 Aubry-Harper Ed-MetaMater. (a) Linear relationship between Δ0 and γEP. (b) Integrated distribution reported as 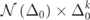 ; axes normalized by their corresponding maxima.
; axes normalized by their corresponding maxima.
Download figure:
Standard image High-resolution imageWe evaluate the probability density function (PDF) 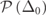 of those EPs. For better statistical processing of these data, we refer to the integrated distribution
of those EPs. For better statistical processing of these data, we refer to the integrated distribution 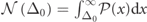 whose derivative
whose derivative  determines the PDF of the frequency split of the EP-pairs and therefore the PDF
determines the PDF of the frequency split of the EP-pairs and therefore the PDF 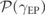 of the gain/loss intensity that is necessary for inducing an EP degeneracy. We find that
of the gain/loss intensity that is necessary for inducing an EP degeneracy. We find that
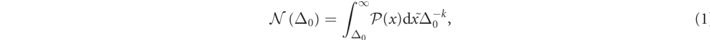
where the best fit parameter k is found to be k = 0.81 ≈ D. Thus, the PDF for the gain/loss intensity scales as 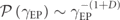 , which is represented by the flat spread in
, which is represented by the flat spread in 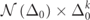 vs Δ0 (figure 3(b)).
vs Δ0 (figure 3(b)).
3.2. The PT-symmetric H-tree geometric fractal Ed-MetaMater
We investigate another class of Ed-MetaMater whose fractal spectrum is originating from a geometric fractality in configuration space [44]. The H-tree geometric fractal Ed-MetaMater is made of two identical planar components made of H-motifs (figure 4(a)). The first generation of this fractal contains two H-shaped structures—each made of three identical cylindrical beams (length: 11.6 cm, radius: 2.38 mm)—coupled by a passive (zero gain/loss) horizontal elastic rod (coupling length: 11.6 cm; length of exterior side ledges: 5.8 cm) such that they form a P-symmetric system. Each subsequent generation adds H-motifs scaled down in length by a factor of 2 (constant diameter) to each tip of the prior H-structure. The analysis of the correlation-dimension of the frequency spectrum indicates that its D converges to 0.80 (see figure S3 in supplementary material).
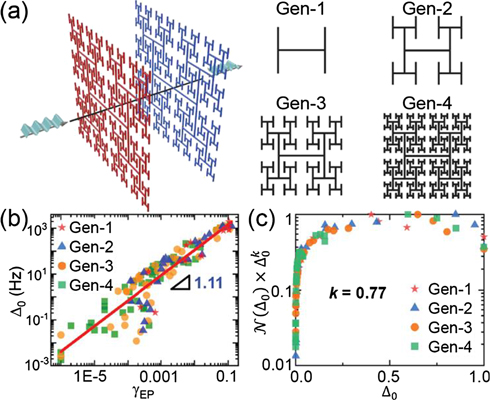
Figure 4. (a) Illustration of a Gen-4 H-tree-fractal Ed-MetaMater and first four generations of its planar component; red/blue represents energy gain/loss. The Gen-1 planar component is made of three identical cylindrical beams (length: 11.6 cm, radius: 2.38 mm). For the subsequent generations, H-motifs are scaled down in length by a factor of 2 (constant diameter) and added to each tip of the prior H-structure. Two identical planar components are then coupled by a passive (zero gain/loss) horizontal elastic rod (coupling length: 11.6 cm; length of exterior side ledges: 5.8 cm) to form a P-symmetric H-tree-fractal Ed-MetaMater. The metamaterial is made of aluminum (Young's modulus: 68.9 GPa, Poisson's ratio: 0.33, density: 2700 kg m−3) to which the gain/loss is introduced by structural anti-damping/damping. (b) Linear relationship between Δ0 and γEP. (c) Integrated distribution reported as 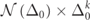 ; axes are normalized by their corresponding maxima.
; axes are normalized by their corresponding maxima.
Download figure:
Standard image High-resolution imageAs previously, the PT-symmetry is created by introducing equal gain/loss (γ = 0.001–1) to the left and right planar components (figure 4(a)). The P-symmetric H-tree-fractal Ed-MetaMater is harmonically excited (0–50 kHz) using a prescribed axial displacement at the left end of the horizontal coupling rod generating a longitudinal wave in the rod, and the corresponding sinusoidal axial reaction force at its fixed-right-end is measured, simulating a steady-state elastic wave dynamics in the metamaterial (see figure S4 in supplementary material). When γ is increased, similar to Aubry-Harper Ed-MetaMater, all four generations of the PT-symmetric H-tree-fractal Ed-MetaMater show the emergence of numerous EPs at 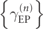 which are proportional to the Δ0 associated with those specific EP-pairs (figure 4(b)). We evaluated the
which are proportional to the Δ0 associated with those specific EP-pairs (figure 4(b)). We evaluated the  which allows estimating the PDF
which allows estimating the PDF 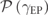 for the critical gain/loss intensity γEP. Figure 4(c) shows the integrated distribution by the variable
for the critical gain/loss intensity γEP. Figure 4(c) shows the integrated distribution by the variable 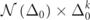 as a function of Δ0. We find that for k = 0.77 ≈ D, the data demonstrate a flat spread, leading to the conclusion that
as a function of Δ0. We find that for k = 0.77 ≈ D, the data demonstrate a flat spread, leading to the conclusion that 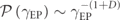 . This finding again demonstrates the intimate relation between the emerging EPs and the fractality of the metamaterial's spectrum.
. This finding again demonstrates the intimate relation between the emerging EPs and the fractality of the metamaterial's spectrum.
3.3. The PT-symmetric aperiodic Fibonacci Ed-MetaMater
To further verify the universal nature of equation (1) we studied another class of Ed-MetaMater with unfolding spectral symmetries—an aperiodic system based on Fibonacci substitutional rule (figure 5(a), details in supplementary material). It is created by equally spaced (3 cm) vertical beams (lengths of A: 8 cm, B: 6 cm; radius: 0.5 cm) organized based on Fibonacci substitutional rule (further details in supplementary material) that are coupled by a horizontal rod (radius: 0.5 cm; exterior ledges: 3 cm) and then mirrored to form a P-symmetric system. The system is harmonically excited (0–50 kHz) using a prescribed axial displacement at the left end of the horizontal coupling rod generating a longitudinal wave in the rod, and the corresponding sinusoidal axial reaction force at its fixed-right-end is measured, simulating a steady-state elastic wave dynamics in the metamaterial (see figure S5 in supplementary material). The correlation-dimension analysis indicates that the frequency spectrum of this system is characterized by D = 0.80 (see figure S6 in supplementary material). The relation between Δ0 and γEP is found to be linear again (figure 5(b)). The 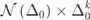 vs Δ0 demonstrates a flat spread with k = 0.80 ≈ D (figure 5(c)), concluding that
vs Δ0 demonstrates a flat spread with k = 0.80 ≈ D (figure 5(c)), concluding that 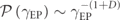 .
.
Figure 5. (a) Illustration of a Gen-7 Fibonacci Ed-MetaMater; red/blue represents energy gain/loss. The right half (blue) of the Ed-MetaMater is made by 13 equally spaced (3 cm) vertical beams (lengths of A: 8 cm, B: 6 cm; radius: 0.5 cm), the number and organization of those beams are based on Fibonacci substitutional rule (see further details in supplementary material). The left half of the Ed-MetaMater (red) is a mirror reflection of the right one. The metamaterial is made of aluminum (Young's modulus: 68.9 GPa, Poisson's ratio: 0.33, density: 2700 kg m−3) to which the gain/loss is introduced by structural anti-damping/damping. (b) Linear relationship between Δ0 and γEP. (c) Integrated distribution reported as 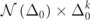 ; axes are normalized by their corresponding maxima.
; axes are normalized by their corresponding maxima.
Download figure:
Standard image High-resolution image3.4. A universal mathematical model for PT-symmetric fractal metamaterials
The intimate relation between 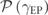 and the spectral fractal dimension of an Ed-MetaMater at γ = 0 implies the existence of an underlying universal route for the creation of EPs in systems with fractal spectrum. To this end, we develop a CMT-based model that utilizes on-site resonant modes that follow an aperiodic Fibonacci substitutional rule (details in figure 6(a) and supplementary material). The CMT Fibonacci model is described by the Hamiltonian:
and the spectral fractal dimension of an Ed-MetaMater at γ = 0 implies the existence of an underlying universal route for the creation of EPs in systems with fractal spectrum. To this end, we develop a CMT-based model that utilizes on-site resonant modes that follow an aperiodic Fibonacci substitutional rule (details in figure 6(a) and supplementary material). The CMT Fibonacci model is described by the Hamiltonian:
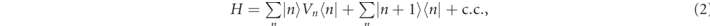
where the coupled resonant frequencies Vn
take only two values ±V arranged in a Fibonacci sequence and {|n⟩} is the local mode basis. This system is known to have a Cantor-set spectrum with zero Lebesgue measure for all V > 0 [48]. A benefit of the Fibonacci CMT modeling is that its spectral fractal dimension D can be tuned by varying on-site resonance of the model, V, thus giving us the possibility to scrutinize the relation 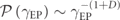 for a variety of spectral fractal dimensions. It turns out that the PDF of the nearest level spacing sn
≡ ωn+1 − ωn
of such family of systems follows a scale-free distribution whose power-law behavior is dictated by the fractality of the spectrum, i.e.
for a variety of spectral fractal dimensions. It turns out that the PDF of the nearest level spacing sn
≡ ωn+1 − ωn
of such family of systems follows a scale-free distribution whose power-law behavior is dictated by the fractality of the spectrum, i.e. 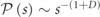 [49–51]. This power law is a signature of level clustering and it is distinct from the PDF
[49–51]. This power law is a signature of level clustering and it is distinct from the PDF 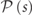 of chaotic or integrable systems [52, 53]. We point out that the realization of this class of systems is not confined only to aperiodic systems like the Fibonacci chain model in equation (2), but also applicable to quasi-periodic systems with metal-insulator transition at some critical value of the on-site resonance (e.g. the Aubry-Harper model) [34, 54, 55], or wave systems with a chaotic classical limit as the kicked Harper model [53]. Therefore, our CMT model represents a typical example of a whole class of systems with fractal spectrum.
of chaotic or integrable systems [52, 53]. We point out that the realization of this class of systems is not confined only to aperiodic systems like the Fibonacci chain model in equation (2), but also applicable to quasi-periodic systems with metal-insulator transition at some critical value of the on-site resonance (e.g. the Aubry-Harper model) [34, 54, 55], or wave systems with a chaotic classical limit as the kicked Harper model [53]. Therefore, our CMT model represents a typical example of a whole class of systems with fractal spectrum.
Figure 6. (a) Illustration of the first five generations of the CMT-based mathematical model with on-site resonances that follow the Fibonacci substitutional rule; red/blue represents energy gain/loss. (b) The linear relation between Δ0 and γEP. (c) Integrated distribution 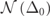 as functions of Δ0 in Gen-17 Fibonacci CMT model.
as functions of Δ0 in Gen-17 Fibonacci CMT model.
Download figure:
Standard image High-resolution imageThe P-symmetric Fibonacci model is implemented by coupling the Hamiltonian of equation (2) with its mirror image. The corresponding effective CMT Hamiltonian takes the form:

where {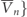 is the mirror-symmetric Fibonacci sequence of {Vn
} and t describes the coupling between two Fibonacci chains. We found that the P-symmetric variant has a fractal frequency spectrum with the same D as the one of the systems of equation (2). Finally, a PT-symmetric CMT model HPT is implemented by introducing uniform gain/loss to the left/right portions of the system in equation (3), i.e. Vn
→ Vn
− iγ and
is the mirror-symmetric Fibonacci sequence of {Vn
} and t describes the coupling between two Fibonacci chains. We found that the P-symmetric variant has a fractal frequency spectrum with the same D as the one of the systems of equation (2). Finally, a PT-symmetric CMT model HPT is implemented by introducing uniform gain/loss to the left/right portions of the system in equation (3), i.e. Vn
→ Vn
− iγ and 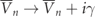 . Because of the simplicity in its structure, this model allows reaching higher generations for more accurate numerical analyses compared to the computationally costly finite element models in previous three examples.
. Because of the simplicity in its structure, this model allows reaching higher generations for more accurate numerical analyses compared to the computationally costly finite element models in previous three examples.
Consider the parametric evolution of frequencies of the P-symmetric model as the coupling constant t that connects the two Fibonacci sub-systems increases. For t = 0, we have two replicas of the same Fibonacci chain in equation (2) and, therefore, the spectrum consists of pairs of degenerate modes. As the coupling t increases, the degeneracy is lifted 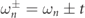 . Simple degenerate perturbation theory with respect to t indicates that the new eigenstates are a linear symmetric/antisymmetric combination of the eigenstates of the Fibonacci Hamiltonian in equation (2). The above perturbative framework is applicable as long as the t is smaller than the distance between nearby frequencies sn
= ωn+1 − ωn
of the uncoupled Hamiltonian H in equation (2). The frequency clustering occurring for fractal spectra, however, enforces a rapid breakdown of the perturbation theory, even for infinitesimal t. Nevertheless, the eigenstates of the Hamiltonian HP(t) are still eigenfunctions of the P-symmetric operator and therefore are symmetric or anti-symmetric with respect to the mirror axis of the total chain. The frequency spacing of nearby levels, however, is not dictated by t but the fractal nature of the spectrum.
. Simple degenerate perturbation theory with respect to t indicates that the new eigenstates are a linear symmetric/antisymmetric combination of the eigenstates of the Fibonacci Hamiltonian in equation (2). The above perturbative framework is applicable as long as the t is smaller than the distance between nearby frequencies sn
= ωn+1 − ωn
of the uncoupled Hamiltonian H in equation (2). The frequency clustering occurring for fractal spectra, however, enforces a rapid breakdown of the perturbation theory, even for infinitesimal t. Nevertheless, the eigenstates of the Hamiltonian HP(t) are still eigenfunctions of the P-symmetric operator and therefore are symmetric or anti-symmetric with respect to the mirror axis of the total chain. The frequency spacing of nearby levels, however, is not dictated by t but the fractal nature of the spectrum.
We treat the inclusion of a small non-Hermitian element ±γ perturbatively. In this case the total Hamiltonian HPT can be written as HPT = HP(t) + iγΓ where the 2N × 2N perturbation matrix Γ has elements Γnm
= δnm
for n ⩽ −1 and Γnm
= −δnm
for n ⩾ 1. Finite γ leads to level shifts proportional to γ2 since the first-order correction vanishes due to the P-symmetry of the corresponding unperturbed eigenmodes of HP(t). For γ = γEP ≃ s = Δ0, the perturbation theory breaks down, signaling level crossing and the appearance of pairs of complex frequencies. It is still intriguing the fact that the non-Hermitian perturbation operator iγΓ couples the nearby levels of Hp(t) in the case of fractal spectrum where the validity of level spacing, and therefore of perturbation theory, is 'blurred'—specifically in the thermodynamic N → ∞ limit. Nevertheless, our detailed numerical investigations confirmed the linear relation γEP ∼ Δ0 for a variety of V-values and find that the linear relation holds with a good approximation in all cases (figure 6(b)). In case of finite system sizes N, some frequency differences Δ0 are still dictated by t, though their weight goes to zero at the thermodynamic limit N → ∞. The above analysis allows us to associate the PDF of the gain/loss intensity that results in EP degeneracy with the distribution of level spacings, leading to the conclusion that 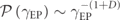 . We tested the validity of the above arguments numerically using the Fibonacci CMT model for a variety of potentials V and corresponding fractal dimensions D(V) and in all cases we find an excellent agreement with the above theoretical results (figure 6(c)).
. We tested the validity of the above arguments numerically using the Fibonacci CMT model for a variety of potentials V and corresponding fractal dimensions D(V) and in all cases we find an excellent agreement with the above theoretical results (figure 6(c)).
The figure 7 comprehensively presents the relationship between the spectral fractal dimensions of all aforementioned P-symmetric systems and the power exponents corresponding to the EPs in the PT-symmetric Fibonacci CMT model with different on-site resonances (indicated by circles; further details see figures S7 and S8 in supplementary material), the PT-symmetric Aubry-Harper Ed-MetaMater (blue star), the PT-symmetric H-tree-fractal Ed-MetaMater (yellow triangle), and the PT-symmetric Fibonacci Ed-MetaMater (purple square). The universality in the relations between the emergence of EPs in these metamaterials and the fractality of their initial spectra is evident in figure 7. The linear fit (black line) with a slope ∼1 signifies the universality of this equality relationship, i.e., the power-law exponent describing a scale-free PDF 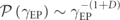 in a PT-symmetric Ed-MetaMater with unfolding spectral symmetries can directly be obtained from its spectral fractal dimension D. This enables a universal route for effectively predicting the emergence of EPs by the initial spectrum itself.
in a PT-symmetric Ed-MetaMater with unfolding spectral symmetries can directly be obtained from its spectral fractal dimension D. This enables a universal route for effectively predicting the emergence of EPs by the initial spectrum itself.
Figure 7. The universal relations between the best-fit power exponents k of the integrated distribution  and the spectral fractal dimensions D of various fractal metamaterials.
and the spectral fractal dimensions D of various fractal metamaterials.
Download figure:
Standard image High-resolution imageThe linear relation found between the critical gain/loss required for creating EPs and the initial split between the mode pairs that coalesce, shows that the high-signal-quality hypersensitive sensors that exploit EPs in PT-symmetric metamaterials can be engineered by appropriate interacting mode pairs that facilitate experimentally realizable low gain/loss. Such systems can be realized via active materials, for example by using piezoelectric elements embedded in the crossbeams that are controlled by non-Foster circuits to provide balanced gain/loss [56] or in combination with passive materials with highly tunable loss [57]. Gain in ultrasonic frequency regime can also be achieved through electroacoustic amplification via phonon-electron interaction in piezoelectric semiconductor [58–60]. The classical noise in Ed-MetaMater (in contrast to quantum noise) may not be a significant concern towards achieving high signal-to-noise ratio as it has been indicated by recent studies on non-Foster circuits [61] that the noise is in same level as in typical diabolic degeneracies.
4. Conclusions
In summary, we designed three PT-symmetric metamaterials with fractal frequency spectrum—a quasi-periodic Aubry-Harper Ed-MetaMater, an H-tree geometric fractal Ed-MetaMater, and an aperiodic Fibonacci Ed-MetaMater—and investigated them using steady-state dynamic finite element approach. The scale-free emergence of numerous EPs is seen in all metamaterials, showing an intimate relation between the scale-free distribution of critical gain/loss intensities and the spectral fractal dimension of the corresponding Hermitian spectra. Particularly, the linear relation we found between the critical gain/loss required for creating EPs and the initial split between the mode pairs that coalesce, shows that the high-signal-quality hypersensitive sensors that exploit EPs in PT-symmetric metamaterials can be engineered by appropriate interacting mode pairs that facilitate experimentally realizable low gain/loss.
We further verified the findings from the specific classes of quasi-periodic, fractal, and aperiodic metamaterials and generalized them to a universal law using a CMT-based PT-symmetric fractal mathematical model. The universal relations among the creation of EPs, the scale-free probability distribution of critical gain/loss intensity, and the fractal dimension of the underlying Hermitian spectrum in these PT-symmetric Ed-MetaMater provide a powerful and convenient tool for predicting the emergence of EPs. Our findings are applicable beyond the elastodynamic realm to PT-symmetric metamaterials in acoustic, optical, microwave, and radiofrequency domains as well. We expect that our detailed numerical results will motivate further mathematical investigations on the interplay of PT-symmetry and the systems with unfolding spectral symmetries.
Acknowledgments
We acknowledge the support from the Dynamics, Controls, and System Dynamics (DCSD) Program of the National Science Foundation (NSF) under the awards CMMI-1925530 (RT, YF) and CMMI-1925543 (TK). We also acknowledge the partial support provided by the University of Wisconsin-Madison, Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).