Abstract
We report magnetic deflagration phenomena ocurring in both antiferromagnetic and ferromagnetic phases in a single crystal of the intermetallic compound Nd5Ge3. We have investigated, using a trigger heat pulse, the spatial and time-resolved evolution of induced magnetic avalanches as a function of the applied magnetic field. The experimental data fit well with the theory of magnetic deflagration.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Deflagration is a dynamic combustion process driven by a self-sustained exothermic reaction that propagates at subsonic speed through a flammable substance [1]. In chemistry terms, the initial flammable substance reacts with an oxidizer, resulting in a chemically modified product and a release of heat that promotes the combustion of the adjacent material. Unfortunately, this process is irreversible since the original substance cannot be recovered after burning. However, reversible deflagration has been proven successfully in magnetic systems, thus opening ahead new research opportunities where the combustion process can be controllably studied and reproduced [2–4]. In magnetic deflagration the role of the flammable substance is played by the magnetic moments (spins) of a magnetic material when prepared in a metastable configuration, and the exothermic reaction to the energy released when they flip (or evolve) towards its equilibrium magnetic state [4, 5]. Magnetic deflagration is therefore suitable to occur in highly anisotropic magnetic materials or during first order magnetic phase transitions at low temperatures, where the sample can be driven to a high energy metastable state—thanks to freezing of thermal kinetic relaxations—when in the presence of large energy barriers.
Magnetic deflagration has only been demonstrated to occur in a small number of systems, such as during spin reversal in highly anisotropic molecule magnets—Mn12-ac (see for instance [3, 6, 7]; see [4] for a review) and Fe8 [8, 9]—, in metamagnetic phase-transitions in manganites—LaxPryCa1–x–yMnO3 [10]—, and in structural magnetic phase-transitions in intermetallic compounds—Gd5Ge4 [11, 12].
Note that the spontaneous emergence of a magnetic deflagration results in the appearance of a magnetic jump in the hysteresis cycle. However, not every magnetic jump is necessarily produced by a magnetic deflagration since other processes such as domain wall nucleation and propagation [13] or spin reversal in highly disordered systems—such as in spin ices [14, 15] or in spin glasses [16]—may also result in the appearance of discrete magnetic jumps along an hysteresis cycle. What distinguish a magnetic deflagration than any casual magnetic avalanche process is that a deflagration is driven by a large release of heat and mediated by thermal conduction [5]. These characteristics are mainly dependent on the thermal conductivity of the material, the energy barriers that control the combustion rate and the energy released. An striking feature of magnetic deflagration is that the last two properties can be easily controlled by the external magnetic field, and since the process is non-destructive, one can reset the magnetic state of the material as many times as one aims to [2, 3, 17].
The purpose of this work is to study the dynamics of the fast magnetic reversal processes observed to occur in the intermetallic compound Nd5Ge3 at low temperatures [18–20] and to compare the results with the known magnetic deflagration laws.
The binary compound Nd5Ge3 is an antiferromagnet (AFM) with a magnetic phase transition to a paramagnet at the Néel temperature  [18, 21]. Below
[18, 21]. Below  , and upon the application of a large magnetic field, this compound exhibits an irreversible AFM to (hard) ferromagnetic (FM) phase transition [18]. Interestingly, it has been observed that at much lower temperatures both the AFM→FM transition and the magnetic field-induced FM reversal may become steep (jump-like) [18–20], which is also accompanied with abrupt changes in other physical properties such as the magnetorstriction, the electrical resistance or the specific heat [18, 19, 22]. These studies were however limited to time-scales of ∼10 s in the best scenario, thus preventing resolving its time-evolution. In this work, we will use a set of pick-up coils and a fast data processing acquisition card to explore, for the first time, the dynamics of the magnetization reversal at different positions along a Nd5Ge3 single crystal with a time resolution of 10 μs.
, and upon the application of a large magnetic field, this compound exhibits an irreversible AFM to (hard) ferromagnetic (FM) phase transition [18]. Interestingly, it has been observed that at much lower temperatures both the AFM→FM transition and the magnetic field-induced FM reversal may become steep (jump-like) [18–20], which is also accompanied with abrupt changes in other physical properties such as the magnetorstriction, the electrical resistance or the specific heat [18, 19, 22]. These studies were however limited to time-scales of ∼10 s in the best scenario, thus preventing resolving its time-evolution. In this work, we will use a set of pick-up coils and a fast data processing acquisition card to explore, for the first time, the dynamics of the magnetization reversal at different positions along a Nd5Ge3 single crystal with a time resolution of 10 μs.
2. Experimental details
Polycrystalline ingots were prepared by arc-melting the constituting 99.9%-pure Nd and 99.999%-pure Ge elements under high-purity argon atmosphere. The compounds were found to be single-phase by powder x-ray diffraction. Single crystals were grown by the Czochralski method from single-phase polycrystalline samples using a tri-arc furnace. The sample was cut from one of the single-crystalline grains into a rectangular shape and annealed at 300 °C for 24 h in an evacuated quartz tube. The sample dimensions were  , where the long axis corresponds to the crystallographic c-axis. The crystal orientation was determined by the back-reflection Laue method.
, where the long axis corresponds to the crystallographic c-axis. The crystal orientation was determined by the back-reflection Laue method.
Magnetic characterization was performed using the SQUID magnetometer of a MPMS® system, produced by Quantum Design®. Figure 1 shows the isothermal magnetization, M , curves along the c-axis and on the c-plane of the single crystal at 2 K. The system, cooled in zero magnetic field, is in the AFM state at H = 0. In the c-axis orientation (triangles), as the field is increased, we confirmed the reported spontaneous metamagnetic transition in the AFM→FM transition at the field  of about 32 kOe. Once this transition takes place the system remains in a hard FM state. When the field
of about 32 kOe. Once this transition takes place the system remains in a hard FM state. When the field  (circa −28 kOe) is reached in the opposite direction of the magnetization of the sample the spontaneous reversal of the FM occurs. The fields
(circa −28 kOe) is reached in the opposite direction of the magnetization of the sample the spontaneous reversal of the FM occurs. The fields  and
and  do not correspond to the previously reported critical field (
do not correspond to the previously reported critical field ( ) and to the coercive field (Hc) respectively. They are related and their values are similar, but the latter are defined in a continuous process while the fields both
) and to the coercive field (Hc) respectively. They are related and their values are similar, but the latter are defined in a continuous process while the fields both  and
and  ) fields are just those where the continuity of the magnetization curve disappears. The large, sudden, and self-sustained process that leads to these discontinuities is known as a magnetic avalanche. From the magnetization measurements in the c-plane orientation we also confirm the lack of transitions and remark the strong anisotropy of this system (diamonds in figure 1).
) fields are just those where the continuity of the magnetization curve disappears. The large, sudden, and self-sustained process that leads to these discontinuities is known as a magnetic avalanche. From the magnetization measurements in the c-plane orientation we also confirm the lack of transitions and remark the strong anisotropy of this system (diamonds in figure 1).
Figure 1. Initial magnetization curves and hysteresis loops at 2 K, for magnetic fields applied parallel (triangles) and perpendicular (diamonds) to the c-axis. The spontaneous fields for the AFM→FM transition,  , and for the FM reversal,
, and for the FM reversal,  , are marked on the top axis. Inset: setup made of two resistors
, are marked on the top axis. Inset: setup made of two resistors  , and four equidistant pick-up coils
, and four equidistant pick-up coils  ; the dark-gray rectangle represents the sample.
; the dark-gray rectangle represents the sample.
Download figure:
Standard image High-resolution imageThe schematic of the experimental setup used to study the spatial and time-resolved evolution of induced magnetic avalanches is shown in the inset of figure 1. This consists of four equal, independent and equidistant pick-up coils and two resistors at the ends of the sample (~1 kΩ at room temperature). Each pick-up coil has two turns and is connected to an instrumentation amplifier INA128P. The voltage generated in the pick-up coils is amplified (×100) and then captured with a data-acquisition card. The four signals are recorded simultaneously.
As spontaneous avalanches occur at a certain magnetic field  for a given temperature (see figure 1 and the magnetic field-temperature phase diagram shown in [18]), a way to trigger the process below that field is needed to study the magnetic field dependence of the avalanche. Several methods have been used for this purpose, from surface acoustic waves to heat pulses [7, 10, 11]. In our case one of the resistors at the ends of the sample (figure 1) acted as a thermometer (R2), and the other one acted as a trigger to ignite the avalanches (R1). The trigger is a heat pulse that consists of a 10 ms pulsed current set to produce 100 mW via Joule effect. The signal of the thermometer was captured simultaneously along the signals of the coils. All the assembly was placed inside the MPMS® with the c-axis of the sample parallel to the direction of the applied magnetic field. The magnetic field sweeping rate used in the experiments was 300 Oe s–1.
for a given temperature (see figure 1 and the magnetic field-temperature phase diagram shown in [18]), a way to trigger the process below that field is needed to study the magnetic field dependence of the avalanche. Several methods have been used for this purpose, from surface acoustic waves to heat pulses [7, 10, 11]. In our case one of the resistors at the ends of the sample (figure 1) acted as a thermometer (R2), and the other one acted as a trigger to ignite the avalanches (R1). The trigger is a heat pulse that consists of a 10 ms pulsed current set to produce 100 mW via Joule effect. The signal of the thermometer was captured simultaneously along the signals of the coils. All the assembly was placed inside the MPMS® with the c-axis of the sample parallel to the direction of the applied magnetic field. The magnetic field sweeping rate used in the experiments was 300 Oe s–1.
The experimental procedure to study the induced magnetic avalanches was the following. To study the AFM→FM process, the system was cooled in zero applied magnetic field from 70 K to a certain T value, and then a magnetic field  was applied. The trigger was sent while the voltage induced by the magnetic flux change in the pick-up coils, C i, and the temperature of the thermometer, R2, were recorded. To determine the amount of magnetization change produced in the induced avalanche, the magnetization was measured immediately before the trigger and right after the acquisition time-window was closed. We repeated the whole procedure at different magnetic fields,
was applied. The trigger was sent while the voltage induced by the magnetic flux change in the pick-up coils, C i, and the temperature of the thermometer, R2, were recorded. To determine the amount of magnetization change produced in the induced avalanche, the magnetization was measured immediately before the trigger and right after the acquisition time-window was closed. We repeated the whole procedure at different magnetic fields,  , and temperatures until the trigger had no effect, because the metastability was not large enough to ignite the avalanche (low fields) [3], or because the avalanche took place spontaneously before (high fields). To study the FM reversal process we set the temperature T and then we applied a magnetic field of
, and temperatures until the trigger had no effect, because the metastability was not large enough to ignite the avalanche (low fields) [3], or because the avalanche took place spontaneously before (high fields). To study the FM reversal process we set the temperature T and then we applied a magnetic field of  , large enough to ensure the complete transition AFM→FM. Next, the system was driven to the desired
, large enough to ensure the complete transition AFM→FM. Next, the system was driven to the desired  value, where the magnetization-trigger-recording-magnetization procedure was performed. We repeated the whole method at different magnetic fields and temperatures. From now on, the AFM→FM and the FM reversal processes will be referred simply as AFM and FM processes, respectively.
value, where the magnetization-trigger-recording-magnetization procedure was performed. We repeated the whole method at different magnetic fields and temperatures. From now on, the AFM→FM and the FM reversal processes will be referred simply as AFM and FM processes, respectively.
3. Experimental results and discussion
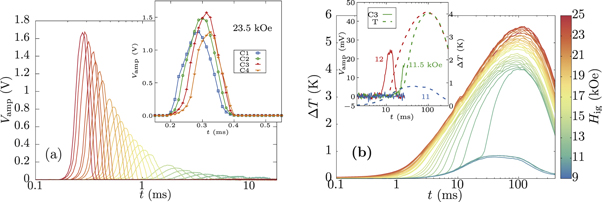
Figure 2 presents the time-resolved measurements of the FM process at 2 K. The panel (a) comprises the voltage generated in the coils, while the temperature increment in the thermometer placed at the end of the sample is shown in panel (b). Panel (a) shows how, as  increases, (i) the time elapsed between the trigger (t = 0) and the rise in the signal decreases, and (ii) that the height of the signal increases and the width of the peak shrinks. The inset in this panel shows the signal of the four coils as a function of time for the avalanche induced at 23.5 kOe. The layout of the curves indicates that the induced avalanche process propagates from one end of the sample to the other. Due the proximity to the edge of the sample and the width of the propagating avalanche, the shapes of the signals of coils C1 and C4 have their height reduced and are also shifted to the 'center'. Therefore we used the signals from coils C2 and C3 to define the value of the experimental speed of the propagation as
increases, (i) the time elapsed between the trigger (t = 0) and the rise in the signal decreases, and (ii) that the height of the signal increases and the width of the peak shrinks. The inset in this panel shows the signal of the four coils as a function of time for the avalanche induced at 23.5 kOe. The layout of the curves indicates that the induced avalanche process propagates from one end of the sample to the other. Due the proximity to the edge of the sample and the width of the propagating avalanche, the shapes of the signals of coils C1 and C4 have their height reduced and are also shifted to the 'center'. Therefore we used the signals from coils C2 and C3 to define the value of the experimental speed of the propagation as  , where
, where  corresponds to the time delay between the half heights of the integrated voltages of C2 and C3, and d23 is the distance between the coils.
corresponds to the time delay between the half heights of the integrated voltages of C2 and C3, and d23 is the distance between the coils.
Figure 2. Time-resolved measurements of the induced FM process as a function of  at 2 K. In all measurements the trigger was sent at t = 0. Panel (a): voltage generated in coil C3 (amplified); the inset details the signals of the four coils at
at 2 K. In all measurements the trigger was sent at t = 0. Panel (a): voltage generated in coil C3 (amplified); the inset details the signals of the four coils at  . Panel (b): temperature increment in R2; the inset details three temperature measurements at consecutive increasing fields (dashed lines), along with their respective coil C3 signal (solid lines). The main plots share the color code, that corresponds to the magnetic field.
. Panel (b): temperature increment in R2; the inset details three temperature measurements at consecutive increasing fields (dashed lines), along with their respective coil C3 signal (solid lines). The main plots share the color code, that corresponds to the magnetic field.
Download figure:
Standard image High-resolution imageFigure 2(b) plots the time evolution of the temperature increment measured by the thermometer placed at the end. It is remarkable the presence of a threshold in the occurrence of the avalanche process. For low fields, the magnetic avalanche cannot be induced by the trigger pulse, but above a certain magnetic field  kOe, a huge increase in the temperature of the thermometer is detected, which occurs together with the emergence of a peak in the signals of the coils (see figure 2(a)). This effect can be clearly seen in the inset of figure 2(b), where the signals of the coil C3 and the thermometer R2 are presented for three consecutive fields. For 11 kOe, the coil signal does not show any relevant peak, while the thermometer presents a small rise mainly due to the heat released by the trigger pulse (a similar temperature rise in the thermometer was detected when the same trigger pulse was send and the sample was in its equilibrium magnetic state, i.e., there was no additional energy released by the crystal). This effect is also consistent with the fact that the contribution of the induced magnetic relaxation due to a thermal rise is very small if the avalanche process is not ignited [3, 17] (see figure 2(b): a very similar thermal rise is observed for
kOe, a huge increase in the temperature of the thermometer is detected, which occurs together with the emergence of a peak in the signals of the coils (see figure 2(a)). This effect can be clearly seen in the inset of figure 2(b), where the signals of the coil C3 and the thermometer R2 are presented for three consecutive fields. For 11 kOe, the coil signal does not show any relevant peak, while the thermometer presents a small rise mainly due to the heat released by the trigger pulse (a similar temperature rise in the thermometer was detected when the same trigger pulse was send and the sample was in its equilibrium magnetic state, i.e., there was no additional energy released by the crystal). This effect is also consistent with the fact that the contribution of the induced magnetic relaxation due to a thermal rise is very small if the avalanche process is not ignited [3, 17] (see figure 2(b): a very similar thermal rise is observed for  ). As the magnetic field is increased up to 11.5 kOe and above, the same small increase in the temperature is observed initially. But when a peak appears in the coil signal, a rapid increase of the temperature begins to develop. This is an indication of the occurrence of the heat mediated magnetic avalanche process. As it is described in the experimental procedure, the magnetization is measured right before the trigger and right after the thermometer adquisition time window is closed. The magnetization change at 11 kOe and below is negligible, but at higher fields , where the avalanche process occurs, a large change in the magnetization is observed (a magnetization reversal for the FM process and a change from nearly zero to saturation magnetization for the AFM one).
). As the magnetic field is increased up to 11.5 kOe and above, the same small increase in the temperature is observed initially. But when a peak appears in the coil signal, a rapid increase of the temperature begins to develop. This is an indication of the occurrence of the heat mediated magnetic avalanche process. As it is described in the experimental procedure, the magnetization is measured right before the trigger and right after the thermometer adquisition time window is closed. The magnetization change at 11 kOe and below is negligible, but at higher fields , where the avalanche process occurs, a large change in the magnetization is observed (a magnetization reversal for the FM process and a change from nearly zero to saturation magnetization for the AFM one).
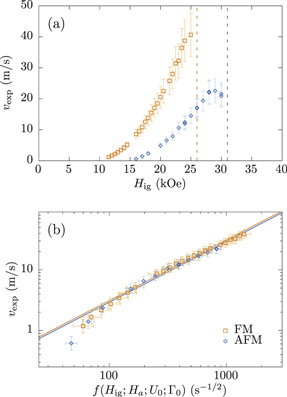
The obtained values  as a function of
as a function of  for the AFM and FM processes are plotted in figure 3(a). In this figure we can see how the speed rapidly increases with increasing
for the AFM and FM processes are plotted in figure 3(a). In this figure we can see how the speed rapidly increases with increasing  up to the corresponding
up to the corresponding  field (dashed vertical lines). The range of speed values measured, ∼10 m s–1, together with the marked nonlinearity dependence and the abrupt, and large heat release, make us to consider the propagation of the magnetization change not related to the dynamics of domain walls [13], but to a magnetic deflagration process [1, 3, 5].
field (dashed vertical lines). The range of speed values measured, ∼10 m s–1, together with the marked nonlinearity dependence and the abrupt, and large heat release, make us to consider the propagation of the magnetization change not related to the dynamics of domain walls [13], but to a magnetic deflagration process [1, 3, 5].
Figure 3. Panel (a): dependence of the experimental speed of the front on the applied magnetic field. The vertical dashed lines correspond to the respective spontaneous deflagration magnetic fields  . Panel (b): log–log plot of the experimental speed versus the theoretical function f (equation (5)), in both AFM (diamonds) and FM (squares) states. Only the experimental speeds with maximum ΔM are used. The lines correspond to the respective linear fits.
. Panel (b): log–log plot of the experimental speed versus the theoretical function f (equation (5)), in both AFM (diamonds) and FM (squares) states. Only the experimental speeds with maximum ΔM are used. The lines correspond to the respective linear fits.
Download figure:
Standard image High-resolution imageThe theory of magnetic deflagration [5, 23] establishes the dependence of the propagation speed of the front on the magnetic field,  in our experiments), as
in our experiments), as

with
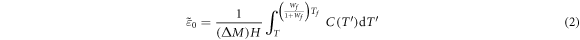
and
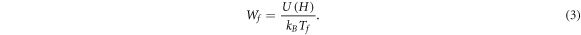
Here Tf is the temperature of the propagating front (or 'flame' temperature), U(H) is the energy barrier,  is the attempt frequency,
is the attempt frequency,  is the Zeeman energy released and C is the specific heat. This expression is obtained considering that the thermal diffusivity κ is independent of temperature in the range of Tf, i.e.
is the Zeeman energy released and C is the specific heat. This expression is obtained considering that the thermal diffusivity κ is independent of temperature in the range of Tf, i.e.  . The value of Tf is obtained solving the equation
. The value of Tf is obtained solving the equation
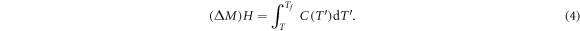
We used the specific heat measurements presented in a recent work [24] to obtain numerically Tf for every field  . The attempt frequency is obtained from relaxation measurements to be
. The attempt frequency is obtained from relaxation measurements to be  [25]. A phenomenological energy barrier U(H) is obtained from isothermal magnetization measurements following the procedure described in the work of Hernàndez et al [26]. It can be approximated to
[25]. A phenomenological energy barrier U(H) is obtained from isothermal magnetization measurements following the procedure described in the work of Hernàndez et al [26]. It can be approximated to  , where U0 corresponds to the energy barrier at zero applied magnetic field and Ha plays the role of an anisotropy field [27]—see supplementary material. This relation corresponds to the energy barrier of a system with uniaxial anisotropy under an external magnetic field H, and describes reasonably well the magnetic behavior of the sample (figure 1). The values obtained for these parameters are presented in table 1.
, where U0 corresponds to the energy barrier at zero applied magnetic field and Ha plays the role of an anisotropy field [27]—see supplementary material. This relation corresponds to the energy barrier of a system with uniaxial anisotropy under an external magnetic field H, and describes reasonably well the magnetic behavior of the sample (figure 1). The values obtained for these parameters are presented in table 1.
Table 1.
Values of the parameters used to compute the theoretical function  (equation (5)), and the deduced thermal diffusivities in the two magnetic states of Nd5Ge3. The number in parenthesis is the statistical uncertainty in the last digit from the least-squares fitting procedure and from error propagation.
(equation (5)), and the deduced thermal diffusivities in the two magnetic states of Nd5Ge3. The number in parenthesis is the statistical uncertainty in the last digit from the least-squares fitting procedure and from error propagation.
| State | U0 (K) | Ha (kOe) |
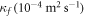
|
|---|---|---|---|
| AFM | 237(4) | 53.1(6) | 8.5(8) |
| FM | 223(7) | 45(1) | 9.6(9) |
The only unknown parameter in equation (1) is  . This equation can be rewritten as
. This equation can be rewritten as
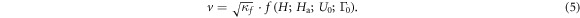
Therefore, if the experimental data matches the theoretical expression, one should expect a linear dependence between the  and the function f. In figure 3(b) we plot the experimental speed
and the function f. In figure 3(b) we plot the experimental speed  versus the function f for both the AFM and FM processes, along with the corresponding linear fits of equation (5). Since the reduction of the total magnetization change that occurs for fields near
versus the function f for both the AFM and FM processes, along with the corresponding linear fits of equation (5). Since the reduction of the total magnetization change that occurs for fields near  can induce firewalls that would reduce the speed of the front, we do not take into account them to the fits. We associate the nonlinearity at small values to slow-deflagration processes where the thermal bath plays an important role [3]. The values of
can induce firewalls that would reduce the speed of the front, we do not take into account them to the fits. We associate the nonlinearity at small values to slow-deflagration processes where the thermal bath plays an important role [3]. The values of  obtained for each phase are shown in table 1 and are of the expected order of magnitude for a metallic compound [28]. We obtain a slightly higher thermal diffusivity in the FM phase, which we consider consequent with the lower heat capacity and electrical resistance of this state [24, 25].
obtained for each phase are shown in table 1 and are of the expected order of magnitude for a metallic compound [28]. We obtain a slightly higher thermal diffusivity in the FM phase, which we consider consequent with the lower heat capacity and electrical resistance of this state [24, 25].
The results presented in this paper correspond to the study of thermally induced magnetic avalanches at 2 K. Nevertheless, we explored different temperatures, and we checked that, for  , at a given field
, at a given field  , the induced deflagration process does not depend on the initial temperature. From the theory of the magnetic deflagration it is known that the initial temperature of the system does not play an important role in the deflagration process when the Zeeman energy and the energy barrier are large, which is the case of Nd5Ge3. Therefore, as we were interested in covering the widest range of magnetic fields, we chose the lowest temperature our system could reach.
, the induced deflagration process does not depend on the initial temperature. From the theory of the magnetic deflagration it is known that the initial temperature of the system does not play an important role in the deflagration process when the Zeeman energy and the energy barrier are large, which is the case of Nd5Ge3. Therefore, as we were interested in covering the widest range of magnetic fields, we chose the lowest temperature our system could reach.
Using the obtained values for the thermal diffusivity we can estimate the deflagration front width  , getting
, getting  for the lowest speed and
for the lowest speed and  for the fastest. Nevertheless, we have calculated the shape of the signal picked up by this setup of coils for those theoretical front widths and the result is that the measured signals of the coils suggest broader fronts. According to Jukimenko et al [29], this observation can be explained by a bending of the propagation front at the boundaries of the sample in contact with the enviorment, thus resulting in a wider effective measured reversal front.
for the fastest. Nevertheless, we have calculated the shape of the signal picked up by this setup of coils for those theoretical front widths and the result is that the measured signals of the coils suggest broader fronts. According to Jukimenko et al [29], this observation can be explained by a bending of the propagation front at the boundaries of the sample in contact with the enviorment, thus resulting in a wider effective measured reversal front.
Finally, with the parameters of the system (see table 1) and taking  equal to the maximum experimental value for all the range of fields (which is equivalent to consider the environment temperature equal to zero) we can extrapolate the theoretical front speed for increasing magnetic fields (see supplementary material for a detailed description). As observed previously in Mn12-ac molecular magnet [30], magnetic deflagration can turn into magnetic detonation. In the case of Nd5Ge3 crystals the larger size and magnetic moment would benefit the investigation of the subsonic to supersonic transition. It should be possible to reach this supersonic regime in a commercial dilution refrigerator with a base temperature of tens of millikelvin and with magnetic fields up to 50 kOe.
equal to the maximum experimental value for all the range of fields (which is equivalent to consider the environment temperature equal to zero) we can extrapolate the theoretical front speed for increasing magnetic fields (see supplementary material for a detailed description). As observed previously in Mn12-ac molecular magnet [30], magnetic deflagration can turn into magnetic detonation. In the case of Nd5Ge3 crystals the larger size and magnetic moment would benefit the investigation of the subsonic to supersonic transition. It should be possible to reach this supersonic regime in a commercial dilution refrigerator with a base temperature of tens of millikelvin and with magnetic fields up to 50 kOe.
4. Conclusions
In this work we show that the change in the magnetization propagates across the system mediated by heat transport. Therefore we state that magnetic avalanches in Nd5Ge3 are actually magnetic deflagrations. We have also shown that the front speed, for the used experimental conditions, is in the range between 0.1–50 m s–1. This fact implies that, for samples of the order on 1–5 mm, the duration of the avalanche process actually lays between 0.1–10 ms, decreasing exponentially with the external magnetic field. This is, therefore, a process much faster than previously suggested.
For the first time a system with a magnetic deflagration process in two different magnetic phases is presented, including, for the first time, the study in a ferromagnetic system. The good agreement between experimental results and the theory allows us to point out the possibility of studying the transition from magnetic deflagration to magnetic detonation within reasonable experimental conditions.
Acknowledgments
This work was financially supported by project MAT2015-69144-P (MINECO/FEDER, UE).