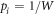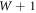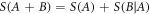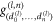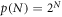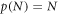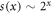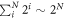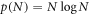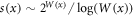Abstract
The nature of statistics, statistical mechanics and consequently the thermodynamics of stochastic systems is largely determined by how the number of states W(N) depends on the size N of the system. Here we propose a scaling expansion of the phasespace volume W(N) of a stochastic system. The corresponding expansion coefficients (exponents) define the universality class the system belongs to. Systems within the same universality class share the same statistics and thermodynamics. For sub-exponentially growing systems such expansions have been shown to exist. By using the scaling expansion this classification can be extended to all stochastic systems, including correlated, constraint and super-exponential systems. The extensive entropy of these systems can be easily expressed in terms of these scaling exponents. Systems with super-exponential phasespace growth contain important systems, such as magnetic coins that combine combinatorial and structural statistics. We discuss other applications in the statistics of networks, aging, and cascading random walks.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Classical statistical physics typically deals with large systems composed of weakly interacting components, which can be decomposed into (practically) independent sub-systems. The phasespace volume W or the number of states of such systems grows exponentially with system size N. For example, the number of configurations in a spin system of N independent spins is W(N) = 2N. For more complicated systems, however, where particles interact strongly, which are path-dependent, or whose configurations become constrained, exponential phasespace growth no-longer occurs, and things become more interesting. For example, in black holes the accessible number of states does not scale with the volume but with surface, which leads to non-standard entropies and thermodynamics [1–3]. A version of entropy that depends on the surface and the volume was recently suggested in [4].
Other examples include systems with interactions on networks, path-dependent processes, co-evolving systems, and many driven non-equilibrium systems. These systems are often non-ergodic and are referred to as complex systems. For these systems, in general, the classical statistical description based on Boltzmann–Gibbs statistical mechanics fails to make correct predictions with respect of the thermodynamic, the information theoretic, or the maximum entropy related aspects [5]. Often the underlying statistics is then dominated by fat-tailed distributions, and power-laws in particular. There have been considerable efforts to understand the origin of power-law statistics in complex systems. Some progress was made for systems with sub-exponentially growing phasespace. It was shown that systems whose phasespace grow as power laws,  , are tightly related to so-called Tsallis statistics [6].
, are tightly related to so-called Tsallis statistics [6].
The tremendous variety and richness of complex systems has led to the question whether it is possible to classify them in terms of their statistical behavior. Given such a classification, is it possible to arrive at a generalized concept of the statistical physics of complex systems, or do we have to establish the statistical physics framework for every particular system independently? For sub-exponentially growing systems such a classification was attempted by characterizing stochastic systems in terms of two scaling exponents of their extensive entropy [7]. The first scaling exponent is recovered from the relation  , which is valid if the first three Shannon–Khinchin (SK) axioms (see appendix) are valid (the fourth, the composition axiom, can be violated), and if the entropy is of so-called trace form, which means that it can be expressed as
, which is valid if the first three Shannon–Khinchin (SK) axioms (see appendix) are valid (the fourth, the composition axiom, can be violated), and if the entropy is of so-called trace form, which means that it can be expressed as  , where pi is the probability for state i, and g some function. The second scaling exponent d is obtained from a scaling relation that involves the re-scaling of the number of states W → Wa. With these two scaling exponents c and d it becomes possible to classify sub-exponentially growing systems that fulfil the first three SK axioms [7]. Further, the exponents c and d characterize the extensive entropy,
, where pi is the probability for state i, and g some function. The second scaling exponent d is obtained from a scaling relation that involves the re-scaling of the number of states W → Wa. With these two scaling exponents c and d it becomes possible to classify sub-exponentially growing systems that fulfil the first three SK axioms [7]. Further, the exponents c and d characterize the extensive entropy,  . Practically all entropies that were suggested within the past three decades, are special cases of this (c, d)-entropy, including Boltzmann–Gibbs–Shannon entropy (c = 1, d = 1), Tsallis entropy (d = 0), Kaniadakis entropy (c = 1, d = 1) [8], Anteneodo–Plastino entropy (c = 1, d > 0) [9], and all others that fulfil the first three SK axioms. In [10] it was then shown that the exponents c and d are tightly related with phasespace growth of the underlaying systems. In fact, they can be derived from the knowledge of W(N),
. Practically all entropies that were suggested within the past three decades, are special cases of this (c, d)-entropy, including Boltzmann–Gibbs–Shannon entropy (c = 1, d = 1), Tsallis entropy (d = 0), Kaniadakis entropy (c = 1, d = 1) [8], Anteneodo–Plastino entropy (c = 1, d > 0) [9], and all others that fulfil the first three SK axioms. In [10] it was then shown that the exponents c and d are tightly related with phasespace growth of the underlaying systems. In fact, they can be derived from the knowledge of W(N),  , and
, and  .
.
For super-exponential systems such a classification is hitherto missing. These systems include important examples of stochastic complex systems that form new states as a result of the interactions of elements. These are systems that—besides their combinatorial number of states (e.g. exponential)—form additional states that emerge as structures from the components. The total number of states then grows super-exponentially with respect to system size, e.g. the number of elements. Stochastic systems with elements that can occupy several states (more than one) and that can form structures with other elements, are generally super-exponential systems. It was pointed out in [11] that such systems might exhibit non-trivial thermodynamical properties.
An example for such systems are magnetic coins of the following kind. Imagine a set of N coins that come in two states, up and down. There are 2N states. However, these coins are 'magnetic', and any two of them can stick to each other, forming a new bond state (neither up nor down). If there are N = 2 coins, there are five states: the usual four states, uu, ud, du, dd, and a fifth state 'bond'. If there are N = 3 coins, there are 14 states, the 23 combinatorial states, and six states involving bond states: state 9 is bond between coin 1 and 2, with the third coin up, state 10 is the same bond state with the third coin down, state 11 is a bond between 1 and 3 with the second con up, 12 the same bond with the second coin down, state 12 is a bond between 2 and 3, with the first state up, and finally, state 14 is the bond between 2 and 3 with the first coin down. It can be easily shown that the recursive formula for the number of states is,  , which, for large N, grows as
, which, for large N, grows as  , see [11].
, see [11].
In this paper we show that it is indeed possible to find a complete classification of complex stochastic systems, including the super-exponential case. By expanding a generic phasespace volume  in a Poincaré expansion, we will see that for any possibility of phasespace growth, there exists a sequence of unique expansion coefficients that are nothing but scaling exponents that describe systems in their large size limit. The set of scaling exponents gives us the full classification of complex systems in the sense that two systems belong to the same universality class, if it is possible to rescale one into the other with exactly these exponents. The framework presented here has been proposed in the appendix of [12] and generalizes the classification approach of [7, 10]. It includes the sub-exponential systems as a special case. We show further that these exponents can be used straight forwardly to express—with a few additional requirements—the corresponding extensive entropy, which is the basis for the thermodynamic properties of the system. Finally, we see in several examples that many systems are fully characterized by a very few exponents. Technical details and auxiliary results are presented in the appendix. We reference the appendix in the corresponding parts of the main text. However, readers may also go through the appendix before they continue reading. We use the following notation for applying a function f for n times,
in a Poincaré expansion, we will see that for any possibility of phasespace growth, there exists a sequence of unique expansion coefficients that are nothing but scaling exponents that describe systems in their large size limit. The set of scaling exponents gives us the full classification of complex systems in the sense that two systems belong to the same universality class, if it is possible to rescale one into the other with exactly these exponents. The framework presented here has been proposed in the appendix of [12] and generalizes the classification approach of [7, 10]. It includes the sub-exponential systems as a special case. We show further that these exponents can be used straight forwardly to express—with a few additional requirements—the corresponding extensive entropy, which is the basis for the thermodynamic properties of the system. Finally, we see in several examples that many systems are fully characterized by a very few exponents. Technical details and auxiliary results are presented in the appendix. We reference the appendix in the corresponding parts of the main text. However, readers may also go through the appendix before they continue reading. We use the following notation for applying a function f for n times,  .
.
2. Rescaling phasespace
Suppose that phasespace volume depends on system size N (e.g. number of elements) as W(N). We use the Poincaré asymptotic expansion for the l + 1 th logarithm of W,
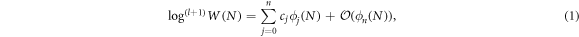
where  for
for  . A uniqueness theorem (see e.g. [13]) states that the asymptotic expansion exists and is uniquely determined for any W(N) for which
. A uniqueness theorem (see e.g. [13]) states that the asymptotic expansion exists and is uniquely determined for any W(N) for which  , see appendix.
, see appendix.
To see how the exponents cj correspond to scaling exponents, let us define a sequence of re-scaling operations,
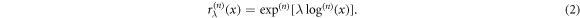
For example  ,
,  , etc. Obviously,
, etc. Obviously,  . The scaling operations obey the composition rule
. The scaling operations obey the composition rule
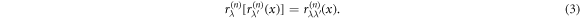
We can now investigate the scaling behavior of the phasespace volume in the thermodynamic limit, N ≫ 1. The leading order of the scaling is given by the first rescaling r0. We show in the appendix that the rescaling of phasespace is asymptotically described by
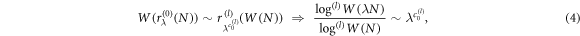
where  is the leading exponent, and l is determined from the condition that
is the leading exponent, and l is determined from the condition that  should be finite. Thus, to leading order, the sample space grows as
should be finite. Thus, to leading order, the sample space grows as  . We now identify the scaling laws for the sub-leading corrections through higher-order rescalings
. We now identify the scaling laws for the sub-leading corrections through higher-order rescalings  . We get (see appendix)
. We get (see appendix)
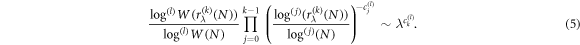
Equivalently, one can express this relation as,  , where
, where  . To extract
. To extract  , take the derivative of equation (4) w.r.t. λ, set λ = 1 and consider the limit
, take the derivative of equation (4) w.r.t. λ, set λ = 1 and consider the limit  . For the leading scaling exponent we obtain
. For the leading scaling exponent we obtain
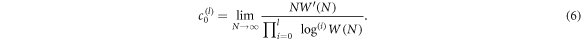
The scaling exponent corresponding to the kth order is obtained in a similar way and reads,
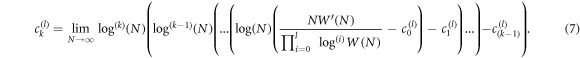
This expression is not identically equal to zero, because the expression on the rhs of equation (6) becomes  only in the limit. As a result, the phasespace volume grows as
only in the limit. As a result, the phasespace volume grows as
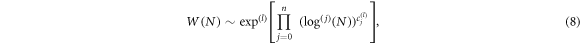
which is nothing but the Poincaré asymptotic expansion in equation (1). In the appendix we show that the formulas for cj, given by the theory of asymptotic expansions, correspond to the formulas for scaling exponents  and therefore it is indeed possible to express any W(N) in terms of an asymptotic expansion that is based on the sequence ϕn(N). The expansion coefficients are scaling exponents determined by the rescaling of phasespace. Here n denotes the minimal number of expansion terms. In the typical situations, only a few scaling exponents are non-zero. If all exponents are non-zero, we can truncate the expansion after a few terms and still preserve a high level of precision. In many realistic situations it is enough to consider n = 2. The estimation of the leading order exponent can be tricky, because looking for the order l incorporates calculation of several infinite limits. Therefore, it is convenient to use an approach based on the corresponding extensive entropy.
and therefore it is indeed possible to express any W(N) in terms of an asymptotic expansion that is based on the sequence ϕn(N). The expansion coefficients are scaling exponents determined by the rescaling of phasespace. Here n denotes the minimal number of expansion terms. In the typical situations, only a few scaling exponents are non-zero. If all exponents are non-zero, we can truncate the expansion after a few terms and still preserve a high level of precision. In many realistic situations it is enough to consider n = 2. The estimation of the leading order exponent can be tricky, because looking for the order l incorporates calculation of several infinite limits. Therefore, it is convenient to use an approach based on the corresponding extensive entropy.
3. The extensive entropy
The extensive entropy can be obtained by following an idea exposed in [7, 10]. Let us assume a so-called trace form entropy for some probability distribution 
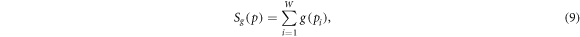
where g is some function. The aim is to find such a function g, for which the entropy functional Sg is extensive for a given W(N). Assuming that no prior information about the system is given, we consider uniform probabilities pi = 1/W. The extensivity condition can be expressed by an equation for g, which is [10]
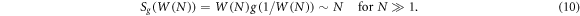
Alternatively, it is possible to define the extensive entropy as the solution of Euler's differential equation, see also [4],
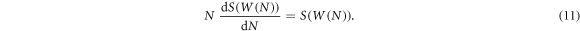
The question now is, how the scaling exponents of W(N) are related to scaling exponents of Sg(W). We begin with the first scaling operation  . One can show that for N ≫ 1, we have
. One can show that for N ≫ 1, we have
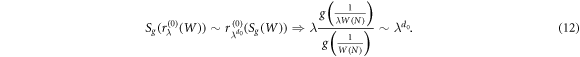
Thus,  for
for  . Again, it is possible to determine the relation for the nth scaling exponent
. Again, it is possible to determine the relation for the nth scaling exponent
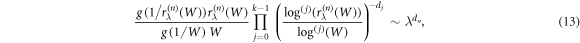
or equivalently,  , where
, where  . We can extract the scaling exponents dn by the same procedure as for
. We can extract the scaling exponents dn by the same procedure as for  by taking the derivative w.r.t. λ, setting λ = 1 and performing the limit. For the first exponent we get
by taking the derivative w.r.t. λ, setting λ = 1 and performing the limit. For the first exponent we get
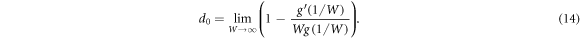
De L'Hospital's rule and applying the extensivity condition of equation (10) gives  , and
, and
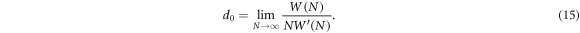
We mentioned this result already above. The nth term can be found analogously to be
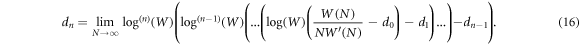
We can now relate the scaling exponents  and dn by comparing equations (7) and (16). For this we use a similar notation as for the exponents
and dn by comparing equations (7) and (16). For this we use a similar notation as for the exponents  and assign
and assign  to the first non-zero exponent,
to the first non-zero exponent,  . All higher terms are denoted by
. All higher terms are denoted by  . Using the fact that
. Using the fact that  , we finally obtain
, we finally obtain
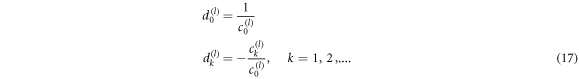
The corresponding extensive entropy can now be characterized by the function g(x), which scales as
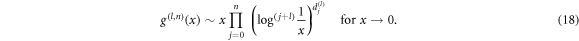
the corresponding entropy scales as
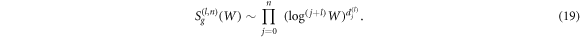
This equation is nothing but the asymptotic expansion of  in terms of
in terms of  the coefficients are again the scaling exponents that correspond to the rescaling of the entropy.
the coefficients are again the scaling exponents that correspond to the rescaling of the entropy.
Note that the entropy approach allows us to obtain additional restrictions for the scaling exponents if further information about the system is available. For example, many systems fulfil the first three of the four SK axioms, see appendix. There we also show that it is possible to find a representation of the entropy that obeys the three axioms and the scaling in equation (19). In this case g(x) can be expressed as
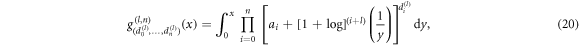
where ai are constants. One possible choice for those is
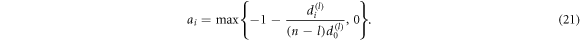
The axioms impose restrictions on the range of scaling exponents. (SK2) requires that  (SK3) requires that
(SK3) requires that  . The resulting entropy can be expressed by equation (12). One can trivially adjust the entropy minimal value, such that for the totally ordered state,
. The resulting entropy can be expressed by equation (12). One can trivially adjust the entropy minimal value, such that for the totally ordered state,  . This is obtained by rescaling
. This is obtained by rescaling
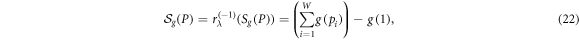
where  . Note that the form of the entropy in equation (20) is equivalent to (c, d)-entropy for c = 1 − d0 and d = d1, and dj = 0 for all j ≥ 2.
. Note that the form of the entropy in equation (20) is equivalent to (c, d)-entropy for c = 1 − d0 and d = d1, and dj = 0 for all j ≥ 2.
4. Examples
We conclude with several examples of systems that are characterized by different sets of scaling exponents.
4.1. Exponential growth: the random walk
Imagine the ordinary random walk with two possibilities at any timestep—a step to the left, or to the right. The number of possible configurations (i.e. possible paths) after N steps is
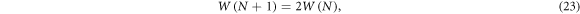
which means exponential phasespace growth,  . We obtain l = 1,
. We obtain l = 1,  and
and  , for j ≥ 1, and for the exponents of the entropy d0 = 0,
, for j ≥ 1, and for the exponents of the entropy d0 = 0,  and dj=0, for j ≥ 2. This set of exponents belongs to the class of (c, d)-entropies described in [7] for c = 1 − d0 = 1, and d = d1 = 1. They correspond to the scaling exponents of the Shannon entropy: from (18) we obtain that
and dj=0, for j ≥ 2. This set of exponents belongs to the class of (c, d)-entropies described in [7] for c = 1 − d0 = 1, and d = d1 = 1. They correspond to the scaling exponents of the Shannon entropy: from (18) we obtain that  and from (19) we get
and from (19) we get  , which is Boltzmann entropy. It is not immediately apparent what the entropy of a random walk should be. However, the random walk is equivalent to spin system of N independent spins, the 2N different paths correspond one-to-one to the 2N configurations in the spin model, where the role entropy of it is clear. Obviously, for the random walk, (SK1–3) are applicable.
, which is Boltzmann entropy. It is not immediately apparent what the entropy of a random walk should be. However, the random walk is equivalent to spin system of N independent spins, the 2N different paths correspond one-to-one to the 2N configurations in the spin model, where the role entropy of it is clear. Obviously, for the random walk, (SK1–3) are applicable.
4.2. Sub-exponential growth: the aging random walk
In this variation of the random walk we impose correlations on the walk. After the first random choice (left or right) the walker goes one step in that direction. The second random choice is followed by two steps in the same direction, the next step is followed by three steps in the same direction, etc. For k independent choices, one has to make  steps. For this walk, we get that the number of possible paths is
steps. For this walk, we get that the number of possible paths is
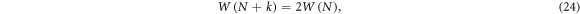
which leads to  . For N ≫ 1, we have
. For N ≫ 1, we have  , and we obtain a stretched exponential (sub-exponential) asymptotic behavior,
, and we obtain a stretched exponential (sub-exponential) asymptotic behavior,  . The order is again l = 1 and the exponents are
. The order is again l = 1 and the exponents are  and
and  , for j ≥ 1. In terms of the d exponents we have d0 = 0 and
, for j ≥ 1. In terms of the d exponents we have d0 = 0 and  . Therefore, the three SK axioms are applicable and the resulting extensive entropy belongs to the class of entropies characterized by the Anteneodo–Plastino entropy, since we have
. Therefore, the three SK axioms are applicable and the resulting extensive entropy belongs to the class of entropies characterized by the Anteneodo–Plastino entropy, since we have  and
and  . This entropy is the special case of the (c, d)-entropy for c = 1 and d = 2, see [7].
. This entropy is the special case of the (c, d)-entropy for c = 1 and d = 2, see [7].
4.3. Super-exponential growth: magnetic coins
Consider N coins with two states (up or down). These coins are magnetic, so that any two can stick to each other to create a pair which is a third state obtained by interactions of elements (one possible configuration). As mentioned before, in [11] it is shown that the phasespace volume can be obtained recursively
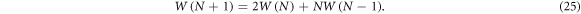
For  , we get
, we get  , which yields l = 1, and the scaling exponents
, which yields l = 1, and the scaling exponents  ,
,  and
and  , for
, for  . The scaling exponents of the entropy are d0 = 0,
. The scaling exponents of the entropy are d0 = 0,  , and
, and  . For the entropy this means, that
. For the entropy this means, that  and
and  . This case is not contained in the class of (c, d)-entropies, because the third exponent, corresponding to the doubly-logarithmic correction, is not zero. Actually we obtain c = 1 and d = 1, which would naively indicate Shannon entropy. However, the correction makes the system clearly super-exponential. The SK axioms are still applicable, the class of accessible entropy formulas is restricted by (SK2). For example, for the representative entropy equation (20) we find that a0 ≥ 0 and a1 ≥ 0, see appendix.
. This case is not contained in the class of (c, d)-entropies, because the third exponent, corresponding to the doubly-logarithmic correction, is not zero. Actually we obtain c = 1 and d = 1, which would naively indicate Shannon entropy. However, the correction makes the system clearly super-exponential. The SK axioms are still applicable, the class of accessible entropy formulas is restricted by (SK2). For example, for the representative entropy equation (20) we find that a0 ≥ 0 and a1 ≥ 0, see appendix.
4.4. Super-exponential growth: random networks
Imagine a random network with N nodes. When a new node is added, there emerge N new possible links, which gives us 2N new possible configurations for each configuration of the network with N links. We obtain the recursive growth equation
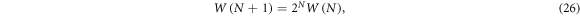
which leads to  , as expected. For this phasespace growth, we obtain l = 1,
, as expected. For this phasespace growth, we obtain l = 1,  and
and  for
for  , and d0 = 0 and
, and d0 = 0 and  . The corresponding entropy can be expressed by
. The corresponding entropy can be expressed by  , and
, and  . The entropy corresponds to the class of compressed exponentials, which are super-exponential, however, the entropy belongs to the class of (c, d)-entropies for c = 1 and d = 1/2. Because all exponents are positive the entropy observes the SK axioms.
. The entropy corresponds to the class of compressed exponentials, which are super-exponential, however, the entropy belongs to the class of (c, d)-entropies for c = 1 and d = 1/2. Because all exponents are positive the entropy observes the SK axioms.
4.5. Super-exponential growth: the cascading random walk
Consider a generalization of the random walk, where a walker can take a left or right step, but it can also split into two walkers, one of which then goes left, the other to the right. Each walker can then go left, right, or split again (multiple walkers can occupy the same position). The number of possible paths after N steps is
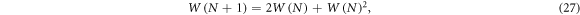
where the first term reflects the left/right decisions, the second the splittings. We have  , and find that l = 2,
, and find that l = 2,  and
and  , for
, for  , and
, and  ,
,  and
and  . The corresponding extensive entropy is
. The corresponding extensive entropy is  and scales as
and scales as  . Because the coefficients are not negative, SK axioms are applicable. However, even though all correction scaling exponents are zero, the system cannot be described in terms of (c, d)-entropies, because l = 2. We would naively obtain that c = 1 and d = 0, which would wrongly correspond to Tsallis entropy. Alternatively, we can think of an example of a spin system with the same scaling exponents. In this case, N would not describe the size of a system, but its dimension. For N = 1, we would have two particles on the line, for N = 2 we have 4 particles forming a square, for N = 3 we have a cube with 8 particles in its vertices, etc. In general, we can think of a spin system of particles sitting on the vertices of a N-dimensional hypercube. The number of particles is naturally 2N and for two possible spins we obtain
. Because the coefficients are not negative, SK axioms are applicable. However, even though all correction scaling exponents are zero, the system cannot be described in terms of (c, d)-entropies, because l = 2. We would naively obtain that c = 1 and d = 0, which would wrongly correspond to Tsallis entropy. Alternatively, we can think of an example of a spin system with the same scaling exponents. In this case, N would not describe the size of a system, but its dimension. For N = 1, we would have two particles on the line, for N = 2 we have 4 particles forming a square, for N = 3 we have a cube with 8 particles in its vertices, etc. In general, we can think of a spin system of particles sitting on the vertices of a N-dimensional hypercube. The number of particles is naturally 2N and for two possible spins we obtain  .
.
5. Conclusions
We introduced a comprehensive classification of complex systems in the thermodynamic limit based on the rescaling properties of their phasespace volume. From a scaling-expansion of the phasespace growth with system size, we obtain a set of scaling exponents, which uniquely characterize the statistical structure of the given system. Restrictions on the scaling exponents can be obtained with further information about the system. In this context we discuss the first three SK axioms, which are valid for many complex systems. The set of exponents further determine the scaling exponents of the corresponding extensive entropy, which plays a central role in the thermodynamics of statistical systems. Thermodynamics is not the only context where entropy appears. As was shown in [5] for many complex systems the functional expressions for entropy depend on the context, in particular if one talks about the thermodynamic (extensive) entropy, the information theoretic entropy, or the entropy that appears in the maximum entropy principle. It remains to be seen if for super-exponential systems there exists an underlying relation between the scaling exponents of the extensive entropy, and the exponents obtained from a information theoretic, or maximum entropy description of the same complex systems.
Acknowledgments
We thank the participants of CSH workshop for helpful initial discussion, in particular Henrik Jeldtoft Jensen, Tamás Sándor Biró, Piergiulio Tempesta and Jan Naudts. This work was supported by the Austrian Science Fund (FWF) under project I3073.
: Appendix
A.1. SK axioms
The SK axioms read:
- (SK1) Entropy is a continuous function of the probabilities pi only, and should not explicitly depend on any other parameters.
- (SK2) Entropy is maximal for the equi-distribution
 .
. - (SK3) Adding a state
 to a system with
to a system with  does not change the entropy of the system.
does not change the entropy of the system. - (SK4) Entropy of a system composed of 2 sub-systems A and B, is
 .
.
They state requirements that must be fulfilled by any entropy. For ergodic systems all four axioms hold. For non-ergodic ones the composition axiom (SK4) is explicitly violated, and only the first three (SK1–SK3) hold. If all four axioms hold the entropy is uniquely determined to be Shannon's; if only the first three axioms hold, the entropy is given by the (c, d)-entropy [7, 10]. The SK axioms were formulated in the context of information theory but are also sensible for many physical and complex systems.
Given a trace form of the entropy as in equation (9), the SK axioms imply the restrictions on g(x): (SK1) implies that g is a continuous function, (SK2) means that g(x) is concave, and (SK3) that  . For details, see [7].
. For details, see [7].
A.2. Rescaling in the thermodynamic limit
We first prove a theorem which determines the general form of rescaling relations in the thermodynamic limit for any general function.
Theorem. Let g(x) be a positive, continuous function on  . Let us define the function
. Let us define the function 
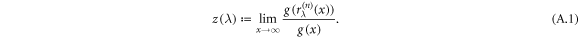
Then,  for some
for some  .
.
Proof. From the definition of  , it is straightforward to show that
, it is straightforward to show that  , because
, because
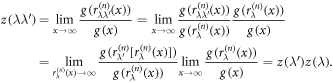
For the computation we used the group property of rescaling in equation (3) and the continuity of g. The only class of functions satisfying the functional equation above are power functions,  . □
. □
Let us take the first scaling relation of the sample space  . From the previous theorem we obtain
. From the previous theorem we obtain
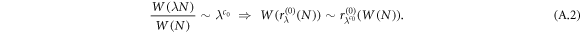
It may happen that c0 is infinite. Thus, we may need to use higher-order scaling for the sample space, i.e.,  , as shown in the main text. l is determined by the condition that the scaling exponent should be finite. The first correction term is given by the scaling
, as shown in the main text. l is determined by the condition that the scaling exponent should be finite. The first correction term is given by the scaling  . To obtain the sub-leading correction, we have to factor out the leading growth term. This means that the scaling relation for the first sub-leading correction looks like
. To obtain the sub-leading correction, we have to factor out the leading growth term. This means that the scaling relation for the first sub-leading correction looks like
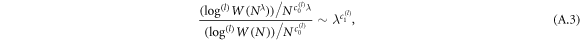
which is again a consequence of the above theorem. To obtain the corresponding scaling relations for higher-order scaling exponents for the sample space (A.4), we need to factor out all previous terms corresponding to lower-order scalings, so the scaling relation looks like
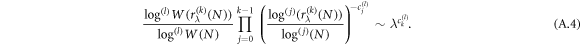
Because the left-hand side of this relation has the form of the function z appearing in the theorem, the validity of the relation is satisfied for  . Similarly, we can deduce the relations for scaling exponents that are associated with the extensive entropy.
. Similarly, we can deduce the relations for scaling exponents that are associated with the extensive entropy.
A.3. Asymptotic expansion in terms of nested logarithms
The asymptotic representation of W(N) is obtained by the rescaling that corresponds to the Poincaré asymptotic expansion [13] of  in terms of
in terms of  for
for  . Let us consider a function f(x) with a singular point at x0. It is possible to express its asymptotic properties in the neighborhood of x0 in terms of the asymptotic series of functions
. Let us consider a function f(x) with a singular point at x0. It is possible to express its asymptotic properties in the neighborhood of x0 in terms of the asymptotic series of functions  , if
, if  and
and  . The series is given as
. The series is given as
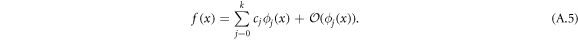
The coefficients can be calculated from the formulas in [13]
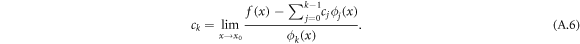
In our case, i.e., for  and
and  the function
the function  can be expressed (for appropriate l) in terms of this series, and the coefficients
can be expressed (for appropriate l) in terms of this series, and the coefficients  are given by
are given by
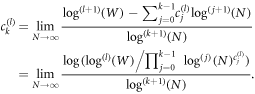
Using L'Hospital's rule and the derivative of the nested logarithm
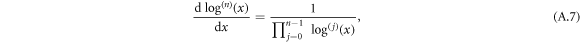
a straightforward calculation yields equation (7).
A.4. Derivation of 
Which entropy functional that fulfills axioms (SK1–3)? The choice is not unique, but a concrete entropy functional serves as a representative of the class in the thermodynamic limit. The requirements imposed by the first three SK axioms are: g(x) is continuous, g(x) is concave, and  . From equation (18) we have,
. From equation (18) we have, ![$g(x)\sim x{\prod }_{j=0}^{n}{\left[{\mathrm{log}}^{(j+l)}\left(\tfrac{1}{x}\right)\right]}^{{d}_{j}^{(l)}}$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn117.gif) for
for  , which gives us the scaling for the values around zero. Unfortunately, the presented form cannot be extended to the full interval
, which gives us the scaling for the values around zero. Unfortunately, the presented form cannot be extended to the full interval ![$[0,1]$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn119.gif) , because the domain of
, because the domain of  is
is  . This can be fixed by replacing
. This can be fixed by replacing  by
by ![${[1+\mathrm{log}]}^{(n)}=1+\mathrm{log}(1+\mathrm{log}(...))$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn123.gif) , which is defined on the whole domain
, which is defined on the whole domain ![$(0,1]$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn124.gif) , where
, where ![${\mathrm{lim}}_{x\to 0}{[1+\mathrm{log}]}^{(n)}(1/x)=+\infty $](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn125.gif) and
and ![${[1+\mathrm{log}]}^{(n)}(1)=1$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn126.gif) . The scaling remains unchanged for
. The scaling remains unchanged for  .
.
The second problem is that in general the function is not concave. For this we introduce the transformation
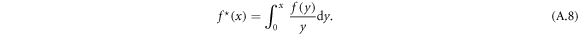
The original function can be obtained by
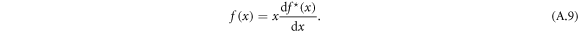
This transform turns an increasing/decreasing function to a convex/concave function, while the scaling for  remains unchanged. Let us write the function g in the form of the transform
remains unchanged. Let us write the function g in the form of the transform
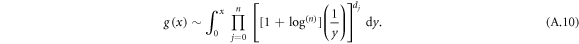
Axiom (SK3) means  . This requires that the integrand should not diverge faster than
. This requires that the integrand should not diverge faster than  for
for  . This can be fulfilled for
. This can be fulfilled for  .
.
Because ![${[1+\mathrm{log}]}^{(n)}(1/x)$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn133.gif) is a decreasing function, g(x) is automatically concave if
is a decreasing function, g(x) is automatically concave if  , since a product of positive, decreasing functions is also decreasing. However, for
, since a product of positive, decreasing functions is also decreasing. However, for  ,
, ![${[1+\mathrm{log}]}^{(n)}{(1/x)}^{{d}_{n}}$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn136.gif) is an increasing function from zero to one and the whole product may not be decreasing. In order to solve this issue, we introduce a set of constants ai and write g(x) in the form
is an increasing function from zero to one and the whole product may not be decreasing. In order to solve this issue, we introduce a set of constants ai and write g(x) in the form
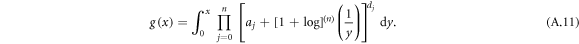
The constants ai can be chosen to ensure that the integrand is a decreasing function. We assume  to avoid problems with powers of negative numbers. The second derivative of g(x), i.e., the first derivative of the integrand is an increasing function and
to avoid problems with powers of negative numbers. The second derivative of g(x), i.e., the first derivative of the integrand is an increasing function and  for
for  . For
. For  , the entropy cannot be concave, so
, the entropy cannot be concave, so  is the restriction given by (SK2). To obtain a negative second derivative on the whole domain
is the restriction given by (SK2). To obtain a negative second derivative on the whole domain ![$[0,1]$](https://content.cld.iop.org/journals/1367-2630/20/9/093007/revision2/njpaadcbeieqn142.gif) , it is therefore enough to investigate
, it is therefore enough to investigate  , which leads to the condition
, which leads to the condition
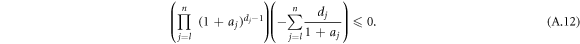
Because  , we can choose al = 0. In the following terms, i.e., for
, we can choose al = 0. In the following terms, i.e., for  , di can be both positive and negative. Positive di pose no problem, because the term corresponding to di, i.e.
, di can be both positive and negative. Positive di pose no problem, because the term corresponding to di, i.e.  is negative, so we can choose ai = 0. When all di are negative we can compensate the positive contribution of the negative terms by diminishing them through choice of appropriate ai. If we choose
is negative, so we can choose ai = 0. When all di are negative we can compensate the positive contribution of the negative terms by diminishing them through choice of appropriate ai. If we choose
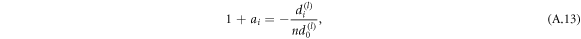
then equation (A.12) becomes zero. If this is given together with previous results and we summarize it as
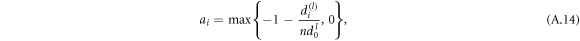
which has been presented in equation (21) in the main text. Clearly, this is not the only possible choice. Note that for all  , one may even choose
, one may even choose  . On the other hand, for the case of the magnetic coin model, one obtains that for
. On the other hand, for the case of the magnetic coin model, one obtains that for  ,
,  as well.
as well.
Finally, let us show the connection to (c, d)-entropy derived in [7]. In this case, we assume only d0 and d1 can be non-zero, which leads to
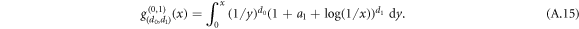
By the choice  , we get
, we get
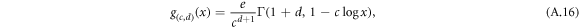
for  and
and  , which is nothing else than the gamma entropy of [7].
, which is nothing else than the gamma entropy of [7].
A.5. Ordering of processes and classes of equivalence
The set of scaling exponents form natural classes of equivalence with natural ordering. Consider two discrete random processes X(N) and Y(N) with sample spaces WX(N) and WY(N), respectively. The corresponding sets of scaling exponents are denoted by  , and
, and  . One can introduce an ordering based on the scaling exponents. We write
. One can introduce an ordering based on the scaling exponents. We write
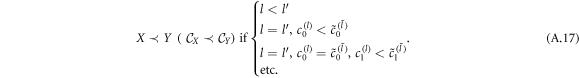
This is equivalent to lexicographic ordering. One can also introduce an ordering, which takes into account only certain a number of correcting terms. So, for example
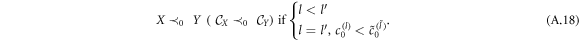
Similarly, one can define ≺k, which takes into account only k correction terms. Additionally, it is possible to introduce an equivalence relation
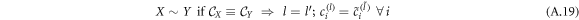
and also equivalence up to certain correction
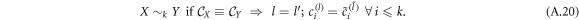
As an example, for magnetic coin model and random walk we have that  , but
, but  .
.
A.6. Construction of a 'representative process'
To understand the mechanism of how the scaling exponents correspond to the structure of a random process, let us discuss a simple procedure to generally obtain processes with given scaling exponents  . We start with a random variable X0 with N possible outcomes, so that
. We start with a random variable X0 with N possible outcomes, so that  . The scaling exponents of this process are naturally
. The scaling exponents of this process are naturally  and
and  for
for  . Let us construct a new variable by choosing subsets of
. Let us construct a new variable by choosing subsets of  .
.
First we can create all possible subsets of  . This defines a new variable X1 with
. This defines a new variable X1 with  , and we get
, and we get  . Generally, the transform
. Generally, the transform
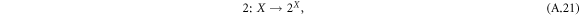
where  denotes a variable on all subsets of X. One can easily show that this results in a shift of scaling exponents
denotes a variable on all subsets of X. One can easily show that this results in a shift of scaling exponents  , and
, and  , because
, because  . The interpretation of this transformation is the following: consider an ordinary random walk with two possible steps. If
. The interpretation of this transformation is the following: consider an ordinary random walk with two possible steps. If  denotes a number of steps of a random walker, then
denotes a number of steps of a random walker, then  denotes the number of possible paths. When we apply the transform again, we obtain
denotes the number of possible paths. When we apply the transform again, we obtain  . This denotes the number of possible configurations of a random walk cascade, etc. As a result, by more applications of
. This denotes the number of possible configurations of a random walk cascade, etc. As a result, by more applications of  , we obtain processes with more complicated structure of the respective phasespace.
, we obtain processes with more complicated structure of the respective phasespace.
To construct processes with arbitrary exponents, let us think about a procedure, where we create only partial subsets, which number p(N) can be between N (no partitioning) and  (full partitioning). We denote this procedure by
(full partitioning). We denote this procedure by  . This can be understood as a process corresponding to a correlated random walk. This means that not every step of the walk is independent, but some steps can be determined by the previous steps, which diminishes the number of possible configurations when compared to the uncorrelated random walk. The resulting random process is obtained as the composition of l uncorrelated random walks (full partitioning) and a correlated random walk
. This can be understood as a process corresponding to a correlated random walk. This means that not every step of the walk is independent, but some steps can be determined by the previous steps, which diminishes the number of possible configurations when compared to the uncorrelated random walk. The resulting random process is obtained as the composition of l uncorrelated random walks (full partitioning) and a correlated random walk
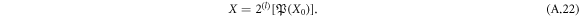
Let us now focus on the construction of correlated random walk with a pre-determined number of states given by p(N).
First we consider the full set of subsets of N elements with natural ordering,
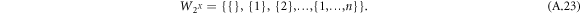
The correlations can be represented by merging subsets to p(N) sequences of length  , i.e.,
, i.e.,
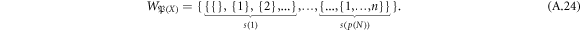
This means that after one independent step, there are  dependent steps, after the second independent step, there are
dependent steps, after the second independent step, there are  dependent steps, etc. Let us determine the form of function s for given p(N). The function s can be obtained from
dependent steps, etc. Let us determine the form of function s for given p(N). The function s can be obtained from
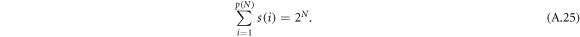
In the limit of large N we can assume that the function s does not depend on N, i.e., is a priori given by the scaling exponents of the system. Let us also assume, without loss of generality, that s is an increasing function (we can neglect the last cell, because its size is determined by the size of previous cells). For  , we approximate the sum by the integral and obtain
, we approximate the sum by the integral and obtain
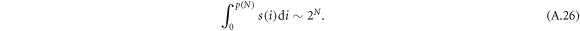
Denoting  , and substituting
, and substituting  , we recast the previous equation as,
, we recast the previous equation as,  , where
, where  denotes the inverse function of p. The function s(x) can be therefore determined as
denotes the inverse function of p. The function s(x) can be therefore determined as
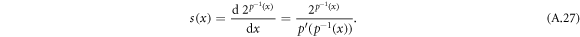
Some examples for s(x) for a corresponding p(N) are
-
 , i.e., full partitioning corresponding to uncorrelated random walk. In this case, we obtain that
, i.e., full partitioning corresponding to uncorrelated random walk. In this case, we obtain that  , as expected.
, as expected. -
 , i.e., no partitioning to maximally correlated random walk. We obtain that
, i.e., no partitioning to maximally correlated random walk. We obtain that  , which can be seen from the relation
, which can be seen from the relation  .
. -
 , which corresponds to the correction in the magnetic coin model. In this case,
, which corresponds to the correction in the magnetic coin model. In this case,  , where W(x) is the Lambert W-function.
, where W(x) is the Lambert W-function.