Abstract
Motivated by the need for quantum computers to communicate between multiple, well separated qubits, we introduce the task of routing the quantum state from one input mode to a superposition of several output modes coherently. We report an experimental demonstration of a deterministic photonic routing protocol applied to an entangled state. We show in a quantum walk architecture, quantum networks perfectly route entangled states from an initial input mode to an arbitrary output mode coherently and deterministically. Our results demonstrate the key principle of a perfect router, opening a route toward data routing and transferring for quantum computing systems. The routing algorithm in our work can be applied to a wide range of physical systems, which provides a way for effective design of efficient routing protocols on practical quantum networks.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Compared to quantum computers and quantum communications, little notice has been made of work on what is known as quantum routers. That is because routing quantum information has been very difficult because of the peculiar nature of the quantum world [1, 2]. Compared to its classical counterpart—a classical router, the obstacle is in creating devices capable of routing information from a signal that tells a router where to send data without destroying either data or signal [3]. By taking the advantages of superposition and entanglement, one can get around the problem and build a quantum router [4–8].
Recently, there have been growing interests and algorithmic developments for quantum routers [9–23]. Several schemes use light–matter interaction in order to achieve quantum routing. For instance, an optical switch routes single-photon pulses based on micro-electromechanical or optical control [24, 25]. In a cavity quantum electrodynamic system, single trapped ions and superconducting circuits are able to route the spatial modes of single photons [26–31]. An ionic routing algorithm has been provided in [32]. In [33–35], single photonic quantum routers using the platform of optical interactions to accomplish the routing have been demonstrated.
Based on the requirements to be suitable for quantum information processing, five standards of building a successful quantum router have been summarized [36–38]: (i) any state can be routed from an input mode to an arbitrary output mode. (ii) The signal state is not changed under routing. The signal information is kept undisturbed. (iii) During the process of routing, the information of the signal is encoded into coherent superposition of the output modes, which is one of pure quantum features. (iv) Quantum router works without postselection. (v) The less resource cost, the better.
In this paper, we develop an algorithm for a router acting as quantum data bus [39–44] and entanglement distributor [45–50]. Our algorithm is based on a discrete-time quantum walk (QW) with time- and position-dependent coin flipping [51–57]. Via executing a properly engineered QW, we control the internal degree of freedom of two-level coins, quantum data encoded in the coin states are carried by the walker and routed in a coherent way to an arbitrary position on demand deterministically.
Compared to a conventional quantum router, in which both control and signal information would be encoded into qubits, we release the requirement of control qubits and the control information is physically encoded in coin parameters which are determined by the algorithm. Thus, we prefer calling our router as a 'semi-quantum router' as it meets five standards of quantum routers but without a control qubit.
We implement this algorithm and realize photonic routing using entangled photons and linear optics. It is confirmed that the coin states are well preserved by the router through quantum process tomography. We also demonstrate the physical nature of this photonic router by showing the entanglement between the coin states in different positions. Thus, our photonic router meets all the five standards and will represent an essential building block in future quantum information networks [58–70].
2. Results
2.1. Semi-quantum routing algorithm
As illustrated in figure 1(a), a standard model of a one-dimensional QW consists of a walker carrying a coin which is flipped before each step [71–74]. The time- and position-dependent coin rotation for the tth step 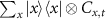 (here
(here  with the coin-state basis
with the coin-state basis 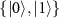 ) is applied, followed by a conditional position shift
) is applied, followed by a conditional position shift 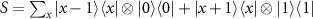 due to the outcome of the coin rotation. The unitary operation for the tth step is
due to the outcome of the coin rotation. The unitary operation for the tth step is 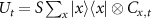 .
.
Figure 1. Routing problem statement via QWs. (a) Schematic of a one-dimensional QW. The red and blue lines indicate the information flow of α and β. The red and blue dots indicate that the coin flipping is not identity in this position. The black dots indicate that the coin flipping is identity in the position. The probability amplitude of the walker walking from the initial position to the x position along the blue path corresponds to the left-hand side of equation (3), while the probability amplitude along the red path corresponds to the right-hand side of equation (3). (b) QW with two walkers walking along x and y axes, respectively.
Download figure:
Standard image High-resolution imageThe quantum data are encoded in the initial coin state 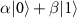 (
(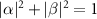 ) and sent to an arbitrary position on a one-dimensional lattice on demand. Suppose the walker starts from the original position
) and sent to an arbitrary position on a one-dimensional lattice on demand. Suppose the walker starts from the original position  . The formalized description of the semi-quantum routing task can be written as
. The formalized description of the semi-quantum routing task can be written as

That is, after t steps, the signal information encoded in the coin state can be routed from the input mode x = 0 to an arbitrary coherent superposition of the output modes  (or 0) for an odd number of steps t (or even t) in a deterministic way.
(or 0) for an odd number of steps t (or even t) in a deterministic way.
We can divide the routing task into three stages as illustrated in figure 1(a). First, we apply the coin rotation 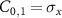 to the initial coin state and it is flipped into
to the initial coin state and it is flipped into 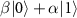 . Second, for the ith step (
. Second, for the ith step (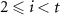 ), the position-dependent coin rotation
), the position-dependent coin rotation
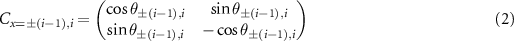
is applied to the coin for 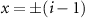 and
and 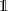 is applied for other cases, and θ is the parameter of coin rotation. Third, for the last step t, the coin rotation
is applied for other cases, and θ is the parameter of coin rotation. Third, for the last step t, the coin rotation 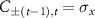 is applied to the coin for
is applied to the coin for  and
and 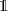 is applied for other cases. The parameters Ax
satisfy the following relations
is applied for other cases. The parameters Ax
satisfy the following relations
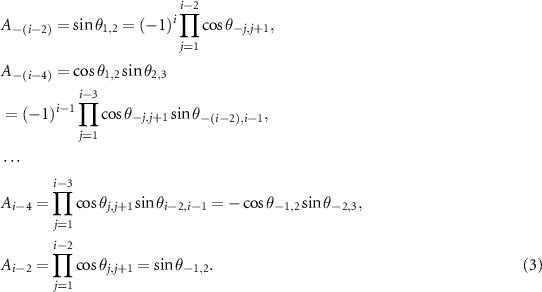
Next, we extend the algorithm to that for an entanglement router based on a QW in figure 1(b), which consists of two walkers and two coins [75, 76]. The routing task in each direction is the same as the one-dimensional routing task in equation (1). The basis state is of the form 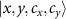 describing the position (x, y) of the walkers and the corresponding coin states with
describing the position (x, y) of the walkers and the corresponding coin states with  . The time evolution for each step is then
. The time evolution for each step is then
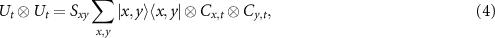
where 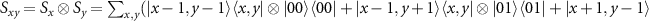
 , and the choices of the coin operators
, and the choices of the coin operators 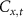 and
and 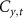 are same as those for the one-dimensional QW in equation (2). The quantum data are encoded in the initial coin state
are same as those for the one-dimensional QW in equation (2). The quantum data are encoded in the initial coin state 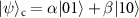 and sent to the position (x, y) on demand, deterministically and coherently. The entanglement routing task can be written as
and sent to the position (x, y) on demand, deterministically and coherently. The entanglement routing task can be written as
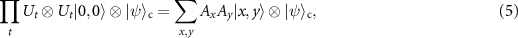
where 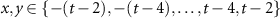 after the tth step in the evolution. The parameters Ax
and Ay
satisfy the relations in equation (3). The user informs two walkers of the demand of Ax
and Ay
according to equation (5), and then two walkers can precisely adjust the coin parameters θ according to equation (3). That is, after t steps of a two-dimensional QW, the signal information encoded in the entangled state
after the tth step in the evolution. The parameters Ax
and Ay
satisfy the relations in equation (3). The user informs two walkers of the demand of Ax
and Ay
according to equation (5), and then two walkers can precisely adjust the coin parameters θ according to equation (3). That is, after t steps of a two-dimensional QW, the signal information encoded in the entangled state 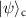 is routed from the position
is routed from the position 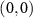 to (x, y) or a superposition of all output modes, where
to (x, y) or a superposition of all output modes, where 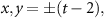
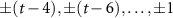 (or 0) for an odd number of steps t (or even t).
(or 0) for an odd number of steps t (or even t).
In this algorithm, all the five standards of building a successful quantum router are met. An arbitrary single-qubit (two-qubit) state can be routed from an input mode to an arbitrary output mode via QWs with single walker (two walkers). The signal state is not changed under routing and the signal information encoded in the coin state is kept undisturbed. During the routing process, the signal information is routed to a coherent superposition of the output modes on demand [37, 77], which is completely different from the task of quantum state transfer, transferring a quantum state from one input mode to one output mode. No postselection is required, nor is ancilla. Thus, our semi-quantum router works in a deterministic way.
2.2. Experimental demonstration
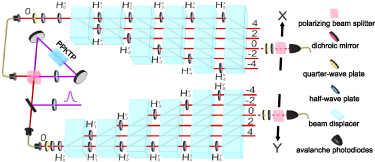
The experimental setup for realization of a deterministic photonic router is illustrated in figure 2, consists of an entangled photon source, two cascaded interferometric networks and measurement devices. For generating polarization-entangled photons, a type-II periodically poled potassium titanyl phosphate (PPKTP) crystal in a Sagnac interferometer configuration is used, which is pumped by a continuous wave (CW) diode laser operating at 405 nm. Two interference filters with a bandwidth of 3 nm are used to filter the photons. The state parameter is controlled simply by the polarization of the pumping laser which is tuned by an ultraviolet half-wave plate (HWP). The measured pump power at the input face of the PPKTP crystal is 2.71 mW and the coincidence count rate of 14 000 pair per second is achieved. The coin states are represented by the horizontal 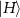 and vertical
and vertical 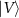 polarization states of the photon pairs, and the walker states are encoded in their spatial modes. The initial coin state is prepared in one of the Bell states
polarization states of the photon pairs, and the walker states are encoded in their spatial modes. The initial coin state is prepared in one of the Bell states 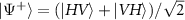 with fidelity
with fidelity 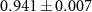 .
.
Figure 2. Experimental setup. Polarization-entangled photon pairs are generated via spontaneous parametric down-conversion. The parameters of the initial two-qubit entangled states are controlled via the setting angle of the ultraviolet HWP. For a QW with two walkers, each photon of an entangled photon pair is steered into the optical modes of the beam-displacer interferometric network. Tomographic measurement of quantum states is performed by wave plates and a PBS. Output photons are then detected by two APDs, registering the two-photon coincidence events.
Download figure:
Standard image High-resolution imageEach photon of an entangled photon pair is steered into the optical modes of a cascaded interferometric network formed by a series of birefringent calcite beam displacers (BDs) and HWPs. The conditional position shift Sx
(Sy
) is implemented by a BD, whose axis is cut so that vertically polarized photons are directly transmitted, and horizontally polarized ones move up a lateral displacement into a neighboring mode and interfere with the vertically polarized photons in the same mode. The site-dependent coin rotations 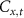 or
or 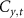 for the tth step can be realized via HWPs with certain setting angles placed in mode x or y. The angles of the first HWP (H
for the tth step can be realized via HWPs with certain setting angles placed in mode x or y. The angles of the first HWP (H
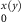 ) is set to 45∘ to realize σx
and the angles of the other HWPs (H
) is set to 45∘ to realize σx
and the angles of the other HWPs (H
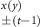 ) are set to
) are set to 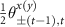 to realize
to realize 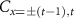 (
(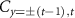 ) in equation (2) (see supplemental materials for details). Output photons are detected using avalanche photo-diodes (APDs) whose coincidence signals, monitored using commercially available counting logic, are used to collect two single-photon events. The walker position probabilities are obtained by normalizing the coincidence counts on each mode with respect to the total count for each respective step. A tomographic reconstruction of the coin state is performed to demonstrate a perfect router.
) in equation (2) (see supplemental materials for details). Output photons are detected using avalanche photo-diodes (APDs) whose coincidence signals, monitored using commercially available counting logic, are used to collect two single-photon events. The walker position probabilities are obtained by normalizing the coincidence counts on each mode with respect to the total count for each respective step. A tomographic reconstruction of the coin state is performed to demonstrate a perfect router.
In our experiment, we realize six-step QWs with two walkers. The first task is to route the quantum information encoded in the entangled coin state coherently to total 25 output modes. The final state of the QW evolves to a product state of an equal superposition state of the walkers and the unchanged coin state, i.e. 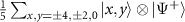 . For each output mode, we perform a tomographic reconstruction of the coin state to demonstrate a perfect router. The resultant fidelities [78]
. For each output mode, we perform a tomographic reconstruction of the coin state to demonstrate a perfect router. The resultant fidelities [78]

between the reduced coin state ρf
and the initial coin state ρin are shown in figure 3(a), ranging from 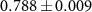 to
to 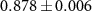 , which indicate an efficient demonstration of a photonic router. The position distribution of the QW after six steps is shown in figure 3(b). We obtain the experimental results of the probabilities ranging from
, which indicate an efficient demonstration of a photonic router. The position distribution of the QW after six steps is shown in figure 3(b). We obtain the experimental results of the probabilities ranging from 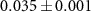 to
to 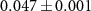 , which agree well with the theoretical prediction 0.04. In figures 3(c) and (d), real and imaginary parts of the experimentally reconstructed density matrix of the reduced coin state at the output mode
, which agree well with the theoretical prediction 0.04. In figures 3(c) and (d), real and imaginary parts of the experimentally reconstructed density matrix of the reduced coin state at the output mode  , which merely indicate that the final coin state has been routed from the input mode
, which merely indicate that the final coin state has been routed from the input mode 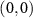 to the output mode
to the output mode 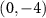 with the coin state well preserved during the process.
with the coin state well preserved during the process.
Figure 3. Experimental results of the photonic router. (a) Fidelities of the reduced coin states at each of total 25 output modes. (b) Probability distribution of the 6-step QW with two walkers. Real (c) and imaginary (d) parts of the reconstructed density matrix of the reduced coin state at the output mode 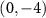 . Colored bars represent the experimental results and the hollow caps denote the theoretical predictions. Error bars indicate the statistical uncertainty, obtained from Monte Carlo simulations assuming Poissonian photon-counting statistics.
. Colored bars represent the experimental results and the hollow caps denote the theoretical predictions. Error bars indicate the statistical uncertainty, obtained from Monte Carlo simulations assuming Poissonian photon-counting statistics.
Download figure:
Standard image High-resolution imageThe second task is to route the signal information from the input mode 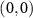 coherently to two output modes A
coherently to two output modes A
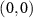 and B
and B
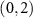 with equal probabilities. Thus, the final state of the QW is
with equal probabilities. Thus, the final state of the QW is  . For each mode, we reconstruct the reduced coin state via 2-qubit quantum state tomography. We also perform a 3-qubit tomographic measurement to reconstruct the final state of walker-coin
. For each mode, we reconstruct the reduced coin state via 2-qubit quantum state tomography. We also perform a 3-qubit tomographic measurement to reconstruct the final state of walker-coin 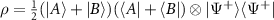 , in which we define
, in which we define 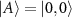 and
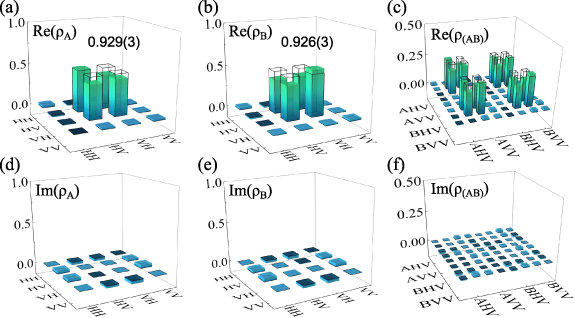
and 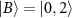 as a qubit. The experimentally reconstructed density matrices of the reduced coin state at either of two output modes are shown in figure 4, so is that of the final state of walker-coin. By comparing the experimentally reconstructed state of the walker-coin and its theoretical prediction, the fidelity is
as a qubit. The experimentally reconstructed density matrices of the reduced coin state at either of two output modes are shown in figure 4, so is that of the final state of walker-coin. By comparing the experimentally reconstructed state of the walker-coin and its theoretical prediction, the fidelity is  . By tracing out the coin state, the fidelity of the position-qubit state is as high as
. By tracing out the coin state, the fidelity of the position-qubit state is as high as 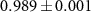 , which confirms coherence between the two output modes. The fidelities of the experimentally reconstructed coin states compared to the initial coin state ρin are
, which confirms coherence between the two output modes. The fidelities of the experimentally reconstructed coin states compared to the initial coin state ρin are  and
and 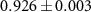 , respectively.
, respectively.
Figure 4. Experimentally reconstructed density matrices of the reduced coin state. Real (a), (b) and imaginary (d), (e) parts of the reconstructed density matrix of the reduced coin state at the output modes 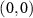 and
and  . (c), (f) Experimental results of a 3-qubit tomographic measurement to reconstruct the final state of walker-coin. Colored bars represent the experimental results and the hollow caps denote the theoretical predictions.
. (c), (f) Experimental results of a 3-qubit tomographic measurement to reconstruct the final state of walker-coin. Colored bars represent the experimental results and the hollow caps denote the theoretical predictions.
Download figure:
Standard image High-resolution imageA photonic router is described by a completely positive map which routes an arbitrary initial state to the corresponding final state. In quantum process tomography, a fixed set of basis operators is chosen so that the map is identified with a process matrix χ. Here we take the progress of the third task in which the signal information is routed from the input mode 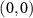 to the output mode
to the output mode 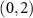 as an example and experimentally reconstruct χ through the maximum likelihood technique. We choose the basis operators
as an example and experimentally reconstruct χ through the maximum likelihood technique. We choose the basis operators  (
(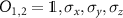 ), which require measurements on the evolved states of the sixteen different initial states
), which require measurements on the evolved states of the sixteen different initial states 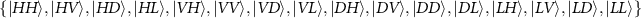 (here
(here 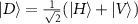 and
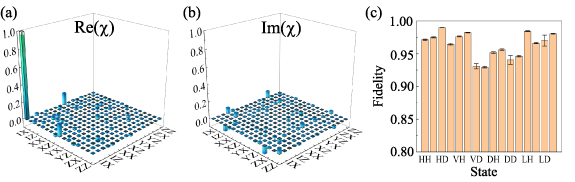
and 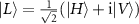 ). Real and imaginary parts of the reconstructed process matrix elements are shown in figures 5(a) and (b). The photonic router preserves the coin state. Thus, in the ideal case the process equals an identity operator. The experimentally reconstructed process matrices χexp are characterized by the process fidelity [79]
). Real and imaginary parts of the reconstructed process matrix elements are shown in figures 5(a) and (b). The photonic router preserves the coin state. Thus, in the ideal case the process equals an identity operator. The experimentally reconstructed process matrices χexp are characterized by the process fidelity [79]

In our experiment, the process fidelity is 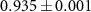 , which indicates a successful photonic router.
, which indicates a successful photonic router.
Figure 5. Experimental results of quantum process tomography. Real (a) and imaginary (b) parts of the reconstructed process matrix elements for the photonic router. The photonic router preserves the coin state, so in the ideal case the operation is represented by an identity operator with its elements shown by hollow caps. (c) Fidelities of total 16 reduced coin states at the output mode 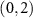 .
.
Download figure:
Standard image High-resolution imageFinally, we choose total 16 product states as the initial coin states, which are routed from 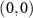 to
to 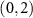 after the evolution of the 6-step QW. Our results in figure 5(c) exhibit all the fidelities are larger than
after the evolution of the 6-step QW. Our results in figure 5(c) exhibit all the fidelities are larger than 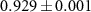 , which indicate that our routing algorithm also works for product states.
, which indicate that our routing algorithm also works for product states.
3. Error analysis
The imperfections cause the difference between the experimental results of the disturbances and their theoretical predictions. There are three sources of imperfections in our experiment: fluctuations in the counts of photons, inaccurate wave plates and decoherence (dephasing) caused by the imperfect interferometers. We perform numerical simulations by considering all the experimental imperfections. First, the imperfection caused by photon-number fluctuations decreases with increasing photon counts. In our experiment, the total photon count for each task is larger than 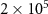 . It can be seen from the data plots that the error bars caused by photon number fluctuations in our experiments are small, so we focus on the remaining two factors below. Second, for each wave plate, we assume an uncertainty in the setting angle
. It can be seen from the data plots that the error bars caused by photon number fluctuations in our experiments are small, so we focus on the remaining two factors below. Second, for each wave plate, we assume an uncertainty in the setting angle 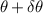 , where δθ is randomly chosen from the interval
, where δθ is randomly chosen from the interval ![$\left[-1.719^{\circ},1.719^{\circ} \right]$](https://content.cld.iop.org/journals/1367-2630/25/5/053011/revision2/njpacd270ieqn77.gif) . The range of these intervals is determined through Monte Carlo simulations to fit the deviations of experimental data from their theoretical predictions. On the other hand, the dephasing due to the imperfection of the five-stage interferometer affects the experimental results through a noisy channel
. The range of these intervals is determined through Monte Carlo simulations to fit the deviations of experimental data from their theoretical predictions. On the other hand, the dephasing due to the imperfection of the five-stage interferometer affects the experimental results through a noisy channel 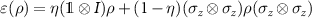 acting on the polarization state in different output modes, where ρ (
acting on the polarization state in different output modes, where ρ (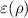 ) is the density matrix of the input (output) state of the noisy channel. By numerically minimizing the difference between the numerical results and the corresponding experiment data, we estimate η to be 0.913.
) is the density matrix of the input (output) state of the noisy channel. By numerically minimizing the difference between the numerical results and the corresponding experiment data, we estimate η to be 0.913.
There are three sources of photon losses in our experiment: the fiber coupling efficiency, the transmissivity of optical elements and the efficiency of the single-photon APDs. The fiber coupling efficiency is about  . The transmissivity of the set-up involving all the optical elements is about
. The transmissivity of the set-up involving all the optical elements is about 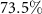 . The detection efficiency of single-photon APDs is about
. The detection efficiency of single-photon APDs is about 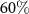 . Thus, the global detection efficiency in our experiment is about
. Thus, the global detection efficiency in our experiment is about 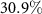 . The photon losses do not change the coin state and only affect the efficiency of routing tasks.
. The photon losses do not change the coin state and only affect the efficiency of routing tasks.
4. Discussion and conclusion
Goals of a quantum (or semi-quantum) routing protocol is to enable high rate entanglement among multiple users on demand. The main achievements of our work are two-fold: first, we develop an algorithm for a semi-quantum router based on a discrete-time QW with time- and position-dependent coin flipping. The routing algorithm is general, which can not only be applied to photons or light at different wavelengths including communication in optical systems, but also be directly applied to a wide range of physical systems, such as chip-scale waveguide circuits, superconducting quantum circuits, nuclear magnetic resonance systems and trapped ions, etc. The routing algorithm can be executed via a well-designed QW operating at telecom wavelength. The data encoded in photons can then be distributed to different locations. Coupling the photons into the telecom fibers, the data can be transmitted to users over significant distances, thereby achieving the application of telecommunication in quantum networks. The routing algorithm can be extended to coherently route an arbitrary N-qubit state from an input mode to an arbitrary superposition of output modes. Second, we implement this algorithm and realize a photonic router using entangled photons and linear optics, routing entangled states from one input mode to an arbitrary superposition of output modes coherently and deterministically. The polarization states of the routed photons are maintained during the routing operation. Our photonic router has the advantage of high efficiency and determinacy. It is the most efficient photonic router developed to this date. This work would spur the potential applications of QWs, bringing together quantum information theory and computer network theory.
Acknowledgments
This work has been supported by the National Natural Science Foundation of China (92265209, 12025401, 12088101, U2230402). K K W acknowledges support from the National Natural Science Foundation of China (Grant No. 12104009).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Conflict of interest
The authors declare that there are no competing interests.
Author contributions
H X G and K K W performed the experiments with contributions from D K Q and Q L. P X designed the experiments, analyzed the results, and wrote the paper.
Supplementary data (8.8 MB PDF)