Abstract
Universal spectral properties of multiplex networks allow us to assess the nature of the transition between disease-free and endemic phases in the SIS epidemic spreading model. In a multiplex network, depending on a coupling parameter, p, the inverse participation ratio (IPR) of the leading eigenvector of the adjacency matrix can be in two different structural regimes: (i) layer-localized and (ii) delocalized. Here we formalize the structural transition point, p*, between these two regimes, showing that there are universal properties regarding both the layer size n and the layer configurations. Namely, we show that IPR ∼ n−δ, with δ ≈ 1, and revealed an approximately linear relationship between p* and the difference between the layers' average degrees. Furthermore, we showed that this multiplex structural transition is intrinsically connected with the nature of the SIS phase transition, allowing us to both understand and quantify the phenomenon. As these results are related to the universal properties of the leading eigenvector, we expect that our findings might be relevant to other dynamical processes in complex networks.
Export citation and abstract BibTeX RIS
1. Introduction
Universality is at the core of physics [1, 2]. Universal properties do not change from one system to another but represent an entire class of them. They allow us to go beyond the observation of macro variables towards the understanding of the mechanisms that trigger a given behavior. Another notable consequence of universality is that by understanding the behavior of one system, we are able to make conclusions about other systems of the same class or governed by the same set of symmetries. Universality in multilayer networks was firstly explored in [3], where the eigenvector properties of the corresponding adjacency matrix were shown to follow a simple scaling law. Complementarily, the spectral properties of multiplex networks have been recently explored in [4–6]. In addition, de Arruda et al [7] reported a non-trivial relationship between the eigenvalues of a relatively simple multiplex network composed of two layers. However, the analysis carried out in [7] mainly focused on the eigenvalues and their bounds rather than eigenvectors, which may provide additional valuable information about the network structure. Although here we focus on the analysis of the adjacency matrix in multiplex networks, we must also remark that the spectral properties of the Laplacian matrix were studied in [8–11] and were applied to the study of diffusion processes in [12]. From the dynamical viewpoint, the concept of layer-localization in multiplex networks was introduced in [5]. That is, when a disease is on top of a multiplex network, it can be localized in one or a subset of layers. This phenomenon depends on the intra-layer configurations and also on the coupling strength between layers. Moreover, it is intrinsically linked to the localization properties of the eigenvectors of the network adjacency matrix, commonly measured by the inverse participation ratio (IPR). Although this phenomenon was well-characterized in [5], the mechanism driving it was not fully understood. In more technical words, the leading eigenvector of a multiplex network can be in one of two different regimes as a function of the coupling parameter between layers: layer-localized regime and delocalized regime. However, the precise definition of the structural transition between those regimes, to the best of our knowledge, is still lacking in the literature. Therefore, here we propose a definition for the transition point between layer-localization to delocalization, showing that it can be used to collapse the IPR curves in a wide range of network configurations. This collapsing also reveals the universality of the transition. Finally, as an application, we analyze the disease spreading on multiplex networks, providing a dynamical condition for the layer-localization to the delocalization phase transition.
2. Universality of eigenvector delocalization
In its more general form, multiplex networks are composed by m layers [13–16]. Each layer has at most n nodes which might have a counterpart in the other layers. Here, we restrict to 2-layer multiplex networks (i.e. m = 2) where each layer has n nodes and each node has a counterpart on the other layer. Formally, these networks can be represented by the adjacency matrix A whose eigenvalue problem is given as
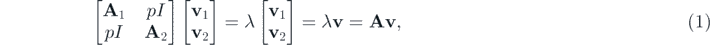
where A1,2 are the individual adjacency matrices, v1,2 are the respective sub-vector components, p is the coupling weight, and ∥v∥ = 1. Furthermore, we focus on the case where there is layer dominance [6, 17], i.e. λ1 ≫ λ2, where λ1 and λ2 are the leading eigenvalues of the individual layers. As a consequence, the components of the leading eigenvector of A2 should be relatively small, i.e.  . This can be easily seen using perturbation theory, see e.g. [17].
. This can be easily seen using perturbation theory, see e.g. [17].
In network theory [18–22], the IPR is commonly used to characterize the localization features of a network [5, 24, 25]. It is defined as

It is instructive to recall the IPR(v) behavior in single-layer networks. If the leading eigenvector is fully delocalized, IPR(v) ∼ N−1, which is the case of ER networks above the percolation transition. On the other hand, if IPR(v) ∼ N−δ
, with δ < 1, then some form of localization is present, which is the case of power-law (PL) networks, P(k) ∼ k−γ
, where  , as demonstrated in [23]. While, in the localized regime the leading eigenvector is concentrated in one or a finite number of nodes and IPR(v) ∼ O(1). For the sake of notation, we denote the IPR of the dominating and non-dominating layers as IPRDL and IPRNDL, respectively: IPRDL ≡ IPR(v1) and IPRNDL ≡ IPR(v2). Furthermore, since A is a function of p, both, their eigenvalues and eigenvectors also depend on p, therefore, IPR ≡ IPR(p). Consequently, by tuning p we can observe two different eigenvector regimes characterized by the IPR [5]: (i) layer-localized, where, as discussed in [5, 24],
, as demonstrated in [23]. While, in the localized regime the leading eigenvector is concentrated in one or a finite number of nodes and IPR(v) ∼ O(1). For the sake of notation, we denote the IPR of the dominating and non-dominating layers as IPRDL and IPRNDL, respectively: IPRDL ≡ IPR(v1) and IPRNDL ≡ IPR(v2). Furthermore, since A is a function of p, both, their eigenvalues and eigenvectors also depend on p, therefore, IPR ≡ IPR(p). Consequently, by tuning p we can observe two different eigenvector regimes characterized by the IPR [5]: (i) layer-localized, where, as discussed in [5, 24],  and (ii) delocalized, where
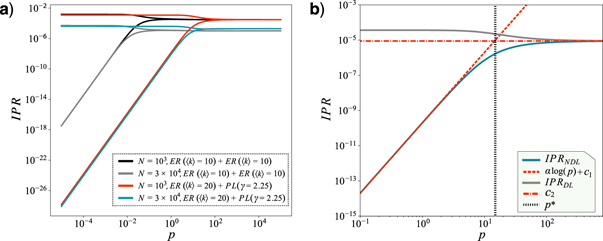
and (ii) delocalized, where  . This statement is exemplified in figure 1(a) where, without loss of generality, we consider homogeneous layers, so we cannot observe node localization. Next, we define p* as the crossover point between the layer-localized and localized regimes. Thus, when p ≪ p*, the eigenvector components are concentrated in a sub-extensive part of the eigenvector. Such part of the eigenvector corresponds to the dominating layer. However, the density of non-negligible eigenvector components corresponding to the non-dominating layer increases with the coupling parameter p. Indeed, from figure 1(a), we observe that in the localized regime, p < p*, the IPR's contribution of the non-dominating layer can be characterized by a PL (i.e. a linear trend in log–log scale), that is, log(IPRNDL(p < p*)) ≈ α log(p) + c1 with α ≈ 4. We also verified that α is independent of N, while c1 is dependent on the system size. Moreover, in the delocalized regime, p > p*, the states are evenly extended and do not change anymore with p and they are characterized by log(IPR(p > p*)) ≈ c2. In this regime, the inter-layer connections play the major role, while the intra-layer connections can be interpreted as perturbations. Hence, all the nodes contribute similarly to the leading eigenvector, making it delocalized. Therefore, the coupling p*, characterizing the delocalization transition, can be defined as the value of p such that IPRNDL(p < p*) = IPR(p > p*). This is illustrated in figure 1(b). With this prescription, we were able to systematically characterize the structural transition of the eigenvectors of our 2-layer network by means of the IPR. Importantly, figure 1 also shows that different network configurations produce different IPR functions. Note that, although all the curves have similar behavior, they are shifted in both axes. Aside from the dependence of the IPR on p, it also depends on the system size as IPR(p, n) ∼ n−δ
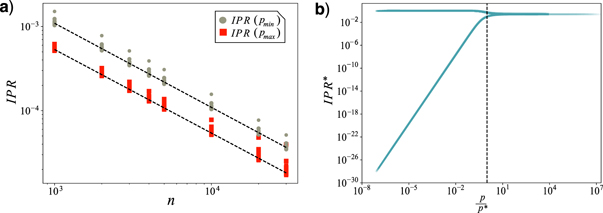
; as shown in figure 2(a). Thus, for a fixed number of layers and in the thermodynamic limit, both regimes scale similarly with δ ≈ 1 (see figure 2(a)). We remark that, in the thermodynamic limit, both IPRNDL(p < p*) and IPR(p > p*) vanish, however, since they obey the same scaling we are also able to define the structural transition in the thermodynamic limit.
. This statement is exemplified in figure 1(a) where, without loss of generality, we consider homogeneous layers, so we cannot observe node localization. Next, we define p* as the crossover point between the layer-localized and localized regimes. Thus, when p ≪ p*, the eigenvector components are concentrated in a sub-extensive part of the eigenvector. Such part of the eigenvector corresponds to the dominating layer. However, the density of non-negligible eigenvector components corresponding to the non-dominating layer increases with the coupling parameter p. Indeed, from figure 1(a), we observe that in the localized regime, p < p*, the IPR's contribution of the non-dominating layer can be characterized by a PL (i.e. a linear trend in log–log scale), that is, log(IPRNDL(p < p*)) ≈ α log(p) + c1 with α ≈ 4. We also verified that α is independent of N, while c1 is dependent on the system size. Moreover, in the delocalized regime, p > p*, the states are evenly extended and do not change anymore with p and they are characterized by log(IPR(p > p*)) ≈ c2. In this regime, the inter-layer connections play the major role, while the intra-layer connections can be interpreted as perturbations. Hence, all the nodes contribute similarly to the leading eigenvector, making it delocalized. Therefore, the coupling p*, characterizing the delocalization transition, can be defined as the value of p such that IPRNDL(p < p*) = IPR(p > p*). This is illustrated in figure 1(b). With this prescription, we were able to systematically characterize the structural transition of the eigenvectors of our 2-layer network by means of the IPR. Importantly, figure 1 also shows that different network configurations produce different IPR functions. Note that, although all the curves have similar behavior, they are shifted in both axes. Aside from the dependence of the IPR on p, it also depends on the system size as IPR(p, n) ∼ n−δ
; as shown in figure 2(a). Thus, for a fixed number of layers and in the thermodynamic limit, both regimes scale similarly with δ ≈ 1 (see figure 2(a)). We remark that, in the thermodynamic limit, both IPRNDL(p < p*) and IPR(p > p*) vanish, however, since they obey the same scaling we are also able to define the structural transition in the thermodynamic limit.
Figure 1. (a) Contribution of the dominating and non-dominating network layers to the IPR as a function of p for several 2-layer network configurations considering Erdös–Rényi (ER) and power-law (PL) layers. In (b), we present an example, where the layer-localized and delocalized regimes are characterized by log(IPRNDL(p < p*)) ≈ α log(p) + c1 and log(IPRDL(p > p*)) ≈ c2 (dashed and dot-dashed lines), respectively, and the delocalization transition coupling p* is given as the crossing of these two curves (vertical dotted line). Here α ≈ 4, c1 = −9.698 and c2 ≈ 8.92 × 10−6.
Download figure:
Standard image High-resolution imageFigure 2. (a) Scaling of the IPR with n, IPR ∼ n−δ , for both the minimum and maximum values of p calculated: IPR(pmin) and IPR(pmax). In both cases we estimated δ ≈ 1. The network sizes used here are n = 1 × 103, 2 × 103, 3 × 103, 4 × 103, 5 × 103, 10 × 103, 20 × 103, and 30 × 103. (b) Collapsing of the curves IPR versus p by the use of IPR* = n × IPR (see (a)) and p' = p/p*. In the homogeneous layer configurations (ER networks) we used all the combinations of k1 = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100} and k2 = {10, 20, 30, 40}. In the mixed case, where one layer is an ER network and the other is a PL network, we considered all the combinations of γ1 = {2.25, 2.5, 3.5} for the PL layer and k2 = {20, 30, 40} for the ER layer.
Download figure:
Standard image High-resolution imageAs a consequence of the IPR behavior described above, and taking into account both the dependencies on the system size n and on the coupling parameter p (see also [5, 24]), we define


Under these scalings, all the IPR* versus p' curves should collapse on top of a universal curve. Indeed, the scaling of the IPR is shown in figure 2(b).
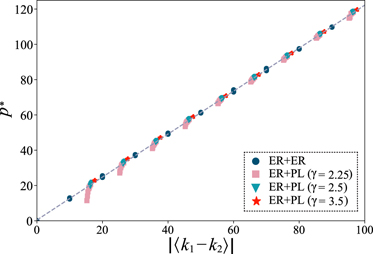
It is relevant to stress that the quantity driving the IPR scaling, for a fixed p and fixed layer structure (i.e. the class of network considered), is the network size. For example, the IPR of an ER single-layer network scales as n−1 and node-localization is absent [23]. Furthermore, for PL networks, P(k) ∼ k−γ , depending on the value of γ, one can observe different scaling laws that depend on n; namely, the network can present k-core or hub localization [23]. In multiplex networks, the layer-localization phenomena were already discussed in [5], in the context of disease localization. There, it was shown that the states could be localized in one or more layers. Moreover, in the multiplex case, p* depends on the layer configurations. For instance, note that considering a fixed value of p, by changing the average degree of a layer in the multiplex, the eigenstates can transit from localization to delocalization (the opposite is also true); see for example figure 1. Thus, the universality shown in figure 2(a) could not be robust against the inner configuration of the layers. We remark that this behavior is adjusted by rescaling p as proposed in equation (4), as shown in figure 2(b). Moreover, a detailed study of the IPR as a function of p, allows relating the structural properties of the multiplex with the delocalization transition coupling p*. Interestingly enough, we found that p* is approximately linearly described by the difference between the average degree of the layers; that is

as can be clearly seen in figure 3 for a wide range of parameter combinations. This relationship describes the change of the IPR curves with the inner configuration of the layers. Surprisingly, despite the local structures that might appear inside the multiplex (cycles), for the range of parameters studied, the average degree difference describes reasonably well the eigenvector's structural transition.
Figure 3. Delocalization transition coupling p* as a function of the absolute degree difference of the two layers forming the multiplex. The dashed line is p* = β1⟨k1 − k2⟩ + β2, with β1 = 1.218 and β2 = 0.430. Same network parameters as in figure 2.
Download figure:
Standard image High-resolution imageTo the best of our knowledge, a definition of the eigenvector structural transition, from layer-localization to delocalization, is not available in the literature. This concept might seem natural at first glance, but, since there is no abrupt transition on the spectral properties of the adjacency matrix nor a singularity to look for, a transition in the strict sense is hard to define. In the following, we formalize this transition and provide a definition for it. It is important to stress that this structural change, characterized by the IPR*, is continuous, and the IPR*(p = p*) does not vanish in the thermodynamic limit. This behavior contrasts with second-order phase transitions, where the transition is associated with a divergence, and it gets better defined as the system size increases. Here, in the layer-localization transition, measured by IPR*, this phenomenon does not occur. However, as we have two clearly defined regimes associated only with the structure, layer-localized, and delocalized regimes, we call it a structural transition. We also remark that a similar nomenclature was used on the analysis of the so-called abrupt structural transition found in the Laplacian matrix [8–12]. Moreover, the adjacency and the Laplacian matrices concern different dynamical processes. So, our interest here is the adjacency matrix due to its relevance to the SIS epidemic spreading process.
3. Application to the SIS phase transition
In [5] it was shown that the disease spreading, more precisely the SIS model, on a multilayer network might present a transition from layer-localization to delocalization. This phenomenon depends on the layer configurations, as well as the spreading parameters [5]. Motivated by [25], the authors extended the concept of localization from node localization to layer-localization. Here, by establishing IPR* as in equation (3), we go one step further since this quantity does not vanish in the thermodynamic limit. Notably, the most important contribution of our analysis regards the nature of the SIS transition on multiplex networks. From the quenched mean-field (QMF) theory, where we assume that the individual probabilities are independent, (see [5, 24]) we have
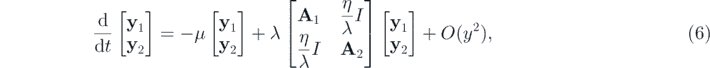
where the transition from a disease-free state to an endemic state occurs at the critical point given by λc = μ/Λ1, with Λ1 being the leading eigenvalue of A, see equation (1), and p = η/λ in our context. Therefore, p* = η/λc = ηΛ1. Moreover, we know that if p > p* the eigenvectors of the multiplex are in the delocalized regime. Conversely, if p < p* the eigenvectors show layer localization. We can now translate this condition into the SIS epidemic spreading context. Thus, from the QMF theory, if

where η is the inter-layer spreading rate, the disease is delocalized, and the whole multiplex is active. Notice that if equation (7) is not satisfied a transition from a disease-free state to a layer-localized state is still present. Aside from that, note that the evaluation of equation (7) is not trivial since p* and Λ1 depend on η. We also remark that, since the delocalization transition is continuous, i.e. it is not characterized by a divergence on a given derivative (see for instance figure 2, where the finite size effects are not present and the curves for different network sizes collapse), the corresponding dynamics is also expected to suffer a smooth transition. This is very relevant, because it might be easier to study localization–delocalization transitions through spectral properties than from dynamical properties, which usually involves more refined and cumbersome numerical techniques. We also want to stress that an important consequence of the renormalization defined in equations (3) and (4) is that they allow for the analysis of finite systems. In other words, these definitions do not require the thermodynamic limit. For the sake of rigor, however, we remark that a true critical point is properly defined only in the infinite size limit.
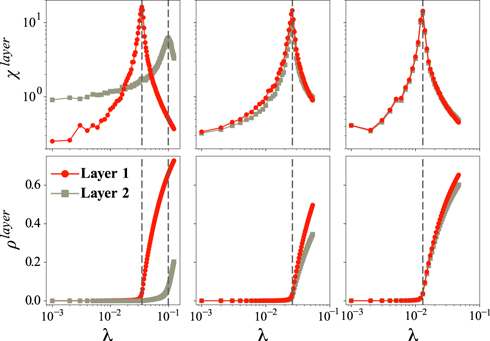
Furthermore, in figure 4, we present Monte Carlo simulations using the quasi-stationary algorithm [5, 24, 26, 27], where the absorbing state is avoided, conferring a numerical validation to our analysis. Here we are interested in the order parameter, and the susceptibility, defined as

and

respectively, where nI is the number of infected individuals, ρ is the average fraction of individuals, and χ is the coefficient of variation of the number of infected individuals. Importantly, in a second-order phase transition, χ presents a peak, and this peak diverges in the thermodynamic limit [5, 24, 26, 27]. Besides, these quantities can also be defined considering the number of infected individuals in each layer individually, here denoted by ρLayer and χLayer. From the structural viewpoint, we evaluate the dynamical response of the SIS model on the different structural regimes: (i) the layer-localized regime, ηΛ1 < p*, (ii) near the structural transition point, ηΛ1 ≈ p* and (iii) the delocalized regime, ηΛ1 > p*. Note that, in the layer-localized regime, the epidemics play a role similar to an external field for the non-dominating layer. Thus, the non-dominating layer plays a minor role. This behavior can be observed in both, the order parameter (for each layer) ρ, and the susceptibility (also calculated individually for each layer) χ, see the left panels of figure 4. In the susceptibility curves, we can even see a second peak, as predicted in [5]. As discussed before, the eigenvector transition from layer-localization to delocalization is not a sharp transition. This is also illustrated in the middle panels of figure 4. In the transition regime, a small change in η does not imply an important change of behavior. Note that at the critical point (peak of susceptibility), the fraction of infected individuals, ρ, is similar in both layers. Besides, these two curves have different growth rates for larger values of λ. Finally, in the right panels of figure 4, we present the delocalized structural regime, where the curves of χ and ρ are practically the same for both layers. In this regime, as we increase η, we are also increasing the leading eigenvalue of A and, thus, moving the critical point to the left. Therefore for large η, using perturbative analysis, we can interpret the block diagonal matrices as a perturbation on the off-diagonal ones.
Figure 4. Quasi stationary simulation of an SIS epidemic spreading. Susceptibility χ (upper panels) and order parameter ρ (lower panels) as a function of λ, for each layer. The multiplex network used in this simulation is composed by two ER networks with ⟨k⟩ = 30 and ⟨k⟩ = 10. From the left to the right we have three different structural regimes: (i) the layer-localized regime with η = 0.01, (ii) near the structural delocalization transition point, ηΛ1 ≈ p* with η = 0.85, p* = 24.795 (from equation (5)) and Λ1 = 31.058, and (iii) the delocalized regime with η = 3.0. The gray dashed lines mark the susceptibility peaks.
Download figure:
Standard image High-resolution image4. Conclusions
In this paper, we have formalized the layer-localization to delocalization transition in bilayer multiplex networks. This process was already anticipated in [5]; however, a proper definition was lacking. In the latter study, the different structural regimes (layer-localized and delocalized) were characterized, but the transition point between them was not defined. In order to properly define the transition, we first performed a scaling analysis of the IPR of the eigenvectors of the adjacency matrix of the bilayer multiplex network as a function of the parameter associated to the coupling between the layers. Furthermore, we also found a linear relationship between the delocalization transition point, p*, and the difference of the average degree between the layers. We remark that this relationship is valid for the set of parameters evaluated here. That is, for homogeneous-layer settings and mixed-layer settings both with a reasonably high average degree, since in order to observe layer-localization, layer dominance is needed.
Finally, we have also applied our results on the universality of layer delocalization to the disease spreading. By using the QMF approach, we were able to define a criterion for disease layer-localization, which was validated through Monte Carlo simulations. This constitutes a step towards a better understanding of the delocalization transition reported for disease dynamics on multilayer networks [5]. We hope that our work could also motivate further research on the impact of the layer delocalization transition in dynamical processes, as well as on the universality of other properties of multiplex networks.
Acknowledgments
GFA and YM acknowledge partial support from Intesa Sanpaolo Innovation Center. JAM-B acknowledges financial support from FAPESP (Grant No. 2019/ 06931-2), Brazil, CONACyT (Grant No. 2019-000009-01EXTV-00067) and PRODEP-SEP (Grant No. 511-6/2019-11821), Mexico. FAR acknowledge support from CNPq (Grant No. 309266/2019-0) and Fapesp (Grant No. 13/07375-0). YM acknowledges partial support from the Government of Aragón, Spain through Grant E36-17R, and by MINECO and FEDER funds (Grant No. FIS2017-87519-P). Research carried out using the computational resources of the Center for Mathematical Sciences Applied to Industry (CeMEAI) funded by FAPESP (Grant No. 2013/07375-0). The funders had no role in study design, data collection, and analysis, decision to publish, or preparation of the manuscript.