Abstract
We consider PT-symmetric quantum graphs, in which the branching points provide PT-symmetric boundary conditions for the Schrödinger equation on a graph. For such branched quantum wires, we derive general boundary conditions, which keep the Hamiltonian as PT-symmetric with real eigenvalues and positively defined norm of the eigenfunctions. Secular equations for finding the eigenvalues of the quantum graph are derived. Breaking the Kirchhoff rule at the branching points in such systems is shown. Experimental realization of PT-symmetric quantum graphs on branched optical waveguides is discussed.
Export citation and abstract BibTeX RIS
1. Introduction
PT-symmetric quantum systems have attracted much attention since the pioneering paper [1], where the authors showed that a quantum system with a non-Hermitian, but PT-symmetric Hamiltonian can have a set of eigenstates with real eigenvalues (a real spectrum). Later, it was shown that the Hermiticity of the Hamiltonian is not a necessary condition for the realness of its eigenvalues. The quantum mechanics of such systems has become a rapidly developing topic called PT-symmetric quantum mechanics (see papers [2–23] for review of recent developments on the topic). Different aspects of PT-symmetric quantum physics have been studied in a huge number of papers published during the past two decades. These studies allowed one to construct the complete theory of the PT-symmetric quantum system, including PT-symmetric field theory [8, 12]. Experimental realization of such systems was also the subject of extensive research. The latter has been done mainly in optics [24–27]. Some other PT-symmetric systems have been discussed recently in the literature [29, 30]. PT-symmetric relativistic systems are also studied in [19, 20]. General conditions for PT-symmetry have been derived in terms of the so-called PT-symmetric inner product. However, since such a condition does not provide a positively defined norm of the eigenvalues, its extension in terms of a CPT-symmetric inner product was proposed in [5, 10, 12]. Similarly to the case of Hermiticity, PT-symmetry can be introduced either through the complex potential, or by imposing proper boundary conditions, which provide such symmetry via the inner product [5, 12]. Different types of complex potentials that provide PT-symmetry in the Hamiltonian have been considered in [10, 12]. Introducing PT-symmetry in terms of proper boundary conditions was studied for the particle-in-box system in [14, 21–23]. Progress has also been made in the nonlinear extension of PT-symmetric systems [26–28]. Spectral properties of the Laplace operators on a graph in the presence of PT- and reflection symmetry have been considered in [31, 32].
In this paper we consider the problem of PT-symmetric quantum graphs, which are branched quantum wires, where the branching points provide PT-symmetry of the systems. The latter means imposing PT-symmetric boundary conditions at the branching points (vertices) of the quantum graph. The quantum graph itself can be determined as a branched system of quantum wires. The branching (connection) rule is called topology of a graph and given in terms of the adjacency matrix [36, 37]. When length is assigned to the bonds of a graph, it is called a metric graph. In the Hermitian case, the vertex (branching point) boundary conditions for the Schrödinger equation are imposed in such a way that they provide self-adjointness of the Hamiltonian operator. First, strict study of quantum graphs as branched quantum wires was presented in [33]. General boundary conditions for the Schrödinger equation on graphs were derived in terms of the Hermitian inner product [34]. Later, such boundary conditions have been derived for the Dirac equation on graphs in [35]. Spectral statistics and manifestation of quantum chaos in quantum graphs was studied in [36, 37]. Different aspects of the Schrödinger operator on graphs have been studied in [38–41]. Experimental realization of quantum graphs in optical microwave networks has been presented in [42]. Nonlinear extension of the wave dynamics in networks is considered in [43–49]. Quantum graphs with transparent vertices were studied recently in [48]. Here we derive PT-symmetric analogs of the Hermitian boundary conditions for quantum graphs, which have been derived earlier in [34]. Such conditions are needed for construction of PT-symmetric quantum graphs. Also, we consider special cases of the boundary conditions, which are consistent with the general ones and obtain a secular equation for finding the eigenvalues of the Schrödinger operator on graphs. By solving numerically such a secular equation we show that the eigenvalues of the problem are real, the norm is positively defined and the Kirchhoff rule is broken at the branching points of a graph. Motivation for the study of PT-symmetric quantum graphs mainly comes from the possibility of their experimental realization in optical waveguide networks. Such networks can be constructed by connecting optical waveguides via dissipative, optically absorbing material. Also, condensed matter realizations using branched graphene nanoribbons or branched polymers can be considered. This paper is organized as follows. In the next section we briefly recall the problem of Hermitian (self-adjoint) quantum graphs. Section 3 presents formulation and explicit solution of the problem of the PT-symmetric quantum star graph. Section 4 extends this study for arbitrary graph topologies. Section 5 briefly discusses possible experimental realization of the model. Finally, section 6 presents some concluding remarks.
2. Hermitian quantum graphs
Let us first recall construction of the Hermitian boundary conditions for quantum graphs, which were derived in [34]. The Schrödinger equation on a metric star graph with N finite bonds (figure 1), 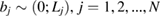 can be written as (in units
can be written as (in units  )
)

where Lj are length of the j th bond.
Figure 1. Sketch of a metric star graph. Lj is the length of the j th bond with  .
.
Download figure:
Standard image High-resolution imageThe inner product of two functions, 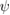 and
and  on a graph can be written as [34]
on a graph can be written as [34]

Here we introduce a so-called skew-Hermitian product on the graph, which is defined for the arbitrary differential operator H as [34]

Then, general Hermitian boundary conditions for equation (3) on the metric star graph can be written as [34]
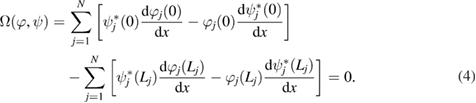
Equation (4) provides the boundary conditions keeping the Schrödinger operator on the metric star graph as self-adjoint and can be rewritten in the compact form as [34]

where  and
and 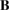 are
are  matrices that fulfill the relations
matrices that fulfill the relations

3. PT-symmetric quantum star graph
Our purpose is to derive PT-symmetric analogs of equations (3) and (4). To do this, one should use the CPT-symmetric inner product in equation (2), instead of the Hermitian inner product. Such an inner product can be written as [5, 10, 12]
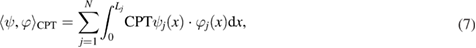
where
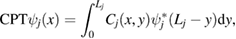
and using
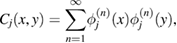
where  are the eigenfunctions of equation (1), we can write CPT-symmetric boundary conditions for equation (1) as
are the eigenfunctions of equation (1), we can write CPT-symmetric boundary conditions for equation (1) as
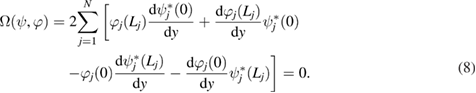
In the derivation of equation (8) we took into account that the eigenvalues of equation (1) are real. It is clear that equation (8) can be written in compact form given by equation (5).
Let us now obtain explicit solutions of equation (1) for some PT-symmetric boundary conditions. The general (without boundary conditions) solution of equation (1) can be written as
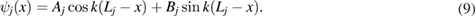
The eigenvalues kn and constants Aj , Bj can be found from the boundary conditions. A set of boundary conditions, which are consistent with equation (8) can be written as (here, for simplicity we consider a metric star graph with three bonds)
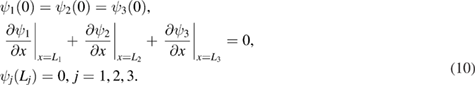
Such boundary conditions have been derived in [21]. Another set of boundary conditions, which is consistent with the general ones given by equation (8) is
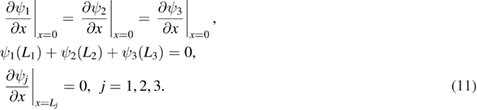
Both sets of boundary conditions lead to the same secular equation, which is given by
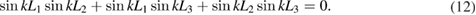
The eigenfunctions corresponding to boundary conditions equation (10) can be written as

while for the boundary conditions (11) we have the eigenfunctions

where An and Bn are the normalization constants given by

and
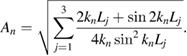
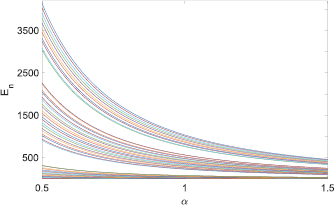
It is clear that the norms of the eigenfunctions given by equations (13) and (14) are positively defined. Direct numerical computation of the roots of equation (12) shows that they are indeed real. This implies that the eigenvalues of equation (1) for the boundary conditions (10) and (11) are real. In figure 2 the energy levels,  , determined by equation (12) are plotted as a functions of the parameter
, determined by equation (12) are plotted as a functions of the parameter  , which is introduced through the relations
, which is introduced through the relations  The eigenvalues are real and their values decay, as the bond lengths increase.
The eigenvalues are real and their values decay, as the bond lengths increase.
Figure 2. First 50 energy levels of PT-symmetric star graph versus the parameter  , which is given by
, which is given by  for
for 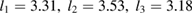 .
.
Download figure:
Standard image High-resolution imageWe note that unlike Hermitian quantum graphs (see, e.g. [34, 36, 37, 41]), the boundary conditions given by equations (10) and (11) do not provide Kirchhoff rules. This implies breaking of the current conservation at the branching point that can be directly checked by computing numerically the total current at the vertex (x = 0) given by
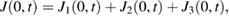
where
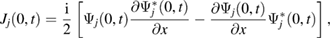
is the current on each bond and
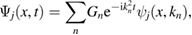
is the total wave function, which is represented as the linear combination of the complete set of the eigenfucntions of the problem given by equations (1) and (11), with coefficients Gn to be found from the initial condition.
In figure 3 the total current at the vertex,  for the boundary conditions (10) and (11) are plotted as a function of time. It is clear that current conservation (the Kirchhoff rule) is broken.
for the boundary conditions (10) and (11) are plotted as a function of time. It is clear that current conservation (the Kirchhoff rule) is broken.
Figure 3. Total current at the vertex for the boundary conditions (10) (blue) and (11) (red) as a function of time.
Download figure:
Standard image High-resolution image4. Extension to arbitrary graph topologies
The above treatment of a PT-symmetric quantum star graph can be extended to arbitrary graph topology by introducing a general CPT-symmetric inner product for such graphs. Topology of a graph consisting of  vertices is given in terms of the adjacency matrix, which can be written as [36, 37]:
vertices is given in terms of the adjacency matrix, which can be written as [36, 37]:
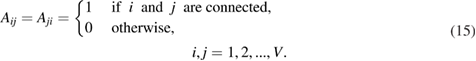
In terms of the adjacency matrix, the CPT-symmetric inner product can be written as
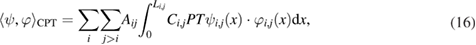
where
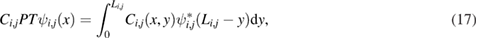
and

 are the eigenfunctions of equation (1) fulfilling the vertex boundary conditions.
are the eigenfunctions of equation (1) fulfilling the vertex boundary conditions.
The skew-CPT-symmetric form can be written as
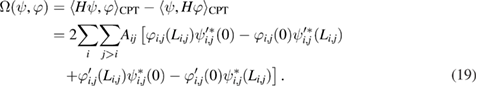
Furthermore, we introduce the following notations:

Then for the skew-CPT-symmetric form we have
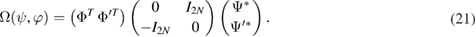
To provide the PT-symmetry of the problem, one needs to fulfill the condition
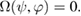
Equivalently, this condition can be written in the form of equations (5) and (6).
Equation (5) presents the most general boundary condition that provides PT-symmetry in the Schrödinger equation on a metric star graph of arbitrary topology. Different special versions of the explicit boundary conditions, which are consistent with equation (5) can be formulated. A special set of the boundary conditions, which are consistent with the general one given by equation (5) can be written, e.g. in the form
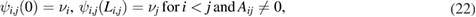
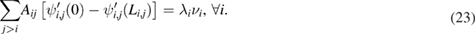
The first condition here provides continuity of the wave function at the graph branching points. The solution of equation (1), fulfilling the continuity condition, (22), can be written as (for i < j )
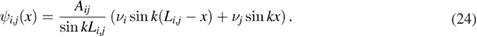
Fulfilling this solution the boundary condition (23) leads to the following linear homogeneous system of equations
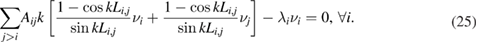
Requiring that this system has non-trivial solutions we obtain the secular equation for finding the eigenvalues, kn:

where

It is easy to check (numerically) that all the roots of equation (26) are real. Hence the eigenvalues of the PT-symmetric quantum graph given by the boundary conditions (22) and (23) are also real. Having found the eigenfunctions and eigenvalues, one can compute the current through the each (ith) vertex of a graph using the following relations:
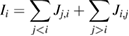

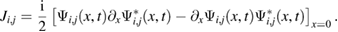
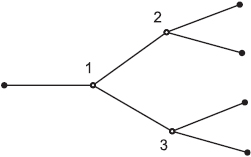
Here we apply the above results to the tree graph, presented in figure 4 Similarly to the case of the star graph, one can check breaking of the Kirchhoff rule at each vertex. In figure 5, the current through each vertex of the tree graph is plotted as a function of time. It is clear that current conservation is broken for this case, too.
Figure 4. Tree graph with three vertices (branching points).
Download figure:
Standard image High-resolution image5. Experimental realization on branched optical waveguides
Some models for PT-symmetric networks have been discussed earlier in the literature [50, 51]. However, the above model of the PT-symmetric quantum graph can be easily realized using branched (Y-junction) optical waveguides, which are connected according to the boundary conditions given by equations (10) or (11). It is clear that both set of boundary conditions provide absence of current at the end of the branches and the continuity of the wave function at the branching point. Taking into account breaking of Kirchhoff rules for these boundary conditions, one may construct such a PT-symmetric quantum graph by connecting three optical waveguides via the small-size partially absorbing optical material. The ends of the branches of the waveguides should provide a total reflection of the wave. Similarly, one may consider experimental realization in a general (more than three branched) star graph of optical waveguides and arbitrary graph topology such as, e.g. tree, loop and complete graphs. In this case all the branching points should be optically absorbing material, while the edge branches should provide zero-current at the ends. One of the options for dissipatively coupled optical waveguides have been recently discussed in [52]. Different branched versions of such a system can also be a good candidate for the PT-symmetric quantum graph.
Figure 5. Total current as a function of time at the three vertices of tree graph shown in figure 4.
Download figure:
Standard image High-resolution image6. Conclusions
In this paper we have studied the problem called 'PT-symmetric quantum graphs', which represents branched quantum wires, whose branches are connected according to PT-symmetric rules. The latter implies that the boundary condition at the branching points and ends of the bonds provide PT-symmetry of the Schrödinger operator on a graph. General boundary conditions providing PT-symmetry of the Schrödinger operator on a graph and having real eigenvalues, as well as positively defined norm of the eigenfunctions are derived. Eigenvalues and eigenfunctions of a quantum star graph are found explicitly for special types of the boundary conditions, which follow from such general conditions. It is shown that the eigenvalue spectrum of the Schrödinger equation on metric graphs for such boundary conditions is real. The approach is extended to the graphs of arbitrary topologies and general boundary conditions providing PT-symmetry for arbitrary graphs are derived. Breaking of Kirchhoff rules for the PT-symmetric quantum tree graph is shown using direct numerical calculation of current through each vertex of the graph. Experimental realization of the PT-symmetric quantum graph using branched optical waveguides is discussed. Finally, we note that extension to the relativistic case can be easily done for PT-symmetric quantum graphs described by Dirac and Klein–Gordon equations.
Acknowledgments
We thank Carl M Bender for his valuable comments on the paper. This work is partially supported by a grant of the Ministry of Innovation Development of Uzbekistan (Ref. No. BF-2-022).