Quantum Fisher information matrix and multiparameter estimation

The traditional derivation of QFIM usually assumes the rank of the density matrix is full, i.e. all the eigenvalues of the density matrix are positive. Specifically if we write $\rho =\sum\nolimits_{i=0}^{\dim(\rho)-1} \lambda_{i}|\lambda_{i}\rangle\langle\lambda_{i}|$, with $\lambda_{i}$ and $|\lambda_{i}\rangle$ the eigenvalue and the corresponding eigenstate, it is usually assumed that $\lambda_{i}>0$ for all $0\leqslant i\leqslant \dim(\rho)-1$. Under this assumption the QFIM can be obtained as follows.

Theorem 2.1. The entry of QFIM for a full-rank density matrix with the spectral decomposition $\rho =\sum\nolimits_{i=0}^{d-1} \lambda_{i}|\lambda_{i}\rangle\langle\lambda_{i}|$ can be written as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\sum^{d-1}_{i,j=0}\frac{2\mathrm{Re}(\langle\lambda_{i} |\partial_{a}\rho |\lambda_{j}\rangle\langle\lambda_{j}|\partial_{b} \rho |\lambda_{i}\rangle)}{\lambda_{i}+\lambda_{j}}, \nonumber \end{align} \tag{ 10 }$$

where $d:=\dim(\rho)$ is the dimension of the density matrix.

One can easily see that if the density matrix is not of full rank, there can be divergent terms in the above equation. To extend it to the general density matrices which may not have full rank, we can manually remove the divergent terms as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\sum^{d-1}_{i,j=0,\lambda_{i}+\lambda_{j}\neq 0} \frac{2\mathrm{Re}(\langle\lambda_{i}|\partial_{a}\rho |\lambda_{j}\rangle \langle\lambda_{j}|\partial_{b}\rho |\lambda_{i}\rangle)}{\lambda_{i}+\lambda_{j}}. \label{eq:tradition_QFIM} \nonumber \end{align} \tag{ 11 }$$

By substituting the spectral decomposition of $\rho$ into the equation above, it can be rewritten as [5]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\sum^{d-1}_{i=0}\frac{(\partial_{a}\lambda_{i}) (\partial_{b}\lambda_{i})}{\lambda_{i}}+\sum_{i\neq j,\lambda_{i}+\lambda_{j}\neq 0} \frac{2(\lambda_{i}-\lambda_{j})^{2}}{\lambda_{i} +\lambda_{j}}\mathrm{Re}\left(\langle\lambda_{i}|\partial_{a}\lambda_{j}\rangle \langle\partial_{b}\lambda_{j}|\lambda_{i}\rangle\right). \label{eq:QFIM_Paris} \nonumber \end{align} \tag{ 12 }$$

Recently, it has been rigorously proved that the QFIM for a finite dimensional density matrix can be expressed with the support of the density matrix [31]. The support of a density matrix, denoted by $\mathcal{S}$, is defined as $\mathcal{S}:=\{\lambda_{i}\in\{\lambda_{i}\}|\lambda_{i}\neq 0\}$ ($\{\lambda_{i}\}$ is the full set of $\rho$'s eigenvalues), and the spectral decomposition can then be modified as $\rho =\sum\nolimits_{\lambda_{i}\in\mathcal{S}}\lambda_{i}|\lambda_{i}\rangle\langle \lambda_{i}|$. The QFIM can then be calculated via the following theorem.

Theorem 2.2. Given the spectral decomposition of a density matrix, $\rho=\sum\nolimits_{\lambda_{i}\in\mathcal{S}} |\lambda_{i}\rangle\langle\lambda_{i}|$ where $\mathcal{S}=\{\lambda_{i}\in\{\lambda_{i}\}|\lambda_{i}\neq 0\}$ is the support, an entry of QFIM can be calculated as [31]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}&=\sum_{\lambda_{i}\in \mathcal{S}}\frac{(\partial_{a}\lambda_{i})(\partial_{b}\lambda_{i})} {\lambda_{i}}+\sum_{\lambda_{i}\in\mathcal{S}}4\lambda_{i}\mathrm{Re} \left(\langle\partial_{a}\lambda_{i} |\partial_{b}\lambda_{i}\rangle\right) \nonumber \\ & -\sum_{\lambda_{i},\lambda_{j}\in \mathcal{S}}\frac{8\lambda_{i}\lambda_{j}} {\lambda_{i}+\lambda_{j}}\mathrm{Re}(\langle\partial_{a}\lambda_{i}|\lambda_{j}\rangle \langle\lambda_{j}|\partial_{b}\lambda_{i}\rangle). \label{eq:QFIM_nonfullrank} \nonumber \end{align} \tag{ 13 }$$

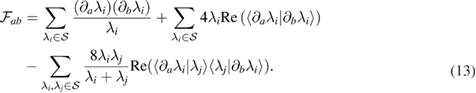
The detailed derivation of this equation can be found in appendix B. It is a general expression of QFIM for a finite-dimensional density matrix of arbitrary rank. Due to the relation between the QFIM and QFI, one can easily obtain the following corollary.

Corollary 2.2.1. Given the spectral decomposition of a density matrix, $\rho=\sum\nolimits_{\lambda_{i}\in\mathcal{S}} |\lambda_{i}\rangle\langle\lambda_{i}|$, the QFI for the parameter x_a can be calculated as [32–36]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{aa}=\sum_{\lambda_{i}\in \mathcal{S}}\frac{(\partial_{a}\lambda_{i})^{2}} {\lambda_{i}}+\sum_{\lambda_{i}\in \mathcal{S}}4\lambda_{i}\langle\partial_{a}\lambda_{i} |\partial_{a}\lambda_{i}\rangle-\sum_{\lambda_{i},\lambda_{j} \in \mathcal{S}}\frac{8\lambda_{i}\lambda_{j}}{\lambda_{i}+\lambda_{j}}|\langle \partial_{a}\lambda_{i}|\lambda_{j}\rangle|^{2}. \label{eq:QFI_nonfullrank} \nonumber \end{align} \tag{ 14 }$$

The first term in equations (12) and (13) can be viewed as the counterpart of the classical Fisher information as it only contains the derivatives of the eigenvalues which can be regarded as the counterpart of the probability distribution. The other terms are purely quantum [5, 36]. The derivatives of the eigenstates reflect the local structure of the eigenspace on $\vec {x}$. The effect of this local structure on QFIM can be easily observed via equations (12) and (13).

The SLD operator is important since it is not only related to the calculation of QFIM, but also contains the information of the optimal measurements and the attainability of the quantum Cramér–Rao bound, which will be further discussed in sections 3.1.2 and 3.1.3. In terms of the eigen-space of $\rho$, the entries of the SLD operator for $\lambda_{i}, \lambda_{j} \in \mathcal{S}$ can be obtained as follows⁸

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \langle\lambda_{i}|L_{a}|\lambda_{j}\rangle=\delta_{ij}\frac{\partial_{a}\lambda_{i}} {\lambda_{i}}+\frac{2(\lambda_{j}-\lambda_{i})}{\lambda_{i}+\lambda_{j}}\langle\lambda_{i} |\partial_{a}\lambda_{j}\rangle; \nonumber \end{align} \tag{ 15 }$$

for $\lambda_{i}\in\mathcal{S}$ and $\lambda_{j}\not\in\mathcal{S}$, $\langle\lambda_{i}|L_{a}|\lambda_{j}\rangle=-2\langle\lambda_{i}|\partial_{a}\lambda_{j}\rangle$; and for $\lambda_{i},\lambda_{j}\not\in\mathcal{S}$, $\langle\lambda_{i}|L_{a}|\lambda_{j}\rangle$ can take arbitrary values. Fujiwara and Nagaoka [29, 37] first proved that this randomness does not affect the value of QFI and all forms of SLD provide the same QFI. As a matter of fact, this conclusion can be extended to the QFIM for any quantum state [31, 38], i.e. the entries that can take arbitrary values do not affect the value of QFIM. Hence, if we focus on the calculation of QFIM we can just set them zeros. However, this randomness plays a role in the search of optimal measurement, which will be further discussed in section 3.1.3.

In control theory, equation (2) is also referred to as the Lyapunov equation and the solution can be obtained as [5]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle L_{a}=2\int^{\infty}_{0}{\rm e}^{-\rho s}\left(\partial_{a}\rho \right){\rm e}^{\rho s}\mathrm{d}s, \nonumber \end{align} \tag{ 16 }$$

which is independent of the representation of $\rho$. This can also be written in an expanded form [38]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle L_{a}=-2\lim_{s\rightarrow\infty}\sum_{n=0}^{\infty}\frac{\left(-s\right)^{n+1}}{(n+1)!} \mathcal{R}^{n}_{\rho}(\partial_{a}\rho), \label{eq:SLD_expand} \nonumber \end{align} \tag{ 17 }$$

here $\mathcal{R}_{\rho}(\cdot):=\{\rho,\cdot\}$ denotes the anti-commutator. Using the fact that $\mathcal{R}^{n}_{\rho}(\partial_{a}\rho) =\sum\nolimits_{m=0}^{n}{n\choose m}\rho^{m}\left(\partial_{a}\rho \right)\rho^{n-m}$, where ${n\choose m}=\frac{n!}{m!(n-m)!}$, equation (17) can be rewritten as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle L_{a}=-2\lim_{s\rightarrow\infty}\sum_{n=0}^{\infty}\sum^{n}_{m=0} \frac{\left(-s\right)^{n+1}}{(n+1)!}{n\choose m}\rho^{m}\left(\partial_{a}\rho \right)\rho^{n-m}. \nonumber \end{align} \tag{ 18 }$$

This form of SLD can be easy to calculate if $\rho^{m}(\partial_{a}\rho)\rho^{n-m}$ is only non-zero for limited number of terms or has some recursive patterns.

Recently, Safránek [39] provided another method to compute the QFIM utilizing the density matrix in Liouville space. In Liouville space, the density matrix is a vector containing all the entries of the density matrix in Hilbert space. Denote $\mathrm{vec}(A)$ as the column vector of A in Liouville space and $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}\mathrm{vec}(A){}^{\dagger}$ as the conjugate transpose of $\mathrm{vec}(A)$. The entry of $\mathrm{vec}(A)$ is $[\mathrm{vec}(A)]_{id+j}=A_{ij}$ ($i,j\in[0,d-1]$). The QFIM can be calculated as follows.

Theorem 2.3. For a full-rank density matrix, the QFIM can be expressed by [39]

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \newcommand{\openone}{\mathbb {1}} \displaystyle \mathcal{F}_{ab}=2\mathrm{vec}(\partial_{a}\rho)^{\dagger}\left(\rho \otimes{\openone} +{\openone}\otimes\rho^{*}\right)^{-1}\mathrm{vec}(\partial_{b}\rho), \nonumber \end{align} \tag{ 19 }$$

where $\rho^{*}$ is the conjugate of $\rho$, and the SLD operator in Liouville space, denoted by $\mathrm{vec}(L_{a})$, reads

$$\begin{align} \newcommand{\e}{{\rm e}} \newcommand{\openone}{\mathbb {1}} \displaystyle \mathrm{vec}(L_{a})=2\left(\rho \otimes{\openone} +{\openone}\otimes\rho^{*}\right)^{-1}\mathrm{vec}(\partial_{a}\rho). \nonumber \end{align} \tag{ 20 }$$

This theorem can be proved by using the facts that $\newcommand{\openone}{\mathbb {1}} \mathrm{vec}(AB\openone) =(A\otimes\openone)\mathrm{vec}(B)=$$\newcommand{\openone}{\mathbb {1}} (\openone\otimes B^{\mathrm{T}})\mathrm{vec}(A)$ ($B^{\mathrm{T}}$ is the transpose of B) [40–42] and $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}\mathrm{Tr}(A^{\dagger}B)=\mathrm{vec}(A){}^{\dagger}\mathrm{vec}(B)$.

Bloch representation is another well-used tool in quantum information theory. For a d-dimensional density matrix, it can be expressed by

$$\begin{align} \newcommand{\e}{{\rm e}} \newcommand{\openone}{\mathbb {1}} \displaystyle \rho=\frac{1}{d}\left(\openone+\sqrt{\frac{d(d-1)}{2}}\vec {r}\cdot\vec {\kappa}\right), \nonumber \end{align} \tag{ 21 }$$

where $\vec {r}=(r_1,r_2...,r_m,...){}^{\mathrm{T}}$ is the Bloch vector ($|\vec {r}|^2\leqslant 1$) and $\vec {\kappa}$ is a (d²  −  1)-dimensional vector of $\mathfrak{su}(d)$ generator satisfying $\mathrm{Tr}(\kappa_i)=0$. The anti-commutation relation for them is $\newcommand{\openone}{\mathbb {1}} \{\kappa_i,\kappa_j\}=\frac{4}{d}\delta_{ij}\openone +\sum\nolimits_{m=1}^{d^2-1}\mu_{ijm}\kappa_m$, and the commutation relation is $\newcommand{\e}{{\rm e}} \left[\kappa_i,\kappa_j\right]= {\rm i}\sum\nolimits_{m=1}^{d^2-1}\epsilon_{ijm}\kappa_m$, where $\mu_{ijm}$ and $\newcommand{\e}{{\rm e}} \epsilon_{ijm}$ are the symmetric and antisymmetric structure constants. Watanabe et al recently [43–45] provided the formula of QFIM for a general Bloch vector by considering the Bloch vector itself as the parameters to be estimated. Here we extend their result to a general case as the theorem below.

Theorem 2.4. In the Bloch representation of a d-dimensional density matrix, the QFIM can be expressed by

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=(\partial_{b} \vec {r})^{\mathrm{T}} \left(\frac{d}{2(d-1)}G-\vec {r}\,\vec {r}^{\,\mathrm{T}}\right)^{-1}\partial_{a}\vec {r}, \nonumber \end{align} \tag{ 22 }$$

where G is a real symmetric matrix with the entry

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle G_{ij}=\frac{1}{2}\mathrm{Tr}(\rho\{\kappa_i,\kappa_j\}) =\frac{2}{d}\delta_{ij}+\sqrt{\frac{d-1}{2d}}\sum_{m}\mu_{ijm}r_m. \nonumber \end{align} \tag{ 23 }$$

The most well-used scenario of this theorem is single-qubit systems, in which $\newcommand{\openone}{\mathbb {1}} \rho=(\openone+\vec {r}\cdot\vec {\sigma})/2$ with $\vec {\sigma}=(\sigma_{x},\sigma_{y},\sigma_{z})$ the vector of Pauli matrices. For a single-qubit system, we have the following corollary.

Corollary 2.4.1. For a single-qubit mixed state, the QFIM in Bloch representation can be expressed by

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}= (\partial_{a}\vec {r})\cdot(\partial_{b}\vec {r}) +\frac{(\vec {r}\cdot\partial_{a}\vec {r})(\vec {r}\cdot\partial_{b}\vec {r})} {1-|\vec {r}|^{2}}, \label{eq:bloch_singlequbit} \nonumber \end{align} \tag{ 24 }$$

where $|\vec {r}|$ is the norm of $\vec {r}$. For a single-qubit pure state, $\mathcal{F}_{ab}=(\partial_{a}\vec {r})\cdot(\partial_{b}\vec {r})$.

The diagonal entry of equation (24) is exactly the one given by [47]. The proofs of the theorem and corollary are provided in appendix C.

A pure state satisfies $\rho=\rho^{2}$, i.e. the purity $\mathrm{Tr}(\rho^{2})$ equals 1. For a pure state $|\psi\rangle$, the dimension of the support is 1, which means only one eigenvalue is non-zero (it has to be 1 since $\mathrm{Tr\rho=1}$), with which the corresponding eigenstate is $|\psi\rangle$. For pure states, the QFIM can be obtained as follows.

Theorem 2.5. The entries of the QFIM for a pure parameterized state $|\psi\rangle:=|\psi(\vec {x})\rangle$ can be obtained as [1, 2]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=4\mathrm{Re}(\langle\partial_{a}\psi|\partial_{b}\psi\rangle- \langle\partial_{a}\psi|\psi\rangle\langle\psi|\partial_{b}\psi\rangle). \label{eq:purestate_general} \nonumber \end{align} \tag{ 25 }$$

The QFI for the parameter x_a is just the diagonal element of the QFIM, which is given by

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{aa}=4(\langle\partial_{a}\psi|\partial_{a}\psi\rangle -|\langle\partial_{a}\psi|\psi\rangle|^{2}), \nonumber \end{align} \tag{ 26 }$$

and the SLD operator corresponding to x_a is $L_{a}=2\left(|\psi\rangle\langle\partial_{a}\psi| +|\partial_{a}\psi\rangle\langle\psi|\right)$.

The SLD formula is obtained from the fact $\rho^{2}=\rho$ for a pure state, then $\partial_a \rho=\rho \partial_a \rho+(\partial_a \rho) \rho$. Compared this equation to the definition equation, it can be seen that $L=2\partial_a \rho$. A simple example is $|\psi\rangle={\rm e}^{-{\rm i}\sum\nolimits_{j}H_{j}x_{j}t}|\psi_{0}\rangle$ with $[H_{a},H_{b}]=0$ for any a and b, here $|\psi_{0}\rangle$ denotes the initial probe state. In this case, the QFIM reads

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=4t^{2}\mathrm{cov}_{|\psi_{0}\rangle}(H_{a},H_{b}), \nonumber \end{align} \tag{ 27 }$$

where $\mathrm{cov}_{|\varphi\rangle}(A,B)$ denotes the covariance between A and B on $|\varphi\rangle$, i.e.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{cov}_{|\varphi\rangle}(A,B):=\frac{1}{2}\langle\varphi|\{A,B\}|\varphi\rangle -\langle\varphi|A|\varphi\rangle\langle\varphi|B|\varphi\rangle. \label{eq:cov_definition} \nonumber \end{align} \tag{ 28 }$$

A more general case where H_a and H_b do not commute will be discussed in section 2.3.4.

The simplest few-qubit system is the single-qubit system. A single-qubit pure state can always be written as $\cos\theta|0\rangle+\sin\theta {\rm e}^{{\rm i}\phi}|1\rangle$ ($\{|0\rangle,|1\rangle\}$ is the basis), i.e. it only has two degrees of freedom, which means only two independent parameters ($\vec {x}=(x_{0},x_{1}){}^{\mathrm{T}}$) can be encoded in a single-qubit pure state. Assume $\theta$, $\phi$ are the parameters to be estimated, the QFIM can then be obtained via equation (25) as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{\theta\theta}=4,~\mathcal{F}_{\phi\phi}=\sin^{2}(2\theta), ~\mathcal{F}_{\theta\phi}=0. \nonumber \end{align} \tag{ 29 }$$

If the unknown parameters are not $\theta,\phi$, but functions of $\theta,\phi$, the QFIM can be obtained from formula above with the assistance of Jacobian matrix.

For a single-qubit mixed state, when the number of encoded parameters is larger than three, the determinant of QFIM would be zero, indicating that these parameters cannot be simultaneously estimated. This is due to the fact that there only exist three degrees of freedom in a single-qubit mixed state, thus, only three or fewer independent parameters can be encoded into the density matrix $\rho$. However, more parameters may be encoded if they are not independent. Since $\rho$ here only has two eigenvalues $\lambda_{0}$ and $\lambda_{1}$, equation (13) then reduces to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\frac{(\partial_{a}\lambda_{0})(\partial_{b}\lambda_{0})} {\lambda_{0}(1-\lambda_{0})}+4(1-2\lambda_{0})^{2}\mathrm{Re} \left(\langle\partial_{a}\lambda_{0}|\lambda_{1}\rangle\langle \lambda_{1}|\partial_{b}\lambda_{0}\rangle\right). \label{eq:qubit_mixed} \nonumber \end{align} \tag{ 30 }$$

In the case of single qubit, equation (30) can also be written in a basis-independent formula [46] below.

Theorem 2.6. The basis-independent expression of QFIM for a single-qubit mixed state $\rho$ is of the following form

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\mathrm{Tr}\left[(\partial_{a}\rho)(\partial_{b}\rho)\right] +\frac{1}{\det(\rho)}\mathrm{Tr}\left[\rho(\partial_{a}\rho)\rho(\partial_{b}\rho)\right], \label{eq:qubit_QFIM} \nonumber \end{align} \tag{ 31 }$$

where $\det(\rho)$ is the determinant of $\rho$. For a single-qubit pure state, $\mathcal{F}_{ab}=2\mathrm{Tr}[(\partial_a\rho)(\partial_b\rho)]$.

Equation (31) is the reduced form of the one given in [46]. The advantage of the basis-independent formula is that the diagonalization of the density matrix is avoided. Now we show an example for single-qubit. Consider a spin in a magnetic field which is in the z-axis and suffers from dephasing noise also in the z-axis. The dynamics of this spin can then be expressed by

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \partial_{t}\rho=-{\rm i}[B\sigma_{z},\rho]+\frac{\gamma}{2}(\sigma_{z}\rho\sigma_{z}-\rho), \nonumber \end{align} \tag{ 32 }$$

where $\sigma_{z}$ is a Pauli matrix. B is the amplitude of the field. Take B and $\gamma$ as the parameters to be estimated. The analytical solution for $\rho(t)$ is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \rho(t)=\left(\begin{array}{@{}cc@{}} \rho_{00}(0) & \rho_{01}(0){\rm e}^{-{\rm i}2Bt-\gamma t} \nonumber \\ \rho_{10}(0){\rm e}^{{\rm i}2Bt-\gamma t} & \rho_{11}(0) \end{array}\right). \label{eq:qubit_dephasing} \nonumber \end{align} \tag{ 33 }$$

The derivatives of $\rho(t)$ on both B and $\gamma$ are simple in this basis. Therefore, the QFIM can be directly calculated from equation (31), which is a diagonal matrix ($\mathcal{F}_{B\gamma}=0$) with the diagonal entries

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{BB} = 16 |\rho_{01}(0)|^{2} {\rm e}^{-2\gamma t}t^{2}, \nonumber \end{align} \tag{ 34 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{\gamma\gamma} = \frac{4\rho_{00}(0)\rho_{11}(0)|\rho_{01}(0)|^{2}t^{2}} {\rho_{00}(0)\rho_{11}(0){\rm e}^{2\gamma t}-|\rho_{01}(0)|^{2}}. \nonumber \end{align} \tag{ 35 }$$

For a general two-qubit state, the calculation of QFIM requires the diagonalization of a 4 by 4 density matrix, which is difficult to solve analytically. However, some special two-qubit states, such as the X state, can be diagonalized analytically. An X state has the form (in the computational basis $\{|00\rangle, |01\rangle,|10\rangle, |11\rangle\}$) of

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \rho =\left(\begin{array}{@{}cccc@{}} \rho_{00} & 0 & 0 & \rho_{03} \nonumber \\ 0 & \rho_{11} & \rho_{12} & 0 \nonumber \\ 0 & \rho_{21} & \rho_{22} & 0 \nonumber \\ \rho_{30} & 0 & 0 & \rho_{33} \end{array}\right). \nonumber \end{align} \tag{ 36 }$$

By changing the basis into $\{|00\rangle, |11\rangle, |01\rangle,|10\rangle\}$, this state can be rewritten in the block diagonal form as $\rho =\rho^{(0)}\oplus\rho^{(1)}$, where $\oplus$ represents the direct sum and

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \rho^{(0)}=\left(\begin{array}{@{}cc@{}} \rho_{00} & \rho_{03} \nonumber \\ \rho_{30} & \rho_{33} \end{array}\right),\quad \rho^{(1)}=\left(\begin{array}{@{}cc@{}} \rho_{11} & \rho_{12} \nonumber \\ \rho_{21} & \rho_{22} \end{array}\right). \nonumber \end{align} \tag{ 37 }$$

Note that $\rho^{(0)}$ and $\rho^{(1)}$ are not density matrices as their trace is not normalized. The QFIM for this block diagonal state can be written as $\mathcal{F}_{ab}=\mathcal{F}^{(0)}_{ab}+\mathcal{F}^{(1)}_{ab}$ [36], where $\mathcal{F}^{(0)}_{ab}$ ($\mathcal{F}^{(1)}_{ab}$) is the QFIM for $\rho^{(0)}$ ($\rho^{(1)}$). The eigenvalues of $\rho^{(i)}$ are $\lambda^{(i)}_{\pm}=\frac{1}{2} \Big(\mathrm{Tr}\rho^{(i)}\pm\sqrt{\mathrm{Tr}^{2}\rho^{(i)} -4\det\rho^{(i)}}\Big)$ and corresponding eigenstates are

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle |\lambda^{(i)}_{\pm}\rangle= \mathcal{N}^{(i)}_{\pm}\left(\frac{1}{2\mathrm{Tr}(\rho^{(i)}\sigma_{+})} \left[\mathrm{Tr}\left(\rho^{(i)}\sigma_{z}\right)\pm \sqrt{\mathrm{Tr}^{2}\rho^{(i)}-4\det\rho^{(i)}}\right], 1\right)^{\mathrm{T}}, \nonumber \end{align} \tag{ 38 }$$

for non-diagonal $\rho^{(i)}$ with $\mathcal{N}^{(i)}_{\pm}$ ($i=0,1$) the normalization coefficient. Here the specific form of $\sigma_{z}$ and $\sigma_{+}$ are

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sigma_{z}=\left(\begin{array}{@{}cc@{}} 1 & 0 \nonumber \\ 0 & -1 \end{array}\right),\quad \sigma_{+}=\left(\begin{array}{@{}cc@{}} 0 & 1 \nonumber \\ 0 & 0 \end{array}\right). \nonumber \end{align} \tag{ 39 }$$

Based on above information, $\mathcal{F}^{(i)}_{ab}$ can be specifically written as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}^{(i)}_{ab} &= \sum_{k=\pm}\frac{(\partial_{a}\lambda^{(i)}_{k})(\partial_{b} \lambda^{(i)}_{k})}{\lambda^{(i)}_{k}}+\lambda^{(i)}_{k}\mathcal{F}_{ab} \left(|\lambda^{(i)}_{k}\rangle\right) \nonumber \\ & \quad -\frac{16\det\rho^{(i)}}{\mathrm{Tr}\rho^{(i)}}\mathrm{Re}(\langle\partial_a \lambda^{(i)}_{+}| \lambda^{(i)}_{-}\rangle\langle\lambda^{(i)}_{-}|\partial_b \lambda^{(i)}_{+}\rangle), \nonumber \end{align} \tag{ 40 }$$

where $\mathcal{F}_{ab}(|\lambda^{(i)}_{k}\rangle)$ is the QFIM entry for the state $|\lambda^{(i)}_{k}\rangle$. For diagonal $\rho^{(i)}$, $|\lambda^{(i)}_{\pm}\rangle$ is just $(0,1){}^{\mathrm{T}}$ and only the classical contribution term remains in above equation.

Unitary processes are the most fundamental dynamics in quantum mechanics since it can be naturally obtained via the Schrödinger equation. For a $\vec {x}$-dependent unitary process $U=U(\vec {x})$, the parameterized state $\rho$ can be written as $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}\rho =U\rho_{0}U^{\dagger}$, where $\rho_{0}$ is the initial probe state which is $\vec {x}$-independent. For such a process, the QFIM can be calculated via the following theorem.

Theorem 2.7. For a unitary parametrization process U, the entry of QFIM can be obtained as [48]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab} &= \sum_{\eta_{i}\in\mathcal{S}}4\eta_{i} \mathrm{cov}_{|\eta_{i}\rangle}(\mathcal{H}_{a},\mathcal{H}_{b}) \nonumber \\ & -\sum_{\eta_{i},\eta_{j}\in\mathcal{S}, i\neq j}\frac{8\eta_{i}\eta_{j}}{\eta_{i} +\eta_{j}}\mathrm{Re}\left(\langle\eta_{i}|\mathcal{H}_{a} |\eta_{j}\rangle\langle\eta_{j}|\mathcal{H}_{b}|\eta_{i} \rangle\right), \label{eq:QFIM_unitary} \nonumber \end{align} \tag{ 41 }$$

where $\newcommand{\e}{{\rm e}} \eta_{i}$ and $\newcommand{\e}{{\rm e}} |\eta_{i}\rangle$ are ith eigenvalue and eigenstate of the initial probe state $\rho_{0}$. $\newcommand{\e}{{\rm e}} \mathrm{cov}_{|\eta_{i}\rangle} (\mathcal{H}_{a},\mathcal{H}_{b})$ is defined in equation (28). The operator $\mathcal{H}_{a}$ is defined as [49, 50]

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \mathcal{H}_{a}:={\rm i}\left(\partial_{a}U^{\dagger}\right)U =-{\rm i}U^{\dagger}\left(\partial_{a}U\right). \label{eq:unitary_H} \nonumber \end{align} \tag{ 42 }$$

$\mathcal{H}_{a}$ is a Hermitian operator for any parameter x_a due to above definition.

For the unitary processes, the parameterized state will remain pure for a pure probe state. The QFIM for this case is given as follows.

Corollary 2.7.1. For a unitary process U with a pure probe state $|\psi_{0}\rangle$, the entry of QFIM is in the form

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=4\mathrm{cov}_{|\psi_{0}\rangle}(\mathcal{H}_{a},\mathcal{H}_{b}), \nonumber \end{align} \tag{ 43 }$$

where $\mathrm{cov}_{|\psi_{0}\rangle}(\mathcal{H}_{a},\mathcal{H}_{b})$ is defined by equation (28) and the QFI for x_a can then be obtained as $\mathcal{F}_{aa}=4\mathrm{var}_{|\psi_{0}\rangle}(\mathcal{H}_{a})$. Here $\mathrm{var}_{|\psi_{0}\rangle}(\mathcal{H}_{a}):=\mathrm{cov}_{|\psi_{0}\rangle} (\mathcal{H}_{a},\mathcal{H}_{a})$ is the variance of $\mathcal{H}_{a}$ on $|\psi_{0}\rangle$.

For a single-qubit mixed state $\rho_{0}$ under a unitary process, the QFIM can be written as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=4\left[2\mathrm{Tr}(\rho^{2}_{0})-1\right] \mathrm{cov}_{|\eta_{0}\rangle}(\mathcal{H}_{a},\mathcal{H}_{b}) \nonumber \end{align} \tag{ 44 }$$

with $\newcommand{\e}{{\rm e}} |\eta_{0}\rangle$ an eigenstate of $\rho_{0}$. This equation is equivalent to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=4\left[2\mathrm{Tr}(\rho^{2}_{0})-1\right]\mathrm{Re} \left(\langle \eta_{0}|\mathcal{H}_{a}|\eta_{1}\rangle \langle\eta_{1}|\mathcal{H}_{b}|\eta_{0}\rangle\right). \nonumber \end{align} \tag{ 45 }$$

The diagonal entry reads $\newcommand{\e}{{\rm e}} \mathcal{F}_{aa}=4\left[2\mathrm{Tr} (\rho^{2}_{0})-1\right]|\langle\eta_{0}|\mathcal{H}_{a}|\eta_{1}\rangle|^{2}.$ Recall that theorem 2.6 provides the basis-independent formula for single-qubit mixed state, which leads to the next corollary.

Corollary 2.7.2. For a single-qubit mixed state $\rho_{0}$ under a unitary process, the basis-independent formula of QFIM is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}&=\mathrm{Tr}(\rho^{2}_{0}\{\mathcal{H}_{a},\mathcal{H}_{b}\}) -2\mathrm{Tr}(\rho_{0}\mathcal{H}_{a}\rho_{0}\mathcal{H}_{b}) \nonumber \\ & \quad +\frac{1}{\det\rho_{0}}\left[\mathrm{Tr}\left(\rho_{0}\mathcal{H}_{a}\rho_{0} \left\{\rho_{0}^{2},\mathcal{H}_{b}\right\}\right)-2\mathrm{Tr} (\rho^{2}_{0}\mathcal{H}_{a}\rho^{2}_{0}\mathcal{H}_{b})\right]. \nonumber \end{align} \tag{ 46 }$$

The diagonal entry reads

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{aa}&= 2\mathrm{Tr}(\rho^{2}_{0}\mathcal{H}^{2}_{a}) -2\mathrm{Tr}[(\rho_{0}\mathcal{H}_{a})^{2}] \nonumber \\ & \quad +\frac{2}{\det\rho_{0}}\left[\mathrm{Tr}\left(\rho_{0}\mathcal{H}_{a}\rho^{3}_{0} \mathcal{H}_{a}\right)-\mathrm{Tr}[(\rho^{2}_{0}\mathcal{H}_{a})^{2}]\right]. \nonumber \end{align} \tag{ 47 }$$

Under the unitary process, the QFIM for pure probe states, as given in equation (1), can be rewritten as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\frac{1}{2}\langle\psi_{0}|\left\{L_{a,\mathrm{eff}}, L_{b,\mathrm{eff}} \right\}|\psi_{0}\rangle, \nonumber \end{align} \tag{ 48 }$$

where $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}L_{a,\mathrm{eff}}:=U^{\dagger} L_{a}U$ can be treated as an effective SLD operator, which leads to the following theorem.

Theorem 2.8. Given a unitary process, U, with a pure probe state, $|\psi_{0}\rangle$, the effective SLD operator $L_{a,\mathrm{eff}}$ can be obtained as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle L_{a,\mathrm{eff}}={\rm i}2\left[\mathcal{H}_{a},|\psi_{0}\rangle\langle\psi_{0}|\right]. \nonumber \end{align} \tag{ 49 }$$

In equation (41), all the information of the parameters is involved in the operator set $\{\mathcal{H}_{a}\}$, which might benefit the analytical optimization of the probe state in some scenarios. Generally, the unitary operator can be written as $\newcommand{\e}{{\rm e}} \exp(-{\rm i}tH)$ where $H=H(\vec {x})$ is a time- independent Hamiltonian for the parametrization. $\mathcal{H}_{a}$ can then be calculated as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{H}_{a}=-\int^{t}_{0}{\rm e}^{{\rm i}sH}\left(\partial_{a}H\right) {\rm e}^{-{\rm i}sH} \mathrm{d}s, \nonumber \end{align} \tag{ 50 }$$

where the technique $\partial_{x}{\rm e}^{A}=\int^{1}_{0}{\rm e}^{sA}\partial_{x}A{\rm e}^{(1-s)A}{\rm d}s$ (A is an operator) is applied. Denote $H^{\times}(\cdot):=[H,\cdot]$, the expression above can be rewritten in an expanded form [48]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{H}_{a}=-\sum^{\infty}_{n=0}\frac{t^{n+1}}{(n+1)!}\left({\rm i} H^{\times}\right)^{n} \partial_{a}H. \label{eq:unitary_Hx} \nonumber \end{align} \tag{ 51 }$$

In some scenarios, the recursive commutations in expression above display certain patterns, which can lead to analytic expressions for the $\mathcal{H}$ operator. The simplest example is $H=\sum\nolimits_{a}x_{a}H_{a}$, with all H_a commute with each other. In this case $\mathcal{H}_{a}=-t H_{a}$ since only the zeroth order term in equation (51) is nonzero. Another example is the interaction of a collective spin system with a magnetic field with the Hamiltonian $H=-B J_{\vec {n}_{0}}$, where B is the amplitude of the external magnetic field, $J_{\vec {n}_{0}}=\vec {n}_{0}\cdot\vec {J}$ with $\vec {n}_{0}=(\cos\theta,0,\sin\theta)$ and $\vec {J}=(J_{x},J_{y},J_{z})$. $\theta$ is the angle between the field and the collective spin. $J_{i}=\sum\nolimits_{k}\sigma^{(k)}_{i}/2$ for $i=x,y,z$ is the collective spin operator. $\sigma^{(k)}_{i}$ is the Pauli matrix for kth spin. In this case, the $\mathcal{H}$ operator for $\theta$ can be analytically calculated via equation (51), which is [48]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{H}_{\theta}=-2\sin\left(\frac{1}{2}Bt\right)J_{\vec {n}_{1}}, \nonumber \end{align} \tag{ 52 }$$

where $J_{n_{1}}=\vec {n}_{1}\cdot\vec {J}$ with $\vec {n}_{1}=(\cos(Bt/2)\sin\theta,\sin(Bt/2),-\cos(Bt/2)\cos\theta)$.

Recently, Sidhu and Kok [51, 52] use this $\mathcal{H}$-representation to study the spatial deformations, epecially the grid deformations of classical and quantum light emitters. By calculating and analyzing the QFIM, they showed that the higher average mode occupancies of the classical states performs better in estimating the deformation when compared with single photon emitters.

An alternative operator that can be used to characterize the precision limit of unitary process is [50, 53, 54]

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \mathcal{K}_{a}:={\rm i}\left(\partial_{a}U\right)U^{\dagger} =-{\rm i}U\left(\partial_{a}U^{\dagger}\right). \nonumber \end{align} \tag{ 53 }$$

As a matter of fact, this operator is the infinitesimal generator of U of parameter x_a. Assume $\vec {x}$ is shifted by ${\rm d}x_{a}$ along the direction of x_a and other parameters are kept unchanged. Then $U(\vec {x}+{\rm d}x_{a})$ can be expanded as $U(\vec {x}+ {\rm d}x_{a})\partial_{a}U(\vec {x})$. The density matrix $\rho_{\vec {x}+{\rm d}x_{a}}$ can then be approximately calculated as $\rho_{\vec {x}+{\rm d}x_{a}}={\rm e}^{-{\rm i}\mathcal{K}_{a}{\rm d}x_{a}}\rho {\rm e}^{{\rm i}\mathcal{K}_{a}{\rm d}x_{a}}$ [53], which indicates that $\mathcal{K}_{a}$ is the generator of U along parameter x_a. The relation between $\mathcal{H}_{a}$ and $\mathcal{K}_{a}$ can be easily obtained as

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \mathcal{K}_{a}=-U\mathcal{H}_{a}U^{\dagger}. \nonumber \end{align} \tag{ 54 }$$

With this relation, the QFIM can be easily rewritten with $\mathcal{K}_{a}$ as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}&= \sum_{\lambda_{i}\in\mathcal{S}}4\lambda_{i} \mathrm{cov}_{|\lambda_{i}\rangle}(\mathcal{K}_{a},\mathcal{K}_{b}) \nonumber \\ &\quad -\sum_{\lambda_{i},\lambda_{j}\in\mathcal{S}, i\neq j}\frac{8\lambda_{i}\lambda_{j}}{\lambda_{i} +\lambda_{j}}\mathrm{Re}\left(\langle\lambda_{i}|\mathcal{K}_{a}|\lambda_{j}\rangle \langle\lambda_{j}|\mathcal{K}_{b}|\lambda_{i}\rangle\right), \nonumber \end{align} \tag{ 55 }$$

where $\newcommand{\e}{{\rm e}} |\lambda_{i}\rangle=U|\eta_{i}\rangle$ is the ith eigenstate of the parameterized state $\rho$. And $\mathrm{cov}_{|\lambda_{i}\rangle} (\mathcal{K}_{a},\mathcal{K}_{b})$ is defined by equation (28). The difference between the calculation of QFIM with $\{\mathcal{K}_{a}\}$ and $\{\mathcal{H}_{a}\}$ is that the expectation is taken with the eigenstate of the probe state $\rho_{0}$ for the use of $\{\mathcal{H}_{a}\}$ but with the parameterized state $\rho$ for $\{\mathcal{K}_{a}\}$. For a pure probe state $|\psi_{0}\rangle$, the expression above reduces to $\mathcal{F}_{ab}=4\mathrm{cov}_{|\psi\rangle}(\mathcal{K}_{a},\mathcal{K}_{b})$ with $|\psi\rangle=U|\psi_{0}\rangle$. Similarly, for a mixed state of single qubit, the QFIM reads $\mathcal{F}_{ab}=4\left(2\mathrm{Tr}\rho^{2}_{0}-1\right) \mathrm{cov}_{|\lambda_{0}\rangle}(\mathcal{K}_{a},\mathcal{K}_{b})$.

Gaussian state is a widely-used quantum state in quantum physics, particularly in quantum optics, quantum metrology and continuous variable quantum information processes. Consider a m-mode bosonic system with a_i ($\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}a^{\dagger}_{i}$) as the annihilation (creation) operator for the ith mode. The quadrature operators are [55, 56] $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}\hat{q}_{i}:=\frac{1}{\sqrt{2}}(a_{i}+a^{\dagger}_{i})$ and $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}\hat{p}_{i}:=\frac{1} {i\sqrt{2}}(a_{i}-a^{\dagger}_{i})$, which satisfy the commutation relation $\left[\hat{q}_{i}, \hat{p}_{j}\right]={\rm i}\delta_{ij}$ ($\hbar=1$). A vector of quadrature operators, $\vec {R}=(\hat{q}_{1},\hat{p}_{1},..., \hat{q}_{m},\hat{p}_{m}){}^{\mathrm{T}}$ satisfies

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \left[R_{i}, R_{j}\right]={\rm i}\Omega_{ij} \nonumber \end{align} \tag{ 56 }$$

for any i and j  where $\Omega$ is the symplectic matrix defined as $\Omega:={\rm i}\sigma^{\oplus m}_{y}$ where $\oplus$ denote the direct sum. Now we introduce the covariance matrix $C(\vec {R})$ with the entries defined as $C_{ij}:=\mathrm{cov}_{\rho}(R_{i},R_{j})=\frac{1}{2}\mathrm{Tr}(\rho \{R_{i},R_{j}\}) -\mathrm{Tr}(\rho R_{i})\mathrm{Tr}(\rho R_{j})$. C satisfies the uncertainty relation $C+\frac{\rm i}{2}\Omega \geqslant 0$ [57, 58]. According to the Williamson's theorem, the covariance matrix can be diagonalized utilizing a symplectic matrix S [58, 59], i.e.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle C=SC_{\mathrm{d}}S^{\mathrm{T}}, \nonumber \end{align} \tag{ 57 }$$

where $\newcommand{\openone}{\mathbb {1}} \newcommand{\bi}{\boldsymbol} C_{\mathrm{d}}=\bigoplus\nolimits_{k=1}^{m}c_{k}\openone_{2}$ with c_k the kth symplectic eigenvalue and $\newcommand{\openone}{\mathbb {1}} \newcommand{\bi}{\boldsymbol} \openone_2$ is a 2-dimensional identity matrix. S is a 2m-dimensional real matrix which satisfies $S\Omega S^{\mathrm{T}}=\Omega$.

A very useful quantity for Gaussian states is the characteristic function

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \chi(\vec {s})=\mathrm{Tr}\left(\rho ~{\rm e}^{{\rm i}\vec {R}^{\,\mathrm{T}}\Omega \vec {s}}\right), \nonumber \end{align} \tag{ 58 }$$

where $\vec {s}$ is a 2m-dimensional real vector. Another powerful function is the Wigner function, which can be obtained by taking the Fourier transform of the characteristic function

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle W(\vec {R})=\frac{1}{(2\pi)^{2m}}\int_{\mathbb{R}^{2m}}{\rm e}^{-{\rm i} \vec {R}^{\,\mathrm{T}} \Omega \vec {s}}~\chi(\vec {s})~\mathrm{d}^{2m}\vec {s}. \nonumber \end{align} \tag{ 59 }$$

Considering the scenario with first and second moments, a state is a Gaussian state if $\chi(\vec {s})$ and $W(\vec {R})$ are Gaussian, i.e. [55, 56, 58, 60, 61]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \chi(\vec {s}) = {\rm e}^{-\frac{1}{2}\vec {s}^{\,\mathrm{T}}\Omega C\Omega^{\mathrm{T}}\vec {s} -{\rm i}(\Omega\langle\vec {R}\rangle)^{\mathrm{T}}\vec {s}}, \nonumber \end{align} \tag{ 60 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle W(\vec {R}) = \frac{1}{(2\pi)^{m}\sqrt{\det C}}{\rm e}^{-\frac{1}{2}\left(\vec {R}-\langle \vec {R}\rangle\right)^{\mathrm{T}}C^{-1}\left(\vec {R}-\langle \vec {R}\rangle\right)}, \nonumber \end{align} \tag{ 61 }$$

where $\langle\vec {R}\rangle_{j}=\mathrm{Tr}(R_{j}\rho)$ is the first moment. A pure state is Gaussian if and only if its Wigner function is non-negative [58].

The study of QFIM for Gaussian states started from the research of QFI. The expression of QFI was first given in 2013 by Monras for the multi-mode case [62] and Pinel et al for the single-mode case [63]. In 2018, Nichols et al [65] and Šafránek [66] provided the expression of QFIM for multi-mode Gaussian states independently, which was obtained based on the calculation of SLD [7]. The SLD operator for Gaussian states has been given in [62, 65, 67], and we organize the corresponding results in the following theorem.

Theorem 2.9. For a continuous variable bosonic m-mode Gaussian state with the displacement vector (first moment) $\langle \vec {R}\rangle$ and the covariance matrix (second moment) C, the SLD operator is [62, 64–67, 69]

$$\begin{align} \newcommand{\e}{{\rm e}} \newcommand{\openone}{\mathbb {1}} \displaystyle L_{a}=L^{(0)}_{a}\openone_{2m}+\vec {L}^{(1),\mathrm{T}}_{a}\vec {R} +\vec {R}^{\,\mathrm{T}}G_{a}\vec {R}, \label{eq:SLD_Gaussian} \nonumber \end{align} \tag{ 62 }$$

where $\newcommand{\openone}{\mathbb {1}} \openone_{2m}$ is the 2m-dimensional identity matrix and the coefficients read

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle G_{a} = \sum^{m}_{j,k=1}\sum^{3}_{l=0}\frac{g^{(\,jk)}_{l}} {4 c_{j}c_{k}+(-1)^{l+1}}\left(S^{\mathrm{T}}\right)^{-1}A^{(\,jk)}_{l}S^{-1}, \nonumber \end{align} \tag{ 63 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \vec {L}^{(1)}_{a} = C^{-1}(\partial_{a}{\langle\vec {R}\rangle})-2G_{a} \langle\vec {R}\rangle, \nonumber \end{align} \tag{ 64 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle L^{(0)}_{a} = \langle\vec {R}\rangle^{\mathrm{T}}G_{a}\langle\vec {R}\rangle -(\partial_{a}\langle\vec {R}\rangle)^{\mathrm{T}}C^{-1}\langle\vec {R}\rangle -\mathrm{Tr}(G_{a}C). \nonumber \end{align} \tag{ 65 }$$

Here

$$\begin{align} \newcommand{\e}{{\rm e}} \newcommand{\openone}{\mathbb {1}} \displaystyle A^{(\,jk)}_{l}=\frac{1}{\sqrt{2}} {\rm i}\sigma^{(\,jk)}_{y},~\frac{1}{\sqrt{2}} \sigma^{(\,jk)}_{z},~\frac{1}{\sqrt{2}}\openone^{(\,jk)}_{2},~\frac{1}{\sqrt{2}} \sigma^{(\,jk)}_{x} \nonumber \end{align} \tag{ 66 }$$

for $l=0,1,2,3$ and $g^{(\,jk)}_{l}=\mathrm{Tr}[S^{-1}(\partial_{a}C)(S^{\mathrm{T}}){}^{-1} A^{(\,jk)}_{l}]$. $\sigma^{(\,jk)}_{i}$ is a 2m-dimensional matrix with all the entries zero expect a $2\times 2$ block, shown as below

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sigma^{(\,jk)}_{i} = \left(\begin{array}{@{}ccccc@{}} & 1\mathrm{st} & \cdots & k\mathrm{th} & \cdots \nonumber \\ 1\mathrm{st} & 0_{2\times2} & 0_{2\times2} & 0_{2\times2} & 0_{2\times2} \nonumber \\ \vdots & 0_{2\times2} & \vdots & \vdots & \vdots \nonumber \\ j\mathrm{th} & 0_{2\times2} & \cdots & \sigma_{i} & \cdots \nonumber \\ \vdots & \vdots & \vdots & \vdots & \vdots \end{array}\right), \nonumber \end{align} \tag{ 67 }$$

where $0_{2\times 2}$ represents a 2 by 2 block with zero entries. $\newcommand{\openone}{\mathbb {1}} \openone^{(\,jk)}_{2}$ is similar to $\sigma^{(\,jk)}_{i}$ but replace the block $\sigma_{i}$ with $\newcommand{\openone}{\mathbb {1}} \openone_{2}$⁹.

Being aware of the expression of SLD operator given in theorem 2.9, the QFIM can be calculated via equation (1). Here we show the result explicitly in following theorem.

Theorem 2.10. For a continuous variable bosonic m-mode Gaussian state with the displacement vector (first moment) $\langle \vec {R}\rangle$ and the covariance matrix (second moment) C, the entry of QFIM can be expressed by [64–66]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{ab}=\mathrm{Tr}\left(G_{a}\partial_{b}C\right) +(\partial_{a}\langle\vec {R}\rangle^{\mathrm{T}}) C^{-1}\partial_{b}\langle\vec {R}\rangle, \label{eq:QFIM_Gaussian} \nonumber \end{align} \tag{ 68 }$$

and the QFI for an m-mode Gaussian state with respect to x_a can be immediately obtained as [62]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}_{aa}=\mathrm{Tr}\left(G_{a}\partial_{a}C\right)+(\partial_{a} \langle\vec {R}\rangle^{\mathrm{T}})C^{-1}\partial_{a}\langle\vec {R}\rangle. \nonumber \end{align} \tag{ 69 }$$

The expression of right logarithmic derivative for a general Gaussian state and the corresponding QFIM was provided by Gao and Lee [64] in 2014, which is an appropriate tool for the estimation of complex numbers [25], such as the number $\alpha$ of a coherent state $|\alpha\rangle$. The simplest case is a single-mode Gaussian state. For such a state, G_a can be calculated as following.

Corollary 5. For a single-mode Gaussian state G_a can be expressed as¹⁰

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle G_{a}=\frac{4c^{2}-1}{4c^{2}+1}\Omega(\partial_{a}J)\Omega, \nonumber \end{align} \tag{ 70 }$$

where $c=\sqrt{\det C}$ is the symplectic eigenvalue of C and

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle J=\frac{1}{4c^{2}-1}C. \nonumber \end{align} \tag{ 71 }$$

For pure states, $\det C$ is a constant, G_a then reduces to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle G_{a}=\frac{1}{4c^{2}+1}\Omega(\partial_{a}C)\Omega. \nonumber \end{align} \tag{ 72 }$$

From this G_a, $\vec {L}^{(1)}_{a}$ and $L^{(0)}_{a}$ can be further obtained, which can be used to obtain the SLD operator via equation (62) and the QFIM via equation (68).

Another widely used method to obtain the QFI for Gaussian states is through the fidelity (see section 2.4.2 for the relation between fidelity and QFIM). The QFI for pure Gaussian states is studied in [68]. The QFI for single-mode Gaussian states has been obtained through the fidelity by Pinel et al in [63], and for two-mode Gaussian states by Šafránek et al in [69] and Marian et al [70] in 2016, based on the expressions of the fidelity given by Scutaru [71] and Marian et al in [72]. The expressions of the QFI and the fidelity for multi-mode Gaussian states are given by Monras [62], Safranek et al [69] and Banchi et al [73], and reproduced by Oh et al [74] with a Hermitian operator related to the optimal measurement of the fidelity.

There are other approaches, such as the exponential state [76], Husimi Q function [77], that can obtain the QFI and the QFIM for some specific types of Gaussian states. Besides, a general method to find the optimal probe states to optimize the QFIM of Gaussian unitary channels is also provided by Šafránek and Fuentes in [78], and Matsubara et al [75] in 2019. Matsubara et al performed the optimization of the QFI for Gaussian states in a passive linear optical circuit. For a fixed total photon number, the optimal Gaussian state is proved to be a single-mode squeezed vacuum state and the optimal measurement is a homodyne measurement.

In quantum mechanics, the pure states is a normalized vector because of the basic axiom that the norm square of its amplitude represents the probability. The pure states thus can be represented as rays in the projective Hilbert space, on which Fubini–Study metric is a Kähler metric. The squared infinitesimal distance here is usually expressed as [79]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{d}s^{2}=\frac{\langle\mathrm{d}\psi|\mathrm{d}\psi\rangle} {\langle\psi|\psi\rangle}-\frac{\langle\mathrm{d}\psi|\psi\rangle \langle\psi|\mathrm{d}\psi\rangle}{\langle\psi|\psi\rangle^{2}}. \nonumber \end{align} \tag{ 73 }$$

As $\langle\psi|\psi\rangle=1$ and $|\mathrm{d}\psi\rangle =\sum\nolimits_{\mu}|\partial_{x_{\mu}}\psi\rangle \mathrm{d}x_{\mu}$, $\mathrm{d}s^{2}$ can be expressed as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{d}s^{2}=\sum_{\mu\nu}\frac{1}{4}\mathcal{F}_{\mu\nu}\mathrm{d}x_{\mu} \mathrm{d}x_{\nu}, \nonumber \end{align} \tag{ 74 }$$

here $\mathcal{F}_{\mu\nu}$ is the $\mu\nu$ element of the QFIM. This means the Fubini–Study metric is a quarter of the QFIM for pure states. This is the intrinsic reason why the QFIM can depict the precision limit. Intuitively, the precision limit is just a matter of distinguishability. The best precision means the maximum distinguishability, which is naturally related to the distance between the states. The counterpart of Fubini-study metric for mixed states is the Bures metric, a well-known metric in quantum information and closely related to the quantum fidelity, which will be discussed below.

In quantum information, the fidelity $f(\rho_{1},\rho_{2})$ quantifies the similarity between two quantum states $\rho_{1}$ and $\rho_{2}$, which is defined as [80]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle f(\rho_{1},\rho_{2}):=\mathrm{Tr}\sqrt{\sqrt{\rho_{1}}\rho_{2}\sqrt{\rho_{1}}}. \label{eq:fidelity_def} \nonumber \end{align} \tag{ 75 }$$

Here $f\in[0,1]$ and f   =  1 only when $\rho_{1}=\rho_{2}$. Although the fidelity itself is not a distance measure, it can be used to construct the Bures distance, denoted as $D_{\mathrm{B}}$, as [80]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle D^{2}_{\mathrm{B}}(\rho_{1},\rho_{2})=2-2 f(\rho_{1},\rho_{2}). \nonumber \end{align} \tag{ 76 }$$

The relationship between the fidelity and the QFIM has been well studied in the literature [30, 31, 81–84]. In the case that the rank of $\rho(\vec {x})$ is unchanged with the varying of $\vec {x}$, the QFIM is related to the infinitestmal Bures distance in the same way as the QFIM related to the Fubini-study metric¹¹

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle D^{2}_{\mathrm{B}}(\rho(\vec {x}),\rho({\vec {x}+\mathrm{d}\vec {x}}))=\frac{1}{4}\sum_{\mu\nu} \mathcal{F}_{\mu\nu} {\rm d}x_{\mu}{\rm d}x_{\nu}. \nonumber \end{align} \tag{ 77 }$$

In recent years it has been found that the fidelity susceptibility, the leading order (the second order) of the fidelity, can be used as an indicator of the quantum phase transitions [18]. Because of this deep connection between the Bures metric and the QFIM, it is not surprising that the QFIM can be used in a similar way. On the other hand, the enhancement of QFIM at the critical point indicates that the precision limit of the parameter can be improved near the phase transition, as shown in [85, 86].

In the case that the rank of $\rho(\vec {x})$ does not equal to that of $\rho(\vec {x}+\mathrm{d}\vec {x})$, Šafránek recently showed [87] that the QFIM does not exactly equal to the fidelity susceptibility. Later, Seveso et al further suggested [88] that the quantum Cramér–Rao bound may also fail at those points.

Besides the Fubini–Study metric and the Bures metric, the QFIM is also closely connected to the Riemannian metric due to the fact that the state space of a quantum system is actually a Riemannian manifold. In more concrete terms, the QFIM belongs to a family of contractive Riemannian metric [24, 26, 89, 90], associated with which the infinitesimal distance in state space is $\mathrm{d}s^{2}=\sum\nolimits_{\mu}g_{\mu\nu}\mathrm{d}x_{\mu}\mathrm{d}x_{\nu}$ with $g_{\mu\nu}$ as the contractive Riemannian metric. In the eigenbasis of the density matrix $\rho$, $g_{\mu\nu}$ takes the form as [91–93]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle g_{\mu\nu}=\frac{1}{4}\sum_{i}\frac{\langle\lambda_{i}|\mathrm{d}\rho|\lambda_{i}\rangle^{2}} {\lambda_{i}}+\frac{1}{2}\sum_{i<j}\frac{|\langle\lambda_{i}|\mathrm{d}\rho|\lambda_{j}\rangle|^{2}} {\lambda_{j}h(\lambda_{i}/\lambda_{j})}, \label{eq:Bures_Riemannian} \nonumber \end{align} \tag{ 78 }$$

where $h(\cdot)$ is the Morozova–Čencov function, which is an operator monotone (for any positive semi-definite operators), self inverse ($xh(1/x)=1/h(x)$) and normalized ($h(1)=1$) real function. When $h(x)=(1+x)/2$, the metric above reduces to the QFIM (based on the SLD). The QFIMs based on right and left logarithmic derivatives can also be obtained by taking $h(x)=x$ and $h(x)=1$. The Wigner–Yanase information metric can be obtained from it by taking $h(x)=\frac{1}{4}(\sqrt{x}+1){}^{2}$.

The quantum geometric tensor originates from a complex metric in the projective Hilbert space, and is a powerful tool in quantum information science that unifies the QFIM and the Berry connection. For a pure state $|\psi\rangle=|\psi(\vec {x})\rangle$, the quantum geometric tensor Q is defined as [23, 95]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle Q_{\mu\nu}=\langle\partial_{\mu}\psi|\partial_{\nu}\psi\rangle -\langle\partial_{\mu}\psi|\psi\rangle\langle\psi|\partial_{\nu}\psi\rangle. \nonumber \end{align} \tag{ 79 }$$

Recall the expression of QFIM for pure states, given in equation (25), the real part of $Q_{\mu\nu}$ is actually the QFIM up to a constant factor, i.e.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{Re}(Q_{\mu\nu})=\frac{1}{4}\mathcal{F}_{\mu\nu}. \nonumber \end{align} \tag{ 80 }$$

In the mean time, due to the fact that

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle (\langle\partial_{\mu}\psi|\psi\rangle\langle\psi|\partial_{\nu}\psi\rangle)^{*} =\langle\psi|\partial_{\mu}\psi\rangle\langle\partial_{\nu}\psi|\psi\rangle =\langle\partial_{\mu}\psi|\psi\rangle\langle\psi|\partial_{\nu}\psi\rangle, \nonumber \end{align} \tag{ 81 }$$

i.e. $\langle\partial_{\mu}\psi|\psi\rangle\langle\psi|\partial_{\nu}\psi\rangle$ is real, the imaginary part of $Q_{\mu\nu}$ then reads

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{Im}(Q_{\mu\nu})=\mathrm{Im}(\langle\partial_{\mu}\psi|\partial_{\nu}\psi\rangle) =-\frac{1}{2}\left(\partial_{\mu}\mathcal{A}_{\nu}-\partial_{\nu}\mathcal{A}_{\mu}\right), \nonumber \end{align} \tag{ 82 }$$

where $\mathcal{A}_{\mu}:={\rm i}\langle\psi|\partial_{\mu}\psi\rangle$ is the Berry connection [96] and $\Upsilon_{\mu\nu}:=\partial_{\mu} \mathcal{A}_{\nu}-\partial_{\nu}\mathcal{A}_{\mu}$ is the Berry curvature. The geometric phase can then be obtained as [97]

where the integral is taken over a closed trajectory in the parameter space.

Recently, Guo et al [98] connected the QFIM and the Berry curvature via the Robertson uncertainty relation. Specifically, for a unitary process with two parameters, $\Upsilon_{\mu\nu}={\rm i}\langle\psi_{0}| [\mathcal{H}_{\mu},\mathcal{H}_{\nu}]|\psi_{0}\rangle$ with $\mathcal{H}_{\mu}$ defined in equation (42) and $|\psi_{0}\rangle$ the probe state, the determinants of the QFIM and the Berry curvature should satisfy

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \det\mathcal{F}+4\det\Upsilon \geqslant 0. \nonumber \end{align} \tag{ 84 }$$

Quantum speed limit aims at obtaining the smallest evolution time for quantum processes [6, 49, 93, 116–121]. It is closely related to the geometry of quantum states since the dynamical trajectory with the minimum evolution time is actually the geodesic in the state space, which indicates that the QFIM should be capable to quantify the speed limit. As a matter of fact, the QFI and the QFIM have been used to bound the quantum speed limit in recent studies [6, 49, 116, 117]. For a unitary evolution, $\newcommand{\e}{{\rm e}} U=\exp(-{\rm i}Ht)$, to steer a state away from the initial position with a Bures angle $D_{\mathrm{B}}=\arccos(\,f)$ (f  is the fidelity defined in equation (75)), the evolution time t needs to satisfy [6, 49, 122]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle t \geqslant \frac{2D_{\mathrm{B}}}{\sqrt{\mathcal{F}_{tt}}}, \nonumber \end{align} \tag{ 94 }$$

where $\mathcal{F}_{tt}$ is the QFI for the time t. For a more general case, that the Hamiltonian is time-dependent, Taddei et al [49] provided an implicit bound based on the QFI,

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sqrt{\frac{1}{2}\frac{\mathrm{d}^2\mathcal{D}(\,f)}{\mathrm{d}f^2} \left(\frac{\mathrm{d}\mathcal{D}}{\mathrm{d}f}\right)^{-3}}\Bigg|_{f\rightarrow 1} \mathcal{D}(\,f(\rho(0),\rho(t)))\leqslant \int^{t}_0\sqrt{\frac{\mathcal{F}_{\tau\tau}}{4}}\mathrm{d}\tau, \nonumber \end{align} \tag{ 95 }$$

where $\mathcal{D}$ is any metric on the space of quantum states via the fidelity f . In 2017, Beau and del Campo [123] discussed the nonlinear metrology of many-body open systems and established the relation between the QFI for coupling constants and the quantum speed limit, which indicates that the quantum speed limit directly determines the amplitude of the estimation error in such cases.

Recently, Pires et al [93] established an infinite family of quantum speed limits based on a contractive Riemannian metric discussed in section 2.4.2. In the case that $\vec {x}$ is time-dependent, i.e. $\vec {x}=\vec {x}(t)$, the geodesic distance $D(\rho_{0},\rho_{t})$ gives a lower bound of general trajectory,

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle D(\rho_{0},\rho_{t})\leqslant\int^{t}_{0}\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)\mathrm{d}t =\int^{t}_{0}\mathrm{d}t\sqrt{\sum_{\mu\nu}g_{\mu\nu}\frac{\mathrm{d}x_{\mu}}{{\rm d}t} \frac{\mathrm{d}x_{\nu}}{{\rm d}t}}, \nonumber \end{align} \tag{ 96 }$$

where $g_{\mu\nu}$ is defined in equation (78). Taking the maximum Morozova–Čencov function, the above inequality leads to the quantum speed limit with time-dependent parameters given in [49].

Non-Markovianity is an emerging concept in open quantum systems. Many different quantification of the non-Markovianity based on monotonic quantities under the completely positive and trace-preserving maps have been proposed [124–126]. The QFI can also be used to characterize the non-Markovianity since it also satisfies the monotonicity [6]. For the master equation

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \partial_{t}\rho=-{\rm i}[H_{\vec {x}},\rho]+\sum_{j}\gamma_{j}(t) \left(\Gamma_{j}\rho\Gamma^{\dagger}_{j}-\frac{1}{2} \left\{\Gamma^{\dagger}_{j}\Gamma_{j},\rho\right\}\right), \nonumber \end{align} \tag{ 97 }$$

the quantum Fisher information flow

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \partial_{t}\mathcal{F}_{aa}=-\sum_{j}\gamma_{j}(t) \mathrm{Tr}\left(\rho[L_{a},\Gamma_{j}]^{\dagger}[L_{a},\Gamma_{j}]\right) \nonumber \end{align} \tag{ 98 }$$

given by Lu et al [127] in 2010 is a valid witness for non-Markovianity. Later in 2015, Song et al [128] utilized the maximum eigenvalue of average QFIM flow to construct a quantitative measure of non-Markovianity. The average QFIM flow is the time derivative of average QFIM $\bar{\mathcal{F}} =\int\mathcal{F} \mathrm{d}\vec {x}$. Denote $\lambda_{\max}(t)$ as the maximum eigenvalue of $\partial_{t}\bar{\mathcal{F}}$ at time t, then the non-Markovianity can be alternatively defined as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{N}:=\int_{\lambda_{\max}>0} \lambda_{\max}\mathrm{d}t. \nonumber \end{align} \tag{ 99 }$$

One may notice that this is not the only way to define non-Makovianity with the QFIM, similar constructions would also be qualified measures for non-Markovianity.

The main application of the QFIM is in the quantum multiparameter estimation, which has shown very different properties and behaviors compared to its single-parameter counterpart [16]. The quantum multiparameter Cramér–Rao bound, also known as Helstrom bound, is one of the most widely used asymptotic bound in quantum metrology [1, 2].

Theorem 3.1. For a density matrix $\rho$ in which a vector of unknown parameters $\vec {x}=(x_{0},x_{1},...,x_{m},...){}^{\mathrm{T}}$ is encoded, the covariance matrix $\mathrm{cov}(\hat{\vec {x}},\{\Pi_{y}\})$ of an unbiased estimator $\hat{\vec {x}}$ under a set of POVM, $\{\Pi_{y}\}$, satisfies the following inequality¹³

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{cov}(\hat{\vec {x}},\{\Pi_{y}\}) \geqslant \frac{1}{n}\mathcal{I}^{-1}(\{\Pi_{y}\}) \geqslant \frac{1}{n}\mathcal{F}^{-1}, \nonumber \end{align} \tag{ 100 }$$

where $\mathcal{I}(\{\Pi_{y}\})$ is the CFIM, $\mathcal{F}$ is the QFIM and n is the repetition of the experiment.

The second inequality is called the quantum multiparameter Cramér–Rao bound. In the derivation, we assume the QFIM can be inverted, which is reasonable since a singular QFIM usually means not all the unknown parameters are independent and the parameters cannot be estimated simultaneously. In such cases one should first identify the set of parameters that are independent, then calculate the corresponding QFIM for those parameters.

For cases where the number of unknown parameters is large, it may be difficult or even meaningless to know the error of every parameter, and the total variance or the average variance is a more appropriate macroscopic quantity to study. Recall that the ath diagonal entry of the covariance matrix is actually the variance of the parameter x_a. Thus, the bound for the total variance can be immediately obtained as following.

Corollary 3.1.1. Denote $\mathrm{var}(\hat{x}_{a},\{\Pi_{y}\})$ as the variance of x_a, then the total variance $\sum\nolimits_{a}\mathrm{var}(x_{a},\{\Pi_{y}\})$ is bounded by the trace of $\mathcal{F}^{-1}$, i.e.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sum_{a}\mathrm{var}(\hat{x}_{a},\{\Pi_{y}\}) \geqslant \frac{1}{n}\mathrm{Tr} \left(\mathcal{I}^{-1}(\{\Pi_{y}\})\right) \geqslant \frac{1}{n}\mathrm{Tr}\left(\mathcal{F}^{-1}\right). \nonumber \end{align} \tag{ 101 }$$

The inverse of QFIM sometimes is difficult to obtain analytically and one may need a lower bound of $\mathrm{Tr}(\mathcal{F}^{-1})$ to roughly evaluate the precision limit. Being aware of the property of QFIM (given in section 2.1) that $[\mathcal{F}^{-1}]_{aa} \geqslant 1/\mathcal{F}_{aa}$, one can easily obtain the following corollary.

Corollary 3.1.2. The total variance is bounded as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sum_{a}\mathrm{var}(\hat{x}_{a},\{\Pi_{y}\}) \geqslant \frac{1}{n}\mathrm{Tr} \left(\mathcal{F}^{-1} \right) \geqslant \sum_{a} \frac{1}{n \mathcal{F}_{aa}}. \nonumber \end{align} \tag{ 102 }$$

The second inequality can only be attained when $\mathcal{F}$ is diagonal. Similarly,

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sum_{a}\mathrm{var}(\hat{x}_{a},\{\Pi_{y}\}) \geqslant \frac{1}{n}\mathrm{Tr} \left(\mathcal{I}^{-1}(\{\Pi_{y}\})\right) \geqslant \sum_{a} \frac{1}{n \mathcal{I}_{aa}(\{\Pi_{y}\})}. \nonumber \end{align} \tag{ 103 }$$

The simplest example for the multi-parameter estimation is the case with two parameters. In this case, $\mathcal{F}^{-1}$ can be calculated analytically as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{F}^{-1}=\frac{1}{\det(\mathcal{F})}\left(\begin{array}{@{}cc@{}} \mathcal{F}_{bb} & -\mathcal{F}_{ab} \nonumber \\ -\mathcal{F}_{ab} & \mathcal{F}_{aa} \end{array}\right). \nonumber \end{align} \tag{ 104 }$$

Here $\det(\cdot)$ denotes the determinant. With this equation, the corollary above can reduce to the following form.

Corollary 3.1.3. For two-parameter quantum estimation, corollary 3.1.1 reduces to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sum_{a}\mathrm{var}(\hat{x}_{a},\{\Pi_{y}\})\geqslant \frac{1}{n I_{\mathrm{ef\,\!f}} (\{\Pi_{y}\})}\geqslant \frac{1}{n F_{\mathrm{ef\,\!f}}}, \nonumber \end{align} \tag{ 105 }$$

where $I_{\mathrm{ef\,\!f}}(\{\Pi_{y}\})=\det(\mathcal{I})/\mathrm{Tr}(\mathcal{I})$ and $F_{\mathrm{ef\,\!f}}=\det(\mathcal{F})/\mathrm{Tr}(\mathcal{F})$ can be treated as effective classical and quantum Fisher information.

In statistics, the mean error given by $\sum\nolimits_{a}\mathrm{var}(\hat{x}_a,\{\Pi_y\})$ is not the only way for the characterization of mean error. Recently Lu et al [129] considered the generalized-mean, including the geometric and harmonic means, and provided the corresponding multiparameter Cramér–Rao bounds.

Attainability is a crucial problem in parameter estimation. An unattainable bound usually means the given precision limit is too optimistic to be realized in physics. In classical statistical estimations, the classical Cramér–Rao bound can be attained by the maximum likelihood estimator in the asymptotic limit, i.e. $\lim\nolimits_{n\rightarrow \infty} n\mathrm{cov}(\hat{\vec {x}}_{\mathrm{m}}(n)) =\mathcal{I}^{-1}$, where $\hat{\vec {x}}_{\mathrm{m}}(n)$ is the local maximum likelihood estimator and a function of repetition or sample number, which is unbiased in the asymptotic limit. Because of this, the parameter estimation based on Cramér–Rao bound is an asymptotic theory and requires infinite samples or repetition of the experiment. For a finite sample case, the maximum likelihood estimator is not unbiased and the Cramér–Rao bound may not be attainable as well. Therefore, the true attainability in quantum parameter estimation should also be considered in the sense of asymptotic limit since the attainability of quantum Cramér–Rao bound usually requires the QFIM equals the CFIM first. The general study of quantum parameter estimation from the asymptotic aspect is not easy, and the recent progress can be found in [90] and references therein. Here in the following, the attainability majorly refers to that if the QFIM coincides with the CFIM in theory. Besides, another thing that needs to emphasize is that the maximum likelihood estimator is optimal in a local sense [129], i.e. the estimated value is very close to the true value, and a locally unbiased estimator only attains the bound locally but not globally in the parameter space, thus, the attainability and optimal measurement discussed below are referred to the local ones.

For the single-parameter quantum estimations, the quantum Cramér–Rao bound can be attained with a theoretical optimal measurement. However, for multi-parameter quantum estimation, different parameters may have different optimal measurements, and these optimal measurements may not commute with each other. Thus there may not be a common measurement that is optimal for the estimation for all the unknown parameters. The quantum Cramér–Rao bound for the estimation of multiple parameters is then not necessary attainable, which is a major obstacle for the utilization of this bound in many years. In 2002, Matsumoto [131] first provided the necessary and sufficient condition of attainability for pure states. After this, its generalization to mixed states was discussed in several specific scenarios [28, 132–134] and rigorously proved via the Holevo bound firstly with the theory of local asymptotic normality [135] and then the direct minimization of one term in Holevo bound [136]. We first show this condition in the following theorem.

Theorem 3.2. The necessary and sufficient condition for the saturation of the quantum multiparameter Cramér–Rao bound is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{Tr}\left(\rho [L_{a},L_{b}]\right)=0,~\forall~a,b. \nonumber \end{align} \tag{ 106 }$$

For a pure parameterized state $|\psi\rangle:=|\psi(\vec {x})\rangle$, this condition reduces to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \langle\psi|[L_{a},L_{b}]|\psi\rangle=0,~\forall~a,b, \nonumber \end{align} \tag{ 107 }$$

which is equivalent to the form

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{Im}(\langle\partial_{a}\psi|\partial_{b}\psi\rangle)=0. \nonumber \end{align} \tag{ 108 }$$

When this condition is satisfied, the Holevo bound is also attained and equivalent to the Cramér–Rao bound [135, 136]. Recall that the Berry curvature introduced in section 2.4.3 is of the form

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Upsilon_{ab}&={\rm i}\partial_{a}(\langle\psi|\partial_{b}\psi\rangle) -{\rm i}\partial_{b}(\langle\psi|\partial_{a}\psi\rangle) \nonumber \\ &= -2\mathrm{Im}(\langle \partial_{a}\psi|\partial_{b}\psi\rangle). \nonumber \end{align} \tag{ 109 }$$

Hence, the above condition can also be expressed as following.

Corollary 3.2.1. The multi-parameter quantum Cramér–Rao bound for a pure parameterized state can be saturated if and only if

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Upsilon=0, \nonumber \end{align} \tag{ 110 }$$

i.e. the matrix of Berry curvature is a null matrix.

For a unitary process U with a pure probe state $|\psi_{0}\rangle$, this condition can be expressed with the operator $\mathcal{H}_{a}$ and $\mathcal{H}_{b}$, as shown in the following corollary [48].

Corollary 3.2.2. For a unitary process U with a pure probe state $|\psi_{0}\rangle$, the necessary and sufficient condition for the attainability of quantum multiparameter Cramér–Rao bound is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \langle\psi_{0}|\left[\mathcal{H}_{a},\mathcal{H}_{b}\right]|\psi_{0}\rangle=0, ~\forall~a,b. \nonumber \end{align} \tag{ 111 }$$

Here $\mathcal{H}_{a}$ was introduced in section 2.3.4.

The satisfaction of attainability condition theoretically guarantees the existence of some CFIM that can reach the QFIM. However, it still requires an optimal measurement. The search of practical optimal measurements is always a core mission in quantum metrology, and it is for the best that the optimal measurement is independent of the parameter to be estimated. The most well studied measurement strategies nowadays include the individual measurement, adaptive measurement and collective measurement, as shown in figure 3. The individual measurement refers to the measurement on a single copy (figure 3(a)) or local systems (black lines in figure 3(d)), and can be easily extend the sequential scenario (figure 3(c)), which is the most common scheme for controlled quantum metrology. The collective measurement, or joint measurement, is the one performed simultaneously on multi-copies or on the global system (orange lines in figure 3(d)) in parallel schemes. A typical example for collective measurement is the Bell measurement. The adaptive measurement (figure 3(b)) usually uses some known tunable operations to adjust the outcome. A well-studied case is the optical Mach–Zehnder interferometer with a tunable path in one arm. The Mach–Zehnder interferometer will be thoroughly introduced in the next section.

Zoom In Zoom Out Reset image size

For the single parameter case, a possible optimal measurement can be constructed with the eigenstates of the SLD operator. Denote $\{|l_{i}\rangle\langle l_{i}|\}$ as the set of eigenstates of L_a, if we choose the set of POVM as the projections onto these eigenstates, then the probability for the ith measurement result is $\langle l_{i}|\rho |l_{i}\rangle$. In the case where $|l_{i}\rangle$ is independent of x_a, the CFI then reads

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{I}_{aa}= \sum_{i}\frac{\langle l_{i}|\partial_{a}\rho |l_{i}\rangle^{2}} {\langle l_{i}|\rho |l_{i}\rangle}. \nonumber \end{align} \tag{ 112 }$$

Due to the equation $2\partial_{a}\rho =\rho L_{a}+L_{a}\rho$, the equation above reduces to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathcal{I}_{aa}= \sum_{i}l^{2}_{i} \langle l_{i}|\rho |l_{i}\rangle =\mathrm{Tr}(\rho L^{2}_{a})=\mathcal{F}_{aa}, \nonumber \end{align} \tag{ 113 }$$

which means the POVM $\{|l_{i}\rangle\langle l_{i}|\}$ is the optimal measurement to attain the QFI. However, if the eigenstates of the SLD are dependent on x_a, it is no longer the optimal measurement. In the case with a high prior information, the CFI with respect to $\{|l_{i}(\hat{x}_{a})\rangle\langle l_{i}(\hat{x}_{a})|\}$ ($\hat{x}_{a}$ is the estimated value of x_a) may be very close to the QFI. In practice, this measurement has to be used adaptively. Once we obtain a new estimated value $\hat{x}_{a}$ via the measurement, we need to update the measurement with the new estimated value and then perform the next round of measurement. For a non-full rank parameterized density matrix, the SLD operator is not unique, as discussed in section 2.3.1, which means the optimal measurement constructed via the eigenbasis of SLD operator is not unique. Thus, finding a realizable and simple optimal measurement is always the core mission in quantum metrology. Update to date, only known states in single-parameter estimation that own parameter-independent optimal measurement is the so-called quantum exponential family [27, 90], which is of the form

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \rho={\rm e}^{\frac{1}{2}\left(\int^{x}_{0}c(x^{\prime})\mathrm{d}x^{\prime} O -\int^{x}_{0}x^{\prime}c(x^{\prime})\mathrm{d}x^{\prime}\right)} \rho_0{\rm e}^{\frac{1}{2}(\int^{x}_{0}c(x^{\prime})\mathrm{d}x^{\prime} O -\int^{x}_{0}x^{\prime}c(x^{\prime})\mathrm{d}x^{\prime})}, \nonumber \end{align} \tag{ 114 }$$

where $c(x)$ is a function of the unknown parameter x, $\rho_{0}$ is a parameter-independent density matrix, and O is an unbiased observable of x, i.e. $\langle O\rangle=x$. For this family of states, the SLD is L_x  =  c(x)(O  −  x) and the optimal measurement is the eigenstates of O.

For multiparameter estimation, the SLD operators for different parameters may not share the same eigenbasis, which means $\{|l_{i}(\hat{x}_{a})\rangle\langle l_{i}(\hat{x}_{a})|\}$ is no longer an optimal choice for the estimation of all unknown parameters, even with the adaptive strategy. Currently, most of the studies in multiparameter estimation focus on the construction of the optimal measurements for a pure parameterized state $|\psi\rangle$. In 2013, Humphreys et al [152] proposed a method to construct the optimal measurement, a complete set of projectors containing the operator $|\psi_{\vec {x}_{\mathrm{true}}}\rangle\langle\psi_{\vec {x}_{\mathrm{true}}}|$ ($\vec {x}_{\mathrm{true}}$ is the true value of $\vec {x}$). Here $|\psi_{\vec {x}_{\mathrm{true}}}\rangle$ equals the value of $|\psi\rangle$ by taking $\vec {x}=\vec {x}_{\mathrm{true}}$. All the other projectors can be constructed via the Gram–Schmidt process. In practice, since the true value is unknown, the measurement has to be performed adaptively with the estimated values $\hat{\vec {x}}$, similar as the single parameter case. Recently, Pezzè et al [137] provided the specific conditions this set of projectors should satisfy to be optimal, which is organized in the following three theorems.

Theorem 3.3. Consider a parameterized pure state $|\psi\rangle$. $|\psi_{\vec {x}_{\mathrm{true}}}\rangle:=|\psi(\vec {x}=\vec {x}_{\mathrm{true}})\rangle$ with $\vec {x}_{\mathrm{true}}$ the true value of $\vec {x}$. The set of projectors $\{|m_{k}\rangle\langle m_{k}|, |m_{0}\rangle=|\psi_{\vec {x}_{\mathrm{true}}}\rangle\}$ is an optimal measurement to let the CFIM reach QFIM if and only if [137]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \lim_{\vec {x}\rightarrow\vec {x}_{\mathrm{true}}} \frac{\mathrm{Im}(\langle \partial_{a}\psi |m_{k}\rangle\langle m_{k}|\psi \rangle)} {|\langle m_{k}|\psi \rangle|}=0,~\forall x_{a}~\mathrm{and}~k\neq 0, \label{eq:optimal_measurement_0} \nonumber \end{align} \tag{ 115 }$$

which is equivalent to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{Im}(\langle\partial_{a}\psi|m_{k}\rangle\langle m_{k}|\partial_{b}\psi\rangle)=0, ~\forall x_{a},x_{b}~\mathrm{and}~k\neq 0. \nonumber \end{align} \tag{ 116 }$$

The proof is given in appendix I. This theorem shows that if the quantum Cramér–Rao bound can be saturated then it is always possible to construct the optimal measurement with the projection onto the probe state itself at the true value and a suitable choice of vectors on the orthogonal subspace [137].

Theorem 3.4. For a parameterized state $|\psi\rangle$, the set of projectors $\{|m_{k}\rangle\langle m_{k}|,\langle\psi |m_{k}\rangle\neq 0~\forall k\}$ is an optimal measurement to let the CFIM reach QFIM if and only if [137]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathrm{Im}(\langle\partial_{a}\psi |m_{k}\rangle\langle m_{k}|\psi\rangle) =|\langle\psi |m_{k}\rangle|^{2}\mathrm{Im}(\langle\partial_{a}\psi|\psi\rangle), ~\forall k, x_{a}. \label{eq:optimal_measurement_1} \nonumber \end{align} \tag{ 117 }$$

For the most general case that some projectors are vertical to $|\psi\rangle$ and some not, we have following theorem.

Theorem 3.5. For a parameterized pure state $|\psi\rangle$, assume a set of projectors $\{|m_{k}\rangle\langle m_{k}|\}$ include two subsets $A=\{|m_{k}\rangle\langle m_{k}|, \langle\psi|m_{k}\rangle=0~\forall k\}$ and $B=\{|m_{k}\rangle\langle m_{k}|, \langle\psi|m_{k}\rangle\neq 0~\forall k\}$, i.e. $\{|m_{k}\rangle\langle m_{k}|\}=A\cup B$, then it is an optimal measurement to let the CFIM to reach the QFIM if and nly if [137] equation (115) is fulfilled for all the projectors in set A and (117) is fulfilled for all the projectors in set B.

Apart from the QFIM, the CFIM is also bounded by a measurement-dependent matrix with the abth entry $\sum\nolimits_{k}\mathrm{Re}[\mathrm{Tr}(\rho L_{a}\Pi_{k}L_{b})]$ [138], where $\{\Pi_{k}\}$ is a set of POVM. Recently, Yang et al [138] provided the attainable conditions for the CFIM to attain this bound by generalizing the approach in [30].

A double-phase MZI consists of two beam splitters and a phase shift in each path, as shown in figure 4(b). In this setup, the operator of the two phase shifts is $\newcommand{\re}{{\rm Re}} \newcommand{\e}{{\rm e}} \renewcommand{\dag}{\dagger}P(\phi_{a},\phi_{b})=\exp({\rm i}(\phi_{a}\hat{a}^{\dagger}\hat{a}+\phi_{b}\hat{b}^{\dagger}\hat{b}))$. According to proposition 2.1, the QFIM for the phases is not affected by the second beam splitter $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}B^{\dagger}$ since it is independent of the phases. Thus, the second beam splitter can be neglected for the calculation of QFIM. Now take $\phi_{\mathrm{tot}}=\phi_{a}+\phi_{b}$ and $\phi_{\mathrm{d}}=\phi_{a}-\phi_{b}$ as the parameters to be estimated. For a separable input state $|\alpha\rangle\otimes|\chi\rangle$ with $|\alpha\rangle$ as a coherent state, the entries of QFIM reads [145]

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \mathcal{F}_{\phi_{\mathrm{tot}},\phi_{\mathrm{tot}}}= |\alpha|^{2}+\mathrm{var}_{|\chi\rangle}(b^{\dagger}b), \nonumber \end{align} \tag{ 118 }$$

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \mathcal{F}_{\phi_{\mathrm{d}},\phi_{\mathrm{d}}}= 2|\alpha|^{2}\mathrm{cov}_{|\chi\rangle}(b,b^{\dagger}) -2\mathrm{Re}\left(\alpha^{2}\mathrm{var}_{|\chi\rangle}(b^{\dagger})\right)+\langle b^{\dagger}b\rangle, \nonumber \end{align} \tag{ 119 }$$

$$\begin{align} \renewcommand{\dag}{\dagger} \newcommand{\e}{{\rm e}} \newcommand{\re}{{\rm Re}} \displaystyle \mathcal{F}_{\phi_{\mathrm{tot}},\phi_{\mathrm{d}}}= -{\rm i}\alpha^{*}\langle b\rangle-{\rm i}\mathrm{Im}(\alpha^{*}(\langle b^{\dagger}b^{2}\rangle -\langle b^{\dagger}b\rangle\langle b\rangle)). \nonumber \end{align} \tag{ 120 }$$

Focusing on the maximization of $\mathcal{F}_{\phi_{\mathrm{d}},\phi_{\mathrm{d}}}$ subject to a constraint of fixed mean photon number on b mode, Lang and Caves [145] proved that the squeezed vacuum state is the optimal choice for $|\chi\rangle$ which leads to the maximum sensitivity of $\phi_{\mathrm{d}}$.

Since Caves already pointed out that the vacuum fluctuation will affect the phase sensitivity [142], it is then interesting to ask the question that how bad the phase sensitivity could be if one input port keeps vacuum? Recently Takeoka et al [146] considered this question and gave the answer by proving a no-go theorem stating that in the double phase MZI, if one input port is the vacuum state, the sensitivity can never be better than the standard quantum limit regardless of the choice of quantum state in the other port and the detection scheme. However, this theorem does not hold for a single phase shift scenario in figure 4(a). Experimentally, Polino et al [147] recently demonstrated quantum-enhanced double-phase estimation with a photonic chip.

Besides the two-phase estimation, another practical two-parameter scenario in interometry is the joint measurement of phase and phase diffusion. In 2014, Vidrighin et al [132] provide a trade-off bound on the statistical variances for the joint estimation of phase and phase diffusion. Later in 2015, Altorio et al [148] addressed the usefulness of weak measurements in this case and in 2018 Hu et al [149] discussed the SU(1,1) interferometry in the presence of phase diffusion. In the same year, Roccia et al [150] experimentally showed that some collective measurement, like Bell measurement, can benefit the joint estimation of phase and phase diffusion.

Apart from double phase estimation, multi-phase estimation is also an important scenario in multiparameter estimation. The multi-phase estimation is usually considered in the multi-phase interferometer shown in figure 5(a). Another recent review on this topic is [16]. In this case, the total variance of all phases is the major concern, which is bounded by $\frac{1}{n}\mathrm{Tr}(\mathcal{F}^{-1})$ according to corollary 3.1.1. For multiple phases, the probe state undergoes the parameterization, which can be represented by $\newcommand{\e}{{\rm e}} U=\exp({\rm i} \sum\nolimits_{j}x_{j}H_{j})$ where H_j is the generator of the j th mode. In the optical scenario, this operation can be chosen as $\newcommand{\re}{{\rm Re}} \newcommand{\e}{{\rm e}} \renewcommand{\dag}{\dagger}\exp({\rm i} \sum\nolimits_{j}x_{j}a^{\dagger}_{j}a_{j})$ with $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}a^{\dagger}_{j}$ (a_j) as the creation (annihilation) operator for the j th mode. For a separable state $\newcommand{\bi}{\boldsymbol} \sum\nolimits_{k}p_{k}\bigotimes\nolimits_{i=0}^{d}\rho^{(i)}_{k}$ where $\rho^{(i)}_{k}$ is a state of the ith mode, and p _k is the weight with p _k  >  0 and $\sum\nolimits_{k}p_{k}=1$, the QFI satisfies $\mathcal{F}_{jj}\leqslant d (h_{j,\mathrm{max}}-h_{j,\mathrm{min}}){}^{2}$ [151] with $h_{j,\mathrm{max}}$ ($h_{j,\mathrm{min}}$) as the maximum (minimum) eigenvalue of H_j. From corollary 3.1.2, the total variance is then bounded by [151]

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \sum_{j}\mathrm{var}(\hat{x}_{j}, \{\Pi_{y}\})\geqslant \frac{1}{d}\sum^{d}_{j=1} \frac{1}{(h_{j,\mathrm{max}}-h_{j,\mathrm{min}})^{2}}. \nonumber \end{align} \tag{ 121 }$$

Zoom In Zoom Out Reset image size

This bound indicates that the entanglement is crucial in the multi-phase estimation to beat the standard quantum limit.

N00N state is a well known entangled state in quantum metrology which can saturate the Heisenberg limit. In 2013, Humphreys et al [152] discussed a generalized $(d+1)$-mode N00N state in the form $c_{0}|N_{0}\rangle+c_{1}\sum\nolimits_{i}|N_{i}\rangle$ where $|N_{i}\rangle=|0...0N0...0\rangle$ is the state in which only the ith mode corresponds to a Fock state and all other modes are left vacuum. c₀ and c₁ are real coefficients satisfying $c^{2}_{0}+dc^{2}_{1}=1$. The 0-mode is the reference mode and the parametrization process is $\newcommand{\re}{{\rm Re}} \newcommand{\e}{{\rm e}} \renewcommand{\dag}{\dagger}\exp({\rm i} \sum\nolimits_{j=1}^{d} x_{j}a^{\dagger}_{j}a_{j})$. The generation of this state has been proposed in [153]. Since this process is unitary, the QFIM can be calculated via corollary 2.7.1 with $\newcommand{\re}{{\rm Re}} \renewcommand{\dag}{\dagger}\mathcal{H}_{j}=-a^{\dagger}_{j}a_{j}$. It is then easy to see that the entry of QFIM reads [152] $\mathcal{F}_{ij} =4N^{2}(\delta_{ij}c^{2}_{1}-c^{4}_{1})$, which further gives

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \min_{c_{1}}\mathrm{Tr}(\mathcal{F}^{-1})=\frac{(1+\sqrt{d})^{2}d}{4N^{2}}, \nonumber \end{align} \tag{ 122 }$$

where the optimal c₁ is $1/\sqrt{d+\sqrt{d}}$.

Apart from the scheme in figure 5(a) with the simultaneous estimation, the multi-phase estimation can also be performed by estimating the phases independently, using the ith mode and the reference mode, as shown in figure 5(b). In this scheme, the phases are estimated one by one with the N00N state, which provides the total precision limit $d^{3}/N^{2}$ [152]. Thus, the simultaneous estimation scheme in figure 5(a) shows a $\mathcal{O}(d)$ advantage compared to the independent scheme in figure 5(b). However, the performance of the simultaneous estimation may be strongly affected by the noise [154, 155] and the $\mathcal{O}(d)$ advantage may even disappear under the photon loss noise [156].

In the single phase estimation, it is known that the entangled coherent state $\mathcal{N}(|0\alpha\rangle+|\alpha 0\rangle)$ ($|\alpha\rangle$ is a coherent state and $\mathcal{N}$ is the normalization) can provide a better precision limit than the N00N state [157]. Hence, it is reasonable to think the generalization of entangled coherent state may also outperform the generalized N00N state. This result was theoretically confirmed in [158]. For a generalized entangled coherent state written in the form $c_{0}|\alpha_{0}\rangle+c_{1}\sum\nolimits_{j=1}^{d}|\alpha_{j}\rangle$ with $|\alpha_{j}\rangle=|0...0\alpha0...0\rangle$, the QFIM is $\mathcal{F}_{ij}=4|c_{1}|^{2} |\alpha|^{2}[\delta_{ij}(1+|\alpha|^{2})-|c_{1}|^{2}|\alpha|^{2}]$ [158]. For most values of d and $|\alpha|$, the minimum $\mathrm{Tr}(\mathcal{F}^{-1})$ can be written as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \min_{c_{1}}\mathrm{Tr}(\mathcal{F}^{-1})=\frac{(1+\sqrt{d})^{2}d}{4(1+|\alpha|^{2})^{2}}, \nonumber \end{align} \tag{ 123 }$$

which is smaller than the counterpart of the generalized N00N state, indicating the performance of the generalized entangled coherent state is better than the generalized N00N state. For a large $|\alpha|$, the total particle number  ∼$|\alpha|^{2}$ and the performances of both states basically coincide. With respect to the independent scheme, the generalized entangled coherent also shows a $\mathcal{O}(d)$ advantage in the absence of noise.

In 2017, Zhang et al [159] considered a general balanced state $c\sum\nolimits_{j}|\psi_{j}\rangle$ with $|\psi_{j}\rangle=|0...0\psi0...0\rangle$. c is the normalization coefficient. Four specific balanced states: N00N state, entangled coherent state, entangled squeezed vacuum state and entangled squeezed coherent state, were calculated and they found that the entangled squeezed vacuum state shows the best performance, and the balanced type of this state outperforms the unbalanced one in some cases.

A linear network is another common structure for multi-phase estimation [160, 161]. Different with the structure in figure 5(a), a network requires the phase in each arm can be detected independently, meaning that each arm needs a reference beam. The calculation of Cramér–Rao bound in this case showed [161] that the linear network for miltiparameter metrology behaves classically even though endowed with well-distributed quantum resources. It can only achieve the Heisenberg limit when the input photons are concentrated in a small number of input modes. Moreover, the performance of a mode-separable state $\mathcal{N}(|N\rangle+v|0\rangle)$ may also shows a high theoretical precision limit in this case if $v\propto \sqrt{d}$.

Recently, Gessner [162] considered a general case for multi-phase estimation with multimode interferometers. The general Hamiltonian is $H=\sum\nolimits_{j=1}^{N} h^{(\,j)}_{k}$ with $h^{(\,j)}_{k}$ a local Hamiltonian for the ith particle in the kth mode. For the particle-separable states, the maximum QFIM is a diagonal matrix with the ith diagonal entry $\langle n_{i}\rangle$ being the ith average particle number (n_i is the ith particle number operator). This bound could be treated as the shot-noise limit for the multi-phase estimation. For the mode-separable states, the maximum QFIM is also diagonal, with the ith entry $\langle n^{2}_{i}\rangle$, which means the maximum QFIM for mode-separable state is larger than the particle-separate counterpart. Taking into account both the particle and mode entanglement, the maximum QFIM is in the form $\mathcal{F}_{ij}=\mathrm{sgn} (\langle n_{i}\rangle)\mathrm{sgn}(\langle n_{j}\rangle)\sqrt{\langle n^{2}_{i}\rangle \langle n^{2}_{j}\rangle}$, which gives the Heisenberg limit in this case.

The comparison among the performances of different strategies usually requires the same amount of resources, like the same sensing time, same particle number and so on. Generally speaking, the particle number here usually refers to the average particle number, which is also used to define the standard quantum limit and Heisenberg limit in quantum optical metrology. Although the Heisenberg limit is usually treated as a scaling behavior, people still attempt to redefine it as an ultimate bound given via quantum mechanics by using the expectation of the square of number operator to replace the square of average particle number [163], i.e. the variance should be involved in the Heisenberg limit [163, 164] and be treated as a resource.