Abstract
To properly represent the interplay and coupling of optical and material chirality at the photon-molecule or photon-nanoparticle level invites a recognition of quantum facets in the fundamental aspects and mechanisms of light–matter interaction. It is therefore appropriate to cast theory in a general quantum form, one that is applicable to both linear and nonlinear optics as well as various forms of chiroptical interaction including chiral optomechanics. Such a framework, fully accounting for both radiation and matter in quantum terms, facilitates the scrutiny and identification of key issues concerning spatial and temporal parity, scale, dissipation and measurement. Furthermore it fully provides for describing the interactions of structured or twisted light beams with a vortex character, and it leads to the complete identification of symmetry conditions for materials to provide for chiral discrimination. Quantum considerations also lend a distinctive perspective to the very different senses in which other aspects of chirality are recognized in metamaterials. Duly attending to the symmetry principles governing allowed or disallowed forms of chiral discrimination supports an objective appraisal of the experimental possibilities and developing applications.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since the turn of the present century, advances in the science and technology of structured light and plasmonics have brought a renewed focus upon the principles of chiral interaction and their underlying mechanisms, as has been exhibited in numerous recent studies [1–8]. Operating over nanoscale dimensions, there is a wide variety of fundamental light–matter processes with a capacity to exhibit chiral features. Traditionally such features have been primarily associated with molecules [9–11], although the development of metamaterials and other nanostructures has significantly expanded the scope for not only bulk, but also surface and layer manifestations [12–15]. As the quantum nature of matter is primarily evident over sub-wavelength scales—even in laser experiments there are usually very few photons, at any instant, over the span of an optical wavelength—it is perhaps surprising to find that many emergent proofs or conjectures of new phenomena are still often described in terms of essentially classical frames of representation. A strong case can be made that, to understand the interplay and coupling of optical and material chirality on the nanoscale, it is not only desirable but in fact necessary to fully account for the quantum aspects of light–matter interaction. When both parts of the system are treated with the same systematic regard for quantum behavior, the full power of symmetry arguments can be fully harnessed.
Optical chirality is a flourishing subject with a long history. It can be argued that the origins of its modern understanding lie in Pasteur's painstaking separation of right-and left-handed tartrate crystals, and his identification of their capacity to turn the plane of polarized light in opposite directions [16]. Given the long passage of time since those pioneering studies, it might be supposed that the general framework of theory for describing all forms of chiroptical interaction would by now be well understood and straightforward to apply. However, episodes of erroneous analysis suggests that this is not universally the case. Moreover, the emergence at intervals of new concept and experiments, with systems and phenomena that have no previous parallel, invites a periodic reappraisal of recognized principles and the extent of their validity. Indeed, much of the recent activity in this field can be attributed to a renewed interest in optical chirality prompted in many instances by the development and promise of structured light [17]. The following analysis aims to clarify the key principles in generic form, and to illustrate their application through some examples relating to recent developments.
By adopting a quantum theory approach to both the matter and the radiation, i.e. utilizing a quantum electrodynamical representation, it is possible to faithfully render the characteristics of photon interactions, spotlighting and addressing the key principles and issues including both spin and orbital angular momentum. It emerges that generalized results can be formulated in a form that not only affords rigor and simplicity, but that also facilitate considerations of fundamental symmetry. Specifically of interest are the behavior of each system and its composite parts under the operations of charge conjugation, parity inversion and time reversal (combining as universal  symmetry), with Hermitian conjugation. This broad perspective helps to bring clarity to some of the less readily understood issues that arise in the field of chiroptical interactions, readily revealing the scope and limitations of chiral specificity, while also having the capacity to demonstrate the viability or non-viability of various proposals for enantiomer resolution (separation of chiral image molecules). One of the most widely vaunted contexts for such studies is the need, especially prominent in health and diet related sectors, to achieve the speciation and separation of enantiomers, given that chiral forms of opposite handedness often have very different effects in the human body. However, the scope for application and development of general principles may hold more promise in other connections, as the wider field of chiroptical phenomena links with developments in metamaterials, nanophotonics and optical technology.
symmetry), with Hermitian conjugation. This broad perspective helps to bring clarity to some of the less readily understood issues that arise in the field of chiroptical interactions, readily revealing the scope and limitations of chiral specificity, while also having the capacity to demonstrate the viability or non-viability of various proposals for enantiomer resolution (separation of chiral image molecules). One of the most widely vaunted contexts for such studies is the need, especially prominent in health and diet related sectors, to achieve the speciation and separation of enantiomers, given that chiral forms of opposite handedness often have very different effects in the human body. However, the scope for application and development of general principles may hold more promise in other connections, as the wider field of chiroptical phenomena links with developments in metamaterials, nanophotonics and optical technology.
2. Structure and scale
At the outset it is worth emphasizing how important it is to identify the physical boundaries, scale and internal constitution of any system in which light engages with matter, as well as the specific quantities that can be directly measured—or which provide the basis for any secondary, derivative effect that is sought. The issues of measurability that characterize any quantum treatment develop a special prominence, and they can also acquire a greater clarity when optical methods are involved.
To begin with the simplest material components, the manifestation of chirality generally signifies a lack of any improper rotation axes: no inversion, mirror reflection or other rotation-reflection symmetry elements can be present in the relevant point group or space group [18]. The Schoenflies classification encapsulates these conditions in a rule precluding any Sn symmetry elements, where the symbol signifies invariance under reflection coupled with rotation about a perpendicular axis, through an angle of 2π/n. (S1 relates to simple reflection and S2 is inversion: the latter is consistent with the parity operation 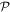 to be fully discussed in the following section.) Molecules lacking these symmetry elements can exist in either of two nominally 'left' and 'right' handed enantiomeric forms, each a mirror image of the other. These are designations that relate to the entirety of a molecule, or unit cell in the case of a solid.
to be fully discussed in the following section.) Molecules lacking these symmetry elements can exist in either of two nominally 'left' and 'right' handed enantiomeric forms, each a mirror image of the other. These are designations that relate to the entirety of a molecule, or unit cell in the case of a solid.
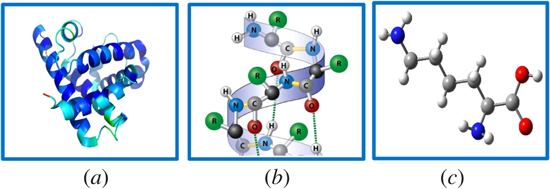
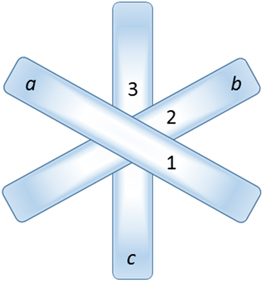
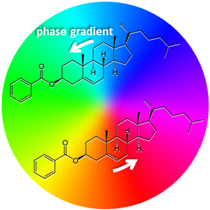
It should immediately be stressed that other senses of structural chirality can become meaningful by reference to another specific scale of measurement. For example, although the fundamental amino acid building blocks of proteins are almost invariably left-handed, the polypeptide chains formed by their linkage frequently form secondary structures such as alpha-helices of right-handed conformation—see figure 1. These in turn may be folded into tertiary structures of another distinct handedness. Equally, for finely layered chiral structures such as smectic or nematic (cholesteric) liquid crystals [19], or chiral sculptured thin films [20], the relative handedness of adjacent layers can be evinced in more than one sense [21], as schematically indicated in figure 2.
Figure 1. Illustration of increasing spatial resolution within a protein segment displaying: (a) twisted helices in a left-handed tertiary (polypeptide) structure; (b) part of an individual right-handed secondary (alpha helix) structure, R signifying a side-group of atoms; (c) left-handed structure of a component amino acid.
Download figure:
Standard image High-resolution imageFigure 2. Schematic illustration of axially aligned but progressively rotated molecules or other fundamental units, as for example in a chiral structured thin film, (axis perpendicular to the figure), in which the sense of rotation depends on the labeling: sequence a, b, c indicates clockwise rotation whereas 1, 2, 3 indicates anticlockwise.
Download figure:
Standard image High-resolution imageOn planar surfaces (more generally, planar interfaces), molecules and other discrete sub-wavelength scale structures are subject to less restrictive conditions for chirality to be exhibited. Since any system components 'above and below' the surface are not related by any symmetry operation, the sole requirement is a preclusion of reflection symmetry in any plane perpendicular to the surface; this serves to satisfy the absence of any Sn axes. Even this minor condition for '2D chirality' can be superseded in certain metamaterial surfaces, as will be discussed in section 14.
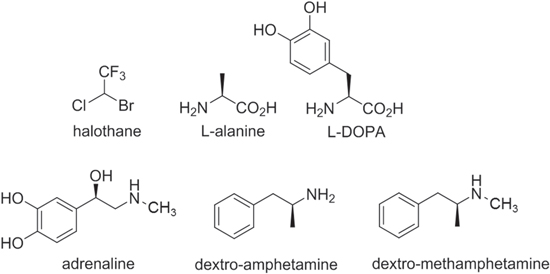
To address in detail the chirality of molecular structures, it is important to pay heed to the complexity of the system, avoiding a compromise of fundamental symmetry arguments by unphysical representations. The spatial dimensions of the individual molecules play a role that is often overlooked. Some relatively small chiral molecules associated with medical or health issues, governed by their left–right-handed form, are illustrated in figure 3. Chiroptical effects in the visible, near-UV and near-IR regions necessarily relate to the engagement of electromagnetic fields with material electronic configurations, and as molecular size increases the most prominent forms of optical response are usually less associated with the entirety of the molecule, more with specific 'chromophore' regions of locally distinctive electronic response (the only significant exceptions are molecules such as polyenes with an extensively delocalized electronic structure). Such chromophores are not directly identifiable with the 'chiral centers' designated as R or S (from the Latin rectus or sinister) in the well-established rules for identifying and classifying chirality in organic compounds [22].
Figure 3. Molecular structures of some simple chiral compounds that can be formed in either right-or left-handed enantiomeric form, and whose handedness (with the exception of halothane, the smallest) significantly affects their medical action. Wedge-shaped lines represent bonds projecting forwards, in front of the figure plane; shortened lines signify bonds projecting backwards.
Download figure:
Standard image High-resolution imageAnother, more general aspect deserves mention: the multiplicity of nuclear framework vibrational modes that generally rise in tiers within every electronic state. For example, the relatively small drug molecule L-DOPA with 22 atoms, illustrated in figure 3, has sixty distinct vibrational frequencies. As a result of this feature, the frequency dispersion properties of all but the very smallest molecules (and even for those, except at very low temperatures) are associated with significantly broad and often overlapped line-shapes. Due to computational complexity, vibrational structure is seldom considered in computing molecular response functions, even today, although a parametric dependence on various stable or semi-stable configurations can be taken into account in density functional theory calculations [23]. Nonetheless, the specific effect of nuclear vibrations is customarily ignored even in calculating molecular polarizabilities—despite their importance being previously flagged in numerous publications: see for example [24]. There is no reason to suppose that such factors should not prove just as significant for the other electronic response tensors associated with chiroptical response.
For all of these reasons, it is frequently misleading to suppose that as a whole, despite its discrete structural integrity, any multi-chromophore molecule could necessarily be simply described as unambiguously 'left' or 'right' handed. In a molecule comprising several chromophore groups, the combined effect of two achiral groups can itself generate chiral behavior—a feature that has long been exploited in the classic 'two-group' model of chiral species. (More detail on this is given later, in section 7.) However, if the separate groups are intrinsically chiral but structurally different, then their chiroptical responses need not necessarily be of the same sign; they may also prove to be strongest at different optical wavelengths.
There is no absolute measure of molecular chirality [11]. Although various metrics have been proposed for the quantification of chirality—generally algorithms based on the mathematics of molecular geometry and symmetry point groups [25, 26]—none of them relate directly to the observations of chiroptical interaction. This is not entirely surprising: optical methods based on optical rotation—circular dichroism or any other kind of measurement—all relate to molecular parameters that vary with the wavelength of incident light. Even the most fundamental and universal forms of interaction between molecules, which occur whether or not light is ostensibly present, depend on the dispersive behavior of molecular tensors that are intimately connected with optical response [27]. In fact, for such reasons any chiral molecule may ultimately be characterized by an infinite set of chiral pseudoscalars, (scalar parameters that are odd with respect to spatial parity 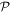 ), and even these may have different signs for a single given object [28].
), and even these may have different signs for a single given object [28].
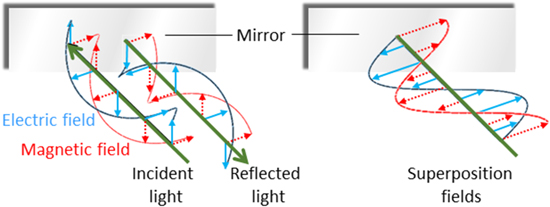
In contrast to the complexities of definition for material chirality, much more precise and unequivocal formulations can be given for the chirality associated with light—as will be detailed in quantum operator form in section 5. Nonetheless, issues of scale are again important regarding the electromagnetic radiation. Novel features can emerge in localized applications—principally in optical interactions with matter in regions that preclude free-space propagation. In fact, cavity and near-field photonics have relatively few features to distinctively register molecular chirality, but close to a source the electric and magnetic fields of electromagnetic radiation do exhibit properties quite different from their wave-zone behavior [29]. The effects are manifested, for example, in the fields radiating from a chiral source exhibiting significant differences between near- and far-field helicity [30]. Indeed, chiral near-fields can be generated in the vicinity of plasmonic nanoantennas that are structurally achiral, for example [31]. Surprising effects also arise in optically very simple optical systems. One striking instance, illustrated in figure 4, occurs in the proximity of a mirror, when circularly polarized light impinges at normal incidence; it has been shown that the self-interference of reflected photons produces electromagnetic field distributions with a capacity to produce chiroptical interactions on a locally anomalous scale [9, 32, 33]. In addition to all of these features, novel experimental effects can also arise over the physical scale represented by the cross-section of a structured beam, as will emerge in later sections.
Figure 4. Circularly polarized light reflected at normal incidence from a mirror (left) produces a superposition in which the electric (blue) and magnetic (red) field vectors are out of phase plane waves, and hence a spatially varying capacity to exhibit chiroptical interactions.
Download figure:
Standard image High-resolution image3. Symmetry and parity in electrodynamics
There is a wide variety of ways through which chiral matter can exhibit distinctive interactions with light. Prominent amongst the governing principles, fundamental symmetry proves powerfully effective, often entirely determining the allowed or forbidden character of a known or conjectured form of interaction. By entertaining such considerations it is possible to identify processes that are intrinsically displayed only by matter of a certain symmetry type. However, interest most often focuses on other, more common kinds of interactions—simple absorption for example—that occur in all kinds of media, yet which in chiral systems exhibit specific differences in optical response according to handedness. As observed earlier, the most familiar chiroptical (gyrotropic) phenomena include optical rotation and circular dichroism [34].
We now focus specific attention upon the general symmetry features of the quantum state vector for a closed light–matter system, evolving under a complete Hamiltonian. The aim is to show how parity determines the interplay of optical and material chirality, with special regard to chirally selective interactions. The fundamental symmetries of significance to optical and electromagnetic phenomena are the parities with respect to charge, space and time inversion—operations denoted by 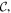
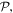 and
and  , respectively [35–37]. Each of these has the cast of an Abelian group Z2, with eigenvalues of ±1 signifying even or odd parity, such that double operation is an identity. Since light is subject to relativistic equations, it is necessary to ensure the use of a Lorentz-invariant local quantum field theory—from which it emerges that a Hermitian Hamiltonian is invariant under the combined
, respectively [35–37]. Each of these has the cast of an Abelian group Z2, with eigenvalues of ±1 signifying even or odd parity, such that double operation is an identity. Since light is subject to relativistic equations, it is necessary to ensure the use of a Lorentz-invariant local quantum field theory—from which it emerges that a Hermitian Hamiltonian is invariant under the combined 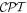 operation. All electromagnetic interactions exhibit this symmetry, and a symmetry analysis with the inclusion of charge conjugation affords some interesting fundamental insights [38]. However, charge conjugation is of less practical concern for addressing the interactions of light with conventional matter; the matter invariably has positively charged nuclei and negative electrons surrounding them, and the converse case simply does not arise in our normal world. Thus, it will suffice from here onwards to specifically consider
operation. All electromagnetic interactions exhibit this symmetry, and a symmetry analysis with the inclusion of charge conjugation affords some interesting fundamental insights [38]. However, charge conjugation is of less practical concern for addressing the interactions of light with conventional matter; the matter invariably has positively charged nuclei and negative electrons surrounding them, and the converse case simply does not arise in our normal world. Thus, it will suffice from here onwards to specifically consider  symmetry.
symmetry.
Since a symmetry-preserving, even character for the product operation 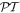 must mean the same character—both either even or both odd—with respect to
must mean the same character—both either even or both odd—with respect to 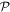 and
and  individually, it is often expedient to focus on just one of them. The conditions and constraints imposed through the behavior under space inversion are therefore the same as those delivered by entertaining the results of time inversion, assuming a closed system. Nonetheless, additional insights are sometimes afforded by keeping both under review, and that is the intention in much of what follows. Moreover, when individual components of the system are considered in isolation, the additional constraints of Hermitian conjugation
individually, it is often expedient to focus on just one of them. The conditions and constraints imposed through the behavior under space inversion are therefore the same as those delivered by entertaining the results of time inversion, assuming a closed system. Nonetheless, additional insights are sometimes afforded by keeping both under review, and that is the intention in much of what follows. Moreover, when individual components of the system are considered in isolation, the additional constraints of Hermitian conjugation  are best subsumed into the formulation of a suitably antilinear time reversal operator
are best subsumed into the formulation of a suitably antilinear time reversal operator 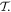
Before proceeding further, the spatial operation 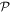 is worth examining in a little more detail. In any number of dimensions its operation can be represented by a coordinate transformation matrix whose determinant is −1. In three-dimensional space this can be effected in two ways: by the reversal of either one, or all three, Cartesian basis vectors
is worth examining in a little more detail. In any number of dimensions its operation can be represented by a coordinate transformation matrix whose determinant is −1. In three-dimensional space this can be effected in two ways: by the reversal of either one, or all three, Cartesian basis vectors 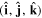 . Reversing just one basis vector equates to mirror reflection in the plane containing the other two; reversing all three directly corresponds to spatial inversion operation i, resulting in
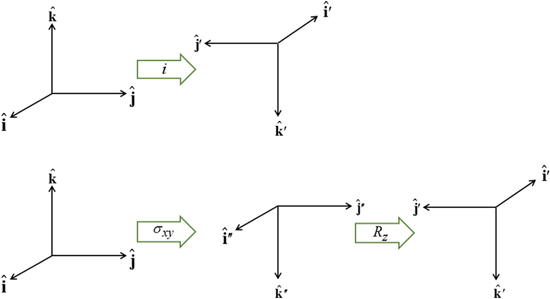
. Reversing just one basis vector equates to mirror reflection in the plane containing the other two; reversing all three directly corresponds to spatial inversion operation i, resulting in 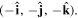 The former option, when followed by a rotation of π radians about the selected axis, leads to the same result—see figure 5. Designating parity in terms of reflection symmetry is more familiar in the field of chemistry, where molecular chirality is commonly described in terms of mirror image enantiomers, and free molecules have no fixed orientation. However, a consideration of reflection alone can be misleading, as its physical consequence for a particular structure may appear to depend on an arbitrary choice of plane, whose normal is reversed in sign. Moreover, inversion, reflection and rotation are specifically separate symmetry operations in point and space groups. Therefore, the operation of
The former option, when followed by a rotation of π radians about the selected axis, leads to the same result—see figure 5. Designating parity in terms of reflection symmetry is more familiar in the field of chemistry, where molecular chirality is commonly described in terms of mirror image enantiomers, and free molecules have no fixed orientation. However, a consideration of reflection alone can be misleading, as its physical consequence for a particular structure may appear to depend on an arbitrary choice of plane, whose normal is reversed in sign. Moreover, inversion, reflection and rotation are specifically separate symmetry operations in point and space groups. Therefore, the operation of 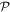 is specifically identified with the inversion in the following. In either representation—inverting just one or all three basis vectors—special consideration has to be given to the fact that its operation compromises the conventional 'right-hand rule' for the vector cross-product
is specifically identified with the inversion in the following. In either representation—inverting just one or all three basis vectors—special consideration has to be given to the fact that its operation compromises the conventional 'right-hand rule' for the vector cross-product  inversion changes 'right-handed' to 'left-handed' space.
inversion changes 'right-handed' to 'left-handed' space.
Figure 5. Equivalence of: (top) the spatial inversion operation i, and (bottom) mirror reflection σxy with rotation Rz about the mirror normal.
Download figure:
Standard image High-resolution imageAlthough it may seem physically obvious, it needs to be asserted that the robust character of the fundamental 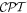 symmetry rules in the province of optics (weak interactions notwithstanding) clearly precludes any spontaneous generation of chirality. A system that is intrinsically achiral cannot become chiral without some form of chiral input or stimulus. For example, light without a degree of handedness or helicity cannot produce any effect that leads to an enantiomeric excess (a difference in the number of right-and left-handed forms), or any response that differentiates between such individual forms, as will clearly emerge from the mathematics that follows. It is important not to underplay the strength of this condition [39], which is physically comprehensible as 'dressing' an achiral system with chiral light, as for example in induced circular dichroism [40, 41]. However, when two or more chiral species are present, whose mutual interaction depends on their relative handedness even when no light is present [42], then light either with or without helical character can elicit a correspondingly differential response [43].
symmetry rules in the province of optics (weak interactions notwithstanding) clearly precludes any spontaneous generation of chirality. A system that is intrinsically achiral cannot become chiral without some form of chiral input or stimulus. For example, light without a degree of handedness or helicity cannot produce any effect that leads to an enantiomeric excess (a difference in the number of right-and left-handed forms), or any response that differentiates between such individual forms, as will clearly emerge from the mathematics that follows. It is important not to underplay the strength of this condition [39], which is physically comprehensible as 'dressing' an achiral system with chiral light, as for example in induced circular dichroism [40, 41]. However, when two or more chiral species are present, whose mutual interaction depends on their relative handedness even when no light is present [42], then light either with or without helical character can elicit a correspondingly differential response [43].
It is also worth emphasizing that it is entirely possible for 'optical activity' to be exhibited by any intrinsically achiral materials or metamaterials [44]. Consideration of the entire light–matter system nonetheless readily shows that such effects can only arise under the influence of optical fields with their own helical character—through chirally configured beams, circular polarizations, or within optical nanofibres for example [45]. Equally, when circularly polarized light impinges upon such a material with a suitably asymmetric structure, its propagation in directly opposite directions may differ; the two light–matter configurations are not equivalent under 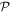 [46]. From a classical perspective, the presence of a static magnetic field is often described as 'symmetry breaking' in other such connections, where Helmholtz reciprocity (backward–forward equivalence) is found lacking—the historically most notable example being the Faraday effect. However, due inclusion of the field as a component of the system shows that its linear involvement is still entirely consistent with overall
[46]. From a classical perspective, the presence of a static magnetic field is often described as 'symmetry breaking' in other such connections, where Helmholtz reciprocity (backward–forward equivalence) is found lacking—the historically most notable example being the Faraday effect. However, due inclusion of the field as a component of the system shows that its linear involvement is still entirely consistent with overall 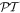 symmetry. We return to these issues in sections 13 and 14.
symmetry. We return to these issues in sections 13 and 14.
To finally set the scene for applying these principles to optical processes, it is worth re-emphasizing that their legitimate application must have regard to the full quantum system comprising both matter and radiation. There are numerous pitfalls if only the material system is considered in formulating theory. For example, in one eminent source we find the surprising and clearly incorrect assertion that 'the observation of a permanent EDM (electric dipole moment) of a neutron, atom or molecule would imply 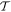 -violation' [47]. The latter case, suggesting the preclusion of a permanent electric dipole in any molecule, is patently untrue; the water molecule is an obvious example, and the operation of liquid crystal displays graphically exhibits the effects of molecular orientation specifically due to permanent dipoles. (Indeed the majority of molecules—even a simple heteronuclear diatomic species such as hydrogen fluoride—have a permanent electric dipole: NIST lists common experimental values at cccbdb.nist.gov/diplistx.asp.) The error in the deduction, that
-violation' [47]. The latter case, suggesting the preclusion of a permanent electric dipole in any molecule, is patently untrue; the water molecule is an obvious example, and the operation of liquid crystal displays graphically exhibits the effects of molecular orientation specifically due to permanent dipoles. (Indeed the majority of molecules—even a simple heteronuclear diatomic species such as hydrogen fluoride—have a permanent electric dipole: NIST lists common experimental values at cccbdb.nist.gov/diplistx.asp.) The error in the deduction, that  symmetry would be compromised by a polar molecule, may partly come from failing to account for having less than spherical symmetry—but it appears to be primarily due to an application of symmetry principles that fails to include, along with matter, the electric or electromagnetic fields necessary to register the dipole.
symmetry would be compromised by a polar molecule, may partly come from failing to account for having less than spherical symmetry—but it appears to be primarily due to an application of symmetry principles that fails to include, along with matter, the electric or electromagnetic fields necessary to register the dipole.
4. Dynamics
The detailed theory now to be presented will clarify an important distinction between processes for which there is a directly identifiable evolution of the system state vector, such that an intrinsic rate can be determined, and other kinds of interaction responsible for energy shifts. The former are generally associated with detectable transitions between electronic states of the material, and/or changes in the state of the radiation field. Energy shifts can only give rise to subsidiary processes: for example, when an optically induced energy shift has a well-defined spatial, orientational or temporal variation it will often lead to measurable response to the resultant force fields [10]. However the latter kinds of mechanical effect are necessarily dependent on bulk properties of the local media, e.g. dielectric constant, viscosity and temperature or pressure. In such a context, it is even possible to conceive an interplay between structural and chiroptical properties mediated by a phase change [48].
It will be helpful to begin with an enumeration of the key equations, whose symmetry character is to be explored. An obvious and appropriate starting point is the time-dependent Schrödinger equation:
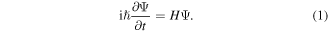
The Hamiltonian operator H and wavefunction Ψ are understood to refer to an entire system—encompassing all of the matter and all of the radiation within a closed system, within which the interactions of interest take place (the complication of losses is to be considered subsequently). Accordingly, equation (1) affords an exact representation of the system dynamics, and its symmetry properties are easily understood. We can focus on the operators on the right-and left-hand sides alone, since the wavefunction appears in both of them. The Hamiltonian operator on the right is necessarily of even parity with respect to both 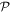 and
and 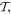 since it delivers an energy. For the operator on the left, the identification of even parity with respect to space inversion is obvious, whilst time reversal both changes the sign of time t and effects complex conjugation, with the result that
since it delivers an energy. For the operator on the left, the identification of even parity with respect to space inversion is obvious, whilst time reversal both changes the sign of time t and effects complex conjugation, with the result that  is also time-even. (Time reversal has several alternative interpretations; here it is used in the sense of combining the reversal of explicit time variables with Hermitian conjugation, which also subsumes complex variable conjugation [49, 50].) Here and in the following we assume 'closed-shell' states of time-even parity, for simplicity excluding states with unpaired electron spin. By far the majority of stable molecules and larger assemblies are of this kind.
is also time-even. (Time reversal has several alternative interpretations; here it is used in the sense of combining the reversal of explicit time variables with Hermitian conjugation, which also subsumes complex variable conjugation [49, 50].) Here and in the following we assume 'closed-shell' states of time-even parity, for simplicity excluding states with unpaired electron spin. By far the majority of stable molecules and larger assemblies are of this kind.
Before proceeding further it is important to recognize that, for either the molecular or optical field components of the system, the symmetry signatures under the operations of  and
and  will commonly not be the same as those of the Hamiltonian. When we are dealing with chiral materials it is necessarily the case that the wavefunction for either individual enantiomer (even in its electronic ground state) lacks the full symmetry of the corresponding molecular Hamiltonian [51], and indeed cannot be an eigenstate of
will commonly not be the same as those of the Hamiltonian. When we are dealing with chiral materials it is necessarily the case that the wavefunction for either individual enantiomer (even in its electronic ground state) lacks the full symmetry of the corresponding molecular Hamiltonian [51], and indeed cannot be an eigenstate of  Similarly, there is no requirement for any specific optical field to satisfy the constraints of parity that are demanded of the quantum field operators. More on this later, but for the present let it be noted that for simplicity—and applicability to the majority of applications—it is to be assumed that the material components individually lack unpaired electron spin [52, 53]. The temporally odd signature of a free unpaired electron for example, as may feature in Kramers states, can be accommodated in a generalized symmetry analysis at the cost of additional complication.
Similarly, there is no requirement for any specific optical field to satisfy the constraints of parity that are demanded of the quantum field operators. More on this later, but for the present let it be noted that for simplicity—and applicability to the majority of applications—it is to be assumed that the material components individually lack unpaired electron spin [52, 53]. The temporally odd signature of a free unpaired electron for example, as may feature in Kramers states, can be accommodated in a generalized symmetry analysis at the cost of additional complication.
To continue in general, the time evolution of the system wavefunction has to be tackled by an optimal and appropriate method of approximation. Time-dependent perturbation theory is an appropriate vehicle for applying symmetry principles; it represents one of the most widely used approaches, and is accordingly chosen for the analysis that follows. For the present purposes, assuming explicit coupling between molecules is not necessitated by the photophysics, it will suffice to consider just a single molecule interacting with light. (The correct formulation of theory for cases where explicit pairwise coupling is important has been discussed in another recent paper [54].) The system Hamiltonian can thus be expressed as a simple sum of three Hermitian terms, two of which together represent an 'unperturbed' system operator H0:
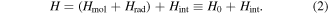
Then the product eigenstates of the molecular and radiation energy operators, Hmol and Hrad respectively, form a basis for perturbation by the coupling term Hint. As the symmetry issues are explored, it is encouraging to observe at the outset that the same principles must apply even under conditions that would invalidate the usual assumptions of perturbation theory. Entertaining such cases explicitly at this stage would complicate symmetry analysis, without changing in any way the parity-based conclusions that are to be drawn.
In the light of earlier remarks, anticipating the analysis that will ensue, it is expedient to consider a general interaction that takes the system from an initial state 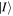 to a final state
to a final state 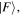 without imposing any condition that either the state of the radiation or that of the matter necessarily changes overall. In any event, since
without imposing any condition that either the state of the radiation or that of the matter necessarily changes overall. In any event, since  and
and 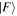 are system states they are, over any measurable time interval, isoenergetic, with energy EI. The matrix element MFI that signifies the electrodynamic coupling involved in a given form of interaction is conveniently cast in a resolvent operator formalism as an infinite series [55];
are system states they are, over any measurable time interval, isoenergetic, with energy EI. The matrix element MFI that signifies the electrodynamic coupling involved in a given form of interaction is conveniently cast in a resolvent operator formalism as an infinite series [55];
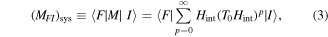
where the subscript sys emphasizes the use of full system states in equation (3), and the propagator  Implementing the completeness relation gives:
Implementing the completeness relation gives:
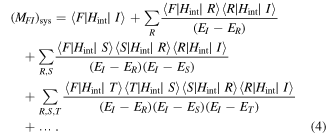
Here, the intermediate virtual states of the particle are denoted by  upon which operates H0 to deliver system energies ER, ES, ET, etc.
upon which operates H0 to deliver system energies ER, ES, ET, etc.
When the initial and final system states are the same, and diagonal elements of the matrix element arise, the result represents an energy component. Trivially, it is evident that effecting time reversal  leaves the result unchanged. However, when
leaves the result unchanged. However, when  and
and 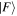 differ, off-diagonal elements arise and the matrix elements MFI represent a directly identifiable evolution of the system state—leading to a process rate that is, in principle always, experimentally determinable. Commonly the rate equation is established by use of the Fermi rule [56], (as will be discussed later), within which MFI features through its modulus square. Here, in consequence, operation of
differ, off-diagonal elements arise and the matrix elements MFI represent a directly identifiable evolution of the system state—leading to a process rate that is, in principle always, experimentally determinable. Commonly the rate equation is established by use of the Fermi rule [56], (as will be discussed later), within which MFI features through its modulus square. Here, in consequence, operation of 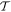 upon the matrix element leads to the same rate result for the state evolution
upon the matrix element leads to the same rate result for the state evolution 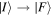 as for
as for 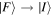 —which is a feature exemplified by the equivalence between the Einstein B-coefficients, B12 and B21, for stimulated emission and absorption. This underscores the fact that the system so described is necessarily a closed system, with no outlet for energy dissipation. Indeed, this is implicit in representing the entirety of the system in equation (1) by a system Hamiltonian of Hermitian form. More generally, and for computational purposes, it is also worth observing that the time-reversal operation
—which is a feature exemplified by the equivalence between the Einstein B-coefficients, B12 and B21, for stimulated emission and absorption. This underscores the fact that the system so described is necessarily a closed system, with no outlet for energy dissipation. Indeed, this is implicit in representing the entirety of the system in equation (1) by a system Hamiltonian of Hermitian form. More generally, and for computational purposes, it is also worth observing that the time-reversal operation 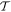 has the effect of inverting the sequence and temporal sense of the Feynman diagrams typically used to evaluate matrix element contributions in equation (4), equivalent to their being mirrored on the time axis: equally, state-sequence diagrams become mirrored left to right [57]. An example is shown in figure 6.
has the effect of inverting the sequence and temporal sense of the Feynman diagrams typically used to evaluate matrix element contributions in equation (4), equivalent to their being mirrored on the time axis: equally, state-sequence diagrams become mirrored left to right [57]. An example is shown in figure 6.
Figure 6. Representative Feynman diagrams for: (a) second harmonic generation; (b) degenerate down-conversion. In each case, time runs upwards from an initial state I to a final state F; also in each case, two other diagrams with permuted sequences of interaction also contribute to calculations of the matrix element MFI.
Download figure:
Standard image High-resolution image5. Quantized fields
To pursue the implications of fundamental symmetry, both the matter and the radiation components of the system have to be brought into consideration. It is expedient for their mutual interactions to be cast in the form of multipolar coupling in the Coulomb gauge. This choice facilitates physical interpretations in terms of electric and magnetic transition multipoles, readily related to a Cartesian expression of the symmetry properties of molecules: its introduction signifies no loss of generality, since the full multipolar series is an exact representation [58, 59]. Moreover, all observables can then be cast in terms that engage the electric and magnetic fields of the radiation, alone. The former is formally odd with respect to parity 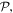 even with respect to
even with respect to  the magnetic field has the opposite character in both respects. As shown in table 1, these features follow from the nature of their relation to the electromagnetic vector potential, and they are also consistent with the physical meaning of the Poynting vector (linear momentum density) yielded by their cross product.
the magnetic field has the opposite character in both respects. As shown in table 1, these features follow from the nature of their relation to the electromagnetic vector potential, and they are also consistent with the physical meaning of the Poynting vector (linear momentum density) yielded by their cross product.
Table 1. Spatial and temporal symmetries of electromagnetic operators. For optical vortex modes, the spatial parity properties of individual modes within the field expansion depend on the topological charge l, as given by (−1)l+1 for the electric field and (−1)l for the magnetic field [203].
| Operators |
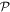 -even -even |
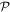 -odd -odd |
|---|---|---|
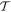 -even -even |
Hamiltonian H | Electric field e |
| Chirality density χ | ||
| Optical helicity κ | ||
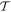 -odd -odd |
Magnetic field b | |
| Angular momentum densities J, L, S | Vector potential a | |
| Chirality flux φ | Poynting vector P |
For general applicability, the electromagnetic fields of light are commonly cast in terms of mode expansions—essentially Fourier decompositions—and to exploit symmetry principles that are valid at the photon level invites the use of quantum field theory. Indeed, there is no other framework in which use of the photon concept is entirely defensible, and a quantum representation of the radiation in its interactions with matter leads to the most direct and transparent analysis. To this end it is helpful to identify a couple of the main features of the mode expansions for the electric and magnetic fields of optical radiation. For convenience, we begin with the plane-wave expansions of the fields at position r, within an arbitrary quantization volume V, as follows:
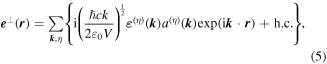

where h.c. denotes the Hermitian conjugate. This is essentially a vacuum formulation; the effects of dissipation are considered later. Here, k is the wave-vector, and η is a label for polarization state—its sum being taken over a basis chosen from any two states represented by opposing points on the Poincaré sphere [60]. Commonly these are chosen as left and right circular polarizations, or horizontal and vertical plane polarizations. Deploying an alternative but equivalent representation based on the Bloch sphere [61], an arbitrary basis of orthonormal polarization vectors is generically and most simply expressible as the unit vector pair
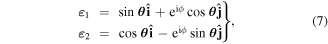
where θ and ϕ are angular coordinates defining a point on the unit sphere (noting that θ here equates to θ/2 in standard Bloch coordinates). Circular polarizations, representing the important case, θ = π/4, ϕ = π/2, are to be examined in more detail in the following section.
Both electromagnetic fields, (5) and (6), are solutions of Maxwell's equations; they also both satisfy the time-independent Helmholtz equation;
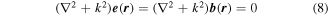
which expresses a form satisfied by other kinds of paraxial beam. For each mode (k, η) above,  is the unit polarization vector (necessarily complex for any other than plane polarization) and
is the unit polarization vector (necessarily complex for any other than plane polarization) and 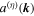 is the photon annihilation operator—the corresponding creation operator appearing in each Hermitian conjugate term. From the operator expressions given above, it is clear that both field operators have specific signatures of space and time parity: e is odd and b is even with respect to inversion
is the photon annihilation operator—the corresponding creation operator appearing in each Hermitian conjugate term. From the operator expressions given above, it is clear that both field operators have specific signatures of space and time parity: e is odd and b is even with respect to inversion  (which reverses e, k and r). Under time reversal
(which reverses e, k and r). Under time reversal  effected by complex conjugation of variables and Hermitian conjugation of operators, the opposite behavior duly occurs; the exhibited terms on exchange with their Hermitian conjugates preserve sign for e, but reverse it for b. The odd parity of the electric field (which is therefore represented by a polar vector) and its invariance to time reversal are intuitive; the opposite parity signatures of the magnetic field are rather less so. The latter field is formally represented by an axial vector, as befits its divergence-free (solenoidal) character (Gauss's law). In both cases, the zero-frequency limit correctly describes the behavior of the corresponding static field; the case of a static magnetic field receives more attention in section 13.
effected by complex conjugation of variables and Hermitian conjugation of operators, the opposite behavior duly occurs; the exhibited terms on exchange with their Hermitian conjugates preserve sign for e, but reverse it for b. The odd parity of the electric field (which is therefore represented by a polar vector) and its invariance to time reversal are intuitive; the opposite parity signatures of the magnetic field are rather less so. The latter field is formally represented by an axial vector, as befits its divergence-free (solenoidal) character (Gauss's law). In both cases, the zero-frequency limit correctly describes the behavior of the corresponding static field; the case of a static magnetic field receives more attention in section 13.
Next, we can note that circular polarizations represent radiation states that are eigenfunctions of the operator for spin angular momentum, whose density operator is a field given by;
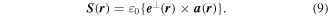
As such, each circularly polarized photon conveys a well-defined quantum spin, precisely 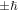 according to the left/right helicity [62]. Circular polarizations are most familiarly associated with chiroptical response. They are, for example, commonly argued as the basis for optical rotation, in which an angular rotation of the polarization in plane polarized light is considered in terms of a differential response to a superposition of left-and right-handed circular polarizations [63]. (The theory can in fact be cast directly in terms of plane polarizations [64]. A pair of orthogonal polarizations V, H identified with
according to the left/right helicity [62]. Circular polarizations are most familiarly associated with chiroptical response. They are, for example, commonly argued as the basis for optical rotation, in which an angular rotation of the polarization in plane polarized light is considered in terms of a differential response to a superposition of left-and right-handed circular polarizations [63]. (The theory can in fact be cast directly in terms of plane polarizations [64]. A pair of orthogonal polarizations V, H identified with 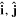 respectively, on rotation through an angle ψ, become equivalent to a right-circular polarization component advanced by a phase
respectively, on rotation through an angle ψ, become equivalent to a right-circular polarization component advanced by a phase  and left-circular component retarded by
and left-circular component retarded by  .)
.)
The assumption of an implicit connection between material chirality and circular polarizations is in principle an obstacle if one is to entertain more general states of light, including those with a complex modal structure, and for this purpose more robust and general formulations can be secured in expanded quantum operator form. Moreover, whilst the plane waves represented above have no capacity to convey orbital angular momentum, many of the most interesting 'twisted' or 'vortex' forms of structured light do exhibit this capacity—in principle representing eigenstates of the orbital angular momentum density operator written as follows with the repeated subscript i denoting summation over Cartesian coordinates;
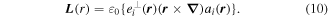
Both equations (9) and (10) are gauge-dependent fields, here written in terms of the vector potential a(r). Accordingly, a significant caveat is that the separation of angular momentum into spin and orbital parts, each vector directed along the propagation direction, is a simplification that strictly applies only in the paraxial approximation. More generally the separation is not absolute; there are transverse components and spin–orbit coupling in any significantly structured beam [65, 66], and there is recent experimental proof of their interconversion in a cylindrically symmetric optical fiber [67].
It is therefore expedient to introduce more definitive, generalized measures of chirality for the radiation field. One suitable measure is the optical chirality density, 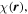 an operator with the physical dimensions of a pseudoscalar that is even under time reversal,
an operator with the physical dimensions of a pseudoscalar that is even under time reversal,  Conventionally defined as;
Conventionally defined as;
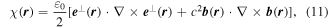
this operator satisfies a continuity equation [68],
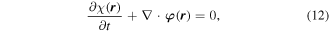
with respect to the φ(r), the latter representing a space-even, time-odd optical chirality flux;
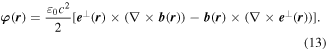
In both equations (11) and (13), the two terms on the right deliver equal contributions. It then emerges that the volume integrals of both χ(r) and φ(r) are directly related to a conserved quantity [69], the scalar field helicity [70],
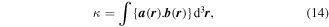
by direct proportionality in the case of monochromatic radiation. Both χ(r) and φ(r) operators are odd with respect to the symmetry operator 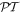 —a property they crucially share with the angular momentum density—see table 1.
—a property they crucially share with the angular momentum density—see table 1.
It has been shown that the ratio of expectation values for the chirality density and energy density, cast in cognate units, has to lie in the range [−1, 1] [71]. For any field of radiation, an effective volumetric measure of chirality is given by the eigenvalue (or expectation value) for any of the above representations, each of which represents a conserved quantity in the absence of material interactions, and in addition a passive measure of electromagnetic field chirality in the vicinity of nanostructures [72]. For monochromatic plane waves, it has been shown that both χ and φ effectively quantify a difference in the number of left-and right-handed photons [73]. Specifically cast in terms of photon number operators,  we have:
we have:
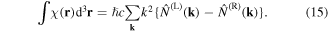
Each measure of optical helicity is accordingly diminished by the absorption of a circular photon with a specific handedness, so that a direct link can indeed be established between the volume integral of χ and the rate of circular dichroic absorption [9]. However, it is not to be supposed that this indicates any more general principle of helicity conservation, applicable to the system as a whole. For example in the process of absorbing a left-handed photon, a chiral molecule in no meaningful sense acquires an additional measure of material chirality from the radiation field, though it can acquire angular momentum. As always, symmetry rules can give no guidance on quantitative measures.
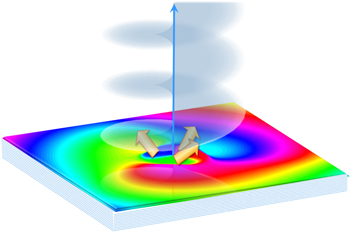
Furthermore, it is important to recognize that other types of basis for the radiation modes may be formulated, and that these may have a separate parity signature of their own. This issue can cause confusion—for in a sum over modes, the overall character of a field need not be the same as any individual component. In the context of chiral structures and interactions, an especially significant class of modes to consider are those that have a helicoidal wavefront, associated with a topological charge l that designates the number of intertwined wavefront surfaces. Laguerre–Gaussian modes, illustrated in figure 7, provide an important and most widely studied instance: as a result of its vortex wavefront, these modes have different field parity signatures for even and odd topological charge, as also indicated in table 1, the last two rows. (An analogy can be drawn to the quantum mechanics of a simple 1D harmonic oscillator—for which the Hamiltonian has even spatial parity, but the allowed wavefunctions alternate between even and odd character.)
Figure 7. Vortex beam propagation: color depiction of the instantaneous phase distribution of simple 'donut' mode, weighted by intensity, exhibiting the typical core singularity along the beam axis.
Download figure:
Standard image High-resolution imageIn the paraxial approximation the appropriate operator expansions, cast as functions of cylindrical coordinates comprising the off-axis radial distance r, axial position z and azimuthal angle ϕ, are as follows—in which l and p are the principal and secondary indices of the associated Laguerre polynomial featured in the radial distribution function fl,p [74]:
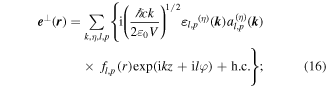
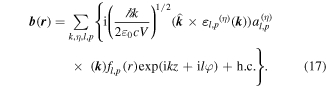
Once again, there is a symmetry feature to note: whereas the full summations for each operator retain their necessary symmetries under 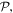 the expressions for individual modes do not. Taking for example the electric field, modes with even l are of odd parity whereas modes with odd l are even; for the magnetic field the converse is true. Terms of the 'wrong' parity vanish on the addition in pairs for l values of opposite sign. This behavior signifies another key difference between the symmetries of operators and of their eigenvalues, similar to the earlier observation concerning the material Hamiltonian.
the expressions for individual modes do not. Taking for example the electric field, modes with even l are of odd parity whereas modes with odd l are even; for the magnetic field the converse is true. Terms of the 'wrong' parity vanish on the addition in pairs for l values of opposite sign. This behavior signifies another key difference between the symmetries of operators and of their eigenvalues, similar to the earlier observation concerning the material Hamiltonian.
With field operator expansions explicitly cast is terms of modes such as equations (16) and (17), the presence of the phase factor exp(±ilφ), (with the plus sign in each annihilation operator term and minus in its photon creation counterpart, not explicitly shown) the corresponding eigenvalues of the angular momentum operator L indicate that these eigenmodes have the capacity to convey orbital lħ per photon [75]. Whilst beams of light with this vortex structure can routinely be produced by passing conventional Gaussian light through a variety of optical elements—notably spatial light modulators [76], it has been shown that rotationally symmetric chiral arrays can deliver vortex photons by direct emission [5, 77–79], as illustrated in figure 8. There is in fact a wide variety of other beams conveying orbital angular momentum, some including several kinds of modified-Gaussian vortex [80] described as having a perfect optical vortex structure [81], and others with the propagation-invariant character of Bessel beams [82]. With regards to the symmetry properties of such modes, however, it is worth observing that when mode structures are mathematically cast in a form that necessarily involves summation over an additional parameter (as is the case with the perfect vortex beams, for example), the associated quanta are correspondingly associated with state superpositions, and a distinct parity signature is generally lost.
Figure 8. Depiction of twisted photon emission from the electronic decay of a 'twisted exciton' state; the initial excitation (whose phase distribution is indicated by colors in the plane) is delocalized within a chromophore array that has C3 symmetry.
Download figure:
Standard image High-resolution imageBefore considering specific polarization issues in more detail, it is worth observing that field operator expansions such as those represented by equations (5), (6), (16) and (17) can be cast in a more complicated form that fully takes account of local fields and allows for dissipation and refraction through the incorporation of a complex refractive index [50]. The detailed theory and explicit mode expansions have been detailed elsewhere [74]. For the present, it is expedient to retain the simpler, vacuum formulations, since their unequivocal parity signatures facilitate the identification of symmetry and selection rule principles—which usually remain applicable in optically dense media. Specific exceptions will be identified along the way; the wider significance of damping and dissipation will be examined in section 12.
6. Circular polarizations
It is already apparent from the preceding analysis that circular polarization states have an importance that warrants a special focus on their properties. It follows from equation (7) that the corresponding electric polarization vectors can be represented as on a Cartesian basis with unit vectors  as:
as:

and accordingly the magnetic polarizations are
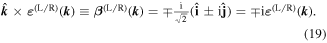
The 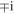 factor on the right in (19) signifies a
factor on the right in (19) signifies a  phase difference between the electric and magnetic fields.
phase difference between the electric and magnetic fields.
Care has to be taken in ascertaining how these field vectors transform under the spatial and temporal symmetry operations 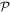 and
and 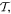 since space inversion undermines the right-handedness of the triad
since space inversion undermines the right-handedness of the triad  As noted in section 3, the Cartesian unit-vector identity
As noted in section 3, the Cartesian unit-vector identity 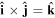 is not invariant on spatial inversion, as the operation changes 'right-handed' to 'left-handed' space. One axis must then be inverted to retain the right-hand rule to consistently determine the sign of the Poynting vector, P(r) = ε0{e(r) × b(r)}. To duly account for this feature, use is made of the following polarization vector identity [83]:
is not invariant on spatial inversion, as the operation changes 'right-handed' to 'left-handed' space. One axis must then be inverted to retain the right-hand rule to consistently determine the sign of the Poynting vector, P(r) = ε0{e(r) × b(r)}. To duly account for this feature, use is made of the following polarization vector identity [83]:
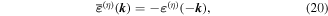
from which the transformation properties emerge as follows;


As required, spatial inversion changes the sign of the electric, but not the magnetic polarization vectors, while the opposite is true for time reversal, and the combined 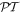 operation results in a change in sign and in handedness for both kinds of vector.
operation results in a change in sign and in handedness for both kinds of vector.
It is worth a brief look at genuine connections between angular momentum and chirality, prompted by the fact that two forms of angular momentum have been noted previously [9]. First, it should be evident that there is no connection between either of these angular momentum terms as applied to optical radiation, and the meaning of the same terms in atomic or molecular electronic (or even rotational) structure. For example, although circularly polarized light has the capacity to elicit chiroptical discrimination—as in the absorption involved in circular dichroism for example—the corresponding spin angular momentum of 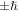 is transferred according to the handedness of the light, irrespective of the enantiomer employed. It is remarkable that in optical rotation, the archetypal optical manifestation of molecular chirality, a conventional beam of light undergoing a rotation in its plane of polarization has no angular momentum either before or after the interaction, and hence of course none is imparted to the system.
is transferred according to the handedness of the light, irrespective of the enantiomer employed. It is remarkable that in optical rotation, the archetypal optical manifestation of molecular chirality, a conventional beam of light undergoing a rotation in its plane of polarization has no angular momentum either before or after the interaction, and hence of course none is imparted to the system.
A more informative interpretation gives another perspective: since a sense of circulation about the propagation axis features in both circular polarizations (circulation of the electric and magnetic field vectors) and vortex light (circulation of optical phase), and since the radiation does indeed propagate, the associated isosurfaces of helical and helicoidal form clearly lack spatial parity. Nonetheless, any direct linking with material structures that have helical structures of a similar dimension cannot be generally assumed, because full-scale oscillations occur at any fixed point over the course of each optical cycle.
It is also timely to recall that any directed beam of light—whether or not it conveys angular momentum—necessarily also carries linear momentum. Neither property alone has the capacity to induce or register chirality, but their concerted involvement can and does, in both respects. It will emerge in the following that a more intricate form of the same principle determines distinctively chiral properties to be exhibited by material systems.
7. Light–matter interactions
A key consequence of the mode expansions such as (5) and (6), or (15) and (16), is that each and every linear operation of the electromagnetic field must result in exactly one radiation mode suffering either the annihilation or the creation of a single photon. The significance emerges as we now return to the matrix element (3), to focus upon the specific details of the multipolar interaction Hamiltonian.
For the present, it will be expedient to use a standard 'dilute gas' approximation, affording lucidity in the determination and application of major spatiotemporal symmetry principles. Local fields that would require consideration of complex electric permittivities, for example, can substantially compromise such arguments, as will be shown in section 12. In the Power–Zienau–Woolley formulation of quantum electrodynamics, matter–light coupling comprises just three terms [84, 85]:
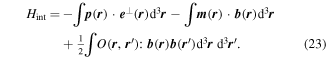
Interactions of the full electric and magnetic polarizations p(r) and m(r) are accounted for in the first two terms, from which series expansions deliver the series of familiar electric and magnetic multipoles, En and Mn respectively. Before focusing on the leading terms, we can note that the electric multipoles En are all even under  and of parity (–1)n under
and of parity (–1)n under 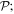 the magnetic multipoles Mn are all odd under
the magnetic multipoles Mn are all odd under 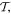 and of parity (–1)n+1 under
and of parity (–1)n+1 under  It has to be emphasized that the above representation of coupling is exact and complete. It has recently been proven, for example, that there is no other toroidal radiation or independent form of toroidal electromagnetic coupling; all of the interactions that are expressible as such [86] are in fact subsumed within the above series [87]. The leading toroidal multipole, odd under both
It has to be emphasized that the above representation of coupling is exact and complete. It has recently been proven, for example, that there is no other toroidal radiation or independent form of toroidal electromagnetic coupling; all of the interactions that are expressible as such [86] are in fact subsumed within the above series [87]. The leading toroidal multipole, odd under both 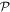 and
and  is associated with magnetic quadrupole interactions.
is associated with magnetic quadrupole interactions.
Before continuing further, it is worth focusing on the third, generally less familiar, term in (23), which uniquely signifies a diamagnetization form of interaction. Whereas the electric and magnetic series engage the corresponding radiation fields and their spatial derivatives linearly, this third term is clearly distinguished by a quadratic dependence on the magnetic field. Consequently, it has fully even 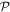 and
and 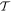 character with regard to its radiation involvement (and the same accordingly has to apply for the matter tensor O(r, r'), in view of the overall Hamiltonian symmetry). Since each field interaction has to involve the creation or annihilation of a photon, this term is only present in processes that fundamentally involve two or more photon events [88]. However, it is usually much smaller in magnitude than the leading multipole forms of coupling—and since its symmetry is even in both space and time, it offers no scope for distinctive involvement in chiral phenomena unless other M1 or E2 transitions are also involved. Clearly, we can therefore dispense with it in the current analysis.
character with regard to its radiation involvement (and the same accordingly has to apply for the matter tensor O(r, r'), in view of the overall Hamiltonian symmetry). Since each field interaction has to involve the creation or annihilation of a photon, this term is only present in processes that fundamentally involve two or more photon events [88]. However, it is usually much smaller in magnitude than the leading multipole forms of coupling—and since its symmetry is even in both space and time, it offers no scope for distinctive involvement in chiral phenomena unless other M1 or E2 transitions are also involved. Clearly, we can therefore dispense with it in the current analysis.
Adopting the Taylor series expansions of the first two terms in equation (23) now separates each coupling into multipolar orders. To the same overall level of approximation the leading contributions, to be designated E1, E2 and M1, invoke the following quantum operators: the electric dipole μ; electric quadrupole Q, and magnetic dipole m, respectively. The former vector operator gives the leading contribution in any application where its matrix elements are non-zero; compared to this, the latter pair (the symmetric second-rank tensor Q and vector m) are involved in couplings of significantly lower magnitude (but broadly equivalent, deriving from the same level of expansion in the alternative minimal coupling representation) [89]. The leading terms of (23) are thus as follows, assuming for convenience a Cartesian coordinate system centered on the molecule of interest;

Here, as earlier, there is an implied summation over subscript Cartesian component indices. Since the above interaction Hamiltonian Hint is linear in the electromagnetic fields, the term with (p + 1) = n in equation (3)—manifest as the nth in equation (4)—delivers the leading contribution for any process involving n photons—indeed this is usually the only significant contributor to the corresponding quantum amplitude.
In the following, attention will be focused on interaction terms that involve terms of no higher order than the three identified in equation (24), which suffice to represent all currently known forms of molecular chiroptical behavior. A selection of some prominent examples, illustrated by representative members of their Feynman diagrammatic depictions, is shown in figure 9. To gauge the relative magnitudes of the terms in (24), one contrivance is to regard each electron as having a radial distribution of the order of the Bohr radius, so that its electric dipole is ea0, its quadrupole  and its magnetic dipole consistent with an orbital angular momentum ħ. Simple back of the envelope calculations then suggest that the magnitudes of M1 and E2 are both smaller than E1 coupling by a factor of the fine structure constant, ∼1/137. In practice, each molecular transition produces a different result, and the significance of both M1 and E2 is usually a little smaller than this calculation suggests.
and its magnetic dipole consistent with an orbital angular momentum ħ. Simple back of the envelope calculations then suggest that the magnitudes of M1 and E2 are both smaller than E1 coupling by a factor of the fine structure constant, ∼1/137. In practice, each molecular transition produces a different result, and the significance of both M1 and E2 is usually a little smaller than this calculation suggests.
Figure 9. Representative time-ordered diagrams for key chiroptical interactions: (a) dominant electric dipole term (interaction labeled E1), and (b) magnetic dipole (M1), both involved in single-photon circular dichroism; (c) and (d) magneto-optical effect contributions to the E1M1 transition tensor  (e) and (f) both contributions to the E12Rayleigh scattering and optical binding (polarizability) tensor
(e) and (f) both contributions to the E12Rayleigh scattering and optical binding (polarizability) tensor 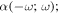 (g)–(j) two pairs of E1M1 differential contributions
(g)–(j) two pairs of E1M1 differential contributions 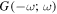 and
and  (k) and (l) two of the 48 time-orderings for circular differential optical binding,
(k) and (l) two of the 48 time-orderings for circular differential optical binding, 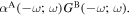 In each of the diagrams where M1 coupling appears, counterpart diagrams for E2 coupling generally also need to be taken into account.
In each of the diagrams where M1 coupling appears, counterpart diagrams for E2 coupling generally also need to be taken into account.
Download figure:
Standard image High-resolution imageAs a consequence of the operator structure for the electromagnetic fields, it transpires that for a position R = (Rx, Ry, Rz) in Cartesian coordinates—or (zR, ρR, ϕR) in cylindrical, beam-reference) coordinates—each contribution to the quantum amplitude entails the same phase factor exp{−i(Δk.R + ϕRΔl)}, where Δk is the difference of the final, compared to the initial, wave-vector sum of all the photons involved (reflecting the number of photon creations and annihilations), and Δl signifies any corresponding change in orbital angular momentum; the latter term only arises in connection with optical vortex radiation. Accounting for the complete multipolar series of interaction terms, the quantum amplitude MFI for a specific n-photon interaction then emerges in the form of a linear combination of scalar terms, each one the inner product of a radiation tensor and a molecular tensor in the form of a generalized nonlinear transition optical susceptibility.
The considerable complexity that ensues in the general case is tempered by focusing on the leading multipole terms, explicitly given in equation (24). Developing from equation (4), we can write the matrix element in the following generic form, a sum of inner products between radiation and molecular tensors;

Here, for later purposes, it is worth noting that the involvement of topological charge is primarily apparent in the exponential phase factor—here in the paraxial approximation. In equation (25), labels (e, m, q) correspond to the number of E1, M1, and E2 interactions, respectively, and the radiation tensor 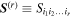 comprises an outer product of radiation components, (specifically, a product of components of vectors potentially including the electric field, the magnetic field, and the wave-vector of each relevant optical mode). However, it also includes factors indicated by the set {ql} that register the topological charge for each photon involved in any electric quadrupole interaction: this is a feature that was overlooked in the earliest formulation of general theory [1]. As a counterpart to S(r), the corresponding molecular tensor
comprises an outer product of radiation components, (specifically, a product of components of vectors potentially including the electric field, the magnetic field, and the wave-vector of each relevant optical mode). However, it also includes factors indicated by the set {ql} that register the topological charge for each photon involved in any electric quadrupole interaction: this is a feature that was overlooked in the earliest formulation of general theory [1]. As a counterpart to S(r), the corresponding molecular tensor  can be written in a form that entails a product of n molecular transition integrals, with energy difference denominators resulting from the structure of terms in equation (4). The detailed equations can be derived using time-ordered diagrams [90], or from the more recently developed state-sequence diagrams [57], by direct application of a standard methodology [91]. Thus, both the S(r) and T(r) tensors are distinguished by the same labels (e, m, q), whose sum equals the number of photon interactions involved in the process, n = (e + m + q), whilst the rank r of each tensor is given by r = (e + m + 2q). The molecular tensor T(r) itself incorporates in each of its composite terms a numerator comprising n products of transition multipole moments, and a denominator product of (n – 1) energy factors.
can be written in a form that entails a product of n molecular transition integrals, with energy difference denominators resulting from the structure of terms in equation (4). The detailed equations can be derived using time-ordered diagrams [90], or from the more recently developed state-sequence diagrams [57], by direct application of a standard methodology [91]. Thus, both the S(r) and T(r) tensors are distinguished by the same labels (e, m, q), whose sum equals the number of photon interactions involved in the process, n = (e + m + q), whilst the rank r of each tensor is given by r = (e + m + 2q). The molecular tensor T(r) itself incorporates in each of its composite terms a numerator comprising n products of transition multipole moments, and a denominator product of (n – 1) energy factors.
Within a phase factor, the matrix element (14) has the properties of a scalar energy, even in time and in space. Accordingly, with regard to each parity operation, 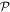 and
and 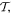 the S(r) and T(r) tensors must also both be either even or odd. In fact, the signatures of each tensor are (–1)e+2q under
the S(r) and T(r) tensors must also both be either even or odd. In fact, the signatures of each tensor are (–1)e+2q under  and (–1)m under
and (–1)m under 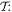 these results are determined by the space-odd, time-even character of the electric field, and the space-even, time-odd character of the magnetic field. For example in second harmonic generation (SHG) the S(r) and T(r) tensors have odd spatial parity for terms involving three electric dipole interactions, E13, but even parity for E12E2 contributions; both cases have even temporal parity. Whenever the S(r) and T(r) tensors are odd with respect to both
these results are determined by the space-odd, time-even character of the electric field, and the space-even, time-odd character of the magnetic field. For example in second harmonic generation (SHG) the S(r) and T(r) tensors have odd spatial parity for terms involving three electric dipole interactions, E13, but even parity for E12E2 contributions; both cases have even temporal parity. Whenever the S(r) and T(r) tensors are odd with respect to both 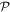 and
and  parity operations, their product will remain the same if both radiation and matter are inverted in space, physically representing opposite parity enantiomers together with opposite helicity radiation. However, as illustrated in figure 10, a difference results if either of the components (radiation or matter) is spatially inverted, thereby signifying chiral discrimination.
parity operations, their product will remain the same if both radiation and matter are inverted in space, physically representing opposite parity enantiomers together with opposite helicity radiation. However, as illustrated in figure 10, a difference results if either of the components (radiation or matter) is spatially inverted, thereby signifying chiral discrimination.
Figure 10. Representation of the effects of separately changing the handedness of molecular and optical components in a simple tetrahedral chiroptical system, such as a tri-substituted methane. Wedge-shaped lines represent bonds projecting in front of the figure plane; dashed lines signify bonds projecting backwards.
Download figure:
Standard image High-resolution imageNotice that, because the transition integrals involved in S(r) and T(r) are generally implemented for states representing the conditions of a specific experimental interaction, they can exhibit a lower symmetry than that of the field operators they contain. For example, an element of S(r) might exhibit the helical symmetry properties of a particular circular polarization, if that polarization alone is present in the radiation (whereas the mode expansion would have both helicities equally represented, and thus no overall helical character). Equally for T(r), the foremost symmetry considerations relate to the set of operations determined by the molecular point group [38]—which for chiral species precludes spatial inversion. For any process, the product of symmetry representations for the connected states must span one or more irreducible representations under which components of the n transition moment products themselves transform. Mapping the irreducible representations of the full three-dimensional rotation-inversion group O(3) onto a lower symmetry is surjective, and in consequence frequently permits transitions to occur between states of more than one symmetry class—a necessary condition for molecules to exhibit chirality.
Before moving on, it is worth making mention of a primitive (but still sometimes utilized) 'two-group' model of material chirality [92]. This is a simplified theory cast in terms of a coupling between dissymmetrically oriented transition electric dipoles, illustrated in figure 11. The quantum interference of transition electric dipoles A and B separated by a positional displacement RAB engages the linear (and higher order odd-rank terms) in the Taylor series expansion of the associated phase factors in the electric field expansion, equation (16). So for example in an expression for the rate of single-photon absorption, the leading E12 term (even under  ) is corrected by an interference term
) is corrected by an interference term 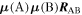 (which is odd under
(which is odd under  ). Developing symmetry arguments to this level only delivers one element of the necessary criteria, of course. Additionally, the two transition dipoles and the positional displacement vector must form a non-coplanar set and therefore lack any mirror symmetry, as befits a locally chiral structure. A similar logic applies to the corresponding radiation field constructs. The result is that circular dichroism can be supported without the explicit involvement of localized E2 or M1 transition moments [93].
). Developing symmetry arguments to this level only delivers one element of the necessary criteria, of course. Additionally, the two transition dipoles and the positional displacement vector must form a non-coplanar set and therefore lack any mirror symmetry, as befits a locally chiral structure. A similar logic applies to the corresponding radiation field constructs. The result is that circular dichroism can be supported without the explicit involvement of localized E2 or M1 transition moments [93].
Figure 11. The 'two-group' model for molecular chirality: coupling of two mutually displaced electric dipole transition moments in a non-coplanar configuration.
Download figure:
Standard image High-resolution image8. Transitions and motions
The implementations of equation (25), which lie at the heart of all discrete photon-particle interactions, now hold the key to applications of the symmetry principles discussed in previous sections. A chiral molecule, for example, has no properties that are eigenstates of the symmetry operator  Consequently both its static and its transition attributes can only be described in terms of mixtures—quantum superpositions—of that operator. Yet, the quantum amplitude in which such properties appear is necessarily even in
Consequently both its static and its transition attributes can only be described in terms of mixtures—quantum superpositions—of that operator. Yet, the quantum amplitude in which such properties appear is necessarily even in  —signifying a condition that a quantum interference of
—signifying a condition that a quantum interference of  -odd and
-odd and  -even radiation constructs is also necessary, to elicit forms of interaction that will permit differentiation between systems of opposite handedness. Physically, this relates to the same symmetry principles that were anticipated, regarding optical angular momentum, at the end of section 5.
-even radiation constructs is also necessary, to elicit forms of interaction that will permit differentiation between systems of opposite handedness. Physically, this relates to the same symmetry principles that were anticipated, regarding optical angular momentum, at the end of section 5.
At this juncture, it is important to distinguish between two quite distinct applications of the quantum matrix elements that emerge from the generic form of equation (25), as more fully discussed elsewhere [10, 94, 95]. The evaluation of a rate for any chiroptical process entails a matrix element connecting physically different states; conversely, in dealing with applications where the initial and final states are identical, only diagonal elements of the matrix element MII are significant and the result represents an expectation value with respect to the operator M. Figures 9(e) and (f) provide an example of how the Feynman framing of a given interaction can in fact play into entirely different phenomena—one a directly observable photophysical event, and the other an ensuing motion. In each effect, both diagrams contribute.
Key features of this difference are illustrated in figure 12. Here, the quantum field representation gives clarity to an issue that is easily obscured by any quasi-classical approach, in which attention focuses only upon the material response: the equality of initial and final system states has to mean that both the matter and the radiation states are unchanged, or else a process occurs, as detailed below. Under such circumstances there can be no direct transfer of energy, linear or angular momentum from the radiation field to the molecule (or molecules); the occupancy of each radiation mode is unchanged, as are the populations of each molecular state. Nonetheless, a force can emerge as an observable, since there is a physically meaningful electronic energy shift (or potential energy), ΔE, identified with the real part of MII,

once again with r = e + m + 2q. In the above product, the phase factor that featured at the front of equation (25) necessarily disappears, and the crescent symbol over the molecular tensor signifies that the material response is an intrinsic, not a transition property—one whose non-zero components therefore transform under the totally symmetric representation of the molecular point group. If the radiation field responsible has a locally variable strength there will be a resulting gradient force given by;

This is the expression used to determine an optical trapping force—also, potentially misleadingly, termed dipole force when E12 interactions alone are involved. This force can be regarded as conservative in the traditional dynamical sense [96]. We can now consider what is necessary in order for chiral discrimination to be exhibited, and how that discrimination arises.
Figure 12. Processing a quantum amplitude for different kinds of application.
Download figure:
Standard image High-resolution imageConsider for example the simplest form of optical interaction responsible for trapping cold molecules, in which a force towards the center or focus of a laser beam derives from the higher intensity there—where it experiences a larger downward shift in energy. At the fundamental level, this is forward elastic scattering, a polarizability effect involving the coupled annihilation and creation of individual photons from the beam [97]. Each photon event can in principle involve any order of electric or magnetic interaction, so the associated energy shift comprises a series of terms involving E12, E1–M1, E1–E2, and so on;

Each term in this series, which has the structure indicated by equation (26), is necessarily positive in parity with respect to both  and
and  as befits an energy. In the leading (invariably non-zero) E12 term, the
as befits an energy. In the leading (invariably non-zero) E12 term, the 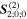 and
and 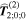 tensors (the latter a polarizability often written as α or χ(e−e)) are individually both of even parity with respect to
tensors (the latter a polarizability often written as α or χ(e−e)) are individually both of even parity with respect to 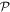 and
and 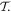 However, the following E1–M1 term, non-vanishing for a chiral species, is constructed from the product of
However, the following E1–M1 term, non-vanishing for a chiral species, is constructed from the product of 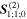 with
with  (the latter representing a 'mixed' polarizability commonly written as G or χ(e−m))—and both are of odd parity in both
(the latter representing a 'mixed' polarizability commonly written as G or χ(e−m))—and both are of odd parity in both 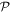 and
and 
It now becomes apparent that if we change from one enantiomer to another, the 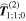 tensor and all others in the odd molecular-parity terms change sign, whereas
tensor and all others in the odd molecular-parity terms change sign, whereas  and all others in the even molecular-parity terms remain unchanged in value. Since some terms change and others do not, the energy shift—while still dominated by the E12 term—will differ in absolute value for opposite enantiomers, thus exhibiting chiral discrimination. The same logic applies if we change the handedness of the incident light, in a system comprising only one enantiomer; the radiation tensor changes in odd radiation-parity terms but not the others, and all of the molecular tensors remain unchanged (again, see figure 10). A variety of means by which the associated differences in local force might be used to engineer the separation of molecular enantiomers, and of chiral nanoparticles, have been proposed in recent years [43, 98–110], and the principles will be further discussed in section 11.
and all others in the even molecular-parity terms remain unchanged in value. Since some terms change and others do not, the energy shift—while still dominated by the E12 term—will differ in absolute value for opposite enantiomers, thus exhibiting chiral discrimination. The same logic applies if we change the handedness of the incident light, in a system comprising only one enantiomer; the radiation tensor changes in odd radiation-parity terms but not the others, and all of the molecular tensors remain unchanged (again, see figure 10). A variety of means by which the associated differences in local force might be used to engineer the separation of molecular enantiomers, and of chiral nanoparticles, have been proposed in recent years [43, 98–110], and the principles will be further discussed in section 11.
Now let us observe how the matrix element feeds into an observable when the initial and final states differ—even if only in the state of the radiation field (as for example occurs in Rayleigh scattering or optical rotation). If the sum of input photon momenta differs from that of the output, or if the corresponding angular momentum sums differ, then forces and torques can result: these are sometimes known as scattering forces. Although they might be regarded as non-conservative in the sense of classical dynamics, the distinction is less clear or useful in the present connection. Whether or not motion ensues, any observable will in this case have a direct relation to the process rate, with the latter normally derived directly from the Fermi rule;
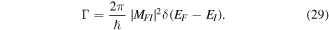
Here, the Dirac delta function serves to ensure energy conservation by the molecule-radiation system as a whole, on integration within the limits of experimental measurability. From equation (25), we therefore determine the following;
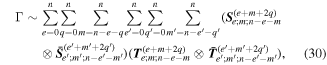
where an overbar denotes complex conjugation, and the symbol ⨂ signifies a tensor outer product. Although the disappearance of the phase factor is obvious, there is, latent within the S tensors only when quadrupole transitions are involved, a dependence on helicity associated with a vortex topological charge.
For the simplest process, single-photon absorption, this conclusion has indeed borne out by recent experimental evidence [111]. For higher order processes involving more than single-photon events, studied under conditions that invalidate the paraxial approximation—including a near-field configuration or in the vicinity of a beam focus—the presence of longitudinal fields [65] and any additional Gouy phase [112] admit an additional dependence on l, not exhibited in the present simplified analysis. Such a feature may permit quadrupole interactions that are sensitive to the associated off-axis components of the wave-vector [113]. Given the scant experimental evidence, it is tempting to conclude that, despite its link to vortex structures, orbital angular momentum is not routinely detected in differential chiroptical behavior [114]. However, a distinction arises between studies of solid or ordered media, and fluid media such as solutions—with the latter a more common focus for studies of molecular chirality. The significance of this difference will emerge in the next two sections, where more stringent conditions are shown to apply.
Despite its apparent complexity, it is straightforward to elicit symmetry principles from the structure of equation (30). As has already been commented in connection with energy shift calculations, chiral discrimination arises when an observable represented by such a sum of terms comprises components that vary in parity signature, in their material or radiation constructs. In (30), the  construct may be regarded as a radiation tensor
construct may be regarded as a radiation tensor  of rank (r + r') in its own right, and
of rank (r + r') in its own right, and 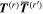 the corresponding material tensor expressible as
the corresponding material tensor expressible as  For example in the leading (E1) contribution to single-photon absorption producing a molecular transition α ← 0, these two constructs take the form of the polarization vector component product
For example in the leading (E1) contribution to single-photon absorption producing a molecular transition α ← 0, these two constructs take the form of the polarization vector component product  and a transition electric dipole product
and a transition electric dipole product  where the subscript indices denote components referred to an arbitrary Cartesian frame.
where the subscript indices denote components referred to an arbitrary Cartesian frame.
Clearly, each  and matching
and matching  tensor product in (30) have even parity when r = r', both with respect to space inversion and time reversal—and in consequence their product delivers no chiroptical features. But in the quantum interference terms, r ≠ r', some products may have odd parity. This is a distinctive feature of a chiral material; it is a necessary (though not sufficient) condition for the exhibition of chiroptical discrimination that such terms arise. As detailed elsewhere [10], and illustrated with specific regard to circular dichroism, it suffices for the analysis of this condition to focus on the spatial parity, since the conditions supporting a non-zero pseudoscalar value for the optical chirality density χ, equation (11), clearly also support odd-parity instances of
tensor product in (30) have even parity when r = r', both with respect to space inversion and time reversal—and in consequence their product delivers no chiroptical features. But in the quantum interference terms, r ≠ r', some products may have odd parity. This is a distinctive feature of a chiral material; it is a necessary (though not sufficient) condition for the exhibition of chiroptical discrimination that such terms arise. As detailed elsewhere [10], and illustrated with specific regard to circular dichroism, it suffices for the analysis of this condition to focus on the spatial parity, since the conditions supporting a non-zero pseudoscalar value for the optical chirality density χ, equation (11), clearly also support odd-parity instances of  As we have seen, this necessitates a circularly or elliptically polarized radiation field, with a non-zero difference in the occupation of left- and right-handed radiation modes effectively maximized in the circular basis. For example, in the simple case of single-photon absorption, the structure of the leading terms can be written in a similar form to equation (28);
As we have seen, this necessitates a circularly or elliptically polarized radiation field, with a non-zero difference in the occupation of left- and right-handed radiation modes effectively maximized in the circular basis. For example, in the simple case of single-photon absorption, the structure of the leading terms can be written in a similar form to equation (28);
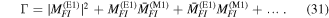
The first term, expressing 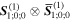
 retains its sign irrespective of the enantiomeric form or the circular handedness of the input radiation. This is almost invariably the term that generates the largest rate contribution. However, the E1M1 interference terms,
retains its sign irrespective of the enantiomeric form or the circular handedness of the input radiation. This is almost invariably the term that generates the largest rate contribution. However, the E1M1 interference terms, 
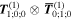 and its complex conjugate, clearly change sign either on substituting the opposite enantiomer (necessarily changing the sign of
and its complex conjugate, clearly change sign either on substituting the opposite enantiomer (necessarily changing the sign of  ), or inverting the circularity of the input (producing the same effect on
), or inverting the circularity of the input (producing the same effect on  ). In either case, the absolute value of the sum (31) changes, resulting in the absorption differential we know as circular dichroism.
). In either case, the absolute value of the sum (31) changes, resulting in the absorption differential we know as circular dichroism.
9. Fluid media
For several reasons, the chiroptical responses of molecules are most often monitored in solution form, whether the purpose is chiral speciation or enantiomer separation. The alternative phases of matter all have major disadvantages: the gas phase represents low sample density, and optical systems associated with low throughput and weak signal strength; the solid state represents a variability of response according to grain or crystal dimensions and—compared to the relative mobility of individual molecules in the liquid phase—a considerably more ponderous response to any subtle optomechanical forces. But the liquid phase also confers other, often very substantial advantages; the theory of optical interactions can be developed to a further level and generally becomes very much simpler.
First, let us consider the mathematical constructs for an optical process in which the matter and/or the radiation change their quantum state. The structure of the process rate equation (30) is formally that of an inner product between the two tensors,  and
and  recall that
recall that  entails components of the input and/or output radiation fields; it contains all the information on the disposition of radiation vectors, whilst
entails components of the input and/or output radiation fields; it contains all the information on the disposition of radiation vectors, whilst 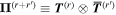 involves components of transition dipoles and/or quadrupoles; it embodies the directional aspects of molecular response. The occurrence of the product signifies that observables will generally depend on the angular disposition of the molecule with respect to laboratory-fixed directions—the latter usually being established by the configuration on an optical table. If, for example, the system under scrutiny were to be a molecular crystal, whose response would usually depend on the angle of the crystal with respect to the radiation, then the net signal would essentially be scaled up from the orientationally dependent responses of each component in the unit cell.
involves components of transition dipoles and/or quadrupoles; it embodies the directional aspects of molecular response. The occurrence of the product signifies that observables will generally depend on the angular disposition of the molecule with respect to laboratory-fixed directions—the latter usually being established by the configuration on an optical table. If, for example, the system under scrutiny were to be a molecular crystal, whose response would usually depend on the angle of the crystal with respect to the radiation, then the net signal would essentially be scaled up from the orientationally dependent responses of each component in the unit cell.
In a fluid medium comprising randomly oriented molecules, however, the ergodic theorem decrees that the ensemble response for incoherent processes will be the same as the scaled up response of any individual molecule, averaged over a timescale beyond the rotational diffusion time. We therefore need to evaluate the three-dimensional orientational average of the appropriate tensor products [115]. Revisiting the well-established calculational procedure [116, 117], the underlying symmetry principles can now be developed. The general theory is addressed before exhibiting the simplicity of a specific application to circular dichroism. (The only significant exceptions to the following, to be examined at the end of this section, are parametric nonlinear optical processes, whose difference in treatment will be shown to arise due to the fulfillment of a phase-matching condition.)
The duly orientation-averaged radiation and molecular parameters must assume the form of scalar quantities, and as such these are determined by contracting each tensor, 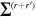 and
and 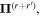 with an isotropic tensor of the same rank (r + r'). Isotropic tensors [118, 119] essentially embed scalars in a higher dimensional space; with no angular character they are termed 'weight 0' in the sense of essentially representing zero angular momentum. There is no rank 1 isotropic tensor: for higher ranks in their simplest irreducible form, isotropic tensors of even rank comprise products of Kronecker deltas; rank 3 has the form of a Levi-Civita (fully index-antisymmetric) tensor; for higher order odd rank they comprise one Levi-Civita tensor with one or more Kronecker deltas. Beyond rank 3, there are several different isomers of the isotropic tensors; for example in rank 4 there is the triad
with an isotropic tensor of the same rank (r + r'). Isotropic tensors [118, 119] essentially embed scalars in a higher dimensional space; with no angular character they are termed 'weight 0' in the sense of essentially representing zero angular momentum. There is no rank 1 isotropic tensor: for higher ranks in their simplest irreducible form, isotropic tensors of even rank comprise products of Kronecker deltas; rank 3 has the form of a Levi-Civita (fully index-antisymmetric) tensor; for higher order odd rank they comprise one Levi-Civita tensor with one or more Kronecker deltas. Beyond rank 3, there are several different isomers of the isotropic tensors; for example in rank 4 there is the triad  where the indices represent Cartesian coordinates. If we now designate the isotropic tensors in the laboratory-fixed space as
where the indices represent Cartesian coordinates. If we now designate the isotropic tensors in the laboratory-fixed space as 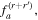 and in a molecule-fixed frame as
and in a molecule-fixed frame as 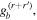 where the subscript identifies one member of the isotropic tensor set, then rotationally averaging the result of equation (30) and expressing the same summations more concisely gives the following linear combination of scalars;
where the subscript identifies one member of the isotropic tensor set, then rotationally averaging the result of equation (30) and expressing the same summations more concisely gives the following linear combination of scalars;
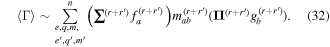
The bracketed terms on the right in equation (32), each a tensor inner product, are scalar measures of the radiation and the molecule, sometimes termed 'invariants'; their products are weighted by a matrix of coefficients 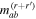 whose numerical values are fully detailed elsewhere [117, 118]. It is straightforward to elicit the symmetry principles for any particular process. Table 2 exemplifies the results for circular dichroism, showing that although both E1–M1 and E1–E2 interference terms are generally involved in the effect in ordered materials, only the former survives in fluid (randomly oriented) media: electric quadrupoles then play no part. Further analysis is given in the next section.
whose numerical values are fully detailed elsewhere [117, 118]. It is straightforward to elicit the symmetry principles for any particular process. Table 2 exemplifies the results for circular dichroism, showing that although both E1–M1 and E1–E2 interference terms are generally involved in the effect in ordered materials, only the former survives in fluid (randomly oriented) media: electric quadrupoles then play no part. Further analysis is given in the next section.
Table 2. Key optical and molecular constructs for (single-photon) circular dichroism in an isotropic fluid, for simplicity omitting superscripts denoting transitions and ranks.
| Multipole interference tensor Π | Contraction to invariant | Radiation product tensor Σ | Plane polarization | L/R polarization | |
|---|---|---|---|---|---|
|
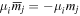
|

|
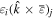
|
|
±i |
|
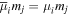
|

|
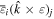
|

|

|
|
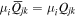
|

|
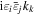
|
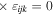
|
−ik |

|

|
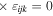
|

|

|
ik |
The importance of establishing a general mathematical structure for a fluid ensemble rate is that it properly exhibits the rotational average being effected with respect to the tensors  and
and 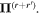 When, on the other hand, we consider optically conferred potential energies, it is very evident that a major difference arises. The form of equation (32) is in clear distinction to an average which is cast as;
When, on the other hand, we consider optically conferred potential energies, it is very evident that a major difference arises. The form of equation (32) is in clear distinction to an average which is cast as;
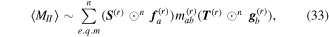
which signifies an orientationally averaged energy shift, the above expression being applicable in cases where no material or radiation transitions occur. Here, the radiation and molecular invariants (respectively represented by the terms in the first and second pairs of brackets) are yet simpler, and they are strikingly different in form from those that appear in the rate equation (32). Such differences can prove highly significant. For example, consider once again Rayleigh scattering, where for each scatterer two photons are involved (one in and one out) and the leading term in the matrix element has E12 form. As we have seen, forward scattering with no change in the throughput radiation wave-vector or polarization generates an energy shift as given by (33), such as can be responsible for cold molecule trapping; conversely, when the radiation is scattered off-axis, the rate equation (32) determines the associated temporal attenuation of the optical throughput.
The analysis of systems with partial orientational order is understandably more complicated than either isotropic fluids or solids, but follows along broadly similar lines to the procedure described above. Commonly there is a weighted distribution of orientations, centered on one specifically favored direction serving as a director vector. A familiar example is a nematic liquid crystal, partially oriented by a weak electric field. The theory for such cases under equilibrium conditions at typical laboratory temperatures can be addressed by weighting the orientational averages, such as feature in equations (32) and (33), with a suitable Boltzmann factor. In the liquid crystal case, this factor takes the exponential form 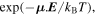 where μ is the static molecular dipole moment and E is the applied static field. The effect of introducing the exponential is most readily appreciated by considering successive terms in its Taylor series expansion. Clearly, terms in successive powers of the numerator alternate between even and odd character in spatial parity, correspondingly modifying the parity of the molecular and radiation constructs with which these terms are multiplied. In consequence, there is additional scope to introduce chiroptical behavior whose leading term results in a Curie's law dependence on temperature. Essentially, this is equivalent to securing a linear combination of 'weight 1' vector products—in the case of process rates, by contracting the radiation and material forms
where μ is the static molecular dipole moment and E is the applied static field. The effect of introducing the exponential is most readily appreciated by considering successive terms in its Taylor series expansion. Clearly, terms in successive powers of the numerator alternate between even and odd character in spatial parity, correspondingly modifying the parity of the molecular and radiation constructs with which these terms are multiplied. In consequence, there is additional scope to introduce chiroptical behavior whose leading term results in a Curie's law dependence on temperature. Essentially, this is equivalent to securing a linear combination of 'weight 1' vector products—in the case of process rates, by contracting the radiation and material forms  and
and  with isotropic tensors of rank (r + r' + 1). Full details of the exact theory, without resort to approximation, are given in [120]. For oriented systems, it also emerges that there is a capacity for differential response to different regions across a phase-structured beam, since the phase gradient may vary in its spatial direction; this is discussed further in the next section.
with isotropic tensors of rank (r + r' + 1). Full details of the exact theory, without resort to approximation, are given in [120]. For oriented systems, it also emerges that there is a capacity for differential response to different regions across a phase-structured beam, since the phase gradient may vary in its spatial direction; this is discussed further in the next section.
It is also possible for suitably configured light fields to generate a chirality for which they also serve as probe. In studies on dye-loaded polymer film, it has been shown that the interference of counterpropagating circularly polarized light engenders helically distributed local forces, locally orienting dye molecules of intrinsically achiral structure, and so producing a medium with chiroptical behavior similar to that of a twisted nematic liquid crystal [121]. This is a case of an intrinsically achiral system exhibiting chiroptical behavior through laser-induced circular dichroism due to local molecular reorientation, rather than an originally conceived method of 'dressing' molecular states with another circularly polarized beam [40].
Finally, as indicated earlier, a significant difference in approach for fluid media is required for parametric nonlinear optical processes—those in which ground-state molecules mediate a change in the radiation state that conserves the photon wave-vector sum. For coherent and elastic processes of this kind, the molecular tensors must be supported by the totally symmetric representation of the appropriate point group; for example sum-frequency and second harmonic generation, (SFG and SHG), require a non-zero hyperpolarizability that is odd under  and which are therefore precluded by a center of symmetry and are therefore usually polar. (In fact, amongst the common non-polar molecular point-groups only the following additionally permit such processes: D2, D2d, C3h, D3h, S4, D4, D6, T and Td [50, 122].)
and which are therefore precluded by a center of symmetry and are therefore usually polar. (In fact, amongst the common non-polar molecular point-groups only the following additionally permit such processes: D2, D2d, C3h, D3h, S4, D4, D6, T and Td [50, 122].)
Such processes essentially redistribute radiation energy between different modes with the fulfillment of a phase-matching condition, such that the generic phase factor in the quantum amplitude generated by equation (25) disappears. In consequence, although there is a weak contribution to the process rate given by the analysis above, it is dominated by terms in which the tensors associated with primed and unprimed parameters in (30) may relate to different molecules. In other words, the signal has coherence terms arising from the interference of quantum amplitudes from innumerable pairs of molecules in different spatial locations. But in the context of fluids the key difference from incoherent processes is that rotational averaging is now performed according to the right-hand side of equation (33), i.e. involving a rank n rather than a rank 2n isotropic average. Full details are given in [50].
Thus, in the leading E13 order for a coherent three-photon process, mediated by a molecular hyperpolarizability, the third rank tensor average cast in terms of a Levi-Civita antisymmetric tensor annuls coherent SHG because the two input photon annihilations with which it is engaged are intrinsically interchangeable. The only second harmonic signal from an isotropic fluid (in the absence of any static field) is the much weaker form known as hyper-Rayleigh scattering, involving the sixth rank average [123]; chiral behavior can only arise through the involvement of an M1 or E2 interaction. However, with sum-frequency generation, in which conversion of two dissimilar photons into another occurs,  symmetry can be broken at the E13 level, and it is possible to observe not only local molecular ordering [124] but also chiral discrimination [125]. This diagnostic capacity has for example recently been applied in the characterization of a helical structure in water molecules clustering around DNA [126].
symmetry can be broken at the E13 level, and it is possible to observe not only local molecular ordering [124] but also chiral discrimination [125]. This diagnostic capacity has for example recently been applied in the characterization of a helical structure in water molecules clustering around DNA [126].
10. The complex role of M1 and E2 transitions
As has been shown in section 8, no individual level of electric or magnetic dipole interaction can be solely responsible for the exhibition of optical chirality in matter; a product or interference of terms having different spatial or temporal character is required. In the light of the symmetry character and magnitudes discussed above, it is evident that the leading terms with the necessary capacity will be E1(m−1)–M1 and E1(m−1)–E2 where, if n photons are involved, m = n for an energy, or m = 2n for a transition rate.
To delve further, more clarity can be gained by assuming for the present that all material wavefunctions are real, and that damping losses can be ignored. The former condition can be satisfied by all non-degenerate states—and even when degeneracy is present, a change of basis always enables linear combinations with real wavefunctions to be found. (A classic example in simple atomic orbital theory is the use of px, py in the basis set for p orbitals, instead of p1 and p−1.) The effect of removing the latter condition—allowing for dispersion and line-shape issues to emerge—is to be examined in section 12.
The condition of real wavefunctions leads to the result that all transition electric dipole moments are real, and all magnetic ones are imaginary. This follows from the defining equations for those moment operators, and is a direct consequence of the correspondingly real and imaginary characters of the quantum operators for position and angular momentum, respectively. Thus, it becomes evident that, since every material tensor has terms with real energy difference-based denominators, as follows on development from equation (4) [91], tensors of the form  are real whilst
are real whilst 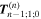 are pure imaginary. However, since it is necessary to properly account for the effect of the gradient operator associated with E2 coupling, which delivers a factor of ±i on application to any of the mode expansions, (5), (6), (16) or (17), it is expedient to assimilate this imaginary factor into the structure of the molecular tensor and so regard both forms of tensors, i.e. for both E1(n−1)–M1 and E1(n−1)–E2 couplings, as imaginary.
are pure imaginary. However, since it is necessary to properly account for the effect of the gradient operator associated with E2 coupling, which delivers a factor of ±i on application to any of the mode expansions, (5), (6), (16) or (17), it is expedient to assimilate this imaginary factor into the structure of the molecular tensor and so regard both forms of tensors, i.e. for both E1(n−1)–M1 and E1(n−1)–E2 couplings, as imaginary.
It now becomes apparent that for chiral discrimination to be possible, the appropriate radiation invariants formed from the right-hand bracketed terms in equation (32) must be complex (i.e. have a non-zero imaginary component) in order to secure a non-zero differential rate observable. By the same logic, an identical rule applies to the E1(n−1)–M1 and E1(n−1)–E2 radiation invariants on the right in equation (33); no other way can a finite differential energy arise. Whilst the specific details have to be secured for each type of experiment (e.g. circular dichroism, or circular differentials in scattering, trapping or binding forces), it is evident that, where gases, liquids or other isotropic systems are concerned, no discrimination should be possible without the use of circular (or at least elliptical) polarizations. As noted in section 5, plane polarizations are the only form that can be represented by entirely real polarization vectors. This conclusion is at odds with predictions based on the use of multiple beams with plane polarization.
Table 2 exhibits how the molecular and radiation tensors, and their invariants, arise in the specific case of single-photon circular dichroism in an isotropic fluid. Two features in particular now warrant renewed attention. In connection with both of the E1–E2 rate interference terms, it is notable from the column on the right how the factor of i becomes manifest in the radiation invariants for the case of circular polarization (whilst for plane polarized light the corresponding result is zero). Thus, the same character with respect to time inversion appears as with the E1–M1 terms where they are to be anticipated. Secondly, also in connection with the E1–E2 terms, it transpires that irrespective of the radiation feature—including non-paraxial conditions, such as may be associated with structured light—the molecular invariants are necessarily zero, and therefore these terms play no part in generating circular dichroism in a fluid of randomly oriented molecules [2, 3]. The reason is readily understood: the only isotropic tensor of rank 3 is the fully index-antisymmetric Levi-Civita ε tensor, which is here contracted with a term involving an index-symmetric quadrupole transition moment; in consequence the result vanishes identically.
The situation is potentially different, however, in aligned media such as poled liquid crystals, or other fluid systems where for example there may be a locally non-uniform distribution of molecular orientations in the proximity of a solid interface [127]. Here, it is possible for molecules in different regions of a phase-structured (e.g. Laguerre–Gaussian) beam to experience an optical phase gradient of locally varying direction, schematically illustrated in figure 13. As has been shown by work on the prototypical case of circular dichroism, this can enable the topological charge to engage with and modify the extent of chiroptical discrimination—a feature that has been dubbed circular vortex dichroism [128]. Measured as usual as the differential response to left- and right-handed circular polarizations, this is a dichroism that can display a weak variation with topological charge l, when the effect is studied with vortex light, due to the implicit dependence on q in the radiation tensor S({ql}) in equation (25). However, the effect will vanish unless the method of experimental detection can resolve the absorption at different locations within the beam cross-section.
Figure 13. Illustration of the different directional sense of the phase gradient experienced by locally ordered chiral molecules (here represented by cholesteryl benzoate) sited at different locations in a cross-section around the axis of a vortex beam—color here representing the optical phase of a beam with topological charge l = 1. When such a beam is circularly polarized it enables circular dichroism, for example, to vary with position—see text and [128].
Download figure:
Standard image High-resolution imageThe separation of effects associated with M1 and E2 is obscured in a minimal coupling formulation; this feature exhibits an advantage of working with the electric and magnetic multipole forms of coupling. Significantly, this facet of the theory also means that to simply prove the capacity for chiral differentiation, in any given form of interaction, it usually suffices to evaluate non-vanishing results with reference to M1 or E2 interferences alone—since any counterpart terms could only provide exact cancellation under an impossibly rare condition: the accidental coincidence of equal and opposite quantities. There is no general quantitative connection between magnetic dipole and electric quadrupole moments. Of course, as we have seen, it is both illogical and potentially wrong to make the inverse inference (a supposed impossibility of chiral discrimination) based alone on a lack of M1 involvement—or equally, to make any such deduction solely from the absence of E2.
The analysis of processes involving higher orders of interaction becomes rapidly more intricate with any increase in the number of photon interactions. This is true event for the next simplest process of higher order, namely circular differential (Rayleigh and Raman) scattering, normally studied in the solution phase [129, 130]. At the molecular level each fundamental process involves one input and one output photon, and the leading rate contributions with the potential to generate a differential response to left-and right-handed input are E12–E1M1 and E12–E1E2 interference terms. The respectively corresponding molecular invariants accordingly relate to isotropic tensors of rank 4 (which are outer products of two Kronecker deltas, δ2) and rank 5 (εδ products). In the latter case, some rate contributions with a dependence on topological charge persist, in the case of vortex light—though only when associated with circular polarizations to support an optical chirality density—as established in equation (15). A weak dependence of exactly this kind has been observed in experimental studies [131, 132].
11. Relevance to enantiomer separation
One of the main or implicit motivations for several of the recent studies in this area is the prospect of achieving, by optical means, a separation of particles—especially chiral molecules—of opposite handedness [7, 10, 43, 98–108, 133–145]. Certainly such a capacity might have important commercial applications—notably in the pharmaceutical industry, where oppositely handed compounds can deliver drastically different effects. Synthetic methods often lead to a racemic product, i.e. one containing the two forms in equal measure, and separation following production is extremely important. The key measure of product purity in such processes is the enantiomeric excess (often reported as 'ee'), defined by a scale on which a racemic mixture has a value of zero, whilst the objective of 100% represents complete enantiomeric purity. The continual development of new drugs, and the increasing use of functionalized nanoparticles in medicine, is constantly extending the range of materials requiring processing to secure a safe level of enantiomeric excess.
However, there are numerous factors that have to be taken into serious consideration in realistically assessing the viability of any scheme for enantiomer distinction and separation, based on optical forces. Consider, for example, optical trapping with a circularly polarized beam, where the optical force experienced by two oppositely handed enantiomers slightly differs—so that an optical separation is in principle possible. Estimates of the difference in force suggest figures in the 10−16–10–15 N range for a trapping beam intensity of 5 × 1011 W cm−2 [142, 146]—disappointingly small, though experimentally distinguishable. Although the levels of achievable intensity are readily extended by compressive ultrafast pulsing, there is no net gain because of the associated reduction in irradiation intervals since chiral separation schemes are almost invariably based on linear optical response.
The basic principle of one potential setup is shown in figure 14. Elegant schemes have been proposed based on plasmonic apertures and nanoantennas, enabling one enantiomer to be trapped and the other repelled by a potential energy barrier [108, 147, 148], whilst a quantum electrodynamical theory has also proposed chiral discrimination associated with the pairwise interactions involved in optical binding, illustrated in figure 15 [149]. But attempts to enhance the efficiency of such methods are fraught with difficulty. To give one further example, it emerges that one potentially promising system based on sample exposure to counterpropagating beams of opposite circular polarization requires the chiral molecules to exhibit an essentially simultaneous absorptive (single-photon) response to photons from each direction, raising issues of the necessary levels of intensity. The authors of one such study conclude that the proposed method is unsuitable for direct separation of chiral molecules, though it might be viable for molecules attached to chiral nanoparticles [150].
Figure 14. Optically induced differential forces acting within a racemic solution produce different equilibrium concentrations of the two enantiomeric species, within and outside the volume illuminated by the circularly polarized light. Molecules of both enantiomeric forms are drawn by a mean force F towards the axis of a beam with a Gaussian spatial profile, but their individual forces differ from the mean force by a component ΔF. Enantiomers with a positive ΔF result move to produce a positive concentration gradient towards the axis; the opposite enantiomers are displaced away from it, producing enantiomeric excess towards the beam edges.
Download figure:
Standard image High-resolution imageFigure 15. Optical binding potential variation with distance, measured in terms of kR where R is the inter-particle displacement and k is the wave-number of the throughput radiation. Inset shows the small differential around the first minimum, for chiral particles of the same or opposite handedness to the light. © 2015 IEEE. Reprinted, with permission, from [142].
Download figure:
Standard image High-resolution imageWhereas in most respects the physical properties of opposite enantiomers are identical—their weakly differential response to circularly polarized light is a rare exception—it is nonetheless the case that intermolecular interactions can be strongly sensitive to relative handedness [151–154]. This is in a sense the weak-association limit of a selectivity which, when if chemical bonding were to occur, would be manifest in the physically distinct properties of diasteroisomers. A host of enantiomer separation techniques is based on this general principle [155, 156]. Techniques such as liquid chromatography with a chiral stationary phase offer a much more effective means of resolution than most conjectured optical methods, while fluidic systems based on the differential hydrodynamical forces can resolve micro-sized chiral particles [157–160]. It has been emphasized that chiroptical discrimination is generally weak [142], and most resonance or plasmonic enhancement mechanisms do not change the fractional difference in response between enantiomers. Currently, no optics-based approach appears to represent serious competition to existing methodologies.
12. Dissipation and damping
In a number of applications—often those with significant device associations—optical systems exhibit processes associated with gains or losses: as such, they are sometimes referred to as 'breaking time symmetry'. Such systems are technically regarded as 'closed' in a thermodynamic sense; they may exchange energy with the surroundings, though not matter. Here, a formulation of theory in terms of an explicitly non-Hermitian Hamiltonian generally undermines the application of conventional 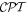 symmetry arguments. The corollary is that certain effects that would otherwise be symmetry-forbidden thus become allowed.
symmetry arguments. The corollary is that certain effects that would otherwise be symmetry-forbidden thus become allowed.
In the most common forms of quantum representation, the non-conservation of energy within the directly modeled system is accommodated in principle by one of two contrivances; either by explicitly adding phenomenological loss or gain terms to the Schrödinger equation, or by adding to the system Hamiltonian an unspecified term, written as Hbath for example, to signify the principle of quantization over a realm beyond the bounds of explicit calculation. To reconcile the two approaches, we first return to equation (2), rewritten as appropriate for an arbitrary system of electrically neutral particles labeled ξ;
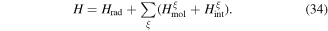
Note that, in the Power–Zienau–Woolley formulation that fully supports multipole expansion, all forms of electronic coupling between components occur only through the interaction of the molecular sub-systems with the quantized radiation field; there is no inter-particle term in the Hamiltonian [84, 161].
While the system as a whole is clearly subject to the corresponding time-dependent Schrödinger equation, its explicit compartmentalizing into stimulus, material subject, and bath means that the latter will (usually) be regarded as a source of net loss. The material particles can therefore be considered as sub-groups; those comprising the material part of the system of interest, a system set {S} [162], and the rest which are physically separate. For example, {S} might represent all the material within given physical boundaries, or the illuminated part of a continuous system, with all other particles beyond: in other applications {S} might represent optically significant solute molecules, or guests in a host lattice, counting the other particles as solvent, or host lattice. (In broader applications, the term 'bath' may even include internal vibrations, where material is modeled only in terms of its electronic structure.) So, we write;
Clearly H0 no longer represents an isolated system within which energy can be exchanged with a radiation field through the  operations of its constituent particles. Particles of matter within the system {S} can lose (or gain) energy from the 'external' set of particles through their mutual engagement with the radiation field. (This principle extends to 'radiationless' energy exchange mediated by the vacuum field.) The upshot is that the time-dependence of the basis functions for perturbation theory expands from the intrinsically energy-conserving form
operations of its constituent particles. Particles of matter within the system {S} can lose (or gain) energy from the 'external' set of particles through their mutual engagement with the radiation field. (This principle extends to 'radiationless' energy exchange mediated by the vacuum field.) The upshot is that the time-dependence of the basis functions for perturbation theory expands from the intrinsically energy-conserving form  consistent with equation (1), to accommodate an additional, real part of the exponent. This is formally equivalent to writing
consistent with equation (1), to accommodate an additional, real part of the exponent. This is formally equivalent to writing  where
where  signifies a 'complex energy' with an imaginary component that has a negative sign for losses (damping the resonance response), or a positive one for gain. This in turn effectively plays into the energies of individual electronic states
signifies a 'complex energy' with an imaginary component that has a negative sign for losses (damping the resonance response), or a positive one for gain. This in turn effectively plays into the energies of individual electronic states  as
as  in the case of losses, this construction denotes association with an effective decay lifetime
in the case of losses, this construction denotes association with an effective decay lifetime 
The manifestations of line-shape and damping mostly become evident in scattering and other processes involving more than one photon per molecular event—multiphoton absorption, or frequency-mixing processes for example. As discussed in section 7, the energy denominators that appear in the expressions for the terms in any molecular response tensor T, for processes fundamentally involving more than a single photon in each molecular event, owe their structure to the forms that arise in equation (4). These are generally terms, or products of terms, that essentially express a difference in value between one of the molecular excited states energies, and one or more photon energies. Essentially, when there is a state 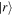 that closely matches the latter, a resonance arises. Phenomenologically tempering the material wavefunctions with the damping factor as described above ensures a Lorentzian lineshape with a half-width at half-maximum of Ωr [163].
that closely matches the latter, a resonance arises. Phenomenologically tempering the material wavefunctions with the damping factor as described above ensures a Lorentzian lineshape with a half-width at half-maximum of Ωr [163].
As previously observed, a wide variety of distinct factors contributes to spectral damping, including intramolecular vibrational redistribution involving a manifold of vibrational states, so the concept of coupling taking place outside the system is again generally considered in terms of a generalized external bath. For pragmatic reasons, partly reflecting the multiplicity of media influences that can contribute to spectral line broadening, the associated damping factors are usually regarded as phenomenological. Due to the non-Hermitian nature of the implicitly non-conservative system Hamiltonian, it is then impossible to reconcile any internally consistent form of damping with both the Hermitian character that befits measurable electromagnetic fields and the demands of time-reversal invariance [164, 165]: attempts to reconcile any ensuing cast of theory with full temporal symmetry must ultimately fail, unless assumptions are made that are rarely applicable to molecules [162, 166].
A classic example of how the symmetry-breaking inclusion of damping can lead to chiroptical phenomena that would otherwise be forbidden is the case of circular polarization-specific surface-reflection second harmonic generation [167, 168]. Under conditions approaching resonance with an electronic excited state, and as a result of the associated damping, the conventional (E13) hyperpolarizability tensor  acquires through its denominator structures a significant imaginary component: the result is that an analog of optical rotation can be clearly observed even from chiral monolayers—without involving any interference from M1 or E2 transition multipoles [50]. The same conclusion can be drawn by deploying field expansions modified by a complex index of refraction, as noted earlier.
acquires through its denominator structures a significant imaginary component: the result is that an analog of optical rotation can be clearly observed even from chiral monolayers—without involving any interference from M1 or E2 transition multipoles [50]. The same conclusion can be drawn by deploying field expansions modified by a complex index of refraction, as noted earlier.
13. Magnetic fields 'breaking symmetry'
As has been seen, the effects of dissipation or gain can compromise temporal symmetry at the bulk, if not the microscopic, level. For very different reasons, the effects of applying a static magnetic field can also be described as 'breaking time symmetry'. However, pursuing the parity aspects of a static magnetic field is an intricate matter—far less intuitive than for an electric field, whose space-odd (polar) and time-even character is quite clear. To illustrate this, we may recall that magnetic field lines are commonly depicted as being directed from a North towards a South pole, suggesting that spatial inversion will change the sign of the field. However, this is thoroughly misleading: the symmetry operation exchanging poles is time inversion, as is readily appreciated when the spin angular momentum-related source of magnetism is considered (again, see table 1). Moreover, the 3D operation of  is not simply reflection in a 2D plane.
is not simply reflection in a 2D plane.
To more fully appreciate the problem, and its resolution, consider the familiar classically formed Lorentz force law:

in which the force f on a charge q is determined by electric and magnetic fields expressed as vector variables rather than operators. The force on the left-hand side of equation (36) is self-evidently odd under  and even under
and even under  The velocity v is odd under both
The velocity v is odd under both  and
and  and accordingly the magnetic field b has to be even in
and accordingly the magnetic field b has to be even in  (it is an axial vector, as noted earlier) and odd in
(it is an axial vector, as noted earlier) and odd in 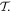 This is consistent with taking the zero-frequency limit of an oscillatory magnetic field, whose +1 signature under
This is consistent with taking the zero-frequency limit of an oscillatory magnetic field, whose +1 signature under  and –1 under
and –1 under 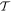 was established in section 5.
was established in section 5.
The foremost, historic example of 'breaking time-reversal symmetry' is the Faraday effect, in which an optical rotation of plane polarized light occurs when a static magnetic field is aligned with the direction of optical propagation, generally on passage through achiral solids. In the same way as with conventional optical activity attributable to material chirality, a beam of light passing through such a system and then reflected back experiences double the rotation, rather than the reverse passage undoing the effect. This is again consistent with the axial property of the magnetic field vector; the material property responsible can be regarded as a zero-frequency limit of a three-interaction scattering tensor of E12M1 form, engaging in coherent forward scattering.
Another familiar and well-established methodology exploiting the temporal parity of a static magnetic field for spectroscopic purposes is magnetic circular dichroism, in which applying the static field to a sample (again, not necessarily chiral) engenders a differential response in the absorption of left-and right-handed light. Most experimental studies exploit the lifting of spin degeneracy in systems with unpaired electrons, such that the wavelengths of maximum absorption slightly differ for 'spin up' and 'spin down' transitions [169]. In connection with quantum dot emission, the principle of deploying a static magnetic field to lift spin degeneracy finds more recent application as a conceived means of adding a chiral dimension to photonic circuitry. Here, the field undermines the energetic symmetry of a V-type three-level system, permitting emission to occur with a high degree of tailored helicity [170]. However, a much simpler magneto-optical effect, though incoherent and therefore weaker, can occur in absorption. With chiral molecules it is possible for a static magnetic field to directly participate in a weak E1M1 interaction—see figures 9(c) and (d)—that electronically excites a molecule through single-photon absorption, as originally predicted [171] and then experimentally observed [172].
14. Metamaterial chirality
In the broad context of metamaterials and other kinds of mesoscopically structured materials, there are further aspects of loss and gain to consider. In general, these are systems characterized by arrays of micron-or nanometer-sized components, each of individual electronic integrity, and fabricated into specific shapes and dimensions for tailored electrodynamic properties. In a sense the description given by equation (34) still applies, but the material properties are now best represented in terms of essentially macroscopic response, involving the electric permittivity, magnetic susceptibility and tensor susceptibilities [173]. Physically fabricated as optical elements, such systems do not usually exhibit identifiable quantum transitions, and the material 'initial' and 'final' states can therefore be considered identical. Where metallic components are involved, and microwave radiation is commonly deployed, chiroptical response is most readily observed as a differential response to left-and right-circularly polarized light (opposite in signature under 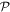 ). Such an effect, termed the 'optical Rashba effect' can result from the removal of surface wave degeneracy on an inversion asymmetric metamaterial, for example [174]. In this respect, helical gold 'metamolecules' have been shown to offer exceptional levels of such discrimination [175]. For many such metamaterials, surface plasmons dominate the optical characteristics and behavior, and magnetic effects gain much greater prominence [176]. The general principles and scope for exploring optical chirality in metallic nanostructures are the subject of a thorough recent review [177].
). Such an effect, termed the 'optical Rashba effect' can result from the removal of surface wave degeneracy on an inversion asymmetric metamaterial, for example [174]. In this respect, helical gold 'metamolecules' have been shown to offer exceptional levels of such discrimination [175]. For many such metamaterials, surface plasmons dominate the optical characteristics and behavior, and magnetic effects gain much greater prominence [176]. The general principles and scope for exploring optical chirality in metallic nanostructures are the subject of a thorough recent review [177].
One recent example is a scheme, whose viability has been verified by theoretical analysis and simulation, in which short diagonal slots are formed in a layer above the surface of a mirror. On illumination with plane polarized light, chiral near-fields arise—whose presence, it is suggested, might enable enantiomeric selectivity to be displayed in their vicinity. As depicted in figure 16, the system is structurally achiral, but each slot is 2D chiral in the sense of lacking mirror symmetry, and retro-reflection relieves the local electromagnetic fields of inversion symmetry [178]. Structures with such 2D chirality can differentially engage not only with circularly polarized light [179] but also with the wavefront twist of suitably structured complex light [180]. Furthermore, a differential response to oppositely handed polarizations can arise at surfaces that do not conform to the usual conditions for 2D or 3D chirality as described in section 2. At an appropriate glancing (off-normal) angle of incidence, surface chirality can also be evident in that the light impinges from a direction that itself breaks mirror symmetry, a condition termed extrinsic chirality [86].
Figure 16. The chiral structure on the left retains a capacity for chiral discrimination when reduced to the simpler structure on the right, which fulfills the criteria for reflective chirality (a lack of mirror planes normal to the surface). Adapted with permission from [178]. Copyright 2016 American Chemical Society.
Download figure:
Standard image High-resolution imageIn a number of entirely separate developments, issues of chirality are linked in significantly different ways with spatial and temporal symmetry [181]. This is an area with a notable capacity to generate confusion: for example even the term 'symmetry breaking' does not, in this sphere of optics, denote instances of dynamical instability—nor any of the fundamental field theory aspects associated with uses of the same term in elementary particle physics. In some papers, the specific term 'chiral' is in a sense misappropriated to denote no more than a lack of mirror symmetry—a difference between forward and backward propagation characteristics [182]. Use of the term 'chiral' to simply signify direction-dependent propagation [45] is especially to be regretted, when it signifies changing a well-established scientific terminology first introduced more than a hundred years before [183].
More commonly, when certain metamaterials are referred to as 'left-handed' or 'chiral', the terms are then being used to signify a system in which the refractive index is negative, more informatively termed 'negative index metamaterials' [176, 184]. To fulfill this criterion, it is necessary for both the effective electric susceptibility εeff and the magnetic permeability μeff to be negative. In this connection, 'left-handed' and 'chiral' have nothing to do with a lack of reflection symmetry or any improper rotation axes; the usage alludes to the fact that the electric field vector, the magnetic field vector and the propagation vector (e, h, k) constitute a left-, rather than the usual right-handed orthogonal set. The significance of the 'handedness' in this sense is argued from the form of the Poynting vector operator which, instead of the commonly used vacuum formulation 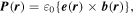 is now defined as [185]:
is now defined as [185]:
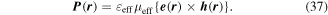
Since the prefactor product is positive, and the negative value of μeff signifies that h(r) is antiparallel to b(r), it follows that the momentum and corresponding energy flux are both in the opposite direction to the  result, signifying backward propagation. Equally, the helicity of a circularly polarized beam entering a negative index material is reversed; in a zero-index medium angular momentum and helicity measures identically vanish.
result, signifying backward propagation. Equally, the helicity of a circularly polarized beam entering a negative index material is reversed; in a zero-index medium angular momentum and helicity measures identically vanish.
Returning to the topic of media exhibiting optical gain or losses; in some circumstances, computational practicalities suggest the representation of a system in terms of an explicitly non-Hermitian Hamiltonian. It has been established that it is nonetheless possible for such systems to still be subject to  symmetry, and so to be associated with real observables [186–189]. This observation hinges on an optomechanical analogy—formally a mathematical equivalence between the quantum mechanical time-independent Schrödinger equation and the optical wave equation. To understand this perspective, consider a vacuum formulation of the latter, paraxially expressible for rectilinear propagation in the time-independent Helmholtz form, equation (8). For adaptation to account for losses or gains, a source or sink term can be added; the propagation distance can then play the role of time in conventional Schrödinger quantum mechanics. (Recall how Beer's law extinction derives from a linear dependence of an absorption rate on intensity.) In such a formulation, the electric field loosely plays the role of wavefunction, but not in the conventional sense; this is not a formulation in which light itself is truly quantized, nor are the solutions to be regarded as any kind of 'photon wavefunctions' [190].
symmetry, and so to be associated with real observables [186–189]. This observation hinges on an optomechanical analogy—formally a mathematical equivalence between the quantum mechanical time-independent Schrödinger equation and the optical wave equation. To understand this perspective, consider a vacuum formulation of the latter, paraxially expressible for rectilinear propagation in the time-independent Helmholtz form, equation (8). For adaptation to account for losses or gains, a source or sink term can be added; the propagation distance can then play the role of time in conventional Schrödinger quantum mechanics. (Recall how Beer's law extinction derives from a linear dependence of an absorption rate on intensity.) In such a formulation, the electric field loosely plays the role of wavefunction, but not in the conventional sense; this is not a formulation in which light itself is truly quantized, nor are the solutions to be regarded as any kind of 'photon wavefunctions' [190].
The way this works in the emerging field of non-Hermitian optics connects to the construction of optical materials with periodic modulations in structure, which are fundamentally important for controlling the flow of light in photonics. In particular it exploits materials designed such that variations in the real and imaginary parts of their refractive index take the specific form,  In other words, one part of the index transforms into the other on spatial inversion—here equivalent to mirror reflection in a plane perpendicular to the propagation axis. In the Schrödinger equation analog, the optical fields are therefore subjected to an effective potential with this same inversion property; the complex conjugation associated with time reversal thus enables complete satisfaction of
In other words, one part of the index transforms into the other on spatial inversion—here equivalent to mirror reflection in a plane perpendicular to the propagation axis. In the Schrödinger equation analog, the optical fields are therefore subjected to an effective potential with this same inversion property; the complex conjugation associated with time reversal thus enables complete satisfaction of  -symmetry [191, 192]. Materials of this kind can exhibit a variety of exotic optical phenomena [193]; more recently they have been supplemented by reports of
-symmetry [191, 192]. Materials of this kind can exhibit a variety of exotic optical phenomena [193]; more recently they have been supplemented by reports of  -symmetry breaking in other forms of complex optical potential [194, 195].
-symmetry breaking in other forms of complex optical potential [194, 195].
As we have seen, it is frequently asserted that a static magnetic field enables temporal symmetry to be 'broken' as it is intrinsically odd under  —though this is simply another aspect of arbitrarily compartmentalizing the system as a whole, regarding the field as specifically extrinsic. The commonly weak character of material coupling with magnetic fields in the key near-IR to near-UV regions, and in non-metals, has prompted the search for other methods to achieve efficient optical diodes and isolators, for example, and this has led to another development in the sphere of metamaterials. To break reciprocity in the sense of time-and path-reversal invariance, systems such as nano-ring assemblies (a little misleadingly described as 'angular momentum biased' materials) are designed to introduce a helical phase similar to that of an optical vortex [196, 197].
—though this is simply another aspect of arbitrarily compartmentalizing the system as a whole, regarding the field as specifically extrinsic. The commonly weak character of material coupling with magnetic fields in the key near-IR to near-UV regions, and in non-metals, has prompted the search for other methods to achieve efficient optical diodes and isolators, for example, and this has led to another development in the sphere of metamaterials. To break reciprocity in the sense of time-and path-reversal invariance, systems such as nano-ring assemblies (a little misleadingly described as 'angular momentum biased' materials) are designed to introduce a helical phase similar to that of an optical vortex [196, 197].
15. Conclusion
The field of optical chirality has been enlivened, and greatly enriched, by a range of recent developments in both optical and material physics—notably in structured light and metamaterials. Each has brought numerous fresh insights into the origins, measurements and applications in this field, leading to wide-ranging explorations of theory and experiment. An overview of this activity from a quantum optical perspective clarifies the fundamental distinction between chiroptical effects based on processes destined for the study and development of material substances—many ultimately aimed at photonic system design—and other effects whose mechanisms achieve mechanical motion, often promoted as potentially significant for the pharmaceutical and other health-related industries.
The role of theory is not only to account for the results and mechanisms behind observed phenomena: it also provides a framework to identify potentially new effects, and to assess their fundamental viability and practical utility. As indicated in the present survey—and the focus of section 11—the potential relevance of optical schemes for the commercial separation of enantiomers is questionable. It is impacted by three main factors: the intrinsic weakness of the optical phenomena with the necessary molecular selectivity; the very small scale of operational volume in processes based on laser light; the efficiency of existing procedures already widely deployed in industry. The first two criteria essentially rule out any process based on gas-phase implementation. In terms of current practice, for example, commercial multi-component implementations of chromatography using a chiral stationary phase can achieve a daily turnover in the range of 1–10 kg of pure product, for each kilogram of a continually reusable column material [198]. This figure is to be viewed in the light of many drugs that are prescribed in full-course doses of much less than a gram.
The speed, scale and efficiency of chromatographic and other non-optical methods significantly undermines even the most optimistic assessments of commercial viability for optical separation methods. However, another kind of advance in the field of synthetic organic chemistry also, to a significant extent, now undermines the value and purpose of all enantiomer separation schemes. This is a technique known as desymmetrization, implemented by catalytic means. In many examples, intrinsically chiral enzymes are introduced to an achiral precursor that has been synthesized by conventional achiral means, to directly isolate an enantiomerically pure chiral product. The chiral product is commonly secured by selectively removing one of a pair of symmetrically disposed functional groups from the precursor, thereby removing mirror symmetry. Numerous reviews of such techniques are now available—see for example [199–201].
It is therefore other, more fundamental aspects of this subject, and their prospective applications in photonic circuitry, that attract and deserve primary attention. We have seen how considerations of fundamental spatial and temporal symmetry can elucidate the determination of mechanism and provide a secure pathway to avoid misleading conclusions. In several respects, the analysis described in sections 1–7 has also exhibited the lack of direct 1:1 mapping (despite strong correlation) between chiroptical behavior in molecules, and optical angular momentum—whether designated as either spin or orbital in nature. The same principles apply to larger particles such as quantum dots: for example, optical vortices can induce a rotational current in spherical semiconductor nanoparticles, generating a magnetic field that could in principle be used to control spin polarization [202]—but the process does not require the nanoparticle to be chiral.
In other respects, the development of symmetry-based theory based on quantum electrodynamics brings a more novel perspective to the understanding of optically induced transitions and motions. The former are generally considered to be of primary interest for their spectroscopic connections, but the analysis in section 8 has highlighted means by which both kinds of interaction can additionally result in motion that differs according to the relative handedness of radiation and matter. Although a distinction is commonly drawn between conservative and non-conservative forces, the present analysis identifies a more crucial difference in the methods needed to evaluate observables—namely either a linear or quadratic dependence on the quantum amplitude. The distinction becomes especially clear when accounting for observations of chiroptical behavior in fluids or orientationally disordered media, such as the solution phase in which the majority of molecular systems are studied. The analysis in sections 9 and 10 show why, and how, entirely different constructs for the associated rotational averages then come into play; it also becomes apparent why the reduction of symmetry associated with structured light can locally enable novel effects such as circular vortex dichroism to occur: this is an area that appears to warrant more extensive experimental investigation.
Section 12 introduced the complication of losses or gains, whose phenomenological development leads to a Hamiltonian lacking Hermitian character, so that time-reversal invariance is inevitably compromised. This even applies to the inclusion of resonance damping, such as in the treatment of optical susceptibilities and molecular response tensors. The accommodation of frequency dispersion and an associated linewidth leads to the impossibility of formulating theory that can simultaneously satisfy time reversal symmetry, and support the Hermiticity that befits measurable electromagnetic fields. Following a discussion of the special role of static magnetic fields in section 13, the survey has concluded with a brief overview of the different constructs of theory associated with the development of metamaterial photonics. With its strongly emerging role in platforms for photonic circuitry, this very much represents a cutting edge in the wide spectrum of chiroptical nanoscale phenomena.
Acknowledgments
I am very grateful to David Bradshaw, Matt Coles, Kayn Forbes, Jack Ford, A Ganesan, Alan Haines and Roger Grinter for numerous comments and valuable insights reflected in this work. Jamie Leeder, Mathew Williams and Silvana Matei are also thanked for contributions to the graphics.