Abstract
Superoscillations are band-limited functions with the counterintuitive property that they can vary arbitrarily faster than their fastest Fourier component, over arbitrarily long intervals. Modern studies originated in quantum theory, but there were anticipations in radar and optics. The mathematical understanding—still being explored—recognises that functions are extremely small where they superoscillate; this has implications for information theory. Applications to optical vortices, sub-wavelength microscopy and related areas of nanoscience are now moving from the theoretical and the demonstrative to the practical. This Roadmap surveys all these areas, providing background, current research, and anticipating future developments.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Faster than Fourier (p)revisited
M V Berry
University of Bristol, Bristol, United Kingdom
Past
The modern study of superoscillations was kick-started by Aharonov et al [1], who, in a still-unpublished 1991 preprint related to the then-new quantum weak measurements, envisaged a box containing only red light, which would emit gamma radiation when a window is opened. It was soon realised [2] that underlying this apparently paradoxical scenario was a deep mathematical phenomenon: a band-limited function ('red light') can vary arbitrarily faster than its fastest Fourier component ('gamma radiation'), over arbitrarily long intervals. Where superoscillations occur, the functions are exponentially weak (in the degree and extent of their 'faster than Fourier' variation), because the different Fourier components exhibit almost-perfect destructive interference. This weakness is the mechanism by which superoscillations evade the uncertainty principle (Fourier duality), because the principle is a relation between variances, and variances are insensitive to exponentially small values.
It is easy to create superoscillatory functions. Perhaps the simplest—certainly the most studied—is the periodic function
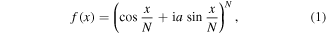
in which N is a large even integer and a > 1. This is periodic with period Nπ, and is band-limited, because when expanded in a Fourier series, the component oscillations are all of the form exp(iknx) with ∣kn∣ ≤ 1. It is superoscillatory, because for ∣x∣ < √N it can be approximated by exp(iax). Outside the interval ∣x∣ < √N, f(x) first increases anti-Gaussianly and then rises to its enormous maximum value ∣f(±Nπ/2)∣ = aN. The meaning of the parameters a and N is: a represents the degree of superoscillation in the region near x = 0, and N measures the extent of this superoscillatory region.
Superoscillations were anticipated in at least two other contexts. During World War II, research in microwave theory demonstrated that it was possible to design a radar antenna, consisting of many radiating elements in an arbitrarily small region, whose radiation pattern represents a beam whose angular width is arbitrarily small ('narrower than Rayleigh'). This 'superdirectivity' or 'supergain' is now understood in terms of superoscillations: in suitable variables, the radiation pattern is band-limited. But superdirectivity comes at a price, which has prevented extensive practical application: the individual elements must be driven very strongly, resulting in a near field that is exponentially more powerful than the narrow beam that reaches the far field.
Toraldo di Francia realised [3] that this microwave research has implications for optics, suggesting a lens with a focal spot small enough to enable superresolution (sub-wavelength) microscopy—performance beyond the Abbe resolution limit. The lens he designed required delicate fabrication, unavailable at that time. In 2000, the technology began to be available, and now the 'superoscillatory lens' (SOL) is being intensively developed, and the resulting superresolution microscopy is becoming practical [4]. An advantage of the SOL is that the microscopy is label-free, in contrast to STED microscopy which involves fluorescence, i.e. labelling. (STED also relies on superoscillation, in the sense that the depletion beam responsible for selective deactivation of fluorescence contains an optical vortex (see below), which can be arbitrarily narrow: there is no Abbe limit for dark light.)
The second early context was phase singularities (=wave vortices, nodal points and lines, or wave dislocations), understood as topologically stable features of waves of all kinds [5]. Around a circuit of such a singular point P in the plane, the phase changes by 2π; so, close to P, the local phase gradient can be arbitrarily larger than any of the wavevectors in the Fourier superposition representing the wave. Therefore, all band-limited waves, in particular monochromatic ones, are superoscillatory near their phase singularities. This understanding emerged belatedly, in 2007; since then, research in superoscillations and phase singularities have merged. Dennis calculated [6] that superoscillations in waves are unexpectedly common: for random monochromatic light in the plane (e.g. speckle patterns), 1/3 of the area is superoscillatory, with similar fractions for these 'natural superoscillations' in more dimensions. A monochromatic superoscillatory wave is illustrated in figures 1 and 2.
Figure 1. Superoscillatory fine detail in one square wavelength of the monochromatic wave ψ = Jm(r)exp(imϕ) + εJ0(r) for m = 1, ε = 10−7 over one square wavelength, The phase argψ is colour-coded, and the optical vortices are the ten points where all colours meet; superimposed are the lines of local wavevector grad(argψ).
Download figure:
Standard image High-resolution imageFigure 2. As figure 1, showing the intensity log∣ψ∣.
Download figure:
Standard image High-resolution imageThe large phase gradient that characterises superoscillations is alternatively described as the local wavevector. This illustrates the quantum 'weak measurement' scheme introduced by Aharonov and his colleagues, involving an operator with a finite spectrum, and pre- and postselected states, leading to a 'weak value' that lies outside the spectrum of the operator. In optics, the local wavevector is the weak value of the momentum operator, the preselected state is the wavefield and the postselected state represents position.
Present and future
The term superoscillation is slightly misleading, because not only fast oscillations but also fast-varying functions of any form can be reproduced band-limitedly. Examples are: the SOL, which generates a sub-wavelength spot; the possibility of reproducing Beethoven's Ninth Symphony with 1 Hz bandlimited signal [2]; and—a recent and extreme example—reproducing fractal functions to any desired accuracy.
A natural question arising in quantum applications is: if an initial state is a superoscillatory function of position, how long do the superoscillations persist under evolution according to the Schrödinger equation? An answer, obtained in 2006 [7], was that if the superoscillations extend over an interval √N (where N is the large integer in (1)), the superoscillations persist for a time proportional to N. After this, they are destroyed by a rogue saddlepoint in the evolution integral. An implication is that for N → ∞ the superoscillations would survive forever. The limit is strongly singular, and rigorous proof requires more sophisticated mathematics [8], being developed for a variety of evolutions.
In optics, the analogy between Schrödinger evolution in time and paraxial propagation in space suggested [7] that the √N persistence might enable sub-wavelength microscopy without evanescent waves, because subwavelength detail in an object could reach a distant image plane. But paraxial propagation fails for superoscillatory light, and must be replaced by exact propagation according to the Helmholtz equation. It turns out, however, that there exists a class of initial waves, which can represent subwavelength detail, that propagate to repeat exactly at any chosen distance, and multiples of it.
Two fundamental obstructions to all extreme applications of superoscillations arise from their origin as a phenomenon of near-perfect destructive interference. The first is that such interference is inherently delicate, and survives only in the region (of size √N, mentioned earlier) where the Fourier amplitudes are phase-coherent. Outside this region, functions rapidly grow to values vastly greater than where they superoscillate. One implication is a difficulty for SOL microscopy: the dark ring around the narrow focal spot is surrounded by a ring of light that is exponentially brighter than the spot, threatening to burn vulnerable speciments.
Another consequence is that near-destructive interference is vulnerable to noise. This vulnerability has now been quantified for superoscillations contaminated by phase noise. As the noise increases through a tiny critical value, the phase coherence is destroyed; the local phase gradient decreases from its superoscillatory values and the tiny intensity increases, to magnitudes representative of the band-limited Fourier content.
These obstructions should be regarded positively, as challenges to the ingenuity of experimentalists. Particularly important is to develop ways of using superoscillations to go beyond the rather modest sub-wavelength resolutions currently obtainable in microscopy.
The original claim that gamma radiation can be released from a box containing red light has now been supported at the level of classical optics [9]. In a box (actually a tube) where superoscillatory red light is confined, a window is opened and closed as the superoscillations (moving with speed c) pass by. An analogy is with a curtain that is briefly opened in a lit room at night, releasing light allowing people in the darkness outside to see what is inside; but this is less straightforward when the light within is superoscillatory. Nevertheless, the exact solution of the relevant causal scattering problem shows that the superoscillations do escape into the far field as 'gamma radiation': the time-dependent window converts the fake frequencies in the superoscillations into genuine frequencies outside. An experiment to demonstrate this phenomenon would be worthwhile, though probably not easy.
At the quantum level, it is more difficult to understand how the escaping gamma photons get their energy, given that the box contains only red photons with much lower energy. This is the subject of a new paper by the original authors [10], arguing that the question opens basic issues concerning the interpretation of conservation laws in quantum physics.
2. Mathematical aspects of superoscillations
Yakir Aharonov1, Fabrizio Colombo2, Irene Sabadini2, Daniele C Struppa1,3 and Jeff Tollaksen1
1Chapman University, Orange, CA, United States of America
2Politecnico di Milano, Milano, Italy
3Donald Bren Distinguished Chair in Mathematics, Chapman University, CA, United States of America
Status
The formal study of the mathematical properties of superoscillations begins by considering a real variable  a fixed real number
a fixed real number  and the superoscillating sequence
and the superoscillating sequence
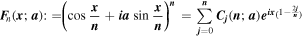
where
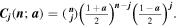
It is easy to show that  converges to
converges to  on all of
on all of  but that the convergence is uniform only on compact sets in
but that the convergence is uniform only on compact sets in  More precisely [11], it is possible to obtain precise estimates on the speed of convergence by showing that, on compact sets,
More precisely [11], it is possible to obtain precise estimates on the speed of convergence by showing that, on compact sets, 
The mathematical study of superoscillations has currently been focused on three main problems: the study of superoscillations when evolved using the Schrödinger equation, the search for larger classes of superoscillations, and finally the use of superoscillations to approximate important classes of functions and generalized functions.
Evolution of superoscillations
Consider the Cauchy problem associated to the Schrödinger equation
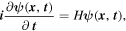
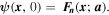
We ask whether the solution to this Cauchy problem remains superoscillatory. The first pioneering work on this problem is [2], where the author shows that the superoscillating phenomenon persists for a time of order 
Equally important, in [2], one sees that for finite  the functions under consideration rise to values
the functions under consideration rise to values  outside the range
outside the range  and are ultimately destroyed for times greater than
and are ultimately destroyed for times greater than 
In a series of papers that began with [12], the authors demonstrate that it is possible to take the limit as  and thus demonstrate superoscillatory behavior for all values of
and thus demonstrate superoscillatory behavior for all values of  Specifically, two case were analyzed: first, we take
Specifically, two case were analyzed: first, we take  to be a constant coefficients differential operator (or a convolution operator) in the variable
to be a constant coefficients differential operator (or a convolution operator) in the variable  , which can be represented, for suitable coefficients
, which can be represented, for suitable coefficients  as
as

In this case [12, 13], it was shown that superoscillatory behavior continued in a very large class of cases, and all values of t. The idea behind the proof of such permanence consists in showing that the solution of the Cauchy problem can be written in the form
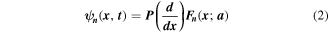
where  is a convolution operator (in some case an infinite order differential operator) whose specific definition reflects the definition of the Hamiltonian H. One then complexifies equation (2) and demonstrates that the complexified operator
is a convolution operator (in some case an infinite order differential operator) whose specific definition reflects the definition of the Hamiltonian H. One then complexifies equation (2) and demonstrates that the complexified operator  acts continuously on an appropriate space of entire functions to which the complexified superoscillating functions
acts continuously on an appropriate space of entire functions to which the complexified superoscillating functions  belong. The fact that this is indeed possible is non-trivial and relies on some subtle properties of multipliers on spaces of entire functions with growth. The desired result is then obtained by restricting back to the real axis. A recent survey of this approach is given in [14].
belong. The fact that this is indeed possible is non-trivial and relies on some subtle properties of multipliers on spaces of entire functions with growth. The desired result is then obtained by restricting back to the real axis. A recent survey of this approach is given in [14].
A different approach consists in considering Hamiltonians that originate from clear physical situations. This includes the case of the Hamiltonians describing the harmonic oscillator of mass m and time dependent frequency  subject to an external time dependent force
subject to an external time dependent force  namely
namely
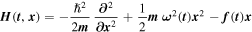
which was extensively treated in [18], as well as the cases of Hamiltonians representing uniform electric field [12], and uniform magnetic field [19].
The study of these Hamiltonians is still based on the ideas described above, but the complexity of the Green functions associated with the corresponding Cauchy problems has often led to the study of delicate new phenomena. We refer the reader to [13, 15] for details.
New classes of superoscillations
The techniques that are used to show the longevity of superoscillations also allow the construction of large new classes of superoscillating functions. For example, when the Hamiltonian is a convolutor whose symbol is a holomorphic function  it can be shown [16] that one can construct superoscillations of the form
it can be shown [16] that one can construct superoscillations of the form
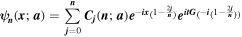
which converge uniformly on compact sets in R to  Given the rather weak constraints on the function G, this allows the construction of a large class of new superoscillating functions.
Given the rather weak constraints on the function G, this allows the construction of a large class of new superoscillating functions.
Approximation of generalized functions
The fact that superoscillations can be used to approximate exponentials, and that exponentials are a basis for most spaces of functions, suggests that one should be able to approximate functions (and generalized functions) in many spaces in a natural way. That this is indeed the case was shown first in [11], where the authors show how to approximate the value of a band limited function φ in the Schwartz space S(R) of rapidly decreasing functions at an arbitrary point  when one only knows the values of φ near the origin.
when one only knows the values of φ near the origin.
Later on (the reader is referred to [16] and the references therein), it has been shown that in fact one can approximate Schwartz tempered functions as well as Schwartz tempered distributions by using superoscillations. In this case, the key technique consists in utiliziing the Hermite orthonormal basis for the space  (R), and replace in it the exponentials with their superoscillating approximants. One can use the same technique, and the fact that we can characterize complex tempered distributions in R via the asymptotic behavior of the coefficients in their spectral Hermite development, to prove a similar result for tempered distributions.
(R), and replace in it the exponentials with their superoscillating approximants. One can use the same technique, and the fact that we can characterize complex tempered distributions in R via the asymptotic behavior of the coefficients in their spectral Hermite development, to prove a similar result for tempered distributions.
Finally, there is current work being done by the authors in collaboration with Yger that shows that a similar process can be used to approximate hyperfunctions. The case of pointwise supported hyperfunctions can be easily addressed, at least in the compact case, by noticing that every such hyperfunction is a suitable sum of infinite derivatives of Dirac's deltas. The general case is still under investigation.
Current and future challenges
There are many open problems concerning the mathematical aspects of the theory of superoscillations. One was proposed by Berry and Morley-Short in [17]: we know that the Weierstrass function that generates fractals can be expressed as a series of exponentials; since exponentials can be replaced by superoscillating sequences, the question is whether fractal functions can be expressed in terms of superoscillations. The proof of this conjecture is not trivial because, as it relies on the ability to prove the continuity of a differential (or convolution) operator, as we indicated in the previous section, and as of now this has not been proved yet. A second question worth investigating is the ability to generate superoscillations within the theory of classical groups. In [12], we describe a joint work with Nussinov to show that superoscillations arise naturally in SO(3); it is not clear how to generalize those ideas to different classical groups. Another interesting question regards the issue of optimization of superoscillations, as well as the problems connected with noise and how noise may indeed lead to a rapid disappearnce of superoscillations, as well as issues of numerical stability. Finally, on the basis of some physical considerations, one of us (Y A) has postulated that superoscillations should be able to offer approximations to rapidly decreasing exponentials. So far, we have not seen yet a mathematical confirmation for this phenomenon.
3. Optical superoscillatory focusing and imaging technologies
Edward T F Rogers1 and Nikolay I Zheludev1,2
1University of Southampton, Southampton, United Kingdom
2Nanyang Technological University, Singapore
The not-so-old history of the superoscillatory lens
The next disruptive step in nanoscale imaging, after the invention of the acclaimed stimulated emission depletion and single-molecule microscopies, will be the development of a far-field super-resolution label-free technique. The Abbe-Rayleigh diffraction limit of conventional optical instruments has long been a barrier for studies of micro and nano-scale objects. The earliest attempts to overcome it exploited recording of the evanescent field of object: contact photography [20] and scanning near-field imaging (SNOM) [21]. Such near-field techniques can provide nanoscale resolution, but capturing evanescent fields requires a probe (or photosensitive material) to be in the immediate proximity of the object. Therefore, these techniques cannot be used to image inside cells or silicon chips, for example. More recently, other techniques have been proposed to reconstruct and capture evanescent fields: including the far-field Veselago-Pendry 'super-lens', which uses a slab of negative index metamaterial as a lens to image the evanescent waves of an object to a camera [22, 23]. This approach, however, faces substantial technological challenges in its optical implementation and has not yet been developed as practical imaging technique. Biological super-resolution imaging is dominated by the powerful stimulated emission depletion (STED) [24] and single-molecule localization (SML) [25] microscopies: far-field techniques that have demonstrated the possibility of nanoscale imaging without capturing evanescent fields (which decay over a scale of about one wavelength away from the object). These techniques, while they have become widely used, also have their own limitations: both STED and some of the SML techniques use an intense beam to deplete or bleach fluorophores in the sample. Indeed, the resolution of STED images is fundamentally linked to the intensity of the depletion beam. The harmful influence of these intense beams is known as phototoxicity, as they damage samples, particularly living samples, either stressing or killing them. SML is also inherently slow, requiring thousands of images to be captured to build a single high resolution image Moreover, STED and SML require fluorescent reporters within the sample, usually achieved by genetic modification or immune labelling with fluorescent dyes or quantum dots [26]. These labels cannot be applied to solid nanostructures such as silicon chips and are known to change the behaviour of molecules or biological systems being studied [27].
Far-field super-resolution is also possible with the phenomenon of superoscillations, when interference of multiple coherent waves diffracted on a mask creates an, in principle, arbitrarily small hot-spot.
It started in 2006 when Berry and Popescu found theoretically that an optical field with a subwavelength structure, which was created by coherent illumination of diffraction grating with subwavelength features, can propagate paraxially in the space beyond the grating, retaining its sub-wavelength structure without evanescent waves [28]. Almost concurrently, this phenomenon was observed experimentally at the University of Southampton when patterns of subwavlength hotspots in free space were discovered by scanning a sub-wavelength aperture over a quasi-crystal array of nanoholes illuminated with coherent light [29, 30], and shortly afterwards, it was shown that such sub-diffraction hotspots can be used for imaging [31, 32]. It was quickly realized that an optical mask can be designed that creates a superoscillatory constructive interference of waves leading to a subwavelength focus of arbitrary prescribed size and shape in an arbitrary field of view beyond the evanescent fields, when illuminated by a monochromatic wave [33]. Moreover, the same work demonstrated that such a mask may be used not only as a focusing device but also as a part of a super-resolution imaging apparatus. Recently, it was demonstrated that the wave function of a single photon can exhibit superoscillatory behaviour upon transmission through an appropriately designed mask [34].
Initially, superoscillatory focusing and imaging technologies were developed using binary zone plates: masks comprised of a complex and elaborate structure of concentric rings fabricated from a thin metal film [35, 36]. Later, it was found that binary superoscillatory lenses can generate optical needles, a class of superoscillatory field localizations resembling a needle of a subdiffraction diameter that extend for tens of wavelengths along the axial direction [36–38]. Such lenses have been explored for high-density data storage applications [39, 40]. Dielectric and metallic superoscillatory lenses for the visible and infrared parts of the spectrum have since been manufactured on silicon wafers, silica substrates and optical fiber tips. Focusing in such lenses has been achieved in both achromatic (at two wavelengths) and apochromatic (at three different wavelengths) regimes [41]. Binary masks are robust and may even be fabricated from optically rewritable media such as phase change chalcogenide glass [42, 43]. We shall note that in a very different context Di Francia also theoretically proposed using a phase mask in the pupil plane of a lens to achieve small hot-spots [44].
The mechanism of superoscillatory focusing is now well understood, and is related to the formation of nanoscale vortices and the energy backflow zones pinned to the focal area, where the backflow depletes the area where flow propagates in the forward direction and thus narrows the focus beyond the conventional diffraction limit [45].
Current state of superoscillatory imaging and challenges ahead
The first practical imaging apparatus using a superoscillatory lens was reported in 2012. It was based on a conventional microscope where the object was illuminated by a binary superoscillatory lens. The drawback of any superoscillatory lens is that the hotspots are surrounded by sidebands (the halo). In imaging applications, the role of such sidebands can be suppressed by using a confocal technique: the image was formed by scanning the object against superoscillatory hot-spot and re-imaging the transmitted light onto a small pinhole. In spite of the limited bandwidth of the optical instrument, far-field images taken with superoscillatory illumination are themselves superoscillatory and hence can reveal fine structural details of the object that are lost in conventional imaging. A resolution of about 1/6 of the wavelength was demonstrated on arrays of randomly placed nanoholes in a metal screen [4]. Other groups followed shortly [46].
However, the practicality of using the sub-wavelength superoscillatory foci to image unlabelled biological samples has never been tested. Would the precise interference of multiple waves forming the superoscillatory focus be robust enough to image complex samples? Would light scattering from the sidebands accompanying the superoscillatory focus be sufficiently supressed to allow for accurate direct imaging without prior knowledge of the sample? Could superoscillatory imaging be combined with a contrast technique that allows study of unlabelled transparent biological samples? And finally, could a practical version of the microscope be developed which allows for video rate imaging? To the triumph of optical superoscillations, such microscopy was recently developed. A high-frame-rate polarisation-contrast microscope for imaging of living unlabelled biological samples with resolution significantly exceeding resolution of the same microscope with conventional illumination has been developed and demonstrated on living biological samples such as mouse bone cells and neurons [47–49]. Figure 3 shows an example of such image. To provide superoscillatory illumination of the object, the laser wavefront was shaped with spatial light-modulators allowing fast and easy reconfiguration of the hotspot and high-speed beam scanning. With this microscope, we demonstrated for the first time simultaneously that superoscillatory imaging: (1) provides greater spatial resolution than microscopy with conventional lenses even in complex biological samples; (2) gives radically more information on the fine details of the object than confocal microscopy; (3) can be combined with polarization contrast imaging for transparent objects (e.g. cells); (4) can be performed simultaneously with epi-fluorescent imaging; (5) is possible at video framerates and at low optical intensities. Thus, the new imaging technology allows non-algorithmic, super-resolution, unlabelled biological imaging at low laser intensities with negligible phototoxicity and will be of interest in numerous biomedical applications.
Figure 3. Superoscillatory imaging of a living unlabelled bone cell (MG63 cell line). False colour is given by polarisation contrast, where brightness represents magnitude of local anisotropy and hue represents local orientation angle. The white ellipse highlights a filopodium, a narrow actin-filled protrusion that the cell uses to sense its environment. Image courtesy of E T F Rogers, S Quraishe, K S Rogers, T A Newman, P J S Smith and N I Zheludev.
Download figure:
Standard image High-resolution imageThe next advances in superoscillatory imaging will be associated with the development of compact and inexpensive superoscillatory lenses that are based on nanoscale-resolution optical transmission and phase retardation masks. Such masks will achieve much better, smaller and more energy-efficient hotspots than binary zone-plate masks that can only control either the intensity or phase profile of the wavefront in a binary fashion, and for which no direct instructive mathematical design algorithm exists. However, no technology currently exists that could deliver transmission and phase retardation masks with the necessary nanoscale finesse.
Recently, a radically new type of metamaterial 'super-lens', a planar array of discrete sub-wavelength metamolecules with individual scattering characteristics that have been engineered to vary spatially was demonstrated, which allows the creation of superoscillatory foci of arbitrary shape and size [50]. The new principle of the far-field metamaterial 'super-lens' is demonstrated by fabricating and characterizing free-space lenses with previously unattainable effective numerical apertures as high as 1.52 and foci as small as 0.33λ in size. This approach will make direct retrofitting of superoscillatory lenses to conventional commercial confocal microscopes possible. Conventional lenses are limited to NA = 1, and approaching this limit requires expensive, complex and bulky lenses. The far-field metamaterial super-lens is a radical step forward.
Concluding remarks on the great future of the technology
Superoscillatory imaging is advancing rapidly, and is currently entering the all-important field of bio-imaging. Further applications, in particular for imaging inside microchips and nanodevices, can be expected. Recent advances have shown that the technology is practical, but further work is required to make high throughput efficient achromatic lenses that will be simple inexpensive 'drop in' replacements for conventional lenses.
Acknowledgments
This work was supported by the Singapore Ministry of Education (Grant MOE2011-T3-1-005), ASTAR QTE Program Grant SERC A1685b0005, and the Engineering and Physical Sciences Research Council UK (Grant EP/G060363/1). The authors would like to thank Guanghui Yuan and Peter J S Smith for fruitful collaborations and discussions.
4. Far-field label-free super-resolution imaging via superoscillation
Fei Qin1 and Minghui Hong2
1Jinan University, Guangzhou, People's Republic of China
2National University of Singapore, Singapore
Status
Optical microscopy has always been an active research area since its invention in the end of the 16th century. Numerous techniques have been proposed in the past century to realize super-resolution imaging in far field, but most of them comes at the price of labelling the samples with fluorescent dyes, which limits their applications. The superoscillation effect provides a new route to achieve label-free super-resolution imaging. Following the mathematical concept of optical superoscillation proposed by Michael Berry, a superoscillatory lens (SOL) optical microscope was experimentally demonstrated soon after. Such lenses rely on the fabricating of a concentric binary amplitude mask with optimized widths and diameters, which can produce a sub-diffractive limit focal spot [4]. Combining with the confocal microscopy technique, super-resolution imaging results have been demonstrated, as shown in figure 4. To further surmount several limitations of this technique to make it more applicable, the development of supercritical lens microscopy closely followed [51–53], which enables imaging of the large scale non-periodic samples at high imaging speeds. As shown in figure 5, the imaging capability of supercritical lens microscopy overwhelms the commercial laser scanning confocal microscope, validating its super-resolution property. Such results are achieved by a totally non-invasive manner, free of any pre-processing to the samples and post-processing to the imaging results.
Figure 4. (a) Configuration of superoscillatory lens and (b) its focal spot distribution. (c), (d) Super-resolution imaging results by a superoscillatory lens microscope. Reprinted by permission from Springer Nature: Nature Materials [4], (2012).
Download figure:
Standard image High-resolution imageFigure 5. (a) Intensity distributions of focal spots for sorts of planar metalens. (b) Schematic of Supercritical lens microscope (SCL MS). (c), (f) Imaging capability of SCL microscopy. [52] John Wiley & Sons. © 2017 WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim.
Download figure:
Standard image High-resolution imageCurrent and future challenges
Although the breakthrough of far-field label-free super-resolution imaging has been made through superoscillation, there are still considerable challenges which need to be addressed, including chromatic dispersion, off-axis aberration, and low energy efficiency.
Chromatic dispersion is an issue that all diffractive optical devices have to confront, which refers to the wavelength dependent focal shift of a lens. A superoscillatory lens is a diffractive optics essentially, and the focusing effect comes from the interference phenomenon of the light components passing through each of transmission belts. The phase of the light components has wavelength dependent values at the focal plane even after propagating over the same distance. The chromatic problem severely hampers its practical applications for superoscillation based optical imaging. Recently, an achromatic SOL has been demonstrated in infrared and visible ranges, through delicately controlling the interference of the propagating waves [54]. This is because the SOL could create an extremely long depth of focus, so the foci of different wavelengths can be partially overlapped. Another strategy to surpass the chromatic phenomenon is to generate multiple discrete focal spots along the optical axis for each wavelength, then some of the focal spots for different wavelengths may be located at the same places. However, these strategies are only temporary and preliminary solutions, which may be very difficult to apply in the imaging process. The chromatic dispersion has still not been fundamentally solved.
Due to the existence of aberration, the imaging process for the SOL microscopy currently is performed through sample scanning. The relatively low scanning speed of the piezo-stage makes it not applicable for some occasions with high speed requirements. In contrast, the beam scanning manner could achieve much a higher speed, but needs an imaging system without off-axis aberration. However, the design and optimization for the SOL are usually based on the on-axis condition, because of the complicated interference condition of the superoscillatory lens. Previous demonstration shows that the lens-like function of the SOL only holds the sub-diffractive limit focusing effect for very small off-axis displacement [36]. The distortion of the focal spot profile greatly increases with the enlarged off-axis distance, especially for high-NA case, which is unacceptable for the imaging process.
So far, almost all the SOL is constructed by binary amplitude or phase type concentric belts with optimized parameters. The binary configuration leads to the multi-order diffraction effect, which makes the energy utilization efficiency of the focal spot at a very low level. In addition, as we can see from figures 4(b) and 5(a), the superoscillation central hot-spot is usually accompanied by a strong sidelobe, which greatly lowers the energy utilization efficiency for the applications. Only less than 10% of the incident energy can be effectively used in the imaging process. Moreover, the halo effect from the strongest first sidelobe is difficult to be completely eliminated by the pinhole in the confocal system, which significantly spoils the imaging contrast and field of view. Pushing the strongest sidelobe away from the central hotspot could be an effective way, as illustrated by the recent works, however the focusing and imaging efficiencies are further decreased [55].
Advances in science and technology to meet challenges
Those above-mentioned issues might partly be resolved through further optimization in the lens design. For example, instead of the binary configuration, constructing the superoscillation lens with a multi-level phase, the sidelobe effect and the energy efficiency might be improved to some extent, but will not get to the root of those problems. Further development of a new approach will be required.
Metasurfaces are the latest advance in light wave manipulation. The phase and amplitude of the light beam could be flexibly modulated by a planar metasurface structure. Applying this advanced strategy into the construction of a superoscillatory lens, those essential problems are possible to solve. An ultrabroadband superoscillatory lens for wavelength spanning across visible and near-infrared spectra has already been proposed by utilizing the plasmonics metasurface [56, 57]. It claims that the ultrabroadband property arises from the nearly dispersionless phase profile of transmitted light from the arrayed nanorectangular apertures with variant orientations. However, the focusing efficiency of this device is still subjected to the ohm loss. Dielectric metasurface metalenses have already successfully shown their potential in the diffraction-limited domain, on the aspects of high energy efficiency, achromatic focusing and imaging, as well as the off-axis aberration correction, and could be the most promising technique to surmount these roadblocks for SOL microscopy. To modify the current design theory and construct the SOL by dielectric metasurface, the settlement of confronting problems for the SOL microscopy can reasonably be expected [58].
Concluding remarks
Superoscillation is the most promising way to realize the far-field label-free super-resolution imaging. Significant progress has been made, and a few of proof-of-principle experiments have already been shown in the past few years. Nevertheless, some challenges still remain to be overcome in terms of dispersion, aberration and efficiency, which are important in the practical applications of optical imaging. These issues could be tackled by the emerging concept of dielectric metasurface. By using the metasurface strategy into the design of the superoscillatory lens, an achromatic, aberration-free and high efficiency superoscillatory lens microscopy is really predictable. It is arguable that the advances in superoscillatory lens microscopy are extensive to rewrite the definition of the diffraction limit in optical textbooks, and also provide a route for the development of next generation confocal microscopy.
Acknowledgments
The author acknowledges the support from the National Natural Science Foundation of China (Grant No. 61705085), the Guangdong Innovative and Entrepreneurial Research Team Program (Grant No. 2016ZT06D081), and the National Research Foundation, Prime Minister's Office, Singapore under its Competitive Research Program (CRP Award No. NRF-CRP10-2012-04).
5. Superoscillatory interference for super-resolution telescope
Xiangang Luo
Chinese Academy of Sciences, People's Republic of China
Status
As one of the most essential characteristics of all kinds of waves, the interference effect plays an important role in both fundamental physics and functional devices. Unfortunately, the interference of light has resulted in some insurmountable barriers like the Abbe-Rayleigh diffraction limit for classic optical imaging instruments. In recent decades, many efforts have been devoted to break the hurdle of traditional interference theory, and one excellent example can be found in the extraordinary Young's interference (EYI) experiments involving the near-field surface plasmon polaritons (SPPs) and metasurface waves (M-waves) [59–61], where the interference period could be shrunk into deep-subwavelength scale. Unlike these subwavelength interferences, superoscillation is another kind of anomalous interference phenomenon which occurs in both the near field and far field. Proper manipulation of the wavelets could make light intensity function oscillate much quicker than its highest Fourier component, leading to a theoretically unlimited resolution in localized space.
In practice, the key point to design a superoscillatory element relies on the optimization and realization of complex light fields, including their phase and amplitude distributions, by special means such as spatial light modulators, diffractive optical elements, and phase-type metasurfaces. Figure 6 illustrates three main kinds of phase modulating techniques. The first one is based on propagation retardation in the vertical direction. Since the effective refractive index and the coupling fields depend on the geometric parameters, one can shape the two dimensional structures for various phase generation. In particular, for the plasmonic nanoslits where the dispersion line is located below the light line [62], the thickness of the device could be reduced to much smaller than the operating wavelength. The second modulation scheme is related to the detoured phase in binary structures including Fresnel zone plate, which is also denoted as amplitude mask [52]. By varying the positions of these transparent slits or apertures, part of the incoming beams are redirected to predefined directions to form a focal spot or holographic pattern. The third route to realize phase modulation relies on another intrinsic property of electromagnetic waves, i.e. the polarization or spin state of photons. By converting circular polarization to its opposite handedness through inhomogeneous anisotropic structures, the outgoing beam will possess an additional phase term known as the geometric or Pancharatnam-Berry phase. For instance, the catenary of equal strength has been demonstrated to be an ideal candidate to realize true linear and broadband phase shift [63].
Figure 6. Three kinds of phase modulation techniques used for superoscillation interference. (a) Nanoslits array and the catenary optical fields. (b) Detoured phase. (c) Geometric phase in a single catenary aperture.
Download figure:
Standard image High-resolution imageCurrent and future challenges
Despite the fact that the current interests in superoscillatory optical imaging are mainly triggered by the demands for super-resolution optical microscopy and data recording, the requirement to build a super-resolution telescope seems to be more urgent. In fact, there are many approaches can be readily exploited for super-resolution microscopy. But few methods could be used to break the resolution limit of optical telescopes.
When used in telescopes, the sub-diffraction-limited superoscillation faces two grand challenges. First, the superoscillation is weak and accompanied with strong side lobes. The smaller the main beam width, the higher the side lobe will be, which poses a great challenge for engineering applications where the Strehl ratio is important. Consequently, it is necessary to make a compromise between the side lobe and gain. Second, traditional SOLs usually exhibit great fragility to the change of light fields due to the delicate wavelength-dependent interference behaviors, especially for the spot size much smaller than the Abbe diffraction limit. Consequently, most SOLs just realize its subdiffraction focusing within a narrowband.
Advances in science and technology to meet challenges
In principle, the narrow bandwidth is an inevitable drawback of traditional phase modulation techniques based on propagation accumulation. In the last decade, some innovative techniques have been proposed to overcome it. Perhaps the most ingenious way may be the utilization of photonic spin–orbit interaction in structures like rotated nano-antennas/apertures and optical catenaries [63–65]. Compared to discrete subwavelength structures, the continuous metasurface enabled by catenary optics shows great improvement of diffraction efficiency and operating bandwidth, and thus is a promising candidate to meet the grand challenges stated above.
In the superoscillatory telescope, the dispersionless property of geometric phase was utilized to construct the phase profile required for superoscillatory imaging [65]. Unlike common phase retardation mechanisms, the geometric phase of these rotated apertures is nearly independent of the wavelength, and the diffraction efficiency is maintained a constant over the entire frequency band. However, a constant phase gradient means a varying propagating direction at different wavelengths, which leads to a strong chromatic change of the focal length. Thus far, many efforts have been paid to realize achromatic flat lens. Besides utilizing space or polarization multiplexing to focus several wavelengths to the same point [66], one could take advantages of the dispersion of the resonant structures and compensate dispersion induced by diffraction [62, 64]. These achromatic lens (either flat or not) can be combined with the geometric phase to realize true achromatic SOLs. As demonstrated in a more recent work [67], achromatic superoscillatory imaging was realized by combining a geometric metasurface filter with an achromatic lens. Figure 7(a) illustrates the experimental setup of the system. Firstly, the point spread function (PSF) is measured by using a 20 μm size transparent circular hole on an opaque screen. For the case without the metasurface filters, the PSF at CCD plane is an Airy spot with a full width of 82.8 μm, as shown in figure 7(c). As the filter group is inserted in the optical system, the PSF in figure 7(d) exhibits an obvious superoscillation pattern with a much smaller bright central spot surrounded by a wide ring. The superoscillation central spot size is about 51.75 μm, being 0.625 times of the Airy spot and slightly larger than the design (0.6).
Figure 7. Achromatic superoscillation under white light illumination. (a) Experimental setup. AL: achromatic lens. LP: linear polarizer. (b) Metasurface filter based on rotated gratings. (c), (d) Normal and superoscillatory images of a hole. (e) Catenary optics for Bessel lens. The blue curve is a schematic of the phase distribution. (a)–(d) [67] John Wiley & Sons. © 2017 WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim. (e) Reprinted by permission from Macmillan Publishers Ltd: Scientific Advances [63], Copyright (2015).
Download figure:
Standard image High-resolution imageAnother concept related to SOLs is the Bessel lens whose phase is composed of a radial linear function and a parabolic function. As depicted in figure 7(e), such a lens could be constructed using dielectric catenaries with simultaneously high transmission coefficient and broadband response [63]. Similar to the supercritical lens [52], such designs may ensure a better compromise between the side lobe and resolution.
Concluding remarks
Superoscillation is an exciting manifestation of the extraordinary interference of light, which in turn provides the key to break the fundamental limit of far-field imaging resolution in Abbe's interference theory. The future development of superoscillation needs finer and broadband phase modulation based on various fantastic structures like the nanoslits and optical catenaries. Although evanescent waves do not exist in the far field, the interaction between low and high spatial optical components mediated by subwavelength structures is crucial to control the phase and amplitude at a scale below the diffraction limit, which forms one essential ingredient for engineering optics 2.0 [60].
Acknowledgments
This work was partly sponsored by the National Basic Research (973) Program of China under Grant No. 2013CBA01700.
6. The simplest realization of superoscillation and its cross-disciplinary implementations
Roei Remez and Ady Arie
Tel Aviv University, Israel
Status
The topic of superoscillation gained attention following a paper by Berry [2], who presented few mathematical expressions for functions that oscillate faster than their highest Fourier component. However, probably the simplest function that contains a superoscillation is the square of a shifted cosine [68] (see figure 8(a)):
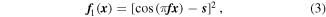
where  The highest frequency at the Fourier transform of this function is
The highest frequency at the Fourier transform of this function is  However, around
However, around  , this function contains an oscillation which has the following width:
, this function contains an oscillation which has the following width:
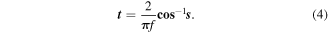
Importantly, the width of the oscillation  can be arbitrarily small by taking
can be arbitrarily small by taking  to be closer to 1, while the highest Fourier component
to be closer to 1, while the highest Fourier component  remains unchanged. The concept here is simple: the shifted cosine function intersects the zero line in two points which are spaced a distance
remains unchanged. The concept here is simple: the shifted cosine function intersects the zero line in two points which are spaced a distance  apart; a distance that is easily controllable by changing the shift
apart; a distance that is easily controllable by changing the shift  The squaring of the function does not change the zero nodes, but makes all the values positive, therefore creating an oscillation. We note that the same principle can be used to increase the number of (super) oscillations, simply by shifting the function by half of the amplitude of the oscillation and squaring again:
The squaring of the function does not change the zero nodes, but makes all the values positive, therefore creating an oscillation. We note that the same principle can be used to increase the number of (super) oscillations, simply by shifting the function by half of the amplitude of the oscillation and squaring again:

In each increasing order  the maximum Fourier component of
the maximum Fourier component of  doubles, however the width of the superoscillations also decreases by factor of 2 or more.
doubles, however the width of the superoscillations also decreases by factor of 2 or more.
Figure 8. (a) (Left) The shifted cosine function (dashed black) and its square value (solid red, equation (3)), showing super oscillation. (Right) Zoom in on the superoscillating region (solid red), in comparison to the fastest sine wave of the function (dashed blue). (b) A standard periodically modulated crystal (top) and a superoscillating nonlinear crystal (bottom) and their corresponding spectral response function. The superoscillating crystal can have arbitrarily narrow central lobe, allowing high-precision filtering.
Download figure:
Standard image High-resolution imageHere, we show four implementations of this simple function and its 2D manifestation, which has the same principle but is written in terms of Bessel functions [69].
Nonlinear frequency conversion
Nonlinear crystals are used to convert a laser beam into a beam with a different wavelength. One of the methods to achieve high efficiency in the conversion is to periodically modulate the sign of the nonlinear coefficient along the propagation of the beam, a process known as quasi-phase matching. The spectral width of the converted beam in this case is inversely proportional to the crystal length. In fact, there is a Fourier transform relation between the spectral width of the converted beam and the shape of the nonlinear coefficient (which is zero outsize the crystal) [70]. Therefore, a longer crystal is needed for a narrow frequency response. Unfortunately, longer crystals are more expensive, consume a larger physical size and moreover, the maximum length of most crystals is limited to a few centimeters at most.
However, decoding the Fourier transform of the superoscillating function  in the modulation pattern of the nonlinear crystal allows for a frequency response, which is a super oscillating function (see figure 8(b)) [68], while the function remains band limited in the spatial (crystal length) coordinates. This means that the efficiency response has two zero nodes placed arbitrarily close to one another, and therefore allows for filtering of two arbitrarily close wavelengths, while transferring the central wavelength. Experimentally, we have demonstrated it by modulating the nonlinear coefficient of a KTiOPO4 nonlinear crystal, obtaining a spectral response that is narrower by 39% and 69% compared to the side lobes and main lobe of the sinc function response of a standard frequency doubling crystal with the same length.
in the modulation pattern of the nonlinear crystal allows for a frequency response, which is a super oscillating function (see figure 8(b)) [68], while the function remains band limited in the spatial (crystal length) coordinates. This means that the efficiency response has two zero nodes placed arbitrarily close to one another, and therefore allows for filtering of two arbitrarily close wavelengths, while transferring the central wavelength. Experimentally, we have demonstrated it by modulating the nonlinear coefficient of a KTiOPO4 nonlinear crystal, obtaining a spectral response that is narrower by 39% and 69% compared to the side lobes and main lobe of the sinc function response of a standard frequency doubling crystal with the same length.
Superoscillating electron wavefunction
The typical de-Broglie wavelength of the electron in a transmission electron microscope is only 2 picometer, about 5 orders of magnitude smaller than that of visible lightwave. Nevertheless, a quantum treatment of free-electron paraxial beam shows that it follows the same diffraction laws as light. Therefore, the radius of the smallest electron spot achievable using a magnetic lens with converging semi-angle  is
is  where
where  and
and  is the de-Broglie wavelength of the electron [71]. This is a result of the Fourier relation between the aperture of the lens and the spot shape at its focal plane.
is the de-Broglie wavelength of the electron [71]. This is a result of the Fourier relation between the aperture of the lens and the spot shape at its focal plane.
Using holographic methods to design an amplitude or phase masks [72], the aperture function of the lens can be decoded with the Fourier transform of a superoscillating probe. Then, placing such a hologram next to a magnetic lens will create electron probes with central hotspot having arbitrarily small width [73] (see figure 9(a)). Experimentally, we have generated a superoscillating beam having a central spot with a radius of 106 pm. Furthermore, by simple modification of the hologram, we generated a superoscillating vortex hotspot that carries orbital angular momentum.
Figure 9. (a) Electron wavefunction showing a hotspot smaller than the diffraction limit, created by placing a holographic mask close to the magnetic lens. Reprinted figure with permission from [73], Copyright (2017) by the American Physical Society. (b) The same holography concept creates a hotspot in a light beam, which is used for highly precise particle trapping.
Download figure:
Standard image High-resolution imageParticle trapping
The same concept described above can be used for high precision particle trapping and manipulation at the superoscillating hotspot of an optical light beam [74]. It is well known that light beam can apply a gradient force that will trap micro-particles. In the case of a superoscillating beam, the narrower central feature can provide a larger gradient force, with respect to the wider, diffraction limited Gaussian beam with the same peak intensity (figure 9(b)). The leads to improved localization of the trapped particle and to stiffer trap when the superoscillating beam is used. Another advantage is that the sidelobes that surround the central hotspot do not disturb the trapping of the particle at the hotspot, since their contribution to the force at the particle location is negligible.
As in the case of electron beam, simple modification of the hologram enables us to structure the sub-diffraction hotspot of the superoscillating light beam. Specifically, we utilized Hermite–Gaussian functions to generate superoscillating beam with a multiple number of hotspot, thus enabling us to trap multiple particles. We also used Laguerre–Gaussian functions to generate vortex superoscillating beams that carry orbital angular momentum, and utilized them to rotate the trapped particles clockwise or anti-clockwise.
Ultrafast optics
The shifted cosine function of equation (3) can also be used in the time domain to generate light pulses with features that are shorter than the temporal width of transform limited pulses [75]. This can be done using a pulse shaper, by adding a  phase shift to central part of the pulse spectrum. Furthermore, as in the cases discussed above, the superoscillating pulse can be structured. More details are provided in the section of this Roadmap (section 9), entitled 'Applications of superoscillations in ultrafast optics', by Eliezer and Bahabad.
phase shift to central part of the pulse spectrum. Furthermore, as in the cases discussed above, the superoscillating pulse can be structured. More details are provided in the section of this Roadmap (section 9), entitled 'Applications of superoscillations in ultrafast optics', by Eliezer and Bahabad.
Current and future challenges
As we have shown here, a very simple function is sufficient in order to obtain arbitrary fast local oscillations that locally exceed the bandwidth limit. Moreover, these local oscillations can be structured, hence multiple hot spots, or a vortex hot spot can be obtained. However, as the local superoscillations become faster, their amplitude decreases, and, moreover, the sidelobes that surround the hotspot region become larger. These unwanted effects are not unique to the simple function we are using, and in fact occur in all the superoscillating functions. A major challenge, which is shared by many potential applications of superoscillation, is how to benefit from the local increase in the frequency, while avoiding the unwanted effect of the strong sidebands. One possibility is to identify applications in which the local features of the function are those that play the key role. An example we showed above is that of particle trapping, where the local gradient force of the superoscillating hotspot governs the trapping mechanism. However, there are other applications in which the sidebands do play an unwanted role. One important example is scanning probe microscopy with a superoscillating beam. Here, the challenge is that scattering from the strong sidelobes adjacent to the main superoscillating lobe. When scanning with the superoscillating probe, scattering from these sidelobes create strong artifacts in the image. While pushing the sidelobe away from the central lobe is mathematically possible, the resulting functions have extremely high intensity at the sidelobes, which makes the superoscillation area highly sensitive to noise and manufacturing errors of the generating holograms.
Advances in science and technology to meet challenges
On the theoretical front, it is required to study superoscillating functions in which the strong sidelobes are located far away from the central, high frequency regime, as well as functions that contain an arbitrary number of hotspots. The tradeoffs in terms of efficiency and the span of the superoscillation region with respect to the entire span of the function should be understood and quantified [76].
Concluding remarks
The advantage of the function presented here is in its simplicity, which allows for relatively easy implementation of the superoscillation concept to different disciplines. Here, we discussed its implementation in nonlinear optics, electron microscopy, particle manipulation and ultrafast optics The inherent limitations are the decrease of efficiency when the oscillations becomes narrower ( closer to 1) and the large sidelobes that accompany the superoscillation region. Future research should concentrate on strategies and applications that can benefit from the fast oscillating region, and avoid the unwanted contributions of the sidelobes.
closer to 1) and the large sidelobes that accompany the superoscillation region. Future research should concentrate on strategies and applications that can benefit from the fast oscillating region, and avoid the unwanted contributions of the sidelobes.
Acknowledgments
This work was supported by Deutsch-Israelische Projektkooperation (DIP), and by the Israeli Science Foundation, Grant No. 1310/13.
7. Superoscillations and optical beam shifts
Jörg B Götte1, 2 and Mark R Dennis3
1University of Glasgow, United Kingdom
2Nanjing University, People's Republic of China
3University of Birmingham, United Kingdom
Status
In the widest sense, the concept of beam shifts describes all deviations from the laws of geometrical optics for reflection and transmission. In particular, they refer to polarisation dependent, spatial and angular shifts either in the plane of incidence, the Goos-Hänchen shift, or transverse to it, the Imbert-Fedorov shift [77] (see figure 10). They come about because the collective behaviour of plane waves bundled into an optical light beam is altered by the presence of an interface or constrained by the transversality condition [78].
Figure 10. Schematic of a beam shift for a beam with an embedded superoscillatory region (optical vortex). The Goos-Hänchen (GF) and Imbert-Fedorov (IF) shifts are widely exaggerated for clarity. Beam shifts affect the position, propagation angle, profile of the beam envelope and shape of the superoscillatory region. In particular, the dark core containing the superoscillatory region may shift differently to the beam centroid. Without weak value amplification, spatial beam shifts are of the order of the wavelength of the light, to which they are proportional.
Download figure:
Standard image High-resolution imageRegions of superoscillatory behaviour were discovered at an early stage of the research on optical beam shifts, when in 1950 Wolter published a study of the details of the optical energy flow for total internal reflection, by considering the displacement of a fringe (nodal line) formed from the minimal interference of two plane waves [79]. Wolter also noted the presence of a circulating wave in the superposition of incident and reflected fields, which we would identify today as an optical vortex. With its emphasis on the behaviour of nodal structures, Wolter's work anticipates the modern notion of superoscillations (see section 1).
Wolter's assertion is still relevant today for a number of different reasons. Firstly, regions of superoscillation and optical backflow, as well as polarization singularities, have recently been found in a variety of reflection and refraction settings, extending Wolter's approach to transverse and angular beam shifts and partial reflection [80]. Secondly, on a fundamental level, there exists a formal analogy between beam shifts for light beams with polarization selection and filtering and quantum weak measurements based on an operator description [81]. This analogy has been exploited in the precision metrology of optical beam shifts to enhance them by orders of magnitude [82] giving rise to observed shifts well outside the spectrum of the associated operators; a signature of superoscillation. Lastly, optical beam shifts for light beams with embedded optical vortices, and hence regions of superoscillations, have proven to be a particularly interesting case in this research area, as they inherently combine spatial and angular shifts in the longitudinal and transverse direction in a vortex induced beam shift [83]. They highlight the difference between shifts of the singularities and the envelope to the light beam [84] and even provide a testing ground for the depth of the analogy between beam shifts and optical vortices [80].
Current opportunities and challenges
The intricacies of a vortex induced beam shift in particular offer a number of interesting challenges for optical precision metrology. Wolter's approach to use destructive interference to mark changes in the light beam shows that structured light is a good probe for Goos-Hänchen and Imbert-Fedorov shifts [80]. Transferring his idea from two plane waves to light beams suggests that the shift of the nodal line transverse to the plane of incidence in a Hermite-Gaussian HG10 beam would probe the Goos-Hänchen shift, while a suitably polarised HG01 with an orthogonally orientated nodal line would be sensitive to the Imbert-Fedorov shift (see figure 11). This serves as an illustrative explanation as to why vortex beams are of particular interest in the study of optical beam shifts: a complex superposition of a HG10 and HG01 produces a first order Laguerre–Gaussian beam, with a superoscillatory region of destructive interference at its centre. Such a superposition is therefore able to probe beam shifts in both directions, while the complex character combines spatial and angular shifts, which are associated with the real and angular part of the corresponding operators [81, 83].
Figure 11. Differently structured light probes different relative shifts between the centroid and internal structure, e.g. a nodal line. Upon reflection (or refraction), the nodal line of a HG10 beam is sensitive to a relative Goos-Hänchen (GH) shift, whereas a relative Imbert-Fedorov (IF) shift can be measured using the nodal line of a HG01 beam. This explains why a vortex beam, as a complex superposition of these two beams, offers sensitivity in both directions.
Download figure:
Standard image High-resolution imageBecause optical beam shifts are sensitive to the refractive index, they can generally be used to probe optical interfaces. A challenge for measurements lies in isolating the shifts from other effects affecting the beam stability and the lack of an absolute reference point. This makes it often necessary to use differential measurements, for example by quickly switching between different polarizations. Because the dark vortex is in general shifted differently to the bright background of the beam envelope [81], using a superoscillatory region embedded in a light beam overcomes some of these challenges and forms the underlying principle of a vortex microscope [85].
A vortex microscope's sensitivity can be enhanced by using optical vortices of higher order, as the vortex induced shift of the beam envelope scales with the order of the embedded vortex [83] (an enhancement scheme based on the analogy to weak measurements). As a superoscillation-like phenomenon, the higher-order vortex induced shift generates increasingly larger displacements than the fundamental beam shifts. A drawback of using high-order vortex beams is that they are unstable under perturbation, and even a simple interaction, such as reflection, leads to splitting of a higher order vortex into a constellation of vortices [84]. However, this splitting can be determined and accounted for, and potentially might be used a probe in its own right. A disruption to a low-intensity superoscillatory structure would similarly occur on oblique reflection or refraction.
In short, the sensitivity of superoscillatory regions to perturbation provides a new method of optical precision metrology, but the general principle that reflection, transmission and scattering typically generate, alter and destroy regions of superoscillation constitutes a formidable challenge which requires both a comprehensive theoretical understanding and excellent control over light preparation and detection.
Future developments
The framework of beam shifts is very general. Beyond spatial or angular deviations, there are subtle effects concerning circular birefringence or delays in the time domain. Beam shifts are not restricted to optics and can occur for other frequency regions and for particle beams [86]. Recent years have seen the generation of electron, neutron and atom vortex beams, all of which have a region of darkness at the centre along the beam axis. All the necessary components to explore the connection between beam shifts and superoscillatory regions in particle beams are therefore in place (see section 6), and it will be interesting to see how the framework of beam shifts can be transferred to particle beams. Of course, the implementation of interfaces will differ from case to case; beam shifts only require an interaction which affects constituent parts of a beam differently. It is likely that because of the small wavelength of particle beams, beam propagation effects play an even more prominent role [82] for particle beam shifts than for light beams.
Electron vortex beams in particular can readily be manipulated with electromagnetic fields, but also neutrons could interact with them via the anomalous magnetic moment. In the latter case, beams shifts are likely to be small, which suggest that amplification schemes based on weak measurements may be needed to measure such shifts. This in turn requires control over the polarization of particle beams, which, given the current interest in vortex beam of fermionic particles, such as electron and neutron, is a topical area of research activity with direct relevance for the development of beam shifts for particle beams.
As particles have mass it is necessary to distinguish between the non-relativistic and relativistic regime in the study of particle vortex beams. For the former, the wavefunction is identical to the paraxial Laguerre–Gaussian beams in the optical regime with a well-defined superoscillatory region at the centre of the beam. For massive relativistic spin ½ particles, free space spin–orbit locking can destroy the vortex at the centre of the beam. Combined with the inevitable vortex splitting on reflection and scattering [84] for particle beams will no doubt reveal interesting new superoscillation-related physics.
Concluding remarks
Starting with the work of Wolter almost 70 years ago, deep and multifaceted connections between superoscillations and beam shifts have been discovered. In optics, this has been explored in both theory and experiment, and is now in the process of being exploited as a technique in precision metrology. There is still much scope for discoveries and we can expect exciting developments in the future, such as applications of weak measurement enhancement and higher order vortex probes. The wavefunction of increasingly more fundamental particles can be shaped into a vortex beam, creating in general a superoscillatory region within the beam, which can be used to characterise the path of the beam or perhaps even scattering events. Applying the framework of beam shifts to these cases may uncover new connections between these fundamental concepts.
Acknowledgments
We would like to thank Konstantin Bliokh and Andrea Aiello for useful comments and we acknowledge funding from the Newton International Fellowship and its alumnus programme. J B G acknowledges funding from the National Key Research and Development Program of China under Contract. No. 2017YFA0303700.
8. An antenna array approach to superoscillations
Alex M H Wong1 and George V Eleftheriades2
1Department of Electronic Engineering, State Key Laboratory of Terahertz and Millimeter Waves, City University of Hong Kong, Hong Kong
2Department of Electrical and Computer Engineering, University of Toronto, Canada
Status
It is widely accepted that initial works on superoscillation took place in the early 1960s in a series of works on bandlimited and time delimited signals, published by Slepian et al at Bell Labs [87]. It was rediscovered around 1990 in a series of works by Aharonov et al in the context of weak values of electron spin in quantum physics (see section 2). This rediscovery initiated studies on the manifestation and application of superoscillations in wide-ranging mathematical and scientific fields (see section 3). In this context, it was understood that ideas pertinent to superoscillations actually surfaced in the 1930s—about a quarter century before the first recognized studies on superoscillations—in the study of superdirective antennas [88, 89].
We first point out that similar mathematical forms describe the radiation from antenna arrays and the fields from the spatial superposition of plane waves. The radiation pattern from an array of  isotropic sources is given by its array factor
isotropic sources is given by its array factor
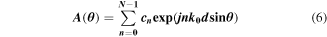
where  is the radiation angle,
is the radiation angle,  is the free-space wavenumber,
is the free-space wavenumber,  is the separation between adjacent antenna elements and
is the separation between adjacent antenna elements and  is the weighted excitation current on the nth antenna. An electric field profile as a superposition of
is the weighted excitation current on the nth antenna. An electric field profile as a superposition of  plane waves can be written as
plane waves can be written as
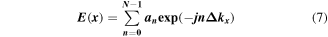
where  is the weighted complex amplitude of the nth plane wave and
is the weighted complex amplitude of the nth plane wave and  is the change in spatial frequency between adjacent plane waves (adjacent in terms of the propagation angle). The transverse spatial frequency is related to the wave propagation angle through
is the change in spatial frequency between adjacent plane waves (adjacent in terms of the propagation angle). The transverse spatial frequency is related to the wave propagation angle through
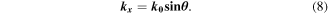
A superdirective antenna is typically built from an array of closely-spaced elements ( ) driven by alternating currents (figure 12(a)). When adjacent elements are driven with opposite phase and a tapered amplitude, an antenna beam of arbitrarily narrow angular width can, in principle, be generated (figure 12(b)), which seemingly violates the angular diffraction limit [88, 89].
) driven by alternating currents (figure 12(a)). When adjacent elements are driven with opposite phase and a tapered amplitude, an antenna beam of arbitrarily narrow angular width can, in principle, be generated (figure 12(b)), which seemingly violates the angular diffraction limit [88, 89].
Figure 12. Superdirectivity versus superoscillation. (a) A set of current excitations to a superdirective antenna array with  plotted with respect to antenna position. (b) The corresponding antenna beam pattern. The shaded area indicates the invisible region. (c) The spectral distribution of several plane waves. (d) The spatial electric field profile formed by their superposition. A superoscillatory subwavelength hotspot is generated.
plotted with respect to antenna position. (b) The corresponding antenna beam pattern. The shaded area indicates the invisible region. (c) The spectral distribution of several plane waves. (d) The spatial electric field profile formed by their superposition. A superoscillatory subwavelength hotspot is generated.
Download figure:
Standard image High-resolution imageAdopting a spatial frequency perspective, one sees that this sub-diffraction angular beamwidth is achieved by hiding most of the waveform's energy in the invisible region (i.e. the region of evanescent waves). Figure 12 compares the operation of a superdirective antenna with that of a spatial domain superoscillation: a superdirective antenna has limited support in the spatial domain (figure 12(a)), but has sharp oscillations in the angular domain, which maps to the spatial frequency domain via (8) (figure 12(b)); a spatial superoscillation waveform has limited bandwidth in the spatial frequency domain (figure 12(c)), but sharp oscillations in the spatial domain (figure 12(d)). Both phenomena achieve unconventionally sharp waveform variations in a region of interest (ROI) at the price of pushing most of the wave's energy outside the ROI. With superdirectivity, most of the wave's energy is kept in the invisible region (near-field) and hence is hidden from the antenna far-field. This leads to a practical difficulty, since the excitation of a very strong near-field often leads to severe mismatch losses and power dissipation from metallic antenna components. On the other hand, with spatial superoscillation, the high-energy region still resides in the visible space, but appears outside the field of view of the imaging system. While its presence may be undesirable, it does not suffer the same sensitivity problems that have heretofore precluded the widespread application of superdirective antennas. Notwithstanding this physical difference, this comparison clarifies that a superdirectivity is achieved by constructing a superoscillation waveform in the spatial frequency ( ) domain.
) domain.
Realizing the strong connection between the concepts of superdirectivity and superoscillation, established antenna design methodologies can be adapted to design superoscillation waveforms, as illustrated in the following cases. Wong et al [89] experimentally demonstrated a subwavelength-focused microwave hotspot ( GHz) at a working distance of five wavelengths—an order of magnitude increased from previous subwavelength focusing devices (figure 13(a)). Wong et al [46] also used a superoscillation filter to build an optical super-microscope (OSM), which performed far-field super-resolution microscopy at 633 nm (figure 13(b)). Unlike previous works, the OSM generated a superoscillating point spread function as opposed to a superoscillating focal spot. This enabled one to image, in real-time, an object within the field of view without any scanning and data post-processing whatsoever, and hence paved way to capturing super-resolution images and videos of moving objects. Other works in this direction included a microscope that featured superoscillating ripples [90] and a formulation for broadband 3D superoscillation microscopy [91]. These varied applications demonstrate the viability of the zero-based antenna design approach to both (i) design superoscillation features and (ii) control the non-superoscillatory high amplitude region outside the ROI.
GHz) at a working distance of five wavelengths—an order of magnitude increased from previous subwavelength focusing devices (figure 13(a)). Wong et al [46] also used a superoscillation filter to build an optical super-microscope (OSM), which performed far-field super-resolution microscopy at 633 nm (figure 13(b)). Unlike previous works, the OSM generated a superoscillating point spread function as opposed to a superoscillating focal spot. This enabled one to image, in real-time, an object within the field of view without any scanning and data post-processing whatsoever, and hence paved way to capturing super-resolution images and videos of moving objects. Other works in this direction included a microscope that featured superoscillating ripples [90] and a formulation for broadband 3D superoscillation microscopy [91]. These varied applications demonstrate the viability of the zero-based antenna design approach to both (i) design superoscillation features and (ii) control the non-superoscillatory high amplitude region outside the ROI.
Figure 13. Examples of antenna-based approach to spatial superoscillation design. (a) 1D subwavelength hotspot in a waveguide. Schematic (left) and the simulated subwavelength focus (right). © IEEE. Reprinted, with permission, from [89]. (b) Experimental measurements using the optical super-microscope (OSM). The OSM's point-spread function (left) and the resolving of two apertures (right: top row = OSM, bottom row = diffraction limit). Reprinted by permission from Springer Nature: Scientific Reports [46], (2013).
Download figure:
Standard image High-resolution imageCurrent and future challenges
The following overviews promising research directions which apply an antenna-based approach to design and synthesize superoscillations. Firstly, while most antenna array methods pertain to the design of 1D antenna arrays, it remains unclear as to what is the optimal way of extending such designs to higher dimensions. As demonstrated in [92], the method of separable functions can indeed be used to generate a higher-order superoscillation function. However, this method causes the amplitude of the non-superoscillatory region to be squared (for 2D) or cubed (for 3D) from the 1D counterpart. In this perspective, it is more energy-efficient to construct the superoscillation waveform with radially symmetric functions, as was done in [46, 91] for 2D and 3D superoscillations, respectively. In these works, radially symmetric superoscillation waveforms are constructed by applying a null matching procedure to a 1D superoscillation waveform constructed from the antenna array design approach. Using this method, the amplitude ratio between the hotspot and the non-superoscillatory region remains by and large unchanged when one extends from the 1D superoscillation waveform into a 2D or 3D counterpart. Notwithstanding, it remains unclear how a similar extension is best accomplished when the desired superoscillation waveform does not have radial symmetry.
Another area worthy of investigation is the application of the antenna-based approach to facilitate the practical construction of extreme superoscillation features, for example, a hotspot with a spot width ten times beyond the diffraction limit. It has been theorized that such waveforms feature a non-superoscillatory region with very high energy [93]. The non-superoscillatory region typically has orders-of-magnitude larger field amplitudes compared to the superoscillatory features. Hence, the generation of such superoscillation features requires systems of exorbitantly high signal-to-noise (SNR) ratios. However, it has been shown that using the antenna-based approach, one can lower the maximum amplitude of the non-superoscillatory region and thereby reduce the required SNR for the construction of superoscillation waveforms [46]. It would be of profound impact to design and construct practical superoscillation waveforms with features markedly improved from the diffraction limit; we think the antenna-based approach has proven itself as a valuable design tool for such desirable extreme waveforms.
A third research direction applies the antenna-based approach to design complex and arbitrary superoscillations. Whilst traditional works on antenna design generate a single radiated beam, ample works exist on designing multiple custom-shaped radiation patterns from antenna arrays in all kinds of geometrical arrangements. For example, satellite antennas often aim to optimize their power efficiencies by tuning their antenna beam shapes to match the geographical contours of a country (e.g. India) or region (e.g. California) which they service. The lessons learned from designing and optimizing these elaborate antenna pattern can be leveraged to help design intricate superoscillation waveforms with widely-varying support in the spectral domain.
Finally, we envision that impactful research can be performed on the use of antennas to synthesize superoscillation waveforms. Antenna arrays and metasurfaces can synthesize electromagnetic waveforms with high-fidelity. Previous works have demonstrated that when deployed in planar formation, antenna arrays can generate superoscillation waveforms in the radiating near-field [89]. An important future direction is to demonstrate the generation of superoscillation waveforms with an antenna array or a metasurface deployed in a 3D formation. Successful efforts in this area can lead to the experimental generation of 3D sub-wavelength hotspots [91] and superoscillation features without the high-energy region [94]. These systems would be very useful for 3D sub-diffraction medical imaging and RF hyperthermia therapy.
Concluding remarks
In this article, we have reviewed the strong connection between superoscillations and superdirective antennas. This strong connection can be leveraged to design superoscillations using established antenna design methodologies. We have reviewed examples of antenna-based designs for generating superoscillation hotspots, with applications in electromagnetic-wave focusing, super-resolution imaging and radar (depth) imaging. Promising research directions include the design of (i) efficient 2D and 3D superoscillations, (ii) practical superoscillations with deep subwavelength features and (iii) complex and arbitrary superoscillations, as well as (iv) their practical implementation, particularly in a 3D environment. The antenna-based approach leverages the vast resource in antenna design and application. This makes it a powerful tool for designing and synthesizing superoscillation waveforms.
9. Applications of superoscillations in ultrafast optics
Yaniv Eliezer and Alon Bahabad
Tel-Aviv University, Israel
Status
To date, most of the applications of superoscillations in optics were realized in the spatial domain, applicable to optical microscopy, while generating small volumes of focused light [46, 95–97]. However, it is only recently that superoscillations have started to emerge in the optical temporal domain and more specifically in the realm of ultrafast optics where the available bandwidth is wide enough to allow synthesis of superoscillating waveforms. The first work in this field suggested to modulate the carrier frequency of a light field by superposing together several monochromatic fields whose frequencies are harmonics of a given fundamental frequency [98]. Although each field by itself is monochromatic with an infinitesimal bandwidth, the superposition of the waves spans a significant bandwidth, and so formally such a signal is in the realm of ultrafast optics. Such a superoscillatory field carries local oscillations whose local frequency exceeds the frequency of the fastest mode in the superposition. If this field is propagated through a medium while the superoscillatory local frequency matches a resonance of the medium, it can still propagate with hardly any absorption of the superoscillation, realizing 'super-transmission' [98]. This corresponds to the spatial case in which a local frequency in a beam of light matches the frequency of an evanescent wave, but can still be carried to the far field [28]. In the temporal domain, dispersion in the medium dephases the signal and eventually destroys the superoscillation. However, the superoscillation can revive, where the dynamics of revivals depend on the number of modes comprising the superoscillation and the dispersion properties of the medium [98].
Modulating the carrier frequency of a light field is a major challenge requiring the generation of different harmonic orders of a given fundamental and then controlling the amplitude and relative phase of these harmonics. It is much easier to modulate the envelope of a given pulse—that is, to modify a phase locked spectrum around a single harmonic. Indeed, recently the first experimental demonstrations of synthesizing a superoscillating optical pulse envelope were carried out by using a standard pulse-shaping technique in which the spectral amplitude and phase of a pulse envelope are directly modified. Two different approaches were used for this purpose—the first was just a straightforward adaptation of the real part of the canonical superoscillatory function [28]: ![${\boldsymbol{f}}({\boldsymbol{t}})={\left[{\bf{c}}{\bf{o}}{\bf{s}}({\boldsymbol{t}})+{\boldsymbol{ia}}{\bf{s}}{\bf{i}}{\bf{n}}({\boldsymbol{t}})\right]}^{{\boldsymbol{N}}}$](https://content.cld.iop.org/journals/2040-8986/21/5/053002/revision1/joptab0191ieqn56.gif) with
with  for the functional form of the envelope of the pulse, where each Fourier mode in the expansion of
for the functional form of the envelope of the pulse, where each Fourier mode in the expansion of  is translated to a beat mode overlaid on the envelope [99]. The benefit of this method is that the superoscillatory region can be designed analytically. The result of using this method to synthesize a superoscillating pulse is shown in the bottom panel of figure 14. The second approach for synthesizing a superoscillatory optical envelope used a windowed spectral phase-shift transformation [75]. This method is general in the sense that it can be applied to pulses in almost any initial functional form, but it does not provide for a simple analytical characterization of the superoscillation.
is translated to a beat mode overlaid on the envelope [99]. The benefit of this method is that the superoscillatory region can be designed analytically. The result of using this method to synthesize a superoscillating pulse is shown in the bottom panel of figure 14. The second approach for synthesizing a superoscillatory optical envelope used a windowed spectral phase-shift transformation [75]. This method is general in the sense that it can be applied to pulses in almost any initial functional form, but it does not provide for a simple analytical characterization of the superoscillation.
Figure 14. Pulse synthesis: theoretical (dashed lines) and experimental synthesis (continuous line) of different temporal ultrafast waveforms sharing the same bandwidth. Left column: frequency domain. Right column: temporal domain. From top to bottom: a Gaussian, a Sinc, a single beat (temporal double slit) and a superoscillating optical beat. Reprinted figure with permission from [99], Copyright (2017) by the American Physical Society.
Download figure:
Standard image High-resolution imageMost importantly, the synthesis of superoscillating pulses allowed us to experimentally demonstrate temporal super-resolution detection in the time domain [99]. This demonstration relied on an analogy with microscopy. In microscopy, the image of an object is the result of convolution of the point-spread-function of the system and the function describing the object. Similarly, in the time domain, the temporal image was realized as the cross-correlation of a test (object) signal comprised of two close-by consecutive pulses with a synthesized signal playing the role of a temporal point spread function. It was verified that when the synthesized probe signal was superoscillatory, it could better resolve the existence of a double-pulse test signal than when the probe signal was a transform limited Gaussian with the same bandwidth (see figure 15). It is noteworthy that in the time domain there are, at the moment, no competing super-resolution schemes which do not involve post-processing. Further, temporal optical superoscillations have the potential to impact many activities relying on femtosecond light sources—such as spectroscopy, nonlinear optics and metrology.
Figure 15. Demonstration of temporal super resolution. A series of test signals comprised of a pair of time-delayed Gaussian pulses with different delays (top row) are cross-correlated with one of two probing signals having the same bandwidth (left column): a superoscillating beat and a Gaussian pulse. The theoretically calculated (dashed lines) and experimentally measured (continuous lines) cross-correlation are shown in the middle. A minimum in the middle of the cross-correlation attest to the existence of two distinct temporal events. The Gaussian only resolves case III, while the superoscillating beat resolves both cases II and III. Reprinted figure with permission from [99], Copyright (2017) by the American Physical Society.
Download figure:
Standard image High-resolution imageCurrent and future challenges
In order to advance the use of superoscillations in ultrafast optics, better pulse synthesis methods are required. The superoscillating beat that was demonstrated in [99] used only two modes for its construction. The advance in the usage of superoscillations for imaging came when many modes were combined together to create a superoscillatory region which was well isolated from the large side lobes accompanying such signals. We can similarly expect that advances would follow in the time domain once temporal optical waveform synthesis would be on par with its spatial counterpart. However, it is more difficult to generate complex optical temporal waveforms than spatial waveforms due to two main reasons. First, pulse shapers suffer from aberrations, which are not simple to compensate for. Second, pulse characterization is much more involved than beam characterization as it requires complicated setups involving nonlinear interactions. When considering synthesizing the carrier of the field instead of its envelope, matters gets much worse as the shaping and analysis need to be performed over an enormous bandwidth.
Another major future challenge lies in finding ways for utilizing temporal superoscillations. As superoscillations are a local interference phenomenon, there are two ways in which they can be utilized. The first is to use them to measure or manipulate temporal events which are short enough in time that they will not interact with the slow intense side lobes of the superoscillatory signal. The second way is to find and employ some gating mechanisms that would be susceptible to the fast local dynamics of the superoscillation [100]. Such a gating mechanism in effect would project, so to speak, the superoscillation unto an actual Fourier component and it would no longer be an interference of other Fourier components. Such a gating can be the result of some dephasing mechanism acting on time scales similar or shorter than the duration of the superoscillation. A gating can also be realized as some externally applied nonlinear interaction.
Advances in science and technology to meet challenges
In recent years, there have been significant advances in the ability to synthesize the carrier of light waves based on nonlinear optical systems [101]. Such methods can help us realize experimentally waveforms with a superoscillating carrier. For superoscillating envelope synthesis, there is a need for higher spectral resolution pulse shapers with better treatment of ailing aberrations. Such an advance can either be gained by modifying the applied modulation functions to compensate for the aberrations, or by looking for compensating optical hardware. Additionally, better understanding through analytical and numerical methods is required for the ways in which local superoscillations can be utilized and/or 'projected' to a Fourier component so they can efficiently interact with different media. Initial steps in such directions have already started [100, 102].
Concluding remarks
The use of superoscillations in ultrafast optics has only seen its first steps. There is still much to explore and to gain in this field, especially if superoscillations would be used to measure rapid spectroscopic transients. The are several possible interesting directions in which this field can progress; for example, by connecting superoscillations to other unique temporal optical phenomena such as fast and slow light. Additionally, the complementary phenomenon of suboscillations [103], where a signal can oscillate locally at a rate below its slowest Fourier components, might be utilized to produce THz local oscillations by interfering optical fields.
10. Superoscillation focusing of cylindrically polarized light
Gang Chen, Zhongquan Wen and Gaofeng Liang
Chongqing University, People's Republic of China
Status
The earliest recorded use of lenses can be traced back to the ancient Romans. Conventional simple lenses have two curved surfaces of different curvatures, which can be positive, negative, or infinite. The properties of such lenses are determined by the refractive indexes of its materials and the curvature of the two surfaces. One major function of a lens is to focus light to form a localized hot spot with high optical intensity, and tight focusing of light waves is of a major interest in a variety of applications, including microcopy, materials processing, optical micro-machining, optical storage, and optical manipulation. The conventional way to generate tight focal spots is to utilize a high-numerical-aperture objective lens to focus light in combination with optical filters, π-phase shift plates, and other components. Polarization plays an important role in the tight focusing of light. Recently, there has been increasing interest in cylindrical vector (CV) beams because of their excellent focusing properties. CV beams exhibit a cylindrical symmetry in their polarization distribution on the beam cross-sections. CV beams can be treated as a linear superposition of radially and azimuthally polarized beams. It is well known that radially polarized light can be focused into longitudinally polarized spots of sub-diffraction size [104], and the superposition of radially and azimuthally polarized waves allows flexible shaping of the three-dimensional (3D) profile of the optical field around the focus [105]. However, due to the diffraction property of conventional lenses, it is challenging to further reduce the focal spot size. In addition, conventional optics are bulky, and have difficulty in optically aligning CV beams, especially in the case in which an additional filter mask is required. Superoscillation is a phenomenon in which a local oscillation can be faster than the highest global Fourier component. Theoretically, superoscillation enables the creation of arbitrary small optical structures in propagating waves [33], and provides an alternative way to generate sub-diffraction and sub-wavelength features in far-field optical fields. The past few decades have seen growing interest in developing a variety of optical devices based on the concept of superoscillation. Most superoscillation focusing devices are designed in the binary-amplitude and binary-phase planar mask configuration for ease of fabrication. Their design critically depends on vectorial diffraction methods and optimization approaches, such as particle swarm and genetic algorithms. Figure 16(a) illustrates focusing of CV beam by a binary mask. For cylindrically polarized light, 2D sub-diffraction azimuthally polarized hollow spots and longitudinal polarized focal spots have been experimentally demonstrated. Figure 16(b) depicts the experimental results of a longitudinal polarized optical needle generated by focusing radially polarized beam with a binary-phase mask. As shown in figure 16(c), a 3D hollow spot of sub-diffraction transverse size was also realized with a cylindrically polarized wave by optimizing the ratio between the radial and azimuthal polarization components. Based on the concept of normalized angular spectrum compression (NASC), as shown in figure 16(d), superoscillation quasi-non-diffraction (QND) beams can be generated with azimuthal polarization and a smallest transverse size of 0.34λ by carefully designed binary phase planar lenses [106]. This concept also enables executing a rapid design of a single lens with an ultra-long working distance for generation of sub-diffraction QND beams for multiple types of polarization, such as circular, azimuthal, and radial polarizations, which is critical for practical applications in super-resolution microscopy [107] and high-density optical storage [108].
Current and future challenges
The design approaches for a superoscillation focusing lens for cylindrically polarized light mainly rely on optimization algorithms, which give a limited physical picture of the nature of superoscillations. Although the feature size of superoscillation optical fields has no theoretical limit, a trade-off has to be made among the field of view, efficiency, sidelobe intensity and spot size. Using band-limited circular prolate spheroidal wave functions to construct the scalar superoscillation wave can reduce the spot size down to approximately λ/4 [109]; however, the same approach is not directly applicable to waves with cylindrical polarization. It is still a challenge to design a superoscillation lens to achieve feature sizes of approximately or below λ/4 for cylindrically polarized light, especially for QND beams. In the generation of a superoscillation QND CV beam, the NASC approach offers no flexible control of the transverse size within the beam-propagation distance, while the existing controllable design methods are extremely time-consuming, even for a propagation distance of a few wavelengths.
Since the phase distribution plays a key role in reducing the spatial frequency of complex optical fields [110], the manipulation of phase is of great importance in superoscillation focusing. Up to now, the experimentally reported focusing planar lenses for cylindrically polarized light have mainly been based on binary amplitude or phase masks. Because the diffraction behavior is quite different for radial and azimuthal components, the independent manipulation of the wavefront of each polarization component is essential for the 3D shaping of a CV beam consisting of hybrid polarizations, which cannot be achieved with commonly employed amplitudes or phase masks. In addition, the precise characterization of a superoscillation CV optical field is still a great challenge due to the polarization-selective response of present testing systems.
Figure 16. (a) Superoscillation focusing of cylindrically polarized light: (b) lingitudinally polarized focus, (c) 3D hollow spot with sub-diffraction transverse size, and (d) azimuthally polarized superoscillation quasi-non-diffraction beam.
Download figure:
Standard image High-resolution imageAll the reported superoscillation and sub-diffraction focusing lenses for cylindrical polarization have been made in the form of either amplitude or phase modulation without any control of wave polarization (see figure 16). Since the symmetrical optical configuration requires extremely precise alignment in generating cylindrically polarized superoscillation focus, particularly when the spot size is much smaller than a wavelength, any slight misalignment will lead to deformation in the intensity profile of the focal spot and destroy the superoscillation features. One possible solution to this problem is the integration of both phase and polarization manipulations in a single lens, which offers independent control of phase and polarization of light, and hence the alignment is automatically guaranteed in the lens design and fabrication.
Achromatic performance is a challenging issue in superoscillation focusing, and it was not until very recently that such lenses with sub-wavelength focusing ability were demonstrated with binary dielectric and metallic planar lenses [111]. However, such lenses are only designed for several working wavelengths, and the contribution to the focus comes from different parts of the lens at different wavelengths, greatly reducing efficiency. Moreover, the superoscillation features only consist of the transverse component of the total optical field.
Broadband performance is not only necessary for achromatic operation, but it is indispensable in the generation of 3D superoscillation features. Current demonstrated superoscillation features of CV light are only restricted to the 2D plane for a single wavelength, because 3D shaping requires superposition of light waves with broadband wave vectors, which are necessary to span a 3D spatial frequency domain [91].
Advances in science and technology to meet challenges
Full control of light waves, including independent manipulation of the phase and polarization, is essential in shaping light waves with cylindrical polarization. Recent advances in metasurfaces provide a promising way of efficiently manipulating light waves on the sub-wavelength scale. In particular, all-dielectric metasurfaces offer high-efficiency building blocks for quasi-continuously tuning the light-wave phase profile for broadband operation. In addition, all-dielectric metasurfaces also provide a promising solution for broadband achromatic operation by compensating the chromatic aberration with carefully designed structural dispersion. Metasurfaces also enable continuous tuning of the polarization of transmitted waves for incident waves with circular polarization, which can be done with metallic stripe gratings and glass nano-gratings. In addition, polarization convertors, such as quarter-wave plates, half-wave plates, polarization rotators, and vector wave polarization convertors, have been demonstrated in the form of metasurfaces. Independent manipulation of phase and polarization is also implementable with specially designed birefringent metasurfaces. Hence, metasurfaces offer an irreplaceable way of meeting the challenges in achieving broadband, achromatic, high-efficiency 3D superoscillation shaping of cylindrically polarized light waves.
Concluding remarks
Optical superoscillation has emerged as a hot topic in present optical research, but it is still in its infancy, notwithstanding a variety of theoretical and experimental demonstrations of superoscillation focusing, imaging, and microscopy applications. A wide range of challenges remain to be overcome both theoretically and experimentally. We expect future advances in superoscillation focusing of CV beams that will lead to breakthroughs in far-field super-resolution applications in fields such as microscopy, data storage, materials processing, micro-nano fabrication, and others.
Acknowledgments
The authors acknowledge the financial support of the National Key Basic Research and Development Program of China (Program 973) (2013CBA01700), China National Natural Science Foundation (61575031, 61177093), and Fundamental Research Funds for the Central Universities (106112016CDJXZ238826, 106112016CDJZR125503)
11. Superoscillations in magnetic holography and acoustics
Chenglong Hao and C-W Qiu
National University of Singapore, Singapore
Status
Superoscillation phenomena have triggered curiosity in exploring intrinsic mathematics as well as man-made generation mechanisms for niche applications. Optics is thus far one of the few areas to which intensive effort of the superoscillation research has been dedicated [4, 112, 113]. It was discovered that a superoscillatory lens can break the diffraction and reach the resolution of λ/6 [4]. Superoscillations in optics have opened up possible avenues of application and are actively being pursued for super-resolution imaging [4, 112, 113], high-resolution photography, and ultrafast pulse generations.
Beyond optical realms, other forms of superoscillation and its related concept—the supercritical phenomenon—have been addressed recently, such as magnetization [114] and acoustics. Therefore, it is necessary to cast a holistic outlook for superoscillation and supercritical phenomena.
Current and future challenges
Superoscillations have been widely investigated in optical realms. It is imperative to give clear demonstrations as to how small a focal spot has to be so that it can be considered as a superoscillatory spot. Although both the Rayleigh criterion (RC) and Berry and Denis's method [6] have been used to define the superoscillation, both criteria have their limitations. On one hand, the RC is very rough since superoscillation is involved. On the other hand, Berry and Dennis's suggestion only predicts the superoscillation at the zero-intensity position for some cases. Therefore, it is better to give a definition of optical superoscillation by measuring the phase-changing rate in a certain region.
Although superoscillation could generate an infinitesimal hot spot theoretically, the price needing to be paid is the high energy sidelobes, resulting in very low energy efficiency. Thus, an approach which could achieve enhanced resolution and acceptable sidelobes simultaneously becomes a natural question. The supercritical phenomenon gives the answer. The supercritical applications work in the intermediate zone between Rayleigh limit and superoscillation. Therefore, they gain benefits of superoscillation and avoid the unfavorable high energy sidelobes, which are highly desired for applications requiring enhanced resolution and high energy efficiency, for example, light induced magnetic data storage.
In the era of big data, there exists a growing gap between data generated and limited storage capacity using two-dimensional magnetic storage technologies (e.g. hard disk drive), since they have reached their performance saturation. Three-dimensional (3D) volumetric all-optical magnetic holography has rapidly emerged as a promising roadmap to realizing high-density capacity for its fast magnetization control and sub-wavelength magnetization volume. However, most of the reported light-induced magnetization confronts the problems of impure longitudinal magnetization, diffraction-limited spot, and uncontrollable magnetization reversal. Therefore, new approaches, e.g. supercritical resolved light induced magnetization, are proposed to overcome these challenges.
Lastly, similar to optical focusing, the diffraction limit also sets an ultimate limit for acoustic focusing, which greatly hinders the applications of acoustic imaging and particle manipulation via acoustic forces. Few approaches are available to transcend this limit. Therefore, superoscillation based far-field focusing provides a practical roadmap for super-resolved acoustic applications.
Advances in science and technology to meet challenges
Generally, for the spherical-lens-based optical imaging system, the lateral size of its focal spot is limited by 0.61λ/NA (above the diffraction limit, where NA is numerical aperture), which is well known as the RC mentioned in the previous section. Sub-diffraction focusing is feasible at the cost of the increasing side lobes. For unpolarized incident beams, light with higher spatial frequencies corresponds to a smaller spot. The extreme case is that light with only the maximum spatial frequency can be focused into a hotspot with intensity distribution similar to that of  which is named as the 'maximum-frequency spot', where k = 2π/λ and λ is the wavelength [112]. The first zero point of this zero-order Bessel function gives the superoscillatory criterion, which is 0.38λ/NA. This criterion is shown in figure 17(a), which is a finely distinguished roadmap providing an instructive guide that the cyan area between Rayleigh and superoscillation criterion is the best choice with superresolution and moderate side lobes in the far-field. This region is defined as the supercritical region.
which is named as the 'maximum-frequency spot', where k = 2π/λ and λ is the wavelength [112]. The first zero point of this zero-order Bessel function gives the superoscillatory criterion, which is 0.38λ/NA. This criterion is shown in figure 17(a), which is a finely distinguished roadmap providing an instructive guide that the cyan area between Rayleigh and superoscillation criterion is the best choice with superresolution and moderate side lobes in the far-field. This region is defined as the supercritical region.
Figure 17. (a) Superoscillation criterion; (b) schematic of 3D light-induced-magnetic holography in 4Pi microscopy; (c) schematic and principles of acoustic superoscillation; (d) experimental and simulation results on focal plane. (a) From [114]. © The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. Distributed under a CC BY-NC 4.0. license. (b) [55] John Wiley & Sons. © 2013 WILEY‐VCH GmbH & Co. KGaA, Weinheim.
Download figure:
Standard image High-resolution imageBased on this criterion, an optimization-free superoscillatory lens (SOL) with phase and amplitude masks [112], a SOL using nanosieves with circular symmetry, a supercritical lens with ultra-long working distances [52], and a 3D supercritical resolved light-induced-magnetic holography [114] have been proposed and validated experimentally or numerically. Next, we will briefly introduce applications with this criterion with supercritical resolved magnetic holography and acoustic SOL in far field.
Due to the low energy main lobe and high energy sidelobes in superoscillation, it cannot be implemented in applications requiring superresolution and high energy main lobes, such as light induced magnetic holography for data storage. To address the challenges in light induced magnetic data storage, a novel roadmap for all-optical magnetic holography based on the conceptual supercritical design with multi-beam combination in 4π microscopic system was proposed, which is shown in figure 17(b). A 3D deep super-resolved (∼λ3/59, λ = 800 nm) pure-longitudinal magnetization spot by focusing six coherent circularly polarized beams with two opposing high numerical aperture objectives was demonstrated theoretically. That allows 3D magnetic holography with volumetric storage density up to 1872 Tb/in3. It was also revealed that the number and locations of the super-resolved magnetization spots are controllable and thus desired magnetization arrays in 3D volume can be produced with properly designed phase filters. Moreover, flexible magnetization reversals were also demonstrated in multifocal arrays by utilizing different illuminations with opposite light helicity. In additional to data storage, this magnetic holography may find application in information security, such as identity verification for credit cards with a magnetic stripe.
Beyond optical and magnetic realms, superoscillation has been successfully implemented to acoustics based on the superoscillation criterion. By employing the quantum-acoustical analog to investigate the ultrasound version of quantum superoscillation and utilizing an optimization-free groove-structured meta-lens, Qiu's group successfully focused underwater ultrasound into a diffraction-limit-broken spot in the far field with a superoscillatory pattern. The schematic of this acoustic superoscillatory lens and the experimental result are shown in figures 17(c) and (d), respectively. A superoscillatory spot with 0.3λ (λ = 1.5 mm) radius is focused at z = 7.8 mm. This acoustic superoscillation ensures the generation of a nontrivial acoustic radiation force, which is verified through the robust ring-shaped trapping of micro-particles.
Concluding remarks
In summary, this report gives a mini review on superoscillation criterion, super-critical resolved light-induced-magnetic holography, and acoustic superoscillation. New realms of superoscillation beyond optics by using superoscillatory and supercritical criterion are anticipated to empower future developments in interdisciplinary fields between optics, magnetics, acoustics, information, and biotechnology.
Acknowledgments
C W Q acknowledges the support by the National Research Foundation, Prime Minister's Office, Singapore, under its Competitive Research Programme (CRP Award No. NRF-CRP15-2015-03).
12. Superoscillations and information theory
Achim Kempf
University of Waterloo, Canada
Status
Waves are commonly used to carry information, in particular, for purposes of communication or measurement. In this context, it is a curious fact that among the waves of a fixed bandwidth, there are waves that locally oscillate arbitrarily fast [115, 116]. The existence of these so-called superoscillatory waveforms is challenging our understanding of how densely information can be packed for a given bandwidth.
This suggests that the study of superoscillations could lead to a deeper understanding of information theory and that it could also inspire the development of new information-theoretic tools. Conversely, adopting an information-theoretic perspective on the phenomenon of superoscillations may help the practitioner to determine how superoscillatory waveforms may best be deployed.
To begin with, let us recall a central theorem of information theory: the noisy channel coding theorem.
The noisy channel coding theorem [117] states the maximum rate at which information can be transmitted through a noisy communication channel for any given tolerance of error probability. Concretely, the theorem states that as long as the data transmission rate, R, is smaller than the channel capacity, R < C, any arbitrarily small error probability E > 0 can be chosen and there will exist an encoding/decoding scheme such that the information is transmitted with at most the error rate E. Here, the channel capacity, C, is defined via the mutual information, I(Y;X), between the input and the output of the channel through C = supp(X) I(Y;X). The supremum is taken over all probability distributions p(X) for X. The theorem is sweepingly general but in practice it can be unwieldy. On one hand, this is because it is hard to find optimized coding schemes. On the other hand, and this will be our concern here, it can be hard to explicitly calculate the capacity, C.
A special case of great practical importance where C can be calculated is the case of communication channels that are based on the transmission of waves. For simplicity, let us first consider the case of scalar waves in one dimension, such as time, e.g. electric current in a wire. In this context, the Shannon–Hartley theorem provides a very useful explicit expression for the channel capacity, C, of a bandlimited channel with Gaussian additive white noise.
Concretely, consider a channel of bandwidth B with Gaussian additive white noise with average power N. Furthermore, assume that the average power of the signal is S. Then, the Shannon–Hartley theorem states that the channel capacity is given by:
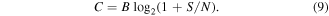
For later reference, we note here that while the Shannon–Hartley theorem is of great practical importance, it suffers from the drawback that is assumes one particular noise model; that of Gaussian additive bandlimited white noise. For any other type of noise, a new theorem of the type of the Shannon–Hartley theorem needs to be derived.
Let us now consider how equation (9) of the Shannon–Hartley theorem can be compatible with the existence of arbitrarily strongly superoscillatory signals, f(t), among the signals with bandlimit B. In fact, it has been shown [118] that within any interval of finite length, an arbitrarily large number nmax of points {tn} and amplitudes {an} can be chosen and there will always exist signals, f(t), of finite energy and of bandwidth, B, which pass through these N prescribed points: f(tn) = an for all n = 1...nmax. This implies, for example, that a function, f(t), exists which possesses bandwidth 1 Hz but whose amplitudes coincide with those of a 20 KHz recording of a Beethoven symphony at 10^100 points in time, e.g. spread out evenly within a recording of T = 30 min duration. The two signals would not be practically distinguishable in that 30 min time interval.
Indeed, for any arbitrary bandwidth B, signals can be found which in an arbitrarily chosen finite time interval pass through arbitrarily many prescribed points. Since it would appear that the amplitudes of these prescribed points can be chosen to carry arbitrarily large amounts information, the challenge arises to determine how this phenomenon is consistent with the Shannon–Hartley theorem.
Current and future challenges
The reason why the Shannon–Hartley theorem is not violated by superoscillatory waveforms is subtle and it points towards an opportunity to generalize the Shannon–Hartley theorem to a new theorem that is independent of any choice of noise model.
First, to see why there is no contradiction to the Shannon–Hartley theorem we begin by considering one of these low-bandwidth signals, f, that is designed to carry a high density of information in a time interval T by passing, in the time interval, T, through prescribed points whose number far exceeds the number of Nyquist points inside the time interval T. Since the prescribed amplitudes are to carry information, they will generally be uncorrelated and as a consequence the signal, f, will generally oscillate in the time interval T at local frequencies that far exceed the bandwidth. Here, the term local oscillation frequency refers to the Fourier spectrum obtained from a Fourier transform that is windowed to the time interval T. In other words, the signal, f, is superoscillatory.
Now in order for this low-bandwidth superoscillatory signal, f, to pass through a channel of its low bandwidth, it is important to note that the signal, f, cannot be truncated, as its truncation, for example, a truncation to the main interval of interest, T, would not obey the original low bandwidth. In particular, the superoscillations would not pass through the channel.
It is necessary, therefore, to send the entire superoscillatory signal through the channel in order to ensure that its superoscillatory interval, T, with its information cargo, passes through the low bandwidth channel. This may appear to be a small price to pay but in fact it is known that every superoscillatory signal possesses extremely large amplitudes before and after the superoscillatory stretch, T. The following scaling behavior of superoscillatory functions was proven in [93, 119, 120]: the L2 norm of a superoscillatory signal must grow at least exponentially with the number of superoscillations (and polynomially with the frequency of the superoscillations). It was also shown that these large norms are achieved not by a slow decay of the signal towards the infinite past or future. Instead, the large norm is obtained because of large amplitudes just before and after the superoscillatory stretch.
The price to pay, therefore, for being able to send a low-bandwidth signal with a superoscillating stretch, T, through a low-bandwidth channel is, therefore, that along with the superoscillatory interval T, parts of the signal also must be transmitted whose amplitudes are excessively large. Given the above-discussed scaling behavior, this means that superoscillatory signals possess a dynamic range (i.e. amplitude range) that grows exponentially with the number of superoscillations, i.e. with the length of the superoscillating stretch. For a channel to be able to transmit such a superoscillating signal well enough for the receiver to be able to resolve the then relatively small superoscillatory amplitudes, the channel's signal-to-noise ratio must also exponentially grow with the number of superoscillations, and therefore with the amount of information that is to be encoded in the superoscillatory amplitudes.
This observation shows why superoscillatory signals are consistent with the Shannon–Hartley theorem. The Shannon–Hartley theorem states that even when holding the bandwidth fixed, the channel capacity can be increased arbitrarily—at the expense of requiring an exponential improvement in the signal-to-noise ratio.
The scaling behavior of the phenomenon of superoscillations, is, therefore, expressing the same tradeoff as is expressed by the Shannon–Hartley theorem: keeping the channel capacity fixed, the bandwidth can be reduced at the cost of a necessarily exponentially increase of the dynamic range.
Crucially, however, the Shannon–Hartley theorem makes specific assumptions regarding the noise model, namely that the noise is additive Gaussian bandlimited noise, and any other noise model requires a fresh derivation of a Shannon–Hartley type theorem. In contrast, the scaling behavior of superoscillatory functions is expressing this exponential tradeoff between dynamic range and bandwidth in a noise-model independent way.
This suggests that there exists a generalization of the Shannon–Hartley theorem for bandlimited signals which does not require an assumption of any particular noise model. To find this generalized channel capacity theorem, the challenges will include finding definitions that suitably relate the descriptors of superoscillatory functions to the descriptors of noisy channels. These relationships are intuitively relatively clear but there remains the challenge to make those relationships quantitative. In particular, it will be necessary to quantitatively relate the concept of dynamic range to that of signal-to-noise ratio and the concept of prescribing nmax number of amplitudes of a superoscillating signal to encoding a certain number of bits.
Advances in science and technology to meet challenges
Both the Shannon–Hartley theorem and the scaling behavior of superoscillations describe a trade-off between bandwidth on one hand and dynamic range and signal-to-noise ratio on the other hand. In practice, different circumstances can require one to work in various ranges of the trade-off spectrum. For example, if bandwidth is scarce, the signal-to-noise ratio must be improved to raise the capacity. Conversely, if signal power is scarce, e.g. in communication with far-away space probes, it can be preferable to increase the bandwidth in order to raise the capacity.
Superoscillations appear to be at the extreme end of the tradeoff, where the bottleneck is bandwidth while there is large freedom in the dynamic range. The bandwidth bottleneck could be, for example, a bandlimitation in time. In practice, and mathematically equivalently, a bandwidth bottleneck may arise for various other reasons, such as an aperture or a diffraction limit in spatial or angular resolution. A bandwidth bottleneck may also arise, for example, from the need to propagate waves through media that possess inconvenient absorption bands. As was pointed out in [32], suitably large dynamic ranges can possibly be utilized in such cases of a bandwidth bottleneck, for example, for optical measurements. There, it is realistic to produce beams of, for example, 1020 photons per second while even single photons can be detected. In [121], it was pointed out that superoscillations may also be useful for probing or utilizing the very absorption processes that cause bandwidth bottlenecks in media, e.g. in optogenetics.
Concluding remarks
From the perspective of the information-theory of continuous channels, superoscillatory signal waveforms arise at the extreme end of the regime characterized by low bandwidth and high signal-to-noise ratio. Correspondingly, the study of superoscillations may inspire new coding schemes for this regime, and it may lead to a generalized Shannon–Hartley theorem that is noise model independent. The role of superoscillations in the transmission of classical and quantum information through quantum fields is starting to be explored [122].
Acknowledgments
A K acknowledges support through the Discovery Program of the National Science and Engineering Research Council of Canada.
13. Optimising superoscillations
Eytan Katzav1 and Moshe Schwarts2
1The Hebrew University of Jerusalem, Israel
2Tel-Aviv University, Israel
Status
Since the invention of superoscillations by Aharonov [1] and Berry [116], it was clear that the common belief that bandlimited signals cannot exhibit an oscillation which exceeds the band limit is strictly speaking invalid. However, at the same time it was realized that from a practical point of view, there is some truth in this belief, in the sense that the energetic efficiency of generating superoscillatory (SO) signals was very low. Gradually, it became clear that designing the superoscillations to more desirable/applicable shapes was possible, e.g. via interpolating superoscillations [93]. Ferreira [93] also allowed some understanding of the basic energetic limitations involved in exceeding the Nyquist rate. Further theoretical progress [123] revealed that superoscillations are actually much more abundant than previously realized, namely that any random band-limited function naturally contains many superoscillatory intervals, implying that in a sense the high energetic price tag attached to superoscillations is related to the need to concentrate them in a-priori well-defined region(s) with a given SO frequency. This can be (morally) interpreted as an entropic effect. A major breakthrough that ignited the current wide interest in superoscillations was the theoretical [28] and experimental [124] insight that optical superoscillations could be used to obtain superresolution without evanescent waves—or using a paraphrase on the provocative title of [124]: 'superoscillations can fair and square beat the diffraction limit'.
However, although superoscillations suggest many practical applications, their uses are presently rather limited, because SO signals exist in limited intervals and the amplitude of the superoscillations in those regions is extremely small compared to typical values of the amplitude in non-superoscillating regions. In an attempt to quantify and control this effect, the concept of the superoscillatory yield [76] has been introduced. Within the context of periodic superoscillations, forcing a signal to superoscillate with a given frequency in a prescribed subinterval ![$\left[-a,a\right]$](https://content.cld.iop.org/journals/2040-8986/21/5/053002/revision1/joptab0191ieqn60.gif) within the unit cell
within the unit cell ![$\left[-\pi ,\pi \right],$](https://content.cld.iop.org/journals/2040-8986/21/5/053002/revision1/joptab0191ieqn61.gif) the superoscillatory yield is defined by
the superoscillatory yield is defined by  namely as the energy of the superoscillatory part of the signal normalized by its total energy per period. As explained above, one expects that the SO-yield would be 'exponentially' small, or more precisely should be orders of magnitude smaller than unity. The basic question underlying our research is whether this situation can be ameliorated, or: what are the fundamental limits on the SO yield?
namely as the energy of the superoscillatory part of the signal normalized by its total energy per period. As explained above, one expects that the SO-yield would be 'exponentially' small, or more precisely should be orders of magnitude smaller than unity. The basic question underlying our research is whether this situation can be ameliorated, or: what are the fundamental limits on the SO yield?
In [76], a method to generate interpolating SO signals, which are optimal with regards to the yield was developed. From a mathematical point of view, the method can be cast as some generalized eigenvalue problem, with the largest eigenvalue representing the optimal yield. In figure 18(a), we show an example for the yield-optimised signal that is designed to pass through  equally spaced points within the interval
equally spaced points within the interval ![$\left[-1,1\right]$](https://content.cld.iop.org/journals/2040-8986/21/5/053002/revision1/joptab0191ieqn64.gif) where we have used
where we have used  Fourier components in
Fourier components in  In figure 18(b), we demonstrate that the superoscillatory interval can actually be composed of two (or more) subintervals at the same level of mathematical complexity. Interestingly, within this framework the subleading generalized eigenvalues and eigenvectors have a very simple meaning. It turns out that two consecutive eigenvalues differ by another zero crossing, which enters the SO interval in the corresponding eigenfunctions. This leads to the surprising conclusion that absolute upper-bound on the yield for a signal with a given frequency within a certain SO interval is given by an eigenvalue of the problem where no constraint is imposed at all.
In figure 18(b), we demonstrate that the superoscillatory interval can actually be composed of two (or more) subintervals at the same level of mathematical complexity. Interestingly, within this framework the subleading generalized eigenvalues and eigenvectors have a very simple meaning. It turns out that two consecutive eigenvalues differ by another zero crossing, which enters the SO interval in the corresponding eigenfunctions. This leads to the surprising conclusion that absolute upper-bound on the yield for a signal with a given frequency within a certain SO interval is given by an eigenvalue of the problem where no constraint is imposed at all.
Figure 18. Two SO yield-optimised signals composed of  Fourier components and interpolating over
Fourier components and interpolating over  points in (a) a single SO interval
points in (a) a single SO interval ![$\left[-1,1\right]$](https://content.cld.iop.org/journals/2040-8986/21/5/053002/revision1/joptab0191ieqn69.gif) and (b) a union of two SO intervals
and (b) a union of two SO intervals ![$\left[-1,-0.5\right]\cup \left[0.5,1\right].$](https://content.cld.iop.org/journals/2040-8986/21/5/053002/revision1/joptab0191ieqn70.gif)
Download figure:
Standard image High-resolution imageFurther analysis [125] reveals that optimising the yield can be very profitable, and result in a SO signal which is orders of magnitude more energetic than that of a randomly chosen (interpolating) signal with the same SO frequency. In addition, a stability analysis [125] shows that the generated SO signals are sensitive to noise in their Fourier coefficients but less than expected, in the sense that the generation of the interpolating SO signal is far more sensitive and requires a much more precise calculation than the one needs to reproduce such a signal given the coefficients.
In the above, we have emphasized the importance of superoscillations in imaging, however the scientific and technological potential of superoscillations goes far beyond, and is relevant to any effort in focusing energy into sub-wavelength structures, such as nano-drilling. Actually, optimisation is even more crucial in this case, because in this case not only is the yield (i.e. the energy ratio) important, but also absolute power. A light beam with  photons per second can suffer a damping factor of
photons per second can suffer a damping factor of  and still allow imaging, while drilling necessitates the maximal possible power.
and still allow imaging, while drilling necessitates the maximal possible power.
Current and future challenges
In spite of the big progress, there are still many challenges in optimising SO signals which are of great importance both theoretically and experimentally, and are actually crucial for technological applications. Below, we identify a few such important directions which could impact the field significantly.
- 1.Consolidation and extensions of the energetic aspects: Currently, the optimisation of the yield requires significant numerical precision, which limits its implementation to high precision platforms, such as MATHEMATICA running on a computer. It would be important to improve the implementation of these procedures such that they could be performed using double-precision (or even lower), and on standalone hardware platforms. This could be achieved via analytical results combined with iterative methods. Furthermore, it is important to extend these results beyond one-dimensional signals so that they could be used to construct 2D beams (radially symmetric or not), which are often needed experimentally. From a fundamental point of view, the holy-grail is to establish absolute upper bounds for the yield of a superoscillatory signal with a given frequency in a given subinterval, among all signals. This can be thought of as 'Heisenberg uncertainly relations' between frequency and yield. A related question worth mentioning is determining the smallest (sub-wavelength) hotspot possible with a given yield? Needless to say that a constructive procedure, which is able to realize these upper bounds, would be desirable. Further questions related to energetic optimisation are: (a) how does the discreteness of the spectrum affect the yield, namely to what extent can the existence of a continuous set of oscillatory signals up to the band-limit improve the yield compared to a signal composed of a discrete set? (b) If we allow a small fraction of frequencies above the bandlimit (even such that we cannot control, but do know its properties), can that be used to improve the SO yield?
- 2.Optimisation of the shape: The current experience with SO functions shows that very often the shape, even if optimised with regards to the yield, is irregular in ways that limit their applicability. Common artefacts are an amplitude that grows towards the boundaries of the SO region (e.g. figure 18) and a frequency that is irregular across that region. The basic challenge would be to devise an effective tool to control the shape of the signal with as low an energetic price as possible. More generally, determining the minimal energetic cost for shaping the superoscillatory signal, such that it would match a desirable shape at a prescribed level of similarity. For example, in imaging, it would be greatly advantageous for the signal to resemble as close as possible a perfect sinusoidal function. A related, less demanding improvement could be made by spreading the zero crossings as regularly as possible, or control the amplitude at a uniform level across the SO region.
- 3.Interaction of SO signals with matter: A major challenge in the application and the design of useful SO signals comes from the fact that the current description of interactions of light and matter is based on perturbation theory and hence may be not precise enough for an adequate understanding of the way such violently fluctuating waves affect matter. Such effects can sometimes limit the relevance of superoscillations [126] and sometimes be utilized to stabilize them [68]. At any rate, a better understanding of the interaction can imply novel optimisation criteria which target more directly the desired effect rather than just controlling the yield or the shape. This challenge is obviously at a much higher level and hence much more prospective.
Concluding Remarks
Optimisation of SO signals is of great importance in both theory and applications of superoscillations. In this section, we tried to portray recent developments in this subject. The introduction of the concept of the superoscillatory yield marks a milestone in energetic optimisation, which demonstrated improvement of the energetic loss by orders of magnitude. We believe that further experimental progress in the coming years will go hand-in-hand with achievements related to optimisation of the yield and shape of SO signals. Furthermore, we believe that a better quantitative understanding of the interaction between light and matter is needed to allow a more principled design of superoscillations to target the goals we assign to them.
Figure 19. Professors Sir Michael Berry, Yakir Aharonov and Nikolay Zheludev at the first international workshop on 'The Physics and Technology of Superoscillations' at the Institute of Physics, London, 16 October 2017. Used with permission.
Download figure:
Standard image High-resolution image


















