Abstract
Hybrid entangled states exhibit non-local correlations between photons with independent degrees of freedom and are currently gaining much interest. In particular, hybrid entanglement between polarisation and spatial modes of two photons are promising candidates for future heterogeneous quantum channels, but their versatility is limited by current generation methods that rely on static elements. Here, we present a technique that exploits polarisation and spatial mode dependent phase modulation in an all-digital approach using spatial light modulators. We show that we can tailor hybrid entangled states using spatial modes with Cylindrical and Cartesian symmetry, making our approach flexible, dynamic, and adaptable.
Export citation and abstract BibTeX RIS
1. Introduction
Generating entanglement beyond single degrees of freedom (DoFs) of photons has enabled cutting edge demonstrations that would otherwise not be possible with a single DoF, e.g. complete Bell state measurements enabled by hyper-entanglement [1, 2] and heterogeneous quantum channels enabled by hybrid entanglement [3]. While the former features non-local correlations between all the DoFs of a photon, the latter, hybrid entanglement, is characterised by entanglement between two photons that have independent DoFs. Remarkably, applications of hybrid entanglement include quantum key distribution [4], quantum repeaters [5], entanglement swapping [3] and quantum teleportation [6] and quantum memories [7], raising the demand for more robust generation methods.
The first and simplest preparation of hybrid entanglement was realised in early quantum eraser experiments, where the polarisation of one photon was used to control the visibility of interference fringes of its entangled twin that resulted from traversing a double slit marked with polarisers [8]. In this case, the hybrid entanglement was between the polarisation and the path DoF of two photons [9]. Today, hybrid entangled states are also generated between time-polarisation [10], frequency-spatial [11], and polarisation-spatial mode DoFs [12, 13]. The attraction towards polarisation-spatial mode hybrid entanglement is motivated by the fact that polarisation states can be controlled with linear optics while the transverse spatial DoF gives access to larger information alphabets, which is beneficial for quantum communication protocols due to the demand for high information capacities [14, 15]. However, generation methods for hybrid spatial and polarisation modes are limited in their versatility.
Current methods for generating polarisation-spatial mode hybrid entanglement are usually borrowed from techniques that are used for preparing vectorial structured light fields [16–19], e.g. interference [20], geometric phase static q-plates [21, 22], static metasurfaces [23–25], and spatial light modulators (SLMs) [26]. However, interferometers can be sophisticated or unstable, and static elements are not versatile enough, therefore imposing restrictions when tailoring arbitrary hybrid entangled states. On the other hand, SLMs are currently being used to advance generation methods for structured light fields across numerous disciplines, i.e. for classical laser beams [27], single photon fields [28], and for controlling up-conversion and down-conversion processes in nonlinear crystals (NCs) [29, 30]. In quantum entanglement experiments, SLMs are a main tool for most spatial mode entanglement experiments, spanning a wide range of transverse spatial modes, e.g. pixel position basis [31, 32], Ince-Gaussian [33], Bessel-Gaussian [34], and Hermite-Gaussian (HG) [35] modes, because they are digitally addressed. Significantly, the intrinsic polarisation dependent birefringence due to the liquid crystals has not been fully utilised for hybrid entanglement generation. So far, the polarisation dependent response of liquid crystal SLMs has been characterised as a quantum channel [36] and have been explored in order to implement optical computations [37, 38] and spatially resolved photon-coincidence measurements [39, 40].
In this paper, we make full use of the phase control and linear polarisation dependent birefringence of SLMs to demonstrate a novel tool for generating hybrid entangled states of photons. We will show that the intrinsic SLM birefringence can be used for dynamic polarisation control of spatial and polarisation DoFs of entangled photons. We demonstrate the method using spatially entangled photons generated from spontaneous parametric down-conversion (SPDC) and map one of the photons from the entangled pair onto the polarisation basis while its twin inherits desired transverse spatial profiles. We show that the resulting spatial mode of the photon is transferred to its twin by performing a complete quantum state tomography (QST) of the resulting hybrid states.
2. Concepts and implementation
2.1. Hybrid entanglement
We outline our method for tailoring hybrid entangled states through spatial-to-polarisation conversion (SPC). It is instructive to first introduce the concept of polarisation-spatial mode hybrid entanglement. A typical hybrid entangled state of this kind has the form

where  and
and  are the horizontal and vertical polarisation states of photon A, while
are the horizontal and vertical polarisation states of photon A, while  and
and  are the orthogonal transverse spatial modes of photon B. Here the factor a varies the state from being completely separable (a = 0 and a = 1) to maximally entangled (a = 0.5), provided
are the orthogonal transverse spatial modes of photon B. Here the factor a varies the state from being completely separable (a = 0 and a = 1) to maximally entangled (a = 0.5), provided 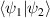 = 0.
= 0.
Each photon occupies an independent DoF and the corresponding Hilbert spaces,  and
and  , are two-dimensional and can be represented on independent Bloch-spheres as shown in figure 1. Photon A is restricted to a two-dimensional subspace, however, multiple subspaces can be formed for photon B. Consequently, one can construct various hybrid subspaces by tailoring the spatial modes of photon B. In this paper, we demonstrate the adaptive control of the spatial DoF of photon B.
, are two-dimensional and can be represented on independent Bloch-spheres as shown in figure 1. Photon A is restricted to a two-dimensional subspace, however, multiple subspaces can be formed for photon B. Consequently, one can construct various hybrid subspaces by tailoring the spatial modes of photon B. In this paper, we demonstrate the adaptive control of the spatial DoF of photon B.
Figure 1. Concept of polarisation-transverse spatial hybrid entanglement where photon A is defined in the polarisation basis, while photon B is defined in the transverse spatial basis. Since the spatial degree of freedom spans a high-dimensional state space, there are a variety of transverse spatial basis modes with various symmetries to choose from, e.g. Cartesian (HG modes) or Cylindrical (LG modes).
Download figure:
Standard image High-resolution imageTo demonstrate the versatility of our approach and the corresponding diversity in hybrid states we can create, we use two mode families as exemplars: the Laguerre–Gaussian (LG) and HG modes, having Cylindrical and Cartesian symmetry, respectively. At the waist plane the LG basis modes have the field profiles

Here the factor 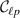 is a normalisation constant, the function
is a normalisation constant, the function 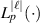 is the Associated Laguerre polynomial with radial number
is the Associated Laguerre polynomial with radial number 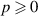 ,
, 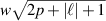 is the second-moment radius of the mode and w is the size of the Gaussian envelope (
is the second-moment radius of the mode and w is the size of the Gaussian envelope (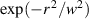 ). The azimuthally dependent factor,
). The azimuthally dependent factor,  , is associated with photon fields that carry an orbital angular momentum of
, is associated with photon fields that carry an orbital angular momentum of  per photon where
per photon where 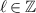 is an unbounded integer, called the topological charge, characterising the helicity of the photon field. The LG basis forms a complete set over the azimuthal (
is an unbounded integer, called the topological charge, characterising the helicity of the photon field. The LG basis forms a complete set over the azimuthal (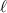 ) and radial indexes (
) and radial indexes (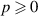 ). We will select the subspaces of photon B as
). We will select the subspaces of photon B as 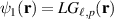 and
and 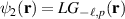 , for the LG basis, and use the shorthand notation
, for the LG basis, and use the shorthand notation 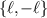 to refer to the individual subspaces. Note that we will select fixed radial indices for each subspace.
to refer to the individual subspaces. Note that we will select fixed radial indices for each subspace.
The HG basis modes can be expressed in Cartesian coordinates, 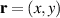 ,
,

indexed by the positive integers 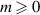 and
and 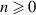 , where
, where 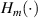 denotes the Hermite polynomials and
denotes the Hermite polynomials and 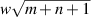 is the second-moment radius of the mode and, once again, w is the size of the Gaussian envelope, while
is the second-moment radius of the mode and, once again, w is the size of the Gaussian envelope, while 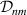 is a normalisation constant. We will select the subspaces of photon B as
is a normalisation constant. We will select the subspaces of photon B as 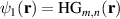 and
and 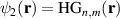 , and adopt the notation
, and adopt the notation 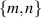 to refer to the HG subspaces.
to refer to the HG subspaces.
2.2. Spatial-to-polarisation mode conversion
To create the hybrid modes in equation (1), we first begin by generating entangled photons from SPDC using a NC that is pumped with a high-energy photon, thereafter producing two lower-energy photons that conserve the energy and momentum of the input photon. The schematic for achieving this is shown in figure 2(a). Crucially, the SPDC photons are correlated in the position basis and their state can be described as
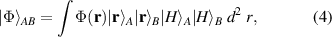
where 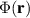 is the two-photon probability amplitude due to the down-conversion process, while the position basis vectors,
is the two-photon probability amplitude due to the down-conversion process, while the position basis vectors, 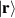 , are complete and satisfy
, are complete and satisfy 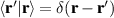 , where
, where 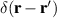 is the Dirac delta function.
is the Dirac delta function.
Figure 2. (a) To generate hybrid entanglement, we prepare two photons using a NC. The photons are spatially separated using a 50:50 beamsplitter (BS). Photon A undergoes a SPC and is measured with polarisation optics and coupled to a single-mode fibre (SMF), while photon B remains in the spatial mode basis and is measured using a SLM and a single-mode fibre. Photon A is measured in the polarisation basis using linear polarisation optics (PO). Each single-mode fibre is coupled to a single-photon detector (D) and measured in coincidence (C.C). (b) The SPC conversion is executed with an SLM. A lens (L) images side ψ2 (encoding 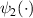 ) to side ψ1 (encoding
) to side ψ1 (encoding  ), while the quarter waveplate and mirror flip the polarisation components of the incoming field ensuring that each mode is coupled to a unique polarisation. Examples of photon fields, initially having a Gaussian profile, emerging from a single-mode fibre and marked with orthogonal linear polarisation states, traversing the SPC optics and resulting in the (c) LG (
), while the quarter waveplate and mirror flip the polarisation components of the incoming field ensuring that each mode is coupled to a unique polarisation. Examples of photon fields, initially having a Gaussian profile, emerging from a single-mode fibre and marked with orthogonal linear polarisation states, traversing the SPC optics and resulting in the (c) LG (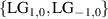 ) and (d) HG (
) and (d) HG (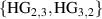 ) basis modes. Such transformation can be achieved by tailoring the phase profile of digital holograms encoded on SLM B. The reverse process (right to left) maps the spatial modes to specific polarisations and the SMF filters the fundamental mode.
) basis modes. Such transformation can be achieved by tailoring the phase profile of digital holograms encoded on SLM B. The reverse process (right to left) maps the spatial modes to specific polarisations and the SMF filters the fundamental mode.
Download figure:
Standard image High-resolution imageWhile the assumptions we will make simplify the calculations that follow, in general, the two photon field amplitude of the SPDC state is determined by the phase matching conditions and pump photon profile [41]. This can have an impact on the spatial bandwidth of the SPDC state [42]. In practise, it is crucial to ensure that the spatial bandwidth of source is high enough. The theory [43], and experimental tools [44, 45], for achieving this are well established.
Next, we define an operator, 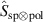 , that maps the SPDC state to a tailored hybrid state corresponding to equation (1) by coupling the internal DoF of photon A using spatial-to-polarisation coupling (SPC) as illustrated in figure 2 (b). The mapping due to the SPC transformation takes a single position basis vector,
, that maps the SPDC state to a tailored hybrid state corresponding to equation (1) by coupling the internal DoF of photon A using spatial-to-polarisation coupling (SPC) as illustrated in figure 2 (b). The mapping due to the SPC transformation takes a single position basis vector, 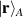 , and transforms it following
, and transforms it following

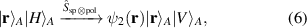
where 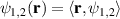 and
and 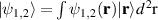 , so that the final output states are imprinted with independent spatial modes depending on the input polarisation states. The operator can therefore be summarised as
, so that the final output states are imprinted with independent spatial modes depending on the input polarisation states. The operator can therefore be summarised as
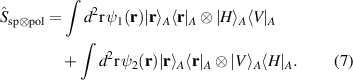
To show that the resulting state of the SPDC photon can be mapped to a hybrid state using the operator  , we will first assume that the two-photon amplitude is uniform and normalised over a bounded domain, and therefore photon A and B have non-local correlations that approximate a maximally entangled state, i.e.
, we will first assume that the two-photon amplitude is uniform and normalised over a bounded domain, and therefore photon A and B have non-local correlations that approximate a maximally entangled state, i.e. 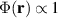 . While this approximation simplifies the calculation, it is imperative to include the phase-matching function and pump profile for a general treatment [43].
. While this approximation simplifies the calculation, it is imperative to include the phase-matching function and pump profile for a general treatment [43].
Before applying the operator on the SPDC state, polarisation of photon A in equation (4) is first rotated to the diagonal polarisation state, 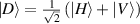 , using a half-wave plate. As a result, the SPDC state is now
, using a half-wave plate. As a result, the SPDC state is now

After applying our operator, 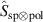 , on photon A, we obtain the state
, on photon A, we obtain the state
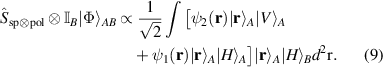
To complete the transformation, we have to integrate over the position vectors in photon A. To achieve this, we use a single-mode fibre (SMF) to perform a partial inner product, enabling us to remove the spatial information of photon A. The SMF filters the fundamental mode, 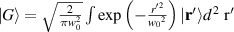 , resulting in
, resulting in
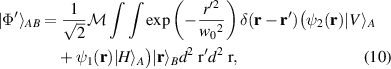
where 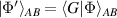 and
and 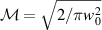 . Next, we integrate over the spatial coordinates of photon A and ignore the polarisation of photon B because it is factorisable and subsequently arrive at the state
. Next, we integrate over the spatial coordinates of photon A and ignore the polarisation of photon B because it is factorisable and subsequently arrive at the state
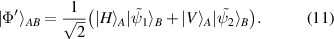
Here  is the modulated version of the spatial modes in our hybrid state from equation (1) (with a = 0.5). If the fields,
is the modulated version of the spatial modes in our hybrid state from equation (1) (with a = 0.5). If the fields, 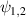 , are sufficiently smaller than the fundamental mode, then
, are sufficiently smaller than the fundamental mode, then 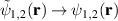 and therefore equations (11) and (1) are equivalent (for a = 0.5). Next, we show how adaptive control of the operator
and therefore equations (11) and (1) are equivalent (for a = 0.5). Next, we show how adaptive control of the operator 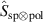 can be achieved using an SLM and linear optical elements.
can be achieved using an SLM and linear optical elements.
2.3. Digital control of spatial-to-polarisation mapping
The transition from the SPDC state to the hybrid entangled state in equation (1) requires the construction of the operator 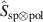 . We achieve this with a SLM and linear polarisation optics (PO) as illustrated in figure 2(b). We rewrite the operator using Jones calculus and project
. We achieve this with a SLM and linear polarisation optics (PO) as illustrated in figure 2(b). We rewrite the operator using Jones calculus and project 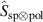 onto the position basis. Assuming that the polarisation basis vectors are
onto the position basis. Assuming that the polarisation basis vectors are 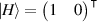 and
and 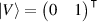 , the corresponding Jones matrix can be written as
, the corresponding Jones matrix can be written as
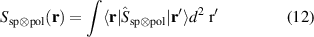
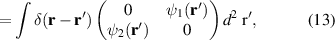

Conveniently, we can decompose the operator into three independent transformations
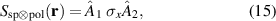
where

Here, 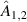 encodes the field profiles that map onto the states
encodes the field profiles that map onto the states 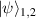 , by modulating the horizontal components of the incoming field, while the vertical component is unaffected. Then, the X Pauli gate (σx
) flips between the linear polarisation basis states so that the field profile encoded by
, by modulating the horizontal components of the incoming field, while the vertical component is unaffected. Then, the X Pauli gate (σx
) flips between the linear polarisation basis states so that the field profile encoded by 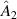 is transferred to the vertical polarisation component while
is transferred to the vertical polarisation component while 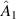 only acts on the horizontal component.
only acts on the horizontal component.
We use an SLM separated into two halves to perform the SPC conversion, as shown in figure 2(b). Since the SLM is birefringent and transfers the desired phase onto the horizontal polarisation component, while the vertical component is unaffected, we can apply the operation 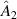 on the first reflection and
on the first reflection and 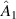 on the second reflection. Importantly, the photon field is modulated on axis and there is no grating. For this reason, we encode the phase of the desired modes, although an inverted grating can be applied to achieve the desired amplitude modulation. We apply the σx
gate by transmitting the field through the quarter-wave plate (QWP) at
on the second reflection. Importantly, the photon field is modulated on axis and there is no grating. For this reason, we encode the phase of the desired modes, although an inverted grating can be applied to achieve the desired amplitude modulation. We apply the σx
gate by transmitting the field through the quarter-wave plate (QWP) at 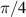 twice, but with a mirror in between. This is because the QWP maps between the linear polarisation basis and the circular polarisation (CP) basis, while the mirror flips the handedness of the incident CP state. The subsequent transmission through the same QWP maps the polarisation state back to the linear polarisation state, but with the initial polarisation now orthogonal to the input. This allows us to apply
twice, but with a mirror in between. This is because the QWP maps between the linear polarisation basis and the circular polarisation (CP) basis, while the mirror flips the handedness of the incident CP state. The subsequent transmission through the same QWP maps the polarisation state back to the linear polarisation state, but with the initial polarisation now orthogonal to the input. This allows us to apply  to the remaining photon field, on the second side of the SLM screen, enabling us to perform polarisation to spatial mode coupling. The lens (L) is used to image the plane of the first half of the SLM to second half.
to the remaining photon field, on the second side of the SLM screen, enabling us to perform polarisation to spatial mode coupling. The lens (L) is used to image the plane of the first half of the SLM to second half.
We illustrate the working principle of the technique graphically in figures 2(c) and (d) for the LG (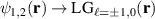 ) and HG (
) and HG ( ) basis. We can think of photon A in the retroactive picture (back-projection) as though it were emanating from the detection SMF fibre and passing through the SPC system to produce the desired target state. The reverse process filters the desired spatial and polarisation mode, therefore converting spatial information to polarisation information. This means that we can couple the photon fields
) basis. We can think of photon A in the retroactive picture (back-projection) as though it were emanating from the detection SMF fibre and passing through the SPC system to produce the desired target state. The reverse process filters the desired spatial and polarisation mode, therefore converting spatial information to polarisation information. This means that we can couple the photon fields 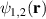 to desired polarisation states by controlling the modes encoded on each half of SLM A.
to desired polarisation states by controlling the modes encoded on each half of SLM A.
2.4. QST of the hybrid entangled states
In this work we reconstruct each generated hybrid entangled state, ρ, using QST. To achieve this, we perform spatially separated measurements  , where
, where 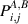 are local projections of photon A and photon B, respectively. The detection probabilities on a system with a corresponding density matrix (ρ) are
are local projections of photon A and photon B, respectively. The detection probabilities on a system with a corresponding density matrix (ρ) are
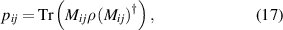
where 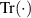 represents the trace operation. In the experiment, photon A is projected onto the spin basis states
represents the trace operation. In the experiment, photon A is projected onto the spin basis states 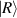 and
and 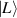 , along with their equally weighted superpositions of linear anti-diagonal, diagonal, horizontal, vertical polarisation states, i.e.
, along with their equally weighted superpositions of linear anti-diagonal, diagonal, horizontal, vertical polarisation states, i.e. 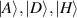 and
and 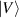 , respectively. Similarly, photon B is locally projected onto the spatial eigenstates
, respectively. Similarly, photon B is locally projected onto the spatial eigenstates 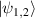 along with superpositions
along with superpositions
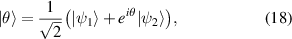
for relative phase 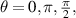 and
and  . We perform these projections digitally using SLMs and linear optical elements only.
. We perform these projections digitally using SLMs and linear optical elements only.
The measurement outcomes are then used to reconstruct the state by employing a maximum likelihood algorithm [46]. In this work, the density matrix reconstruction assumes the decomposition given by
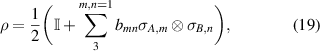
where 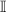 is the four dimensional identity matrix and
is the four dimensional identity matrix and 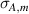 and
and 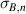 are the Pauli matrices that span the two-dimensional hybrid space for polarisation and spatial DoF respectively.
are the Pauli matrices that span the two-dimensional hybrid space for polarisation and spatial DoF respectively.
2.5. Concurrence
We quantify the degree of entanglement of our reconstructed density matrices by calculating their concurrences [47]. For a reconstructed density matrix ρ, the concurrence is given by
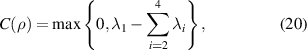
where ρ is the density matrix, λ are the eigenvalues of the operator  in descending order with
in descending order with 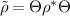 and
and  denotes a complex conjugation. The operator Θ represents any arbitrary anti-unitary operator satisfying
denotes a complex conjugation. The operator Θ represents any arbitrary anti-unitary operator satisfying 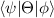 =
=  for any state
for any state 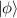 and
and 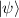 , if
, if 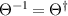 .
.
For pure states, the concurrence can be simplified as
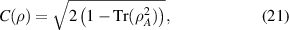
where ρA is the reduced density matrix found by computing the partial trace of ρ. For the state in equation (1), the concurrence is given by
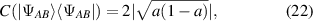
where C = 0 when a = 0 or 1, and C = 1 for a = 0.5.
3. Experimental setup
A conceptual illustration for our experimental setup is shown in figure 2(a). We used a pulsed laser, having a central wavelength of 355 nm to pump on a 3 mm type-I β-barium borate NC. The crystal produced collinear 710 nm photon pairs. The photons where filtered with a bandpass filter and spatially separated by a 50:50 beam splitter. The crystal plane was imaged onto the SLMs for spatial imaging of photon B and for the SPC mapping in Photon A (see figure 2(b)), by a 4F system of lenses. Importantly, photon A was measured with PO using waveplates and polarisers after the SPC mapping. Finally, the modulated photons were directed and imaged by another 4F system and collected with SMFs that where coupled to single photon detectors (D) and subsequently time correlated with coincidence counters (C.C).
We used computer generated holograms that were loaded onto HoloEye Pluto SLMs to encode the desired spatial profiles for photon A and B. The holograms where computed from [48]
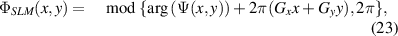
in Cartesian coordinates, (x, y), where 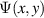 is the field profile of the desired mode while
is the field profile of the desired mode while 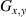 is the grating frequency. The grating frequency was set to zero for SLM A in order to perform on axis modulation of the horizontal and vertical polarisation components of photon A as discussed in section 2.3. For photon B, the grating was non-zero and therefore the first diffraction order contained the desired modulated field. While this technique is a binary phase approximation of the detection modes, complex amplitude modulation can be be adapted for full amplitude and phase control [48, 49].
is the grating frequency. The grating frequency was set to zero for SLM A in order to perform on axis modulation of the horizontal and vertical polarisation components of photon A as discussed in section 2.3. For photon B, the grating was non-zero and therefore the first diffraction order contained the desired modulated field. While this technique is a binary phase approximation of the detection modes, complex amplitude modulation can be be adapted for full amplitude and phase control [48, 49].
4. Results and discussion
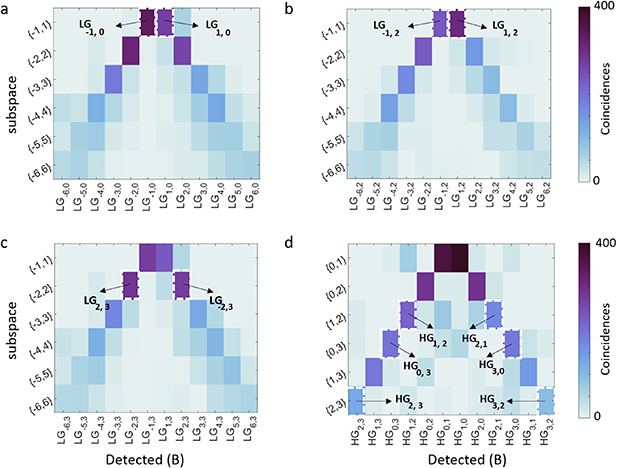
To demonstrate our method we generated hybrid entangled states in the LG and HG basis and confirm that we can post-select various hybrid states using SPC on photon A in the desired basis, by projecting photon B onto the superposition state 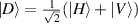 , collapsing the spatial modes of photon B onto the superposition state
, collapsing the spatial modes of photon B onto the superposition state 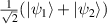 . We then measured the spatial modes of photon B holographically with SLM B and an SMF. The results are shown in figures 3(a)–(d). For each spectrum plot, the columns show the basis modes that were measured for photon B, while the rows represent the post-selected subspaces. The subspaces are labelled with,
. We then measured the spatial modes of photon B holographically with SLM B and an SMF. The results are shown in figures 3(a)–(d). For each spectrum plot, the columns show the basis modes that were measured for photon B, while the rows represent the post-selected subspaces. The subspaces are labelled with, 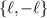 for the LG basis (figures 3(a)–(c)), for
for the LG basis (figures 3(a)–(c)), for 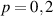 and 3, respectively, and
and 3, respectively, and 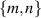 for the HG basis (figure 3(d)). The two peaks observed in each figure, correspond to the modes present in the superposition state after the polarisation projection, indicating that photon B occupies two orthogonal states, as desired. The purity for the
for the HG basis (figure 3(d)). The two peaks observed in each figure, correspond to the modes present in the superposition state after the polarisation projection, indicating that photon B occupies two orthogonal states, as desired. The purity for the 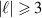 subspaces are lower than
subspaces are lower than 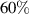 and can be as high as
and can be as high as  otherwise. For the HG basis, we only decomposed the modes into the HG modes with a mode order less than N = 6 (
otherwise. For the HG basis, we only decomposed the modes into the HG modes with a mode order less than N = 6 (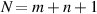 ) and found the mode purities to be as high as
) and found the mode purities to be as high as 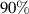 for the
for the 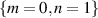 and
and 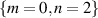 . The reduction in purity for higher order modes in both bases, is due to the phase only encoding of the modes, which can result in loss of orthogonality, and the spatial bandwidth of the SPDC state. These limitations can be overcome by making moderate adjustments of the pump field size, crystal length and the angular spectrum of the imaging system in order to access higher order modes [44, 50].
. The reduction in purity for higher order modes in both bases, is due to the phase only encoding of the modes, which can result in loss of orthogonality, and the spatial bandwidth of the SPDC state. These limitations can be overcome by making moderate adjustments of the pump field size, crystal length and the angular spectrum of the imaging system in order to access higher order modes [44, 50].
Figure 3. Decomposition of photon B when photon A is collapsed onto the superposition state 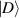 for various subspaces in the
for various subspaces in the 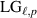 basis for fixed (a) p = 0 , (b) p = 2, (c) p = 3, and (d) the HG basis. The highlighted states are the subspaces chosen for performing QST.
basis for fixed (a) p = 0 , (b) p = 2, (c) p = 3, and (d) the HG basis. The highlighted states are the subspaces chosen for performing QST.
Download figure:
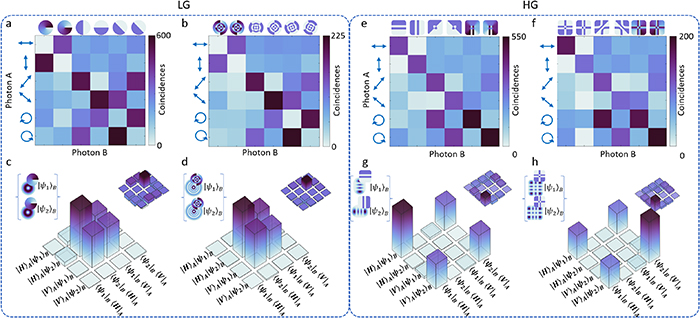
Standard image High-resolution imageTo confirm that the generated hybrid states are indeed entangled, we performed a full QST. The results are presented in figure 4. We highlighted the modes used for QST in figure 3. Figures 4(a) and (b) show the overcomplete set of measurements for the 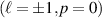 and
and 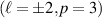 subspace, while the corresponding density matrices are shown in figures 4(c) and (d), respectively. The measured fidelities, compared to a maximally entangled state are 90% and 94% for each subspace, while the degree of entanglement (concurrence, C) is 0.81 and 0.90, respectively. Similarly, for the HG basis, we show the overcomplete set of measurements for the
subspace, while the corresponding density matrices are shown in figures 4(c) and (d), respectively. The measured fidelities, compared to a maximally entangled state are 90% and 94% for each subspace, while the degree of entanglement (concurrence, C) is 0.81 and 0.90, respectively. Similarly, for the HG basis, we show the overcomplete set of measurements for the 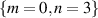 and
and 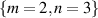 subspaces in figures 4(e) and (f), respectively. The corresponding density matrices are also shown in figures 4(g) and (h). We also calculated the fidelities, and found them to be 87% and 81% for each subspace. The corresponding concurrences were calculated to be 0.78 and 0.65, for each subspace, indicating that the states are entangled but present some degree of mixture.
subspaces in figures 4(e) and (f), respectively. The corresponding density matrices are also shown in figures 4(g) and (h). We also calculated the fidelities, and found them to be 87% and 81% for each subspace. The corresponding concurrences were calculated to be 0.78 and 0.65, for each subspace, indicating that the states are entangled but present some degree of mixture.
Figure 4. QST in the LG and HG basis where the spatial basis modes are (a)  and (b)
and (b) 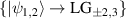 , and (e)
, and (e)  and (f)
and (f) 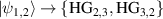 . The corresponding real and imaginary (insets) parts of the reconstructed density matrix are shown below each tomography plot ((c)–(d) and (g)–(h)).
. The corresponding real and imaginary (insets) parts of the reconstructed density matrix are shown below each tomography plot ((c)–(d) and (g)–(h)).
Download figure:
Standard image High-resolution imageWe present a summary of all the measured subspaces in table 1, which also includes the linear entropy, 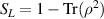 , where 0 corresponds to a pure state. Our calculated linear entropies were all below 0.18, with the lowest being 0.005, indicating that we can produce states that approximate pure hybrid entangled states. The source of the errors in the system were due to the Possonian nature of the detected signals. Accordingly, we computed the errors from
, where 0 corresponds to a pure state. Our calculated linear entropies were all below 0.18, with the lowest being 0.005, indicating that we can produce states that approximate pure hybrid entangled states. The source of the errors in the system were due to the Possonian nature of the detected signals. Accordingly, we computed the errors from 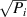 , where Pi
are the photon counts and therefore through error propagation, we obtained uncertainties in the range of
, where Pi
are the photon counts and therefore through error propagation, we obtained uncertainties in the range of  for each fidelity, concurrence and entropy measurement.
for each fidelity, concurrence and entropy measurement.
Table 1. Fidelity (F), concurrence (C) and linear entropy (SL ) for selected subspaces.
| LG | HG | |||||
|---|---|---|---|---|---|---|
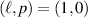
|

|
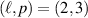
|
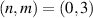
|

|
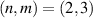
| |
| F | 0.90 | 0.86 | 0.94 | 0.87 | 0.90 | 0.81 |
| C | 0.81 | 0.76 | 0.90 | 0.73 | 0.78 | 0.65 |
| SL | 0.08 | 0.09 | 0005 | 0.17 | 0.13 | 0.17 |
Further improvements to the purity and quality of the entangled states can be made by using complete amplitude and phase control, and by tuning the generational and detection spiral bandwidth to increase the number of basis modes in the system [44]. Moreover, we acknowledge that photon loss and low mode fidelity can be a limitation owing to pixelation on the SLM [51], as well as inefficient photon generation and detectors. However, we envisage that such challenges can be overcome in the future thanks to accelerating growth in liquid crystal display technologies and development of high efficiency detectors [52].
We believe that our work is well placed for applications in heterogeneous quantum communication channels [53, 54], where the hybrid entangled states can be tailored for the medium, i.e. turbulence [55], underwater, [56] and multi-mode optical fibre [32]. This is because the spatial modes of photon B can be chosen appropriately when performing the SPC coupling, therefore making our approach more robust since digital holography is the main workhorse of our technique. Moreover, our work paves the way for the creation of entangled photons beyond single DoF, therefore showcasing the advantage of employing tools for tailoring structured photons [15], by controlling the internal DoF of photons. Our method advances the toolbox for creating exotic hybrid entangled states, while simultaneously overcoming the limitations imposed by traditional static optical elements for achieving the same task.
Regarding applications, our measured fidelities are above the error thresholds and classical bounds of typical quantum communication and information processing protocols. For example, the most error resistant protocol with well devised privacy amplification can tolerate quantum error rates close to 27% [57] when the six state protocol is employed, translating to a fidelities of roughly 73%. Another relevant application can be quanutm teleportation, where the classical bound for fidelity is 66% [58]. This indicates that our generation technique if is immediately deploy-able and can be of practical use.
5. Conclusion
We demonstrated the generation of polarisation-spatial mode hybrid entangled states of photons in an all-digital approach by harnessing the polarisation dependent birefringence and phase control of SLMs. Our approach is versatile and enables the tailoring of a diverse range of complex hybrid entangled states, surpassing many of the limitations of static optical elements methods currently in use.
We deem our work to be a robust contribution to the field of structured quantum states of light, and we hope it paves the way to novel and more dynamic applications of hybrid entangled states in quantum communications.
Acknowledgments
A F acknowledges financial support from the DSI-CSIR Rental Pool Programme administered by the NRF. A G O and P H S R would like to thank the Brazilian Agencies, Conselho Nacional de Desenvolvimento Tecnológico (CNPq), Fundação de Amparo à Pesquisa e Inovação do Estado de Santa Catarina (FAPESC), and the Brazilian National Institute of Science and Technology of Quantum Information (INCT/IQ), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.