Abstract
The properties of self-assembled molecular layers (SAMs) on weakly interacting substrates depend on a delicate balance between intermolecular and molecule–substrate interactions. In this paper, combining STM experiments and first principle calculations, we study 1,3,5-triazine layers grown on both graphite and G/Pt(111). We have carried out ab initio DFT calculations trying standard and hybrids functionals as well as different approaches for the van der Waals (vdW) interactions to fully characterize the intermolecular—H-bonds and vdW– and molecule–substrate–vdW attraction and Pauli repulsion—interactions. Our results confirm that, regarding the SAM formation, the molecule–substrate interaction is strong enough to fix a relative molecule–substrate orientation even though the intermolecular interaction, which fixes the triangular lattice symmetry of the SAM, is larger. This game between these two interactions explains the appearance of very large moiré patterns between SAM and substrate. However, our simulations, even testing several approaches for the vdW and XC interactions, do not reproduce neither the value of diffusion barriers nor differences between substrates found in the experiments.
Export citation and abstract BibTeX RIS
1. Introduction
The ability of some molecules to self assemble on ordered networks is a remarkable property that allows bottom-up fabrication of functional structures in a size range of 1–100 nm [1–4]. Self-assembled molecular layers (SAMs) represent a versatile and cheap source of surface coatings useful for several applications, such as wetting and adhesion tuning, biocompatibility, molecular recognition for sensor applications, chemical resistance and sensitization for photon harvesting [1–8].
The formation of SAMs on different substrates is controlled by a delicate balance between the intermolecular and the molecule–substrate interactions. The strength of this last interaction is highly dependent upon the chemical nature of both molecule and substrate. For very weak molecule–substrate interaction, the SAM structure is practically the same as the isolated monolayer, while if it is very strong, each molecule will be adsorbed on a substrate preferential site regardless of the intermolecular interaction. There are multiple studies of SAMs on reactive surfaces [1–3, 5–7, 9]. However, the formation of SAMs of organic molecules on non-reactive surfaces—the very weakly interacting limit—is still not well understood [3, 4, 7].
Here we fill this gap and present a comprehensive study of the SAMs formed by the small molecule 1,3,5-triazine (hereafter referred as triazine, see figure 2(a)) on different graphene-terminated substrates: single layer graphene (G), graphite and G/Pt(111). Triazine ( ) is essentially a benzene ring where three of the carbon (C) atoms (and the corresponding hydrogen (H) atoms attached) have been replaced by nitrogen (N) atoms. This makes it an outstanding candidate for this study: it is small, planar, highly symmetric, and, at variance with benzene, it supports strong intermolecular interactions through N–H hydrogen bonds that give rise to stable SAMs. The low reactivity and flatness of G makes it an ideal substrate to understand SAMs formation on a weakly interacting substrate. Moreover, adsorption of molecules on G has been proposed as one of the most promising and effective methods to tune the properties of G sheets [10–13].
) is essentially a benzene ring where three of the carbon (C) atoms (and the corresponding hydrogen (H) atoms attached) have been replaced by nitrogen (N) atoms. This makes it an outstanding candidate for this study: it is small, planar, highly symmetric, and, at variance with benzene, it supports strong intermolecular interactions through N–H hydrogen bonds that give rise to stable SAMs. The low reactivity and flatness of G makes it an ideal substrate to understand SAMs formation on a weakly interacting substrate. Moreover, adsorption of molecules on G has been proposed as one of the most promising and effective methods to tune the properties of G sheets [10–13].
There are numerous previous experimental and theoretical studies on the adsorption of single molecules—particularly benzene and other polycyclic aromatic hydrocarbons (PAHs)—on G (see [9–12] and references therein). Most of them are focused on the molecule–substrate binding interaction, with very few works addressing the properties that control the formation of SAMs. The adsorption of triazine on G has already been studied theoretically [14–17], but none of these works has specifically tried to unveil the mechanisms of the SAMs formation. Further motivation comes from recent STM experiments on the formation of triazine SAMs on highly ordered pyrolytic graphite (HOPG) [18], on G/Pt(111) [19], and on G/Rh(111) [20]. These experiments revealed different surface diffusion barriers for the same molecule on the three substrates, opening the way to explore not only the competition between intermolecular and molecular-G interactions but also the subtle changes induced in the graphene by the support. The influence of the support has been recently confirmed by experiments that show that the binding energy of a naphthalene molecule on G on Ir changes by the intercalation of atoms between the G sheet and the metal [21].
The adsorption of PAHs on G, whose behavior is quite similar to the case of the triazine molecules, is controlled by the π–π interplay, one of the most intriguing non covalent interactions [10] on which attraction is driven by van der Waals (vdW) dispersion forces while repulsion is controlled by the electronic overlap between the π wave functions of the molecules and G. Thermal desorption spectroscopy shows that the adsorption energy of PAHs on HOPG has a contribution of ∼52 ± 5 meV per C atom and ∼31 meV per H atom (i.e. adsorption energy for benzene is ∼500 meV/molecule [22]). The theoretical determination of these small binding energies, resulting from the balance between vdW forces and subtle short range electron–electron interactions, is a challenge. Recent calculations show that the most accurate approaches for vdW interactions are needed in order to achieve an accuracy better than 2 meV per C atom [23–26] when comparing adsorption energies for PAHs on graphite to experiments.
In this work, we have characterized by state-of-the-art DFT approaches the formation of triazine SAMs on G, graphite and G/Pt(111). We have used the most recent developments to include the relevant interactions: gradient corrected (GGA) and hybrid exchange-correlation (XC) functionals to describe the short range chemical forces, and a battery of different methodologies—from the semiempirical D2 and D3 [27, 28] to the many-body dispersion (MBD) framework [25, 29]—to account for the long-range electronic correlations that are responsible for vdW interactions. In the case of triazine on graphite and G/Pt(111), on top of these methodological issues and the tight convergence parameters needed to determine energy differences of the order of a few meV, we have to cope with the large unit cells needed to represent the observed moiré patterns. To tackle this problem, we have developed a methodology to extract, from two different sets of manageable calculations, the necessary information to characterize separately the molecule–substrate and intermolecular interactions.
The rest of the paper is organized as follows. Firstly, we summarize the relevant experimental information on the triazine SAMs on graphite and G/Pt(111) (section 2). Then, we describe our methodological approach to characterize the two interactions separately (section 3) and the computational methods chosen to perform the calculations (section 4). Section 5 presents a thorough study of the simplest case: a free-standing G sheet as substrate. Next, we deal with the realistic substrates characterized in the experiments: graphite and G/Pt(111) (section 6). Based on these results, in section 7, we (i) compare our theoretical predictions with the experimental evidence, (ii) characterize the role played by the different interactions on the SAM formation, and (iii) address the accuracy of the theoretical approaches that we have used. Section 8 presents our conclusions.
2. Experimental evidence on the adsorption of triazine on graphite and G/Pt(111)
The adsorption and SAM formation of triazine has been investigated experimentally for the present work by variable temperature scanning tunneling microscopy (VT-STM) under ultra-high vacuum conditions (UHV) on two different graphene-type substrates: HOPG and G/Pt(111) surfaces. HOPG samples were cleaved in situ, under UHV, by means of a homemade device. G/Pt(111) surfaces were grown under UHV by ethylene decomposition at high temperature (typically,  Torr, 1 min,
Torr, 1 min,  ). Pt(111) surfaces were previously cleaned by repeated cycles of argon ion sputtering (1 keV) and annealing under an oxygen atmosphere (10−6 Torr, 870 K), followed by flashing, under the same oxygen partial pressure, at 1270 K. Triazine was deposited at low temperatures (substrates between 40 and 150 K) from a glass container, separated from the main UHV chamber by a leak valve; the triazine container was cleaned, previous to deposition, by repeated freeze-pump-thaw cycles. More details can be found in [18, 19]. STM measurements were done with a homemade VT-STM [18, 30] at low temperature (typically 40 K). All data acquisition and image processing were performed using the WSxM software [31].
). Pt(111) surfaces were previously cleaned by repeated cycles of argon ion sputtering (1 keV) and annealing under an oxygen atmosphere (10−6 Torr, 870 K), followed by flashing, under the same oxygen partial pressure, at 1270 K. Triazine was deposited at low temperatures (substrates between 40 and 150 K) from a glass container, separated from the main UHV chamber by a leak valve; the triazine container was cleaned, previous to deposition, by repeated freeze-pump-thaw cycles. More details can be found in [18, 19]. STM measurements were done with a homemade VT-STM [18, 30] at low temperature (typically 40 K). All data acquisition and image processing were performed using the WSxM software [31].
In previous studies, we have already characterized triazine growth on HOPG [18], G/Pt(111) [19] and G/Rh(111) [20]. In these previous studies the focus was on the diffusion barrier for single triazine molecules, and a significant difference among the three substrates was detected: 55 ± 8 meV for the HOPG case, 68 ± 9 meV for G/Pt(111), and 80 ± 9 meV for the G/Rh(111) system. In the present work, we have analyzed in more detail the formation of SAMs on HOPG versus G/Pt(111).
The expected triangular molecular lattice due to the three-fold symmetry of the triazine can be observed in the experiments but, more importantly, different large moiré patterns, i.e. superperiodicity patterns due to the mismatch between the SAM and the substrate, can be clearly identified on HOPG and G/Pt(111) (see figure 1). Both moirés have large lattice parameters, ≈4.0 nm and ≈4.4 nm for graphite and G/Pt(111) respectively (see the supporting information for a detailed analysis of the experimentally observed moiré structures, which is available online at stacks.iop.org/NANOF/2/045002/mmedia), and form large domains that extend several tens of nm. The intermolecular distance is different for each substrate, 6.1 Å, and 6.25 Å for HOPG, and G/Pt(111), respectively, even though, in both cases, the uppermost layer of the substrate is G. As already mentioned above, the diffusion energy barriers are different. These differences are presumably responsible for alternative growth mechanisms that result on the observation of triazine islands with different morphologies during growth: in HOPG, the boundary of the islands shows a very irregular, fractal-like shape [18] while, for G/Pt(111) [19], the islands present a much more regular, round shape. This smooth boundary suggests a smaller intermolecular interaction than in the HOPG case, that is also consistent with the larger lattice parameter observed in G/Pt(111).
Figure 1. Experimental STM images for the triazine on the HOPG (a) and on the G/Pt(111) (b) substrate. Both the full system moiré (black dashed line) and the intermolecular (light green solid line) cells are depicted. Acquisition parameters: (a) Vs = +2.26 V, It = 60 pA, size: 10 × 10 nm2 ; (b) Vs = +0.27 V, It = 290 pA, size: 9.6 × 9.6 nm2. The bias voltage was applied to the sample.
Download figure:
Standard image High-resolution image3. Methodological approach
A direct calculation of the large moirés found on the experiments for the triazine SAMs on graphite and G/Pt(111) is out of the capabilities of current DFT methods. This section describes our methodological approach to characterize the two interactions separately: (1) study of the molecule–substrate interaction (section 3.1), and (2) a characterization of the molecule–molecule interaction (section 3.2). First, we have applied the general procedure outlined below to characterize the intermolecular interaction and binding to the case where the substrate is a single G sheet. This study identifies the atomistic mechanisms controlling the triazine SAM formation. Based on these results, we extend our study to the cases of graphite and G/Pt(111) in order to understand the role played by the G support.
3.1. Adsorption of a single molecule: molecule–substrate interaction characterized through the binding energy
For this study, a single molecule of triazine is adsorbed on a G(3 × 3) cell (see figure 2(b)). This cell corresponds to the smallest and most frequent moiré pattern observed on G/Pt(111). It allows an intermolecular distance larger than the equilibrium distance in isolated layers of triazine molecules, but the size is not enough to completely eliminate the intermolecular interaction. In order to remove this contribution and retain just the molecule–substrate interaction, we will focus on the binding energy, Ebind, defined as
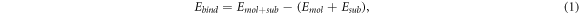
where  is the energy of the full system in the G(3 × 3) cell and Emol and Esub are the energies of the molecular layer and the substrate calculated separately on the G(3 × 3) cell using the geometry obtained during the relaxation of the whole system. Subtracting Emol, that includes the residual intermolecular interaction, Ebind just provides information about the molecule–substrate interaction.
is the energy of the full system in the G(3 × 3) cell and Emol and Esub are the energies of the molecular layer and the substrate calculated separately on the G(3 × 3) cell using the geometry obtained during the relaxation of the whole system. Subtracting Emol, that includes the residual intermolecular interaction, Ebind just provides information about the molecule–substrate interaction.
Figure 2. (a) Scheme of the triazine molecule and its LUMO and HOMO orbital geometries. (b) Ball-and-stick models for the equilibrium structures for the G(3 × 3) and G(6 × 6) cells of G used for the study of the molecule–substrate and molecule–molecule interactions, respectively. The G monolayer C atoms are colored in pink while for the triazine molecule the same color code in (a) has been used. The unit cell is highlighted in red.
Download figure:
Standard image High-resolution imageWe have also calculated the standard adsorption energy, Eads, that includes both the binding energy and the intermolecular interaction. The latter obviously depends on the relative orientation between molecules. It is given by

where the new energy references, E0mol and E0sub, are the energies for a molecule in the gas phase and the isolated substrate respectively, both relaxed to their equilibrium configuration. The single molecule energy, E0mol, is computed in a much larger cell (30 × 30 × 30 Å3) to minimize any intermolecular interaction.
If a localized atomic orbital scheme is used, in particular when dealing with calculations performed with the CRYSTAL code, the adsorption energy is affected by the basis set superposition error (BSSE). In order to correct for the BSSE, the counter-poise (CP) method can be used [32]. The CP-corrected energy ECPbind, has then the form [33]

where  is the computed total energy, and
is the computed total energy, and  and
and  are the energies of the molecule and the substrate calculated respectively in the presence of the ghosted atoms of the substrate and of the molecule. In the same way, the corrected adsorption energy ECPads can be written as follows
are the energies of the molecule and the substrate calculated respectively in the presence of the ghosted atoms of the substrate and of the molecule. In the same way, the corrected adsorption energy ECPads can be written as follows
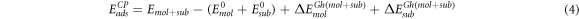
being  and
and  the corrected energies of the substrate and the molecule at the geometry adopted in the adsorbate-substrate system that can be expressed
the corrected energies of the substrate and the molecule at the geometry adopted in the adsorbate-substrate system that can be expressed

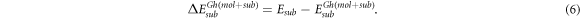
We have characterized the potential energy surface (PES) profile by calculating these energies and adsorption distances for several high symmetry adsorption sites of the molecule on the G layer. Apart from the analysis on the plane parallel to the substrate (the xy-plane), we have also studied the energy variation upon changes in the adsorption distance. Starting from the geometry of the ground state of the system we have modified homogeneously the adsorption distance of the molecule letting the atoms relax but freezing the z coordinate of all atoms in the molecule. This procedure allows us to unveil the PES as a function of the molecule–substrate separation as well as to disclose the different contributions (short range, vdW or intramolecular energy changes) to both the binding energy and the energy barriers.
3.2. SAM characterization: intermolecular interaction
The study of the intermolecular interaction in an isolated layer of triazine molecules can be easily performed by a simulation with a small unit cell including just one molecule. However, the large sizes of the moiré patterns found in the experiments are out of the possibilities of the current implementations of the DFT codes. Our characterization of the intermolecular interaction among triazine molecules adsorbed on different G-terminated substrates is based on simulations of islands formed by three triazine molecules, the smallest combination needed to preserve the triangular symmetry of the SAM lattice. Our calculations have been carried out with a G(6 × 6) cell (see figure 2(b)). With this cell size, there is still a residual interaction between neighboring islands, but it is very small compared to the interaction among molecules inside the island. A larger simulation cell able to include more molecules would be superior to reproduce the intermolecular interactions of the realistic moirés. However, first, the cell size, once the substrate is included, would be too large for DFT calculations; and second, we have tested that the effect of both, the position of the island respect to the substrate and the inclusion of more neighbors (an increase of the molecule coordination) are small and do not change the main conclusions. The validity of this approach is confirmed by the comparison of the energetics and structure of a triazine monolayer with our three-molecule island: the H-bond distances are identical (2.35 Å) for both cases, and the interaction energy per H-bond are very similar (127 meV and 131 meV respectively), with just an expected small change due to the different coordination number (see inset of figure 5(b)).
Our goal is to determine the intermolecular energy as a function of the H-bond distance between the molecules in the island. Our starting point is a full relaxation of the island on top of each of the different substrates to determine the equilibrium structure. Then, we use this optimized geometry to prepare a set of configurations where we displace the molecules from their equilibrium positions in the xy-plane while preserving the symmetry of the island and its orientation with respect to the substrate. Each of these configurations is subsequently relaxed, keeping fixed the xy position of a C and a N atom from each molecule (to enforce the constraint on the H-bond distance) and allowing the rest of the atoms in the molecule and substrate to move freely.
For each configuration, we determine the intermolecular interaction among the molecules on the island, Eintermol, using the equation:
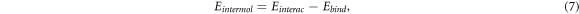
where we subtract the molecule–substrate interaction, Ebind, from the total interaction energy, Einterac. The total interaction energy is calculated by subtracting from the total energy of the system,  , the energy of the isolated substrate, Esub, and the energy of the isolated molecules,
, the energy of the isolated substrate, Esub, and the energy of the isolated molecules,  :
:
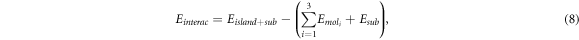
where the reference energies Esub and  are calculated using the geometries corresponding to the equilibrium configuration of the whole system.
are calculated using the geometries corresponding to the equilibrium configuration of the whole system.
As the chemical environment of each molecule in the island is different, we have to perform three independent simulations to determine the binding energy of each molecule. Each of these simulations includes only one of the molecules of the island interacting with the substrate. Its contribution to the binding energy is obtained from the total energy  by subtracting the total energies of the substrate, Esub, and the isolated molecule
by subtracting the total energies of the substrate, Esub, and the isolated molecule 
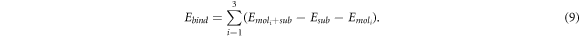
4. Computational methods
We have characterized these systems with first principle calculations based in DFT as implemented in the VASP [34] and CRYSTAL [35, 36] codes. We have used very fine convergence criteria to reach an accuracy of 1 meV per molecule. In our VASP calculations, we have used the 5.3 version with projector augmented wave pseudopotentials [37] and a plane-wave cutoff of 600 eV. The energy convergence is better than 10−7 eV/atom and residual forces smaller than 0.007 eV Å−1. We have used a 6 × 6 × 1 Γ-centered Monkhorst–Pack grid for the calculations in the G(3 × 3) cell and an equivalent grid (3 × 3 × 1) for the bigger G(6 × 6) cell.
We have also employed CRYSTAL14, an all-electron linear combination of atomic orbital code [35, 36]. We have used consistent Gaussian basis sets of triple-zeta valence with polarization. Integration was carried out over reciprocal space using a shrinking factor of 24 to form a Monkhorst–Pack mesh of k points. This grid converges the integrated charge density to an accuracy of about 10−6 electrons per unit cell. The Coulomb and exchange series are summed directly and truncated using overlap criteria with thresholds of (7, 7, 7, 7, 14). The self-consistent field algorithm was set to converge at the point at which the change in energy was less than 10−7 Hartree.
We performed the calculations in three different substrates and for the different cells. For the smaller G(3 × 3) cells the G sheet is composed by 18 C atoms, the graphite substrate is a 4-layer slab of G sheets with the AB stacking corresponding to this material and finally the G/Pt(111) consists on a G layer with a slab of Pt(111) underneath formed by 4 layers with 7 atoms each. Building the G(6 × 6) cells is trivial from these smaller G(3 × 3) ones. For the structural relaxations, only the two lower layers of the slab were fixed to their bulk-like positions (except for the simplest case of the single sheet of G on which all the atoms of the substrate were free to move).
In order to find the best description of the electron–electron interaction, we have used various implementations to incorporate the contribution of dispersive (vdW) interactions and test different exchange-correlation (XC) functionals to describe the chemical interaction.
4.1. Chemical interaction description
For most of our calculations, we have used the PBE functional [38] supplemented by different vdW approaches. Some calculations have been done with XC functionals like optB86b [39] (see below) that include a different exchange contribution and a kernel that accounts for vdW interactions. We have also explored the possible role of an improved description of the short range contributions using hybrid functionals, in particular HSE06 [40], PBE0 [41] and B3LYP [42, 43]. These last calculations were performed using CRYSTAL14 as the convergence with hybrid functionals is more optimized in this code. For these simulations, we carried out only static calculations using the geometry from the PBE+vdW result but optimizing the adsorption distance.
4.2. Van der Waals approaches
There are two ways to include this interaction in the calculations: either as a correction to the final energy or through a kernel in the electronic XC functional that includes these effects in the self-consistency process.
From the first group of vdW implementations we have used the simplest Grimme approach (PBE-D2) [27] and also an advanced implementation by the same authors (PBE-D3) [28]. For the PBE-D2 calculations, we have used the default values given in [27] for all the chemical species except for the Pt, which is not tabulated. For this metal, we have used the parameters C6(Pt) = 20 J nm6 mol−1 and R0(Pt) = 1.9 Å which successfully reproduce the G–Pt distance [44]. In the case of the PBE-D3 implementation (for which we used the Becke–Johnson damping [45–47]), the vdW C6 parameter takes into account the local environment of the atom through its coordination number—which means that it may change during the simulation—and is determined by the program. We have also performed calculations with the TS+SCS [48]—similar to D2, apart from the fact that in this approach the parameters are charge-density dependent, accounting in this way for screening effects—and the MBD approach [25, 29]—which contains both the many-body energy and the screening which are missing in simple pairwise approaches—which are the more sophisticated methods to date. From the second group—the so-called DFT-DF functionals—we have used the Klimes optB86b functional [39] which is able to partially account for screening effects and has proven to work very well for G systems [49].
Table 1 shows the variation on the characteristic distances of our systems depending on the vdW approach used. The mismatch between the C and Pt lattices in the G(3 × 3) moiré of G/Pt(111) is small (0.6%) (see table 1) and we decided to fix the size of the supercell to match the relaxed G lattice calculated with each functional-vdW scheme.
Table 1. Values of characteristic parameters to describe the substrates that we have simulated for different functionals and vdW flavors. The first two columns correspond to the values for Pt and G lattice parameters and the third an fourth are the G-metal distance and graphite interlayer distance respectively
| A0 (Å) | dnn (Å) |
 (Å) (Å) |
 (Å) (Å) |
|
|---|---|---|---|---|
| Bulk Pt | Graphene | G/Pt(111) | Graphite | |
| Exp | 3.913 [50] | 2.46 [51] | 3.30 [52] | 3.35 [53] |
| PBE-D2 | 3.953 | 2.458 | 3.345 | 3.229 |
| PBE-D3 | 3.927 | 2.470 | 3.317 | 3.384 |
| PBE-TS+SCS | 3.951 | 2.466 | 3.325 | 3.382 |
| PBE-MBD | 3.968 | 2.465 | 3.427 | 3.410 |
| optB86b | 3.958 | 2.468 | 3.361 | 3.324 |
5. SAMs formation in graphene
We start the study of the SAMs formation with the simplest case—the substrate being a single sheet of G. We first show our characterization of the relevant adsorption sites, the PES profile and the diffusion energy of the molecules. After that, we analyze the intermolecular energy per H-bond and the bond distances of the triazine molecules adsorbed on the G layer.
5.1. Molecule–substrate interaction
5.1.1. Triazine adsorption sites
We have characterized the preferential adsorption sites on a G(3 × 3) cell, in order to make contact with the literature. We have checked that the results for PBE-D2 in the G(3 × 3) cell are consistent to what is found in a bigger G(6 × 6) cell and, in order to minimize the computational cost, we stuck to the G(3 × 3) cell to perform the molecule adsorption characterization. Figure 3 displays the high symmetry adsorption sites considered in our study and the final orientation of the molecule with respect to the G honeycomb lattice. The molecular symmetry directions are aligned with those of the underlying G substrate for the three top and one of the bridge configurations, while they are rotated by 30° in the Cross(R) and Bridge(R) geometries in order to maximize the intermolecular interaction with molecules in neighboring cells. Adsorption energies and adsorption distances for the PBE-D2 approach are shown in table 2. The Bridge(R), followed by the Cross(R), are the most stable configurations due precisely to the intermolecular interaction, in good agreement with previous calculations [16].
Figure 3. Ball-and-stick models for the high symmetry adsorption sites studied. All top, C top, Bridge and N top adsorption sites share the same molecule-G orientation, while Cross(R) and Bridge(R) (labeled with a gray border) are rotated 30° with respect to the other sites.
Download figure:
Standard image High-resolution imageTable 2. Characteristic binding energies and mean adsorption distances calculated for different adsorption sites of triazine on G depicted in figure 3 using the PBE [38] functional with the Grimme-D2 [27] vdW implementation. The values of the adsorption energies agree with previous works [16]. The energy differences with respect to C top (minimum energy site) for each site are shown in brackets next to the absolute energies.
| Site | Ebinding | Eads | dads | ||
|---|---|---|---|---|---|
| (meV) | (meV) | (Å) | |||
| C top | −404 | (0) | −388 | (0) | 3.15 |
| N top | −377 | (27) | −361 | (27) | 3.20 |
| All top | −344 | (60) | −327 | (61) | 3.28 |
| Bridge(R) | −367 | (37) | −494 | (−106) | 3.21 |
| Cross(R) | −339 | (65) | −464 | (−76) | 3.29 |
In order to obtain the relevant molecule–substrate interaction for the energetic analysis of the SAMs, we need to remove the intermolecular interaction, which is still important in the G(3 × 3) cell. We follow the procedure outlined in section 3 to obtain for each adsorption site the corresponding binding energy. Table 2 shows that, in terms of the binding energy, the most favorable adsorption configuration is the C top, followed by the N top. In the case of a PAH molecule, benzene would be the comparable molecule in this case, these two most favorable positions would be equivalent—there would be no N atoms but more C atoms instead. In the case of triazine, the charge density is larger in the N atoms, on the contrary of what happens in π–π interacting molecules, which breaks the equivalence between these two sites. The C top binding energy, ∼400 meV/molecule, is similar to the cohesive energy measured for a benzene molecule on HOPG, ∼500 meV/molecule [22], which points out that adsorption in both cases is ruled by the same mechanism: non covalent interactions.
We have studied the adsorption and binding energies of the C top and N top configurations using different XC functionals and vdW implementations. Results are shown in table 3. They all predict the C top to have the largest binding energy, but significant differences in absolute binding energies and adsorption distances are found among the different approaches.
Table 3. Characteristic binding energies and mean adsorption distances calculated for the C top and N top adsorption sites (see figure 3) of triazine on G using different vdW flavors (DFT-D2 [27], DFT-D3 [28], DFT-DF(optB86b) [39], TS+SCS [48], and MBD [25, 29]) (see section 4). The energy differences with respect to C top (diffusion energy barriers) are shown in brackets.
| Functional | Site | Ebinding | dads | |
|---|---|---|---|---|
| (meV) | (Å) | |||
| PBE-D2 | C top | −404 | (0) | 3.15 |
| N top | −377 | (27) | 3.20 | |
| PBE-D3 | C top | −400 | (0) | 3.30 |
| N top | −381 | (18) | 3.34 | |
| PBE-TS+SCS | C top | −574 | (0) | 3.43 |
| N top | −551 | (22) | 3.49 | |
| PBE-MBD | C top | −360 | (0) | 3.30 |
| N top | −342 | (17) | 3.35 | |
| optB86b | C top | −562 | (0) | 3.19 |
| N top | −537 | (26) | 3.25 | |
The PBE-D2 is the one with lower adsorption distances although it yields similar binding energies to PBE-D3 (∼400 meV). The rest of the vdW implementations place the molecule much farther from the substrate. This second approach—PBE-D3—along with the PBE-MBD method result in very similar adsorption distances and, although the binding energies are smaller for the MBD approach, the energy differences are very similar for these two methods. The PBE-TS+SCS and optB86b schemes produce bigger binding energies than the other methods (∼550 meV). However, while the optB86b adsorption distances are somewhere in between the PBE-D2 and PBE-D3 cases, the PBE-TS+SCS is the method that results in the farthest distances between molecule and substrate.
5.1.2. Energy barrier calculation
The calculation of the diffusion energy barrier for triazine on G requires to characterize the PES and to determine the minimum energy path. The results of this study are shown in figure 4, where a triangular path that goes through the high symmetry adsorption positions framed in black in figure 3 is explored. These results suggest that the C top-N top-C top path yields the lower energy barrier. We have confirmed this point by performing calculations with the PBE-D2 approach using the nudged elastic band method [54, 55], and, thus, we restrict the study to determine the energy barrier with the other XC+vdW approaches to the path between these two configurations.
Figure 4. Energy landscape calculated for triazine molecules on G with PBE-D2 for in-plane (top image) and out-of-plane (bottom plot) displacements of the molecule. In the top image the PES is shown for an All top-C top-N top-All top trajectory. Both the adsorption energy (blue) and distance (green) are shown for each point of the path. The graph on the bottom shows the energy behavior with the variation of the adsorption distance for the two geometries that define the diffusion energy of the molecule (C top in blue and N top in green). In the total energy curves (solid color), the minima, whose difference is the energy barrier, are circled in black. The short range and vdW contributions are also plotted. The points shown in this graph correspond to actual calculations and the lines are spline interpolations from points belonging to an adsorption distance range of [2.15:3.70] Å some of them not shown in the figure.
Download figure:
Standard image High-resolution imageAccording to the results shown in table 3, the biggest barriers are obtained for the cases where the D2 vdW implementation is used. This is due to the known overestimation of the dispersion forces associated with this vdW approach. This behavior pushes the molecule closer to the surface towards a more repulsive chemical interaction range which results into a bigger barrier. The rest of the methods used yield to smaller but similar barriers on the order of 15–25 meV.
In summary, diffusion energy barriers are always underestimated by the calculations regardless of the method used, similarly to what was found in benzene on G. For that case, some DFT approaches predict a barrier of less than 10 meV [24], which is small compared to the experimental measurements (17 ± 12 meV) [56], although compatible with them given the large experimental uncertainty.
In order to understand the interactions that are controlling the molecule–substrate interaction, we have determined the adsorption energy and the short range and vdW contributions as a function of the adsorption distance for the triazine on the C top and N top sites using the PBE-D2 functional (figure 4(b)). The molecule adsorbs at a distance of 3.15 Å (3.20 Å) with respect to the G on the C top (N top) configuration. We can recognize a very similar behavior to what is found in π–π interacting systems: the driving attractive force is the vdW—which is very similar in the two cases—while the short range contribution is responsible for the PES corrugation and determines the difference in equilibrium adsorption distance (∼0.05 Å) between the two sites. Notice that the minimum of both curves is located in the repulsive region of the short range interaction due to the effect of the vdW contribution that pushes the molecule closer to the surface. We will come back to these energy curves in the discussion presented in section 7.
5.2. Intermolecular interaction
In order to analyze the role of the intermolecular interaction in the SAM formation, we first optimize the structure of the system including both the 3-molecule island and the G substrate on a G(6 × 6) unit cell. The resultant equilibrium geometry is depicted in figure 2(b). The molecules are not exactly on the most stable adsorption configuration for a single adsorbed triazine, the C top site, as the interaction with other molecules induces a small displacement on each molecule from the C top configuration of around 0.3 Å.
We have characterized the strength of the intermolecular interaction following the procedure described in the section 3.2. Figure 5 shows the different energy contributions as a function of the separation (defined as the length of the N–H hydrogen bond) between the three molecules of the island. In figure 5(a), we plot the total interaction energy (Einterac), the binding energy (Ebind)—the sum of the interaction energies of each molecule with the substrate, as defined by equation (9)—and the intermolecular energy calculated as  . Figure 5(b) compares the intermolecular energy per H-bond of the isolated island with the energy of the island adsorbed on G. Although both interactions are very similar, the substrate has the effect of slightly weakening the intermolecular interaction, reducing the H-bond energy from ∼−131 to ∼−119 meV, and increasing the H-bond distance from 2.35 to 2.36 Å.
. Figure 5(b) compares the intermolecular energy per H-bond of the isolated island with the energy of the island adsorbed on G. Although both interactions are very similar, the substrate has the effect of slightly weakening the intermolecular interaction, reducing the H-bond energy from ∼−131 to ∼−119 meV, and increasing the H-bond distance from 2.35 to 2.36 Å.
Figure 5. Intermolecular interaction. (a) Decomposition of the interaction energy per H-bond for the G versus the H-bond distance. All the energies are referred to its minimum value in the represented range to make it easier to visualize. (b) Comparison of the intermolecular energy per H-bond between the G (red) and the isolated island (gray). The minimum of the case with substrate (2.36 Å) is slightly displaced with respect to the isolated island (2.35 Å) and there is an energy shift of ∼11 meV between both cases being the H-bond softer in the G case. In the inset we compare the isolated monolayer (black) and the isolated island (gray). The behavior is very similar except for a shift of ∼4 meV in the energy per H-bond being stronger for the case of the island.
Download figure:
Standard image High-resolution image6. Realistic graphene growth environments: graphite and G/Pt(111)
In this section, we will explore how changes on the G properties induced by the supporting substrate may affect the formation of SAMs [7, 9]. Before that, let us recall the main experimental results with triazine molecules [18, 19]. SAMs grown on HOPG and G/Pt(111) have different equilibrium intermolecular distances (C–H···N), 2.39 Å for HOPG versus 2.49 Å for G/Pt(111), and diffusion energy barriers—55 (68) meV for HOPG (G/Pt(111)). Which are the characteristic properties of each of these substrates that could induce differences in the SAM formation and molecule diffusion? It is well-known that the properties of a G layer are modified by the substrate underneath. In the case of graphite, the Bernal stacking makes the two C atoms in the unit cell inequivalent and a gap is opened in the electronic states of one of the sublattices. Thus, this loss of symmetry converts the massless fermion dispersion of G into massive fermions. This effect can be already seen in bilayer G, and is certainly present in our 4-layer slab [57].
For G/Pt(111), although a weakly G-metal interacting system, there are important changes induced by the substrate on G [58]. The difference between the G and metal work functions and their interaction induce a dipole in the interface with its positive pole at the G layer [58] and the metal dopes G with holes, inducing a shift of the Dirac point which is ∼0.5 eV above the Fermi level when calculated with DFT [44]. In terms of geometry, there is another fundamental difference with respect to the free-standing G and the graphite. The relative orientation between the G layer and the metal surface induces moiré patterns. The G(3 × 3) moiré ( for Pt) is the most common in G/Pt(111) [59]. C atoms inside the moiré unit cell have different coordination with surface metal atoms. This induces differences on its relative heights as well as in their local electronic properties. The height corrugation is subtle for weakly interacting systems (height differences below ∼2 pm for G/Pt(111), see figure 6), anyway, even in these systems, morié patterns can be clearly observed with STM due to electronic effects [44]. Thus, the moiré pattern breaks the symmetry among the different equivalent sites (e.g. the C top sites) and makes the adsorption dependent on its position within the moiré unit cell.
for Pt) is the most common in G/Pt(111) [59]. C atoms inside the moiré unit cell have different coordination with surface metal atoms. This induces differences on its relative heights as well as in their local electronic properties. The height corrugation is subtle for weakly interacting systems (height differences below ∼2 pm for G/Pt(111), see figure 6), anyway, even in these systems, morié patterns can be clearly observed with STM due to electronic effects [44]. Thus, the moiré pattern breaks the symmetry among the different equivalent sites (e.g. the C top sites) and makes the adsorption dependent on its position within the moiré unit cell.
Figure 6. Ball-and-stick scheme of the G/Pt(111) moiré cell simulated. It corresponds to the G(3 × 3) moiré pattern, the one seen in the experiments [19], which is the more common in G/Pt(111). In the top sight an extra color range varying from red (for the lower) to white (for the highest) represents the relative height of the corrugated G sheet. The molecule depicted corresponds to the lower energy—among all the G-equivalent positions in the G(3 × 3) moiré—C top adsorption geometry. In the side view (bottom right corner) the slab structure and the relative distances between the metal, the G and the triazine are shown.
Download figure:
Standard image High-resolution imageBefore addressing local changes induced by the different chemical environment of the G atoms, we consider whether global processes, in particular charge transfer between the molecule and the substrate, could be responsible for differences among the substrates. As the work functions of graphite and G/Pt(111) differ, this charge transfer could be different and make stronger/weaker both the intermolecular H-bonds and the coupling with the substrate. We have calculated the charge transfer for triazine on G, graphite and G/Pt(111) (see the integrated charge density difference in figure 7). We did not find any relevant global charge transfer. However, we did observe a small charge redistribution with the formation of a small dipole in the area between the molecules and the G sheet that is slightly different for each substrate. This small dipole is consistent with the small decrease of the calculated work function (183 meV and 159 meV for graphite and G/Pt(111) respectively). Nevertheless, we will show below that these variations do not modify neither the molecule–substrate coupling nor the strength of the H-bonds.
Figure 7. xy-integrated charge density difference,  , along the z axis for the three systems that we have studied. The vertical dashed lines represent the position of the G sheet (left) and the triazine monolayer (right). The change of sign of the dipole that appears between the substrate and the molecule is highlighted with a change in the background color from blue to red.
, along the z axis for the three systems that we have studied. The vertical dashed lines represent the position of the G sheet (left) and the triazine monolayer (right). The change of sign of the dipole that appears between the substrate and the molecule is highlighted with a change in the background color from blue to red.
Download figure:
Standard image High-resolution image6.1. Molecule–substrate interaction
6.1.1. Triazine adsorption sites
We follow the same procedure used for the case of the free-standing G. We first determine the molecule–substrate binding configuration and energy for a single triazine molecule on the different adsorption sites using a G(3 × 3) unit cell. Table 4 presents the results for different sites on graphite and G/Pt(111) calculated with the PBE-D2 functional. Comparing with the free-standing G case, there are no significant differences induced by the presence of the substrate, apart from a small rigid shift of the binding energies, −40 (−60) meV for graphite (G/Pt(111)), and small variations (less than 5 pm) in the adsorption distances. In the case of G/Pt(111), those results correspond to sites on the most favorable adsorption area (the lower area of the moiré see figure 6). However, we have analyzed all of the equivalent sites within the moiré unit cell (e.g. all the C top sites) and confirmed that the variations induced by the moiré are extremely small (less than ∼2 meV in the binding energy and ∼0.02 Å in the adsorption distance). Results with other vdW approaches are very similar.
Table 4. Molecule–substrate binding energy and mean adsorption distance for the different high symmetry adsorption sites studied for the three different substrates we are characterizing calculated with PBE-D2.
| Graphene | Graphite | G/Pt(111) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| meV | Å | meV | Å | meV | Å | ||||
| C top | −404 | (0) | 3.15 | −445 | (0) | 3.13 | −466 | (0) | 3.11 |
| N top | −377 | (27) | 3.20 | −417 | (27) | 3.20 | −440 | (25) | 3.17 |
| All top | −344 | (60) | 3.28 | −382 | (63) | 3.28 | −402 | (64) | 3.28 |
| Bridge(R) | −367 | (37) | 3.21 | −407 | (38) | 3.20 | −428 | (38) | 3.20 |
| Cross(R) | −339 | (65) | 3.29 | −377 | (68) | 3.28 | −398 | (67) | 3.26 |
6.1.2. Energy barrier calculation
Contrary to the experimental evidence, we have not found with the PBE-D2 functional any difference in the diffusion energy barriers by changing the substrate. We have calculated the diffusion barrier with other more sophisticated vdW approaches that take into account the different chemical environment and/or screening/polarizabiliy effects. However, none of these approaches leads to significant differences among the different substrates (see table 5). Changes in the diffusion barrier are also very small (less than for ∼4 meV) when considering C top and N top sites on different areas of the G/Pt(111) 3 × 3 moiré unit cell, in line with the conclusions of the previous section. Thus, simulation provides diffusion barriers that are approximately 50% smaller than the ones found in the experiment and essentially independent of the support of the G layer.
6.2. Intermolecular interaction
Finally, we analyze the effect of the substrate on the intermolecular interaction. We have followed the same procedure applied for the adsorption on G. Figure 8 presents the energy per H-bond as a function of the bond length for G, graphite, G/Pt(111) and the isolated three-molecule island. Experiments show a change on the intermolecular distance of ∼10 pm between the triazine molecules adsorbed on graphite and on G/Pt(111). Calculations yield distance variations between substrates one order of magnitude smaller (<1 pm) and almost identical bond energies (differences less than 1 meV). Therefore, although the presence of G does induce some small changes in the intermolecular interaction, the substrate underneath seems not to play any role.
Figure 8. Intermolecular energy per H-bond versus the H-bond distance calculated with PBE-D2 for simulations with the isolated 3-molecule island of triazines (gray), the island on top of G (red), the island on top of graphite (orange) and the island on top of G/Pt(111) (blue). Note that the energy axis for the three substrates (left) is different from the energy axis of the isolated island (right) but both axis represent the same energy increment. The minimum for the case of the isolated island is at a H-bond distance of ∼2.35 Å while for the three substrates it slightly increases up to ∼2.36 Å.
Download figure:
Standard image High-resolution image7. Discussion
All this exhaustive theoretical study of the adsorption of the triazine molecule over different G-based substrates, having the experimental evidence as a reference, allows us to unveil some of the basic properties driving the SAM formation on G layers. However, we are still unable to address the influence on the SAM formation—found in the experiments—of the material on which the G has been grown. Despite this, we have learnt relevant notions on the SAMs formation and we have also been able to point out the possible origins of the discrepancies with the experiments.
7.1. Which is the interaction that controls the SAMs formation?
For all the systems considered, G, graphite and G/Pt(111), the clearly preferred configuration for the adsorption of a single triazine molecule is the C top site. The orientation of the triazine molecule with respect to G (the relative angle between the directions that are equivalent under the three-fold symmetry of the molecule and the honeycomb lattice) defined by the C top configuration is consistent with the molecular orientation observed experimentally on the triazine SAMs formed both on HOPG and G/Pt(111). This suggests that the molecule–substrate interaction, although weak, plays a key role in fixing the SAM orientation with respect to the G.
One would be tempted to conclude that the molecule–substrate interaction controls the SAM formation. If this was the case, we should observe supercells like the  shown in figure 9(a). This configuration accommodates all the triazine molecules close to C top sites in order to maximize the substrate–molecule interaction, although they are slightly rotated from the perfect C top configuration to favor the correct alignment of the H-bonds. Although retaining the proper orientation, this favorable substrate binding configuration imposes intermolecular N–H distances of ∼2.7 Å that are large compared to the intermolecular distance in the isolated triazine monolayer (2.35 Å). This results in a high cost in intermolecular binding: using the results of figure 8, the intermolecular energy in the
shown in figure 9(a). This configuration accommodates all the triazine molecules close to C top sites in order to maximize the substrate–molecule interaction, although they are slightly rotated from the perfect C top configuration to favor the correct alignment of the H-bonds. Although retaining the proper orientation, this favorable substrate binding configuration imposes intermolecular N–H distances of ∼2.7 Å that are large compared to the intermolecular distance in the isolated triazine monolayer (2.35 Å). This results in a high cost in intermolecular binding: using the results of figure 8, the intermolecular energy in the  moiré is reduced by 3 H-bonds/molecule × ∼23 meV/H-bond = 69 meV/molecule.
moiré is reduced by 3 H-bonds/molecule × ∼23 meV/H-bond = 69 meV/molecule.
Figure 9. (a) Ball-and-stick scheme of the  supercell of triazine on graphene (the triazine network is commensurated to the G lattice) obtained from DFT (PBE-D2) simulations. The intermolecular distance is shown and the triazine molecules are adsorbed close to the C top position but slightly rotated by the effect of the H-bonds alignment. (b), (c) Experimental STM images for the triazine on the HOPG (a) and on the G/Pt(111) (b) substrate. Both the full system moiré (black dashed line) and the intermolecular (light green solid line) cells are depicted. In both images both the SAM and the substrate can be observed enabling us to obtain from them the relative orientations of the two networks. Acquisition parameters: (b) Vs = +1.16 V, It = 40 pA, size: 6.7 × 6.7 nm2 ; (c) Vs = +0.27 V, It = 760 pA, size: 5.3 × 5.3 nm2. The bias voltage was applied to the sample.
supercell of triazine on graphene (the triazine network is commensurated to the G lattice) obtained from DFT (PBE-D2) simulations. The intermolecular distance is shown and the triazine molecules are adsorbed close to the C top position but slightly rotated by the effect of the H-bonds alignment. (b), (c) Experimental STM images for the triazine on the HOPG (a) and on the G/Pt(111) (b) substrate. Both the full system moiré (black dashed line) and the intermolecular (light green solid line) cells are depicted. In both images both the SAM and the substrate can be observed enabling us to obtain from them the relative orientations of the two networks. Acquisition parameters: (b) Vs = +1.16 V, It = 40 pA, size: 6.7 × 6.7 nm2 ; (c) Vs = +0.27 V, It = 760 pA, size: 5.3 × 5.3 nm2. The bias voltage was applied to the sample.
Download figure:
Standard image High-resolution imageThe analysis above points out to a dominant role for the intermolecular interaction. In fact, our calculations show that the strength of molecule–substrate and intermolecular interactions are similar. For G, for example, the binding energy in the C top position (−404 meV with PBE-D2) is of the order of the H-bond contribution per molecule (6/2 H-bonds/molecule × −119 meV/H-bond = −357 meV/molecule). The SAM formation is ruled by the subtle balance between changes in both the binding energy and the intermolecular interaction that are controlled by (i) the corrugation of the binding PES, and (ii) the distance dependence of the intermolecular interaction, and result in large moirés. The latter is the key factor according to our analysis of the equilibrium configuration of the three-molecule island on all of the substrates: we found lateral displacements with respect to the C top site in order to keep the intermolecular distances very close to those of the isolated triazine monolayer. This is also consistent with the experimental results. In the large moiré patterns observed in the experiments, the intermolecular distances are close to its optimum value—with an intermolecular energy loss of less than 3 meV per molecule (see figure 8)—while the molecules are not placed on optimal C top adsorption configurations but distributed along the binding PES that has a corrugation around 60 meV (figure 4). Assuming a uniform distribution, this would result on an average binding energy loss of ∼30 meV/molecule, that is compensated by the more favorable intermolecular interaction. This subtle balance explains the preferential stability of large moiré patterns. Notice that for this system we predict a variation of the adsorption distances of ∼15 pm inside these large moirés (figure 4) and that molecules on non-highly-symmetric sites should be slightly tilted. These features could be confirmed in future STM experiments.
7.2. Does the G support play a role? Insights from the experiments
Having understood the role of the molecule–substrate and intermolecular interactions, we address the possible reasons behind the discrepancy found between our calculations and the experimental evidence about the influence of the substrate on the SAM formation. The different moiré patterns found in the experiments for HOPG and G/Pt(111) can be explained phenomenologically in terms of the mismatch between the different lattice periodicities involved [59]. We have analyzed the experimental STM images in order to determine the moiré periodicity (see figures 9(b) (c)), the commensurability and the relative orientation of the molecular and substrate lattices. For graphite, the images can be reproduced with a  periodicity (lattice parameter 40.3 Å), where the molecular layer is rotated 19.8° with respect to the graphite lattice (see figures S1 and S2 on the supporting information). The same analysis for the G/Pt(111) case, gives a periodicity of
periodicity (lattice parameter 40.3 Å), where the molecular layer is rotated 19.8° with respect to the graphite lattice (see figures S1 and S2 on the supporting information). The same analysis for the G/Pt(111) case, gives a periodicity of  (lattice parameter 43.7 Å), and a relative angle of 21.2° (see figures S3 and S4 on the supporting information). In graphite, the lattice mismatch between the molecular layer and the G lattice is very small (−0.02%). When Pt is introduced, a new lattice periodicity has to be taken into account. If the moiré pattern for G-triazine were preserved, there would be a mismatch of more than 2% between the metal and the G-triazine system. Thus, it is favorable for the system to choose a different moiré pattern with a unit cell that slightly increases the mismatch of the triazine monolayer with the G (0.05%), and consequently the intermolecular distance, but considerably reduces the mismatch with the Pt underneath (0.2%).
(lattice parameter 43.7 Å), and a relative angle of 21.2° (see figures S3 and S4 on the supporting information). In graphite, the lattice mismatch between the molecular layer and the G lattice is very small (−0.02%). When Pt is introduced, a new lattice periodicity has to be taken into account. If the moiré pattern for G-triazine were preserved, there would be a mismatch of more than 2% between the metal and the G-triazine system. Thus, it is favorable for the system to choose a different moiré pattern with a unit cell that slightly increases the mismatch of the triazine monolayer with the G (0.05%), and consequently the intermolecular distance, but considerably reduces the mismatch with the Pt underneath (0.2%).
7.3. Why we do not observe any support influence in the calculations?
The analysis presented above clearly shows the effect of the Pt support through the interaction of the molecules with the Pt atoms either directly or through the modulation created in the G by the Pt surface. Our calculations should capture this effect: the SAM should be trading the loss of some intermolecular bonding energy to accommodate the adsorption positions to the Pt lattice or to the G(3 × 3)/Pt(111) moiré. Remember that the only trace of the Pt in our calculations on this substrate is a difference of ∼2 meV/molecule in the binding energy among equivalent adsorption sites located on different areas of the G(3 × 3)/Pt(111) moiré.
A simple estimate of the energy difference between the moiré patterns observed on graphite and G/Pt(111) does not support the preferential stability of the latter for the G/Pt(111) case: the larger intermolecular distances would result on a reduction of the intermolecular energy of ∼2 meV/H-bond×3 H-bond/molecule ∼6 meV/molecule (figure 8), that cannot be compensated by the ∼2 meV/molecule adsorption energy corrugation of the G/Pt(111) moiré. This result is consistent with the theoretical underestimation of the diffusion barriers and seems not to be essentially modified by the use of other XC functionals and vdW implementations.
The evolution of the diffusion barriers with the adsorption distance (figure 10) suggests that we can increase significantly those barriers if we push the triazine molecule towards the G layer: a rigid reduction of the adsorption distance for all the sites by ∼0.2 (∼0.3) Å for graphite (G/Pt(111)) would bring those barriers to agreement with the experimental values. Thus, our calculations point out to an underestimation of the molecule–substrate interaction, larger in the presence of Pt, as a possible explanation for the discrepancies with experiments in the value of the diffusion barriers and the influence of the G support.
Figure 10. Energy difference between the C top and N top adsorption positions calculated with PBE-D2 plotted for different adsorption distances. The results for the three substrates (G in red, graphite in orange and G/Pt(111) in blue) are shown. The range of adsorption distances that was got in the calculations is highlighted in gray. The regions colored with light orange and light blue are those on which the adsorption distances should reproduce the experimental barrier for the graphite and G/Pt(111) respectively. The inset shows the increase in energy difference when the adsorption distance decreases between the most repulsive and most attractive moiré sites for the same geometry (C top in black and N top in gray) in the G/Pt(111) substrate.
Download figure:
Standard image High-resolution imageWe can analyze the implications of this idea by exploring the evolution of the N top-C top energy difference versus the adsorption distance as is shown in figure 10 for the three different substrates using PBE-D2. According to this test, we can predict the adsorption distance ranges for which the experimental barriers would be reproduced. At the new predicted equilibrium adsorption distances (different for each site), the binding PES for the G/Pt(111) case has a larger corrugation (difference in binding energy among equivalent sites on different areas of the G(3 × 3) moiré) needed (∼10 meV/molecule, see the inset on figure 10) to compensate the intermolecular energy loss (∼6 meV, see above), required to accommodate the triazine SAM to the Pt lattice and stabilize the  moiré observed on the G/Pt(111) case.
moiré observed on the G/Pt(111) case.
Our results clearly show that the effect of the short range interaction should be larger in order to get a good comparison with the experimental evidences. The first candidate to explain this would be that the attraction, provided by the vdW dispersion forces, yielded by our calculations is being underestimated: an increase of the vdW contribution would decrease the adsorption distances towards the values that are required to reproduce the experiments.
Notice that what it is needed is an increase of the vdW force, as it is the one that should compensate the repulsive short range force to fix the adsorption position of the molecules.
Nevertheless, the most accurate vdW implementations that we have tried, D3 and MBD approaches, show similar forces (see figure 11) [13]. Even the D2 scheme, which is well-known to overestimate the vdW contributions [28, 29], is unable to reduce the adsorption distances enough to reproduce the experimental data. Indeed, it would be needed to increase the vdW-D2 by a factor of 2 (3) for the graphite (G/Pt(111)) substrate to get to the required adsorption distances. The good agreement between the most reliable vdW implementations, that have been well tested in other systems [13, 25, 28, 29], lead us to think that assuming errors on the calculation of this contribution of 200%–300% is not reasonable.
Figure 11. Comparison between the different vdW approaches contributions for the PBE functional versus the adsorption distance for the case of the molecule on a C top on top a graphene substrate. The most advanced D3 and MBD yield very similar results, D2 overestimates and TS+SCS underestimate the force respect to the D3 and MBD schemes [13].
Download figure:
Standard image High-resolution imageAfter discarding the vdW as the prime suspect, we need to consider other sources of disagreement. The next candidate left is the short range interaction. In order to characterize the system with more sophisticated XC functionals we have used the CRYSTAL code which is more optimized than VASP for simulations with hybrids.
To check the comparison between the two codes we first perform a benchmark calculation with PBE-D2. In the top panel of figure 12 the results of the calculations with VASP and CRYSTAL are compared. It can be observed that, as expected, the vdW contribution matched exactly between the two codes (the D2 implementation is purely geometrical) while there is an evident difference in the short range interaction. This discrepancy can be explained in terms of the basis set used: the decay of the Gaussian wave functions of CRYSTAL is more steep than that of the plane waves of VASP. As a consequence, the equilibrium adsorption distances are pushed farther from the substrate in the case of CRYSTAL than in the case of VASP (see figure 12). Once we have clarified this difference between codes let us analyze the results obtained with CRYSTAL for hybrid XC functionals.
Figure 12. (a) Comparison between the variation of adsorption energy with the adsorption distance for PBE-D2 calculations in VASP (in solid lines) and in CRYSTAL (in dashed lines) for the graphene substrate. The different contributions are plotted with different symbols: vdW with triangles, short range with circles and the total energy with squares. The results for the C top geometry are depicted in green colors and the N top ones appear in purple. In both cases, lighter colors correspond to VASP results and darker colors correspond to CRYSTAL results. The positions of the minima for the total energy curves are marked with red (VASP) and black (CRYSTAL) circles. (b) The difference of energies between the C top and N top adsorption positions for the graphene substrate is plotted for different adsorption distances. The results for the different XC approaches tried are shown.
Download figure:
Standard image High-resolution imageThree different well-tested functionals have been used in these calculations (HSE06, PBE0 and B3LYP). In the lower panel of figure 12 we compare the N top-C top energy differences between the different functionals including the results for PBE obtained with both VASP and CRYSTAL—the difference between codes previously discussed is evident too. The obvious conclusion from this figure is that there is no significant change in the energy differences originated for the use of different XC functionals: the energy differences are larger than the one calculated with VASP but all the CRYSTAL results are very similar among them.
We are, then, unable to address the source of our lack of interaction because the two main suspects—the vdW and the chemical interactions—separately seem to be not enough to explain the discrepancies with the experiment.
8. Conclusions
We have studied the formation of triazine SAMs on G, graphite and G/Pt(111) substrates with the more advanced DFT techniques. In the three cases, we have characterized both the molecule–substrate and the intermolecular interactions. Our results show that the SAM formation in these weakly interacting systems is ruled by a subtle balance between both interactions, which are of the same order. Thus, the theory shows that the molecular orientation found in the experiments, the same that characterizes the minimum energy adsorption site for a single molecule, is driven by the molecule–substrate interaction. However, the intermolecular contribution leads to large moiré patterns instead of the smaller periodicities favored by the molecule–substrate interaction.
The experiments show that the SAMs of triazine form moiré patterns which try to minimize the mismatch not only with the G layer but also with the substrate underneath. Our calculations do not capture this effect. Neither the diffusion energy barriers in any substrate. We have shown that these discrepancies with the experiment are related with a theoretical underestimation of the molecule–substrate interaction. However, neither the vdW description nor different approaches for XC functionals are able to solve the discrepancies with the experiments in both the value of the energy barriers and the effect of the substrate underneath graphene.
Our study shows that molecule-G systems are a paradigmatic example to test the accuracy of new XC functionals and vdW implementations to describe the short- and long-range electron–electron correlations needed to describe weakly interacting systems. On these large systems first principles simulations cannot deal the whole cell and has to be complemented with approaches to simplify the calculation of the interactions. However, experimental results have not been reproduced even with the actual state-of-the-art DFT-based methods. Binding energies, diffusion barriers, and the subtle balance between intermolecular and molecule–substrate interactions are excellent benchmarks to guide the development of the next generation of DFT tools.
Acknowledgments
We thank A Tkatchenko for fruitful discussions. Financial support from the Spanish MINECO under grants MAT2014-54484-P, MAT2013-41636-P, MAT2016-77852-C2-2-R and CSD2010-00024 is gratefully acknowledged. Computer time provided by the Spanish Supercomputing Network (RES) in the CeSViMa-UPM (Magerit) is gratefully acknowledged. AJM-G was supported by the Juan de la Cierva program.













