Abstract
The optical radiation force, spin and orbital torques exerted on a subwavelength prolate gold spheroid coated by a layer of plasmonic material with negative permittivity and illuminated by either a zeroth-order (non-vortex) or a first-order vector Bessel (vortex) beam are computed in the framework of the electric dipole approximation method. Calculations for the Cartesian components of the optical radiation force on a subwavelength spheroid with arbitrary orientation in space are performed, with emphasis on the order (or topological charge), half-cone angle of the beam, and the plasmonic layer thickness on- and off-resonance. A repulsive (pushing) force is predicted for the layered subwavelength prolate spheroid, on- and off-resonance along the direction of wave propagation. Moreover, the Cartesian components of the spin radiation torque are computed where a negative longitudinal spin torque component can arise, suggesting a rotational twist of the spheroid around its center of mass in either the counter-clockwise or the clockwise (negative) direction of spinning. In addition, the longitudinal component of the orbital radiation torque exhibits sign reversal, indicating a revolution around the beam axis in either the counter-clockwise or the clockwise directions. The results show that the plasmonic resonance strongly alters the force, spin and orbital torque components, causing major amplitude enhancements, signs twists, and complex distributions in the transverse plane.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Elongated gold (Au) spheroidal nanoparticles coated by a metallic plasmonic layer (such as silver, copper, or other artificial materials etc) are particularly useful in various inorganic chemistry, metamaterials, drug delivery, biosensing [1] and biophysics applications to name a few examples. A carefully-designed conformal plasmonic layer coating of such particles provides the capability of detecting single-molecule events [2] by monitoring the shift of the plasmonic resonance. In practice, these particles can be rotated and transported before they get released to the desired site using optical tweezers [3] and tractor beams [4, 5], due to the transfer of linear and angular momenta carried by light waves [6].
Optimal design often relies on the computational modeling [7, 8] of the induced optical force, spin and orbital torques [9–14] as a priori information used for experimental guidance. Thus, numerical simulations constitute indispensable tools for guiding and improving the functionalities of the technological devices and experimental setups.
Several investigations considered computational analyses for the optical force and torques on spheroidal particles in optical tweezers [15–21], including the long-wavelength (Rayleigh) limit in Gaussian [22] and focused beams [23], Bessel beams [24, 25], and light-sheets [26] as well as the geometrical optics regime [27, 28]. Tailoring the incident wave field and beam profile to enhance or reduce light scattering from the particle can create a paradigm shift in optical manipulation procedures, such that negative pulling or positive pushing forces can be generated, and used to advantage depending on the application in mind. Such beams include circularly-polarized [29] or helicoidal (vortex) beams [30] possessing a phase singularity.
A high-order Bessel vector beam (HOBVB) [31] possesses an axial phase singularity (i.e., a null in amplitude or intensity) at the central region [32]. Such a beam is characterized by an integer positive or negative topological charge (or order) m ≠ 0, and a half-cone angle β such that below 20°, the paraxial approximation holds [33]. Notice that the dimensions of the singularity in the axial region increase as m increases [34]. Moreover, the HOBVB resists diffraction over an extended distance of several wavelengths, and has the capability to reform [35–38] after encountering an obstruction, as long as the whole beam is not blocked. In addition, a HOBVB has the capability of inducing a negative pulling radiation force [39–44] as well as spin [45, 46] and orbital [46] torque reversal [45–48] depending on the beam parameters.
All these properties make the optical HOBVB an attractive candidate from the standpoint of particle manipulation and handling applications. Various investigations recognizing the importance and utility of the HOBVB considered the case of a sphere, and examined the resonance scattering [49], radiation forces [42, 43, 50, 51] and torques [45, 46, 48]. Nonetheless, in some instances, the actual shapes of a variety of objects deviate significantly from the spherical geometry. Thus, applying the standard formulations devoted initially to spheres leads to significant miscalculations of the force, spin and orbital torque components for elongated aggregates. Recognizing the need to fill this gap, numerous investigations considered the spheroidal elongated particle geometry in plane waves and Gaussian beams [15, 17–21, 27, 28].
The aim of this work is therefore directed towards providing a formalism to predict numerically the mechanical effects induced by an optical HOBVB interacting with a coated prolate subwavelength spheroid (figure 1) in the framework of the electric dipole approximation, although recent works considered the optically-active [24], semiconducting [25] and dielectric [26] spheroidal particles. The particular case of a subwavelength spheroid coated by a plasmonic layer of material with a refractive index different from that of the surrounding medium is of particular interest in various biophysical [2, 52], bio-sensing [1], nanomaterials [53–55] and other applications since a new class of biosensors can emerge, which consists of detecting molecular events at the early stage. The plasmonic resonance effect can be harnessed from the standpoint of particle manipulation and handling applications in order to achieve high-performance optical devices and systems. Therefore, it is of some importance to examine the features of a plasmonic coating, combined with those of a dielectric core material in a single object, such as the layered spheroid, from the standpoint of the optical radiation force, spin and orbital torque theories.
Figure 1. The schematic describing the interaction of an optical high-order Bessel vortex beam with a coated prolate spheroid with arbitrary orientation in space. The internal/external major and minor semi-axes are ai, ae and bi, be, respectively, where the relative thickness factor is e = be/bi ≥ 1.
Download figure:
Standard image High-resolution imageSection 2 provides a description of the method in the framework of the electric dipole approximation method and from the standpoint of the radiation force, spin and orbital torque theories where the modified electric polarizability for the coated spheroid is defined as a tensor of rank two, and includes the radiative correction of the electric field. Section 3 is devoted to numerical examples for a layered spheroid in a HOBVB with particular emphasis on the beam parameters and the plasmonic layer thickness. The electric field components for the HOBVB [56, 57] are determined based on the dual-field method [56] stemming from the Lorenz gauge condition [58] and Maxwell's equations [59]. Adequate discussions of the results are also provided, while section 4 concludes this work.
2. Method
A dielectric subwavelength coated spheroid subjected to an incident optical beam develops an electric dipole moment, such that the resulting electric radiation force F in a medium of wave propagation that is nonmagnetic and nonelectric (with a unit index of refraction) such as vacuum, is expressed as [60],
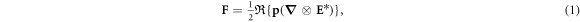
where  is the real part of a complex number, the symbol
is the real part of a complex number, the symbol  denotes a tensor product,
denotes a tensor product,  represents the electric dipole moment,
represents the electric dipole moment,  is the modified electric polarizability, which accounts for the radiative nature of the field, the double over-bar denotes a tensor of rank two [61], E is the incident electric field, and the superscript * denotes the conjugate of a complex number. The modified electric polarizability tensor is generally a complex number, given as [62],
is the modified electric polarizability, which accounts for the radiative nature of the field, the double over-bar denotes a tensor of rank two [61], E is the incident electric field, and the superscript * denotes the conjugate of a complex number. The modified electric polarizability tensor is generally a complex number, given as [62],
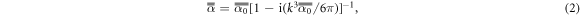
where the matrix representing  for a coated spheroid is expressed as,
for a coated spheroid is expressed as,
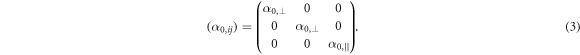
The coefficients  and
and  are the components of the static electric molecular polarizability tensor, which are expressed as,
are the components of the static electric molecular polarizability tensor, which are expressed as,
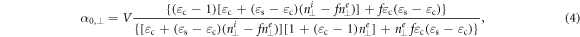
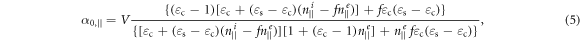
where 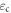 and
and  are the permittivities of the coating and the bare spheroid, respectively. Notice that for optically-absorptive (or active) coating and/or core materials,
are the permittivities of the coating and the bare spheroid, respectively. Notice that for optically-absorptive (or active) coating and/or core materials,  and
and 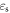 are generally complex numbers. The parameter
are generally complex numbers. The parameter  is the volume of the coated spheroid,
is the volume of the coated spheroid,  is the fraction of particle volume occupied by the internal spheroid, the parameters
is the fraction of particle volume occupied by the internal spheroid, the parameters  and
and 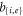 are the internal and external semi-major and semi-minor axes of the coated spheroid, respectively (figure 1), and the depolarizing factors are given as [61],
are the internal and external semi-major and semi-minor axes of the coated spheroid, respectively (figure 1), and the depolarizing factors are given as [61],
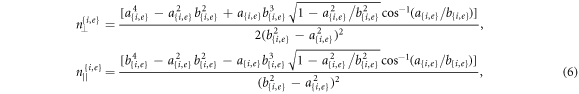
where the interior and exterior semi-axes satisfy the confocal condition [63]  which leads to a layer of non-uniform thickness across the surface of the prolate spheroid.
which leads to a layer of non-uniform thickness across the surface of the prolate spheroid.
The rotation of the spheroid with respect to its center of mass is described by two additional angular parameters (θ0, ϕ0), where θ0 and ϕ0 are the polar and azimuthal angles of the major axis, respectively (figure 1). The rotation of the spheroid in space affects the modified and static polarizability tensors  and
and  respectively, such that in matrix notation,
respectively, such that in matrix notation,  and
and  where the rotation matrix is given by [28],
where the rotation matrix is given by [28],
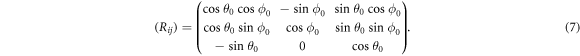
In addition to the radiation force, the layered spheroid experiences a spin radiation torque vector  causing its spinning around its center mass, as well as a longitudinal orbital torque component
causing its spinning around its center mass, as well as a longitudinal orbital torque component 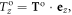 (known also as the torque of revolution [10]) causing its rotation around the main axis of the incident beam, in the plane perpendicular to the direction of wave propagation, where
(known also as the torque of revolution [10]) causing its rotation around the main axis of the incident beam, in the plane perpendicular to the direction of wave propagation, where  is the unit vector along the direction of wave propagation. Unlike the case of a (coated) sphere [64] for which energy absorption in its coating/core materials is required in order that it experiences a spin torque causing its rotation around its center of mass [10], the (layered) spheroid considered here, which is made of lossless coating/core materials, is subjected to a non-zero spin torque depending on its orientation in space. Furthermore, the orbital torque only has a longitudinal component
is the unit vector along the direction of wave propagation. Unlike the case of a (coated) sphere [64] for which energy absorption in its coating/core materials is required in order that it experiences a spin torque causing its rotation around its center of mass [10], the (layered) spheroid considered here, which is made of lossless coating/core materials, is subjected to a non-zero spin torque depending on its orientation in space. Furthermore, the orbital torque only has a longitudinal component  as the orbiting of the spheroid around the beam axis occurs solely in the transversal plane (x, y). The total radiation torque is expressed as,
as the orbiting of the spheroid around the beam axis occurs solely in the transversal plane (x, y). The total radiation torque is expressed as,
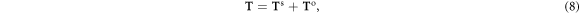
where the spin torque [65, 66] is expressed as
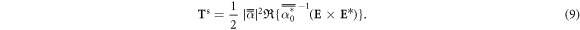
The longitudinal orbital torque component (along the direction of wave propagation z) is calculated from the transverse components of the force given by equation (1), such that
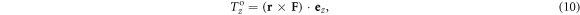
where r is the vector position.
Equations (1), (9), and (10) show that the radiation force and torque expressions depend directly on the incident electric E = (Ex, Ey, Ez) of the HOBVB. For an unpolarized HOBVB [56, 57] with a harmonic time-dependence in the form of  omitted from the equations for convenience, the expressions for the Cartesian components of the electric field are given by,
omitted from the equations for convenience, the expressions for the Cartesian components of the electric field are given by,

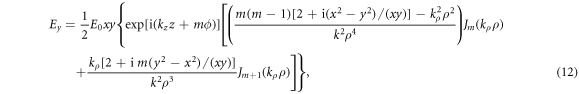
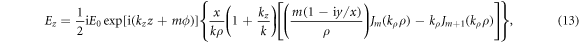
where 
 is an amplitude factor,
is an amplitude factor, 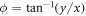 is the azimuthal angle,
is the azimuthal angle, 

 is the radial distance to a point in the transverse plane (x, y), β is the half-cone angle of the beam, and
is the radial distance to a point in the transverse plane (x, y), β is the half-cone angle of the beam, and  is the cylindrical Bessel function of the first kind of order m, which determines also the topological charge (or order) of the HOBVB.
is the cylindrical Bessel function of the first kind of order m, which determines also the topological charge (or order) of the HOBVB.
3. Numerical results and discussions
The analysis is started by developing a MATLAB numerical code to implement equations (1)–(13) and compute the optical radiation force, spin and orbital torque components for a gold (Au) spheroid in air with a permittivity coefficient εs = −50, coated by a plasmonic layer of material with a permittivity coefficient εc. The Cartesian components of the optical radiation force and radiation spin and orbital torques are computed in the ranges −10 ≤ (kx, ky) ≤ 10.
Initially, a Rayleigh prolate spheroid is considered, with kae = 0.25 > kbe = 0.1. To characterize the properties of the layered spheroid, computational plots for the components of the modified electric polarizability given by equation (2) are evaluated, by varying the relative thickness (be/bi ≥ 1) of the layer as well as its permittivity. The chosen bandwidths are 1 ≤ (be/bi) ≤ 10 and −5 ≤ εc ≤ 0. Panels (a)–(d) of figure 2 illustrate the results for this example where the real part of the transverse  and longitudinal
and longitudinal  modified polarizability components (i.e., panels (a) and (c)) display positive and negative values while the imaginary part (shown in panels (b) and (d)) only show positive values. Those plots show that each of the modified polarizability component for the subwavelength spheroid coated by a layer of a plasmonic material, exhibits a particular resonance determined by the values of the layer thickness and its permittivity. It is anticipated that these effects significantly modify the radiation force, spin and orbital torques, as will be further examined in the following.
modified polarizability components (i.e., panels (a) and (c)) display positive and negative values while the imaginary part (shown in panels (b) and (d)) only show positive values. Those plots show that each of the modified polarizability component for the subwavelength spheroid coated by a layer of a plasmonic material, exhibits a particular resonance determined by the values of the layer thickness and its permittivity. It is anticipated that these effects significantly modify the radiation force, spin and orbital torques, as will be further examined in the following.
Figure 2. The plots corresponding to the transverse  and longitudinal
and longitudinal  complex modified electric polarizability components for a subwavelength gold (Au) spheroid with kae = 0.25, kbe = 0.1, and a permittivity εs = −50, coated by a layer of a plasmonic material. A resonance appears clearly in each panel by varying the thickness ratio (be/bi) and the layer permittivity εc. The marks A and B in panel (c) correspond to the numerical values chosen for the thickness ratio (be/bi) and εc in the subsequent computations for the off- and on-resonance cases, respectively.
complex modified electric polarizability components for a subwavelength gold (Au) spheroid with kae = 0.25, kbe = 0.1, and a permittivity εs = −50, coated by a layer of a plasmonic material. A resonance appears clearly in each panel by varying the thickness ratio (be/bi) and the layer permittivity εc. The marks A and B in panel (c) correspond to the numerical values chosen for the thickness ratio (be/bi) and εc in the subsequent computations for the off- and on-resonance cases, respectively.
Download figure:
Standard image High-resolution imageThe first example considers the case of a gold prolate spheroid with kae = 0.25, kbe = 0.1 and εs = −50, coated by a layer of a plasmonic material such that (be/bi) = 1.2 and εc = −4.134. The layer material properties are selected based upon the plots of figure 2 (denoted by mark A in figure2(c)), such that no resonance occurs for this set of parameters. The subwavelength spheroid in air is illuminated by an optical zeroth-order (i.e., m = 0) Bessel beam with β = 35°, and its orientation angles in space are (θ0, ϕ0) = (45°, 0°) chosen to illustrate the analysis. Panel (a) of figure 3 displays the results for the radiation force components, where the background corresponds to the longitudinal component Fz of the force vector, while the vector arrows superimposed on the plot denote the transverse radiation force vector field F⊥ = (Fx, Fy). As observed from the background plot, the longitudinal force component is always positive, which tends to push the coated prolate spheroid away from the source along the direction of wave propagation. Moreover, the transverse vector force field (represented by the vector arrows) converges towards the main axis, and has the tendency of pushing the prolate spheroid to the central region. Panel (b) of figure 3 shows the plots for the spin radiation torque components, where the background is for the longitudinal component  while the vector arrows superimposed on the plot denote the transverse spin radiation torque vector field
while the vector arrows superimposed on the plot denote the transverse spin radiation torque vector field  The background plot for the longitudinal spin torque component shows that
The background plot for the longitudinal spin torque component shows that  is negative over well-defined regions around the main axis and as the radial distance ρ increases. The transverse vector field denoted by the arrows points towards the positive ky direction suggesting a transverse spin torque component
is negative over well-defined regions around the main axis and as the radial distance ρ increases. The transverse vector field denoted by the arrows points towards the positive ky direction suggesting a transverse spin torque component  larger than
larger than  Panel (c) of figure 3 displays the longitudinal orbital torque component over which the transverse radiation force vector field F⊥ = (Fx, Fy) is superimposed. Also,
Panel (c) of figure 3 displays the longitudinal orbital torque component over which the transverse radiation force vector field F⊥ = (Fx, Fy) is superimposed. Also,  displays negative values suggesting a sense of rotation in the counter-clockwise direction, not in phase with those of the spin radiation torque component
displays negative values suggesting a sense of rotation in the counter-clockwise direction, not in phase with those of the spin radiation torque component  as shown in panel (b). Moreover, the longitudinal spin radiation torque component is an order of magnitude smaller than its orbital counterpart.
as shown in panel (b). Moreover, the longitudinal spin radiation torque component is an order of magnitude smaller than its orbital counterpart.
Figure 3. Panel (a) displays the plot for the longitudinal radiation force of a zeroth-order Bessel beam, over which the transverse radiation force vector field is superimposed. Panel (b) displays the plot for the longitudinal spin radiation torque, over which the transverse spin radiation torque vector field is superimposed. Panel (c) shows the longitudinal orbital torque component over which the transverse radiation force vector field is superimposed. For this example, the physical parameters used off-resonance are kae = 0.25, kbe = 0.1, εs = −50, (be/bi) = 1.2 and εc = −4.134.
Download figure:
Standard image High-resolution imageGuided by the plots of figure 2, a layer of a plasmonic material is chosen such that (be/bi) = 4 and εc = −4.134 (denoted by mark B in figure 2(c)). This choice of parameters indicates the emergence of a plasmonic resonance in the plots of α∣∣. Keeping all the other parameters of the prolate spheroid and incident beam the same, numerical simulations for the force and torque components are performed, and the results are displayed in figure 4. Panel (a) of figure 4 displays the longitudinal force component at resonance, which is about five orders of magnitudes larger than its counterpart, away from the plasmonic resonance (i.e., panel (a) of figure 3). Moreover, the transverse vector force field denoted by the arrows converges no longer to the main central region as observed in panel (a) of figure 3, rather it has a tendency to push the prolate spheroid along the negative kx-direction. In addition, a quasi-vortex behavior of the transverse vector field is manifested from either side of the main axis (kx, ky) = (0, 0), such that for ky > 0, a clockwise sense of rotation is observed, whereas for ky < 0, a counter-clockwise sense of rotation is exhibited. The plots for the longitudinal spin and orbital torque components displayed in panels (b) and (c) of figure 4 also show an amplitude increase of about two orders of magnitudes compared to those of figure 3, and negative longitudinal spin and orbital torques can still occur at the plasmonic resonance. Moreover, panel (b) shows that the transverse spin torque vector field is oriented towards the positive ky direction for kx > 0, while the sign of the vector arrows is reversed for kx < 0.
Figure 4. The same as is figure 3, but for a layered spheroid having a plasmonic resonance (for α∣∣) such that (be/bi) = 4 and εc = −4.134.
Download figure:
Standard image High-resolution imageThe effect of increasing the order of the beam to m = 1 is further investigated for the prolate spheroid having kae = 0.25, kbe = 0.1 and εs = −50, and coated by a layer of a plasmonic material such that (be/bi) = 1.2 and εc = −4.134. The half-cone angle of the first-order Bessel vortex beam is β = 35°, and the orientation angles of the spheroid in space are (θ0, ϕ0) = (45°, 0°). Panel (a) of figure 5 shows an asymmetric behavior of the longitudinal force component in the form of a crescent in the transverse plane (kx, ky), where the transverse vector force field converges for the maximal value of Fz. Nevertheless, it diverges radially below the crescent, suggesting that the prolate spheroid may be pushed outside that zone. This behavior is different from panel (a) of figure 3 for the zeroth-order Bessel beam. Moreover, Fz > 0 suggests the emergence of a pushing/repulsive longitudinal force acting in the forward direction of wave propagation. The background plot in panel (b) shows the longitudinal spin radiation torque component, which displays negative and positive values, suggesting a counter-clockwise or a clockwise sense of rotation around the center of mass of the layered spheroid, respectively. An asymmetry in the plot of  also arises versus the central axis kx = 0. Moreover, the transverse vector force field denoted by the arrows is directed towards the positive ky direction, suggesting that
also arises versus the central axis kx = 0. Moreover, the transverse vector force field denoted by the arrows is directed towards the positive ky direction, suggesting that  >
>  as observed previously in panel (b) of figure 3 for the zeroth-order Bessel beam. Panel (c) displays the plot for the longitudinal radiation torque component, which is also asymmetric with respect to the axis kx = 0.
as observed previously in panel (b) of figure 3 for the zeroth-order Bessel beam. Panel (c) displays the plot for the longitudinal radiation torque component, which is also asymmetric with respect to the axis kx = 0.  exhibits negative and positive values suggesting a counter-clockwise and clockwise sense of revolution around the beam axis centered at (kx, ky) = (0, 0), respectively. Comparison between panels (b) and (c) of figure 5 shows that the longitudinal spin and orbital torque components are not in phase; i.e. in the region where
exhibits negative and positive values suggesting a counter-clockwise and clockwise sense of revolution around the beam axis centered at (kx, ky) = (0, 0), respectively. Comparison between panels (b) and (c) of figure 5 shows that the longitudinal spin and orbital torque components are not in phase; i.e. in the region where  is positive,
is positive,  is negative and vice versa.
is negative and vice versa.
Figure 5. The same as is figure 3, but the layered spheroid is illuminated by a first-order (m = 1) Bessel vortex beam (off-resonance).
Download figure:
Standard image High-resolution imageAdditional computations are performed for the first-order Bessel vortex beam with β = 35° illuminating the layered prolate spheroid at the plasmonic resonance, similarly to the case treated for figure 4, for which kae = 0.25, kbe = 0.1, εs = −50, (be/bi) = 4 and εc = −4.134. Panel (a) of figure 6 shows about a five orders of magnitudes increase in the longitudinal force amplitude, while the transverse vector force field exhibits a quasi-vortex-like structure in the counter-clockwise direction. Compared with panel (a) of figure 5, it can be concluded that the plasmonic resonance affects the behavior of the force vector components. Panel (b) displays the spin radiation torque components where  can alternate between positive and negative values, while the transverse spin torque vector field behaves similarly to its counterpart for the zeroth-order Bessel beam at the plasmonic resonance (i.e., panel (b) of figure 4). Interestingly, panel (c) of figure 6 for the longitudinal orbital torque component
can alternate between positive and negative values, while the transverse spin torque vector field behaves similarly to its counterpart for the zeroth-order Bessel beam at the plasmonic resonance (i.e., panel (b) of figure 4). Interestingly, panel (c) of figure 6 for the longitudinal orbital torque component  shows a behavior comparable to that of Fz of panel (a) with the emergence of a crescent region of large amplitude, nonetheless, it reverses sign depending on the shift from the center of the beam (where it vanishes therein) in the transverse plane. The transverse radiation force vector field is superimposed and denoted by the arrows that display the same quasi-vortex-like structure in the counter-clockwise direction, shown in panel (a).
shows a behavior comparable to that of Fz of panel (a) with the emergence of a crescent region of large amplitude, nonetheless, it reverses sign depending on the shift from the center of the beam (where it vanishes therein) in the transverse plane. The transverse radiation force vector field is superimposed and denoted by the arrows that display the same quasi-vortex-like structure in the counter-clockwise direction, shown in panel (a).
Figure 6. The same as is figure 4, but the layered spheroid is illuminated by a first-order (m = 1) Bessel vortex beam at the plasmonic resonance.
Download figure:
Standard image High-resolution imageThe effect of increasing the half-cone angle to β = 85° is further investigated, and the corresponding radiation force and torque results for the layered spheroid for which kae = 0.25, kbe = 0.1, εs = −50, (be/bi) = 4 and εc = −4.134, in a first-order Bessel vortex beam, are shown in the panels of figure 7. The one-to-one comparison of each of the panels with those of figure 6 shows that the longitudinal force, spin and orbital torque components are reduced, and the amplitude maxima are narrower for panels (a) and (b). Complex patterns arise as the half-cone angle of the beam increases.
Figure 7. The same as is figure 6, but the half-cone angle of the beam is increased to β = 85° at the plasmonic resonance.
Download figure:
Standard image High-resolution imageFinally, the variations of the radiation force, spin and orbital torque components versus the orientation angles have been computed in the ranges 0° ≤ θ0 ≤ 180° and 0° ≤ ϕ0 ≤ 360°. The same layered prolate spheroid parameters considered previously for figure 6 are used, such that kae = 0.25, kbe = 0.1, εs = −50, (be/bi) = 4 and εc = −4.134, considering a zeroth-order Bessel beam with β = 85°. The shift from the center of the beam is (kx, ky) = (0.1, 2.5) chosen as an example to illustrate the analysis. The corresponding results are displayed in panels (a)–(g) of figure 8 for the Cartesian components of the force and torques. As the shift from the center of the beam is non-zero, the transverse components of the optical force shown in panels (a) and (b) do not vanish. Nonetheless, along some specific polar and azimuthal orientation directions, the transverse components vanish due to symmetry consideration. Notice also that the longitudinal force component shown in panel (c) is positive, regardless of the values of the orientation angles. Thus, the repulsive beam effect on the layered prolate subwavelength spheroid is manifested regardless of the orientation angles. Similar variations have been also observed for the spin torque components shown in panels (d)–(f) of figure 8. The longitudinal spin torque component vanishes along symmetry orientation directional lines for θ0 = 0° or 180°, as required by symmetry. Similarly, the longitudinal orbital torque component shown in panel (g) vanishes for θ0 = 0° or 180°.
Figure 8. The plots for the Cartesian components of the radiation force, spin and orbital torque vectors for a layered subwavelength prolate spheroid at the plasmonic resonance, placed in the field of an optical zeroth-order Bessel beam with β = 85°, with a shift (kx, ky) = (0.1, 2.5) from the center of the beam, versus the orientation angles θ0 and ϕ0.
Download figure:
Standard image High-resolution imageThe effect of increasing the order of the beam to m = 1 and keeping all the other parameters the same, is also examined, and the corresponding results are displayed in the panels of figure 9. The one-to-one comparison of each of the panels with those of figure 8 shows that the force, spin and orbital torque components are significantly altered as more complex variations arise as m increases.
Figure 9. The same as in figure 8, but the layered subwavelength prolate spheroid is illuminated by an optical first-order Bessel vortex beam at the plasmonic resonance.
Download figure:
Standard image High-resolution imageOne aspect in which the calculations for the optical radiation force, spin and orbital torque components obtained here can be beneficial is the prediction of the translational and rotational dynamics of the subwavelength layered spheroid in a HOBVB. Depending on the incident beam parameters and field intensity as well as the physical properties of the spheroid, Brownian motion [67], viscous drag [68–70], optical streaming [71], a nearby boundary/wall, buoyancy and other elements can influence the translational and rotational dynamics. Typically, pre-calculated force, spin and orbital torque vector components at any position in space are used in applying Newton's second law of motion to compute the trajectories. Examples can be found for an infinite cylinder of circular cross-section in Hermite–Gaussian light-sheets [72], a sphere in Airy [73] or a coated sphere in Bessel-pincers light-sheets [64], large ellipsoids in collimated and focused beams [74], and multiple spheroidal particles in a circularly polarized dual beam trap [21] to mention a few. The scope of the present analysis can be further extended to include particle dynamics computations, and this work should assist along that direction of research.
It should be also noted here that the generation of negative optical spin and orbital torques is in complete agreement with energy conservation since computations (not shown here) for the rates of energy extinction and scattering [75] by the lossless spheroid coated by a non-absorptive plasmonic layer of material have shown equal results. Notice that the rate of energy absorption by the subwavelength spheroid considered here is zero. It must be recalled here that the spin torque reversal has been observed initially in the context of a scalar (acoustical) HOBVB incident upon a viscous sphere located arbitrarily in space (figure 4 in [47]), as well as vector (optical) HOBVBs on dielectric absorptive and semiconducting spheres [45, 48, 76] satisfying energy conservation. Furthermore, the orbital torque sign reversal, initially observed in the context of a circularly polarized Gaussian laser beam incident upon an absorptive sphere (figure 7 in [10]), and predicted previously for vector HOBVBs [46] on a semiconducting lossy sphere, is anticipated here on a subwavelength layered lossless spheroid as shown by the results of the present study. Notice, on the other hand, that for a scalar (acoustical) HOBVB incident on a subwavelength (Rayleigh) viscous fluid sphere, the orbital torque sign reversal does not occur [77].
4. Conclusion
Within the framework of the dielectric dipole approximation method, analytical solutions for the optical radiation force, spin and orbital torques are used to compute the mechanical effects of optical Bessel beams of zeroth and first orders on a non-absorptive prolate subwavelength spheroid, coated by a plasmonic layer of lossless material. In contrast to the cases dealing with Bessel beam illumination of an optically-active [24] or a semiconducting [25] subwavelength spheroid where negative pulling longitudinal forces arise (i.e. displaying a tractor beam effect), the lossless dielectric subwavelength spheroid coated by a plasmonic layer of non-absorptive material considered here always experiences a pushing longitudinal force component directed in the forward direction of wave propagation, and the transverse forces induce a collimating effect toward the central axis of the beam, off the plasmonic resonance. Nevertheless, this effect does not occur at the plasmonic resonance, where large amplitude enhancements of the positive longitudinal force component occur. Moreover, the layered spheroid is shown to experience negative spin and orbital torques causing rotation around its center of mass and revolution around the beam axis, respectively, in either the counter-clockwise or the clockwise directions. Unlike the case of a sphere, the subwavelength spheroid experiences a rotation around its center of mass in the ideal case of no-absorption inside its coating/core materials when located arbitrarily in the field of optical Bessel beams, depending on the polar and azimuthal orientation angles. The results of this analysis find potential applications in optical tweezers, tractor beams and other related topics in particle manipulation and handling.










