Deciphering the origin of nonlocal resistance in multiterminal graphene on hexagonal-boron-nitride with ab initio quantum transport: Fermi surface edge currents rather than Fermi sea topological valley currents

The recent measurements [1] of a sharply peaked nonlocal resistance R_NL in a narrow energy range near the Dirac point (DP) of multiterminal graphene on hexagonal-boron nitride (G/hBN) heterostructures have been interpreted as the manifestation of the valley Hall effect (VHE) [2–5]. In this interpretation, injecting charge current I₃ between leads 3 and 4 of the device illustrated in figure 1 generates a VH current in the first crossbar flowing from lead 1 to lead 2, which traverses the channel of length L (≃4 μm in the experiments [1]), and is finally converted into a nonlocal voltage V_NL between leads 5 and 6 by the inverse VHE in the second crossbar. The corresponding nonlocal resistance R_NL = V_NL/I₃ has been observed previously also near the DP in multiterminal graphene due to an external magnetic field inducing edge states in the quantum Hall regime or the Zeeman spin Hall effect at higher temperatures [6–10], as well as due to the spin Hall effect [10–12]. However, none of these mechanisms is operational in the experiment of [1].

Zoom In Zoom Out Reset image size

Instead, the physics of graphene on hBN with their crystallographic axes aligned is expected to be governed by the broken spatial inversion symmetry due to different potentials on two triangular sublattices of carbon atoms induced by the hBN substrate. This opens a gap E_g at the DP of two valleys K and K' in the band structure of an infinite two-dimensional sheet of graphene, where ab initio calculations have estimated E_g ≃ 58 meV [13]. In addition, the finite Berry curvature [14] of opposite sign at the two valleys was predicted to generate valley-dependent transverse conductivities, ${\sigma }_{{xy}}^{K}={e}^{2}/h$ and ${\sigma }_{{xy}}^{K^{\prime} }=-{e}^{2}/h$ [2–4]. The VH current is characterized by the transverse VH conductivity, ${\sigma }_{{xy}}^{v}={\sigma }_{{xy}}^{K}-{\sigma }_{{xy}}^{K^{\prime} }=2{e}^{2}/h$, and zero transverse charge conductivity, ${\sigma }_{{xy}}={\sigma }_{{xy}}^{K}+{\sigma }_{{xy}}^{K^{\prime} }\equiv 0$, within the gap [3, 4, 15]. Such charge-neutral valley currents, denoted also as 'topological' [1–4] due to the involvement of the Berry curvature hot spots in reciprocal space, are not conserved but are expected to be long-ranged when the intervalley scattering is weak [15].

However, ${\sigma }_{{xy}}^{v}$ is not directly observable. An attempt to connect ${\sigma }_{{xy}}^{v}$ to observable nonlocal resistance is made [1, 4, 5]

$$\begin{eqnarray}&&{R}_{\mathrm{NL}}\propto {({\sigma }_{{xy}}^{v})}^{2}{\rho }_{{xx}}^{3}{e}^{-L/{{\ell }}_{v}},\end{eqnarray} \tag{ 1 }$$

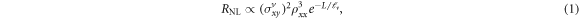
using semiclassical transport theory [16], which assumes diffusive transport with ℓ_v as the valley diffusion length [5]. However, semiclassical transport theory is not applicable [17, 18] to electronic transport near the DP. In the case of G/hBN, this is further emphasized [19] by the presence of the gap forcing electrons to tunnel through the system, which is a phenomenon with no classical analog.

The Landauer–Büttiker (LB) formalism [20–22], which offers quantum transport framework to compute V_NL and R_NL directly and has been used for decades to model nonlocal transport measurements [23, 24], yields R_NL ≡ 0 near the DP in figure 2(c) in multiterminal geometries whose channel length is larger than its width (L/W ≃ 4 in the experiments of [1]). Note that in geometries with L < W, we (as well as [19]) get ${R}_{\mathrm{NL}}\ne 0$ in figure 2(c). Nevertheless, this is trivially explained by transport through evanescent wave-functions able to propagate from the first to the second crossbar through the gap in such geometries [12, 19].

Zoom In Zoom Out Reset image size

The numerically exact result in figure 2(c), for a G/hBN system described by the same simplistic Hamiltonian employed [1–4, 15] to obtain ${\sigma }_{{xy}}^{v}\ne 0$, is clearly incompatible with the interpretation of ${R}_{\mathrm{NL}}\ne 0$ based on the picture of topological valley currents carried by the Fermi sea states just beneath the gap [3]. Such currents are conjectured to be persistent and circulating in equilibrium [3], but they become mediative VH currents connecting the two crossbars in figure 1 under the application of a bias voltage. Thus, this concept circumvents the absence of electronic states around the DP, but at a very high price—it demands a major overhaul of the LB theory [21] in which the absence of states within the gap is a fundamental reason for R_NL ≡ 0 in figure 2(c).

Another long-standing puzzle is the metallic-like ordinary longitudinal resistivity, ρ_xx ∼ 10 kΩ, commonly measured experimentally [1, 25] for the G/hBN channel between the two crossbars despite the expected finite gap in its bulk. This suggests the presence of additional conduction pathways, such as edge currents observed very recently [26, 27], which shunt the highly insulating state at low temperatures. However, previous studies have concluded that edge states are either absent [3] or, when they are present due to zigzag [28, 29] or chiral [30, 31] arrangement of edge carbon atoms, they become gapped near the DP and dispersionless away from it so they cannot carry any current [32]. The latter conclusion is reproduced in figure A1(f) in appendix A where we compute the band structure of a G/hBN wire with zigzag edges using the same simplistic Hamiltonian employed in prior theoretical studies [1–4, 15, 19, 32].

In this work, we demonstrate how to resolve both puzzles:

• R_NL ≡ 0 (figure 2(c)) obtained for multiterminal G/hBN whose bulk counterpart exhibits ${\sigma }_{{xy}}^{v}\ne 0$ (figure 4(a)),
• metallic-like ρ_xx usually measured experimentally [1, 25] despite the presumed gap opening around the DP,

using ab initio quantum transport where we perform density functional theory (DFT) calculations combined with both the multiterminal LB formula (figures 2, 3 and 5) and the Kubo formula (figure 4).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

These puzzles turn out to be an artifact of the simplistic Hamiltonian [1–4, 15, 19, 32], which inadequately describes G/hBN wires. For example, in contrast to previously obtained [32] gapped band structure for all types of G/hBN wires, the ab initio band structure (figure 3(a)) of G/hBN wires with zigzag edges has no gap. The ab initio Hamiltonian combined with the LB formula yields R_NL (figure 2(a)) and ρ_xx (figure 2(b)) whose features closely match those measured in [1]:

• the ρ_xx peak is wider than the R_NL peak,
• the magnitude of the R_NL peak decays exponentially with increasing L (figure 5(b)),
• aligned hBN is necessary to obtain ${R}_{\mathrm{NL}}\ne 0$ in figure 2(a)—an isolated zigzag graphene wire also has edge states (figure B1(a)–(f) in appendix B), but its band structure leads to R_NL ≡ 0 (figure B2 in appendix B).

Since the resolution of the two puzzles relies on an accurate Hamiltonian for G/hBN wires, as well as its combination with a proper quantum theory of observable transport quantities, we first summarize inconsistencies arising in previous theoretical analyses. The seminal arguments [2] for the VHE are based on the semiclassical transport theory describing the motion of a narrow wave-packet constructed by superposing [2, 33] eigenstates of gapped Dirac Hamiltonian ${\hat{H}}_{{\rm{D}}}$ with dispersion _k. This assumes that each valley of G/hBN can be described by

$$\begin{eqnarray}&&{\hat{H}}_{{\rm{D}}}={\hslash }{v}_{F}(\hat{{\boldsymbol{\sigma }}}\cdot \hat{{\bf{k}}})+{\rm{\Delta }}{\hat{\sigma }}_{z},\end{eqnarray} \tag{ 2 }$$

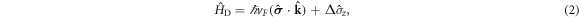
where v_F is the Fermi velocity, $\hat{{\boldsymbol{\sigma }}}=({\hat{\sigma }}_{x},{\hat{\sigma }}_{y})$ is the vector of the Pauli matrices corresponding to the sublattice degree of freedom and ${\hslash }\hat{{\bf{k}}}$ is the momentum operator. The wave-packet velocity

$$\begin{eqnarray}&&{{\bf{v}}}_{{\bf{k}}}=\displaystyle \frac{1}{{\hslash }}\displaystyle \frac{\partial {\epsilon }_{{\bf{k}}}}{\partial {\bf{k}}}+\displaystyle \frac{d{\bf{k}}}{{dt}}\times {{\boldsymbol{\Omega }}}_{{\bf{k}}},\end{eqnarray} \tag{ 3 }$$

acquires an anomalous (second) term [14] due to the Berry curvature Ω_k hot spot near the apex of the valley described by ${\hat{H}}_{{\rm{D}}}$. Since ${{\boldsymbol{\Omega }}}_{{\bf{k}}}$ in valley K has opposite direction to that in valley $K^{\prime}$, electrons belonging to two valleys will be separated [33] in the opposite transverse directions in the presence of an applied electric field E, which is required to accelerate electrons according to ${\hslash }d{\bf{k}}/{dt}=e{\bf{E}}$. This gives rise [2] to

$$\begin{eqnarray}&&{\sigma }_{{xy}}^{K,K^{\prime} }=\displaystyle \frac{{e}^{2}}{\pi h}\int {d}^{2}{\bf{k}}\,f({\varepsilon }_{{\bf{k}}}){{\rm{\Omega }}}_{{\bf{k}}},\end{eqnarray} \tag{ 4 }$$

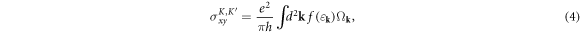
where f(ε_k) is the Fermi function forcing the integration over the whole Fermi sea, i.e. from the bottom of the band to the Fermi level E_F.

However, it has already been pointed out in [19] that nonzero E cannot appear in the linear-response limit of the multiterminal LB formula [20–22]. The experiments measuring R_NL are carefully kept [1] in the linear-response regime in order to avoid heating of the device and the ensuing thermoelectric effects that can add large spurious contributions to R_NL [7]. The multiterminal LB formula

$$\begin{eqnarray}&&{I}_{p}=\displaystyle \sum _{q}{G}_{{pq}}({V}_{p}-{V}_{q}),\end{eqnarray} \tag{ 5 }$$

relates the total charge current I_p in lead p to voltages V_q in all other leads via the conductance coefficients

$$\begin{eqnarray}&&{G}_{{pq}}=\displaystyle \frac{2{e}^{2}}{h}\int {dE}\left(-\displaystyle \frac{\partial f}{\partial E}\right){T}_{{pq}}(E),\end{eqnarray} \tag{ 6 }$$

where the negative derivative of the Fermi function confines the integration to a shell of states of width ∼k_BT around E_F [21]. The transmission functions T_pq(E) do not include any effect of ${\bf{E}}$ [20–22]. We use the multiterminal LB formula implemented in KWANT package [22, 34] to compute

$$\begin{eqnarray}&&{V}_{\mathrm{NL}}={V}_{5}-{V}_{6},\end{eqnarray} \tag{ 7 }$$

and

$$\begin{eqnarray}&&{R}_{\mathrm{NL}}=\displaystyle \frac{{V}_{\mathrm{NL}}}{{I}_{3}},\end{eqnarray} \tag{ 8 }$$

in response to an injected charge current I₃ = − I₄ [12] while keeping I_p ≡ 0 in the other four leads. A similar procedure allows us to compute the longitudinal resistivity

$$\begin{eqnarray}&&{\rho }_{{xx}}={R}_{4{\rm{T}}}\displaystyle \frac{W}{L},\end{eqnarray} \tag{ 9 }$$

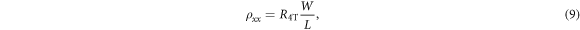
from the four-terminal resistance

$$\begin{eqnarray}&&{R}_{4{\rm{T}}}=\displaystyle \frac{{V}_{3}-{V}_{5}}{{I}_{1}},\end{eqnarray} \tag{ 10 }$$

obtained by injecting the current I₁ = −I₂ into the device of figure 1 and by imposing voltage probe conditions, I_p ≡ 0, in leads p = 3–6.

The semiclassical arguments for the origin of ${\sigma }_{{xy}}^{v}$ can be replaced by quantum transport theory based on the Kubo formula [15, 35], which requires to first obtain [36, 37] the velocity operator $\hat{{\bf{v}}}$. The physical consequences of the equation of motion for $\hat{{\bf{v}}}={v}_{F}\hat{{\boldsymbol{\sigma }}}$ defined by ${\hat{H}}_{{\rm{D}}}$ [15]

$$\begin{eqnarray}&&\displaystyle \frac{d{\bf{v}}}{{dt}}=\displaystyle \frac{1}{i{\hslash }}[\hat{{\bf{v}}},{\hat{H}}_{{\rm{D}}}]=2{v}_{F}^{2}(\hat{{\bf{k}}}\times \hat{{\boldsymbol{\sigma }}})-\displaystyle \frac{{E}_{g}}{{\hslash }}\hat{{\bf{v}}}\times {{\bf{e}}}_{z},\end{eqnarray} \tag{ 11 }$$

are extracted by finding its expectation value in a suitably prepared wave-packet [33, 38] injected with given initial velocity into G/hBN, where it can propagate even in the absence of any external electric field [38]. The first term of dv/dt causes Zitterbewegung motion of the center of the wave-packet, while the second one acts on it like a Lorentz force due to an effective magnetic field in the direction of the unit vector e_z perpendicular to the graphene plane. For electrons from the $K^{\prime}$ valley, ${\hat{v}}_{y}=-{v}_{F}{\hat{\sigma }}_{y}$, leading to opposite direction of this force.

The gapped Dirac Hamiltonian ${\hat{H}}_{{\rm{D}}}$ is a long wavelength limit of a more general tight-binding Hamiltonian (TBH). This latter accounts for both valleys and can, therefore, be used to capture intervalley scattering effects. The TBH, which is preferred for numerical calculations using the LB [19] or the Kubo formula (as well as for simulations of wave-packet dynamics [33]), is defined on a honeycomb lattice hosting a single p_z-orbital per site

$$\begin{eqnarray}&&{\hat{H}}_{\mathrm{TB}}=\displaystyle \sum _{i}{\varepsilon }_{i}{\hat{c}}_{i}^{\dagger }{\hat{c}}_{i}-{t}_{1}\displaystyle \sum _{\langle {ij}\rangle }{\hat{c}}_{i}^{\dagger }{\hat{c}}_{j}.\end{eqnarray} \tag{ 12 }$$

Here, ${\hat{c}}_{i}^{\dagger }$ (${\hat{c}}_{i}$) creates (annihilates) an electron at site i; the hopping energy t₁ = 2.7 eV is nonzero between nearest-neighbor (NN) carbon atoms; and the on-site energy ε_i = ±Δ, responsible for the gap E_g = 2Δ, is positive on one atom of the graphene unit cell and negative on the other one to take into account the staggered potential induced by the hBN substrate (while neglecting any reorganization of chemical bonding or change in the atomic order of graphene and hBN layers). We use Δ = 29 meV [13] to compute R_NL in figure 2(c) for G/hBN channel with zigzag edges, as well as to compute its band structure (figure A1(f) in appendix A) exhibiting gapped flat bands [32].

Figure 4(a) shows ${\sigma }_{{xy}}^{v}$, computed using the Kubo formula [35, 37] combined with a valley-projection scheme [10, 39], for a rhomboid supercell of G/hBN with periodic boundary conditions described by ${\hat{H}}_{\mathrm{TB}}$ in equation (12). The supercell is either clean or it contains long- or short-range disorder (delineated in appendix D) as additional terms in the on-site energy ε_i. In the clean limit, we confirm [15] that σ_xy^v = 2e²/h is quantized inside the gap (figure 4(a)), as well as that the Fermi sea states just beneath the gap provide the main contribution to it [3]. For long-range disorder that does not mix valleys, σ_xy^v remains close to the clean limit, but within a smaller energy range than E_g (figure 4(a)) due to disorder-induced broadening of the states [15]. High concentration of valley mixing short-range disorder slightly reduces σ_xy^v (figure 4(a)).

In order to replace ${\hat{H}}_{\mathrm{TB}}$ with a more accurate Hamiltonian, we proceed by computing the ab initio band structure of G/hBN wires using local-orbital pseudopotential DFT, as implemented in ATK [40] and OpenMX [41] packages, whose Kohn–Sham (KS) Hamiltonian can be also easily combined with the LB formula [42]. We assume stacking where one C atom is over a B atom and the other C atom in the unit cell is centered above the hBN hexagon, as the energetically most stable configuration found in DFT calculations [13]. The DFT Hamiltonian for a wire—composed of C, B and N atoms, as well as H atoms passivating dangling bonds along the zigzag edges—produces the gapless band structure in figure 3(a) and the corresponding zero-temperature two-terminal conductance ${G}_{21}=5\times 2{e}^{2}/h$ (figure 3(b)) near the DP (at E − E_F = 0). This value is insensitive to the presence of a nanopore within the bulk (figure 3(d)), signifying edge transport, but it is reduced to ${G}_{21}\lesssim 2{e}^{2}/h$ in the presence of edge vacancies (figure 3(e)) or quantum interferences generated by edge vacancies in series (figure 3(f)) due to lack of topological protection against backscattering [32, 43]. The valley-polarized states [44] above and below the DP are bulk states since G₂₁ is reduced at those energies by the presence of the bulk nanopore (figure 3(d)). The edge states are visualized by plotting the local density of states (LDOS) in figures 3(c)–(f), which is peaked near the edges but it remains nonzero in the bulk [31]. This can be contrasted with topologically protected edge states in quantum (ordinary [10], spin [45, 46] and anomalous [47]) Hall insulators,where LDOS in the bulk vanishes. The corresponding local current distributions (figure C1 in appendix C) shows that edge currents can survive edge disorder breaking G/hBN wire into short zigzag-edge segments, as suggested also by experiments [26]. The G/hBN wires with pristine armchair edges do not exhibit any edge states (figures B1(g)–(l) in appendix B), which, therefore, leads to R_NL ≡ 0 in multiterminal geometries with L > W.

It is worth mentioning that even in systems with nonzero topological invariants in the bulk band structure, such as the Chern number ${ \mathcal C }$ in quantum Hall and quantum anomalous Hall insulators, which counts the number of metallic edge states [32] (note that ${ \mathcal C }\equiv 0$ in the case of G/hBN [32]), zigzag edges of the honeycomb lattice play a special role due to their ability to modify the energy–momentum dispersion and the corresponding conductance carried by edge states [47]. They also shrink the spatial extent of edge states [45, 47, 48]. Nevertheless, the presence of nonzero ${ \mathcal C }$ guarantees that the quantized conductance ${ \mathcal C }\times 2{e}^{2}/h$ will survive disorder [47], while no such topological protection exists in the case of G/hBN wires whose two-terminal conductance is nonquantized $\lesssim 2{e}^{2}/h$ in the presence of edge disorder (figure 3(b)).

Since the usage of the full DFT Hamiltonian is prohibitively expensive for large number of atoms (∼10⁶ in our LB or Kubo formula calculations), we derive simpler ab initio TBHs [49]. A widely used approach for this purpose is to transform the DFT Hamiltonian to a basis of maximally localized Wannier functions in a selected energy window around E_F [50]. We combine Wannier TBH (truncated [49] to third NN hoppings without loss of accuracy in the energy window considered in figure 4) with the Kubo formula in figure 4(b), where we find quantized ${\sigma }_{{xy}}^{v}$ in the gap. Furthermore, due to longer range hoppings, ${\sigma }_{{xy}}^{v}$ in figure 4(b) has a surprising resilience to short-range disorder that was not exhibited in figure 4(a) for the simplistic TBH of equation (12). However, the same Wannier TBH applied to G/hBN wires generates much larger group velocity $\partial {\varepsilon }_{{k}_{x}}/{\hslash }\partial {k}_{x}$ of edge state bands near the DP (figure A1(d) in appendix A) than in figure 3(a) due to lack of information about atoms (like H) passivating bonds of edge carbon atoms. Nevertheless, such Wannier TBH could be useful for fully encapsulated G/hBN wires, where edges are not exposed to the environment [1, 26].

Therefore, we derive an alternative ab initio TBH that precisely fits (figure A1(c) in appendix A) the bands around the DP in figure 3(a). This requires up to the fifth NN hoppings and on-site energies in equation (12), with adjusted values along the edges (figure A2 in appendix A). The ab initio 5NN TBH combined with the multiterminal LB formula leads to ${R}_{\mathrm{NL}}\ne 0$, with a sharp peak (figure 2(a)) near the DP in the case of ballistic G/hBN channel. In addition, we also calculate R_NL and ρ_xx in the presence of disordered edges, where we remove 50% of edge tight-binding sites and also use an additional on-site energy on the remaining edge sites, which is distributed randomly in the range ±1 eV in order to model binding of different chemical species to the outermost carbon atoms [43] (see figure C1(b) in appendix C for illustration), or bulk of different range (in the model delineated in appendix D). The disorder reduces the height of the R_NL peak (figure 2(a)), while concurrently generating a peak in ρ_xx (figure 2(b)). Although metallic-like ρ_xx in figure 2(b) could arise due to trivial reasons, such as charge inhomogeneity induced by chemical or electrostatic doping at the edges [27], recent imaging [26] of proximity-induced supercurrents flowing near the edges of G/hBN wires is in accord with LDOS in figures 3(c)–(f) or local current distributions in figure C1 in appendix C.

It has been argued [1, 4, 5] that experimental confirmation of topological valley currents carried by the Fermi sea states just beneath the bulk gap E_g is achieved by observing different dependences encoded in equation (1), such as ${R}_{\mathrm{NL}}\propto {\rho }_{{xx}}^{3}$ and ${R}_{\mathrm{NL}}\propto {e}^{-L/{{\ell }}_{v}}$. However, such dependences were originally derived [16] for the diffusive spin Hall current as the mediative current between the two crossbars, and they can be observed for different types of mediative currents as long as they propagate by diffusion (as demonstrated by the measurements of nonlocal resistance in multiterminal graphene due to direct and inverse spin Hall effect [11]). This is exemplified by figure 5(a) where we find that our mediative edge currents can display ${R}_{\mathrm{NL}}\propto {\rho }_{{xx}}^{3}$ dependence in the presence of experimentally relevant long-range disorder, as well as by figure 5(b) where R_NL decays exponentially with increasing channel length L in the presence of strong edge disorder (illustrated in figure C1(b) in appendix C). Interestingly, the very recent experiments [25] on quasiballistic hBN/G/hBN heterostructures exhibiting metallic-like ${\rho }_{{xx}}$ have measured R_NL that does not scale as $\propto {\rho }_{{xx}}^{3}$ at low temperatures T ≃ 1.5 K (such cubic scaling is restored at T ≃ 40 K). Also, deep into the insulating regime (i.e., with large ρ_xx) R_NL becomes independent of ρ_xx [5].

Zoom In Zoom Out Reset image size

Thus, confirming unambiguously that R_NL originates [1, 4, 5] from topological valley currents carried by the Fermi sea states just beneath the bulk gap E_g requires to demonstrate the scaling ${R}_{\mathrm{NL}}\propto {({\sigma }_{{xy}}^{v})}^{2}$ in the same regime where ${R}_{\mathrm{NL}}\propto {\rho }_{{xx}}^{3}$ and ${R}_{\mathrm{NL}}\propto {e}^{-L/{{\ell }}_{v}}$ is found [5]. This, however, is impossible experimentally since ${\sigma }_{{xy}}^{v}$ is not directly measurable. Nevertheless, R_NL(E_F) and ${\sigma }_{{xy}}^{v}({E}_{F})$ can be calculated independently in a chosen interval of Fermi energies E_F, while using the same long-range or short-range disorder in both the LB and Kubo formula calculations. Figure 2(d) plots R_NL(E_F) from figure 2(a) computed using the multiterminal LB formula versus ${\sigma }_{{xy}}^{v}({E}_{F})$ from figure 4(b) computed using the Kubo formula. In both of these calculations, we employ the ab initio 5NN TBH delineated in appendix A in order to avoid R_NL ≡ 0 in figure 2(c) obtained for the case of the simplistic NN TBH in equation (12).

In conclusion, the R_NL peak exists in the clean limit (where ${\rho }_{{xx}}\to 0$) and it is reduced by disorder, whereas ${\sigma }_{{xy}}^{v}$ is insensitive to disorder at the DP (figure 4(b)). Furthermore, plotting ${R}_{\mathrm{NL}}({E}_{F})$ versus ${\sigma }_{{xy}}^{v}({E}_{F})$ in figure 2(d), computed for a range of E_F ≥ 0 independently while using the same long-range or short-range disorder in both the LB and Kubo formula calculations, reveals that these two quantities are not related in the way conjectured by equation (1). This strengthens our principal conclusion—the observed R_NL is driven by a particular gapless band structure and its edge eigenstates carrying current near the DP while not being protected by any nontrivial topology of bulk band structure [66], rather than by the Fermi sea dissipationless topological valley currents conjectured [1–5, 32] for the gapped Dirac spectra.

Acknowledgments

Appendix A.: Ab initio versus tight-binding band structure of G/hBN wires with zigzag edges

The diagonalization of the KS Hamiltonian in DFT to obtain the ab initio band structure proceeds by approximating the Hilbert space of all single-electron eigenfunctions with a finite set of basis functions. A popular basis set is composed of plane-waves (PWs), where varying the energy cutoff makes it possible to improve the basis systematically. Linear combination of atomic orbitals (LCAO) basis sets [51, 41] require more tuning. However, they make it possible to treat supercells containing a large number of atoms with O(N) computational complexity [52, 53]. They also simplify ab initio quantum transport device simulations—based on the LB formula combined with the KS Hamiltonian [42]—where one has to spatially separate the devices into a central region and semi-infinite leads (as illustrated by figure 1).

A commonly used minimal LCAO basis set for graphene systems is composed of single-zeta polarized (SZP) pseudoatomic orbitals [51] on C atoms [54]. However, when this is applied to G/hBN wires—together with double-zeta polarized (DZP) orbitals [51] on B and N atoms, and SZP orbitals on edge passivating H atoms—it leads to the valence band of hBN being pushed toward the Fermi level E_F, which incorrectly generates conduction through the hBN substrate. Therefore, we first perform DFT calculations for G/hBN wires with zigzag edges of width W = 13 nm using a large LCAO basis set provided in the OpenMX package [41] consisting of s2p1 orbitals on H atoms and s2p2d1 on C, B and N atoms with cutoff radius 5.0 and 7.0 a.u, respectively. This gives an accurate reference band structure shown in figure A1(a). The same is reproduced by a medium SG15 basis set [55] implemented in the ATK package [40], as shown in figure A1(b). For both calculations in figures A1(a) and (b) we use the Perdew–Burke–Ernzerhof (PBE) parametrization of the generalized gradient approximation (GGA) for the exchange-correlation (XC) functional and norm-conserving pseudopotentials for describing electron–core interactions.

Zoom In Zoom Out Reset image size

However, the matrix representations of the KS Hamiltonian in both the OpenMX and in the smaller SG15 basis sets are still too large for computationally efficient quantum transport simulations. Therefore, we perform additional calculations using DZP orbitals on all atoms C, B, N, and H and Perdew–Zunger parametrization of the local density approximation (LDA) for the XC functional, which produces a reasonably small KS Hamiltonian matrix. The corresponding band structure in figure A1(c) matches the band structure obtained in figures A1(a) and (b) in the energy interval ±0.1 eV around the DP at E − E_F = 0, which is of interest to quantum transport studies in the linear-response regime. The same match (not shown explicitly) remains valid for G/hBN wires of width W = 50 nm employed as the channel of the device in figure 1. The matrix representation of the KS Hamiltonian in the basis of DZP orbitals is employed to obtain LDOS and conductance of two-terminal wires in figures 3 and B1.

The very large number of atoms ∼10⁶ in our Kubo or multiterminal LB formula calculations makes the direct usage of KS Hamiltonian prohibitively expensive [42]. Instead, a Hamiltonian with a minimal number of orbitals per atom, as provided by semi-empirical or ab initio TBHs, is required. A widely used approach to derive an accurate ab initio TBH [49] is to project the KS Hamiltonian onto a basis of maximally localized Wannier functions, which faithfully retains the overlap matrix elements and their phases, the orbital character of the bands and the accuracy of the original DFT calculations [50]. We compute the KS Hamiltonian in the PW basis using the VASP package [56, 57], where we consider p_x, p_y and p_z orbitals on C atoms for bands around the DP of an infinite G/hBN heterostructure. In the VASP calculations, we choose a PW cutoff energy 500 eV, the PBE parametrization of the GGA for the XC functional, and the projector augmented wave method for describing electron–core interactions [58, 59]. The k-point mesh of size 8 × 6 × 1 is used for the Brillouin zone (BZ) sampling of a rectangular unit cell consisting of four C atoms.

Thus, the derived Wannier TBH, truncated [49] to third NN hoppings without loss of accuracy of band structure in the interval considered in figure 4(b), is useful for the Kubo formula calculations (figure 4(b)) on rhomboid supercells with periodic boundary conditions. However, the Wannier TBH generates a too large group velocity $\partial {\varepsilon }_{{k}_{x}}/{\hslash }\partial {k}_{x}$ of edge state bands near the DP in figure A1(d) when compared to those in figures A1(a)–(c) obtained directly from DFT calculations. This is because the VASP calculations for the periodic supercell of G/hBN used to construct the Wannier TBH did not include information about edges and edge passivating atoms. Nevertheless, the Wannier TBH could be useful for fully encapsulated hBN/G/hBN wires [25, 26], where edges are not exposed to the environment and where a large group velocity of edge state bands near the DP in figure A1(d) would make edge currents more resilient to disorder.

Therefore, we resort to the construction of another ab initio TBH via the least square fitting [60] of the bands around the DP, as shown in figure A1(c), while keeping in mind possible problems with overfitting [49]. Such ab initio TBH with single p_z-orbital per site includes up to fifth NN hoppings and on-site energies illustrated in figure A2(a) and listed in figure A2(b). The ab initio 5NN TBH is used in the computation of R_NL in figures 2(a), 2(d), 5 and B2; ρ_xx in figure 2(b); and local current distribution in figure C1.

Zoom In Zoom Out Reset image size

Figures A1(e) and (f) plot the band structure of isolated graphene and G/hBN wires, both with zigzag edges and width W = 50 nm, respectively, obtained by diagonalizing the simplistic TBH in equation (12), which includes only the NN hopping [32]. The same band structures are recomputed in figures A1(g) and (h), respectively, using the ab initio 5NN TBH from figure A2. The nonlocal resistances R_NL for channels of multiterminal device in figure 1 with band structures shown in figures A1(h), (f) and (g) are plotted in figures 2(a), (c) and B2, respectively. The gapped band structure in figure A1(f) for the simplistic NN TBH in equation (12) was obtained previously in [32]. The flat bands connecting the two valleys at the gap boundary correspond to edge states, and they are inherited from the band structure of an isolated graphene wire with zigzag edges shown in figure A1(e). That is, simulating the presence of hBN by using the staggered on-site energy ε_i = ±Δ in NN TBN in equation (12) simply opens the gap between the flat bands in figure A1(e) to produce the band structure in figure A1(f). Both of these band structures, which are an artifact of the simplistic NN TBH [31, 61] or continuous Dirac Hamiltonian with appropriate boundary conditions [62], do not generate edge currents [63]. This contradicts experimental observation of edge currents near the DP in isolated graphene wires with zigzag edges [28] or in G/hBN wires where some zigzag segments are present [26]. These edge currents [26] are responsible for the metallic-like resistivityρ_xx in figure 2(b), which is also observed experimentally [1, 25, 26].

Appendix B.: Ab initio band structure and quantum transport through isolated graphene wire with zigzag edges or G/hBN wire with armchair edges

For comparison with figure 3, we provide identically calculated panels in figures B1(a)–(f) for an isolated graphene wire with zigzag edges and in figures B1(g)–(l) for a G/hBN wire with armchair edges, both of the same width W = 13 nm. For this purpose, we use LCAO pseudopotential DFT implemented in the ATK package [40], where the KS Hamiltonian is represented in the basis of DZP orbitals on C, B, N and H atoms, LDA is used for XC functional and the energy mesh cutoff for the real-space grid is chosen as 75.0 Hartree. Careful comparison shows that the hBN substrate splits the edge bands near the DP—see inset in figure 3(a)—and also slightly changes the spatial extension of the corresponding eigenstates. This helps to make conductance in figure 3(b) more resilient to quantum interference effects in the case of a series of edge vacancies in figure 3(f), thereby evading antiresonance in the conductance at the DP in figure B1(b).

Zoom In Zoom Out Reset image size

Despite the existence of edge eigenstates in isolated graphene wires with zigzag edges, using its ab initio 5NN TBH to describe the channel of the device in figure 1 leads to R_NL ≡ 0 in figure B2 for L ≫ W geometry. This is in accord with experiments of [1] or figure 2(a), where aligned hBN is necessary to obtain ${R}_{\mathrm{NL}}\ne 0$ by modifying the energy–momentum dispersion of edge eigenstates from that shown in figure A1(g) to the one shown in figure A1(h).

Zoom In Zoom Out Reset image size

In contrast to the simplistic NN TBH for an isolated graphene wire with armchair edges, which predicts that those composed of $3p+2$ dimers are metallic [61], DFT calculations show that armchair wires of all widths have an energy gap [61]. The energy gap in figure B1(g) of G/hBN wires with armchair edges can be larger (depending on the wire width) than the gap E_g ≃ 58 meV [13] of bulk G/hBN because of transverse confinement in the case of wire geometry. As shown in figures B1(i)–(l), such gapped wires have no edge states around the DP. Since their two-terminal conductance G₂₁ in figure B1(h) is zero within the gap, using G/hBN wires with armchair edges as the channel between the two crossbars in the device in figure 1 leads to ${R}_{\mathrm{NL}}\equiv 0$ for L ≫ W geometry.

Appendix C.: Local current distribution in clean or edge-disordered G/hBN wires with zigzag edges

Figure C1 plots the local current distribution in G/hBN wires with zigzag edges, where current at a site of the tight-binding lattice is obtained by summing all bond currents [63, 64] flowing from that site to all other sites to which it is connected by nonzero hoppings of the ab initio 5NN TBH in figure A2. In the case of an infinite clean homogeneous G/hBN wire with zigzag edges, figure C1(a) reveals edge currents flowing in narrow strips near the edge with minuscule value flowing through the bulk [31]. Upon introducing edge disorder [43], whose properties are defined in figure C1(b) and which is also used to compute edge disorder effects on R_NL and ρ_xx in figures 2 and 5(b), we find that some part of the electron flux is deflected into the bulk of the wire. Nevertheless, as long as the G/hBN wire contains short zigzag-edge segments local current is confined near the edges, in agreement with very recent experimental imaging [26] of proximity-induced supercurrents in G/hBN wires.

Zoom In Zoom Out Reset image size

Appendix D.: Models for long-range and short-range disorder in the bulk

The long-range and short-range disorder—employed in the LB formula calculations in figures 2 and 5(a), as well as in the Kubo formula calculations in figure 4—is modeled as additional on-site energy terms in TBHs

$$\begin{eqnarray}&&\hat{V}=\displaystyle \sum _{n=1}^{{N}_{p}}{V}_{i}({{\bf{R}}}_{n}){\hat{c}}_{i}^{\dagger }{\hat{c}}_{i},\end{eqnarray} \tag{ D.1 }$$

where N_p is the number of impurities, ${\hat{c}}_{i}^{\dagger }$ (${\hat{c}}_{i}$) creates (annihilates) an electron at site i and

$$\begin{eqnarray}&&{V}_{i}({{\bf{R}}}_{n})=\displaystyle \frac{{U}_{n}}{{\displaystyle \sum }_{i=1}^{{N}_{\mathrm{tot}}}{e}^{-{({{\bf{r}}}_{i}-{{\bf{R}}}_{n})}^{2}/2{\xi }^{2}}}{e}^{-{({{\bf{r}}}_{i}-{{\bf{R}}}_{n})}^{2}/2{\xi }^{2}},\end{eqnarray} \tag{ D.2 }$$

is the contribution at site i due to an impurity placed at position R_n. Here N_tot is the total number of lattice sites, U_n is a uniform random variable in the interval [−U_p, U_p] and ξ is the spatial range of the impurity potential. Using this definition, the parameter K₀ in the Gaussian correlator ($\langle \ldots \rangle$ denotes disorder averaging)

$$\begin{eqnarray}&&\displaystyle \sum _{n,m}\langle {V}_{i}({{\bf{R}}}_{m}){V}_{j}({{\bf{R}}}_{n})\rangle ={K}_{0}\displaystyle \frac{{({\hslash }{v}_{F})}^{2}}{2\pi {\xi }^{2}}{{\rm{e}}}^{-{({{\bf{r}}}_{i}-{{\bf{r}}}_{j})}^{2}/2{\xi }^{2}},\end{eqnarray} \tag{ D.3 }$$

is given by K₀ ∼ N_p N_tot U_p⁴/t₁⁴ (t₁ is NN hopping) and it is independent of the spatial range ξ. This definition is similar to the one used in previous studies [17, 18, 65], but it employs a range-dependent strength of the impurity potential, which allows us to compare impurity potentials with the same U_p but different ξ parameters. The short-range disorder employed in figures 2, 4 and 5(a) is modeled using ξ = 0.1a_C−C and strength U_p = 1.275 eV, while for long-range disorder we use ξ = 10a_C−C and effective strength ≃0.005 × U_p, where a_C−C ≈ 1.42 Å is the carbon–carbon bond length. Thus, such long-range disorder can capture puddles induced by charged impurities of effective strength ∼10 meV, which is similar to realistic samples where the depth of the charged puddles is of the same order as the gap E_g.

Appendix E.: Valley-projection scheme for Kubo formula calculations

The valley-projection scheme [10, 39] we employ for numerically exact calculations of the VH conductivity ${\sigma }_{{xy}}^{v}$ in figure 4 via the real-space Kubo formula [36, 37] relies on the artificial separation of the BZ of graphene into K and ${K}^{{\prime} }$ regions with different chirality. In this scheme, the current defined over the whole BZ is separated into an electronic current due electrons in the K($K^{\prime}$) valley. This can be done by projecting the α-component of the velocity operator in the following way

$$\begin{eqnarray}&&{\hat{v}}_{\alpha }^{\overrightarrow{K}(\overrightarrow{K}^{\prime} )}\equiv {P}_{\overrightarrow{K}(\overrightarrow{K}^{\prime} )}{\hat{v}}_{\alpha }{P}_{\overrightarrow{K}(\overrightarrow{K}^{\prime} )},\end{eqnarray} \tag{ E.1 }$$

where

$$\begin{eqnarray}&&{P}_{\overrightarrow{K}(\overrightarrow{K}^{\prime} )}=\displaystyle \sum _{\overrightarrow{q}}{w}_{\overrightarrow{q}}^{\overrightarrow{K}(\overrightarrow{K}^{\prime} )}| q\rangle \langle q| ,\end{eqnarray} \tag{ E.2 }$$

with the sum going over the whole BZ. The weight, ${w}_{\overrightarrow{q}}^{\overrightarrow{K}}={\rm{\Theta }}[(\overrightarrow{q}-\overrightarrow{M})\cdot (\overrightarrow{K}-\overrightarrow{M})/| \overrightarrow{K}-\overrightarrow{M}{| }^{2}]$, breaks the BZ into two regions, one containing the $\overrightarrow{K}$ point, which has unit weight, and another which contains the $\overrightarrow{K}^{\prime}$ point with zero weight. The weight ${w}_{\overrightarrow{q}}^{\overrightarrow{K}^{\prime} }$ is defined as ${w}_{\overrightarrow{q}}^{\overrightarrow{K}^{\prime} }\equiv 1-{w}_{\overrightarrow{q}}^{\overrightarrow{K}}$. As shown in figure E1, when computing the Hall conductivities for each of the two valleys, ${\sigma }_{{xy}}^{K}$ and ${\sigma }_{{xy}}^{K^{\prime} }$, a lot of noise is generated from stochastic calculation of the trace in the real-space Kubo formula [36, 37]. These fluctuations are random and as such do not obey any symmetry of the system. But once we compute the VH conductivity, ${\sigma }_{{xy}}^{v}={\sigma }_{{xy}}^{K}-{\sigma }_{{xy}}^{K^{\prime} }$, this noise is filtered away because it does not have opposite chirality. However, when we introduce disorder effects that scatter electrons between the two valleys, such a property is removed and one should proceed to smooth out these fluctuations by averaging over many disorder realizations.

Zoom In Zoom Out Reset image size