-
PDF
- Split View
-
Views
-
Cite
Cite
David Ellerman, Logical information theory: new logical foundations for information theory, Logic Journal of the IGPL, Volume 25, Issue 5, October 2017, Pages 806–835, https://doi.org/10.1093/jigpal/jzx022
Close - Share Icon Share
Abstract
There is a new theory of information based on logic. The definition of Shannon entropy as well as the notions on joint, conditional and mutual entropy as defined by Shannon can all be derived by a uniform transformation from the corresponding formulas of logical information theory. Information is first defined in terms of sets of distinctions without using any probability measure. When a probability measure is introduced, the logical entropies are simply the values of the (product) probability measure on the sets of distinctions. The compound notions of joint, conditional and mutual entropies are obtained as the values of the measure, respectively, on the union, difference and intersection of the sets of distinctions. These compound notions of logical entropy satisfy the usual Venn diagram relationships (e.g. inclusion–exclusion formulas) since they are values of a measure (in the sense of measure theory). The uniform transformation into the formulas for Shannon entropy is linear so it explains the long-noted fact that the Shannon formulas satisfy the Venn diagram relations—as an analogy or mnemonic—since Shannon entropy is not a measure (in the sense of measure theory) on a given set. What is the logic that gives rise to logical information theory? Partitions are dual (in a category-theoretic sense) to subsets, and the logic of partitions was recently developed in a dual/parallel relationship to the Boolean logic of subsets (the latter being usually mis-specified as the special case of ‘propositional logic’). Boole developed logical probability theory as the normalized counting measure on subsets. Similarly the normalized counting measure on partitions is logical entropy—when the partitions are represented as the set of distinctions that is the complement to the equivalence relation for the partition. In this manner, logical information theory provides the set-theoretic and measure-theoretic foundations for information theory. The Shannon theory is then derived by the transformation that replaces the counting of distinctions with the counting of the number of binary partitions (bits) it takes, on average, to make the same distinctions by uniquely encoding the distinct elements—which is why the Shannon theory perfectly dovetails into coding and communications theory.
1 Introduction
This article develops the logical theory of information-as-distinctions. It can be seen as the application of the logic of partitions [15] to information theory. Partitions are dual (in a category-theoretic sense) to subsets. George Boole developed the notion of logical probability [7] as the normalized counting measure on subsets in his logic of subsets. This article develops the normalized counting measure on partitions as the analogous quantitative treatment in the logic of partitions. The resulting measure is a new logical derivation of an old formula measuring diversity and distinctions, e.g., Corrado Gini’s index of mutability or diversity [19], that goes back to the early 20th century. In view of the idea of information as being based on distinctions (see next section), I refer to this logical measure of distinctions as ‘logical entropy’.
This raises the question of the relationship of logical entropy to Claude Shannon’s entropy ([40], [41]). The entropies are closely related since they are both ultimately based on the concept of information-as-distinctions—but they represent two different way to quantify distinctions. Logical entropy directly counts the distinctions (as defined in partition logic) whereas Shannon entropy, in effect, counts the minimum number of binary partitions (or yes/no questions) it takes, on average, to uniquely determine or designate the distinct entities. Since that gives (in standard examples) a binary code for the distinct entities, the Shannon theory is perfectly adapted for applications to the theory of coding and communications.
The logical theory and the Shannon theory are also related in their compound notions of joint entropy, conditional entropy and mutual information. Logical entropy is a measure in the mathematical sense, so as with any measure, the compound formulas satisfy the usual Venn diagram relationships. The compound notions of Shannon entropy were defined so that they also satisfy similar Venn diagram relationships. However, as various information theorists, principally Lorne Campbell, have noted [9], Shannon entropy is not a measure (outside of the standard example of |$2^{n}$| equiprobable distinct entities where it is the count |$n$| of the number of yes/no questions necessary to unique determine or encode the distinct entities)—so one can conclude only that the ‘analogies provide a convenient mnemonic’ [9, p. 112] in terms of the usual Venn diagrams for measures. Campbell wondered if there might be a ‘deeper foundation’ [9, p. 112] to clarify how the Shannon formulas can be defined to satisfy the measure-like relations in spite of not being a measure. That question is addressed in this article by showing that there is a transformation of formulas that transforms each of the logical entropy compound formulas into the corresponding Shannon entropy compound formula, and the transform preserves the Venn diagram relationships that automatically hold for measures. This ‘dit-bit transform’ is heuristically motivated by showing how average counts of distinctions (‘dits’) can be converted in average counts of binary partitions (‘bits’).
Moreover, Campbell remarked that it would be ‘particularly interesting’ and ‘quite significant’ if there was an entropy measure of sets so that joint entropy corresponded to the measure of the union of sets, conditional entropy to the difference of sets, and mutual information to the intersection of sets [9, p. 113]. Logical entropy precisely satisfies those requirements.
2 Logical information as the measure of distinctions
There is now a widespread view that information is fundamentally about differences, distinguishability and distinctions. As Charles H. Bennett, one of the founders of quantum information theory, put it:
So information really is a very useful abstraction. It is the notion of distinguishability abstracted away from what we are distinguishing, or from the carrier of information. [5, p. 155]
This view even has an interesting history. In James Gleick’s book, The Information: A History, A Theory, A Flood, he noted the focus on differences in the 17th century polymath, John Wilkins, who was a founder of the Royal Society. In |$1641$|, the year before Isaac Newton was born, Wilkins published one of the earliest books on cryptography, Mercury or the Secret and Swift Messenger, which not only pointed out the fundamental role of differences but noted that any (finite) set of different things could be encoded by words in a binary code.
For in the general we must note, That whatever is capable of a competent Difference, perceptible to any Sense, may be a sufficient Means whereby to express the Cogitations. It is more convenient, indeed, that these Differences should be of as great Variety as the Letters of the Alphabet; but it is sufficient if they be but twofold, because Two alone may, with somewhat more Labour and Time, be well enough contrived to express all the rest. [47, Chap. XVII, p. 69]
Wilkins explains that a five letter binary code would be sufficient to code the letters of the alphabet since |$2^{5}=32$|.
Thus any two Letters or Numbers, suppose |$A.B$|. being transposed through five Places, will yield Thirty Two Differences, and so consequently will superabundantly serve for the Four and twenty Letters ... .[47, Chap. XVII, p. 69]
As Gleick noted:
Any difference meant a binary choice. Any binary choice began the expressing of cogitations. Here, in this arcane and anonymous treatise of |$1641$|, the essential idea of information theory poked to the surface of human thought, saw its shadow, and disappeared again for [three] hundred years. [20, p. 161]
Thus counting distinctions [12] would seem the right way to measure information,1 and that is the measure which emerges naturally out of partition logic—just as finite logical probability emerges naturally as the measure of counting elements in Boole’s subset logic.
Although usually named after the special case of ‘propositional’ logic, the general case is Boole’s logic of subsets of a universe |$U$| (the special case of |$U=1$| allows the propositional interpretation since the only subsets are |$1$| and |$\emptyset$| standing for truth and falsity). Category theory shows there is a duality between sub-sets and quotient-sets (= partitions = equivalence relations), and that allowed the recent development of the dual logic of partitions ([13], [15]). As indicated in the title of his book, An Investigation of the Laws of Thought on which are founded the Mathematical Theories of Logic and Probabilities [7], Boole also developed the normalized counting measure on subsets of a finite universe |$U$| which was finite logical probability theory. When the same mathematical notion of the normalized counting measure is applied to the partitions on a finite universe set |$U$| (when the partition is represented as the complement of the corresponding equivalence relation on |$U\times U$|) then the result is the formula for logical entropy.
In addition to the philosophy of information literature [4], there is a whole sub-industry in mathematics concerned with different notions of ‘entropy’ or ‘information’ ([2]; see [45] for a recent ‘extensive’ analysis) that is long on formulas and ‘intuitive axioms’ but short on interpretations. Out of that plethora of definitions, logical entropy is the measure (in the technical sense of measure theory) of information that arises out of partition logic just as logical probability theory arises out of subset logic.
The logical notion of information-as-distinctions supports the view that the notion of information is independent of the notion of probability and should be based on finite combinatorics. As Andrey Kolmogorov put it:
Information theory must precede probability theory, and not be based on it. By the very essence of this discipline, the foundations of information theory have a finite combinatorial character. [27, p. 39]
Logical information theory precisely fulfills Kolmogorov’s criterion.2 It starts simply with a set of distinctions defined by a partition on a finite set |$U$|, where a distinction is an ordered pair of elements of |$U$| in distinct blocks of the partition. Thus the ‘finite combinatorial’ object is the set of distinctions (‘ditset’) or information set (‘infoset’) associated with the partition, i.e., the complement in |$U\times U$| of the equivalence relation associated with the partition. To get a quantitative measure of information, any probability distribution on |$U$| defines a product probability measure on |$U\times U$|, and the logical entropy is simply that probability measure of the information set.
3 Duality of subsets and partitions
Logical entropy is to the logic of partitions as logical probability is to the Boolean logic of subsets. Hence we will start with a brief review of the relationship between these two dual forms of mathematical logic.
Modern category theory shows that the concept of a subset dualizes to the concept of a quotient set, equivalence relation, or partition. F. William Lawvere called a subset or, in general, a subobject a ‘part’ and then noted: ‘The dual notion (obtained by reversing the arrows) of ‘part’ is the notion of partition.’ [31, p. 85] That suggests that the Boolean logic of subsets (usually named after the special case of propositions as ‘propositional’ logic) should have a dual logic of partitions ([13], [15]).
A partition|$\pi=\left\{B_{1},...,B_{m}\right\}$| on |$U$| is a set of subsets, called cells or blocks, |$B_{i}$| that are mutually disjoint and jointly exhaustive (|$\cup_{i}B_{i}=U$|). In the duality between subset logic and partition logic, the dual to the notion of an ‘element’ of a subset is the notion of a ‘distinction’ of a partition, where |$\left( u,u^{\prime}\right) \in U\times U$| is a distinction or dit of |$\pi$| if the two elements are in different blocks, i.e., the ‘dits’ of a partition are dual to the ‘its’ (or elements) of a subset. Let |$\operatorname*{dit}\left( \pi\right) \subseteq U\times U$| be the set of distinctions or ditset of |$\pi$|. Thus the information set or infoset associated with a partition |$\pi$| is ditset |$\operatorname*{dit}\left( \pi\right)$|. Similarly an indistinction or indit of |$\pi$| is a pair |$\left(u,u^{\prime}\right) \in U\times U$| in the same block of |$\pi$|. Let |$\operatorname*{indit}\left(\pi\right) \subseteq U\times U$| be the set of indistinctions or inditset of |$\pi$|. Then |$\operatorname*{indit}\left( \pi\right) $| is the equivalence relation associated with |$\pi$| and |$\operatorname*{dit}\left( \pi\right) =U\times U-\operatorname*{indit} \left( \pi\right) $| is the complementary binary relation that has been called an apartness relation or a partition relation.
4 Classical subset logic and partition logic
The algebra associated with the subsets |$S\subseteq U$| is the Boolean algebra |$\wp\left( U\right) $| of subsets of |$U$| with the inclusion of elements as the partial order. The corresponding algebra of partitions |$\pi$| on |$U$| is the partition algebra|$\prod\left( U\right) $| defined as follows:
the partial order|$\sigma\preceq\pi$| of partitions |$\sigma=\left\{ C,C^{\prime},...\right\} $| and |$\pi=\left\{ B,B^{\prime },...\right\} $| holds when |$\pi$|refines|$\sigma$| in the sense that for every block |$B\in\pi$| there is a block |$C\in\sigma$| such that |$B\subseteq C$|, or, equivalently, using the element-distinction pairing, the partial order is the inclusion of distinctions: |$\sigma\preceq\pi$| if and only if (iff) |$\operatorname*{dit}\left( \sigma\right) \subseteq\operatorname*{dit}\left( \pi\right) $|;
the minimum or bottom partition is the indiscrete partition (or blob) |$\mathbf{0}=\left\{ U\right\} $| with one block consisting of all of |$U$|;
the maximum or top partition is the discrete partition|$\mathbf{1}=\left\{ \left\{ u_{j}\right\} \right\} _{j=1,...,n}$| consisting of singleton blocks;
the join|$\pi\vee\sigma$| is the partition whose blocks are the non-empty intersections |$B\cap C$| of blocks of |$\pi$| and blocks of |$\sigma$|, or, equivalently, using the element-distinction pairing, |$\operatorname*{dit} \left( \pi\vee\sigma\right) =\operatorname*{dit}\left( \pi\right) \cup\operatorname*{dit}\left( \sigma\right) $|;
the meet|$\pi\wedge\sigma$| is the partition whose blocks are the equivalence classes for the equivalence relation generated by: |$u_{j}\sim u_{j^{\prime}}$| if |$u_{j}\in B\in\pi$|, |$u_{j^{\prime}}\in C\in\sigma$|, and |$B\cap C\neq\emptyset$|; and
|$\sigma\Rightarrow\pi$| is the implication partition whose blocks are: (1) the singletons |$\left\{ u_{j}\right\} $| for |$u_{j}\in B\in\pi$| if there is a |$C\in\sigma$| such that |$B\subseteq C$|, or (2) just |$B\in\pi$| if there is no |$C\in\sigma$| with |$B\subseteq C$|, so that trivially: |$\sigma\Rightarrow\pi=\mathbf{1}$| iff |$\sigma\preceq\pi$|.3
The logical partition operations can also be defined in terms of the corresponding logical operations on subsets. A ditset |$\operatorname*{dit} \left( \pi\right)$| of a partition on |$U$| is a subset of |$U\times U$| of a particular kind, namely the complement of an equivalence relation. An equivalence relation is reflexive, symmetric and transitive. Hence the ditset complement, i.e., a partition relation (or apartness relation), is a subset |$P\subseteq U\times U$| that is:
(1) irreflexive (or anti-reflexive), |$P\cap\Delta=\emptyset$| (where |$\Delta=\left\{ \left( u,u\right) :u\in U\right\} $| is the diagonal), i.e., no element |$u\in U$| can be distinguished from itself;
(2) symmetric, |$\left( u,u^{\prime}\right) \in P$| implies |$\left(u^{\prime},u\right) \in P$|, i.e., if |$u$| is distinguished from |$u^{\prime}$|, then |$u^{\prime}$| is distinguished from |$u$|; and
(3) anti-transitive (or co-transitive), if |$\left( u,u^{\prime\prime}\right) \in P$| then for any |$u^{\prime}\in U$|, |$\left( u,u^{\prime}\right) \in P$| or |$\left( u^{\prime},u^{\prime\prime}\right) \in P$|, i.e., if |$u$| is distinguished from |$u^{\prime\prime}$|, then any other element |$u^{\prime}$| must be distinguished from |$u$| or |$u^{\prime\prime}$| because if |$u^{\prime}$| was equivalent to both, then by transitivity of equivalence, |$u$| would be equivalent to |$u^{\prime\prime}$| contrary to them being distinguished.
That is how distinctions work at the logical level, and that is why the ditset of a partition is the ‘probability-free’ notion of an information set or infoset in the logical theory of information-as-distinctions.
Given any subset |$S\subseteq U\times U$|, the reflexive-symmetric-transitive (rst) closure|$\overline{S^{c}}$| of the complement |$S^{c}$| is the smallest equivalence relation containing |$S^{c} $|, so its complement is the largest partition relation contained in |$S$|, which is called the interior|$\operatorname*{int}\left( S\right) $| of |$S$|. This usage is consistent with calling the subsets that equal their rst-closures closed subsets of |$U\times U$| (so closed subsets = equivalence relations) so the complements are the open subsets (= partition relations). However it should be noted that the rst-closure is not a topological closure since the closure of a union is not necessarily the union of the closures, so the ‘open’ subsets do not form a topology on |$U\times U$|.
Since the same operations can be defined for subsets and partitions, one can interpret a formula |$\Phi\left( \pi,\sigma,...\right) $| either way as a subset or a partition. Given either subsets or partitions of |$U$| substituted for the variables |$\pi$|, |$\sigma$|,..., one can apply, respectively, subset or partition operations to evaluate the whole formula. Since |$\Phi\left(\pi,\sigma,...\right) $| is either a subset or a partition, the corresponding proposition is ‘|$u$| is an element of |$\Phi\left( \pi ,\sigma,...\right)$|’ or ‘|$\left( u,u^{\prime}\right) $| is a distinction of |$\Phi\left( \pi,\sigma,...\right)$|’. And then the definitions of a valid formula are also parallel, namely, no matter what is substituted for the variables, the whole formula evaluates to the top of the algebra. In that case, the subset |$\Phi\left( \pi,\sigma,...\right) $| contains all elements of |$U$|, i.e., |$\Phi\left( \pi,\sigma,...\right) =U$|, or the partition |$\Phi\left( \pi,\sigma,...\right) $| distinguishes all pairs |$\left( u,u^{\prime}\right) $| for distinct elements of |$U$|, i.e., |$\Phi\left( \pi,\sigma,...\right) =\mathbf{1}$|. The parallelism between the dual logics is summarized in the following Table 1.
Duality between subset logic and partition logic
| Table 1 . | Subset logic . | Partition logic . |
|---|---|---|
| ‘Elements’ (its or dits) | Elements |$u$| of |$S$| | Dits |$\left(u,u^{\prime }\right) $| of |$\pi$| |
| Inclusion of ‘elements’ | Inclusion |$S\subseteq T$| | Refinement: |$\operatorname*{dit}\left( \sigma\right)\subseteq\operatorname*{dit}\left( \pi\right) $| |
| Top of order = all ‘elements’ | |$U$| all elements | |$\operatorname*{dit}(\mathbf{1)}=U^{2}-\Delta$|, all dits |
| Bottom of order = no ‘elements’ | |$\emptyset$| no elements | |$\operatorname*{dit}(\mathbf{0)=\emptyset}$|, no dits |
| Variables in formulas | Subsets |$S$| of |$U$| | Partitions |$\pi$| on |$U$| |
| Operations: |$\vee,\wedge,\Rightarrow,...$| | Subset ops. | Partition ops. |
| Formula |$\Phi(x,y,...)$| holds | |$u$| element of |$\Phi(S,T,...)$| | |$\left( u,u^{\prime}\right) $| dit of |$\Phi(\pi,\sigma,...)$| |
| Valid formula | |$\Phi(S,T,...)=U$|, |$\forall S,T,...$| | |$\Phi(\pi ,\sigma,...)=\mathbf{1}$|, |$\forall\pi,\sigma,...$| |
| Table 1 . | Subset logic . | Partition logic . |
|---|---|---|
| ‘Elements’ (its or dits) | Elements |$u$| of |$S$| | Dits |$\left(u,u^{\prime }\right) $| of |$\pi$| |
| Inclusion of ‘elements’ | Inclusion |$S\subseteq T$| | Refinement: |$\operatorname*{dit}\left( \sigma\right)\subseteq\operatorname*{dit}\left( \pi\right) $| |
| Top of order = all ‘elements’ | |$U$| all elements | |$\operatorname*{dit}(\mathbf{1)}=U^{2}-\Delta$|, all dits |
| Bottom of order = no ‘elements’ | |$\emptyset$| no elements | |$\operatorname*{dit}(\mathbf{0)=\emptyset}$|, no dits |
| Variables in formulas | Subsets |$S$| of |$U$| | Partitions |$\pi$| on |$U$| |
| Operations: |$\vee,\wedge,\Rightarrow,...$| | Subset ops. | Partition ops. |
| Formula |$\Phi(x,y,...)$| holds | |$u$| element of |$\Phi(S,T,...)$| | |$\left( u,u^{\prime}\right) $| dit of |$\Phi(\pi,\sigma,...)$| |
| Valid formula | |$\Phi(S,T,...)=U$|, |$\forall S,T,...$| | |$\Phi(\pi ,\sigma,...)=\mathbf{1}$|, |$\forall\pi,\sigma,...$| |
Duality between subset logic and partition logic
| Table 1 . | Subset logic . | Partition logic . |
|---|---|---|
| ‘Elements’ (its or dits) | Elements |$u$| of |$S$| | Dits |$\left(u,u^{\prime }\right) $| of |$\pi$| |
| Inclusion of ‘elements’ | Inclusion |$S\subseteq T$| | Refinement: |$\operatorname*{dit}\left( \sigma\right)\subseteq\operatorname*{dit}\left( \pi\right) $| |
| Top of order = all ‘elements’ | |$U$| all elements | |$\operatorname*{dit}(\mathbf{1)}=U^{2}-\Delta$|, all dits |
| Bottom of order = no ‘elements’ | |$\emptyset$| no elements | |$\operatorname*{dit}(\mathbf{0)=\emptyset}$|, no dits |
| Variables in formulas | Subsets |$S$| of |$U$| | Partitions |$\pi$| on |$U$| |
| Operations: |$\vee,\wedge,\Rightarrow,...$| | Subset ops. | Partition ops. |
| Formula |$\Phi(x,y,...)$| holds | |$u$| element of |$\Phi(S,T,...)$| | |$\left( u,u^{\prime}\right) $| dit of |$\Phi(\pi,\sigma,...)$| |
| Valid formula | |$\Phi(S,T,...)=U$|, |$\forall S,T,...$| | |$\Phi(\pi ,\sigma,...)=\mathbf{1}$|, |$\forall\pi,\sigma,...$| |
| Table 1 . | Subset logic . | Partition logic . |
|---|---|---|
| ‘Elements’ (its or dits) | Elements |$u$| of |$S$| | Dits |$\left(u,u^{\prime }\right) $| of |$\pi$| |
| Inclusion of ‘elements’ | Inclusion |$S\subseteq T$| | Refinement: |$\operatorname*{dit}\left( \sigma\right)\subseteq\operatorname*{dit}\left( \pi\right) $| |
| Top of order = all ‘elements’ | |$U$| all elements | |$\operatorname*{dit}(\mathbf{1)}=U^{2}-\Delta$|, all dits |
| Bottom of order = no ‘elements’ | |$\emptyset$| no elements | |$\operatorname*{dit}(\mathbf{0)=\emptyset}$|, no dits |
| Variables in formulas | Subsets |$S$| of |$U$| | Partitions |$\pi$| on |$U$| |
| Operations: |$\vee,\wedge,\Rightarrow,...$| | Subset ops. | Partition ops. |
| Formula |$\Phi(x,y,...)$| holds | |$u$| element of |$\Phi(S,T,...)$| | |$\left( u,u^{\prime}\right) $| dit of |$\Phi(\pi,\sigma,...)$| |
| Valid formula | |$\Phi(S,T,...)=U$|, |$\forall S,T,...$| | |$\Phi(\pi ,\sigma,...)=\mathbf{1}$|, |$\forall\pi,\sigma,...$| |
5 Classical logical probability and logical entropy
George Boole [7] extended his logic of subsets to finite logical probability theory where, in the equiprobable case, the probability of a subset |$S$| (event) of a finite universe set (outcome set or sample space) |$U=\left\{ u_{1},...,u_{n}\right\} $| was the number of elements in |$S$| over the total number of elements: |$\Pr\left( S\right) =\frac{\left\vert S\right\vert }{\left\vert U\right\vert }=\sum_{u_{j}\in S}\frac{1}{\left\vert U\right\vert }$|. Pierre-Simon Laplace’s classical finite probability theory [30] also dealt with the case where the outcomes were assigned real point probabilities |$p=\left\{ p_{1},...,p_{n}\right\} $| so rather than summing the equal probabilities |$\frac{1}{\left\vert U\right\vert }$|, the point probabilities of the elements were summed: |$\Pr\left( S\right) =\sum_{u_{j}\in S}p_{j}=p\left( S\right) $|–where the equiprobable formula is for |$p_{j}=\frac{1}{\left\vert U\right\vert }$| for |$j=1,...,n$|. The conditional probability of an event |$T\subseteq U$| given an event |$S$| is |$\Pr\left( T|S\right) =\frac{p\left( T\cap S\right) }{p\left( S\right)}$|.
Since ‘Probability is a measure on the Boolean algebra of events’ that gives quantitatively the ‘intuitive idea of the size of a set’, we may ask by ‘analogy’ for some measure to capture a property for a partition like ‘what size is to a set.’ Rota goes on to ask:
How shall we be led to such a property? We have already an inkling of what it should be: it should be a measure of information provided by a random variable. Is there a candidate for the measure of the amount of information? [38, p. 67]
Since |$1=\left( \sum_{i=1}^{n}p_{i}\right) ^{2}=\sum_{i}p_{i} ^{2}+\sum_{i\neq j}p_{i}p_{j}$|, we again have the logical entropy |$h\left(p\right) $| as the probability |$\sum_{i\neq j}p_{i}p_{j}$| of drawing a distinction in two independent samplings of the probability distribution |$p$|.
Then the logical entropy |$h\left( p\right) =\mu\left(\operatorname*{dit}(\mathbf{1}_{U})\right) $| is just the product measure of the information set or ditset |$\operatorname*{dit}\left( \mathbf{1}_{U}\right) =U\times U-\Delta$| of the discrete partition |$\mathbf{1}_{U}$| on |$U$|.
There are also parallel ‘element |$\leftrightarrow$| distinction’ probabilistic interpretations:
|$\Pr\left( S\right) =\sum_{u_{i}\in S}p_{i}$| is the probability that a single draw from |$U$| gives a element|$u_{j}\ $|of |$S$|, and
|$h_{p}\left( \pi\right) =\mu\left( \operatorname*{dit}\left(\pi\right) \right) =\sum_{\left( u_{j},u_{k}\right) \in\operatorname*{dit}\left( \pi\right) }p_{j}p_{k}$| is the probability that two independent (with replacement) draws from |$U$| gives a distinction|$\left( u_{j},u_{k}\right) $| of |$\pi$|.
The duality between logical probabilities and logical entropies based on the parallel roles of ‘its’ (elements of subsets) and ‘dits’ (distinctions of partitions) is summarized in Table 2.
Classical logical probability theory and classical logical information theory
| Table 2 . | Logical probability theory . | Logical information theory . |
|---|---|---|
| ‘Outcomes’ | Elements |$u\in U$| finite | Dits |$\left( u,u^{\prime}\right) \in U\times U$| finite |
| ‘Events’ | Subsets |$S\subseteq U$| | Ditsets |$\operatorname*{dit}\left( \pi\right) \subseteq U\times U$| |
| Equiprobable points | |$\ \Pr\left( S\right) =\frac{|S|}{\left\vert U\right\vert }$| | |$h\left( \pi\right) =\frac{\left\vert \operatorname*{dit}\left( \pi\right) \right\vert }{\left\vert U\times U\right\vert }$| |
| Point probabilities | |$\ \Pr\left( S\right) =\sum\left\{ p_{j}:u_{j}\in S\right\} $| | |$h\left( \pi\right) =\sum\left\{ p_{j}p_{k}:\left(u_{j},u_{k}\right) \in\operatorname*{dit}\left( \pi\right) \right\}$| |
| Interpretation | |$\Pr(S)=$||$1$|-draw prob. of |$S$|-element | |$h\left(\pi\right) =$||$2$|-draw prob. of |$\pi$|-distinction |
| Table 2 . | Logical probability theory . | Logical information theory . |
|---|---|---|
| ‘Outcomes’ | Elements |$u\in U$| finite | Dits |$\left( u,u^{\prime}\right) \in U\times U$| finite |
| ‘Events’ | Subsets |$S\subseteq U$| | Ditsets |$\operatorname*{dit}\left( \pi\right) \subseteq U\times U$| |
| Equiprobable points | |$\ \Pr\left( S\right) =\frac{|S|}{\left\vert U\right\vert }$| | |$h\left( \pi\right) =\frac{\left\vert \operatorname*{dit}\left( \pi\right) \right\vert }{\left\vert U\times U\right\vert }$| |
| Point probabilities | |$\ \Pr\left( S\right) =\sum\left\{ p_{j}:u_{j}\in S\right\} $| | |$h\left( \pi\right) =\sum\left\{ p_{j}p_{k}:\left(u_{j},u_{k}\right) \in\operatorname*{dit}\left( \pi\right) \right\}$| |
| Interpretation | |$\Pr(S)=$||$1$|-draw prob. of |$S$|-element | |$h\left(\pi\right) =$||$2$|-draw prob. of |$\pi$|-distinction |
Classical logical probability theory and classical logical information theory
| Table 2 . | Logical probability theory . | Logical information theory . |
|---|---|---|
| ‘Outcomes’ | Elements |$u\in U$| finite | Dits |$\left( u,u^{\prime}\right) \in U\times U$| finite |
| ‘Events’ | Subsets |$S\subseteq U$| | Ditsets |$\operatorname*{dit}\left( \pi\right) \subseteq U\times U$| |
| Equiprobable points | |$\ \Pr\left( S\right) =\frac{|S|}{\left\vert U\right\vert }$| | |$h\left( \pi\right) =\frac{\left\vert \operatorname*{dit}\left( \pi\right) \right\vert }{\left\vert U\times U\right\vert }$| |
| Point probabilities | |$\ \Pr\left( S\right) =\sum\left\{ p_{j}:u_{j}\in S\right\} $| | |$h\left( \pi\right) =\sum\left\{ p_{j}p_{k}:\left(u_{j},u_{k}\right) \in\operatorname*{dit}\left( \pi\right) \right\}$| |
| Interpretation | |$\Pr(S)=$||$1$|-draw prob. of |$S$|-element | |$h\left(\pi\right) =$||$2$|-draw prob. of |$\pi$|-distinction |
| Table 2 . | Logical probability theory . | Logical information theory . |
|---|---|---|
| ‘Outcomes’ | Elements |$u\in U$| finite | Dits |$\left( u,u^{\prime}\right) \in U\times U$| finite |
| ‘Events’ | Subsets |$S\subseteq U$| | Ditsets |$\operatorname*{dit}\left( \pi\right) \subseteq U\times U$| |
| Equiprobable points | |$\ \Pr\left( S\right) =\frac{|S|}{\left\vert U\right\vert }$| | |$h\left( \pi\right) =\frac{\left\vert \operatorname*{dit}\left( \pi\right) \right\vert }{\left\vert U\times U\right\vert }$| |
| Point probabilities | |$\ \Pr\left( S\right) =\sum\left\{ p_{j}:u_{j}\in S\right\} $| | |$h\left( \pi\right) =\sum\left\{ p_{j}p_{k}:\left(u_{j},u_{k}\right) \in\operatorname*{dit}\left( \pi\right) \right\}$| |
| Interpretation | |$\Pr(S)=$||$1$|-draw prob. of |$S$|-element | |$h\left(\pi\right) =$||$2$|-draw prob. of |$\pi$|-distinction |
This concludes the argument that logical information theory arises out of partition logic just as logical probability theory arises out of subset logic. Now we turn to the formulas of logical information theory and the comparison to the formulas of Shannon information theory.
6 Entropy as a measure of information
Shannon entropy and the many other suggested ‘entropies’ are routinely called ‘measures’ of information [2]. The formulas for mutual information, joint entropy and conditional entropy are defined so these Shannon entropies satisfy Venn diagram formulas (e.g. [1, p. 109]; [35, p. 508]) that would follow automatically if Shannon entropy were a measure in the technical sense. As Lorne Campbell put it:
Certain analogies between entropy and measure have been noted by various authors. These analogies provide a convenient mnemonic for the various relations between entropy, conditional entropy, joint entropy, and mutual information. It is interesting to speculate whether these analogies have a deeper foundation. It would seem to be quite significant if entropy did admit an interpretation as the measure of some set. [9, p. 112]
For any finite set |$X$|, a measure|$\mu$| is a function |$\mu:\wp\left( X\right) \rightarrow \mathbb{R}$| such that:
(1) |$\mu\left( \emptyset\right) =0$|,
(2) for any |$E\subseteq X$|, |$\mu\left( E\right) \geq0$|, and
(3) for any disjoint subsets |$E_{1}$| and |$E_{2}$|, |$\mu(E_{1}\cup E_{2})=\mu\left( E_{1}\right) +\mu\left( E_{2}\right)$|.
Considerable effort has been expended to try to find a framework in which Shannon entropy would be a measure in this technical sense and thus would satisfy the desiderata:
that |$H\left( \alpha\right) $| and |$H\left( \beta\right) $| are measures of sets, that |$H\left( \alpha,\beta\right)$| is the measure of their union, that |$I\left(\alpha,\beta\right) $| is the measure of their intersection, and that |$H\left( \alpha|\beta\right)$| is the measure of their difference. The possibility that |$I\left(\alpha ,\beta\right)$| is the entropy of the “intersection” of two partitions is particularly interesting. This “intersection,” if it existed, would presumably contain the information common to the partitions |$\alpha$| and |$\beta$|. [9, p. 113]
But these efforts have not been successful beyond special cases such as |$2^{n}$| equiprobable elements where, as Campbell notes, the Shannon entropy is just the counting measure |$n$| of the minimum number of binary partitions it takes to distinguish all the elements. In general, Shannon entropy is not a measure on a set.6
In contrast, it is ‘quite significant’ that logical entropy is a measure such as the normalized counting measure on the ditset |$\operatorname*{dit}(\pi)$| representation of a partition |$\pi$| as a subset of the set |$U\times U$|. Thus all of Campbell’s desiderata are true when:
‘sets’ = ditsets, the set of distinctions of partitions (or, in general, information sets of distinctions), and
‘entropies’ = normalized counting measure of the ditsets (or, in general, product probability measure on the infosets), i.e. the logical entropies.
7 The dit-bit transform
The logical entropy formulas for various compound notions (e.g. conditional entropy, mutual information and joint entropy) stand in certain Venn diagram relationships because logical entropy is a measure. The Shannon entropy formulas for these compound notions, e.g. |$H(\alpha,\beta)=H\left( \alpha\right) +H\left( \beta\right) -I\left( \alpha,\beta\right)$|, are defined so as to satisfy the Venn diagram relationships as if Shannon entropy was a measure when it is not. How can that be? Perhaps there is some ‘deeper foundation’ [9, p. 112] to explain why the Shannon formulas still satisfy those measure-like Venn diagram relationships.
Indeed, there is such a connection, the dit-bit transform. This transform can be heuristically motivated by considering two ways to treat the standard set |$U_{n}$| of |$n$| elements with the equal probabilities |$p_{0}=\frac{1}{n}$|. In that basic case of an equiprobable set, we can derive the dit-bit connection, and then by using a probabilistic average, we can develop the Shannon entropy, expressed in terms of bits, from the logical entropy, expressed in terms of (normalized) dits, or vice versa.
That is the dit-count or logical measure of the information in a set of |$n$| distinct elements (think of it as the logical entropy of the discrete partition on |$U_{n}$| with equiprobable elements).
The dit-bit connection is that the Shannon-Hartley entropy |$H\left( p_{0}\right) =\log\left( \frac{1}{p_{0}}\right) $| will play the same role in the Shannon formulas that |$h\left( p_{0}\right) =1-p_{0}$| plays in the logical entropy formulas—when both are formulated as probabilistic averages or expectations.
The common thing being measured is an equiprobable |$U_{n}$| where |$n=\frac {1}{p_{0}}$|.7 The dit-count for |$U_{n}$| is |$h\left( p_{0}\right) =1-p_{0}$| and the bit-count for |$U$| is |$H\left( p_{0}\right) =\log\left(\frac{1}{p_{0}}\right) $|, and the dit-bit transform converts one count into the other. Using this dit-bit transform between the two different ways to quantify the ‘information’ in |$U_{n}$|, each entropy can be developed from the other. Nevertheless, this dit-bit connection should not be interpreted as if it was just converting a length using centimeters to inches or the like. Indeed, the (average) bit-count is a ‘coarser-grid’ that loses some information in comparison to the (exact) dit-count as shown by the analysis (below) of mutual information. There is no bit-count mutual information between independent probability distributions but there is always dit-count information even between two (non-trivial) independent distributions (see below the proposition that non-empty supports always intersect).
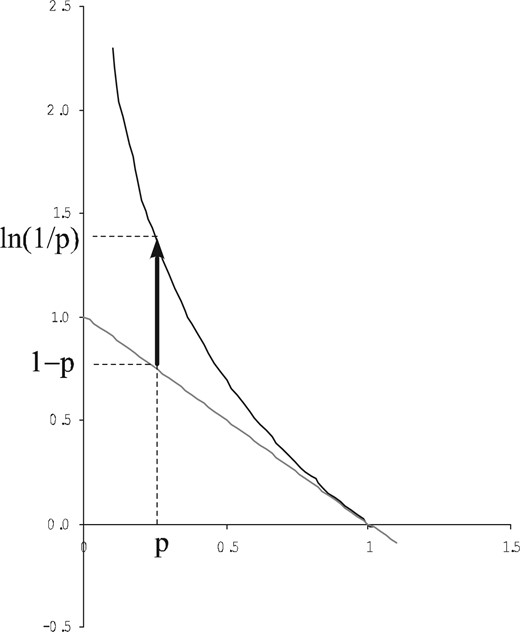
The graph of the dit-bit transform is familiar in information theory from the natural log inequality: |$\ln p_{i}\leq p_{i}-1$|. Taking negatives of both sides gives the graph (Figure 1) of the dit-bit transform for natural logs: |$1-p_{i}\rightsquigarrow\ln\left( \frac{1}{p_{i}}\right) $|.
The dit-bit transform |$1-p\rightsquigarrow\ln\left(\frac{1}{p}\right)$| (natural logs).
The dit-bit connection carries over to all the compound notions of entropy so that the Shannon notions of conditional entropy, mutual information, cross-entropy and divergence can all be developed from the corresponding notions for logical entropy. Since the logical notions are the values of a probability measure, the compound notions of logical entropy have the usual Venn diagram relationships. And then by the dit-bit transform, those Venn diagram relationships carry over to the compound Shannon formulas since the dit-bit transform preserves sums and differences (i.e. is, in that sense, linear). That is why the Shannon formulas can satisfy the Venn diagram relationships even though Shannon entropy is not a measure.
The logical entropy formula |$h\left( p\right) =\sum_{i}p_{i}\left(1-p_{i}\right) $| (and the corresponding compound formulas) are put into that form of an average or expectation to apply the dit-bit transform. But logical entropy is the exact measure of the information set |$S_{i\neq i^{\prime}}=\left\{ \left( i,i^{\prime}\right) :i\neq i^{\prime}\right\}\subseteq\left\{ 1,...,n\right\} \times\left\{ 1,...,n\right\} $| for the product probability measure |$\mu:\wp\left( \left\{ 1,...,n\right\}^{2}\right) \rightarrow\left[ 0,1\right] $| where for |$S\subseteq\left\{1,...,n\right\} ^{2}$|, |$\mu\left( S\right) =\sum\left\{ p_{i}p_{i^{\prime}}:\left( i,i^{\prime}\right) \in S\right\} $|, i.e., |$h\left( p\right)=\mu\left( S_{i\neq i^{\prime}}\right) $|.
8 Information algebras and joint distributions
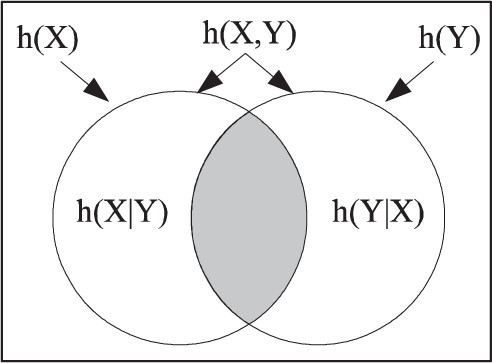
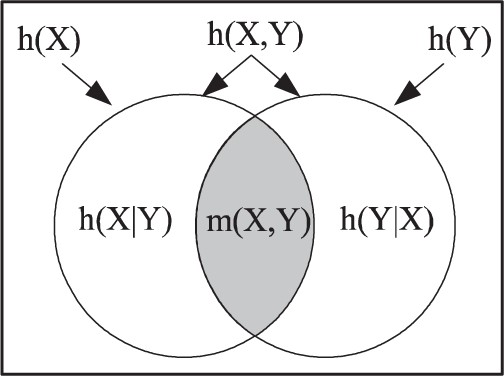
The four atoms |$S_{X}\cap S_{Y}=S_{X\wedge Y}$|, |$S_{X}\cap S_{\lnot Y}=S_{X\wedge\lnot Y}$|, |$S_{\lnot X}\cap S_{Y}=S_{\lnot X\wedge Y}$|, and |$S_{\lnot X}\cap S_{\lnot Y}=S_{\lnot X\wedge\lnot Y}$| in the information Boolean algebra are non-empty and correspond to the four rows in the truth table (Table 3) for the two propositions |$x\neq x^{\prime}$| and |$y\neq y^{\prime}$|(and to the four disjoint areas in the Venn diagram of Figure 2).
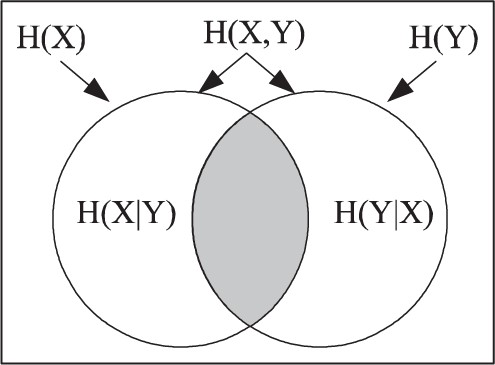
|$h\left(X,Y\right) =h\left( X|Y\right) +h\left( Y\right) =h\left( Y|X\right) +h\left( X\right)$|.
Truth table for atoms in the information algebra
| Atoms . | |$x\neq x^{\prime}$| . | |$y\neq y^{\prime}$| . | |$X\not \equiv Y$| . | |$X\supset Y$| . |
|---|---|---|---|---|
| |$S_{X\wedge Y}$| | T | T | F | T |
| |$S_{X\wedge\lnot Y}$| | T | F | T | F |
| |$S_{Y\wedge\lnot X}$| | F | T | T | T |
| |$S_{\lnot X\wedge\lnot Y}$| | F | F | F | T |
| Atoms . | |$x\neq x^{\prime}$| . | |$y\neq y^{\prime}$| . | |$X\not \equiv Y$| . | |$X\supset Y$| . |
|---|---|---|---|---|
| |$S_{X\wedge Y}$| | T | T | F | T |
| |$S_{X\wedge\lnot Y}$| | T | F | T | F |
| |$S_{Y\wedge\lnot X}$| | F | T | T | T |
| |$S_{\lnot X\wedge\lnot Y}$| | F | F | F | T |
Truth table for atoms in the information algebra
| Atoms . | |$x\neq x^{\prime}$| . | |$y\neq y^{\prime}$| . | |$X\not \equiv Y$| . | |$X\supset Y$| . |
|---|---|---|---|---|
| |$S_{X\wedge Y}$| | T | T | F | T |
| |$S_{X\wedge\lnot Y}$| | T | F | T | F |
| |$S_{Y\wedge\lnot X}$| | F | T | T | T |
| |$S_{\lnot X\wedge\lnot Y}$| | F | F | F | T |
| Atoms . | |$x\neq x^{\prime}$| . | |$y\neq y^{\prime}$| . | |$X\not \equiv Y$| . | |$X\supset Y$| . |
|---|---|---|---|---|
| |$S_{X\wedge Y}$| | T | T | F | T |
| |$S_{X\wedge\lnot Y}$| | T | F | T | F |
| |$S_{Y\wedge\lnot X}$| | F | T | T | T |
| |$S_{\lnot X\wedge\lnot Y}$| | F | F | F | T |
For |$n=2$| variables |$X$| and |$Y$|, there are |$2^{\left( 2^{n}\right) }=16$| ways to fill in the T’s and F’s to define all the possible Boolean combinations of the two propositions so there are |$16$| subsets in the information algebra |$\mathcal{I}\left( X\times Y\right)$|. The |$15$| non-empty subsets in |$\mathcal{I}\left( X\times Y\right) $| are defined in disjunctive normal form by the union of the atoms that have a T in their row. For instance, the set |$S_{X\not \equiv Y}$| corresponding to the symmetric difference or inequivalence |$\left( x\neq x^{\prime}\right) \not \equiv \left( y\neq y^{\prime}\right) $| is |$S_{X\not \equiv Y}=S_{X\wedge\lnot Y}\cup S_{Y\wedge\lnot X}=\left( S_{X}-S_{Y}\right) \cup\left( S_{Y} -S_{X}\right) $|.
The information algebra |$\mathcal{I}\left( X\times Y\right) $| is a finite combinatorial structure defined solely in terms of |$X\times Y$| using only the distinctions and indistinctions between the elements of |$X$| and |$Y$|. Any equivalence between Boolean expressions that is a tautology, e.g., |$x\neq x^{\prime}\equiv\left( x\neq x^{\prime}\wedge\lnot\left( y\neq y^{\prime }\right) \right) \vee\left( x\neq x^{\prime}\wedge y\neq y^{\prime}\right) $|, gives a set identity in the information Boolean algebra, e.g., |$S_{X}=\left( S_{X}\cap S_{\lnot Y}\right) \cup\left( S_{X}\cap S_{Y}\right) $|. Since that union is disjoint, any probability distribution on |$X\times Y$| gives the logically necessary identity |$h\left( X\right) =h\left( X|Y\right) +m\left( X,Y\right) $| (see below).
Consider |$S_{X\supset Y}=$||$S_{X\wedge Y}\cup S_{Y\wedge\lnot X}\cup S_{\lnot X\wedge\lnot Y}$| and suppose that the probability distribution gives |$\mu\left( S_{X\supset Y}\right) =1$| so that |$\mu\left( S_{X\wedge\lnot Y}\right) =0$|. That means in a double draw of |$\left( x,y\right) $| and |$\left( x^{\prime},y^{\prime}\right) $|, if |$x\neq x^{\prime}$|, then there is zero probability that |$y=y^{\prime}$|, so |$x\neq x^{\prime}$| implies (probabilistically) |$y\neq y^{\prime}$|. In terms of the Venn diagram, the |$h\left( X\right) $| area is a subset of the |$h\left( Y\right) $| area. i.e., |$Supp\left( S_{X}\right) \subseteq Supp\left( S_{Y}\right) $| in terms of the underlying sets.
9 Conditional entropies
9.1 Logical conditional entropy
All the compound notions for Shannon and logical entropy could be developed using either partitions (with point probabilities) or probability distributions of random variables as the given data. Since the treatment of Shannon entropy is most often in terms of probability distributions, we will stick to that case for both types of entropy. The formula for the compound notion of logical entropy will be developed first, and then the formula for the corresponding Shannon compound entropy will be obtained by the dit-bit transform.
The general idea of a conditional entropy of a random variable |$X$| given a random variable |$Y$| is to measure the information in |$X$| when we take away the information contained in |$Y$|, i.e., the set difference operation in terms of information sets.
9.2 Shannon conditional entropy
Since the dit-bit transform preserves sums and differences, we will have the same sort of Venn diagram formula for the Shannon entropies and this can be illustrated in the analogous ‘mnemonic’ Venn diagram (Figure 3).
|$H\left( X,Y\right)=H\left( X|Y\right) +H\left( Y\right) =H\left( Y|X\right)+H\left(X\right)$|.
10 Mutual information
10.1 Logical mutual information
It is a non-trivial fact that two non-empty partition ditsets always intersect [12]. The same holds for the positive supports of the basic infosets |$S_{X}$| and |$S_{Y}$|.
(Two non-empty supports always intersect) If |$h\left( X\right) h\left( Y\right) >0$|, then |$m\left( X,Y\right) >0$|.
Assuming |$h\left( X\right) h\left( Y\right) >0$|, the support |$Supp\left( S_{X}\right) $| is non-empty and thus there are two pairs |$\left( x,y\right) $| and |$\left( x^{\prime},y^{\prime}\right) $| such that |$x\neq x^{\prime}$| and |$p\left( x,y\right) p\left(x^{\prime},y^{\prime}\right) >0$|. If |$y\neq y^{\prime}$| then |$\left( \left( x,y\right) ,\left(x^{\prime},y^{\prime}\right) \right) \in Supp\left( S_{Y}\right) $| as well and we are finished, i.e., |$Supp\left( S_{X}\right) \cap Supp\left( S_{Y}\right) \neq\emptyset$|. Hence assume |$y=y^{\prime}$|. Since |$Supp\left( S_{Y}\right) $| is also non-empty and thus |$p\left(y\right) \neq1$|, there is another |$y^{\prime\prime}$| such that for some |$x^{\prime\prime}$|, |$p\left( x^{\prime\prime},y^{\prime\prime}\right) >0$|. Since |$x^{\prime\prime}$| cannot be equal to both |$x$| and |$x^{\prime}$| (by the anti-transitivity of distinctions), at least one of the pairs |$\left( \left( x,y\right) ,\left( x^{\prime\prime},y^{\prime\prime}\right) \right) $| or |$\left( \left( x^{\prime},y\right) ,\left( x^{\prime\prime},y^{\prime\prime}\right) \right) $| is in both |$Supp\left( S_{X}\right) $| and |$Supp\left( S_{Y}\right) $|, and thus the product measure on |$S_{\wedge\left\{ X,Y\right\} }=\left\{ \left( \left( x,y\right) ,\left( x^{\prime },y^{\prime}\right) \right) :x\neq x^{\prime}\wedge y\neq y^{\prime }\right\} $| is positive, i.e., |$m\left( X,Y\right) >0$|. ■
10.2 Shannon mutual information
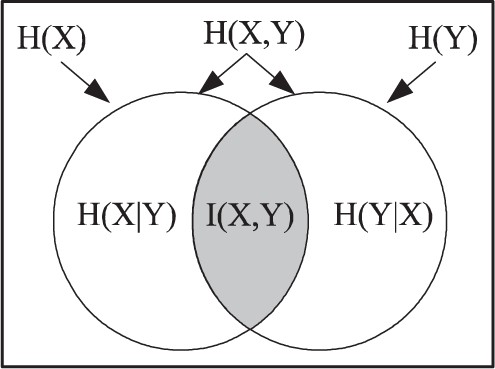
|$H\left(X,Y\right) =H\left( X|Y\right) +H\left( Y|X\right) +I\left( X,Y\right)$|.
This is the usual Venn diagram for the Shannon entropy notions that needs to be explained—since the Shannon entropies are not measures. Of course, one could just say the relationship holds for the Shannon entropies because that is how they were defined. It may seem a happy accident that the Shannon definitions all satisfy the measure-like Venn diagram formulas, but as one author put it: ‘Shannon carefully contrived for this “accident” to occur’ [39, p. 153]. As noted above, Campbell asked if ‘these analogies have a deeper foundation’ [9, p. 112] and the dit-bit transform answers that question.
11 Independent joint distributions
A joint probability distribution |$\left\{ p\left( x,y\right) \right\} $| on |$X\times Y$| is independent if each value is the product of the marginals: |$p\left( x,y\right) =p\left( x\right) p\left( y\right) $|.
Independence means the joint probability |$p\left( x,y\right) $| can always be separated into |$p\left( x\right) $| times |$p\left( y\right) $|. This carries over to the standard two-draw probability interpretation of logical entropy. Thus independence means that in two draws, the probability |$m\left( X,Y\right) $| of getting distinctions in both |$X$| and |$Y$| is equal to the probability |$h\left( X\right) $| of getting an |$X$|-distinction times the probability |$h\left( Y\right) $| of getting a |$Y$|-distinction. Similarly, Table 4 shows that, under independence, the four atomic areas in Figure 4 can each be expressed as the four possible products of the areas |$\left\{ h\left( X\right) ,1-h\left( X\right) \right\} $| and |$\left\{ h\left( Y\right) ,1-h\left( Y\right) \right\} $| that are defined in terms of one variable.
|$h\left( X,Y\right) =h\left( X|Y\right) +h\left( Y|X\right) +m\left( X,Y\right)$|.
Logical entropy relationships under independence
| Atomic areas . | |$X$| . | |$Y$| . |
|---|---|---|
| |$m\left( X,Y\right) =$| | |$h\left( X\right) \times$| | |$h\left( Y\right)$| |
| |$h\left( X|Y\right) =$| | |$h\left( X\right) \times$| | |$\left[1-h\left( Y\right) \right] $| |
| |$h\left( Y|X\right) =$| | |$\left[1-h\left( X\right) \right] \times$| | |$h\left( Y\right) $| |
| |$1-h\left( X,Y\right) =$| | |$\left[ 1-h\left( X\right) \right] \times$| | |$\left[ 1-h\left( Y\right) \right] $| |
| Atomic areas . | |$X$| . | |$Y$| . |
|---|---|---|
| |$m\left( X,Y\right) =$| | |$h\left( X\right) \times$| | |$h\left( Y\right)$| |
| |$h\left( X|Y\right) =$| | |$h\left( X\right) \times$| | |$\left[1-h\left( Y\right) \right] $| |
| |$h\left( Y|X\right) =$| | |$\left[1-h\left( X\right) \right] \times$| | |$h\left( Y\right) $| |
| |$1-h\left( X,Y\right) =$| | |$\left[ 1-h\left( X\right) \right] \times$| | |$\left[ 1-h\left( Y\right) \right] $| |
Logical entropy relationships under independence
| Atomic areas . | |$X$| . | |$Y$| . |
|---|---|---|
| |$m\left( X,Y\right) =$| | |$h\left( X\right) \times$| | |$h\left( Y\right)$| |
| |$h\left( X|Y\right) =$| | |$h\left( X\right) \times$| | |$\left[1-h\left( Y\right) \right] $| |
| |$h\left( Y|X\right) =$| | |$\left[1-h\left( X\right) \right] \times$| | |$h\left( Y\right) $| |
| |$1-h\left( X,Y\right) =$| | |$\left[ 1-h\left( X\right) \right] \times$| | |$\left[ 1-h\left( Y\right) \right] $| |
| Atomic areas . | |$X$| . | |$Y$| . |
|---|---|---|
| |$m\left( X,Y\right) =$| | |$h\left( X\right) \times$| | |$h\left( Y\right)$| |
| |$h\left( X|Y\right) =$| | |$h\left( X\right) \times$| | |$\left[1-h\left( Y\right) \right] $| |
| |$h\left( Y|X\right) =$| | |$\left[1-h\left( X\right) \right] \times$| | |$h\left( Y\right) $| |
| |$1-h\left( X,Y\right) =$| | |$\left[ 1-h\left( X\right) \right] \times$| | |$\left[ 1-h\left( Y\right) \right] $| |
The non-empty-supports-always-intersect proposition shows that |$h\left( X\right) h\left(Y\right) >0$| implies |$m\left( X,Y\right) >0$|, and thus that logical mutual information |$m\left(X,Y\right) $| is still positive for independent distributions when |$h\left( X\right) h\left(Y\right) >0$|, in which case |$m\left( X,Y\right) =h\left( X\right) h\left( Y\right) $|. This is a striking difference between the average bit-count Shannon entropy and the dit-count logical entropy. Aside from the waste case where |$h\left( X\right) h\left( Y\right) =0$|, there are always positive probability mutual distinctions for |$X$| and |$Y$|, and that dit-count information is not recognized by the coarser-grained average bit-count Shannon entropy.
12 Cross-entropies and divergences
The logical cross entropy is the same as the logical entropy when the distributions are the same, i.e., if |$p=q$|, then |$h\left( p\Vert q\right) =h\left( p\right) =\mu_{p}\left( S_{i\neq i^{\prime}}\right) $|.
Since the logical divergence |$d\left(p||q\right)$| is symmetrical, it develops via the dit-bit transform to the symmetrized version |$D_{s}\left( p||q\right) $| of the Kullback–Leibler divergence. The logical divergence |$d\left(p||q\right)$| is clearly a distance function (or metric) on probability distributions, but even the symmetrized Kullback–Leibler divergence |$D_{s}\left( p||q\right) $| may fail to satisfy the triangle inequality [11, p. 58] so it is not a distance metric.
13 Summary of formulas and dit-bit transforms
The Table 5 summarizes the concepts for the Shannon and logical entropies.
Comparisons between Shannon and logical entropy formulas
| . | |$\text{Shannon entropy}$| . | |$\text{Logical entropy}$| . |
|---|---|---|
| Entropy | |$H(p)=\sum p_{i}\log\left(1/p_{i}\right) $| | |$h\left( p\right) =\sum p_{i}\left( 1-p_{i}\right) $| |
| Mutual Info. | |${\small I(X,Y)=H}\left( X\right) +H\left( Y\right)-H\left( X,Y\right) $| | |$m\left( X,Y\right) =h\left( X\right) +h\left( Y\right) -h\left(X,Y\right) $| |
| Cond. entropy | |$H\left( X|Y\right)=H(X)-I\left( X,Y\right) $| | |$h\left( X|Y\right) =h\left( X\right) -m\left( X,Y\right)$| |
| Independence | |$I\left( X,Y\right) =0$| | |$m\left(X,Y\right) =h\left( X\right) h\left( Y\right) $| |
| Indep. Relations | |$H\left( X|Y\right) =H\left( X\right) $| | |$h\left( X|Y\right) =h\left( X\right)\left( 1-h\left( Y\right) \right) $| |
| Cross entropy | |${\small H}\left( p\Vert q\right) =\sum p_{i}\log\left( 1/q_{i}\right) $| | |${\small h}\left( p\Vert q\right) =\sum p_{i}\left( 1-q_{i}\right) $| |
| Divergence | |${\small D}\left( p\Vert q\right)=\sum_{i}p_{i}\log\left( \frac{p_{i}}{q_{i}}\right) $| | |${\small d}\left( p||q\right) =\sum_{i}\left( p_{i}-q_{i}\right) ^{2}$| |
| Relationships | |${\small D}\left( p\Vert q\right) ={\small H}\left( p\Vert q\right) {\small -H}\left( p\right) $| | |${\small d}\left( p\Vert q\right) =2{\small h}\left( p\Vert q\right){\small -}\left[ {\small h}\left( p\right) {\small +h}\left( q\right)\right] $| |
| Info. Inequality | |${\small D}\left( p\Vert q\right) \geq{\small 0}\text{ with }=\text{ iff }p=q$| | |$d\left( p\Vert q\right) \geq0\text{ with }=\text{ iff }p=q$| |
| . | |$\text{Shannon entropy}$| . | |$\text{Logical entropy}$| . |
|---|---|---|
| Entropy | |$H(p)=\sum p_{i}\log\left(1/p_{i}\right) $| | |$h\left( p\right) =\sum p_{i}\left( 1-p_{i}\right) $| |
| Mutual Info. | |${\small I(X,Y)=H}\left( X\right) +H\left( Y\right)-H\left( X,Y\right) $| | |$m\left( X,Y\right) =h\left( X\right) +h\left( Y\right) -h\left(X,Y\right) $| |
| Cond. entropy | |$H\left( X|Y\right)=H(X)-I\left( X,Y\right) $| | |$h\left( X|Y\right) =h\left( X\right) -m\left( X,Y\right)$| |
| Independence | |$I\left( X,Y\right) =0$| | |$m\left(X,Y\right) =h\left( X\right) h\left( Y\right) $| |
| Indep. Relations | |$H\left( X|Y\right) =H\left( X\right) $| | |$h\left( X|Y\right) =h\left( X\right)\left( 1-h\left( Y\right) \right) $| |
| Cross entropy | |${\small H}\left( p\Vert q\right) =\sum p_{i}\log\left( 1/q_{i}\right) $| | |${\small h}\left( p\Vert q\right) =\sum p_{i}\left( 1-q_{i}\right) $| |
| Divergence | |${\small D}\left( p\Vert q\right)=\sum_{i}p_{i}\log\left( \frac{p_{i}}{q_{i}}\right) $| | |${\small d}\left( p||q\right) =\sum_{i}\left( p_{i}-q_{i}\right) ^{2}$| |
| Relationships | |${\small D}\left( p\Vert q\right) ={\small H}\left( p\Vert q\right) {\small -H}\left( p\right) $| | |${\small d}\left( p\Vert q\right) =2{\small h}\left( p\Vert q\right){\small -}\left[ {\small h}\left( p\right) {\small +h}\left( q\right)\right] $| |
| Info. Inequality | |${\small D}\left( p\Vert q\right) \geq{\small 0}\text{ with }=\text{ iff }p=q$| | |$d\left( p\Vert q\right) \geq0\text{ with }=\text{ iff }p=q$| |
Comparisons between Shannon and logical entropy formulas
| . | |$\text{Shannon entropy}$| . | |$\text{Logical entropy}$| . |
|---|---|---|
| Entropy | |$H(p)=\sum p_{i}\log\left(1/p_{i}\right) $| | |$h\left( p\right) =\sum p_{i}\left( 1-p_{i}\right) $| |
| Mutual Info. | |${\small I(X,Y)=H}\left( X\right) +H\left( Y\right)-H\left( X,Y\right) $| | |$m\left( X,Y\right) =h\left( X\right) +h\left( Y\right) -h\left(X,Y\right) $| |
| Cond. entropy | |$H\left( X|Y\right)=H(X)-I\left( X,Y\right) $| | |$h\left( X|Y\right) =h\left( X\right) -m\left( X,Y\right)$| |
| Independence | |$I\left( X,Y\right) =0$| | |$m\left(X,Y\right) =h\left( X\right) h\left( Y\right) $| |
| Indep. Relations | |$H\left( X|Y\right) =H\left( X\right) $| | |$h\left( X|Y\right) =h\left( X\right)\left( 1-h\left( Y\right) \right) $| |
| Cross entropy | |${\small H}\left( p\Vert q\right) =\sum p_{i}\log\left( 1/q_{i}\right) $| | |${\small h}\left( p\Vert q\right) =\sum p_{i}\left( 1-q_{i}\right) $| |
| Divergence | |${\small D}\left( p\Vert q\right)=\sum_{i}p_{i}\log\left( \frac{p_{i}}{q_{i}}\right) $| | |${\small d}\left( p||q\right) =\sum_{i}\left( p_{i}-q_{i}\right) ^{2}$| |
| Relationships | |${\small D}\left( p\Vert q\right) ={\small H}\left( p\Vert q\right) {\small -H}\left( p\right) $| | |${\small d}\left( p\Vert q\right) =2{\small h}\left( p\Vert q\right){\small -}\left[ {\small h}\left( p\right) {\small +h}\left( q\right)\right] $| |
| Info. Inequality | |${\small D}\left( p\Vert q\right) \geq{\small 0}\text{ with }=\text{ iff }p=q$| | |$d\left( p\Vert q\right) \geq0\text{ with }=\text{ iff }p=q$| |
| . | |$\text{Shannon entropy}$| . | |$\text{Logical entropy}$| . |
|---|---|---|
| Entropy | |$H(p)=\sum p_{i}\log\left(1/p_{i}\right) $| | |$h\left( p\right) =\sum p_{i}\left( 1-p_{i}\right) $| |
| Mutual Info. | |${\small I(X,Y)=H}\left( X\right) +H\left( Y\right)-H\left( X,Y\right) $| | |$m\left( X,Y\right) =h\left( X\right) +h\left( Y\right) -h\left(X,Y\right) $| |
| Cond. entropy | |$H\left( X|Y\right)=H(X)-I\left( X,Y\right) $| | |$h\left( X|Y\right) =h\left( X\right) -m\left( X,Y\right)$| |
| Independence | |$I\left( X,Y\right) =0$| | |$m\left(X,Y\right) =h\left( X\right) h\left( Y\right) $| |
| Indep. Relations | |$H\left( X|Y\right) =H\left( X\right) $| | |$h\left( X|Y\right) =h\left( X\right)\left( 1-h\left( Y\right) \right) $| |
| Cross entropy | |${\small H}\left( p\Vert q\right) =\sum p_{i}\log\left( 1/q_{i}\right) $| | |${\small h}\left( p\Vert q\right) =\sum p_{i}\left( 1-q_{i}\right) $| |
| Divergence | |${\small D}\left( p\Vert q\right)=\sum_{i}p_{i}\log\left( \frac{p_{i}}{q_{i}}\right) $| | |${\small d}\left( p||q\right) =\sum_{i}\left( p_{i}-q_{i}\right) ^{2}$| |
| Relationships | |${\small D}\left( p\Vert q\right) ={\small H}\left( p\Vert q\right) {\small -H}\left( p\right) $| | |${\small d}\left( p\Vert q\right) =2{\small h}\left( p\Vert q\right){\small -}\left[ {\small h}\left( p\right) {\small +h}\left( q\right)\right] $| |
| Info. Inequality | |${\small D}\left( p\Vert q\right) \geq{\small 0}\text{ with }=\text{ iff }p=q$| | |$d\left( p\Vert q\right) \geq0\text{ with }=\text{ iff }p=q$| |
The Table 6 summarizes the dit-bit transforms.
The dit-bit transform from logical entropy to Shannon entropy
| . | The dit-bit Transform: |$1-p_{i}\rightsquigarrow\log\left( \frac {1}{p_{i}}\right) $| . |
|---|---|
| |$h\left( p\right) =$| | |$\sum_{i}p_{i}\left( 1-p_{i}\right) $| |
| |$H\left( p\right) =$| | |$\sum_{i}p_{i}\log\left( 1/p_{i}\right)$| |
| |$h\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right)\left[ \left( 1-p\left( x,y\right) \right) -\left( 1-p\left( y\right) \right) \right]$| |
| |$H\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[\log\left( \frac{1}{p\left( x,y\right) }\right) -\log\left( \frac{1}{p\left( y\right)}\right) \right] $| |
| |$m\left( X,Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[ \left[ 1-p\left( x\right) \right] +\left[ 1-p\left(y\right) \right] -\left[ 1-p\left( x,y\right) \right] \right] $| |
| |$I(X,Y)=$| | |$\sum_{x,y}p\left( x,y\right) \left[ \log\left(\frac{1}{p\left( x\right) }\right) +\log\left( \frac {1}{p\left( y\right) }\right)-\log\left( \frac{1}{p\left( x,y\right) }\right) \right] $| |
| |$h\left( p\Vert q\right) =$| | |$\frac{1}{2}\left[\sum_{i}p_{i}(1-q_{i})+\sum_{i}q_{i}\left( 1-p_{i}\right) \right] $| |
| |$H_{s}(p||q)=$| | |$\frac{1}{2}\left[ \sum_{i}p_{i}\log\left( \frac{1}{q_{i}}\right) +\sum_{i}q_{i}\log\left( \frac{1}{p_{i}}\right) \right] $| |
| |$d\left( p||q\right) =$| | |$2h\left( p||q\right)-\left[ \left( \sum_{i}p_{i}\left( 1-p_{i}\right) \right) +\left(\sum_{i}q_{i}\left( 1-q_{i}\right) \right) \right] $| |
| |$D_{s}\left( p||q\right) =$| | |$2H_{s}\left(p||q\right) -\left[ \sum_{i}p_{i}\log\left( \frac{1}{p_{i}}\right)+\sum_{i}q_{i}\log\left( \frac{1}{q_{i}}\right) \right] $| |
| . | The dit-bit Transform: |$1-p_{i}\rightsquigarrow\log\left( \frac {1}{p_{i}}\right) $| . |
|---|---|
| |$h\left( p\right) =$| | |$\sum_{i}p_{i}\left( 1-p_{i}\right) $| |
| |$H\left( p\right) =$| | |$\sum_{i}p_{i}\log\left( 1/p_{i}\right)$| |
| |$h\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right)\left[ \left( 1-p\left( x,y\right) \right) -\left( 1-p\left( y\right) \right) \right]$| |
| |$H\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[\log\left( \frac{1}{p\left( x,y\right) }\right) -\log\left( \frac{1}{p\left( y\right)}\right) \right] $| |
| |$m\left( X,Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[ \left[ 1-p\left( x\right) \right] +\left[ 1-p\left(y\right) \right] -\left[ 1-p\left( x,y\right) \right] \right] $| |
| |$I(X,Y)=$| | |$\sum_{x,y}p\left( x,y\right) \left[ \log\left(\frac{1}{p\left( x\right) }\right) +\log\left( \frac {1}{p\left( y\right) }\right)-\log\left( \frac{1}{p\left( x,y\right) }\right) \right] $| |
| |$h\left( p\Vert q\right) =$| | |$\frac{1}{2}\left[\sum_{i}p_{i}(1-q_{i})+\sum_{i}q_{i}\left( 1-p_{i}\right) \right] $| |
| |$H_{s}(p||q)=$| | |$\frac{1}{2}\left[ \sum_{i}p_{i}\log\left( \frac{1}{q_{i}}\right) +\sum_{i}q_{i}\log\left( \frac{1}{p_{i}}\right) \right] $| |
| |$d\left( p||q\right) =$| | |$2h\left( p||q\right)-\left[ \left( \sum_{i}p_{i}\left( 1-p_{i}\right) \right) +\left(\sum_{i}q_{i}\left( 1-q_{i}\right) \right) \right] $| |
| |$D_{s}\left( p||q\right) =$| | |$2H_{s}\left(p||q\right) -\left[ \sum_{i}p_{i}\log\left( \frac{1}{p_{i}}\right)+\sum_{i}q_{i}\log\left( \frac{1}{q_{i}}\right) \right] $| |
The dit-bit transform from logical entropy to Shannon entropy
| . | The dit-bit Transform: |$1-p_{i}\rightsquigarrow\log\left( \frac {1}{p_{i}}\right) $| . |
|---|---|
| |$h\left( p\right) =$| | |$\sum_{i}p_{i}\left( 1-p_{i}\right) $| |
| |$H\left( p\right) =$| | |$\sum_{i}p_{i}\log\left( 1/p_{i}\right)$| |
| |$h\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right)\left[ \left( 1-p\left( x,y\right) \right) -\left( 1-p\left( y\right) \right) \right]$| |
| |$H\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[\log\left( \frac{1}{p\left( x,y\right) }\right) -\log\left( \frac{1}{p\left( y\right)}\right) \right] $| |
| |$m\left( X,Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[ \left[ 1-p\left( x\right) \right] +\left[ 1-p\left(y\right) \right] -\left[ 1-p\left( x,y\right) \right] \right] $| |
| |$I(X,Y)=$| | |$\sum_{x,y}p\left( x,y\right) \left[ \log\left(\frac{1}{p\left( x\right) }\right) +\log\left( \frac {1}{p\left( y\right) }\right)-\log\left( \frac{1}{p\left( x,y\right) }\right) \right] $| |
| |$h\left( p\Vert q\right) =$| | |$\frac{1}{2}\left[\sum_{i}p_{i}(1-q_{i})+\sum_{i}q_{i}\left( 1-p_{i}\right) \right] $| |
| |$H_{s}(p||q)=$| | |$\frac{1}{2}\left[ \sum_{i}p_{i}\log\left( \frac{1}{q_{i}}\right) +\sum_{i}q_{i}\log\left( \frac{1}{p_{i}}\right) \right] $| |
| |$d\left( p||q\right) =$| | |$2h\left( p||q\right)-\left[ \left( \sum_{i}p_{i}\left( 1-p_{i}\right) \right) +\left(\sum_{i}q_{i}\left( 1-q_{i}\right) \right) \right] $| |
| |$D_{s}\left( p||q\right) =$| | |$2H_{s}\left(p||q\right) -\left[ \sum_{i}p_{i}\log\left( \frac{1}{p_{i}}\right)+\sum_{i}q_{i}\log\left( \frac{1}{q_{i}}\right) \right] $| |
| . | The dit-bit Transform: |$1-p_{i}\rightsquigarrow\log\left( \frac {1}{p_{i}}\right) $| . |
|---|---|
| |$h\left( p\right) =$| | |$\sum_{i}p_{i}\left( 1-p_{i}\right) $| |
| |$H\left( p\right) =$| | |$\sum_{i}p_{i}\log\left( 1/p_{i}\right)$| |
| |$h\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right)\left[ \left( 1-p\left( x,y\right) \right) -\left( 1-p\left( y\right) \right) \right]$| |
| |$H\left( X|Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[\log\left( \frac{1}{p\left( x,y\right) }\right) -\log\left( \frac{1}{p\left( y\right)}\right) \right] $| |
| |$m\left( X,Y\right) =$| | |$\sum_{x,y}p\left( x,y\right) \left[ \left[ 1-p\left( x\right) \right] +\left[ 1-p\left(y\right) \right] -\left[ 1-p\left( x,y\right) \right] \right] $| |
| |$I(X,Y)=$| | |$\sum_{x,y}p\left( x,y\right) \left[ \log\left(\frac{1}{p\left( x\right) }\right) +\log\left( \frac {1}{p\left( y\right) }\right)-\log\left( \frac{1}{p\left( x,y\right) }\right) \right] $| |
| |$h\left( p\Vert q\right) =$| | |$\frac{1}{2}\left[\sum_{i}p_{i}(1-q_{i})+\sum_{i}q_{i}\left( 1-p_{i}\right) \right] $| |
| |$H_{s}(p||q)=$| | |$\frac{1}{2}\left[ \sum_{i}p_{i}\log\left( \frac{1}{q_{i}}\right) +\sum_{i}q_{i}\log\left( \frac{1}{p_{i}}\right) \right] $| |
| |$d\left( p||q\right) =$| | |$2h\left( p||q\right)-\left[ \left( \sum_{i}p_{i}\left( 1-p_{i}\right) \right) +\left(\sum_{i}q_{i}\left( 1-q_{i}\right) \right) \right] $| |
| |$D_{s}\left( p||q\right) =$| | |$2H_{s}\left(p||q\right) -\left[ \sum_{i}p_{i}\log\left( \frac{1}{p_{i}}\right)+\sum_{i}q_{i}\log\left( \frac{1}{q_{i}}\right) \right] $| |
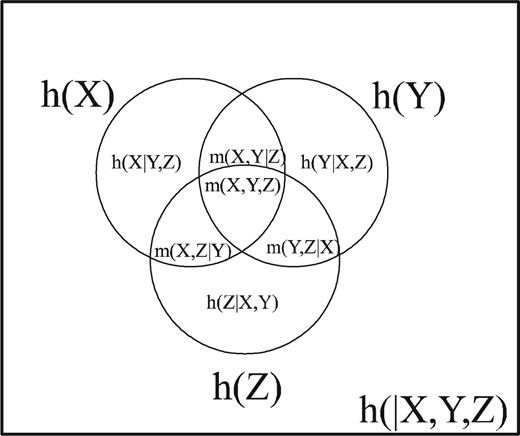
14 Entropies for multivariate joint distributions
Then all the logical entropies for this |$n$|-variable case are given as the product measure of certain infosets |$S$|. Let |$I,J\subseteq N$| be subsets of the set of all variables |$N=\left\{ X_{1},...,X_{n}\right\} $| and let |$x=\left( x_{1},...,x_{n}\right) $| and |$x^{\prime}=\left( x_{1} ^{\prime},...,x_{n}^{\prime}\right) $|.
As before, the information algebra |$\mathcal{I}\left( X_{1}\times...\times X_{n}\right) $| is the Boolean subalgebra of |$\wp\left( \left( X_{1} \times...\times X_{n}\right) ^{2}\right) $| generated by the basic infosets |$S_{X_{i}}$| for the variables and their complements |$S_{\lnot X_{i}}$|.
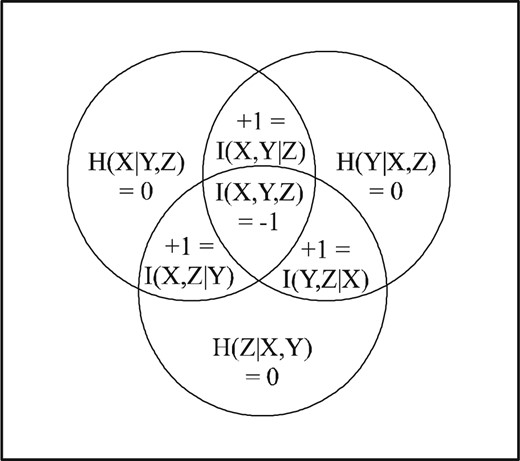
To emphasize that Venn-like diagrams are only a mnemonic analogy, Norman Abramson gives an example [1, pp. 130–1] where the Shannon mutual information of three variables is negative.12
Consider the joint distribution |$\left\{ p\left( x,y,z\right) \right\} $|on |$X\times Y\times Z$| where |$X=Y=Z=\left\{ 0,1\right\} $|. Suppose two dice are thrown, one after the other. Then |$X=1$| if the first die came up odd, |$Y=1$| if the second die came up odd, and |$Z=1$| if |$X+Y$| is odd [18, Exercise 26, p. 143]. Then the probability distribution is in Table 7.
Abramson’s example giving negative Shannon mutual information |$I\left(X,Y,Z\right)$|
| |$X$| . | |$Y$| . | |$Z$| . | |$p(x,y,z)$| . | |$p(x,y),p(x,z),p\left( y,z\right) $| . | |$p(x),p(y),p\left( z\right) $| . |
|---|---|---|---|---|---|
| |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$0$| | |$0$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
| |$X$| . | |$Y$| . | |$Z$| . | |$p(x,y,z)$| . | |$p(x,y),p(x,z),p\left( y,z\right) $| . | |$p(x),p(y),p\left( z\right) $| . |
|---|---|---|---|---|---|
| |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$0$| | |$0$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
Abramson’s example giving negative Shannon mutual information |$I\left(X,Y,Z\right)$|
| |$X$| . | |$Y$| . | |$Z$| . | |$p(x,y,z)$| . | |$p(x,y),p(x,z),p\left( y,z\right) $| . | |$p(x),p(y),p\left( z\right) $| . |
|---|---|---|---|---|---|
| |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$0$| | |$0$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
| |$X$| . | |$Y$| . | |$Z$| . | |$p(x,y,z)$| . | |$p(x,y),p(x,z),p\left( y,z\right) $| . | |$p(x),p(y),p\left( z\right) $| . |
|---|---|---|---|---|---|
| |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$0$| | |$0$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$0$| | |$1$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$0$| | |$0$| | |$1/4$| | |$1/2$| |
| |$1$| | |$0$| | |$1$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/4$| | |$1/2$| |
| |$1$| | |$1$| | |$1$| | |$0$| | |$1/4$| | |$1/2$| |
All the simple and compound notions of logical entropy have a direct interpretation as a two-draw probability. The logical mutual information |$m\left( X,Y,Z\right) $| is the probability that in two independent samples of |$X\times Y\times Z$|, the outcomes would differ in all coordinates. This means the two draws would have the form |$\left( x,y,z\right) $| and |$\left(1-x,1-y,1-z\right) $| for the binary variables, but it is easily seen by inspection that |$p\left(x,y,z\right) =0$| or |$p\left( 1-x,1-y,1-z\right) =0$|, so the products of those two probabilities are all |$0$| as computed—and thus there is no three-way overlap. The two-way overlaps are |$m\left( X,Y\right) =h\left( X\right) +h\left( Y\right) -h\left( X,Y\right)=\frac{1}{2}+\frac{1}{2}-\frac{3}{4}=\frac{1}{4}$| or since each pair of variables is independent, |$m\left( X,Y\right) =h\left( X\right) h\left( Y\right)=\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$|, and similarly for the other pairs of variables. The non-empty-supports-always-intersect result holds for any two variables, but the example shows that there is no necessity in having a three-way overlap, i.e., |$h\left( X\right) h\left( Y\right) h\left( Z\right) >0$| does not imply |$m\left( X,Y,Z\right) >0$|.13
It is unclear how that can be interpreted as the mutual information contained in the three variables or how the corresponding ‘Venn diagram’ (Figure 7) can be anything more than a mnemonic. Indeed, as Imre Csiszar and Janos Körner remark:
The set-function analogy might suggest to introduce further information quantities corresponding to arbitrary Boolean expressions of sets. E.g., the ‘information quantity’ corresponding to |$\mu\left(A\cap B\cap C\right) =\mu\left( A\cap B\right) -\mu\left( \left(A\cap B\right) -C\right)$| would be |$I(X,Y)-I(X,Y|Z)$|; this quantity has, however, no natural intuitive meaning. [11, pp. 53–4]
Note how the supposed ‘intuitiveness’ of independent random variables giving disjoint or at least ‘zero overlap’ Venn diagram areas in the two-variable Shannon case comes at the cost of possibly having ‘no natural intuitive meaning’ and negative ‘areas’ in the multivariate case. In probability theory, for a joint probability distribution of |$3$| or more random variables, there is a distinction between the variables being pair-wise independent and being mutually independent. In any counterexample where three variables are pairwise but not mutually independent [18, p. 127], the Venn diagram areas for |$H(X)$|, |$H(Y)$| and |$H(Z)$| have to have pairwise zero overlaps, but since they are not mutually independent, all three areas have a non-zero overlap. The only way that can happen is for the pairwise overlaps such as |$I\left( X,Y\right) =0$| between |$H\left( X\right)$| and |$H\left(Y\right)$| to have a positive part |$I\left( X,Y|Z\right) $| (always non-negative [49, Theorem 2.34, p. 23]) and a negative part |$I(X,Y,Z)$| that add to |$0$| as in Figure 7.
15 Logical entropy and some related notions
A similar relationship holds in the quantum case between the von Neumann entropy |$S\left( \rho\right) =-\operatorname*{tr}\left[ \rho \ln\left( \rho\right) \right] $| and the quantum logical entropy|$h\left( \rho\right) =\operatorname*{tr}\left[ \rho\left( 1-\rho\right) \right] =1-\operatorname*{tr}\left[ \rho^{2}\right] $| which is defined by having a density matrix |$\rho$| replace the probability distribution |$p$| and the trace replace the sum.
This relationship between the Shannon/von Neumann entropies and the logical entropies in the classical and quantum cases is responsible for presenting the logical entropy as a ‘linear’ approximation to the Shannon or von Neumann entropies since |$1-p_{i}$| is the linear term in the series for |$-\ln\left( p_{i}\right) $| [before the multiplication by |$p_{i}$| to make the term quadratic!]. And |$h\left( p\right) =1-\sum_{i}p_{i}^{2}$| or it quantum counterpart |$h\left(\rho\right) =1-\operatorname*{tr}\left[ \rho ^{2}\right] $| are even called ‘linear entropy’ (e.g. [8]) even though the formulas are obviously quadratic.14 Another name for the quantum logical entropy found in the literature is ‘mixedness’ [26, p. 5] which at least does not call a quadratic formula ‘linear.’ It is even called ‘impurity’ since the complement |$1-h\left( \rho\right) =\operatorname*{tr}\left[\rho^{2}\right] $| (i.e. the quantum version of Alan Turing’s repeat rate |$\sum_{i}p_{i}^{2}$| [21]) is called the ‘purity.’
Quantum logical entropy is beyond the scope of this article but it might be noted that some quantum information theorists have been using that concept to rederive results previously derived using the von Neumann entropy such as the Klein inequality, concavity, and a Holevo-type bound for Hilbert–Schmidt distance ([42], [43]). Moreover, the logical derivation of the logical entropy formulas using the notion of distinctions gives a certain naturalness to the notion of quantum logical entropy.
We find this framework of partitions and distinction most suitable (at least conceptually) for describing the problems of quantum state discrimination, quantum cryptography and in general, for discussing quantum channel capacity. In these problems, we are basically interested in a distance measure between such sets of states, and this is exactly the kind of knowledge provided by logical entropy ([12], [42]).
There are many older results derived under the misnomer ‘linear entropy’ or derived for the quadratic special case of the Tsallis–Havrda–Charvat entropy ([24], [44], [45]). Those parameterized families of entropy formulas are sometimes criticized for lacking a convincing interpretation, but we have seen that the quadratic case is interpreted simply as a two-draw probability of a ‘dit’ of the partition—just as in the dual case, the normalized counting measure of a subset is the one-draw probability of an ‘it’ in the subset.
In accordance with its quadratic nature, logical entropy is the logical special case of C. R. Rao’s quadratic entropy [36]. Two elements from |$U=\left\{ u_{1},...,u_{n}\right\} $| are either identical or distinct. Gini [19] introduced |$d_{ij}$| as the ’distance’ between the |$i^{th}$| and |$j^{th}$| elements where |$d_{ij}=1$| for |$i\not =j$| and |$d_{ii} =0$|—which might be considered the ‘logical distance function’ |$d_{ij} =1-\delta_{ij}$|, so logical distance is complement of the Kronecker delta. Since |$1=\left( p_{1}+...+p_{n}\right) \left( p_{1}+...+p_{n}\right) =\sum_{i}p_{i}^{2}+\sum_{i\not =j}p_{i}p_{j}$|, the logical entropy, i.e., Gini’s index of mutability, |$h\left( p\right) =1-\sum_{i}p_{i}^{2} =\sum_{i\not =j}p_{i}p_{j}$|, is the average logical distance between distinct elements. But in 1982, C. R. Rao [36] generalized this as quadratic entropy by allowing other distances |$d_{ij}=d_{ji}$| for |$i\not =j$| (but always |$d_{ii}=0$|) so that |$Q=\sum_{i\not =j}d_{ij}p_{i}p_{j}$| would be the average distance between distinct elements from |$U$|.
Rao’s treatment also includes (and generalizes) the natural extension of logical entropy to continuous probability density functions |$f\left( x\right) $| for a random variable |$X$|: |$h\left(X\right) =1-\int f\left( x\right) ^{2}dx$|. It might be noted that the natural extension of Shannon entropy to continuous probability density functions |$f(x)$| through the limit of discrete approximations contains terms |$1/\log\left( \Delta x_{i}\right) $| that blow up as the mesh size |$\Delta x_{i}$| goes to zero (see [34, pp. 34–38]).15 Hence the definition of Shannon entropy in the continuous case is defined not by the limit of the discrete formula but by the analogous formula |$H\left( X\right) =-\int f\left( x\right) \log\left( f\left( x\right) \right) dx$| which, as Robert McEliece notes, ‘is not in any sense a measure of the randomness of |$X$|’ [34, p. 38] in addition to possibly having negative values [46, p. 74].
16 The statistical interpretation of Shannon entropy
Shannon, like Ralph Hartley [23] before him, starts with the question of how much ‘information’ is required to single out a designated element from a set |$U$| of equiprobable elements. Alfréd Rényi formulated this in terms of the search [37] for a hidden designated element like the answer in a Twenty Questions game. But being able to always find the designated element is equivalent to being able to distinguish all elements from one another.
How can that extrapolation and averaging be made rigorous to offer a more convincing interpretation? Shannon uses the law of large numbers. Suppose that we have a three-letter alphabet |$\left\{ a,b,c\right\} $| where each letter was equiprobable, |$p_{a}=p_{b}=p_{c}=\frac{1}{3}$|, in a multi-letter message. Then a one-letter or two-letter message cannot be exactly coded with a binary |$0,1$| code with equiprobable |$0$|’s and |$1$|’s. But any probability can be better and better approximated by longer and longer representations in the binary number system. Hence we can consider longer and longer messages of |$N$| letters along with better and better approximations with binary codes. The long-run behaviour of messages |$u_{1}u_{2}...u_{N}$| where |$u_{i}\in\left\{ a,b,c\right\} $| is modelled by the law of large numbers so that the letter |$a$| on average occur |$p_{a}N=\frac{1}{3}N$| times and similarly for |$b$| and |$c$|. Such a message is called typical.
Hence the number of such typical messages is |$3^{N}$|.
This example shows the general pattern.
In the general case, let |$p=\left\{ p_{1},...,p_{n}\right\} $| be the probabilities over a |$n$|-letter alphabet |$A=\left\{ a_{1},...,a_{n}\right\} $|. In an |$N$|-letter message, the probability of a particular message |$u_{1}u_{2}...u_{N}$| is |$\Pi_{i=1}^{N}\Pr\left( u_{i}\right) $| where |$u_{i}$| could be any of the symbols in the alphabet so if |$u_{i}=a_{j}$| then |$\Pr\left( u_{i}\right) =p_{j}$|.
Dividing by the number |$N$| of letters gives the average bit-count interpretation of the Shannon entropy; |$H\left( p\right) =\log\left[E\left( p\right) \right] =\sum_{k=1}^{n}p_{k}\log\left( \frac{1}{p_{k} }\right) $| is the average number of bits necessary to distinguish, i.e., uniquely encode, each letter in a typical message.
This result, usually called the Noiseless Coding Theorem, allows us to conceptually relate the logical and Shannon entropies (the dit-bit transform gives the quantitative relationship). In terms of the simplest case for partitions, the Shannon entropy |$H\left( \pi\right) =\sum_{B\in\pi} p_{B}\log_{2}\left( 1/p_{B}\right) $| is a requantification of the logical measure of information |$h\left( \pi\right) =\frac {|\operatorname*{dit}\left( \pi\right) |}{\left\vert U\times U\right\vert }=1-\sum_{B\in\pi}p_{B}^{2}$|. Instead of directly counting the distinctions of |$\pi$|, the idea behind Shannon entropy is to count the (minimum) number of binary partitions needed to make all the distinctions of |$\pi$|. In the special case of |$\pi$| having |$2^{m}$| equiprobable blocks, the number of binary partitions |$\beta_{i}$| needed to make the distinctions |$\operatorname*{dit} \left( \pi\right) $| of |$\pi$| is |$m$|. Represent each block by an |$m$|-digit binary number so the |$i^{th}$| binary partition |$\beta_{i}$| just distinguishes those blocks with |$i^{th}$| digit |$0$| from those with |$i^{th}$| digit |$1$|.18 Thus there are |$m$| binary partitions |$\beta_{i}$| such that |$\vee_{i=1}^{m}\beta_{i}=\pi$| (|$\vee$| is here the partition join) or, equivalently, |$\cup_{i=1}^{m}\operatorname*{dit}\left( \beta_{i}\right) =\operatorname*{dit}\left(\vee_{i=1}^{m}\beta_{i}\right) =\operatorname*{dit}\left( \pi\right) $|. Thus |$m$| is the exact number of binary partitions it takes to make the distinctions of |$\pi$|. In the general case, Shannon gives the above statistical interpretation so that |$H\left( \pi\right) $| is the minimum average number of binary partitions or bits needed to make the distinctions of |$\pi$|.
Note the difference in emphasis. Logical information theory is only concerned with counting the distinctions between distinct elements, not with uniquely designating the distinct entities. By requantifying to count the number of binary partitions it takes to make the same distinctions, the emphasis shifts to the length of the binary code necessary to uniquely designate the distinct elements. Thus the Shannon information theory perfectly dovetails into coding theory and is often presented today as the unified theory of information and coding (e.g. [34] or [22]). It is that shift to not only making distinctions but uniquely coding the distinct outcomes that gives the Shannon theory of information, coding and communication such importance in applications.
It might be noted that Shannon formula is often connected to (and even sometimes identified with) the Boltzmann–Gibbs entropy in statistical mechanics–which was the source for Shannon’s nomenclature. But that connection is only a numerical approximation, not an identity in functional form, where the natural logs of factorials in the Boltzmann formula are approximated using the first two terms in the Stirling approximation [14]. Indeed, as pointed out by David J. C. MacKay, one can use the next term in the Stirling approximation to give a ‘more accurate approximation’ [32, p. 2] to the entropy of statistical mechanics–but no one would suggest using such a formula in information theory. While the use of the ‘entropy’ terminology is here to stay in information theory, the Shannon Noiseless Coding Theorem gives the basis to interpret the Shannon formula, not numerical approximations to the Boltzmann-Gibbs entropy in statistical mechanics.
17 Concluding remarks
Logical information theory is based on the notion of information-as-distinctions. It starts with the finite combinatorial information sets which are the ditsets of partitions on a finite |$U$| or the infosets |$S_{X}$| and |$S_{Y}$| associated with a finite |$X\times Y$|—and that calculus of identities and differences is expressed in the information Boolean algebra |$\mathcal{I}\left( U\right)$| or |$\mathcal{I}\left(X\times Y\right)$|. No probabilities are involved in the definition of the information sets of distinctions. But when a probability distribution is defined on |$U$| or on |$X\times Y$|, then the product probability distribution is determined on |$U^{2}$| or |$\left( X\times Y\right)^{2}$| respectively. The quantitative logical entropy of an information set is the value of the product probability measure on the set.
Since conventional information theory has heretofore been focused on the original notion of Shannon entropy (and quantum information theory on the corresponding notion of von Neumann entropy), much of the article has compared the logical entropy notions to the corresponding Shannon entropy notions.
Logical entropy, like logical probability, is a measure, while Shannon entropy is not. The compound Shannon entropy concepts nevertheless satisfy the measure-like Venn diagram relationships that are automatically satisfied by a measure. This can be explained by the dit-bit transform so that by putting a logical entropy notion into the proper form as an average of dit-counts, one can replace a dit-count by a bit-count and obtain the corresponding Shannon entropy notion—which shows a deeper relationship behind the Shannon compound entropy concepts.
In sum, the logical theory of information-as-distinctions is the ground level logical theory of information stated first in terms of sets of distinctions and then in terms of two-draw probability measures on the sets. The Shannon information theory is a higher-level theory that requantifies distinctions by counting the minimum number of binary partitions (bits) that are required, on average, to make all the same distinctions, i.e., to encode the distinguished elements—and is thus well-adapted for the theory of coding and communication.
References
Footnotes
1This article is about what Adriaans and van Benthem call ‘Information B: Probabilistic, information-theoretic, measured quantitatively’, not about ‘Information A: knowledge, logic, what is conveyed in informative answers’ where the connection to philosophy and logic is built-in from the beginning. Likewise, the paper is not about Kolmogorov-style ‘Information C: Algorithmic, code compression, measured quantitatively’ [4, p. 11].
2Kolmogorov had something else in mind such as a combinatorial development of Hartley’s |$\log\left( n\right) $| on a set of |$n$| equiprobable elements [28].
3There is a general method to define operations on partitions corresponding to the Boolean operations on subsets ([13], [15]) but the lattice operations of join and meet, and the implication are sufficient to define a partition algebra |$\prod\left( U\right) $| parallel to the familiar powerset Boolean algebra |$\wp\left( U\right) $|.
6Perhaps, one should say that Shannon entropy is not the measure of any independently defined set. The fact that the Shannon formulas ‘act like a measure on a set’ can, of course, be formalized by formally associating an (indefinite) ‘set’ with each random variable |$X$| and then defining the measure value on the ‘set’ as |$H\left( X\right) $|. But since there is no independently defined ‘set’ with actual members and this ‘measure’ is defined by the Shannon entropy values (rather than the other way around), nothing is added to the already-known fact that the Shannon entropies act like a measure in the Venn diagram relationships. This formalization exercise seems to have been first carried out by Guo Ding Hu [25] but was also noted by Imre Csiszar and Janos Körner [11], and redeveloped by Raymond Yeung ([48], [49]).
7Note that |$n=1/p_{0}$| need not be an integer. We are following the usual practice in information theory where an implicit ‘on average’ interpretation is assumed since actual ‘binary partitions’ or ‘binary digits’ (or ‘bits’) only come in integral units. The ‘on average’ provisos are justified by the ‘Noiseless Coding Theorem’ covered in the later section on the statistical interpretation of Shannon entropy.
8Note that |$S_{\lnot X}$| and |$S_{\lnot Y}$| intersect in the diagonal |$\Delta\subseteq\left( X\times Y\right) ^{2}$|.
9In a context where the logical distance |$d\left(X,Y\right) =h\left( X|Y\right) +h\left( Y|X\right) $| and the logical divergence |$d\left( p||q\right) $| are both defined, e.g., two partitions |$\pi$| and |$\sigma$| on the same set |$U$|, then the two concepts are the same, i.e., |$d\left( \pi,\sigma\right) =d\left( \pi||\sigma\right) $|.
10The usual version of the inclusion–exclusion principle would be: |$h(X,Y,Z)=h(X)+h\left( Y\right) +h\left( Z\right) -m\left( X,Y\right) -m\left(X,Z\right) -m\left( Y,Z\right) +m\left( X,Y,Z\right) $| but |$m\left( X,Y\right) =h(X)+h\left( Y\right) -h\left( X,Y\right) $| and so forth, so substituting for |$m\left(X,Y\right) $|, |$m\left( X,Z\right) $|, and |$m\left( Y,Z\right) $| gives the formula.
11The multivariate generalization of the ‘Shannon’ mutual information was developed not by Shannon but by William J. McGill [33] and Robert M. Fano ([16], [17]) at MIT in the early 1950s and independently by Nelson M. Blachman [6]. The criterion for it being the ‘correct’ generalization seems to be that it satisfied the generalized Venn diagram formulas that are automatically satisfied by any measure and are thus also obtained from the multivariate logical mutual information using the dit-bit transform—as is done here.
12Fano had earlier noted that, for three or more variables, the mutual information could be negative [17, p. 58].
13The simplest example suffices. There are three non-trivial partitions on a set with three elements and those partitions have no dits in common.
14Sometimes the misnomer ‘linear entropy’ is applied to the rescaled logical entropy |$\frac{n}{n-1}h\left(\pi\right)$|. The maximum value of the logical entropy is |$h(\mathbf{1})=1-\frac{1}{n}=\frac{n-1}{n}$| so the rescaling gives a maximum value of |$1$|. In terms of the partition-logic derivation of the logical entropy formula, this amounts to sampling without replacement and normalizing |$\left\vert \operatorname*{dit}\left( \pi\right) \right\vert $| by the number of possible distinctions |$\left\vert U\times U-\Delta\right\vert =n^{2}-n$| (where |$\Delta=\left\{ \left( u,u\right) :u\in U\right\} $| is the diagonal) instead of |$\left\vert U\times U\right\vert =n^{2}$| since: |$\frac{\left\vert \operatorname*{dit}\left( \pi\right) \right\vert }{\left\vert U\times U-\Delta\right\vert }=\frac{\left\vert \operatorname*{dit}\left(\pi\right) \right\vert }{n\left( n-1\right) }=\frac{n}{n-1}\frac{\left\vert\operatorname*{dit}\left( \pi\right) \right\vert }{n^{2}}=\frac{n}{n-1}h\left( \pi\right) $|.
15For expository purposes, we have restricted the treatment to finite sample spaces |$U$|. For some countably infinite discrete probability distributions, the Shannon entropy blows up to infinity [49, Example 2.46, p. 30], while the countable logical infosets are always well-defined and the logical entropy is always in the half-open interval |$[0,1)$|.
16This is the special case where Campbell [9] noted that Shannon entropy acted as a measure to count that number of binary partitions.
17When an event or outcome has a probability |$p_{i}$|, it is intuitive to think of it as being drawn from a set of |$\frac{1}{p_{i}}$| equiprobable elements (particularly when |$\frac{1}{p_{i}}$| is an integer) so |$\frac{1}{p_{i}}$| is called the numbers-equivalentof the probability|$p_{i}$| [3]. For a development of |$E\left( p\right) $| from scratch, see [12], [14].
18Thus as noted by John Wilkins in 1641, five letter words in a two-letter code would suffice to distinguish |$2^{5}=32$| distinct entities [47].