-
PDF
- Split View
-
Views
-
Cite
Cite
J. Ted Mackereth, Jo Bovy, Ricardo P. Schiavon, Gail Zasowski, Katia Cunha, Peter M. Frinchaboy, Ana E. García Perez, Michael R. Hayden, Jon Holtzman, Steven R. Majewski, Szabolcs Mészáros, David L. Nidever, Marc Pinsonneault, Matthew D. Shetrone, The age–metallicity structure of the Milky Way disc using APOGEE, Monthly Notices of the Royal Astronomical Society, Volume 471, Issue 3, November 2017, Pages 3057–3078, https://doi.org/10.1093/mnras/stx1774
Close - Share Icon Share
Abstract
The measurement of the structure of stellar populations in the Milky Way disc places fundamental constraints on models of galaxy formation and evolution. Previously, the disc's structure has been studied in terms of populations defined geometrically and/or chemically, but a decomposition based on stellar ages provides a more direct connection to the history of the disc, and stronger constraint on theory. Here, we use positions, abundances and ages for 31 244 red giant branch stars from the Sloan Digital Sky Survey (SDSS)-APOGEE survey, spanning 3 < Rgc < 15 kpc, to dissect the disc into mono-age and mono-[Fe/H] populations at low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$|. For each population, with Δage < 2 Gyr and Δ[Fe/H] < 0.1 dex, we measure the structure and surface-mass density contribution. We find that low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| mono-age populations are fit well by a broken exponential, which increases to a peak radius and decreases thereafter. We show that this profile becomes broader with age, interpreted here as a new signal of disc heating and radial migration. High |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations are well fit as single exponentials within the radial range considered, with an average scalelength of 1.9 ± 0.1 kpc. We find that the relative contribution of high to low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations at R0 is |$f_\Sigma = 18\hbox{ per cent} \pm 5\hbox{ per cent}$|; high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| contributes most of the mass at old ages, and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at young ages. The low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations overlap in age at intermediate [Fe/H], although both contribute mass at R0 across the full range of [Fe/H]. The mass-weighted scaleheight hZ distribution is a smoothly declining exponential function. High |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations are thicker than low |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, and the average hZ increases steadily with age, between 200 and 600 pc.
1 INTRODUCTION
The understanding of the present day spatial, kinematic and chemical configuration of the stars of the Milky Way disc is a cornerstone of Galactic archaeology, placing key constraints on models of galaxy disc formation and evolution. Much of our understanding of the time evolution of galaxy discs like that of the Milky Way has arisen from studies that match galaxies of a given stellar mass at z = 0 to their progenitors at higher z (and therefore, lookback time, e.g. van Dokkum et al. 2013; Papovich et al. 2015; Huertas-Company et al. 2016). However, the Sun's position in the Milky Way presents a high-fidelity insight into the structure of a Galactic disc on a star by star basis, which has provided a great many insights into the problem (e.g. Eggen, Lynden-Bell & Sandage 1962; Edvardsson et al. 1993; Haywood et al. 2013). Data for large numbers of disc stars over a wide range of Galactocentric distances, including positions, chemical abundances and stellar ages are now becoming readily available, due to the advent of modern spectroscopic surveys such as APOGEE (Majewski et al. 2015), Gaia-ESO (Gilmore et al. 2012) and GALAH (Martell et al. 2017), with future instruments aiming to bolster the ESA-Gaia data releases (Gaia Collaboration 2016), such as WEAVE (Dalton et al. 2014) and MOONS (Cirasuolo et al. 2012).
Galaxy discs are commonly considered to have stellar density distributions described by exponential laws of some form (e.g. de Vaucouleurs 1959; Freeman 1970; Gilmore & Reid 1983; Pohlen & Trujillo 2006), assumed classically as the result of gas collapse with angular momentum conservation (e.g. Fall & Efstathiou 1980), and more recently, the redistribution or ‘scrambling’ of the angular momentum of individual stars (e.g. Elmegreen & Struck 2013, 2016; Herpich, Tremaine & Rix 2017). External discs have relatively well-constrained photometric scalelengths (e.g. Fathi et al. 2010), but estimates of that of the Milky Way vary greatly (see Bland-Hawthorn & Gerhard 2016, for a review), and seem to be in tension with those in external galaxies that are assumed to be similar to the Milky Way. This suggests a discord between internal and external scalelength measurement methods, or that the Milky Way has a structure distinct from the bulk of disc galaxies.
In the Milky Way, the definition of the measured population appears to have a great effect on this estimate, with thicker, geometrically defined populations having generally flatter radial profiles (e.g. Jurić et al. 2008) than, for example, the populations enhanced in α-element abundances (e.g. Bovy et al. 2012b, 2016b; Cheng et al. 2012b). Theoretical results have suggested that these geometric thick discs are formed from embedded flaring of co-eval populations (Minchev et al. 2015). The discrepant scalelengths between geometric and abundance-selected thick discs was framed most recently by Martig et al. (2016b) as the result of a hitherto unaccounted-for radial age gradient in the disc.
When considered in toto, nearby galaxy discs, and the Milky Way disc, are observed to have a two-component vertical spatial structure, commonly referred to as the geometric ‘thick’ and ‘thin’ discs (Burstein 1979; Tsikoudi 1979; Yoshii 1982; Gilmore & Reid 1983; Jurić et al. 2008). Classically, the ‘thick’ components have been characterized by older, kinematically hotter stellar populations, enriched in |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, whereas the ‘thin’ populations assume lower, near solar |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and are kinematically cooler (e.g. Bensby et al. 2005). It has, however, also been posited that these populations are in fact composed of multiple subpopulations that smoothly span this range of properties (e.g. Norris 1987; Nemec & Nemec 1991; Bovy et al. 2012c,b, 2016b), thus, in terms of structural parameters, the disc cannot be characterized as the superposition of two distinct structures with different scaleheights (Bovy, Rix & Hogg 2012a). It has been shown that the total vertical stellar spatial distribution resulting from the overlap of such subpopulations is consistent with a double exponential (see e.g. fig. 14 of Rix & Bovy 2013). It is difficult to explain the presence of a continuity in structure alongside the discontinuity in chemistry seen in the Milky Way.
The Milky Way's disc has a complex chemical structure, with a bimodality in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| seen at fixed [Fe/H] across many of the observable regions of the disc (Bensby, Feltzing & Lundström 2003; Bensby et al. 2005; Nidever et al. 2014; Hayden et al. 2015). This characteristic is difficult to explain using one-zone Galactic chemical evolution (GCE) models (most recently shown by Andrews et al. 2017), giving rise to attempts to explain it by means other than pure chemical evolution. Examples of such models include the heating of the old disc by high-redshift mergers (e.g. Brook et al. 2004; Villalobos & Helmi 2008; Kazantzidis et al. 2009; Minchev, Chiappini & Martig 2013) and the formation of a dual disc by gradual accretion of stars into disc orbits (e.g. Abadi et al. 2003). More recent work has also framed this bimodality as a consequence of discontinuous radial migration of stars in the disc (Toyouchi & Chiba 2016).
However, such chemical structure can be replicated in part by invoking various GCE models that do not rely on a ‘one-zone’ approximation (e.g. Chiappini, Matteucci & Gratton 1997; Portinari & Chiosi 2000; Andrews et al. 2017; Weinberg, Andrews & Freudenburg 2017). For example, Andrews et al. (2017) showed that a combination of GCE models with varying outflow mass loading parameters and inflow time-scales (intended to represent enrichment histories at varying Galactocentric radii) could make a roughly bimodal |$\mathrm{[ \alpha \mathrm{/Fe]}}$| distribution. The same models were shown to present a good explanation of the APOGEE |$\mathrm{[ \alpha \mathrm{/Fe]}}$|–[Fe/H] plane by Nidever et al. (2014). A deeper understanding of the connection between spatial structure in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and stellar age selected populations in the Milky Way is necessary to link these results.
In this paper, we present the first dissection of radially extended samples of Milky Way disc stars in age, [Fe/H] and |$\mathrm{[ \alpha \mathrm{/Fe]}}$|. A strong correlation is observed between stellar age and |$\mathrm{[ \alpha \mathrm{/Fe]}}$| in the solar vicinity (Haywood et al. 2013). On the other hand, but also in the solar vicinity, no correlation is found between age and [Fe/H] (e.g. Edvardsson et al. 1993; Nordström et al. 2004), which may be explained by the occurrence of radial migrations. Thickening of the Galactic disc has been invoked as a consequence of outward stellar radial migration (e.g. Schönrich & Binney 2009b). However, Minchev et al. (2012) argue that the effect is small and that such migration in fact only makes discs flare by a small amount. Similarly, Bovy et al. (2016b) measured the flaring profile of low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stars to only slowly exponentially increase with Galactocentric radius, and suggest that radial migration is likely not a viable mechanism for forming thickened disc components. Flaring has also been shown to arise as a result of satellite infall, which can be a stronger flaring agent than migrations (e.g. Bournaud, Elmegreen & Martig 2009). The understanding of flaring and its connection to the evolution of the Galactic disc is essential, but as yet incomplete. In this paper, we present new constraints on models of radial migration in the disc by studying its effects on the Milky Way's mono-age stellar populations.
Many theoretical studies have attempted to understand the observed structure of mono-abundance populations (MAPs) through the use of hydrodynamics and N-body simulations. Few reproduce the observed bimodality in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at fixed [Fe/H], and so an understanding of this has so far proved difficult. However, certain characteristics of the Milky Way |$\mathrm{[ \alpha \mathrm{/Fe]}}$| distribution are beginning to emerge in the most recent cosmological simulations (Ma et al. 2017). Structurally, the mono-age populations of simulated galaxies show good agreement with the Milky Way (e.g. Bird et al. 2013; Stinson et al. 2013; Martig, Minchev & Flynn 2014a,b). More recent work has brought into question the applicability of MAPs as a proxy for mono-age populations (Minchev et al. 2017), showing that, particularly at low |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, MAPs may have significant age spreads due to the differential nature of star formation in the disc. We show in this paper that the structures of mono-age and MAPs in the Milky Way disc differ, but present complementary insights into the temporal and chemical evolution processes in the disc.
Previous work has studied MAPs in the Milky Way by analysing samples of SEGUE G-dwarfs (Bovy et al. 2012c,b,a) and APOGEE red-clump (RC) giants (Bovy et al. 2016b). In this work, we map the spatial distribution of mono-age, mono-[Fe/H] populations at low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| using a catalogue containing [Fe/H] and |$\mathrm{[ \alpha \mathrm{/Fe]}}$| from the APOGEE survey (Majewski et al. 2015) and ages from Martig et al. (2016a) for 31 244 red giant stars. We complement earlier work by adapting the method developed by Bovy et al. (2016b) for RC stars, to enable its application to the full red giant branch (RGB) sample from APOGEE. Stars in the RGB are better tracers of the underlying stellar population than their RC counterparts because of reduced uncertainties in the stellar evolution models, and because they are generally brighter, and so are observed at greater distances. On the other hand, this means that the method developed by Bovy et al. (2016b) must be adapted to account for the spread in absolute magnitude over the RGB (whereas RC stars can be considered as a near-standard candle). On the basis of these measurements, we establish the local mass-weighted age–[Fe/H] distribution, showing the contributions from both low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stellar populations.
In Section 2, we discuss the APOGEE data and the distance and age catalogues used for this work. Section 3 describes the stellar density fitting method, drawing greatly on work by Bovy et al. (2016a,b). Specifically, we describe the generalities of the maximum likelihood fitting procedure and the calculation of the effective survey selection function for RGB stars in Section 3.1, the adopted parametric stellar density model in Section 3.2, and the method for calculating stellar surface-mass densities in Section 3.3. We present the fits in Section 4, along with the calculated surface-mass density contributions for each mono-age, mono-[Fe/H] population. In Section 5, we compare our findings to those in the literature and discuss possible scenarios for the formation of the Milky Way's disc in light of our findings. Section 6 summarizes our results and conclusions.
2 DATA
2.1 The APOGEE catalogue
We use data from the twelfth data release (DR12, Alam et al. 2015) of the SDSS-III APOGEE survey (Majewski et al. 2015), a high-signal-to-noise ratio (SNR >100 pixel−1), high-resolution (R ∼ 22 500) spectroscopic survey of over 150 000 Milky Way stars in the near-infrared H Band (1.5–1.7μm). Stars were observed during bright time with the APOGEE spectrograph (Wilson et al. 2010) on the 2.5-m Sloan Foundation Telescope (Gunn et al. 2006) at Apache Point Observatory. Targets were selected in general from the 2MASS point-source catalogue, employing a dereddened (J − KS)0 ≥ 0.5 colour cut (in the fields that are of interest here) in up to three apparent H magnitude bins (for a full description of the APOGEE target selection, see Zasowski et al. 2013). Reddening corrections were determined for the colour cut via the Rayleigh–Jeans Colour Excess method (RJCE; Majewski, Zasowski & Nidever 2011). Corrections are found by applying the method to 2MASS (Skrutskie et al. 2006) and mid-IR data from Spitzer-IRAC GLIMPSE-I, -II, and -3D (Churchwell et al. 2009) when available and from WISE (Wright et al. 2010) otherwise. For this work, we use distance moduli (which use the aforementioned reddening corrections) from the Hayden et al. (2015) distance catalogue for DR12 (see Section 2.2).
All APOGEE data products employed in this paper are those output by the standard data reduction and analysis pipeline used for DR12. The data were processed (Nidever et al. 2015), then fed into the APOGEE Stellar Parameters and Chemical Abundances Pipeline (ASPCAP; García Pérez et al. 2016), which makes use of a specifically computed spectral library (Zamora et al. 2015), calculated using a customised H-band line-list (Shetrone et al. 2015). Outputs from ASPCAP are analysed, calibrated and tabulated (Holtzman et al. 2015). The output |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and [Fe/H] abundances for DR12 have been shown to have a high degree of precision (at least between 4500 ≲ Teff ≲ 5200 K), such that σ[Fe/H] = 0.05 dex and σ[α/Fe] = 0.02 dex (Bovy et al. 2016b). We apply here the same external calibrations to |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and [Fe/H] as Bovy et al. (2016b), constant offsets of −0.05 and −0.1 dex, respectively. We use the tabulated [Fe/H] value rather than the globally fit [M/H] which is included in the table.
We select stars from the DR12 catalogue which were targeted as part of the main disc survey (i.e. were subject to the (J − KS)0 ≥ 0.5 cut), have reliably measured abundances (i.e. no warning or error bits set in the ASPCAPFLAG field) and have a well-defined distance modulus and age measurement (see Sections 2.2 and 2.3). We apply a secondary cut at 1.8 < log g < 3.0 to restrict the sample to stars on the RGB, removing most contaminating dwarfs, and very evolved stars near the tip of the RGB. The high end of our log g cut is more conservative than other studies in this regime; however, we find that this gives the best agreement between the data and stellar evolution models, without significantly reducing the sample size or introducing unwanted bias. These cuts give a final sample of 31 244 stars, spanning 4200 ≲ Teff ≲ 5050 K for which the effective survey selection function can be reconstructed.
We further divide the sample into low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples, as it has been shown in previous work that the two populations have quite different structural parameters (Bovy et al. 2016b), and as such it makes sense to fit their mono-age subpopulations separately. We separate visually the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, leaving a gap between the two samples of 0.05 dex in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at each [Fe/H] (our separation is shown in Fig. 1), to minimize contamination between the subsamples, particularly at the high [Fe/H] end, where the two populations partially overlap. The final density fits are performed on finer bins in age and [Fe/H], which we define in Section 2.3. As the adopted separation in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| removes 6532 stars from the full count, when calculating the surface-mass density contributions from the stellar number counts in each age–[Fe/H] bin, we remove the separation in |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, using the star counts as if the populations were separated along the mid-point of the division (as shown by the dot–dashed line in Fig. 1).
The full RGB sample in |$\mathrm{[ \alpha \mathrm{/Fe]}}$|–[Fe/H] space. The coloured regions show our division between low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples. At each [Fe/H] the division between the samples is |$\mathrm{[ \alpha \mathrm{/Fe]}}$| = 0.05 dex, roughly twice the mean uncertainty on |$\mathrm{[ \alpha \mathrm{/Fe]}}$| abundance determinations in APOGEE DR12. The bimodality in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at fixed [Fe/H] is visible across many [Fe/H], and the lower number of stars in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sample is clear from this plot.
Our method, discussed in Section 3, corrects for selection effects induced by interstellar extinction (in addition to the RJCE reddening corrections) using 3D dust maps for the Milky Way derived by Marshall et al. (2006) for the inner disc plane, combined with those for a large majority of the APOGEE footprint by Green et al. (2015), adopting conversions |$A_H/A_{K_{\rm S}}=1.48$| and AH/E(B − V) = 0.46 (Schlafly & Finkbeiner 2011; Yuan, Liu & Xiang 2013). Fields with no dust data (of which there are ∼10) are removed from the analysis. Bovy et al. (2016b) discuss the relative merits and limitations of these dust maps as opposed to others that are available, and determine that this combination of dust maps provides the best density fits.
2.2 Distance estimates
We use distance estimates from Hayden et al. (2014, but see also Hayden et al. 2015 for further description). Distances are estimated by computing the probability distribution function (PDF) of all distance moduli to a given star using a Bayesian method applied to the spectroscopic and photometric parameters from the DR12 catalogue and the PARSEC isochrones (Bressan et al. 2012). The distance estimates are found to have accuracy at the 15–20 per cent level, upon comparison with cluster members of well-known distance observed by APOGEE.
We use the median of the posterior PDF (which is given in the output catalogue) as the estimate for the distance modulus, and compute the Galactocentric cylindrical coordinates, R, ϕ and Z for each star using the l, b coordinates provided in the APOGEE-DR12 catalogue. The spatial distribution of the two |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples is shown in Fig. 2. We perform a simple cross match between our sample and the APOGEE RC value added catalogue (Bovy et al. 2014) and plot the RC-derived distance (DRC) against the estimate from Hayden et al. (2014, DMH) in Fig. 3. The RC catalogue has precise distance estimates, which can be determined due to the RC having a near constant absolute magnitude. The majority of the Hayden et al. (2014) distances compare well to the RC distances, but there are notable differences. The Hayden et al. (2014) distances can be underestimated by as much as 50 per cent, and we find that ∼20 per cent of our sample have distances underestimated by more than 10 per cent. Our density fitting method is insensitive to uncertainties on the distances at these scales, as the scale of any variations in the density distribution can be assumed to be far greater than the distance uncertainties.
2D histograms of the spatial distribution (in Galactocentric R and Z) of the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples shown in Fig. 1. The high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sample appears more diffuse and extended in height even before selection effects are accounted for. Readers should notice the different colour scale adopted for each panel, due to the much lower number of stars in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sample.
Comparison of APOGEE RC catalogue (APOGEE-RC) distances DRC with distances derived by Hayden et al. (2015), DMH. The top panel directly compares the distances, where the bottom panel shows the difference as a fraction of DMH, as a function of that distance. There are many stars with good agreement, but a distinct fraction of MH distances are underestimated compared to RC (∼20 per cent with distances underestimated by more than ∼10 per cent). As the variations in the density occur on scales which are, in general, far larger than these discrepancies, these are not problematic in our analysis. The two distance scales differ systematically by a factor of ∼5 per cent, but we do not correct for this in the following discussion and it does not impact any of our results.
Fig. 3 also shows that there is a systematic offset between the RC and Hayden et al. (2014) distances of the order of ∼5 per cent across the full range of distances. We find that adopting this offset as a correction to the distances makes little impact on the final results, merely broadening fitted density profiles slightly, spreading the star counts over a wider Galactocentric distance, meaning that the final stellar surface-mass density estimates are unchanged.
2.3 Age estimates
We use age estimates for APOGEE DR12 catalogued by Martig et al. (2016a), who derive an empirical model for the [C/N]–M* relation using asteroseismic masses from Kepler and abundances from APOGEE for their overlapping samples (APOKASC; Pinsonneault et al. 2014). Masses are predicted for DR12 stars which meet quality and stellar parameter criteria outlined in Martig et al. (2016a), and ages are estimated from that mass using the PARSEC isochrones with the nearest metallicity to that of the given star. Martig et al. (2016a) use this empirical relation to build a model that predicts mass and age as a function of [[M/H], [C/M], [N/M], [(C + N)/M],log g, Teff]. It is important to note here that Martig et al. (2016a) derive a model and fit for the ages in DR12 using the uncalibrated, raw stellar parameters, found in the FPARAM arrays in the APOGEE catalogue. This is difficult to account for when using the age catalogue alongside the calibrated parameters, and must be borne in mind in future comparisons of this work with models and observational results. In addition to this, Martig et al. (2016a) also mention that care should be taken when applying these ages to regions of the Milky Way where the chemical evolution may have been complex (e.g. the bulge/bar region). However, in their fig. 12, they compare the [C/N] ratio as a function of [M/H] in a sample of pre-dredge-up giants in the inner and outer disc, showing that the shapes of the distributions are similar. This suggests that differences in chemical evolution do not affect the [C/N]–age relation within a wide range of galactocentric distances. Therefore, the assumption that it is safe to adopt the Martig et al. (2016a) ages over the extent of the disc covered by our sample is robust, regardless of the fact that they are trained on the Kepler sample, which is limited in its spatial extent.
Although individual uncertainties on ages are not given in the catalogue, Martig et al. (2016a) state that the model predicts ages with rms errors of ∼40 per cent. Although uncertainties are potentially very large at high age, our sample is binned with Δage = 2 Gyr in order to gauge general trends with age. It should be understood that such trends are smoothed by the age uncertainties, particularly at high age, and detailed comparisons to models should take the age uncertainty into account. We discuss the effect of these uncertainties on our recovered trends with age in Appendix B, showing that our methodology can still reliably recover such trends, even though mixing between bins may be present in the data.
Fig. 11 of Martig et al. (2016a) shows that there is a significant bias in the ages returned by the model, such that ages are underpredicted at high age when compared to the training set. For this reason, we fit for and apply a correction to the catalogued ages before performing the density fitting. Using table 1 of Martig et al. (2016a), we perform a non-parametric lowess fit to the predicted age–true age distribution. This fit is then used to derive age corrections as a function of predicted age. We show the fitted correction in Fig. 4 in both predicted versus true age space and also in Δ age against the predicted age. The correction as a function of predicted age is then applied to each of the ages in the DR12 catalogue. In all further analysis, we refer only to the corrected ages. The main effect of this correction is to make the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stars older. Consequently, our surface-mass density estimates (presented in Section 4.3) become more conservative, as the mass contribution per star in older bins is lower (as discussed in Section 5.1). Martig et al. (2016a) comment on the bias in the context that the ages returned for high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stars appear younger than previous estimates (from Haywood et al. 2013; Bensby, Feltzing & Oey 2014; Bergemann et al. 2014). Our correction brings these data more in line with those estimates.
Asteroseismically determined ages from APOKASC against the [C/M] and [N/M] based ages from Martig et al. (2016a). The line gives the fitted correction for ages from Martig et al. (2016a), based on the values for the APOKASC training set, given in their table 1. We fit the data using a non-parametric lowess fit. Before corrections, older ages are underpredicted, and young ages are overpredicted. The corrections mainly change the scaling of the ages, such that the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sample occupies an age range more in line with the existing literature (e.g. Haywood et al. 2013; Anders et al. 2016)
It is also important to account for all other cuts made by Martig et al. (2016a) on the stellar parameters in the APOGEE catalogue, outlined in full at the beginning of their section 6.2. While we account for cuts in Teff and log g by applying the same cuts to the isochrone grid when calculating surface-mass density contributions, it is not possible to properly account for cuts made on the stellar abundances in this way. We find that 9041 stars are removed from the 40 285 star catalogue (those with distances, after the log g cut mentioned above) by these abundance cuts, to give our final catalogue size of 31 244. This means that ∼25 per cent of star counts are missing from the age catalogue, and therefore unaccounted for by our analysis. With no robust method for determining the age distribution of these missing stars, we are forced to make the assumption that these star counts can be added uniformly to each age–[Fe/H] bin. We make this correction by simply increasing the counts in each bin by 25 per cent when calculating the surface-mass density. This correction simply increases the final surface-mass density values systematically by 25 per cent.
Another important consideration when using this set of ages regards stars whose chemical compositions are such that the ages fit from the model (after making the corrections) would be higher than 13 Gyr and left out of our analysis. As the age estimates are computed based on the surface parameters and abundances of the stars using a fitting function, many stars with strongly outlying abundances and parameters can be assigned ages that are greater than 13 Gyr. We find that the 3020 such stars (in the final sample) have an average [C/Fe] which is lower than the general sample, and an average [N/Fe] which is enhanced with respect to the stars with reliably measured ages. We also find that at fixed [Fe/H] and log g these stars have warmer Teff. While these properties are expected given their age measurements, we believe that there is a distinct possibility of some peculiarity of these stars. For example, if such stars were early AGB stars (having gone through the second dredge-up, reducing the surface C abundance, e.g. Boothroyd & Sackmann 1999), which had been fit as RGB stars, their actual age may be considerably younger, and their counts missed in the younger bins (where mass contribution per star is higher). As the nature of these stars is debatable and a correction cannot be made confidently before carrying out the full analysis, we regard the missing counts from these stars as a contribution to the systematic error budget, which we discuss fully in Section 5.1.
We demonstrate the adopted binning in (age,[Fe/H]) space in Fig. 5, showing also the number of stars that fall in each bin and the general distribution of stars in (age,[Fe/H]) space. There is a notable separation in age between the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples.
2D histograms showing the raw number of stars in each (age,[Fe/H]) bin of the low (left) and high (right) |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples. We draw the reader's attention to the difference in amplitude between the two subsamples (and the associated difference in colour scale normalization). Although the majority of bins are well sampled (≳ 30 stars), there are some greatly undersampled bins, for which well-defined fits are not possible.
3 METHOD
In this section, we describe the method for fitting the underlying number density of stars in the Milky Way from APOGEE observations, which we represent here as ν*(X, Y, Z|θ), in units of stars kpc−3. The calculation of this quantity requires allowances to be made for the survey selection function, which is non-trivial due to the presence of inhomogeneous dust extinction along lines of sight observed by APOGEE, the target selection invoking different H magnitude limits, and the use of RGB stars as a tracer, which cannot be considered as standard candles. The quantity that we are ultimately interested in is the surface-mass density of stars at the solar radius, |$\Sigma _{R_0}$|, in units of M⊙ pc−2, which we infer from the number of stars in the APOGEE sample as a function of position. We describe the method for this calculation in Section 3.3. Our methodology consists of an adaptation of that used by Bovy et al. (2016b), employing a modified version of their publicly available code.1 Although the general method is identical, we describe again the key components for clarity and completeness.
As some readers may find it unnecessary to read in full the details of the methodology (which are described in the following sections), we summarize the procedure as follows:
We fit parametric density models to the APOGEE star counts using a maximum likelihood fitting procedure, based on the assumption that star counts are well modelled as an inhomogeneous Poisson point process. The density models that we assume throughout the paper are described by radially broken exponentials, with scalelengths hR, [in, out] either side of a break radius Rpeak (where hR, in denotes the scalelength of the inner profile and vice versa), and a vertical distribution that is a single exponential with scaleheight hZ, which is modified as a function of R by an exponential flaring term with scalelength Rflare. We show that, in general, if the density is better fit by a single exponential, it is recovered as so by our procedure.
We obtain a best-fitting density model for every bin in age and [Fe/H], at high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$|. This best-fitting model is then used to initiate an MCMC sampling of the posterior PDF. We then use the median and standard deviation of one-dimensional projections of the MCMC chain as our adopted parameter values and uncertainties.
As the fitting procedure does not fit for the normalization of the density |$N_{R_0}$|, the number surface density of stars at the solar radius in stars pc−2, we calculate this value by comparing the observed number of stars in each bin to that which would be observed in APOGEE for the fitted density model if |$N_{R_0} = 1$| star pc−2. We then convert |$N_{R_0}$| for each bin into the surface-mass density in visible stars at the solar radius |$\Sigma _{R_0}$| by converting the mass in RGB stars observed to the total mass using stellar evolution models.
Readers can then pick up the results in Section 4.
3.1 Density fitting procedure
We evaluate |$\mathfrak {S}({\rm field}, D)$| on a grid of distances for each APOGEE field for simple computation of ∫dOλ(O|θ). We then optimize the likelihood function in equation (2) for a given density model and data set using a downhill-simplex algorithm, to obtain the best-fitting set of parameters θ. A Markov Chain Monte Carlo (MCMC) sampling of the posterior PDF is then initiated using this optimal solution. This is implemented with an affine-invariant ensemble MCMC sampler (Goodman & Weare 2010; Foreman-Mackey et al. 2013). All parameter values and associated uncertainties for individual (age,[Fe/H]) bins that are reported in the following sections represent the median and standard deviation σ, respectively, of one-dimensional projections of the MCMC chain.
3.2 Adopted stellar number density models
We also note here that our sample is not limited to stars that are members of any specific Galactic component, and as such, may include small numbers of halo stars in the very high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and low [Fe/H] regimes. However, our fitting procedure is agnostic to these contaminants, which would only cause the fits to have larger uncertainty (from the MCMC exploration) about the best fit from the dominant population in a given bin.
3.3 Stellar surface-mass densities
Our final surface-mass density estimate is strongly dependent on the conversion factors in the above equations, the average RGB star mass, 〈MRGB〉, and the fractional contribution from giants, ω. We find that the average giant masses in our range of ages and [Fe/H] span 0.9 ≲ 〈MRGB〉 ≲ 2.1M⊙. The most metal-poor and oldest populations have the lowest average mass, and the youngest, most metal-rich populations have the highest. The fractional contribution from giants in this regime ranges between 0.002 ≲ ω ≲ 0.02. The oldest and most metal-poor populations have the least giants, whereas the youngest, metal-rich populations have the most. These values appear to sit well with recent inventories of the solar neighbourhood, which suggest giants should make up of the order of a few percent of the mass (McKee, Parravano & Hollenbach 2015). We discuss the potential systematics introduced by the use of stellar evolution models in Section 5.1.
4 RESULTS
We now present results from the density fitting procedure, and the subsequent calculation of the surface-mass density contribution of each mono-age, mono-[Fe/H] population in Fig. 5. Density fitting is performed on all populations, but we only display the fits for populations with >30 stars, as data below this level become too noisy to render reliable fits. Although the remaining fits can be noisy when star counts are near this limit, this is reflected in the error analysis arising from the MCMC exploration of the posterior PDF of the fitted parameters. We refer the reader to Appendix A for a comparison between the data and the fitted models for each mono-age, mono-[Fe/H] bin, and a qualitative discussion regarding the rationale behind the decision to discuss fits to only the broken exponential density profile.
4.1 The radial profile of mono-age, mono-[Fe/H] populations
We first show the fits to the surface density in the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples in Fig. 6. We display fits for all age and [Fe/H] bins with >30 stars. By shading the profiles by their surface-mass density contribution (as shown in Section 4.3), we intend to draw the eye to the profiles that contribute most to the mass of the Milky Way disc. We defer a discussion of the individual mass contributions of each bin to Section 4.3, concentrating in this section on trends in the shapes of the density profiles.
The fitted surface density profiles for the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| (top) and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| (bottom) subsamples as a function of [Fe/H] (colour) and age (increasing from left to right). The coloured bands represent the 95 per cent uncertainty range. Only profiles for bins containing >30 stars are shown. The profiles have a transparency according to the surface-mass density calculated for each bin in Section 4.3, normalized separately for each row (i.e. in each [Fe/H] bin), to draw the eye to those profiles which contribute most to the Milky Way surface-mass density. High |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles are described well by a single exponential, whereas young, low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles are broken exponentials with a peak density that varies in radius in the disc.
Although fit with the broken exponential, high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles are generally better described by near-single exponentials, either showing no break in the radial range or being fit by a profile with a break at low significance (i.e. a single line could be drawn through the coloured band). Many of the outer profiles (after Rpeak) in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample appear to have a similar slope, suggesting that they may all be represented by the same exponential. The mean outer scalelength for the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations is hR, out = 1.9 ± 0.1 kpc. The picture is noticeably different in the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample, with profiles showing clear breaks, at well-defined radii. Any trends in break radius in this regime are determined with high significance.
Low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles have a density that increases with radius out to the break radius, and declines outward of this radius. We do not constrain the fits to behave in this way, and this indicates that mono-age, mono-[Fe/H] populations at low [Fe/H] are shaped approximately as donut-like annuli. The variation of the break radius then represents the moving peak of stellar density as a function of age and [Fe/H]. Concentrating on the bins youngest bin (1 < age < 3 Gyr), the break radius is a declining function of metallicity, moving between Rpeak = 10 kpc at −0.6 < [Fe/H] < −0.5 dex down to Rpeak < 8 kpc at 0.1 < [Fe/H] < 0.2 dex. This trend is also present in older bins but with decreased amplitude. In a fixed [Fe/H] bin, Rpeak appears to remain roughly constant (within ∼1 kpc) at ages between 1 and 6 Gyr. At ages older than this Rpeak varies in unexpected ways, but there is much less mass contribution from these populations, and we attribute much of this behaviour to noise from the narrow age bins.
On the other hand, the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles change shape (either side of Rpeak) with age in a fixed [Fe/H] bin. The youngest populations show a sharp peak, with a steep increase and decline either side of Rpeak. As populations grow older, the profile broadens significantly, becoming almost flat in the lowest [Fe/H] bins. We show this behaviour by finding the inverse of the difference between the inverse outer and inner scalelength3, such that a low value denotes a sharper peak, whereas a broader profile has a higher value. We show how this value changes with age for the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations in Fig. 7. The peak is sharpest in the younger populations, and becomes broader with age. Old populations have artificially sharpened peaks in this diagnostic due to their being better described by single exponentials. Notably also, in Fig. 6, at low [Fe/H] the inner profiles flatten faster than the outer profile, whereas the higher [Fe/H] populations show the opposite behaviour. For example, in the −0.3 < [Fe/H] < −0.2 dex bin, the outer profile appears to remain roughly constant in slope between 1 and 6 Gyr, while the inner profile flattens significantly. The opposite is seen in the 0.1 < [Fe/H] < 0.2 dex bin, where the outer profile flattens considerably with age.
The profile width |$(h_{R,\mathrm{out}}^{-1} - h_{R,\mathrm{in}}^{-1})^{-1}$| against age for the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations (this diagnostic is irrelevant for the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, which are generally fitted by single exponentials). We add a small random jitter to the central age of each age bin, to make individual points and their uncertainty clearer. The relations and coloured band show the running surface-mass density weighted mean and standard deviation in the age bins. The profile width increases with age. A higher value of this diagnostic suggests a broader surface density profile, showing that older populations are flatter and broader around the peak density.
4.2 The vertical profile of the disc
We now examine the variation of hZ as a function of radius in mono-age, mono-[Fe/H] populations. Because mono-age, mono-[Fe/H] populations are well described by a single scaleheight, which is modified by a flaring term Rflare, this means that hZ is weakly dependent on R for profiles that flare. We show vertical profiles for age–[Fe/H] bins with >30 stars in Fig. 8, adopting the same shading as Fig. 6 to draw the eye to the profiles with greater mass contribution, and adding a dashed line representing 0.3 kpc for reference.
Vertical profiles for the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| (top) and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| (bottom) subsamples as a function of [Fe/H] (colour) and age (increasing from left to right). The coloured bands represent the 95 per cent uncertainty range. Only profiles for bins with >30 stars are shown, with profiles shaded according to their surface-mass density contributions (discussed in Section 4.3). The dashed lines represent hZ = 0.3 kpc, for reference.
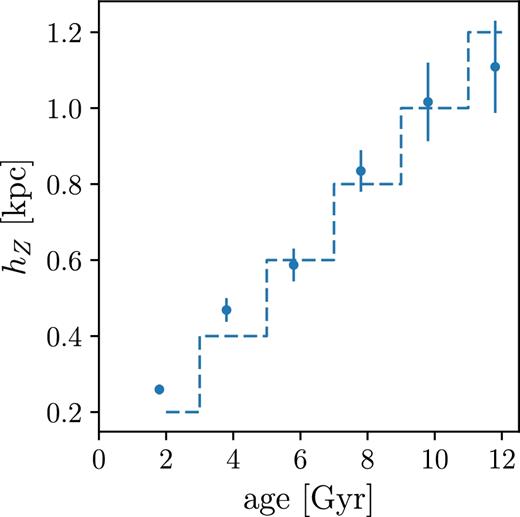
Fig. 8 suggests that the disc is thicker as traced by older populations. All [Fe/H] bins show a thickening as age increases. This is clear in the left-hand panel of Fig. 9, which shows the surface-mass density weighted mean variation of hZ with age. The mean hZ spans the range between 0.8 and 0.2 kpc. The high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations show a bump in the mean hZ at 8 Gyr, but hZ generally increases with age, similarly to the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. The shapes of the profiles of the youngest populations in Fig. 8 in the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample show little variation with [Fe/H], and this trend generally continues to older ages. This is also reflected in the low uncertainties associated with the blue points in the left-hand panel of Fig. 9.
Mean hZ at R0 (left) and Rflare− 1 (right) against age. The mean value in each age bin is calculated by multiplying together the posterior PDFs of the density fits. The panels show both the low (purple) and high (green) |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. The left-hand panel shows the total surface-mass density weighted mean as a dashed line, which demonstrates that the vertical distribution of the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population is only important at the solar radius at old ages due to its low surface-mass density contribution. hZ increases with age for both low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. Rflare− 1 behaves similarly for the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population, meaning flaring decreases with age, but the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population shows an opposite behaviour.
The high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles are generally flat, indicating that these populations show little flaring. By multiplying together the PDFs of the posterior distribution of fits to Rflare, we determine that the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations have an average Rflare− 1 = −0.06 ± 0.02. The low alpha populations flare more strongly, with an average Rflare− 1 = −0.12 ± 0.01. There is, however, some variation in the flaring as a function of age, so it may not be sensible to ascribe a single Rflare− 1 to all the populations. We show the variation of Rflare− 1 with age in the right-hand panel of Fig. 9, showing Rflare− 1 rather than Rflare so that values close to 0 are represented properly. The surface-mass density weighted mean Rflare− 1 of the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations increases as a function of age, meaning that the most flared populations are the youngest. The behaviour appears opposite for the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, whose mean Rflare− 1 seems to decrease with age, but this is determined with low significance as Rflare− 1 measurements are noisier for these populations.
4.3 The mass contribution of mono-age, mono-[Fe/H] populations
We now present the results from the calculation of the surface-mass density at the solar radius using the method described in Section 3.3. We compute surface-mass density |$\Sigma _{R_0}$| estimates for each age–[Fe/H] bin, for the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| samples. When quoting the surface-mass densities, we also quote estimates of the systematic uncertainties. We evaluate the sources of these uncertainties in Section 5.1.
We combine the mass contributions of the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| mono-age, mono-[Fe/H] populations, and plot the estimates as a function of age and [Fe/H] in Fig. 10. This figure essentially represents the mass-weighted age–[Fe/H] distribution at the solar radius, that is, the probability distribution for age and [Fe/H] for a randomly selected mass element. The distribution varies smoothly with no sharp peaks, and the surface-mass density increases linearly with both age and [Fe/H], peaking at 1 < age < 3 Gyr, 0.0 < [Fe/H] < 0.1 dex. The mass increases more smoothly with [Fe/H] than with age, but there is little mass in the highest [Fe/H] bin, creating a ridge in the marginalized distribution. The marginalized distributions as a function of age and [Fe/H] show no sign of bimodality, and there is little sign of a bimodality in age at fixed [Fe/H]. It should be mentioned again here that the age uncertainties may be larger than the bin width, particularly in older bins, which would cause an artificial blurring of a density edge in the distribution along the age axis. Therefore, we cannot presently determine to high significance that there are no discontinuities in this distribution.
The surface-mass density contribution of mono-age, mono-[Fe/H] populations at R0 (where low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| are combined). The total contribution |$\Sigma _{R_0,\ \mathrm{tot}}$| is displayed at the top of the main panel. The colour scale is linear and spans the surface-mass density range between |$0 < \Sigma _{R_0} < 1.5\ \mathrm{M_{{\odot }}\ pc^{-2}}$|. The marginalized distributions along each axis are shown above and to the right. The mass at the solar radius increases monotonically with both age and [Fe/H].
An alternative way to look at the surface-mass density distributions is to retain the division in |$\mathrm{[ \alpha \mathrm{/Fe]}}$|. We find that the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations contribute |$\Sigma _{R_0,\ \mathrm{tot}} = 3.0_{-0.5}^{+0.4}\mathrm{(stat.)}_{-0.6}^{+0.6}\mathrm{(syst.)}\ \mathrm{M_{{\odot }}\ pc^{-2}}$| to the total surface-mass density at the solar radius, whereas the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations contribute |$\Sigma _{R_0,\ \mathrm{tot}} = 17.1_{-2.4}^{+2.0}\mathrm{(stat.)}_{-1.9}^{+4.4}\mathrm{(syst.)}\ \mathrm{M_{{\odot }}\ pc^{-2}}$|, giving a total surface-mass density in stars at R0 of |$\Sigma _{R_0,\ \mathrm{tot}} = 20.0_{-2.9}^{+2.4}\mathrm{(stat.)}_{-2.4}^{+5.0}\mathrm{(syst.)}\ \mathrm{M_{{\odot }}\ pc^{-2}}$|. We plot the individual surface-mass contributions for the separated low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations in Fig. 11, adopting different colour scales in each panel, to highlight the behaviour of the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, which contribute little mass in comparison to the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$|. The low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| mass is mostly concentrated at young age and towards higher [Fe/H], although there is mass even at the oldest ages. The high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| mass is concentrated towards older ages, but interestingly the distribution extends to high [Fe/H], and we detect mass at some [Fe/H] in every age bin, but at much lower levels. The tails of the distributions of the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations overlap somewhat in age-[Fe/H] space, around 6 Gyr ago, and there is a hint of a sequence extending from old, low [Fe/H] and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, to young, high [Fe/H] and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, which is somewhat visible in the combined histogram. There is no clear bimodality in age at fixed [Fe/H] in the combined histogram, owing to the very low mass contribution of the old, high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations.
The surface-mass density contributions of the low (left) and high (right) |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsamples. The total contributions |$\Sigma _{R_0,\ \mathrm{tot}}$| are displayed at the top of each panel. We draw the attention of the reader to the difference in colour scale between the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| panels, which differs by an order of magnitude, and is adopted to better show the behaviour in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sample. The low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample has mass at all ages and [Fe/H] but is concentrated mostly at young ages. The high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample contributes far less mass and is concentrated at old age.
We have established that the vertical spatial distributions of mono-age, mono-[Fe/H] populations are well described by single exponentials with characteristic hZ. Next, we use this information to generate the mass-weighted distribution of hZ, which is representative of the PDF for hZ, p(hZ). For a random stellar mass element, this function gives the probability density for the hZ of the component to which it belongs. We show this relation in Fig. 12, where coloured points represent the individual density contributions of mono-age, mono-[Fe/H] populations, and the coloured histograms represent their co-addition within ∼0.1 kpc wide bins in hZ for the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations (purple and green, respectively). The dashed histogram represents the resulting total p(hZ). Scatter points are coloured by the age of the population they represent. The total distribution is smooth, resulting from the superposition of the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| distributions, which overlap significantly. The total |$\Sigma _{R_0}$| (dashed histogram) declines exponentially with hZ, and is unimodal with no gaps. The trends of both hZ and |$\Sigma _{R_0}$| with age seen in Figs 7 and 10 are recovered here, although it is surprising that the trend of hZ with age at the high hZ end does not appear as obvious here.
The mass-weighted vertical scaleheight hZ distribution. The individual points represent the hZ and |$\Sigma _{R_0}$| for each mono-age, mono-[Fe/H] population. We colour the points, which represent both the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, by the central age of the mono-age, mono-[Fe/H] bin that they represent. The coloured histograms represent the hZ distributions for the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations from the sum of the individual contributions. The dashed histogram represents the total distribution. The total distribution smoothly decreases with hZ, with no hints of bimodality.
We can also now mass-weight and combine the fitted density profiles to attain the surface-mass density profile of the Milky Way as a function of age, [Fe/H] and |$\mathrm{[ \alpha \mathrm{/Fe]}}$|. The resulting profiles are displayed in Fig. 13. The different nature of the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations in terms of spatial structure is clear here, with the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profile having a clear break between 8 and 10 kpc, and the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| declining exponentially with R. It is interesting to note that extrapolation by eye of the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| profiles to low R would result in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population becoming dominant over the low. The total profile appears roughly flat out to ∼10 kpc. However, we strongly emphasize that this is not determined to high significance, as even when only the uncertainties from the fitting procedure are included, one could describe the profile as exponentially declining with R within R < R0. The inclusion of the other sources of uncertainty on the surface-mass density estimates would further decrease the significance of the apparent flattening. For example, the systematic uncertainties (discussed in Section 5.1) act to increase the fraction of surface-mass density contributed by the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, which would only increase the slope of the inner exponential. Using dynamical tracers, Bovy & Rix (2013) find that the surface density should decline exponentially with R, so it seems logical to assume that the inner profile should not be increasing with R.
The radial surface-mass density profile of the Milky Way, as a function of |$\mathrm{[ \alpha \mathrm{/Fe]}}$| (top), age (middle) and [Fe/H] (bottom). The profiles are the result of a mass-weighted combination of the fitted density profiles along different axes in age–[Fe/H] space and (in the top panel) for the combined low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. We show the combined uncertainties from the fitting procedure in the top panel, which are sufficient (without addition of the individual statistical and systematic errors on the surface-mass densities, which are substantial) to show that the apparent flattening at R < R0 is not found to high significance. The surface-mass density of low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stars extends to a higher radius than the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stars. The youngest populations show a clearly peaked surface-mass density around the solar radius, whereas the older populations peak more centrally. Behaviour with [Fe/H] is complex, with flat profiles at low R, becoming exponentially decreasing at high R.
As a function of age, the peak in the surface-mass density visible in the youngest population becomes less prominent, and the profile becomes a roughly single exponential at the oldest ages (i.e. it monotonically decreases with R). The behaviour with [Fe/H] is more complex, but the variation of the peak radius with [Fe/H] is obvious, and the turnover in the total profile at ∼10 kpc appears to be a result of the outermost breaks.
5 DISCUSSION
In the above analysis, we have, for the first time, determined the detailed structure of the Milky Way's disc as a function of stellar age and [Fe/H]. In our method, we have drawn heavily from previous dissections of the disc into its mono-abundance constituents (MAPs; Bovy et al. 2012b, 2016b), and so use these previous findings as a benchmark with which to compare these results. We also show that our results are also broadly consistent with other measurements, whilst shedding new light on to the problem of the formation of the Milky Way disc.
5.1 Surface-mass density systematics
We first address the sources of systematic uncertainty in our surface-mass density estimates, which are pertinent to the following discussions. Our total local surface-mass density, including the correction for stars missing from the age catalogue, but before accounting for any other systematic uncertainties, is |$\Sigma _{R_0, {\rm tot}} = 20.0_{-2.9}^{+2.4}\ \mathrm{M_{{\odot }} \ pc^{-2}}$|. This result is roughly two-thirds as large as previous estimates, which are of the order of |$\Sigma _{R_0, {\rm tot}} \sim 30\ \mathrm{M_{{\odot }} \ pc^{-2}}$| (e.g. Flynn et al. 2006; Bovy et al. 2012a; McKee et al. 2015). From canonical stellar evolution, it is known that giants contribute very little to the total stellar mass in any population. For instance, McKee et al. (2015) find that giants make up ∼2 per cent of the local stellar mass. By virtue of this fact, conversions of the stellar mass inferred from giant-star counts to that of the total underlying stellar population require a multiplication of the observed counts by a factor of ∼50, meaning that any uncertainty in the star counts is amplified in the final surface-mass density estimate. Our quoted statistical error estimates, however, which account for Poisson fluctuations in the stellar counts cannot fully account for the discrepancy.
We first evaluate whether such a discrepancy may be due to the assumed IMF or stellar evolution model. Tests adopting exponential Chabrier (2003) and Kroupa (2001) IMFs for the mass calculation resulted in variations of the final |$\Sigma _{R_0, {\rm tot}}$| estimate of the order of ∼1 M⊙ pc−2, which we incorporate into the systematic error budget. We also re-ran our analysis on the basis of the BaSTI stellar evolution models (Pietrinferni et al. 2004), for which there also exists calculations for α-enhanced stars (Pietrinferni et al. 2006), which produced comparable estimates to the PARSEC models (after correcting for the fact that the lowest mass in the BaSTI isochrones is 0.5M⊙ as opposed to 0.1M⊙ in the PARSEC models). We also compute the mass using only APOGEE fields away from the plane (with |b| ≥ 6°), to test for the effects of extinction on the star counts, but attain results within the Poisson uncertainties of the original estimate.
We also apply our analysis procedure to a basic Monte Carlo mock sample, to check the method for converting observed counts to the real number density N(R0). We sample stars on a broken exponential density distribution with exponential flare then select points within APOGEE fields out to an imposed distance cut (which allows a simple reconstruction of the selection, and calculation of the effective volume). We calculate N(R0) analytically, and via our method, and find results that are consistent with the input parameters of the model broken exponential profiles, within the Poisson errors, for a wide variety of input parameters.
As mentioned in Section 2.3, we find that, after making corrections to the ages, the model returns ages greater than 13 Gyr for a sizeable number of stars (Martig et al. 2016a, limit ages to 13 Gyr in their table). While these stars make up approximately 10 per cent of the final sample (3020 stars), they are not included in the number counts in each mono-age mono-[Fe/H] bin for calculation of the surface-mass density. Adding an extra 10 per cent of counts to each bin (in the same way as the extra 25 per cent is added in Section 2.3) introduces an extra systematic uncertainty of roughly 1 M⊙ pc−2 in each |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample. However, readers should take into account that this simple correction does not account for a scenario where the stars with ages fitted >13 Gyr might have a specific distribution in age, casting more counts in some bins (which might have more mass contribution per star) than others. For example, if these stars were all old, then the actual surface mass density in older bins would be higher than that found here, which would increase the total surface-mass density estimate.
From the above, we conclude that the majority of the systematic discrepancy is likely not due to the assumed IMF, stellar evolution model, dust extinction, or some peculiarity in the age measurements which affects star counts in the bins used. At this stage, it is difficult to understand what is the possible origin of this discrepancy with other works in the literature. Interestingly, our study is the only one employing giant stars as the stellar population tracer, which may point to possible systematics in the theoretical isochrones, or the APOGEE stellar parameters, or a combination thereof. It has recently been demonstrated by Masseron & Hawkins (2017) that there may be significant issues with the spectroscopic determination of stellar surface gravity, which is dependent on the star's evolutionary state. We find some discrepancy between the log g of the RC between the PARSEC isochrones and the data, of the order of ∼0.2 to 0.3 dex (similar to that found by Masseron & Hawkins 2017, albeit based on APOGEE-DR13 data), which could conceivably lead to problems in our conversion. We test for the effect of systematics in the log g scale, shifting the log g cut of the isochrones to lower and higher log g by 0.3 dex. We find that shifting the log g cut by −0.3 dex increases the surface-mass density estimate by 5.0 M⊙ pc−2. Increasing the log g cut by 0.3 dex results in a decrease of 2.4 M⊙ pc−2. It therefore seems plausible that the discrepancy results from a systematic difference between the log g scales of the theoretical isochrones and APOGEE, and so we incorporate these shifts into the systematic error estimate.
Upon inclusion of the systematic uncertainties from IMF variations and differences in the surface gravity scales, we attain a final estimate of the total local surface-mass density in visible stars of |$\Sigma _{R_0, {\rm tot}} = 20.0_{-2.9}^{+2.4}\mathrm{(stat.)}_{-2.4}^{+5.0}\mathrm{(syst.)}\ \mathrm{M_{{\odot }} \ pc^{-2}}$|, from the addition of the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| surface-mass density of |$\Sigma _{R_0, {\rm tot}} = 17.1_{-2.4}^{+2.0}\mathrm{(stat.)}_{-1.9}^{+4.4}\mathrm{(syst.)}\ \mathrm{M_{{\odot }} \ pc^{-2}}$|, and the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| value of |$\Sigma _{R_0, {\rm tot}} = 3.0_{-0.5}^{+0.4}\mathrm{(stat.)}_{-0.6}^{+0.6}\mathrm{(syst.)}\ \mathrm{M_{{\odot }} \ pc^{-2}}$|. If the log g systematics are as large as −0.3 dex, then our result is in agreement with the recent estimate from McKee et al. (2015) of 27 ± 2.7 M⊙ pc−2.
A recent compilation of measurements of the thick and thin discs found that the thick–thin disc surface density ratio at R0 is fΣ = 15 per cent ± 6 per cent (Bland-Hawthorn & Gerhard 2016). Our results find fΣ = 18 per cent ± 5 per cent for high–low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| disc surface-mass density ratio, consistent with that estimate. While a better understanding of the possible systematics between the theoretical isochrones and APOGEE is beyond the scope of this paper, we have shown that even a slight difference in the log g scale can bring our results in line with existing estimates. This suggests that our surface-mass density measurement discrepancy is indeed systematic, and that the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| discs may still have some relation to the thick and thin components measured by these studies, which are mainly based on geometric decompositions of the disc.
5.2 Comparison with maps results
We first discuss our density fits in comparison to the MAP measurements of Bovy et al. (2012b, 2016b). Such a comparison is important because our method is based on an extension of that developed by Bovy et al. (2016b) to the case of RGB stars, whose distances are far more uncertain than those of RC stars. Bovy et al. (2016b) used the APOGEE RC sample, to find the structure of populations in narrow bins of |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and [Fe/H], or MAPs. These MAPs represent stellar populations with a distribution of ages, but their interpretation assumes a significant relationship between age, |$\mathrm{[ \alpha \mathrm{/Fe]}}$| and [Fe/H]. We can now compare results when the third parameter, age, is known.
Bovy et al. (2016b) showed that the radial distribution of low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| MAPs is well described by a broken exponential, and we confirm this result, showing that each of the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, mono-age, mono-metallicity populations is also described by a radially broken exponential. We also show that the older, high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations are instead described by a single exponential, which is in good agreement with the findings of Bovy et al. (2016b).
The dependence of the radial distribution of mono-[Fe/H] populations on age is interesting in this regard. The low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population, for which our sample covers a wide range of ages with high signal to noise, shows a broadening of the profile around a density peak towards older populations, at all [Fe/H]. This effect does not appear to be present in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population (although some populations have slight evidence of a break at low significance), which suggests that it was formed and evolved differently. We discuss the implications of these findings in Section 5.4.
We also confirm the results of Bovy et al. (2016b) which showed that the break radius, Rpeak, is a declining function of [Fe/H]. We show that, in the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population, at fixed age, Rpeak moves to smaller radii as [Fe/H] increases. As a function of age, the amplitude of this variation increases. The difference in Rpeak at the highest and lowest [Fe/H] in the 6 Gyr bin is ∼6 kpc, which is identical with that of the profiles shown in fig. 11 of Bovy et al. (2016b).
Bovy et al. (2016b) found that low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| MAPs were fitted well with an hZ(R) which was slowly exponentially flaring with Rflare− 1 = −0.12 ± 0.01 kpc− 1. We confirm this result, finding also that low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations have, on average, Rflare− 1 = −0.12 ± 0.01 kpc− 1, but we also find that Rflare− 1 shows considerable variation with age (around this mean) in the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. While Bovy et al. (2016b) found that high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations were consistent with Rflare− 1 = 0.0 ± 0.02 kpc− 1, we find that these populations have Rflare− 1 = −0.06 ± 0.02 kpc− 1, showing some evidence of flaring, albeit at a lower level and lower significance than the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations.
It was also shown by Bovy et al. (2012b, 2016b) that the hZ(|$\mathrm{[ \alpha \mathrm{/Fe]}}$|,[Fe/H]) of MAPs smoothly spans the range between 0.2 and 1 kpc. We also confirm and extend this result, showing that hZ(age,|$\mathrm{[ \alpha \mathrm{/Fe]}}$|,[Fe/H]) varies smoothly between a maximum hZ of ∼1.2 kpc in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, low [Fe/H], older populations, down to a minimum of ∼0.2 kpc in the youngest, low |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, [Fe/H] rich populations. We can also directly compare our Fig. 12 with fig. 2 of Bovy et al. (2012a), which showed that the mass-weighted hZ distribution is not bimodal but smoothly declines with hZ. We confirm that result, demonstrating that for mono-age, mono-metallicity populations, the mass-weighted hZ distribution shows no sign of bimodality; the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations’ hZ distributions are distinct but overlap significantly, generating a smooth distribution. This presents an interesting new look at the interplay between spatial and chemical structure in the disc, as there is a clear mixing spatially of the two chemically separated populations. The implications of this finding are intriguing, and we discuss them further in Section 5.4.
Bovy et al. (2012a) also made a measurement of the local surface-mass density, finding (in the original application of the method used here) that SEGUE G-type dwarfs yield an estimate of |$\Sigma _{R_0,{\rm tot}} = 30 \pm 1\ \mathrm{M_{{\odot }}\ pc^{-2}}$|, which is in good agreement with other studies based on different samples (e.g. Flynn et al. 2006; McKee et al. 2015). Comparatively, our result is somewhat smaller, even when systematics are taken into account. There are a number of differences between this study and that of Bovy et al. (2012a). For example, the increased radial coverage, adoption of RGB stars as a tracer and the fits based on mono-age, mono-metallicity (rather than mono-abundance) populations. However, as mentioned in Section 5.1, our results, after accounting for systematic uncertainties, appear in good agreement with other more recent estimates (McKee et al. 2015).
5.3 Comparison with other Milky Way disc studies
We now compare qualitatively the findings of our analysis with the broader body of knowledge regarding the Milky Way disc structure (see, e.g. Rix & Bovy 2013; Bland-Hawthorn & Gerhard 2016, for recent reviews). In comparing our results with those from previous studies, we are constrained to making mostly qualitative considerations, as previous work is based on fits of single exponentials to the radial component of the stellar density distribution.
This work strongly constrains the structure of both the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| components in the Galactic disc, which are commonly considered to be interchangeable with the thin and thick components (as asserted by, e.g. Fuhrmann 1998; Bensby, Feltzing & Lundström 2004; Adibekyan et al. 2012). We have shown that the |$\mathrm{[ \alpha \mathrm{/Fe]}}$| rich component, while corresponding to a thicker configuration, in general, is the product of individual mono-age populations of varying thickness. We find that the |$\mathrm{[ \alpha \mathrm{/Fe]}}$| rich populations span the range 0.4 < hZ < 1 kpc, with hZ increasing with age. Studies of the vertical disc structure which fit a double exponential find a thick disc scaleheight of ∼1 kpc (e.g. Gilmore & Reid 1983; Jurić et al. 2008), which is fully consistent with measurements of the thickest high |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, old, mono-age populations in our analysis. However, we again stress here that the age uncertainties at old ages may be significantly larger than the bin size, which may cause a blurring of these trends, and should be accounted for when comparing these results to models. As an example, in the worst case scenario, assuming Gaussian errors, the oldest bins (between 7 and 13 Gyr) may be contaminated by up to 50 per cent of the stars which should be assigned to neighbouring bins, at the oldest end, with the fraction dropping off quickly at younger ages. We briefly discuss the implications of the worst case blurring on our interpretation of these trends in Appendix B
Regarding the radial scalelength of the thick component, we find an obvious discrepancy with literature values, whereby our thick, high |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, populations have an average hR, out = 1.9 ± 0.1 kpc, while the aforementioned studies, who define the thick disc geometrically, find values of the order of ∼4 kpc (Ojha 2001; Jurić et al. 2008). This discrepancy appears to arise in the choice of definition of the measured population between a geometric or chemical abundance selection, with many studies finding a scalelength for the abundance-selected α-rich disc in the range hR = 2.0 ± 0.2 kpc (Cheng et al. 2012b; Bland-Hawthorn & Gerhard 2016; Bovy et al. 2016b, 2012b). It should be noted here that our hR, out would likely be in even better agreement with this value, had we accounted for the 5 per cent systematic discrepancy in the distances (shown in Fig. 3). Martig et al. (2016b) recently showed evidence for a radial age gradient in the Milky Way, suggesting this as a source of disagreement between abundance-selected and geometric studies of the thick disc components, where the geometric-selected studies see an extended thick disc that is made up of flared low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations.
We also examine claims of a sharp decline in the stellar density at R ∼ 13.5 kpc (e.g. Reylé et al. 2009; Sale et al. 2010) in light of our results. Sale et al. (2010) fit a single exponential density profile with scalelength ∼3 kpc to A stars (which preferentially selects stars younger than ∼100 Myr old) and found that after R ∼ 13 kpc, a model with shorter scalelength was necessary to explain the increased rate of decline in stellar density. Our total profile in Fig. 13 begins to decline after R ∼ 10 kpc. The uncertainties in the measurement of the mass contribution of each profile may cause some discrepancy here, as implying a higher mass on older or more metal-poor populations would shift this turnover to higher radii. We also fit older populations than Sale et al. (2010), which, under the inside-out formation paradigm, might suggest another reason for such a discrepancy, as older populations would be more centrally concentrated. We confirm the assertion of Bovy et al. (2016b) that this break, clearly visible in the total stellar distribution, is attributable to the outermost break of the mono-[Fe/H] profiles – which are shown in the bottom panel of Fig. 13. External disc galaxies are also observed to have such a truncation in their stellar density profiles (e.g. Pohlen & Trujillo 2006).
5.4 Implications for the formation of the Galactic disc
In light of the above discussion, we now present the implications of our results for the formation of the Galactic disc. In this paper, we present a detailed dissection of the disc by age, [Fe/H] and |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, and as such, present a previously unseen picture of the dominant structure of the Milky Way. In studying mono-age populations, we can perform a more direct comparison than previously possible with numerical simulations of Milky Way type galaxies, which tend to use age information in the absence of detailed chemical modelling.
5.4.1 Disc flaring, profile broadening and radial migration
By estimating the density profiles of mono-age populations, we place novel constraints on radial migration and its effects on the structure and evolution of the disc. We have two key observables that provide this insight: the flaring of the disc, which has been considered as an effect of vertical action conserving radial migration (where stars have greater vertical excursions as they migrate outward, e.g. Minchev et al. 2012), and the broadening of the density profiles around the peak with time, which we discuss as a potential new indicator of radial migration. The right-hand panel of Fig. 9 shows a clear trend of increasing Rflare− 1 with age such that the youngest populations flare most. This behaviour is distinct from the results of Bovy et al. (2016b), which found that low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations were described by a single Rflare− 1. It is, however, conceivable that if low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations of all ages are combined, the resulting population may have a similar behaviour as that in Bovy et al. (2016b). Indeed, we find an average Rflare− 1 = −0.12 ± 0.01 kpc− 1, which is in good agreement with the value from Bovy et al. (2016b). If populations become more flared as radial migration proceeds, then it becomes difficult to reconcile our result with that of a disc whose stars continually underwent radial migration, largely unperturbed by any mergers that might cause structural discontinuity (e.g. Martig et al. 2014a), especially under suggestions that mergers actually reduce flaring from radial migration (e.g. Minchev, Chiappini & Martig 2014a). In this context, this result is indicative of an old population in the Milky Way which has undergone some mergers, reducing the flaring in the oldest populations. It should be noted here, however, that the age uncertainties (which can be as large as 40 per cent) could effectively artificially increase the age bin size, superimposing populations with different scaleheights and flare, and reducing the overall flaring profile.
We showed in Figs 6 and 7 that the radial surface density profiles of low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations become smoother with age. Interestingly, the position of the break radius does not vary monotonically with age. Assuming that the peak radius is at the equilibrium point of chemical evolution for a given population (where the consumption of gas and its dilution are balanced, as discussed in Bovy et al. 2016b), then one might consider that such a broadening would occur if stars that formed near the equilibrium point migrated inwards and outwards over time. If these assumptions are correct, then the specific surface density profile shapes might provide insights into how radial migration has proceeded in the disc. For example, if the slope of the inner or outer profile changes slope differently, this might suggest that migration has been asymmetric (i.e. more mass has moved in than out or vice versa). Comparing the −0.2 < [Fe/H] < −0.1 dex and 0.0 < [Fe/H] < 0.1 dex bins in Fig. 6, it seems that the inner slope of the former profile decreases more with age, whereas the outer slope of the latter decreases more strongly, suggesting that the former population has preferentially migrated in, whereas the latter migrated out. It is important to point out that under the interpretation that the increasing profile width is due to migration efficiency, we make an assumption that stars of a given [Fe/H] and |$\mathrm{[ \alpha \mathrm{/Fe]}}$| must have been born with the same width throughout cosmic time (as discussed by, e.g. Minchev et al. 2017).
This picture is also consistent with the suggestion by, e.g. Hayden et al. (2015) and Loebman et al. (2011) that the changing skew in the MDF as a function of Galactocentric radius is caused by such a mechanism. We show the mass-weighted [Fe/H] distribution for the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| fits at different Galactocentric radii in Fig. 14, showing that our results both find a radial metallicity gradient and qualitatively reproduce the skew found by Hayden et al. (2015). Unlike Hayden et al. (2015), our analysis fully corrects for sample-selection and stellar-population biases in reconstructing the MDF. Grand et al. (2016) also found similar behaviour in a simulated galaxy, finding that spiral structure induces different migration patterns, dependent on birth radius.
The surface-mass density weighted [Fe/H] distribution (MDF) at 3 radii for profiles fit to the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. The distribution shown is marginalized in age across all our age bins. The coloured bands give the 95 per cent uncertainty ranges, where uncertainties are dominated by those on the fitted density profiles. The mean [Fe/H] is lower at greater R. Qualitatively, the skew of the MDF's changes with R, such that the innermost R has a tail going to low [Fe/H], and the outermost R has a tail going to high [Fe/H].
Interestingly, we detect the possible flaring of old, high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, with average Rflare− 1 = −0.06 ± 0.02 kpc− 1. However, the right-hand panel of Fig. 9 shows that the flaring of the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations does not vary as strongly with age as the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations (although it should be noted that most of the mass in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations is concentrated at older age anyway). The detection of even a slight flare in these populations is surprising, as Bovy et al. (2016b) found that the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| MAPs did not have flare. Again, this may be an effect of the superposition of multiple mono-age populations within the MAPs. Minchev et al. (2015), for example, found that co-eval populations in simulated galaxies always flare, and suggested that the superposition of such flares might be an explanation for thickened disc components. Minchev et al. (2017) showed that the superposition of mono-age populations within MAPs can introduce decreased flaring in high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, whilst the mono-age populations themselves still flare. Comparison of these results with Bovy et al. (2016b) seems to present a consistent scenario. It should be noted here, however, that Stinson et al. (2013) found that MAPs in their simulation were coeval in general.
Our results show that the oldest populations are thicker, centrally concentrated and display the least flaring, whilst the youngest populations, which show the most flaring, have the thinnest vertical distribution (smallest hZ). Between these extremes, consecutive populations in age form a continuum, when the combined low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| structure is considered (see Fig. 9). Then, it is clearly conceivable that the geometrically defined thick disc, found to have large scalelength (e.g. Jurić et al. 2008; Jayaraman et al. 2013), may be the superposition of these flared (young) and naturally thick (old) components. An obvious consequence of this scenario would be an age-gradient at high Z above the disc plane, which has been recently shown to be present in the APOGEE data by Martig et al. (2016b). It was also recently shown that in the Gaia-ESO survey data, the mean structural characteristics of the abundance-selected thick and thin discs appear to overlap at [M/H] ∼ −0.25 dex and |$\mathrm{[ \alpha \mathrm{/Fe]}}$| ∼0.1 dex (Recio-Blanco et al. 2014), further presenting a scenario where the thick and thin disc components are not necessarily separable from one another, or at least not in abundance space.
5.4.2 Inside-out formation and the overall vertical disc structure
The formation of the Galactic disc is commonly framed in the paradigm of inside-out formation (e.g. Larson 1976; Matteucci & Francois 1989; Kobayashi & Nakasato 2011; Bird et al. 2013). More recently, the effects of radial migration (e.g. Sellwood & Binney 2002) were added, in order to produce models that agree better with the observations (e.g. Schönrich & Binney 2009a; Loebman et al. 2011; Kubryk, Prantzos & Athanassoula 2015; Spitoni et al. 2015). Our measurements of the peak radius of mono-age populations place strong empirical constraints on the evolution of the Milky Way disc over time. The behaviour of Rpeak with age and [Fe/H] is shown in Fig. 15. We find that the surface-mass density weighted mean Rpeak of low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations remains roughly constant with age, whilst the dispersion about the mean increases with age. This finding is qualitatively consistent with that of e.g. Anders et al. (2017), who show that the radial metallicity gradient decreases with the age of the population considered. Our results show that the density peaks of mono-[Fe/H] populations become more separated with age. As the mean [Fe/H] at a given R is dictated by the dominant population in stellar density at that radius, this indicates that we also see a shallowing gradient in [Fe/H] with age. This is reinforced by our finding (also shown in Fig. 15) that the mean Rpeak decreases with [Fe/H].
The behaviour of Rpeak with age and [Fe/H] for the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. The high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations are better fit by single exponentials, and so Rpeak is not an informative diagnostic of these populations. The coloured lines and bands give the surface-mass density weighted mean and standard deviation within an age or [Fe/H] bin. The mean Rpeak does not vary significantly with age, whereas it shows a clear decrease with [Fe/H]. However, the dispersion in Rpeak does increase with age for low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. High |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations show a slight increasing trend for increasing age and [Fe/H], albeit at low significance.
Our results also place strong constraints on models for the formation of the vertical disc structure. We have already discussed that the vertical structure of the disc is commonly framed as having two geometrically distinct (but overlapping) vertical components (e.g. Gilmore & Reid 1983). Our results confirm previous work (e.g. Bovy et al. 2012a) that shows that this picture, while providing an acceptable description of the data when analysing the whole population, is not complete when individual populations, either abundance selected or age selected, are considered. We have shown (in Fig. 12) that for a random mass element, the probability that it belongs to a population of a given hZ exponentially declines as hZ increases. There are no apparent breaks in this relation at the resolution that we measure, strongly suggesting that the spatial vertical disc structure is continuous. This finding, in stark contrast to the distinct discontinuities seen in the chemical structure of the entire disc (e.g. Nidever et al. 2014; Hayden et al. 2015), presents an interesting conundrum for galaxy formation theory. How is it possible that the spatial structure of the disc be smooth and continuous, whilst the chemical structure portrays a clear discontinuity?
Theoretical studies have, thus far, presented some clues as to how galaxy discs such as that of the Milky Way might form. As most studies fit single exponential radial profiles to simulated discs, quantitative comparisons are difficult, yet qualitative considerations can be made. Stinson et al. (2013) used a maximum likelihood method similar to Bovy et al. (2012b) to fit density profiles to MAPs in a simulated galaxy and found a continuous distribution of scaleheights, but also found that their simulation showed a strongly geometrically distinct thick disc component. Bird et al. (2013) made detailed measurements of the mono-age populations in a high-resolution hydrodynamic Milky Way like galaxy simulation and found, similarly to our results, that their scaleheights gradually decreased with time, while the scalelengths increased, with populations forming thick and retaining that thickness in an ‘upside-down and inside-out’ disc formation. Our results also find evidence of flaring in the thick components (as discussed in Section 5.2), which may point towards some structural evolution (via a process such as radial migration) after their formation. However, work on simulations by Bournaud et al. (2009) suggests early, turbulent gas as the origin for thicker disc components. A flare in the gas disc of the Milky Way, associated with the stellar component, is also observed in numerous studies (e.g. Lozinskaya & Karadashev 1963; Feast et al. 2014; Kalberla et al. 2014), suggesting a formation of the disc with structural parameters similar to its progenitor gas disc.
5.4.3 The age–[Fe/H] distribution and the evolution of the disc
We now discuss how the present day structural parameters, in combination with the emergent picture of the mass distribution in age–[Fe/H] space at the solar radius, might offer deeper insights into the formation and evolution of the disc.
We find, as may be expected, that the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations contribute the majority of their mass at the solar radius at ages older than ∼6 Gyr, although the mass contribution by old stars is extremely low compared to the younger populations. The middle panel of Fig. 13 shows that if the populations follow the density models that we fit then the older stars become more dominant closer to the Galactic Centre, which is suggestive of a weak mean radial age gradient, in qualitative agreement with theoretical predictions (e.g. Minchev et al. 2015) and observations of the thick disc (e.g. Martig et al. 2016b). It is therefore not surprising that the bottom panel of Fig. 13 shows a clear variation in mean metallicity, in agreement with findings in other works (e.g. Cheng et al. 2012a; Hayden et al. 2015; Anders et al. 2017). Only with high-resolution hydrodynamical simulations, which accurately reproduce the stellar populations in galaxies, will it be possible to reconstruct the right combination of star formation history and radial mixing that led to these age and metallicity gradients to gain a better understanding of the details of their formation.
In Fig. 11, an overlap in age–[Fe/H] space is visible between the high and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations. While there appears to be mass at many [Fe/H] bins in the old populations, the overlap in age occurs at intermediate [Fe/H] at the solar radius. Previous studies have found that the youngest stars in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sequence overlap in age with the oldest and most [Fe/H] poor stars in the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population (e.g. Haywood et al. 2013), and our findings appear to be consistent with that result. It should, however, be noted that at least some of this overlap is likely caused by the age uncertainties, which can be as high as 40 per cent. If the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population emerged from the remnants of the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, then it is likely that some sort of infall event must have occurred to return the ISM to low [Fe/H] and low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| before forming those stars (as expressed by, e.g. Chiappini et al. 1997). These scenarios are also discussed in the context of the APOGEE results by Nidever et al. (2014). To fully understand this, however, we will likely require a chemodynamical model that reproduces the bimodality in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at fixed [Fe/H].
6 CONCLUSIONS
We have performed the first detailed dissection of the stellar populations of the Milky Way disc in age, [Fe/H] and |$\mathrm{[ \alpha \mathrm{/Fe]}}$| space, bridging the gap between the detailed observational understanding of MAPs (e.g. Bovy et al. 2012b, 2016b) and the plethora of studies of co-eval stellar populations in simulated galaxies (e.g Bird et al. 2013; Stinson et al. 2013; Martig et al. 2014a). We have placed novel constraints on models for the formation of the Milky Way disc by combining detailed density models fit to the mono-age, mono-[Fe/H] populations of the low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| disc, with surface mass density contributions calculated on the basis of these density fits and stellar evolution models. We summarize our key results as follows:
Radial and vertical profiles: The mono-age, mono-[Fe/H] populations of the |$\mathrm{[ \alpha \mathrm{/Fe]}}$| poor disc are well fitted by a radially broken exponential, with a peak radius, Rpeak, that varies as a function of age and [Fe/H]. We find that the distance between Rpeak's of the low and high [Fe/H] populations increases with age, which we interpret as evidence for a decreasing [Fe/H] gradient with time (e.g. Anders et al. 2017). The radial variation of the stellar surface density of the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| mono-age populations is found to have insignificant breaks, and they are better fit by a single exponential in this disc region. As these populations are the oldest, this may be a sign of the disc evolution washing out the density peak over time, or may point to a different formation scenario for high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| stars, where no density peak ever existed. These findings are in good agreement with earlier studies of MAPs (Bovy et al. 2016b). We measure an average high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| population scalelength of hR, in = 1.9 ± 0.1 kpc, and find scaleheights between 600 and 1000 pc, in good agreement with current measures of the |$\mathrm{[ \alpha \mathrm{/Fe]}}$| rich disc scalelength and scaleheight (e.g. those outlined in Bland-Hawthorn & Gerhard 2016).
Profile broadening: We show that the radial surface density profile of the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations broadens with age in a given [Fe/H] bin, which we interpret as evidence of the gradual dispersal of mono-[Fe/H] populations, presumably due to radial migration and radial heating. The variation in shape of the broken exponential profile changes differently depending on the population [Fe/H], with low [Fe/H] populations inner profiles flattening faster, whereas the high [Fe/H] outer profiles flatten faster. We interpret this effect as tentative evidence for [Fe/H] dependent radial migration arising from pre-existing [Fe/H] gradients in the star-forming disc. We showed that our results qualitatively reproduce those of Hayden et al. (2015), finding a skewed MDF that varies as a function of R.
Flaring: We find that flaring seems to be present in almost all mono-age populations, at differing levels. We have shown that the inverse flaring scalelength Rflare− 1 increases with age, meaning that the youngest populations flare most strongly. This finding appears inconsistent with that above, under the assumption that flaring is the result of radial migration. However, these results may be reconciled by invoking a more active accretion history in the early life of the disc, which could have suppressed flaring (e.g. Minchev et al. 2014b).
The surface-mass density at R0: We have measured the surface mass density at the solar radius for each mono-age, mono-[Fe/H] population, finding a total surface mass density of |$\Sigma _{R_0, {\rm tot}} = 20.0_{-2.9}^{+2.4}\mathrm{(stat.)}_{-2.4}^{+5.0}\mathrm{(syst.)}\ \mathrm{M_{{\odot }} \ pc^{-2}}$|. Before allowing for systematics, this value is less than current estimates (e.g. Flynn et al. 2006; Bovy et al. 2012a; McKee et al. 2015), however, the systematic uncertainties are large, mainly due to a mismatch between the log g scales in APOGEE and the PARSEC models, and as such, we find our value to be consistent within the uncertainties. The relative contribution of high to low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations, |$f_\Sigma$|, is 18 per cent ± 5 per cent, which is consistent with existing measurements (e.g. Bland-Hawthorn & Gerhard 2016).
The hZ distribution at R0: The shape of the mass-weighted hZ distribution found by this study is in good agreement with that of Bovy et al. (2012a), calling into question the existence of a vertical structural discontinuity in the Milky Way disc. The reconciliation of this finding with the discontinuity in chemical space (e.g. the bimodality in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at fixed [Fe/H]: Nidever et al. 2014; Hayden et al. 2015) may shed new light on our understanding of the formation of the Galactic disc.
The surface-mass density profile of the Milky Way: We have found the combined (from mono-age, mono-[Fe/H] populations at low and high |$\mathrm{[ \alpha \mathrm{/Fe]}}$|) surface-mass density-weighted profiles of the Milky Way disc as a function of |$\mathrm{[ \alpha \mathrm{/Fe]}}$|, age and [Fe/H], and found that the total surface density is also described by a broken exponential. We find that our results fail to determine the sign of the inner exponential to high significance out to ∼10 kpc, but detect a turnover to a declining exponential, at high significance, thereafter. We find evidence of a radial mean age and [Fe/H] gradient driven by the changing dominant population as a function of radius. A detailed comparison of these findings with numerical simulations is necessary for a proper interpretation. Our finding of a decline in stellar density may be consistent with that found in other studies (e.g. Reylé et al. 2009; Sale et al. 2010), albeit at shorter radii.
These findings are strongly constraining to future theoretical work. With the recent (Lindegren et al. 2016) and future releases of Gaia data, and the ongoing APOGEE-2 survey (Sobeck et al. 2014), which will include an updated APOKASC sample (Pinsonneault et al. 2014), access to improved positions, abundances and age estimates is within reach. We again stress here that the age uncertainties in this data set can be as large as 40 per cent, and so until more precise ages are attained for similarly sized samples, our conclusions must be considered under the caveat that the mono-age populations at old age are likely mixed to some extent. It will be possible to investigate this issue better once better ages for a larger sample are released by APOGEE and APOKASC (Pinsonneault et al. 2014).
Future studies of simulations which accurately track chemical evolution, gas and stellar dynamics, and the feedback processes that are dominant in galaxies will no doubt lead to a deeper insight into the physical processes leading to the present day structure of the Milky Way. The understanding of discontinuity in chemical space, namely the bimodality in |$\mathrm{[ \alpha \mathrm{/Fe]}}$| at fixed [Fe/H], and how this can be reconciled with the apparent structural continuity that we find here poses an interesting challenge to models of the formation of the Milky Way disc. By performing a first mapping of the 3D distribution of stellar populations as a function of age, metallicity and [a/Fe], we hope that this work provides the kind of data needed for a comparison with numerical simulations that is unencumbered by the complexities associated with corrections for the survey selection function.
Acknowledgements
It is a pleasure to thank Marie Martig for helpful comments and discussion, and also for providing the catalogue of ages for APOGEE DR12 in digital format. We also thank Ivan Minchev, Misha Haywood and Paola Di Matteo for insightful discussion and comments that improved the clarity of the manuscript. The analysis and plots in the paper used ipython, and packages in the scipy ecosystem (Jones et al. 2001; Hunter 2007; Perez & Granger 2007; van der Walt, Colbert & Varoquaux 2011). JTM is funded by a Science and Technology Facilities Council (UK) studentship and was hosted at the University of Toronto for a short period while completing this work. JB received support from the Natural Sciences and Engineering Research Council of Canada, an Alfred P. Sloan Fellowship and from the Simons Foundation. SM has been supported by the Premium Postdoctoral Research Program of the Hungarian Academy of Sciences, and by the Hungarian NKFI Grants K-119517 of the Hungarian National Research, Development and Innovation Office.
Funding for SDSS-III was provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation and the U.S. Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/.
Available at https://github.com/jobovy/apogee-maps
Available at https://github.com/jobovy/apogee.
Taking a ratio of the sum of the density at fixed ΔR either side of Rpeak to that at Rpeak would give some measure of width. Then, assuming ΔR ≪ hR, [in, out], a Taylor expansion of this ratio |${\sim } \Delta R (h_{R,{\rm out}}^{-1}-h_{R,{\rm in}}^{-1})$|. We then plot the inverse of this factor such that it increases for broader profiles.
REFERENCES
APPENDIX A: DENSITY FITS
For completeness, we briefly discuss the quality of the fits performed with the method outlined in Section 3. Figs A1 and A2 show the distance modulus distribution of the APOGEE data in each of our mono-age and mono-[Fe/H] bins (grey histograms) and the resulting distance modulus distribution when the best-fitting density model for each bin is run through the calculated effective selection function (which is the space in which models are fit in our procedure). The red line represents a single exponential fit to the radial and vertical spatial distribution and the black lines give the best-fitting broken-exponential density model (upon which we base our results). We show the single exponential fit in order to demonstrate that, in most cases, this does not provide a good fit to the data, and that when a single exponential is a better fit, the broken-exponential density fit matches it.
Comparison between the best-fitting models and the APOGEE data for mono-age, mono-[Fe/H] populations in the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample. The grey histogram shows the distance modulus distribution of the APOGEE data for the mono-age, mono-[Fe/H] bin indicated by the ([Fe/H] [dex], age [Gyr]) coordinate given in each panel. The coloured curves show the distance modulus distribution found when the best-fitting broken exponential (black) and single exponential (red) density model is run through the effective selection function. It is clear that the broken exponential density model provides a qualitatively better fit to the data in all cases.
Comparison between the best-fitting models and the APOGEE data for mono-age, mono-[Fe/H] populations in the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subsample. The grey histogram shows the distance modulus distribution of the APOGEE data for the mono-age, mono-[Fe/H] bin indicated by the ([Fe/H] [dex], age [Gyr]) coordinate given in each panel. The coloured curves show the distance modulus distribution found when the best-fitting broken exponential (black) and single exponential (red) density model is run through the effective selection function. In many cases the red and black curves are indistinguishable (only red is seen), or very similar. In cases where the black and red curves are different, the red curve provides a qualitatively better fit. Bins with less than 30 stars (which we disregard for the majority of the analysis) are hatched out.
Regarding Fig. A1, which shows the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subpopulations, it is clear that the black curve (broken exponential) represents a far better model for the data than the red curve (single exponential), in all mono-age, mono-[Fe/H] bins. While the black curve is not perfect in all cases, the peak of the distribution tends to lie at the correct μ, whereas the red curve finds a peak at higher μ in most cases (due to the higher than necessary density at low Galactocentric radius in this model).
Fig. A2 demonstrates the fits for the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| subpopulations. The greyed out panels reflect those with less than 30 stars, which we deem too noisy to render reliable fits. In many of the remaining panels, the red curve is similar or identical to the black, due to the fact that many of the high |$\mathrm{[ \alpha \mathrm{/Fe]}}$| populations are better described by single exponentials, and the broken exponential generally recovers this result. In most of the cases where the curves differ greatly, the red curve recovers the peak of the distribution better than the black – suggesting that breaks that were fit in the radial range we consider are artificial, and due to the noisy data in this regime. We discuss the broken exponential fits in the main text in order to make proper comparison with the low |$\mathrm{[ \alpha \mathrm{/Fe]}}$| sample, although it seems plausible that the single exponential model provides a better explanation of the data.
APPENDIX B: THE EFFECT OF UNCERTAINTIES ON TRENDS WITH AGE
In order to demonstrate and characterize the effect that the age errors have on our interpretation of the trends between structural parameters and age, we created a mock data set from a set of randomly sampled density distributions. We created a mock data set with an input trend of hZ with age which increased monotonically with age from 0.2 to 1.2 kpc. Ages were assigned to each hZ population, sampling uniformly in bins of width 2 Gyr, to which we then added a random Gaussian error of 40 per cent, replicating the shifting of stars with different hZ into each age bin. In each bin, we sample a single exponential (a broken exponential with Rpeak = 0) with scalelength 8 kpc. This higher scalelength is required to make the test computationally efficient, to produce realistic numbers of stars when selecting stars in APOGEE fields and does not impact on the results of this test. We assume no error on the stellar positions, in order to isolate the effect of the age errors.
While this test is a somewhat simplistic representation of the underlying processes, it serves as a good example of the effect of the age uncertainties that are expected in the present data. One example of its simplicity is the assignment of a single hZ to relatively wide bins in age. It seems logical to assume that if there is an age–hZ relation, then the change in hZ should be somewhat continuous with age. Our test assigns the same hZ to stars at bin edges (which should have hZ close to that of the bin-edge stars in the neighbouring bin). This may artificially increase the amount of blurring of the age–hZ trend. We also simplify the test by assuming that the only changing parameter is the scaleheight. Realistic structural parameters would change the relative number of stars within each bin observed by APOGEE (and considered in our test), and may change the level of contamination between bins. However, we assume that our simple approximation represents a ‘worst case’ scenario, where the mixing between bins is maximal.
We restrict the mock data to the APOGEE fields, simplifying the selection to a distance cut (assuming the selection fraction is 1 out to a distance that corresponds to MH = −1.5, assuming no extinction). We apply the method described in Section 3 to our mock data, fitting a broken exponential profile, and using the best-fitting solution to initiate an MCMC sampling of the posterior probability distribution. As in the main body of the paper, the reported parameter values reflect the median and σ of the one-dimensional projections of the MCMC chain. The resulting age–hZ relation is shown in Fig. B1. A clear trend is recovered between age and hZ. The trend is still recovered at high age, regardless of the high level of mixing between bins, which increases the size of the error bars. The higher scaleheight components are recovered by the analysis, but results are scattered around the input values, with large error bars. This serves to show that even in the face of large age uncertainties causing mixing between the adopted bins, our method is still able to recover the underlying trends of parameters with age.
The resulting age–hZ trend from the Monte Carlo sampling of a set of mock density distributions. The input density models had hZ increasing monotonically with age (in bins of Δage = 2 Gyr) from 0.2 to 1.2 kpc (shown by the blue dashed line). After sampling of the density distribution, we applied random errors of 40 per cent to the mock ages, and measured the structural parameters using the exact density fitting method applied to the APOGEE data. The method is able to approximately recover the general shape of the input age–hZ relation, showing a clear trend with age. The age errors increase the error bar sizes significantly where mixing does occur, but the results are consistent with the input in most cases.



![The full RGB sample in $\mathrm{[ \alpha \mathrm{/Fe]}}$–[Fe/H] space. The coloured regions show our division between low and high $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsamples. At each [Fe/H] the division between the samples is $\mathrm{[ \alpha \mathrm{/Fe]}}$ = 0.05 dex, roughly twice the mean uncertainty on $\mathrm{[ \alpha \mathrm{/Fe]}}$ abundance determinations in APOGEE DR12. The bimodality in $\mathrm{[ \alpha \mathrm{/Fe]}}$ at fixed [Fe/H] is visible across many [Fe/H], and the lower number of stars in the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ sample is clear from this plot.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig1.jpeg?Expires=1716465206&Signature=LN4wgE1Y11flkG5ppUAp0hEiKMkin8d8ap28RcfoJDld4TlqORg1poHADaXgGDVnYL7BYjD2iVb7zbKzouLqRVmhG1ZI2O97TyBjTDfi7-gNXDOMyZzDL3EzElfmoDoqe1Df-ubDAMaNNFMCDbVSWNYOC3VaWpGWxeSr5TKQ58K1Xy49VciPcXxprUOE3sy9hnxpLJoDD7Lkas1cTCb-2Qxzl4Zuo3TJgC2Bh0HsTKkiJDP2RxaQwZuRnNCHFnX01toHE~FsTlAG0Sf0O~TkfwRPi238mUEwjCjXhUSwqQ8slr9fNA1PKP8TnyFQW2tEcsI~kpx3WW9pK9T7~n6uKQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![2D histograms of the spatial distribution (in Galactocentric R and Z) of the high and low $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsamples shown in Fig. 1. The high $\mathrm{[ \alpha \mathrm{/Fe]}}$ sample appears more diffuse and extended in height even before selection effects are accounted for. Readers should notice the different colour scale adopted for each panel, due to the much lower number of stars in the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ sample.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig2.jpeg?Expires=1716465206&Signature=d456~aY6f1cdhRnuPgA1aaN~OJ-KwO-fMu939aE7I-ryqj~MGSCCkZuOvZf5dUY5mg~it18-nzzmztanDjagZ7l~16ICMbL3WR1lQnKW~JAkWPlzD~eQcVtr5k7lEQAZbUJlWw7CjMVRLkWHxH9WFJUwDlCConj0ZTt~iSUzvZ6JQlhOmMYWrreDE6ra20JD167NrxIu~JS49AfreqXWBBaP-EPtXENoERo48lyZhVUqnXx0cT0QNFNJRRosxQfRbhqbuEwbluIQ6rlZapdFGD-ibnuJG1owiPD-Qdh-LfNWaHm9vDUEp3V5w15GMFjRXhyK62aeZaMseqywlihOeA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
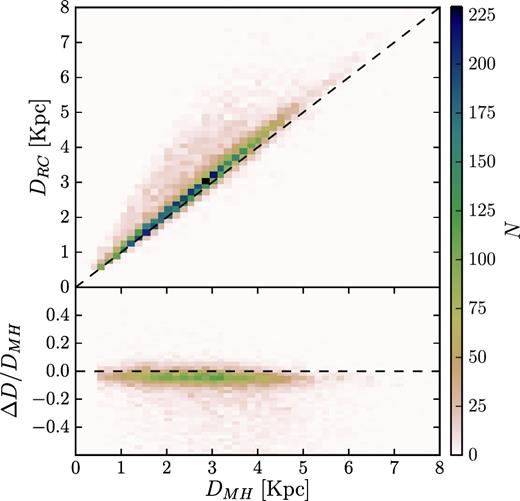
![Asteroseismically determined ages from APOKASC against the [C/M] and [N/M] based ages from Martig et al. (2016a). The line gives the fitted correction for ages from Martig et al. (2016a), based on the values for the APOKASC training set, given in their table 1. We fit the data using a non-parametric lowess fit. Before corrections, older ages are underpredicted, and young ages are overpredicted. The corrections mainly change the scaling of the ages, such that the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ sample occupies an age range more in line with the existing literature (e.g. Haywood et al. 2013; Anders et al. 2016)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig4.jpeg?Expires=1716465206&Signature=176PzXdWSOMJ-NCRZjOMM2Uc812ifaSsQdOmJofne1ExRX8l1EUdmvm5NOmJNF0LYDVmF7Ofx8UeXXZI-FN04doY0cEXpaknCJBydanrgVxyLGqMusa17ESC6BJ5jn1juUyKvFNH2AZzUE9cnz4nVLfpuKZ-EEtDcPpIOgyivrwg33YwNGL-R71BjCCPilI2u8zPPrdHaPc6Nvl8~qtYGYWECunntpuDaErHB6hBWqbZaW5lbogBhtvtWckY217gWfl-Ftta2Kaw3~H0mAtDmexdIrIWLQnsejU6pahjsH-x-qh7ZhBK-8El94tgh8NNf0cw8Rirgjtze~f0bC~i2Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![2D histograms showing the raw number of stars in each (age,[Fe/H]) bin of the low (left) and high (right) $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsamples. We draw the reader's attention to the difference in amplitude between the two subsamples (and the associated difference in colour scale normalization). Although the majority of bins are well sampled (≳ 30 stars), there are some greatly undersampled bins, for which well-defined fits are not possible.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig5.jpeg?Expires=1716465206&Signature=Rim0-VVrd1ivbqTxAnTH-xj~gsHNoj~tC~EmiHDNUwmwoyDztlf2RKKw3zby6e1ZYqGnpT~jpI2a74qw5dU-wM9m7clJ-bGon3ZjBfxvajmDRb0W7-sSYKApKug8Ullw~-u2dlhMIxlkMQBl1PY-bQUB-y2SwC2QapAyjmL3S5gmujrLZ~IDmDfk82VTmZAhPDY6-OhUzA7161pmMr4lupB4ZFpfq4t2RLXrpc9YqZ1UXFS-2T157cXtVtKhKNLLfD6BDDDtQeVWTLYTSEMe5re1biMUoUjEsEUypQ7wAC8i9kDxGsbpCKx1AxhZzYMh1PorKIQqeZSI8lvwOfP9Xw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The fitted surface density profiles for the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ (top) and low $\mathrm{[ \alpha \mathrm{/Fe]}}$ (bottom) subsamples as a function of [Fe/H] (colour) and age (increasing from left to right). The coloured bands represent the 95 per cent uncertainty range. Only profiles for bins containing >30 stars are shown. The profiles have a transparency according to the surface-mass density calculated for each bin in Section 4.3, normalized separately for each row (i.e. in each [Fe/H] bin), to draw the eye to those profiles which contribute most to the Milky Way surface-mass density. High $\mathrm{[ \alpha \mathrm{/Fe]}}$ profiles are described well by a single exponential, whereas young, low $\mathrm{[ \alpha \mathrm{/Fe]}}$ profiles are broken exponentials with a peak density that varies in radius in the disc.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig6.jpeg?Expires=1716465206&Signature=IEmgthLcyAJ7n-sVpXr-L-74f4btT6H2E3DW0vGiTbArJBUttRpCnWXtNoP9EIOzp3r1hTDStt2DB4fZVPSntRKQE9aHZAa8~NKsN3cJdI6qWs1rnGMNBgeNEjSyS9DGGCceKi2FuaPNETRDvBbio5ROWvAhVXtWcKJOb0JRpPSHdhPMN8zYSaePs5swHJamKW8wANhkR8mhqyjDrjLY1AHVGE98VQmXu1-KtzBkbP8BGvPPjxGoAgOujBosCHQz5QUoVsL0TYKbTNYwr3ZHc5W~h2RTDrYPEE3RUQnQE9uAcD6azdUnPnDJjvc6x2ye6Ux-Hs5WfjbK0Mm-e6~rBw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The profile width $(h_{R,\mathrm{out}}^{-1} - h_{R,\mathrm{in}}^{-1})^{-1}$ against age for the low $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations (this diagnostic is irrelevant for the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations, which are generally fitted by single exponentials). We add a small random jitter to the central age of each age bin, to make individual points and their uncertainty clearer. The relations and coloured band show the running surface-mass density weighted mean and standard deviation in the age bins. The profile width increases with age. A higher value of this diagnostic suggests a broader surface density profile, showing that older populations are flatter and broader around the peak density.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig7.jpeg?Expires=1716465206&Signature=I~nNfnqEK5qqvnUl1ENn~hWoyfrfzyKPoMRIV~AB5ni2x8hSgAmatJqp5rfKjCqNHmkHgboIL8V143gkSh1H~Xl6pN1y9rSK65~4gYwjnxL4T8utx1kvcvPVBt4XzyIzGtzR8pOfpV0Xs1ApiYzqhnplXHTFTTfYxn7KVnKJ0G88Nr1z2zzt-23W1obtvieDdsJQDDO2BE5Lab22Z9~xt181PcNrP3XoQafCTIAo~xYbqT3DZ1nu969c7ZfueS3-znrt4awq3BqFeUGB1e2mk87V7IkVM9~iSXnFzgzlnPR4Imnm0SogCT2R2CkFujs86-Nm4SoQG490cbXo8ESHRA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Vertical profiles for the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ (top) and low $\mathrm{[ \alpha \mathrm{/Fe]}}$ (bottom) subsamples as a function of [Fe/H] (colour) and age (increasing from left to right). The coloured bands represent the 95 per cent uncertainty range. Only profiles for bins with >30 stars are shown, with profiles shaded according to their surface-mass density contributions (discussed in Section 4.3). The dashed lines represent hZ = 0.3 kpc, for reference.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig8.jpeg?Expires=1716465206&Signature=hGybBdz9-KfSk0bZ-vFS1rExhw-rVAaXFK40Cmj1Gw1XTkq666hfJqG-xlLUasBtMtUD6oOT2isnDM8v6iopIVbYYDFZOx2LfQ7sQtcbelZeZ3jkihHfZUeOGdD8zXozwo2woOmJLbezegHvoDtCbEpphcHTxV3UlWM6W9EYXu~2ip4OPbuXCxIEF36IGA~z4NOihjdxzivVugTvQVCg9q1L6TqnovbGd05mBy7CpZkDeCMgqKJGquAMD2WJyv2Z13SAleRYL4K9vFxh8Ol2IzPRyqMFwda40N5L1-T3hVpbDRbiJELt4U4delCNyIDyeDZa6AlMSg-u8WluBzNmew__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Mean hZ at R0 (left) and Rflare− 1 (right) against age. The mean value in each age bin is calculated by multiplying together the posterior PDFs of the density fits. The panels show both the low (purple) and high (green) $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations. The left-hand panel shows the total surface-mass density weighted mean as a dashed line, which demonstrates that the vertical distribution of the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ population is only important at the solar radius at old ages due to its low surface-mass density contribution. hZ increases with age for both low and high $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations. Rflare− 1 behaves similarly for the low $\mathrm{[ \alpha \mathrm{/Fe]}}$ population, meaning flaring decreases with age, but the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ population shows an opposite behaviour.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig9.jpeg?Expires=1716465206&Signature=TnTo1Op8~u3wivRJDw~XwLNqS99icdPv9p95q-E6PoBjG3VYCQ98nEsLj7zg3UeHVBk6X9njDOqISPfVWjxhcVzkW28exjlO7RPZxzUNHiSgbiHFv9fDGBcD-V-aNWT5RXtakVwb2F7KNlnd4HFbSnvyWQmKQER8EsrNsHWu~7JzAR837a7Poep-TZZVL~lzz~5751YufnzQKnQjHnQ~TK9XRW6pqIwt7galowPH2dKiCN90ycJkiStZLJDJEu6A8YnAj9r2Sc5pyxyCdMfeqF9apA7GmyfU559XHaL-G9g7OJy0S4xRvFfDK5Ig0VM1kVDkUr2NP~z4zQLs0Jtocg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The surface-mass density contribution of mono-age, mono-[Fe/H] populations at R0 (where low and high $\mathrm{[ \alpha \mathrm{/Fe]}}$ are combined). The total contribution $\Sigma _{R_0,\ \mathrm{tot}}$ is displayed at the top of the main panel. The colour scale is linear and spans the surface-mass density range between $0 < \Sigma _{R_0} < 1.5\ \mathrm{M_{{\odot }}\ pc^{-2}}$. The marginalized distributions along each axis are shown above and to the right. The mass at the solar radius increases monotonically with both age and [Fe/H].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig10.jpeg?Expires=1716465206&Signature=Z2TZaPUjHrWomKgaiC687fFaqLaDGajvYMdBJ8UWH2h48jO95txVY-WI9Ml6ZXeBx08FrVrAJ8~-xVg9aXs7txUOEoK4ky8Cr4N696QnZoa4fRBDFZ3nG8kT5R9Dvesyj0BYAILHe2h6Gs~q0EQG2Emkn3jW1uNwxTcGAR~vu9UxypAvBbULo0v~OzEIibaZ-~sI0YIk8IFaxIsZ0YLKLKP2SvMg174TFuxmHpNd68wzfFtLFAXI-ABYwM~39CswJIBjyr1WSLreYyp1bLexLypkT6Wm6r3vfVdqO5IeNnoTIzUetgczpONGsxopRJS7jSe~LIwjT6r66KLxdlzVAw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The surface-mass density contributions of the low (left) and high (right) $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsamples. The total contributions $\Sigma _{R_0,\ \mathrm{tot}}$ are displayed at the top of each panel. We draw the attention of the reader to the difference in colour scale between the high and low $\mathrm{[ \alpha \mathrm{/Fe]}}$ panels, which differs by an order of magnitude, and is adopted to better show the behaviour in the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ sample. The low $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsample has mass at all ages and [Fe/H] but is concentrated mostly at young ages. The high $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsample contributes far less mass and is concentrated at old age.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig11.jpeg?Expires=1716465206&Signature=e9qyz~7v4LG4rPnKZXrutb7qethdNq5j9aH1W~e8w8DLQVc5MBnrCEykoxbTPLHEFAK7GHlKfSCcg7jO6pUfPlm-JSVAl437yBO~I6NCPmizzGK-kABjmyj7ajceXGi8PY-NwM~yJk1HLaJamPRanU7sIT6iALLCqCxzNewgNDvFVzvvoWJih0ZI0zlXjCUlqeRnYN19uJYfbM-GpVhEKn8Ad6HLRFsPpeEy38YNA2q1a8Lo1Q5CWMHXUbk3-NxcsJQW6awqpCL5cyN1Db6sVd-~t0okiAzhHtfiPaeu17-IQG-oBmXLXZXwCrjR-EVHf7pYEQPk0PW3QqimQWxhjw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The mass-weighted vertical scaleheight hZ distribution. The individual points represent the hZ and $\Sigma _{R_0}$ for each mono-age, mono-[Fe/H] population. We colour the points, which represent both the low and high $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations, by the central age of the mono-age, mono-[Fe/H] bin that they represent. The coloured histograms represent the hZ distributions for the low and high $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations from the sum of the individual contributions. The dashed histogram represents the total distribution. The total distribution smoothly decreases with hZ, with no hints of bimodality.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig12.jpeg?Expires=1716465206&Signature=CMxOVtE6DRdtlFbK7jS6m~S-OECCNUmOu1zUlM1aa2CAm7OZR1XEgD5fIRPM1LhrxPjbCwoOXC6VUv~FCpMN8bnYhIu0NcCV7IHoXssKKzrd1UqGWL6G9O0Ah3axbXAmyzrqLSip-HaFBMCdx-QkpNm52FzAKDElzCCUpiJb~AMUihWce1~UjfM99TWZ1cpt~wkiyFw0vuutIcQ9Ate0CMczt8ivbkaqxY6k29RwYL5l~cOwPwntdep18r66FJjby~L0YGOAJil3qw53seOOlWGwdVnoK0Ad5LaDLnomKGKcOqgrwQRaKw1jCd5srnL7-PIVxpVat96PRR7R6pY2wg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The radial surface-mass density profile of the Milky Way, as a function of $\mathrm{[ \alpha \mathrm{/Fe]}}$ (top), age (middle) and [Fe/H] (bottom). The profiles are the result of a mass-weighted combination of the fitted density profiles along different axes in age–[Fe/H] space and (in the top panel) for the combined low and high $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations. We show the combined uncertainties from the fitting procedure in the top panel, which are sufficient (without addition of the individual statistical and systematic errors on the surface-mass densities, which are substantial) to show that the apparent flattening at R < R0 is not found to high significance. The surface-mass density of low $\mathrm{[ \alpha \mathrm{/Fe]}}$ stars extends to a higher radius than the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ stars. The youngest populations show a clearly peaked surface-mass density around the solar radius, whereas the older populations peak more centrally. Behaviour with [Fe/H] is complex, with flat profiles at low R, becoming exponentially decreasing at high R.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig13.jpeg?Expires=1716465206&Signature=n1tmAyCAwJ8uVvYYSw0AL0OrHm~eL6i54B-pnirJTrvHMwowFdCE9HOmvo-iY4Ab5A8fBKi5kG3JNzzdgP0mncs5~syeVcxrA~vv07KOF1YnCXbajYdfgyrjEY52M3Q~w22~wSq7jjJ~RSIoozwfME4MR2KIAhTMlMTAxkEQv2BpVFadM8ujADKh2~X7aWUMWx1pgOIlbgJuuneFiXv6jZi2xZ1SC~eSQpJa5aZEIqsVta4eqm7xu0FzYiT4A0omaxdf-a-JT5-rielTfzFHOmnKB3Wh8G7qBoGN588K3-mgVA-uP88kbT6E-MA-KdaUDmt9KlsTYhllIv5Wcp6eng__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The surface-mass density weighted [Fe/H] distribution (MDF) at 3 radii for profiles fit to the low $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations. The distribution shown is marginalized in age across all our age bins. The coloured bands give the 95 per cent uncertainty ranges, where uncertainties are dominated by those on the fitted density profiles. The mean [Fe/H] is lower at greater R. Qualitatively, the skew of the MDF's changes with R, such that the innermost R has a tail going to low [Fe/H], and the outermost R has a tail going to high [Fe/H].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig14.jpeg?Expires=1716465206&Signature=kDbdU4TN-SalVjhexLIArAM4ZjfEiyKfSz7aynmQBfcYBJ3Vq2iIGAj70vU1LrEKirCamkTMrGBoS1UoSO622E1Z1XIy0XD7Ft6t8YpCflDUgpXApRx-ljlz6mNMayKbGfemievABw6avg0yW3QfGoE4M0JjLFMOejN8xguxbtp4S1HfRZBnKackfWhvLdstvwdZmm5bsK6mf2C4IjkFTT1CZc6pX21VGvoAS7pv1kHFY0FUrOGiLYFqOmTHMOSp2p5baAgpTx~58A~wX4F4F2Vgpuu6ynd9WPvfwaAgSyOL0bhc0tkGgBLTUC4-f2~XpVwPWmVX-18b8CUXkWzATQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![The behaviour of Rpeak with age and [Fe/H] for the low $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations. The high $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations are better fit by single exponentials, and so Rpeak is not an informative diagnostic of these populations. The coloured lines and bands give the surface-mass density weighted mean and standard deviation within an age or [Fe/H] bin. The mean Rpeak does not vary significantly with age, whereas it shows a clear decrease with [Fe/H]. However, the dispersion in Rpeak does increase with age for low $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations. High $\mathrm{[ \alpha \mathrm{/Fe]}}$ populations show a slight increasing trend for increasing age and [Fe/H], albeit at low significance.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774fig15.jpeg?Expires=1716465206&Signature=P8Sbv7lzVf1Uw7v~vW3n37HWMK59CngZl2jFxgWgt7SeEUx-B-avkiZ70~TYLZQjhECZLla51prY32awVRjNbZDx4jpRh7W~-ihaL9rKviDV4RpytIHVF5LVpEm5skoaA18TKdMGDhAt3C7bOitRHiSWp-lw9w6S0cKoyFUhY8jpjnCixz-Vboz3jJkM9IGJmUxKwi194GBYXkv2MfdP3BfTi~DiBuSTXbb~9gVRRwjMABqSj85KLkLZLd1qx4onW8~o4nLz4C3AOK7O2lSCKZqlVj~RBc~PyvzVBu39we7-jLyy41KnYrlX5RpXetb8mPhgIOQuFv84rH~4Kzbzpw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Comparison between the best-fitting models and the APOGEE data for mono-age, mono-[Fe/H] populations in the low $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsample. The grey histogram shows the distance modulus distribution of the APOGEE data for the mono-age, mono-[Fe/H] bin indicated by the ([Fe/H] [dex], age [Gyr]) coordinate given in each panel. The coloured curves show the distance modulus distribution found when the best-fitting broken exponential (black) and single exponential (red) density model is run through the effective selection function. It is clear that the broken exponential density model provides a qualitatively better fit to the data in all cases.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774figa1.jpeg?Expires=1716465206&Signature=Km-Lp0UDxDZJvyLJEcuQn1TG2A6qivNad5O2lXPPrahrsnjudzPupAMW40PDFjDA5ZV4Qnw8iU9op9RmeK-mQ6mFPVKy4idg7BhCe5kC6nUxlNdPCxV43EKaxkf8gj5O6296sENai~nJFymmtkz4si127MlDVMkEjLSwbGVWngT0lxH5GeYV9Z6wtICJLY4-Ueupiuwd~8Oa8Md7HaD-jrYbS2bZk4lEIT3ALdURsyiuK9g~9xUvNdbzexKadcLvLPZlcEQp3AQhle54A-h63Rm1VnT6weDqSr3IbGotX2qnvs-J3fiyAIQKOwRuyjqSKzUkT0M8ExUivt9WHgaFNw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
![Comparison between the best-fitting models and the APOGEE data for mono-age, mono-[Fe/H] populations in the high $\mathrm{[ \alpha \mathrm{/Fe]}}$ subsample. The grey histogram shows the distance modulus distribution of the APOGEE data for the mono-age, mono-[Fe/H] bin indicated by the ([Fe/H] [dex], age [Gyr]) coordinate given in each panel. The coloured curves show the distance modulus distribution found when the best-fitting broken exponential (black) and single exponential (red) density model is run through the effective selection function. In many cases the red and black curves are indistinguishable (only red is seen), or very similar. In cases where the black and red curves are different, the red curve provides a qualitatively better fit. Bins with less than 30 stars (which we disregard for the majority of the analysis) are hatched out.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/471/3/10.1093_mnras_stx1774/1/m_stx1774figa2.jpeg?Expires=1716465206&Signature=C5u8rXkGrlYz1QlBqwnd22wGtlJoFgtR~ZKMdEXyVBpDZAxUvbYsGKl7b5ZbpjRraao-fH1gi7jLQ9Yd1AUvEsGZSKYaKoLzExkXSSvCXGJS~C-PZU3L1ajSmV3aGvc9ETFgJCEoOTpnZV8OGfMSoy33JM-3l7ash4wQb36eOtoYipPdIbirv4Ab32CwE6WnxIbU1AtJD-JFgUWRgtLh~0VqmFOyV05UDxJYPMTMBDKmFJh-YiW2hGZXAtl478hZLtFD2dWkDstfok6kGWVd0l3XFZ79ilvRnA9c5Hn2n1xLT5-Req37Fa833k2D3XA2EzYLqH1NpJz8c6myx1z6xQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)