-
PDF
- Split View
-
Views
-
Cite
Cite
Niels G. Becker, Agus Salim, Christopher W. Kelman, Analysis of a potential trigger of an acute illness, Biostatistics, Volume 7, Issue 1, January 2006, Pages 16–28, https://doi.org/10.1093/biostatistics/kxi037
Close - Share Icon Share
Abstract
Sometimes certain short-term risk exposures are postulated to act as a trigger for the onset of a specific acute illness. When the incidence of the illness is low it is desirable to investigate this possible association using only data on cases detected during a specific observation period. Here we propose an analysis for such a study based on a model expressed in terms of the probability that the exposure triggers the illness and a random delay from a triggered illness until its diagnosis. Both the natural hazard rate for the illness and the probability that the exposure triggers the illness are assumed to be small and possibly dependent on age and covariates such as sex and duration or severity of the exposure. The method of analysis is illustrated with a study of the association between long flights and hospitalization for venous thromboembolism.
1 INTRODUCTION
A study of the association between air travel and onset of venous thromboembolism (VTE) by Kelman et al. (2003) and Becker et al. (2004) analyzes data on cases only, using a model that temporarily enhances the hazard rate for VTE following each flight. Their analysis has the attraction of being robust with respect to any constant predisposition to VTE that individuals might have and being straightforward to implement via likelihood inferences. The approach extends one proposed in Feldman (1993), by allowing for aging during the course of the observation period, and is contained in the very general formulation of Farrington (1995). Here we propose an alternative analysis that has an additional advantage. It is based on a model whose parameters are more directly related to the characteristics of major interest in such studies, which assists when formulating parameters appropriately in terms of covariates and with the interpretation of results.
The type of study considered has a wide range of applications, so it is useful to describe the approach in general terms. We are concerned with episodes of an adverse health event (illness) that may occur at any time. Its hazard rate at any point in time is assumed to be small. The illness is possibly triggered by a specified short-term risk exposure, such as an episode of strenuous exercise, a trauma event, long-haul air travel, or exposure to air pollution. To provide the opportunity to assess the possible association of onset of the illness with the exposure we assume that the illness is acute, by which we mean that its onset occurs relatively rapidly (within days or a few weeks of being ‘triggered’). It also needs to be clearly identifiable by an agreed clinical investigation. Adverse health effects that have been investigated by the type of study envisaged here include myocardial infarction, injuries, adverse drug events, and death; see Mittleman et al. (1993, 1995, 1999), Muller et al. (1996), Petridou et al. (1998), Roberts et al. (1995), Vinson et al. (1995), Barbone et al. (1998), Farrington (2004), Lee & Schwartz (1999), Neas et al. (1999), and Maclure and Mittleman (2000).
The form of the data, the model formulation, and the likelihood function are presented in Section 2. An application to the Western Australian linked-data study of the association between air travel and VTE is given in Section 3. It illustrates an analysis based on the present model and has some new features, including estimation of the probability that VTE was induced by air travel as a function of the time since the most recent flight and age. This is followed, in Section 4, by a comparison of the present model formulation with that used in earlier analyses.
2 DATA, MODEL, AND LIKELIHOOD FUNCTION
Suppose cases of illness occurring in a window of time [0, τ] are identified from hospital records, for example, and for each of these cases one is able to determine their history of transient risk exposures over the same interval, as well as values of covariates such as age and sex.
Let Ti be the time from the beginning of the observation period until the first onset of illness for an individual labeled i. The illness may have been triggered by a transient risk exposure or be a consequence of natural causes, by which we mean a cause not related to the specified risk exposure. The Ti will have different distributions because individuals have different risk exposure patterns and individuals may have inherent differences.
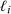 exposures in [0, τ], at times
exposures in [0, τ], at times 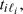 , where these are ordered from smallest to largest. For convenience, we define
, where these are ordered from smallest to largest. For convenience, we define 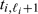 to be τ. Let Wij be an indicator of the event that the exposure at tij triggers the illness, with Pr(Wij = 1) = πij = 1 − Pr(Wij = 0). An illness triggered at time tij is followed by a random delay from this trigger until diagnosis of the illness. These random delays are assumed to be independently and identically distributed, with density function f and distribution function F. The distribution of Ti can now be described by
to be τ. Let Wij be an indicator of the event that the exposure at tij triggers the illness, with Pr(Wij = 1) = πij = 1 − Pr(Wij = 0). An illness triggered at time tij is followed by a random delay from this trigger until diagnosis of the illness. These random delays are assumed to be independently and identically distributed, with density function f and distribution function F. The distribution of Ti can now be described by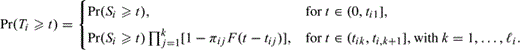
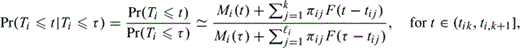
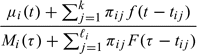
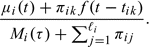
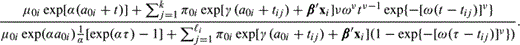
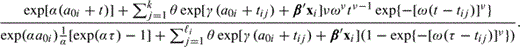
A major goal in this kind of study is to weigh the evidence that θ is positive, which implies that the risk exposure does trigger the illness. A positive value for α indicates that the baseline hazard function for the illness increases with age. The values of γ and
The above derivation of the likelihood contribution from data on individual i assumes that there was no transient risk exposure just prior to the start of the observation period [0, τ]. In applications such risk exposures are rare, but some adjustment to the expression is needed when they do occur. To accommodate such exposures it is convenient if data on the exposure history begins a little prior to the period [0, τ].
Note from (2.4) that πij depends on covariate xi. To explain why μi(t) of (2.3) do not depend on covariate xi, consider a one-dimensional covariate x that does not change over time. By looking at the likelihood function we see that multiplicative terms exp(βπx) and exp(βμx) in πij and μi(t), respectively, give the same likelihood as a model with multiplicative terms exp [(βπ−βμ)x] and 1 in πij and μi(t), respectively. In other words, we can only estimate the difference in the coefficients from this kind of data. In contrast, the coefficients α and γ of age can be estimated separately because age is a time-dependent covariate.
The model for the analysis would need to be enhanced if we wished to include other triggers of the illness that are also observed over the observation period. Potential triggers of the illness that are not observed can be accommodated by assuming them to be part of the underlying natural hazard. However, our parameter estimates could become biased if such triggers are correlated with the observed trigger of interest.
3 APPLICATION: IS AIR TRAVEL A TRIGGER OF VTE?
VTE arises from the formation of blood clots in a peripheral vein. These clots may have locally obstructive effects (deep vein thrombosis, DVT) or may migrate to the heart and lungs (pulmonary embolism, PE). PE occurs in about 40% of VTE episodes and has a fatality rate of about 2%. Onset of VTE in the ambulant population is rare, implying a low baseline hazard rate per individual and making it costly and time consuming to conduct cohort studies. A study of the association of air travel and VTE is therefore well suited to the type of analysis described above. Linked data available for individuals in Western Australia, see Kelman et al. (2003), are well suited to this study because their hospital records are of excellent quality and international travel to and from Perth, Western Australia, involves a long flight.
3.1 The data
Let [0, τ] be the time interval from the start of 1981 to the end of 1999. A total of 13 184 distinct patients were admitted to Western Australian hospitals with a diagnosis of VTE during that period. Individuals from this data set were probabilistically, and confidentially, matched with those in records of the Australian Department of Immigration, Multicultural, and Indigenous Affairs on 4.8 million flight arrivals by Australian citizens during that period. The sensitivity for matching flight arrivals to individuals on the hospital admission list was set to ensure a low false-match rate. Individuals with a history of international flights who were not Australian citizens were excluded from the study, because flight histories and incidence of VTE episodes are likely to be incomplete for these individuals. This left 2279 Australian citizens who had both a hospital admission for VTE and at least one arrival flight in the period 1981–1999. It also left 8197 Australian citizens who had no overseas travel records during this period.
The total time spent overseas by Australian travellers is assumed to be small compared with the observation period of 19 years. As Australian records are unlikely to contain information on VTE episodes that occurred to individuals while overseas, only an arrival flight is counted as a risk exposure.
The data on the 2279 Australian travellers were analyzed by Kelman et al. (2003) to provide evidence of an association between air travel and VTE, using a model with a transiently enhanced hazard (TEH) function. We refer to this as the TEH model. Becker et al. (2004) showed that it is necessary to allow for aging in the baseline hazard function, to prevent bias in parameter estimates. The analysis presented here differs in four aspects. Firstly, it is based on the Probability-of-Trigger (PoT) model and so provides an alternative analysis, with a focus on parameters that are more directly related to the study aims. Secondly, we attempt to enhance parameter estimation by including data on the 8197 VTE cases without a history of international air travel during the observation period. Data on these cases are informative about α. Thirdly, we explore the effect of different assumptions about the delay distribution on the precision of parameter estimates. Finally, we present results on other quantities of interest, such as estimates of the probability that VTE was induced by air travel as a function of the time since the most recent flight, for travellers of different ages.
3.2 Results
In our discussion we do not include sex as a covariate, because the analysis by Becker et al. (2004) found that the postflight enhancement of the hazard function does not depend on sex, and we found no evidence of an association by using the analysis described here. The covariate age is permitted distinct coefficients in the baseline hazard function and the probability that a flight triggers VTE. The parameters of the model are θ, α, γ, ν, and ω. To facilitate comparison with the previous analyses based on the TEH model we present estimates of the age coefficients in terms of exp(α), the proportionate change in the hazard function for naturally acquired VTE per year of age, and exp(γ), the proportionate change in the probability of flight-induced VTE per year of age.
The set of parameter estimates (a) in Table 1 are based on contributions to the likelihood by 2279 Australian VTE cases with a flight history and 8197 VTE cases without an international flight during the observation period. It is interesting to observe that the estimates of α and γ differ significantly, which suggests that the effect of age on naturally acquired VTE differs from its effect on flight-induced VTE. However, we note that the estimate of exp(α) found by Becker et al. (2004) is 1.063, with 95% confidence interval (1.055, 1.072), which is larger than the estimate 1.041 shown in Table 1. While different models are used in these two analyses, the interpretation of α is the same and the reason for the significant difference deserves investigation.
Parameter estimates, with 95% confidence intervals, for the PoT model
Parameter . | Estimates (a) . | Estimates (b) . | Estimates (c) . |
|---|---|---|---|
. | Including nontravellers . | Travellers only . | Travellers only (γ = α) . |
| θ | 19.8 (9.4, 30.3) | 19.8 (9.0, 30.6) | 45.6 (15.0, 76.0) |
| exp(α) | 1.041 (1.036, 1.046) | 1.063 (1.049, 1.078) | 1.063 (1.053, 1.074) |
| exp(γ) | 1.060 (1.055, 1.065) | 1.081 (1.066, 1.096) | [equal to exp(α)] |
| ν | 1.00 (0.86, 1.15) | 1.02 (0.87, 1.17) | 1.09 (0.45, 1.72) |
| ω | 0.100 (0.066, 0.206) | 0.100 (0.065, 0.210) | 0.119 (0.073, 0.320) |
Parameter . | Estimates (a) . | Estimates (b) . | Estimates (c) . |
|---|---|---|---|
. | Including nontravellers . | Travellers only . | Travellers only (γ = α) . |
| θ | 19.8 (9.4, 30.3) | 19.8 (9.0, 30.6) | 45.6 (15.0, 76.0) |
| exp(α) | 1.041 (1.036, 1.046) | 1.063 (1.049, 1.078) | 1.063 (1.053, 1.074) |
| exp(γ) | 1.060 (1.055, 1.065) | 1.081 (1.066, 1.096) | [equal to exp(α)] |
| ν | 1.00 (0.86, 1.15) | 1.02 (0.87, 1.17) | 1.09 (0.45, 1.72) |
| ω | 0.100 (0.066, 0.206) | 0.100 (0.065, 0.210) | 0.119 (0.073, 0.320) |
Parameter estimates, with 95% confidence intervals, for the PoT model
Parameter . | Estimates (a) . | Estimates (b) . | Estimates (c) . |
|---|---|---|---|
. | Including nontravellers . | Travellers only . | Travellers only (γ = α) . |
| θ | 19.8 (9.4, 30.3) | 19.8 (9.0, 30.6) | 45.6 (15.0, 76.0) |
| exp(α) | 1.041 (1.036, 1.046) | 1.063 (1.049, 1.078) | 1.063 (1.053, 1.074) |
| exp(γ) | 1.060 (1.055, 1.065) | 1.081 (1.066, 1.096) | [equal to exp(α)] |
| ν | 1.00 (0.86, 1.15) | 1.02 (0.87, 1.17) | 1.09 (0.45, 1.72) |
| ω | 0.100 (0.066, 0.206) | 0.100 (0.065, 0.210) | 0.119 (0.073, 0.320) |
Parameter . | Estimates (a) . | Estimates (b) . | Estimates (c) . |
|---|---|---|---|
. | Including nontravellers . | Travellers only . | Travellers only (γ = α) . |
| θ | 19.8 (9.4, 30.3) | 19.8 (9.0, 30.6) | 45.6 (15.0, 76.0) |
| exp(α) | 1.041 (1.036, 1.046) | 1.063 (1.049, 1.078) | 1.063 (1.053, 1.074) |
| exp(γ) | 1.060 (1.055, 1.065) | 1.081 (1.066, 1.096) | [equal to exp(α)] |
| ν | 1.00 (0.86, 1.15) | 1.02 (0.87, 1.17) | 1.09 (0.45, 1.72) |
| ω | 0.100 (0.066, 0.206) | 0.100 (0.065, 0.210) | 0.119 (0.073, 0.320) |
A major difference between the two analyses is that data on 8197 nontravellers are included in the present analysis, specifically to improve the precision of the estimate of α. The lower estimate obtained after including nontravellers suggests that there is a difference between travellers and nontravellers. To explore this possibility we allowed the value of α to differ for these two groups. Under this expanded model, data on nontravellers do not contribute to the estimation of the α for travellers, nor do they contribute to the estimation of γ, ν, and ω. The set of parameter estimates (b) in Table 1 is obtained using only data on the 2279 travellers. The estimate of 1.063 obtained for exp(α) is in good agreement with that found by Becker et al. (2004). In contrast, the estimate of exp(α) obtained from the data on nontravellers (not shown in Table 1) is 1.035, with 95% confidence interval (1.029, 1.040), which is significantly lower. This means that our attempt to enhance the precision of parameter estimates by including data on nontravellers has not succeeded. Instead, we found that the rate of increase with age in the hazard function for naturally acquired VTE is lower among nontravellers. Plausible reasons for this difference deserve investigation, but we will not pursue this here.
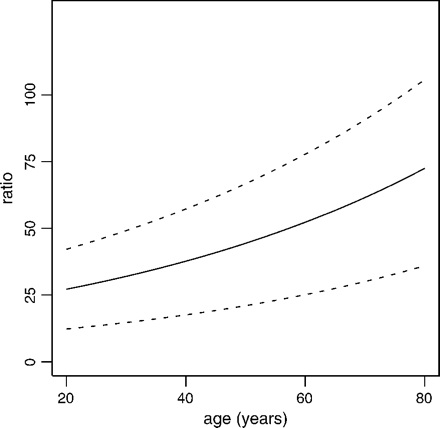
The parameter θ is of major interest in this study. For its interpretation it is useful to remember that θ exp[(γ − α)at] is the ratio of the probability of acquiring VTE from a flight to the probability of naturally acquired VTE on any given day for someone aged at years at time t. Therefore, θ corresponds to this ratio for an individual aged ‘zero’. The fact that the estimate of θ is significantly larger than zero supports the hypothesis that long flights trigger some VTE hospitalizations, but the value 19.8 of the estimate does not, by itself, reflect the size of the triggering effect. In this fitted model, the size of the effect depends appreciably on age as is seen by the estimate of θ exp[(γ − α)at] being 28.4 for someone aged 20 years and 83.6 for someone aged 80 years. Figure 1 shows the estimate of θ exp[(γ − α)at] as a function of age at, with 95% confidence bands computed by the 2.5th and 97.5th percentiles of 1000 bootstrap samples of
Ratio of probability of flight-induced and naturally occurring VTE across age with 95% confidence bands.
The Weibull distribution (2.5) describes the time from a flight-induced blood clot until hospitalization for VTE in this model. We have assumed that this distribution does not depend on age. With values of parameters ν and ω given by estimates (b) of Table 1, this delay distribution has 50th, 90th, and 95th percentiles of 7.0, 22.7, and 29.5 days, respectively.
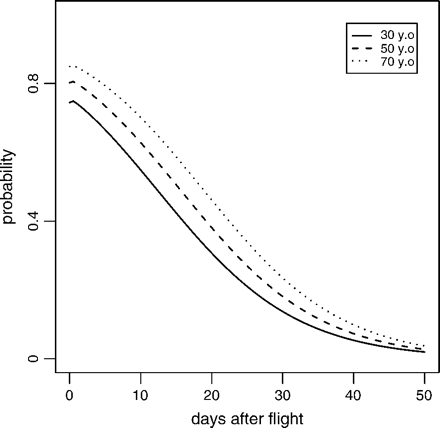
Probability that the VTE was induced by air travel, as a function of the time since the most recent flight.
After allowing for the dependence of the baseline hazard rate on age, Becker et al. (2004) found that age does not significantly affect the proportionate enhancement in the postflight hazard rate. For the specific PoT model fitted here, this conclusion corresponds to γ = α. Inspection of the confidence intervals for exp(α) and exp(γ) suggests that γ = α is plausible under the present analysis. The maximum likelihood estimates (c) of Table 1 correspond to the model with γ set equal to α, again using only data on Australian travellers. As the likelihood ratio (LR) test statistic for the hypothesis γ = α is 1.2 on 1 degree of freedom (df), the hypothesis can be accepted. The estimate of exp(α) is now virtually the same as its estimate under the corresponding TEH model. The estimate of ω is larger under model (c) so that the 50th, 90th, and 95th percentiles of the distribution of the time from a flight-induced blood clot until hospitalization for VTE are reduced to 6.0, 18.1, and 23.1 days, respectively.
A dramatically different estimate of θ is found under the reduced model (c). This arises because θ exp[(γ − α)at], the ratio of the probability of acquiring VTE from a flight to the probability of naturally acquired VTE on any given day for someone aged at, no longer depends on age when γ = α and the interpretation of θ becomes the common ratio across all ages. This value of θ probably best reflects the true risk of acquiring VTE from a long flight. It is estimated that an individual is about 45 times as likely to acquire a blood clot, leading to hospitalization, on the day of a long flight when compared to a day that is flight-free. The confidence interval for θ is (15.0, 76.0), which is very wide. However, even the lower confidence bound of 15 represents a very substantial enhancement in risk.
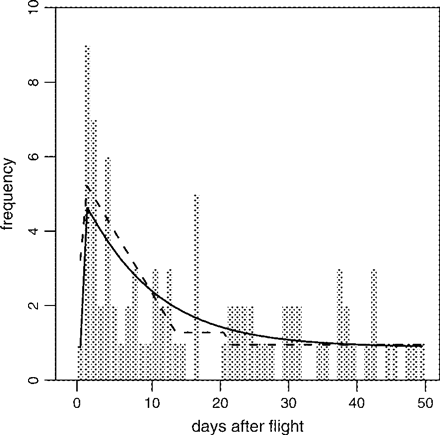
Observed and fitted frequency distributions of VTE hospitalization over the 50 days following a flight.
The other parameter estimates, when the discrete distribution (3.7) is used instead of the Weibull distribution, are given in Table 2. We see that they are very similar to the corresponding estimates in Table 1, when taking their precision (as reflected by the width of each confidence interval) into account. Furthermore, the hypothesis γ = α is also accepted under this model (LR test statistic of 1.0 on 1 df). A noteworthy feature is that by restricting the permissible range of the delay U, one obtains narrower interval estimates, particularly for θ under the model with γ = α. The LR statistic for the hypothesis p = 0 is 0.4 on 1 df, which suggests that a delay distribution with all of its probability mass in the first two weeks after the flight is plausible. This is in accordance with the result under the TEH model, that there is no significant evidence of an increased hazard function for hospitalization beyond the first two weeks after a flight. The similarity of the parameter estimates shown in Tables 1 and 2 suggests that they are robust with respect to the choice of delay distribution used in the analysis.
Parameter estimates when the delay has discrete distribution(3.7)
Parameter . | Model with α and γ distinct . | . | Model with α = γ . | . | ||
|---|---|---|---|---|---|---|
. | Estimate . | 95% confidence interval . | Estimate . | 95% confidence interval . | ||
| θ | 19.8 | (11.0, 28.6) | 38.5 | (21.3, 55.7) | ||
| exp(α) | 1.064 | (1.049, 1.078) | 1.064 | (1.053, 1.074) | ||
| exp(γ) | 1.077 | (1.068, 1.086) | [equal to exp(α)] | |||
Parameter . | Model with α and γ distinct . | . | Model with α = γ . | . | ||
|---|---|---|---|---|---|---|
. | Estimate . | 95% confidence interval . | Estimate . | 95% confidence interval . | ||
| θ | 19.8 | (11.0, 28.6) | 38.5 | (21.3, 55.7) | ||
| exp(α) | 1.064 | (1.049, 1.078) | 1.064 | (1.053, 1.074) | ||
| exp(γ) | 1.077 | (1.068, 1.086) | [equal to exp(α)] | |||
Parameter estimates when the delay has discrete distribution(3.7)
Parameter . | Model with α and γ distinct . | . | Model with α = γ . | . | ||
|---|---|---|---|---|---|---|
. | Estimate . | 95% confidence interval . | Estimate . | 95% confidence interval . | ||
| θ | 19.8 | (11.0, 28.6) | 38.5 | (21.3, 55.7) | ||
| exp(α) | 1.064 | (1.049, 1.078) | 1.064 | (1.053, 1.074) | ||
| exp(γ) | 1.077 | (1.068, 1.086) | [equal to exp(α)] | |||
Parameter . | Model with α and γ distinct . | . | Model with α = γ . | . | ||
|---|---|---|---|---|---|---|
. | Estimate . | 95% confidence interval . | Estimate . | 95% confidence interval . | ||
| θ | 19.8 | (11.0, 28.6) | 38.5 | (21.3, 55.7) | ||
| exp(α) | 1.064 | (1.049, 1.078) | 1.064 | (1.053, 1.074) | ||
| exp(γ) | 1.077 | (1.068, 1.086) | [equal to exp(α)] | |||
3.3 Discussion
In Table 1 of Becker et al. (2004) the association between international flights and VTE is quantified by enhancing the hazard function for hospitalization by a factor of 4.03 for each of the first 7.5 days following an international flight and by a factor of 2.32 for each of the next 7 days. Here this association is expressed by the estimate
In epidemiological terms, the estimated relative risk
The PoT model allows individuals to have inherent predisposition to VTE, as long as it affects the hazard rate for naturally acquired VTE and the probability that exposure triggers VTE proportionately, i.e. π0i/μ0i = θ does not depend on i. More general forms of predisposition can be allowed for by use of random effects or mixed models, i.e. letting some or all of θ, α, and γ be random variables. For example, we might adopt a frailty model where θ varies across individuals, which could be implemented by use of a hierarchical likelihood approach, see Lee and Nelder (1996) and Ha et al. (2001).
The fact that the method gives sensible results, with a precision that is of practical value, when the delay distribution does not have a restricted range is noteworthy. However, it is clear from the application that a restriction on the range of possible delays can greatly improve precision of estimates. Hence, such a restriction should be made when there is objective external evidence that the restriction is meaningful.
The analysis presented here is based on the time from the start of the observation period until hospitalization for VTE, discarding (for each individual) the time remaining until the end of the observation period. This is not likely to be a significant loss in information because VTE is a rare condition and additional episodes of VTE are infrequent. Among the 2279 Australian travellers there were 86 who had a second episode. There are two potential ways to incorporate data on the part of the observation period remaining, after removing 6 months to allow for a period of therapy with anticoagulants following the first VTE. One approach is to restrict attention to the 86 individuals with a second episode, conditioned on the fact that they had a VTE hospitalization in the remaining observation period and utilize data on the time until the second VTE in the manner described above. A second approach is to view the time until the second VTE episode or the end of the observation period, as a survival time and apply standard survival analysis techniques. Survival times are censored by the end of the observation period. No conditioning is required because the condition that there must be a VTE episode in the observation period has been met by the first VTE.
4 COMPARISON WITH THE TEH MODEL
It is useful to compare the model proposed here, referred to as the PoT model, with that used in the analysis by Becker et al. (2004), referred to as the TEH model.
4.1 Hazard Functions
One way to compare the two models is to determine what the PoT model implies about the hazard function for Ti, and compare the hazard functions. We make this comparison with a simple illustrative example, to avoid complicated expressions.
4.2 Interpretation of Results
We now explain why parameter estimates of the PoT model tend to enable questions of interest in such studies to be addressed more directly.
The PoT model separates the risk of the exposure and the delay until diagnosis quite clearly. In contrast, to assess the risk of the exposure from a fitted TEH model one needs to make use of both the magnitude of the postexposure enhancement to the hazard function for onset and the duration of the enhancement. The distribution of the delay until diagnosis also depends on the ‘shape’ of the enhancement to the hazard function for onset. A simple illustrative example helps to clarify this. Suppose that every individual in the study has only one exposure during the observation period and each of these occurs at the same time t′. The variable delay until diagnosis translates the spike of triggers at t′ to a smoothed bump for the incidence of diagnosis. The TEH model uses the hazard function to describe this smoothed incidence. In other words, the TEH model is a direct description of the convolution and to get at the risk and the delay distribution one needs to ‘deconvolve’ this description.
For another illustration of the more direct interpretation of the PoT description, suppose that the hazard function for naturally occurring illness increases with age, e.g. μ(t) = μ0 exp[α(a0 + t)]. Assume that occurrences of exposure-triggered illness do not depend on age. The PoT model captures this naturally by γ = 0. In contrast, the TEH model needs a negative value for its βA parameter, to compensate for the fact that μ(t) increases with age. A correct interpretation of this negative βA requires an adjustment for the value of α.
The application in Section 3 uses at, the age at time t, as covariate. As a result, θ is the ratio of the probability of acquiring VTE from a flight to the probability of naturally acquired VTE on any given day for someone aged ‘zero’. By using
Here we have taken the distribution f, for the delay until diagnosis, to be common to all cases. One may need to allow f to depend on patient characteristics, such as age and distance residing from health services. This can be done more naturally in the PoT model because f enters its formulation quite explicitly.
4.3 The predisposition factor
We now take a closer look at the assumption π0i = θμ0i, made in Section 2. Consider πij, the probability that an exposure at time tij triggers an illness. In practice, the exposure is often not instantaneous, but occurs over a short time interval. For example, an international flight might last for half of one day. Let the hazard rate for the exposure-induced trigger of the illness be ηi(u) for individual i, where u is the time from the start of the transient exposure period. The probability that one transient exposure triggers the illness is then
Funding from Australian National Health and Medical Research Council grant 268015 is gratefully acknowledged. Data was supplied by the Health Department of Western Australia and the Department of Immigration and Multicultural Affairs. The original project was funded by the Department of Transport and Regional Affairs.
References
BARBONE, F., MCMAHON, A. D., DAVEY, P. G., MORRIS, A. D., REID, I. C., MCDEVITT, D. G. AND MCDONALD, T. M. (
BECKER, N. G., LI, Z. AND KELMAN, C. W. (
FARRINGTON, C. P. (
FARRINGTON, C. P. (
FELDMAN, U. (
HA, I. D., LEE, Y. AND SONG, J.-K. (
KELMAN, C. W., KORTT, M. A., BECKER, N. G., LI, Z., MATHEWS, J. D., GUEST, C. S. AND HOLMAN, C. D. J. (
LEE, Y. AND NELDER, J. A. (
LEE, J. T. AND SCHWARTZ, J. (
MACLURE, M. AND MITTLEMAN, M. A. (
MITTLEMAN, M. A., MACLURE, M., SHERWOOD, J. B., MULRY, R. P., TOFLER, G. H., JACOBS, S. C., FRIEDMAN, R., BENSON, H. AND MULLER, J. E. (
MITTLEMAN, M. A., MACLURE, M., TOFLER, G. H., SHERWOOD, J. B., GOLDBERG, R. J. AND MULLER, J. E. (
MITTLEMAN, M. A., MINTZER, D., MACLURE, M., TOFLER, G. H., SHERWOOD, J. B. AND MULLER, J. E. (
MULLER, J. E., MITTLEMAN, M. A., MACLURE, M., SHERWOOD, J. B. AND TOFLER, G. H. (
NEAS, L. M., SCHWARTZ, J. AND DOCKERY, D. (
PETRIDOU, E., MITTLEMAN, M. A., TROHANIS, D., DESSYPRIS, N., KARPATHIOS, T. AND TRICHOPOULOS, D. (
ROBERTS, I., MARSHALL, R. AND LEE-JOE, T. (