Search
Close
Search
Advanced Search
Search Menu

Abstract

Understanding the universal accretion history of dark matter haloes is the first step towards determining the origin of their structure. We use the extended Press–Schechter formalism to derive the halo mass accretion history from the growth rate of initial density perturbations. We show that the halo mass history is well described by an exponential function of redshift in the high-redshift regime. However, in the low-redshift regime the mass history follows a power law because the growth of density perturbations is halted in the dark energy dominated era due to the accelerated expansion of the Universe. We provide an analytic model that follows the expression |${M(z)=M_{0}(1+z)^{af(M_{0})}{\rm e}^{-f(M_{0})z}}$|⁠, where M0 = M(z = 0), a depends on cosmology and f(M0) depends only on the linear matter power spectrum. The analytic model does not rely on calibration against numerical simulations and is suitable for any cosmology. We compare our model with the latest empirical models for the mass accretion history in the literature and find very good agreement. We provide numerical routines for the model online (available at https://bitbucket.org/astroduff/commah).

methods: analytical, galaxies: haloes, cosmology: theory

1 INTRODUCTION

Throughout the last decade, there have been many attempts to quantify halo mass accretion histories using catalogues of haloes from numerical simulations (Wechsler et al. 2002; McBride, Fakhouri & Ma 2009; Wang & White 2009; Fakhouri, Ma & Boylan-Kolchin 2010; Genel et al. 2010; Faucher-Giguère, Kereš & Ma 2011; van de Voort et al. 2011; Benson et al. 2012; Johansson 2013; Behroozi, Wechsler & Conroy 2013; Wu et al. 2013). Wechsler et al. (2002) characterized the mass history of haloes more massive than 1012 M⊙ at z = 0 using a one-parameter exponential form eβz. In their work, Wechsler et al. (2002) limited their analysis to the build-up of clusters through progenitors already larger than the Milky Way halo. Similarly, McBride et al. (2009) limited their analysis to massive haloes and found that a large fraction were better fitted when an additional factor of (1 + z)α was added to the Wechsler et al. (2002) exponential parametrization, yielding a mass history of the form M ∝ (1 + z)αeβz. Wong & Taylor (2012) investigated whether the mass history can be described by a single parameter function or whether more variables are required. They utilized principal component analysis and found that despite the fact that the McBride et al. (2009) two-parameter formula presents an excellent fit to halo mass histories, the parameters α and β are not a natural choice of variables as they are strongly correlated. Recently, van den Bosch et al. (2014) studied halo mass histories extracted from N-body simulations and semi-analytical merger trees. However, so far no universal and physically motivated model of a universal halo mass history function has been provided.

An alternative method to interpret the complex numerical results and to unravel the physics behind halo mass growth, is the extended Press–Schechter (EPS) formalism. EPS theory provides a framework that allows us to connect the halo mass accretion history to the initial density perturbations. Neistein, van den Bosch & Dekel (2006) showed in their work that it is possible to create halo mass histories directly from EPS formalism by deriving a useful analytic approximation for the average halo mass growth. In this work, we aim to provide a physical explanation for the ‘shape’ of the halo mass history using the EPS theory and the analytic formulation of Neistein et al. (2006). The resulting model for the halo mass history, which is suitable for any cosmology, depends mainly on the linear power spectrum.

This paper is organized as follows. We show in Section 2 that the halo mass history is naturally described by a power law and an exponential as originally suggested from fits to cosmological simulation data by McBride et al. (2009). We then provide a simple analytic model based on the EPS formalism and compare it to the latest empirical halo mass history models from the literature. Finally, we provide a summary of formulae and discuss our main findings in Section 3.

In a companion paper, Correa et al. (2015a, hereafter Paper II), we explore the relation between the structure of the inner dark matter halo and halo mass history using a suite of cosmological simulations. We provide a semi-analytic model for halo mass history that combines analytic relations for the concentration and formation time with fits to simulations, to relate halo structure to the mass accretion history. This semi-analytic model has the functional form, M = M0(1 + z)αeβz, where the parameters α and β are directly correlated with the dark matter halo concentration. Finally, in a forthcoming paper (Correa et al. 2015b, hereafter Paper III), we combine the semi-analytic model of halo mass history with the analytic model described in Section 2.3 of this paper to predict the concentration–mass relation and its dependence on cosmology.

2 ANALYTIC MODEL FOR THE HALO MASS HISTORY

In order to provide a physical motivation for the ‘shape’ of the halo mass history, we begin in Section 2.1 with an analytic study of dark matter halo growth using the EPS formalism (Bond et al. 1991; Lacey & Cole 1993). In Section 2.2, we show that the halo mass history is well described by an exponential at high redshift, and by a power law at low redshift. In Section 2.3, we then adopt the power-law exponential form and use it to provide a simple analytic model for halo mass histories. Finally, we compare our results with the latest models of halo mass history from the literature in Section 2.4.

2.1 Theoretical background of EPS theory

The EPS formalism is an extension of the Press–Schechter (PS) formalism (Press & Schechter 1974), which provides an approximate description of the statistics of merger trees using a stochastic process. The EPS formalism has been widely used in algorithms for the construction of random realizations of merger trees (Kauffmann & White 1993; Benson, Kamionkowski & Hassani 2005; Cole et al. 2008; Neistein & Dekel 2008).

In the standard model of cosmology, the structures observed today are assumed to have grown from small initial density perturbations due to the action of gravity. The initial density contrast, defined as |$\delta ({{\boldsymbol x}},t)=\rho ({{\boldsymbol x}},t)/\bar{\rho }-1$| (with |$\rho ({{\boldsymbol x}},t)$| density field and |$\bar{\rho }$| mean density), is considered to be a Gaussian random field completely specified by the power spectrum P(k), where k is a spatial frequency. In the linear regime (δ ≪ 1), the perturbations determined by |$\delta ({{\boldsymbol x}},t)$| evolve as |$\delta ({{\boldsymbol x}},t)=\delta _{0}({{\boldsymbol x}})D(t)$|⁠, where |$\delta _{0}({{\boldsymbol x}})$| is the density contrast field linearly extrapolated to the present time and D(t) is the linear growth factor. According to the spherical collapse model, once |$\delta ({{\boldsymbol x}},t)$| exceeds a critical threshold |$\delta _{\rm {crit}}^{0}\simeq 1.69$| (with a weak dependence on redshift and cosmology) the perturbation starts to collapse. Regions that have collapsed to form a virialized object at redshift z are then associated with those regions for which
\begin{equation} \delta _{0}>\delta _{\rm c}(z)\equiv \frac{\delta _{\rm {crit}}^{0}}{D(z)}=\frac{1.686\Omega _{\rm m}(z)^{0.0055}}{D(z)}. \end{equation}
(1)
Here |$\Omega _{\rm m}(z)=\Omega _{\rm m,0}(1+z)^{3}H_{0}^{2}/H(z)^{2}$|⁠, H(z) = H0[Ωm, 0(1 + z)3 + ΩΛ, 0]1/2 and the linear growth factor D(z) is computed by performing the integral
\begin{equation} D(z)\propto H(z)\int _{z}^{\infty }\frac{1+z^{\prime }}{H(z^{\prime })^{3}}{\rm d}z^{\prime }, \end{equation}
(2)
where D(z) is normalized to unity at the present day. The collapsed regions are assigned masses by smoothing the density contrast δ0 with a spatial window function. In what follows, instead of using the halo mass as the independent variable, we adopt the variance of the smoothed density field, σ2(M).
The EPS model developed by Bond et al. (1991) is based on the excursion set formalism. For each collapsed region one constructs random ‘trajectories’ of the linear density contrast δ(M) as a function of the variance σ2(M). Defining
\begin{equation} \omega \equiv \delta _{\rm c}(z)\quad {\rm {and}}\quad S\equiv \sigma ^{2}(M), \end{equation}
(3)
we use ω and S to label redshift and mass, respectively. If the initial density field is a Gaussian random field smoothed under a sharp k-space filter, increasing S (corresponding to a decreased in the filter mass M) results in δ(M) starting to wander away from zero, executing a random walk. The fraction of matter in collapsed objects in the mass interval M, M + dM at redshift z is associated with the fraction of trajectories that have their first upcrossing through the barrier ω in the interval S, S + dS, which is given by (Bond et al. 1991; Bower 1991; Lacey & Cole 1993)
\begin{equation} f(S,\omega ){\rm d}S=\frac{1}{\sqrt{2\pi }}\frac{\omega }{S^{3/2}}\rm {exp}\left[-\frac{\omega ^{2}}{2S}\right]dS, \end{equation}
(4)
where S is defined as
\begin{equation} S(M) = \frac{1}{2\pi ^{2}}\int _{0}^{\infty }P(k)\hat{W}^{2}(k;R)k^{2}{\rm d}k. \end{equation}
(5)
Here P(k) is the linear power spectrum and |$\hat{W}(k;R)$| is the Fourier transform of a top hat window function. The probability function in equation (4) yields the PS mass function and gives the probability for a change ΔS in a time-step Δω, since for random walks the upcrossing probabilities are a Markov process (i.e. are independent of the path taken). The analytic function given by equation (4) provides the basis for the construction of merger trees. Neistein et al. (2006) derived a differential equation for the average halo mass history over an ensemble of merger trees from the EPS formalism. Defining MEPS(z) to be the mass of the most massive halo (main progenitor), along the main branch of the merger tree, as a function of redshift, they obtained the differential equation (see derivation in Appendix A)
\begin{eqnarray} \frac{{\rm d}M_{\rm {EPS}}}{{\rm d}z}&=& \sqrt{\frac{2}{\pi }}\frac{M_{\rm {EPS}}}{\sqrt{S_{q}-S}}\frac{1.686}{D(z)^{2}}\frac{{\rm d}D(z)}{{\rm d}z}, \end{eqnarray}
(6)
where Sq = S(MEPS(z)/q) and S = S(MEPS(z)). The value of q needs to be obtained empirically so that MEPS reproduces halo mass histories from cosmological simulations. Neistein et al. (2006) showed that the uncertainty of q is an intrinsic property of EPS theory, where different algorithms for constructing merger trees may correspond to different values of q.

2.2 Mass accretion in the high- and low-z regimes

In this section, we analyse how the evolution of MEPS(z) given by equation (6) is governed by the growth factor. We provide two practical approximations for the growth factor in the high- and low-redshift regimes and investigate the ‘shape’ of MEPS(z) in these regimes by integrating equation (6).

In addition to the redshift dependence of the growth factor (D(z)), in equation (6) an extra redshift dependence is introduced through the quantity [Sq − S]−1/2 = [S(M(z)/q) − S(M(z))]−1/2. Before integrating equation (6), we calculate how the value of [S(M(z)/q) − S(M(z))]−1/2 changes with redshift to find a suitable first-order approximation to simplify the calculations.

We replace S = σ2 and approximate σ ≈ Mγ, where γ = −0.063 for M ≤ 1012 M⊙ and γ = −0.21 for M > 1012 M⊙, to obtain
\begin{eqnarray} \frac{[S(M(z)/q)-S(M(z))]^{-1/2}}{[S(M_{0}/q)-S(M_{0})]^{-1/2}} &=&\left(\frac{M(z)}{M_{0}}\right)^{-\gamma }, \end{eqnarray}
(7)
where M0 = M(z = 0).

Given the weak dependence on mass in the right part of equation (9), we simplify the expression [S(M(z)/q) − S(M(z))]−1/2 in our analysis using the approximation [S(M(z)/q) − S(M(z))]−1/2 ≈ [S(M0/q) − S(M0)]−1/2. It is important to note that as the MEPS(z) evolution (given by equation 6) is only governed by the growth factor in equation (2), we find that in the latter part of the accretion history, where most mass is accreted, the approximation [S(M(z)/q) − S(M(z))]−1/2 ≈ [S(M0/q) − S(M0)]−1/2, will carry an ∼5 per cent error for M(z) ≤ 1012 M⊙ and 15 per cent error for M(z) > 1012 M⊙. Earlier in the accretion history, the errors may be as large as ∼20 per cent and 40 per cent for M(z) ≤ 1012 M⊙ and M(z) > 1012 M⊙, respectively. We demonstrate in Section 2.4 that these errors do not affect the final M(z) model, which we show provides very good agreement with simulation-based mass history models from the literature.

The growth factor can be approximated with high accuracy by
\begin{equation} D(z) = \left\lbrace \begin{array}{cl}\frac{1.34}{1+z} & {\rm {if}}\quad z \gg 1,\\ \\ \frac{1}{\ln (e+1.5z)} & {\rm {if}}\quad z \ll 1, \end{array} \right. \end{equation}
(8)
for all cosmologies. Fig. 1 shows the growth factor as given by equation (2) (solid dark blue line), together with the approximations in the high- and low-redshift regimes (solid green and purple lines, respectively). The high-redshift approximation for D(z) is an exact solution for an Einstein-de Sitter (EdS) cosmology (ΩΛ = 0). However, the growth rate slows down in the cosmological constant dominated phase, so that linear perturbations grow faster in an EdS universe.
Figure 1.
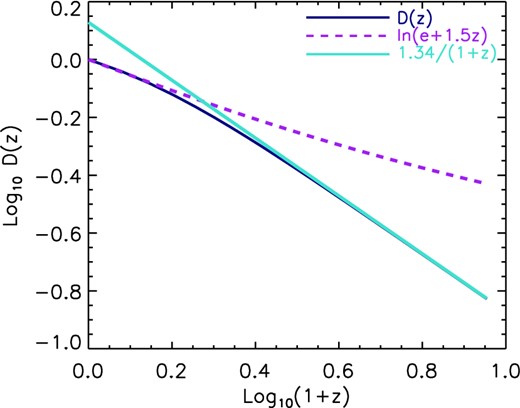
Linear growth factor against redshift. The dark blue solid line shows the growth factor obtained by performing the integral given by equation (2). The purple dashed line corresponds to the low-redshift approximation in equation (8). Similarly, the green solid line shows the approximation of the growth factor in the high-redshift regime.
Open in new tabDownload slide

Linear growth factor against redshift. The dark blue solid line shows the growth factor obtained by performing the integral given by equation (2). The purple dashed line corresponds to the low-redshift approximation in equation (8). Similarly, the green solid line shows the approximation of the growth factor in the high-redshift regime.

We can estimate MEPS(z) in the high- and low-redshift regimes by substituting the two expressions from equation (8) into equation (6). In the high-redshift regime (where z ≫ 1),
\begin{eqnarray} \frac{{\rm d}M_{\rm {EPS}}}{M_{\rm {EPS}}} &=& \sqrt{\frac{2}{\pi }}\frac{1}{\sqrt{S_{q}-S}}\frac{1.686}{D(z)^{2}}\frac{{\rm d}D(z)}{{\rm d}z}\mathrm{d}z,\nonumber \\ \frac{{\rm d}M_{\rm {EPS}}}{M_{\rm {EPS}}} & = & -f(M_{0})\mathrm{d}z, \end{eqnarray}
(9)
where |$f(M_{0})=1/\sqrt{S(M_{0}/q)-S(M_{0})}$| is a function of halo mass. Integrating this last equation, we obtain
\begin{eqnarray} M_{\rm {EPS}}(z) &=& M_{0}{\rm e}^{-f(M_{0})z}\quad {\rm {at}} \quad z\gg 1. \end{eqnarray}
(10)
Thus, we conclude that the halo mass history is well described by an exponential (M(z) ∼ eβz), as suggested by Wechsler et al. (2002) in the high-redshift regime. In the low-redshift regime, from equation (9) and the bottom part of equation (8), we find
\begin{eqnarray*} \nonumber \frac{{\rm d}M_{\rm {EPS}}}{M_{\rm {EPS}}} & = & -\frac{1.34}{1.8+z}f(M_{0})\mathrm{d}z.\nonumber \end{eqnarray*}
Integrating the above expression yields
\begin{equation} M_{\rm {EPS}}(z)= M_{0}(1+0.5z)^{-1.34f(M_{0})}\quad {\rm {at}} \quad z\ll 1. \end{equation}
(11)

Therefore, in the low-redshift regime, a power law (M(z) ∼ (1 + z)α) is necessary because the growth of density perturbations is halted in the dark energy dominated era due to the accelerated expansion of the Universe.

2.3 Analytic mass accretion history model based on the EPS formalism

In this subsection, we provide an analytic model for the halo mass history based on the EPS formalism. This model is not calibrated against numerical simulations and allows an exploration of the physical processes involved in the halo mass growth. Based on our analysis above, we begin by assuming that the halo mass history is well described by the simple form
\begin{equation} M(z)=M_{0}(1+z)^{\alpha }{\rm e}^{\beta z}. \end{equation}
(12)
The presence of the function S(M0) in both the high-redshift exponential and the low-redshift power law explains the correlation between α and β found by Wong & Taylor (2012). We estimate the relation between α, β and S(M0) by replacing MEPS(z) in equation (6) with the above expression. Evaluating at z = 0 we obtain
\begin{equation} \alpha +\beta = 1.686(2/\pi )^{1/2}f(M_{0})\frac{{\rm d}D}{{\rm d}z}|_{z=0}. \end{equation}
(13)
Assuming β follows the relation with S(M0) shown in equation (10) for the high-z regime we find
\begin{eqnarray} \beta &=& -f(M_{0}), \end{eqnarray}
(14)
\begin{eqnarray} \alpha &=& af(M_{0}), \end{eqnarray}
(15)
with |$a=\left[1.686(2/\pi )^{1/2}\frac{{\rm d}D}{{\rm d}z}|_{z=0}+1\right]$|⁠. The above equations introduce a halo mass history model directly derived from the EPS theory, where the parameters α and β are related through the variance of the smoothed density field, S(M0). The quantity q is a free parameter which can be determined by adding an extra equation that restricts the model. We do this by defining the halo formation redshift, |$\tilde{z}_{\rm f}$|⁠, as the redshift, where |$M(\tilde{z}_{\rm f})=M_{0}/q$|⁠. From equation (12) we obtain
\begin{equation} \frac{1}{q} = (1+\tilde{z}_{\rm f})^{af(M_{0})}{\rm e}^{-f(M_{0})\tilde{z}_{\rm f}}, \end{equation}
(16)
where |$f(M_{0})=1/\sqrt{S(M_{0}/q)-S(M_{0})}$|⁠.
The general relation between formation time and q was introduced by Lacey & Cole (1993), using the expression
\begin{equation} M(z)=M_{0}\left[1-{\rm {erf}}\left(\frac{\delta _{\rm c}(z)-\delta _{\rm c}(0)}{\sqrt{2(S(M_{0}/q)-S(M_{0})}}\right)\right], \end{equation}
(17)
which describes the average mass of the main progenitors in the EPS merger tree. We use equation (17) to evaluate the halo mass at |$\tilde{z}_{\rm f}$| and find the distribution of formation times. We follow the approach of Lacey & Cole (1993) and find
\begin{equation} \delta _{\rm c}(\tilde{z}_{\rm f})=\delta _{\rm c}(0)+\sqrt{2}f^{-1}(M_{0}){\rm {erf}}^{-1}(1-1/q). \end{equation}
(18)
We solve equations (16) and (18) and find q and |$\tilde{z}_{\rm f}$| for various halo masses. We then fit the q–M0 and |$\tilde{z}_{\rm f}{\rm -}q$| relations using a second-order polynomial in log10M for |$\tilde{z}_{\rm f}$|⁠, and obtain the following set of equations that describe the halo mass history,
\begin{eqnarray} M(z)&=&M_{0}(1+z)^{af(M_{0})}{\rm e}^{-f(M_{0})z}, \end{eqnarray}
(19)
\begin{eqnarray} a&=&\left[1.686(2/\pi )^{1/2}\frac{{\rm d}D}{{\rm d}z}|_{z=0}+1\right], \end{eqnarray}
(20)
\begin{eqnarray} f(M_{0})&=&1/\sqrt{S(M_{0}/q)-S(M_{0})}, \end{eqnarray}
(21)
\begin{eqnarray} q&=&4.137\tilde{z}^{-0.9476}_{{\rm f}}, \end{eqnarray}
(22)
\begin{eqnarray} \tilde{z}_{\rm f}&=&-0.0064(\log _{10}M_{0})^{2}+0.0237(\log _{10}M_{0})\nonumber \\ && +\,1.8837. \end{eqnarray}
(23)
The equations that relate q, |$\tilde{z}_{\rm f}$| and M0 are calculated assuming the WMAP5 cosmology, but work for others cosmologies1 because the halo mass histories are mainly driven by the change in σ8 and Ωm. We reiterate that unlike previous models based on EPS theory (e.g. van den Bosch 2002), the analytic model specified in the above equations was not calibrated against any simulation data.

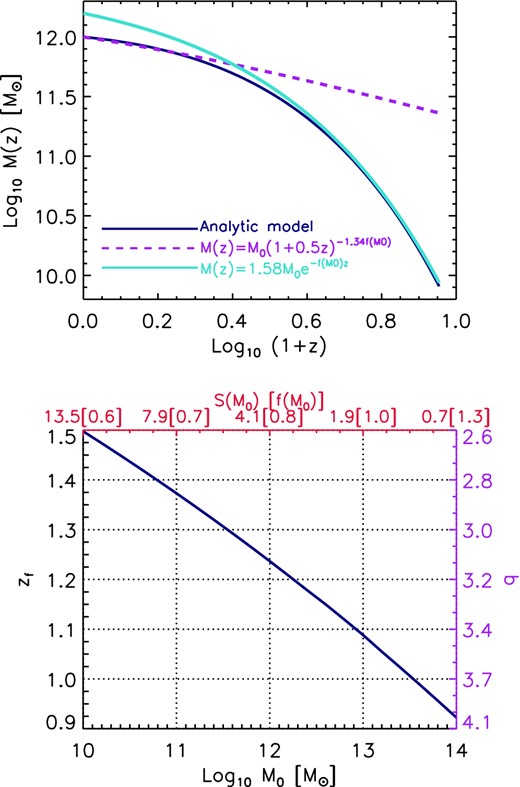
The top panel of Fig. 2 shows a comparison between the analytic model given by equations (19)–(23) (blue solid line), and the limiting case for the halo mass histories given by equation (11) for the low-redshift regime (purple dashed line) and by equation (10) for the high-redshift regime (green solid line). In the last case, we renormalized the mass history curve to match that given by the analytic model at z = 7. This figure demonstrates how exponential growth dominates the mass history at high redshift, and power-law growth dominates at low redshift, as concluded in the previous section.

Figure 2.
Top panel: comparison between halo mass histories predicted by the analytic model $M(z)=M_{0}(1+z)^{af(M_{0})}{\rm e}^{-f(M_{0})z}$, given by equations (19)–(23) (blue solid line), and the approximated halo mass histories given by equation (11), for the low-redshift regime (purple dashed line), and by equation (10), for the high-redshift regime (green solid line). Bottom panel: formation redshift against halo mass. Here the formation redshifts were obtained by solving equations (16) and (18). The right Y-axis shows the values of ‘q’ obtained when calculating the formation redshift, whereas the top X-axis shows the variance of the smoothed density field of a region that encloses the mass indicated by the bottom X-axis. The values of the function $f(M_{0})=1/\sqrt{S(M_{0}/q)-S(M_{0})}$ are shown in brackets.
Open in new tabDownload slide

Top panel: comparison between halo mass histories predicted by the analytic model |$M(z)=M_{0}(1+z)^{af(M_{0})}{\rm e}^{-f(M_{0})z}$|⁠, given by equations (19)–(23) (blue solid line), and the approximated halo mass histories given by equation (11), for the low-redshift regime (purple dashed line), and by equation (10), for the high-redshift regime (green solid line). Bottom panel: formation redshift against halo mass. Here the formation redshifts were obtained by solving equations (16) and (18). The right Y-axis shows the values of ‘q’ obtained when calculating the formation redshift, whereas the top X-axis shows the variance of the smoothed density field of a region that encloses the mass indicated by the bottom X-axis. The values of the function |$f(M_{0})=1/\sqrt{S(M_{0}/q)-S(M_{0})}$| are shown in brackets.

The bottom panel of Fig. 2 shows the formation time obtained from equations (16) and (18), as a function of halo mass. As expected, larger mass haloes form later. The right Y-axis shows the values of q obtained when calculating formation time, whereas the top X-axis shows the variance of the smoothed density field of a region that encloses the mass indicated by the bottom X-axis. The values of the function |$f(M_{0})=1/\sqrt{S(M_{0}/q)-S(M_{0})}$| are included in brackets. As can be seen from this figure, the larger the halo mass, the lower the variance S(M0), the larger f(M0), and so the larger the factor in the exponential that makes the halo mass halt its rapid growth at low redshift. For example, a 1014 M⊙ halo has a mass history mostly characterized by an exponential growth (⁠|${\sim } {\rm e}^{-f(M_{0})z}$|⁠) until redshift z = 1/f(M0) = 0.7, whereas a 1010 M⊙ halo only has an exponential growth until redshift z = 1.6. Note, however, that our analytic model is not limited to the halo mass ranges shown in the bottom panel of Fig. 2, it can be extended to any halo masses and redshifts and the q–M0 and |$\tilde{z}_{\rm f}{\rm -}M_{0}$| relations still hold.

In addition to the halo mass history, it is possible to calculate the accretion rate of a halo at a particular redshift. In order to do that we differentiate equation (12) with respect to time and replace dz/dt by −H0[Ωm(1 + z)5 + ΩΛ(1 + z)2]1/2 to obtain
\begin{eqnarray*} \nonumber \frac{{\rm d}M(z)}{{\rm d}t} &=& 71.6{\rm {M}}_{\odot }{\rm {yr}}^{-1} \left(\frac{M(z)}{10^{12}\,\rm {M}_{\odot }}\right)\left(\frac{h}{0.7}\right) \\ \nonumber &&\times \ f(M_{0})[(1+z)-a][\Omega _{\rm {m}}(1+z)^{3}+\Omega _{\Lambda }]^{1/2}, \end{eqnarray*}
where a is given by equation (20) and f(M0) is given by equation (21). Note that the above formula will give the accretion rate at redshift z of a halo that has mass M0 at redshift z = 0, and mass M(z) at redshift z.

The physical relation derived between the parameters describing the exponential and power-law behaviour implies that a single parameter accretion history formula should be seen in numerical simulations. In Paper II, we investigate the α and β parameter dependence in more detail, and we determine the intrinsic relation (which cannot be explored under the EPS formalism) between halo assembly history and inner halo structure.

2.4 Comparison with previous studies

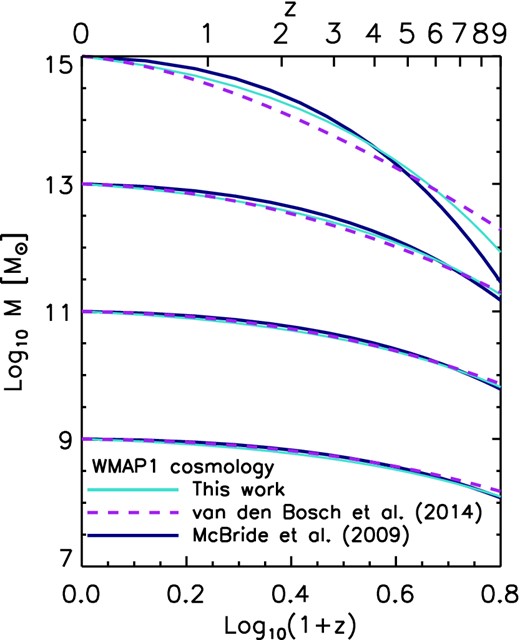
In this section, we briefly describe the simulation-based halo mass history models presented in van den Bosch et al. (2014, hereafter vdB14) and McBride et al. (2009, hereafter MB09), and contrast them with our analytic model given by equations (19)–(23). Fig. 3 shows a comparison of our mass history model (turquoise solid lines) to the models of vdB14 (purple dashed lines) and MB09 (dark blue solid lines). vdB14 used the mass histories from the Bolshoi simulation (Klypin, Trujillo-Gomez & Primack 2011) and extrapolated them below the resolution limit using EPS merger trees. They then used a semi-analytic model to transform the average or median mass accretion history for a halo of a particular mass taken from the Bolshoi simulation, to another cosmology, via a simple transformation of the time coordinate. Using their publicly available code, we calculated the mass histories of 109, 1011, 1013 and 1015 M⊙ haloes for the WMAP1 cosmology. We find good agreement between our model and vbB14 for all halo masses. The main difference occurs for the mass histories of high-mass haloes (M0 > 1013 M⊙), where vdB14 seems to underpredict the mass growth above z = 4 by a factor of ∼1.2. In addition, vdB14 compared their model to those of Zhao et al. (2009) and Giocoli, Tormen & Sheth (2012), and found that both works predict smaller halo mass growth at z > 1.5.

Figure 3.
Comparison of halo mass history models. The analytic model presented in this work (turquoise solid lines) is compared with the median mass history obtained from the Bolshoi simulation and merger trees from vdB14 (purple dashed lines) and the best-fitting relations from the Millennium simulation from MB09 (dark blue solid lines). The comparisons are shown for four halo masses and for consistency with MB09 we assumed in our model and in the vdB14 model the WMAP1 cosmology.
Open in new tabDownload slide

Comparison of halo mass history models. The analytic model presented in this work (turquoise solid lines) is compared with the median mass history obtained from the Bolshoi simulation and merger trees from vdB14 (purple dashed lines) and the best-fitting relations from the Millennium simulation from MB09 (dark blue solid lines). The comparisons are shown for four halo masses and for consistency with MB09 we assumed in our model and in the vdB14 model the WMAP1 cosmology.

We also compare our model to the MB09 mass history curves. MB09 used the Millennium simulation (Springel 2005) and separated their halo sample into categories depending on the ‘shape’ of the mass histories, from late-time growth that is steeper than exponential to shallow growth. We find that the fitting function that best matches our results is from their type IV category. We find good agreement with the MB09 formula.

Fig. 3 demonstrates that the physically motivated analytic model presented in this work yields mass histories that are in good agreement with the results obtained from numerical simulations. However, in contrast to the models based on fits to simulation results, our analytic model can be extrapolated to very low masses and is suitable for any cosmology.

3 SUMMARY AND CONCLUSION

In this work, we have demonstrated how halo mass histories are determined by the initial power spectrum of density fluctuations, and the growth factor. We found that the halo mass history is well described by an exponential (M(z) ∼ eβz, as suggested by Wechsler et al. 2002) in the high-redshift regime, but that the accretion slows to a power law at low redshift (M(z) ∼ (1 + z)α) because the growth of density perturbations is halted in the dark-energy-dominated era due to the accelerated expansion of the Universe. The resulting expression,
\begin{equation} M(z)= M_{0}(1+z)^{\alpha }{\rm e}^{\beta z}, \end{equation}
(24)
accurately captures all halo mass histories (Fig. 3). Adopting this expression, we provided an analytic mass history model based on the EPS formalism, in which the parameters α and β are related to the power spectrum by
\begin{eqnarray*} \nonumber \beta &=& -f(M_{0}),\\ \nonumber \alpha &=& \left[1.686(2/\pi )^{1/2}\frac{{\rm d}D}{{\rm d}z}|_{z=0}+1\right]f(M_{0}),\\ \nonumber f(M_{0}) &=& [S(M_{0}/q)-S(M_{0})]^{-1/2},\\ \nonumber S(M) &=& \frac{1}{2\pi ^{2}}\int _{0}^{\infty }P(k)\hat{W}^{2}(k;R)k^{2}{\rm d}k,\nonumber \end{eqnarray*}
where D is the linear growth factor, P is the linear power spectrum and q is related to the total halo mass as
\begin{eqnarray*} \nonumber q &=& 4.137\tilde{z}^{-0.9476}_{f},\\ \nonumber \tilde{z}_{\rm f} &=& -0.0064(\log _{10}M_{0})^{2}+0.0237(\log _{10}M_{0})\\ \nonumber && +\,1.8837. \end{eqnarray*}

We found very good agreement between the halo mass histories predicted by our analytic model and published fits to simulation results (Fig. 3). The reader may find a step-by-step description on how to implement both models in Appendix B, as well as numerical routines online.2

The relation of the parameters α and β with the linear power spectrum explains the correlation between the dark matter halo concentration and the linear rms fluctuation of the primordial density field that was previously noted in numerical simulations (Prada et al. 2012; Diemer & Kravtsov 2015). We show it in Paper II, where we derive a semi-analytic model for the halo mass history that relates halo structure to the mass accretion history. In that work, we combine the semi-analytic model with the analytic model presented here to establish the physical link between halo concentrations and the initial density perturbation field. Finally, in Paper III we combine the analytic and semi-analytic description to predict the concentration–mass relation of haloes and its dependence on cosmology.

We are grateful to the referee Aaron Ludlow for fruitful comments that substantially improved the original manuscript. CAC acknowledges the support of the 2013 John Hodgson Scholarship and the hospitality of Leiden Observatory. JSBW is supported by an Australian Research Council Laureate Fellowship. JS acknowledges support by the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement 278594-GasAroundGalaxies. We are grateful to the OWLS team for their help with the simulations.

1

We verified that the MAHs predicted by equations (19)–(23) are in excellent agreement with the simulations for the WMAP1/3/9 and Planck cosmologies.

2

Available at https://bitbucket.org/astroduff/commah.

REFERENCES

Behroozi
P. S.
, 
Wechsler
R. H.
, 
Conroy
C.
. , 
ApJ
, 
2013
, vol. 
770
 pg. 
57
 
Crossref
Search ADS
 
Benson
A. J.
, 
Kamionkowski
M.
, 
Hassani
S. H.
. , 
MNRAS
, 
2005
, vol. 
357
 pg. 
847
 
Crossref
Search ADS
 
Benson
A. J.
, 
Borgani
S.
, 
De Lucia
G.
, 
Boylan-Kolchin
M.
, 
Monaco
P.
. , 
MNRAS
, 
2012
, vol. 
419
 pg. 
3590
 
Crossref
Search ADS
 
Bond
J. R.
, 
Cole
S.
, 
Efstathiou
G.
, 
Kaiser
N.
. , 
ApJ
, 
1991
, vol. 
379
 pg. 
440
 
Crossref
Search ADS
 
Bower
R. G.
. , 
MNRAS
, 
1991
, vol. 
248
 pg. 
332
 
Crossref
Search ADS
 
Cole
S.
, 
Helly
J.
, 
Frenk
C. S.
, 
Parkinson
H.
. , 
MNRAS
, 
2008
, vol. 
383
 pg. 
546
 
Crossref
Search ADS
 
Correa
C. A.
, 
Wyithe
J. S. B.
, 
Schaye
J.
, 
Duffy
A. R.
. , 
MNRAS
, 
2015a
, vol. 
450
 pg. 
1521
  
Paper II
Crossref
Search ADS
 
Correa
C. A.
, 
Wyithe
J. S. B.
, 
Schaye
J.
, 
Duffy
A. R.
. , 
2015b
 
preprint (arXiv:1502.00391) (Paper III)
Diemer
B.
, 
Kravtsov
A. V.
. , 
ApJ
, 
2015
, vol. 
799
 pg. 
108
 
Crossref
Search ADS
 
Eisenstein
D. J.
, 
Hu
W.
. , 
ApJ
, 
1998
, vol. 
496
 pg. 
605
 
Crossref
Search ADS
 
Fakhouri
O.
, 
Ma
C.-P.
, 
Boylan-Kolchin
M.
. , 
MNRAS
, 
2010
, vol. 
406
 pg. 
2267
 
Crossref
Search ADS
 
Faucher-Giguère
C.-A.
, 
Kereš
D.
, 
Ma
C.-P.
. , 
MNRAS
, 
2011
, vol. 
417
 pg. 
2982
 
Crossref
Search ADS
 
Genel
S.
, 
Bouché
N.
, 
Naab
T.
, 
Sternberg
A.
, 
Genzel
R.
. , 
ApJ
, 
2010
, vol. 
719
 pg. 
229
 
Crossref
Search ADS
 
Giocoli
C.
, 
Tormen
G.
, 
Sheth
R. K.
. , 
MNRAS
, 
2012
, vol. 
422
 pg. 
185
 
Crossref
Search ADS
 
Johansson
P. H.
. 
Thomas
D.
, 
Pasquali
A.
, 
Ferreras
I.
. , 
Proc. IAU Symp. 295, The Intriguing Life of Massive Galaxies
, 
2013
Cambridge
Cambridge Univ. Press
pg. 
354
 

Google Scholar

OpenURL Placeholder Text

 
Kauffmann
G.
, 
White
S. D. M.
. , 
MNRAS
, 
1993
, vol. 
261
 pg. 
921
 
Crossref
Search ADS
 
Klypin
A. A.
, 
Trujillo-Gomez
S.
, 
Primack
J.
. , 
ApJ
, 
2011
, vol. 
740
 pg. 
102
 
Crossref
Search ADS
 
Lacey
C.
, 
Cole
S.
. , 
MNRAS
, 
1993
, vol. 
262
 pg. 
627
 
Crossref
Search ADS
 
McBride
J.
, 
Fakhouri
O.
, 
Ma
C.-P.
. , 
MNRAS
, 
2009
, vol. 
398
 pg. 
1858
  
MB09
Crossref
Search ADS
 
Neistein
E.
, 
Dekel
A.
. , 
MNRAS
, 
2008
, vol. 
388
 pg. 
1792
 
Crossref
Search ADS
 
Neistein
E.
, 
van den Bosch
F. C.
, 
Dekel
A.
. , 
MNRAS
, 
2006
, vol. 
372
 pg. 
933
 
Crossref
Search ADS
 
Prada
F.
, 
Klypin
A. A.
, 
Cuesta
A. J.
, 
Betancort-Rijo
J. E.
, 
Primack
J.
. , 
MNRAS
, 
2012
, vol. 
423
 pg. 
3018
 
Crossref
Search ADS
 
Press
W. H.
, 
Schechter
P.
. , 
ApJ
, 
1974
, vol. 
187
 pg. 
425
 
Crossref
Search ADS
 
Springel
V.
. , 
MNRAS
, 
2005
, vol. 
364
 pg. 
1105
 
Crossref
Search ADS
 
van de Voort
F.
, 
Schaye
J.
, 
Booth
C. M.
, 
Haas
M. R.
, 
Dalla Vecchia
C.
. , 
MNRAS
, 
2011
, vol. 
414
 pg. 
2458
 
Crossref
Search ADS
 
van den Bosch
F. C.
. , 
MNRAS
, 
2002
, vol. 
331
 pg. 
98
 
Crossref
Search ADS
 
van den Bosch
F. C.
, 
Jiang
F.
, 
Hearin
A.
, 
Campbell
D.
, 
Watson
D.
, 
Padmanabhan
N.
. , 
MNRAS
, 
2014
, vol. 
445
 pg. 
1713
  
vdB14
Crossref
Search ADS
 
Wang
J.
, 
White
S. D. M.
. , 
MNRAS
, 
2009
, vol. 
396
 pg. 
709
 
Crossref
Search ADS
 
Wechsler
R. H.
, 
Bullock
J. S.
, 
Primack
J. R.
, 
Kravtsov
A. V.
, 
Dekel
A.
. , 
ApJ
, 
2002
, vol. 
568
 pg. 
52
 
Crossref
Search ADS
 
Wong
A. W. C.
, 
Taylor
J. E.
. , 
ApJ
, 
2012
, vol. 
757
 pg. 
102
 
Crossref
Search ADS
 
Wu
H.-Y.
, 
Hahn
O.
, 
Wechsler
R. H.
, 
Mao
Y.-Y.
, 
Behroozi
P. S.
. , 
ApJ
, 
2013
, vol. 
763
 pg. 
70
 
Crossref
Search ADS
 
Zhao
D. H.
, 
Jing
Y. P.
, 
Mo
H. J.
, 
Börner
G.
. , 
ApJ
, 
2009
, vol. 
707
 pg. 
354
 
Crossref
Search ADS
 

APPENDIX A: DIFFERENTIAL EQUATION FOR MEPS

To construct the mass history of a given parent halo mass, it is most convenient to begin from the parent halo and go backwards in time following the merger events of the most massive progenitor. We begin by assuming that a halo of mass Mj (corresponding to a mass variance Sj) at time ωj takes a small time-step Δω back in time (note that Δω < 0). At the time ωj + 1 = ωj + Δω, we calculate the average mass of the main progenitor Mj + 1 (Sj + 1) following an excursion set approach and computing the probability for a random walk originating at (Sj, ωj) and executing a first upcrossing of the barrier ωj + 1 at Sj + 1. Hence the probability we want is given by equation (4) upon replacing S by Sj + 1 − Sj and ω by ωj + 1 − ωj. Converting from mass weighting to number weighting, one obtains the average number of progenitors at zj + 1 in the mass interval (Mj + 1, Mj + 1 + dM) which by time zj have merged to form a halo of mass Mj,
\begin{eqnarray} &&{P(M_{j+1},z_{j+1}|M_{j},z_{j})dM_{j+1}=\frac{M_{j}}{M_{j+1}}}\nonumber \\ &&{\quad\times f(S_{j+1},\omega _{j+1}|S_{j},\omega _{j})\left|\frac{{\rm d}S_{j+1}}{{\rm d}M_{j+1}}\right|{\rm d}M_{j+1}.} \end{eqnarray}
(A1)
As a first approximation, we assume that P(Mj + 1, zj + 1|Mj, zj) = 0 for Mj + 1 < Mj/q, so that the main progenitor always has a mass Mj + 1 ≥ Mj/q for a given q value. Therefore, the average mass of the main progenitor can be written as
\begin{equation*} M_{j+1}(z_{j+1})=\int _{M_{j}/q}^{M_{j}}P(M|M_{j},z_{j})M{\rm d}M. \end{equation*}
We then replace P(M|Mj, zj) by equation (A1) and integrate
\begin{equation*} M_{j+1}(z_{j+1})=\int _{M_{j}/q}^{M_{j}}\frac{M_{j}}{M}\frac{1}{\sqrt{2\pi }}\frac{\Delta \omega }{\Delta S^{3/2}}\rm {exp}\left[-\frac{\Delta \omega ^{2}}{2\Delta S}\right]\left|\frac{{\rm d}S}{{\rm d}M}\right|M{\rm d}M, \end{equation*}
where Δω = wj + 1 − wj, that correspond to the redshift interval (zj + 1, zj), and ΔS = S − Sj. Defining u2 = Δω2/2ΔS, the above integral yields
\begin{equation*} M_{j+1}(z_{j+1})=\frac{2}{\sqrt{\pi }}M_{j}\int _{u_{j+1}}^{u_{j}}{\rm e}^{-u^{2}}{\rm d}u, \end{equation*}
here |$u_{j}=\Delta \omega /\sqrt{2(S_{j}-S_{j})}\rightarrow \infty$| and |$u_{j+1}=\Delta \omega /\sqrt{2(S(M_{j}/q)-S_{j})}$|⁠. Therefore, the integral can be written in terms of the error function
\begin{equation} M_{j+1}(z_{j+1})=M_{j}\left[1-\rm {erf}\left(\frac{\Delta \omega }{\sqrt{2S(M_{j}/q)-2S_{j}}}\right)\right]. \end{equation}
(A2)
This equation becomes linear in Δω for small enough Δω, therefore the mass history can be constructed by iterating
\begin{equation*} M_{\rm {EPS}}(\Delta \omega _{i}+\Delta \omega _{j}|M_{0})=M_{\rm {EPS}}(\Delta \omega _{i}|M_{\rm {EPS}}(\Delta \omega _{j}|M_{0})), \end{equation*}
where we term M0 as the mass of the parent halo. Then the rate of change, dMEPS/dω, can be computed as
\begin{eqnarray*} \nonumber \frac{{\rm d}M_{\rm {EPS}}}{{\rm d}\omega } &=& \lim _{\Delta \omega \rightarrow 0}\frac{M_{\rm {EPS}}(\Delta \omega )-M_{0}}{\Delta \omega },\\ \nonumber &=& -M_{0}\lim _{\Delta \omega \rightarrow 0}\frac{1}{\Delta \omega }\rm {erf}\left(\frac{\Delta \omega }{\sqrt{2(S_{q}-S)}}\right), \end{eqnarray*}
with Sq = S(MEPS/q) and S = S(MEPS). Using the fact that |$\lim _{x\rightarrow 0}\rm {erf}(x)\rightarrow 2x/\sqrt{\pi }$|⁠, yields
\begin{equation} \frac{{\rm d}M_{\rm {EPS}}}{{\rm d}\omega }=-\sqrt{\frac{2}{\pi }}\frac{M_{\rm {EPS}}}{\sqrt{S_{q}-S}}. \end{equation}
(A3)
The differential equation for MEPS (equation A3) can be written in terms of redshift by replacing dω = d(δ0/D(z)) (given by equation 1),
\begin{eqnarray} \frac{{\rm d}M_{\rm {EPS}}}{{\rm d}z}&=& -\sqrt{\frac{2}{\pi }}\frac{M_{\rm {EPS}}}{\sqrt{S_{q}-S}}\frac{1.686\Omega _{\rm {m}}(z)^{0.0055}}{D(z)}\nonumber \\ &&\times \left[\frac{0.0055{\rm d}\Omega _{\rm {m}}(z)/{\rm d}z}{\Omega _{\rm {m}}(z)}-\frac{{\rm d}D(z)/\mathrm{d}z}{D(z)}\right]. \end{eqnarray}
(A4)
The above equation simplifies since 0.0055(dΩm(z)/dz)/Ωm(z) ∼ 0 and Ωm(z)0.0055 can well be approximated by 1, then the rate of change gives
\begin{eqnarray} \frac{{\rm d}M_{\rm {EPS}}}{{\rm d}z}&=& \sqrt{\frac{2}{\pi }}\frac{M_{\rm {EPS}}}{\sqrt{S_{q}-S}}\frac{1.686}{D(z)^{2}}\frac{{\rm d}D(z)}{{\rm d}z}. \end{eqnarray}
(A5)

APPENDIX B: Step-by-step guide to compute halo mass histories

B0.1 Analytic model based on EPS

This appendix provides a step-by-step procedure that details how to calculate the halo mass histories using the analytic model presented in Section 2.

  • Calculate the linear power spectrum P(k). In this work, we use the approximation of Eisenstein & Hu (1998).

  • Perform the integral
    \begin{equation} S(R)=\frac{1}{2\pi ^{2}}\int _{0}^{\infty }P(k)\hat{W}^{2}(k;R)k^{2}{\rm d}k, \end{equation}
    (B1)

    where |$\hat{W}^{2}(k;R)$| is the Fourier transform of a top hat window function and R defines S in a sphere of mass M = (4π/3)ρm, 0R3, where ρm, 0 is the mean background density today.

  • Given M0, the halo mass today, calculate the mass history by first obtaining |$\tilde{z}_{\rm f}$|
    \begin{equation} \tilde{z}_{\rm f}=-0.0064(\log _{10}M_{0})^{2}+0.0237(\log _{10}M_{0})+1.8837 \end{equation}
    (B2)
    and
    \begin{equation} q=4.137\tilde{z}^{-0.9476}_{{\rm f}}. \end{equation}
    (B3)
  • Use the parameter q to calculate f(M0), the function that relates the power spectrum to the mass history through the mass variance S,
    \begin{equation} f(M_{0})=1/\sqrt{S(M_{0}/q)-S(M_{0})}. \end{equation}
    (B4)
  • Finally, the mass history can be calculated as follows,
    \begin{eqnarray} M(z)&=&M_{0}(1+z)^{af(M_{0})}{\rm e}^{-f(M_{0})z}, \end{eqnarray}
    (B5)
    \begin{eqnarray} a&=&\left[1.686(2/\pi )^{1/2}\frac{{\rm d}D}{{\rm d}z}|_{z=0}+1\right], \end{eqnarray}
    (B6)
    where dD/dz is the derivative of the linear growth factor, which can be computed by performing the integral
    \begin{equation} D(z)\propto H(z)\int _{z}^{\infty }\frac{1+z^{\prime }}{H(z^{\prime })^{3}}{\rm d}z^{\prime }. \end{equation}
    (B7)
    D(z) is normalized to unity at the present.

The above model is suitable for any adopted cosmology and halo mass range.

© 2015 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides