Search
Close
Search
Advanced Search
Search Menu

Abstract

Annihilating dark matter (DM) models offer promising avenues for future DM detection, in particular via modification of astrophysical signals. However, when modelling such potential signals at high redshift, the emergence of both DM and baryonic structure, as well as the complexities of the energy transfer process, needs to be taken into account. In the following paper, we present a detailed energy deposition code and use this to examine the energy transfer efficiency of annihilating DM at high redshift, including the effects on baryonic structure. We employ the pythia code to model neutralino-like DM candidates and their subsequent annihilation products for a range of masses and annihilation channels. We also compare different density profiles and mass–concentration relations for 105–107 M⊙ haloes at redshifts 20 and 40. For these DM halo and particle models, we show radially dependent ionization and heating curves and compare the deposited energy to the haloes’ gravitational binding energy. We use the ‘filtered’ annihilation spectra escaping the halo to calculate the heating of the circumgalactic medium and show that the mass of the minimal star-forming object is increased by a factor of 2–3 at redshift 20 and 4–5 at redshift 40 for some DM models.

dark ages, reionization, first stars, dark matter

1 INTRODUCTION

The potential impact of annihilating and decaying dark matter (DM) in the context of standard astrophysics has shown itself to be a promising avenue in the exploration of DM phenomenology (Chen & Kamionkowski 2004; Padmanabhan & Finkbeiner 2005; Furlanetto, Oh & Pierpaoli 2006; Slatyer 2013; Valdés et al. 2013; Bertone & Hooper 2016). This is in part because annihilating models are well motivated from a particle physics perspective, often arising naturally within new theoretical frameworks for physics beyond the standard model (Bertone, Hooper & Silk 2005; Bergstrom 2012; Roos 2012), but also because their non-gravitational interactions make them attractive candidates for possible future detection.

Indirect searches for annihilating and decaying DM focus on the detection of the highly energetic annihilation products that maybe used to infer the existence of the parent particles. As any non-gravitational interaction such as annihilation is assumed to be at or around the weak scale, in general a high-density region, such as found at the centre of Milky Way, is required for detectable particle excesses (Prada et al. 2004; Grasso et al. 2009; Cohen et al. 2012).

While the Galactic Centre presents a relatively accessible overdense region of DM, it is also home of one of the most astrophysically rich regions in the Milky Way. This highlights an ongoing complication with these kinds of experiments as they rely on meticulous treatment of the underlying astrophysics in order to disentangle a potential DM signal. More often that underlying physics is not yet fully understood or the signal may even be degenerate with a standard process. Similarly, uncertainty in the underlying DM structure (Mack 2014) makes for further complications, though non-detections from dwarf spheroidal galaxies occupying the Milky Way's subhaloes have been used to constrain the annihilation cross-section for some DM models.

Instead of focusing on a single, dense, and sufficiently near region of DM to detect an excess in the associated annihilation products, another possibility is to look for the potential global impact DM annihilation may have on standard cosmic evolution. One of the most exciting is the potential modification of the 21  cm signal associated with the epoch of reionzation. There are a number of ways in which the additional injected energy from DM annihilation and decay could produce changes including direct heating and ionization of the intergalactic medium (IGM; Evoli, Mesinger & Ferrara 2014; Poulin, Serpico & Lesgourgues 2015; Lopez-Honorez et al. 2016) as well as secondary effects from DM modification of baryonic structure. A number of next-generation radio telescopes such as the Square Kilometre Array (Mellema et al. 2013), Precision Array for Probing the Epoch of Reionization (Pober et al. 2013), and the Low-Frequency Array (Chapman et al. 2012) are preparing to probe the epoch of reionization using the 21  cm signal (Mesinger, Ewall-Wice & Hewitt 2014).

The following work is motivated by the prospect of using global signals such as the 21  cm line of neutral hydrogen or other observables such as galaxy properties to constrain annihilating DM models. One of the pivotal aspects of this is the integration of DM annihilation with standard astrophysical processes, such as star formation and the heating of the IGM, as well as potential complex feedback mechanisms between forming structure and the injected annihilation products. The impact of DM annihilation on individual haloes has previously been discussed in Mapelli & Ripamonti (2007), Spolyar, Freese & Gondolo (2008), Natarajan, Tan & O'Shea (2009), Gondolo et al. (2013) as well as our previous work (Schön et al. 2015, , from here on S15).

In S15, we performed a first-order calculation to gauge the impact of DM annihilation on early structure formation. We employed a simplified energy transfer process based on the medeaii code (Evoli et al. 2012) to cover a wide parameter space and a range of DM halo and particle models. We showed that in small, high-redshift objects, the energy input from DM annihilation over the Hubble time is comparable to the gravitational binding energy of the object. In this paper, we foremost look to update the energy transfer code used in S15 to allow the full evolution of the injected annihilation products, including the secondary particle cascades. The new version of the code also determines the radial distribution of the deposited energy in and outside the halo.

To demonstrate the use of the code, we revisited the halo parameter space from our previous work. This paper is structured in the following manner: Sections 2 and 3 outline the DM halo and particle models employed throughout the work and Section 4 introduces the Monte Carlo code used to calculate the energy transfer in and around the chosen haloes. The ionization and heating curves are calculated, showing the radial distribution of deposited energy within the halo and presented in Section 5 along with the comparison to the haloes’ gravitational binding energy. Section 6 shows how the initial injection spectra of the different annihilation models are changed by the gas component of the halo and how the energy that escapes into the circumgalactic medium (CGM) can heat the surrounding gas sufficiently to increase the mass of the minimal baryonic object for some haloes. The paper concludes with a discussion in Section 7 of results.

Throughout the paper, we take the cosmological parameters to be in keeping with the Planck Collaboration XIII (2016) so that h = 0.71, ΩΛ, 0 = 0.6825, Ωb, 0h2 = 0.022 068, and Ωdm, 0h2 = 0.120 29.

2 DM MODEL

We employ the same effective, self-annihilating, neutralino-like DM particle model as in S15, albeit with an additional 130 MeV, 10 GeV, and 100 GeV particle annihilating directly to an electron/positron pair. A natural choice of cross-section is close to that of the weak interaction as this gives the correct current-day density if DM is assumed to be a thermal relic. In this work, it is assumed that DM is cold and the velocity-averaged annihilation cross-section is taken as constant, regardless of environment. We set the annihilation cross-section for the 130 MeV model annihilating to an electron/positron pair to be 1.0 × 10−28 cm−3 s−1 to be in keeping with the latest DM annihilation limits from cosmic microwave background (CMB) measurements (Madhavacheril, Sehgal & Slatyer 2014; Planck Collaboration XIII 2016). The cross-section for all other mass models is adjusted so that the total annihilation power is the same as that of the 130 MeV model to allow for comparison of the energy transfer efficiency of DM models with different masses and annihilation channels.

2.0.1 Annihilation power

The annihilation power per unit volume of the DM component is then given by
\begin{equation} P_{\text{dm}}(\boldsymbol {x}) = \frac{c^{2}}{m_{\text{dm}}} \langle v \sigma \rangle \rho _{\text{dm}}^{2}(\boldsymbol {x}), \end{equation}
(1)
where mdm is the mass of the DM particle, ρdm is the DM volume density at point |$\boldsymbol {x}$| in the halo, and 〈vσ〉 is the velocity-averaged annihilation cross-section.

2.0.2 Annihilation channels

We consider annihilation via muons, quarks, tau lepton, and W bosons as well as annihilation straight to electron–positron pairs. To implement this, an electron and a positron are collided to produce the immediate annihilation product, where the centre of mass energy of the e− and e+ is used as a proxy for the DM candidate mass. In the case of unstable annihilation products, the particles were further evolved in pythia (Sjostrand, Mrenna & Skands 2006, 2008) until only stable particles remain (see appendix A of S15 for detailed final electron, positron, and photon energy distributions). The different DM annihilation models are summarized in Table 1.

Table 1.

Summary of the different DM annihilation models considered in this paper.

DMmdmAnnihilationCross-section
model(GeV)channel(⁠|$\mathrm{cm^{3}\, \mathrm{s^{-1}}}$|⁠)
DM10.13–100e−10−28 to 7.7 × 10−26
DM25, 20, 50τ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM35, 20, 50μ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM45.5, 20, 50q4.2 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM583, 110W6.4 × 10−26, 8.5 × 10−26
DMmdmAnnihilationCross-section
model(GeV)channel(⁠|$\mathrm{cm^{3}\, \mathrm{s^{-1}}}$|⁠)
DM10.13–100e−10−28 to 7.7 × 10−26
DM25, 20, 50τ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM35, 20, 50μ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM45.5, 20, 50q4.2 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM583, 110W6.4 × 10−26, 8.5 × 10−26
Open in new tab
Table 1.

Summary of the different DM annihilation models considered in this paper.

DMmdmAnnihilationCross-section
model(GeV)channel(⁠|$\mathrm{cm^{3}\, \mathrm{s^{-1}}}$|⁠)
DM10.13–100e−10−28 to 7.7 × 10−26
DM25, 20, 50τ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM35, 20, 50μ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM45.5, 20, 50q4.2 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM583, 110W6.4 × 10−26, 8.5 × 10−26
DMmdmAnnihilationCross-section
model(GeV)channel(⁠|$\mathrm{cm^{3}\, \mathrm{s^{-1}}}$|⁠)
DM10.13–100e−10−28 to 7.7 × 10−26
DM25, 20, 50τ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM35, 20, 50μ3.8 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM45.5, 20, 50q4.2 × 10−27, 1.5 × 10−26, 3.8 × 10−26
DM583, 110W6.4 × 10−26, 8.5 × 10−26
Open in new tab

The annihilation process can also produce a significant fraction of neutrinos. However, as these only interact on the weak scale with the surrounding gas, we assume that they do not contribute in a significant fashion to the energy transfer process and we thus do not consider them further in this work.

3 HALO MODELS

In order to investigate the degree to which DM annihilation transfers energy into the halo and CGM, we require models for the DM and gas distribution within the halo as well as a density profile for the gas immediately surrounding the halo. We note that since we are primarily interested in high-redshift haloes with masses well below the general resolution limit of N-body simulations, there is a considerable degree of uncertainty involved in these models (Mack 2014).

3.1 DM density profiles

The radially dependent density profile of DM haloes has been shown to be well described by a universal profile wholly determined by the mass and redshift of the halo. This profile was first fitted as a broken power law by Navarro, Fenk & White (1996) and consequently named the ‘Navarro–Frenk–White’ profile,
\begin{equation} \rho _{\text{NFW}} = \frac{\rho _{\text{NFW},0}}{\frac{r}{r_{\text{s}}}(1 + \frac{r}{r_{\text{s}}})^{2}}. \end{equation}
(2)
Later work has shown that this fit can further be improved (Merritt et al. 2005, 2006) by the Einasto profile (Einasto 1965)
\begin{equation} \rho _{\text{E}} = \rho _{\text{E},0}\text{e}^{-\frac{2}{\alpha _{e}}[(\frac{r}{r_{\text{s}}})^{\alpha }-1]}. \end{equation}
(3)
Both the NFW and Einasto profile fit haloes with high-density cusps. For comparison, we also include the Burkert profile (Burkert 1995) that has a flat core inwards of the scale-radius rs,
\begin{equation} \rho _{\text{B}} = \frac{\rho _{\text{B},0}}{(1+\frac{r}{r_{\text{s}}})(1+\frac{r^{2}}{r_{\text{s}}^{2}})}, \end{equation}
(4)
where ρNFW, 0, ρE, 0, and ρB, 0 are the appropriate DM density normalization parameters for each profile. For all models,
\begin{equation} r_{\text{s}} = \frac{r_{\text{vir}}}{c}. \end{equation}
(5)
Here rvir is the virial radius defined in the standard manner, where the average density enclosed in a sphere of radius rvir is 200 times the critical density ρcrit. The Einasto profile contains an addition shape parameter αe = 0.17, which is in general only weakly dependent on the mass and redshift of the halo and taken to be a constant.

3.1.1 Mass–concentration relation

The mass–concentration parameter c is a free parameter of the profiles described above, which sets the turn-over of the density gradient. It is of particular interest in DM annihilation calculations because it can significantly enhance the overall power output in individual haloes by increasing the DM density at its core.

The concentration parameter is well described (Comerford & Natarajan 2007; Duffy et al. 2008; Ludlow et al. 2013) for galaxy hosting haloes at low redshifts. However, simply extrapolating these mass–concentration relations to the required masses and redshifts can lead to haloes with extremely dense cores, which in turn could potentially overestimate the DM annihilation signal. The evolution of the mass–concentration parameter for the small masses and high redshifts reviewed in this work is less well constrained (Prada et al. 2012; Dutton & Macciò 2014; van den Bosch et al. 2014; Diemer & Kravtsov 2015). The determination of the behaviour for low-mass haloes in particular is restricted by the mass resolution of N-body simulations. In addition to mass resolution, different equilibrium cuts (Neto et al. 2007) imposed on the respective halo samples could be a further factor contributing to the discrepancies found between the mass–concentration relations cited above. The impact of these unsettled haloes on the mass–concentration relation becomes more pronounced at high redshift where a large fraction of the halo population is not in a relaxed state due to elevated merger rates.

We use the semi-analytic model based on the mass–concentration relation of Correa et al. (2015) that predicts c for redshifts z = 0–20 and masses M/M⊙ = [10−2, 1016]:
\begin{equation} \mathrm{log}_{10}c = \alpha + \beta \mathrm{log}_{10}(M/\mathrm{M}_{{\odot }}) \end{equation}
(6)
\begin{eqnarray*} \alpha &=& 1.226 - 0.1009(1 + z) + 0.003\, 78(1 + z)^{2} \\ \beta &=& 0.008\, 634 - 0.088\, 14(1 + z)^{-0.588\, 16}. \end{eqnarray*}
Fig. 1 shows the mass–concentration relation produced by Correa et al. (2015) at different redshifts (solid coloured lines). In addition, the mass–concentration relation at redshift 7 (Angel et al. 2016) from N-body simulations is shown in comparison by the dashed pink line. The dashed black line shows c extrapolated from the semi-analytic model to redshift 40.
Figure 1.
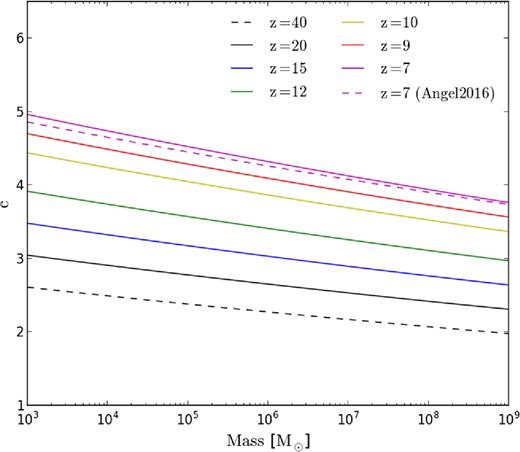
The fiducial mass–concentration relation used in this work. Solid lines show the semi-analytic model from Correa et al. (2015) at various redshifts with the dashed black curve showing an extrapolation to redshift 40. The dashed pink line shows results from Angel et al. (2016) that were extracted from N-body simulations.
Open in new tabDownload slide

The fiducial mass–concentration relation used in this work. Solid lines show the semi-analytic model from Correa et al. (2015) at various redshifts with the dashed black curve showing an extrapolation to redshift 40. The dashed pink line shows results from Angel et al. (2016) that were extracted from N-body simulations.

Lastly, we summarize the different halo models in Table 2. Throughout the paper, the ‘fiducial’ and ‘Burkert’ models refer to haloes with the Correa mass–concentration relation and an Einasto and Burkert density profile, respectively. The ‘high’ and ‘Burkert-high’ models refer to haloes with Einasto and Burkert profiles as well as an increased c parameter, here taken to be double that of the Correa model. The highly concentrated model was chosen to account for the uncertainty in the mass–concentration relation, as well as natural scatter found in the relevant halo population (Angel et al. 2016).

Table 2.

Summary of the different DM halo models considered in this work.

Halo modelMassRedshiftcProfile
log10[M⊙](z)
Fiducial5–720, 40CorreaEinasto
Burkert5–720, 40CorreaBurkert
High5–720, 40Correa × 2Einasto
Burkert-high5–720, 40Correa × 2Burkert
Halo modelMassRedshiftcProfile
log10[M⊙](z)
Fiducial5–720, 40CorreaEinasto
Burkert5–720, 40CorreaBurkert
High5–720, 40Correa × 2Einasto
Burkert-high5–720, 40Correa × 2Burkert
Open in new tab
Table 2.

Summary of the different DM halo models considered in this work.

Halo modelMassRedshiftcProfile
log10[M⊙](z)
Fiducial5–720, 40CorreaEinasto
Burkert5–720, 40CorreaBurkert
High5–720, 40Correa × 2Einasto
Burkert-high5–720, 40Correa × 2Burkert
Halo modelMassRedshiftcProfile
log10[M⊙](z)
Fiducial5–720, 40CorreaEinasto
Burkert5–720, 40CorreaBurkert
High5–720, 40Correa × 2Einasto
Burkert-high5–720, 40Correa × 2Burkert
Open in new tab

3.1.2 Dynamic haloes

At this point, a brief mention should be made about the assumption that the haloes under consideration here are in a static state of equilibrium, and that both the underlying DM structure and the baryonic content of the halo remain unchanged. More realistically, haloes after collapse will grow through a combination of merger events and inflowing gas. At high redshifts especially, the rapid merger rate means that a significant fraction of haloes are not relaxed, and moreover, recovery takes place over a number of dynamical times (Poole et al. 2016).

The disruption of both the DM and gas density distributions associated with mergers could subsequently impact both the DM annihilation power and the absorption efficiency. In addition, self-consistent modelling of the halo incorporating the potential ongoing effects due to the halo self-heating, such as expulsion of gas, is not accounted for. These concerns are anticipated to be included in future work.

3.2 Gas model

3.2.1 Baryonic density distribution within the halo

In S15, the gas component of the halo was assumed to follow that of the DM distribution. We update our gas profile to that of a pseudo-isothermal sphere, as it makes a reasonable first-order approximation for the mass distribution of halo-type objects (Binney & Tremaine 1987) and avoids a divergent core density in the case of the NFW profile,
\begin{equation} \rho _{\text{gas}}(r) = \displaystyle\frac{\rho _{\text{bar},0}}{r_{0}^2 +r^{2}}. \end{equation}
(7)
Here ρbar, 0 gives the appropriate baryon density normalization and |$r_{0}^2 = r_{\text{vir}}/10^4$|⁠. The total baryon fraction of the halo is taken to be fb = 0.15 for all haloes so that |$M_{\text{gas}} = \frac{f_{\text{b}}}{1 - f_{\text{b}}}M_{\text{DM}}$|⁠, where Mgas and MDM are the total gas and DM mass contained in the halo.

3.2.2 Circumgalactic density distribution

The gas density of the CGM gas follows the fit by Dijkstra, Lidz & Wyithe (2007) and Bruns et al. (2012),
\begin{equation} \rho _{\text{CGM}}(r, r_{\text{vir}}) =\left\lbrace \begin{array}{@{}l@{\quad }l@{}}20 \bar{\rho } (r/r_{\text{vir}})^{-1} & r < 10r_{\text{vir}}, \\ \bar{\rho }[1 + \text{exp}(2-r/5r_{\text{vir}})] & r \ge 10r_{\text{vir}},\\ \end{array}\right. \end{equation}
(8)
where |$\bar{\rho }$| is the average gas density of the IGM. We consider haloes at redshifts corresponding to the very onset of star and galaxy formation and assume that the gas in and around the haloes can be treated as neutral and only consisting of hydrogen and helium. As the gas begins to be ionized, the energy deposition would be pushed towards heating as Coulomb interactions become prominent while electro- and photoionization are suppressed.

4 ENERGY TRANSFER CODE

We update the energy transfer code used in S15 to more fully model the paths of the injected particles (as well as the secondary particles created in the subsequent cascades) throughout the halo. In addition, the updated code allows us to record the spatial distribution of the deposited energy in the form of heating, ionization, and Lyman photons as well as keep a record of the energy distribution of the particles that escape the halo.

4.1 Processes

In our treatment of the relevant interaction processes, we closely follow the treatment of Evoli et al. (2012) and Slatyer, Padmanabhan & Finkbeiner (2009).

4.1.1 Electrons and positrons

At high energies, electrons and positrons predominantly lose energy through inverse Compton (IC) scattering off CMB photons (Blumenthal & Gould 1970) while lower energy electrons undergo collisional interaction with the gas atoms. These collisions lead to ionization (Arnaud & Rothenflug 1985; Shah, Elliott & Gilbody 1987; Shah et al. 1988; Kim & Rudd 1994), atomic excitation (Bransden & Noble 1976; Fisher et al. 1997; Stone, Kim & Desclaux 2002; Hirata 2006; Chuzhoy & Shapiro 2007), and Coulomb scattering (Spitzer & Scott 1969; Shull & Steenberg 1985; Furlanetto & Stoever 2010). Recombination (Karzas & Latter 1961) is also included, though subdominant compared to the other processes.

At high energies, positrons behave in the same manner as electrons. At low energies, they also undergo collisional interactions in addition to forming positronium via charge exchange (Heitler 1954; Guessoum, Jean & Gillard 2005).

4.1.2 Photons

In a similar fashion, photons photoionize the surrounding gas (Verner et al. 1996), Compton scatter off free electrons (Heitler 1954; Chen & Kamionkowski 2004), and at high enough energies undergo electron–positron pair production (PP). We here distinguish the cross-section for PP off of the CMB (Agaronyan, Atoyan & Nagapetyan 1987; Ferrigno, Blasi & De Marco 2005), atomic and ionized hydrogen and helium, as well as free electrons (Joseph & Rohrlich 1958; Motz, Olsen & Koch 1969; Zdziarski & Svensson 1989). Photons also undergo photon–photon scattering where the injected photon transfers part of its energy to a CMB photon (Svensson & Zdziarski 1990); however, this process is highly subdominant in the redshift range considered here.

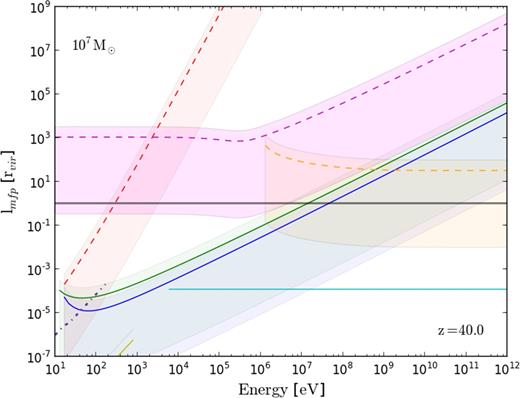
The mean free paths (mfp) at mean gas density for selected processes undergone by injected electrons, positrons, and photons are outlined in Fig. 2 for a neutral 107 M⊙ halo at redshift 40. Solid and dot–dashed lines show interactions for the leptons while the dashed show those for photons. The dashed red, magenta, and orange lines show photoionization, Compton scattering, and pair creation off of the gas field, respectively. Electroionization and excitation are shown in green and blue, IC scattering in black, and annihilation via positronium for positron in purple. For a fully ionized halo, the yellow line shows the mfp for Coulomb interaction. For each process, the lines indicate the mfp at the average density of the halo while the shading either side of the curves shows the mfp at rvir and rvir/100.

Figure 2.
mfpin units of the virial radius for the various interactions undergone by injected particles within a neutral gas 107 M⊙ halo at redshift 40. Solid lines show interactions for charged particles and dashed for photons. The grey line indicates the virial radius of the halo. Processes shown are photoionization (red), Compton scattering (magenta), and pair creation off of the gas (orange) for photons and ionization and excitation (green and blue) for electrons, as well as IC scattering (cyan) and annihilation via positronium for positrons (purple, dot–dashed line). In all cases, lines show the mfp for the process at the average density of the halo, while the shaded regions either side indicate the mfp at rvir and rvir/100. For reference, the yellow curve shows the mfp for Coulomb scattering in an equivalent, fully ionized halo.
Open in new tabDownload slide

mfpin units of the virial radius for the various interactions undergone by injected particles within a neutral gas 107 M⊙ halo at redshift 40. Solid lines show interactions for charged particles and dashed for photons. The grey line indicates the virial radius of the halo. Processes shown are photoionization (red), Compton scattering (magenta), and pair creation off of the gas (orange) for photons and ionization and excitation (green and blue) for electrons, as well as IC scattering (cyan) and annihilation via positronium for positrons (purple, dot–dashed line). In all cases, lines show the mfp for the process at the average density of the halo, while the shaded regions either side indicate the mfp at rvir and rvir/100. For reference, the yellow curve shows the mfp for Coulomb scattering in an equivalent, fully ionized halo.

The grey line is indicative of the halo's virial radius. Particles with energies such that their interaction mfp are no longer smaller than or comparable to the virial radius will readily escape the halo without either interacting with the gas and/or depositing energy. For the DM annihilation products considered here, the primary interaction of the injected electrons and positrons is IC scattering (injected photons first undergo electron/positron pair creation off of the gas field). The actual energy transfer process occurs via the secondary particle produced in those interactions, in this case, the upscattered IC photons. Therefore, the energy spectrum of the secondary cascade products induced by the injected particles plays an important role in determining the relative efficiency with which the different DM models are able to deposit energy into the halo.

4.2 Particle evolution

The step-wise evolution of the particle follows the methodology of the GEANT4 simulation toolkit (Agostinelli et al. 2003; Allison et al. 2006). At the beginning of each calculation, the code takes a particle (in this case, an electron, photon, or positron) with a given energy and injects it at point |$\boldsymbol {x}$| in direction (θ, ϕ). The particle then takes a straight line step of size determined by the step-size function in this specified direction. The code then selects a random point along this straight line step and uses the densities at this point to calculate the relevant mfp that characterize the distance the particle travels before said interactions take place. For each potential process, random numbers are used to determine at what point the interaction takes place. If none of the interactions take place within the step size, the particle travels to the end of the straight line, the next step is taken, and the process is repeated. If one or more interactions do occur within the step, the process corresponding to the shortest distance to interaction will be executed. At the end of the process, the code records the location of any energy that has been deposited as well as the type, energy, position, and orientation of the remaining/newly created particles. The process repeats until either all particles’ energies drop below all interaction thresholds (or if one is defined, the particle escapes a pre-defined spatial boundary).

The initial particle can be evolved as often as required to achieve the necessary level of convergence. At the end of the Monte Carlo run, the code outputs the average energy deposited into heating, ionization, and Lyman α photons in each pre-defined spatial bin as a fraction of the original injected particle's energy. If a physical boundary is defined, the code will give a similarly normalized spectrum of the escaped electrons, positrons, and photons.

In this calculation, we assume that both the halo and the CGM are spherically symmetric. We thus define the step-size function the following way:
\begin{equation} S(\boldsymbol {r}) = \epsilon _{0} \boldsymbol {r}, \end{equation}
(9)
where ε0 is an adjustable parameter setting the length of the step. Fig. 3 shows the code output for a 104 keV electron in a 105 M⊙ halo at redshift 20 for different values of ε. Results are given as the fraction of the original injected particle energy deposited in each respective radial bin. The magenta, green, blue, and black curves show results for ε = 0.5, 0.1, 0.05, and 0.01, respectively. For ε < 0.1, the results appear to converge. In contrast, for larger ε, the change in density across the resultant step size is no longer sufficiently close to constant. For a radially, monotonically decreasing density, the code will then underestimate the mfp for particles heading towards the centre of the halo, while overestimating those for particles heading outwards resulting in the shifted, magenta curve shown in Fig. 3. An ε = 0.01 was used throughout this paper.
Figure 3.
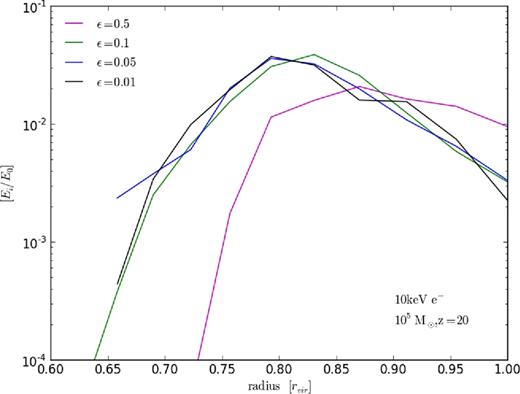
Outputs for a 10 keV electron injected into 105 M⊙ halo at redshift 20 for different step-size scale parameters ε. Magenta, green, blue, and black curves, respectively, refer to ε = 0.5, 0.1, 0.05, and 0.01. Results are given as the fraction of the original injected particle energy deposited in each respective radial bin.
Open in new tabDownload slide

Outputs for a 10 keV electron injected into 105 M⊙ halo at redshift 20 for different step-size scale parameters ε. Magenta, green, blue, and black curves, respectively, refer to ε = 0.5, 0.1, 0.05, and 0.01. Results are given as the fraction of the original injected particle energy deposited in each respective radial bin.

5 HALO SELF-HEATING

We now use the code to calculate the energy deposited within 105, 106, and 107 M⊙ haloes at redshifts 20 and 40.

5.1 Heating and ionization

In order to determine the total energy transfer for each DM model, the deposition fractions for each particle species α, with energy Ej injected at radius ri, are first calculated,
\begin{equation} \begin{array}{lcc} \boldsymbol {h}_{ijk}^{\alpha }, & \boldsymbol {x}_{ijk}^{\alpha }, & \boldsymbol {l}_{ijk}^{\alpha }\\ \boldsymbol {e}_{ijk}^{\alpha }, & \boldsymbol {f}_{ijk}^{\alpha }, & \boldsymbol {p}_{ijk}^{\alpha }. \end{array} \end{equation}
(10)
Here |$\boldsymbol {h}$|⁠, |$\boldsymbol {x}$|⁠, and |$\boldsymbol {l}$| denote the fraction deposited as heating, ionization, and Lyman photons at each radius rk, and |$\boldsymbol {e}$|⁠, |$\boldsymbol {f}$|⁠, and |$\boldsymbol {p}$| the energy distribution of escaped electrons, photons, and positrons in energy bin Ek. The energy transfer code was run for the range of injected particles in each of the different mass haloes at redshifts 20 and 40 and the subsequent deposition fractions calculated separately for each halo. These act as elements of a kind of pseudo-basis that are then weighted by the appropriate halo and DM models. The total, halo-summed energy deposition for a particle α with energy Ej is then given by
\begin{equation} \boldsymbol {H}_{jk}^{\alpha } {=} \sum _{i} w_{i} \boldsymbol {h}_{ijk}^{\alpha }, \quad \boldsymbol {\chi }_{jk}^{\alpha } {=} \sum _{i} w_{i} \boldsymbol {x}_{ijk}^{\alpha }, \quad \boldsymbol {L}_{jk}^{\alpha } {=} \sum _{i} w_{i} \boldsymbol {l}_{ijk}^{\alpha }, \end{equation}
(11)
where wi is the fraction of the total DM annihilation power produced within the shell at radius ri. The coefficients wi will naturally vary depending on the halo model, with concentrated models (such as those with an Einasto profile) injecting more of their total annihilation energy close to the centre of the halo while in haloes with the flat-core Burkert profile the injected energy is distributed closer to the edge. This means that more concentrated haloes not only have greater total annihilation power, but they are also more efficient at energy transfer as more of their energy is injected close to the haloes’ centre where the gas density is greatest.
The code outputs can now be used to calculate the radially dependent heating |$\mathfrak {H}$|⁠, ionization |$\mathfrak {X}$|⁠, and Lyman photon |$\mathfrak {L}$| production for different DM models,
\begin{eqnarray} \mathfrak {H}_{k} &=& \sum _{\alpha } f_{j\alpha } \sum _{j} \boldsymbol {H}_{jk}^{\alpha }\nonumber\\ \mathfrak {X}_{k} &=& \sum _{\alpha } f_{j \alpha }\sum _{j} \boldsymbol {\chi }_{jk}^{\alpha }\nonumber\\ \mathfrak {L}_{k} &=& \sum _{\alpha } f_{j \alpha } \sum _{j} \boldsymbol {L}_{jk}^{\alpha }, \end{eqnarray}
(12)
where fjα is the fraction of the annihilation spectrum carried by particle α with energy Ej. fjα depends on the annihilation channel of the DM model.

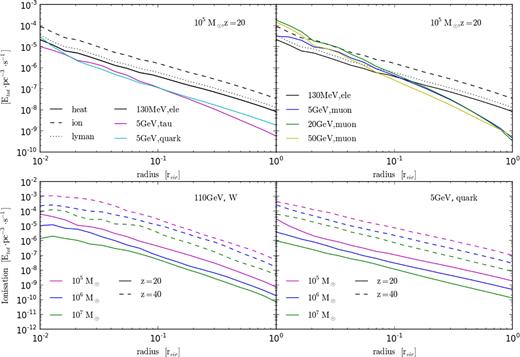
Fig. 4 shows selected heating and ionization curves for different halo and DM particle models. All results are given as the fraction of the total annihilation power of the halo deposited per unit volume. Upper plots show the outputs for a 105 M⊙ halo at redshift 20. The figure on the left shows a 5 GeV particle annihilating via tau leptons (magenta) and quarks (cyan) while the figure on the right shows models annihilating via muons with 5, 20, and 50 GeV shown in blue, green, and yellow. In both plots, the black curves show the 130 MeV model annihilating directly to an electron/positron pair with the solid, dashed, and dotted lines showing energy going into heating, ionization, and Lyman photons for reference.

Figure 4.
Heating and ionization curves for different haloes and DM models. All results are given as the fraction of the total annihilation power of the halo deposited per unit volume. Upper plots show the outputs for a 105 M⊙ halo at redshift 20. The figure on the left shows a 5 GeV particle annihilating via tau leptons (magenta) and quarks (cyan) while the figure on the right shows models annihilating via muons with 5, 20, and 50 GeV shown in blue, green, and yellow. In both plots, the black curves show the 130 MeV model annihilating directly to an electron/positron pair with the solid, dashed, and dotted lines showing energy going into heating, ionization, and Lyman photons for reference. The lower-left plot shows results for a 110 GeV DM particle annihilating via W bosons and the lower right shows those for a 5 GeV particle annihilating via quarks, In each of the lower plots, magenta, blue, and green curves show the ionization curves for 105, 106, and 107 M⊙ haloes where solid lines indicate outputs at redshift 20 and dashed those at redshift 40.
Open in new tabDownload slide

Heating and ionization curves for different haloes and DM models. All results are given as the fraction of the total annihilation power of the halo deposited per unit volume. Upper plots show the outputs for a 105 M⊙ halo at redshift 20. The figure on the left shows a 5 GeV particle annihilating via tau leptons (magenta) and quarks (cyan) while the figure on the right shows models annihilating via muons with 5, 20, and 50 GeV shown in blue, green, and yellow. In both plots, the black curves show the 130 MeV model annihilating directly to an electron/positron pair with the solid, dashed, and dotted lines showing energy going into heating, ionization, and Lyman photons for reference. The lower-left plot shows results for a 110 GeV DM particle annihilating via W bosons and the lower right shows those for a 5 GeV particle annihilating via quarks, In each of the lower plots, magenta, blue, and green curves show the ionization curves for 105, 106, and 107 M⊙ haloes where solid lines indicate outputs at redshift 20 and dashed those at redshift 40.

As mentioned previously, the relative energy transfer efficiency of the various DM models is strongly dependent on the energy distribution of the secondary cascade particles. Of particular note is the 130 MeV model annihilating via an electron/positron pair shown in black in the upper row of Fig. 4. Electrons/positrons injected at 130 MeV will produce upscattered IC photons with energies low enough to undergo photoionization so that even the lower density regions at the edge of the halo can be heated. This, along with the fact that none of the annihilation power is lost to neutrinos, makes it a very attractive DM candidate as far as possible detection goes.

For somewhat heavier DM models (1–5 GeV), the peak of upscattered IC photons will fall into the energy regime of Compton scattering, which is only efficient at the high gas densities found at the centre of the halo. Even heavier candidates will eventually produce IC photons sufficiently energetic to undergo pair creation themselves leading to more complex cascades. In both of those scenarios, the energy deposition in the outer parts of the haloes is less efficient due to a significant fraction of the resultant cascade particles falling into energy regimes in which interaction with the gas is poor. Lastly for neutral gas, the majority of the deposited energy is partitioned into ionization as is indicated by the black dashed line in the upper plots of Fig. 4. However, as the halo becomes ionized, Coulomb heating very rapidly becomes a dominant interaction process and the energy partition becomes skewed towards heating instead.

The lower-left plot shows results for a 110 GeV DM particle annihilating via W bosons and the lower right shows those for a 5 GeV particle annihilating via quarks, In each of the lower plots, magenta, blue, and green curves show the ionization curves for 105, 106, and 107 M⊙ haloes where solid lines indicate outputs at redshift 20 and dashed those at redshift 40. As expected, the energy deposition efficiency at higher redshifts is greater due to the increase in both the gas and CMB number density.

5.1.1 Lyman photons

As shown in Fig. 4, our code also tracks the production of Lyman photons. Photons with energy below the Lyman limit (13.6  eV) are assumed to cease direct interaction with their surrounding medium. However, their production through DM annihilation can still play an important role in baryonic structure formation when taking gas cooling into account. For instance, photons with energies between 11.2 and 13.6  eV are classified as Lyman–Werner photons. These photons maybe absorbed by molecular hydrogen and through excitation and subsequent radiative decay lead to its disassociation. Before the production of metals, the formation and destruction of H2 play an important role in molecular cooling at high redshifts (Abel et al. 1997) and are thus vital for early star (Abel, Bryan & Norman 2002) and galaxy formation (Bromm et al. 2009). For the calculation performed here, all photons with energy between 10.2 and 13.6 eV were counted towards the Lyman photon output. Those with energy below 10.2 eV were taken to no longer interact with the halo's gas component and discarded.

5.2 Binding energy comparison

The above results allow for the comparison of the halo's gravitational binding energy and the DM energy input to be revisited. However, unlike in the work conducted in S15, the comparison will be made for individual shells rather than the total halo. The energy produced due to DM annihilation over the Hubble time tH, in the spherical shell between rk and rk + 1, is
\begin{equation} U_{\text{dm,shell}}(r_{k}) = \int P_{\text{dm}}(r_{k}) \mathrm{d}S \cdot t_{\text{H}}. \end{equation}
(13)
The gravitational binding energy is given by
\begin{equation} U_{\text{G,shell}}(r_{k}) = \frac{G M_{\text{shell}}(r_{k}) M(<r)}{r_{k}} \end{equation}
(14)
so that the ratio between the energy going into heating and the gravitational binding energy is
\begin{equation} R_{\text{g}}(r_{k}) = \frac{U_{\text{dm,shell}}(r_{k})}{U_{\text{G, shell}}(r_{k})} \cdot \mathfrak {H}_{k}, \end{equation}
(15)
where |$\mathfrak {H}$| is the heating term previously calculated.

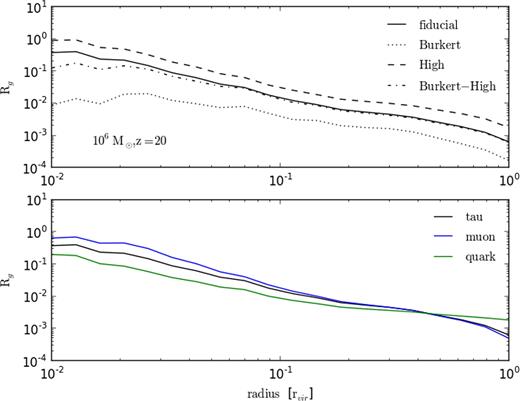
Fig. 5 shows the comparison Rg between the energy deposited over the Hubble time and the gravitational binding energy of the haloes at different radii. For a 106 M⊙ halo at redshift 20, the upper plots compare different halo models where the solid, dotted, dashed, and dot–dashed lines show the results for the fiducial, Burkert, high, and Burkert-high models, respectively. As previously discussed, models with more concentrated mass profiles both produce more annihilation power and are more efficient at depositing energy into the halo. This can be seen here when comparing the high model to the others. Also of interest is that the Burkert-high model is, with exception of the behaviour very close to the halo centre, nigh indistinguishable from the fiducial model. In this scenario, doubling the mass–concentration parameter allows the flat-core Burkert profile to mimic the behaviour of the cuspy Einasto profile, again highlighting the potential impact underlying uncertainties in the DM models have on results. The lower plot shows results for different annihilation channels where black, blue, and green show the tau lepton, muon, and quark models.

Figure 5.
The ratio Rg comparing the energy deposited as heat over the Hubble time with the gravitational binding energy of shells at different radii in a 106 M⊙ halo at redshift 20. The upper plot compares different DM haloes models for a 20 GeV DM particle annihilating via tau leptons. The fiducial halo model is shown by the solid black line and the Burkert model is shown by the dotted curve. The high and Burkert-high models are given by the dashed and dot–dashed curves, respectively. The lower plot shows Rg for the fiducial halo model but with the black, blue, and green lines showing models annihilating via tau leptons, muons, and quarks.
Open in new tabDownload slide

The ratio Rg comparing the energy deposited as heat over the Hubble time with the gravitational binding energy of shells at different radii in a 106 M⊙ halo at redshift 20. The upper plot compares different DM haloes models for a 20 GeV DM particle annihilating via tau leptons. The fiducial halo model is shown by the solid black line and the Burkert model is shown by the dotted curve. The high and Burkert-high models are given by the dashed and dot–dashed curves, respectively. The lower plot shows Rg for the fiducial halo model but with the black, blue, and green lines showing models annihilating via tau leptons, muons, and quarks.

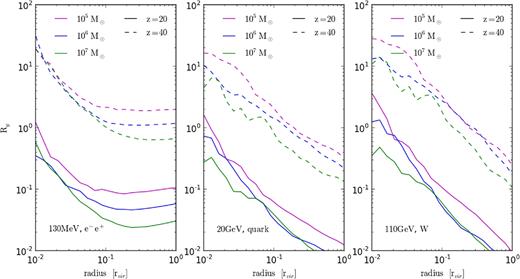
Fig. 6 also shows Rg but here haloes at different redshifts are compared. From left to right, the plots show results for 130 MeV particle annihilating to an electron/positron pair, 20 GeV annihilating to quarks, and 110 GeV annihilation to a W boson. As before, magenta, blue, and green curves correspond to 105, 106, and 107 M⊙ haloes while solid lines refer to results at redshift 20 and dashed to those at redshift 40. Also as before, Rg is greater at high redshift due to the higher energy transfer efficiency. The sustained heating of the 130 MeV model out to the edges of the halo is also demonstrated again.

Figure 6.
The ratio Rg of heating from DM annihilation over the Hubble time and gravitational binding energy at different radii. From left to right, the plots show results for 130 MeV particle annihilating to an electron/positron pair, 20 GeV annihilating to quarks, and 110 GeV annihilation to a W boson. As before, magenta, blue, and green curves correspond to 105, 106, and 107 M⊙ haloes while solid lines refer to results at redshift 20 and dashed to those at redshift 40.
Open in new tabDownload slide

The ratio Rg of heating from DM annihilation over the Hubble time and gravitational binding energy at different radii. From left to right, the plots show results for 130 MeV particle annihilating to an electron/positron pair, 20 GeV annihilating to quarks, and 110 GeV annihilation to a W boson. As before, magenta, blue, and green curves correspond to 105, 106, and 107 M⊙ haloes while solid lines refer to results at redshift 20 and dashed to those at redshift 40.

As a whole, this matches the findings of the work in S15, albeit with a more precise estimate of the deposition fractions. Having an additional, not insignificant heating source during the early stages of these micro-haloes’ development could result in gas being expelled, or alternatively heated to a degree that prevents/delays star formation. A dynamic model would be required to ascertain how impactful the heating from DM turns out to be. While this is beyond the scope of this work, the heating curves calculated here are an important first step towards fully quantifying the impact DM annihilation has on early star formation.

6 HEATING OF THE CGM

While it was here shown that energy comparable to that of the binding energy is deposited inside the halo over the Hubble time, most of the injected energy will escape the halo. In this section, the results from this calculation are used to determine the changes to the particle distribution of the original annihilation spectrum as a consequence of traversing the halo. These new spectra are then injected into the CGM to establish whether there is sufficient heating to curtail the infall of gas on to the halo, and therefore affect structure formation.

Loeb (2006) gives an expression for the baryon overdensity inside a collapsed DM structure after virialization as
\begin{equation} \delta _{\text{b}} \equiv \frac{\rho _{\text{b}}}{\bar{\rho }_{\text{b}}} - 1 = \left( 1 + \frac{6}{5} \frac{T_{\text{vir}}}{\bar{T}_{\text{g}}} \right) ^{3/2} -1, \end{equation}
(16)
where the background gas temperature |$\bar{T}_{\text{g}}$| can be written as
\begin{equation} \bar{T}_{\text{gas}} \approx 170[(1+z)/100]^{2} \, \mathrm{K}, \quad \text{for } z< 160. \end{equation}
(17)
Using the result above, a critical value for δb can be set to indicate the collapse of the gas. This value is to a certain degree arbitrary so for example when δb > 100, then >50 per cent of the gas that would be present if there were no pressure accrues on to the halo. Having set a critical δb to indicate collapse, a minimal baryonic mass can be defined. Regardless of what δb is chosen, if the background temperature of the halo |$\bar{T}_{\text{g}}$| is increased, the virial temperature Tvir (which is a proxy for the total mass of the halo) needs to increase along with it to maintain the same δb. Having a source of heating of the CGM such as DM annihilation could, if efficient enough, reduce the amount of gas accreted on to the halo or in even more extreme cases raise the minimal halo mass required for baryonic collapse. Unlike for calculations of the Jeans mass, the above expression takes into account shell crossing, though it does neglect shock heating that is critical when calculating the DM-modified δb for the larger of our haloes.

6.1 Filtered spectra

We assume the primary source of heating of the CGM due to DM annihilation to come from within the halo itself. When considering the actual energy input into the CGM, one has to take into consideration that some of the injected energy will have been lost to the halo's gas component, and some will have been down-scattered through the IC-induced particle cascades. The modified annihilation spectra are calculated in much the same manner as the total heating and ionization curves so that the escaped distributions of electrons, photons, and positrons for particle α with energy Ei are
\begin{equation} \boldsymbol {E}_{jk}^{\alpha } {=} \sum _{i} w_{i} \boldsymbol {e}_{ijk}^{\alpha }, \quad \boldsymbol {F}_{jk}^{\alpha } {=} \sum _{i} w_{i} \boldsymbol {f}_{ijk}^{\alpha }, \quad \boldsymbol {P}_{jk}^{\alpha } {=} \sum _{i} w_{i} \boldsymbol {p}_{ijk}^{\alpha } \end{equation}
(18)
and the total distributions of electrons, photons, and positrons for the different annihilation models are
\begin{eqnarray} \mathfrak {E}_{k} &=& \sum _{\alpha } \sum _{j} f_{j \alpha } \boldsymbol {E}_{jk}^{\alpha }\nonumber\\ \mathfrak {F}_{k} &=& \sum _{\alpha } \sum _{j} f_{j \alpha } \boldsymbol {F}_{jk}^{\alpha }\nonumber\\ \mathfrak {P}_{k} &=& \sum _{\alpha } \sum _{j} f_{j \alpha } \boldsymbol {P}_{jk}^{\alpha }, \end{eqnarray}
(19)
where wi and fjα are the same coefficients as used in Section 5.1.

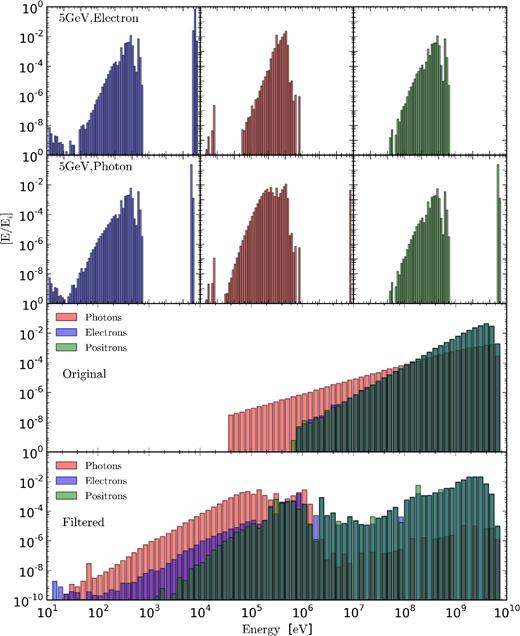
Fig. 7 demonstrates the code output showing the energy distribution of particles escaping a 106 M⊙ halo at redshift 20. The uppermost plot shows the distribution of escaped electrons (left), photons (middle), and positrons (right) for 5 GeV electrons injected into the halo. The plots directly below show the same but for a 5 GeV photon. The lower two plots show the total spectrum where the third row shows the original, unmodified injected annihilating spectrum for a 5 GeV DM particle annihilating via muons. The lowest plot shows the spectra after the injected particles have passed through the halo. In both plots, the pink columns show photons, blue electron, and green positrons, and results are given as a fraction of the halo's total annihilation power.

Figure 7.
Code output showing the energy distribution of particles escaping a 106 M⊙ halo at redshift 20. The uppermost plot shows the distribution of escaped electrons (left), photons (middle), and positrons (right) for 5 GeV electrons injected into the halo. The plots directly below show the same but for a 5 GeV photon. The lower two plots show the total spectrum where the third row shows the original, unmodified injected annihilating spectrum for a 5 GeV DM particle annihilating via muons. The lowest plot shows the spectrum after the injected particles have passed through the halo. In both plots, the pink columns show photons, blue electron, and green positrons, and results are given as a fraction of the halo's total annihilation power.
Open in new tabDownload slide

Code output showing the energy distribution of particles escaping a 106 M⊙ halo at redshift 20. The uppermost plot shows the distribution of escaped electrons (left), photons (middle), and positrons (right) for 5 GeV electrons injected into the halo. The plots directly below show the same but for a 5 GeV photon. The lower two plots show the total spectrum where the third row shows the original, unmodified injected annihilating spectrum for a 5 GeV DM particle annihilating via muons. The lowest plot shows the spectrum after the injected particles have passed through the halo. In both plots, the pink columns show photons, blue electron, and green positrons, and results are given as a fraction of the halo's total annihilation power.

As can be seen in the modified spectra, the original electron/positron distribution is largely retained as only a small fraction of energy is actually lost to the halo, though it is somewhat broadened towards lower energies. In contrast, the original high-energy photons undergo pair creation and only those photons injected close to the virial radius are retained. The secondary population of pair-created electrons and positrons can be observed around 104–106 eV. Electrons also feature a low-energy tail due to ionization from those IC photons that fall below the pair-creation limit. IC scattering will create an extensive secondary population of photons with those IC photons below the pair-creation limit comprising the prominent mid- to low-energy tail.

While we focus here on the impact on a halo's immediate environment, this modification of the spectrum also has implications for the impact of annihilation products on the mean IGM evolution. The efficiency of energy deposition depends strongly on the energy spectrum of the photons and particles, suggesting that the filtering must be taken into account in studies of DM's impact on reionization.

6.2 Raising Jeans mass

The CGM is well approximated by a monatomic, ideal gas for which the internal energy can be written as |$U = \frac{3}{2} N k_{\text{b}} T$|⁠. Here N denotes the total number of particles and kb is the Boltzmann constant. Given the total energy produced through DM annihilation by the halo over the Hubble time, Udm, the heating |$\boldsymbol {H}_{k}$|⁠, and ionization |$\boldsymbol {X}_{k}$| fractions calculated above, the average change in temperature of the shell at |$\boldsymbol {r}_{k}$| is given by
\begin{equation} \Delta T(\boldsymbol {r}_{k}) = \frac{2 \boldsymbol {H}_{k} U_{\text{dm}}}{3 N_{k} k_{\text{b}} }. \end{equation}
(20)
To show the potential increase in the minimal baryonic mass, we use equation (16) so that the new δb with DM annihilation is given by
\begin{equation} \delta _{\text{mod}} = \frac{\rho _{\text{b}}}{\bar{\rho }_{\text{b}}} - 1 = \left( 1 + \frac{6}{5} \frac{T_{\text{vir}}}{\bar{T}_{\text{g}} + \Delta T_{\text{DM}}} \right) ^{3/2} -1, \end{equation}
(21)
where ΔTdm is the extra heating due to dark matter annihilation. The ΔTdm used here is the average change in temperature taken over the first five radial bins from the CGM results.

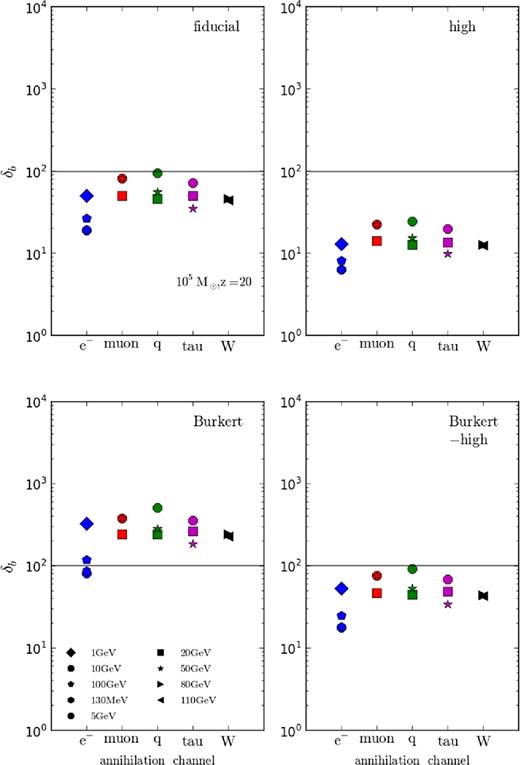
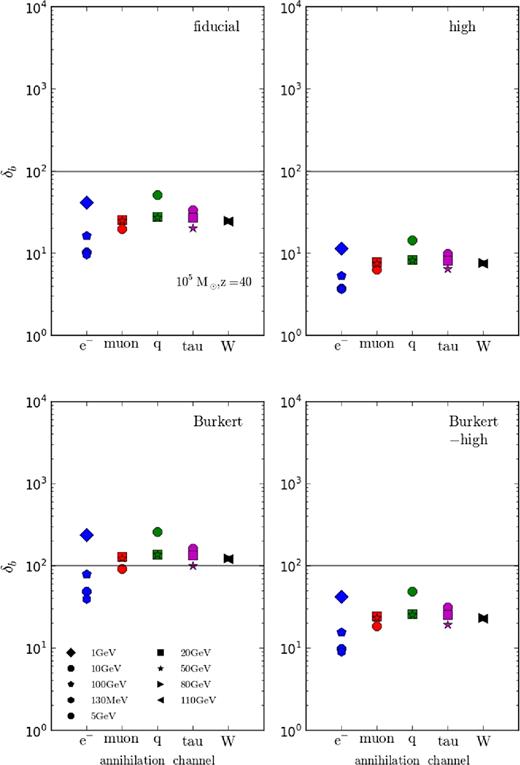
Figs 8 and 9 show the modified δb from DM annihilation for a 105 M⊙ halo at redshifts 20 and 40. Different colours correspond to different DM annihilating channels with blue, red, green, magenta, and black showing the electron/positron, muon, quark, tau, and W boson channels, respectively. Different symbols as indicated in the bottom-left plot indicate different DM masses. From left to right, the top plots show the fiducial and high halo models and the lower show results for Burkert and Burkert-high models.

Figure 8.
Modification of δb from DM annihilation for a 105 M⊙ halo at redshift 20. Different colours correspond to different DM annihilating channels with blue, red, green, magenta, and black showing the electron/positron, muon, quark, tau, and W boson channels, respectively. Different symbols as indicated in the bottom-left plot indicate different DM masses. From left to right, the top plots show the fiducial and high halo models and the lower show results for Burkert and Burkert-high models. The grey horizontal line shows the critical δb chosen to indicate the minimal δb required for baryonic collapse.
Open in new tabDownload slide

Modification of δb from DM annihilation for a 105 M⊙ halo at redshift 20. Different colours correspond to different DM annihilating channels with blue, red, green, magenta, and black showing the electron/positron, muon, quark, tau, and W boson channels, respectively. Different symbols as indicated in the bottom-left plot indicate different DM masses. From left to right, the top plots show the fiducial and high halo models and the lower show results for Burkert and Burkert-high models. The grey horizontal line shows the critical δb chosen to indicate the minimal δb required for baryonic collapse.

Figure 9.
Same as Fig. 8 but for a 105 M⊙ halo at redshift 40.
Open in new tabDownload slide

Same as Fig. 8 but for a 105 M⊙ halo at redshift 40.

The results for the 105 M⊙ haloes in Figs 8 and 9 suggest that for a number of DM particle and halo models, the additional heating from DM annihilation will lower δb below 100. As expected, this effect is most pronounced for the highly concentrated Einasto-high halo model due to the increase in annihilation power. In comparison, results for the standard Burkert model show the impact to be reduced by about an order of magnitude. Understandably, the fiducial model falls between the two extremes with the concentrated Burkert profile again producing results comparable to that of the fiducial model.

In terms of DM particles, the 130 MeV model annihilating to an electron/positron pair is the most effective in reducing δb due to both its efficiency in depositing energy into the gas locally and the fact that none of the annihilation energy is siphoned into neutrinos. Amongst the remaining annihilation channels, heavier candidates provide a greater change in δb compared to models with masses from 1to5 GeV. This is in keeping with the previous discussion that showed that electrons and positrons within that energy range produce IC photons that tend to free stream at IGM densities. Results for the halo at redshift 40 are qualitatively similar to those at redshift 20 but with δb reduced even further.

While not shown here, results indicate that δb is not significantly impacted for the 106 and 107 M⊙ haloes, though again the results are comparable to the lower mass cases in their general behaviour. However, as was briefly alluded to earlier, the method of calculating δb does not take into account the virialization shocks surrounding the haloes and for 107 M⊙ haloes shock heating of the surrounding gas becomes significant. The derivation of δmod in equation (16) however assumes that the gas temperature remains at the temperature of the IGM, and therefore the method does not produce reliable results for haloes of this mass.

6.3 Change in the minimal baryonic mass

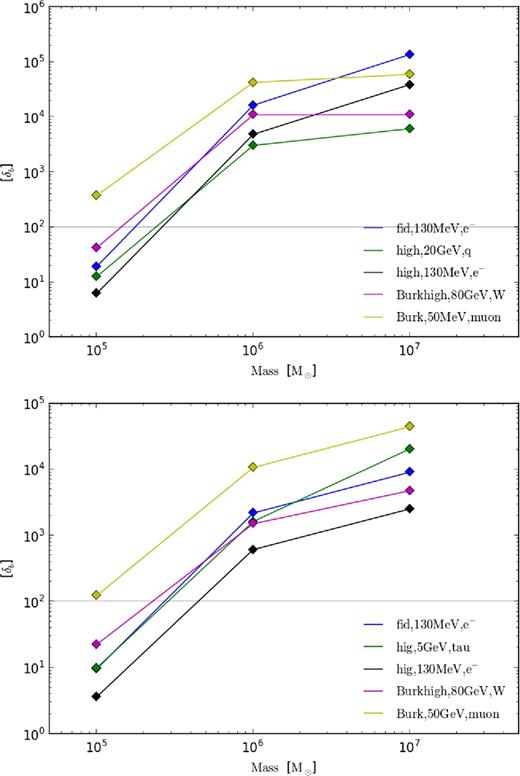
If δb is sufficiently reduced due to DM annihilation in 105 M⊙ haloes at redshifts 20 and 40, what consequences does this suggest for the minimal baryonic objects? Fig. 10 again shows the annihilation-modified δb though this time as a function of halo mass. The top panel shows the results at redshift 20 and the lower panel at redshift 40. In both plots, the grey, horizontal line denotes δb = 100, which gives the chosen critical value for the collapse of baryonic structures. Different coloured curves show the outputs for different halo/DM models.

Figure 10.
Modification of δb from DM annihilation for different halo masses and DM models. The grey horizontal line again shows the critical δb chosen to indicate the minimum δb for sufficient gas accretion on to the halo.
Open in new tabDownload slide

Modification of δb from DM annihilation for different halo masses and DM models. The grey horizontal line again shows the critical δb chosen to indicate the minimum δb for sufficient gas accretion on to the halo.

For δb = 100 as the critical value, a number of DM candidates would reduce the infall of gas on to the halo to a degree that potential baryonic structure formation could be affected. For the DM model with the most pronounced impact on δb, a 130 MeV particle with a concentrated Einasto profile (black curve), a 105 M⊙ halo would have to increase in mass by a factor of 2–3 at redshift 20 and 4–5 at redshift 40 to recover a δb of 100. It is again important to note that the large δb produced for haloes with mass >106 M⊙ arise due to the non-inclusion of virialization shocks and the subsequent shock heating of the gas surrounding the haloes. The derivation of δmod in equation (21) however assumes that the CGM gas temperature remains at the temperature of the IGM (which gives rise to the large δb in Fig. 10), and therefore the method does not produce reliable results for haloes of this mass. This however does not impact the conclusions drawn for the 105 M⊙ haloes.

7 DISCUSSION

In this paper, we revisited the energy deposition from DM annihilation in small, high-redshift haloes, as well as calculating the heating of the haloes’ CGM due to DM annihilation in the halo proper. A key aspect of this work is the updated energy transfer Monte Carlo code that allows for injected electrons, positrons, and photons to interact with an arbitrary, three-dimensional number density distribution of atomic hydrogen, helium, free electrons, and CMB photons. The code calculates the fraction and location of the energy deposited into heating, ionization, and Lyman photons in a pre-defined volume such as a halo.

Overall, the broad conclusions drawn in the earlier calculation are supported in the detailed study. We find that the total annihilation power is increased for more concentrated haloes, with the total annihilation power being significantly impacted by the precise distribution of DM within the halo. We also find the existence of a parameter space in which DM annihilation could modify baryonic structure formation. In our previous paper, the choice of annihilation channel influenced outcomes predominantly through the fraction of the total annihilation power partitioned into electrons/positrons and photons, as opposed to the non-interacting neutrinos. Since the updated energy transfer method is sensitive to the energy-dependent mfp, both the DM particle mass (for an annihilation cross-section adjusted to give the same total power integrated over the halo) and choice of annihilation channel also impact the overall energy deposition by changing the energy distribution of annihilation products. The 130 MeV DM model annihilating via electron/positron pairs was particularly efficient at depositing energy with haloes due to the favourable interaction mfp of the upscattered IC photons produced by the injected particles.

We built on our detailed examination of self-heating haloes by calculating the heating of the haloes’ CGM. Sufficient increase in temperature of the CGM can lead to the suppression of gas infall on to the halo and formation of baryonic structure. δmod was calculated for the different DM models. At redshifts 20 and 40, a 105 M⊙ halo is no longer massive enough for δb > 100, instead objects more massive by a factor of 3–5 are required. An important caveat is that the method used in the work breaks down for more massive haloes as it does not take into account shock heating haloes, which results in an inflated value of δb.

The work completed here aims to contribute to the identification of the parameter space in which DM annihilation impacts early structure formation as well as developing tools to assist with the rigorous treatment of energy transfer in non-homogeneous density fields. While the analysis of a single halo cannot predict the accumulative effect DM annihilation has on hierarchical structure formation over time, it does aid in the formulation of models that will be compatible with simulations and allow for testable predictions to be made.

In order to identify a signal indicative of new physics, careful modelling is required to account for both uncertainties in the DM and astrophysical models. It is crucial that predictions whether they be of a DM-modified 21  cm signal or general galaxy properties integrate DM annihilation into the emergence of structure starting at high redshifts. A number of challenges remain before the latter can be fully realized, but the prospective comparisons to be made with future observations will provide valuable constraints to guide the ongoing quest to uncover the fundamental nature of DM.

Acknowledgements

We would like to thank Tracy Slatyer and Hongwan Liu for insightful discussions. Part of the energy transfer calculation was performed using the gSTAR national facility at Swinburne University of Technology, which is funded by Swinburne and the Australian Government's Education Investment Fund. KM is supported by the Australian Research Council Discovery Early Career Research Award. Lastly, we would like to thank the anonymous referee for their valuable comments.

REFERENCES

Abel
T.
,
Anninos
P.
,
Zhang
Y.
,
Norman
M. L.
,
1997
,
New Astron.
,
2
,
181

Crossref
Search ADS
 

Abel
T.
,
Bryan
G. L.
,
Norman
M. L.
,
2002
,
Science
,
295
,
93

Crossref
Search ADS
PubMed
 

Agaronyan
F. A.
,
Atoyan
A. M.
,
Nagapetyan
A. M.
,
1987
,
Astrophysics
,
19
,
187

Crossref
Search ADS
 

Agostinelli
S.
et al. ,
2003
,
Nucl. Instrum. Methods Phys. Res. A
,
506
,
250

Crossref
Search ADS
 

Allison
J.
et al. ,
2006
,
IEEE Trans. Nucl. Sci.
,
53
,
270

Crossref
Search ADS
 

Angel
P. W.
et al. ,
2016
,
MNRAS
,
459
,
2106

Crossref
Search ADS
 

Arnaud
M.
,
Rothenflug
R.
,
1985
,
A&AS
,
60
,
425

 

Bergstrom
L.
,
2012
,
preprint (arXiv:1202.1170)

Bertone
G.
,
Hooper
D.
,
2016
,
preprint (arXiv:1605.04909)

Bertone
G.
,
Hooper
D.
,
Silk
J.
,
2005
,
Phys. Rep.
,
405
,
279

Crossref
Search ADS
 

Binney
J.
,
Tremaine
S.
,
1987
,
Galactic Dynamics
.
Princeton Univ. Press
,
Princeton, NJ

Google Scholar

OpenURL Placeholder Text

 

Blumenthal
G. R.
,
Gould
R. J.
,
1970
,
Rev. Mod. Phys.
,
42
,
237

Crossref
Search ADS
 

Bransden
B. H.
,
Noble
C. J.
,
1976
,
J. Phys. B: At. Mol. Phys.
,
9
,
1507

Crossref
Search ADS
 

Bromm
V.
,
Yoshida
N.
,
Hernquist
L.
,
McKee
C. F.
,
2009
,
Nature
,
459
,
49

Crossref
Search ADS
PubMed
 

Bruns
L. R.
,
Jr
,
Wyithe
J. S. B.
,
Bland-Hawthorn
J.
,
Dijkstra
M.
,
2012
,
MNRAS
,
421
,
2543

Crossref
Search ADS
 

Burkert
A.
,
1995
,
ApJ
,
447
,
L25

Crossref
Search ADS
 

Chapman
E.
et al. ,
2012
,
MNRAS
,
423
,
2518

Crossref
Search ADS
 

Chen
X.
,
Kamionkowski
M.
,
2004
,
Phys. Rev. D
,
70
,
043502

Crossref
Search ADS
 

Chuzhoy
L.
,
Shapiro
P. R.
,
2007
,
ApJ
,
655
,
843

Crossref
Search ADS
 

Cohen
T.
,
Lisanti
M.
,
Slatyer
T. R.
,
Wacker
J. G.
,
2012
,
J. High Energy Phys.
,
10
,
134

Crossref
Search ADS
 

Comerford
J. M.
,
Natarajan
P.
,
2007
,
MNRAS
,
379
,
190

Crossref
Search ADS
 

Correa
C. A.
,
Wyithe
J. S. B.
,
Schaye
J.
,
Duffy
A. R.
,
2015
,
MNRAS
,
452
,
1217

Crossref
Search ADS
 

Diemer
B.
,
Kravtsov
A. V.
,
2015
,
ApJ
,
799
,
108

Crossref
Search ADS
 

Dijkstra
M.
,
Lidz
A.
,
Wyithe
J. S. B.
,
2007
,
MNRAS
,
377
,
1175

Crossref
Search ADS
 

Duffy
A. R.
,
Schaye
J. S.
,
Kay
S. T.
,
Vecchua
C. D.
,
2008
,
MNRAS
,
390
,
L64

Crossref
Search ADS
 

Dutton
A. A.
,
Macciò
A. V.
,
2014
,
MNRAS
,
441
,
3359

Crossref
Search ADS
 

Einasto
J.
,
1965
,
Tr. Astrofiz. Inst. Alma-Ata
,
5
,
87

 

Evoli
C.
,
Valdes
M.
,
Ferrara
A.
,
Yoshida
N.
,
2012
,
MNRAS
,
422
,
420

Crossref
Search ADS
 

Evoli
C.
,
Mesinger
A.
,
Ferrara
A.
,
2014
,
J. Cosmol. Astropart. Phys.
,
11
,
024

Crossref
Search ADS
 

Ferrigno
C.
,
Blasi
P.
,
De Marco
D.
,
2005
,
Astropart. Phys.
,
23
,
211

Crossref
Search ADS
 

Fisher
V. I.
,
Ralchenko
Y. V.
,
Bernshtam
V. A.
,
Goldgirsh
A.
,
Maron
Y.
,
Vainshtein
L. A.
,
Bray
I.
,
Golten
H.
,
1997
,
Phys. Rev. A
,
55
,
329

Crossref
Search ADS
 

Furlanetto
S. R.
,
Stoever
S. J.
,
2010
,
MNRAS
,
404
,
1869

 

Furlanetto
S. R.
,
Oh
S. P.
,
Pierpaoli
E.
,
2006
,
Phys. Rev. D
,
74
,
103502

Crossref
Search ADS
 

Gondolo
P.
,
Freese
K.
,
Spolyar
D.
,
Bodenheimer
P.
,
2013
,
preprint (arXiv:1304.7415)

Grasso
D.
et al. ,
2009
,
Astropart. Phys.
,
32
,
140

Crossref
Search ADS
 

Guessoum
N.
,
Jean
P.
,
Gillard
W.
,
2005
,
MNRAS
,
436
,
171

 

Heitler
W.
,
1954
,
Quantum Theory of Radiation
.
Clarendon Press
,
Oxford

Google Scholar

OpenURL Placeholder Text

 

Hirata
C. M.
,
2006
,
MNRAS
,
367
,
259

Crossref
Search ADS
 

Joseph
J.
,
Rohrlich
F.
,
1958
,
Rev. Mod. Phys.
,
30
,
354

Crossref
Search ADS
 

Karzas
W. J.
,
Latter
R.
,
1961
,
ApJS
,
6
,
167

Crossref
Search ADS
 

Kim
Y.
,
Rudd
M. E.
,
1994
,
Phys. Rev. A
,
50
,
3954

Crossref
Search ADS
PubMed
 

Loeb
A.
,
2006
,
preprint (astro-ph/0603360)

Lopez-Honorez
L.
,
Mena
O.
,
Moliné
Á.
,
Palomares-Ruiz
S.
,
Vincent
A. C.
,
2016
,
J. Cosmol. Astropart. Phys.
,
08
,
004

Crossref
Search ADS
 

Ludlow
A. D.
et al. ,
2013
,
MNRAS
,
432
,
1103

Crossref
Search ADS
 

Mack
K. J.
,
2014
,
MNRAS
,
439
,
2728

Crossref
Search ADS
 

Madhavacheril
M. S.
,
Sehgal
N.
,
Slatyer
T. R.
,
2014
,
Phys. Rev. D
,
89
,
103508

Crossref
Search ADS
 

Mapelli
M.
,
Ripamonti
E.
,
2007
,
Mem. Soc.  Astron. Ital.
,
78
,
800

 

Mellema
G.
et al. ,
2013
,
Exp. Astron.
,
36
,
235

Crossref
Search ADS
 

Merritt
D.
,
Navarro
J. F.
,
Ludlow
A.
,
Jenkins
A.
,
2005
,
ApJ
,
624
,
L85

Crossref
Search ADS
 

Merritt
D.
,
Graham
A. W.
,
Moore
B.
,
Diemand
J.
,
Terzić
B.
,
2006
,
AJ
,
132
,
2685

Crossref
Search ADS
 

Mesinger
A.
,
Ewall-Wice
A.
,
Hewitt
J.
,
2014
,
MNRAS
,
439
,
3262

Crossref
Search ADS
 

Motz
J. W.
,
Olsen
H. A.
,
Koch
H. W.
,
1969
,
Rev. Mod. Phys.
,
41
,
581

Crossref
Search ADS
 

Natarajan
A.
,
Tan
J. C.
,
O'Shea
B. W.
,
2009
,
ApJ
,
692
,
574

Crossref
Search ADS
 

Navarro
J. F.
,
Fenk
C. S.
,
White
S. D. M.
,
1996
,
ApJ
,
462
,
563

Crossref
Search ADS
 

Neto
A. F.
et al. ,
2007
,
MNRAS
,
381
,
1450

Crossref
Search ADS
 

Padmanabhan
N.
,
Finkbeiner
D. P.
,
2005
,
Phys. Rev. D
,
72
,
023508

Crossref
Search ADS
 

Planck Collaboration XIII
,
2016
,
A&A
,
594
,
A13

Crossref
Search ADS
 

Pober
J. C.
et al. ,
2013
,
ApJ
,
768
,
L36

Crossref
Search ADS
 

Poole
G. B.
,
Angel
P. W.
,
Mutch
S. J.
,
Power
C.
,
Duffy
A. R.
,
Geil
P. M.
,
Mesinger
A.
,
Wyithe
S. B.
,
2016
,
MNRAS
,
459
,
3025

Crossref
Search ADS
 

Poulin
V.
,
Serpico
P. D.
,
Lesgourgues
J.
,
2015
,
J. Cosmol. Astropart. Phys.
,
12
,
041

Crossref
Search ADS
 

Prada
F.
,
Klypin
A.
,
Flix
J.
,
Martínez
M.
,
Simonneau
E.
,
2004
,
Phys. Rev. Lett.
,
93
,
241301

Crossref
Search ADS
PubMed
 

Prada
F.
,
Klypin
A. A.
,
Cuesta
A. J.
,
Betancort-Rijo
J. E.
,
Primack
J.
,
2012
,
MNRAS
,
423
,
3018

Crossref
Search ADS
 

Roos
M.
,
2012
,
J. Mod. Phys.
,
3
,
1152

Crossref
Search ADS
 

Schön
S.
,
Mack
K. J.
,
Avram
C. A.
,
Wyithe
J. S. B.
,
Barberio
E.
,
2015
,
MNRAS
,
451
,
2840
(S15)

Crossref
Search ADS
 

Shah
M. B.
,
Elliott
D. S.
,
Gilbody
H. B.
,
1987
,
J. Phys. B: At. Mol. Phys.
,
20
,
3501

Crossref
Search ADS
 

Shah
M. B.
,
Elliott
D. S.
,
McCallion
P.
,
Gilbody
H. B.
,
1988
,
J. Phys. B: At. Mol. Phys.
,
21
,
2751

Crossref
Search ADS
 

Shull
J. M.
,
Steenberg
M. E.
,
1985
,
ApJ
,
298
,
268

Crossref
Search ADS
 

Sjostrand
T.
,
Mrenna
S.
,
Skands
P.
,
2006
,
J. High Energy Phys.
,
5
,
26

Crossref
Search ADS
 

Sjostrand
T.
,
Mrenna
S.
,
Skands
P.
,
2008
,
Comput. Phys. Commun.
,
178
,
852

Crossref
Search ADS
 

Slatyer
T. R.
,
2013
,
Phys. Rev. D
,
87
,
123513

Crossref
Search ADS
 

Slatyer
T. R.
,
Padmanabhan
N.
,
Finkbeiner
D. P.
,
2009
,
Phys. Rev. D
,
80
,
043526

Crossref
Search ADS
 

Spitzer
L.
,
Jr
,
Scott
E. H.
,
1969
,
ApJ
,
158
,
161

Crossref
Search ADS
 

Spolyar
D.
,
Freese
K.
,
Gondolo
P.
,
2008
,
Phys. Rev. Lett.
,
100
,
051101

Crossref
Search ADS
PubMed
 

Stone
P. M.
,
Kim
Y. R.
,
Desclaux
J. P.
,
2002
,
J. Res. Natl. Inst. Stand. Technol.
,
107
,
327

Crossref
Search ADS
PubMed
 

Svensson
R.
,
Zdziarski
A. A.
,
1990
,
ApJ
,
349
,
415

Crossref
Search ADS
 

Valdés
M.
,
Evoli
C.
,
Mesinger
A.
,
Ferrara
A.
,
Yoshida
N.
,
2013
,
MNRAS
,
429
,
1705

Crossref
Search ADS
 

van den Bosch
F. C.
,
Jiang
F.
,
Hearin
A.
,
Campbell
D.
,
Watson
D.
,
Padmanabhan
N.
,
2014
,
MNRAS
,
445
,
1713

Crossref
Search ADS
 

Verner
D. A.
,
Ferland
G. J.
,
Korista
K. T.
,
Yakovlev
D. G.
,
1996
,
ApJ
,
465
,
487

Crossref
Search ADS
 

Zdziarski
A. A.
,
Svensson
R.
,
1989
,
ApJ
,
344
,
551

Crossref
Search ADS
 
© 2017 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides