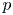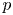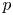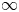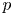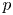1. Introduction
Let ![]() $p$ be a prime and let
$p$ be a prime and let ![]() $D/\mathbb {Q}$ be the (unique up to isomorphism) quaternion algebra ramified at
$D/\mathbb {Q}$ be the (unique up to isomorphism) quaternion algebra ramified at ![]() $p$ and
$p$ and ![]() $\infty$. Let
$\infty$. Let ![]() $\mathbb {A}$ denote the adèles of
$\mathbb {A}$ denote the adèles of ![]() $\mathbb {Q}$,
$\mathbb {Q}$, ![]() $\mathbb {A}_f$ the finite adèles, and
$\mathbb {A}_f$ the finite adèles, and ![]() $\mathbb {A}_f^{(p)}$ the finite prime-to-
$\mathbb {A}_f^{(p)}$ the finite prime-to-![]() $p$ adèles. Let
$p$ adèles. Let ![]() $K^p \subset D^\times (\mathbb {A}_f^{(p)})$ be a compact open subgroup. For
$K^p \subset D^\times (\mathbb {A}_f^{(p)})$ be a compact open subgroup. For ![]() $R$ a topological ring (e.g.
$R$ a topological ring (e.g. ![]() $\mathbb {C}$,
$\mathbb {C}$, ![]() ${\overline {\mathbb {F}}_p}$,
${\overline {\mathbb {F}}_p}$, ![]() $\mathbb {Q}_p$, or
$\mathbb {Q}_p$, or ![]() $\mathbb {C}_p$), we consider the space of continuous
$\mathbb {C}_p$), we consider the space of continuous ![]() $p$-adic automorphic forms on
$p$-adic automorphic forms on ![]() $D^\times$ with coefficients in
$D^\times$ with coefficients in ![]() $R$ and prime-to-
$R$ and prime-to-![]() $p$ level
$p$ level ![]() $K^p$,
$K^p$,
For ![]() $R$ totally disconnected (e.g.
$R$ totally disconnected (e.g. ![]() ${\overline {\mathbb {F}}_p}$,
${\overline {\mathbb {F}}_p}$, ![]() $\mathbb {Q}_p$, or
$\mathbb {Q}_p$, or ![]() $\mathbb {C}_p$), the archimedean component can be removed, and we have an identification
$\mathbb {C}_p$), the archimedean component can be removed, and we have an identification
Note that ![]() $D^\times (\mathbb {Q}) \backslash D^\times (\mathbb {A}_f) / K^p$ is a profinite set. Moreover, by choosing coset representatives, it can be identified with a finite disjoint union of compact open subgroups of
$D^\times (\mathbb {Q}) \backslash D^\times (\mathbb {A}_f) / K^p$ is a profinite set. Moreover, by choosing coset representatives, it can be identified with a finite disjoint union of compact open subgroups of ![]() $D^\times (\mathbb {Q}_p)$, so that it is essentially a
$D^\times (\mathbb {Q}_p)$, so that it is essentially a ![]() $p$-adic object.
$p$-adic object.
The space ![]() $\mathcal {A}_{R}^{K^p}$ admits an action of the abstract double-coset Hecke algebra
$\mathcal {A}_{R}^{K^p}$ admits an action of the abstract double-coset Hecke algebra
and a commuting action of ![]() $D^\times (\mathbb {Q}_p)$. In this work, we study the spectral decomposition of
$D^\times (\mathbb {Q}_p)$. In this work, we study the spectral decomposition of ![]() $\mathcal {A}_{R}^{K_p}$ under the action of
$\mathcal {A}_{R}^{K_p}$ under the action of ![]() $\mathbb {T}_{\mathrm {abs}}$.
$\mathbb {T}_{\mathrm {abs}}$.
The classical Jacquet–Langlands correspondence [Reference Jacquet and LanglandsJL70], proved using analytic techniques, implies that, up to twisting, the eigensystems for ![]() $\mathbb {T}_{\mathrm {abs}}$ acting on
$\mathbb {T}_{\mathrm {abs}}$ acting on ![]() $\mathcal {A}_{\mathbb {C}}^{K^p}$ are a strict subset of those appearing in classical complex modular forms. The eigensystem attached to a cuspidal modular form appears on the quaternionic side if and only if the corresponding automorphic representation of
$\mathcal {A}_{\mathbb {C}}^{K^p}$ are a strict subset of those appearing in classical complex modular forms. The eigensystem attached to a cuspidal modular form appears on the quaternionic side if and only if the corresponding automorphic representation of ![]() $\mathrm {GL}_2$ is discrete series at
$\mathrm {GL}_2$ is discrete series at ![]() $p$.
$p$.
On the other hand, arguing with the geometry of mod ![]() $p$ modular curves, Serre [Reference SerreSer96] showed that the eigensystems arising in
$p$ modular curves, Serre [Reference SerreSer96] showed that the eigensystems arising in ![]() $\mathcal {A}_{{\overline {\mathbb {F}}_p}}^{K^p}$ are the same as those appearing in the space of mod
$\mathcal {A}_{{\overline {\mathbb {F}}_p}}^{K^p}$ are the same as those appearing in the space of mod ![]() $p$ modular forms (see Theorem 1.1.1 for a slight refinement of Serre's result). In particular, the gaps in the Jacquet–Langlands correspondence over
$p$ modular forms (see Theorem 1.1.1 for a slight refinement of Serre's result). In particular, the gaps in the Jacquet–Langlands correspondence over ![]() $\mathbb {C}$ disappear when working mod
$\mathbb {C}$ disappear when working mod ![]() $p$.
$p$.
The main result of this work is a natural lift of Serre's result to ![]() $\mathbb {Q}_p$: we use the geometry of the perfectoid modular curve at infinite level to show that the completed Hecke algebra of
$\mathbb {Q}_p$: we use the geometry of the perfectoid modular curve at infinite level to show that the completed Hecke algebra of ![]() $\mathcal {A}_{\mathbb {Q}_p}^{K^p}$ is isomorphic to the completed Hecke algebra of
$\mathcal {A}_{\mathbb {Q}_p}^{K^p}$ is isomorphic to the completed Hecke algebra of ![]() $p$-adic modular forms (see Theorem A for a precise statement).
$p$-adic modular forms (see Theorem A for a precise statement).
Theorem A is compatible with the classical Jacquet–Langlands correspondence: the eigensystems appearing in classical complex quaternionic automorphic forms can be identified with the eigensystems appearing in ![]() $\mathcal {A}_{\mathbb {Q}_p}^{K_p}$ such that the corresponding eigenspace contains a vector which, up to a twist, transforms via an algebraic representation of
$\mathcal {A}_{\mathbb {Q}_p}^{K_p}$ such that the corresponding eigenspace contains a vector which, up to a twist, transforms via an algebraic representation of ![]() $D^\times (\mathbb {Q}_p)$ after restriction to a sufficiently small compact open subgroup. Thus, Theorem A can be interpreted as saying that there is a
$D^\times (\mathbb {Q}_p)$ after restriction to a sufficiently small compact open subgroup. Thus, Theorem A can be interpreted as saying that there is a ![]() $p$-adic Jacquet–Langlands correspondence that fills in the gaps in the classical Jacquet–Langlands correspondence. As our proof of the
$p$-adic Jacquet–Langlands correspondence that fills in the gaps in the classical Jacquet–Langlands correspondence. As our proof of the ![]() $p$-adic correspondence is independent of the classical correspondence, we also obtain a new proof that Galois representations can be attached to quaternionic automorphic forms (Corollary B).
$p$-adic correspondence is independent of the classical correspondence, we also obtain a new proof that Galois representations can be attached to quaternionic automorphic forms (Corollary B).
Both Theorems 1.1.1 and A are purely spectral Jacquet–Langlands correspondences, in the sense that they compare spectral information for a family of prime-to-![]() $p$ Hecke operators acting on two different spaces but say little else relating the structure of these spaces; in particular, we make no attempt here to describe the local
$p$ Hecke operators acting on two different spaces but say little else relating the structure of these spaces; in particular, we make no attempt here to describe the local ![]() $D^\times (\mathbb {Q}_p)$-representation appearing in a fixed Hecke eigenspace. Nevertheless, some of the methods employed in the proofs of Theorems 1.1.1 and A can be used provide significant information about these local representations, and we plan to return to this in future work (see § 1.3 for further discussion).
$D^\times (\mathbb {Q}_p)$-representation appearing in a fixed Hecke eigenspace. Nevertheless, some of the methods employed in the proofs of Theorems 1.1.1 and A can be used provide significant information about these local representations, and we plan to return to this in future work (see § 1.3 for further discussion).
1.1 Serre's spectral mod  $p$ Jacquet–Langlands correspondence
$p$ Jacquet–Langlands correspondence
Before discussing our results and techniques further, we take a detour to give a precise statement of Serre's [Reference SerreSer96] mod ![]() $p$ correspondence.
$p$ correspondence.
If we fix an isomorphism
then we obtain an action of the Hecke algebra ![]() $\mathbb {T}_\mathrm {abs}$ on the space
$\mathbb {T}_\mathrm {abs}$ on the space ![]() $\mathcal {M}_{{\overline {\mathbb {F}}_p}}^{K^p}$ of mod
$\mathcal {M}_{{\overline {\mathbb {F}}_p}}^{K^p}$ of mod ![]() $p$ modular forms of prime-to-
$p$ modular forms of prime-to-![]() $p$ level
$p$ level ![]() $K^p$. In a 1987 letter to Tate, Serre [Reference SerreSer96] proved a mod
$K^p$. In a 1987 letter to Tate, Serre [Reference SerreSer96] proved a mod ![]() $p$ Jacquet–Langlands correspondence comparing the spectral decompositions of
$p$ Jacquet–Langlands correspondence comparing the spectral decompositions of ![]() $\mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}$ and
$\mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}$ and ![]() $\mathcal {M}_{{\overline {\mathbb {F}}_p}}^{K^p}$. We state below a slight strengthening of his result, which follows essentially from Serre's proof.Footnote 1 First, some notation.
$\mathcal {M}_{{\overline {\mathbb {F}}_p}}^{K^p}$. We state below a slight strengthening of his result, which follows essentially from Serre's proof.Footnote 1 First, some notation.
Suppose ![]() $\mathbb {T}' \subset \mathbb {T}_{\mathrm {abs}}$ is a commutative sub-algebra and
$\mathbb {T}' \subset \mathbb {T}_{\mathrm {abs}}$ is a commutative sub-algebra and ![]() $\chi : \mathbb {T}' \rightarrow {\overline {\mathbb {F}}_p}$ is a character. Then, if
$\chi : \mathbb {T}' \rightarrow {\overline {\mathbb {F}}_p}$ is a character. Then, if ![]() $\mathbb {T}'$ acts on an
$\mathbb {T}'$ acts on an ![]() ${\overline {\mathbb {F}}_p}$-vector space
${\overline {\mathbb {F}}_p}$-vector space ![]() $V$, we may consider the
$V$, we may consider the ![]() $\chi$-eigenspace
$\chi$-eigenspace ![]() $V[\chi ]$. If we write
$V[\chi ]$. If we write ![]() $\mathfrak {m}_\chi := \ker \chi$, we may also consider the generalized
$\mathfrak {m}_\chi := \ker \chi$, we may also consider the generalized ![]() $\chi$-eigenspace
$\chi$-eigenspace ![]() $V_{\mathfrak {m}_\chi }$ (that is, the subset of elements killed by a power of
$V_{\mathfrak {m}_\chi }$ (that is, the subset of elements killed by a power of ![]() $\mathfrak {m}_\chi$).
$\mathfrak {m}_\chi$).
Theorem 1.1.1 (Serre)
Let ![]() $\mathbb {T}' \subset \mathbb {T}_{\mathrm {abs}}$ be a commutative sub-algebra. Then, there is a finite collection of characters
$\mathbb {T}' \subset \mathbb {T}_{\mathrm {abs}}$ be a commutative sub-algebra. Then, there is a finite collection of characters ![]() $\chi _i: \mathbb {T}' \rightarrow {\overline {\mathbb {F}}_p}$ with kernels
$\chi _i: \mathbb {T}' \rightarrow {\overline {\mathbb {F}}_p}$ with kernels ![]() $\mathfrak {m}_i$ such that:
$\mathfrak {m}_i$ such that:
(i) for each
 $i$,
$i$,  $\big (\mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}\big )_{\mathfrak {m}_i}$ and
$\big (\mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}\big )_{\mathfrak {m}_i}$ and  $\big (\mathcal {M}^{K^p}_{{\overline {\mathbb {F}}_p}}\big )_{\mathfrak {m}_i}$ are non-zero; in particular
$\big (\mathcal {M}^{K^p}_{{\overline {\mathbb {F}}_p}}\big )_{\mathfrak {m}_i}$ are non-zero; in particular
 \[ \mathcal{A}^{K^p}_{{\overline{\mathbb{F}}_p}}[\chi_i] \neq 0 \quad \text{and} \quad \mathcal{M}^{K^p}_{{\overline{\mathbb{F}}_p}}[\chi_i] \neq 0; \]
\[ \mathcal{A}^{K^p}_{{\overline{\mathbb{F}}_p}}[\chi_i] \neq 0 \quad \text{and} \quad \mathcal{M}^{K^p}_{{\overline{\mathbb{F}}_p}}[\chi_i] \neq 0; \](ii) there are direct sum decompositions
 \[ \mathcal{A}^{K^p}_{{\overline{\mathbb{F}}_p}} = \bigoplus_i \big( \mathcal{A}^{K^p}_{{\overline{\mathbb{F}}_p}} \big)_{\mathfrak{m}_{\chi_i}} \quad \text{and} \quad \mathcal{M}_{{\overline{\mathbb{F}}_p}}^{K^p} = \bigoplus_i \big( \mathcal{M}_{{\overline{\mathbb{F}}_p}}^{K^p}\big)_{\mathfrak{m}_{\chi_i}}. \]
\[ \mathcal{A}^{K^p}_{{\overline{\mathbb{F}}_p}} = \bigoplus_i \big( \mathcal{A}^{K^p}_{{\overline{\mathbb{F}}_p}} \big)_{\mathfrak{m}_{\chi_i}} \quad \text{and} \quad \mathcal{M}_{{\overline{\mathbb{F}}_p}}^{K^p} = \bigoplus_i \big( \mathcal{M}_{{\overline{\mathbb{F}}_p}}^{K^p}\big)_{\mathfrak{m}_{\chi_i}}. \]
In other words, the Hecke eigensystems appearing in mod ![]() $p$ quaternionic automorphic forms are precisely those appearing in mod
$p$ quaternionic automorphic forms are precisely those appearing in mod ![]() $p$ modular forms. This stands in contrast to the classical Jacquet–Langlands correspondence, where the eigensystems appearing in quaternionic forms are a strict subset of those appearing in modular forms. The following example gives a concrete illustration.
$p$ modular forms. This stands in contrast to the classical Jacquet–Langlands correspondence, where the eigensystems appearing in quaternionic forms are a strict subset of those appearing in modular forms. The following example gives a concrete illustration.
Example 1.1.2 The discriminant form, represented by the Ramanujan series
is a weight 12 level-one cuspidal eigenform whose corresponding automorphic representation is principal series at every prime ![]() $p$. Thus, the classical Jacquet–Langlands correspondence says that its Hecke eigensystem, encoded by the coefficients
$p$. Thus, the classical Jacquet–Langlands correspondence says that its Hecke eigensystem, encoded by the coefficients ![]() $\tau (\ell )$ for
$\tau (\ell )$ for ![]() $\ell$ prime, does not appear in the space of classical automorphic forms on
$\ell$ prime, does not appear in the space of classical automorphic forms on ![]() $D^\times$ for any prime
$D^\times$ for any prime ![]() $p$ (recall
$p$ (recall ![]() $p$ appears in the definition of
$p$ appears in the definition of ![]() $D^\times$). By contrast, Theorem 1.1.1 shows that the coefficients
$D^\times$). By contrast, Theorem 1.1.1 shows that the coefficients ![]() $\tau (\ell ) \mod p$ for
$\tau (\ell ) \mod p$ for ![]() $\ell \neq p$ are remembered by a mod
$\ell \neq p$ are remembered by a mod ![]() $p$ quaternionic automorphic form on
$p$ quaternionic automorphic form on ![]() $D^\times$. A similar phenomenon occurs in our
$D^\times$. A similar phenomenon occurs in our ![]() $p$-adic correspondence, which remembers the numbers
$p$-adic correspondence, which remembers the numbers ![]() $\tau (\ell )$ on the nose.
$\tau (\ell )$ on the nose.
1.2 A spectral  $p$-adic Jacquet–Langlands correspondence
$p$-adic Jacquet–Langlands correspondence
1.2.1 Serre's question
Serre ended his letter to Tate with a list of questions inspired by the mod ![]() $p$ Jacquet–Langlands correspondence. One of these suggests an analogous study relating
$p$ Jacquet–Langlands correspondence. One of these suggests an analogous study relating ![]() $\mathcal {A}_{\overline {\mathbb {Q}_p}}^{K^p}$ to
$\mathcal {A}_{\overline {\mathbb {Q}_p}}^{K^p}$ to ![]() $p$-adic modular forms.
$p$-adic modular forms.
Analogues ![]() $p$-adiques. Au lieu de regarder les fonctions localement constantes sur
$p$-adiques. Au lieu de regarder les fonctions localement constantes sur ![]() $D_\mathbb {A}^\times / D_{\mathbb {Q}}^\times$ á valeurs dans
$D_\mathbb {A}^\times / D_{\mathbb {Q}}^\times$ á valeurs dans ![]() $\mathbb {C}$, il serait plus amusant de regarder celles à valeurs dans
$\mathbb {C}$, il serait plus amusant de regarder celles à valeurs dans ![]() $\overline {\mathbb {Q}}_p$. Si l'on décompose
$\overline {\mathbb {Q}}_p$. Si l'on décompose ![]() $\mathbb {A}$ en
$\mathbb {A}$ en ![]() $\mathbb {Q}_p \times \mathbb {A}'$, on leur imposerait d’être localement constantes par rapport à la variable dans
$\mathbb {Q}_p \times \mathbb {A}'$, on leur imposerait d’être localement constantes par rapport à la variable dans ![]() $D_{\mathbb {A}'}$ et d’être continues (ou analytiques, ou davantage) par rapport à la variable dans
$D_{\mathbb {A}'}$ et d’être continues (ou analytiques, ou davantage) par rapport à la variable dans ![]() $D_p$…Y aurait-il des représentations galoisiennes
$D_p$…Y aurait-il des représentations galoisiennes ![]() $p$-adiques associées a de telles fonctions, supposées fonctions propres des opérateurs de Hecke? Peut-on interpréter les constructions de Hida (et Mazur) dans un tel style? Je n'en ai aucune idée. (Serre [Reference SerreSer96, paragraph (26)].)
$p$-adiques associées a de telles fonctions, supposées fonctions propres des opérateurs de Hecke? Peut-on interpréter les constructions de Hida (et Mazur) dans un tel style? Je n'en ai aucune idée. (Serre [Reference SerreSer96, paragraph (26)].)
Our main result, Theorem A, shows that the answers to Serre's questions are, largely, yes. In particular, Theorem A implies that Galois representations can be attached to ![]() $p$-adic quaternionic eigenforms (Corollary B).
$p$-adic quaternionic eigenforms (Corollary B).
1.2.2 A homeomorphism of completed Hecke algebras
The space ![]() $\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ of
$\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ of ![]() $p$-adic quaternionic automorphic forms is a
$p$-adic quaternionic automorphic forms is a ![]() $\mathbb {Q}_p$-Banach space with respect to the sup norm and the action of
$\mathbb {Q}_p$-Banach space with respect to the sup norm and the action of ![]() $\mathbb {T}_\mathrm {abs}$ is by bounded linear operators. For any subalgebra
$\mathbb {T}_\mathrm {abs}$ is by bounded linear operators. For any subalgebra ![]() $\mathbb {T}'\subset \mathbb {T}_\mathrm {abs}$ we thus obtain a completed Hecke algebra
$\mathbb {T}'\subset \mathbb {T}_\mathrm {abs}$ we thus obtain a completed Hecke algebra ![]() ${\mathbb {T}'}^\wedge _{\mathcal {A}^{K^p}_{\mathbb {Q}_p}}$ by taking the closure of the image of
${\mathbb {T}'}^\wedge _{\mathcal {A}^{K^p}_{\mathbb {Q}_p}}$ by taking the closure of the image of ![]() $\mathbb {T}'$ in the algebra of bounded linear operators on
$\mathbb {T}'$ in the algebra of bounded linear operators on ![]() $\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ (equipped with the topology of pointwise convergence; see § 2.4 for details). It is a topological
$\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ (equipped with the topology of pointwise convergence; see § 2.4 for details). It is a topological ![]() $\mathbb {Z}_p$-algebra.
$\mathbb {Z}_p$-algebra.
As in the mod ![]() $p$ case, we would like to compare the Hecke action on
$p$ case, we would like to compare the Hecke action on ![]() $\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ to a Hecke action on a space of modular forms; in this case, we do so by comparing completed Hecke algebras. To that end: Serre [Reference SerreSer73] constructed natural spaces of
$\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ to a Hecke action on a space of modular forms; in this case, we do so by comparing completed Hecke algebras. To that end: Serre [Reference SerreSer73] constructed natural spaces of ![]() $p$-adic modular forms by completing spaces of classical modular forms for the
$p$-adic modular forms by completing spaces of classical modular forms for the ![]() $p$-adic topology on
$p$-adic topology on ![]() $q$-expansions (these spaces were then interpreted geometrically by Katz [Reference KatzKat75a, Reference KatzKat75b]). In particular, one obtains a natural
$q$-expansions (these spaces were then interpreted geometrically by Katz [Reference KatzKat75a, Reference KatzKat75b]). In particular, one obtains a natural ![]() $\mathbb {Q}_p$-Banach space
$\mathbb {Q}_p$-Banach space ![]() $\mathcal {M}_{p\text {-}\mathrm {adic}}^{K^p}$ of
$\mathcal {M}_{p\text {-}\mathrm {adic}}^{K^p}$ of ![]() $p$-adic modular forms of prime-to-
$p$-adic modular forms of prime-to-![]() $p$ level
$p$ level ![]() $K^p$ equipped with an action of
$K^p$ equipped with an action of ![]() $\mathbb {T}_\mathrm {abs}$ by bounded linear operators and, thus, a completed Hecke algebra
$\mathbb {T}_\mathrm {abs}$ by bounded linear operators and, thus, a completed Hecke algebra ![]() ${\mathbb {T}'}^\wedge _{\mathcal {M}^{K^p}_{p\text {-}\mathrm {adic}}}$. Our main result is as follows.
${\mathbb {T}'}^\wedge _{\mathcal {M}^{K^p}_{p\text {-}\mathrm {adic}}}$. Our main result is as follows.
Theorem A For any sub-algebra ![]() $\mathbb {T}' \subset \mathbb {T}_\mathrm {abs}$, the identity map
$\mathbb {T}' \subset \mathbb {T}_\mathrm {abs}$, the identity map ![]() $\mathbb {T}' \rightarrow \mathbb {T}'$ extends to a canonical isomorphism of topological
$\mathbb {T}' \rightarrow \mathbb {T}'$ extends to a canonical isomorphism of topological ![]() $\mathbb {Z}_p$-algebras
$\mathbb {Z}_p$-algebras
Theorem A implies Theorem 1.1.1 (as essentially explained in § 4.5; the point is that the maximal ideals in Theorem 1.1.1 correspond to the open maximal ideals in the corresponding completed Hecke algebras), and gives a natural lift to characteristic zero suitable, e.g., for the construction of Galois representations. Our proof lifts Serre's approach via the mod ![]() $p$ geometry of modular curves to characteristic zero by using the
$p$ geometry of modular curves to characteristic zero by using the ![]() $p$-adic geometry of infinite level modular curves.
$p$-adic geometry of infinite level modular curves.
Remark 1.2.3 The completed Hecke algebras do not change if we replace ![]() $\mathbb {Q}_p$ with a finite extension, or even
$\mathbb {Q}_p$ with a finite extension, or even ![]() $\mathbb {C}_p$ (and, indeed, this invariance under base change plays an important role in our proof). Thus, although Serre in his letter quoted above suggests the study of
$\mathbb {C}_p$ (and, indeed, this invariance under base change plays an important role in our proof). Thus, although Serre in his letter quoted above suggests the study of ![]() $\mathcal {A}^{K^p}_{\overline {\mathbb {Q}}_p}$, it is natural in our setup to work over
$\mathcal {A}^{K^p}_{\overline {\mathbb {Q}}_p}$, it is natural in our setup to work over ![]() $\mathbb {Q}_p$. In particular, an eigenform in
$\mathbb {Q}_p$. In particular, an eigenform in ![]() $\mathcal {A}^{K^p}_{\overline {\mathbb {Q}}_p}$ will still give rise to a
$\mathcal {A}^{K^p}_{\overline {\mathbb {Q}}_p}$ will still give rise to a ![]() $\overline {\mathbb {Q}}_p$-valued character of
$\overline {\mathbb {Q}}_p$-valued character of ![]() ${\mathbb {T}'}^\wedge _{\mathcal {A}^{K^p}_{\mathbb {Q}_p}}$.
${\mathbb {T}'}^\wedge _{\mathcal {A}^{K^p}_{\mathbb {Q}_p}}$.
1.2.4 Completed cohomology
By a result of Emerton [Reference EmertonEme11] (building on work by Hida), ![]() ${{\mathbb {T}}'}^\wedge _{\mathcal {M}^{K^p}_{p\text {-}\mathrm {adic}}}$ is equal to the completed Hecke algebra of
${{\mathbb {T}}'}^\wedge _{\mathcal {M}^{K^p}_{p\text {-}\mathrm {adic}}}$ is equal to the completed Hecke algebra of ![]() $\mathbb {T}'$ acting on the completed cohomology of modular curves. On the other hand,
$\mathbb {T}'$ acting on the completed cohomology of modular curves. On the other hand, ![]() $\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ is the completed cohomology at level
$\mathcal {A}^{K^p}_{\mathbb {Q}_p}$ is the completed cohomology at level ![]() $K^p$ for
$K^p$ for ![]() $D^\times$. Hence, we also obtain a homeomorphism between the completed Hecke algebras for the completed cohomology of
$D^\times$. Hence, we also obtain a homeomorphism between the completed Hecke algebras for the completed cohomology of ![]() $\mathrm {GL}_2$ and
$\mathrm {GL}_2$ and ![]() $D^\times$. In fact, our proof passes first through this equivalence then uses the result of Emerton, which we establish more carefully along with some other identifications in § 5.7.
$D^\times$. In fact, our proof passes first through this equivalence then uses the result of Emerton, which we establish more carefully along with some other identifications in § 5.7.
1.2.5 Galois representations
Let ![]() $\mathbb {T}_{\mathrm {tame}} \subset \mathbb {T}_\mathrm {abs}$ be the tame Hecke algebra of level
$\mathbb {T}_{\mathrm {tame}} \subset \mathbb {T}_\mathrm {abs}$ be the tame Hecke algebra of level ![]() $K^p$, i.e. the commutative sub-algebra generated by the Hecke operators at
$K^p$, i.e. the commutative sub-algebra generated by the Hecke operators at ![]() $\ell$ for primes
$\ell$ for primes ![]() $\ell \neq p$ at which
$\ell \neq p$ at which ![]() $K^p$ factors as
$K^p$ factors as ![]() $K^{p,\ell }K_\ell$ for
$K^{p,\ell }K_\ell$ for ![]() $K^{p,\ell } \subset D^\times (\mathbb {A}_f^{(pl)})$ and
$K^{p,\ell } \subset D^\times (\mathbb {A}_f^{(pl)})$ and ![]() $K_\ell \subset D^\times (\mathbb {Q}_l)$ a maximal compact subgroup. For each such
$K_\ell \subset D^\times (\mathbb {Q}_l)$ a maximal compact subgroup. For each such ![]() $\ell$ we write
$\ell$ we write ![]() $T_\ell$ for the standard Hecke operator. Combining Theorem A with known results for
$T_\ell$ for the standard Hecke operator. Combining Theorem A with known results for ![]() ${\mathbb {T}'}^\wedge _{\mathcal {M}^{K^p}_{p\text {-}\mathrm {adic}}}$ gives the following result.
${\mathbb {T}'}^\wedge _{\mathcal {M}^{K^p}_{p\text {-}\mathrm {adic}}}$ gives the following result.
Corollary B If ![]() $\chi : \mathbb {T}^\wedge _{\mathrm {tame}, \mathcal {A}^{K^p}_{\mathbb {Q}_p}} \rightarrow \mathbb {C}_p$ is a continuous character then there exists a unique semisimple continuous representation
$\chi : \mathbb {T}^\wedge _{\mathrm {tame}, \mathcal {A}^{K^p}_{\mathbb {Q}_p}} \rightarrow \mathbb {C}_p$ is a continuous character then there exists a unique semisimple continuous representation
unramified at ![]() $\ell$ as above and such that
$\ell$ as above and such that ![]() $\mathrm {Tr}(\rho (\mathrm {Frob}_\ell ))=\chi (T_\ell )$.
$\mathrm {Tr}(\rho (\mathrm {Frob}_\ell ))=\chi (T_\ell )$.
One can obtain such a ![]() $\chi$ from a quaternionic eigenform as in Remark 1.2.3, and thus Corollary B attaches Galois representations to these eigenforms.
$\chi$ from a quaternionic eigenform as in Remark 1.2.3, and thus Corollary B attaches Galois representations to these eigenforms.
1.2.6 Work of Emerton
Corollary B can also be deduced from the classical Jacquet–Langlands correspondence. In fact, a version of Theorem A after localizing at a maximal ideal was first shown by Emerton [Reference EmertonEme14, 3.3.2] by reversing this argument: the classical correspondence gives rise to a surjective map of completed Hecke algebras
(which is enough to obtain Corollary B), and then strong results in the deformation theory of Galois representations can be used to deduce that this map is an isomorphism after localizing at a maximal ideal ![]() $\mathfrak {m}$ (under minor hypotheses on
$\mathfrak {m}$ (under minor hypotheses on ![]() $\mathfrak {m}$).
$\mathfrak {m}$).
By contrast, our proof is based entirely on the ![]() $p$-adic geometry of modular curves. Thus, we obtain a new proof of Corollary B that is independent of the classical Jacquet–Langlands correspondence, and our proof of Theorem A does not use any
$p$-adic geometry of modular curves. Thus, we obtain a new proof of Corollary B that is independent of the classical Jacquet–Langlands correspondence, and our proof of Theorem A does not use any ![]() $R=\mathbb {T}$ theorems or other results on Galois deformations.
$R=\mathbb {T}$ theorems or other results on Galois deformations.
1.3 Eigenspaces and the local  $p$-adic Jacquet–Langlands correspondence
$p$-adic Jacquet–Langlands correspondence
One failing of Theorem A as stated is that it says nothing about the ![]() $D^\times (\mathbb {Q}_p)$-representation appearing in the eigenspace in
$D^\times (\mathbb {Q}_p)$-representation appearing in the eigenspace in ![]() $\mathcal {A}^{K^p}_{\overline {\mathbb {Q}}_p}$ attached to a character of
$\mathcal {A}^{K^p}_{\overline {\mathbb {Q}}_p}$ attached to a character of ![]() ${\mathbb {T}'}^\wedge _{\mathcal {A}^{K^p}_{\mathbb {Q}_p}}$ valued in a finite extension of
${\mathbb {T}'}^\wedge _{\mathcal {A}^{K^p}_{\mathbb {Q}_p}}$ valued in a finite extension of ![]() $\mathbb {Q}_p$. Indeed, because completed Hecke algebras are formed by compiling congruences of eigensystems, which may not be reflected in congruences of eigenvectors, one does not even know whether such an eigenspace is non-empty. On the other hand, one expects that it is always non-empty, and that the
$\mathbb {Q}_p$. Indeed, because completed Hecke algebras are formed by compiling congruences of eigensystems, which may not be reflected in congruences of eigenvectors, one does not even know whether such an eigenspace is non-empty. On the other hand, one expects that it is always non-empty, and that the ![]() $D^\times (\mathbb {Q}_p)$-representation appearing is essentially that constructed in the local correspondences of Knight [Reference KnightKni16] and Scholze [Reference ScholzeSch18].
$D^\times (\mathbb {Q}_p)$-representation appearing is essentially that constructed in the local correspondences of Knight [Reference KnightKni16] and Scholze [Reference ScholzeSch18].
In the course of the proof of Theorem A, we produce explicit eigenvectors that show this eigenspace is non-empty at least for eigensystems attached to classical modular forms. In the author's thesis [Reference HoweHow17], it was explained how to refine this construction so that it applies more generally to overconvergent modular forms, and it was also verified that the eigenvectors obtained are never locally algebraic for the action of ![]() $D^\times (\mathbb {Q}_p)$ (and, thus, in some sense are new, i.e. not obtainable by combining the classical Jacquet–Langlands correspondence and Gross's [Reference GrossGros99] theory of algebraic automorphic forms, which together furnish a complete description of the locally algebraic vectors). One can now do better in at least two ways.
$D^\times (\mathbb {Q}_p)$ (and, thus, in some sense are new, i.e. not obtainable by combining the classical Jacquet–Langlands correspondence and Gross's [Reference GrossGros99] theory of algebraic automorphic forms, which together furnish a complete description of the locally algebraic vectors). One can now do better in at least two ways.
(i) An overconvergent modular form more canonically gives rise to a non-zero map to the corresponding eigenspace in quaternionic automorphic forms from a purely local representation of
 $D^\times (\mathbb {Q}_p)$ constructed as a space of distributions on the Lubin–Tate tower. The eigenvector referred to above is obtained as the image of a Dirac delta function under this map. By studying this local representation we can obtain considerably more, though still incomplete, information about the eigenspace.
$D^\times (\mathbb {Q}_p)$ constructed as a space of distributions on the Lubin–Tate tower. The eigenvector referred to above is obtained as the image of a Dirac delta function under this map. By studying this local representation we can obtain considerably more, though still incomplete, information about the eigenspace.(ii) Combining this with recent results of Pan [Reference PanPan22] on the ubiquity of overconvergent modular forms, we find that, under some minor hypotheses on the associated Galois representation, the eigenspace is always non-empty.
Both points will be explained further in future work.
1.4 Outline
In § 2 we give some preliminaries, including in § 2.4 some results on comparing completed Hecke algebras that will be essential in the proof of Theorem A. In § 3 we set up our moduli problems for elliptic curves and recall the basic adelic setup for modular forms (classical, mod ![]() $p$, and
$p$, and ![]() $p$-adic). The main result of the section is Theorem 3.7.1, which identifies the supersingular Igusa variety with a quaternionic coset, one of the key ingredients in the proof of both the mod
$p$-adic). The main result of the section is Theorem 3.7.1, which identifies the supersingular Igusa variety with a quaternionic coset, one of the key ingredients in the proof of both the mod ![]() $p$ and
$p$ and ![]() $p$-adic correspondence. Some aspects of the way we set up our moduli problems may be of independent interest; for more, we refer the reader to the introduction of § 3.
$p$-adic correspondence. Some aspects of the way we set up our moduli problems may be of independent interest; for more, we refer the reader to the introduction of § 3.
In § 4 we prove the version of Serre's mod ![]() $p$ Jacquet–Langlands correspondence stated above as Theorem 1.1.1. The proof we give is essentially that of Serre, but we emphasize carefully from the beginning the role of uniformization of the supersingular locus by the supersingular Igusa variety, which, by the above, is just a quaternionic coset. In particular, modular forms can be evaluated to quaternionic automorphic forms after choosing a trivialization of the modular bundle along the Igusa variety. A mod
$p$ Jacquet–Langlands correspondence stated above as Theorem 1.1.1. The proof we give is essentially that of Serre, but we emphasize carefully from the beginning the role of uniformization of the supersingular locus by the supersingular Igusa variety, which, by the above, is just a quaternionic coset. In particular, modular forms can be evaluated to quaternionic automorphic forms after choosing a trivialization of the modular bundle along the Igusa variety. A mod ![]() $p$ modular form can have zeros or poles along the supersingular locus, but these can be cleared Hecke-equivariantly using the Hasse invariant in order to obtain a clean comparison of the corresponding Hecke algebras. When
$p$ modular form can have zeros or poles along the supersingular locus, but these can be cleared Hecke-equivariantly using the Hasse invariant in order to obtain a clean comparison of the corresponding Hecke algebras. When ![]() $p =2 \text { or } 3$, this proof actually falls just short of the full Theorem 1.1.1, but in § 4.5 we explain how to obtain the full statement as a consequence of Theorem A.
$p =2 \text { or } 3$, this proof actually falls just short of the full Theorem 1.1.1, but in § 4.5 we explain how to obtain the full statement as a consequence of Theorem A.
In § 5 we prove Theorem A. Here the quaternionic coset, again in its avatar as the supersingular Igusa variety, arises naturally as a fiber of the Hodge–Tate period map in the infinite level perfectoid modular curve (as in [Reference Caraiani and ScholzeCS17]). Thus, we can evaluate modular forms to ![]() $p$-adic quaternionic automorphic forms after choosing a trivialization of the modular bundle on this fiber. A simple argument shows this evaluation map is injective; the other key property we need is density of the image. We establish this with the help of Scholze's fake Hasse invariants.Footnote 2 These properties of the evaluation map are combined with the results of § 2.4 to deduce Theorem A.
$p$-adic quaternionic automorphic forms after choosing a trivialization of the modular bundle on this fiber. A simple argument shows this evaluation map is injective; the other key property we need is density of the image. We establish this with the help of Scholze's fake Hasse invariants.Footnote 2 These properties of the evaluation map are combined with the results of § 2.4 to deduce Theorem A.
2. Preliminaries
2.1 Numbers
We fix a prime number ![]() $p$ and an algebraic closure
$p$ and an algebraic closure ![]() $\overline {\mathbb {Q}}_p$ of
$\overline {\mathbb {Q}}_p$ of ![]() $\mathbb {Q}_p$. We write
$\mathbb {Q}_p$. We write ![]() $\mathbb {C}_p$ for the completion of
$\mathbb {C}_p$ for the completion of ![]() $\overline {\mathbb {Q}}_p$. We denote by
$\overline {\mathbb {Q}}_p$. We denote by ![]() $\breve {\mathbb {Q}}_p\subset \mathbb {C}_p$ the completion of the maximal unramified extension of
$\breve {\mathbb {Q}}_p\subset \mathbb {C}_p$ the completion of the maximal unramified extension of ![]() $\mathbb {Q}_p$ in
$\mathbb {Q}_p$ in ![]() $\overline {\mathbb {Q}}_p$, and by
$\overline {\mathbb {Q}}_p$, and by ![]() $\breve {\mathbb {Z}}_p \subset \breve {\mathbb {Q}}_p$ the completion of the ring of integers in the maximal unramified extension. We write
$\breve {\mathbb {Z}}_p \subset \breve {\mathbb {Q}}_p$ the completion of the ring of integers in the maximal unramified extension. We write ![]() ${\overline {\mathbb {F}}_p}$ for
${\overline {\mathbb {F}}_p}$ for ![]() $\breve {\mathbb {Z}}_p/p$, an algebraically closed extension of
$\breve {\mathbb {Z}}_p/p$, an algebraically closed extension of ![]() $\mathbb {F}_p = \mathbb {Z}_p/p$. There is a canonical identification
$\mathbb {F}_p = \mathbb {Z}_p/p$. There is a canonical identification ![]() $W({\overline {\mathbb {F}}_p})=\breve {\mathbb {Z}}_p$, where
$W({\overline {\mathbb {F}}_p})=\breve {\mathbb {Z}}_p$, where ![]() $W(\bullet )$ denotes Witt vectors.
$W(\bullet )$ denotes Witt vectors.
We write ![]() $\mathbb {A}$ for the adèles of
$\mathbb {A}$ for the adèles of ![]() $\mathbb {Q}$,
$\mathbb {Q}$, ![]() $\mathbb {A}_f$ for the finite adèles, and
$\mathbb {A}_f$ for the finite adèles, and ![]() $\mathbb {A}_f^{(p)}$ for the finite prime-to-
$\mathbb {A}_f^{(p)}$ for the finite prime-to-![]() $p$ adèles. We write
$p$ adèles. We write ![]() $\widehat {\mathbb {Z}}$ for the profinite completion of
$\widehat {\mathbb {Z}}$ for the profinite completion of ![]() $\mathbb {Z}$ and
$\mathbb {Z}$ and ![]() $\widehat {\mathbb {Z}}^{(p)}$ for the prime-to-
$\widehat {\mathbb {Z}}^{(p)}$ for the prime-to-![]() $p$ profinite completion. We have canonical identifications
$p$ profinite completion. We have canonical identifications
and inclusions ![]() $\widehat {\mathbb {Z}} \subset \mathbb {A}_f$ and
$\widehat {\mathbb {Z}} \subset \mathbb {A}_f$ and ![]() $\widehat {\mathbb {Z}}^{(p)} \subset \mathbb {A}_f^{(p)}$ inducing isomorphisms
$\widehat {\mathbb {Z}}^{(p)} \subset \mathbb {A}_f^{(p)}$ inducing isomorphisms
Here ![]() $\mathbb {Z}_{(p)}$ is interpreted via the notation
$\mathbb {Z}_{(p)}$ is interpreted via the notation ![]() $R_{\mathfrak {p}}$ for
$R_{\mathfrak {p}}$ for ![]() $R$ a ring and
$R$ a ring and ![]() $\mathfrak {p}$ a prime ideal of
$\mathfrak {p}$ a prime ideal of ![]() $R$, which means the localization of
$R$, which means the localization of ![]() $R$ by the multiplicative system
$R$ by the multiplicative system ![]() $R\backslash \mathfrak {p}$.
$R\backslash \mathfrak {p}$.
2.2 Topological spaces, lisse sheaves, and torsors
Given a topological space ![]() $T$, we denote by
$T$, we denote by ![]() $\underline {T}$ the topological constant sheaf with value
$\underline {T}$ the topological constant sheaf with value ![]() $T$, that is, the functor on schemes
$T$, that is, the functor on schemes
where ![]() $|S|$ denotes the underlying topological space of
$|S|$ denotes the underlying topological space of ![]() $S$. When
$S$. When ![]() $T$ is a profinite set, it is represented by
$T$ is a profinite set, it is represented by ![]() $\operatorname {SpecCont}(T, \mathbb {Z})$, where
$\operatorname {SpecCont}(T, \mathbb {Z})$, where ![]() $\mathbb {Z}$ is equipped with the discrete topology (so that the continuous functions are just locally constant). It is, in particular, a sheaf for the pro-étale topology of [Reference Bhatt and ScholzeBS15].
$\mathbb {Z}$ is equipped with the discrete topology (so that the continuous functions are just locally constant). It is, in particular, a sheaf for the pro-étale topology of [Reference Bhatt and ScholzeBS15].
We also adopt the framework of [Reference Bhatt and ScholzeBS15] as our formalism for lisse adelic sheaves.Footnote 3 Thus, by a lisse ![]() $\mathbb {A}_f$-sheaf on a scheme
$\mathbb {A}_f$-sheaf on a scheme ![]() $S$, we mean a locally free of finite rank
$S$, we mean a locally free of finite rank ![]() $\underline {\mathbb {A}_f}$ module on
$\underline {\mathbb {A}_f}$ module on ![]() $S_\mathrm {pro\acute {e}t}$, and similarly for
$S_\mathrm {pro\acute {e}t}$, and similarly for ![]() $\widehat {\mathbb {Z}}$,
$\widehat {\mathbb {Z}}$, ![]() $\mathbb {A}_f^{(p)}$,
$\mathbb {A}_f^{(p)}$, ![]() $\widehat {\mathbb {Z}}^{(p)}$,
$\widehat {\mathbb {Z}}^{(p)}$, ![]() $\mathbb {Q}_p,$
$\mathbb {Q}_p,$ ![]() $\mathbb {Z}_p$, etc. A lisse
$\mathbb {Z}_p$, etc. A lisse ![]() $\widehat {\mathbb {Z}}$-sheaf is equivalent to a compatible system of locally free
$\widehat {\mathbb {Z}}$-sheaf is equivalent to a compatible system of locally free ![]() $\underline {\mathbb {Z}/n\mathbb {Z}}$ modules of finite rank (on either
$\underline {\mathbb {Z}/n\mathbb {Z}}$ modules of finite rank (on either ![]() $S_\mathrm {\acute {e}t}$ or
$S_\mathrm {\acute {e}t}$ or ![]() $S_\mathrm {pro\acute {e}t}$: a locally free
$S_\mathrm {pro\acute {e}t}$: a locally free ![]() $\underline {\mathbb {Z}/n\mathbb {Z}}$ module on
$\underline {\mathbb {Z}/n\mathbb {Z}}$ module on ![]() $S_\mathrm {pro\acute {e}t}$ is automatically classical because
$S_\mathrm {pro\acute {e}t}$ is automatically classical because ![]() $\mathbb {Z}/n\mathbb {Z}$ is discrete), and similarly for
$\mathbb {Z}/n\mathbb {Z}$ is discrete), and similarly for ![]() $\widehat {\mathbb {Z}}^{(p)}$ and
$\widehat {\mathbb {Z}}^{(p)}$ and ![]() $\mathbb {Z}_p$.
$\mathbb {Z}_p$.
For ![]() $K$ a topological group, a (right)
$K$ a topological group, a (right) ![]() $K$-torsor on
$K$-torsor on ![]() $S_\mathrm {pro\acute {e}t}$ is a sheaf
$S_\mathrm {pro\acute {e}t}$ is a sheaf ![]() $\mathcal {K}$ equipped with an action
$\mathcal {K}$ equipped with an action ![]() $\mathcal {K} \times \underline {K} \rightarrow \mathcal {K}$ such that locally on
$\mathcal {K} \times \underline {K} \rightarrow \mathcal {K}$ such that locally on ![]() $S_\mathrm {pro\acute {e}t}$,
$S_\mathrm {pro\acute {e}t}$, ![]() $\mathcal {K} \cong \underline {K}$ with the action by right multiplication. In particular, if
$\mathcal {K} \cong \underline {K}$ with the action by right multiplication. In particular, if ![]() $A=\mathbb {A}_f, \widehat {\mathbb {Z}}, \mathbb {A}_f^{(p)}, \widehat {\mathbb {Z}}^{(p)}, \mathbb {Z}_p,\text {or } \mathbb {Q}_p,$ and
$A=\mathbb {A}_f, \widehat {\mathbb {Z}}, \mathbb {A}_f^{(p)}, \widehat {\mathbb {Z}}^{(p)}, \mathbb {Z}_p,\text {or } \mathbb {Q}_p,$ and ![]() $V$ is a lisse
$V$ is a lisse ![]() $A$-sheaf of rank
$A$-sheaf of rank ![]() $n$, then
$n$, then
is a ![]() $\mathrm {GL}_n(A)$-torsor (as in these cases
$\mathrm {GL}_n(A)$-torsor (as in these cases ![]() $\underline {\mathrm {Isom}}(\underline {A}^n, \underline {A}^n)= \underline { \mathrm {GL}_n(A) })$.
$\underline {\mathrm {Isom}}(\underline {A}^n, \underline {A}^n)= \underline { \mathrm {GL}_n(A) })$.
The following lemma will be used as a technical tool for moving between infinite-level and finite-level moduli problems for elliptic curves. When ![]() $G=\mathrm {GL}_m(\mathbb {Z}_\ell )$ and
$G=\mathrm {GL}_m(\mathbb {Z}_\ell )$ and ![]() $H=\{e\}$, it amounts to the statement that a rank
$H=\{e\}$, it amounts to the statement that a rank ![]() $m$ lisse
$m$ lisse ![]() $\mathbb {Z}_\ell$-sheaf is the same as a compatible family of rank
$\mathbb {Z}_\ell$-sheaf is the same as a compatible family of rank ![]() $m$ lisse
$m$ lisse ![]() $\mathbb {Z}/\ell ^n\mathbb {Z}$-sheafs, which will surprise nobody.
$\mathbb {Z}/\ell ^n\mathbb {Z}$-sheafs, which will surprise nobody.
Lemma 2.2.1 Let ![]() $G$ be a profinite group,
$G$ be a profinite group, ![]() $H\leq G$ a closed subgroup, and
$H\leq G$ a closed subgroup, and ![]() $\mathcal {G}$ a
$\mathcal {G}$ a ![]() $G$-torsor on
$G$-torsor on ![]() $\operatorname {Spec}\!R_\mathrm {pro\acute {e}t}$. The map
$\operatorname {Spec}\!R_\mathrm {pro\acute {e}t}$. The map
is a bijection between the set of ![]() $H$-torsors in
$H$-torsors in ![]() $\mathcal {G}$ and compatible systems of
$\mathcal {G}$ and compatible systems of ![]() $U$-torsors in
$U$-torsors in ![]() $G$ for
$G$ for ![]() $H \leq U \leq G,$
$H \leq U \leq G,$ ![]() $U$ a compact open subgroup.
$U$ a compact open subgroup.
Proof. It suffices to consider a cofinal system of ![]() $U$; thus we take a neighborhood basis of the identity in
$U$; thus we take a neighborhood basis of the identity in ![]() $G$ consisting of open normal subgroups
$G$ consisting of open normal subgroups ![]() $G_\epsilon$,
$G_\epsilon$, ![]() $\epsilon \in I$, and consider only
$\epsilon \in I$, and consider only ![]() $U$ of the form
$U$ of the form ![]() $H_\epsilon := H \cdot G_\epsilon$. Note that
$H_\epsilon := H \cdot G_\epsilon$. Note that ![]() $\bigcap _{\epsilon \in I} H_\epsilon = H$.
$\bigcap _{\epsilon \in I} H_\epsilon = H$.
The key point is to show that if ![]() $(\mathcal {H}_\epsilon \subset \mathcal {G})_\epsilon$ is a compatible system of
$(\mathcal {H}_\epsilon \subset \mathcal {G})_\epsilon$ is a compatible system of ![]() $H_\epsilon$-torsors, then
$H_\epsilon$-torsors, then ![]() $\bigcap _{\epsilon \in I} \mathcal {H}_\epsilon$ admits a section on a pro-étale cover. Indeed, then because
$\bigcap _{\epsilon \in I} \mathcal {H}_\epsilon$ admits a section on a pro-étale cover. Indeed, then because ![]() $\bigcap _{\epsilon \in I}\underline {H_\epsilon } = \underline {H}$,
$\bigcap _{\epsilon \in I}\underline {H_\epsilon } = \underline {H}$, ![]() $\bigcap _{\epsilon \in I} \mathcal {H}_\epsilon$ will automatically be an
$\bigcap _{\epsilon \in I} \mathcal {H}_\epsilon$ will automatically be an ![]() $H$-torsor, and it is straightforward to check this is a two-sided inverse to (2.2.1).
$H$-torsor, and it is straightforward to check this is a two-sided inverse to (2.2.1).
For this key point, by passing to a pro-étale cover we may assume ![]() $\mathcal {G}$ is trivial, i.e. we can take
$\mathcal {G}$ is trivial, i.e. we can take ![]() $\mathcal {G}=\underline {G}$. We now choose a compatible family of splittings of
$\mathcal {G}=\underline {G}$. We now choose a compatible family of splittings of ![]() $G \rightarrow G/H_\epsilon$ (this is possible because for each
$G \rightarrow G/H_\epsilon$ (this is possible because for each ![]() $\epsilon$ the set of splittings is a finite set and the transition maps are surjective), thus we obtain a compatible family of homeomorphisms, each equivariant for the right multiplication actions of
$\epsilon$ the set of splittings is a finite set and the transition maps are surjective), thus we obtain a compatible family of homeomorphisms, each equivariant for the right multiplication actions of ![]() $H_\epsilon$,
$H_\epsilon$,
and, passing to the limit over ![]() $\epsilon$, a homeomorphism
$\epsilon$, a homeomorphism
equivariant for the right multiplication action of ![]() $H$.
$H$.
From this it follows that the ![]() $\underline {H_\epsilon }$-torsors in
$\underline {H_\epsilon }$-torsors in ![]() $\mathcal {G}$ are identified with
$\mathcal {G}$ are identified with ![]() $\underline {G/H_\epsilon }(\operatorname {Spec}\!R)$, the
$\underline {G/H_\epsilon }(\operatorname {Spec}\!R)$, the ![]() $\underline {H}$-torsors in
$\underline {H}$-torsors in ![]() $\mathcal {G}$ are identified with
$\mathcal {G}$ are identified with ![]() $\underline {G/H}(\operatorname {Spec}\!R)$, and the map
$\underline {G/H}(\operatorname {Spec}\!R)$, and the map ![]() $\mathcal {H} \mapsto \mathcal {H} \cdot \underline {H_\epsilon }$ is induced by the canonical projection
$\mathcal {H} \mapsto \mathcal {H} \cdot \underline {H_\epsilon }$ is induced by the canonical projection ![]() $G/H \rightarrow G/H_\epsilon$. The result then follows as
$G/H \rightarrow G/H_\epsilon$. The result then follows as ![]() $G/H = \lim _{\epsilon \in I} G/H_\epsilon$.
$G/H = \lim _{\epsilon \in I} G/H_\epsilon$.
2.3 Elliptic curves and quasi-isogenies
For ![]() $R$ a ring, we will consider the category
$R$ a ring, we will consider the category ![]() $\operatorname {Ell}(R)$ of elliptic curves over
$\operatorname {Ell}(R)$ of elliptic curves over ![]() $R$. It is
$R$. It is ![]() $\mathbb {Z}$-linear. The isogeny category
$\mathbb {Z}$-linear. The isogeny category
has the same objects but homomorphisms are tensored with ![]() $\mathbb {Q}$. For
$\mathbb {Q}$. For ![]() $E$ an elliptic curve, we sometimes write
$E$ an elliptic curve, we sometimes write ![]() $E \otimes \mathbb {Q}$ for the corresponding element of
$E \otimes \mathbb {Q}$ for the corresponding element of ![]() $\operatorname {Ell}(R) \otimes \mathbb {Q}$, so
$\operatorname {Ell}(R) \otimes \mathbb {Q}$, so
An isogeny from ![]() $E_1$ to
$E_1$ to ![]() $E_2$ is a morphism
$E_2$ is a morphism ![]() $f: E_1 \rightarrow E_2$ such that
$f: E_1 \rightarrow E_2$ such that ![]() $f \otimes \mathbb {Q}: E_1 \otimes \mathbb {Q} \rightarrow E_2 \otimes \mathbb {Q}$ is invertible. A quasi-isogeny from
$f \otimes \mathbb {Q}: E_1 \otimes \mathbb {Q} \rightarrow E_2 \otimes \mathbb {Q}$ is invertible. A quasi-isogeny from ![]() $E_1$ to
$E_1$ to ![]() $E_2$ is an invertible morphism
$E_2$ is an invertible morphism ![]() $f:E_1 \otimes \mathbb {Q} \rightarrow E_2 \otimes \mathbb {Q}$; we often write instead, e.g., ‘
$f:E_1 \otimes \mathbb {Q} \rightarrow E_2 \otimes \mathbb {Q}$; we often write instead, e.g., ‘![]() $f:E_1 \rightarrow E_2$ is a quasi-isogeny’.
$f:E_1 \rightarrow E_2$ is a quasi-isogeny’.
Similarly, we consider the prime-to-![]() $p$ isogeny category
$p$ isogeny category ![]() $\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}$ by replacing
$\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}$ by replacing ![]() $\mathbb {Q}$ everywhere above with
$\mathbb {Q}$ everywhere above with ![]() $\mathbb {Z}_{(p)}$. A prime-to-
$\mathbb {Z}_{(p)}$. A prime-to-![]() $p$ isogeny from
$p$ isogeny from ![]() $E_1$ to
$E_1$ to ![]() $E_2$ is a morphism
$E_2$ is a morphism ![]() $f: E_1 \rightarrow E_2$ such that
$f: E_1 \rightarrow E_2$ such that ![]() $f \otimes \mathbb {Z}_{(p)}: E_1 \otimes \mathbb {Z}_{(p)} \rightarrow E_2 \otimes \mathbb {Z}_{p}$ is invertible. A prime-to-
$f \otimes \mathbb {Z}_{(p)}: E_1 \otimes \mathbb {Z}_{(p)} \rightarrow E_2 \otimes \mathbb {Z}_{p}$ is invertible. A prime-to-![]() $p$ quasi-isogeny from
$p$ quasi-isogeny from ![]() $E_1$ to
$E_1$ to ![]() $E_2$ is an invertible morphism
$E_2$ is an invertible morphism ![]() $f:E_1 \otimes \mathbb {Z}_{(p)} \rightarrow E_2 \otimes \mathbb {Z}_{(p)}$; we often write instead, e.g., ‘
$f:E_1 \otimes \mathbb {Z}_{(p)} \rightarrow E_2 \otimes \mathbb {Z}_{(p)}$; we often write instead, e.g., ‘![]() $f:E_1\rightarrow E_2$ is a prime-to-
$f:E_1\rightarrow E_2$ is a prime-to-![]() $p$ quasi-isogeny’.
$p$ quasi-isogeny’.
Remark 2.3.1 When ![]() $R$ is not normal, this is not quite the category of elliptic curves up-to-isogeny (respectively, prime-to-
$R$ is not normal, this is not quite the category of elliptic curves up-to-isogeny (respectively, prime-to-![]() $p$ isogeny) considered in [Reference DeligneDel71, § 3], but rather the full subcategory consisting of objects with a genuine underlying elliptic curve. In general, one also formally enforces effectivity of étale descent. This full subcategory will suffice for our needs as our moduli problems typically include rigidifying data.
$p$ isogeny) considered in [Reference DeligneDel71, § 3], but rather the full subcategory consisting of objects with a genuine underlying elliptic curve. In general, one also formally enforces effectivity of étale descent. This full subcategory will suffice for our needs as our moduli problems typically include rigidifying data.
2.3.2 Tate modules
If ![]() $R/\mathbb {Q}$ (i.e.
$R/\mathbb {Q}$ (i.e. ![]() $R$ is of characteristic zero) and
$R$ is of characteristic zero) and ![]() $E/R$ is an elliptic curve, we consider the
$E/R$ is an elliptic curve, we consider the ![]() $p$-adic and adelic integral and rational Tate modules
$p$-adic and adelic integral and rational Tate modules
These are lisse rank-two sheaves on ![]() $\operatorname {Spec}\!R$ over
$\operatorname {Spec}\!R$ over ![]() $\mathbb {Z}_p, \mathbb {Q}_p, \widehat {\mathbb {Z}},$ and
$\mathbb {Z}_p, \mathbb {Q}_p, \widehat {\mathbb {Z}},$ and ![]() $\mathbb {A}_f$, respectively. All are functors on
$\mathbb {A}_f$, respectively. All are functors on ![]() $\operatorname {Ell}(R)$, and
$\operatorname {Ell}(R)$, and ![]() $V_p$ and
$V_p$ and ![]() $V_{\mathbb {A}_f}$ factor through
$V_{\mathbb {A}_f}$ factor through ![]() $\operatorname {Ell}(R) \otimes \mathbb {Q}$.
$\operatorname {Ell}(R) \otimes \mathbb {Q}$.
If ![]() $R/\mathbb {Z}_{(p)}$ (i.e. all primes
$R/\mathbb {Z}_{(p)}$ (i.e. all primes ![]() $\ell \neq p$ are invertible in
$\ell \neq p$ are invertible in ![]() $R$) and
$R$) and ![]() $E/\operatorname {Spec}\!R$ is an elliptic curve, then we may still form the prime-to-
$E/\operatorname {Spec}\!R$ is an elliptic curve, then we may still form the prime-to-![]() $p$ integral and adelic Tate modules
$p$ integral and adelic Tate modules
These are lisse rank-two sheaves on ![]() $\operatorname {Spec}\!R$ over
$\operatorname {Spec}\!R$ over ![]() $\widehat {\mathbb {Z}}^{(p)}$ and
$\widehat {\mathbb {Z}}^{(p)}$ and ![]() $\mathbb {A}_f^{(p)}$, respectively. Both are functors on
$\mathbb {A}_f^{(p)}$, respectively. Both are functors on ![]() $\operatorname {Ell}(R)$, and
$\operatorname {Ell}(R)$, and ![]() $V_{\mathbb {A}_f^{(p)}}$ factors through
$V_{\mathbb {A}_f^{(p)}}$ factors through ![]() $\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}$.
$\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}$.
2.3.3 Relative differentials
For ![]() $\pi :E\rightarrow \operatorname {Spec}\!R$ an elliptic curve,
$\pi :E\rightarrow \operatorname {Spec}\!R$ an elliptic curve, ![]() $\omega _{E/R}:=\pi _* \Omega _{E/R}$ is a line bundle on
$\omega _{E/R}:=\pi _* \Omega _{E/R}$ is a line bundle on ![]() $S$. Restriction induces canonical isomorphisms
$S$. Restriction induces canonical isomorphisms
where, here, ![]() $1_E: \operatorname {Spec}\!R \rightarrow E$ is the identity section.
$1_E: \operatorname {Spec}\!R \rightarrow E$ is the identity section.
The assignment ![]() $E/R \rightarrow \omega _{E/R}$ is a functor from
$E/R \rightarrow \omega _{E/R}$ is a functor from ![]() $\operatorname {Ell}(R)$ to line bundles on
$\operatorname {Ell}(R)$ to line bundles on ![]() $\operatorname {Spec}\!R$. If
$\operatorname {Spec}\!R$. If ![]() $R/\mathbb {Q}$, then it factors through
$R/\mathbb {Q}$, then it factors through ![]() $\operatorname {Ell}(R) \otimes \mathbb {Q}$, and if
$\operatorname {Ell}(R) \otimes \mathbb {Q}$, and if ![]() $R/\mathbb {Z}_{(p)}$, it factors through
$R/\mathbb {Z}_{(p)}$, it factors through ![]() ${\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}}$; indeed, for
${\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}}$; indeed, for ![]() $n \in \mathbb {Z}$, the multiplication map by
$n \in \mathbb {Z}$, the multiplication map by ![]() $n$ map
$n$ map ![]() $[n]:E \rightarrow E$ induces ring multiplication by
$[n]:E \rightarrow E$ induces ring multiplication by ![]() $n$ on
$n$ on ![]() $\omega _{E/R}$, thus is invertible if
$\omega _{E/R}$, thus is invertible if ![]() $n$ is invertible in
$n$ is invertible in ![]() $R$.
$R$.
2.3.4  $p$-divisible groups
$p$-divisible groups
For ![]() $R$ a ring, a
$R$ a ring, a ![]() $p$-divisible group
$p$-divisible group ![]() $G$ of height
$G$ of height ![]() $h \in \underline {\mathbb {N}}(\operatorname {Spec}\!R)$ is, following Tate [Reference TateTat67, 2.1] and Messing [Reference MessingMes72, I.2], an inductive system
$h \in \underline {\mathbb {N}}(\operatorname {Spec}\!R)$ is, following Tate [Reference TateTat67, 2.1] and Messing [Reference MessingMes72, I.2], an inductive system
of finite locally free commutative group schemes ![]() $G_i$ of degree
$G_i$ of degree ![]() $p^{ih}$ over
$p^{ih}$ over ![]() $\operatorname {Spec}\!R$, equipped with closed immersions
$\operatorname {Spec}\!R$, equipped with closed immersions ![]() $\iota _i: G_i \rightarrow G_{i+1}$ identifying
$\iota _i: G_i \rightarrow G_{i+1}$ identifying ![]() $G_i$ with the kernel of multiplication by
$G_i$ with the kernel of multiplication by ![]() $p^i$ on
$p^i$ on ![]() $G_{i+1}$.
$G_{i+1}$.
We write ![]() $p\text {-}\mathrm {div}(R)$ for the
$p\text {-}\mathrm {div}(R)$ for the ![]() $\mathbb {Z}_p$-linear category of
$\mathbb {Z}_p$-linear category of ![]() $p$-divisible groups over
$p$-divisible groups over ![]() $R$. There is a natural functor
$R$. There is a natural functor
This functor factors through ![]() $\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}$. We also form the isogeny category
$\operatorname {Ell}(R) \otimes \mathbb {Z}_{(p)}$. We also form the isogeny category ![]() $p\text {-}\mathrm {div}(R) \otimes \mathbb {Q}_p$ and define isogenies and quasi-isogenies in the obvious way. The functor
$p\text {-}\mathrm {div}(R) \otimes \mathbb {Q}_p$ and define isogenies and quasi-isogenies in the obvious way. The functor ![]() $E \mapsto E[p^\infty ] \otimes \mathbb {Q}_p$ then factors through
$E \mapsto E[p^\infty ] \otimes \mathbb {Q}_p$ then factors through ![]() $\operatorname {Ell}(R) \otimes \mathbb {Q}$.
$\operatorname {Ell}(R) \otimes \mathbb {Q}$.
If ![]() $R$ is a
$R$ is a ![]() $p$-adically complete ring, then we write
$p$-adically complete ring, then we write ![]() $\mathrm {Nilp}_R$ for the category of
$\mathrm {Nilp}_R$ for the category of ![]() $R$-algebras where
$R$-algebras where ![]() $p$ is nilpotent and we view a
$p$ is nilpotent and we view a ![]() $p$-divisible group
$p$-divisible group ![]() $G=(G_i)$ over
$G=(G_i)$ over ![]() $R$ as the functor on
$R$ as the functor on ![]() $\mathrm {Nilp}_R$
$\mathrm {Nilp}_R$
In this case, because ![]() $E[p^\infty ]_{R/p^n}$ and
$E[p^\infty ]_{R/p^n}$ and ![]() $E_{R/p^n}$ have the same tangent space for any
$E_{R/p^n}$ have the same tangent space for any ![]() $n$ and
$n$ and ![]() $R$ is
$R$ is ![]() $p$-adically complete, the functor
$p$-adically complete, the functor ![]() $E \mapsto \omega _{E/S}$ factors through
$E \mapsto \omega _{E/S}$ factors through ![]() $E \mapsto E[p^\infty ]$.
$E \mapsto E[p^\infty ]$.
2.4 Completing algebra actions
In this section, we develop the basic definitions for completing algebra actions and some tools for comparing completions. This material is used in § 5.7, where it is essential for the final deduction of Theorem A from the key geometric input, Corollary 5.6.3. Some results are also used in § 4.5 when we explain how Theorem 1.1.1 can be deduced from Theorem A.
The statements we give here are likely well known to experts and the proofs are, for the most part, elementary exercises in analysis. Nonetheless we include a full treatment because we are not aware of another suitable source in the literature.
We begin with some basic definitions in non-archimedean functional analysis. In the following, ![]() $L$ is any complete non-archimedean field.
$L$ is any complete non-archimedean field.
Definition 2.4.1
(i) An
 $L$-Banach space is a complete topological
$L$-Banach space is a complete topological  $L$-vector space
$L$-vector space  $V$ whose topology is induced by an ultrametric norm; we refer to the choice of such a norm on
$V$ whose topology is induced by an ultrametric norm; we refer to the choice of such a norm on  $V$ as a Banach norm.
$V$ as a Banach norm.(ii) A bounded collection of vectors
 $\{e_i \}_{i \in I}$ in an
$\{e_i \}_{i \in I}$ in an  $L$-Banach space
$L$-Banach space  $V$ is an orthonormal basis if every
$V$ is an orthonormal basis if every  $v \in V$ can be written uniquely as
(2.4.1)
$v \in V$ can be written uniquely as
(2.4.1) \begin{equation} v = \sum_{i \in I} v_i e_i,\quad v_i \in L, v_i \rightarrow 0. \end{equation}
\begin{equation} v = \sum_{i \in I} v_i e_i,\quad v_i \in L, v_i \rightarrow 0. \end{equation}(iii) We say that
 $V$ is orthonormalizable if it admits an orthonormal basis.
$V$ is orthonormalizable if it admits an orthonormal basis.
Note that because in Definition 2.4.1(ii) we assumed ![]() $\{e_i\}_{i \in I}$ was bounded, all sums of the form (2.4.1) converge, and then the open mapping theorem implies that the sup norm
$\{e_i\}_{i \in I}$ was bounded, all sums of the form (2.4.1) converge, and then the open mapping theorem implies that the sup norm ![]() $|v|=\sup _{i \in I} |v_i|_L$ is a Banach norm. For
$|v|=\sup _{i \in I} |v_i|_L$ is a Banach norm. For ![]() $L$ discretely valued (or, more generally, spherically complete), every
$L$ discretely valued (or, more generally, spherically complete), every ![]() $L$-Banach space is orthonormalizable; cf. [Reference SerreSer62, Corollaire of Proposition 1 and Remarques after Proposition 2].
$L$-Banach space is orthonormalizable; cf. [Reference SerreSer62, Corollaire of Proposition 1 and Remarques after Proposition 2].
Definition 2.4.2 For ![]() $V$ and
$V$ and ![]() $W$ two
$W$ two ![]() $L$-Banach spaces, we write
$L$-Banach spaces, we write ![]() $B(V,W)$ for the space of bounded (equivalently, continuous) linear operators from
$B(V,W)$ for the space of bounded (equivalently, continuous) linear operators from ![]() $V$ to
$V$ to ![]() $W$.
$W$.
(i) The choice of Banach norms on
 $V$ and
$V$ and  $W$ induces an operator norm on
$W$ induces an operator norm on  $B(V,W)$ defined by
The operator norms for different choices of Banach norms on
$B(V,W)$ defined by
The operator norms for different choices of Banach norms on \[ |T|=\sup_{v\in V, v\neq0} |T(v)|/|v|. \]
\[ |T|=\sup_{v\in V, v\neq0} |T(v)|/|v|. \] $V$ and
$V$ and  $W$ are equivalent and with the induced topology
$W$ are equivalent and with the induced topology  $B(V,W)$ is a Banach space.
$B(V,W)$ is a Banach space.(ii) The topology of pointwise convergence Footnote 4 on
 $B(V,W)$ is defined by the family of seminorms
$B(V,W)$ is defined by the family of seminorms  $T \mapsto |T(v)|$ indexed by
$T \mapsto |T(v)|$ indexed by  $v\in V$ (for any Banach norm on
$v\in V$ (for any Banach norm on  $W$).
$W$).
The topology of pointwise convergence is uniquely determined by the property that a net ![]() $(T_j)_{j \in J}$ in
$(T_j)_{j \in J}$ in ![]() $B(V,W)$ converges to
$B(V,W)$ converges to ![]() $T\in B(V,W)$ if and only if
$T\in B(V,W)$ if and only if ![]() $T_j(v) \rightarrow T(v)$ for all
$T_j(v) \rightarrow T(v)$ for all ![]() $v \in V$. It is through this characterization that we access it.
$v \in V$. It is through this characterization that we access it.
Definition 2.4.3 We say ![]() $\mathcal {T} \subset B(V,W)$ is bounded if it is bounded in the operator norm topology.
$\mathcal {T} \subset B(V,W)$ is bounded if it is bounded in the operator norm topology.
The following lemma is elementary but extremely useful.
Lemma 2.4.4 Suppose ![]() $V$ and
$V$ and ![]() $W$ are
$W$ are ![]() $L$-Banach spaces,
$L$-Banach spaces, ![]() $S \subset V$ is such that the set
$S \subset V$ is such that the set ![]() $L[S]$ of finite linear combinations of elements of
$L[S]$ of finite linear combinations of elements of ![]() $S$ is dense in
$S$ is dense in ![]() $V$,
$V$, ![]() $(T_{j})_{j \in J}$ is a bounded net of operators in
$(T_{j})_{j \in J}$ is a bounded net of operators in ![]() $B(V,W)$, and
$B(V,W)$, and ![]() $T \in B(V,W)$. Then
$T \in B(V,W)$. Then ![]() $T_j \rightarrow T$ in the in the topology of pointwise convergence if and only if
$T_j \rightarrow T$ in the in the topology of pointwise convergence if and only if
Proof. As previously, we have ![]() $T_j \rightarrow T$ in the topology of pointwise converge if and only if, for every
$T_j \rightarrow T$ in the topology of pointwise converge if and only if, for every ![]() $v \in V$,
$v \in V$, ![]() $\lim _{j \in J} T_j(v)=T(v)$. Thus, one direction is immediate. For the other, suppose that (2.4.2) holds and fix Banach norms on
$\lim _{j \in J} T_j(v)=T(v)$. Thus, one direction is immediate. For the other, suppose that (2.4.2) holds and fix Banach norms on ![]() $V$ and
$V$ and ![]() $W$. By the boundedness hypothesis, we can then choose a common bound
$W$. By the boundedness hypothesis, we can then choose a common bound ![]() $C\geq 1$ for the operator norms of all
$C\geq 1$ for the operator norms of all ![]() $T_j,\ j \in J$, and
$T_j,\ j \in J$, and ![]() $T$.
$T$.
Let ![]() $v \in V$. By the density hypothesis, for any
$v \in V$. By the density hypothesis, for any ![]() $\epsilon > 0$ we can find
$\epsilon > 0$ we can find
such that ![]() $|v-v'| \leq \epsilon$. By (2.4.2), for each
$|v-v'| \leq \epsilon$. By (2.4.2), for each ![]() $v_i$, there is a
$v_i$, there is a ![]() $j_i \in J$ such that, for
$j_i \in J$ such that, for ![]() $j\geq j_i$,
$j\geq j_i$,
Thus, taking ![]() $j' \geq j_1, \ldots, j_k$ (the fundamental property of the directed set indexing a net is that there is always an upper bound for any finite collection of elements), we obtain that for
$j' \geq j_1, \ldots, j_k$ (the fundamental property of the directed set indexing a net is that there is always an upper bound for any finite collection of elements), we obtain that for ![]() $j \geq j'$,
$j \geq j'$,
 \begin{align*} |T(v)-T_j(v)| &= | (T(v') - T_j(v')) + T(v-v') - T_j(v-v')|\\ &= \biggl|\sum_{i=1}^k(T(\ell_i v_i)-T_j(\ell_i v_i)) + T(v-v') - T_j(v-v')\biggr|\\ &\leq \max(\epsilon, |T(v-v')|, |T_j(v-v')|) \leq C\epsilon. \end{align*}
\begin{align*} |T(v)-T_j(v)| &= | (T(v') - T_j(v')) + T(v-v') - T_j(v-v')|\\ &= \biggl|\sum_{i=1}^k(T(\ell_i v_i)-T_j(\ell_i v_i)) + T(v-v') - T_j(v-v')\biggr|\\ &\leq \max(\epsilon, |T(v-v')|, |T_j(v-v')|) \leq C\epsilon. \end{align*}
We conclude that ![]() $\lim _{j\in J} T_j(v) = T(v)$, as desired.
$\lim _{j\in J} T_j(v) = T(v)$, as desired.
Definition 2.4.5 If ![]() $A$ is a ring,
$A$ is a ring, ![]() $L$ is a non-archimedean field, and
$L$ is a non-archimedean field, and ![]() $(W_i)_{i \in I}$ is family of
$(W_i)_{i \in I}$ is family of ![]() $L$-Banach spaces equipped with actions of
$L$-Banach spaces equipped with actions of ![]() $A$ by operators in
$A$ by operators in ![]() $B(W_i,W_i)$, the completion Footnote 5 of
$B(W_i,W_i)$, the completion Footnote 5 of ![]() $A$ acting on
$A$ acting on ![]() $(W_i)_{i \in I}$ is the closure
$(W_i)_{i \in I}$ is the closure ![]() $\widehat {A}_{(W_i)_{i \in I}}$ of the image of
$\widehat {A}_{(W_i)_{i \in I}}$ of the image of ![]() $A$ in
$A$ in
where ![]() $B(W_i, W_i)$ is equipped with the topology of pointwise convergence and the product is equipped with the product topology. Concretely,
$B(W_i, W_i)$ is equipped with the topology of pointwise convergence and the product is equipped with the product topology. Concretely, ![]() $(T_i)_{i \in I} \in \widehat {A}_{(W_i)_{i \in I}}$ if and only if there exists a net
$(T_i)_{i \in I} \in \widehat {A}_{(W_i)_{i \in I}}$ if and only if there exists a net ![]() $(a_j)_{j \in J}$ in
$(a_j)_{j \in J}$ in ![]() $A$ whose image converges to
$A$ whose image converges to ![]() $(T_i)_{i \in I}$. The latter is equivalent to asking that, for any
$(T_i)_{i \in I}$. The latter is equivalent to asking that, for any ![]() $i \in I$ and any
$i \in I$ and any ![]() $w_i \in W_i$,
$w_i \in W_i$,
Lemma 2.4.6 Using notation as before, if the action of ![]() $A$ on each
$A$ on each ![]() $W_i$ is bounded (i.e. the image of
$W_i$ is bounded (i.e. the image of ![]() $A$ in
$A$ in ![]() $B(W_i, W_i)$ is bounded in the operator norm topology), then
$B(W_i, W_i)$ is bounded in the operator norm topology), then ![]() $\widehat {A}_{(W_i)_{i \in I}}$ is a closed subring of
$\widehat {A}_{(W_i)_{i \in I}}$ is a closed subring of ![]() $\prod _{i \in I} B(W_i, W_i)$.
$\prod _{i \in I} B(W_i, W_i)$.
Proof. It is always a closed subgroup, so it remains just to see that under the boundedness hypothesis it is closed under composition.
Suppose given ![]() $(T_i)_{i \in I}$ and
$(T_i)_{i \in I}$ and ![]() $(S_i)_{i \in I}$ in
$(S_i)_{i \in I}$ in ![]() $\widehat {A}_{(W_i)_{i \in I}}$, and choose nets
$\widehat {A}_{(W_i)_{i \in I}}$, and choose nets ![]() $(a_{j_T})_{j_T \in J_T}$ and
$(a_{j_T})_{j_T \in J_T}$ and ![]() $(b_{j_S})_{j_{S} \in J_S}$ whose images in
$(b_{j_S})_{j_{S} \in J_S}$ whose images in ![]() $\prod _{i \in I} \mathrm {End}(W_i)$ converge to
$\prod _{i \in I} \mathrm {End}(W_i)$ converge to ![]() $(T_i)_{i \in I}$ and
$(T_i)_{i \in I}$ and ![]() $(S_i)_{i \in I}$, respectively. Then we claim that the image of
$(S_i)_{i \in I}$, respectively. Then we claim that the image of
converges to ![]() $(T_i \circ S_i)_{i \in I}$. It suffices to show that for any
$(T_i \circ S_i)_{i \in I}$. It suffices to show that for any ![]() $i \in I$ and
$i \in I$ and ![]() $w_i \in W_i$,
$w_i \in W_i$,
We suppress the ![]() $i$ now and write
$i$ now and write ![]() $W_i=W$,
$W_i=W$, ![]() $w_i=w$,
$w_i=w$, ![]() $T_i=T$, and
$T_i=T$, and ![]() $S_i=S$.
$S_i=S$.
To see the convergence, fix a Banach norm on ![]() $W$ and, by boundedness of the action, a
$W$ and, by boundedness of the action, a ![]() $C\geq 1$ such that
$C\geq 1$ such that ![]() $|a \cdot v|\leq C|v|$ for all
$|a \cdot v|\leq C|v|$ for all ![]() $a \in A$ and
$a \in A$ and ![]() $v \in W$. Then, for any
$v \in W$. Then, for any ![]() $\epsilon > 0$, we may choose
$\epsilon > 0$, we may choose ![]() $j_{T,0} \in j_T$ and
$j_{T,0} \in j_T$ and ![]() $j_{S,0} \in J_S$ such that:
$j_{S,0} \in J_S$ such that:
(i)
 $|a_{j_T} \cdot S(w) - T(S(w))| \leq \epsilon$ for all
$|a_{j_T} \cdot S(w) - T(S(w))| \leq \epsilon$ for all  $j_T \geq j_{T,0}$; and
$j_T \geq j_{T,0}$; and(ii)
 $|b_{j_S} \cdot w -S(w)| \leq \epsilon$ for all
$|b_{j_S} \cdot w -S(w)| \leq \epsilon$ for all  $j_S \geq j_{S,0}$.
$j_S \geq j_{S,0}$.
Then, for ![]() $(j_S,j_T)\geq (j_{S,0}, j_{T,0})$,
$(j_S,j_T)\geq (j_{S,0}, j_{T,0})$,
 \begin{align*} |a_{j_T}b_{j_S} \cdot w - T(S(w))| &= \big|a_{j_T}\cdot(b_{j_S} \cdot w - S(w)) + (a_{j_T}\cdot S(W) - T(S(w))) \big|\\ & \leq \max(|a_{j_T}\cdot(b_{j_S} \cdot w - S(w))|,\, |a_{j_T}\cdot S(W) - T(S(w))| ) \\ & \leq \max( C\epsilon, \epsilon ) \\ & \leq C\epsilon \end{align*}
\begin{align*} |a_{j_T}b_{j_S} \cdot w - T(S(w))| &= \big|a_{j_T}\cdot(b_{j_S} \cdot w - S(w)) + (a_{j_T}\cdot S(W) - T(S(w))) \big|\\ & \leq \max(|a_{j_T}\cdot(b_{j_S} \cdot w - S(w))|,\, |a_{j_T}\cdot S(W) - T(S(w))| ) \\ & \leq \max( C\epsilon, \epsilon ) \\ & \leq C\epsilon \end{align*}and we conclude.
The following lemma allows for comparison with other definitions in the literature, in particular the definition given in [Reference EmertonEme14, 2.1.4].
Lemma 2.4.7 Using notation as before, suppose ![]() $L$ is discretely valued and write
$L$ is discretely valued and write ![]() $\mathcal {O}_L$ for the ring of integers and
$\mathcal {O}_L$ for the ring of integers and ![]() $\mathfrak {p}$ for its maximal ideal. If each
$\mathfrak {p}$ for its maximal ideal. If each ![]() $W_i$ is finite dimensional and, for each
$W_i$ is finite dimensional and, for each ![]() $i$,
$i$, ![]() $A$ preserves an
$A$ preserves an ![]() $\mathcal {O}_L$-lattice
$\mathcal {O}_L$-lattice ![]() $W_i^\circ \subset W_i$, then the action is bounded and
$W_i^\circ \subset W_i$, then the action is bounded and ![]() $\widehat {A}_{(W_i)_{i \in I}}$ is naturally identified with the closure of the image of
$\widehat {A}_{(W_i)_{i \in I}}$ is naturally identified with the closure of the image of ![]() $A$ in
$A$ in
equipped with the product topology (each term is equipped with the discrete topology).
Proof. Boundedness is clear. For the rest, first note the image of ![]() $A$ in
$A$ in ![]() $\prod _{i \in I} B(W_i, W_i)$ factors through
$\prod _{i \in I} B(W_i, W_i)$ factors through ![]() $\prod _{i \in I} \mathrm {End}_{\mathcal {O}_K}(W_i^\circ )$, where we identify
$\prod _{i \in I} \mathrm {End}_{\mathcal {O}_K}(W_i^\circ )$, where we identify ![]() $\mathrm {End}_{\mathcal {O}_K}(W_i^\circ )$ with the subset of
$\mathrm {End}_{\mathcal {O}_K}(W_i^\circ )$ with the subset of ![]() $B(W_i, W_i)$ preserving
$B(W_i, W_i)$ preserving ![]() $W_i^\circ$. This subset is closed, so we can form
$W_i^\circ$. This subset is closed, so we can form ![]() $\widehat {A}_{V}$ by taking the closure of the image of
$\widehat {A}_{V}$ by taking the closure of the image of ![]() $A$ in
$A$ in ![]() $\prod _{i \in I} \mathrm {End}_{\mathcal {O}_K}(W_i^\circ )$. Then, for each
$\prod _{i \in I} \mathrm {End}_{\mathcal {O}_K}(W_i^\circ )$. Then, for each ![]() $i$ we have
$i$ we have
where each term on the right is equipped with the discrete topology. Thus,
is closed so we may compute ![]() $\widehat {A}_V$ by taking the closure in the space on the right.
$\widehat {A}_V$ by taking the closure in the space on the right.
The following lemma says that completion is insensitive to base extension. This is useful as our comparisons of Hecke modules take place over very large extensions of ![]() $\mathbb {Q}_p$, whereas one is typically interested in Hecke algebras over
$\mathbb {Q}_p$, whereas one is typically interested in Hecke algebras over ![]() $\mathbb {Z}_p$.
$\mathbb {Z}_p$.
Lemma 2.4.8 Let ![]() $L \subset L'$ be an extension of complete non-archimedean fields, and let
$L \subset L'$ be an extension of complete non-archimedean fields, and let ![]() $A$ be a ring. Suppose
$A$ be a ring. Suppose ![]() $(W_i)$ is a family of orthonormalizable
$(W_i)$ is a family of orthonormalizable ![]() $L$-Banach spaces equipped with bounded actions of
$L$-Banach spaces equipped with bounded actions of ![]() $A$. Then the identity map
$A$. Then the identity map ![]() $A \rightarrow A$ extends uniquely to a topological isomorphism
$A \rightarrow A$ extends uniquely to a topological isomorphism
Proof. Immediate by applying Lemma 2.4.4 to an orthonormal basis and using the fact that an orthonormal basis remains an orthonormal basis under completed base change.
The following is our main technical tool for comparing completed Hecke algebras.
Lemma 2.4.9 Suppose ![]() $V$ is an orthonormalizable
$V$ is an orthonormalizable ![]() $L$-Banach space equipped with a bounded action of a ring
$L$-Banach space equipped with a bounded action of a ring ![]() $A$, and
$A$, and ![]() $(W_i)_{i \in I}$ is a collection of
$(W_i)_{i \in I}$ is a collection of ![]() $A$-invariant closed subspaces such that the span of
$A$-invariant closed subspaces such that the span of ![]() $\bigcup _i W_i$ is dense in
$\bigcup _i W_i$ is dense in ![]() $V$. Then
$V$. Then ![]() $\widehat {A}_{(W_i)_{i\in I}} = \widehat {A}_{V}$.
$\widehat {A}_{(W_i)_{i\in I}} = \widehat {A}_{V}$.
Remark 2.4.10 In this setup, each ![]() $W_i$ is automatically a Banach space as a closed subspace of a Banach space and the action on
$W_i$ is automatically a Banach space as a closed subspace of a Banach space and the action on ![]() $W_i$ is automatically bounded.
$W_i$ is automatically bounded.
Proof. We abbreviate ![]() $\widehat {A}_W := \widehat {A}_{(W_i)_{i\in I}}\subset \prod B(W_i, W_i)$. We then obtain a map
$\widehat {A}_W := \widehat {A}_{(W_i)_{i\in I}}\subset \prod B(W_i, W_i)$. We then obtain a map ![]() $\widehat {A}_V \rightarrow \widehat {A}_W$ via restriction: if the image of
$\widehat {A}_V \rightarrow \widehat {A}_W$ via restriction: if the image of ![]() $(a_j)_{j \in J}$ in
$(a_j)_{j \in J}$ in ![]() $B(V,V)$ converges to
$B(V,V)$ converges to ![]() $T$, then, in particular, the image of
$T$, then, in particular, the image of ![]() $(a_j)_{j \in J}$ in
$(a_j)_{j \in J}$ in ![]() $B(W_i, W_i)$ converges to
$B(W_i, W_i)$ converges to ![]() $T|_{W_i}$. This restriction map is injective by the density hypothesis.
$T|_{W_i}$. This restriction map is injective by the density hypothesis.
We show now that it is surjective. The key observation that makes this possible is that, by the density hypothesis, we may choose an orthonormal basis ![]() $(e_m)_{m \in M}$ for
$(e_m)_{m \in M}$ for ![]() $V$ consisting of vectors
$V$ consisting of vectors ![]() $e_m$ each of which is a finite linear combination of vectors in the subspaces
$e_m$ each of which is a finite linear combination of vectors in the subspaces ![]() $W_i$: indeed, if we fix a pseudo-uniformizer
$W_i$: indeed, if we fix a pseudo-uniformizer ![]() $\pi$ in
$\pi$ in ![]() $\mathcal {O}_L$ and an arbitrary orthonormal basis
$\mathcal {O}_L$ and an arbitrary orthonormal basis ![]() $(f_m)_{m \in M}$, then any collection of vectors
$(f_m)_{m \in M}$, then any collection of vectors ![]() $(e_m)_{m \in M}$ with
$(e_m)_{m \in M}$ with ![]() $|f_m - e_m| \leq |\pi |$ will also be an orthonormal basis.
$|f_m - e_m| \leq |\pi |$ will also be an orthonormal basis.
Now, suppose ![]() $(T_i)_{i \in I} \in \widehat {A}_W$, and fix a net
$(T_i)_{i \in I} \in \widehat {A}_W$, and fix a net ![]() $a_j$ of elements of
$a_j$ of elements of ![]() $A$ whose image converges to
$A$ whose image converges to ![]() $(T_i)_{i \in I}$. Then we find that for each
$(T_i)_{i \in I}$. Then we find that for each ![]() $m$,
$m$, ![]() $\lim _j a_j \cdot e_m$ exists in
$\lim _j a_j \cdot e_m$ exists in ![]() $V$, call it
$V$, call it ![]() $v_m$ and, by boundedness of the action, the set of
$v_m$ and, by boundedness of the action, the set of ![]() $v_m$ is bounded. There is, thus, a unique bounded linear operator
$v_m$ is bounded. There is, thus, a unique bounded linear operator ![]() $T:V\rightarrow V$ such that
$T:V\rightarrow V$ such that ![]() $T(e_m)=v_m$. We conclude by Lemma 2.4.4 that the image of
$T(e_m)=v_m$. We conclude by Lemma 2.4.4 that the image of ![]() $a_j$ in
$a_j$ in ![]() $B(V,V)$ converges to
$B(V,V)$ converges to ![]() $T$, and then by restriction that, in fact,
$T$, and then by restriction that, in fact, ![]() $T|_{W_i}=T_i$.
$T|_{W_i}=T_i$.
Now, a topology is uniquely determined by the knowledge of which nets converge to which points. With this bijection established, Lemma 2.4.4 tells us that the same nets converge to the same points, so the bijection is a homeomorphism.
The following lemma combines some of the results given previously, and is used in § 4.5 to deduce Theorem 1.1.1 from Theorem A.
Lemma 2.4.11 Suppose ![]() $L$ is discretely valued and write
$L$ is discretely valued and write ![]() $\mathcal {O}_L$ for the ring of integers and
$\mathcal {O}_L$ for the ring of integers and ![]() $\mathfrak {p}$ for the maximal ideal. Suppose
$\mathfrak {p}$ for the maximal ideal. Suppose ![]() $V$ is an
$V$ is an ![]() $L$-Banach space and
$L$-Banach space and ![]() $A$ acts on
$A$ acts on ![]() $V$ preserving a bounded open
$V$ preserving a bounded open ![]() $\mathcal {O}_K$-lattice
$\mathcal {O}_K$-lattice ![]() $V^\circ$, and
$V^\circ$, and ![]() $(W_i)_{i \in I}$ is a filtered system of finite-dimensional
$(W_i)_{i \in I}$ is a filtered system of finite-dimensional ![]() $A$-invariant subspaces such that
$A$-invariant subspaces such that ![]() $\bigcup _{i \in I} W_i$ is dense in
$\bigcup _{i \in I} W_i$ is dense in ![]() $V$. Then, writing
$V$. Then, writing
and ![]() $A_{i,n}$ for the image of
$A_{i,n}$ for the image of ![]() $A$ in
$A$ in ![]() $\mathrm {End}_{\mathcal {O}_K}( \overline {W}_{i,n})$, we have
$\mathrm {End}_{\mathcal {O}_K}( \overline {W}_{i,n})$, we have
where each term in the limit is equipped with the discrete topology.
3. Modular curves and Igusa varieties
In this section, we study some moduli problems for elliptic curves. In § 3.1 we give isogeny formulations for some classical moduli problems and recall the standard representability results. In § 3.2 we recall the construction of the modular bundle and the adelic representations on modular forms, as well as the construction of the Hasse invariant. In § 3.3, we recall the construction of the supersingular and ordinary loci on the mod ![]() $p$ modular curve. In § 3.4, we recall some Igusa moduli problems over the ordinary locus and their relation with mod
$p$ modular curve. In § 3.4, we recall some Igusa moduli problems over the ordinary locus and their relation with mod ![]() $p$ and
$p$ and ![]() $p$-adic modular forms as developed by Katz [Reference KatzKat75a].
$p$-adic modular forms as developed by Katz [Reference KatzKat75a].
In §§ 3.5–3.7, we undertake a study of the supersingular Igusa variety, culminating with the identification of the supersingular Igusa variety with a quaternionic coset in Theorem 3.7.1. Everything here except this final identification is a very special case of results of Caraiani–Scholze [Reference Caraiani and ScholzeCS17]. However, following our treatment of modular curves, we take a resolutely ‘top-down’ approach, and for the most partFootnote 6 our treatment here is independent of the results of [Reference Caraiani and ScholzeCS17]. We lean instead on the Hasse invariant and other ideas specific to this special case.
As to the identification with a quaternionic coset, the basic idea is already present in Serre's letter [Reference SerreSer96], so our main contribution is a careful treatment by exploiting the group action at infinite level. This identification is a key ingredient in both the mod ![]() $p$ correspondence in § 4 and the
$p$ correspondence in § 4 and the ![]() $p$-adic correspondence in § 5.
$p$-adic correspondence in § 5.
Finally, we remark that, motivated by our specific needs, we have made what appear to be some non-standard choices in defining our moduli problems.
(i) We allow level defined by an arbitrary closed adelic subgroup, which facilitates the free usage of large group actions on infinite-level moduli problems and, in particular, transparent passage between the infinite-level prime-to-
 $p$ moduli problem over
$p$ moduli problem over  $\mathbb {Z}_{(p)}$ and infinite-level moduli problem over
$\mathbb {Z}_{(p)}$ and infinite-level moduli problem over  $\mathbb {Q}$.
$\mathbb {Q}$.(ii) We give an up to isogeny definition of level structure that does not require the base scheme to be locally noetherian (i.e. does not use the (pro)-étale fundamental group). In particular, this is necessary to allow arbitrary closed subgroups as before, but also allows us to evaluate on, e.g., perfectoid rings and other very non-noetherian objects without appealing behind the scenes to noetherian approximation.
We accomplish both of these goals by interpreting the sentence ‘level ![]() $K$ structure on
$K$ structure on ![]() $E$ is a
$E$ is a ![]() $K$-orbit of trivializations of
$K$-orbit of trivializations of ![]() $V_{\mathbb {A}_f}(E)$’ literally, i.e. as the choice of a
$V_{\mathbb {A}_f}(E)$’ literally, i.e. as the choice of a ![]() $K$-torsor in
$K$-torsor in ![]() $\underline {\mathrm {Isom}}(\underline {\mathbb {A}_f}^2, V_{\mathbb {A}_f}(E))$. All representability statements are deduced from classical results on finite-level curves, and ultimately all of our arguments could be run in a more classical setup, as the diligent reader will have no trouble verifying.
$\underline {\mathrm {Isom}}(\underline {\mathbb {A}_f}^2, V_{\mathbb {A}_f}(E))$. All representability statements are deduced from classical results on finite-level curves, and ultimately all of our arguments could be run in a more classical setup, as the diligent reader will have no trouble verifying.
3.1 Modular curves
Definition 3.1.1 (The level  $K$ elliptic moduli functor)
$K$ elliptic moduli functor)
Let ![]() $K \subset \mathrm {GL}_2(\mathbb {A}_f)$ be a closed subgroup. Let
$K \subset \mathrm {GL}_2(\mathbb {A}_f)$ be a closed subgroup. Let ![]() $Y_K$ be the functor on
$Y_K$ be the functor on ![]() $\mathbb {Q}$-algebras
$\mathbb {Q}$-algebras
sending ![]() $R/\mathbb {Q}$ to the set of equivalence classes of pairs
$R/\mathbb {Q}$ to the set of equivalence classes of pairs ![]() $(E, \mathcal {K})$ where:
$(E, \mathcal {K})$ where:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\mathcal {K} \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f})^2, V_{\mathbb {A}_f }(E))$ is a
$\mathcal {K} \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f})^2, V_{\mathbb {A}_f }(E))$ is a  $K$-torsor;
$K$-torsor;(iii) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E,\mathcal {K}) \sim (E', \mathcal {K}')$ if there is a quasi-isogeny
$(E,\mathcal {K}) \sim (E', \mathcal {K}')$ if there is a quasi-isogeny  $q: E \rightarrow E'$ such that
$q: E \rightarrow E'$ such that  $q(\mathcal {K}) = \mathcal {K}'$.
$q(\mathcal {K}) = \mathcal {K}'$.
The topological constant sheaf on the normalizer of ![]() $K$,
$K$, ![]() $\underline {N_{\mathrm {GL}_2(\mathbb {A}_f)}(K)}$, acts on
$\underline {N_{\mathrm {GL}_2(\mathbb {A}_f)}(K)}$, acts on ![]() $Y_K$, and for
$Y_K$, and for ![]() $K_1 \leq K_2$ we have the obvious map
$K_1 \leq K_2$ we have the obvious map
Example 3.1.2 (Infinite level)
Take ![]() $K=\{e\}$. Then the
$K=\{e\}$. Then the ![]() $K$-torsor
$K$-torsor ![]() $\mathcal {K}$ appearing in the moduli problem
$\mathcal {K}$ appearing in the moduli problem ![]() $Y_{K}$ is just a section of
$Y_{K}$ is just a section of
i.e. an isomorphism ![]() $\varphi _{\mathbb {A}_f}:\underline {\mathbb {A}_f}^2 \xrightarrow {\sim } V_{\mathbb {A}_f}(E)$, and the condition in the equivalence relation becomes
$\varphi _{\mathbb {A}_f}:\underline {\mathbb {A}_f}^2 \xrightarrow {\sim } V_{\mathbb {A}_f}(E)$, and the condition in the equivalence relation becomes ![]() $q \circ \varphi _{\mathbb {A}_f} = \varphi '_{\mathbb {A}_f}$. The group action is by all of
$q \circ \varphi _{\mathbb {A}_f} = \varphi '_{\mathbb {A}_f}$. The group action is by all of ![]() $\underline {\mathrm {GL}_2(\mathbb {A}_f)}$, and in this notation it acts by composition with
$\underline {\mathrm {GL}_2(\mathbb {A}_f)}$, and in this notation it acts by composition with ![]() $\varphi _{\mathbb {A}_f}$. When
$\varphi _{\mathbb {A}_f}$. When ![]() $K=\{e\}$, we typically omit it from the notation and write simply
$K=\{e\}$, we typically omit it from the notation and write simply ![]() $Y=Y_{\{e\}}$.
$Y=Y_{\{e\}}$.
Removing any level structure at ![]() $p$, we obtain a variant over
$p$, we obtain a variant over ![]() $\mathbb {Z}_{(p)}$.
$\mathbb {Z}_{(p)}$.
Definition 3.1.3 (The integral level  $K^p$ elliptic moduli functor)
$K^p$ elliptic moduli functor)
Let ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. Let
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. Let ![]() $\mathfrak {Y}_{K^p}$ be the functor on
$\mathfrak {Y}_{K^p}$ be the functor on ![]() $\mathbb {Z}_{(p)}$-algebras
$\mathbb {Z}_{(p)}$-algebras
sending ![]() $R/\mathbb {Z}_{(p)}$ to the set of equivalence classes of pairs
$R/\mathbb {Z}_{(p)}$ to the set of equivalence classes of pairs ![]() $(E, \mathcal {K}^p)$ where:
$(E, \mathcal {K}^p)$ where:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E))$ is a
$\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E))$ is a  $K^p$-torsor;
$K^p$-torsor;(iii) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E, \mathcal {K}^p) \sim (E', {\mathcal {K}^p}')$ if there is a prime-to-
$(E, \mathcal {K}^p) \sim (E', {\mathcal {K}^p}')$ if there is a prime-to- $p$ quasi-isogeny
$p$ quasi-isogeny  $q: E \rightarrow E'$ such that
$q: E \rightarrow E'$ such that  $q(\mathcal {K}^p) = {\mathcal {K}^p}'$.
$q(\mathcal {K}^p) = {\mathcal {K}^p}'$.
The topological constant sheaf on the normalizer of ![]() $K$,
$K$, ![]() $\underline {N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$, acts on
$\underline {N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$, acts on ![]() $\mathfrak {Y}_{K^p}$, and for
$\mathfrak {Y}_{K^p}$, and for ![]() $K^p_1 \leq K^p_2$ we have the obvious map
$K^p_1 \leq K^p_2$ we have the obvious map
Example 3.1.4 (Integral infinite level)
As in Example 3.1.2, when ![]() $K^p=\{e\}$,
$K^p=\{e\}$, ![]() $\mathcal {K}^p$ is simply the choice of an isomorphism
$\mathcal {K}^p$ is simply the choice of an isomorphism ![]() $\varphi _{\mathbb {A}_f^{(p)}}:\underline {\mathbb {A}_f^{(p)}}^2 \xrightarrow {\sim } V_{\mathbb {A}_f^{(p)}}(E)$. When
$\varphi _{\mathbb {A}_f^{(p)}}:\underline {\mathbb {A}_f^{(p)}}^2 \xrightarrow {\sim } V_{\mathbb {A}_f^{(p)}}(E)$. When ![]() $K^p=\{e\}$, we typically omit it from the notation and write simply
$K^p=\{e\}$, we typically omit it from the notation and write simply ![]() $\mathfrak {Y}=\mathfrak {Y}_{\{e\}}$.
$\mathfrak {Y}=\mathfrak {Y}_{\{e\}}$.
Arguing as in [Reference DeligneDel71, Corollaire 3.5], we find the following.
Lemma 3.1.5 Let ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. The assignment
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. The assignment
induces an isomorphism
Example 3.1.6 Lemma 3.1.5 gives ![]() $\mathfrak {Y}_{\mathbb {Q}}=Y_{\mathrm {GL}_2(\mathbb {Z}_p)},$ where on the right-hand side
$\mathfrak {Y}_{\mathbb {Q}}=Y_{\mathrm {GL}_2(\mathbb {Z}_p)},$ where on the right-hand side ![]() $\mathrm {GL}_2(\mathbb {Z}_p)$ is viewed as a closed subgroup of
$\mathrm {GL}_2(\mathbb {Z}_p)$ is viewed as a closed subgroup of ![]() $\mathrm {GL}_2(\mathbb {A}_f)$, and, as previously,
$\mathrm {GL}_2(\mathbb {A}_f)$, and, as previously, ![]() $\mathfrak {Y}=\mathfrak {Y}_{\{e\}}$. This identification explains one reason why it is convenient to allow an arbitrary closed subgroup in the formulation of the moduli problem.
$\mathfrak {Y}=\mathfrak {Y}_{\{e\}}$. This identification explains one reason why it is convenient to allow an arbitrary closed subgroup in the formulation of the moduli problem.
Definition 3.1.7 A closed subgroup ![]() $K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$) is sufficiently small if it stabilizes a
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$) is sufficiently small if it stabilizes a ![]() $\widehat {\mathbb {Z}}$-lattice
$\widehat {\mathbb {Z}}$-lattice ![]() $\mathcal {L} \subset \mathbb {A}_f^2$ (respectively, a
$\mathcal {L} \subset \mathbb {A}_f^2$ (respectively, a ![]() $\widehat {\mathbb {Z}}^{(p)}$-lattice
$\widehat {\mathbb {Z}}^{(p)}$-lattice ![]() $\mathcal {L} \subset (\mathbb {A}_f^{(p)})^2$) and lies in the kernel of the map
$\mathcal {L} \subset (\mathbb {A}_f^{(p)})^2$) and lies in the kernel of the map ![]() $\mathrm {GL}(\mathcal {L}) \rightarrow \mathrm {GL}(\mathcal {L}/n\mathcal {L})$ for some
$\mathrm {GL}(\mathcal {L}) \rightarrow \mathrm {GL}(\mathcal {L}/n\mathcal {L})$ for some ![]() $n \geq 3$ (respectively, and
$n \geq 3$ (respectively, and ![]() $(n,p)=1$).
$(n,p)=1$).
Note that if ![]() $K_2 \leq K_1 \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$K_2 \leq K_1 \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $K_2^p \leq K_1^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$), are closed subgroups and
$K_2^p \leq K_1^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$), are closed subgroups and ![]() $K_1$ (respectively,
$K_1$ (respectively, ![]() $K_1^p$) is sufficiently small, then so is
$K_1^p$) is sufficiently small, then so is ![]() $K_2$ (respectively,
$K_2$ (respectively, ![]() $K_2^p$). Moreover, the property of being a sufficiently small closed subgroup of
$K_2^p$). Moreover, the property of being a sufficiently small closed subgroup of ![]() $\mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$\mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$) is preserved under conjugation by
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$) is preserved under conjugation by ![]() $\mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$\mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$). Because any lattice
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$). Because any lattice ![]() $\mathcal {L}$ is in the
$\mathcal {L}$ is in the ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-orbit of
$\mathrm {GL}_2(\mathbb {A}_f)$-orbit of ![]() $\widehat {\mathbb {Z}}^2$ (respectively,
$\widehat {\mathbb {Z}}^2$ (respectively, ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-orbit of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-orbit of ![]() $(\widehat {\mathbb {Z}}^{(p)})^2$), being sufficiently small is equivalent to being contained in a conjugate of the standard principal congruence subgroup of level
$(\widehat {\mathbb {Z}}^{(p)})^2$), being sufficiently small is equivalent to being contained in a conjugate of the standard principal congruence subgroup of level ![]() $n \geq 3$ (respectively,
$n \geq 3$ (respectively, ![]() $(n,p)=1$).
$(n,p)=1$).
The main representability results are as follows.
Proposition 3.1.8 If ![]() $K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$) is a sufficiently small closed subgroup, then
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$) is a sufficiently small closed subgroup, then ![]() $Y_K$ (respectively,
$Y_K$ (respectively, ![]() $\mathfrak {Y}_{K^p}$) is represented by an affine scheme over
$\mathfrak {Y}_{K^p}$) is represented by an affine scheme over ![]() $\operatorname {Spec}\!\mathbb {Q}$ (respectively,
$\operatorname {Spec}\!\mathbb {Q}$ (respectively, ![]() $\operatorname {Spec}\!\mathbb {Z}_{(p)}$), and the natural map
$\operatorname {Spec}\!\mathbb {Z}_{(p)}$), and the natural map
 \begin{equation} Y_K \rightarrow \lim_{\substack{K' \text{ compact open}\\ K \leq K' \leq \mathrm{GL}_2(\mathbb{A}_f)}} Y_{K'} \quad \text{ (respectively, } \mathfrak{Y}_{K^p} \rightarrow \lim_{\substack{{K^p}' \text{ compact open}\\ {K^p} \leq {K^p}' \leq \mathrm{GL}_2(\mathbb{A}_f^{(p)})}} \mathfrak{Y}_{{K^p}'} \text{)} \end{equation}
\begin{equation} Y_K \rightarrow \lim_{\substack{K' \text{ compact open}\\ K \leq K' \leq \mathrm{GL}_2(\mathbb{A}_f)}} Y_{K'} \quad \text{ (respectively, } \mathfrak{Y}_{K^p} \rightarrow \lim_{\substack{{K^p}' \text{ compact open}\\ {K^p} \leq {K^p}' \leq \mathrm{GL}_2(\mathbb{A}_f^{(p)})}} \mathfrak{Y}_{{K^p}'} \text{)} \end{equation}
is a ![]() $\underline {N_{\mathrm {GL}_2(\mathbb {A}_f)}(K)}$-equivariant (respectively,
$\underline {N_{\mathrm {GL}_2(\mathbb {A}_f)}(K)}$-equivariant (respectively, ![]() $\underline {N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$-equivariant) isomorphism, where the action on the right-hand side is induced by the action on the tower that permutes the terms by conjugation (i.e. right multiplication by
$\underline {N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$-equivariant) isomorphism, where the action on the right-hand side is induced by the action on the tower that permutes the terms by conjugation (i.e. right multiplication by ![]() $h$ sends
$h$ sends ![]() $Y_{K'}$ to
$Y_{K'}$ to ![]() $Y_{h^{-1}K'h}$).
$Y_{h^{-1}K'h}$).
If ![]() $K$ (respectively,
$K$ (respectively, ![]() $K^p$) is furthermore compact open, then
$K^p$) is furthermore compact open, then ![]() $Y_K$ (respectively,
$Y_K$ (respectively, ![]() $\mathfrak {Y}_{K^p}$) is a smooth affine curve. Moreover, for
$\mathfrak {Y}_{K^p}$) is a smooth affine curve. Moreover, for ![]() $K_1 \leq K_2$ (respectively,
$K_1 \leq K_2$ (respectively, ![]() $K_1^p \leq K_2^p$) sufficiently small closed subgroups the natural map
$K_1^p \leq K_2^p$) sufficiently small closed subgroups the natural map ![]() $Y_{K_1} \rightarrow Y_{K_2}$ (respectively,
$Y_{K_1} \rightarrow Y_{K_2}$ (respectively, ![]() $\mathfrak {Y}_{K_1^p} \rightarrow \mathfrak {Y}_{K_2^p}$) is profinite étale, and, if
$\mathfrak {Y}_{K_1^p} \rightarrow \mathfrak {Y}_{K_2^p}$) is profinite étale, and, if ![]() $K_1 \trianglelefteq K_2$ (respectively,
$K_1 \trianglelefteq K_2$ (respectively, ![]() $K_1^p \trianglelefteq K_2^p$) it is Galois with group
$K_1^p \trianglelefteq K_2^p$) it is Galois with group ![]() $K_1/K_2$ (respectively,
$K_1/K_2$ (respectively, ![]() $K_1^p/K_2^p$).
$K_1^p/K_2^p$).
Proof. We argue only in the case over ![]() $\mathbb {Q}$, as the argument over
$\mathbb {Q}$, as the argument over ![]() $\mathbb {Z}_{(p)}$ is essentially the same. If we fix a
$\mathbb {Z}_{(p)}$ is essentially the same. If we fix a ![]() $\widehat {\mathbb {Z}}$ lattice
$\widehat {\mathbb {Z}}$ lattice ![]() $\mathcal {L}\subset \mathbb {A}_f^{2}$ preserved by
$\mathcal {L}\subset \mathbb {A}_f^{2}$ preserved by ![]() $K$, then, as in [Reference DeligneDel71, Corollaire 3.5], we see that the moduli problem can be replaced with an equivalent up to isomorphism moduli problem by taking
$K$, then, as in [Reference DeligneDel71, Corollaire 3.5], we see that the moduli problem can be replaced with an equivalent up to isomorphism moduli problem by taking ![]() $\mathcal {K}$ in
$\mathcal {K}$ in ![]() $\underline {\mathrm {Isom}}(\mathcal {L}, T_{\widehat {\mathbb {Z}}^{\bullet }}(E))$. The assertion that (3.1.1) is an isomorphism then amounts to the following: for
$\underline {\mathrm {Isom}}(\mathcal {L}, T_{\widehat {\mathbb {Z}}^{\bullet }}(E))$. The assertion that (3.1.1) is an isomorphism then amounts to the following: for ![]() $E/R$ an elliptic curve, if we consider the
$E/R$ an elliptic curve, if we consider the ![]() $\underline {\mathrm {GL}(\mathcal {L})}$-torsor
$\underline {\mathrm {GL}(\mathcal {L})}$-torsor ![]() $\mathcal {G}:=\underline {\mathrm {Isom}}(\mathcal {L}, T_{\widehat {\mathbb {Z}}^{\bullet }}(E))$, we must show that the following data are equivalent:
$\mathcal {G}:=\underline {\mathrm {Isom}}(\mathcal {L}, T_{\widehat {\mathbb {Z}}^{\bullet }}(E))$, we must show that the following data are equivalent:
(i) a
 $K$–torsor inside
$K$–torsor inside  $\mathcal {G}$;
$\mathcal {G}$;(ii) a system of
 $K'$-torsors inside
$K'$-torsors inside  $\mathcal {G}$ for
$\mathcal {G}$ for  $K'$ compact open,
$K'$ compact open,  $K \leq K' \leq \mathrm {GL}(\mathcal {L})$, compatible under inclusion.
$K \leq K' \leq \mathrm {GL}(\mathcal {L})$, compatible under inclusion.
This equivalence is provided by Lemma 2.2.1.
As we have established that (3.1.1) is an isomorphism, the rest of the claim for general ![]() $K$ is essentially formal if we can establish the representability claims for
$K$ is essentially formal if we can establish the representability claims for ![]() $K$ compact open. However, for
$K$ compact open. However, for ![]() $K$ compact open, we can conjugate to assume the lattice
$K$ compact open, we can conjugate to assume the lattice ![]() $\mathcal {L}$ as previously is
$\mathcal {L}$ as previously is ![]() $\widehat {\mathbb {Z}}^2$, and then the representability statements are consequences of the classical theory of finite level modular curves as in, e.g., [Reference Katz and MazurKM85].
$\widehat {\mathbb {Z}}^2$, and then the representability statements are consequences of the classical theory of finite level modular curves as in, e.g., [Reference Katz and MazurKM85].
Definition 3.1.9 (Compactified modular curves)
For ![]() $K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $K^p \leq \mathrm {GL}_2 (\mathbb {A}_f^{(p)})$) a sufficiently small compact open subgroup, we form compactifications
$K^p \leq \mathrm {GL}_2 (\mathbb {A}_f^{(p)})$) a sufficiently small compact open subgroup, we form compactifications ![]() $X_K$ (respectively,
$X_K$ (respectively, ![]() $\mathfrak {X}_{K^p}$) as in [Reference Katz and MazurKM85, 8.6] after fixing a lattice
$\mathfrak {X}_{K^p}$) as in [Reference Katz and MazurKM85, 8.6] after fixing a lattice ![]() $\mathcal {L} \subset \mathbb {A}_f^2$ (respectively,
$\mathcal {L} \subset \mathbb {A}_f^2$ (respectively, ![]() $\mathcal {L} \subset (\mathbb {A}_f^{(p)})^2$) preserved by
$\mathcal {L} \subset (\mathbb {A}_f^{(p)})^2$) preserved by ![]() $K$ (respectively,
$K$ (respectively, ![]() $K^p$) to relate to classical finite-level moduli problems as in the previous proof. We obtain smooth projective curves
$K^p$) to relate to classical finite-level moduli problems as in the previous proof. We obtain smooth projective curves ![]() $X_K/\mathbb {Q}$ (respectively,
$X_K/\mathbb {Q}$ (respectively, ![]() $\mathfrak {X}_{K^p}/\mathbb {Z}_{(p)}$), and the finite étale maps in the tower of
$\mathfrak {X}_{K^p}/\mathbb {Z}_{(p)}$), and the finite étale maps in the tower of ![]() $Y_K$ (respectively,
$Y_K$ (respectively, ![]() $\mathfrak {Y}_{K^p}$) for
$\mathfrak {Y}_{K^p}$) for ![]() $K$ (respectively,
$K$ (respectively, ![]() $K^p$) sufficiently small compact open extend to finite maps in the tower of
$K^p$) sufficiently small compact open extend to finite maps in the tower of ![]() $X_K$ (respectively,
$X_K$ (respectively, ![]() $\mathfrak {X}_{K^p}$).
$\mathfrak {X}_{K^p}$).
It can be checked that the natural group actions also extend. For ![]() $X_K$ and
$X_K$ and ![]() $\mathfrak {X}_{K^p,\mathbb {F}_p}$ this is even immediate because the smooth compactifications of smooth curves are functorial over a perfect field: using this, we could also define
$\mathfrak {X}_{K^p,\mathbb {F}_p}$ this is even immediate because the smooth compactifications of smooth curves are functorial over a perfect field: using this, we could also define ![]() $X_K$ and
$X_K$ and ![]() $\mathfrak {X}_{K^p,\mathbb {F}_p}$ with no reference to the moduli problem.
$\mathfrak {X}_{K^p,\mathbb {F}_p}$ with no reference to the moduli problem.
We extend these definitions to ![]() $K$ (respectively,
$K$ (respectively, ![]() $K^p$) sufficiently small closed by taking limits as in Proposition 3.1.8, and the resulting objects are schemes because the transition maps are affine.
$K^p$) sufficiently small closed by taking limits as in Proposition 3.1.8, and the resulting objects are schemes because the transition maps are affine.
We refer to the boundary ![]() $X_K\backslash Y_K$ (respectively,
$X_K\backslash Y_K$ (respectively, ![]() $\mathfrak {X}_{K^p} \backslash \mathfrak {Y}_{K^{p}}$) with its reduced subscheme structure as the cusps. The cusps can also be described as filling in the punctures corresponding to level structure on the Tate curve as in [Reference Katz and MazurKM85, 8.11].
$\mathfrak {X}_{K^p} \backslash \mathfrak {Y}_{K^{p}}$) with its reduced subscheme structure as the cusps. The cusps can also be described as filling in the punctures corresponding to level structure on the Tate curve as in [Reference Katz and MazurKM85, 8.11].
3.2 Modular forms
For any sufficiently small closed ![]() $K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively,
$K \leq \mathrm {GL}_2(\mathbb {A}_f)$ (respectively, ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$), we have a universal elliptic curve
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$), we have a universal elliptic curve ![]() $E_K/Y_K$ (respectively,
$E_K/Y_K$ (respectively, ![]() $\mathfrak {E}_{K^p} / \mathfrak {Y}_{K^p}$), determined up to unique isogeny (respectively, prime-to-
$\mathfrak {E}_{K^p} / \mathfrak {Y}_{K^p}$), determined up to unique isogeny (respectively, prime-to-![]() $p$ isogeny). We write simply
$p$ isogeny). We write simply ![]() $\omega$ for the line bundle
$\omega$ for the line bundle ![]() $\omega _{E/K} / Y_K$ (respectively,
$\omega _{E/K} / Y_K$ (respectively, ![]() $\omega _{\mathfrak {E}_{K^p}/\mathfrak {Y}_{K^p}}/\mathfrak {Y}_{K^p}$): it is determined up to unique isomorphism compatibly with all pullbacks, base change, and group actions discussed so far, so that this notation will cause no confusion.
$\omega _{\mathfrak {E}_{K^p}/\mathfrak {Y}_{K^p}}/\mathfrak {Y}_{K^p}$): it is determined up to unique isomorphism compatibly with all pullbacks, base change, and group actions discussed so far, so that this notation will cause no confusion.
For every sufficient small compact open ![]() $K$ (respectively,
$K$ (respectively, ![]() $K^p$), we extend
$K^p$), we extend ![]() $\omega$ to
$\omega$ to ![]() $X_K$ (respectively, to
$X_K$ (respectively, to ![]() $\mathfrak {X}_{K^p}$) in the standard way by allowing sections with holomorphic
$\mathfrak {X}_{K^p}$) in the standard way by allowing sections with holomorphic ![]() $q$-expansions at each cusp. Direct computation shows this is compatible with all pullbacks, base change, and group actions discussed so far, so that we can extend this definition to any sufficiently small closed
$q$-expansions at each cusp. Direct computation shows this is compatible with all pullbacks, base change, and group actions discussed so far, so that we can extend this definition to any sufficiently small closed ![]() $K$ (respectively,
$K$ (respectively, ![]() $K^p$) and again no confusion will be caused by referring to the extended line bundle also as
$K^p$) and again no confusion will be caused by referring to the extended line bundle also as ![]() $\omega$.
$\omega$.
We consider the smooth ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-representation of modular forms,
$\mathrm {GL}_2(\mathbb {A}_f)$-representation of modular forms,
For ![]() $K$ any sufficiently small closed subgroup, pullback from level
$K$ any sufficiently small closed subgroup, pullback from level ![]() $K$ identifies
$K$ identifies
Applied to ![]() $K$ sufficiently small compact open, we deduce that
$K$ sufficiently small compact open, we deduce that ![]() $M_{k,\mathbb {Q}}$ is an admissible representation of
$M_{k,\mathbb {Q}}$ is an admissible representation of ![]() $\mathrm {GL}_2(\mathbb {A}_f)$. Applied to
$\mathrm {GL}_2(\mathbb {A}_f)$. Applied to ![]() $K=\mathrm {GL}_2(\mathbb {Z}_p)$, we obtain
$K=\mathrm {GL}_2(\mathbb {Z}_p)$, we obtain
In particular, if we write
an admissible ![]() $\mathbb {F}_p$-representation of
$\mathbb {F}_p$-representation of ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ by the same argument as previously, then
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ by the same argument as previously, then ![]() $H^0(\mathfrak {X}, \omega ^k)$ is a natural
$H^0(\mathfrak {X}, \omega ^k)$ is a natural ![]() $\mathbb {Z}_{(p)}$-lattice in
$\mathbb {Z}_{(p)}$-lattice in ![]() $M_{k,\mathbb {Q}}^{\mathrm {GL}_2(\mathbb {Z}_p)}$ equipped with a
$M_{k,\mathbb {Q}}^{\mathrm {GL}_2(\mathbb {Z}_p)}$ equipped with a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant reduction map to
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant reduction map to ![]() $M_{k,\mathbb {F}_p}$.
$M_{k,\mathbb {F}_p}$.
Remark 3.2.1 Neither ![]() $M_{k,\mathbb {F}_p}$ nor the image of reduction is what is typically referred to as mod
$M_{k,\mathbb {F}_p}$ nor the image of reduction is what is typically referred to as mod ![]() $p$ modular forms. We recall this definition in § 3.4.
$p$ modular forms. We recall this definition in § 3.4.
3.2.2 The Hasse invariant
We now recall how, to any elliptic curve ![]() $E/R$ for
$E/R$ for ![]() $R/\mathbb {F}_p$, one can attach a canonical section
$R/\mathbb {F}_p$, one can attach a canonical section ![]() $\mathrm {Ha}(E/R) \in \omega ^{p-1}_{E/R}$, the Hasse invariant. We follow one of the approaches described in [Reference Katz and MazurKM85, 12.3].
$\mathrm {Ha}(E/R) \in \omega ^{p-1}_{E/R}$, the Hasse invariant. We follow one of the approaches described in [Reference Katz and MazurKM85, 12.3].
As the section ![]() $\mathrm {Ha}(E/R)$ can be constructed Zariski locally, it suffices to assigns to any pair
$\mathrm {Ha}(E/R)$ can be constructed Zariski locally, it suffices to assigns to any pair ![]() $(E/R, \alpha )$ where
$(E/R, \alpha )$ where ![]() $R$ is an
$R$ is an ![]() $\mathbb {F}_p$-algebra,
$\mathbb {F}_p$-algebra, ![]() $E/ R$ is an elliptic curve and
$E/ R$ is an elliptic curve and ![]() $\alpha \in \omega _{E/R}$ is a non-vanishing invariant differential, an element
$\alpha \in \omega _{E/R}$ is a non-vanishing invariant differential, an element ![]() $\mathrm {Ha}(E/ R,\alpha )$ of
$\mathrm {Ha}(E/ R,\alpha )$ of ![]() $R$ such that, for
$R$ such that, for ![]() $a \in A^\times$,
$a \in A^\times$,
and whose formation is functorial in base change and isomorphism. In this case, to give our rule we first take the invariant derivation ![]() $\partial _{\alpha }$ that is dual to
$\partial _{\alpha }$ that is dual to ![]() $\alpha$, then form
$\alpha$, then form
which is also an invariant derivation and thus a multiple of ![]() $\partial$. Then the equation
$\partial$. Then the equation
defines ![]() $\mathrm {Ha}(E/ R, \alpha )$, and it is straightforward to check this satisfies the desired transformation rule if we scale
$\mathrm {Ha}(E/ R, \alpha )$, and it is straightforward to check this satisfies the desired transformation rule if we scale ![]() $\alpha$ and is functorial in base change and isomorphism.
$\alpha$ and is functorial in base change and isomorphism.
In fact, the construction is also functorial in prime-to-![]() $p$ quasi-isogenies: it suffices to observe that a prime-to-
$p$ quasi-isogenies: it suffices to observe that a prime-to-![]() $p$ quasi-isogeny induces an isomorphism of
$p$ quasi-isogeny induces an isomorphism of ![]() $p$-divisible groups and, in particular, of formal groups, and that the action of an invariant derivation is completely determined by its action on the formal group. This observation also has the important consequence that the resulting section
$p$-divisible groups and, in particular, of formal groups, and that the action of an invariant derivation is completely determined by its action on the formal group. This observation also has the important consequence that the resulting section ![]() $\mathrm {Ha}(E/R)$ can be constructed entirely in terms of
$\mathrm {Ha}(E/R)$ can be constructed entirely in terms of ![]() $E[p^\infty ]$.
$E[p^\infty ]$.
Applying this construction to the universal elliptic curve over ![]() $\mathfrak {Y}_{\mathbb {F}_p}$, we obtain a
$\mathfrak {Y}_{\mathbb {F}_p}$, we obtain a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-invariant section of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-invariant section of ![]() $\omega ^{p-1}$. A direct computation on the Tate curve (see [Reference Katz and MazurKM85, Theorem 12.4.2]) shows that its
$\omega ^{p-1}$. A direct computation on the Tate curve (see [Reference Katz and MazurKM85, Theorem 12.4.2]) shows that its ![]() $q$-expansions are constant equal to
$q$-expansions are constant equal to ![]() $1$ at every cusp, thus it extends to
$1$ at every cusp, thus it extends to
3.3 Supersingular and ordinary loci
Let
Let ![]() $\mathbb {X}_{\mathrm {ss}} / \mathbb {F}_p$ (respectively,
$\mathbb {X}_{\mathrm {ss}} / \mathbb {F}_p$ (respectively, ![]() $\mathbb {X}_{\mathrm {ord}}/\mathbb {F}_p$) be the
$\mathbb {X}_{\mathrm {ord}}/\mathbb {F}_p$) be the ![]() $p$-divisible group corresponding to the covariant Dieudonné module
$p$-divisible group corresponding to the covariant Dieudonné module ![]() $\mathbb {Z}_p^2$ with Frobenius
$\mathbb {Z}_p^2$ with Frobenius ![]() $F$ acting by
$F$ acting by ![]() $b_{\mathrm {ss}}$ (respectively,
$b_{\mathrm {ss}}$ (respectively, ![]() $b_\mathrm {ord}$). Then
$b_\mathrm {ord}$). Then ![]() $\mathbb {X}_{\mathrm {ss}}$ is a connected one-dimensional height-two
$\mathbb {X}_{\mathrm {ss}}$ is a connected one-dimensional height-two ![]() $p$-divisible group, whereas
$p$-divisible group, whereas ![]() $\mathbb {X}_{\mathrm {ord}}=\mu _{p^\infty } \times \mathbb {Q}_p/\mathbb {Z}_p$ is a one-dimensional height-two
$\mathbb {X}_{\mathrm {ord}}=\mu _{p^\infty } \times \mathbb {Q}_p/\mathbb {Z}_p$ is a one-dimensional height-two ![]() $p$-divisible group with non-trivial étale part. It follows from the classification of
$p$-divisible group with non-trivial étale part. It follows from the classification of ![]() $p$-divisible groups by Dieudonné modules that, for any algebraically closed
$p$-divisible groups by Dieudonné modules that, for any algebraically closed ![]() $\kappa /\mathbb {F}_p$, every height-two one-dimensional
$\kappa /\mathbb {F}_p$, every height-two one-dimensional ![]() $p$-divisible group over
$p$-divisible group over ![]() $\kappa$ is quasi-isogenous/isomorphicFootnote 7 to exactly one of
$\kappa$ is quasi-isogenous/isomorphicFootnote 7 to exactly one of ![]() $\mathbb {X}_{\mathrm {ord}, \kappa }$ and
$\mathbb {X}_{\mathrm {ord}, \kappa }$ and ![]() $\mathbb {X}_{\mathrm {ss}, \kappa }$.
$\mathbb {X}_{\mathrm {ss}, \kappa }$.
In particular, this applies to ![]() $E[p^\infty ]$ for
$E[p^\infty ]$ for ![]() $E/\kappa$ an elliptic curve. It thus makes sense, for any
$E/\kappa$ an elliptic curve. It thus makes sense, for any ![]() $K^p$ sufficiently small, to define the supersingular (respectively, ordinary) locus
$K^p$ sufficiently small, to define the supersingular (respectively, ordinary) locus ![]() $\mathfrak {Y}_{K^p,\mathbb {F}_p}^\mathrm {ss}$ (respectively,
$\mathfrak {Y}_{K^p,\mathbb {F}_p}^\mathrm {ss}$ (respectively, ![]() $\mathfrak {Y}_{K^p,\mathbb {F}_p}^\mathrm {ord}$) in
$\mathfrak {Y}_{K^p,\mathbb {F}_p}^\mathrm {ord}$) in ![]() $\mathfrak {Y}_{K^p,\mathbb {F}_p}$ as the locus whose geometric points are such that the
$\mathfrak {Y}_{K^p,\mathbb {F}_p}$ as the locus whose geometric points are such that the ![]() $p$-divisible group of universal elliptic curve is quasi-isogenous/isomorphic to
$p$-divisible group of universal elliptic curve is quasi-isogenous/isomorphic to ![]() $\mathbb {X}_\mathrm {ss}$ (respectively,
$\mathbb {X}_\mathrm {ss}$ (respectively, ![]() $\mathbb {X}_\mathrm {ord}$). We then have
$\mathbb {X}_\mathrm {ord}$). We then have
and it can be shown that the supersingular locus is closed (and, thus, the ordinary locus is open). In fact, a local computation as in [Reference Katz and MazurKM85, Theorem 12.4.3] gives the following result.
Lemma 3.3.1 For ![]() $K^p$ sufficiently small, the vanishing locus of
$K^p$ sufficiently small, the vanishing locus of ![]() $\mathrm {Ha}$, viewed as a section of
$\mathrm {Ha}$, viewed as a section of ![]() $H^0(\mathfrak {X}_{K^p}, \mathbb {F}_p)$, is
$H^0(\mathfrak {X}_{K^p}, \mathbb {F}_p)$, is ![]() $\mathfrak {Y}_{K^p,\mathbb {F}_p}^\mathrm {ss}$ with its reduced closed subscheme structure.
$\mathfrak {Y}_{K^p,\mathbb {F}_p}^\mathrm {ss}$ with its reduced closed subscheme structure.
We write also
3.4 Ordinary Igusa varieties, mod  $p$, and
$p$, and  $p$-adic modular forms
$p$-adic modular forms
Following Katz [Reference KatzKat75a], we define mod ![]() $p$ and
$p$ and ![]() $p$-adic modular forms as functions on certain moduli problems. This has the advantage of rendering group actions transparent, and mirrors our approach to the supersingular Igusa variety and quaternionic
$p$-adic modular forms as functions on certain moduli problems. This has the advantage of rendering group actions transparent, and mirrors our approach to the supersingular Igusa variety and quaternionic ![]() $p$-adic automorphic forms. Functions on these moduli problems have
$p$-adic automorphic forms. Functions on these moduli problems have ![]() $q$-expansions, and the connection with the completion of
$q$-expansions, and the connection with the completion of ![]() $q$-expansions of classical modular forms as in Serre's [Reference SerreSer73] perspective then comes from evaluation along a canonical trivialization of
$q$-expansions of classical modular forms as in Serre's [Reference SerreSer73] perspective then comes from evaluation along a canonical trivialization of ![]() $\omega$ and the
$\omega$ and the ![]() $q$-expansion principle.
$q$-expansion principle.
We begin by treating mod ![]() $p$ modular forms.
$p$ modular forms.
Definition 3.4.1 (The  $\mu _p$-Igusa moduli problem)
$\mu _p$-Igusa moduli problem)
Let ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. Let
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. Let ![]() $\mathrm {Ig}^{\mu _p}_{K^p}$ be the functor on
$\mathrm {Ig}^{\mu _p}_{K^p}$ be the functor on ![]() $\mathbb {F}_{p}$-algebras
$\mathbb {F}_{p}$-algebras
sending ![]() $R/\mathbb {F}_p$ to the set of equivalence classes of triples
$R/\mathbb {F}_p$ to the set of equivalence classes of triples ![]() $(E, \varphi _p, \mathcal {K}^p)$ where:
$(E, \varphi _p, \mathcal {K}^p)$ where:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\varphi _p: \mu _p \xrightarrow {\sim } \hat {E}[p]$ is an isomorphism;
$\varphi _p: \mu _p \xrightarrow {\sim } \hat {E}[p]$ is an isomorphism;(iii)
 $\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E))$ is a
$\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E))$ is a  $K^p$-torsor;
$K^p$-torsor;(iv) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E, \mathcal {K}^p) \sim (E', {\mathcal {K}^p}')$ if there is a prime-to-
$(E, \mathcal {K}^p) \sim (E', {\mathcal {K}^p}')$ if there is a prime-to- $p$ quasi-isogeny
$p$ quasi-isogeny  $q: E \rightarrow E'$ such that
$q: E \rightarrow E'$ such that  $q\circ \varphi _p = \varphi _p'$ and
$q\circ \varphi _p = \varphi _p'$ and  $q(\mathcal {K}^p) = {\mathcal {K}^p}'$.
$q(\mathcal {K}^p) = {\mathcal {K}^p}'$.
As usual, when ![]() $K^p=\{e\}$ we drop it from the notation. For
$K^p=\{e\}$ we drop it from the notation. For ![]() $K^p$ sufficiently small, the functor
$K^p$ sufficiently small, the functor ![]() $\mathrm {Ig}^{\mathrm {ord}}_{K^p,\mu _p}$ is a finite étale
$\mathrm {Ig}^{\mathrm {ord}}_{K^p,\mu _p}$ is a finite étale ![]() $(\mathbb {Z}/p\mathbb {Z})^\times$ cover of
$(\mathbb {Z}/p\mathbb {Z})^\times$ cover of ![]() $\mathfrak {Y}^{\mathrm {ord}}_{K^p, \mathbb {F}_p}$, where
$\mathfrak {Y}^{\mathrm {ord}}_{K^p, \mathbb {F}_p}$, where ![]() $(\mathbb {Z}/p\mathbb {Z})^\times$ acts by precomposition with
$(\mathbb {Z}/p\mathbb {Z})^\times$ acts by precomposition with ![]() $\varphi _p$. A direct computation on the Tate curve, whose formal group is canonically
$\varphi _p$. A direct computation on the Tate curve, whose formal group is canonically ![]() $\widehat {\mathbb {G}}_m$, shows the cover is unramified at the cusps and, thus, extends canonically to a finite étale
$\widehat {\mathbb {G}}_m$, shows the cover is unramified at the cusps and, thus, extends canonically to a finite étale ![]() $(\mathbb {Z}/p\mathbb {Z})^\times$-cover
$(\mathbb {Z}/p\mathbb {Z})^\times$-cover ![]() $\mathrm {Ig}^{\mathrm {ord},c}_{K^p,\mu _p}$ of
$\mathrm {Ig}^{\mathrm {ord},c}_{K^p,\mu _p}$ of ![]() $\mathfrak {X}^{\mathrm {ord}}_{K^p, \mathbb {F}_p}$.
$\mathfrak {X}^{\mathrm {ord}}_{K^p, \mathbb {F}_p}$.
Definition 3.4.2 (Mod  $p$ modular forms)
$p$ modular forms)
The space of mod ![]() $p$ modular forms is the
$p$ modular forms is the ![]() $(\mathbb {Z}/p\mathbb {Z})^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant ring
$(\mathbb {Z}/p\mathbb {Z})^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant ring ![]() $\mathcal {M}_{\mathbb {F}_p}:=H^0(\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}, \mathcal {O})$.
$\mathcal {M}_{\mathbb {F}_p}:=H^0(\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}, \mathcal {O})$.
The pullback ![]() $(\varphi _p^{-1})^*({dt}/{t})$ of the invariant differential
$(\varphi _p^{-1})^*({dt}/{t})$ of the invariant differential ![]() ${dt}/{t}$ on
${dt}/{t}$ on ![]() $\mu _p=\operatorname {Spec}\!\mathbb {F}_p[t]/(t^p-1)$ is
$\mu _p=\operatorname {Spec}\!\mathbb {F}_p[t]/(t^p-1)$ is ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant trivialization of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant trivialization of ![]() $\omega$ on
$\omega$ on ![]() $\mathrm {Ig}^{\mathrm {ord}}_{\mu _p}$ and extends to a trivialization over
$\mathrm {Ig}^{\mathrm {ord}}_{\mu _p}$ and extends to a trivialization over ![]() $\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}$. In particular, we can use it to evaluate modular forms to functions on
$\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}$. In particular, we can use it to evaluate modular forms to functions on ![]() $\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}$ and we obtain the following version of a well-known result (cf., e.g., [Reference GrossGros90]).
$\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}$ and we obtain the following version of a well-known result (cf., e.g., [Reference GrossGros90]).
Lemma 3.4.3 Evaluation along ![]() $(\varphi _p^{-1})^*({dt}/{t})$ induces a
$(\varphi _p^{-1})^*({dt}/{t})$ induces a ![]() $(\mathbb {Z}/p\mathbb {Z})^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism of rings
$(\mathbb {Z}/p\mathbb {Z})^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism of rings
 \[ \biggl( \bigoplus_{k \geq 0} M_{k,\mathbb{F}_p} \biggr) / (\mathrm{Ha} - 1) \cong \mathcal{M}_{\mathbb{F}_p}, \]
\[ \biggl( \bigoplus_{k \geq 0} M_{k,\mathbb{F}_p} \biggr) / (\mathrm{Ha} - 1) \cong \mathcal{M}_{\mathbb{F}_p}, \]
where ![]() $(\mathbb {Z}/p\mathbb {Z})^\times$ acts on
$(\mathbb {Z}/p\mathbb {Z})^\times$ acts on ![]() $M_{k,\mathbb {F}_p}$ by the character
$M_{k,\mathbb {F}_p}$ by the character ![]() $z \mapsto z^{k}$.
$z \mapsto z^{k}$.
Proof. First note that the evaluation map on ![]() $M_{k,\mathbb {F}_p}$ factors through
$M_{k,\mathbb {F}_p}$ factors through ![]() $H^0(\mathfrak {X}^\mathrm {ord}_{\mathbb {F}_p},\omega ^k)$. One computes that
$H^0(\mathfrak {X}^\mathrm {ord}_{\mathbb {F}_p},\omega ^k)$. One computes that ![]() $((\varphi _p^{-1})^*({dt}/{t}))^{p-1}=\mathrm {Ha}$, so that the evaluation map factors as
$((\varphi _p^{-1})^*({dt}/{t}))^{p-1}=\mathrm {Ha}$, so that the evaluation map factors as
 \[ \bigoplus_{k\geq 0} M_{k,\mathbb{F}_p} \rightarrow \bigoplus_{k=0}^{p-2} H^0(\mathfrak{X}^\mathrm{ord}_{\mathbb{F}_p},\omega^k) \xrightarrow{\sim} H^0(\mathrm{Ig}^{\mathrm{ord}, c}_{\\\mu_p}, \mathcal{O}) = \mathcal{M}_{\mathbb{F}_p}, \]
\[ \bigoplus_{k\geq 0} M_{k,\mathbb{F}_p} \rightarrow \bigoplus_{k=0}^{p-2} H^0(\mathfrak{X}^\mathrm{ord}_{\mathbb{F}_p},\omega^k) \xrightarrow{\sim} H^0(\mathrm{Ig}^{\mathrm{ord}, c}_{\\\mu_p}, \mathcal{O}) = \mathcal{M}_{\mathbb{F}_p}, \]
where the first arrow is restriction followed by division by ![]() $\mathrm {Ha}^{\lfloor k/(p-1)\rfloor }$. The second arrow is an isomorphism because we can decompose
$\mathrm {Ha}^{\lfloor k/(p-1)\rfloor }$. The second arrow is an isomorphism because we can decompose ![]() $H^0(\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}, \mathcal {O})$ according to the characters of
$H^0(\mathrm {Ig}^{\mathrm {ord}, c}_{\mu _p}, \mathcal {O})$ according to the characters of ![]() $(\mathbb {Z}/p\mathbb {Z})^\times$ in
$(\mathbb {Z}/p\mathbb {Z})^\times$ in ![]() $\mathbb {F}_p$ and if
$\mathbb {F}_p$ and if ![]() $f$ is in the character space for
$f$ is in the character space for ![]() $z^{k}$, then
$z^{k}$, then ![]() $f( (\varphi _p^{-1})^*({dt}/{t}))^k$ is invariant under
$f( (\varphi _p^{-1})^*({dt}/{t}))^k$ is invariant under ![]() $(\mathbb {Z}/p\mathbb {Z})^\times$ thus descends to a section over
$(\mathbb {Z}/p\mathbb {Z})^\times$ thus descends to a section over ![]() $\mathfrak {X}^\mathrm {ord}_{\mathbb {F}_p}$.
$\mathfrak {X}^\mathrm {ord}_{\mathbb {F}_p}$.
The first map is clearly surjective because multiplying by a sufficient power of ![]() $\mathrm {Ha}$ will clear any poles along the supersingular locus. On the other hand, any element in the kernel can be multiplied by
$\mathrm {Ha}$ will clear any poles along the supersingular locus. On the other hand, any element in the kernel can be multiplied by ![]() $1+\mathrm {Ha} + \mathrm {Ha}^2 + \mathrm {Ha}^3 + \cdots$ (the condition of being in the kernel, when written out, guarantees that this product is zero in sufficiently large degree) to show that it is, in fact, in the ideal generated by
$1+\mathrm {Ha} + \mathrm {Ha}^2 + \mathrm {Ha}^3 + \cdots$ (the condition of being in the kernel, when written out, guarantees that this product is zero in sufficiently large degree) to show that it is, in fact, in the ideal generated by ![]() $(1-\mathrm {Ha})$.
$(1-\mathrm {Ha})$.
Remark 3.4.4 The ideal ![]() $(\mathrm {Ha}-1)$ on the left can also be interpreted as the kernel of the total
$(\mathrm {Ha}-1)$ on the left can also be interpreted as the kernel of the total ![]() $q$-expansion map, and indeed the original definition of mod
$q$-expansion map, and indeed the original definition of mod ![]() $p$ modular forms was by passing to
$p$ modular forms was by passing to ![]() $q$-expansions.
$q$-expansions.
We now define ![]() $p$-adic modular forms.
$p$-adic modular forms.
Definition 3.4.5 (The Katz–Igusa moduli problem)
Let ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. Let
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a closed subgroup. Let ![]() $\mathrm {Ig}^{\mathrm {ord}}_{K^p, \widehat {\mathbb {G}}_m}$ be the functor on
$\mathrm {Ig}^{\mathrm {ord}}_{K^p, \widehat {\mathbb {G}}_m}$ be the functor on ![]() $\mathrm {Nilp}_{\mathbb {Z}_p}$
$\mathrm {Nilp}_{\mathbb {Z}_p}$
sending ![]() $R/\mathbb {Z}_p$ to the equivalence classes of triples
$R/\mathbb {Z}_p$ to the equivalence classes of triples ![]() $(E, \varphi _p, \mathcal {K}^p)$ such that:
$(E, \varphi _p, \mathcal {K}^p)$ such that:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\varphi _p: \widehat {\mathbb {G}}_m \xrightarrow {\sim } \widehat {E}$ is an isomorphism of formal groups;
$\varphi _p: \widehat {\mathbb {G}}_m \xrightarrow {\sim } \widehat {E}$ is an isomorphism of formal groups;(iii)
 $\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E) )$ is a
$\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E) )$ is a  $K^p$-torsor; and
$K^p$-torsor; and(iv) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E, \varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a prime-to-
$(E, \varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a prime-to- $p$ quasi-isogeny
$p$ quasi-isogeny  $q: E \rightarrow E'$ such that
$q: E \rightarrow E'$ such that  $q\circ \varphi _p = \varphi _p'$ and
$q\circ \varphi _p = \varphi _p'$ and  $q(\mathcal {K}^p)=\mathcal {K}^p$.
$q(\mathcal {K}^p)=\mathcal {K}^p$.
As usual, when ![]() $K^p=\{e\}$ we drop it from the notation. The main source is [Reference KatzKat75a], which works with the geometrically connected variant with full level
$K^p=\{e\}$ we drop it from the notation. The main source is [Reference KatzKat75a], which works with the geometrically connected variant with full level ![]() $n$ structure. As in [Reference KatzKat75a], for
$n$ structure. As in [Reference KatzKat75a], for ![]() $K^p$ sufficiently small,
$K^p$ sufficiently small, ![]() $\mathrm {Ig}^{\mathrm {ord}}_{K^p, \widehat {\mathbb {G}}_m}$ is represented by an affine
$\mathrm {Ig}^{\mathrm {ord}}_{K^p, \widehat {\mathbb {G}}_m}$ is represented by an affine ![]() $p$-adic formal scheme, a pro-étale
$p$-adic formal scheme, a pro-étale ![]() $\mathbb {Z}_p^\times$-torsor over the formal ordinary locus
$\mathbb {Z}_p^\times$-torsor over the formal ordinary locus ![]() $\mathfrak {Y}_{K^p}^{\wedge, \mathrm {ord}}/\mathrm {Spf}\mathbb {Z}_p$; here, the action of
$\mathfrak {Y}_{K^p}^{\wedge, \mathrm {ord}}/\mathrm {Spf}\mathbb {Z}_p$; here, the action of ![]() $\underline {\mathbb {Z}_p^\times }$ is by precomposition with
$\underline {\mathbb {Z}_p^\times }$ is by precomposition with ![]() $\varphi _p$. For the same reason as the
$\varphi _p$. For the same reason as the ![]() $\mu _p$-Igusa moduli problem, it is unramified at the cusps and thus extends canonically over
$\mu _p$-Igusa moduli problem, it is unramified at the cusps and thus extends canonically over ![]() $\mathfrak {X}^{\wedge,\mathrm {ord}}_{K^p} /\mathrm {Spf} \mathbb {Z}_p$ to an affine formal scheme
$\mathfrak {X}^{\wedge,\mathrm {ord}}_{K^p} /\mathrm {Spf} \mathbb {Z}_p$ to an affine formal scheme ![]() $\mathrm {Ig}^{\mathrm {ord}, c}_{K^p, \widehat {\mathbb {G}}_m}$.
$\mathrm {Ig}^{\mathrm {ord}, c}_{K^p, \widehat {\mathbb {G}}_m}$.
Definition 3.4.6 The space of ![]() $p$-adic modular forms is the unitary
$p$-adic modular forms is the unitary ![]() $\mathbb {Z}_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ representation on the
$\mathbb {Z}_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ representation on the ![]() $\mathbb {Q}_p$-Banach space
$\mathbb {Q}_p$-Banach space
In the introduction, we used the notation ![]() $\mathcal {M}_{p-adic}$, which we do not employ further. We note also that
$\mathcal {M}_{p-adic}$, which we do not employ further. We note also that ![]() $\mathbb {V}_{\mathbb {Z}_p}$ is
$\mathbb {V}_{\mathbb {Z}_p}$ is ![]() $p$-torsion free.
$p$-torsion free.
The ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representation
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representation ![]() $\mathbb {V}_{\mathbb {Q}_p}$ is not smooth, but one can check that the smooth vectors are dense and, for
$\mathbb {V}_{\mathbb {Q}_p}$ is not smooth, but one can check that the smooth vectors are dense and, for ![]() $K^p$ a sufficiently small closed subgroup, already at the integral level we have
$K^p$ a sufficiently small closed subgroup, already at the integral level we have
The bundle ![]() $\omega$ is
$\omega$ is ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariantly trivialized over
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariantly trivialized over ![]() $\mathrm {Ig}^{\mathrm {ord}}_{\widehat {\mathbb {G}}_m}$ by
$\mathrm {Ig}^{\mathrm {ord}}_{\widehat {\mathbb {G}}_m}$ by ![]() $(\varphi _p^{-1})^*({dt}/{t})$ and this trivialization extends to
$(\varphi _p^{-1})^*({dt}/{t})$ and this trivialization extends to ![]() $\mathrm {Ig}^{\mathrm {ord},c}_{\widehat {\mathbb {G}}_m}$. We can, thus, evaluate modular forms to elements of
$\mathrm {Ig}^{\mathrm {ord},c}_{\widehat {\mathbb {G}}_m}$. We can, thus, evaluate modular forms to elements of ![]() $\mathbb {V}_{\mathbb {Q}_p}$ and, as in [Reference KatzKat75a, especially Theorem 2.1], one obtains the following result.
$\mathbb {V}_{\mathbb {Q}_p}$ and, as in [Reference KatzKat75a, especially Theorem 2.1], one obtains the following result.
Lemma 3.4.7 Evaluation on ![]() $(\varphi _p^{-1})^*({dt}/{t})$ induces a
$(\varphi _p^{-1})^*({dt}/{t})$ induces a ![]() $\mathbb {Z}_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant injection
$\mathbb {Z}_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant injection
where we let ![]() $\mathbb {Z}_p^\times$ act by
$\mathbb {Z}_p^\times$ act by ![]() $z^{k}$ on
$z^{k}$ on ![]() $M_{k, \mathbb {Q}_p}$. The induced map on
$M_{k, \mathbb {Q}_p}$. The induced map on ![]() $K^p$-invariants has dense image for any compact open subgroup
$K^p$-invariants has dense image for any compact open subgroup ![]() $K^p$.
$K^p$.
Remark 3.4.8 If we write ![]() $\mathbb {V}_{\mathbb {F}_p}=\mathbb {V}_{\mathbb {Z}_p}/(p)$, then it is clear by comparing moduli problems that the invariants
$\mathbb {V}_{\mathbb {F}_p}=\mathbb {V}_{\mathbb {Z}_p}/(p)$, then it is clear by comparing moduli problems that the invariants ![]() $\mathbb {V}_{\mathbb {F}_p}^{1+p\mathbb {Z}_p}$ represent
$\mathbb {V}_{\mathbb {F}_p}^{1+p\mathbb {Z}_p}$ represent ![]() $\mathrm {Ig}^{\mathrm {ord},c}_{\mu _p}$. The following obvious diagram comparing Lemmas 3.4.3 and 3.4.7 then commutes.
$\mathrm {Ig}^{\mathrm {ord},c}_{\mu _p}$. The following obvious diagram comparing Lemmas 3.4.3 and 3.4.7 then commutes.

This diagram summarizes why in [Reference KatzKat75a] one must pass to divided congruences to see all of ![]() $\mathbb {V}$, which in our presentation corresponds to the fact that it is crucial to invert
$\mathbb {V}$, which in our presentation corresponds to the fact that it is crucial to invert ![]() $p$ to obtain the density statement in Lemma 3.4.7.
$p$ to obtain the density statement in Lemma 3.4.7.
Remark 3.4.9 For ![]() $K^p$ a sufficiently small compact open, if we fix a set of cusps
$K^p$ a sufficiently small compact open, if we fix a set of cusps ![]() $c_1, \ldots, c_m$, one in each connected component of
$c_1, \ldots, c_m$, one in each connected component of ![]() $X_{\mathrm {GL}_2(\mathbb {Z}_p)K^p, \breve {\mathbb {Q}}_p}$, then we obtain
$X_{\mathrm {GL}_2(\mathbb {Z}_p)K^p, \breve {\mathbb {Q}}_p}$, then we obtain ![]() $q$-expansion maps
$q$-expansion maps
 \[ M_{k, \mathbb{Q}_p}^{\mathrm{GL}_2(\mathbb{Z}_p)K^p} \rightarrow \prod_{i=1}^{m} \breve{\mathbb{Z}}_p[[q]][1/p]. \]
\[ M_{k, \mathbb{Q}_p}^{\mathrm{GL}_2(\mathbb{Z}_p)K^p} \rightarrow \prod_{i=1}^{m} \breve{\mathbb{Z}}_p[[q]][1/p]. \]
A generalization of Serre's [Reference SerreSer73] original definition of ![]() $p$-adic modular forms of level
$p$-adic modular forms of level ![]() $K^p$ would be to take the completion of the span of the images of these maps over all
$K^p$ would be to take the completion of the span of the images of these maps over all ![]() $k$. The
$k$. The ![]() $q$-expansion principle combined with Lemma 3.4.7 implies that this agrees with the definition given above (see [Reference KatzKat75a] for related discussions).
$q$-expansion principle combined with Lemma 3.4.7 implies that this agrees with the definition given above (see [Reference KatzKat75a] for related discussions).
3.5 The supersingular Caraiani–Scholze Igusa variety
We now turn our attention to the main player in our story. Though it would be possible to work over ![]() $\mathbb {F}_p$, from here on out it will be cleaner and more convenient to work over
$\mathbb {F}_p$, from here on out it will be cleaner and more convenient to work over ![]() $\overline {\mathbb {F}}_p$ (essentially because the endomorphisms of
$\overline {\mathbb {F}}_p$ (essentially because the endomorphisms of ![]() $\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p}$ are not all defined over
$\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p}$ are not all defined over ![]() $\mathbb {F}_p$).
$\mathbb {F}_p$).
Definition 3.5.1 (The supersingular Caraiani–Scholze Igusa moduli problem)
Let ![]() $K^p \leq \mathrm {GL}_2 (\mathbb {A}_f^{(p)})$ be a closed subgroup. Let
$K^p \leq \mathrm {GL}_2 (\mathbb {A}_f^{(p)})$ be a closed subgroup. Let ![]() $\mathrm {Ig}_{K^p}^\mathrm {ss}$ be the functor on
$\mathrm {Ig}_{K^p}^\mathrm {ss}$ be the functor on ![]() $\overline {\mathbb {F}}_p$-algebras
$\overline {\mathbb {F}}_p$-algebras
sending ![]() $R/\overline {\mathbb {F}}_p$ to the set of equivalence classes of triples
$R/\overline {\mathbb {F}}_p$ to the set of equivalence classes of triples ![]() $(E, \varphi _p, \mathcal {K}^p )$ where:
$(E, \varphi _p, \mathcal {K}^p )$ where:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\varphi _p: \mathbb {X}_{\mathrm {ss}, R} \otimes \mathbb {Q}_p \xrightarrow {\sim } E[p^\infty ] \otimes \mathbb {Q}_p$ is a quasi-isogeny;
$\varphi _p: \mathbb {X}_{\mathrm {ss}, R} \otimes \mathbb {Q}_p \xrightarrow {\sim } E[p^\infty ] \otimes \mathbb {Q}_p$ is a quasi-isogeny;(iii)
 $\mathcal {K}^p \subset \underline {\mathrm {Isom}}\bigl ((\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E)\bigr )$ is a
$\mathcal {K}^p \subset \underline {\mathrm {Isom}}\bigl ((\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E)\bigr )$ is a  $K^p$-torsor; and
$K^p$-torsor; and(iv) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E,\varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a quasi-isogeny
$(E,\varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a quasi-isogeny  $q: E \otimes \mathbb {Q} \xrightarrow {\sim } E'\otimes \mathbb {Q}$ such that
$q: E \otimes \mathbb {Q} \xrightarrow {\sim } E'\otimes \mathbb {Q}$ such that
 \[ q(\mathcal{K}^p) = {\mathcal{K}^p}' \text{ and } q \circ \varphi_p = \varphi'_p. \]
\[ q(\mathcal{K}^p) = {\mathcal{K}^p}' \text{ and } q \circ \varphi_p = \varphi'_p. \]
As usual, when ![]() $K^p=\{e\}$ we drop it from the notation and write
$K^p=\{e\}$ we drop it from the notation and write ![]() $\mathrm {Ig}^\mathrm {ss} := \mathrm {Ig}_{\{e\}}^\mathrm {ss}$. In this case, we also identify the prime-to-
$\mathrm {Ig}^\mathrm {ss} := \mathrm {Ig}_{\{e\}}^\mathrm {ss}$. In this case, we also identify the prime-to-![]() $p$ level data with the choice of an isomorphism
$p$ level data with the choice of an isomorphism ![]() $\varphi _{\mathbb {A}_f^{(p)}}: \underline {(\mathbb {A}_f^{(p)})^2} \rightarrow V_{\mathbb {A}_f^{(p)}}(E)$ as in Example 3.1.4.
$\varphi _{\mathbb {A}_f^{(p)}}: \underline {(\mathbb {A}_f^{(p)})^2} \rightarrow V_{\mathbb {A}_f^{(p)}}(E)$ as in Example 3.1.4.
This up to quasi-isogeny moduli problem is well-adapted for comparison with the quaternionic coset, as we show in § 3.7. To compare with modular curves, however, it is useful to also have an up to prime-to-![]() $p$ quasi-isogeny moduli interpretation. Similarly to Lemma 3.1.5 (see also [Reference Caraiani and ScholzeCS17, Lemma 4.3.4]), we obtain the following result.
$p$ quasi-isogeny moduli interpretation. Similarly to Lemma 3.1.5 (see also [Reference Caraiani and ScholzeCS17, Lemma 4.3.4]), we obtain the following result.
Lemma 3.5.2 For ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ a closed subgroup, consider the functor
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ a closed subgroup, consider the functor
sending ![]() $R/\overline {\mathbb {F}}_p$ to the set of equivalence classes of triples
$R/\overline {\mathbb {F}}_p$ to the set of equivalence classes of triples ![]() $(E, \varphi _p, \mathcal {K}^p)$ where:
$(E, \varphi _p, \mathcal {K}^p)$ where:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\varphi _p: \mathbb {X}_{\mathrm {ss},R} \xrightarrow {\sim } E[p^\infty ]$ is an isomorphism;
$\varphi _p: \mathbb {X}_{\mathrm {ss},R} \xrightarrow {\sim } E[p^\infty ]$ is an isomorphism;(iii)
 $\mathcal {K}^p \subset \underline {\mathrm {Isom}}\bigl ((\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E)\bigr )$ is a
$\mathcal {K}^p \subset \underline {\mathrm {Isom}}\bigl ((\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E)\bigr )$ is a  $K^p$-torsor; and
$K^p$-torsor; and(iv) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E,\varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a prime-to-
$(E,\varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a prime-to-  $p$ quasi-isogeny
$p$ quasi-isogeny  $q: E \otimes \mathbb {Z}_{(p)} \xrightarrow {\sim } E'\otimes \mathbb {Z}_{(p)}$ such that
$q: E \otimes \mathbb {Z}_{(p)} \xrightarrow {\sim } E'\otimes \mathbb {Z}_{(p)}$ such that
 \[ q(\mathcal{K}^p) = {\mathcal{K}^p}' \quad \text{and} \quad q \circ \varphi_p = \varphi'_p. \]
\[ q(\mathcal{K}^p) = {\mathcal{K}^p}' \quad \text{and} \quad q \circ \varphi_p = \varphi'_p. \]
The assignment
induces an isomorphism
We write ![]() $\mathcal {O}_p = \mathrm {End}(\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p})$ and
$\mathcal {O}_p = \mathrm {End}(\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p})$ and ![]() $D_p := \mathcal {O}_p \otimes \mathbb {Q}_p$, so that
$D_p := \mathcal {O}_p \otimes \mathbb {Q}_p$, so that ![]() $\mathcal {O}_p$ is the maximal order in
$\mathcal {O}_p$ is the maximal order in ![]() $D_p$, a ramified quaternion algebra over
$D_p$, a ramified quaternion algebra over ![]() $\mathbb {Q}_p$. Then
$\mathbb {Q}_p$. Then ![]() $D_p$ acts on
$D_p$ acts on ![]() $\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p} \otimes \mathbb {Q}_p$, and there is a natural action of
$\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p} \otimes \mathbb {Q}_p$, and there is a natural action of ![]() $D_p^\times$ on
$D_p^\times$ on ![]() $\mathrm {Ig}^\mathrm {ss}_K$ by composition with
$\mathrm {Ig}^\mathrm {ss}_K$ by composition with ![]() $\varphi _p$. The action of
$\varphi _p$. The action of ![]() $\mathcal {O}_p^\times \subset D_p^\times$ preserves the prime-to-
$\mathcal {O}_p^\times \subset D_p^\times$ preserves the prime-to-![]() $p$ moduli interpretation of Lemma 3.5.2.
$p$ moduli interpretation of Lemma 3.5.2.
In fact, what acts most naturally are the functors on ![]() $\overline {\mathbb {F}}_p$-algebras
$\overline {\mathbb {F}}_p$-algebras
The following lemma says we have not missed anything.
Lemma 3.5.3 The actions of ![]() $D_p^\times$ and
$D_p^\times$ and ![]() $\mathcal {O}_p^\times$ described previously factor through isomorphisms
$\mathcal {O}_p^\times$ described previously factor through isomorphisms ![]() $\underline {\mathcal {O}_p^\times } \rightarrow \underline {\mathrm {Aut}}(\mathbb {X}_{\mathrm {ss},\overline {\mathbb {F}}_p})$ and
$\underline {\mathcal {O}_p^\times } \rightarrow \underline {\mathrm {Aut}}(\mathbb {X}_{\mathrm {ss},\overline {\mathbb {F}}_p})$ and ![]() $\underline {D_p^\times } \rightarrow \underline {\mathrm {Aut}}(\mathbb {X}_{\mathrm {ss},\overline {\mathbb {F}}_p} \otimes \mathbb {Q}_p)$.
$\underline {D_p^\times } \rightarrow \underline {\mathrm {Aut}}(\mathbb {X}_{\mathrm {ss},\overline {\mathbb {F}}_p} \otimes \mathbb {Q}_p)$.
Proof. This is established in a more general context in the proof of [Reference Caraiani and ScholzeCS17, Proposition 4.2.11]. The key point is that on ![]() $\overline {\mathbb {F}}_p$-algebras, by [Reference Caraiani and ScholzeCS17, Lemma 4.1.7, Corollary 4.1.10], the endomorphisms of
$\overline {\mathbb {F}}_p$-algebras, by [Reference Caraiani and ScholzeCS17, Lemma 4.1.7, Corollary 4.1.10], the endomorphisms of ![]() $\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p}$ are given by the Tate module of an étale
$\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p}$ are given by the Tate module of an étale ![]() $p$-divisible group over
$p$-divisible group over ![]() ${\overline {\mathbb {F}}_p}$, and are thus equal to the constant sheaf on the
${\overline {\mathbb {F}}_p}$, and are thus equal to the constant sheaf on the ![]() ${\overline {\mathbb {F}}_p}$-points of that Tate module.
${\overline {\mathbb {F}}_p}$-points of that Tate module.
Remark 3.5.4 One can also define an ordinary Caraiani–Scholze Igusa variety. We do not use this here, but see Remark 5.7.2 for some connections to the present work and [Reference HoweHow20] for an application to the study of ![]() $p$-adic modular forms.
$p$-adic modular forms.
3.6 Uniformization of the supersingular locus
Proposition 3.6.1 For ![]() $K^p$ a sufficiently small closed subgroup, the assignment
$K^p$ a sufficiently small closed subgroup, the assignment
induces a ![]() $\underline {D_p^\times \times N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$-equivariant map
$\underline {D_p^\times \times N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$-equivariant map
where ![]() $\underline {D_p^\times }$ acts on
$\underline {D_p^\times }$ acts on ![]() $\mathfrak {Y}^\mathrm {ss}_{K^p, \overline {\mathbb {F}}_p}$ by
$\mathfrak {Y}^\mathrm {ss}_{K^p, \overline {\mathbb {F}}_p}$ by ![]() $\mathrm {Frob}^{v_p\circ \operatorname {Nrd}}$ (here
$\mathrm {Frob}^{v_p\circ \operatorname {Nrd}}$ (here ![]() $\mathrm {Frob}: \mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p} \rightarrow \mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p}$ is the relative Frobenius and
$\mathrm {Frob}: \mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p} \rightarrow \mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p}$ is the relative Frobenius and ![]() $\operatorname {Nrd}: D_p \rightarrow \mathbb {Q}_p$ denotes the reduced norm). Moreover,
$\operatorname {Nrd}: D_p \rightarrow \mathbb {Q}_p$ denotes the reduced norm). Moreover, ![]() $\mathrm {unif}_{\mathbb {X}_{\mathrm {ss}}}$ is a trivializable
$\mathrm {unif}_{\mathbb {X}_{\mathrm {ss}}}$ is a trivializable ![]() $\underline {\mathcal {O}_p^\times }$-torsor, and the maps compile to a
$\underline {\mathcal {O}_p^\times }$-torsor, and the maps compile to a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism of towers as the sufficiently small closed subgroup
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism of towers as the sufficiently small closed subgroup ![]() $K^p$ varies.
$K^p$ varies.
Proof. We first show that the map factors through ![]() $\mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p}^\mathrm {ss}$: given a point
$\mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p}^\mathrm {ss}$: given a point
we find ![]() $\mathrm {Ha}(E/R)$ is identically zero because
$\mathrm {Ha}(E/R)$ is identically zero because ![]() $E[p^\infty ] \cong \mathbb {X}_{\mathrm {ss},R}$ and, as observed in § 3.2.2, the Hasse invariant only depends on
$E[p^\infty ] \cong \mathbb {X}_{\mathrm {ss},R}$ and, as observed in § 3.2.2, the Hasse invariant only depends on ![]() $E[p^\infty ]$. However,
$E[p^\infty ]$. However, ![]() $\mathrm {Ha}(E/R)$ is the pullback of
$\mathrm {Ha}(E/R)$ is the pullback of ![]() $\mathrm {Ha}$ under the induced map
$\mathrm {Ha}$ under the induced map ![]() $\operatorname {Spec}\!R \rightarrow \mathfrak {Y}_{K^p, \overline {\mathbb {F}}_p}$, so by Lemma 3.3.1 this induced map factors through
$\operatorname {Spec}\!R \rightarrow \mathfrak {Y}_{K^p, \overline {\mathbb {F}}_p}$, so by Lemma 3.3.1 this induced map factors through ![]() $\mathfrak {Y}^\mathrm {ss}_{K^p, \overline {\mathbb {F}}_p}$, as desired.
$\mathfrak {Y}^\mathrm {ss}_{K^p, \overline {\mathbb {F}}_p}$, as desired.
It is also clear from the definitions of the moduli problems and the identification ![]() $\underline {\mathrm {Aut}}(\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p})=\underline {\mathcal {O}_p^\times }$ in Lemma 3.5.3 that the map is a quasi-torsor; to conclude it is a trivializable torsor it thus suffices to produce a section.
$\underline {\mathrm {Aut}}(\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p})=\underline {\mathcal {O}_p^\times }$ in Lemma 3.5.3 that the map is a quasi-torsor; to conclude it is a trivializable torsor it thus suffices to produce a section.
To obtain this, we observe that the ![]() $p$-divisible group of the universal elliptic curve over
$p$-divisible group of the universal elliptic curve over ![]() $\mathfrak {Y}_{K^p, \overline {\mathbb {F}}_p}^\mathrm {ss}$ is isomorphic to
$\mathfrak {Y}_{K^p, \overline {\mathbb {F}}_p}^\mathrm {ss}$ is isomorphic to ![]() $\mathbb {X}_{\mathrm {ss}, \mathfrak {Y}_{K^p, \overline {\mathbb {F}}_p}^\mathrm {ss}}$: indeed, it is pulled back from
$\mathbb {X}_{\mathrm {ss}, \mathfrak {Y}_{K^p, \overline {\mathbb {F}}_p}^\mathrm {ss}}$: indeed, it is pulled back from ![]() $\mathfrak {Y}_{{K^p}', \overline {\mathbb {F}}_p}^\mathrm {ss}$ for any sufficiently small compact open subgroup
$\mathfrak {Y}_{{K^p}', \overline {\mathbb {F}}_p}^\mathrm {ss}$ for any sufficiently small compact open subgroup ![]() ${K^p}' \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ containing
${K^p}' \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ containing ![]() $K^p$, and
$K^p$, and ![]() $\mathfrak {Y}_{{K^p}', \overline {\mathbb {F}}_p}^\mathrm {ss}$ is just a finite union of
$\mathfrak {Y}_{{K^p}', \overline {\mathbb {F}}_p}^\mathrm {ss}$ is just a finite union of ![]() $\overline {\mathbb {F}}_p$-points. We can choose an isomorphism at each of these points (because
$\overline {\mathbb {F}}_p$-points. We can choose an isomorphism at each of these points (because ![]() $\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p}$ is the unique up to isomorphism connected one-dimensional height-two
$\mathbb {X}_{\mathrm {ss}, \overline {\mathbb {F}}_p}$ is the unique up to isomorphism connected one-dimensional height-two ![]() $p$-divisible group over
$p$-divisible group over ![]() $\overline {\mathbb {F}}_p$), and then assemble these and pull back to
$\overline {\mathbb {F}}_p$), and then assemble these and pull back to ![]() $\mathfrak {Y}_{K^p}^\mathrm {ss}$ to obtain the desired isomorphism. This is exactly the data of a section.
$\mathfrak {Y}_{K^p}^\mathrm {ss}$ to obtain the desired isomorphism. This is exactly the data of a section.
It is left only to verify the action of ![]() $\underline {D_p^\times }/\underline {\mathcal {O}_p^\times }$ is as described on
$\underline {D_p^\times }/\underline {\mathcal {O}_p^\times }$ is as described on ![]() $\mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p}^\mathrm {ss}$, and this is a direct computation from the definitions that we leave to the reader (we do not use this part of the statement in any of what follows).
$\mathfrak {Y}_{K^p,\overline {\mathbb {F}}_p}^\mathrm {ss}$, and this is a direct computation from the definitions that we leave to the reader (we do not use this part of the statement in any of what follows).
As a consequence, one finds that for each sufficiently small ![]() $K^p$,
$K^p$, ![]() $\mathrm {Ig}_{K^p}^\mathrm {ss}$ is a profinite set, thus, in particular, a perfect affine scheme over
$\mathrm {Ig}_{K^p}^\mathrm {ss}$ is a profinite set, thus, in particular, a perfect affine scheme over ![]() $\overline {\mathbb {F}}_p$. Our next goal is to identify this profinite set explicitly with a quaternionic coset.
$\overline {\mathbb {F}}_p$. Our next goal is to identify this profinite set explicitly with a quaternionic coset.
3.7 Supersingular Igusa variety as quaternionic coset
We now identify ![]() $\mathrm {Ig}^\mathrm {ss}$ with a quaternionic coset using the orbit map for the action of
$\mathrm {Ig}^\mathrm {ss}$ with a quaternionic coset using the orbit map for the action of ![]() $\underline {D_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})}$. To that end, fix a supersingular elliptic curve
$\underline {D_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})}$. To that end, fix a supersingular elliptic curve ![]() $E_0 / \overline {\mathbb {F}}_p$ and level structure to obtain
$E_0 / \overline {\mathbb {F}}_p$ and level structure to obtain
We write ![]() $D=\mathrm {End}(E_0) \otimes \mathbb {Q}$. As explained, e.g., in [Reference SilvermanSil92, Theorem V.3.1], this a quaternion algebra over
$D=\mathrm {End}(E_0) \otimes \mathbb {Q}$. As explained, e.g., in [Reference SilvermanSil92, Theorem V.3.1], this a quaternion algebra over ![]() $\mathbb {Q}$, and because it is non-split and acts faithfully on the
$\mathbb {Q}$, and because it is non-split and acts faithfully on the ![]() $\ell$-adic Tate module for all
$\ell$-adic Tate module for all ![]() $\ell \neq p$, it must be ramified exactly at
$\ell \neq p$, it must be ramified exactly at ![]() $p$ and
$p$ and ![]() $\infty$.
$\infty$.
By definition, ![]() $D^\times$ is identified with the self quasi-isogenies of
$D^\times$ is identified with the self quasi-isogenies of ![]() $E_0 \otimes \mathbb {Q}$. The actions of
$E_0 \otimes \mathbb {Q}$. The actions of ![]() $D$ on
$D$ on ![]() $E_0[p^\infty ]\otimes \mathbb {Q}_p$ and
$E_0[p^\infty ]\otimes \mathbb {Q}_p$ and ![]() $V_{\mathbb {A}_f^{(p)}}(E)$, transported by
$V_{\mathbb {A}_f^{(p)}}(E)$, transported by ![]() $\varphi _{p,0}$ and
$\varphi _{p,0}$ and ![]() $\varphi _{\mathbb {A}_f^{(p)},0}$, thus induce an identification
$\varphi _{\mathbb {A}_f^{(p)},0}$, thus induce an identification
In particular, we obtain a map ![]() $D^\times (\mathbb {Q}) \hookrightarrow D^\times (\mathbb {A}_f)$.
$D^\times (\mathbb {Q}) \hookrightarrow D^\times (\mathbb {A}_f)$.
The action on the point ![]() $x_0$ induces an orbit map
$x_0$ induces an orbit map
and we show that the following holds.
Theorem 3.7.1 The orbit map ( 3.7.1) factors through a ![]() ${D^\times (\mathbb {A}_f)=D^\times (\mathbb {Q}_p) \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})}$-equivariant isomorphism
${D^\times (\mathbb {A}_f)=D^\times (\mathbb {Q}_p) \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})}$-equivariant isomorphism
Before proving Theorem 3.7.1, it is helpful to recall the following basic structural result for quaternionic double cosets. We write ![]() $\mathcal {O} = \mathrm {End}(E_0)$, a maximal order in
$\mathcal {O} = \mathrm {End}(E_0)$, a maximal order in ![]() $D$, and consider the finite class set of right fractional ideals in
$D$, and consider the finite class set of right fractional ideals in ![]() $\mathcal {O}$
$\mathcal {O}$
We may fix a finite set of representatives for the class set ![]() $I$ and corresponding representatives
$I$ and corresponding representatives ![]() $\gamma _\mathcal {I} \in D^\times (\mathbb {A}_f),\ \mathcal {I} \in I$, for the double cosets. The stabilizer of
$\gamma _\mathcal {I} \in D^\times (\mathbb {A}_f),\ \mathcal {I} \in I$, for the double cosets. The stabilizer of ![]() $\mathcal {I}$ for left multiplication in
$\mathcal {I}$ for left multiplication in ![]() $D^\times (\mathbb {Q})$ is the units in a maximal order
$D^\times (\mathbb {Q})$ is the units in a maximal order ![]() $\mathcal {O}_\mathcal {I}$, and we find
$\mathcal {O}_\mathcal {I}$, and we find
where the isomorphisms on the right-hand side are of right ![]() $\mathcal {O} \otimes \widehat {\mathbb {Z}}$-modules. Because each group
$\mathcal {O} \otimes \widehat {\mathbb {Z}}$-modules. Because each group ![]() $\mathcal {O}_\mathcal {I}^\times$ is finite, if we replace
$\mathcal {O}_\mathcal {I}^\times$ is finite, if we replace ![]() $\mathcal {O} \otimes \widehat {\mathbb {Z}}$ with a small enough compact open subgroup
$\mathcal {O} \otimes \widehat {\mathbb {Z}}$ with a small enough compact open subgroup ![]() $K \subset \mathcal {O} \otimes \widehat {\mathbb {Z}}^\times$, we obtain a finite set of representatives
$K \subset \mathcal {O} \otimes \widehat {\mathbb {Z}}^\times$, we obtain a finite set of representatives ![]() $\gamma _{\mathcal {I}, i}$ such that
$\gamma _{\mathcal {I}, i}$ such that
In other words, we obtain a topological splitting of the locally profinite set ![]() $D^\times (\mathbb {A}_f)$ as a product of a discrete set and a profinite set,
$D^\times (\mathbb {A}_f)$ as a product of a discrete set and a profinite set,
compatible with the left action of ![]() $D^\times (\mathbb {Q})$ and the right action of
$D^\times (\mathbb {Q})$ and the right action of ![]() $K$.
$K$.
We also need to understand the quasi-isogenies of ![]() $E_0$ after arbitrary base change. To this end, we observe that, for any
$E_0$ after arbitrary base change. To this end, we observe that, for any ![]() $S$, there is a natural map from
$S$, there is a natural map from ![]() $\underline {D^\times (\mathbb {Q})}(R)$ to
$\underline {D^\times (\mathbb {Q})}(R)$ to ![]() $\underline {\mathrm {Aut}}(E_0\otimes \mathbb {Q})(R)=\mathrm {Aut}(E_{0,R} \otimes \mathbb {Q})$; indeed, because
$\underline {\mathrm {Aut}}(E_0\otimes \mathbb {Q})(R)=\mathrm {Aut}(E_{0,R} \otimes \mathbb {Q})$; indeed, because ![]() $D^\times (\mathbb {Q})$ is discrete, an element of
$D^\times (\mathbb {Q})$ is discrete, an element of ![]() $\underline {D^\times (\mathbb {Q})}(R)$ is a locally constant on
$\underline {D^\times (\mathbb {Q})}(R)$ is a locally constant on ![]() $\operatorname {Spec}\!R$ choice of element in
$\operatorname {Spec}\!R$ choice of element in ![]() $D^\times (\mathbb {Q})$.
$D^\times (\mathbb {Q})$.
Lemma 3.7.2 The natural map defined previously identifies ![]() $\underline {D^\times (\mathbb {Q})}$ with
$\underline {D^\times (\mathbb {Q})}$ with ![]() $\underline {\mathrm {Aut}}(E\otimes \mathbb {Q})$.
$\underline {\mathrm {Aut}}(E\otimes \mathbb {Q})$.
Proof. It suffices to verify this on ![]() $\operatorname {Spec}\!R$ points, and we may moreover assume
$\operatorname {Spec}\!R$ points, and we may moreover assume ![]() $R$ is of finite type over
$R$ is of finite type over ![]() ${\overline {\mathbb {F}}_p}$, and then that
${\overline {\mathbb {F}}_p}$, and then that ![]() $R$ is reduced using that quasi-isogenies lift along nilpotent ideals containing
$R$ is reduced using that quasi-isogenies lift along nilpotent ideals containing ![]() $p$. Then, the result follows from the computation over algebraically closed fields.
$p$. Then, the result follows from the computation over algebraically closed fields.
Proof of Theorem 3.7.1 By Lemma 3.7.2, we deduce that the orbit map factors as an injection on ![]() $R$-points
$R$-points
From (3.7.3), we deduce
and thus the orbit map factors through an injection
It remains to show the map is surjective. To do so, it suffices to show that the universal elliptic curve over ![]() $\mathrm {Ig}_\mathrm {ss}$ is quasi-isogenous to
$\mathrm {Ig}_\mathrm {ss}$ is quasi-isogenous to ![]() $E_{0,\mathrm {Ig}^\mathrm {ss}}$. However, the universal elliptic curve is the pullback from
$E_{0,\mathrm {Ig}^\mathrm {ss}}$. However, the universal elliptic curve is the pullback from ![]() $Y^\mathrm {ss}_{\overline {\mathbb {F}}_p}$ along the map
$Y^\mathrm {ss}_{\overline {\mathbb {F}}_p}$ along the map ![]() $\mathrm {unif}_{\mathbb {X}_\mathrm {ss}}$ of Proposition 3.6.1, and the statement follows as in the proof of Proposition 3.6.1 by reduction to a finite set of points at finite level and the fact that any two supersingular elliptic curves over
$\mathrm {unif}_{\mathbb {X}_\mathrm {ss}}$ of Proposition 3.6.1, and the statement follows as in the proof of Proposition 3.6.1 by reduction to a finite set of points at finite level and the fact that any two supersingular elliptic curves over ![]() ${\overline {\mathbb {F}}_p}$ are isogenous.
${\overline {\mathbb {F}}_p}$ are isogenous.
Remark 3.7.3 We can avoid the use of any Grothendieck topology above because our torsors are all trivializable. In particular, this sidesteps the following question: for ![]() $X$ a topological space and
$X$ a topological space and ![]() $\Gamma$ a topological group acting on
$\Gamma$ a topological group acting on ![]() $X$, for which Grothendieck topologies does
$X$, for which Grothendieck topologies does ![]() $\underline {X}/\underline {\Gamma }=\underline {X/\Gamma }$? Indeed, when
$\underline {X}/\underline {\Gamma }=\underline {X/\Gamma }$? Indeed, when ![]() $X \rightarrow X/\Gamma$ is a trivializable
$X \rightarrow X/\Gamma$ is a trivializable ![]() $\Gamma$-torsor, this is already true at the level of presheaves.
$\Gamma$-torsor, this is already true at the level of presheaves.
Corollary 3.7.4 For any sufficiently small closed subgroup ![]() $K^p\leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$, the map of Theorem 3.7.1 induces a
$K^p\leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$, the map of Theorem 3.7.1 induces a ![]() $\underline {D_p^\times \times N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$-equivariant isomorphism
$\underline {D_p^\times \times N_{\mathrm {GL}_2(\mathbb {A}_f^{(p)})}(K^p)}$-equivariant isomorphism
and, combined with Proposition 3.6.1,
These maps compile to ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphisms of towers as the closed subgroup
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphisms of towers as the closed subgroup ![]() $K^p$ varies over all sufficiently small closed subgroups.
$K^p$ varies over all sufficiently small closed subgroups.
4. Serre's mod  $p$ correspondence
$p$ correspondence
In this section we give a proof of Theorem 1.1.1, roughly following Serre [Reference SerreSer96]. The main difference between our presentation and that of [Reference SerreSer96] is that we emphasize from the beginning the role of the supersingular Igusa variety as quaternionic coset in the uniformization of the supersingular locus established in Corollary 3.7.4. When ![]() $p=2 \text { or } 3$ the proof is only valid for
$p=2 \text { or } 3$ the proof is only valid for ![]() $K^p$ sufficiently small, however, in § 4.5 we explain how to deduce the full result directly from Theorem A.
$K^p$ sufficiently small, however, in § 4.5 we explain how to deduce the full result directly from Theorem A.
In this section, ![]() $D/\mathbb {Q}$ is the specific quaternion algebra ramified at
$D/\mathbb {Q}$ is the specific quaternion algebra ramified at ![]() $p$ and
$p$ and ![]() $\infty$ defined in § 3.7. Up to isomorphism, there is a unique quaternion algebra over
$\infty$ defined in § 3.7. Up to isomorphism, there is a unique quaternion algebra over ![]() $\mathbb {Q}$ ramified only at
$\mathbb {Q}$ ramified only at ![]() $p$ and
$p$ and ![]() $\infty$, so this specific choice is made only to normalize with the results of § 3.7. Recall that we have also fixed in § 3.7 identifications
$\infty$, so this specific choice is made only to normalize with the results of § 3.7. Recall that we have also fixed in § 3.7 identifications ![]() $D^\times (\mathbb {A}_f^{(p)})=\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ and
$D^\times (\mathbb {A}_f^{(p)})=\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ and ![]() $D^\times (\mathbb {Q}_p)=D_p^\times$. As in the introduction, we write
$D^\times (\mathbb {Q}_p)=D_p^\times$. As in the introduction, we write
which we view as an admissible ![]() $D^\times (\mathbb {A}_f)=D_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representation.
$D^\times (\mathbb {A}_f)=D_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representation.
4.1 Mod  $p$ modular forms
$p$ modular forms
We write ![]() $\mathcal {M}_{\overline {\mathbb {F}}_p}$ for the base change to
$\mathcal {M}_{\overline {\mathbb {F}}_p}$ for the base change to ![]() $\overline {\mathbb {F}}_p$ of the space of mod
$\overline {\mathbb {F}}_p$ of the space of mod ![]() $p$ modular forms of Definition 3.4.2. As explained in the proof of Lemma 3.4.3, the evaluation map from modular forms to mod
$p$ modular forms of Definition 3.4.2. As explained in the proof of Lemma 3.4.3, the evaluation map from modular forms to mod ![]() $p$ modular forms factors through an isomorphism of
$p$ modular forms factors through an isomorphism of ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representations
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representations
 \begin{equation} \mathcal{M}_{\overline{\mathbb{F}}_p} = \bigoplus_{k=0}^{p-2} H^0(\mathfrak{X}_{\overline{\mathbb{F}}_p}^\mathrm{ord}, \omega^k). \end{equation}
\begin{equation} \mathcal{M}_{\overline{\mathbb{F}}_p} = \bigoplus_{k=0}^{p-2} H^0(\mathfrak{X}_{\overline{\mathbb{F}}_p}^\mathrm{ord}, \omega^k). \end{equation}
We consider the increasing exhaustive filtration ![]() $F_i \mathcal {M}_{\overline {\mathbb {F}}_p}$ whose
$F_i \mathcal {M}_{\overline {\mathbb {F}}_p}$ whose ![]() $i$th step consists of those sections on the right-hand side of (4.1.1) with poles of order
$i$th step consists of those sections on the right-hand side of (4.1.1) with poles of order ![]() $\leq i$ along
$\leq i$ along ![]() $\mathfrak {X}_{\overline {\mathbb {F}}_p}^\mathrm {ss}$.
$\mathfrak {X}_{\overline {\mathbb {F}}_p}^\mathrm {ss}$.
As in § 3.2, we also write
the admissible ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ representation of weight
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ representation of weight ![]() $k$ modular forms over
$k$ modular forms over ![]() $\overline {\mathbb {F}}_p$. In particular, for
$\overline {\mathbb {F}}_p$. In particular, for ![]() $K^p$ sufficiently small, we have
$K^p$ sufficiently small, we have
From these definitions and Lemma 3.3.1, we find that multiplication by ![]() $\mathrm {Ha}^i$ gives a
$\mathrm {Ha}^i$ gives a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
 \begin{equation} F_i \mathcal{M}_{\overline{\mathbb{F}}_p} \xrightarrow{\sim} \bigoplus_{k=0}^{p-2} M_{k+(p-1)i,\overline{\mathbb{F}}_p}. \end{equation}
\begin{equation} F_i \mathcal{M}_{\overline{\mathbb{F}}_p} \xrightarrow{\sim} \bigoplus_{k=0}^{p-2} M_{k+(p-1)i,\overline{\mathbb{F}}_p}. \end{equation}
Thus, in particular, ![]() $F_i \mathcal {M}_{\overline {\mathbb {F}}_p}$ is an admissible
$F_i \mathcal {M}_{\overline {\mathbb {F}}_p}$ is an admissible ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representation.
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representation.
4.2 Evaluation of modular forms
We now explain how to evaluate modular forms to functions on ![]() $\mathrm {Ig}^\mathrm {ss}$. This works almost exactly as in the evaluation map for mod
$\mathrm {Ig}^\mathrm {ss}$. This works almost exactly as in the evaluation map for mod ![]() $p$ modular forms in Lemma 3.4.3, but we set things up here in a slightly more canonical language.
$p$ modular forms in Lemma 3.4.3, but we set things up here in a slightly more canonical language.
We write ![]() $\omega _{\mathbb {X}_\mathrm {ss}}=\operatorname {Lie}(\mathbb {X}_\mathrm {ss})^*$, equipped with the natural action of
$\omega _{\mathbb {X}_\mathrm {ss}}=\operatorname {Lie}(\mathbb {X}_\mathrm {ss})^*$, equipped with the natural action of ![]() $\mathcal {O}_p^\times$ after base change to
$\mathcal {O}_p^\times$ after base change to ![]() $\overline {\mathbb {F}}_p$. Using the isomorphism
$\overline {\mathbb {F}}_p$. Using the isomorphism ![]() $\varphi _p$ in the prime-to-
$\varphi _p$ in the prime-to-![]() $p$ moduli interpretation (cf. Definition 3.5.1(ii)) and the uniformization in Proposition 3.6.1, we obtain a canonical
$p$ moduli interpretation (cf. Definition 3.5.1(ii)) and the uniformization in Proposition 3.6.1, we obtain a canonical ![]() $\mathcal {O}_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
$\mathcal {O}_p^\times \times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
In particular, we obtain a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
Note that, by the definition of ![]() $\mathbb {X}_\mathrm {ss}$ in terms of the Dieudonné module given in § 3.5, we have an identification of
$\mathbb {X}_\mathrm {ss}$ in terms of the Dieudonné module given in § 3.5, we have an identification of ![]() $\operatorname {Lie} \mathbb {X}_{\mathrm {ss}}$ with
$\operatorname {Lie} \mathbb {X}_{\mathrm {ss}}$ with ![]() $\mathbb {F}_p^2/\langle (1, 0) \rangle$, and of
$\mathbb {F}_p^2/\langle (1, 0) \rangle$, and of ![]() $\mathcal {O}_p$ with the
$\mathcal {O}_p$ with the ![]() $\sigma$-centralizer of
$\sigma$-centralizer of ![]() $b_\mathrm {ss}$ in
$b_\mathrm {ss}$ in ![]() $M_2(\breve {\mathbb {Z}}_p)$. In particular, the image of
$M_2(\breve {\mathbb {Z}}_p)$. In particular, the image of ![]() $(0,1)$ gives a basis element of
$(0,1)$ gives a basis element of ![]() $\operatorname {Lie} \mathbb {X}_\mathrm {ss}$, and a direct computation shows
$\operatorname {Lie} \mathbb {X}_\mathrm {ss}$, and a direct computation shows ![]() $\mathcal {O}_p^\times$ acts on
$\mathcal {O}_p^\times$ acts on ![]() $\operatorname {Lie} \mathbb {X}_{\mathrm {ss},\overline {\mathbb {F}}_p}={\overline {\mathbb {F}}_p}$ through a surjective character
$\operatorname {Lie} \mathbb {X}_{\mathrm {ss},\overline {\mathbb {F}}_p}={\overline {\mathbb {F}}_p}$ through a surjective character ![]() $\epsilon : \mathcal {O}_p^\times \rightarrow \mathbb {F}_{p^2}^\times$ whose kernel is a pro-
$\epsilon : \mathcal {O}_p^\times \rightarrow \mathbb {F}_{p^2}^\times$ whose kernel is a pro-![]() $p$ group we write as
$p$ group we write as ![]() $\mathcal {N}_p$. Combining with Theorem 3.7.1, we obtain a
$\mathcal {N}_p$. Combining with Theorem 3.7.1, we obtain a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism
Then, evaluating homomorphisms in the right-hand side of (4.2.1) on ![]() $1 \in {\overline {\mathbb {F}}_p}$ and passing to
$1 \in {\overline {\mathbb {F}}_p}$ and passing to ![]() $K^p$-invariants, we obtain Serre's map, a Hecke equivariant isomorphism
$K^p$-invariants, we obtain Serre's map, a Hecke equivariant isomorphism
4.3 Hecke algebras and generalized eigenspaces
If ![]() $L$ is a field and
$L$ is a field and ![]() $V$ is a finite-dimensional vector space over
$V$ is a finite-dimensional vector space over ![]() $L$, then for any commutative
$L$, then for any commutative ![]() $L$-algebra
$L$-algebra ![]() $T$ acting on
$T$ acting on ![]() $V$, we have a decomposition into generalized eigenspaces
$V$, we have a decomposition into generalized eigenspaces
where ![]() $\mathfrak {m}$ runs over maximal ideals of
$\mathfrak {m}$ runs over maximal ideals of ![]() $T$ with residue field a finite extension of
$T$ with residue field a finite extension of ![]() $L$ and
$L$ and ![]() $V_\mathfrak {m}$ is the sub-module of
$V_\mathfrak {m}$ is the sub-module of ![]() $\mathfrak {m}$-torsion elements. In particular, if
$\mathfrak {m}$-torsion elements. In particular, if ![]() $V_\mathfrak {m} \neq 0$, the eigenspace
$V_\mathfrak {m} \neq 0$, the eigenspace ![]() $V[\mathfrak {m}]$ consisting of elements annihilated by
$V[\mathfrak {m}]$ consisting of elements annihilated by ![]() $\mathfrak {m}$ is non-empty.
$\mathfrak {m}$ is non-empty.
The same result applies more generally to ![]() $V$ an increasing union of finite-dimensional vector spaces with
$V$ an increasing union of finite-dimensional vector spaces with ![]() $T$-action. In particular, if
$T$-action. In particular, if ![]() $W$ is an increasing union of admissible representations of a locally profinite group
$W$ is an increasing union of admissible representations of a locally profinite group ![]() $G$,
$G$, ![]() $K$ is a compact open subgroup of
$K$ is a compact open subgroup of ![]() $G$, and
$G$, and ![]() $T$ is a commutative subalgebra of the abstract Hecke algebra
$T$ is a commutative subalgebra of the abstract Hecke algebra ![]() $L[K\backslash G/K]$, then the action of
$L[K\backslash G/K]$, then the action of ![]() $T$ on the invariants
$T$ on the invariants ![]() $W^K$ admits a decomposition into generalized eigenspaces.
$W^K$ admits a decomposition into generalized eigenspaces.
This formalism gives a decomposition into generalized eigenspaces for the action of any commutative subalgebra
on ![]() $M_{k, \overline {\mathbb {F}}_p}^{K^p}$,
$M_{k, \overline {\mathbb {F}}_p}^{K^p}$, ![]() $\mathcal {A}^{K^p}_{\overline {\mathbb {F}}_p}$, and
$\mathcal {A}^{K^p}_{\overline {\mathbb {F}}_p}$, and ![]() $\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$. For
$\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$. For ![]() $M_{k,\overline {\mathbb {F}}_p}^{K^p}$ this is immediate because
$M_{k,\overline {\mathbb {F}}_p}^{K^p}$ this is immediate because ![]() $M_{k, \overline {\mathbb {F}}_p}$ is admissible. For
$M_{k, \overline {\mathbb {F}}_p}$ is admissible. For ![]() $\mathcal {A}^{K^p}_{\overline {\mathbb {F}}_p}$ it follows because
$\mathcal {A}^{K^p}_{\overline {\mathbb {F}}_p}$ it follows because ![]() $\mathcal {A}$ is a colimit of admissible
$\mathcal {A}$ is a colimit of admissible ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representations by taking invariants under compact open subgroups of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-representations by taking invariants under compact open subgroups of ![]() $D_p^\times$. For
$D_p^\times$. For ![]() $\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$ it follows using the filtration by the admissible representations
$\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$ it follows using the filtration by the admissible representations ![]() $F_i \mathcal {M}_{\overline {\mathbb {F}}_p}$.
$F_i \mathcal {M}_{\overline {\mathbb {F}}_p}$.
Remark 4.3.1 In order to obtain a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-action on modular forms inducing the standard action of Hecke operators on
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-action on modular forms inducing the standard action of Hecke operators on ![]() $K^p$-invariants, one must twist by the unramified determinant character that appears in the Kodaira–Spencer isomorphism
$K^p$-invariants, one must twist by the unramified determinant character that appears in the Kodaira–Spencer isomorphism ![]() $\omega ^2 = \Omega (\mathrm {cusps})$. This replaces each individual coset Hecke operators with a multiple by an invertible element (because we do not include Hecke operators at
$\omega ^2 = \Omega (\mathrm {cusps})$. This replaces each individual coset Hecke operators with a multiple by an invertible element (because we do not include Hecke operators at ![]() $p$), so it will not change the image under the action map. Thus, this choice is immaterial for our purposes; we prefer not to include the twist because it is less natural to do so except when one is comparing with étale cohomology, where it is baked in.
$p$), so it will not change the image under the action map. Thus, this choice is immaterial for our purposes; we prefer not to include the twist because it is less natural to do so except when one is comparing with étale cohomology, where it is baked in.
4.4 Spectral decompositions
We now compare the spectral decompositions provided by the previous section in order to prove Theorem 1.1.1. The comparison of ![]() $\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$ and
$\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$ and ![]() $\mathcal {A}^{K^p}_{\overline {\mathbb {F}}_p}$ is mediated through comparisons of each with
$\mathcal {A}^{K^p}_{\overline {\mathbb {F}}_p}$ is mediated through comparisons of each with ![]() $\bigoplus _{k\geq 0}M_{k, \overline {\mathbb {F}}_p}^{K^p}$.
$\bigoplus _{k\geq 0}M_{k, \overline {\mathbb {F}}_p}^{K^p}$.
We first treat the simpler case of ![]() $\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$.
$\mathcal {M}_{\overline {\mathbb {F}}_p}^{K^p}$.
Lemma 4.4.1 For ![]() $\mathfrak {m}$ a maximal ideal of
$\mathfrak {m}$ a maximal ideal of ![]() $\mathbb {T}'$,
$\mathbb {T}'$,
Proof. We have ![]() $\big ( \mathcal {M}^{K^p}_{\overline {\mathbb {F}}_p} \big )_\mathfrak {m} \neq 0$ if and only if
$\big ( \mathcal {M}^{K^p}_{\overline {\mathbb {F}}_p} \big )_\mathfrak {m} \neq 0$ if and only if ![]() $\big (F_i \mathcal {M}^{K^p}_{{\overline {\mathbb {F}}_p}} \big )_\mathfrak {m} \neq 0$ for
$\big (F_i \mathcal {M}^{K^p}_{{\overline {\mathbb {F}}_p}} \big )_\mathfrak {m} \neq 0$ for ![]() $i$ sufficiently large. On the other hand, by (4.1.2),
$i$ sufficiently large. On the other hand, by (4.1.2), ![]() $\big (F_i \mathcal {M}^{K^p}_{{\overline {\mathbb {F}}_p}} \big )_\mathfrak {m} \neq 0$ if and only if
$\big (F_i \mathcal {M}^{K^p}_{{\overline {\mathbb {F}}_p}} \big )_\mathfrak {m} \neq 0$ if and only if ![]() $\big (M_{k' + i(p-1)}^{K^p}\big )_\mathfrak {m} \neq 0$ for some
$\big (M_{k' + i(p-1)}^{K^p}\big )_\mathfrak {m} \neq 0$ for some ![]() $0 \leq k' \leq p-2$, and we conclude as varying
$0 \leq k' \leq p-2$, and we conclude as varying ![]() $k'$ and
$k'$ and ![]() $i$ exhausts all possible
$i$ exhausts all possible ![]() $k=k'+i(p-1)$.
$k=k'+i(p-1)$.
On the other hand, using Serre's evaluation map we obtain the following result.
Lemma 4.4.2 Assume either ![]() $K^p$ is sufficiently small or that
$K^p$ is sufficiently small or that ![]() $p \neq 2, 3$. Then, for
$p \neq 2, 3$. Then, for ![]() $\mathfrak {m}$ a maximal ideal of
$\mathfrak {m}$ a maximal ideal of ![]() $\mathbb {T}'$,
$\mathbb {T}'$,
Proof. Suppose ![]() $\bigoplus _{k \geq 0} \big (M_{k,\overline {\mathbb {F}}_p}^{K^p}\big )_\mathfrak {m} \neq 0$. For each
$\bigoplus _{k \geq 0} \big (M_{k,\overline {\mathbb {F}}_p}^{K^p}\big )_\mathfrak {m} \neq 0$. For each ![]() $k \geq 0$, we have a
$k \geq 0$, we have a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant exact sequence
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant exact sequence
Passing to ![]() $K^p$-invariants and localizing at
$K^p$-invariants and localizing at ![]() $\mathfrak {m}$, we obtain the exact sequence
$\mathfrak {m}$, we obtain the exact sequence
By induction on ![]() $k$, we deduce that if
$k$, we deduce that if ![]() $\big (M_{k,\overline {\mathbb {F}}_p}^{K^p}\big )_\mathfrak {m} \neq 0$, then
$\big (M_{k,\overline {\mathbb {F}}_p}^{K^p}\big )_\mathfrak {m} \neq 0$, then ![]() $\bigl (H^0(\mathfrak {X}_{\overline {\mathbb {F}}_p}^\mathrm {ss}, \omega ^{k'})^{K^p}\bigr )_\mathfrak {m} \neq 0$ for some
$\bigl (H^0(\mathfrak {X}_{\overline {\mathbb {F}}_p}^\mathrm {ss}, \omega ^{k'})^{K^p}\bigr )_\mathfrak {m} \neq 0$ for some ![]() $0 \leq k' \leq k$, and, applying (4.2.2), that
$0 \leq k' \leq k$, and, applying (4.2.2), that ![]() $\big (\mathcal {A}^{\mathcal {N}_pK^p}_{{\overline {\mathbb {F}}_p}}\big )_\mathfrak {m} \neq 0$.
$\big (\mathcal {A}^{\mathcal {N}_pK^p}_{{\overline {\mathbb {F}}_p}}\big )_\mathfrak {m} \neq 0$.
Suppose ![]() $\big (\mathcal {A}^{\mathcal {N}_p K^p}_{{\overline {\mathbb {F}}_p}}\big )_\mathfrak {m} \neq 0$. Then, as
$\big (\mathcal {A}^{\mathcal {N}_p K^p}_{{\overline {\mathbb {F}}_p}}\big )_\mathfrak {m} \neq 0$. Then, as
we deduce that for some ![]() $k \geq 0$,
$k \geq 0$, ![]() $\mathcal {A}^{\mathcal {N}_pK^p}_{{\overline {\mathbb {F}}_p}}[\epsilon ^k]_\mathfrak {m} \neq 0$. If
$\mathcal {A}^{\mathcal {N}_pK^p}_{{\overline {\mathbb {F}}_p}}[\epsilon ^k]_\mathfrak {m} \neq 0$. If ![]() $K^p$ is sufficiently small, then because
$K^p$ is sufficiently small, then because ![]() $\omega$ is ample on
$\omega$ is ample on ![]() $\mathfrak {X}_{K^p,\overline {\mathbb {F}}_p}$ and
$\mathfrak {X}_{K^p,\overline {\mathbb {F}}_p}$ and ![]() $\epsilon ^k$ only depends on
$\epsilon ^k$ only depends on ![]() $k$ mod
$k$ mod ![]() $p^2-1$, we may choose this value of
$p^2-1$, we may choose this value of ![]() $k$ large enough that
$k$ large enough that ![]() ${H^1(\mathfrak {X}_{K^p,\overline {\mathbb {F}}_p}, \omega ^{k-(p-1)})=0}$. Then, the sequence (4.4.1) extends to a short exact sequence; indeed, it is obtained by localizing at
${H^1(\mathfrak {X}_{K^p,\overline {\mathbb {F}}_p}, \omega ^{k-(p-1)})=0}$. Then, the sequence (4.4.1) extends to a short exact sequence; indeed, it is obtained by localizing at ![]() $\mathfrak {m}$ the short exact sequence
$\mathfrak {m}$ the short exact sequence
 \[ 0 \rightarrow H^0(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}, \omega^{k-{p-1}}) \xrightarrow{\cdot \mathrm{Ha}} H^0(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}, \omega^{k}) \rightarrow H^0(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}^\mathrm{ss}, \omega^{k}) \rightarrow \underbrace{H^1(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}, \omega^{k-(p-1)})}_{=0}. \]
\[ 0 \rightarrow H^0(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}, \omega^{k-{p-1}}) \xrightarrow{\cdot \mathrm{Ha}} H^0(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}, \omega^{k}) \rightarrow H^0(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}^\mathrm{ss}, \omega^{k}) \rightarrow \underbrace{H^1(\mathfrak{X}_{K^p,\overline{\mathbb{F}}_p}, \omega^{k-(p-1)})}_{=0}. \]In particular, restriction induces a surjection
Applying Serre's isomorphism (4.2.2) we obtain ![]() $H^0(\mathfrak {X}^\mathrm {ss}_{K^p,\overline {\mathbb {F}}_p}, \omega ^{k})_\mathfrak {m} \neq 0$, and thus (4.4.2) implies
$H^0(\mathfrak {X}^\mathrm {ss}_{K^p,\overline {\mathbb {F}}_p}, \omega ^{k})_\mathfrak {m} \neq 0$, and thus (4.4.2) implies ![]() $(M_{k,\overline {\mathbb {F}}_p}^{K^p})_\mathfrak {m} \neq 0$, as desired. If
$(M_{k,\overline {\mathbb {F}}_p}^{K^p})_\mathfrak {m} \neq 0$, as desired. If ![]() $K^p$ is not sufficiently small, then we can still apply the same argument by first passing to a sufficiently small
$K^p$ is not sufficiently small, then we can still apply the same argument by first passing to a sufficiently small ![]() $K_1^p$ that is normal in
$K_1^p$ that is normal in ![]() $K^p$ and such that
$K^p$ and such that ![]() $p$ does not divide
$p$ does not divide ![]() $[K^p:K_1^p]$, then taking
$[K^p:K_1^p]$, then taking ![]() $K^p/K^p_1$ invariants (which are exact because
$K^p/K^p_1$ invariants (which are exact because ![]() $p \nmid |K^p/K^p_1|$). When
$p \nmid |K^p/K^p_1|$). When ![]() $p\neq 2, 3$, such a
$p\neq 2, 3$, such a ![]() $K_1^p$ always exists by adding full level
$K_1^p$ always exists by adding full level ![]() $\ell$ structure for a large enough prime
$\ell$ structure for a large enough prime ![]() $\ell \not \equiv \pm 1 \mod p$.
$\ell \not \equiv \pm 1 \mod p$.
Finally, a purely representation-theoretic argument allows us to pass back and forth between ![]() $\mathcal {A}_{\overline {\mathbb {F}}_p}^{K^p}$ and its
$\mathcal {A}_{\overline {\mathbb {F}}_p}^{K^p}$ and its ![]() $\mathcal {N}_p$-invariants.
$\mathcal {N}_p$-invariants.
Lemma 4.4.3 For ![]() $\mathfrak {m}$ a maximal ideal of
$\mathfrak {m}$ a maximal ideal of ![]() $\mathbb {T}'$,
$\mathbb {T}'$,
Proof. Because ![]() $\mathcal {N}_p$ is a pro-
$\mathcal {N}_p$ is a pro-![]() $p$ group and
$p$ group and ![]() $\big (\mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}\big )_\mathfrak {m} \subset \mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}$ is a smooth characteristic
$\big (\mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}\big )_\mathfrak {m} \subset \mathcal {A}^{K^p}_{{\overline {\mathbb {F}}_p}}$ is a smooth characteristic ![]() $p$ representation of
$p$ representation of ![]() $\mathcal {N}_p$, if the representation is non-zero, then it admits a non-zero
$\mathcal {N}_p$, if the representation is non-zero, then it admits a non-zero ![]() $\mathcal {N}_p$-fixed vector by the standard trick: the
$\mathcal {N}_p$-fixed vector by the standard trick: the ![]() $K_p$-invariants for some
$K_p$-invariants for some ![]() $K_p \trianglelefteq \mathcal {N}_p$ compact open are then non-zero, and then the orbit-stabilizer theorem applied to the action of
$K_p \trianglelefteq \mathcal {N}_p$ compact open are then non-zero, and then the orbit-stabilizer theorem applied to the action of ![]() $\mathcal {N}_p/K_p$ on the finite-dimensional
$\mathcal {N}_p/K_p$ on the finite-dimensional ![]() $\mathbb {F}_p$-vector space spanned by the orbit of a non-trivial
$\mathbb {F}_p$-vector space spanned by the orbit of a non-trivial ![]() $K_p$-fixed vector shows there must be a non-trivial
$K_p$-fixed vector shows there must be a non-trivial ![]() $\mathcal {N}_p$-fixed vector.
$\mathcal {N}_p$-fixed vector.
Remark 4.4.4 One can also obtain a similar statement relating ![]() $\mathcal {M}^{K^p}_{\overline {\mathbb {F}}_p}$ and the mod
$\mathcal {M}^{K^p}_{\overline {\mathbb {F}}_p}$ and the mod ![]() $p$ reduction of
$p$ reduction of ![]() $p$-adic modular forms,
$p$-adic modular forms, ![]() $\mathbb {V}_{\overline {\mathbb {F}}_p}^{K^p}$ (see § 3.4 for the notation). Indeed, as in Remark 3.4.8,
$\mathbb {V}_{\overline {\mathbb {F}}_p}^{K^p}$ (see § 3.4 for the notation). Indeed, as in Remark 3.4.8, ![]() $\mathcal {M}^{K^p}_{\overline {\mathbb {F}}_p}=(\mathbb {V}^{K^p}_{\overline {\mathbb {F}}_p})^{1+p\mathbb {Z}_p}$, and
$\mathcal {M}^{K^p}_{\overline {\mathbb {F}}_p}=(\mathbb {V}^{K^p}_{\overline {\mathbb {F}}_p})^{1+p\mathbb {Z}_p}$, and ![]() $1+p\mathbb {Z}_p$ is a pro-
$1+p\mathbb {Z}_p$ is a pro-![]() $p$-group; however, a little more work is necessary to obtain the finite-dimensionality needed to apply the formalism of the previous section to
$p$-group; however, a little more work is necessary to obtain the finite-dimensionality needed to apply the formalism of the previous section to ![]() $\mathbb {V}^{K^p}_{\overline {\mathbb {F}}_p}$ in the first place. A version of this argument appears in Lemma 4.5.2.
$\mathbb {V}^{K^p}_{\overline {\mathbb {F}}_p}$ in the first place. A version of this argument appears in Lemma 4.5.2.
4.4.5 Consequences
Combining Lemmas 4.4.1, 4.4.2, and 4.4.3, we obtain Theorem 1.1.1 of the introduction with the additional restriction that ![]() $K^p$ be sufficiently small when
$K^p$ be sufficiently small when ![]() $p=2$ or
$p=2$ or ![]() $3$; only a finite number of maximal ideals can appear in the decompositions because
$3$; only a finite number of maximal ideals can appear in the decompositions because ![]() $\mathcal {A}^{\mathcal {N}_p K^p}_{\overline {\mathbb {F}}_p}$ is a finite-dimensional
$\mathcal {A}^{\mathcal {N}_p K^p}_{\overline {\mathbb {F}}_p}$ is a finite-dimensional ![]() ${\overline {\mathbb {F}}_p}$-vector space. We note that this also proves a theorem of Jochnowitz [Reference JochnowitzJoc82] stating that there are only finitely many eigensystems appearing in mod
${\overline {\mathbb {F}}_p}$-vector space. We note that this also proves a theorem of Jochnowitz [Reference JochnowitzJoc82] stating that there are only finitely many eigensystems appearing in mod ![]() $p$ modular forms.
$p$ modular forms.
4.5 Deduction of Theorem 1.1.1 from Theorem A
To finish the section, we explain how one can deduce the mod ![]() $p$ correspondence (Theorem 1.1.1) directly from the
$p$ correspondence (Theorem 1.1.1) directly from the ![]() $p$-adic correspondence (Theorem A), assuming the latter has been established (as is done independently of the mod
$p$-adic correspondence (Theorem A), assuming the latter has been established (as is done independently of the mod ![]() $p$ correspondence in § 5). In fact, it is more natural to deduce the corresponding statement over
$p$ correspondence in § 5). In fact, it is more natural to deduce the corresponding statement over ![]() $\mathbb {F}_p$ instead of
$\mathbb {F}_p$ instead of ![]() $\overline {\mathbb {F}}_p$, but there is no important difference between the two.
$\overline {\mathbb {F}}_p$, but there is no important difference between the two.
We fix a compact open ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ and a commutative subalgebra
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ and a commutative subalgebra ![]() $\mathbb {T}'$ of
$\mathbb {T}'$ of ![]() $\mathbb {T}^\mathrm {abs}$. Then, it suffices to verify that the maximal ideals appearing in the decompositions given by the formalism of § 4.3 for
$\mathbb {T}^\mathrm {abs}$. Then, it suffices to verify that the maximal ideals appearing in the decompositions given by the formalism of § 4.3 for ![]() $\mathcal {A}_{\mathbb {F}_p}^{K^p}$ and
$\mathcal {A}_{\mathbb {F}_p}^{K^p}$ and ![]() $\mathcal {M}_{\mathbb {F}_p}^{K^p}$ are identified with the open maximal ideals in the corresponding completed Hecke algebras. We show this in two lemmas, one for each space.
$\mathcal {M}_{\mathbb {F}_p}^{K^p}$ are identified with the open maximal ideals in the corresponding completed Hecke algebras. We show this in two lemmas, one for each space.
Lemma 4.5.1 The action of ![]() $\mathbb {T}'$ on
$\mathbb {T}'$ on ![]() $\mathcal {A}_{\mathbb {F}_p}^{K^p}$ factors through
$\mathcal {A}_{\mathbb {F}_p}^{K^p}$ factors through ![]() $\mathbb {T}'^\wedge _{\mathcal {A}_{\mathbb {Q}_p}^{K^p}}$ and the maximal ideals such that
$\mathbb {T}'^\wedge _{\mathcal {A}_{\mathbb {Q}_p}^{K^p}}$ and the maximal ideals such that ![]() $\bigl (\mathcal {A}_{\mathbb {F}_p}^{K^p}\bigr )_\mathfrak {m} \neq 0$ are precisely the open ideals of
$\bigl (\mathcal {A}_{\mathbb {F}_p}^{K^p}\bigr )_\mathfrak {m} \neq 0$ are precisely the open ideals of ![]() $\mathbb {T}'^\wedge _{\mathcal {A}_{\mathbb {Q}_p}^{K^p}}$.
$\mathbb {T}'^\wedge _{\mathcal {A}_{\mathbb {Q}_p}^{K^p}}$.
Proof. The union of the finite-dimensional subspaces ![]() $\mathcal {A}_{\mathbb {Q}_p}^{K_pK^p}$ as
$\mathcal {A}_{\mathbb {Q}_p}^{K_pK^p}$ as ![]() $K_p$ ranges over compact open subgroups
$K_p$ ranges over compact open subgroups ![]() $K_p \leq D_p^\times$ is dense in
$K_p \leq D_p^\times$ is dense in ![]() $\mathcal {A}_{\mathbb {Q}_p}^{K^p}$. Thus, if we write
$\mathcal {A}_{\mathbb {Q}_p}^{K^p}$. Thus, if we write ![]() $\mathbb {T}'_{K_pK^p,n}$ for the image of
$\mathbb {T}'_{K_pK^p,n}$ for the image of ![]() $\mathbb {T}'$ in
$\mathbb {T}'$ in ![]() $\mathrm {End}_{\mathbb {Z}/p^n}(\mathcal {A}_{\mathbb {Z}/p^n\mathbb {Z}}^{K_pK^p})$, Lemma 2.4.11 gives
$\mathrm {End}_{\mathbb {Z}/p^n}(\mathcal {A}_{\mathbb {Z}/p^n\mathbb {Z}}^{K_pK^p})$, Lemma 2.4.11 gives
In particular, considering the maps from the limit when ![]() $n=1$, we deduce that the action on
$n=1$, we deduce that the action on ![]() $\mathcal {A}^{K^p}_{\mathbb {F}_p}$ factors over
$\mathcal {A}^{K^p}_{\mathbb {F}_p}$ factors over ![]() $\mathbb {T}'^\wedge _{\mathcal {A}_{\mathbb {Q}_p}^{K^p}}$ as claimed. Moreover, each term in the limit has the discrete topology, so we also find that every open maximal ideal is pulled back from
$\mathbb {T}'^\wedge _{\mathcal {A}_{\mathbb {Q}_p}^{K^p}}$ as claimed. Moreover, each term in the limit has the discrete topology, so we also find that every open maximal ideal is pulled back from ![]() $\mathbb {T}'_{K_pK^p,n}$ for some
$\mathbb {T}'_{K_pK^p,n}$ for some ![]() $n$, and we can take
$n$, and we can take ![]() $n=1$ because any maximal ideal in
$n=1$ because any maximal ideal in ![]() $\mathbb {T}'_{K_pK^p,n}$ contains
$\mathbb {T}'_{K_pK^p,n}$ contains ![]() $p$. But the maximal ideals in
$p$. But the maximal ideals in ![]() $\mathbb {T}'_{K_pK^p,1}$ are precisely those such that
$\mathbb {T}'_{K_pK^p,1}$ are precisely those such that ![]() $(\mathcal {A}_{\mathbb {F}_p}^{K_pK^p})_\mathfrak {m} \neq 0$, so we conclude.
$(\mathcal {A}_{\mathbb {F}_p}^{K_pK^p})_\mathfrak {m} \neq 0$, so we conclude.
Lemma 4.5.2 The action of ![]() $\mathbb {T}'$ on
$\mathbb {T}'$ on ![]() $\mathcal {M}^{K^p}_{\mathbb {F}_p}$ factors through
$\mathcal {M}^{K^p}_{\mathbb {F}_p}$ factors through ![]() $\mathbb {T}'^\wedge _{\mathbb {V}^{K^p}_{\mathbb {Q}_p}}$ and the maximal ideals such that
$\mathbb {T}'^\wedge _{\mathbb {V}^{K^p}_{\mathbb {Q}_p}}$ and the maximal ideals such that ![]() $\bigl (\mathcal {M}^{K^p}_{\mathbb {F}_p}\bigr )_\mathfrak {m} \neq 0$ are precisely the open ideals of
$\bigl (\mathcal {M}^{K^p}_{\mathbb {F}_p}\bigr )_\mathfrak {m} \neq 0$ are precisely the open ideals of ![]() $\mathbb {T}'^\wedge _{\mathbb {V}^{K^p}_{\mathbb {Q}_p}}$.
$\mathbb {T}'^\wedge _{\mathbb {V}^{K^p}_{\mathbb {Q}_p}}$.
Proof. Write ![]() $F_i \mathbb {V}_{\mathbb {Q}_p}^{K^p}$ for the image of
$F_i \mathbb {V}_{\mathbb {Q}_p}^{K^p}$ for the image of ![]() $\bigoplus _{k=0}^{i} M_{k,\mathbb {Q}_p}^{K^p}$ in
$\bigoplus _{k=0}^{i} M_{k,\mathbb {Q}_p}^{K^p}$ in ![]() $\mathbb {V}^{K^p}_{\mathbb {Q}_{p}}$ under the evaluation map. The subspaces
$\mathbb {V}^{K^p}_{\mathbb {Q}_{p}}$ under the evaluation map. The subspaces ![]() $F_i \mathbb {V}_{\mathbb {Q}_p}^{K^p}$ are preserved by
$F_i \mathbb {V}_{\mathbb {Q}_p}^{K^p}$ are preserved by ![]() $\mathbb {T}'$ and their union is dense in
$\mathbb {T}'$ and their union is dense in ![]() $\mathbb {V}_{\mathbb {Q}_p}^{K^p}$. If we write
$\mathbb {V}_{\mathbb {Q}_p}^{K^p}$. If we write ![]() $F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} = F_i \mathbb {V}_{\mathbb {Q}_p}^{K^p} \cap \mathbb {V}_{\mathbb {Z}_p}^{K^p}$ and
$F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} = F_i \mathbb {V}_{\mathbb {Q}_p}^{K^p} \cap \mathbb {V}_{\mathbb {Z}_p}^{K^p}$ and ![]() $\mathbb {T}'_{i,n}$ for the image of
$\mathbb {T}'_{i,n}$ for the image of ![]() $\mathbb {T}'$ in
$\mathbb {T}'$ in ![]() $\mathrm {End}_{\mathbb {Z}/p^n} (F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} / p^n F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p})$, then Lemma 2.4.11 gives
$\mathrm {End}_{\mathbb {Z}/p^n} (F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} / p^n F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p})$, then Lemma 2.4.11 gives ![]() $\mathbb {T}'^\wedge _{\mathbb {V}_{\mathbb {Q}_p}^{K^p}} = \lim _{i,n} \mathbb {T}'_{i,n}$.
$\mathbb {T}'^\wedge _{\mathbb {V}_{\mathbb {Q}_p}^{K^p}} = \lim _{i,n} \mathbb {T}'_{i,n}$.
We write ![]() $F_i\mathbb {V}^{K^p}_{\mathbb {F}_p} := F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} / \bigl (F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} \cap p\mathbb {V}_{\mathbb {Z}_p}^{K^p} \bigr ) = F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} / p F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p}$. Then,
$F_i\mathbb {V}^{K^p}_{\mathbb {F}_p} := F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} / \bigl (F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} \cap p\mathbb {V}_{\mathbb {Z}_p}^{K^p} \bigr ) = F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p} / p F_i \mathbb {V}_{\mathbb {Z}_p}^{K^p}$. Then, ![]() $F_i \mathbb {V}_{\mathbb {F}_p}^{K^p}$ is a finite-dimensional
$F_i \mathbb {V}_{\mathbb {F}_p}^{K^p}$ is a finite-dimensional ![]() $\mathbb {F}_p$-vector space and
$\mathbb {F}_p$-vector space and ![]() $\mathbb {V}_{\mathbb {F}_p}^{K^p} = \bigcup _i F_i \mathbb {V}_{\mathbb {F}_p}^{K^p}$. Taking the maps corresponding to the
$\mathbb {V}_{\mathbb {F}_p}^{K^p} = \bigcup _i F_i \mathbb {V}_{\mathbb {F}_p}^{K^p}$. Taking the maps corresponding to the ![]() $n=1$ terms in the limit above, we deduce that the action of
$n=1$ terms in the limit above, we deduce that the action of ![]() $\mathbb {T}'$ on
$\mathbb {T}'$ on ![]() $\mathbb {V}_{\mathbb {F}_p}^{K^p}$ factors through
$\mathbb {V}_{\mathbb {F}_p}^{K^p}$ factors through ![]() $\mathbb {T}'^\wedge _{\mathbb {V}_{\mathbb {Q}_p}^{K^p}}$.
$\mathbb {T}'^\wedge _{\mathbb {V}_{\mathbb {Q}_p}^{K^p}}$.
Now, because ![]() $\mathcal {M}^{K^p}_{\mathbb {F}_p}=(\mathbb {V}_{\mathbb {F}_p}^{K^p})^{1+p\mathbb {Z}_p}$, the action on
$\mathcal {M}^{K^p}_{\mathbb {F}_p}=(\mathbb {V}_{\mathbb {F}_p}^{K^p})^{1+p\mathbb {Z}_p}$, the action on ![]() $\mathcal {M}_{\mathbb {F}_p}^{K^p}$ also factors through
$\mathcal {M}_{\mathbb {F}_p}^{K^p}$ also factors through ![]() $\mathbb {T}'^\wedge _{\mathbb {V}_{\mathbb {Q}_p}^{K^p}}$. Moreover, arguing as in the proof of the previous lemma, any open maximal ideal is pulled back from
$\mathbb {T}'^\wedge _{\mathbb {V}_{\mathbb {Q}_p}^{K^p}}$. Moreover, arguing as in the proof of the previous lemma, any open maximal ideal is pulled back from ![]() $\mathbb {T}'_{i,1}$ for some
$\mathbb {T}'_{i,1}$ for some ![]() $i$, i.e. from the image of
$i$, i.e. from the image of ![]() $\mathbb {T}'$ in
$\mathbb {T}'$ in ![]() $\mathrm {End}(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})$, so we conclude that the open maximal ideals are exactly those for which
$\mathrm {End}(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})$, so we conclude that the open maximal ideals are exactly those for which ![]() $(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$ for some
$(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$ for some ![]() $i$. On the other hand,
$i$. On the other hand, ![]() $F_i \mathbb {V}_{\mathbb {F}_p}^{K^p}$ is preserved by the action of
$F_i \mathbb {V}_{\mathbb {F}_p}^{K^p}$ is preserved by the action of ![]() $\mathbb {Z}_p^\times$, which commutes with the Hecke action, thus
$\mathbb {Z}_p^\times$, which commutes with the Hecke action, thus ![]() $(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$ is a finite-dimensional
$(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$ is a finite-dimensional ![]() $\mathbb {F}_p$-vector space with an action of
$\mathbb {F}_p$-vector space with an action of ![]() $\mathbb {Z}_p^\times$. Because
$\mathbb {Z}_p^\times$. Because ![]() $1+p\mathbb {Z}_p$ is a pro-
$1+p\mathbb {Z}_p$ is a pro-![]() $p$ group,
$p$ group, ![]() $(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$ if and only if
$(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$ if and only if ![]() $(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})^{1+p\mathbb {Z}_p}_\mathfrak {m} \neq 0$, as in the proof of Lemma 4.4.3. Because
$(F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})^{1+p\mathbb {Z}_p}_\mathfrak {m} \neq 0$, as in the proof of Lemma 4.4.3. Because ![]() $\mathcal {M}_{\mathbb {F}_p}^{K^p} = \bigcup _i (F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})^{1+p\mathbb {Z}_p}$, we find that as
$\mathcal {M}_{\mathbb {F}_p}^{K^p} = \bigcup _i (F_i \mathbb {V}_{\mathbb {F}_p}^{K^p})^{1+p\mathbb {Z}_p}$, we find that as ![]() $i$ varies these are exactly the maximal ideals for which
$i$ varies these are exactly the maximal ideals for which ![]() $(\mathcal {M}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$.
$(\mathcal {M}_{\mathbb {F}_p}^{K^p})_\mathfrak {m} \neq 0$.
Combining Lemmas 4.5.1 and 4.5.2 (and invoking Lemma 4.4.3 still to see that only finitely many maximal ideals appear), we obtain the ![]() $\mathbb {F}_p$-version of Theorem 1.1.1 as a consequence of Theorem A.
$\mathbb {F}_p$-version of Theorem 1.1.1 as a consequence of Theorem A.
5. Spectral  $p$-adic Jacquet–Langlands correspondence
$p$-adic Jacquet–Langlands correspondence
In this section, we prove Theorem A. After recalling some preliminaries on perfectoid modular curves in §§ 5.1–5.3, in §§ 5.4–5.5 we recall the construction of the supersingular perfectoid Igusa variety and its relation to the fibers of the Hodge–Tate period map. In § 5.6 we use this relation to construct an evaluation map from classical modular forms to ![]() $\mathcal {A}_{\mathbb {C}_p}$. The key properties of this evaluation map are that it is injective and has dense image; these are established in Theorem 5.6.2. We conclude in § 5.7 by invoking some of the tools developed in § 2.4; in particular, Theorem 5.7.1 gives the isomorphism of completed Hecke algebras of Theorem A along with some other isomorphisms indicated in the introduction.
$\mathcal {A}_{\mathbb {C}_p}$. The key properties of this evaluation map are that it is injective and has dense image; these are established in Theorem 5.6.2. We conclude in § 5.7 by invoking some of the tools developed in § 2.4; in particular, Theorem 5.7.1 gives the isomorphism of completed Hecke algebras of Theorem A along with some other isomorphisms indicated in the introduction.
5.1 Perfectoid modular curves
Let ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a sufficiently small compact open subgroup. Viewing
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ be a sufficiently small compact open subgroup. Viewing ![]() $K^p$ as a subgroup of
$K^p$ as a subgroup of ![]() $\mathrm {GL}_2(\mathbb {A}_f)$, the (infinite level at
$\mathrm {GL}_2(\mathbb {A}_f)$, the (infinite level at ![]() $p$) schematic modular curves
$p$) schematic modular curves ![]() $Y_{K^p}$ and
$Y_{K^p}$ and ![]() $X_{K^p}$ define functors on affinoid perfectoids over
$X_{K^p}$ define functors on affinoid perfectoids over ![]() $(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$ by
$(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$ by
It is convenient to write out an equivalent definition for ![]() $\mathcal {Y}_{K^p}$, where we separate out the
$\mathcal {Y}_{K^p}$, where we separate out the ![]() $p$ and prime-to-
$p$ and prime-to-![]() $p$ parts of the level.
$p$ parts of the level.
Definition 5.1.1 We define ![]() $\mathcal {Y}_{K^p}$ as the functor on affinoid perfectoid
$\mathcal {Y}_{K^p}$ as the functor on affinoid perfectoid ![]() $\mathrm {Spa}(R,R^+)/\mathrm {Spa}(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$,
$\mathrm {Spa}(R,R^+)/\mathrm {Spa}(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$,
sending ![]() $(R,R^+)$ to the set of equivalence classes of triples
$(R,R^+)$ to the set of equivalence classes of triples ![]() $(E, \varphi _p, \mathcal {K}^p)$ where:
$(E, \varphi _p, \mathcal {K}^p)$ where:
(i)
 $E/R$ is an elliptic curve;
$E/R$ is an elliptic curve;(ii)
 $\varphi _p: \underline {\mathbb {Q}_p}^2 \xrightarrow {\sim } V_{\mathbb {Q}_p}(E)$ is an isomorphism;
$\varphi _p: \underline {\mathbb {Q}_p}^2 \xrightarrow {\sim } V_{\mathbb {Q}_p}(E)$ is an isomorphism;(iii)
 $\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E))$ is a
$\mathcal {K}^p \subset \underline {\mathrm {Isom}}( (\underline {\mathbb {A}_f^{(p)}})^2, V_{\mathbb {A}_f^{(p)}}(E))$ is a  $K^p$-torsor;
$K^p$-torsor;(iv) the relation
 $\sim$ is defined by
$\sim$ is defined by  $(E,\varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a quasi-isogeny
$(E,\varphi _p, \mathcal {K}^p) \sim (E', \varphi _p', {\mathcal {K}^p}')$ if there is a quasi-isogeny  $q: E \rightarrow E'$ such that
$q: E \rightarrow E'$ such that  $q \circ \varphi _p = \varphi _p'$ and
$q \circ \varphi _p = \varphi _p'$ and  $q(\mathcal {K}^p) = {\mathcal {K}^p}'$.
$q(\mathcal {K}^p) = {\mathcal {K}^p}'$.
Both ![]() $\mathcal {Y}_{K^p}$ and
$\mathcal {Y}_{K^p}$ and ![]() $\mathcal {X}_{K^p}$ are represented by perfectoid spaces over
$\mathcal {X}_{K^p}$ are represented by perfectoid spaces over ![]() $\mathbb {C}_p$: in [Reference ScholzeSch15, Theorem 3.3.18] it is shown that there is a perfectoid space
$\mathbb {C}_p$: in [Reference ScholzeSch15, Theorem 3.3.18] it is shown that there is a perfectoid space
where, here, a ![]() $\sim$ limit, as defined in [Reference Scholze and WeinsteinSW13, Definition 2.4.1], in particular implies (via [Reference Scholze and WeinsteinSW13, Proposition 2.4.5]) that for
$\sim$ limit, as defined in [Reference Scholze and WeinsteinSW13, Definition 2.4.1], in particular implies (via [Reference Scholze and WeinsteinSW13, Proposition 2.4.5]) that for ![]() $(R,R^+)$ perfectoid over
$(R,R^+)$ perfectoid over ![]() $(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$,
$(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$,
However, we have the identity
because ![]() $X_{K_pK^p}$ is projective and the line bundles on
$X_{K_pK^p}$ is projective and the line bundles on ![]() $\mathrm {Spa}(R,R^+)$ and
$\mathrm {Spa}(R,R^+)$ and ![]() $\operatorname {Spec}\!R$ are identified via their global sections which are rank-one projectives over
$\operatorname {Spec}\!R$ are identified via their global sections which are rank-one projectives over ![]() $R$ (for affine schemes this is standard, and for
$R$ (for affine schemes this is standard, and for ![]() $\mathrm {Spa}(R,R^+)$ the equivalence between vector bundles and finite projective modules over
$\mathrm {Spa}(R,R^+)$ the equivalence between vector bundles and finite projective modules over ![]() $R$ is given by [Reference Kedlaya and LiuKL15, Theorem 8.2.2]). Thus, we conclude
$R$ is given by [Reference Kedlaya and LiuKL15, Theorem 8.2.2]). Thus, we conclude ![]() $\mathcal {X}_{K^p}=\mathcal {X}_{K^p}',$ so that
$\mathcal {X}_{K^p}=\mathcal {X}_{K^p}',$ so that ![]() $\mathcal {X}_{K^p}$ is a perfectoid space.
$\mathcal {X}_{K^p}$ is a perfectoid space.
Passing to the open modular curves we find
is also represented by an open in ![]() $\mathcal {X}_{K^p}$, which is perfectoid by the above result. It is immediate by construction of the analytification of an affine finite-type scheme over
$\mathcal {X}_{K^p}$, which is perfectoid by the above result. It is immediate by construction of the analytification of an affine finite-type scheme over ![]() $\mathbb {C}_p$ that
$\mathbb {C}_p$ that
so that we conclude ![]() $\mathcal {Y}_{K^p}$ is a perfectoid space.
$\mathcal {Y}_{K^p}$ is a perfectoid space.
Remark 5.1.2 For open modular curves we can then obtain the same result for ![]() $K^p$ closed but not necessarily compact open by using Proposition 3.1.8 and the fact that the limit of a tower of finite étale covers of perfectoid spaces is perfectoid, and similarly for
$K^p$ closed but not necessarily compact open by using Proposition 3.1.8 and the fact that the limit of a tower of finite étale covers of perfectoid spaces is perfectoid, and similarly for ![]() $X$ if this is combined with explicit computations at the cusps. As our main concern is the Hecke action, for which it suffices to have a construction for
$X$ if this is combined with explicit computations at the cusps. As our main concern is the Hecke action, for which it suffices to have a construction for ![]() $K^p$ compact open, we do not go further into these details here.
$K^p$ compact open, we do not go further into these details here.
From the actions on ![]() $Y_{K^p}$ and
$Y_{K^p}$ and ![]() $X_{K^p}$, we obtain an action of
$X_{K^p}$, we obtain an action of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ on
$\mathrm {GL}_2(\mathbb {Q}_p)$ on ![]() $\mathcal {X}_{K^p}$ preserving
$\mathcal {X}_{K^p}$ preserving ![]() $\mathcal {Y}_{K^p}$ and a commuting action of
$\mathcal {Y}_{K^p}$ and a commuting action of ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ on the towers as
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$ on the towers as ![]() $K^p$ varies over sufficiently small compact opens
$K^p$ varies over sufficiently small compact opens ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$.
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$.
5.2 Modular forms
For ![]() $k \geq 0$ recall from § 3.2 that we have the admissible
$k \geq 0$ recall from § 3.2 that we have the admissible ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-representation of weight
$\mathrm {GL}_2(\mathbb {A}_f)$-representation of weight ![]() $k$ modular forms over
$k$ modular forms over ![]() $\mathbb {C}_p$,
$\mathbb {C}_p$,
 \[ M_{k,\mathbb{C}_p} = H^0(X_{\mathbb{C}_p}, \omega^k)\cong\mathrm{colim}_{\substack{K \leq \mathrm{GL}_2(\mathbb{A}_f) \\ K \text{ sufficiently small} \\\text{compact open}}} H^0(X_{K,\mathbb{C}_p}, \omega^k). \]
\[ M_{k,\mathbb{C}_p} = H^0(X_{\mathbb{C}_p}, \omega^k)\cong\mathrm{colim}_{\substack{K \leq \mathrm{GL}_2(\mathbb{A}_f) \\ K \text{ sufficiently small} \\\text{compact open}}} H^0(X_{K,\mathbb{C}_p}, \omega^k). \]
We now relate these to ![]() $\mathcal {X}_{K^p}$.
$\mathcal {X}_{K^p}$.
The ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$-action on
$\mathrm {GL}_2(\mathbb {Q}_p)$-action on ![]() $\mathcal {X}_{K^p}$ can be viewed as induced from the identification
$\mathcal {X}_{K^p}$ can be viewed as induced from the identification
and the action of ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ on the tower. In particular, the analytification of the
$\mathrm {GL}_2(\mathbb {Q}_p)$ on the tower. In particular, the analytification of the ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant modular bundle
$\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant modular bundle ![]() $\omega$ on the tower pulls back to a
$\omega$ on the tower pulls back to a ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant vector bundle on
$\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant vector bundle on ![]() $\mathcal {X}_{K^p}$ which we also denote by
$\mathcal {X}_{K^p}$ which we also denote by ![]() $\omega$. Moreover, these compile to a
$\omega$. Moreover, these compile to a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant bundle on the tower
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant bundle on the tower ![]() $(\mathcal {X}_{K^p})_{K^p}$ as
$(\mathcal {X}_{K^p})_{K^p}$ as ![]() $K^p$ varies.
$K^p$ varies.
For ![]() $K_p \leq \mathrm {GL}_2(\mathbb {Q}_p)$ compact open, we have
$K_p \leq \mathrm {GL}_2(\mathbb {Q}_p)$ compact open, we have
In particular, by pullback to ![]() $\mathcal {X}_{K^p}$ we obtain a
$\mathcal {X}_{K^p}$ we obtain a ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant injection
$\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant injection
Though we do not need any more than this, we note that this is an isomorphism onto the ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$-smooth vectors, as can be checked after restriction to
$\mathrm {GL}_2(\mathbb {Q}_p)$-smooth vectors, as can be checked after restriction to ![]() $\mathcal {Y}_{K^p}$ where it follows from the sheaf property for the completed structure sheaf on the pro-étale site of
$\mathcal {Y}_{K^p}$ where it follows from the sheaf property for the completed structure sheaf on the pro-étale site of ![]() $\mathcal {Y}_{K_pK^p, \mathbb {C}_p}^\mathrm {ad}$ for each compact open subgroup
$\mathcal {Y}_{K_pK^p, \mathbb {C}_p}^\mathrm {ad}$ for each compact open subgroup ![]() $K_p \leq \mathrm {GL}_2(\mathbb {Q}_p)$.
$K_p \leq \mathrm {GL}_2(\mathbb {Q}_p)$.
This isomorphism is compatible with the ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-action on the tower of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-action on the tower of ![]() $\mathcal {X}_{K^p}$ so extends to a
$\mathcal {X}_{K^p}$ so extends to a ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-equivariant injection
$\mathrm {GL}_2(\mathbb {A}_f)$-equivariant injection
Remark 5.2.1 As in Remark 4.3.1, to obtain a ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-action inducing the standard Hecke action, one should introduce a twist by the unramified determinant character that appears in the Kodaira–Spencer isomorphism. This does not change the resulting completed Hecke algebra, so it is reasonable to include the twist only when convenient, that is, when comparing with singular/étale cohomology.
$\mathrm {GL}_2(\mathbb {A}_f)$-action inducing the standard Hecke action, one should introduce a twist by the unramified determinant character that appears in the Kodaira–Spencer isomorphism. This does not change the resulting completed Hecke algebra, so it is reasonable to include the twist only when convenient, that is, when comparing with singular/étale cohomology.
5.3 The Hodge–Tate period map
In [Reference ScholzeSch15], Scholze constructs the Hodge–Tate period map,
We normalize some choices related to the group actions and equivariant structures by requiring that, over ![]() $\mathcal {Y}_{K^p}$,
$\mathcal {Y}_{K^p}$, ![]() $\pi _{\mathrm {HT},K^p}$ is the classifying map for the line
$\pi _{\mathrm {HT},K^p}$ is the classifying map for the line
given by the Hodge–Tate filtration for the universal elliptic curve and the trivialization of its relative Tate module. In particular, ![]() $\pi _{\mathrm {HT},K^p}$ is
$\pi _{\mathrm {HT},K^p}$ is ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant for the action on
$\mathrm {GL}_2(\mathbb {Q}_p)$-equivariant for the action on ![]() $\mathbb {P}^1$ in which
$\mathbb {P}^1$ in which ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ acts by the dual of the standard representation on
$\mathrm {GL}_2(\mathbb {Q}_p)$ acts by the dual of the standard representation on ![]() $H^0(\mathbb {P}^1, \mathcal {O}(1))$. The image of the boundary/cusps
$H^0(\mathbb {P}^1, \mathcal {O}(1))$. The image of the boundary/cusps ![]() $\mathcal {X}_{K^p}\backslash \mathcal {Y}_{K^p}$ is
$\mathcal {X}_{K^p}\backslash \mathcal {Y}_{K^p}$ is ![]() $\mathbb {P}^1(\mathbb {Q}_p)$.
$\mathbb {P}^1(\mathbb {Q}_p)$.
The maps ![]() $\pi _{\mathrm {HT},K^p}$ compile to a
$\pi _{\mathrm {HT},K^p}$ compile to a ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-equivariant map
$\mathrm {GL}_2(\mathbb {A}_f)$-equivariant map
from the tower ![]() $\mathcal {X}_{K^p}$, where
$\mathcal {X}_{K^p}$, where ![]() $\mathbb {P}^1$ is given the trivial action of
$\mathbb {P}^1$ is given the trivial action of ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$. By construction, after fixing a compatible system of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$. By construction, after fixing a compatible system of ![]() $p$-power roots of unity in
$p$-power roots of unity in ![]() $\mathbb {C}_p$, there is a natural isomorphism
$\mathbb {C}_p$, there is a natural isomorphism ![]() $\pi _{\mathrm {HT}}^{*} \mathcal {O}(1) = \omega$ of
$\pi _{\mathrm {HT}}^{*} \mathcal {O}(1) = \omega$ of ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-equivariant line bundles on the tower
$\mathrm {GL}_2(\mathbb {A}_f)$-equivariant line bundles on the tower ![]() $(\mathcal {X}_{K^p})_{K^p}$.
$(\mathcal {X}_{K^p})_{K^p}$.
Remark 5.3.1 Comparing with [Reference Caraiani and ScholzeCS17, Reference Scholze and WeinsteinSW13], over the good reduction locus one can also think of the map ![]() $\pi _\mathrm {HT}$ as the classifying map for the
$\pi _\mathrm {HT}$ as the classifying map for the ![]() $p$-divisible group
$p$-divisible group ![]() $E[p^\infty ]$ equipped with a basis for
$E[p^\infty ]$ equipped with a basis for ![]() $T_p E[p^\infty ]$. A key property of
$T_p E[p^\infty ]$. A key property of ![]() $\pi _\mathrm {HT}$ is that we can construct
$\pi _\mathrm {HT}$ is that we can construct ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant fake Hasse invariants via pullback; this matches well with the perspective on the classical Hasse invariant described in § 3.2.2 which can be read as saying that it is pulled back from the moduli stack of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant fake Hasse invariants via pullback; this matches well with the perspective on the classical Hasse invariant described in § 3.2.2 which can be read as saying that it is pulled back from the moduli stack of ![]() $p$-divisible groups.
$p$-divisible groups.
5.4 The perfectoid supersingular Igusa variety
For a closed subgroup ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$, the supersingular Caraiani–Scholze Igusa moduli problem of Definition 3.5.1 defines a functor on affinoid perfectoids over
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$, the supersingular Caraiani–Scholze Igusa moduli problem of Definition 3.5.1 defines a functor on affinoid perfectoids over ![]() $(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$,
$(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$,
When ![]() $K^p$ is sufficiently small, Corollary 3.7.4 identifies
$K^p$ is sufficiently small, Corollary 3.7.4 identifies ![]() $\mathrm {Ig}_{K^p}^\mathrm {ss}$ with
$\mathrm {Ig}_{K^p}^\mathrm {ss}$ with ![]() $\operatorname {Spec}\!A$ for
$\operatorname {Spec}\!A$ for
Because ![]() $A$ is a perfect ring and
$A$ is a perfect ring and ![]() $R^+$ is
$R^+$ is ![]() $p$-adically complete,
$p$-adically complete,
 \begin{align*} \mathrm{Ig}_{K^p}^\mathrm{ss}(R^+/p) &= \mathrm{Hom}_{\overline{\mathbb{F}}_p}(A, R^+/p) \\ &= \mathrm{Hom}_{\breve{\mathbb{Z}}_p}(W(A), R^+) \\ &= \mathrm{Hom}_{(\breve{\mathbb{Q}}_p, \breve{\mathbb{Z}}_p)}\bigl((W(A)[1/p], W(A)), (R,R^+) \bigr)\\ &= \mathrm{Hom}_{(\breve{\mathbb{Q}}_p, \breve{\mathbb{Z}}_p)}\bigl((\mathcal{A}_{\breve{\mathbb{Q}}_p}^{K^p}, \mathcal{A}_{\breve{\mathbb{Z}}_p}^{K^p}), (R,R^+) \bigr) \\ &= \mathrm{Hom}_{(\mathbb{C}_p, \mathcal{O}_{\mathbb{C}_p})}\bigl((\mathcal{A}_{\mathbb{C}_p}^{K^p}, \mathcal{A}_{\mathcal{O}_{\mathbb{C}_p}}^{K^p}), (R,R^+) \bigr). \end{align*}
\begin{align*} \mathrm{Ig}_{K^p}^\mathrm{ss}(R^+/p) &= \mathrm{Hom}_{\overline{\mathbb{F}}_p}(A, R^+/p) \\ &= \mathrm{Hom}_{\breve{\mathbb{Z}}_p}(W(A), R^+) \\ &= \mathrm{Hom}_{(\breve{\mathbb{Q}}_p, \breve{\mathbb{Z}}_p)}\bigl((W(A)[1/p], W(A)), (R,R^+) \bigr)\\ &= \mathrm{Hom}_{(\breve{\mathbb{Q}}_p, \breve{\mathbb{Z}}_p)}\bigl((\mathcal{A}_{\breve{\mathbb{Q}}_p}^{K^p}, \mathcal{A}_{\breve{\mathbb{Z}}_p}^{K^p}), (R,R^+) \bigr) \\ &= \mathrm{Hom}_{(\mathbb{C}_p, \mathcal{O}_{\mathbb{C}_p})}\bigl((\mathcal{A}_{\mathbb{C}_p}^{K^p}, \mathcal{A}_{\mathcal{O}_{\mathbb{C}_p}}^{K^p}), (R,R^+) \bigr). \end{align*}
However, ![]() $(\mathcal {A}_{\mathbb {C}_p}^{K^p}, \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p})$ is a perfectoid Huber pair, so we conclude that
$(\mathcal {A}_{\mathbb {C}_p}^{K^p}, \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p})$ is a perfectoid Huber pair, so we conclude that ![]() $\mathcal {I}g^\mathrm {ss}_{K^p}$ is represented by the affinoid perfectoid space
$\mathcal {I}g^\mathrm {ss}_{K^p}$ is represented by the affinoid perfectoid space ![]() $\mathrm {Spa}(\mathcal {A}_{\mathbb {C}_p}^{K^p}, \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p})$, which is just the profinite set
$\mathrm {Spa}(\mathcal {A}_{\mathbb {C}_p}^{K^p}, \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p})$, which is just the profinite set ![]() $D^\times (\mathbb {Q})\backslash D^\times (\mathbb {A}_f)/K^p$ viewed as a perfectoid space over
$D^\times (\mathbb {Q})\backslash D^\times (\mathbb {A}_f)/K^p$ viewed as a perfectoid space over ![]() $\mathrm {Spa}(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$.
$\mathrm {Spa}(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$.
Remark 5.4.1 In [Reference Caraiani and ScholzeCS17, § 4] this procedure is carried out in much greater generality to construct perfectoid Igusa varieties (without the explicit identification with a double coset, which, in general, will only occur over the basic locus).
5.5 Uniformization of fibers of  $\pi _{\mathrm {HT}}$
$\pi _{\mathrm {HT}}$
We fix now a one-dimensional connected height-two ![]() $p$-divisible group
$p$-divisible group ![]() $G / \mathcal {O}_{\mathbb {C}_p}$ equipped with a quasi-isogeny
$G / \mathcal {O}_{\mathbb {C}_p}$ equipped with a quasi-isogeny
and a trivialization ![]() $\psi _{G}: \mathbb {Z}_p^2 \xrightarrow {\sim } T_p G (\mathcal {O}_{\mathbb {C}_p})$. By the Scholze–Weinstein classification [Reference Scholze and WeinsteinSW13], the pair
$\psi _{G}: \mathbb {Z}_p^2 \xrightarrow {\sim } T_p G (\mathcal {O}_{\mathbb {C}_p})$. By the Scholze–Weinstein classification [Reference Scholze and WeinsteinSW13], the pair ![]() $(G,\psi _G)$ is equivalent to the point
$(G,\psi _G)$ is equivalent to the point ![]() $x \in \mathbb {P}^1(\mathbb {C}_p) \backslash \mathbb {P}^1(\mathbb {Q}_p)$ determined by the position of the Hodge–Tate filtration. As it will be convenient later, we choose our data so that
$x \in \mathbb {P}^1(\mathbb {C}_p) \backslash \mathbb {P}^1(\mathbb {Q}_p)$ determined by the position of the Hodge–Tate filtration. As it will be convenient later, we choose our data so that ![]() $x$ is in the affinoid ball
$x$ is in the affinoid ball ![]() $B_1: |U/V| \leq 1$, where here
$B_1: |U/V| \leq 1$, where here ![]() $U$ and
$U$ and ![]() $V$ denote the standard basis for
$V$ denote the standard basis for ![]() $O(1)$ (i.e. projective coordinates are
$O(1)$ (i.e. projective coordinates are ![]() $[U:V]$).
$[U:V]$).
As in [Reference Scholze and WeinsteinSW13], there is a perfectoid Lubin–Tate space ![]() $\widehat {\mathcal {M}}_{\mathrm {LT},\infty }$ over
$\widehat {\mathcal {M}}_{\mathrm {LT},\infty }$ over ![]() $\mathrm {Spa}(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$ parameterizing quasi-isogeny lifts
$\mathrm {Spa}(\mathbb {C}_p, \mathcal {O}_{\mathbb {C}_p})$ parameterizing quasi-isogeny lifts ![]() $G$ of
$G$ of ![]() $\mathbb {X}_\mathrm {ss}$ equipped with trivializations of
$\mathbb {X}_\mathrm {ss}$ equipped with trivializations of ![]() $T_pG$. We do not define this space more carefully as we use it only through a citation to [Reference Caraiani and ScholzeCS17] in a proof in the following, but let us recall that there is a local Hodge–Tate period map classifying the Hodge–Tate filtration,
$T_pG$. We do not define this space more carefully as we use it only through a citation to [Reference Caraiani and ScholzeCS17] in a proof in the following, but let us recall that there is a local Hodge–Tate period map classifying the Hodge–Tate filtration,
and ![]() $\rho _G$ determines a point
$\rho _G$ determines a point ![]() $x_\infty \in \widehat {\mathcal {M}}_{\mathrm {LT},\infty }(\mathbb {C}_p)$ lying in
$x_\infty \in \widehat {\mathcal {M}}_{\mathrm {LT},\infty }(\mathbb {C}_p)$ lying in ![]() $\pi _{\mathrm {HT,loc}}^{-1}(x)$.
$\pi _{\mathrm {HT,loc}}^{-1}(x)$.
From these data, we now construct a map
On points in affinoid perfectoid ![]() $(R,R^+)$, it sends
$(R,R^+)$, it sends ![]() $(E, \varphi _p, \mathcal {K}^p)$ to
$(E, \varphi _p, \mathcal {K}^p)$ to ![]() $(E', \varphi _p', {\mathcal {K}^p}')$, where:
$(E', \varphi _p', {\mathcal {K}^p}')$, where:
(i)
 $E'=\mathcal {E}_R$ where
$E'=\mathcal {E}_R$ where  $\mathcal {E}$ is the elliptic curve over
$\mathcal {E}$ is the elliptic curve over  $R^+$ given by the Serre–Tate lifting (cf. [Reference KatzKat81, § 1]) of
$R^+$ given by the Serre–Tate lifting (cf. [Reference KatzKat81, § 1]) of  $E$ to
$E$ to  $R^+$ determined by the quasi-isogeny
$R^+$ determined by the quasi-isogeny
 \[ \rho_G \circ \varphi_{p}^{-1}: E[p^\infty] \otimes \mathbb{Q}_p \rightarrow G_{R^+/p} \otimes \mathbb{Q}_p; \]
\[ \rho_G \circ \varphi_{p}^{-1}: E[p^\infty] \otimes \mathbb{Q}_p \rightarrow G_{R^+/p} \otimes \mathbb{Q}_p; \](ii)
 $\varphi _p'$ is the composition of
$\varphi _p'$ is the composition of  $\psi _G$ with the canonical identification of Tate modules induced by
$\psi _G$ with the canonical identification of Tate modules induced by  $\mathcal {E}[p^\infty ]=G[p^\infty ]_{R^+}$;
$\mathcal {E}[p^\infty ]=G[p^\infty ]_{R^+}$;(iii)
 ${\mathcal {K}^p}'$ is the unique lift of
${\mathcal {K}^p}'$ is the unique lift of  $\mathcal {K}^p$.
$\mathcal {K}^p$.
By construction, ![]() $\mathrm {unif}_{x_\infty }$ factors through the closed subset
$\mathrm {unif}_{x_\infty }$ factors through the closed subset ![]() $\pi _{\mathrm {HT}, K^p}^{-1}(x) \subset \mathcal {X}_{K^p, \mathbb {C}_p}$. The latter is a Zariski closed subset of a perfectoid space and, thus, admits a canonical structure of a perfectoid space through which
$\pi _{\mathrm {HT}, K^p}^{-1}(x) \subset \mathcal {X}_{K^p, \mathbb {C}_p}$. The latter is a Zariski closed subset of a perfectoid space and, thus, admits a canonical structure of a perfectoid space through which ![]() $\mathrm {unif}_{x_\infty }$ factors (because the domain is also a perfectoid space).
$\mathrm {unif}_{x_\infty }$ factors (because the domain is also a perfectoid space).
In addition to the obvious ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariance in the tower, the map
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariance in the tower, the map ![]() $\mathrm {unif}_{x_\infty,K^p}$ also satisfies an equivariance at
$\mathrm {unif}_{x_\infty,K^p}$ also satisfies an equivariance at ![]() $p$: let
$p$: let ![]() $T_x:=\mathrm {Aut}(G \otimes \mathbb {Q}_p)$ be the group of self quasi-isogenies of
$T_x:=\mathrm {Aut}(G \otimes \mathbb {Q}_p)$ be the group of self quasi-isogenies of ![]() $G$. Then, by the Scholze–Weinstein classification,
$G$. Then, by the Scholze–Weinstein classification, ![]() $\psi _G$ identifies
$\psi _G$ identifies ![]() $T_x$ with the stabilizer in
$T_x$ with the stabilizer in ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ of
$\mathrm {GL}_2(\mathbb {Q}_p)$ of ![]() $x\in \mathbb {P}^1(\mathbb {C}_p) \backslash \mathbb {P}^1(\mathbb {Q}_p)$. On the other hand,
$x\in \mathbb {P}^1(\mathbb {C}_p) \backslash \mathbb {P}^1(\mathbb {Q}_p)$. On the other hand, ![]() $\rho _G$ identifies
$\rho _G$ identifies ![]() $T_x$ with a subgroup of the self-quasi-isogenies
$T_x$ with a subgroup of the self-quasi-isogenies
By the interpretation as a stabilizer, ![]() $T_x$ is equal to either
$T_x$ is equal to either ![]() $\mathbb {Q}_p^\times$ or
$\mathbb {Q}_p^\times$ or ![]() $F^\times$ for a quadratic extension
$F^\times$ for a quadratic extension ![]() $F/\mathbb {Q}_p$, and the latter occurs exactly when
$F/\mathbb {Q}_p$, and the latter occurs exactly when ![]() $x \in \mathbb {P}^1(F) - \mathbb {P}^1(\mathbb {Q}_p)$; this follows from an explicit computation after observing that any line preserved by a non-scalar matrix in
$x \in \mathbb {P}^1(F) - \mathbb {P}^1(\mathbb {Q}_p)$; this follows from an explicit computation after observing that any line preserved by a non-scalar matrix in ![]() $\mathrm {GL}_2(\mathbb {Q}_p)$ must be defined over a quadratic extension of
$\mathrm {GL}_2(\mathbb {Q}_p)$ must be defined over a quadratic extension of ![]() $\mathbb {Q}_p$.
$\mathbb {Q}_p$.
Theorem 5.5.1 The maps ![]() $\mathrm {unif}_{x_\infty, K^p}$ induce a
$\mathrm {unif}_{x_\infty, K^p}$ induce a ![]() $T_x\times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism of towers of perfectoid spaces
$T_x\times \mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant isomorphism of towers of perfectoid spaces
as ![]() $K^p$ varies over sufficiently small compact open subgroups of
$K^p$ varies over sufficiently small compact open subgroups of ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$.
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$.
Proof. The equivariance and compatibility in the tower is immediate from the definition, so it suffices to show that for each ![]() $K^p$ the map
$K^p$ the map ![]() $\mathrm {unif}_{x_\infty, K^p}$ is an isomorphism of perfectoid spaces.
$\mathrm {unif}_{x_\infty, K^p}$ is an isomorphism of perfectoid spaces.
We first note that ![]() $\mathrm {unif}_{x_\infty,K^p}$ is the restriction to
$\mathrm {unif}_{x_\infty,K^p}$ is the restriction to ![]() $\mathcal {I}g^\mathrm {ss}_{K^p} \times x_\infty$ of a map
$\mathcal {I}g^\mathrm {ss}_{K^p} \times x_\infty$ of a map
defined similarly in [Reference Caraiani and ScholzeCS17, § 4]; here, ![]() $\mathcal {Y}_{K^p}^\mathrm {ss}$ denotes the closed subspace of
$\mathcal {Y}_{K^p}^\mathrm {ss}$ denotes the closed subspace of ![]() $\mathcal {Y}_{K^p}$ whose
$\mathcal {Y}_{K^p}$ whose ![]() $\mathrm {Spa}(C,C^+)$ points for
$\mathrm {Spa}(C,C^+)$ points for ![]() $C$ complete algebraically closed correspond to triples
$C$ complete algebraically closed correspond to triples ![]() $(E, \rho _p, \mathcal {K}^p)$ such that
$(E, \rho _p, \mathcal {K}^p)$ such that ![]() $E$ extends to an elliptic curve over
$E$ extends to an elliptic curve over ![]() $C^+$ with supersingular reduction at the maximal ideal
$C^+$ with supersingular reduction at the maximal ideal ![]() ${\mathfrak {m}}_{C^+}$ of
${\mathfrak {m}}_{C^+}$ of ![]() $C^+$.
$C^+$.
It follows from [Reference Caraiani and ScholzeCS17, Lemma 4.3.20] (cf. also [Reference Caraiani and ScholzeCS17, Definition 4.3.17]), that the diagram

is Cartesian on perfectoid spaces. Thus, because ![]() $\pi _\mathrm {HT,loc}(x_\infty )=x$, we find that
$\pi _\mathrm {HT,loc}(x_\infty )=x$, we find that ![]() $\mathrm {unif}_{x_\infty, K^p}$ induces an isomorphism between the functors of points of
$\mathrm {unif}_{x_\infty, K^p}$ induces an isomorphism between the functors of points of ![]() $\mathcal {I}g^\mathrm {ss}_{K^p}$ and
$\mathcal {I}g^\mathrm {ss}_{K^p}$ and ![]() $(\pi _{\mathrm {HT},K^p}|_{\mathcal {Y}_{K^p}^\mathrm {ss}})^{-1}(x)$ on perfectoid spaces. Because both are perfectoid spaces, and a perfectoid space is determined by its functor of points on perfectoid spaces, we conclude that
$(\pi _{\mathrm {HT},K^p}|_{\mathcal {Y}_{K^p}^\mathrm {ss}})^{-1}(x)$ on perfectoid spaces. Because both are perfectoid spaces, and a perfectoid space is determined by its functor of points on perfectoid spaces, we conclude that ![]() $\mathrm {unif}_{x_\infty }$ is an isomorphism onto this space.
$\mathrm {unif}_{x_\infty }$ is an isomorphism onto this space.
It remains to show that ![]() $\pi _{\mathrm {HT},K^p}^{-1}(x) \subset \mathcal {Y}_{K^p}^\mathrm {ss}$. Here the point is just that the loci of ordinary and multiplicative reduction map to
$\pi _{\mathrm {HT},K^p}^{-1}(x) \subset \mathcal {Y}_{K^p}^\mathrm {ss}$. Here the point is just that the loci of ordinary and multiplicative reduction map to ![]() $\mathbb {P}^1(\mathbb {Q}_p)$, but let us make this completely precise: suppose given a geometric point
$\mathbb {P}^1(\mathbb {Q}_p)$, but let us make this completely precise: suppose given a geometric point
and write ![]() $t$ for the corresponding point
$t$ for the corresponding point
By [Reference ScholzeSch15, Lemma 3.3.19], because ![]() $x \not \in \mathbb {P}^1(\mathbb {Q}_p)$, there is a rational number
$x \not \in \mathbb {P}^1(\mathbb {Q}_p)$, there is a rational number ![]() $1\geq \epsilon >0$ such that the Hasse invariant vanishes on
$1\geq \epsilon >0$ such that the Hasse invariant vanishes on ![]() $t_{C^+/p^\epsilon }$, which thus factors through the supersingular locus. However, this implies, in particular, that
$t_{C^+/p^\epsilon }$, which thus factors through the supersingular locus. However, this implies, in particular, that ![]() $E$ has supersingular reduction over
$E$ has supersingular reduction over ![]() $C^+/\mathfrak {m}_{C^+}$, so we conclude.
$C^+/\mathfrak {m}_{C^+}$, so we conclude.
5.6 Evaluation of modular forms
Any choice of basis for the fiber of ![]() $\mathcal {O}(1)$ at
$\mathcal {O}(1)$ at ![]() $x \in \mathbb {P}^1(\mathbb {C}_p)$ induces a
$x \in \mathbb {P}^1(\mathbb {C}_p)$ induces a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant trivialization of
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant trivialization of ![]() $\omega |_{\pi _{\mathrm {HT}}^{-1}(x)}$. In particular, if we take as basis the section
$\omega |_{\pi _{\mathrm {HT}}^{-1}(x)}$. In particular, if we take as basis the section ![]() $V|_x$ (recall
$V|_x$ (recall ![]() $U$ and
$U$ and ![]() $V$ are the standard basis for
$V$ are the standard basis for ![]() $O(1)$), we obtain a map from classical modular forms
$O(1)$), we obtain a map from classical modular forms
by first pulling back to ![]() $\mathcal {X}_{K^p}$, then restricting to
$\mathcal {X}_{K^p}$, then restricting to ![]() $\pi _{\mathrm {HT}}^{-1}(x)$ and dividing by
$\pi _{\mathrm {HT}}^{-1}(x)$ and dividing by ![]() $V^k$.
$V^k$.
Remark 5.6.1 Choosing ![]() $G$ to have endomorphisms by
$G$ to have endomorphisms by ![]() $\breve {\mathbb {Z}}_{p^2}$ and scaling the trivialization
$\breve {\mathbb {Z}}_{p^2}$ and scaling the trivialization ![]() $V|_x$ by a
$V|_x$ by a ![]() $p$-adic period of
$p$-adic period of ![]() $G$, one can obtain an evaluation map that, on
$G$, one can obtain an evaluation map that, on ![]() $H^0(\mathfrak {X}_{\breve {\mathbb {Z}}_p, \omega ^k}) \subset M_{k,\mathbb {C}_p}^{K^p}$, reduces modulo
$H^0(\mathfrak {X}_{\breve {\mathbb {Z}}_p, \omega ^k}) \subset M_{k,\mathbb {C}_p}^{K^p}$, reduces modulo ![]() $p$ to Serre's evaluation map described in § 4.
$p$ to Serre's evaluation map described in § 4.
Theorem 5.6.2 For ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ a sufficiently small compact open, the map
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ a sufficiently small compact open, the map ![]() $\mathrm {eval}_{x_\infty }^{K^p}$ is injective and has dense image. Moreover, as
$\mathrm {eval}_{x_\infty }^{K^p}$ is injective and has dense image. Moreover, as ![]() $K^p$ varies they are compatible and induce an injective
$K^p$ varies they are compatible and induce an injective ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant map
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant map
Proof. The compatibility and equivariance as ![]() $K^p$ varies is clear from construction.
$K^p$ varies is clear from construction.
We now show injectivity: because ![]() $z \in \mathbb {Z}_p^\times \subset T_x$ acts as multiplication by
$z \in \mathbb {Z}_p^\times \subset T_x$ acts as multiplication by ![]() $z^{-k}$ on our fixed trivialization
$z^{-k}$ on our fixed trivialization ![]() $V|_x$, we find that for any compact open
$V|_x$, we find that for any compact open ![]() $K_p \subset \mathrm {GL}_2(\mathbb {Q}_p)$, the image of
$K_p \subset \mathrm {GL}_2(\mathbb {Q}_p)$, the image of ![]() $M^{K_pK^p}_{k, \mathbb {C}_p}$ in
$M^{K_pK^p}_{k, \mathbb {C}_p}$ in ![]() $H^0(\pi _\mathrm {HT}^{-1}(x), \mathcal {O})$ transforms under
$H^0(\pi _\mathrm {HT}^{-1}(x), \mathcal {O})$ transforms under ![]() $z^{k}$ for the action of
$z^{k}$ for the action of ![]() $z \in K_p \cap \mathbb {Z}_p^\times$. Thus, by the equivariance of the
$z \in K_p \cap \mathbb {Z}_p^\times$. Thus, by the equivariance of the ![]() $T_x$ action in Theorem 5.5.1, the image of
$T_x$ action in Theorem 5.5.1, the image of ![]() $M^{K^p}_{k, \mathbb {C}_p}$ lands in the subspace
$M^{K^p}_{k, \mathbb {C}_p}$ lands in the subspace ![]() $\mathcal {A}^{K^p}_{\mathbb {C}_p}[k]$ of vectors on which the action of the central
$\mathcal {A}^{K^p}_{\mathbb {C}_p}[k]$ of vectors on which the action of the central ![]() $\mathbb {Z}_p^\times \leq D_p^\times$ is differentiable with derivative
$\mathbb {Z}_p^\times \leq D_p^\times$ is differentiable with derivative ![]() $k$. In particular, there can be no cancellation between the different degrees
$k$. In particular, there can be no cancellation between the different degrees ![]() $k$.
$k$.
To show the map is injective on each ![]() $M_{k,\mathbb {C}_p}$, we first observe that for
$M_{k,\mathbb {C}_p}$, we first observe that for ![]() $K=K_pK^p$ a compact open subgroup of
$K=K_pK^p$ a compact open subgroup of ![]() $\mathrm {GL}_2(\mathbb {A}_f)$, the image of
$\mathrm {GL}_2(\mathbb {A}_f)$, the image of ![]() $\pi _{\mathrm {HT}}^{-1}(x)$ in
$\pi _{\mathrm {HT}}^{-1}(x)$ in ![]() $X_{K, \mathbb {C}_p}^\mathrm {ad}(\mathbb {C}_p)=X_{K, \mathbb {C}_p}(\mathbb {C}_p)$ intersects every connected component of
$X_{K, \mathbb {C}_p}^\mathrm {ad}(\mathbb {C}_p)=X_{K, \mathbb {C}_p}(\mathbb {C}_p)$ intersects every connected component of ![]() $X_{K,\mathbb {C}_p}$ in an infinite set; indeed, the map factors as an injection from
$X_{K,\mathbb {C}_p}$ in an infinite set; indeed, the map factors as an injection from ![]() $D^\times (\mathbb {Q})\backslash D^\times (\mathbb {A}_f) / (K_p \cap T_x) \cdot K^p$, and the connected component of the image in
$D^\times (\mathbb {Q})\backslash D^\times (\mathbb {A}_f) / (K_p \cap T_x) \cdot K^p$, and the connected component of the image in ![]() $X_{K,\mathbb {C}_p}$ is recorded by the map
$X_{K,\mathbb {C}_p}$ is recorded by the map
with values in ![]() $\mathbb {Z}_p^\times$ modulo the image of
$\mathbb {Z}_p^\times$ modulo the image of ![]() $K$.
$K$.
If ![]() $s$ is a non-zero section of a line bundle on
$s$ is a non-zero section of a line bundle on ![]() $X_{K,\mathbb {C}_p}$, then there is at least one connected component where it has only finitely many zeros. Thus, any section of
$X_{K,\mathbb {C}_p}$, then there is at least one connected component where it has only finitely many zeros. Thus, any section of ![]() $\omega ^k$ over
$\omega ^k$ over ![]() $X_{K}$ which vanishes upon restriction to
$X_{K}$ which vanishes upon restriction to ![]() $\pi _{\mathrm {HT},K^p}^{-1}(x)$ is identically zero, and we conclude the map is injective.
$\pi _{\mathrm {HT},K^p}^{-1}(x)$ is identically zero, and we conclude the map is injective.
We now show the map has dense image. By assumption, ![]() $x$ is contained in
$x$ is contained in
and [Reference ScholzeSch15, Theorem 3.3.18(i)] gives that ![]() $\pi _{\mathrm {HT}}^{-1}(B_1)$ is affinoid perfectoid. By [Reference Bhatt and ScholzeBS19, Remark 7.5] (Zariski closed implies strongly Zariski closed; cf. also [Reference ScholzeSch15, Definition II.2.6]), we find that the map
$\pi _{\mathrm {HT}}^{-1}(B_1)$ is affinoid perfectoid. By [Reference Bhatt and ScholzeBS19, Remark 7.5] (Zariski closed implies strongly Zariski closed; cf. also [Reference ScholzeSch15, Definition II.2.6]), we find that the map
is almost surjective; in particular, the image contains ![]() $p \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p}$.
$p \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p}$.
Thus, given ![]() ${f \in p \cdot \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p}}$, we can lift it to
${f \in p \cdot \mathcal {A}_{\mathcal {O}_{\mathbb {C}_p}}^{K^p}}$, we can lift it to ![]() $\tilde {f} \in H^0(\pi _{\mathrm {HT},K^p}^{-1}(B_1), \mathcal {O}^+)$. By Lemma 5.6.4 we find that for any
$\tilde {f} \in H^0(\pi _{\mathrm {HT},K^p}^{-1}(B_1), \mathcal {O}^+)$. By Lemma 5.6.4 we find that for any ![]() $n > 0$ that there is a
$n > 0$ that there is a ![]() $k$ large enough,
$k$ large enough, ![]() $K_p$ small enough, and an element of
$K_p$ small enough, and an element of ![]() $\alpha \in M_{k,\mathbb {C}_p}^{K_pK^p}$ such that
$\alpha \in M_{k,\mathbb {C}_p}^{K_pK^p}$ such that
In particular, ![]() $\mathrm {eval}_{x_\infty }^{K^p}(\alpha ) \equiv f \mod p^n$. Thus, the image of
$\mathrm {eval}_{x_\infty }^{K^p}(\alpha ) \equiv f \mod p^n$. Thus, the image of ![]() $\mathrm {eval}_{x_\infty }^{K^p}$ contains a dense subset of the open ball
$\mathrm {eval}_{x_\infty }^{K^p}$ contains a dense subset of the open ball ![]() $p\mathcal {A}^{K^p}_{\mathcal {O}_{\mathbb {C}_p}}$, so is dense in
$p\mathcal {A}^{K^p}_{\mathcal {O}_{\mathbb {C}_p}}$, so is dense in ![]() $\mathcal {A}^{K^p}_{\mathbb {C}_p}$.
$\mathcal {A}^{K^p}_{\mathbb {C}_p}$.
Corollary 5.6.3 If ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ is any compact open subgroup, then
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})$ is any compact open subgroup, then ![]() $\mathrm {eval}_{x_\infty }$ restricts to a Hecke-equivariant injection with dense image
$\mathrm {eval}_{x_\infty }$ restricts to a Hecke-equivariant injection with dense image
Proof. This statement is immediate from Theorem 5.6.2 except for the density when ![]() $K^p$ is not sufficiently small. To see this density, we pass to a sufficiently small compact open normal subgroup
$K^p$ is not sufficiently small. To see this density, we pass to a sufficiently small compact open normal subgroup ![]() ${K^p}' \trianglelefteq K^p$, then average approximations by
${K^p}' \trianglelefteq K^p$, then average approximations by ![]() ${K^p}'$-invariants over
${K^p}'$-invariants over ![]() $K^p/{K^p}'$ to obtain approximations by
$K^p/{K^p}'$ to obtain approximations by ![]() $K^p$ invariants.
$K^p$ invariants.
The following lemma extracts part of the fake Hasse invariant argument given in [Reference ScholzeSch15, Proof of Theorem 4.3.1, pp. 1028–1031] in the simplest possible case. We make no new contribution, however, as the specific statement we need is significantly simpler than the setup in [Reference ScholzeSch15], we reproduce the proof here in the hopes that it will be helpful for the reader.
Lemma 5.6.4 If ![]() $g \in H^0(\pi _{\mathrm {HT}, K^p}^{-1}(B_1), \mathcal {O}^+)$ and
$g \in H^0(\pi _{\mathrm {HT}, K^p}^{-1}(B_1), \mathcal {O}^+)$ and ![]() $n>0$, then there is a compact open subgroup
$n>0$, then there is a compact open subgroup ![]() $K_p \subset \mathrm {GL}_2(\mathbb {Z}_p)$, a
$K_p \subset \mathrm {GL}_2(\mathbb {Z}_p)$, a ![]() $k>0$, and an
$k>0$, and an ![]() $\alpha \in H^0(X_{K_pK^p}, \omega ^k)$ such that
$\alpha \in H^0(X_{K_pK^p}, \omega ^k)$ such that ![]() $\alpha /V^k \in H^0(\pi _{\mathrm {HT}, K^p}^{-1}(B_1), \mathcal {O}^+)$ and
$\alpha /V^k \in H^0(\pi _{\mathrm {HT}, K^p}^{-1}(B_1), \mathcal {O}^+)$ and ![]() $\alpha /V^k \equiv g \mod p^n$.
$\alpha /V^k \equiv g \mod p^n$.
Proof. We use density of sections to approximate ![]() $g$,
$g$, ![]() $U$, and
$U$, and ![]() $V$ at finite level, then make an argument using formal models and ampleness of
$V$ at finite level, then make an argument using formal models and ampleness of ![]() $\omega$ to extend the approximation of
$\omega$ to extend the approximation of ![]() $g$ to a global section of a power of
$g$ to a global section of a power of ![]() $\omega$ after multiplying by a large enough power of the approximation of
$\omega$ after multiplying by a large enough power of the approximation of ![]() $V$.
$V$.
To better match the notation of [Reference ScholzeSch15], we write
In particular, ![]() $\mathcal {U}_2=\pi _{\mathrm {HT},K^p}^{-1}(B_1)$ in the previous notation.
$\mathcal {U}_2=\pi _{\mathrm {HT},K^p}^{-1}(B_1)$ in the previous notation.
By [Reference ScholzeSch15, Theorem 3.3.18(i)], both ![]() $\mathcal {U}_1$ and
$\mathcal {U}_1$ and ![]() $\mathcal {U}_2$ are affinoid perfectoid and come from finite-level affinoids
$\mathcal {U}_2$ are affinoid perfectoid and come from finite-level affinoids ![]() $\mathcal {U}_{1,K_p}$ and
$\mathcal {U}_{1,K_p}$ and ![]() $\mathcal {U}_{2,K_p}$ in
$\mathcal {U}_{2,K_p}$ in ![]() $X_{K_pK^p,\mathbb {C}_p}^\mathrm {ad}$ for small enough compact open
$X_{K_pK^p,\mathbb {C}_p}^\mathrm {ad}$ for small enough compact open ![]() $K_p \leq \mathrm {GL}_2(\mathbb {Z}_p)$. Moreover, they satisfy
$K_p \leq \mathrm {GL}_2(\mathbb {Z}_p)$. Moreover, they satisfy
The same density statement holds for sections of ![]() $\omega$, thus we can choose, for
$\omega$, thus we can choose, for ![]() $K_p$ small enough, sections
$K_p$ small enough, sections
such that ![]() $s_{i}^{(i)}$ is non-vanishing and the sections
$s_{i}^{(i)}$ is non-vanishing and the sections ![]() $s_{j}^{(i)}$ satisfy
$s_{j}^{(i)}$ satisfy
 \[ \biggl|\frac{s_j - s_{j}^{(i)}}{s_{i}^{(i)}}\biggr| \leq |p^n| \quad \text{on } \mathcal{U}_i. \]
\[ \biggl|\frac{s_j - s_{j}^{(i)}}{s_{i}^{(i)}}\biggr| \leq |p^n| \quad \text{on } \mathcal{U}_i. \]
By possibly taking ![]() $K_p$ smaller still, we may also assume that there is a function
$K_p$ smaller still, we may also assume that there is a function
where we recall that ![]() $g$ is the function we are ultimately trying to approximate.
$g$ is the function we are ultimately trying to approximate.
Now, [Reference ScholzeSch15, Lemma 2.1.1] gives:
(i) a formal model
 $\frak {X}^\mathrm {strange}$ over
$\frak {X}^\mathrm {strange}$ over  $\mathrm {Spf} \mathcal {O}_{\mathbb {C}_p}$ for
$\mathrm {Spf} \mathcal {O}_{\mathbb {C}_p}$ for  $X_{K_pK^p, \mathbb {C}_p}^\mathrm {ad}$;
$X_{K_pK^p, \mathbb {C}_p}^\mathrm {ad}$;(ii) a cover of
 $\frak {X}^\mathrm {strange}$ by affines
$\frak {X}^\mathrm {strange}$ by affines  $\frak {U}_\bullet =\mathrm {Spf} \mathcal {O}^+(\mathcal {U}_{\bullet, K_p})$,
$\frak {U}_\bullet =\mathrm {Spf} \mathcal {O}^+(\mathcal {U}_{\bullet, K_p})$,  $\bullet =1,2$; and
$\bullet =1,2$; and(iii) an ample line bundle
 $\frak {w}/\frak {X}^\mathrm {strange}$ modeling
$\frak {w}/\frak {X}^\mathrm {strange}$ modeling  $\omega /X_{K_pK^p, \mathbb {C}_p}^\mathrm {ad}$ and such that
$\omega /X_{K_pK^p, \mathbb {C}_p}^\mathrm {ad}$ and such that
 \[ \frak{w}(\frak{U}_i) = \mathcal{O}^+(\mathcal{U}_{\bullet, K_p}) \cdot s_{i}^{(i)}. \]
\[ \frak{w}(\frak{U}_i) = \mathcal{O}^+(\mathcal{U}_{\bullet, K_p}) \cdot s_{i}^{(i)}. \]
In particular, the sections ![]() $s_{i}^{(j)}$ glue mod
$s_{i}^{(j)}$ glue mod ![]() $p^n$ to a section
$p^n$ to a section ![]() $\overline {s_i}$ of
$\overline {s_i}$ of ![]() $\frak {w}/p^n$, and
$\frak {w}/p^n$, and ![]() $\frak {U}_i$ is exactly the locus where
$\frak {U}_i$ is exactly the locus where ![]() $\overline {s_i}$ is invertible. We deduce by ampleness that for large enough
$\overline {s_i}$ is invertible. We deduce by ampleness that for large enough ![]() $k$:
$k$:
(i)
 $H^1(\frak {X}^\mathrm {strange}, \frak {w}^k/p^n)=0$; and
$H^1(\frak {X}^\mathrm {strange}, \frak {w}^k/p^n)=0$; and(ii)
 $\bar {h} \cdot \overline {s_{2}}^k$ extends to a global section of
$\bar {h} \cdot \overline {s_{2}}^k$ extends to a global section of  $H^0(\frak {X}^\mathrm {strange}, \frak {w}^k/p^n)$.
$H^0(\frak {X}^\mathrm {strange}, \frak {w}^k/p^n)$.
The first item implies that ![]() $H^0(\frak {X}^\mathrm {strange}, \frak {w}^k) \rightarrow H^0(\frak {X}^\mathrm {strange}, \frak {w}^k/p^n)$ is surjective: consider the exact sequence of cohomology coming from
$H^0(\frak {X}^\mathrm {strange}, \frak {w}^k) \rightarrow H^0(\frak {X}^\mathrm {strange}, \frak {w}^k/p^n)$ is surjective: consider the exact sequence of cohomology coming from
to lift to ![]() $H^0(\frak {X}^\mathrm {strange}, \frak {w}^k/p^{2n})$ and obtain
$H^0(\frak {X}^\mathrm {strange}, \frak {w}^k/p^{2n})$ and obtain ![]() $H^1(\frak {X}, \frak {w}^{k}/p^{2n})=0$, then repeat and pass to the limit. Thus, we can lift
$H^1(\frak {X}, \frak {w}^{k}/p^{2n})=0$, then repeat and pass to the limit. Thus, we can lift ![]() $\bar {h}\cdot \overline {s_2}^k$ to
$\bar {h}\cdot \overline {s_2}^k$ to
and this is the desired section.
5.7 Comparison of completed Hecke algebras
We now prove Theorem A: let ![]() $K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})= D^\times (\mathbb {A}_f^{(p)})$ be compact open, let
$K^p \leq \mathrm {GL}_2(\mathbb {A}_f^{(p)})= D^\times (\mathbb {A}_f^{(p)})$ be compact open, let
and let ![]() $\mathbb {T}' \subset \mathbb {T}^\mathrm {abs}_{K^p}$ be a subring. Corollary 5.6.3 and Lemma 2.4.9 give
$\mathbb {T}' \subset \mathbb {T}^\mathrm {abs}_{K^p}$ be a subring. Corollary 5.6.3 and Lemma 2.4.9 give
Invoking Lemma 2.4.8, we find that we can replace ![]() $\mathbb {C}_p$ with
$\mathbb {C}_p$ with ![]() $\mathbb {Q}_p$ on both sides.
$\mathbb {Q}_p$ on both sides.
On the other hand, combining Lemmas 3.4.7 and 2.4.9, we find that
Thus, to deduce Theorem A, it remains only to show
This is basically a well-known result of Hida [Reference HidaHid86, Equation (1.7)], however, we are not aware of a full proof in the literature. Thus, we include a proof here, arguing with completed cohomology as explained by Emerton [Reference EmertonEme11, Remarks 5.4.2 and 5.4.3]. This argument forms part of the proof of the following result, which encodes all of the isomorphisms indicated previously and in the introduction.
Theorem 5.7.1 The identity map ![]() $\mathbb {T}'\rightarrow \mathbb {T}'$ extends to a topological isomorphism of the completed Hecke algebras
$\mathbb {T}'\rightarrow \mathbb {T}'$ extends to a topological isomorphism of the completed Hecke algebras ![]() $\mathbb {T}'$ acting on the following:
$\mathbb {T}'$ acting on the following:
(i)
 $\big ( M_{k,\mathbb {Q}_p}^{K_p K^p} \big )_{k, K_p}$ for
$\big ( M_{k,\mathbb {Q}_p}^{K_p K^p} \big )_{k, K_p}$ for  $k$ varying over all non-negative integers and
$k$ varying over all non-negative integers and  $K_p$ varying over all compact open subgroups of
$K_p$ varying over all compact open subgroups of  $\mathrm {GL}_2(\mathbb {Q}_p)$;
$\mathrm {GL}_2(\mathbb {Q}_p)$;(ii)
 $\big ( M_{k,\mathbb {Q}_p}^{\mathrm {GL}_2(\mathbb {Z}_p)K^p} \big )_k$ for
$\big ( M_{k,\mathbb {Q}_p}^{\mathrm {GL}_2(\mathbb {Z}_p)K^p} \big )_k$ for  $k$ varying over all non-negative integers;
$k$ varying over all non-negative integers;(iii)
 $\big ( M_{2,\mathbb {Q}_p}^{K_pK^p} \big )$, for
$\big ( M_{2,\mathbb {Q}_p}^{K_pK^p} \big )$, for  $K_p$ varying over all compact open subgroups of
$K_p$ varying over all compact open subgroups of  $\mathrm {GL}_2(\mathbb {Q}_p)$;
$\mathrm {GL}_2(\mathbb {Q}_p)$;(iv) the completed cohomology of the modular curve at level
 $K^p$ (cf. [Reference EmertonEme06]),
$K^p$ (cf. [Reference EmertonEme06]),
 \[ \hat{H}^1_{K^p} = \tilde{H}^1_{K^p}:= \biggl(\varprojlim_m \varinjlim_{K_p} H^i(Y_{K_p K^p}(\mathbb{C}), \mathbb{Z}/p^m)\biggr)[1/p]; \]
\[ \hat{H}^1_{K^p} = \tilde{H}^1_{K^p}:= \biggl(\varprojlim_m \varinjlim_{K_p} H^i(Y_{K_p K^p}(\mathbb{C}), \mathbb{Z}/p^m)\biggr)[1/p]; \](v) the space of quaternionic automorphic forms
 $\mathcal {A}_{\mathbb {Q}_p}^{K^p}$; and
$\mathcal {A}_{\mathbb {Q}_p}^{K^p}$; and(vi) the space of
 $p$-adic modular forms
$p$-adic modular forms  $\mathbb {V}^{K^p}_{\mathbb {Q}_p}$.
$\mathbb {V}^{K^p}_{\mathbb {Q}_p}$.
Proof. We have already established the identities of completed Hecke algebras (i) ![]() ${=}$ (v) and (ii)
${=}$ (v) and (ii) ![]() ${=}$ (vi). We conclude by identifying (iv)
${=}$ (vi). We conclude by identifying (iv) ![]() ${=}$ (i), (iv)
${=}$ (i), (iv) ![]() ${=}$ (ii), and (iv)
${=}$ (ii), and (iv) ![]() ${=}$ (iii).
${=}$ (iii).
For ![]() $K=K_pK^p$ sufficiently small, let
$K=K_pK^p$ sufficiently small, let ![]() $\mathrm {pr}:E_K \rightarrow Y_K(\mathbb {C})$ be the universal elliptic curve over
$\mathrm {pr}:E_K \rightarrow Y_K(\mathbb {C})$ be the universal elliptic curve over ![]() $Y_K(\mathbb {C})$ and let
$Y_K(\mathbb {C})$ and let ![]() $\underline {\mathrm {Sym}^k}$ be the
$\underline {\mathrm {Sym}^k}$ be the ![]() $k$th symmetric power of
$k$th symmetric power of ![]() $R^1 \mathrm {pr}_* \mathbb {Q}$, a
$R^1 \mathrm {pr}_* \mathbb {Q}$, a ![]() $\mathrm {GL}_2(\mathbb {A}_f)$-equivariant local system on the tower
$\mathrm {GL}_2(\mathbb {A}_f)$-equivariant local system on the tower ![]() $(Y_K(\mathbb {C}))_K$. Fixing an isomorphism
$(Y_K(\mathbb {C}))_K$. Fixing an isomorphism ![]() $\overline {\mathbb {Q}}_p \cong \mathbb {C}$, we obtain for each
$\overline {\mathbb {Q}}_p \cong \mathbb {C}$, we obtain for each ![]() $k\geq 2$ and
$k\geq 2$ and ![]() $K_p$ such that
$K_p$ such that ![]() $K=K_pK^p$ is sufficiently small a
$K=K_pK^p$ is sufficiently small a ![]() $\mathbb {T}^\mathrm {abs}$-equivariant injection
$\mathbb {T}^\mathrm {abs}$-equivariant injection
given by composing the maps
where the second arrow comes from the classical Eichler–Shimura isomorphism and the last arrow comes from composition of the isomorphism ![]() $\overline {\mathbb {Q}_p}\cong \mathbb {C}$ with
$\overline {\mathbb {Q}_p}\cong \mathbb {C}$ with ![]() $\overline {\mathbb {Q}_p} \hookrightarrow \mathbb {C}_p$. It follows from the Eichler–Shimura isomorphism that (5.7.1) induces an isomorphism on the image of
$\overline {\mathbb {Q}_p} \hookrightarrow \mathbb {C}_p$. It follows from the Eichler–Shimura isomorphism that (5.7.1) induces an isomorphism on the image of ![]() $\mathbb {T}'$ in the respective endomorphism rings. If we denote by
$\mathbb {T}'$ in the respective endomorphism rings. If we denote by ![]() $\mathbb {T}'^\wedge _\mathrm {aux}$ the completed Hecke algebra for
$\mathbb {T}'^\wedge _\mathrm {aux}$ the completed Hecke algebra for ![]() $\mathbb {T}'$ acting on the family
$\mathbb {T}'$ acting on the family
then we deduce that ![]() $\mathbb {T}'^\wedge _\mathrm {aux}$ is isomorphic to the completed Hecke algebra for part(i). By Lemma 2.4.8,
$\mathbb {T}'^\wedge _\mathrm {aux}$ is isomorphic to the completed Hecke algebra for part(i). By Lemma 2.4.8, ![]() $\mathbb {T}'^\wedge _\mathrm {aux}$ is also the completed Hecke algebra for
$\mathbb {T}'^\wedge _\mathrm {aux}$ is also the completed Hecke algebra for ![]() $\mathbb {T}'$ acting on
$\mathbb {T}'$ acting on
As in [Reference EmertonEme06, Reference EmertonEme11],Footnote 8
Thus, if we fix for each ![]() $k \geq 2$ a non-zero vector in
$k \geq 2$ a non-zero vector in ![]() $(\mathrm {Sym}^{k-2} \mathbb {Q}_p^2)$, then pairing with these vectors gives Hecke–equivariant injections
$(\mathrm {Sym}^{k-2} \mathbb {Q}_p^2)$, then pairing with these vectors gives Hecke–equivariant injections
whose joint image is dense (indeed, it is already so if we fix ![]() $k=2$), and thus we deduce from Lemma 2.4.9 that
$k=2$), and thus we deduce from Lemma 2.4.9 that ![]() $\mathbb {T}'^\wedge _\mathrm {aux}$ is isomorphic to the completed Hecke algebra for part (iv), establishing (i)
$\mathbb {T}'^\wedge _\mathrm {aux}$ is isomorphic to the completed Hecke algebra for part (iv), establishing (i) ![]() ${=}$ (iv). Then, running the same argument using only weight two modular forms, we find (iii)
${=}$ (iv). Then, running the same argument using only weight two modular forms, we find (iii) ![]() ${=}$ (iv).
${=}$ (iv).
Arguing similarly and using the density of ![]() $\mathrm {GL}_2(\mathbb {Z}_p)$-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$-algebraic vectors in ![]() $\hat {H}^1_{K^p}$ as established in [Reference EmertonEme11, Remark 5.4.2] (specifically of those which transform locally as
$\hat {H}^1_{K^p}$ as established in [Reference EmertonEme11, Remark 5.4.2] (specifically of those which transform locally as ![]() $\mathrm {Sym}^{k-2}\mathbb {Q}_p^2$ for some
$\mathrm {Sym}^{k-2}\mathbb {Q}_p^2$ for some ![]() $k$; we do not need to also allow for arbitrary twists by a determinant), we obtain (ii)
$k$; we do not need to also allow for arbitrary twists by a determinant), we obtain (ii) ![]() ${=}$ (iv).
${=}$ (iv).
Remark 5.7.2 From our perspective, instead of ![]() $p$-adic modular forms it is perhaps more natural to consider the larger space of
$p$-adic modular forms it is perhaps more natural to consider the larger space of ![]() $p$-adic automorphic forms given by functions on the Caraiani–Scholze Igusa formal scheme over the ordinary locus, which parameterizes isomorphisms
$p$-adic automorphic forms given by functions on the Caraiani–Scholze Igusa formal scheme over the ordinary locus, which parameterizes isomorphisms
Indeed, an argument nearly identical to that given in this section for the supersingular Igusa variety but starting with the point
shows that the completed Hecke algebra of this space of ![]() $p$-adic automorphic forms is the same as that appearing in Theorem 5.7.1.
$p$-adic automorphic forms is the same as that appearing in Theorem 5.7.1.
Moreover, this space of ![]() $p$-adic automorphic forms admits an action of a very large unipotent group at
$p$-adic automorphic forms admits an action of a very large unipotent group at ![]() $p$, and using this action one can produce a
$p$, and using this action one can produce a ![]() $\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant projection operator (a type of Kirillov functor) to Katz
$\mathrm {GL}_2(\mathbb {A}_f^{(p)})$-equivariant projection operator (a type of Kirillov functor) to Katz ![]() $p$-adic modular forms which can, in turn, be used to deduce an isomorphism of completed Hecke algebras; this will be explained in future work (cf. also [Reference HoweHow20]). In this way, one will be able to obtain a proof of Theorem A that does not pass through singular/étale cohomology to show that level and weight families of classical modular forms give rise to the same completed Hecke algebra.
$p$-adic modular forms which can, in turn, be used to deduce an isomorphism of completed Hecke algebras; this will be explained in future work (cf. also [Reference HoweHow20]). In this way, one will be able to obtain a proof of Theorem A that does not pass through singular/étale cohomology to show that level and weight families of classical modular forms give rise to the same completed Hecke algebra.
Acknowledgements
This article grew out of the author's PhD thesis [Reference HoweHow17], and he thanks Matt Emerton, his thesis advisor, for his profound influence. The author also thanks Rebecca Bellovin, Ana Caraiani, Andrea Dotto, Tianqi Fan, David Hansen, Christian Johannson, Kiran Kedlaya, Erick Knight, Daniel Le, Keerthi Madapusi-Pera, Jay Pottharst, Peter Scholze, Joel Specter, Matthias Strauch, Jan Vonk, Jared Weinstein, and Yiwen Zhou for helpful conversations about this work. The author also thanks two anonymous referees for their helpful comments and suggestions.