Dust Acoustic Solitons in Saturn’s Dust-Filled Magnetosphere

Abstract

The possibility is considered of propagation of localized wave structures, such as dust acoustic solitons, in the plasma of the dust-filled Saturn’s magnetosphere, which contains electrons of two sorts (hot and cold) subject to kappa distribution, ions, and charged dust grains. The ranges of possible velocities and amplitudes of the solitons are determined. Soliton solutions for different sizes and concentrations of dust grains in the dust-filled Saturn’s magnetosphere are found.

1 INTRODUCTION

It is difficult to imagine a plasma-filled region of the Solar system that would be free of finely dispersed dust grains [1]. Nano- and microsized dust grains are found in interplanetary space, in ionospheric and magnetospheric plasma of the planets of the Solar system, in planetary rings, in the vicinity of space bodies devoid of their own atmosphere, and so on. An important object from the viewpoint of dusty plasma studies is Saturn’s magnetosphere [2, 3]. Its plasma parameters were measured as early as in the 1980s by the Voyager 1 and 2 space missions [4]. Also based on the data collected by the Voyager 1 spacecraft [5], it was shown that waves exist in the magnetospheric plasma of Saturn. Theoretical studies of ion acoustic waves in Saturn’s magnetosphere were carried out in [6]. The dusty plasma in the vicinity of Saturn’s satellite Enceladus was discovered during the Cassini mission [2, 3].

The plasma in Saturn’s magnetosphere has a number of specificities compared with other space systems that are now actively studied (studies of the dusty plasma on Moon and Mars see, e.g., in [7, 8]). For example, measurements of the parameters of electrons in Saturn’s magnetosphere obtained by the Voyager [4, 5] and Cassini [9] missions showed the existence of two types (hot and cold) of electrons. It turned out [9] that the velocities of these electron populations are subject to the so-called kappa distribution with independent low values of κ.

All of this indicates the importance of studying the nonlinear wave structures in the dusty plasma under conditions characteristic of Saturn’s magnetosphere, for which, dust acoustic waves are typical. An important type of nonlinear structures observed in space [10, 11] are solitons. In this work, we consider nonlinear sound structures in the dust-filled Saturn’s magnetosphere characteristic of dusty plasma, namely, dust acoustic solitons [12]. We take into account the two types of electrons (hot and cold) that coexist in Saturn’s magnetosphere and are subject to two different κ distributions. The study is carried out for arbitrary (not small) soliton amplitudes, which appears important for interpreting future space observations.

2 BASIC EQUATIONS

To describe dust acoustic solitons (see, e.g., [13–15]), the following set of equations can be used, which includes the continuity equation, the (Euler) motion equation for the dust grains, and Poisson’s equation for the self-consistent electrostatic potential $\varphi$ in the dusty plasma of Saturn’s magnetosphere:

$$\begin{gathered} \frac{{\partial {{n}_{{\text{d}}}}}}{{\partial t}} + \frac{{\partial ({{n}_{{\text{d}}}}{{v}_{{\text{d}}}})}}{{\partial x}} = 0, \\ \frac{{\partial {{v}_{{\text{d}}}}}}{{\partial t}} + {{v}_{{\text{d}}}}\frac{{\partial {{v}_{{\text{d}}}}}}{{\partial x}} = - \frac{{{{Z}_{{\text{d}}}}e}}{{{{m}_{{\text{d}}}}}}\frac{{\partial \varphi }}{{\partial x}}, \\ \frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} = 4\pi e\left( {{{n}_{{{\text{e,c}}}}} + {{n}_{{{\text{e,h}}}}} - {{n}_{{\text{i}}}} - {{n}_{{\text{d}}}}{{Z}_{{\text{d}}}}} \right), \\ \end{gathered} $$

(1)

where the space variable x corresponds to the propagation direction of the wave perturbation, n_d is the concentration of dust grains, ${{v}_{{\text{d}}}}$ is their velocity, m_d and q_d = Z_de is the mass and charge of dust grains, $- e$ is the electron charge, n_e,c(h) is the concentration of hot (cold) electrons, and n_i is the concentration of ions.

Additionally, it is necessary to take into account the ion and electron distributions that have time to get established over the dust acoustic time scale. It was already noted that, in Saturn’s magnetosphere, the electrons have a κ velocity distribution [16]

$$\begin{gathered} {{n}_{{{\text{e,c}}}}} = {{n}_{{{\text{e,c0}}}}}{{\left( {1 - \frac{1}{{{{\kappa }_{{\text{c}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{{e\varphi }}{{{{T}_{{{\text{ec}}}}}}}} \right)}^{{ - {{\kappa }_{{\text{c}}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{n}_{{{\text{e,h}}}}} = {{n}_{{{\text{e,h}}0}}}{{\left( {1 - \frac{1}{{{{\kappa }_{{\text{h}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{{e\varphi }}{{{{T}_{{{\text{eh}}}}}}}} \right)}^{{ - {{\kappa }_{{\text{h}}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $$

(2)

where T_e,c(h) is the temperature of cold (hot) electrons in energy units, index 0 corresponds to unperturbed states, and κ_c and κ_h are the parameters of kappa distributions of the cold and hot electrons, respectively. Note that κ_c, κ_h > 3/2.

The ions are subject to Boltzmann’s distribution

$${{n}_{{\text{i}}}} = {{n}_{{{\text{i0}}}}}e{}^{{ - e\varphi /{{T}_{{\text{i}}}}}},$$

(3)

where T_i is the ion temperature in energy units.

Taking into account that dust acoustic solitons are relatively slow, and consequently, their characteristic time scale significantly exceeds the characteristic time scale of the change of the charge of dust grains (see, e.g., [17]), the dust grain charges have time to adjust to the plasma parameters and can be determined by the equation

$${{I}_{{\text{e}}}}({{Z}_{{\text{d}}}}) + {{I}_{{\text{i}}}}({{Z}_{{\text{d}}}}) = 0,$$

(4)

where the macroscopic currents of cold (hot) electrons on the surface of the dust grain are described by the expression [18]

$$\begin{gathered} {{I}_{{{\text{e,c}}\left( {\text{h}} \right)}}}\left( {{{Z}_{{\text{d}}}}} \right) \\ \, = 2\sqrt \pi {{a}^{2}}e{{n}_{{{\text{e0,c}}\left( {\text{h}} \right)}}}\frac{{\sqrt {{{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} }}{{{{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}}\left( {{{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}} - 1} \right)}}\frac{{\Gamma \left( {{{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}} + 1} \right)}}{{\Gamma \left( {{{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}} \\ \, \times \sqrt {\frac{{{{T}_{{{\text{e,c}}\left( {\text{h}} \right)}}}}}{{{{m}_{{\text{e}}}}}}} {{\left( {1 - \frac{1}{{{{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{{{{e}^{2}}{{Z}_{{\text{d}}}}}}{{a{{T}_{{{\text{e,c}}\left( {\text{h}} \right)}}}}}} \right)}^{{ - {{\kappa }_{{{\text{c}}\left( {\text{h}} \right)}}} + 1}}}, \\ \end{gathered} $$

(5)

and the microscopic ion current has the form [18]

$${{I}_{{\text{i}}}}\left( {{{Z}_{{\text{d}}}}} \right) = 4\pi {{a}^{2}}e{{n}_{{{\text{i0}}}}}\sqrt {\frac{{{{T}_{{\text{i}}}}}}{{2\pi {{m}_{{\text{i}}}}}}} \left( {1 - \frac{{{{e}^{2}}{{Z}_{{\text{d}}}}}}{{a{{T}_{{\text{i}}}}}}} \right).$$

(6)

Here, a is the dust grain size, m_e(i) is the electron (ion) mass, and Γ(κ_c(h)) is the gamma function. Note that the values Z_d in the soliton obtained from Eq. (4), generally speaking, depend on the electrostatic potential φ. However, according to the conducted calculations that take into account the changes of plasma parameters in the soliton, this dependence is not very strong. For example, even in the maximum of the soliton, where the deviation of its charge from its nonperturbed state is maximum, the charge differs less than 5% from its value at the base of the soliton, including in solitons with a high amplitude (see [17]). This fact allows one to consider the charges of dust grains in the soliton approximately constant, which will be used later.

The nonperturbed concentrations are connected by the quasi-neutrality condition

$${{n}_{{{\text{i0}}}}} + {{Z}_{{\text{d}}}}{{n}_{{{\text{d}}0}}} = {{n}_{{{\text{e0,c}}}}} + {{n}_{{{\text{e0,h}}}}}.$$

(7)

It is convenient to introduce the total concentration of nonperturbed cold and hot electrons

$${{n}_{{{\text{eo}}}}} = {{n}_{{{\text{e0,c}}}}} + {{n}_{{{\text{e0,h}}}}}$$

(8)

and the ratio α between the concentrations of hot and cold electrons ($0 \leqslant \alpha \leqslant 1$). Then we have

$${{n}_{{{\text{e0,c}}}}} = \alpha \left( {{{n}_{{{\text{i0}}}}} + {{Z}_{{\text{d}}}}{{n}_{{{\text{d0}}}}}} \right),$$

(9)

$${{n}_{{{\text{e0,h}}}}} = \left( {1 - \alpha } \right)\left( {{{n}_{{{\text{i0}}}}} + {{Z}_{{\text{d}}}}{{n}_{{{\text{d0}}}}}} \right).$$

(10)

3 SOLITON SOLUTIONS

The system of equations (1)–(7) can be solved by the standard method of Sagdeev potential [19]. To determine the localized wave solution that propagates at some constant velocity M, we can transfer to a new system of coordinates $\xi = x - Mt$ connected to the wave. In this case, all the parameters of the problem depend only on the new variable $\xi$. The Sagdeev potential in dimensionless variables ${{e\varphi } \mathord{\left/ {\vphantom {{e\varphi } {{{T}_{{\text{i}}}}}}} \right. \kern-0em} {{{T}_{{\text{i}}}}}} \to \varphi$, ${M \mathord{\left/ {\vphantom {M {{{C}_{{{\text{Sd}}}}}}}} \right. \kern-0em} {{{C}_{{{\text{Sd}}}}}}} \to M$, ${\xi \mathord{\left/ {\vphantom {\xi {{{\lambda }_{{{\text{Di}}}}}}}} \right. \kern-0em} {{{\lambda }_{{{\text{Di}}}}}}} \to \xi$, where ${{C}_{{{\text{Sd}}}}} = \sqrt {{{{{T}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{i}}}}} {{{m}_{{\text{d}}}}}}} \right. \kern-0em} {{{m}_{{\text{d}}}}}}}$ and ${{\lambda }_{{{\text{Di}}}}} = \sqrt {{{{{T}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{i}}}}} {4\pi {{n}_{{{\text{i0}}}}}{{e}^{2}}}}} \right. \kern-0em} {4\pi {{n}_{{{\text{i0}}}}}{{e}^{2}}}}}$ has the form

$$V\left( \varphi \right) = 1 - {{e}^{{ - \varphi }}} + \left( {1 - \alpha } \right)$$

$$\begin{gathered} \times \;\left( {1 + {{Z}_{{\text{d}}}}d} \right){{\tau }_{{\text{h}}}}\left[ {1 - {{{\left( {1 - \frac{1}{{{{\kappa }_{{\text{h}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{\varphi }{{{{\tau }_{{\text{h}}}}}}} \right)}}^{{ - {{\kappa }_{{\text{h}}}} + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right] \\ + \;\alpha \left( {1 + {{Z}_{{\text{d}}}}d} \right){{\tau }_{{\text{c}}}}\left[ {1 - {{{\left( {1 - \frac{1}{{{{\kappa }_{{\text{c}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{\varphi }{{{{\tau }_{{\text{c}}}}}}} \right)}}^{{ - {{\kappa }_{{\text{c}}}} + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right] \\ \end{gathered} $$

(11)

$$\, + Md\left( {M - \sqrt {{{M}^{2}} - 2{{Z}_{{\text{d}}}}\varphi } } \right),$$

where $d = {{{{n}_{{{\text{d}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{\text{d}}0}}}} {{{n}_{{{\text{i0}}}}}}}} \right. \kern-0em} {{{n}_{{{\text{i0}}}}}}}$, ${{\tau }_{{\text{c}}}} = {{{{T}_{{{\text{ec}}}}}} \mathord{\left/ {\vphantom {{{{T}_{{{\text{ec}}}}}} {{{T}_{{\text{i}}}}}}} \right. \kern-0em} {{{T}_{{\text{i}}}}}}$, ${{\tau }_{{\text{h}}}} = {{{{T}_{{{\text{eh}}}}}} \mathord{\left/ {\vphantom {{{{T}_{{{\text{eh}}}}}} {{{T}_{{\text{i}}}}}}} \right. \kern-0em} {{{T}_{{\text{i}}}}}}$.

The soliton solution is found from the relation

$$\frac{1}{2}\varphi _{\xi }^{2} + V(\varphi ) = 0,$$

(12)

where φ_ξ is the first derivative of function φ with respect to ξ.

The scope (${{M}_{{\min }}} < M < {{M}_{{\max }}}$) of localized wave solutions is determined by the conditions of their existence and has the form

$$M > {{M}_{{\min }}} = \sqrt {\frac{{Z_{{\text{d}}}^{2}d}}{{1 + \frac{{\alpha \left( {1 + {{Z}_{{\text{d}}}}d} \right)}}{{{{\tau }_{{\text{c}}}}}}\frac{{{{\kappa }_{{\text{c}}}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{{{{\kappa }_{{\text{c}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}} + \frac{{\left( {1 - \alpha } \right)\left( {1 + {{Z}_{{\text{d}}}}d} \right)}}{{{{\tau }_{{\text{h}}}}}}\frac{{{{\kappa }_{{\text{h}}}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{{{{\kappa }_{{\text{h}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} ,$$

(13)

$$\begin{gathered} 1 - {{e}^{{ - M_{{\max }}^{2}/(2{{Z}_{{\text{d}}}})}}} + \left( {1 - \alpha } \right)\left( {1 + {{Z}_{{\text{d}}}}d} \right){{\tau }_{{\text{h}}}}\left[ {1 - {{{\left( {1 - \frac{1}{{{{\kappa }_{{\text{h}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{{M_{{\max }}^{2}}}{{2{{\tau }_{{\text{h}}}}{{Z}_{{\text{d}}}}}}} \right)}}^{{ - {{\kappa }_{{\text{h}}}} + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right] \\ + \,\alpha \left( {1 + {{Z}_{{\text{d}}}}d} \right){{\tau }_{{\text{c}}}}\left[ {1 - {{{\left( {1 - \frac{1}{{{{\kappa }_{{\text{c}}}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\frac{{M_{{\max }}^{2}}}{{2{{\tau }_{{\text{c}}}}{{Z}_{{\text{d}}}}}}} \right)}}^{{ - {{\kappa }_{{\text{c}}}} + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right] + M_{{\max }}^{2}d > 0. \\ \end{gathered} $$

(14)

Below, results are given for calculations that were carried out for the following parameters of Saturn’s magnetosphere (see [4, 6, 9]): n_i0 = 10 cm^–3, T_i = 100 K, T_ec = 10 eV, T_eh = 700 eV, $\alpha = 0.5$, and κ_c = κ_h = 2.

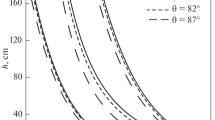
Figure 1 shows the dependences of charge numbers Z_d of the dust grains and total electron concentra-tions n_e0 on dust grain size for different concentrations of dust grains. The values Z_d and n_e0 were obtained at the given value of n_i0 based on the self-consistent solution of Eqs. (4)–(7).

Fig. 1.

Dependences of charge number Z_d of dust grains (curves 1–3) and total electron concentrations n_e0 (curves 1'–3') on dust grain size for different concentrations of dust grains: n_d0 = 10^–4 (curves 1, 1'), 10^–3 (curves 2, 2'), and 10^–2 cm^–3 (curves 3, 3').

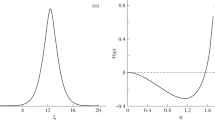
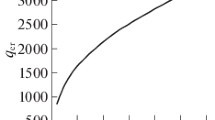
Figure 2 shows the amplitudes of dust acoustic solitons depending on dust grain size in the entire possible range of dimensionless velocities M at different dust grain concentrations. Figures 3–5 show the characteristic types of solitons (panels a) and the corresponding Sagdeev potentials (panels b and c) for the cases with different concentrations and sizes of dust grains and different values of the dimensionless velocity M. It is seen that, in the entire scope of amplitude of the dust acoustic solitons, φ₀ is negative and their amplitudes can be relatively high (of the order of T_i /e).

Fig. 2.

Amplitudes φ₀ of dust acoustic solitons depending on the dust grain size and the dimensionless soliton velocity M at n_d0 = 10^–4, 10^–3, and 10^–2 cm^–3. The thick black lines correspond to the boundaries of the allowed M regions.

Fig. 3.

(a) Dust acoustic solitons and (b, c) the corresponding Sagdeev potentials in the case n_d0 = 10^–2 cm^–3, M = 40. Soliton 1 corresponds to the dust grain size a = 2 μm. Soliton 2 corresponds to the dust grain size a = 0.2 μm.

Fig. 4.

The same as in Fig. 3 for n_d0 = 10^–3 cm^–3, M = 100.

Fig. 5.

The same as in Fig. 3 for n_d0 = 10^–4 cm^–3, M = 300 for soliton 1 and M = 60 for soliton 2.

4 CONCLUSIONS

In this work, the possibility was shown of the propagation of localized wave structures, such as dust acoustic solitons, in the dust-filled Saturn’s magnetosphere, which includes electrons of two types (hot and cold), ions, and charged dust grains. The regions of possible velocities and amplitudes of the solitons were determined. Soliton solutions were found for different sizes and concentrations of dust grains in the dust-filled plasma of Saturn’s magnetosphere. It turns out that in their entire scope, the amplitudes of electrostatic potential of dust acoustic solitons are negative. At the same time, their absolute values can be relatively high (of the order of T_i /e), which indicates that dust acoustic solitons can be observed in Saturn’s magnetosphere by future space missions.