Momentum-dependent two-loop QCD corrections to the neutral Higgs-boson masses in the MSSM

Abstract

Results are presented for the momentum-dependent two-loop contributions of $\mathcal{O}(\alpha _t\alpha _s)$ to the masses and mixing effects in the Higgs sector of the MSSM. They are obtained in the Feynman-diagrammatic approach using a mixed on-shell/$\overline{{\mathrm {DR}}}$ renormalization that can directly be matched onto the higher-order corrections included in the code FeynHiggs. The new two-loop diagrams are evaluated with the program SecDec. The combination of the new momentum-dependent two-loop contribution with the existing one- and two-loop corrections in the on-shell/$\overline{{\mathrm {DR}}}$ scheme leads to an improved prediction of the light MSSM Higgs boson mass and a correspondingly reduced theoretical uncertainty. We find that the corresponding shifts in the lightest Higgs-boson mass $M_h$ are below $1 \,\, \mathrm {GeV}$ in all scenarios considered, but they can extend up to the level of the current experimental uncertainty. The results are included in the code FeynHiggs.

1 Introduction

The ATLAS and CMS experiments at CERN have recently discovered a new boson with a mass around $125.6\,\, \mathrm {GeV}$ [1, 2]. Within the present experimental uncertainties this new boson behaves like the Higgs boson of the Standard Model (SM) [3–6]. However, the newly discovered particle can also be interpreted as the Higgs boson of extended models. The Higgs sector of the Minimal Supersymmetric Standard Model (MSSM) [7–9] with two scalar doublets accommodates five physical Higgs bosons. In lowest order these are the light and heavy $\mathcal{CP}$-even $h$ and $H$, the $\mathcal{CP}$-odd $A$, and the charged Higgs bosons $H^{\pm }$. The measured mass value, having already reached the level of a precision observable with an experimental accuracy of about $500 \,\, \mathrm {MeV}$, plays an important role in this context. In the MSSM the mass of the light $\mathcal{CP}$-even Higgs boson, $M_h$, can directly be predicted from the other parameters of the model. The accuracy of this prediction should at least match the one of the experimental result.

The Higgs sector of the MSSM can be expressed at lowest order in terms of the gauge couplings, the mass of the $\mathcal{CP}$-odd Higgs boson, $M_A$, and $\tan \beta \equiv v_2/v_1$, the ratio of the two vacuum expectation values. All other masses and mixing angles can therefore be predicted. Higher-order contributions can give large corrections to the tree-level relations [10–12]. An upper bound for the mass of the lightest MSSM Higgs boson of $M_h\lesssim 135 \,\, \mathrm {GeV}$ was obtained [13], and the remaining theoretical uncertainty in the calculation of $M_h$, from unknown higher-order corrections, was estimated to be up to $3 \,\, \mathrm {GeV}$, depending on the parameter region. Recent improvements have lead to a somewhat smaller estimate of up to ${\sim }2 \,\, \mathrm {GeV}$ [14, 15] (see below).

Experimental searches for the neutral MSSM Higgs bosons have been performed at LEP [16, 17], placing important restrictions on the parameter space. At Run II of the Tevatron the search was continued but is now superseded by the LHC Higgs searches. Besides the discovery of a SM Higgs-like boson the LHC searches place stringent bounds, in particular in the regions of small $M_A$ and large $\tan \beta$ [18]. At a future linear collider (ILC) a precise determination of the Higgs boson properties (either of the light Higgs boson at ${\sim }125.6\,\, \mathrm {GeV}$ or heavier MSSM Higgs bosons within the kinematic reach) will be possible [19]. In particular a mass measurement of the light Higgs boson with an accuracy below ${\sim }0.05 \,\, \mathrm {GeV}$ is anticipated [20]. The interplay of the LHC and the ILC in the neutral MSSM Higgs sector has been discussed in Refs. [21–23].

For the MSSM¹ the status of higher-order corrections to the masses and mixing angles in the neutral Higgs sector is quite advanced. The complete one-loop result within the MSSM is known [28–35]. The by far dominant one-loop contribution is the $\mathcal{O}(\alpha _t)$ term due to top and stop loops ($\alpha _t\equiv h_t^2 / (4 \pi )$, $h_t$ being the top-quark Yukawa coupling). The computation of the two-loop corrections has meanwhile reached a stage where all the presumably dominant contributions are available [36–53]. In particular, the $\mathcal{O}(\alpha _t\alpha _s)$ contributions to the self-energies—evaluated in the Feynman-diagrammatic (FD) as well as in the effective potential (EP) method—as well as the $\mathcal{O}(\alpha _t^2)$, $\mathcal{O}(\alpha _b\alpha _s)$, $\mathcal{O}(\alpha _t\alpha _b)$ and $\mathcal{O}(\alpha _b^2)$ contributions—evaluated in the EP approach—are known for vanishing external momenta. An evaluation of the momentum dependence at the two-loop level in a pure $\overline{{\mathrm {DR}}}$ calculation was presented in Ref. [54]. A (nearly) full two-loop EP calculation, including even the leading three-loop corrections, has also been published [55–62]. However, within the EP method all contributions are evaluated at zero external momentum, in contrast to the FD method, which in principle allows non-vanishing external momentum. Further, the calculation presented in Refs. [55–62] is not publicly available as a computer code for Higgs-mass calculations. Subsequently, another leading three-loop calculation of $\mathcal{O}(\alpha _t\alpha _s^2)$, depending on the various SUSY mass hierarchies, has been performed [63–65], resulting in the code H3m (which adds the three-loop corrections to the FeynHiggs result). Most recently, a combination of the full one-loop result, supplemented with leading and subleading two-loop corrections evaluated in the Feynman-diagrammatic/effective potential method and a resummation of the leading and subleading logarithmic corrections from the scalar-top sector has been published [14] in the latest version of the code FeynHiggs [13, 14, 24, 38, 66, 67]. While previous to this combination the remaining theoretical uncertainty on the lightest $\mathcal{CP}$-even Higgs boson mass had been estimated to be about $3 \,\, \mathrm {GeV}$ [12, 13], the combined result was roughly estimated to yield an uncertainty of about $2 \,\, \mathrm {GeV}$ [14, 15]; however, more detailed analyses will be necessary to yield a more solid result.

In the present paper we calculate the two-loop $\mathcal{O}(\alpha _t\alpha _s)$ corrections to the Higgs boson masses in a mixed on-shell/$\overline{{\mathrm {DR}}}$ scheme. Compared to previously known results [36–38, 44] we evaluate here corrections that are proportional to the external momentum of the relevant Higgs boson self-energies. These corrections can directly be added to the corrections included in FeynHiggs. An overview of the relevant sectors and the calculation is given in Sect. 2, whereas in Sect. 3 we discuss the size and relevance of the new two-loop corrections. Our conclusions are given in Sect. 4.

2 Calculation

2.1 The Higgs-boson sector of the MSSM

The MSSM requires two scalar doublets, which are conventionally written in terms of their components as follows:

$$\begin{aligned} \mathcal{H}_1&= \left( \begin{array}{c}\mathcal{H}_1^0 \\ \mathcal{H}_1^- \end{array} \right) =\left( \begin{array}{c}v_1 + \frac{1}{\sqrt{2}}(\phi _1^0 - i\chi _1^0) \\ -\phi _1^- \end{array} \right) ,\nonumber \\ \mathcal{H}_2&= \left( \begin{array}{c}\mathcal{H}_2^+\\ \mathcal{H}_2^0 \end{array} \right) =\left( \begin{array}{c}\phi _2^+\\ v_2 + \frac{1}{\sqrt{2}}(\phi _2^0 + i\chi _2^0) \end{array} \right) . \end{aligned}$$

(1)

The Higgs boson sector can be described with the help of two independent parameters (besides the SM gauge couplings), conventionally chosen as $\tan \beta = v_2/v_1$, the ratio of the two vacuum expectation values, and $M_A^2$, the mass of the $\mathcal{CP}$-odd Higgs boson $A$. The bilinear part of the Higgs potential leads to the tree-level mass matrix for the neutral $\mathcal{CP}$-even Higgs boson,

$$\begin{aligned}&M_\mathrm{Higgs}^{2, \mathrm{tree}} = \left( \begin{array}{c@{\quad }c}m_{\phi _1}^2 \quad m_{\phi _1\phi _2}^2 \\ m_{\phi _1\phi _2}^2\quad m_{\phi _2}^2 \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{c@{\quad }c}M_A^2 \sin ^2\!\beta + M_Z^2 \cos ^2\!\beta \quad -(M_A^2 + M_Z^2) \sin \beta \cos \beta \\ -(M_A^2 + M_Z^2) \sin \beta \cos \beta \quad M_A^2 \cos ^2\!\beta + M_Z^2 \sin ^2\!\beta \end{array} \right) ,\nonumber \\ \end{aligned}$$

(2)

in the $(\phi _1, \phi _2)$ basis and being expressed in terms of the parameters $M_Z$, $M_A$ and the angle $\beta$. Diagonalization yields the tree-level masses $m_{h, \mathrm{tree}}$, $m_{H, \mathrm{tree}}$.

The higher-order corrected $\mathcal{CP}$-even Higgs boson masses in the MSSM are obtained from the corresponding propagators dressed by their self-energies. The inverse propagator matrix in the $(\phi _1, \phi _2)$ basis is given by

$$\begin{aligned}&(\Delta _{\text {Higgs}})^{-1} \nonumber \\&\quad = -\text {i} \left( \begin{matrix} p^2 - m_{\phi _1}^2 + \hat{\Sigma }_{\phi _1}(p^2) &{}\quad -m_{\phi _1\phi _2}^2 +\hat{\Sigma }_{\phi _1\phi _2}(p^2)\\ -m_{\phi _1\phi _2}^2 +\hat{\Sigma }_{\phi _1\phi _2}(p^2) &{}\quad p^2 - m_{\phi _2}^2 + \hat{\Sigma }_{\phi _2}(p^2) \end{matrix}\right) ,\nonumber \\ \end{aligned}$$

(3)

where the $\hat{\Sigma }(p^2)$ denote the renormalized Higgs-boson self-energies, $p$ being the external momentum. The renormalized self-energies can be expressed through the unrenormalized self-energies, $\Sigma (p^2)$, and counterterms involving renormalization constants $\delta m^2$ and $\delta Z$ from parameter and field renormalization. With the self-energies expanded up to two-loop order, $\hat{\Sigma }= \hat{\Sigma }^{(1)} + \hat{\Sigma }^{(2)}$, one has for the $\mathcal{CP}$-even part at the $i$-loop level ($i = 1, 2$),

$$\begin{aligned} \hat{\Sigma }_{\phi _1}^{(i)}(p^2)&= \Sigma _{\phi _1}^{(i)}(p^2) + \delta Z_{\phi _1}^{(i)}\, (p^2-m_{\phi _1}^2) - \delta m_{\phi _1}^{2(i)},\end{aligned}$$

(4a)

$$\begin{aligned} \hat{\Sigma }_{\phi _2}^{(i)}(p^2)&= \Sigma _{\phi _2}^{(i)}(p^2) + \delta Z_{\phi _2}^{(i)}\, (p^2-m_{\phi _2}^2) - \delta m_{\phi _2}^{2(i)},\end{aligned}$$

(4b)

$$\begin{aligned} \hat{\Sigma }_{\phi _1\phi _2}^{(i)}(p^2)&= \Sigma _{\phi _1\phi _2}^{(i)}(p^2) - \delta Z_{\phi _1\phi _2}^{(i)}\, m_{\phi _1\phi _2}^2 - \delta m_{\phi _1\phi _2}^{2(i)}. \end{aligned}$$

(4c)

The counterterms are determined by appropriate renormalization conditions and are given in the appendix.

The renormalized self-energies in the $(\phi _1, \phi _2)$ basis can be rotated into the physical $(h,H)$ basis where the tree-level propagator matrix is diagonal, via

$$\begin{aligned} \left( \begin{array}{c@{\quad }c}\hat{\Sigma }_{HH} &{} \hat{\Sigma }_{hH} \\ \hat{\Sigma }_{hH} &{} \hat{\Sigma }_{hh} \end{array} \right) = D(\alpha ) \left( \begin{array}{c@{\quad }c}\hat{\Sigma }_{\phi _1} &{} \hat{\Sigma }_{\phi _1\phi _2} \\ \hat{\Sigma }_{\phi _1\phi _2} &{} \hat{\Sigma }_{\phi _2} \end{array} \right) D^T(\alpha ) \end{aligned}$$

(5)

with the matrix

$$\begin{aligned} D(\alpha ) = \left( \begin{array}{c@{\quad }c}\cos \alpha &{} \sin \alpha \\ -\sin \alpha &{} \cos \alpha \end{array} \right) , \end{aligned}$$

(6)

which diagonalizes the tree-level mass matrix (2). The $\mathcal{CP}$-even Higgs boson masses are determined by the poles of the $(h,H)$-propagator matrix. This is equivalent to solving the equation

$$\begin{aligned}&\left[ p^2 - m_{h, \mathrm{tree}}^2 + \hat{\Sigma }_{hh}(p^2) \right] \left[ p^2 - m_{H, \mathrm{tree}}^2 + \hat{\Sigma }_{HH}(p^2) \right] \nonumber \\&\quad -\left[ \hat{\Sigma }_{hH}(p^2)\right] ^2 = 0, \end{aligned}$$

(7)

yielding the loop-corrected pole masses, $M_h$ and $M_H$. Here we use the implementation in the code FeynHiggs [13, 14, 24, 38, 66, 67], supplemented by the new momentum-dependent $\mathcal{O}(\alpha _t\alpha _s)$ corrections, as described in Sect. 2.4.

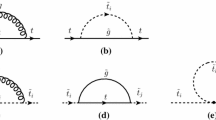
Our calculation is performed in the Feynman-diagrammatic (FD) approach. To arrive at expressions for the unrenormalized self-energies and tadpoles at $\mathcal{O}(\alpha _t\alpha _s)$, the evaluation of genuine two-loop diagrams and one-loop graphs with counterterm insertions is required. Example diagrams for the neutral Higgs-boson self-energies are shown in Fig. 1, and for the tadpoles in Fig. 2. For the counterterm insertions, described in Sect. 2.2, one-loop diagrams with external top quarks/squarks have to be evaluated as well, as displayed in Fig. 3. The complete set of contributing Feynman diagrams has been generated with the program FeynArts [68–71] (using the model file including counterterms from Ref. [72]), tensor reduction and the evaluation of traces was done with support from the programs FormCalc [73] and TwoCalc [74, 75], yielding algebraic expressions in terms of the scalar one-loop functions $A_0, B_0$ [76], the massive vacuum two-loop functions [77], and two-loop integrals which depend on the external momentum. These integrals have been evaluated with the program SecDec [78, 79]; see Sect. 2.3.

Fig. 1

Generic two-loop diagrams and diagrams with counterterm insertions for the Higgs-boson self-energies ($\phi = h, H, A$)

Fig. 2

Generic two-loop diagrams and diagrams with counterterm insertions for the Higgs-boson tadpoles ($\phi = h,H$; $i,j,k = 1,2$)

Fig. 3

Generic one-loop diagrams for subrenormalization counterterms, involving top quarks $t$, top squarks ${\tilde{t}}$, gluons $g$ and gluinos ${\tilde{g}}$ ($i,j,k=1,2$)

2.2 The scalar-top sector of the MSSM

The bilinear part of the top-squark Lagrangian,

$$\begin{aligned} \mathcal{L}_{{\tilde{t}}, \text {mass}}=-\begin{pmatrix} {{{\tilde{t}}}_{L}}^{\dagger }, {{{\tilde{t}}}_{R}}^{\dagger } \end{pmatrix} {\mathbf {M}}_{{\tilde{t}}}\begin{pmatrix}{{\tilde{t}}}_{L}\\ {{\tilde{t}}}_{R} \end{pmatrix}, \end{aligned}$$

(8)

contains the stop mass matrix ${\mathbf {M}}_{{\tilde{t}}}$, given by

$$\begin{aligned} {\mathbf {M}}_{{\tilde{t}}} = \begin{pmatrix} M_{{\tilde{t}}_L}^2 + m_t^2 + M_Z^2 \cos 2\beta \, (T_t^3 - Q_t s_\mathrm {w}^2) &{} m_tX_t\\ m_tX_t&{} M_{{\tilde{t}}_R}^2 + m_t^2 + M_Z^2 \cos 2\beta \, Q_t \, s_\mathrm {w}^2 \end{pmatrix},\nonumber \\ \end{aligned}$$

(9)

with

$$\begin{aligned} X_t= A_t- \mu \,\cot \beta . \end{aligned}$$

(10)

$Q_t$ and $T_t^3$ denote the charge and isospin of the top quark, $A_t$ is the trilinear coupling between the Higgs bosons and the scalar tops, and $\mu$ is the Higgsino mass parameter. Below we use $M_\mathrm{SUSY}:= M_{{\tilde{t}}_L}= M_{{\tilde{t}}_R}$ for our numerical evaluation. However, the analytical calculation has been performed for arbitrary $M_{{\tilde{t}}_L}$ and $M_{{\tilde{t}}_R}$. ${\mathbf {M}}_{{\tilde{t}}}$ can be diagonalized with the help of a unitary transformation matrix ${{\mathbf {U}}}_{{\tilde{t}}}$, parametrized by a mixing angle ${\theta }_{{\tilde{t}}}$, to provide the eigenvalues $m_{{\tilde{t}}_1}^2$ and $m_{{\tilde{t}}_2}^2$ as the squares of the two on-shell top-squark masses.

For the evaluation of the $\mathcal{O}(\alpha _t\alpha _s)$ two-loop contributions to the self-energies and tadpoles of the Higgs sector, renormalization of the top/stop sector at $\mathcal{O}(\alpha _s)$ is required, giving rise to the counterterms for one-loop subrenormalization (see Figs. 1, 2). We follow the renormalization at the one-loop level given in Refs. [40, 80–82], where details can be found. In the context of this paper, we only want to emphasize that on-shell (OS) renormalization is performed for the top-quark mass as well as for the scalar-top masses. This is different from the approach pursued, for example, in Ref. [54], where a $\overline{{\mathrm {DR}}}$ renormalization has been employed. Using the OS scheme allows us to consistently combine our new correction terms with the hitherto available self-energies included in FeynHiggs.

Finally, at $\mathcal{O}(\alpha _t\alpha _s)$, gluinos appear as virtual particles only at the two-loop level (hence, no renormalization for the gluinos is needed). The corresponding soft-breaking gluino mass parameter $M_3$ determines the gluino mass, $M_{{\tilde{g}}}= M_3$.

2.3 The program SecDec

The calculation of the momentum-dependent two-loop corrections to the Higgs-boson masses at order $\mathcal{O}(\alpha _t\alpha _s)$ involves two-loop two-point functions with up to four different masses, in addition to the mass scale given by the external momentum $p^2$. For two-loop diagrams of propagator type, analytical results in four space-time dimensions are known only sparsely if different masses are occurring in the loops [77, 83–90]. The integrals which are lacking analytical results can be classified into four different topologies, shown in Fig. 4. We have calculated these integrals numerically using the program SecDec [78, 79], where up to four different masses in 34 different mass configurations needed to be considered, with differences in the kinematic invariants of several orders of magnitude.

Fig. 4

Topologies which have been calculated numerically using SecDec

The program SecDec is a publicly available tool [91] to calculate multi-loop integrals numerically. Dimensionally regulated poles are factorized by sector decomposition as described in Refs. [92, 93], while kinematic thresholds are handled by a deformation of the integration contour into the complex plane, as described e.g. in Ref. [79]. The numerical integration is done using the Cuba library [94].

The program has also been extended to be able to calculate tensor integrals of any rank [95], and to process efficiently the evaluation of large ranges of kinematic points using the “multinumerics” feature of the program, which is of particular importance for the calculation presented here. This feature allows one to produce input files for large sets of kinematic points automatically, and to process the evaluation of these points in parallel if several cores or a cluster are available, without repeating the algebraic part of the sector decomposition, which can be done once and for all. The evaluation of a single phase space point for the most complicated topology, to reach a relative accuracy of at least $10^{-5}$, ranges between 0.01 and 100 s on an Intel core i7 processor, where the larger timings are for points very close to a kinematic threshold.

2.4 Evaluation and implementation in the program FeynHiggs

The resulting new contributions to the neutral $\mathcal{CP}$-even Higgs-boson self-energies, containing all momentum-dependent and additional constant terms, are assigned to the differences

$$\begin{aligned} \Delta \hat{\Sigma }_{ab}^{(2)}(p^2) \!=\! \hat{\Sigma }_{ab}^{(2)}(p^2) \!-\! \tilde{\Sigma }_{ab}^{(2)}(0),\quad ab \!=\! \{HH,hH,hh\}.\nonumber \\ \end{aligned}$$

(11)

Note the tilde (not hat) on $\tilde{\Sigma }^{(2)}(0)$ which signifies that not only the self-energies are evaluated at zero external momentum but also the corresponding counterterms, following Refs. [36–38]. A finite shift $\Delta \hat{\Sigma }^{(2)} (0)$ therefore remains in the limit $p^2\rightarrow 0$ due to $\delta M_A^{2(2)}= \mathop {\mathrm {Re}}\Sigma _{AA}^{(2)}(M_A^2)$ being computed at $p^2=M_A^2$ in $\hat{\Sigma }^{(2)}$, but at $p^2=0$ in $\tilde{\Sigma }^{(2)}$; for details see Eqs. (22) and (24) in the appendix.

The numerical evaluation to derive the physical masses for $h,H$ as the poles (real parts) of the dressed propagators proceeds on the basis of Eq. (7) in an iterative way.

• In a first step, the squared masses $M_{h,0}^2, M_{H,0}^2$ are determined by solving Eq. (7) excluding the new terms $\Delta \hat{\Sigma }_{ab}^{(2)}(p^2)$ from the self-energies.

• In a second step, the shifts $\Delta \hat{\Sigma }^{(2)}_{ab}(M_{h,0}^2) \equiv c_{ab}^h$ and $\Delta \hat{\Sigma }^{(2)}_{ab}(M_{H,0}^2) \equiv c_{ab}^H$ are calculated and added as constants to the self-energies in Eq. (7), $\hat{\Sigma }_{ab}(p^2) \rightarrow \hat{\Sigma }_{ab}(p^2) + c_{ab}^{h(H)}$.

• In the third step, Eq. (7) is solved again, now including the constant shifts $c_{ab}^{h(H)}$ in the self-energies, to deliver the refined masses $M_h$ (with $c_{ab}^h)$ and $M_H$ (with $c_{ab}^H$).

This procedure can be repeated for improving the accuracy; numerically it turns out that going beyond the first iteration yields only marginal changes.

The corrections of Eq. (11) are incorporated in FeynHiggs by the following recipe, which is more general and in principle applicable also to the case of the complex MSSM with $\mathcal{CP}$ violation.

• 1. Determine Higgs masses $M_{h_{i},0}$ without the momentum-dependent terms of Eq. (11); the index $i=1,\dots ,4$ enumerates the masses of $h, H, A, H^{\pm }$ in the real MSSM. This is done by invoking the FeynHiggs mass-finder.

• 2. Compute the shifts $c_{ab}^{h_k} = \Delta \hat{\Sigma }_{ab}^{(2)} (M_{h_k,0}^2)$ with $a,b,h_k = {h,H}$.

• 3. Run FeynHiggs’ mass-finder again including the $c_{ab}^{h_k}$ as constant shifts in the self-energies to determine the refined Higgs masses $M_{h}$ and $M_{H}$.

This procedure could conceivably be iterated until full self-consistency is reached; yet the resulting mass improvements turn out to be too small to justify extra CPU time.

On the technical side we added an interface for an external program to FeynHiggs which exports relevant model parameters to the external program’s environment, currently:

where the $U_{\tilde{t},1i}$ denote the elements of the stop mixing matrix, $\alpha _s(m_t)$ the running strong coupling at the scale $m_t$, and $G_F$ the Fermi constant. The renormalization scale is defined within FeynHiggs as $\mu _R = m_t \cdot \mathtt{FHscalefactor }$. Invocation of the external program is switched on by providing its path in the environment variable FHEXTSE. The program is executed from inside a temporary directory which is afterwards removed.

The output (stdout) is scanned for lines of the form ‘se@$m$ $c_r$ $c_i$’ which specify the correction $c_r + {\mathrm {i}} c_i$ [with $c_r = \mathrm{Re}(c_{ab}^{h_k}), \; c_i = \mathrm{Im}(c_{ab}^{h_k})$] to self-energy se in the computation of mass $m$, where $m$ is one of Mh0, MHH, MA0, MHp, and se is one of h0h0, HHHH, A0A0, HmHp, h0HH, h0A0, HHA0, G0G0, h0G0, HHG0, A0G0, GmGp, HmGp, F1F1, F2F2, F1F2. The latter three, if given, substitute

$$\begin{aligned} {\mathtt {HHHH}}&= \cos ^2\alpha \,{\mathtt {F1F1}} + \sin ^2\alpha \,{\mathtt {F2F2}} + \sin 2\alpha \,{\mathtt {F1F2}}\,, \end{aligned}$$

(12a)

$$\begin{aligned} {\mathtt {h0h0}}&= \sin ^2\alpha \,{\mathtt {F1F1}} + \cos ^2\alpha \,{\mathtt {F2F2}} - \sin 2\alpha \,{\mathtt {F1F2}}, \end{aligned}$$

(12b)

$$\begin{aligned} {\mathtt {h0HH}}&= \cos 2\alpha \,{\mathtt {F1F2}} + \tfrac{1}{2}\sin 2\alpha \,({\mathtt {F2F2}} - {\mathtt {F1F1}}), \end{aligned}$$

(12c)

where $\alpha$ is the tree-level $2\times 2$ neutral-Higgs mixing angle in Eq. (6). Self-energies not given are assumed zero.

The zero-momentum contributions $\tilde{\Sigma }_{ab}^{(2)}(0)$, $ab=\{HH, hH,hh\}$, are subtracted if the output of the external program contains one or more of ‘sub asat’, ‘sub atat’, ‘sub asab’, ‘sub atab’ for the $\alpha _s\alpha _t$, $\alpha _t^2$, $\alpha _s\alpha _b$, and $\alpha _t\alpha _b$ contributions, respectively. All other lines in the output are ignored.

3 Numerical results

We show results for the subtracted two-loop self-energies $\Delta \hat{\Sigma }_{ab}^{(2)}(p^2)$ given in Eq. (11), as well as for the mass shifts

$$\begin{aligned} \Delta M_h= M_h- M_{h,0}, \quad \Delta M_H= M_H- M_{H,0} \end{aligned}$$

(13)

i.e. the difference in the physical Higgs-boson masses evaluated including and excluding the newly obtained momentum-dependent two-loop corrections. This quantity, in particular $\Delta M_h$ for the light $\mathcal{CP}$-even Higgs boson, can directly be compared with the current experimental uncertainty as well as with the anticipated future ILC accuracy of [20],

$$\begin{aligned} \delta M_h^\mathrm{exp, ILC} \lesssim 0.05 \,\, \mathrm {GeV}. \end{aligned}$$

(14)

The results are obtained for two different scenarios, varying parameters like $\tan \beta ,M_A,M_{{\tilde{g}}}$, and illustrate the impact of these parameters via the new two-loop corrections on the neutral $\mathcal{CP}$-even Higgs boson masses, $M_h$ and $M_H$. The corresponding renormalization scale, $\mu _{\overline{{\mathrm {DR}}}}$, is set to $\mu _{\overline{{\mathrm {DR}}}}= m_t$ in all numerical evaluations. The scale uncertainties are expected to be much smaller than the parametric uncertainties due to variations of parameters like $\tan \beta ,M_A,M_{{\tilde{g}}},m_{{\tilde{t}}}$.

3.1 Scenario 1: $m_h^\mathrm{max}$

Scenario 1 is oriented at the $m_h^\mathrm{max}$ scenario described in Ref. [96]. We use the following parameters:

$$\begin{aligned} m_t&= 173.2\,\, \mathrm {GeV},\quad M_\mathrm{SUSY}=1\,\, \mathrm {TeV},\quad X_t=2\,M_\mathrm{SUSY}, \nonumber \\ M_{{\tilde{g}}}&= 1500\,\, \mathrm {GeV},\quad \mu = 200\,\, \mathrm {GeV}, \end{aligned}$$

(15)

leading to stop mass values of

$$\begin{aligned} m_{{\tilde{t}}_1}= 826.8\,\, \mathrm {GeV},\quad m_{{\tilde{t}}_2}= 1173.2\,\, \mathrm {GeV}. \end{aligned}$$

With the introduction of the momentum dependence, thresholds occur in the self-energy diagrams when the external momentum $p=\sqrt{p^2}$, in the time-like region, is such that a cut of the diagram would correspond to on-shell production of the massive particles of the cut propagators. The resulting imaginary parts enter in the search for the complex poles of the inverse propagator matrix of the Higgs bosons. Therefore it is interesting to study the behavior of the real and imaginary parts of the self-energies. In Fig. 5 we show the momentum-dependent parts of the renormalized two-loop self-energies in the physical basis, Eq. (11) for two different values of $\tan \beta$, $\tan \beta =5$ and $\tan \beta =20$, at a fixed $A$-boson mass $M_A=250$ GeV. The data points are not connected by a line in order to show that each numerical point is obtained from a calculation of the 34 analytically unknown integrals with the program SecDec. The inlays in Fig. 5 magnify the region $p^2\le (125 \,\, \mathrm {GeV})^2$, where one can observe that for $p^2\rightarrow 0$, the subtracted self-energies are not exactly zero. As mentioned in Sect. 2.4, this is due to the fact that the on-shell renormalization condition for the $A$-boson self-energy is defined differently with regard to the calculation without momentum dependence. The resulting constant contributions are additionally suppressed by factors $\sin ^2\!\beta$, $\sin \beta \cos \beta$ and $\cos ^2\!\beta$ appearing in the counter terms $\delta m_{\phi _1}^{2(2)}$, $\delta m_{\phi _1\phi _2}^{2(2)}$ and $\delta m_{\phi _2}^{2(2)}$, respectively, according to Eqs. (24) in the appendix.

Fig. 5

Momentum dependence of the real (left column) and imaginary (right column) parts of the two-loop self-energies $\Delta {\hat{\Sigma }}_{hh},\Delta {\hat{\Sigma }}_{hH},\Delta {\hat{\Sigma }}_{HH}$, within scenario 1, for $\tan \beta =5$ (red squares) and $\tan \beta = 20$ (blue crosses) and $M_A=250 \,\, \mathrm {GeV}$. One can see that the self-energies change substantially beyond the threshold at $p^2= (2m_t)^2$

The imaginary part is independent of the $A$-boson mass, as this mass parameter solely appears in the counterterms of $\overline{{\mathrm {DR}}}$ renormalized quantities and the $\delta M_A^{2(2)}$ counterterm, where only the real part contributes. Therefore, the imaginary parts displayed in Fig. 5 do not contain additional constant terms. As to be expected, the imaginary parts are zero below the $t{\bar{t}}$ production threshold at $p=2\,m_t$, which results from the fact that the top mass is the smallest mass appearing in the loops. Beyond this threshold, the imaginary parts are growing substantially with increasing $p^2$. From these observations, the mass shifts in the region below the first threshold at $p=2\,m_t$ are expected not to be large.

Similar results, now including a variation of $M_A$ are shown in Fig. 6. In the upper plot for $\Delta \hat{\Sigma }_{hh}$ and in the middle plot for $\Delta \hat{\Sigma }_{hH}$ the solid lines depict $M_A\sim 100 \,\, \mathrm {GeV}$, while the dashed lines are for $M_A\sim 900 \,\, \mathrm {GeV}$. In these plots the light shading covers the range for $\tan \beta = 5$, while the dark shading for $\tan \beta = 20$. In the lower plot for $\Delta \hat{\Sigma }_{HH}$ we show results for $M_A\sim 100, 250, 600, 900 \,\, \mathrm {GeV}$ as solid, dotted, dot-dashed, dashed lines, respectively (and shading has been omitted). For $\Delta \hat{\Sigma }_{hh}$ at low $p$ values only a small variation with $M_A$ can be observed. For $p$ and $M_A$ large, the contributions to the self-energy are bigger. In $\Delta \hat{\Sigma }_{hH}$ larger effects are observed at smaller $M_A$ for both small and large $p$ values. For $\Delta \hat{\Sigma }_{HH}$, on the other hand, at low $p$ values, large effects can be observed for large $M_A$ due to the aforementioned counterterm contribution ${\sim } \delta M_A^{2(2)}= \mathop {\mathrm {Re}}\Sigma _{AA}^{(2)}(M_A^2)$. At large $p$, as before, small $M_A$ values give a more sizable contribution.

Fig. 6

Momentum dependence of the real part of the two-loop self-energies $\Delta \hat{\Sigma }_{hh},\Delta \hat{\Sigma }_{hH},\Delta \hat{\Sigma }_{HH}$, within scenario 1, for two different values of $\tan \beta$ and a range of $M_A$ values

We now turn to the effects of our newly computed momentum-dependent two-loop corrections on the Higgs-boson masses $M_{h,H}$ via the mass shifts $\Delta M_h$ and $\Delta M_H$. In Fig. 7 we show $\Delta M_h$ (upper plot) and $\Delta M_H$ (lower plot) as a function of $M_A$ for $\tan \beta = 5$ (blue) and $\tan \beta = 20$ (red). In the $m_h^\mathrm{max}$ scenario for $M_A\gtrsim 200 \,\, \mathrm {GeV}$ we find $\Delta M_h\sim - 60 \,\, \mathrm {MeV}$, i.e. of the size of the future experimental precision; see Eq. (14). The contribution to the heavy $\mathcal{CP}$-even Higgs-boson is suppressed with $\tan \beta$. While the size of $\Delta M_H$ becomes negligible for $M_A\gtrsim 150 \,\, \mathrm {GeV}$ for $\tan \beta = 20$, its variation is more pronounced for $\tan \beta = 5$. $\Delta M_H$ can reach about $-60 \,\, \mathrm {MeV}$ for very small or intermediate values of $M_A$ and steadily decreases for $M_A\gtrsim 500 \,\, \mathrm {GeV}$. The peak in $\Delta M_H$ for $\tan \beta = 5$ originates from a threshold at $2\,m_t$.

Fig. 7

Variation of the mass shifts $\Delta M_h,\Delta M_H$ with the $A$-boson mass $M_A$ within scenario 1, for $\tan \beta =5$ (red) and $\tan \beta = 20$ (blue). The peak in $\Delta M_H$ originates from a threshold at $2\,m_t$

Finally, in scenario 1, we analyze the dependence of $M_h$ and $M_H$ on the gluino mass, $M_{{\tilde{g}}}$. The results are shown in Fig. 8 for $\Delta M_h$ (upper plot) and $\Delta M_H$ (lower plot) for $M_A= 250 \,\, \mathrm {GeV}$, with the same color coding as in Fig. 7. In the upper plot one can observe that the effects are particularly small for the default value of $M_{{\tilde{g}}}$ in scenario 1. More sizeable shifts occur for larger gluino masses, by more than $-400 \,\, \mathrm {MeV}$ for $M_{{\tilde{g}}}\gtrsim 4 \,\, \mathrm {TeV}$, reaching thus the level of the current experimental accuracy in the Higgs-boson mass determination. The corrections to $M_H$, for the given value of $M_A= 250 \,\, \mathrm {GeV}$ do not exceed $-50 \,\, \mathrm {MeV}$ in the considered $M_{{\tilde{g}}}$ range.

Fig. 8

Variation of the mass shifts $\Delta M_h,\Delta M_H$ with the gluino mass, within scenario 1, for two different values of $\tan \beta =5,20$ and $M_A= 250 \,\, \mathrm {GeV}$

The dependence of the light $\mathcal{CP}$-even Higgs-boson mass on $M_{{\tilde{g}}}$ is analyzed in Fig. 9 for $\tan \beta = 5, 20$ and $M_A= 250 \,\, \mathrm {GeV}$. Here we show as dashed lines the results for $M_{h,0}$ (i.e. without the newly obtained momentum-dependent two-loop corrections) and as solid lines the results for $M_h$ (i.e. including the new corrections). While a maximum of the Higgs-boson mass can be observed around $M_{{\tilde{g}}}\sim 800 \,\, \mathrm {GeV}$, in agreement with the original definition of the $m_h^\mathrm{max}$ scenario [97], a downward shift by more than $4 \,\, \mathrm {GeV}$ is found for $M_{{\tilde{g}}}\sim 5 \,\, \mathrm {TeV}$. Such a strong effect is due to a (squared) logarithmic dependence of the $\mathcal{O}(\alpha _t\alpha _s)$ corrections evaluated at $p^2 = 0$, as given in Eq. (73) of Ref. [38]. In Fig. 9 it can be seen that the size of the momentum-dependent two-loop corrections similarly grows with $M_{{\tilde{g}}}$, reaching ${\sim }400 \,\, \mathrm {MeV}$, as was shown above in Fig. 8. Consequently, the logarithmic dependence of the light $\mathcal{CP}$-even Higgs-boson mass on the gluino mass that was found analytically for the $\mathcal{O}(\alpha _t\alpha _s)$ corrections at $p^2 = 0$, is now also found numerically for the momentum-dependent two-loop corrections.

Fig. 9

Variation of $M_h$ and $M_{h,0}$ as a function of $M_{{\tilde{g}}}$ within scenario 1, for $\tan \beta = 5, 20$ and $M_A= 250 \,\, \mathrm {GeV}$

3.2 Scenario 2: light stops

Scenario 2 is oriented at the “light-stop scenario” of Ref. [96].² We use the following parameters:

$$\begin{aligned} m_t&= 173.2\,\, \mathrm {GeV},\quad M_\mathrm{SUSY}= 0.5 \,\, \mathrm {TeV},\quad X_t=2\,M_\mathrm{SUSY}, \nonumber \\ M_{{\tilde{g}}}&= 1600\,\, \mathrm {GeV},\quad \mu = 200\,\, \mathrm {GeV}, \end{aligned}$$

(16)

leading to stop mass values of

$$\begin{aligned} m_{{\tilde{t}}_1}= 326.8 \,\, \mathrm {GeV},\quad m_{{\tilde{t}}_2}= 673.2 \,\, \mathrm {GeV}. \end{aligned}$$

Scenario 2 is analyzed with the same set of plots shown for scenario 1 in the previous subsection. The effects of the new momentum-dependent two-loop contributions on the renormalized Higgs-boson self-energies, $\Delta \hat{\Sigma }_{ab}(p^2)$, are shown in Fig. 10. As before, we show the results separately for the real and imaginary parts of the self-energies. An additional threshold beyond the top-mass threshold appears at $p = 2\, m_{{\tilde{t}}_1}$, where the discontinuity stems from the derivative of the imaginary part of the $B_0$ function(s). Analogously to scenario 1, the largest contributions in the region below $200\,\, \mathrm {GeV}$ arise in the real part of $\Delta {\hat{\Sigma }}_{hh}$ amounting to about $15\,\, \mathrm {GeV}^2$ at $p=125\,\, \mathrm {GeV}$, where the dependence on the value of $\tan \beta \,$ is rather weak.

Fig. 10

Momentum dependence of the real and imaginary parts of the two-loop self-energies $\Delta {\hat{\Sigma }}_{hh},\Delta {\hat{\Sigma }}_{hH},\Delta {\hat{\Sigma }}_{HH}$ within scenario 2, with $\tan \beta =5,20$ and $M_A=250 \,\, \mathrm {GeV}$ with the same color coding as in Fig. 5

The dependence of $\Delta \hat{\Sigma }_{ab}(p^2)$ on $M_A$ is shown in Fig. 11, using the same line styles as in Fig. 6. The curves show the same qualitative behavior as in Fig. 10, exhibiting again the new threshold at $p = 2\, m_{{\tilde{t}}_1}$. In general, outside the threshold region the effects in scenario 2 are slightly smaller than in scenario 1.

Fig. 11

Momentum dependence of the real parts of the two-loop self-energies $\Delta {\hat{\Sigma }}_{hh},\Delta {\hat{\Sigma }}_{hH},\Delta {\hat{\Sigma }}_{HH}$ in scenario 2 for two different values of $\tan \beta$ and various values of $M_A$ (see text)

We now turn to the effects on the physical neutral $\mathcal{CP}$-even Higgs boson masses. In Fig. 12 we show the results for $\Delta M_h$ (upper plot) and $\Delta M_H$ (lower plot) as a function of $M_A$ (with the same line styles as in Fig. 7). As can be expected from the previous figures, the effects on $M_h$ and $M_H$ are in general slightly smaller in scenario 2 than in scenario 1, where $\Delta M_h$ still reaches the anticipated ILC accuracy; see Eq. (14). For $\Delta M_H$ around the threshold $p = 2\,m_{{\tilde{t}}_1}$ the largest shift of ${\sim } - 1 \,\, \mathrm {GeV}$ can be observed. However, this shift is still below the anticipated mass resolution at the LHC [98].

Fig. 12

Variation of the mass shifts $\Delta M_h,\Delta M_H$ with the $A$-boson mass $M_A$ within scenario 2, for two different values of $\tan \beta =5,20$

Finally we analyze the dependence on $M_{{\tilde{g}}}$ in Fig. 13. In the upper plot we show $\Delta M_h$ for $\tan \beta = 5$ and $\tan \beta = 20$, where both values yield very similar results. As in scenario 1, “accidentally” small values of $\Delta M_h$ are found around $M_{{\tilde{g}}}\sim 1600 \,\, \mathrm {GeV}$. For larger gluino mass values the shifts induced by the new momentum-dependent two-loop corrections exceed $- 500 \,\, \mathrm {MeV}$ and are thus larger than the current experimental uncertainty. The results for $\Delta M_H$ are shown in the lower plot. While they are roughly twice as large as in scenario 1, they do not exceed $-100 \,\, \mathrm {MeV}$.

Fig. 13

Variation of the mass shifts $\Delta M_h,\Delta M_H$ with the gluino mass, within scenario 2, for two different values of $\tan \beta =5,20$ and $M_A= 250 \,\, \mathrm {GeV}$

4 Conclusions

We have presented results for the leading momentum-dependent $\mathcal{O}(\alpha _t\alpha _s)$ contributions to the masses of neutral $\mathcal{CP}$-even Higgs bosons in the MSSM. They are obtained by calculating the corresponding contributions to the dressed Higgs-boson propagators obtained in the Feynman-diagrammatic approach using a mixed on-shell/$\overline{{\mathrm {DR}}}$ renormalization scheme. In the Higgs sector a two-loop renormalization has to be carried out for the mass of the neutral Higgs bosons and the tadpole contributions. Furthermore, renormalization of the top/stop sector at $\mathcal{O}(\alpha _s)$ is needed entering at the two-loop level via one-loop subrenormalization. The diagrams were generated with FeynArts and reduced to a set of basic integrals with the help of FormCalc and TwoCalc. The two-loop integrals which are analytically unknown have been calculated numerically with the program SecDec.

We have analyzed numerically the effect of the new momentum-dependent two-loop corrections on the predictions for the $\mathcal{CP}$-even Higgs boson masses. This is particularly important for the interpretation of the scalar boson discovered at the LHC as the light $\mathcal{CP}$-even Higgs state of the MSSM. While currently a precision below the level of ${\sim }500 \,\, \mathrm {MeV}$ is reached, a reduction by about an order of magnitude can be expected at the future $e^+e^-$ International Linear Collider (ILC).

In our numerical analysis we found that the effects on the light $\mathcal{CP}$-even Higgs boson mass, $M_h$, depend strongly on the value of the gluino mass, $M_{{\tilde{g}}}$. For values of $M_{{\tilde{g}}}\sim 1.5 \,\, \mathrm {TeV}$ corrections to $M_h$ of about $-50 \,\, \mathrm {MeV}$ are found, at the level of the anticipated future ILC accuracy. For very large gluino masses, $M_{{\tilde{g}}}\gtrsim 4 \,\, \mathrm {TeV}$, on the other hand, substantially larger corrections are found, at the level of the current experimental accuracy. Consequently, this type of momentum-dependent two-loop corrections should be taken into account in precision analyses interpreting the discovered Higgs boson in the MSSM.

For the heavy $\mathcal{CP}$-even Higgs boson mass, $M_H$, the effects are mostly below current and future anticipated accuracies. Only close to thresholds, e.g. around $p = 2\,m_{{\tilde{t}}_1}$, larger corrections to $M_H$ around ${\sim }1 \,\, \mathrm {GeV}$ are found.

The new results of $\mathcal{O}(\alpha _t\alpha _s)$ have been implemented into the program FeynHiggs. A detailed description of our calculation will be presented in a forthcoming publication [99].

Appendix: Renormalization and counterterms

Renormalization and calculation of the renormalized self-energies is performed in the $(\phi _1, \phi _2)$ basis, which has the advantage that the mixing angle $\alpha$ does not appear and expressions are in general simpler.

Field renormalization is performed by assigning one renormalization constant for each doublet,

$$\begin{aligned} \mathcal{H}_1\rightarrow (1 + \tfrac{1}{2} \delta Z_{\mathcal{H}_1} )\, \mathcal{H}_1, \quad \mathcal{H}_2\rightarrow (1 + \tfrac{1}{2} \delta Z_{\mathcal{H}_2} ) \mathcal{H}_2, \end{aligned}$$

(17)

which can be expanded to one- and two-loop order according to

$$\begin{aligned} \delta Z_{\mathcal{H}_1}=\delta Z_{\mathcal{H}_1}^{(1)} + \delta Z_{\mathcal{H}_1}^{(2)}, \quad \delta Z_{\mathcal{H}_2}=\delta Z_{\mathcal{H}_2}^{(1)} + \delta Z_{\mathcal{H}_2}^{(2)}. \end{aligned}$$

(18)

The field renormalization constants appearing in (4) are then given by

$$\begin{aligned} \begin{aligned}&\delta Z_{\phi _1}^{(i)} = \delta Z_{\mathcal{H}_1}^{(i)}, \quad \delta Z_{\phi _2}^{(i)} = \delta Z_{\mathcal{H}_2}^{(i)},\\&\delta Z_{\phi _1\phi _2}^{(i)} = \tfrac{1}{2}(\delta Z_{\mathcal{H}_1}^{(i)} + \delta Z_{\mathcal{H}_2}^{(i)}). \end{aligned} \end{aligned}$$

(19)

The mass counterterms $\delta m^{2 (i)}_{ab}$ in (4) are derived from the Higgs potential, including the tadpoles, by the following parameter renormalization:

$$\begin{aligned}&M_A^2 \rightarrow M_A^2 + \delta M_A^{2(1)}+ \delta M_A^{2(2)},\nonumber \\&T_1\rightarrow T_1+ \delta T_1^{(1)}+ \delta T_1^{(2)}, \\&M_Z^2 \rightarrow M_Z^2 + \delta M_Z^{2(1)}+ \delta M_Z^{2(2)},\nonumber \\&T_2\rightarrow T_2+ \delta T_2^{(1)}+ \delta T_2^{(2)},\nonumber \\&\tan \beta \rightarrow \tan \beta \left( 1 + \delta \tan \beta ^{(1)} + \delta \tan \beta ^{(2)} \right) .\nonumber \end{aligned}$$

(20)

The parameters $T_1$ and $T_2$ are the terms linear in $\phi _1$ and $\phi _2$ in the Higgs potential. The renormalization of the $Z$ mass $M_Z$ does not contribute to the ${\mathcal {O}}(\alpha _s \alpha _t)$ corrections we are pursuing here; it is listed, however, for completeness.

The basic renormalization constants for parameters and fields have to be fixed by renormalization conditions according to a renormalization scheme. Here we choose the on-shell scheme for the parameters and the $\overline{\mathrm{DR}}$ scheme for field renormalization and give the expressions for the two-loop part.

The tadpole coefficients are chosen to vanish at all orders; hence their two-loop counterterms follow from

$$\begin{aligned} T_{1,2}^{(2)}\!+\! \delta T_{1,2}^{(2)} \!=\! 0, \quad \hbox {i.e.}\ \quad \delta T_1^{(2)}\!=\! -\!{T_1^{(2)}}, \quad \delta T_2^{(2)}\!=\! -\!{T_2^{(2)}},\nonumber \\ \end{aligned}$$

(21)

where $T_1^{(2)}$, $T_2^{(2)}$ are obtained from the two-loop tapole diagrams. The two-loop renormalization constant of the $A$-boson mass reads

$$\begin{aligned} \delta M_A^{2(2)}= \mathop {\mathrm {Re}}\Sigma _{AA}^{(2)}(M_A^2), \end{aligned}$$

(22)

in terms of the $A$-boson unrenormalized self-energy $\Sigma _{AA}$. The appearance of a non-zero momentum in the self-energy goes beyond the $\mathcal{O}(\alpha _t\alpha _s)$ corrections evaluated in Refs. [36–38, 44].

For the renormalization constants $\delta Z_{\mathcal{H}_1}$, $\delta Z_{\mathcal{H}_2}$ and $\delta \tan \beta$ several choices are possible; see the discussion in [100–102]. As shown there, the most convenient choice is a $\overline{\mathrm{DR}}$ renormalization of $\delta \tan \beta$, $\delta Z_{\mathcal{H}_1}$ and $\delta Z_{\mathcal{H}_2}$, which reads at the two-loop level

$$\begin{aligned} \delta Z_{\mathcal{H}_1}^{(2)}&= \delta Z_{\mathcal{H}_1}^{(2)\overline{\mathrm{DR}}}=- \left[ \mathop {\mathrm {Re}}\Sigma ^{\prime (2)}_{\phi _1} \right] ^\mathrm{div}_{|p^2 = 0},\end{aligned}$$

(23a)

$$\begin{aligned} \delta Z_{\mathcal{H}_2}^{(2)}&= \delta Z_{\mathcal{H}_2}^{(2)\overline{\mathrm{DR}}}=-\left[ \mathop {\mathrm {Re}}\Sigma ^{\prime (2)}_{\phi _2} \right] ^\mathrm{div}_{|p^2 = 0},\end{aligned}$$

(23b)

$$\begin{aligned} \delta \tan \beta ^{(2)}&= \delta \tan \beta ^{(2)\overline{\mathrm{DR}}}=\tfrac{1}{2}\left( \delta Z_{\mathcal{H}_2}^{(2)} - \delta Z_{\mathcal{H}_1}^{(2)} \right) . \end{aligned}$$

(23c)

The term in Eq. (23c) is in general not the proper expression beyond one-loop order even in the $\overline{\mathrm{DR}}$ scheme. For our approximation, however, with only the top Yukawa coupling at the two-loop level, it is the correct $\overline{\mathrm{DR}}$ form [103, 104].

The two-loop mass counterterms in the self-energies (4) are now expressed in terms of the parameter renormalization constants determined above as follows:

$$\begin{aligned} \delta m_{\phi _1}^{2(2)}&= \delta M_Z^{2(2)}\, \cos ^2\!\beta + \delta M_A^{2(2)}\sin ^2\!\beta \nonumber \\&- \delta T_1^{(2)}\frac{e}{2 M_Ws_\mathrm {w}} \, \cos \beta (1 + \sin ^2\!\beta ) \nonumber \\&+ \delta T_2^{(2)}\frac{e}{2 M_Ws_\mathrm {w}} \, \cos ^2\!\beta \sin \beta \nonumber \\&+ 2\, \delta \tan \beta ^{(2)}\, \cos ^2\!\beta \sin ^2\!\beta \, (M_A^2 - M_Z^2),\end{aligned}$$

(24a)

$$\begin{aligned} \delta m_{\phi _1\phi _2}^{2(2)}&= - (\delta M_Z^{2(2)}+ \delta M_A^{2(2)}) \sin \beta \cos \beta \nonumber \\&- \delta T_1^{(2)}\frac{e}{2 M_Ws_\mathrm {w}} \, \sin ^3\!\beta - \delta T_2^{(2)}\frac{e}{2 M_Ws_\mathrm {w}} \, \cos ^3\!\beta \nonumber \\&- \! \delta \tan \beta ^{(2)}\, \cos \beta \sin \beta \cos 2\beta (M_A^2 \!+\! M_Z^2),\qquad \end{aligned}$$

(24b)

$$\begin{aligned} \delta m_{\phi _2}^{2(2)}&= \delta M_Z^{2(2)}\sin ^2\!\beta + \delta M_A^{2(2)}\cos ^2\!\beta \nonumber \\&+ \delta T_1^{(2)}\frac{e}{2 M_Ws_\mathrm {w}} \, \sin ^2\!\beta \cos \beta \nonumber \\&- \delta T_2^{(2)}\frac{e}{2 M_Ws_\mathrm {w}} \, \sin \beta (1 + \cos ^2\!\beta ) \nonumber \\&- 2\, \delta \tan \beta ^{(2)}\, \cos ^2\!\beta \sin ^2\!\beta \, (M_A^2 - M_Z^2). \end{aligned}$$

(24c)

Note that the $Z$-mass counterterm is kept for completeness; it does not contribute in the approximation of $\mathcal{O}(\alpha _s\alpha _t)$ considered here.