1 Introduction

Cosmological observations of the cosmic microwave background (CMB) and the large scale distribution of galaxies indicate that the universe is homogeneous and isotropic on scales larger than about 100 megaparsecs [1]. The apparent acceleration of the expansion of the universe deduced from type Ia supernova observations and the CMB, WMAP, and Planck data [2–6] is one of the most striking cosmological observations of recent times. In the context of FLRW models with matter and radiation energy components, the acceleration of our universe cannot be explained and would require either the presence of a cosmological constant or a new form of matter which does not clump and dominates the late time evolution with a negative pressure [7, 8]. However, since there is no explanation for the presence of a cosmological constant of the appropriate value and there is no natural candidate for dark energy, it is tempting to look for alternative explanations by simply taking one step back and noticing one of the fundamental assumptions of cosmology: homogeneity [9]. Recently, inhomogeneous models of the universe have become popular among cosmologists [10]. One of the inhomogeneous cosmological models which is a solution of Einstein equations with perfect fluid source and conformally flat is the Stephani model [10–12]. The matter in these solutions has zero shear and rotation and moves with acceleration [13]. This solution was obtained by Stephani in 1967. His solution emerged as one of the spacetimes that can be embedded in a flat five dimensional space [14]. This universe and some of its subcases have been examined in many papers (see e.g. [10] and the references therein). It has also been used in stellar models [15–19] and some generalizations to FLRW [20, 21]. Other papers have pointed out their singularities [22–26] and the thermodynamics of their fluid source [27–29]. Recently, models with inhomogeneous pressure for testing the astronomical data related to supernovae observations have been put forward [30, 31]. In these solutions, the energy density of matter, \(\rho \), depends only on cosmic time, \(t\), while pressure, \(p\), depends on both \(t\) and \(r\) which means that the temperature varies with spatial position. One of the objections to this model is their incompatibility with a linear barotropic equation of the form \(p(t)=w_{0}\rho (t)\) with a constant \(w_{0}\) [29]. However, this incompatibility would not prohibit one to dismiss this solution since the non-barotropic equation of state cannot be ruled out a priori. The solution has a curvature parameter which is time dependent and does not have any special form. Generally, the curvature parameter can be positive at one time and negative at another time, thus this spacetime is interesting for its topological dynamics among cosmologists. The evolution of the model depends on some arbitrary functions, accordingly it can be named a private universe [32]. In the work by Stelmach and Jakacka [33], they assume that the curvature parameter relates to the scale factor by \(K(t)=\beta R(t)\) where \(\beta \) is a constant. They showed that with \(\beta <0\) a cosmological model with dust source can lead to the accelerated expansion at later times of evolution.

In this paper, we use the energy balance equation to obtain the pressure and energy density. We assume a non-barotropic equation of state to provide a reasonable interpretation for the Stephani universe. We consider an ansatz of the type \(K(t)=\beta (\frac{R}{R_{0}})^n\) for studying the model. We show that the field equation is similar to the Cardassian model where the expansion of the universe is accelerated without postulating any exotic matter field [36]. We find that for some specific values of \(n\) the model exhibits accelerated expansion at later stages of evolution which is in agreement with the recent Planck data [34].

This paper is organized as follows: In Sect. 2, the Stephani universe is studied as an alternative model of the universe. The pressure as a function of spacetime coordinates is derived. In Sect. 3, we calculate observable quantities such as the Hubble and the deceleration parameters. We show that in the considered model a negative deceleration parameter can be observed which is in agreement with the recent observations [34]. We derive a general statement for the age of the universe in the model. We show how a positive accelerated expansion of the universe can appear in the model without using any exotic matter. In the last section, we will draw some conclusions.

2 Spherically symmetric Stephani universe

The line element of the spherically symmetric Stephani universe in comoving coordinates is usually given in such a way as to emphasize its similarity to FLRW models [10]. However, we use the following alternative coordinates [13] which is more appropriate for simplifying our calculations that we are going to do in the next section

$$\begin{aligned} \mathrm{d}s^2&=-D^2\mathrm{d}t^2+V^2[\mathrm{d}r^2+f^2(\mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2)],\nonumber \\ D&=\frac{1+F^2(K-RK_{,R})}{1+KF^2}, \quad V= \frac{R}{1+KF^2}, \end{aligned}$$
(1)

where \(K(t)\) is the curvature parameter, \(R(t)\) is the scale factor and \(K_{,R}=\frac{K_{,t}}{R_{,t}}=\frac{\mathrm{d}K}{\mathrm{d}R}\), and the functions \(f(r), F(r)\) are defined by the three possible combinations

$$\begin{aligned}&f=r,\quad \, F=\frac{r}{2},\nonumber \\&f=\sin r,\quad ~ F=\sin \left( \frac{r}{2}\right) ,\\&f=\sinh r,\quad F=\sinh \left( \frac{r}{2}\right) .\nonumber \end{aligned}$$
(2)

The general transformation that relates the relations (2) with the radial coordinate \(r\) and the radial coordinate of the Stephani universe, \( \tilde{r}\), is given by \(r=\int \dfrac{\mathrm{d} \tilde{r}}{1+k_{0}\tilde{r}^2/4}\) where \(k_{0}=0,\pm 1\). Also we assume that the energy-momentum tensor is that of a perfect fluid,

$$\begin{aligned} T^{\mu \nu }=(\rho +p)u^\mu u^\nu +pg^{\mu \nu }, \end{aligned}$$
(3)

where \(u^\mu =\frac{1}{D}\delta ^{\mu }_{t}\) is the fluid 4-velocity and \(\rho , p\) are the mass–energy density and the pressure, respectively. The time coordinate in the metric (1) has been selected such that the expansion scalar \(\Theta =u^\mu _{~~;\mu }\) reads

$$\begin{aligned} \Theta =3\frac{R,{t}}{R}. \end{aligned}$$
(4)

The matter in this universe has zero shear and rotation but moves with acceleration which is defined as \(\dot{u}_{\mu } \equiv u_{\mu ;\nu }u^{\nu }\), whose value for the metric (1) is

$$\begin{aligned} \dot{u}_{\mu }=\frac{D_{,r}}{D} \delta ^r_{\mu }=-\frac{RK_{,R}f}{2[1+KF^2][1+F^2(K-RK_{,R})]}\delta ^r_{\mu }. \end{aligned}$$
(5)

Hence the covariant form of the energy balance \( u_{\mu }T^{\mu \nu }_{~~~;\nu }=0\) and the momentum balance \(h_{\mu \nu }T^{\mu \sigma }_{~~~;\sigma }=0\) takes the following forms, respectively:

$$\begin{aligned} u_{\mu }T^{\mu \nu }_{~~~;\nu }=\dot{\rho }+(\rho +p)\Theta =0, \end{aligned}$$
(6)

and

$$\begin{aligned} h_{\mu \nu }T^{\nu \sigma }_{~~~;\sigma }=h_{\mu }^{~~\nu }p_{,\nu }+(\rho +p)\dot{u}_{\mu }=0, \end{aligned}$$
(7)

where \(\dot{\rho }=u^{\mu }\rho _{,\mu }\) is the proper time derivative and \(h^{\mu \nu }\) is the projection tensor \(h^{\mu \nu }=u^{\mu }u^{\nu }+g^{\mu \nu }\).

By inserting the line element (1) and the energy-momentum tensor (3) into Einstein field equations the time-time component of the field equations will be

$$\begin{aligned} \left( \frac{R_{,t}}{R}\right) ^2+\frac{\left( K+k_{0}\right) }{R^2}=\frac{8 \pi G}{3}\rho , \end{aligned}$$
(8)

where

$$\begin{aligned} k_{0}={\left\{ \begin{array}{ll} 0,&{} \hbox {for}\, f=r, F=\dfrac{r}{2},\\ 1,&{} \hbox {for}\, f=\sin (r), F=\sin \left( \dfrac{r}{2}\right) ,\\ \,-1,&{} \hbox {for}\, f=\sinh (r), F=\sinh \left( \dfrac{r}{2}\right) . \end{array}\right. } \end{aligned}$$
(9)

Equation (8) shows that \(\rho \) is a function of \(t\) only. We can obtain the form of pressure \(p(r,t)\) from Eq. (6) as

$$\begin{aligned} p(r,t)=-\rho (t)- \frac{R}{3}\frac{\rho _{,t}}{R_{,t}}\left[ \frac{1+KF^2}{1+F^2\left( K-RK_{,R}\right) }\right] , \end{aligned}$$
(10)

and from the equation of momentum balance (7) we arrive at

$$\begin{aligned} \acute{p}+\frac{fR^2\rho _{,R}K_{,R}}{6[1+(K-RK_{,R})F^2]^2}=0, \end{aligned}$$
(11)

where prime denotes derivative with respect to \(r\).

The Stephani universe has two arbitrary functions of time \((K(t), R(t))\) whose values are not prescribed [13]. We suppose that the curvature parameter and the matter energy density have the following power-law forms [36]:

$$\begin{aligned} K\left( t\right) =\beta \left( \frac{R}{R_{0}}\right) ^n, \end{aligned}$$
(12)

and

$$\begin{aligned} \rho =\rho _{0}\left( \frac{R}{R_{0}}\right) ^\alpha , \end{aligned}$$
(13)

we set \(\alpha =-3(1+w_{0})\) where \(w_{0}\) is the equation of state parameter which exists in FLRW models, \(\beta \) and \(n\) are constants, \(R_{0}\) and \(\rho _{0}\) are the present values of the scale factor and matter energy density, respectively. A time derivative of Eq. (8) leads to the Raychaudhuri equation given by

$$\begin{aligned} \frac{R_{,tt}}{R}=-\frac{4\pi G}{3}(1+3w_{0})\rho -\frac{\beta n}{2R_{0}^2}\left( \frac{R}{R_{0}}\right) ^{n-2}. \end{aligned}$$
(14)

Inserting Eqs. (12) and (13) into Eq. (10) leads to

$$\begin{aligned} p(r,t)=\left( -1+\frac{\left( 1+w_{0}\right) (1+\beta (\frac{R}{R_{0}})^nF^2)}{1+\beta (\frac{R}{R_{0}})^n (1-n)F^2}\right) \rho (t). \end{aligned}$$
(15)

Note that at the symmetry center \((r\simeq 0)\) for a matter-dominated universe \((w_{0}=0)\) pressure vanishes, but at large distances from the symmetry center it will be negative, thus in the presence of a non-relativistic matter, due to a negative pressure at large distances, the expansion can be observed. By comparing Eq. (15) with the general equation of state with a non-constant parameter \(w\equiv \dfrac{p}{\rho }\) we get

$$\begin{aligned} w(r,t)=\left( -1+\frac{\left( 1+w_{0}\right) (1+\beta (\frac{R}{R_{0}})^nF^2)}{1+\beta (\frac{R}{R_{0}})^n (1-n)F^2}\right) , \end{aligned}$$
(16)

which can be regarded as the dynamical equation of state parameter for the Stephani universe. For \(\beta =0\) (switching off the inhomogeneities), we have \(w=w_{0}\) and the model reduces to the FLRW universe.

3 Hubble and deceleration parameters

In order to study the cosmological parameters which can be determined via observational data, it is important to derive some of the observational quantities in the Stephani universe. The kinematics of the universe is described by the Hubble parameter \(H\) and the deceleration parameter \(q\). For calculating these parameters we rewrite the metric (1) in the comoving coordinate \([\tau , r, \theta , \phi ]\) which reduces to

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}\tau ^2+V^2[\mathrm{d}r^2+f^2(\mathrm{d}\theta ^2+\sin ^2\theta d\phi ^2)], \end{aligned}$$
(17)

where we have defined

$$\begin{aligned} D^2\mathrm{d}t^2=\mathrm{d}\tau ^2. \end{aligned}$$
(18)

Now the definitions for \(H \) and \(q\) will be

$$\begin{aligned} H=\frac{1}{V}\frac{\partial V}{\partial \tau },~~~~ q=-\frac{1}{H^2V}\frac{\partial ^2V}{\partial \tau ^2}. \end{aligned}$$
(19)

Note that due to the inhomogeneity that occurs in this universe, the Hubble and deceleration parameters will no longer be spatially constant. However, it is possible to choose a time parameter in which the spatial dependence of the Hubble and deceleration parameters can vanish [33]. Consequently, the above definition for the Hubble parameter reduces to

$$\begin{aligned} H=\frac{1}{R}\frac{\mathrm{d}R}{\mathrm{d}t}. \end{aligned}$$
(20)

Also the deceleration parameter reads

$$\begin{aligned} q\left( r,t\right)&= -\frac{1+\beta \left( \frac{R}{R_{0}}\right) ^nF^2}{1+\beta (1-n)\left( \frac{R}{R_{0}}\right) ^n F^2}\frac{R_{,tt}}{H^2 R}\nonumber \\&+\frac{n\beta \left( \frac{R}{R_{0}}\right) ^nF^2}{1+\beta (1-n) \left( \frac{R}{R_{0}}\right) ^n F^2}, \end{aligned}$$
(21)

which can be rewritten as

$$\begin{aligned} q\left( r,t\right) =\frac{\left( 1+\beta \left( \frac{R}{R_{0}}\right) ^nF^2\right) \tilde{q}+n\beta \left( \frac{R}{R_{0}}\right) ^nF^2}{1+\beta (1-n)\left( \frac{R}{R_{0}}\right) ^n F^2}, \end{aligned}$$
(22)

where

$$\begin{aligned} \tilde{q}\!\equiv \!-\dfrac{R_{,tt}}{H^2 R}\!=\!\frac{\frac{4\pi G }{3}\rho _{0}(1\!+\!3w_{0})\left( \!\frac{R}{R_{0}}\!\right) ^{\!-3(1+w_{0})}\!\! +\!\frac{n\beta }{2R_{0}^2}\left( \!\frac{R}{R_{0}}\!\right) ^{n-2}}{\frac{8\pi G}{3}\rho _{0}\left( \!\frac{R}{R_{0}}\!\right) ^{\!-3(1+w_{0})}\!-\! \frac{k_{0}}{R_{0}^2}\left( \frac{R}{R_{0}}\right) ^{\!-2} \!-\!\frac{\beta }{R_{0}^2}\left( \!\frac{R}{R_{0}}\!\right) ^{n-2}}. \end{aligned}$$
(23)

With \(n=1\) Eq. (22) reduces to the deceleration parameter obtained in the work by Stelmach and Jakacka [32] in which they showed that with a negative \(\beta \) the deceleration parameter decreases with increasing distance to the observed galaxy.

The resemblance of Eq. (8) with the first dynamical equation of the FLRW universe allows us to insert Eqs. (12) and (13) into Eq. (8) to get an expression between \(H, H_{0}, \Omega \) and \(R\)

$$\begin{aligned} \left( \frac{H}{H_{0}}\right) ^2&= \Omega _{k_{0},0}\left( \frac{R}{R_{0}}\right) ^{-2}+ \Omega _{0,0}\left( \frac{R}{R_{0}}\right) ^{-3(1+w_{0})}\nonumber \\&+\left( 1-\Omega _{0,0}-\Omega _{k_{0},0}\right) \left( \frac{R}{R_{0}}\right) ^{n-2}, \end{aligned}$$
(24)

where

$$\begin{aligned} \Omega _{0,0}=\frac{\rho _{0}}{\rho _{cr}}\mid _{t=t_{0}}, \quad \Omega _{k_{0,0}}=\frac{-k_{0}}{R_{0}^2H_{0}^2}. \end{aligned}$$
(25)

Moreover, by setting \(t=t_{0}\) in Eq. (24) the value of the constant \(\beta \) is given by

$$\begin{aligned} \beta =\left( \Omega _{0,0}+\Omega _{k_{0},0} -1 \right) R_{0}^2H_{0}^2. \end{aligned}$$
(26)

Now we can find the age of the universe by integrating Eq. (24), which yields

$$\begin{aligned} t_{0}\!=\!\frac{1}{H_{0}}\int ^{1}_{0}\!\frac{dx}{x\sqrt{\Omega _{0,0}x^{-3(1+w_{0})}\!+\! \Omega _{k_{0},0}x^{-2}\!+\!\left( 1\!-\!\Omega _{0}\!-\!\Omega _{k_{0},0}\right) x^{n-2} }}; \end{aligned}$$
(27)

here \(x=\dfrac{R}{R_{0}}\) is the scale of the universe in units \(R_{0}\). With \(n=1\) Eq. (27) corresponds to the age of the universe obtained in the work by Stelmach and Jakacka [33]. For the present epoch we assume that the universe is only composed of dust \((w_{0}=0)\) and for simplicity in our calculations we put \(k_{0}=0\) as we do in flat FLRW models. Accordingly, Eqs. (21), (24), and (27) reduce to

$$\begin{aligned} q(r,t)&= \frac{1}{2}\left( \frac{1+\beta \left( \frac{R}{R_{0}}\right) ^nF^2}{1+\beta (1-n)\left( \frac{R}{R_{0}}\right) ^nF^2}\right) \nonumber \\&\times \left( \frac{ \Omega _{m,0}+n(\Omega _{m,0}-1) \left( \frac{R}{R_{0}}\right) ^{n+1}}{ \Omega _{m,0}-n(\Omega _{m,0}-1) \left( \frac{R}{R_{0}}\right) ^{n+1}}\right) \nonumber \\&+\frac{n\beta \left( \frac{R}{R_{0}}\right) ^nF^2}{1+\beta (1-n)\left( \frac{R}{R_{0}}\right) ^nF^2}, \end{aligned}$$
(28)
$$\begin{aligned} t_{0}=\frac{1}{H_{0}}\int ^{1}_{0}\frac{dx}{x\sqrt{\Omega _{m,0}x^{-3}+ \left( 1-\Omega _{m,0}\right) x^{n-2} }}, \end{aligned}$$
(29)

and

$$\begin{aligned} \left( \frac{H}{H_{0}}\right) ^2=\Omega _{m,0}\left( \frac{R}{R_{0}}\right) ^{-3}+\left( 1-\Omega _{m,0}\right) \left( \frac{R}{R_{0}}\right) ^{n-2}, \end{aligned}$$
(30)

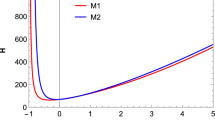
respectively. The lookback time \((t^{\prime }{}=tH_{0})\) as a function of the energy density \(\Omega _{m,0}\) in the model for some specific values of \(n\) and in the FLRW models are presented in Fig. 1. We realize that the age of the universe in the discussed model for \(n>2\) is larger than in FLRW models corresponding to the same values of the parameters \( H_{0}=67\) \({Km Mpc^{-1} s^{-1}}\) and \(\Omega _{m}=0.31\) [34]. As an example according to Eq. (29) by setting \(n=3\) the age of the universe will be \(14.38\) Gyr.

Fig. 1
figure 1

Lookback time \(t^{\prime }{}=tH_{0}\) in the spherically symmetric Stephani cosmological model for some selected values of \(n\) and in FLRW model as a function of the energy density \(\Omega _{m,0}\)

Full size image

At the late stage of the cosmological evolution when the scale factor is large, the first and the second terms in Eq. (30) can dominate and we can apply the following approximations. From now on we assume that \(\mid \beta x^n F^2\mid \gg 1\). We consider Eq. (30) in the late time epoch which can be solved for the scale factor to yield

$$\begin{aligned} \frac{R}{R_{0}}\!\simeq \!{\left\{ \begin{array}{ll} \frac{1}{4}H_{0}^2(1-\Omega _{m,0})t^{2},&{} n=1,\\ \exp [\sqrt{1-\Omega _{m,0}}H_{0}t],&{} n=2,\\ \left[ H_{0}\left( 1-\frac{n}{2}\right) \sqrt{1-\Omega _{m,0}}\right] ^{\frac{2}{2-n} }t^{\frac{2}{2-n}},&{} n\!>\!1,\quad or \quad -1\!<\!n\!<\!0,\\ (\frac{3}{2}H_{0}\sqrt{\Omega _{m,0}})^\frac{2}{3} t^{\frac{2}{3}},&{} n<-1. \end{array}\right. } \end{aligned}$$
(31)

We should point out that the case \(n=2\) has an exponential form for the scale factor in the late time stage which is the same as the vacuum FLRW models with cosmological constant. However, as mentioned before, the universe in this model is only filled with dust which leads to the above expressions. In the case \(n<-1\) we get a sort of dust dominated universe. It follows from Eq. (31) that the deceleration parameter for the late time epoch can be derived for the above stages as

$$\begin{aligned} q\left( r,t\right) \!\simeq \!{\left\{ \begin{array}{ll} \frac{1}{2}(\Omega _{m,0}-1)R_{0}^2H_{0}^2(\frac{R}{R_{0}}) F^2,&{} n=1,\\ -1,&{} n=2,\\ \frac{n}{2(1-n)},&{} n\!>\!1,\quad -1\!<\!n\!<\!0,\\ \frac{1}{1-n}(n+\frac{1}{2}),&{} n<-1. \end{array}\right. } \end{aligned}$$
(32)

For all of the above values of \(n\), the deceleration parameter is negative, thus the accelerated expansion of the universe is obtained without using any exotic matter or cosmological constant. In Fig. 2 the deceleration parameter is plotted for \(n=2.5\) as a function of the dimensionless parameters \(y\equiv R_{0} H_{0}r\) and \(t^{\prime }{}=t_{0}H_{0}\).

Fig. 2
figure 2

The deceleration parameter in the spherically symmetric Stephani cosmological model as a function of the dimensionless parameters \(y\equiv R_{0} H_{0}r\) and \(t^{\prime }{}=t_{0}H_{0}\) for \(n=2.5\)

Full size image

It is seen from Fig. 2 that the acceleration becomes larger as the distance to the observed object is increased. In other words, in the inhomogeneous universe acceleration of the expansion increases with the distance.

It should also be noted that Eqs. (29) and (30) can be rewritten as

$$\begin{aligned} H^2=\frac{8\pi G}{3}\rho _{m}+B\rho _{m}^{\gamma }, \end{aligned}$$
(33)

where the constants \(B\) and \(\gamma \) are defined as

$$\begin{aligned} B=\frac{H_{0}^2(1-\Omega _{m,0})}{\rho ^{\gamma }_{m,0}},\quad \gamma =\frac{2-n}{3}. \end{aligned}$$
(34)

The above equation is similar to the model proposed by Freese and Lewis [34] which is an alternative model explaining the accelerating universe. This model is called Cardassian model where the FLRW equation is modified by the presence of the term \(\rho ^\gamma \). This seems to be interesting as regards the way that the expansion of the universe is accelerated automatically by the presence of the second term without suggesting any unknown form of exotic matter [35].

4 Conclusion

In this paper we considered the inhomogeneous Stephani universe characterized with a time dependent curvature index. Although we obtained results for general \(w\) (equation of state parameter), but we focused our attention on the model with only dust as the fluid component of the universe. We found the age of the universe in the model which was remarkably larger than the corresponding age in the FLRW models without exotic matter. We derived the deceleration parameter which was dependent on the scale factor and radial coordinate, moreover, we showed that the acceleration becomes larger while increasing the distance. The fore-mentioned results were based on the ansatz of the type \(K(t)=\beta \left( \frac{R}{R_{0}}\right) ^n\) for the spatial curvature parameter and we showed that in the late time epoch of evolution, by choosing the appropriate values for \(n\), the power-law solution can be revived in the considered model.