1 Introduction

It is widely believed now that the inclusive hadroproduction of two jets featuring transverse momenta of the same order and much larger than the typical hadronic masses and being separated by a large rapidity gap Y, the so-called Mueller–Navelet jets [1], is a fundamental testfield for perturbative QCD in the high-energy limit, the jet transverse momenta providing us with the hard scales of the process.

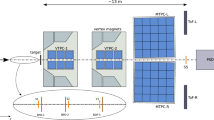
At the LHC energies, the theoretical description of this process lies at the crossing point of two distinct approaches: collinear factorization and BFKL [2–5] resummation. On one side, at leading twist the process can be seen as the hard scattering of two partons, each emitted by one of the colliding hadrons according to the appropriate parton distribution function (PDF); see Fig. 1. Collinear factorization takes care of systematically resumming the logarithms of the hard scale, through the standard DGLAP evolution [6–8] of the PDFs and the fixed-order radiative corrections to the parton scattering cross section.

The other resummation mechanism at work, justified by the large center-of-mass energy \(\sqrt{s}\) available at LHC, is the BFKL resummation of energy logarithms, which are so large as to compensate the small QCD coupling and must therefore be accounted for to all orders of perturbation. These energy logarithms are related with the emission of undetected partons between the two jets (the larges s, the larger the number of partons), which lead to a reduced azimuthal correlation between the two detected forward jets, in comparison to the fixed-order DGLAP calculation, where jets are emitted almost back-to-back.

In the BFKL approach energy logarithms are systematically resummed in the leading logarithmic approximation (LLA), which means all terms \((\alpha _s\ln (s))^n\), and in the next-to-leading logarithmic approximation (NLA), which means resummation of all terms \(\alpha _s(\alpha _s\ln (s))^n\). The process-independent part of such resummation is encoded in the BFKL Green’s function, obeying an iterative integral equation, whose kernel is known at the next-to-leading order (NLO) both for forward scattering (i.e. for \(t=0\) and color singlet in the t-channel) [9, 10] and for any fixed (not growing with energy) momentum transfer t and any possible two-gluon color state in the t-channel [11–17].

To get the cross section for Mueller–Navelet jet production and other related observables, the BFKL Green’s function must be convoluted with two impact factors for the transition from the colliding parton to the forward jet (the so-called “jet vertices”). They were first calculated with NLO accuracy in [18, 19] and the result was later confirmed in [20]. A simpler expression, more practical for numerical purposes, was obtained in [21] adopting the so-called “small-cone” approximation (SCA) [22–24], i.e. for small jet cone aperture in the rapidity-azimuthal angle plane. A critical comparison between the latter result and the exact jet vertex in the cases of \(k_t\) and cone algorithms and their “small-cone” versions has been recently carried out in [25]. We stress that, within NLO accuracy, the jet can be formed by either one or two particles and no more, so that the argument given in [25] about the non-infrared-safety of the all-order extension of the jet algorithm used to obtain the SCA jet vertex in [21] does not apply here.

Fig. 1
figure 1

Mueller–Navelet jet production process

Full size image

The BFKL approach brings along some extra-sources of systematic uncertainties with respect to the fixed-order, DGLAP calculation. First of all, in addition to the renormalization and factorization scales, \(\mu _R\) and \(\mu _F\), which appear also in DGLAP, there is a third, artificial normalization scale, usually called \(s_0\), which must be suitably fixed. Moreover, there is compelling evidence that choosing for these scales the values dictated by the kinematics of the process is not necessarily the best choice when the BFKL resummation is at work. It is well known, indeed, that the NLO BFKL corrections for the \(n=0\) conformal spin have opposite sign with respect to the leading order (LO) result and are large in absolute value. This happens both to the NLO BFKL kernel and to the process-dependent NLO impact factors (see, e.g., Refs. [26–28], for the case of the vector meson photoproduction). This calls for some optimization procedure, which can consist in (i) including some pieces of the (unknown) next-to-NLO corrections, such as those dictated by renormalization group, as in collinear improvement [29–39], or by energy–momentum conservation [40], and/or (ii) suitably choosing the values of the energy and renormalization scales, which, though arbitrary within the NLO, can have a sizeable numerical impact through subleading terms. Common optimization methods are those inspired by the principle of minimum sensitivity [41, 42], the fast apparent convergence [43–45] and the Brodsky–Lepage–Mackenzie method (BLM) [46].

This variety of options reflects in the large number of numerical studies of the Mueller–Navelet jet production process at LHC, both at a center-of-mass energy of 14 TeV [47–49] and 7 TeV [50–53]. All these studies were concerned with the behavior on Y of azimuthal angle correlations between the two measured jets, i.e. average values of \(\cos {(n \phi )}\), where n is an integer and \(\phi \) is the angle in the azimuthal plane between the direction of one jet and the opposite direction of the other jet, and ratios of two such cosines [54, 55]. In particular, one of these analyses [51], based on the use of a collinear improvement and energy scales optimized à la BLM, found a nice agreement with CMS data [56].

In a recent paper [53], some of us stressed that another important source of systematics on should be aware of is the “representation uncertainty”, deriving from the freedom to use different representation of the BFKL cross section, equivalent within the NLO.Footnote 1 The good agreement between CMS data and BLM-optimized theoretical predictions gives us perhaps a hint toward the right direction. In the same paper, a list of issues was presented which, if considered in the experimental analysis, could help the matching between the way Mueller–Navelet are defined in the theory and in the experiment. One of these issue was, for instance, the very measurement of the Mueller–Navelet total cross section, \(C_0\), which, on the theory side, is strongly sensitive both to the representation of the BFKL amplitude and to the optimization procedure.

In this paper we want to further discuss and expand on another of the issues listed in the “Discussion” section of [53], related with the choice of the experimental cuts in the values of the forward jet transverse momenta. Since the Born contribution to the cross section \(C_0\) is present only for back-to-back jets, its effect is maximized when symmetric cuts are used; on the contrary, in the case of asymmetric cuts, the Born term is suppressed, and the effects of the additional undetected hard gluon radiation is enhanced, thus making more visible the BFKL resummation, in comparison to descriptions based on the fixed-order DGLAP approach, in all observables involving \(C_0\).

For this purpose, we compare predictions for several azimuthal correlations and their ratios obtained, on one side, by a fixed-order DGLAP calculation at the NLO and, on the other side, by BFKL resummation in the NLA.

To avoid misunderstanding we note that in what follows our implementation of the NLO DGLAP calculation will be an approximate one. We just use here NLA BFKL expressions for the observables that are truncated to the \(\mathcal{O}\left( \alpha _s^3\right) \) order. In this way we take into account the leading power asymptotic of the exact NLO DGLAP prediction and neglect terms that are suppressed by the inverse powers of the energy of the parton–parton collisions. Such approach is legitimate in the region of large Y which we consider here. The exact implementation of NLO DGLAP for Mueller–Navelet jets is important, because it allows one to understand better the region of applicability of our approach, but it requires more involved Monte Carlo calculations (some first results were reported recently in [57]).

To single out the only effect of transverse momentum cuts, we consider just one representation of the Mueller–Navelet cross section (the exponentiated one) and just one optimization procedure (the BLM one, in the two variants discussed in [58]).

The paper is organized as follows: in the next section we give the kinematics and the basic formulas for the Mueller–Navelet jet process cross section; in Sect. 3 we present our results; finally, in Sect. 4 we draw our conclusions.

2 Theoretical setup

In this section we briefly recall the kinematics of the process and the main formulas, referring the reader to previous papers [48, 53] for the omitted details.

The process under exam is the production of Mueller–Navelet jets [1] in proton–proton collisions

$$\begin{aligned} p(p_1) + p(p_2) \rightarrow \mathrm{jet}(k_{J_1}) + \mathrm{jet}(k_{J_2})+ X , \end{aligned}$$
(1)

where the two jets are characterized by high transverse momenta, \({\vec {k}}_{J_1}^2\sim {\vec {k}}_{J_2}^2\gg \Lambda _{QCD}^2\) and large separation in rapidity; \(p_1\) and \(p_2\) are taken as Sudakov vectors satisfying \(p_1^2=p_2^2=0\) and \(2\left( p_1 p_2\right) =s\).

In QCD collinear factorization the cross section of the process (1) reads

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}x_{J_1}\mathrm{d}x_{J_2}\mathrm{d}^2k_{J_1}\mathrm{d}^2k_{J_2}}=\sum _{i,j=q,{\bar{q}},g}\int _0^1 \mathrm{d}x_1 \int _0^1 \mathrm{d}x_2\ f_i\left( x_1,\mu _F\right) \nonumber \\&\quad \times f_j\left( x_2,\mu _F\right) \frac{\mathrm{d}{\hat{\sigma }}_{i,j}\left( x_1x_2s,\mu _F\right) }{\mathrm{d}x_{J_1}\mathrm{d}x_{J_2}\mathrm{d}^2k_{J_1}\mathrm{d}^2k_{J_2}},\nonumber \\ \end{aligned}$$
(2)

where the i, j indices specify the parton types (quarks \(q = u, d, s, c, b\); antiquarks \(\bar{q} = \bar{u}, \bar{d}, \bar{s}, \bar{c}, \bar{b}\); or gluon g), \(f_i\left( x, \mu _F \right) \) denotes the initial proton PDFs; \(x_{1,2}\) are the longitudinal fractions of the partons involved in the hard subprocess, while \(x_{J_{1,2}}\) are the jet longitudinal fractions; \(\mu _F\) is the factorization scale; \(\mathrm{d}\hat{\sigma }_{i,j}\left( x_1x_2s, \mu _F \right) \) is the partonic cross section for the production of jets and \(x_1x_2s\equiv \hat{s}\) is the squared center-of-mass energy of the parton–parton collision subprocess (see Fig. 1).

The cross section of the process can be represented as

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}y_{J_1}\mathrm{d}y_{J_2}\, \mathrm{d}|{\vec {k}}_{J_1}| \, \mathrm{d}|{\vec {k}}_{J_2}| \mathrm{d}\phi _{J_1} \mathrm{d}\phi _{J_2}}\nonumber \\&\quad =\frac{1}{(2\pi )^2}\left[ \mathcal{C}_0+\sum _{n=1}^\infty 2\cos (n\phi )\, \mathcal{C}_n\right] , \end{aligned}$$
(3)

where \(\phi =\phi _{J_1}-\phi _{J_2}-\pi \), while \(\mathcal{C}_0\) gives the total cross section and the other coefficients \(\mathcal{C}_n\) determine the distribution of the azimuthal angle of the two jets. In the BFKL approach several NLA-equivalent expressions can be adopted for \(\mathcal{C}_n\). A large list of them and of their features can be found in [53]. For the purposes of the present analysis, we concentrate on one representation, the so-called exponentiated representation, and use it in combination with the BLM optimization procedure. We recall that BLM setting means choosing the scale \(\mu _R\) such that it makes vanish completely the \(\beta _0\)-dependence of a given observable. As discussed in [53], we implement two variants of the BLM method, dubbed (a) and (b), derived in [58]. Moreover, we use a common optimal scale for the renormalization scale \(\mu _R\) and for the factorization scale \(\mu _F\). In [53] it was shown that this setup allows a nice agreement with CMS data for several azimuthal correlations and their ratios in the large Y regime.

Introducing, for the sake of brevity, the definitions

$$\begin{aligned} Y=\ln \frac{x_{J_1}x_{J_2}s}{|{\vec {k}}_{J_1}||{\vec {k}}_{J_2}|},\quad Y_0=\ln \frac{s_0}{|{\vec {k}}_{J_1}||{\vec {k}}_{J_2}|}, \end{aligned}$$

we have then the following expressions for the coefficients \(\mathcal{C}_n\), in the two variants of BLM setting:

$$\begin{aligned}&\mathcal{C}_n^{\mathrm{BFKL}_{(a)}}= \frac{x_{J_1}x_{J_2}}{|{\vec {k}}_{J_1}| |{\vec {k}}_{J_2}|}\nonumber \\&\quad \times \int _{-\infty }^{+\infty }\mathrm{d}\nu \ e^{(Y-Y_0)[{\bar{\alpha }}_s(\mu _R)\chi (n,\nu ) +{\bar{\alpha }}_s^2(\mu _R)({\bar{\chi }}(n,\nu )- \frac{T^{\beta }}{C_A}\chi (n,\nu )-\frac{\beta _0}{8C_A} \chi ^2(n,\nu ))]}\nonumber \\&\quad \times \alpha _s^2(\mu _R)c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1}) c_2(n,\nu ,|{\vec {k}}_{J_2}|,x_{J_2})\nonumber \\&\quad \times \left[ 1-\frac{2}{\pi } \alpha _s\left( \mu _R\right) T^{\beta } \right. \nonumber \\&\quad \left. +\, \alpha _s\left( \mu _R\right) \left( \frac{\bar{c}_1^{\left( 1\right) } (n,\nu ,|{\vec {k}}_{J_1}|,x_{J_1})}{c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1})} +\frac{\bar{c}_2^{\left( 1\right) }(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}{c_2(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}\right) \right] , \end{aligned}$$
(4)

with \(\mu _R\) fixed at the value

$$\begin{aligned} (\mu _R^\mathrm{BLM})^2=k_{J_1}k_{J_2}\ \exp \left[ 2\left( 1+\frac{2}{3}I\right) -\frac{5}{3}\right] \; \end{aligned}$$
(5)

and

$$\begin{aligned}&\mathcal{C}_n^{\mathrm{BFKL}_{(b)}}\nonumber \\&\quad =\frac{x_{J_1}x_{J_2}}{|{\vec {k}}_{J_1}| |{\vec {k}}_{J_2}|}\int _{-\infty }^{+\infty }\mathrm{d}\nu \ e^{(Y-Y_0)[{\bar{\alpha }}_s(\mu _R)\chi (n,\nu )+{\bar{\alpha }}_s^2 (\mu _R)({\bar{\chi }}(n,\nu )-\frac{T^{\beta }}{C_A} \chi (n,\nu ))]}\nonumber \\&\qquad \times \alpha _s^2\left( \mu _R\right) c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1}) c_2(n,\nu ,|{\vec {k}}_{J_2}|,x_{J_2})\nonumber \\&\qquad \times \left[ 1+\alpha _s\left( \mu _R\right) \left( \frac{\beta _0}{4\pi } \chi \left( n,\nu \right) - 2\frac{T^{\beta }}{\pi }\right) \right. \nonumber \\&\qquad \left. + \alpha _s\left( \mu _R\right) \left( \frac{\bar{c}_1^{\left( 1\right) } (n,\nu ,|{\vec {k}}_{J_1}|,x_{J_1})}{c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1})} +\frac{\bar{c}_2^{\left( 1\right) }(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}{c_2(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}\right) \right] , \end{aligned}$$
(6)

with \(\mu _R\) fixed at the value

$$\begin{aligned} (\mu _R^\mathrm{BLM})^2=k_{J_1}k_{J_2}\ \exp \left[ 2\left( 1+\frac{2}{3}I\right) -\frac{5}{3}+\frac{1}{2}\chi \left( \nu ,n\right) \right] . \end{aligned}$$
(7)

In Eqs. (4) and (6), \(\bar{\alpha }_s(\mu _R) \equiv \alpha _s(\mu _R) N_c/\pi \), with \(N_c\) the number of colors, and

$$\begin{aligned} \beta _0=\frac{11}{3} N_c - \frac{2}{3}n_f \end{aligned}$$
(8)

is the first coefficient of the QCD \(\beta \)-function,

$$\begin{aligned} \chi \left( n,\nu \right) =2\psi \left( 1\right) -\psi \left( \frac{n}{2} +\frac{1}{2}+i\nu \right) -\psi \left( \frac{n}{2}+\frac{1}{2}-i\nu \right) \end{aligned}$$
(9)

is the LO BFKL characteristic function,

$$\begin{aligned}&c_1(n,\nu ,|{\vec {k}}|,x)=2\sqrt{\frac{C_F}{C_A}} ({\vec {k}}^{\,2})^{i\nu -1/2}\nonumber \\&\quad \times \left( \frac{C_A}{C_F}f_g(x,\mu _F)+\sum _{a=q,\bar{q}}f_q(x,\mu _F)\right) \end{aligned}$$
(10)

and

$$\begin{aligned} c_2(n,\nu ,|{\vec {k}}|,x)=\biggl [c_1(n,\nu ,|{\vec {k}}|,x) \biggr ]^* , \end{aligned}$$
(11)

are the LO jet vertices in the \(\nu \)-representation. The remaining objects are related with the NLO corrections of the BFKL kernel (\(\bar{\chi }(n,\nu )\)) and of the jet vertices in the SCA (\(c_{1,2}^{(1)}(n,\nu ,|{\vec {k}}_{J_{1,2}}|, x_{J_{1,2}})\)) in the \(\nu \)-representation. Their expressions are given in Eqs. (23), (36), and (37) of Ref. [48]. Moreover,

$$\begin{aligned} T^{\beta } = -\frac{\beta _0}{2}\left( 1+\frac{2}{3}I \right) , \end{aligned}$$

where \(I=-2\int _0^1\mathrm{d}x\frac{\ln \left( x\right) }{x^2-x+1}\simeq 2.3439\) and \(\bar{c}_{1,2}^{(1)}(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})\) are the same as \(c_{1,2}^{(1)}(n,\nu ,|{\vec {k}}_{J_{1,2}}|, x_{J_{1,2}})\) with the terms proportional to \(\beta _0\) removed. The scale \(s_0\) entering \(Y_0\) is artificial. It is introduced in the BFKL approach at the time to perform the Mellin transform from the s-space to the complex angular momentum plane and cancels in the full expression, up to terms beyond the NLA. In the following it will always be fixed at the “natural” value \(Y_0=0\).

Table 1 Ratios \(C_n/C_m\) for \(k_{J_1,\mathrm min}=35\) GeV and \(k_{J_2,\mathrm min}=45\) GeV
Full size table
Table 2 Ratios \(C_n/C_m\) for \(k_{J_1,\mathrm min}=35\) GeV and \(k_{J_2,\mathrm min}=50\) GeV
Full size table

In the fixed-order DGLAP approach at the NLO, the expressions for the coefficients \(\mathcal{C}_n\) are nothing but the truncation of the BFKL expressions up to inclusions of NLO terms and read

$$\begin{aligned}&\mathcal{C}_n^\mathrm{DGLAP_{(a)}} = \frac{x_{J_1}x_{J_2}}{|{\vec {k}}_{J_1}| |{\vec {k}}_{J_2}|}\int _{-\infty }^{+\infty }\mathrm{d}\nu \ \alpha _s^2\left( \mu _R\right) \nonumber \\&\quad \quad \times c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1}) c_2(n,\nu ,|{\vec {k}}_{J_2}|,x_{J_2})\nonumber \\&\quad \quad \times \left[ 1 - \frac{2}{\pi } \alpha _s\left( \mu _R\right) T^{\beta } + \bar{\alpha }_s\left( \mu _R\right) \left( Y - Y_0 \right) \chi \left( n,\nu \right) \right. \nonumber \\&\quad \quad +\left. \alpha _s\left( \mu _R\right) \left( \frac{\bar{c}_1^{\left( 1\right) } (n,\nu ,|{\vec {k}}_{J_1}|,x_{J_1})}{c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1})} +\frac{\bar{c}_2^{\left( 1\right) }(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}{c_2(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}\right) \right] ,\nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned}&\mathcal{C}_n^\mathrm{DGLAP_{(b)}} = \frac{x_{J_1}x_{J_2}}{|{\vec {k}}_{J_1}| |{\vec {k}}_{J_2}|}\int _{-\infty }^{+\infty }\mathrm{d}\nu \ \alpha _s^2\left( \mu _R\right) \nonumber \\&\quad \times c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1}) c_2(n,\nu ,|{\vec {k}}_{J_2}|,x_{J_2})\nonumber \\&\quad \times \left[ 1 +\alpha _s\left( \mu _R\right) \left( \frac{\beta _0}{4\pi } \chi \left( n,\nu \right) - 2\frac{T^{\beta }}{\pi }\right) \right. \nonumber \\&\quad +\left. \bar{\alpha }_s\left( \mu _R\right) \left( Y - Y_0 \right) \chi \left( n,\nu \right) +\alpha _s\left( \mu _R\right) \right. \nonumber \\&\quad \times \left. \left( \frac{\bar{c}_1^{\left( 1\right) } (n,\nu ,|{\vec {k}}_{J_1}|,x_{J_1})}{c_1(n,\nu ,|{\vec {k}}_{J_1}|, x_{J_1})} +\frac{\bar{c}_2^{\left( 1\right) }(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}{c_2(n,\nu ,|{\vec {k}}_{J_2}|, x_{J_2})}\right) \right] ,\nonumber \\ \end{aligned}$$
(13)

which we will use in the following with the two possible choices (a) and (b) of the optimal scales, given in Eqs. (5) and (7), respectively. It is worth mentioning that our DGLAP expressions, Eqs. (12) and (13), do not actually depend on \(Y_0\). The corresponding terms in the r.h.s. of (12) and (13) are canceled by similar terms in \(c^{(1)}_{1, 2}\); see [48].

We note that, in our way to implement the BLM procedure (see [58]), the final expressions are given in terms of \(\alpha _s\) in the \(\overline{\mathrm{MS}}\) scheme, although in one intermediate step the MOM scheme was used.

3 Numerical analysis

3.1 Results

In this section we present our results for the dependence on the rapidity separation between the detected jets, \(Y=y_{J_1}-y_{J_2}\), of ratios \(\mathcal{R}_{nm}\equiv \mathcal{C}_n/\mathcal{C}_m\) between the coefficients \(\mathcal{C}_n\). Among them, the ratios of the form \(R_{n0}\) have a simple physical interpretation, being the azimuthal correlations \(\langle \cos (n\phi )\rangle \).

In order to match the kinematic cuts used by the CMS collaboration, we will consider the integrated coefficients given by

$$\begin{aligned} C_n= & {} \int _{y_{1,\mathrm min}}^{y_{1,\mathrm max}}\mathrm{d}y_1 \int _{y_{2,\mathrm min}}^{y_{2,\mathrm max}}\mathrm{d}y_2\int _{k_{J_1,\mathrm min}}^{\infty }\mathrm{d}k_{J_1}\nonumber \\&\times \int _{k_{J_2,\mathrm min}}^{\infty }\mathrm{d}k_{J_2} \delta \left( y_1-y_2-Y\right) \mathcal{C}_n \left( y_{J_1},y_{J_2},k_{J_1},k_{J_2} \right) \nonumber \\ \end{aligned}$$
(14)

and their ratios \(R_{nm}\equiv C_n/C_m\). We will take jet rapidities in the range delimited by \(y_{1,\mathrm min}=y_{2,\mathrm min}=-4.7\) and \(y_{1,\mathrm max}=y_{2,\mathrm max}=4.7\) Footnote 2 and consider \(Y=3\), 6, and 9. As for the jet transverse momenta, differently from all previous analyses, we make two asymmetric choices: (1) \(k_{J_1,\mathrm min} = 35\) GeV, \(k_{J_2,\mathrm min} = 45\) GeV and (2) \(k_{J_1,\mathrm min} = 35\) GeV, \(k_{J_2,\mathrm min} = 50\) GeV. The jet cone size R entering the NLO-jet vertices is fixed at the value \(R=0.5\), the center-of-mass energy at \(\sqrt{s}=7\) TeV and, as anticipated, \(Y_0=0\). We use the PDF set MSTW2008nlo [59] and the two-loop running coupling with \(\alpha _s\left( M_Z\right) =0.11707\).

Fig. 2
figure 2

Y-dependence of several ratios \(C_m/C_n\) for \(k_{J_1,\mathrm min}=35\) GeV and \(k_{J_2,\mathrm min}=45\) GeV, for BFKL and DGLAP in the two variants of the BLM method (data points have been slightly shifted along the horizontal axis for the sake of readability)

Full size image
Fig. 3
figure 3

Y-dependence of several ratios \(C_m/C_n\) for \(k_{J_1,\mathrm min}=35\) GeV and \(k_{J_2,\mathrm min}=50\) GeV, for BFKL and DGLAP in the two variants of the BLM method (data points have been slightly shifted along the horizontal axis for the sake of readability)

Full size image

We summarize our results in Tables 1, 2 and Figs. 2, 3. We can clearly see that, at \(Y=9\), BFKL and DGLAP, in both variants (a) and (b) of the BLM setting, give quite different predictions for all considered ratios except \(C_1/C_0\); at \(Y=6\) this happens in fewer cases, while at \(Y=3\) BFKL and DGLAP cannot be distinguished with given uncertainties. This scenario is similar in the two choices of the transverse momentum cuts.

3.2 Used tools

All numerical calculations were implemented in Fortran, using the corresponding interfaces for the MSTW 2008 PDFs [59]. Numerical integrations and the computation of the polygamma functions were performed using specific CERN program libraries [60]. Furthermore, we used slightly modified versions of the Chyp [61] and Psi [62] routines in order to perform the calculation of the Gauss hypergeometric function \(_2F_1 \) and of the real part of the \(\psi \) function, respectively.

3.3 Uncertainty estimation

The are three main sources of uncertainty in our calculation:

  • The first source of uncertainty is the numerical four-dimensional integration over the variables \(|{\vec {k}}_{J_1}|\), \(|{\vec {k}}_{J_2}|\), \(y_{J_1}\) and \(\nu \) and was directly estimated by Dadmul integration routine [60].

  • The second one is the one-dimensional integration over the longitudinal momentum fraction \(\zeta \) entering the expression for the NLO impact factors \(c_{1,2}^{(1)}(n,\nu ,|{\vec {k}}_{J_{1,2}}|, x_{J_{1,2}})\) given in Eqs. (36) and (37) of Ref. [48] and used in this work. This integration was performed by using the WGauss routine [60]. At first, we fixed the best value of the input accuracy parameter EPS by making comparisons between separate Fortran and Mathematica calculations of the impact factor. Then we verified that, under variations by factors of 10 or 1/10 of the EPS parameter, the \(C_n^\mathrm{BFKL}\) and \(C_n^\mathrm{DGLAP}\) coefficients change by less than 1 permille.

  • The third one is related with the upper cutoff in the integrations over \(|{\vec {k}}_{J_1}|\), \(|{\vec {k}}_{J_2}|\) and \(\nu \). We fixed \(k_{J_1 \mathrm max}=k_{J_2 \mathrm max} = 60\) GeV as in [50], where it was shown that the contribution to the integration from the omitted region is negligible. Concerning the \(\nu \)-integration, we fixed the upper cutoff \(\nu _\mathrm{max}=30\) for the calculation of the \(C_n^\mathrm{BFKL}\) coefficients, after verifying that a larger value does not change the result in appreciable way. The \(C_n^\mathrm{DGLAP}\) coefficients show a more pronounced sensitivity to \(\nu _\mathrm{max}\), due to the fact that the oscillations in the integrand in Eqs. (12) and (13) are not dumped by the exponential factor as in the BFKL expressions (4) and (6). For the same reason, the computational time of \(C_n^\mathrm{DGLAP}\) is much larger than for \(C_n^\mathrm{BFKL}\). We found that the best compromise was to set \(\nu _\mathrm{max} = 50\). We checked in some sample cases, mostly at \(Y=6\) and 9, that, putting \(\nu _\mathrm{max}\) at 60, the ratios \(C_m/C_n\) change always less than 1%, in spite of the fact that the single coefficients \(C_n\) change in a more pronounced way.

Of the three main sources of uncertainty, the first one is, by far, the most significant, therefore the error bars of all data presented in this work are just those given by the Dadmul integration. We checked, however, using some trial functions which mimic the behavior of the true integrands involved in this work, that the error given by the Dadmul integration is a large overestimate of the true one. We are therefore confident that our error estimation is quite conservative.

4 Conclusions

In this paper we have considered the Mueller–Navelet jet production process at LHC at the center-of-mass energy of 7 TeV and have compared predictions for several azimuthal correlations and ratios between them, both in full NLA BFKL approach and in fixed-order NLO DGLAP.

Differently from current experimental analyses of the same process, we have used asymmetric cuts for the transverse momenta of the detected jets. In particular, taking one of the cuts at 35 GeV (as done by the CMS collaboration [56]) and the other at 45 or 50 GeV, we can clearly see that predictions from BFKL and DGLAP become separate for most azimuthal correlations and ratios between them, this effect being more and more visible as the rapidity gap between the jets, Y, increases. In other words, in this kinematics the additional undetected parton radiation between the jets which is present in the resummed BFKL series, in comparison to just one undetected parton allowed by the NLO DGLAP approach, makes its difference and leads to more azimuthal angle decorrelation between the jets, in full agreement with the original proposal of Mueller and Navelet.

This result was not unexpected: the use of symmetric cuts for jet transverse momenta maximizes the contribution of the Born term, which is present for back-to-back jets only and is expected to be large, therefore making less visible the effect of the BFKL resummation. This phenomenon could be at the origin of the instabilities observed in the NLO fixed-order calculations of [63, 64].

Another important benefit from the use of asymmetric cuts, pointed out in [52], is that the effect of violation of the energy–momentum conservation in the NLA is strongly suppressed with respect to what happens in the LLA.

In view of all these considerations, we strongly suggest experimental collaborations to consider also asymmetric cuts in jet transverse momenta in all future analyses of Mueller–Navelet jet production process.