Vacuum stability and naturalness in type-II seesaw

Abstract

We study the vacuum stability and perturbativity conditions in the minimal type-II seesaw model. These conditions give characteristic constraints to the model parameters. In the model, there is a $SU(2)_L$ triplet scalar field, which could cause a large Higgs mass correction. From the naturalness point of view, heavy Higgs masses should be lower than $350\,\mathrm{GeV}$, which may be testable by the LHC Run-II results. Due to the effects of the triplet scalar field, the branching ratios of the Higgs decay ($h\rightarrow \gamma \gamma , Z\gamma$) deviate from the standard model, and a large parameter region is excluded by the recent ATLAS and CMS combined analysis of $h\rightarrow \gamma \gamma$. Our result of the signal strength for $h\rightarrow \gamma \gamma$ is $R_{\gamma \gamma } \lesssim 1.1$, but its deviation is too small to observe at the LHC experiment.

1 Introduction

Current experimental results at the LHC are almost consistent with the predictions in the standard model (SM). However, the discovery of neutrino oscillations established that active neutrinos are massive, and their masses are much smaller than those of the other SM fermions. Since the SM cannot explain nonzero neutrino masses, the existence of nonzero neutrino masses is evidence of physics beyond the SM. The simplest way to obtain nonzero neutrino masses is breaking the global $B-L$ symmetry, which is expressed by an effective dimension-5 operator [1]. There are three ways to induce the effective dimension-5 operator at tree level, that is, the so-called seesaw mechanism. There are additional particles to the SM: the SM gauge singlet Majorana neutrinos, an $SU(2)_L$ triplet scalar field with hypercharge $Y=2$, and an $SU(2)_L$ triplet fermion with hypercharge $Y=0$ in type-I [2–5], II [6–11], and III [12] seesaw mechanism, respectively. Their collider phenomenologies have been studied in Ref. [13] for example.

In this paper, we will focus on the minimal type-II seesaw model with a single $SU(2)_L$ triplet scalar field. The existence of the triplet scalar field can significantly change the electroweak (EW) vacuum structure, and the vacuum can become stable up to the Planck scale [14–20]. The vacuum stability and perturbativity conditions yield characteristic constraints between the model parameters. In addition, since the triplet scalar field couples directly to the SM gauge bosons ($W^\pm$, Z, $\gamma$), its VEV affects $\rho$-parameter at tree level, and decay rates of the SM-like Higgs boson ($h\rightarrow \gamma \gamma , Z\gamma$) are different from the SM case. Thus, the type-II seesaw model is relatively easy to test at the collider experiments compared to type-I and III seesaw models. We will find that large parameter region can be excluded by the recent ATLAS and CMS combined analysis for the signal strength of $h\rightarrow \gamma \gamma$.

On the other hand, the gauge hierarchy problem generally arises when the SM is extended with some heavy particles which couple to the Higgs doublet. In the SM, all operators are renormalizable, and there is no quadratic divergence in terms of the dimensional regularization. Moreover, radiative corrections (or renormalization group evolution) of the Higgs mass term does not change its order of magnitude, and hence, the SM itself is ${ natural}$. However, adding a heavy particle into the SM and integrating it out, the Higgs mass term receives a contribution of the heavy particle. It is proportional to $M^2$, where M is a heavy particle mass. When the contribution is much larger than the EW scale, there should be a fine-tuning to realize the Higgs mass of $125\,\mathrm{GeV}$, unless the Higgs mass term is protected by a symmetry, for example, supersymmetry, shift symmetry, or conformal symmetry (scale invariance). In this paper, we do not consider such a symmetry, but simply impose a naturalness condition that contributions of the heavy triplet scalar field should be lower than the measured Higgs mass. As a result, we will find an upper bound on heavy Higgs masses to be around $350\,\mathrm{GeV}$.

This paper is organized as follows. In Sect. 2, we briefly review the type-II seesaw model and derive mass eigenstates of the scalar sector. In Sect. 3, we summarize the vacuum stability and unitarity conditions, and define our naturalness condition. In Sect. 4, we show the allowed parameter space of scalar quartic couplings and branching ratios of $h\rightarrow \gamma \gamma , Z\gamma$. Our conclusions are given in Sect. 5.

2 Review of the type-II seesaw model

We consider the minimal type-II seesaw model (for more detailed discussion, see e.g., [21]), where, in addition to the SM fields, a triplet scalar field $\Delta$ is introduced, which transforms as $(\mathbf{1},\mathbf{3},2)$ under the $SU(3)_C \times SU(2)_L \times U(1)_Y$ gauge group:

$$\begin{aligned} \Delta = \frac{\sigma ^i}{\sqrt{2}}\Delta _i = \left( \begin{array}{cc} \delta ^+/\sqrt{2} &{} \delta ^{++}\\ \delta ^0 &{} -\delta ^+/\sqrt{2} \end{array} \right) , \end{aligned}$$

(1)

with $\Delta _1=(\delta ^{++}+\delta ^0)/\sqrt{2},~\Delta _2=i(\delta ^{++}-\delta ^0)/\sqrt{2},~\Delta _3=\delta ^+$. The Lagrangian for this model is given by

$$\begin{aligned} \mathcal{L} = \mathcal{L}_\mathrm{kinetic} + \mathcal{L}_Y - \mathcal{V}(\Phi ,\Delta ), \end{aligned}$$

(2)

where the relevant kinetic and Yukawa interaction terms are, respectively,

$$\begin{aligned}&\mathcal{L}_\mathrm{kinetic} = \mathcal{L}_\mathrm{kinetic}^\mathrm{SM} + \mathrm{Tr}\left[ \left( D_\mu \Delta \right) ^\dag \left( D^\mu \Delta \right) \right] ,\end{aligned}$$

(3)

$$\begin{aligned}&\mathcal{L}_Y = \mathcal{L}_Y^\mathrm{SM} - \frac{1}{\sqrt{2}}\left( Y_\Delta \right) _{ij} L_i^\mathsf{T}Ci\sigma _2\Delta L_j+\mathrm{H.c.} . \end{aligned}$$

(4)

Here C is the Dirac charge conjugation matrix with respect to the Lorentz group, and

$$\begin{aligned} D_\mu \Delta = \partial _\mu \Delta + i\frac{g}{2}[\sigma ^a W_\mu ^a,\Delta ] + i\frac{g'}{2}B_\mu \Delta \quad (a=1,2,3)\nonumber \\ \end{aligned}$$

(5)

is the covariant derivative of the scalar triplet field, with the GUT-normalization for the electroweak couplings $g=g_2$ and $g'=\sqrt{3/5}g_1$.

Following the notation of [22, 23], we write the scalar potential in Eq. (2) as¹

$$\begin{aligned} \mathcal{V}(\Phi , \Delta )= & {} - m_\Phi ^2 \Phi ^\dagger \Phi \nonumber \\&+ \frac{\lambda }{2} (\Phi ^\dagger \Phi )^2 + M_\Delta ^2 \mathrm{Tr}(\Delta ^\dagger \Delta ) + \frac{\lambda _1}{2} \left[ \mathrm{Tr}(\Delta ^\dagger \Delta ) \right] ^2 \nonumber \\&+ \frac{\lambda _2}{2} \left( \left[ \mathrm{Tr}(\Delta ^\dagger \Delta ) \right] ^2 - \mathrm{Tr} \left[ (\Delta ^\dagger \Delta )^2 \right] \right) \nonumber \\&+ \lambda _4 (\Phi ^\dagger \Phi ) \mathrm{Tr}(\Delta ^\dagger \Delta ) + \lambda _5 \Phi ^\dagger [\Delta ^\dagger , \Delta ] \Phi \nonumber \\&+ \left( \frac{\Lambda _6}{\sqrt{2}} \Phi ^\mathrm{T} i \sigma _2 \Delta ^\dagger \Phi + \mathrm{H.c}. \right) . \end{aligned}$$

(6)

We have chosen $m_\Phi ^2>0$ in order to ensure the spontaneous EW symmetry breaking. Stationary conditions of the scalar potential lead to

$$\begin{aligned} m_\Phi ^2= & {} \frac{1}{2}\lambda v^2 - \Lambda _6 v_\Delta + \frac{1}{2} (\lambda _4-\lambda _5) v_\Delta ^2, \end{aligned}$$

(7)

$$\begin{aligned} M_\Delta ^2= & {} \frac{1}{2} \frac{\Lambda _6 v^2}{v_\Delta } - \frac{1}{2} (\lambda _4-\lambda _5) v^2 - \frac{1}{2} \lambda _1 v_\Delta ^2, \end{aligned}$$

(8)

where v and $v_\Delta$ are VEVs of neutral components of $\Phi$ and $\Delta$, respectively. The nonzero $v_\Delta$ makes the $\rho$-parameter deviate from unity at the tree level as

$$\begin{aligned} \rho \equiv \frac{M_W^2}{M_Z^2 \cos ^2 \theta _W} = \frac{1+\frac{2v_\Delta ^2}{v^2}}{1+\frac{4v_\Delta ^2}{v^2}}, \end{aligned}$$

(9)

with the gauge boson masses given by

$$\begin{aligned} M_W^2 = \frac{g_2^2}{2} \left( v^2 + 2 v_\Delta ^2 \right) ,\quad M_Z^2 = \frac{g_2^2}{2 \cos ^2 \theta _W} \left( v^2 + 4 v_\Delta ^2 \right) ,\nonumber \\ \end{aligned}$$

(10)

where $g_2$ is the $SU(2)_L$ gauge coupling constant and $\theta _W$ is the Weinberg angle. From the experimental bound $\rho =1.0004^{+0.0003}_{-0.0004}$ [24], $v_\Delta$ is strongly restricted by

$$\begin{aligned} \frac{v_\Delta }{v} \lesssim 0.02,\quad \mathrm{or\ equivalently}\quad v_\Delta \lesssim 5\,\mathrm{GeV}. \end{aligned}$$

(11)

In the limit $v_\Delta \ll v$, we obtain from Eq. (8)

$$\begin{aligned} v_\Delta \approx \frac{\lambda _6 M_\Delta v^2}{2 M_\Delta ^2 + v^2(\lambda _4- \lambda _5)}, \end{aligned}$$

(12)

where we have defined $\lambda _6 \equiv \Lambda _6 /M_\Delta$. Then the neutrino mass matrix is given by

$$\begin{aligned} (M_\nu )_{ij} = v_\Delta (Y_\Delta )_{ij} \approx \frac{\lambda _6 M_\Delta v^2}{2 M_\Delta ^2 + v^2(\lambda _4- \lambda _5)} (Y_\Delta )_{ij}, \end{aligned}$$

(13)

where $i,j = 1, 2, 3$ are flavor indices. On the other hand, $M_\nu$ is written using the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix U [25–27] as $M_\nu = U^\mathrm{T} M_\nu ^\mathrm{diag} U$, where $M_\nu ^\mathrm{diag} = \mathrm{diag}(m_1, m_2, m_3)$ is the diagonal neutrino mass eigenvalue matrix. Using the central values of a recent neutrino oscillation data [28], the order of magnitude of the neutrino Yukawa coupling matrix is estimated as

$$\begin{aligned} Y_\Delta = \frac{10^{-2}\,\mathrm{eV}}{v_\Delta } \times \mathcal {O}(1)_{3\times 3}, \end{aligned}$$

(14)

where the last $3 \times 3$ matrix can be calculated by mass eigenvalues, mixing angles, Dirac CP phase, and two Majorana phases. Since the Yukawa coupling should be less than unity for perturbation theory, $v_\Delta$ is bounded from below as $v_\Delta \gtrsim \mathcal {O}(10^{-2}\,\mathrm{eV})$.

In the rest of this section, we explain masses and mixings of the scalar fields. Expanding the scalar fields $\phi ^0$ and $\delta ^0$ around their VEVs ($\phi ^0=(v+\phi +i\chi )/\sqrt{2}$ and $\delta ^0=(v_\Delta +\delta +i\eta )/\sqrt{2}$), we obtain 10 real-valued field components, which yields a $10\times 10$ squared mass matrix for the scalars. There are seven physical massive eigenstates $H^{\pm \pm },H^\pm ,h,H^0,A^0$ and three massless Goldstone bosons $G^\pm ,G^0$, which are eaten by the SM gauge bosons $W^\pm ,Z$. The physical mass eigenvalues for the scalar sector are given as follows:

$$\begin{aligned}&M^2_{H^{\pm \pm }} = M_\Delta ^2+\frac{1}{2}(\lambda _4+\lambda _5)v^2 +\frac{1}{2}(\lambda _1+\lambda _2)v_\Delta ^2, \end{aligned}$$

(15)

$$\begin{aligned}&M^2_{H^\pm } = \left( M_\Delta ^2+\frac{1}{2}\lambda _4v^2 +\frac{1}{2}\lambda _1v_\Delta ^2\right) \left( 1+\frac{2v^2_\Delta }{v^2}\right) ,\end{aligned}$$

(16)

$$\begin{aligned}&M^2_{A^0} = \left( M_\Delta ^2+\frac{1}{2}(\lambda _4-\lambda _5)v^2 +\frac{1}{2}\lambda _1v_\Delta ^2\right) \left( 1+\frac{4v^2_\Delta }{v^2}\right) ,\nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned}&M^2_h = \frac{1}{2}\left( A+C-\sqrt{(A-C)^2+4B^2}\right) ,\end{aligned}$$

(18)

$$\begin{aligned}&M^2_{H^0} = \frac{1}{2}\left( A+C+\sqrt{(A-C)^2+4B^2}\right) , \end{aligned}$$

(19)

$$\begin{aligned}&\mathrm{with}~~ A = \lambda v^2, B = -\frac{2v_\Delta }{v}\left( M^2_\Delta +\frac{1}{2}\lambda _1 v_\Delta ^2\right) ,~~ \\&C = M^2_\Delta +\frac{1}{2}(\lambda _4-\lambda _5)v^2+\frac{3}{2}\lambda _1 v_\Delta ^2. \\ \end{aligned}$$

Note that among the two CP-even neutral Higgs bosons, $M_{H^0}>M_{h}$ is satisfied for $A<C$, which we will impose in our analysis.

The mixing between the doublet and triplet scalar fields in the charged, CP-even and CP-odd scalar sectors are, respectively, given by

$$\begin{aligned} \left( \begin{array}{c} G^\pm \\ H^\pm \end{array} \right)= & {} \left( \begin{array}{cc} \cos \beta ' &{} \sin \beta '\\ -\sin \beta ' &{} \cos \beta ' \end{array} \right) \left( \begin{array}{c} \phi ^\pm \\ \delta ^\pm \end{array} \right) ,\end{aligned}$$

(20)

$$\begin{aligned} \left( \begin{array}{c} h \\ H^0 \end{array}\right)= & {} \left( \begin{array}{cc} \cos \alpha &{} \sin \alpha \\ -\sin \alpha &{} \cos \alpha \end{array} \right) \left( \begin{array}{c} \phi \\ \delta \end{array} \right) ,\end{aligned}$$

(21)

$$\begin{aligned} \left( \begin{array}{c} G^0 \\ A^0 \end{array}\right)= & {} \left( \begin{array}{cc} \cos \beta &{} \sin \beta \\ -\sin \beta &{} \cos \beta \end{array} \right) \left( \begin{array}{c} \chi \\ \eta \end{array} \right) , \end{aligned}$$

(22)

where the mixing angles are given by

$$\begin{aligned} \tan \beta '= & {} \frac{\sqrt{2} v_\Delta }{v},\end{aligned}$$

(23)

$$\begin{aligned} \tan \beta= & {} \frac{2v_\Delta }{v} = \sqrt{2} \tan \beta ',\end{aligned}$$

(24)

$$\begin{aligned} \tan {2\alpha }= & {} \frac{2B}{A-C} = \frac{4v_\Delta }{v}\frac{M_\Delta ^2+\frac{1}{2}\lambda _1 v_\Delta ^2}{M_\Delta ^2+\frac{1}{2}(\lambda _4-\lambda _5-2\lambda )v^2+\frac{3}{2}\lambda _1v_\Delta ^2} .\nonumber \\ \end{aligned}$$

(25)

Thus, in the limit $v_\Delta \ll v$, the mixing between the doublet and triplet scalars is small, unless the CP-even scalars h and $H^0$ are close to being mass-degenerate. In this limit, the mass of the (dominantly doublet) lightest CP-even scalar is simply given by $M_h^2=\lambda v^2$ (as in the SM) independent of the mass scale $M_\Delta$, whereas the other (dominantly triplet) scalars have $M_\Delta$-dependent mass.

After integrating out the heavy Higgs triplets, the effective scalar potential is given by

$$\begin{aligned} V_\mathrm{eff} = - m_\Phi ^2 \Phi ^\dagger \Phi + \frac{1}{2} (\lambda -\lambda _6^2) (\Phi ^\dagger \Phi )^2. \end{aligned}$$

(26)

At $\mu = M_\Delta$, the following matching condition is satisfied:

$$\begin{aligned} \lambda _\mathrm{SM} = \lambda -\lambda _6^2, \end{aligned}$$

(27)

where $\lambda _\mathrm{SM}$ is the SM Higgs quartic coupling. Note that the EW vacuum can be stable by a sufficiently large $\lambda _6$ as shown later.

3 Vacuum stability and naturalness

Since $\lambda _\mathrm{SM}$ becomes negative at around $\mu =10^{8-10}\,\mathrm{GeV}$ in the SM (see [29] for example), new physics scale, which corresponds to $M_\Delta$ in our case, have to appear before $\lambda _\mathrm{SM}$ becomes negative. To ensure that the scalar potential (6) is bounded from below, the necessary and sufficient conditions are given by [15]

$$\begin{aligned}&\lambda \ge 0,\quad \lambda _1 \ge 0,\quad 2 \lambda _1 + \lambda _2 \ge 0, \nonumber \\&\lambda _4 + \lambda _5 + \sqrt{\lambda \lambda _1} \ge 0,\quad \lambda _4 + \lambda _5 + \sqrt{\lambda \left( \lambda _1 + \frac{\lambda _2}{2} \right) } \ge 0, \nonumber \\&\lambda _4 - \lambda _5 + \sqrt{\lambda \lambda _1} \ge 0,\quad \lambda _4 - \lambda _5 + \sqrt{\lambda \left( \lambda _1 + \frac{\lambda _2}{2} \right) } \ge 0.\nonumber \\ \end{aligned}$$

(28)

In fact, corrections of necessary and sufficient conditions have been recently pointed out by Eq. (19) in Ref. [20]. The major difference would appear in the ($\lambda _4$, $\lambda _5$) plane, that is, the correct conditions can make the allowed parameter region larger than that by Eq. (28). Since the difference is not so large and does not change our main result significantly, we will consider Eq. (28) for a relevant vacuum stability condition.

In addition, the tree-level unitarity of the S-matrix for elastic scattering imposes the following constraints [15]:

$$\begin{aligned}&\lambda \le \frac{8}{3}\pi ,\quad \lambda _1-\lambda _2\le 8\pi ,\quad \nonumber \\&4\lambda _1+\lambda _2\le 8\pi ,\quad 2\lambda _1+3\lambda _2\le 16\pi ,\nonumber \\&|\lambda _5|\le \frac{1}{2} \mathrm{min}\left[ \sqrt{(\lambda \pm 8\pi )(\lambda _1-\lambda _2\pm 8\pi )}\right] ,\nonumber \\&|\lambda _4| \le \frac{1}{\sqrt{2}} \sqrt{\left( \lambda -\frac{8}{3}\pi \right) \left( 4\lambda _1+\lambda _2-8\pi \right) }. \end{aligned}$$

(29)

We also impose the perturbativity condition, that is, all quartic couplings are less than $4\pi$ up to the Planck scale. It turns out that the perturbativity condition more strongly constrains the parameter space than the unitarity condition. The one-loop beta functions of coupling constants are given in the appendix.

In the ordinary type-II seesaw model, the Higgs mass correction is given by [30]

$$\begin{aligned}&\delta m_h^2 = \frac{1}{16\pi ^2} \left[ 3 \lambda _4 \left( \Lambda ^2 - M_\Delta ^2 \log \frac{\Lambda ^2}{M_\Delta ^2}\right) - 3 \lambda _6^2 M_\Delta ^2 \log \frac{\Lambda ^2}{M_\Delta ^2} \right] ,\nonumber \\ \end{aligned}$$

(30)

where $\Lambda$ is a UV cutoff. In our analysis, we neglect the quadratic divergent term, because it does not appear in the dimensional regularization. On the other hand, the logarithmic correction appears in the scheme-independent form, i.e., the coefficient of logarithmic term is the same for any regularization scheme. Thus, we consider only the logarithmic terms in Eq. (30) for a physical correction,

$$\begin{aligned} \delta m_h^2 = - \frac{3}{16\pi ^2} \left( \lambda _4 + \lambda _6^2 \right) M_\Delta ^2 \log \frac{M_\mathrm{Pl}^2}{M_\Delta ^2}, \end{aligned}$$

(31)

where we have set $\Lambda =M_\mathrm{Pl}=2.4\times 10^{18}\,\mathrm{GeV}$. We evaluate a fine-tuning level as $|\delta m_h^2|/M_h^2$, where $M_h=125\,\mathrm{GeV}$ is the experimentally observed Higgs boson mass. We require the fine-tuning level to be less than unity for the naturalness in our analysis.

Here, we mention results from the different naturalness conditions in the literature. In Ref. [31], the authors evaluated the Higgs mass correction at two-loop induced by electroweak interactions, and they obtained the upper bound of triplet scalar around 200 GeV in type-II seesaw, while they have not considered the corrections due to couplings not related to active neutrino masses except for $\lambda _4$ in our notation. However, we will find $\lambda _6$ is also important for the naturalness condition (31) to realize the vacuum stability. On the other hand, in Ref. [32], the authors obtained $M_{H^\pm }<288\,\mathrm{GeV}$ and $M_{H^{\pm \pm }}<351\,\mathrm{GeV}$ by considering the naturalness condition in terms of the Veltman condition [33], which requires a cancellation of quadratic divergences. Since we neglect the quadratic divergences for an unphysical quantity, our method is completely different from that in Ref. [32]. However, we will find that our result is accidentally almost the same as their results.

4 Numerical analysis

In this section, we show some numerical results with scatter plots, which satisfy the vacuum stability condition (28) and the perturbativity condition. In our analysis, we solve the renormalization group equations at two-loop level with a one-loop threshold correction for $\lambda$, and we restrict the regions of some parameters as follows:

$$\begin{aligned}&M_h = 125.09 \pm 0.21 \ (\mathrm{stat.}) \pm 0.11 \ (\mathrm{syst.})\ \mathrm{GeV}~[34],\nonumber \\&M_t = 173.34 \pm 0.27 \ (\mathrm{stat.}) \pm 0.71 \ (\mathrm{syst.})\ \mathrm{GeV}~[35], \nonumber \\&\alpha _s = 0.1184 \pm 0.0007~[36], \nonumber \\&200\,\mathrm{GeV} \le M_\Delta \le 10^{12}\,\mathrm{GeV}, \quad 0.01\,\mathrm{eV} \le v_\Delta \le 5\,\mathrm{GeV}.\nonumber \\ \end{aligned}$$

(32)

Although we take $M_\Delta$ up to $10^{12}\,\mathrm{GeV}$, the following numerical results always satisfy the requirement that $M_\Delta$ is lower than the energy scale, at which $\lambda _\mathrm{SM}$ becomes negative. The upper and lower bounds of $v_\Delta$ are given by $\rho$-parameter bound and naturalness of neutrino Yukawa coupling, respectively, as mentioned in Sect. 2. We also adopt the following constraints for the charged Higgs boson masses:

$$\begin{aligned}&M_{H^{\pm \pm }}>550\,\mathrm{GeV\ for}\ v_\Delta < 10^{-4}\,\mathrm{GeV},\end{aligned}$$

(33)

$$\begin{aligned}&v_\Delta M_{H^{\pm \pm }}>150\,\mathrm{eV\, GeV},\end{aligned}$$

(34)

$$\begin{aligned}&|M_{H^{\pm \pm }}-M_{H^{\pm }}| < 40\,\mathrm{GeV}, \end{aligned}$$

(35)

which correspond to the experimental bounds on decay mode of $H^{\pm \pm }\rightarrow \ell ^{\pm }\ell ^{\pm }$ [37], lepton flavor violating decays [38, 39], and the electroweak precision data [17], respectively.

4.1 Allowed parameter space

Fig. 1

Scatter plots in the ($\lambda _1$, $\lambda _2$) plane (left) and the ($\lambda _4$, $\lambda _5$) plane (right), which satisfy the vacuum stability and perturbativity conditions. For $200\,\mathrm{GeV} \le M_\Delta \le 1\,\mathrm{TeV}$ the allowed parameter space is limited in the green region. The black dots satisfy the naturalness condition of $|\delta m_h^2|<M_h^2$

Figure 1 shows scatter plots in the ($\lambda _1$, $\lambda _2$) plane (left) and the ($\lambda _4$, $\lambda _5$) plane (right), which satisfy the vacuum stability and perturbativity conditions. The green dots in Fig. 1 correspond to the allowed parameter space for $200\,\mathrm{GeV} \le M_\Delta \le 1\,\mathrm{TeV}$, in which the new quartic couplings ($\lambda _i$, $i=1,2,4,5$) should be sufficiently small to keep the perturbativity up to the Planck scale. The black dots satisfy $|\delta m_h^2|<M_h^2$. The lower bound of $\lambda _1$ is $-\lambda _2/2$ because of $2\lambda _1+\lambda _2\ge 0$, and the upper bounds of $\lambda _1$ and $\lambda _2$ come from the perturbativity condition. Since the third terms of the last four inequalities in Eq. (28) are negligible for a sufficiently large $\lambda _4\pm \lambda _5$, the vacuum stability requires $-\lambda _4 \lesssim \lambda _5 \lesssim \lambda _4$. Note that, when both $|\lambda _4|$ and $|\lambda _5|$ are small, the vacuum can become stable only by a sufficiently large $\lambda _6$, which will be explained in detail below. The allowed parameter space shown in Fig. 1 is much smaller than that in Ref. [18], in which only the unitarity condition has been considered.

The left panel of Fig. 2 shows scatter plots in the ($|\lambda _4|$, $\lambda _6$) plane. There is no allowed parameter space for $|\lambda _4| < 0.01$ and $\lambda _6<0.01$. Then we find $\lambda _4+\lambda _6^2 = \mathcal{O}(1)$ for almost all values of $M_\Delta$, which is shown in the right panel of Fig. 2. If both $|\lambda _4|$ and $\lambda _6$ are sufficiently small, the Higgs mass correction would be smaller than the Higgs mass. However, the vacuum stability cannot be realized by such small parameters.

Fig. 2

Scatter plots in the ($|\lambda _4|$, $\lambda _6$) plane (left) and the ($M_\Delta$ [GeV], $\lambda _4 + \lambda _6^2$) plane (right), which satisfy the vacuum stability and perturbativity conditions. The setup is the same as in Fig. 1

Fig. 3

Running of $\lambda _H (=\lambda _\mathrm{SM}\ \mathrm{for\ \mu < M_\Delta }, \lambda \ \mathrm{for\ \mu \ge M_\Delta })$. We have taken $\lambda _4=0.2$ and $\lambda _6=3\times 10^{-4}$ in the left panel, while $\lambda _4=0.1$ and $\lambda _6=0.2$ in the right panel. Other quartic couplings are commonly taken as $\lambda _1=\lambda _2=\lambda _5=0.1$. The black dashed line corresponds to the SM case. The vertical lines show $M_\Delta =10\,\mathrm{TeV}$ and $M_\mathrm{Pl}$, respectively

Fig. 4

$M_\Delta$ dependence of the Higgs mass correction for all allowed region of $M_\Delta$ (left) and $200\,\mathrm{GeV} \le M_\Delta \le 1\,\mathrm{TeV}$ (right). The horizontal line shows the Higgs mass squared, i.e., $M_h^2 = (125\,\mathrm{GeV})^2$

To stabilize the EW vacuum, there are two types of solutions. We show the running of $\lambda _H (=\lambda _\mathrm{SM}\ \mathrm{for\ \mu < M_\Delta }, \lambda \ \mathrm{for}\ \mu \ge M_\Delta )$ for typical input parameters in Fig. 3. The left panel of Fig. 3 corresponds to the large positive contribution to a beta function of $\lambda$ ($\beta _\lambda$), which is realized by a large $|\lambda _4|$ and/or $|\lambda _5|$ [see Eq. (50)]. The right panel of Fig. 3 corresponds to a discontinuous shift between $\lambda _\mathrm{SM}$ and $\lambda$, which is realized by a large $\lambda _6$ [see Eq. (27)]. When $|\lambda _4|$ and $\lambda _6$ are sufficiently small but $|\lambda _5|$ is sufficiently large, the EW vacuum likely become stable, because $\lambda _5$ also positively contributes to $\beta _\lambda$. In that case, however, the last two conditions in Eq. (28) cannot be satisfied. Thus, when the EW vacuum becomes stable, the Higgs mass correction usually becomes larger than the Higgs mass.

Figure 4 shows $M_\Delta$ dependence of the Higgs mass correction, which is calculated by Eq. (31). From the right panel of Fig. 4, we find that the naturalness condition requires $M_\Delta \lesssim 350\,\mathrm{GeV}$. Below this bound, the minimal type-II seesaw model can be testable by the LHC Run-II results [40] (also see Refs. [41–46] for the LHC phenomenology). In the case of $M_{H^{\pm \pm }}<M_{H^\pm }<M_{H^0/A^0}$, from four-lepton signal at the 14 TeV LHC experiment with $300\,\mathrm{fb}^{-1}$, we can potentially probe up to a mass $M_{H^{\pm \pm }}\sim 600\ (700)\,\mathrm{GeV}$ for the normal (inverted) hierarchy of active neutrino masses. In the case of $M_{H^{\pm \pm }}>M_{H^\pm }>M_{H^0/A^0}$, with an integrated luminosity $\sim$ $500\,\mathrm{fb}^{-1}$, the triplet scalars can be fully reconstructed at the 14 TeV LHC.

4.2 Predictions for the decay rate of $h \rightarrow \gamma \gamma$, $Z\gamma$

In the SM, the decay $h\rightarrow \gamma \gamma (Z\gamma )$ at the one-loop level is mediated by the virtual exchange of SM fermions (dominantly the top-quark) and the W-boson. In the type-II seesaw model, there are additional contributions from the new charged Higgs bosons [15].² The decay rates of $h\rightarrow \gamma \gamma$ is given by [47, 48]

$$\begin{aligned} \Gamma (h\rightarrow \gamma \gamma )= & {} \frac{\alpha ^2 G_F M_h^3}{128\sqrt{2}\pi ^3} \bigg | \sum _f N_c Q_f^2 g_{hf\bar{f}}A^{\gamma \gamma }_{1/2}(\tau _h^f) \nonumber \\&+ g_{hW^+W^-} A^{\gamma \gamma }_1(\tau _h^W) + \tilde{g}_{hH^\pm H^\mp } A^{\gamma \gamma }_0(\tau _h^{H^\pm }) \nonumber \\&+ 4 \tilde{g}_{hH^{\pm \pm } H^{\mp \mp }} A^{\gamma \gamma }_0(\tau _h^{H^{\pm \pm }}) \bigg |^2, \end{aligned}$$

(36)

where $\alpha$ is the fine-structure constant, $G_F$ is the Fermi coupling constant, $N_c=3 (1)$ for quarks (leptons), and $Q_f$ is the electric charge of the fermion in the loop. In the same way, the decay rate of $h\rightarrow Z\gamma$ is given by

$$\begin{aligned}&\Gamma (h\rightarrow Z\gamma ) = \frac{\alpha ^2 M_h^3}{128\pi ^3 v^2}\left( 1-\frac{M_Z^2}{M_h^2}\right) ^3 \nonumber \\&\quad \times \bigg | \frac{1}{s_W c_W}\sum _f N_c Q_f (2I_3^f-4Q_fs_W^2) A_{1/2}^{Z\gamma }(\tau _h^f,\tau _Z^f) \nonumber \\&\quad + \cot \theta _W g_{hW^+W^-} A_1^{Z\gamma }(\tau _h^W,\tau _Z^W) \nonumber \\&\quad - 2 g_{ZH^\pm H^\mp } \tilde{g}_{hH^\pm H^\mp } A_0^{Z\gamma }(\tau _h^{H^\pm },\tau _Z^{H^\pm }) \nonumber \\&\quad - 4 g_{ZH^{\pm \pm }H^{\mp \mp }} \tilde{g}_{hH^{\pm \pm }H^{\mp \mp }} A_0^{Z\gamma }(\tau _h^{H^{\pm \pm }},\tau _Z^{H^{\pm \pm }})\bigg |^2, \end{aligned}$$

(37)

where $s_W\equiv \sin \theta _W$, $c_W\equiv \cos \theta _W$, $\tau _h^i=4M_i^2/M_h^2$, $\tau _Z^i=4M_i^2/M_Z^2$ ($i=f,W,H^\pm ,H^{\pm \pm }$), and $I_3^{t,s}$ are the third isospin components of the fermion. In these equations, the first two terms in the squared amplitude are the SM fermion and W-boson contributions, respectively, whereas the last two terms correspond to the $H^\pm$ and $H^{\pm \pm }$ contributions. We consider only the top quark contribution for the SM fermion, because the other fermion contributions are negligible. The relevant loop functions are defined as

$$\begin{aligned} A_0^{\gamma \gamma } (x)= & {} -x^2[x^{-1}-f(x^{-1})], \nonumber \\ A_{1/2}^{\gamma \gamma } (x)= & {} 2x^2[x^{-1}+(x^{-1}-1)f(x^{-1})], \nonumber \\ A_1^{\gamma \gamma }(x)= & {} -x^2[2x^{-2}+3x^{-1}+3(2x^{-1}-1)f(x^{-1})], \nonumber \\ A_0^{Z\gamma }(x,y)= & {} I_1(x,y), \nonumber \\ A_{1/2}^{Z\gamma } (x,y)= & {} I_1(x,y)-I_2(x,y), \nonumber \\ A_1^{Z\gamma }(x,y)= & {} 4(3-\tan ^2\theta _W)I_2(x,y) \nonumber \\&+ [(1+2x^{-1}) \tan ^2 \theta _W-(5+2x^{-1})]I_1(x,y),\nonumber \\ \end{aligned}$$

(38)

where

$$\begin{aligned} I_1(x,y)= & {} \frac{x y}{2(x-y)} + \frac{x^2 y^2}{2(x-y)^2}[f(x^{-1})-f(y^{-1})] \nonumber \\&+\frac{x^2 y}{(x-y)^2}[g(x^{-1})-g(y^{-1})], \nonumber \\ I_2(x,y)= & {} - \frac{x y}{2(x-y)}[f(x^{-1})-f(y^{-1})]\;, \end{aligned}$$

(39)

with the functions f(x) and g(x) in the range $x<1$, given by

$$\begin{aligned} f(x) = (\sin ^{-1}\sqrt{x})^2, \quad g(x) = \sqrt{x^{-1}-1}(\sin ^{-1}\sqrt{x}). \end{aligned}$$

(40)

The couplings of h to the SM fermions and vector bosons relative to the SM Higgs couplings are given by

$$\begin{aligned} g_{hf\bar{f}} = \frac{\cos \alpha }{\cos \beta '} ,\quad g_{hW^+W^-} = \cos \alpha +2\sin \alpha \frac{v_\Delta }{v}. \end{aligned}$$

(41)

From Eqs. (23) and (25), we see in the limit $v_\Delta \ll v$, $\cos \alpha \simeq 1$, $\cos \beta ' \simeq 1$, and hence the couplings of h to the SM fermions and vector bosons are almost identical to the SM case. The couplings of Z to the charged Higgs bosons in Eq. (37) are given by

$$\begin{aligned} g_{Z H^{+} H^{-}} = - \tan \theta _W , \quad g_{Z H^{++} H^{--}} = 2\cot 2\theta _W . \end{aligned}$$

(42)

For the scalar trilinear couplings, we have

$$\begin{aligned}&\tilde{g}_{h H^+H^-} = \frac{M_W}{g M_{H^{\pm }}^2} g_{h H^+H^-}, \nonumber \\&\tilde{g}_{h H^{++}H^{--}} = \frac{M_W}{ g M_{H^{\pm \pm }}^2} g_{h H^{++}H^{--}}, \end{aligned}$$

(43)

with the following definitions in terms of the parameters of the scalar potential (up to $\mathcal{O}(v_\Delta ^2)$) [15]:

(44)

$$\begin{aligned}&g_{hH^{++}H^{--}} = (\lambda _1+\lambda _2)v_\Delta \sin \alpha + (\lambda _4+\lambda _5)v\cos \alpha . \end{aligned}$$

(45)

In the limit $v_\Delta \ll v$, Eqs. (44) and (45) can be written

$$\begin{aligned} g_{hH^{+}H^{-}}\simeq \lambda _4 v , \quad g_{hH^{++}H^{--}} \simeq (\lambda _4+\lambda _5)v . \end{aligned}$$

(46)

Thus, the signs of the couplings $g_{hH^{+}H^{-}}$ and $g_{hH^{++}H^{--}}$, and hence, those of the $H^\pm$ and $H^{\pm \pm }$ contributions to the amplitude in Eq. (36) are fixed by the scalar couplings $\lambda _4$ and $\lambda _4+\lambda _5$, respectively. The allowed parameter space by the vacuum stability and perturbativity conditions is shown in Fig. 1, and we can see that there is a small allowed region in $\lambda _4+\lambda _5<0$.

Table 1 Signs of corresponding amplitudes. Signs of the singly and doubly charged scalar contributions depend on signs of $\lambda _4$ and $\lambda _4 + \lambda _5$, respectively

In the SM, the W-boson contributions to $h\rightarrow \gamma \gamma$ and $h\rightarrow Z\gamma$ dominate over those from the SM fermions, while the signs of the corresponding amplitudes $A^{\gamma \gamma }_1$ and $A^{Z\gamma }_1$ are opposite as shown in Table 1. The doubly charged scalar contribution usually dominates over the singly charged scalar contribution for both $h\rightarrow \gamma \gamma$ and $h\rightarrow Z\gamma$ amplitude because of the enhancement factor of four in Eqs. (36) and (37), which corresponds to the squared electric charge of $H^{\pm \pm }$. Since doubly charged scalar contributions are proportional to $\lambda _4+\lambda _5$ with the opposite sign to the W-boson contribution, the two decay widths are enhanced for $\lambda _4+\lambda _5<0$. For the same reason, the behavior reverses for $\lambda _4 + \lambda _5>0$.

In order to compare the model predictions for the signal strength with the SM value at the LHC, the partial decay widths of the processes $h\rightarrow \gamma \gamma ,~Z\gamma$ can be expressed by

$$\begin{aligned} R_{\gamma \gamma (Z\gamma )}= & {} \frac{\sigma (pp\rightarrow h \rightarrow \gamma \gamma (Z\gamma ))}{\sigma _\mathrm{SM}(pp\rightarrow h \rightarrow \gamma \gamma (Z\gamma ))} \nonumber \\= & {} \frac{\sigma (pp\rightarrow h)}{\sigma _\mathrm{SM}(pp\rightarrow h)} \frac{\mathrm{Br}(h\rightarrow \gamma \gamma (Z\gamma ))}{\mathrm{Br}_\mathrm{SM}(h\rightarrow \gamma \gamma (Z\gamma ))}, \end{aligned}$$

(47)

where $\sigma (pp\rightarrow h)/\sigma _\mathrm{SM}(pp\rightarrow h) = \cos ^2\alpha$ with the mixing angle $\alpha$ given by Eq. (25). Since $\cos \alpha \sim 1$ in the limit $v_\Delta \ll v$, the SM-like Higgs production rate is almost the same as that in the SM. The branching ratios of all the Higgs decay channels are also the same as in the SM, except for $\gamma \gamma$ and $Z\gamma$ channels which may differ significantly, but their contribution to the total decay width remains negligible as in the SM. Hence, for our numerical purposes, we can simply assume $R_{\gamma \gamma }$ defined in Eq. (47) to be the ratio of the partial decay widths for $h\rightarrow \gamma \gamma$ in the type-II seesaw model and in the SM.

Fig. 5

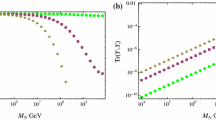
$R_{\gamma \gamma }$ (left) and $R_{Z\gamma }$ (right) versus $M_{H^{\pm \pm }}$. The green and cyan dots correspond to $\lambda _4 + \lambda _5 < 0$ and $\lambda _4 + \lambda _5 >0$, respectively. The black dots satisfy $|\delta m_h^2|<M_h^2$. The red line in the left panel shows the experimental lower bound

Figure 5 shows $R_{\gamma \gamma }$ (left) and $R_{Z\gamma }$ (right) versus $M_{H^{\pm \pm }}$. The green and cyan dots correspond to $\lambda _4 + \lambda _5 < 0$ and $\lambda _4 + \lambda _5 >0$, respectively. The black dots satisfy $|\delta m_h^2|<M_h^2$. The red line in the left panel shows the lower bound on the current signal strength, which is obtained as $R_{\gamma \gamma }=1.16^{+0.20}_{-0.18}$ by the combined analysis of ATLAS and CMS results [51]. Our result of $R_{\gamma \gamma } \lesssim 1.1$ needs more than 10 % precision to see the deviation, while the relative uncertainty on the $R_{\gamma \gamma }$ is 0.1 for the combined Higgs analysis by the LHC experiment at 14 TeV with $3000\,\mathrm{fb}^{-1}$ of integrated luminosity [52]. There is no useful experimental bound for $R_{Z \gamma }$ at present [53]. The expected measured signal for $h \rightarrow Z\gamma \rightarrow \ell \ell \gamma$ is $1.00^{+0.25}_{-0.26}(\mathrm{stat.})^{+0.17}_{-0.15}(\mathrm{sys.})$ by the 14 TeV LHC experiment with $3000\,\mathrm{fb}^{-1}$ [54].

In the $\lambda _4 + \lambda _5 < 0$ case, both $R_{\gamma \gamma }$ and $R_{Z\gamma }$ are larger than unity with $M_{H^{\pm \pm }} < M_\Delta$. The behavior reverses for $\lambda _4 + \lambda _5>0$: in the $\lambda _4 + \lambda _5 > 0$ case, both $R_{\gamma \gamma }$ and $R_{Z\gamma }$ are smaller than unity with $M_{H^{\pm \pm }} > M_\Delta$. Although $R_{\gamma \gamma }$ can be enhanced by both $H^{\pm }$ and $H^{\pm \pm }$ contributions for $\lambda _4<0$, there is no parameter space in $\lambda _4<0$ region for $M_\Delta \le 1\,\mathrm{TeV}$ (see the right panel in Fig. 1). This result comes from the vacuum stability conditions, and we note that $R_{\gamma \gamma }$ is not strongly enhanced compared to the literature; see for example Refs. [55, 56].

In the $\lambda _4 + \lambda _5 \simeq 0$ case, contributions from $H^{\pm \pm }$ to the decay rate vanish, while contributions from $H^{\pm }$ can be seen clearly. We can see from Table 1 that there is an anti-correlation between $R_{\gamma \gamma }$ and $R_{Z\gamma }$ for $\lambda _4 + \lambda _5 \simeq 0$. To see this, we show the relation between $R_{\gamma \gamma }$ and $R_{Z\gamma }$ in Fig. 6. The gray dots correspond to $-0.05< \lambda _4 + \lambda _5 < 0.05$ with $\lambda _4>0$, and they lie in the $R_{\gamma \gamma }<1$ and $R_{Z\gamma }>1$ region. Since there is no allowed parameter space in $-0.05< \lambda _4 + \lambda _5 < 0.05$ with $\lambda _4<0$, the model cannot realize $R_{\gamma \gamma }>1$ and $R_{Z\gamma }<1$ at the same time.

Fig. 6

The relation between $R_{\gamma \gamma }$ and $R_{Z\gamma }$. The green, gray, and cyan dots correspond to $\lambda _4 + \lambda _5 < -0.05$, $-0.05< \lambda _4 + \lambda _5 < 0.05$, and $\lambda _4 + \lambda _5 >0.05$, respectively. The black dots satisfy $|\delta m_h^2|<M_h^2$. The red line shows the experimental lower bound

5 Conclusion

We have studied the vacuum stability and perturbativity conditions in the minimal type-II seesaw model. Their conditions give characteristic constraints between model parameters as in Fig. 1. The vacuum stability can be realized by sufficiently large $|\lambda _4|$ or $\lambda _6$, which leads to large Higgs mass corrections. To realize the naturalness condition ($\delta m_h^2 < M_h^2 = (125\,\mathrm{GeV})^2$), we have found that heavy Higgs masses should be lower than $350\,\mathrm{GeV}$. Below this bound, the minimal type-II seesaw model can be testable by the LHC Run-II results. Due to the triplet scalar field, branching ratios of the Higgs decay for $h\rightarrow \gamma \gamma , Z\gamma$ are different from the standard model case. They strongly depend on the sign of $\lambda _4+\lambda _5$, and there is an anti-correlation between $R_{\gamma \gamma }$ and $R_{Z \gamma }$ for $\lambda _4+\lambda _5 \simeq 0$ with $\lambda _4>0$. From the recent ATLAS and CMS combined analysis for the signal strength of $h\rightarrow \gamma \gamma$, we have also found that a large parameter region is to be excluded. Our result of $R_{\gamma \gamma } \lesssim 1.1$ needs more than 10 % precision to see the deviation, while the relative uncertainty on the $R_{\gamma \gamma }$ is 0.1 for the combined Higgs analysis by the LHC experiment at 14 TeV with $3000\,\mathrm{fb}^{-1}$ of integrated luminosity.

Appendices

Appendix

The beta functions in the minimal type-II seesaw model

The one-loop beta functions for the minimal type-II seesaw model are given by

$$\begin{aligned}&16\pi ^2 \beta _{g_Y} = \frac{47}{6} g_Y^3,\quad 16\pi ^2 \beta _{g_2} = - \frac{5}{2} g_2^3 ,\quad 16\pi ^2 \beta _{g_3} = -7 g_3^3 \nonumber \\ \end{aligned}$$

(48)

$$\begin{aligned}&16\pi ^2 \beta _{y_t} = y_t \left[ \frac{9}{2} y_t^2 - \left( \frac{17}{20} g_1^2 + \frac{9}{4} g_2^2 + 8 g_3^2 \right) \right] , \end{aligned}$$

(49)

$$\begin{aligned}&16\pi ^2 \beta _\lambda = \lambda \left[ 12\lambda - \left( \frac{9}{5}g_1^2 + 9g_2^2 \right) + 12y_t^2 \right] \nonumber \\&\quad + \frac{9}{4} \left( \frac{3}{25}g_1^4 + \frac{2}{5}g_1^2g_2^2 + g_2^4 \right) + 6\lambda _4^2 + 4\lambda _5^2 - 12y_t^4, \end{aligned}$$

(50)

$$\begin{aligned}&16\pi ^2 \beta _{\lambda _1} = \lambda _1 \left[ 14\lambda _1 + 4 \lambda _2 - \left( \frac{36}{5} g_1^2 + 24g_2^2 \right) + 4 \mathrm{tr} \left[ \mathbf{S}_\Delta \right] \right] \nonumber \\&\quad + \frac{108}{25}g_1^4 + \frac{72}{5}g_1^2g_2^2 + 18g_2^4 + 2 \lambda _2^2 + 4 \lambda _4^2 + 4\lambda _5^2 - 8 \mathrm{tr} \left[ \mathbf{S}_\Delta ^2 \right] , \nonumber \\\end{aligned}$$

(51)

$$\begin{aligned}&16\pi ^2 \beta _{\lambda _2} = \lambda _2 \left[ 12 \lambda _1 + 3 \lambda _2 - \left( \frac{36}{5}g_1^2 + 24g_2^2 \right) + 4 \mathrm{tr} \left[ \mathbf{S}_\Delta \right] \right] \nonumber \\&\quad - \frac{144}{5}g_1^2g_2^2 + 12g_2^4 - 8 \lambda _5^2 + 8 \mathrm{tr} \left[ \mathbf{S}_\Delta ^2 \right] , \end{aligned}$$

(52)

$$\begin{aligned}&16\pi ^2\ \beta _{\lambda _4} = \lambda _4 \nonumber \\&\quad \times \left[ 6 \lambda + 8 \lambda _1 + 2 \lambda _2 + 4\lambda _4 - \left( \frac{9}{2}g_1^2 + \frac{33}{2}g_2^2 \right) + 6 y_t^2 + 2 \mathrm{tr} \left[ \mathbf{S}_\Delta \right] \right] \nonumber \\&\quad + \frac{27}{25}g_1^4 + 6g_2^4 + 8 \lambda _5^2 - 4 \mathrm{tr} \left[ \mathbf{S}_\Delta ^2 \right] , \end{aligned}$$

(53)

$$\begin{aligned}&16\pi ^2 \beta _{\lambda _5} = \lambda _5 \nonumber \\&\quad \times \left[ 2 \lambda + 2\lambda _1 - 2\lambda _2 + 8 \lambda _4 - \left( \frac{9}{2}g_1^2 + \frac{33}{2}g_2^2 \right) + 6 y_t^2 + 2 \mathrm{tr}\left[ \mathbf{S}_\Delta \right] \right] \nonumber \\&\quad - \frac{18}{5}g_1^2g_2^2 + 4 \mathrm{tr}\left[ \mathbf{S}_\Delta ^2 \right] , \end{aligned}$$

(54)

where we define $\mathbf{S}_\Delta =Y_\Delta ^\dagger Y_\Delta$ and its beta function is given by

$$\begin{aligned} 16\pi ^2 \beta _{\mathbf{S}_\Delta } = \mathbf{S}_\Delta \left[ 6\, \mathbf{S}_\Delta - 3 \left( \frac{3}{5} g_1^2 + 3 g_2^2 \right) + 2 \mathrm{tr}[\mathbf{S}_\Delta ] \right] .\nonumber \\ \end{aligned}$$

(55)