1 Introduction

The final states of collapsing stars remain an exciting research area in theoretical astrophysics. Now a days it is a well-established theory that the final state of a main-sequence star of mass of more than \(8M_\odot \) is most likely to form a neutron star after a type IIa supernova. However, it is important to keep in mind that such an evolution in single star system is completely different from that of a binary star system. Also accretion onto a white dwarf leads to a type Ia supernova left behind a neutron star as well. Accretion onto a neutron star (NS) can also initiate a collapse once it crossed the Chandrashekhar limit of NS leading to the formation of more dense objects like quark star (QS) and black hole. Neutron stars and quark stars are the most dense objects ever existing in the universe that can be practically observed. Due to their compact nature, many exotic phases are expected to be present in the interior such as pion condensation, neutron superfluid, superconducting protons, asymptotic free quarks, quark gluon plasma etc. Therefore, these compact objects are the only laboratories existing for testing quantum chromodynamics.

New compact stars other than NS and QS such as strange stars (SSs) and boson stars (BSs) have also been proposed by Witten [1], Farhi and Jaffe [2], Kaup [3], Ruffini and Bonazzola [4] and Colpi et al. [5]. The matter at the interior of these compact stars are not necessarily ideal fluids (isotropic pressure); however, assuming non-ideal (anisotropic pressure) fluid would be of more general consideration. The existence of an anisotropic pressure is also highly possible at a density \({\sim }10^{14}~\mathrm{g/cm}^3\) due to relativistic nuclear interaction [6], the presence of solid core or the presence of type 3A superfluid [7], phase transitions [8], meson condensation [9], slow rotation [10], a mixture of two gases [11] or strong magnetic fields [12], and the presence of some electric charge. It is well known that the behavior of a collapsing star is strongly influenced by its initial static configuration. The evolution of a collapsing star can be strongly influenced by the presence of pressure anisotropy, electric charge, EoS, shear, radiations, magnetic field etc. The initial configurations with the same masses and radii for pressure isotropy and anisotropy when undergoing collapse lead to a completely different temperature evolution at their later stages [13]. Hence, to study the complete picture of the initial static configuration it is necessary to track the evolution when collapse happens.

Schwarzschild [14] has shown that an incompressible fluid sphere satisfies the Buchdahl condition \(2M/R \le 8/9\), which implies an upper bound on the redshift \(z_{\max } \le 2\). High redshift can be achieved on account of anisotropic fluid configurations [10, 15]. Lindblom [16] and Haensel et al. [17] have shown that neutron stars with causal equations of state can have a maximum redshift of \(z_{\max }<0.9\).

Embedding of n-dimensional space \(V_n\) into flat \(E_{n+p}\) space captured much attention after the investigation of Randall and Sundrum [18] on brane theory. Embedded spaces are also used by many authors to investigate extrinsic gravity, string and membranes, rigid particles and Zitterbewegung theory [19]. If a n-dimensional at space \(V_n\) can be embedded in \((n + p)\)-dimensional space, where p is a minimum number of extra dimensions, then \(V_n\) is said to be of embedding class p. Many physically important solutions, e.g. Friedmann universe and Schwarzschild’s interior solutions [14] are of class I, the well-known Schwarzschild exterior solution [14] is of class II (\(p = 2\)) and the Kerr metric [20] is of class V (\(p = 5\)). There are only two solutions for an isotropic pressure i.e. the Schwarzschild interior and Kohler–Chao solutions. The Schwarzschild interior solution is conformally flat, which represents a bounded configuration and the Kohler–Chao solution is conformally non-flat, which represents unbounded or cosmological configurations. However, on introducing electric charge and pressure anisotropy many authors have recently presented various conformally non-flat bounded solutions [21,22,23,24,25,26,27,28].

In this article, we are presenting a new conformally non-flat embedding class I solution that represents bounded configurations. For the first time we have obtained an embedding class I solution as special function. The article is organized as follows: Sect. 2 we are discussing concepts on embedding class and Einstein’s field equations, in Sect. 3 we discover a new solution, Sect. 4 is devoted to the physical conditions, Sect. 5 deals with boundary conditions and a determination of constants of integration, Sect. 6 is on physical properties of the new solutions, Sect. 7 discusses the equilibrium condition and stability analysis in detail and in Sect. 8, we present our results and discussions.

2 Concepts of embedding classes and basic field equations

To describe the interior of a static and spherically symmetry object in the canonical coordinate \(x^{\mu }=(t,r,\theta ,\phi )\), we take the line element

$$\begin{aligned} \mathrm{d}s^{2}=\mathrm{e}^{\nu (r)}\mathrm{d}t^{2}-\mathrm{e}^{\lambda (r)}\mathrm{d}r^{2}-r^{2}\left( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2} \right) \end{aligned}$$
(1)

\(\nu \) and \(\lambda \) being the functions of the radial coordinate r.

Kasner [29] has shown that the Schwarzschild exterior spacetime i.e. \(\mathrm{e}^\nu =\mathrm{e}^{-\lambda }=1-2m(r)/r\) in (1) cannot be embeded in 5-D Euclidean space. Adopting the coordinates transformation given as

$$\begin{aligned} x= & {} r \sin \theta \cos \phi , \quad y=r\sin \theta \sin \phi , \quad z=r\cos \theta \end{aligned}$$
(2)

the spacetime (1) reduces to

$$\begin{aligned} \mathrm{d}s^{2}= {r-2m \over r}\mathrm{d}t^2-{2m \over r-2m}\mathrm{d}r^2 -\mathrm{d}x^2-\mathrm{d}y^2-\mathrm{d}z^2 \end{aligned}$$
(3)

where \(r^2=x^2+y^2+z^2\). Further, assuming

$$\begin{aligned} \mathrm{d}R=\sqrt{{2m \over r-2m}}~\mathrm{d}r \quad \text{ or }\quad R=\sqrt{8m(r-2m)} \end{aligned}$$
(4)

Equation (3) reduces to

$$\begin{aligned} \mathrm{d}s^2={R^2 \over R^2+16m^2}~\mathrm{d}t^2-\mathrm{d}R^2-\mathrm{d}x^2-\mathrm{d}y^2-\mathrm{d}z^2. \end{aligned}$$
(5)

Due to the coefficient of the first term in the above line element (5) is not a perfect differential. Hence it is clear that the 4-D spacetime of the form (1) cannot be embedded in 5-D pseudo-Euclidean space. However, if we introduce another coordinate transformation:

$$\begin{aligned}&\mathrm{d}S^2 = -\mathrm{d}R^2+{R^2 \over R^2+16m^2}~\mathrm{d}t^2 =\mathrm{d}X^2+\mathrm{d}Y^2+\mathrm{d}Z^2 \end{aligned}$$
(6)
$$\begin{aligned}&X ={R \sin t \over \sqrt{R^2+16m^2}},~~Y = {R \cos t \over \sqrt{R^2+16m^2}}\end{aligned}$$
(7)
$$\begin{aligned}&Z = \int \sqrt{1+{256m^4 \over (R^2+16m^2)^3}}~\mathrm{d}R. \end{aligned}$$
(8)

Equation (5) finally reduces to

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}x^2-\mathrm{d}y^2-\mathrm{d}z^2+\mathrm{d}S^2. \end{aligned}$$
(9)

Hence the 4-D metric (1) can be embedded in 6-D pseudo-Euclidean space.

Gupta and Goel [30] also have shown that the metric (1) can be embedded in 6-D pseudo-Euclidean space given by

$$\begin{aligned} \mathrm{d}s^2 = -\mathrm{d}x^2-\mathrm{d}y^2-\mathrm{d}z^2+\mathrm{d}X^2+\mathrm{d}Y^2 \pm \mathrm{d}Z^2 \end{aligned}$$
(10)

where

$$\begin{aligned} x= & {} r \sin \theta \cos \phi , ~~y=r\sin \theta \sin \phi , ~~ z=r\cos \theta ,\nonumber \\ X= & {} k \mathrm{e}^{\nu /2} \cosh (t/k),~Y=k \mathrm{e}^{\nu /2} \sinh (t/k), \nonumber \\ Z= & {} f(r) , \end{aligned}$$
(11)

provided \(f'^2(r)=\mp [-(\mathrm{e}^\lambda -1)+k^2\mathrm{e}^\nu \nu '~^2/4]\) and for all \(k>0\).

However, in this transformation it is always possible to find \(\lambda (r)\) and \(\nu (r)\) such that \(\mathrm{d}Z^2=f'^2(r)=0\) or equivalently

$$\begin{aligned} \mathrm{e}^\lambda = 1+{1 \over 4}k^2 \nu '^2 \mathrm{e}^\nu . \end{aligned}$$
(12)

Hence with the transformation (11), the metric (1) can be embedded in 5-D pseudo-Euclidean space (i.e. class I solution) provided the condition (12) is satisfied. This condition (12) is known as the Karmarkar condition; it was presented in terms of components of the Riemann tensor by [31] as

$$\begin{aligned} R_{rtrt}=\frac{R_{r\theta r \theta }R_{\phi t \phi t}+ R_{r \theta \theta t}R_{r \phi \phi t}}{R_{\theta \phi \theta \phi }} \end{aligned}$$
(13)

with \(R_{\theta \phi \theta \phi } \ne 0\) [32].

Now the above components of \(R_{\mu \nu \alpha \beta }\) for the metric (1) are

$$\begin{aligned}&R_{\theta \phi \theta \phi } = r^2 \sin ^{2}\theta ~\left[ 1-\mathrm{e}^{-\lambda }\right] , \\&R_{r\theta r \theta } = \frac{1}{2}~\lambda ' ~r , \\&R_{r \theta \theta t} = 0 ,\\&R_{rtrt} = \mathrm{e}^{\nu }\left[ \frac{1}{2}~\nu ''+\frac{1}{4}~{\nu '}^{2}-\frac{1}{4}\,\lambda '~\nu ' \right] , \\&R_{\phi t \phi t}= \frac{r}{2}\sin ^{2}\theta ~ \nu ' ~\mathrm{e}^{\nu -\lambda } . \end{aligned}$$

We assume that the matter distribution within the star is locally anisotropic and therefore the energy-momentum tensor is described by

$$\begin{aligned} T_{\mu \nu }= (\rho +p_\mathrm{r})v_\mu v_\nu -p_\mathrm{t} g_{\mu \nu }+(p_\mathrm{r}-p_\mathrm{t})\chi _\mu \chi _\nu \end{aligned}$$
(14)

where \(\rho ,\,p_\mathrm{r}\) and \(p_\mathrm{t}\) represent the matter density, radial and transverse pressure of the fluid distribution. The quantities \(v^\mu \) and \(\chi ^\mu \) are four-velocity and the unit spacelike vector in the radial direction satisfying \(-v^\mu v_\mu =\chi ^\mu \chi _\mu =1\).

Assuming \(G=c=1\), for the line element (1) and the matter distribution (14) the Einstein field equations are written as

$$\begin{aligned}&\frac{1-\mathrm{e}^{-\lambda }}{r^{2}}+\frac{\mathrm{e}^{-\lambda }\lambda '}{r}=8\pi \rho (r) , \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\mathrm{e}^{-\lambda }-1}{r^{2}}+\frac{\mathrm{e}^{-\lambda }\nu '}{r}=8\pi p_{r}(r) , \end{aligned}$$
(16)
$$\begin{aligned}&\mathrm{e}^{-\lambda }\left( \frac{\nu ''}{2}+\frac{\nu '^{2}}{4}-\frac{\nu '\lambda '}{4}+\frac{\nu '-\lambda '}{2r} \right) =8\pi p_\mathrm{t}(r) , \end{aligned}$$
(17)

where \((')\) represents differentiation with respect to the radial coordinate r. From Eqs. (16) and (17) the anisotropy factor \(\Delta \) is obtained:

$$\begin{aligned} \Delta (r)= & {} p_\mathrm{t}-p_\mathrm{r}\nonumber \\= & {} \frac{\mathrm{e}^{-\lambda }}{8\pi } \bigg [{\nu '' \over 2}-{\lambda ' \nu ' \over 4}+{\nu '^2 \over 4}-{\nu '+\lambda ' \over 2r} +{\mathrm{e}^\lambda -1 \over r^2}\bigg ]. \end{aligned}$$
(18)

On integration (12) we get the following relationship between the metric potentials \(\nu \) and \(\lambda \):

$$\begin{aligned} \mathrm{e}^{\nu }=\left( A+B\int \sqrt{\mathrm{e}^{\lambda }-1}~\mathrm{d}r\right) ^2 \end{aligned}$$
(19)

where \(A = 3C/2\) and \(B=3/k\) are constants of integration. By using (19) we can rewrite (18) as

$$\begin{aligned} \Delta (r) = {\nu ' \over 4\mathrm{e}^\lambda }\left[ {2\over r}-{\lambda ' \over \mathrm{e}^\lambda -1}\right] ~\left[ {\nu ' \mathrm{e}^\nu \over 2rB^2}-1\right] . \end{aligned}$$
(20)

We have to solve the Einstein field equations (15)–(17) with the help of Eq. (19). One can notice that we have four equations with five unknowns, namely \(\lambda ,~\nu ,~\rho ,~p_\mathrm{r}\) and \(p_\mathrm{t}\).

3 Solutions to the Einstein field equation

To generate the model let us assume a completely new expression for the \(g_{rr}\) metric potential:

$$\begin{aligned} \mathrm{e}^{\lambda }=1 + \frac{a^2r^2}{(1 + b^2r^4)^n} \end{aligned}$$
(21)

where a and b are constants having the dimensions length \(^{-1}\) and length \(^{-2}\), respectively.

Solving Eqs. (19) and (21) we obtain the expression for the metric coefficient \(\mathrm{e}^{\nu }\):

$$\begin{aligned} \mathrm{e}^{\nu }=\left( A + \frac{1}{2} a B r^2~~ _2 F_1\left[ \frac{1}{2}, \frac{n}{2};~ \frac{3}{2};~ -b^2 r^4\right] \right) ^2 \end{aligned}$$
(22)

where \(_2F_1\) is the usual hypergeometric function defined as

$$\begin{aligned} _2F_1 (a,~b;~c;~z) = \sum _{i=0}^\infty {(a)_i (b)_i \over (c)_i} {z^i \over i!}. \end{aligned}$$
(23)

Here \((x)_n\) is the Pochhammer symbol, which is defined as

$$\begin{aligned} (x)_i = \left\{ \begin{array}{lcl} 1 &{} \quad \text{ for } &{} i=0 \\ x(x+1)\ldots (x+i-1) &{}\quad \text{ for } &{} i>0 . \end{array}\right. \end{aligned}$$
(24)

Using Eqs. (21) and (22) the expressions for matter density, radial and transverse pressure are obtained:

$$\begin{aligned} 8\pi \rho= & {} \frac{a^2}{(1 + b^2 r^4)\big [a^2 r^2 + (1 + b^2 r^4)^n\big ]^2}\nonumber \\&\times \Big [(1 + b^2 r^4)^n\big \{3 + b^2 (3 - 4 n) r^4\big \}\nonumber \\&+ a^2 (r^2 + b^2 r^6)\Big ] ,\end{aligned}$$
(25)
$$\begin{aligned} 8\pi p_\mathrm{r}= & {} \frac{a \big [-2 a A +4 B (1 + b^2 r^4)^{n/2}- a^2 B r^2 f_1(r)\big ]}{\big [a^2 r^2 + (1 + b^2 r^4)^n\big ]\big [2 A + a B r^2 f_1(r)\big ]},\end{aligned}$$
(26)
$$\begin{aligned} 8\pi p_\mathrm{t}= & {} \frac{a (1 + b^2 r^4)^{n/2-1}}{\big [a^2 r^2 + (1 + b^2 r^4)^n\big ]^2 \big [2 A + a B r^2 f_1(r)\big ]}\nonumber \\&\times \Big [2 a^2 B r^2 (1 + b^2 r^4)+ 4 B (1 + b^2 r^4)^n \nonumber \\&\times \big \{1-(n-1)b^2 r^4\big \}-a (1 + b^2 r^4)^{n/2}\nonumber \\&\times \big \{1-(2 n-1)b^2 r^4\big \}\big \{2 A + a B r^2 f_1(r)\big \}\Big ], \end{aligned}$$
(27)

where

$$\begin{aligned} f_1(r)= & {} _2 F_1\left[ \frac{1}{2}, \frac{n}{2};~ \frac{3}{2};~ -b^2 r^4\right] . \end{aligned}$$

4 Physical acceptability conditions

For the well-behaved nature of the solution, the following conditions should be satisfied [33]:

  1. (i)

    The metric potentials should be free from singularities inside the radius of the star; moreover, the fluid sphere should satisfy \(\mathrm{e}^{\nu (0)}=\) constant, and \(\mathrm{e}^{-\lambda (0)}=1\).

  2. (ii)

    The density \(\rho \) and pressures \(p_\mathrm{r},\,p_\mathrm{t}\) should be positive inside the fluid configuration.

  3. (iii)

    The radial pressure \(p_\mathrm{r}\) must be vanishing but the tangential pressure \(p_\mathrm{t}\) needs not necessarily vanish at the boundary \(r=r_\Sigma \). However, the radial pressure is equal to the tangential pressure at the center of the fluid sphere, i.e., the pressure anisotropy vanishes at the center, \(\Delta (0)=0\) [34, 35] and \(\displaystyle \Delta (r=r_\Sigma )=p_\mathrm{t}(r_\Sigma )>0\) [36].

  4. (iv)

    The radial pressure gradient \(\mathrm{d}p_\mathrm{r}/\mathrm{d}r\le 0\) for \(0\le r \le r_\Sigma \).

  5. (v)

    The density gradient \(\mathrm{d}\rho /\mathrm{d}r\le 0\) for \(0\le r\le r_\Sigma \).

  6. (vi)

    A physically acceptable fluid sphere must satisfy the causality conditions; the radial and tangential adiabatic speeds of sound should be less than the speed of light. In the unit \(c=1\) the causality conditions take the form \(0<v_{sr}^{2}=\mathrm{d}p_\mathrm{r}/\mathrm{d}\rho \le 1\) and \(0<v_{st}^{2}=\mathrm{d}p_\mathrm{t}/\mathrm{d}\rho \le 1\).

  7. (vii)

    The interior solution should satisfy either:

    • strong energy condition (SEC) \(\rho -p_\mathrm{r}-2p_\mathrm{t}\ge 0,\,\rho -p_\mathrm{r}\ge 0,\,\rho -p_\mathrm{t}\ge 0\) or,

    • dominant energy condition (DEC) \(\rho \ge p_\mathrm{r}\) and \(\rho \ge p_\mathrm{t}\).

  8. (viii)

    The interior solution should continuously match with the exterior Schwarzschild solution.

Conditions (iv) and (v) imply that pressure and density should be maximum at the center and monotonically decreasing towards the surface.

5 Exterior spacetime and boundary condition

To fix the values of the constants \(a,\,b,\,A\) and B we match our interior spacetime to the exterior Schwarzschild line element given by

$$\begin{aligned} \mathrm{d}s^{2}= & {} \left( 1-\frac{2m}{r}\right) \mathrm{d}t^{2}-\left( 1-\frac{2m}{r}\right) ^{-1}\mathrm{d}r^{2}\nonumber \\&-r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}) \end{aligned}$$
(28)

outside the event horizon \(r>2m\), m being the mass of the black hole.

Using the continuity of the metric coefficients \(\mathrm{e}^{\nu },\mathrm{e}^{\lambda }\) across the boundary we get the following three equations (Table 3):

$$\begin{aligned}&1 + \frac{a^2 r_{\Sigma }^2}{(1 + b^2 r_{\Sigma }^4)^n}=\left( 1-\frac{2m}{r_{\Sigma }}\right) ^{-1}, \end{aligned}$$
(29)
$$\begin{aligned}&1-\frac{2m}{r_{\Sigma }}=\left[ A + \frac{1}{2} a B r_{\Sigma }^2 f_1(r_{\Sigma })\right] ^2 , \end{aligned}$$
(30)

and \(p_\mathrm{r}(r=r_{\Sigma })=0\) gives

$$\begin{aligned} -2 a A +4 B (1 + b^2 r_{\Sigma }^4)^{n/2}- a^2 B r_{\Sigma }^2 f_1(r_{\Sigma })=0. \end{aligned}$$
(31)

Solving Eqs. (29)–(31) we get

$$\begin{aligned} a= & {} \frac{(1+b^2r_{\Sigma }^4)^{n/2}}{r_{\Sigma }}\sqrt{\frac{2m/r_{\Sigma }}{1-2m/r_{\Sigma }}},\end{aligned}$$
(32)
$$\begin{aligned} B= & {} \frac{a}{2(1 + b^2r_{\Sigma }^4)^{n/2}} \sqrt{1 - \frac{2m}{r_{\Sigma }}},\end{aligned}$$
(33)
$$\begin{aligned} A= & {} \sqrt{1 - \frac{2m}{r_{\Sigma }} }- \frac{1}{2}a B r_{\Sigma }^2 f_1(r_{\Sigma }). \end{aligned}$$
(34)

6 Physical analysis

At the center of the star the expressions for metric potentials are obtained:

$$\begin{aligned} \mathrm{e}^{\lambda }|_{r=0}=1,\quad \mathrm{e}^{\nu }|_{r=0}=\left( A-\frac{aB}{2b}\right) ^2, \end{aligned}$$

which are constants and

$$\begin{aligned} (\mathrm{e}^{\lambda })'|_{r=0}=0,\quad (\mathrm{e}^{\nu })'|_{r=0}=0. \end{aligned}$$

The central density and central pressure are obtained:

$$\begin{aligned}&8\pi \rho _\mathrm{c} = 3a^2,\end{aligned}$$
(35)
$$\begin{aligned}&8\pi p_{rc} = 8\pi p_{tc}=\frac{a \big [- 2 a A + 4 B \big ]}{2 A }. \end{aligned}$$
(36)

To satisfy Zeldovich’s condition at the interior, \(p_\mathrm{r}/\rho \) at the center must be \({\le }1\). Therefore

$$\begin{aligned} \frac{- 2 a A + 4B}{6A a} \le 1. \end{aligned}$$
(37)

From Eqs. (36) and (37) we get

$$\begin{aligned} \frac{1}{2a} \le \frac{A}{B} < \frac{2}{a}. \end{aligned}$$
(38)

Differentiating Eqs. (25)–(27) we get the density and pressure gradient:

$$\begin{aligned} 8\pi \frac{\mathrm{d}\rho }{\mathrm{d}r}= & {} -\frac{2 a^2 r}{(1 + b^2 r^4)^2 (a^2 r^2 + (1 + b^2 r^4)^n)^3} \nonumber \\&\times \big [2 b^2 n r^2 (1 + b^2 r^4)^{2 n} \big \{7 + b^2 (3 - 4 n) r^4\big \} \nonumber \\&+a^4 (r + b^2 r^5)^2 + a^2 (1 + b^2 r^4)^n f_2(r)\big ] ,\end{aligned}$$
(39)
$$\begin{aligned} 8\pi \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}= & {} -\frac{2ar}{(1 + b^2 r^4)\big [a^2 r^2 + (1 + b^2 r^4)^n\big ]^2 f_6(r)}\nonumber \\&\times \bigg [4 b^2 B n r^2 (1 + b^2 r^4)^{3 n/2} (2 A +a B r^2 f_1(r))\nonumber \\&+4 a^2 B (1 + b^2 r^4)^{n/2} \big \{1 - b^2 (n-1) r^4\big \}\nonumber \\&\times \big \{2 A + a B r^2 f_1(r)\big \} - a^3 (1 + b^2 r^4)f_3(r)\nonumber \\&\times f_4(r)-2 a (1 + b^2 r^4)^n f_5(r) \bigg ],\\ 8\pi \frac{\mathrm{d}\Delta }{\mathrm{d}r}= & {} -\frac{2ar}{(1 + b^2 r^4)^2 (a^2 r^2 + (1 + b^2 r^4)^n)^3 f_6(r)}\nonumber \\&\times \Bigg [4 a^4 A B r^2 (1 + b^2 r^4)^{1 +n/2}\big \{(n-1)b^2 r^4-1\big \} \nonumber \\&-8 A b^2 B n r^2 (1 + b^2 r^4)^{5 n/2} (b^2 n r^4-2) +2 a^5 \nonumber \\&\times (2 A^2 - B^2 r^2)(r + b^2 r^5)^2 +4 a^2 A B\nonumber \\&\times (1 + b^2 r^4)^{3 n/2} f_7(r) -4 a b^2 n r^2 (1 + b^2 r^4)^{2 n} \nonumber \\&f_8(r)- 2 a^3 (1 + b^2 r^4)^n f_9(r) +a B r^2 f_1(r) \nonumber \\&\bigg \{2 \Big (a^4 B r^2(1 + b^2 r^4)^{1+n/2} \big \{(n-1)b^2 r^4-1\big \} \nonumber \\&-f_{10}(r)+8 a A b^2 n r^2 f_{11}(r) +2 a^5 A (r + b^2 r^5)^2 \nonumber \\&+a^2 B(1 + b^2 r^4)^{3 n/2} f_{12}(r) - 2 a^3 A (1 + b^2 r^4)^n \nonumber \\&f_{13}(r)\Big )+a^2 B r^2 f_1(r)f_{16}(r)\bigg \}\Bigg ],\end{aligned}$$
(40)
$$\begin{aligned} {\mathrm{d}p_\mathrm{t} \over \mathrm{d}r}= & {} {\mathrm{d}p_\mathrm{r} \over \mathrm{d}r}+{\mathrm{d}\Delta \over \mathrm{d}r} , \end{aligned}$$
(41)

where

$$\begin{aligned} f_2(r)= & {} 5 - 2 b^2 (-5 + n) r^4 + b^4 \big \{5 + 2 n (-5 + 4 n)\big \} r^8 ,\\ f_3(r)= & {} 2 (A + B r) + a B r^2 f_1(r) , \\ f_4(r)= & {} 2 A - 2 B r + a B r^2 f_1(r) , \\ f_5(r)= & {} -2\big \{-2 A^2 b^2 n r^2 + B^2 (1 + b^2 r^4)\big \}\\&+ a b^2 B n r^4 f_1(r) (4 A + a B r^2 f_1(r)) , \\ f_6(r)= & {} \big \{2 A + a B r^2 f_1(r)\big \}^2 , \\ f_7(r)= & {} (1 + b^2 (2 - 3 n) r^4 \\&+ b^4 (-1 + n) (-1 + 6 n) r^8) , \\ f_8(r)= & {} (B^2 r^2 (1 + b^2 r^4) + A^2 (4 - 4 b^2 n r^4)) , \\ f_9(r)= & {} B^2 r^2 (1 + b^2 r^4)\big \{ 1 + b^2 (1 + 2 n) r^4\big \} \\&+2 A^2 \Big [1 + 2 b^2 (1 - 2 n) r^4 \\&+ b^4 \big \{1 + 4 (-2 + n) n\big \} r^8\Big ] , \\ f_{10}(r)= & {} 2 b^2 B n r^2 (1 + b^2 r^4)^{\frac{5 n}{2}}(b^2 n r^4-2),\\ f_{11}(r)= & {} (1 + b^2 r^4)^{2 n} (b^2 n r^4-1) , \\ f_{12}(r)= & {} 1 + b^2 (2 - 3 n) r^4 + b^4 (-1 + n) (-1 + 6 n) r^8,\\ f_{13}(r)= & {} 1 + 2 b^2 (1 - 2 n) r^4 + b^4 \big \{1 + 4 (-2 + n) n\big \} r^8,\\ f_{14}(r)= & {} (1 + b^2 r^4)^{2 n} (-1 + b^2 n r^4) , \\ f_{15}(r)= & {} 1 + 2 b^2 (1 - 2 n) r^4 + b^4 \big \{1 + 4 (-2 + n) n\big \} , \\ f_{16}(r)= & {} 4 b^2 n r^2 f_{14}(r) + a^4 (r + b^2 r^5)^2 \\&-a^2 (1 + b^2 r^4)^n f_{15}(r) r^8. \end{aligned}$$

The mass function, compactness parameter and redshift can be determined as

$$\begin{aligned} m(r)= & {} 4\pi \int _0^r r^2 \rho (r) ~\mathrm{d}r = \frac{a^2 r^3}{2 \left[ a^2 r^2+(b^2 r^4+1)^n\right] } , \end{aligned}$$
(42)
$$\begin{aligned} u(r)= & {} {2m(r) \over r} = \frac{a^2 r^2}{a^2 r^2+\left( b^2 r^4+1\right) ^n} , \end{aligned}$$
(43)
$$\begin{aligned} z(r)= & {} \mathrm{e}^{-\nu (r) /2}-1 , \nonumber \\= & {} \left( A + \frac{a B r^2}{2} ~ _2 F_1\left[ \frac{1}{2}, \frac{n}{2}; \frac{3}{2}; -b^2 r^4\right] \right) ^{-1}-1. \end{aligned}$$
(44)

7 Equilibrium and stability analysis

7.1 Equilibrium analysis via TOV-equation

Equilibrium condition under three forces, viz. the gravitational, hydrostatic and anisotropic forces, can be analyze via a generalized Tolman–Oppenheimer–Volkoff (TOV) equation expressed as

$$\begin{aligned} -\frac{M_g(r)(\rho +p_\mathrm{r})}{r}\mathrm{e}^{\frac{\nu -\lambda }{2}}-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})=0, \end{aligned}$$
(45)

where \(M_g(r) \) represents the gravitational mass within the radius r. It is defined using the Tolman–Whittaker mass formula through the Einstein field equations as

$$\begin{aligned} M_g(r)= & {} 4 \pi \int _0^r \big (T^t_t-T^r_r-T^\theta _\theta -T^\phi _\phi \big ) r^2 \mathrm{e}^{(\nu +\lambda )/2}\mathrm{d}r \nonumber \\= & {} \frac{1}{2}r\mathrm{e}^{(\lambda -\nu )/2}~\nu '. \end{aligned}$$
(46)

Plugging the value of \(M_g(r)\) in Eq. (46), we get

$$\begin{aligned}&-\frac{\nu '}{2}(\rho +p_\mathrm{r})-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})=0\nonumber \\ \text{ or }~&F_g+F_h+F_a = 0 \end{aligned}$$
(47)

where \(F_g, F_h\) and \(F_a\) represent the gravitational, hydrostatic and anisotropic forces, respectively, and it gives

$$\begin{aligned} F_g= & {} -\frac{\nu '}{2}(\rho +p_\mathrm{r})= \Bigg [ a^2 B r \Big (a^2 B r^2 (b^2 r^4+1)^{n/2} \nonumber \\&\times \big \{b^2 (2 n-1) r^4-1\big \} _2F_1\left[ \frac{1}{2},\frac{n}{2};\frac{3}{2};-b^2 r^4\right] \nonumber \\&- 2 \Big \{a^2 B r^2 (b^2 r^4+1)-a A \big \{b^2 (2 n-1) r^4-1\big \}\nonumber \\&\times (b^2 r^4+1)^{n/2}+B (b^2 r^4+1)^{n+1}\Big \}\Big ) \Bigg ] \nonumber \\&\times \left[ 2 (\pi b^2 r^4+\pi ) \big \{(a^2 r^2+(b^2 r^4+1)^n\big \}^2\right. \nonumber \\&\left. \times \left( a B r^2~ _2F_1\left[ \frac{1}{2},\frac{n}{2};\frac{3}{2};-b^2 r^4\right] +2 A\right) ^2\right] ^{-1} ,\end{aligned}$$
(48)
$$\begin{aligned} F_h= & {} -{1\over 8\pi } {\mathrm{d}p_\mathrm{r} \over \mathrm{d}r}\end{aligned}$$
(49)
$$\begin{aligned} F_a= & {} {2\Delta \over r} = \left[ a r \big \{a^2 (b^2 r^4+1)+2 b^2 n r^2 (b^2 r^4+1)^n\big \} \right. \nonumber \\&\times \left\{ a^2 B r^2 \, _2F_1\left[ \frac{1}{2},\frac{n}{2};\frac{3}{2};-b^2 r^4\right] \right. \nonumber \\&\left. \left. +2 a A-2 B (b^2 r^4+1)^{n/2}\right\} \right] \nonumber \\&\times \left[ 4 \pi (b^2 r^4+1)\big \{a^2 r^2+(b^2 r^4+1)^n\big \}^2 \right. \nonumber \\&\times \left. \left\{ a B r^2 _2F_1\left[ \frac{1}{2},\frac{n}{2};\frac{3}{2};-b^2 r^4\right] +2 A\right\} \right] ^{-1}. \end{aligned}$$
(50)

All the solutions have to satisfy TOV equation if the configurations are at equilibrium.

7.2 Causality condition and stability criterion

In general relativity, since the maximum possible speed is the speed of light, the speed of sound when traveling within the interior of the star has to be less than or equal to the speed of light. This condition is known as the causality condition. The speed of sound can be determined using

$$\begin{aligned} v_r^2 = {\mathrm{d}p_\mathrm{r}/\mathrm{d}r \over \mathrm{d}\rho /\mathrm{d}r}\quad \text{ and }\quad v_t^2 = {\mathrm{d}p_\mathrm{t}/\mathrm{d}r \over \mathrm{d}\rho /\mathrm{d}r} \end{aligned}$$
(51)

and in the light of (39)–(42). To satisfy the causality condition \(v_r^2\) and \(v_t^2\) have to lie in the range of 0 to 1. Using the cracking method of analysis stability by Herrera [37] and Abreu et al. [33] one finds a stability condition in terms of the speed of sound. They have proposed that \(-1 \le v_t^2-v_r^2 \le 0\) is satisfied for stable configurations and \(0 < v_t^2-v_r^2 \le 1\) is satisfied for unstable configurations.

7.3 Stability analysis using relativistic adiabatic index

One of the important parameters needed to analyze whether a configuration is potentially stable or not is the relativistic adiabatic index \(\Gamma _r\) and it is defined as

$$\begin{aligned} \Gamma _r = {\rho +p_\mathrm{r} \over p_\mathrm{r}} ~{\mathrm{d}p_\mathrm{r} \over \mathrm{d}\rho }. \end{aligned}$$
(52)
Fig. 1
figure 1

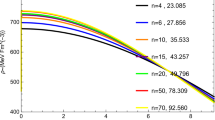
Variation of metric potentials with radial coordinate for the parameters given in Table 1

Full size image
Table 1 Values of the constants for different values of n
Full size table
Table 2 Central values of some physical quantities for different values of n
Full size table
Table 3 Variation of metric potentials with radial coordinates r for different values of n
Full size table

Bondi had clearly mentioned that a stable Newtonian sphere has \(\Gamma _r > 4/3\) and \(\Gamma _r = 4/3\) for a neutral equilibrium. However, Chan et al. [38] have shown that in the general relativistic case the above condition is modified as

$$\begin{aligned} \Gamma _r > \frac{4}{3}+\left[ \frac{4}{3}\frac{(p_{ti}-p_{ri})}{|p_{ri}^\prime |r}+\frac{8\pi }{3}\frac{\rho _ip_{ri}}{|p_{ri}^\prime |}~r\right] _{\max }, \end{aligned}$$
(53)

where \(p_{ri}\), \(p_{ti}\), and \(\rho _i\) are the initial values of radial, tangential and energy densities in static equilibrium satisfying (46). The first and last term inside the square brackets represent the anisotropic and relativistic corrections, respectively, and both quantities are positive increasing the unstable range of \(\Gamma \).

7.4 Static stability criterion

The static stability criterion (Harrison–Zeldovich–Novi–kov) [39, 40] states that any stellar configuration has an increasing mass profile with increasing central density i.e. \(\mathrm{d}M/\mathrm{d}\rho _\mathrm{c} > 0\) represents stable configurations and vice versa. The turning point between stable and unstable region is achieved when the mass remains constant with increase in central density, i.e. \(\mathrm{d}M/\mathrm{d}\rho _\mathrm{c} = 0\). For the new solution \(M(\rho _\mathrm{c})\) and \(\mathrm{d}M/ \mathrm{d}\rho _\mathrm{c}\) we find

$$\begin{aligned}&M(\rho _\mathrm{c}) = {8\pi \rho _\mathrm{c} R^3/3 \over 16\pi \rho _\mathrm{c} R^2/3+2(1+b^2R^4)^n} ,\end{aligned}$$
(54)
$$\begin{aligned}&{\mathrm{d}M \over \mathrm{d}\rho _\mathrm{c}} = \frac{12 \pi R^3 \left( b^2 R^4+1\right) ^n}{\big [3 \left( b^2 R^4+1\right) ^n+8 \pi R^2 \rho _\mathrm{c}\big ]^2} >0. \end{aligned}$$
(55)

Hence the presenting new solutions can represent static stable configurations according to the above discussions.

Fig. 2
figure 2

Variation of density with radial coordinate for the parameters given in Table 1

Full size image
Fig. 3
figure 3

Variation of pressure with radial coordinate for the parameters given in Table 1

Full size image
Fig. 4
figure 4

Variation of anisotropy with radial coordinate for the parameters given in Table 1

Full size image
Fig. 5
figure 5

Variation of mass function with radial coordinate for the parameters given in Table 1

Full size image
Fig. 6
figure 6

Variation of redshift with radial coordinate for the parameters given in Table 1

Full size image
Fig. 7
figure 7

Variation of sound speed with radial coordinate for the parameters given in Table 1

Full size image
Fig. 8
figure 8

Variation of stability factor with radial coordinate for the parameters given in Table 1

Full size image
Fig. 9
figure 9

Variation of \(\rho -p_\mathrm{r}\) with radial coordinate for the parameters given in Table 1

Full size image
Fig. 10
figure 10

Variation of \(\rho -p_\mathrm{t}\) with radial coordinate for the parameters given in Table 1

Full size image
Fig. 11
figure 11

Variation of \(\rho -p_\mathrm{r}-2p_\mathrm{t}\) with radial coordinate for the parameters given in Table 1

Full size image
Fig. 12
figure 12

Variations of gravitational, hydrostatic and anisotropic forces acting on the system with radial coordinate for the parameters given in Table 1

Full size image
Fig. 13
figure 13

Variation of relativistic adiabatic index with radial coordinate for the parameters given in Table 1

Full size image
Fig. 14
figure 14

Variation of mass with central density for \(R=9~\mathrm{km}\) and for the parameters given in Table 1

Full size image
Fig. 15
figure 15

Variation of equation of state parameters with radial coordinate for the parameters given in Table 1

Full size image

8 Results and discussions

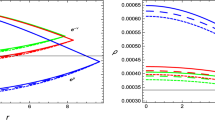
The central values of the metric potentials are regular and finite throughout the interior and free of any singularity (Fig. 1). The values of \(\mathrm{e}^\nu \) are almost the same and \(\mathrm{e}^\lambda \) is slightly changed for \(n=12\) to \(n=12\) (see Table 3). The central density is also regular and finite everywhere inside the boundary; however, \(n=12\) gives lower \(\rho _\mathrm{c}\) than \(n=24\) (Fig. 2; Table 2). The interior pressures are also finite and regular. Here \(n=12\) gives a higher pressure than \(n=24\) (Fig. 3). Since \(n=12\) exerts a higher outward pressure, the corresponding density is also smaller. The increasing nature of anisotropy is shown in Fig. 4; \(n=12\) shows smaller anisotropy than \(n=24\). This anisotropy is zero at the center since the matter is highly packed. The mass function and compactness parameter are shown in Fig. 5 signifying that the maximum mass is \(2.1M_\odot \) and the maximum compactness parameter 0.469 is with Buchdahl limit. The redshift at the center yield by the solutions is minimum for \(n=12\) and maximum for \(n=24\); however, the surface redshift is exactly equal for all values of n (Fig. 6). These solutions obey the causality condition perfectly for \(n=12\) to \(n=24\), being well-behaved, i.e. decreasing radially outward (Fig. 7). The stability factor \(v_t^2-v_r^2\) holds the cracking stability criterion since it lies between \(-1\) and 0 (Fig. 8).

In a previous research article, Herrera et al. [41] proposed that any solution describing a static anisotropic fluid distribution is fully determined by the two generating functions \(\Pi \) and Z given by

$$\begin{aligned} \Pi= & {} 8\pi (p_\mathrm{r}-p_\mathrm{t}) \end{aligned}$$
(56)

and

$$\begin{aligned} \mathrm{e}^{\nu (r)}= & {} \mathrm{e}^{\int \big (2 Z(r)-\frac{2}{r}\big ) \mathrm{d}r}. \end{aligned}$$
(57)

In our present model these two generating functions are obtained:

$$\begin{aligned} \Pi= & {} -8\pi \Delta , \end{aligned}$$
(58)
$$\begin{aligned} Z= & {} \frac{1}{r} + \frac{2 a B r (1 + b^2 r^4)^{-n/2}}{ 2 A + a B r^2 ~_2 F_1\Big [\frac{1}{2}, \frac{n}{2};~ \frac{3}{2};~ -b^2 r^4\Big ]}. \end{aligned}$$
(59)

The satisfaction of the strong energy condition (SEC), null energy condition (NEC), the weak energy condition (WEC) and the dominant energy condition (DEC) ensure that the solution can represent a physically possible matter distribution. The presented new solutions do satisfy all these energy conditions, signifying that these are physical solutions (Figs. 9, 10, 11). The equilibrium condition is possible only when all the applied forces satisfy the TOV equation and balance each other. The solutions present here also satisfy the TOV equation and hence can represents equilibrium conditions (Fig. 12).

These solutions yield an almost equal central adiabatic index \(\Gamma _{rc}\) of about 1.735 (Fig. 13). This central value is larger than 4/3 and hence these solutions can represent stable stellar objects. The static stable criterion also hold good by our solutions. For \(R=9~\mathrm{km}\), the maximum mass allowed by this criterion is 4.46 \(M_\odot \) and it is obtained from about \(\rho _\mathrm{c} = 2.021 \times 10^{17}~\mathrm{g/cm}^3\) (see Fig. 14). The equation of state parameters i.e. \(\omega _r=p_\mathrm{r}/\rho \) and \(\omega _t=p_\mathrm{t}/\rho \) are less than 1, showing that it describes physical matters (Fig. 15). Thus from all these analyses, one can conclude with certainty that the new solutions are physically possible well-behaved solutions that can be used to describe physical compact models.