1 Introduction

The astrophysical data obtained from high redshift surveys of supernovae [1,2,3], Wilkinson Microwave Anisotropy Probe (WMAP) [4, 5] and the large scale structure from Slogan Digital Sky Survey (SDSS) [6, 7] support the existence of dark energy (DE). The DE is considered as an exotic energy component with negative pressure. The cosmological analysis of these observations suggest that the universe consists of about \(70\%\) DE, \(30\%\) dust matter (cold dark matter plus baryons), and negligible radiation. It is the most accepted idea that DE leads to the late-time accelerated expansion of the universe. Nevertheless, the nature of such a DE is still the source of debate. Many theoretical models have been proposed to describe this late-time acceleration of the universe. The most obvious theoretical candidate for DE is the cosmological constant [8], which has the equation of state (EoS) \(\omega _{\Lambda }=-1\). However, it suffers the so-called cosmological constant (CC) problem (the fine-tuning problem) and the cosmic coincidence problem [9,10,11]. Both of these problems are related to the DE density.

In order to solve the cosmological constant problems, many candidates such as quintessence [12, 13], phantom [14], tachyon field [15], quintom [16], holographic dark energy [17, 18], agegraphic dark energy [19, 20] have been proposed to explain the nature of DE phenomenon. Starobinsky [21] and Kerner et al. [22] proposed an another way to explain the accelerated expansion of the universe by modifying the geometrical part of Einstein field equations which is known as modified gravity theory.

In recent years, the considerable interest has been noticed in the study of holographic dark energy (HDE) model to explain the recent phase transition of the universe. The idea of HDE is basically based on the holographic principle [23,24,25]. According to holographic principle a short distance (ultraviolet) cut-off \(\Lambda \) is related to the long distance (infrared) cut-off L due to the limit set by the formation of a black hole [26]. Li [18] argued that the total energy in a region of size L should not exceed the mass of a black hole of same size for a system with ultraviolet (UV) cut-off \(\Lambda \), thus \(L^3\rho _{\Lambda }\le L M^{2}_{pl}\), where \(\rho _{\Lambda }\) is the quantum zero-point energy density caused by UV cot-off \(\Lambda \) and \(M_{pl}\) is the reduced Planck mass \(M^{-2}_{pl}=8\pi G\). The largest L allowed is the one saturating this inequality, thus the HDE density is defined as \(\rho _{\Lambda }=3c^2M^{2}_{pl}L^{-2}\), where c is a numerical constant. The UV cut-off is related to the vacuum energy, and the infrared (IR) cut-off is related to the large scale structure of the universe, i.e., Hubble horizon, particle horizon, event horizon, Ricci scalar, etc. The HDE model suffers the choice of IR cut-off problem. In the Ref. [17], it has been discussed that the HDE model with Hubble horizon or particle horizon can not drive the accelerated expansion of the universe. However, HDE model with event horizon can drive the accelerated expansion of the universe [18]. The drawback with event horizon is that it is a global concept of spacetime and existence of universe, depends on the future evolution of the universe. The HDE with event horizon is also not compatible with the age of some old high redshift objects [27]. Gao et al. [28] proposed IR cut-off as a function of Ricci scalar. So, the length L is given by the average radius of Ricci scalar curvature.

As the origin of the HDE is still unknown, Granda and Oliveros [29] proposed a new IR cut-off for HDE, known as new holographic dark energy (NHDE), which besides the square of the Hubble scale also contains the time derivative of the Hubble scale. The advantage is that this NHDE model depends on local quantities and avoids the causality problem appearing with event horizon IR cut-off. The authors, in their other paper [30], reconstructed the scalar field models for HDE by using this new IR cut-off in flat Friedmann–Robertson–Walker (FRW) universe with only DE content. Karami and Fehri [31] generated the results of Ref. [29] for non-flat FRW universe. Malekjani et al. [32] have studied the statefinder diagnostic with new IR cut-off proposed in [29] in a non-flat model. Sharif and Jawad [33] have investigated interacting NHDE model in non-flat universe. Debnath and Chattopadhyay [34] have considered flat FRW model filled with mixture of dark matter and NHDE, and have studied the statefinder and Om diagnostics. Wang and Xu [35] have obtained the constraints on HDE model with new IR cut-off via the Markov Chain Monte Carlo method with the combined constraints of current cosmological observations. Oliveros and Acero [36] have studied NHDE model with a non-linear interaction between the DE and dark matter (DM) in flat FRW universe.

A large number of models within modified theories can explain the DE phenomenon. It is therefore important to find the ways to discriminate among various competing models. For this purpose, Sahni et al. [37] and Alam et al. [38] introduced an important geometrical diagnostic, known as statefinder pair \(\{r, s\}\) to remove the degeneracy of \(H_0\) and \(q_0\) of different DE models. The statefinder diagnostic has been extensively used in the literature to distinguish among various models of DE and modified theories of gravity. The various DE models have different evolutionary trajectories in (r, s) plane.

In order to complement the statefinder [37, 38], a new diagnostic called \(\textit{Om}\) was proposed by Sahni et al. [39] in 2008, which is used to distinguish among the energy densities of various DE models. The advantage of \(\textit{Om}\) over the statefinder parameters is that, \(\textit{Om}\) involves only the first order derivative of scale factor. For the \(\Lambda CDM\) model \(\textit{Om}\) diagnostic turns out to be constant. We provide the mathematical expressions of statefinder and \(\textit{Om}\) diagnostic in the appropriate section.

Evolution of the universe involves a sequence of dissipative processes. These processes include bulk viscosity, shear viscosity and heat transport. The theory of dissipation was proposed by Eckart [40] and the full causal theory was developed by Israel and Stewart [41]. In the case of isotropic and homogeneous model, the dissipative process is modeled as a bulk viscosity, see Refs. [42,43,44,45,46,47,48,49,50]. Brevik et al. [51] discussed the general account about viscous cosmology for early and late time universe. Norman and Brevik [52] analyze characteristic properties of two different viscous cosmology models for the future universe. In other paper, Norman and Brevik [53] derived a general formalism for bulk viscous and estimated the bulk viscosity in the cosmic fluid. The HDE model has been studied in some recent literatures [54, 55] under the influence of bulk viscosity. Feng and Li [56] have investigated the viscous Ricci dark energy (RDE) model by assuming that there is bulk viscosity in the linear barotropic fluid and RDE. Singh and Kumar [57] have discussed the statefinder diagnosis of the viscous HDE cosmology. The main motive of this work is to explain the acceleration with the help of bulk viscosity for new holographic dark energy (NHDE) in GR which has not been studied sofar.

The bulk viscosity introduces dissipation by only redefining the effective pressure, \(p_{eff}\), according as \(p_{eff}=p-3\zeta H\), where \(\zeta \) is the bulk viscosity coefficient and H is the Hubble parameter. In this paper, we are interested when the universe is dominated by viscous HDE and dark matter with Granda–Oliveros IR cut-off to study the influence of bulk viscosity to the cosmic evolution. We consider the general form of bulk viscosity \(\zeta = \zeta _0 +\zeta _1 H\), where \(\zeta _0\) and \(\zeta _1\) are the constants and H is the Hubble’s parameter, see Refs. [42, 43]. First, we discuss the non-viscous NHDE model to find out the exact solution of the field equations. In the second case, we find out the exact solutions of the field equations with constant and varying bulk viscous term. We find the exact forms of scale factor, deceleration parameter and transition redshift and discuss the evolution through the graphs. We also discuss the geometrical diagnostics like statefinder parameter and Om diagnostic to discriminate our model with \(\Lambda CDM\). We plot the trajectories of these parameters and observe the effect of bulk viscous coefficient.

The paper is organised as follows. In Sect. 2, we discuss the non-viscous HDE model with new IR cut-off. Section 3 presents the viscous NHDE model and is divided into Sects. 3.1 and 3.2. In Sects. 3.1 and 3.2 we present the solutions with constant and time varying bulk viscous term. Section 4 presents the summary of the results.

2 Non-viscous NHDE model

We consider a spatially homogeneous and isotropic flat Friedmann–Robertson–Walker (FRW) space-time, specified by the line element

$$\begin{aligned} ds^2 = dt^2 - a^2(t) \left[ dr^2+r^2(d\theta ^2+sin^2\theta d\phi ^2)\right] , \end{aligned}$$
(1)

where a(t) is the scale factor, t is the cosmic time and \((r, \theta , \phi )\) are the comoving coordinates.

We consider that the Universe is filled with NHDE plus pressureless dark matter (DM) (ignoring the contribution of the baryonic matter here for simplicity). For Einstein field equations \(R_{\mu \nu }-g_{\mu \nu }R/2=T_{\mu \nu }\) in the units where \(8\pi G=c=1\), we obtain the Friedmann equations for the metric (1) as

$$\begin{aligned} 3H^2= & {} \rho _m + \rho _d, \end{aligned}$$
(2)
$$\begin{aligned} 2\dot{H} + 3H^2= & {} -p_d, \end{aligned}$$
(3)

where \(\rho _m\) and \(\rho _d\) are the energy density of DM and NHDE, respectively, and \(p_d\) is the pressure of the NHDE. A relation between \(\rho _{d}\) and \(p_{d} \) is given by equation of state (EoS) parameter \(\omega _d = p_d/\rho _d\). Here, \(H=\dot{a}/a\) is the Hubble parameter. A dot denotes a derivative with respect to the cosmic time t.

As suggested by Granda and Oliveros in paper [29], the energy density of HDE with the new IR cut-off is given by

$$\begin{aligned} \rho _d = 3 (\alpha H^2 +\beta \dot{H}), \end{aligned}$$
(4)

where \(\alpha \) and \(\beta \) are the dimensionless parameters, which must satisfy the restrictions imposed by the current observational data.

Using (4), Eqs. (2) and (3) give

$$\begin{aligned} \dot{H} + \frac{3(1+\alpha \;\omega _d)}{(2+3\beta \;\omega _d)} H^2 = 0. \end{aligned}$$
(5)

The solution of (5) is given by

$$\begin{aligned} H = \frac{1}{c_0+\frac{3(1+\alpha \; \omega _d)}{(2+3\beta \;\omega _d )}t}, \end{aligned}$$
(6)

where \(c_0\) is an integration constant. Equation (6) can be rewritten as

$$\begin{aligned} H = \frac{H_0 }{\left\{ 1+\frac{3 H_0 (1+\alpha \; \omega _d)}{(2+3\beta \;\omega _d )}(t-t_0)\right\} }, \end{aligned}$$
(7)

where \(H_0\) is the present value of the Hubble parameter at \(t=t_{0}\), where NHDE starts to dominate. As we know \(H=\dot{a}/a\), Eq. (7) gives the solution for the scale factor which is given by

$$\begin{aligned} a= & {} a_0 \left\{ 1+\frac{3(1+\alpha \; \omega _d)H_0}{(2+3\beta \;\omega _d)} (t-t_0) \right\} ^{\frac{(2+3\beta \; \omega _d)}{3(1+\alpha \; \omega _d)}}, \nonumber \\&\quad \text {for}\;\alpha \ne -1/\omega _d,\; \beta \ne -2/3\omega _d, \end{aligned}$$
(8)

where \(a_0\) is the present value of the scale factor at a cosmic time \(t=t_0\). Equation (8) shows the power-law \(a\propto t^m\), where m is a constant, type expansion of the scale factor. As we know that the universe will undergo with decelerated expansion for \(m < 1\), i.e., \((2+3\beta \omega _d ) < (3+3\alpha \omega _d)\) in our case whereas it accelerates for \(m > 1\), i.e., \((2+3\beta \omega _d ) > (3+3\alpha \omega _d)\). For \(m = 1\), i.e., \((2+3\beta \omega _d) = (3+3\alpha \omega _d)\), the universe will show marginal inflation. In the absence of NHDE, i.e., for \(\alpha =\beta =0\), we get the dark matter dominated scale factor, \(a=a_0(1+\frac{3}{2}H_0(t-t_0))^{2/3}\).

Let us consider the deceleration parameter (DP) which is very useful parameter to discuss the behaviour of the universe. The sign (positive or negative) of DP explains whether the universe decelerates or accelerates. It is defined as \(q = -\frac{a \ddot{a}}{\dot{a}^2}\). From (8), we get

$$\begin{aligned} q = \frac{3(1+\alpha \omega _d)}{(2+3\beta \omega _d)}-1, \end{aligned}$$
(9)

which is a constant value throughout the evolution of the universe. The universe will expand with decelerated rate for \(q>0\), i.e., \((2+3\beta \omega _d ) < (3+3\alpha \omega _d)\), accelerated rate for \(q<0\), i.e., \((2+3\beta \omega _d ) > (3+3\alpha \omega _d)\) and marginal inflation for \(q=0\), i.e., \((2+3\beta \omega _d ) = (3+3\alpha \omega _d)\). One can explicitly observe the dependence of DP q on the model parameters \(\alpha \), \(\beta \) and EoS parameter \(\omega _d\) under above constraints. Thus, we can obtain a decelerated or accelerated expansion of the universe depending on the suitable choices of these parameters. In this case, the model does not show the phase transition due to power-law expansion or constant DP. The model shows marginal inflation, \(q=0\) when \(\omega _d=1/3(\beta -\alpha )\). Using Markov chain Monte Carlo method on latest observational data, Wang and Xu [35] have constrained the NHDE model and obtained the best fit values of the parameters \(\alpha =0.8502^{+0.0984+0.1299}_{-0.0875-0.1064}\) and \(\beta =0.4817^{+0.0842+0.1176}_{-0.0773-0.0955}\) with \(1\sigma \) and \(2\sigma \) errors in flat model. In the best fit NHDE models, they have obtained the EoS parameter \(\omega _d=-1.1414\pm 0.0608\). Putting these values of parameters (excluding the errors) in Eq.(9), we get \(q=-0.7468\), which shows that our NHDE model is consistent with current observation data given in [35].

In order to discriminate among the various DE models, Sahni et al. [37] and Alam et al. [38] introduced a new geometrical diagnostic pair for DE, which is known as statefinder pair and is denoted as \(\{r,s\}\). The statefinder probes the expansion dynamics of the universe through higher derivatives of the scale factor and is a geometrical diagnosis in the sense that it depends on the scale factor and hence describes the spacetime. The statefinder pair is defined as

$$\begin{aligned} r=\frac{\dddot{a}}{a H^3}\quad \text {and} \quad s= \frac{r-1}{3(q-1/2)}. \end{aligned}$$
(10)

Substituting the required values from (8) and (9) into (10), we get

$$\begin{aligned} r = 1-\frac{9(1+\alpha \omega _d)}{(2+ 3\beta \omega _d)} + \frac{18(1+\alpha \omega _d)^2}{(2+3\beta \omega _d)^2}, \end{aligned}$$
(11)

and

$$\begin{aligned} s = \frac{2(1+\alpha \omega _d)}{2+3\beta \omega _d}. \end{aligned}$$
(12)

From (11) and (12), we can observe that these statefinder parameters are constant whose values depend on \(\alpha \), \(\beta \) and \(\omega _d\). As Sahni et al. [37] and Alam et al. [38] have observed that Lambda cold dark matter (\(\Lambda \)CDM) model and standard cold dark matter (SCDM) model have fixed point values of statefinder parameter \(\{r,s\} = \{1,0\}\) and \(\{r,s\} = \{1,1\}\), respectively. Putting the values of parameters [35] as mentioned above, we observe that this set of data do not favor the NHDE model over the \(\Lambda \)CDM as well as SCDM model. However, NHDE model behaves like SCDM model for \(\alpha =3\beta /2\). We can also observe that this model approaches to \(\{r, s\}\rightarrow \{1, 0\}\) in the limit of \(\alpha \rightarrow -1/\omega _d\) but there is no such value of parameters which would clearly show the \(\Lambda \)CDM.

3 Viscous NHDE model

In the previous section, we have observed that the non-viscous NHDE model gives constant DP which is unable to represent the phase transition. However, the observations show that the phase transition plays a vital role in describing the evolution of the universe. Therefore, it will be interesting to study the NHDE model with viscous to investigate whether a viscous NHDE model with Granda-Oliveros IR cut-off would be able to find the phase transition.

In an isotropic and homogeneous FRW universe, the dissipative effects arise due to the presence of bulk viscosity in cosmic fluids as shear viscosity plays no role. DE with bulk viscosity has a peculiar property to cause accelerated expansion of phantom type in the late time evolution of the universe [58,59,60]. It can also alleviate the problem like age problem and coincidence problem.

Let us assume that the effective pressure of NHDE is a sum of pressure of NHDE and bulk viscosity, i.e., the universe is filled with bulk viscous NHDE plus pressureless dark matter (DM) (ignoring the contribution of the baryonic matter here for simplicity). Then, the field equations (2) and (3) modify to

$$\begin{aligned}&3H^2 = \rho _m + \rho _d, \end{aligned}$$
(13)
$$\begin{aligned}&2\dot{H} + 3H^2 = -\tilde{p_d}, \end{aligned}$$
(14)

where \(\tilde{p_d}=p_d-3H\zeta \) is the effective pressure of NHDE. This form of effective pressure was originally proposed by Eckart [40] in the context of relativistic dissipative process occurring in thermodynamic systems went out of local thermal equilibrium. The term \(\zeta \) is the bulk viscosity coefficient [61,62,63]. On the thermodynamical grounds, \(\zeta \) is conventionally chosen to be a positive quantity and generically depends on the cosmic time t, or redshift z, or the scale factor a, or the energy density \(\rho _d\), or a more complicated combination form. Maartens [64] assumed the bulk viscous coefficient as \(\zeta \propto \rho ^{n}\), where n is a constant. In the Refs. [42,43,44], the most general form of bulk viscosity has been considered with generalized equation of state. Following [42,43,44, 65], we take the bulk viscosity coefficient in the following form.

$$\begin{aligned} \zeta = \zeta _0 + \zeta _1 H, \end{aligned}$$
(15)

where \(\zeta _0\) and \(\zeta _1\) are positive constants. The motivation for considering this bulk viscosity has been discussed in Refs. [42,43,44].

From the dynamical equations (13) and (14), we can formulate a first order differential equation for the Hubble parameter by using Eqs. (4) and (15) as,

$$\begin{aligned} \dot{H}+\frac{3(1+\alpha \omega _d)}{(2+3\beta \omega _d)}H^2-\frac{3\zeta }{(2+3\beta \omega _d)}H=0. \end{aligned}$$
(16)

It can be observed that Eq. (16) reduces to the non-viscous equation (5) for \(\zeta =0\) as discussed in previous section.

In the following subsections, we classify different viscous NHDE models arises due to the constant and variable bulk viscous coefficient. We analyze the behavior of the scale factor, DP, statefinder parameter and \({\textit{Om}}\) diagnostic of these different cases.

3.1 NHDE Model with constant bulk viscosity

The simplest case of viscous NHDE model is to be taken with constant bulk viscous coefficient. Therefore, assuming \(\zeta _1=0\) in Eq. (15), the bulk viscous coefficient reduces to

$$\begin{aligned} \zeta = \zeta _0=\text {const.} \end{aligned}$$
(17)

Using (17) into (16), we get

$$\begin{aligned} \dot{H} + \frac{3(1+\alpha \omega _d)}{(2+3\beta \omega _d)} H^2 - \frac{3 \zeta _0}{(2+3\beta \omega _d)} H =0. \end{aligned}$$
(18)

The solution of (18) in terms of cosmic time t can be given by

$$\begin{aligned} H = e^{\frac{3\zeta _0 t}{(2+3\beta \omega _d)}}\left[ c_1 + \frac{(1+\alpha \omega _d)}{\zeta _0}\;e^{\frac{3\zeta _0 t}{(2+3\beta \omega _d)}}\right] ^{-1}, \end{aligned}$$
(19)

where \(c_1\) is the constant of integration. From (19), we get the evolution of the scale factor as

$$\begin{aligned} a = c_2 \left[ c_1 + \frac{(1+\alpha \omega _d)}{\zeta _0}\;e^{\frac{3\zeta _0 t}{(2+3\beta \omega _d)}} \right] ^{\frac{(2+3\beta \omega _d)}{3(1+\alpha \omega _d)}}, \end{aligned}$$
(20)

where \(c_2\) is an integration constant. The above scale factor can be rewritten as

$$\begin{aligned} a= & {} \left[ 1 + \frac{H_0 (1+\alpha \omega _d)}{\zeta _0}\left\{ e^{\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}-1\right\} \right] ^{\frac{(2+3\beta \omega _d)}{3(1+\alpha \omega _d)}}, \nonumber \\&\quad \text {for}\;\alpha \ne -1/\omega _d,\;\zeta _0\ne 0 \end{aligned}$$
(21)

where \(t_0\) is the present cosmic time. Here, we get exponential form of the scale factor which shows non-singular solution. Equation (21) shows that in early stages of the evolution, the scale factor can be approximated as \(a(t) \sim \left[ 1 + \frac{3H_0 (1+\alpha \omega _d)}{(2+3\beta \omega _d)}(t-t_0) \right] ^{\frac{(2+3\beta \omega _d)}{3(1+\alpha \omega _d)}}\), and as \((t-t_0)\rightarrow \infty \), the scale factor approaches to a form like that of the de Sitter universe, i.e., \(a(t) \rightarrow \exp \left[ \frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}\right] \). Thus, we observe that the universe starts with a finite volume followed by an early decelerated epoch, then making a transition into the accelerated epoch in the late time of the evolution.

From (21), we can obtain the Hubble parameter in terms of scale factor a as

$$\begin{aligned} H(a)= & {} \frac{H_0}{(1+\alpha \omega _d)} \nonumber \\&\times \left[ \frac{\zeta _0}{H_0}+\{(1+\alpha \omega _d)-\frac{\zeta _0}{H_0}\}\;a^{-\frac{(3+3\alpha \omega _d)}{(2+3\beta \omega _d)}}\right] , \end{aligned}$$
(22)

where \(H_0\) is the present value of the Hubble parameter and we have made the assumption that the present value of scale factor is \(a_0=1\). The derivative of \(\dot{a}\) with respect to a can be obtained as [65]

$$\begin{aligned} \frac{d\dot{a}}{da}= & {} \frac{H_0}{(1+\alpha w_d)} \left[ \frac{\zeta _0}{H_0} -\left\{ (1+\alpha w_d)-\frac{\zeta _0}{H_0}\right\} \right. \nonumber \\&\times \left. \left( \frac{(1+3(\alpha -\beta ) w_d)}{2+3\beta w_d}\right) a^{-\frac{3(1+\alpha w_d)}{(2+3\beta w_d)}}\right] . \end{aligned}$$
(23)

Equation (23) to zero, the transition scale factor \(a_T\) can be obtained as

$$\begin{aligned} a_T=\left[ \frac{(1+3(\alpha -\beta )w_d)\left\{ (1+\alpha w_d)H_0-\zeta _0 \right\} }{(2+3\beta w_d)\zeta _0}\right] ^{\frac{(2+3\beta w_d)}{3(1+\alpha w_d)}}.\nonumber \\ \end{aligned}$$
(24)

The corresponding transition redshift \(z_T\), where \(a=(1+z)^{-1}\), is

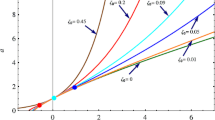
$$\begin{aligned} z_T=\left[ \frac{(1+3(\alpha -\beta ) w_d)\left\{ (1+\alpha w_d)H_0-\zeta _0 \right\} }{(2+3\beta w_d)\zeta _0}\right] ^{-\frac{(2+3\beta w_d)}{3(1+\alpha w_d)}}-1.\nonumber \\ \end{aligned}$$
(25)

From (24) or (25), we observe that for \(\zeta _0=\frac{\{1+3(\alpha -\beta ) w_d\}H_0}{3}\), the transition from decelerated phase to accelerated phase occurs at \(a_T=1\) or \(z_T=0\), which corresponds to the present time of the universe. On taking the observed values of \(\alpha =0.8502\) and \(\beta =0.4817\) [35], \(H_0=1\) and \(\omega _d=-0.5\) in this expression of \(\zeta _0\), we get \(\zeta _0=0.15\). Figure 1 represents the evolution of the scale factor a(t) with respect to time \((t-t_0)\) for different values of \(\zeta _0>0\). It is observed that the transition from decelerated to accelerated phase takes place in late time for small values of \(\zeta _0\), i.e., in \(0<\zeta _0 < 0.15\). The transition from decelerated phase to accelerated one occurs at \(a_T=1\) for \(\zeta _0=0.15\) which corresponds to the present time of the universe. However, the transition takes place in early stages of the evolution for large values of \(\zeta _0\), i.e., \(\zeta _0>0.15\). Thus, as the value of \(\zeta _0\) increases, the scale factor expands more rapidly with exponential rate.

Fig. 1
figure 1

The scale factor evolution for different values of \(\zeta _0>0\) with \(H_0=1\), \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\)

Full size image
Fig. 2
figure 2

a The variation of q with a for different values of \(\zeta _0\) with fixed \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). b The variation of q with a for different values of \(\alpha \) and \(\beta \) with fixed \(\zeta _0=0.2\) and \(\omega _d=-0.5\)

Full size image

The result regarding the transition of the universe into the accelerated epoch discussed above can be further verified by studying the evolution of DP q. In this case, DP is given by

$$\begin{aligned} q=\frac{3 \left\{ (1+\alpha \omega _d)-\frac{\zeta _0}{H_0}\right\} }{(2+3\beta \omega _d )} \; e^{-\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}-1. \end{aligned}$$
(26)

Thus, we find a time-varying DP in the case of constant viscous NHDE, which describes the phase transition of the evolution of the universe. DP must change its sign at \(t=t_0\), i.e., the time at which the viscous NHDE begins to dominate. This time can be achieved if \([1+3(\alpha - \beta )\omega _d]H_0=3\zeta _0\). The universe must decelerate for \(t<t_0\) and accelerate for \(t>t_0\) for any parametric values of \(\alpha \), \(\beta \) and \(\omega _d\).

From (26), DP can be written in terms of scale factor as

$$\begin{aligned} q= & {} \frac{\{3(1+\alpha \omega _d)-3\zeta _0\}}{(2+3\beta \omega _d)} \nonumber \\&\times \left[ \frac{(1+\alpha \omega _d)}{\left( a^{\frac{3+3 \alpha \omega _d}{2+3\beta \omega _d}}-1\right) \zeta _0+(1+\alpha \omega _d)} \right] -1. \end{aligned}$$
(27)

In terms of red shift z, the above equation becomes

$$\begin{aligned} q= & {} \frac{\{3(1+\alpha \omega _d)-3\zeta _0\}}{(2+3\beta \omega _d)} \nonumber \\&\times \left[ \frac{(1+\alpha \omega _d)}{\left( (1+z)^{-\frac{3+3 \alpha \omega _d}{2+3\beta \omega _d}}-1\right) \zeta _0+(1+\alpha \omega _d)} \right] -1.\nonumber \\ \end{aligned}$$
(28)

When the bulk viscous parameter and all other parameters are zero, the deceleration parameter \(q = 1/2\), which corresponds to a decelerating matter-dominated universe with null bulk viscosity. However, when only the bulk viscous term \(\zeta _0=0\), the value of q is same as obtained in Eq. (9) for non-viscous NHDE model.

The present value of q corresponds to \(z = 0\) or \(a = 1\) is,

$$\begin{aligned} q_0=q(a=1)=\frac{3(1+\alpha \omega _d)-3\zeta _0}{(2+3\beta \omega _d)}-1. \end{aligned}$$
(29)

This equation shows that if \(3\zeta _0= [1+3(\alpha -\beta )\omega _d]\), the deceleration parameter \(q_0 = 0\). This implies that the transition into the accelerating phase would occur at the present time. The current DP \(q_0 < 0\) if \(3\zeta _0 > [1+3(\alpha -\beta )\omega _d]\), implying that the present universe is in the accelerating epoch and it entered this epoch at an early stage. But \(q_0 > 0\) if \(3\zeta _0 < [1+3(\alpha -\beta )\omega _d]\) implying that the present universe is decelerating and it will be entering the accelerating phase at a future time. The evolution of q with a is shown in Fig. 2 by taking fixed constant \(\alpha \) and \(\beta \) (or \(\zeta _0\)), from which we can see that the evolution of the universe is from deceleration to acceleration. Figure 2a illustrates the evolutionary history of DP for different value of \(\zeta _0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). On considering \(\alpha =0.8502\), \(\beta =0.4817\) [35] and \(\omega _d=-0.5\) in Eq. (29), we get \(\zeta _0=0.15\) which gives \(q_0=0\). Thus, the transition into accelerating phase would occur at present time. If \(\zeta _0>0.15\), \(q_0<0\), i.e., the universe is in accelerating epoch and it entered this epoch at an early stage. If \(\zeta _0<0.15\), \(q_0>0\), i.e., the universe is in decelerating epoch and it enters in an accelerating phase in future. Thus, the larger the value \(\zeta _0\) is, the earlier acceleration occurs. The similar results for a fixed \(\zeta _0\) also appear in Fig. 2b. The larger the values \(\alpha \) and \(\beta \) is, the earlier q changes it sign from \(q>0\) to \(q<0\) for a fixed \(\zeta _0\). In both Fig. 2a, b, we observe that \(q\rightarrow -1\) in late time of evolution.

Fig. 3
figure 3

a The \(r-s\) trajectories are plotted in \(r-s\) plane for different values of \(\zeta _0>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). The arrows represent the directions of the evolutions of statefinder diagnostic pair with time. The curves are coinciding with each other for smaller and larger values of \(\zeta _0\). b The \(r-q\) trajectories are plotted in \(r-q\) plane for different values of \(\zeta _0>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). The arrows represent the directions of the time evolution pair \(\{r,q\}\) with time. The curves are coinciding with each other for smaller and larger values of \(\zeta _0\)

Full size image

3.2 Statefinder diagnostic

From above discussion we conclude that there is a transition from decelerated phase to accelerated one in future for small bulk viscous coefficient, \(0< \zeta _0<0.15\). It takes place to the present time for \(\zeta =0.15\). However, the transition takes place in past for \(\zeta >0.15\). The behavior of scale factor and deceleration parameter shows that the constant bulk viscous coefficient plays the role of DE. In what follows, we will present the statefinder diagnostic of the viscous NHDE model . In this model, the statefinder parameters defined in (10) can be obtained as

$$\begin{aligned} r= & {} 1+\frac{9\left( \frac{\zeta _0}{H_0}-(1+\alpha \omega _d)\right) \left( 1-\frac{1+\alpha \omega _d}{(2+3\beta \omega _d)}\right) }{\left( 2+3\beta \omega _d\right) }e^{-\frac{3\zeta _0 (t -t_0)}{(2+3\beta \omega _d)}} \nonumber \\&+\frac{9\left( \frac{\zeta _0}{H_0}-(1+\alpha \omega _d)\right) ^2}{\left( 2+3\beta \omega _d\right) ^2}e^{-\frac{6\zeta _0 (t -t_0)}{(2+3\beta \omega _d)}}, \end{aligned}$$
(30)

and

$$\begin{aligned} s = \frac{\frac{2\left( \frac{\zeta _0}{H_0}-(1+\alpha \omega _d) \right) \left( 1-\frac{1+\alpha \omega _d}{(2+3\beta \omega _d)} \right) }{(2+3\beta \omega _d)}e^{-\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}+\frac{2\left( \frac{\zeta _0}{H_0}-(1+\alpha \omega _d) \right) ^2}{(2+3\beta \omega _d)^2}e^{-\frac{6\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}}{\frac{2\left( (1+\alpha \omega _d)-\frac{\zeta _0}{H_0} \right) }{(2+3\beta \omega _d)}e^{-\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}-1}.\nonumber \\ \end{aligned}$$
(31)

Here, these values of statefinder parameter are time-dependent and this is due to the bulk viscous coefficient \(\zeta _0\). In previous Sect. 2, we see that the diagnostic pair is constant in the absence of viscous term. As we can observe from the above two equations that in the limit of \((t-t_0)\rightarrow \infty \), the model approaches to \(\{r,s\}\rightarrow \{1,0\}\) and for this limit we get \(q\rightarrow -1\). We draw the trajectories of the statefinder pair \(\{r, s\}\) in \(r-s\) plane for different values of constant \(\zeta _0\) with \(\omega _d=-0.5\), \(H_0=t_0=1\), \(\alpha =0.8502\) and \(\beta =0.4817\) as shown in Fig. 3a. Here, we observe that the model approaches to \(\{r,s\}\rightarrow \{1,0\}\) for all positive values of \(\zeta _0\). In Fig. 3a, the fixed points \(\{r, s\}=\{1, 1\}\) and \(\{r, s\}=\{1, 0\}\) are shown as SCDM and \(\Lambda CDM\) models, respectively.

Fig. 4
figure 4

a The \(r-s\) trajectories are plotted in \(r-s\) plane for different values of \(\alpha \) and \(\beta \) with \(\omega _d=-0.5\) and \(\zeta _0=0.02\). The arrows represent the directions of the evolutions of statefinder diagnostic pair with time. b The \(r-q\) trajectories are plotted in \(r-q\) plane for different values of \(\alpha \) and \(\beta \) with \(\omega _d=-0.5\) and \(\zeta _0=0.02\). The arrows represent the directions of the time evolution pair \(\{r,q\}\) with time

Full size image

It is observed from figures that the statefinder diagnostic of our model can discriminate from other DE models. For example, in quiessence with constant EoS parameter [37, 38] and the Ricci dark energy (RDE) model [66], the trajectory in \(r-s\) plane is a vertical segment, i.e. s is constant during the evolution of the universe whereas the trajectories for the Chaplygin gas (CG) [67] and the quintessence (inverse power-law) models (Q) [37, 38] are similar to arcs of a parabola (downward and upward) lying in the regions \(s<0\), \(r>1\) and \(s>0\), \(r<1\), respectively. In modified NHDE model [68], the trajectory in \(r-s\) is from left to right. In holographic dark energy model with future event horizon [69, 70] its evolution starts from the point \(s=2/3\), \(r=1\) and ends at \(\Lambda CDM\) model fixed point in future.

In Fig. 3a, the plot reveals that the \(r-s\) plane can be divided into two regions \(r<1, s>0\) and \(r>1, s<0\) which are showing the similar characteristics to Q and CG models, respectively. The present model starts in both regions \(r<1, s>0\) and \(r>1, s<0\), and end on the \(\Lambda CDM\) point in the \(r-s\) plane in far future. The trajectories in the right side of the vertical line correspond to the different values of \(\zeta _0\), i.e., \(\zeta _0=0.02\), \(\zeta _0=0.10\), \(\zeta _0=0.15\) and \(\zeta _0=0.30\) lying in the range \(0<\zeta _0\le 0.57\) whereas the trajectories to the left side of the vertical line correspond to \(\zeta _0> 0.57\), i.e., \(\zeta _0=0.60\), \(\zeta _0=0.70\), \(\zeta _0=0.80\) and \(\zeta _0=1.00\). This reveals that smaller values of \(\zeta _0\) give the model similar to Q model and larger values correspond to the CG model. We find that the evolutions are coinciding each other for all different values of \(\zeta _0\) in both regions.

We also study the evolutionary behaviour of constant viscous NHDE model in \(r-q\) plane. For different values of \(\zeta _0\), as taken in \(\{r, s\}\), the trajectories are shown in Fig. 3b for \(w_d=-0.5\), \(H_0=t_0=1\), \(\alpha =0.8502\) and \(\beta =0.4817\). The SCDM model and steady state (SS) model corresponds to fixed point \(\{r,q\}=\{1,0.5\}\) and \(\{r,q\}=\{1,-1\}\), respectively. It can be seen that there is a sign change of q from positive to negative which explain the recent phase transition. The trajectories show that viscous NHDE models commence evolving from different points for different values of \(\zeta _0\) with respect to \(\Lambda CDM\) which starts from SCDM fixed point. The viscous NHDE model always converges to SS model as \(\Lambda CDM\), Q and CG models in late-time evolution of the universe. Thus, the constant viscous NHDE model is compatible with Q and CG models.

The above discussion concludes the effect of viscous term in NHDE model. Let us discuss the model in view point of model parameters \(\alpha \) and \(\beta \). Figure 4a, b show the trajectories in \(r-s\) and \(r-q\) planes, respectively, for the different values of \(\alpha \) and \(\beta \) with constant \(\omega _d=-0.5\), \(H_0=t_0=1\) and \(\zeta _0=0.02\). The arrows in the diagram denote the evolution directions of the statefinder trajectories and \(r-q\) trajectories. From Fig. 4a, we observe that for this fixed value of \(\zeta _0\) the constant viscous NHDE model always correspond to the Q model. It may start from the vicinity of SCDM model in early time of evolution for some values of \(\alpha \) and \(\beta \), e.g., \((\alpha ,\beta )=(0.8502, 0.55)\). In late-time of evolution the model always converges to \(\Lambda CDM\) model for any values of \((\alpha , \beta )\).

The panel (b) of Fig. 4 shows the time evolution of the \(r-q\) trajectories in \(r-q\) plane. The horizontal line at \(r=1\) corresponds to the time evolution of the \(\Lambda CDM\) model. The signature change from positive to negative in q clearly explain the phase transition of the universe. The constant viscous NHDE model may start from the vicinity of the SCDM model (\(\{r,q\}=\{1,0.5\}\)) for some values of \(\alpha \) and \(\beta \) (e.g., \(\alpha =0.8502, \beta =0.55\)). However, the constant viscous NHDE model approaches to the SS model as the \(\Lambda CDM\) and Q models in future . Thus, the viscous NHDE model is compatible with the \(\Lambda CDM\) and Q models with variables model parameters and constant value of \(\zeta _0\).

Thus, we conclude that our model corresponds to both Q and CG models for the different values of viscous coefficient \(\zeta _0\) whereas for the different values of model parameters \(\alpha \) and \(\beta \) with respect to the fixed value of \(\zeta _0\), our model only corresponds to Q model. Hence, we can conclude that due to the viscosity NHDE model is compatible with the Q and CG models. By above analysis, we can say that the bulk viscous coefficient and model parameters play the important roles in the evolution of the universe, i.e., they both determine the evolutionary behavior as well as the ultimate fate of the universe.

3.3 Om diagnostic

In addition to statefinder \(\{r, s\}\), another diagnostic model, \(\textit{Om(z)}\) is widely used to discriminate DE models. It is a new geometrical diagnostic which combines Hubble parameter H and redshift z. The \(\textit{Om(z)}\) diagnostic [39] has been proposed to differentiate \(\Lambda CDM\) to other DE models. Many authors [71,72,73] have studied the DE models based on \(\textit{Om(z)}\) diagnostic. Its constant behaviour with respect to z represents that DE is a cosmological constant (\(\Lambda CDM\)). The positive slope of \(\textit{Om(z)}\) with respect to z shows that the DE behaves as phantom and negative slope shows that DE behaves like quintessence. According to Ref. [39], \(\textit{Om(z)}\) parameter for spatially flat universe is defined as

$$\begin{aligned} \textit{Om(z)} = \frac{\frac{H^2(z)}{H_0^2}-1}{(1+z)^3-1}, \end{aligned}$$
(32)

where \(H_0\) is the present value of the Hubble parameter. Since the \(\textit{Om(z)}\) involves only the first derivative of scale factor, so it is easier to reconstruct it as compare to statefinder parameters. It has been shown that the slope of \(\textit{Om(z)}\) can distinguish dynamical dark energy from the cosmological constant in a robust manner, both with and without reference to the value of the matter density.

Fig. 5
figure 5

a The \(\textit{Om(z)}\) evolutionary diagram of viscous NHDE for different values of \(\zeta _0>0\) with fixed \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). b The \(\textit{Om(z)}\) evolutionary diagram of viscous NHDE for different values of \(\alpha \) and \(\beta \) with fixed \(\zeta _0=0.02\) with \(\omega _d=-0.5\)

Full size image

On substituting the required value of H(z) from (22) in (32), we get the value of \(\textit{Om(z)}\) as

$$\begin{aligned} \textit{Om(z)} = \frac{\left[ \frac{\zeta _0}{H_0}+\left\{ 1+\alpha \omega _d - \frac{\zeta _0}{H_0}\right\} (1+z)^{\frac{3(1+\alpha \omega _d)}{2+3\beta \omega _d}} \right] ^2 - (1+\alpha \omega _d)^2}{(1+\alpha \omega _d)^2 [(1+z)^3-1]}.\nonumber \\ \end{aligned}$$
(33)

For comparison, we plot \(\textit{Om(z)}\) trajectory with respect to z for different values of \(\zeta _0>0\) (or \(\alpha \) and \(\beta \)) with fixed \(\alpha \) and \(\beta \) (or \(\zeta _0\)), with \(H_0=1\) and \(\omega _d=-0.5\) as shown in Fig. 5. From Fig. 5a, we observe that for \(0<\zeta _0\le 0.57\), the trajectory shows the negative slope, i.e., the DE behaves like quintessence and for \(\zeta _0>0.57\), the positive slope of the \(\textit{Om}\) trajectory is observed, i.e., the DE behaves as phantom. For the late future stage of evolution when \(z=-1\), we get \(\textit{Om(z)}=1-\frac{\zeta _0^2}{H_0^2(1+\alpha \omega _d)^2}\), which is the constant value of \(\textit{Om(z)}\). Thus for \(z=-1\), the DE will correspond to \(\Lambda CDM\).

The Fig. 5b shows the \(\textit{Om(z)}\) trajectory for different values of model parameters \(\alpha \) and \(\beta \) with fixed \(\zeta _0=0.02\), \(\omega _d=-0.5\) and \(H_0=1\). This trajectory only shows the negative curvature which imply that the DE behaves like quintessence.

From the above discussion with constant bulk viscous coefficient, we find that the constant \(\zeta _0\) ( or cosmological parameters \(\alpha \) and \(\beta \) ) play important roles in the evolution of the universe, i.e., they both determine the evolutionary behavior as well as the ultimate fate of the universe.

3.4 Solution for variable bulk viscosity coefficient

In this section, we consider two cases: (i) \(\zeta _0 = 0\) and \(\zeta _{1} \ne 0\), and (ii) \(\zeta _0 \ne 0\) and \(\zeta _1 \ne 0\).

Case (i) \(\zeta _{\mathbf {0}} = \mathbf {0}\) and \(\zeta _{\mathbf {1}} \ne \mathbf {0}\):

In this case, the bulk viscosity coefficient given in (15) reduces to

$$\begin{aligned} \zeta =\zeta _1 H, \end{aligned}$$
(34)

which shows that the bulk viscous coefficient is directly proportional to Hubble parameter.

Using (34) into (16), we get

$$\begin{aligned} \dot{H} + \frac{3(1-\zeta _1+\alpha \omega _d)}{(2+3\beta \omega _d)} H^2 = 0. \end{aligned}$$
(35)

The above equation is similar to the Eq.(5) obtained in the case of non-viscous NHDE model in Sect. 2. The solution of (35) for H in terms of t is given by

$$\begin{aligned} H = \frac{1}{c_3 + \frac{3(1-\zeta _1+\alpha \omega _d)}{(2+3\beta \omega _d)}t}, \end{aligned}$$
(36)

where \(c_3\) represents the constant of integration. The scale factor can be obtained as

$$\begin{aligned} a= & {} a_0 \left[ 1+\frac{3(1-\zeta _1+\alpha \omega _d) H_0}{(2+3\beta \omega _d)} (t-t_0) \right] ^{\frac{(2+3\beta \omega _d)}{3(1-\zeta _1 +\alpha \omega _d)}}, \nonumber \\&\quad \text {for}\;\zeta _1\ne (1+\alpha \omega _d),\quad \beta \ne - \frac{2}{3\omega _d} \end{aligned}$$
(37)

The scale factor varies as power-law expansion. Now, the DP is

$$\begin{aligned} q = \frac{3(1-\zeta _1 +\alpha \omega _d)}{(2+3\beta \omega _d)}-1. \end{aligned}$$
(38)

which is a constant value. Such form of \(\zeta \) gives no transition phase. The positive or negative sign of q depends on whether \(3\zeta _1<(1+3(\alpha -\beta )\omega _d)\) or \(3\zeta _1>(1+3(\alpha -\beta )\omega _d)\), respectively.

Now, the statefinder parameter can be given as

$$\begin{aligned} r = 1-\frac{9(1+\alpha \omega _d-\zeta _1)}{(2+3\beta \omega _d)} + \frac{18(1+\alpha \omega _d-\zeta _1)^2}{(2+3\beta \omega _d)^2}, \end{aligned}$$
(39)

and

$$\begin{aligned} s = \frac{2(1+\alpha \omega _d-\zeta _1)}{(2+3\beta \omega _d)}. \end{aligned}$$
(40)

In this case the statefinder pair is constant. In the limit of \(\zeta _1\rightarrow (1+\alpha \omega _d)\), the statefinder pair \(\{r, s\}\rightarrow \{1, 0\}\) and for \(\zeta _1 = \frac{(2\alpha -3\beta )\omega _d}{2}\), this model behaves as SCDM, i.e., \(\{r, s\}=\{1, 1\}\).

Case (ii) \(\zeta _{\mathbf {0}} \ne \mathbf {0}\) and \(\zeta _1\ne 0\):

Let us consider the more general form of the bulk viscous coefficient, i.e., \(\zeta =\zeta _0+\zeta _1 H\). Using (15) into (16), we get

$$\begin{aligned} \dot{H} + \frac{3(1-\zeta _1+\alpha \omega _d)}{(2+3\beta \omega _d)} H^2 - \frac{3\zeta _0}{(2+3\beta \omega _d)} H = 0. \end{aligned}$$
(41)

Solving the above equation, we get the Hubble parameter in terms of t as

$$\begin{aligned} H= & {} H_0 e^{\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}} \nonumber \\&\times \left[ 1 + \frac{H_0(1-\zeta _1+\alpha \omega _d)}{\zeta _0}\;\left\{ e^{\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}-1\right\} \right] ^{-1},\nonumber \\ \end{aligned}$$
(42)

where \(H_0\) is the present value of the Hubble parameter and we have made the assumption that the present value of scale factor is \(a_0=1\). The solution of (42) for the scale factor a in terms of t is given by

$$\begin{aligned} a= & {} \left[ 1 + \frac{H_0 (1-\zeta _1+\alpha \omega _d)}{\zeta _0}\left\{ e^{\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}-1\right\} \right] ^{\frac{(2+3\beta \omega _d)}{3(1-\zeta _1+\alpha \omega _d)}}, \nonumber \\&\quad \text {for}\;\;\zeta _0\ne 0,\;\;\zeta _1 \ne (1+\alpha \omega _d) \end{aligned}$$
(43)

Here, we get an exponential type scale factor with the viscous terms. As \((t-t_0)\rightarrow 0\), the scale factor behaves as

$$\begin{aligned} a\rightarrow \left[ 1+\frac{3H_0 (1-\zeta _1+\alpha \omega _d)(t-t_0)}{(2+3\beta \omega _d)} \right] ^{\frac{(2+3\beta \omega _d)}{3(1-\zeta _1+\alpha \omega _d)}}, \end{aligned}$$
(44)

which shows power-law expansion in early time. On the other hand, if \(\zeta _0=H_0(1-\zeta _1+\alpha \omega _d)\) or \((t-t_0)\rightarrow \infty \), we obtain

$$\begin{aligned} a(t)=\exp \left( \frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}\right) . \end{aligned}$$
(45)

This case corresponds the de Sitter universe which shows accelerated expansion in the later time of evolution.

Now, with the help of (43), the Hubble parameter in terms of scale factor can be written as

$$\begin{aligned} H(a)= & {} \frac{H_0}{(1-\zeta _1+\alpha \omega _d)} \nonumber \\&\times \left[ \frac{\zeta _0}{H_0}+\left\{ (1-\zeta _1+\alpha \omega _d)-\frac{\zeta _0}{H_0}\right\} \;a^{-\frac{3(1-\zeta _1+\alpha \omega _d)}{(2+3\beta \omega _d)}}\right] .\nonumber \\ \end{aligned}$$
(46)

This equations shows that if both \(\zeta _0\) and \(\zeta _1\) are zero, the Hubble parameter, \(H=H_0 a^{\frac{-3(1+\alpha \omega _d)}{(2+3\alpha \omega _d)}}\), which corresponds to non-viscous NHDE model. When \(\zeta _1=0\), H reduces to Eq. (22) which is the case of constant viscosity.

The derivative of \(\dot{a}\) with respect to a can be obtained from (46), which is given by

$$\begin{aligned} \frac{d\dot{a}}{da}= & {} \frac{H_0}{(1-\zeta _1+\alpha w_d)}\left[ \frac{\zeta _0}{H_0}-\left\{ (1-\zeta _1+\alpha w_d)-\frac{\zeta _0}{H_0}\right\} \right. \nonumber \\&\times \left. \left( \frac{(1+3(\alpha -\beta ) w_d-3\zeta _1)}{2+3\beta w_d}\right) a^{-\frac{3(1-\zeta _1+\alpha w_d)}{(2+3\beta w_d)}}\right] . \end{aligned}$$
(47)

Equating (47) to zero to get the transition scale factor \(a_T\) as

$$\begin{aligned} a_T=\left[ \frac{(1+3(\alpha -\beta )w_d-3\zeta _1)\left\{ (1-\zeta _1+\alpha w_d)H_0-\zeta _0 \right\} }{(2+3\beta w_d)\zeta _0}\right] ^{\frac{(2+3\beta w_d)}{3(1-\zeta _1+\alpha w_d)}}.\nonumber \\ \end{aligned}$$
(48)

The corresponding transition redshift \(z_T\) is

$$\begin{aligned} z_T=\left[ \frac{(1+(\alpha -\beta ) w_d-3\zeta _1)\left\{ (1-\zeta _1+\alpha w_d)H_0-\zeta _0 \right\} }{(2+3\beta w_d)\zeta _0}\right] ^{-\frac{(2+3\beta w_d)}{3(1-\zeta _1+\alpha w_d)}}-1.\nonumber \\ \end{aligned}$$
(49)

It can be observed that for \((\zeta _0+\zeta _1H_0)=\frac{\{1+3(\alpha -\beta ) w_d\}H_0}{3}\), the transition from decelerated phase to accelerated phase occurs at \(a_T=1\) or \(z_T=0\), which corresponds to the present time of the universe. By considering the observational value \(\alpha =0.8502\) and \(\beta =0.4817\) along with \(\omega _d=-0.5\), \(H_0=1\), we get \((\zeta _0+\zeta _1)=0.15\). A plot of the evolution of the scale factor is given in Fig. 6. Thus, for \(0<(\zeta _0+\zeta _1)\le 0.15\) the scale factor has earlier deceleration phase followed by an acceleration phase in later stage of the evolution. The transition from the decelerated to accelerated expansion depends on the viscosity \(\zeta _0\) and \(\zeta _1\) as shown above. For \((\zeta _0+\zeta _1)>0.15\), the transition takes place in past of the universe and the scale factor increases with accelerated rate forever.

Fig. 6
figure 6

The plot of the scale factor with respect to \(t-t_0\) for different values of \(\zeta _0, \zeta _1\) when \(\zeta _0>0\) and \(\zeta _1>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\)

Full size image
Fig. 7
figure 7

a The \(q-a\) graph in \(q-a\) plane for different values of \(\zeta _0>0\) and \(\zeta _1>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). b The \(q-a\) graph in \(q-a\) plane for different values of \(\alpha \) and \(\beta \) with \(\zeta _0=0.2\), \(\zeta _1=0.3\) and \(\omega _d=-0.5\)

Full size image

The transition may also be discussed through the evolution of DP. In this case, we get

$$\begin{aligned} q=\frac{3 \left\{ (1-\zeta _1 +\alpha \omega _d)-\frac{\zeta _0}{H_0}\right\} }{(2+3\beta \omega _d )} e^{-\frac{3\zeta _0 (t -t_0)}{(2+3\beta \omega _d)}}-1, \end{aligned}$$
(50)

which is a time-dependent value of DP, which may describe the transition phase of the universe. It can be observed that DP must change its sign at \(t=t_0\). This time can be achieved if \(3(\zeta _0+\zeta _1H_0)=\{1+3(\alpha -\beta ) w_d\}H_0\). The sign of q is positive for \(t<t_0\) and it is negative for \(t>t_0\). The values of \(\zeta _0\) and \(\zeta _1\) can be obtained for a given values of \(\omega _d\), \(\alpha \) and \(\beta \), which may be obtained from observation, or vice-versa.

From (50), DP can be written in terms of scale factor as

$$\begin{aligned} q(a)= & {} \frac{\{3(1-\zeta _1+\alpha \omega _d)-3\zeta _0\}}{(2+3\beta \omega _d)} \nonumber \\&\times \left[ \frac{(1-\zeta _1+\alpha \omega _d)}{(a^{\frac{3(1-\zeta _1+\alpha \omega _d)}{2+3\beta \omega _d}}-1)\zeta _0+(1-\zeta _1+\alpha \omega _d)} \right] -1.\nonumber \\ \end{aligned}$$
(51)

In terms of red shift z, the above equation becomes

$$\begin{aligned} q(z)= & {} \frac{\{3(1-\zeta _1+\alpha \omega _d)-3\zeta _0\}}{(2+3\beta \omega _d)} \nonumber \\&\times \left[ \frac{(1{-}\zeta _1+\alpha \omega _d)}{\left( (1{+}z)^{-\frac{3(1{-}\zeta _1+\alpha \omega _d)}{2{+}3\beta \omega _d}}-1\right) \zeta _0+(1-\zeta _1+\alpha \omega _d)} \right] {-}1.\nonumber \\ \end{aligned}$$
(52)

When the bulk viscous parameter and all other parameter are zero, the deceleration parameter \(q = 1/2\), which corresponds to a decelerating matter dominated universe with null bulk viscosity. However, when only the bulk viscous term \(\zeta _0=0\) and \(\zeta _1 \ne 0\), the value of q is same as obtained in Eq. (38) for case (i) of variable viscous NHDE model, and when \(\zeta _0\ne 0\) and \(\zeta _1=0\) , Eq. (51) reduces to Eq. (27) of constant viscous coefficient.

The present value of q corresponds to \(z = 0\) or \(a = 1\) is,

$$\begin{aligned} q_0=q(a=1)=\frac{3(1-\zeta _1+\alpha \omega _d)-3\zeta _0}{(2+3\beta \omega _d)}-1. \end{aligned}$$
(53)

This equation shows that if \(3(\zeta _0+\zeta _1)= [1+3(\alpha -\beta )\omega _d]\), the deceleration parameter \(q = 0\). This implies that the transition into the accelerating phase would occur at the present time. The current DP \(q_0 < 0\) if \(3(\zeta _0 +\zeta _1)> [1+3(\alpha -\beta )\omega _d]\), implying that the present universe is in the accelerating epoch and it entered this epoch at an early stage. But \(q_0 > 0\) if \(3(\zeta _0\,+\,\zeta _1) < [1+3(\alpha -\beta )\omega _d]\) implying that the present universe is decelerating and it will be entering the accelerating phase at a future time. For the observational value \(\alpha =0.8502\) and \(\beta =0.4817\) with \(\omega _d=-0.5\) and \(H_0=1\), we get \((\zeta _0+\zeta _1)=0.15\) which gives \(q_0=0\). Thus for this value set, the transition into accelerating phase would occur at present time. If \((\zeta _0+\zeta _1)>0.15\), \(q_0<0\), i.e., the universe is in accelerating phase and it entered this epoch at an early stage. If \((\zeta _0+\zeta _1)<0.15\), \(q_0>0\), i.e., the universe is in decelerating epoch and it will be entered into the accelerated phase in future. This result is verified graphically which is represented by Fig. 7a. The Fig. 7b shows the \(q-a\) graph in \(q-a\) plane to discuss the evolution of the universe with respect to model parameters \(\alpha \) and \(\beta \). Here, the signature change in the value of DP can be seen by the figure. From above discussion we say that both viscous coefficient and model parameter have their own role in the evolution of the universe. Some values of bulk viscous term gives the accelerated phase from the beginning and continues to be accelerated in late time.

3.5 Statefinder diagnostic

As we have mentioned above , the scale factor and deceleration parameter have been discussed to explain the accelerating universe with viscous term or model parameters. So it is necessary to distinguished these models in a model-independent manner. In what follows we will apply two geometrical approaches to viscous NHDE model, i.e., the statefinder and Om diagnostic from which we can compute the evolutionary trajectories with ones of the \(\Lambda CDM\) model to show the difference among them.

In this case, the statefinder parameters defined in Eq. (10) can be evaluated as

$$\begin{aligned} r= & {} 1 + \frac{9\left( \frac{\zeta _0}{H_0}-(1-\zeta _1 +\alpha \omega _d) \right) \left( 1-\frac{(1-\zeta _1+\alpha \omega _d)}{(2+3\beta \omega _d)} \right) e^{-\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}}{(2+3\beta \omega _d)} \nonumber \\&+ \frac{9\left( \frac{\zeta _0}{H_0}-(1-\zeta _1+\alpha \omega _d) \right) ^2e^{-\frac{6\zeta _0 (t-t_0)}{(2+3 \beta \omega _d)}}}{ (2+3\beta \omega _d)^2}, \end{aligned}$$
(54)

and

$$\begin{aligned} s = \frac{\frac{2\left( \frac{\zeta _0}{H_0}-(1-\zeta _1+\alpha \omega _d) \right) \left( 1-\frac{1-\zeta _1+\alpha \omega _d}{(2+3\beta \omega _d)} \right) }{(2+3\beta \omega _d)}e^{-\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}+\frac{2\left( \frac{\zeta _0}{H_0}-(1-\zeta _1+\alpha \omega _d) \right) ^2}{(2+3\beta \omega _d)^2}e^{-\frac{6\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}}{\frac{2\left( (1-\zeta _1+\alpha \omega _d)-\frac{\zeta _0}{H_0} \right) }{(2+3\beta \omega _d)}e^{-\frac{3\zeta _0 (t-t_0)}{(2+3\beta \omega _d)}}-1}. \end{aligned}$$
(55)
Fig. 8
figure 8

a The \(r-s\) trajectories are plotted in \(r-s\) plane for different values of \(\zeta _0>0\) and \(\zeta _1>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). The arrows represent the directions of the evolutions of statefinder diagnostic pair with time. b The \(r-q\) trajectories are plotted in \(r-q\) plane for different values of \(\zeta _0>0\) and \(\zeta _1>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). The arrows represent the directions of the time evolution pair \(\{r,q\}\) with time

Full size image

From (54) and (55) it can be observed that the viscous NHDE model converges to \(\{r, s\}\rightarrow \{1, 0\}\) in the limit of \((t-t_0)\rightarrow \infty \). This can also be achieved at \((\zeta _0 + H_0 \zeta _1) = H_0 (1+\alpha \omega _d)\) but this is a very fixed point. Thus, the statefinder diagnostic fails to discriminate between \(\Lambda CDM\) and the NHDE model. Here, we obtain time-dependent statefinder pair which needs to study the general behavior. Let us see the effect of viscosity coefficients \(\zeta _0, \zeta _1\) and model parameters \(\alpha , \beta \) for the general form of variable viscous NHDE model. Figure 8a shows the \(r-s\) trajectory in \(r-s\) plane for different values of \(\zeta _0\) and \(\zeta _1\) with \(H_0=t_0=1\), \(\alpha =0.8502\) and \(\beta =0.4817\). The model behaviors to Q models for \(0<(\zeta _0+\zeta _1)\le 0.57\) and CG models for \((\zeta _0+\zeta _1)> 0.57\). The trajectories in Q-model and CG-model both converge to the \(\Lambda CDM\) model in late time of evolution.

Figure 8b shows the time evolution of \(\{r,q\}\) pair in \(r-q\) plane for different combinations of the values of \(\zeta _0\) and \(\zeta _1\) with \(H_0=t_0=1\), \(\alpha =0.8502\) and \(\beta =0.4817\). The fixed points \(\{r,q\}=\{1,0.5\}\) and \(\{r,q\}=\{1,-1\}\) represents the SCDM and SS models, respectively. Since q changes its sign from positive to negative with respect to time which shows the phase transition of the universe from deceleration to acceleration. In beginning this model behaves different from the \(\Lambda CDM\) but in future it behaves same as \(\Lambda CDM\) which converges to SS model in late-time. Hence the variable viscous NHDE model always converges to SS model as \(\Lambda CDM\), Q and CG models in late-time evolution of the universe. For all the ranges of \((\zeta _0+\zeta _1)\) the trajectories correspond to Q and CG models as in Fig. 8a. Thus the variable viscous NHDE model is compatible with both Q and CG models.

Thus, the viscosity coefficients are able to correspond to both Q and CG models for different combinations of \(\zeta _0, \zeta _1\) and also explain the phase transition of the universe.

Fig. 9
figure 9

a The \(r-s\) trajectories are plotted in \(r-s\) plane for different values of \(\alpha \) and \(\beta \) with \(\omega _d=-0.5\), \(\zeta _0=0.02\) and \(\zeta _1=0.03\). The arrows represent the directions of the evolutions of statefinder diagnostic pair with time. b The \(r-q\) trajectories are plotted in \(r-q\) plane for different values of \(\alpha \) and \(\beta \) with \(\omega _d=-0.5\), \(\zeta _0=0.02\) and \(\zeta _1=0.03\). The arrows represent the directions of the time evolution pair \(\{r,q\}\) with time

Full size image
Fig. 10
figure 10

a The evolution of \(\textit{Om(z)}\) versus the redshift z for different values of \(\zeta _0>0\) and \(\zeta _1>0\) with \(\omega _d=-0.5\), \(\alpha =0.8502\) and \(\beta =0.4817\). b The evolution of \(\textit{Om(z)}\) versus the redshift z for different values of \(\alpha \) and \(\beta \) with \(\zeta _0=0.02\), \(\zeta _1=0.03\) and \(\omega _d=-0.5\)

Full size image

Now, we are curious to know the behaviour of variable viscous NHDE model with respect to the model parameters \(\alpha \) and \(\beta \). Here, Fig. 9a, b represents the \(r-s\) and \(r-q\) trajectories in \(r-s\) and \(r-q\) plane, respectively, for the different values of \(\alpha \) and \(\beta \) close to it’s observational value with \(\omega _d=-0.5\), \(H_0=t_0=1\), \(\zeta _0=0.02\) and \(\zeta _1=0.03\). The evolutionary directions of both the trajectories are shown in the figures by the arrows. In Fig. 9a, we analysed that for this fixed value of \(\zeta _0\) and \(\zeta _1\) the (r, s) trajectories are lying in the region corresponds to \(r<1\), \(s>0\) which shows that our model is similar to the Q model. It also starts from the vicinity of SCDM model in early time of evolution for some values of \(\alpha \) and \(\beta \), e.g., \((\alpha ,\beta )=(0.8502,0.59)\). It is different from RDE model and quiessence model as it produces the curved trajectories for any values of \((\alpha , \beta )\) close to observational value which approach to \(\Lambda CDM\) in late-time of evolution as the Q model tends to \(\Lambda CDM\) model in late-time of evolution.

The \(r-q\) trajectories in \(r-q\) plane are shown by the Fig. 9b. This model is also able to explain the phase transition of the universe. It also starts from the neighbourhood of the SCDM model for some values of \(\alpha \) and \(\beta \) (e.g., \(\alpha =0.8502, \beta =0.55\)) and approaches to SS model in late-time for any value of \(\alpha \) and \(\beta \) close to the observational value. In future the variable viscous NHDE model approaches to the SS model same as the \(\Lambda CDM\) and Q models. Thus the viscous NHDE model is compatible with the \(\Lambda CDM\) and Q models.

Thus, we observed from Figs. 8 and 9 that viscous NHDE model is compatible to Q and CG models for different ranges of viscosity coefficients in the presence of the fixed observational value of model parameters whereas the model parameter in the presence of fixed value of viscosity coefficients approaches only to Q model.

3.6 Om diagnostic

Let us discuss the another geometrical parameter, i.e., \(\textit{Om(z)}\) diagnostic in viscous NHDE model. By substituting the required values in Eq. (32), we get the \(\textit{Om(z)}\) diagnostic for \(\zeta =\zeta _0+\zeta _1 H\) as

$$\begin{aligned}&\textit{Om(z)} = \frac{\left[ \frac{\zeta _0}{H_0}+\left\{ (1-\zeta _1+\alpha \omega _d) - \frac{\zeta _0}{H_0}\right\} (1+z)^{\frac{3(1-\zeta _1+\alpha \omega _d)}{2+3\beta \omega _d}} \right] ^2 - (1-\zeta _1+\alpha \omega _d)^2}{(1-\zeta _1+\alpha \omega _d)^2 [(1+z)^3-1]}. \end{aligned}$$
(56)

Figure 10a shows the \(\textit{Om(z)}\) trajectory with respect to z for different values of \(\zeta _0>0\) and \(\zeta _1>0\) corresponding to \(\alpha =0.8502\), \(\beta =0.4817\), \(H_0=1\) and \(\omega _d=-0.5\). Here, the trajectory represents the negative curvature, i.e., the viscous NHDE behaves as quintessence for the limit \(0<(\zeta _0+\zeta _1)\le 0.57\) and it shows the positive curvature, i.e., the viscous DE behaves as phantom, for \((\zeta _0+\zeta _1)>0.57\) whereas for \(z=-1\), i.e., in future time we get \(\textit{Om(z)}=1-\frac{\zeta _0^2}{H_0^2(1-\zeta _1+\alpha \omega _d)^2}\), which is the constant value of \(\textit{Om(z)}\). Thus for \(z=-1\), the viscous NHDE will correspond to \(\Lambda CDM\).

Figure 10b plot the \(\textit{Om(z)}\) versus z for different model parameters \(\alpha \) and \(\beta \) correspond to fixed \(\zeta _0\) and \(\zeta _1\). The graph shows that there is always negative curvature for any values of model parameters. This shows that the model behaviors similar to quintessence model.

4 Conclusion

We have studied some viscous cosmological NHDE models on the evolution of the universe, where the IR cutoff is given by the modified Ricci scalar, proposed by Granda and Olivers [29, 30]. It has been tried to demonstrate that the bulk viscosity can also play the role as a possible candidate of DE. We have performed a detailed study of both non-viscous and viscous NHDE models. The component of this model is DE and pressureless DM. We have obtained the solutions for scale factor and deceleration parameter. We have also studied these models from two independent geometrical point of view, namely the statefinder parameter and \(\textit{Om}\) diagnostic. We have studied the different possible scenarios of viscous NHDE and analyzed the evolution of the universe according to the assumption of bulk viscous coefficient \(\zeta \). In the following we summarize the results obtained in different sections for non-viscous and viscous NHDE models.

In Sect. 2, we have investigated non-viscous NHDE in flat FRW universe. We have calculated the relevant cosmological parameters and their evolution. The evolution of scale factor has been studied. We have obtained power-law form of scale factor for which the model may decelerate or accelerate depending on the constraint of model parameters. The deceleration parameter is constant in this case. Therefore, the model can not describe the transition phase of the universe. The statefinder parameters are also constant. We have observed that the observed set of data of model parameters do not favor the NHDE model over the \(\Lambda \)CDM as well as SCDM model. However, NHDE model behaves like SCDM model for \(\alpha \rightarrow 3\beta /2\). It has been observed that this model approaches to \(\{r, s\}\rightarrow \{1, 0\}\) in the limit of \(\alpha \rightarrow -1/\omega _d\) but there is no such value of parameters which would clearly show the \(\Lambda \)CDM.

In viscous NHDE model as discussed in Sect. 3, we have considered that the matter consists of viscous holographic dark energy and pressureless DM. We have assumed a most general form \(\zeta =\zeta _0+\zeta _1 H\) to observe the effect of bulk viscous coefficient in the evolution of the universe during early and late time. We have studied three cases: (\(\zeta _0 \ne 0,\; \zeta _1=0\)); (\(\zeta _0=0,\; \zeta _1\ne 0\)) and (\(\zeta _0\ne 0,\;\zeta _1\ne 0\)).

In the first case where we have constant bulk viscous coefficient, i.e., \(\zeta = \zeta _0\), an exponential form of the scale factor is obtained. Therefore, the universe starts from a finite volume followed by an early decelerated phase and then transits into an accelerated phase in late time of evolution. As \((t-t_0)\rightarrow 0\), the scale factor reduces to the power-law form which corresponds to an early decelerated expansion. As \((t-t_0)\rightarrow \infty \), the scale factor tends to the exponential form which corresponds to acceleration similar to the de Sitter phase. The scale factor and red shift corresponding to the transition from decelerated to accelerated expansion has been obtained. The evolution of scale factor has been shown is Fig. 1. It is clear from Fig. 1 that if \(\zeta _0=0.15\), transition from decelerated phase to accelerated phase occurs at \(a_T=1\) and \(z_T=0\), which corresponds to the present time of the universe. The transition would takes place in past if \(\zeta _0>0.15\) and in future if \(0<\zeta _0<0.15\).

The result regarding the transition of the universe into accelerated epoch discussed above have been further verified by studying the evolution of DP. The viscous NHDE model gives time-dependent DP which would describe the phase transition. We have obtained q in terms of a and z. The variation of q with a has been shown in Fig. 2a, b with varying \(\zeta _0\) and constant model parameters, and varying model parameters and constant \(\zeta _0\), respectively. The evolution of DP shows that the transition from decelerated to accelerated epoch occurs at the present time, corresponding to \(q=0\) if \(\zeta _0=0.15\). The transition would be in recent past, corresponds to \(q<0\) at present \(\zeta _0>0.15\) and the transition into accelerating epoch will be in the future, corresponds to \(q>0\) at present if \(0<\zeta _0<0.15\).

As the model predicts the late time acceleration, we have analyzed the model using statefinder parameter and \(\textit{Om}\) diagnostic to distinguished it from other DE models especially from \(\Lambda CDM\) model. The evolution of the viscous NHDE model in the \(\{r, s\}\) plane is shown in Fig. 3a with different values of \(\zeta _0\) with constant \(\alpha \) and \(\beta \). It shows that the evolution of \(\{r, s\}\) parameter is in such a way that \(r<1\), \(s>0\), a feature of quintessence model where as \(r>1\), \(s<0\) corresponds to the Chaplygin gas model. In both models, the trajectories are coinciding with each other for any value of \(\zeta _0\). The viscous NHDE model behaving quintessence and Chaplygin gas models in early time for different \(\zeta _0\) untimely approaches to \(\Lambda CDM\) model in late time. We have also discussed the evolutionary behavior of \(\{r, q\}\) to discriminate the viscous NHDE model. The trajectory of \(\{r, q\}\) has been plotted in Fig. 3b which shows the phase transition from decelerated to accelerated phase. If \(0<\zeta _0 \le 0.57\), the transition takes place from quintessence region and approaches to SS model in late time as \(\Lambda CDM \) model approaches from SCDM. However, if \(\zeta _0>0.57\), the transition starts from Chaplygin gas model and approaches to SS model in late time. Both the trajectories in Q model and CG model are coinciding on each other for any value of \(\zeta _0\).

A study of \(\textit{Om}\) diagnostic of viscous NHDE model has been carried out in Fig. 5a for different values of \(\zeta _0\) and fixed \(\alpha \) and \(\beta \). The trajectory shows that if \(0<\zeta _0\le 0.57\), the \(\textit{Om(z)}\) trajectory shows the negative slope which means viscous NHDE behaves like quintessence and if \(\zeta _0>0.57\), the positive slope of the \(\textit{Om(z)}\) trajectory is observed, i.e., the viscous NHDE behaves like phantom. In future as \(z\rightarrow -1\), the \(\textit{Om(z)}\) becomes constant, i.e, it may approach to \(\Lambda CDM\) model.

The above discussion shows that effect of bulk viscous coefficient on NHDE model with different values of \(\zeta _0\). We have also discussed the viscous NHDE model with varying model parameters \(\alpha \) and \(\beta \) taking fixed \(\zeta _0\). The trajectory for q versus a as shown in Fig. 2b shows that the transition takes place from decelerated to accelerated phase in future for any values of \(\alpha \) and \(\beta \) and approaches to \(q=-1\) in late-time. The trajectory for \(\{r, s\}\) and \(\{r, q\}\) have also been plotted respectively in Fig. 4a, b for different values of \(\alpha \) and \(\beta \) with fixed value of \(\zeta _0\). The \(\{r, s\}\) trajectory as shown in Fig. 4a shows that the trajectory starts from the quintessence region, even though some starts from the vicinity of SCDM and approaches to \(\Lambda CDM\) in late-time. The signature change of q from positive to negative has been observed in \(r-q\) plane as shown in Fig. 4b. The viscous NHDE model approaches to SS model in late-time as \(\Lambda CDM\) does. The \(\textit{Om}\) trajectory has been plotted in Fig. 5b for different values of \(\alpha \) and \(\beta \) for fixed \(\zeta _0\). This trajectory only shows the negative curvature which imply that the viscous NHDE behaves like quintessence.

From the above discussion with constant bulk viscous coefficient, we find that the constant \(\zeta _0\) (or cosmological parameters \(\alpha \) and \(\beta \)) play important roles in the evolution of the universe i.e., they both determine the evolutionary behavior as well as the ultimate fate of the universe.

In second viscous NHDE model we have assumed \(\zeta =\zeta _1 H\). The solution of this model is similar to the non-viscous NHDE one. We have obtained power-law form of scale factor which gives constant values of DP and statefinder pairs.

In last case we have taken the most general form of bulk viscous coefficient \(\zeta =\zeta _0+\zeta _1 H\). The solution of this model is similar to the constant bulk viscous coefficient \(\zeta _0\). The effect of both non-zero values of \(\zeta _0\) and \(\zeta _1\) have been discussed. We have obtained exponential scale factor which gives time-dependent DP and statefinder pairs. The transition from decelerated to accelerated epoch has been discussed. As \((t-t_0) \rightarrow 0\), the scale factor asymptotically gives the power-law which shows that the model decelerates in early time and accelerates in late-time. As \((t-t_0) \rightarrow \infty \), the model corresponds to de Sitter like. The transition scale factor and hence corresponding transition redshift has been calculated. If \((\zeta _0+\zeta _1)=0.15\), the transition from decelerated to accelerated phase occurs at \(a_T=1\) or \(z_T=0\), i.e., at present time of the universe. Figure 6 shows that evolution of the scale factor with (\(t-t_0\)). If \(0<(\zeta _0+\zeta _1) <0.15\), the scale factor has earlier deceleration phase followed by an acceleration phase in later stage of the evolution. For \((\zeta _0+\zeta _1) > 0.15\), the transition takes place in past of the universe and the scale factor increases with accelerated rate forever.

The DP is time-dependent which shows phase transition from decelerated to accelerated phase. The DP has been written in terms of scale factor or redshift. We have calculated the present value \(q_0\) which gives \(\zeta _0+\zeta _1=0.15\). This shows that the transition into acceleration phase occurs at present time. If \((\zeta _0+ \zeta _1) > 0.15\), \(q_0< 0\), i.e., the universe is in accelerating phase and it entered this epoch at an early stage. If \((\zeta _0+\zeta _1) < 0.15\), \(q_0> 0\), i.e., the universe is in decelerating epoch and it will be entered into the accelerated phase in future. We have plotted q versus a for different values of \((\zeta _0, \zeta _1)\) with fixed model parameters and others as shown in Fig. 7a. The Fig. 7b plots the \(q-a\) for different models parameters \(\alpha , \beta \) with fixed \(\zeta _0, \zeta _1\) and others.

Figure 8a shows the \(r-s\) trajectory in \(r-s\) plane for different values of \(\zeta _0\) and \(\zeta _1\) with constant model parameters and others. The model behaviors to Q models for \(0 < (\zeta _0+ \zeta _1) \le 0.57 \) and CG models for \((\zeta _0+ \zeta _1) > 0.57\). The trajectories in Q-model and CG model both converge to the \(\Lambda CDM\) model in late time of evolution. Figure 8b plots the trajectory of \(q-r\) for different values of \((\zeta _0, \zeta _1)\) with constant model parameters and others. The DP changes its sign from positive to negative with respect to time which shows the phase transition of the universe from deceleration to acceleration. In beginning this model behaves different from the \(\Lambda CDM\) but in future it behaves same as \(\Lambda CDM\) which converges to SS model in late-time. Thus, the variable viscous NHDE model is compatible with both Q and CG model. Figure 9a, b plot the trajectories of \(r-s\) and \(r-q\) for different model parameters \((\alpha , \beta )\) with fixed \(\zeta _0, \zeta _1\) and others. In Fig. 9a, we have analysed that for this fixed value of \(\zeta _0\) and \(\zeta _1\) the \(\{r, s\}\) trajectories are lying in the region corresponds to \(r < 1\), \(s > 0\) which shows that our model is similar to the Q model. Figure 9b shows that this model is also able to explain the phase transition of the universe. It also starts from the neighbourhood of the SCDM model for some values of \(\alpha \) and \(\beta \). In future the variable viscous NHDE model approaches to the SS model same as the \(\Lambda CDM\) and Q models. Thus the viscous NHDE model is compatible with the \(\Lambda CDM\) and Q models.

We conclude that the trajectory of \(s-r\) and \(q-r\) suggest a different behavior as compare to Ricci dark energy done by Feng [16] where it was found that the \(s-r\) trajectory is a vertical segment, i.e., s is constant during the evolution of the universe. The trajectory in our viscous NHDE model is mostly confined a parabolic curve and approaches to \(\{r, s\}=\{1,0\}\) in \(s-r\) plane and \(\{r, q\}=\{1, -1\}\) in \(q-r\) plane.

From \(\textit{Om}\) diagnostic we find that the trajectory represents the negative curvature, i.e, viscous NHDE behaves as a quintessence for \(0<(\zeta _0+\zeta _1) \le 0.57\) and it shows the positive curvature, i.e., the viscous DE behaves as phantom, for \((\zeta _0+ \zeta _1) > 0.57\), which is graphically represented by Fig. 10a. We have also concluded that as \(z\rightarrow -1\), we get the constant value of \(\textit{Om}\), which corresponds to \(\Lambda CDM\) model. However, plot of \(\textit{Om}\) as shown in Fig. 10b for different model parameters with constant \(\zeta _o\) and \(\zeta _1\) reveal that there is always negative curvature for any values of model parameters. This shows that the viscous NHDE behaviors similar to quintessence.

In concluding remarks, let us compare our work with respect to the earlier studied in this direction. Feng and Li [56] who investigated the viscous Ricci DE model by assuming bulk viscous coefficient proportional to the velocity vector of the fluid. Chattopadhyay [55] reported a study on modified Chaplygin gas based reconstructed scheme for extended HDE in the presence of bulk viscosity. In comparison to the said work, the present work lies not only in its choice of different bulk viscous coefficient but also in its different approach to discuss the evolution of the universe. The present viscous NHDE model successfully describes the present accelerated epoch. The \(\Lambda CDM\) model is attainable by present model. The NHDE model behaves quintessence model and Chaplygin gas model inn early time due to viscous effect. However, it behaves only quintessence if we consider the model parameters with fixed viscous coefficient. Our work implies the theoretical basis for future observations to constraint the viscous NHDE.