1 Introduction

Why is gravity so weak compared to the other fundamental forces in nature? This question can be recast in terms of the hierarchy problem, namely the seeming disparity (about 16 orders of magnitude) between the electroweak symmetry breaking scale and the Planck mass. This problem can be overcome by adding new dimensions in the large extra dimension (or the bulk) model, namely the ADD model, which was first developed by Arkani-Hamed, Dimopoulos, and Dvali [1,2,3]. They proposed that the extra dimensions could be as large as a millimeter and the measurements of gravity may observe the deviation from \(1/r^{2}\) Newtonian gravitation. Considering this possibility, they found that their model could describe the hierarchy between the Planck mass and the standard model electroweak scale in terms of the large size of the extra dimensions. Therefore testing general relativity and its Newtonian limit at short distances has become particularly important in recent theoretical developments [4,5,6,7,8,9,10,11,12,13].

On the other hand, significant advances have been witnessed in studying the characteristic and application of the cavity optomechanical system with high-Q mechanical nanoresonators(NRs) [14]. Nano- and micromechanical devices can be coupled to optical cavities directly via radiation pressure, leading to a variety of important properties, such as optical self-focusing [15], optomechanical entanglement [16] and optomechanically induced transparency (OMIT) [17, 18]. Recently, many efforts have been made toward optically levitating nano- and micromechanical oscillators in ultrahigh vacuum, such as nanospheres [19, 20], nanodiamonds [21, 22], microdisk [23, 24], and even living organisms [25]. The laser trapped objects have no physical contact with the environment and can lead to ultralow mechanical damping. In the absence of other noise sources, the quality factors of optical levitation can exceed \(10^{12}\) with pressures of \(10^{-10}\) Torr [19]. Owing to its exceptional mechanical properties, optical levitation appears to be an excellent candidate for the NRs in nanoelectromechanical systems (NEMSs), which are of great interest for applications in fundamental science and precision measurement [26,27,28].

Fig. 1
figure 1

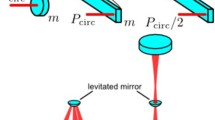
a Schematic diagram of the cavity optomechanical system with two levitated microdisks. The cavity mode is driven by a strong pump laser and probed by a weak probe laser. The levitated microdisks are placed at the antinodes of cavity field with a separation of \(r_{0}=8\upmu m\). b Schematic of the energy-levels for the resonance mode splitting in the cavity

Full size image

In the present work, by combining cavity optomechanics and the ADD model, we investigate the optomechanical system consisting of coupled quantum levitated oscillators and cavity modes. Then we propose a design for non-Newtonian gravity detection at short range with the levitated sensors. The results show that the sharp enhanced transparency peaks with ultra-narrow linewidth can be induced through the coupling between the optical cavity and the levitated resonator. We find that the two transparency peaks are apart near linearly with respect to the gravitational coupling strength. The feature reminds us of a practical application for precisely detecting large extra dimensions at micron separations. We also consider the Casimir effect as the main background force noise in the micro-scale optomechanical system. The constraints on the compactification distances are deduced as last, the super-resolution can be achieved by using the oscillators with high Q factor in vacuum. We expect that the proposed scheme could be applied to probe the large extra dimensions or set a new upper limit on the hypothetical long-range interactions which naturally arise in many extensions to the standard model [29, 30].

2 Theory framework

The micro- or nanoscale objects can be attracted to the anti-node of the field of an optical standing wave. The resulting gradient in the optical field provides a sufficiently deep optical potential well, which allows the object to be confined in a number of possible trapping sites with precise localization [25, 31, 32]. A schematic of our setup is sketched in Fig. 1a, where two dielectric microdisks are optically levitated between the two fixed mirrors by applying two trapping lasers, respectively. A Fabry–Pérot cavity consists of the left fixed mirror and the levitated microdisk 1 (the left one) which couples to the optical cavity field via radiation pressure. This cavity mode is driven by two light fields, one of which is the pump field with frequency \(\omega _{pu} \) and the other of which is the probe field with frequency \(\omega _{pr}\) as shown in Fig. 1a by the purple curve and green curve respectively. The mechanism can be explained as a quantum coupling induced normal mode splitting (NMS) in the four-wave mixing (FWM) process. Figure 1b is the energy level description of this process.

In the present paper, the trapped microdisks are treated as quantum-mechanical harmonic oscillators and their masses are \(m_{1}\) and \( m_{2}\), mechanical frequencies \(\omega _{1}\) and \(\omega _{2}\), and damping rates \(\gamma _{1}\) and \(\gamma _{2}\), respectively. The Hamiltonian can be regarded as \(H_{\omega }=\sum \nolimits _{{j=1,2}} \hbar \omega _{j}a_{j}^{+}a_{j}\), where \(a_{j}^{+}\) and \(a_{j}\) are the bosonic creation and annihilation operators for the two vibrational resonators. We use \( H_{c}=\hbar \omega _{c}c^{+}c\) to describe the Hamiltonian of the cavity mode; here \(\omega _{c}\) and \(c(c^{+})\) denote the oscillation frequency and the annihilation (creation) operator of the cavity. The radiation pressure of the cavity gives rise to the optomechanical coupling \(H_{g}=-\hbar g_{1}c^{+}c(a_{1}^{+}+a_{1})\), where \(g_{1}\) is the single-photon coupling rate between the microdisk 1 and the cavity mode. The parameter \(g_{1}\) has the typical value of \(\sim 2\pi \times 1.2\) Hz [32].

Then we consider the gravity interaction in the system. The ADD theory establishes an effective Planck scale coinciding with the electroweak scale by allowing gravity to travel in extra dimensions. It is possible that all of the particles and fields of the standard model are trapped on this brane, providing an explanation for why we have never observed more than our three spatial dimensions. On the other hand, gravity would be able to travel in \(4+n\) dimensions, where n is the number of extra dimensions. According to this model, the Planck scale is not fundamental but determined by the volume of the extra dimensions,

$$\begin{aligned} M_{Pl}^{2}\sim M_{Pl(4+n)}^{2+n}V_{n}\text { [natural units]}, \end{aligned}$$
(1)

where \(V_{n}\) is the volume of extra dimensions. For equal-size extra dimensions and toroidal compactification, \(V_{n}=(2\pi R_{*})^{n}\) and the size of the extra dimensions,

$$\begin{aligned} R_{*}=10^{30/n-17}\text {mm}\times \left( \frac{1\text { TeV}}{m_{EW}}\right) ^{1+\frac{ 2}{n}}\text { [natural units]}, \end{aligned}$$
(2)

where the electroweak scale \(m_{EW}\), also known as the Fermi scale, is the energy scale around 246 GeV. For \(n=1,\ R_{*}\sim 10^{13}\) cm, implying deviations from Newtonian gravity over solar system distances. In the case of \(n=2\), \(R_{*}\sim 1\) mm. By this process in ADD, the hierarchy problem is nullified and a modification of Newtonian gravity is proposed for the ranges smaller than the compactification length. When the separation between the masses decreases to the point where \(r\ll R_{*}\)(\(R_{*}\) denotes the size of the extra dimensions), the usual inverse-square law of gravity changes to a new power-law [3]

$$\begin{aligned} V(r)=-G_{4+n}\frac{m_{1}m_{2}}{r^{n+1}}, \end{aligned}$$
(3)

where \(G_{4+n}\) is the gravitational constant in the \(4+n\) extra dimensions. Since \(G_{4+n}\sim M_{Pl(4+n)}^{-(2+n)}\) and the Newton constant \( G_{4}\sim M_{pl}^{-2}\), one can obtain the relationship \(G_{4+n}=G_{4}V_{n}\). The separation can be regarded as \(r=r_{0}+x_{1}-x_{2}\), where \(x_{1,2}\) denote the displacements of mechanical oscillators from their equilibrium positions, \(r_{0}\) denotes the distance between equilibrium positions of the two levitated disks.

In our scheme the levitated resonators held in trapping potentials are separated by a distance of \(r_{0}=8\) \(\upmu \hbox {m}\), thus the condition of \(r\ll R_{*}\) can be physically achieved. Expanding Eq. (3) in the condition of \( \left| x_{1}\right| ,\left| x_{2}\right| \ll r_{0}\) and working to the second order, we can obtain the term of gravitational potential for 4+n dimensions, thus

$$\begin{aligned} \begin{aligned} V_{int} \approx&-G_{4+n}m_{1}m_{2}\left[ C_{n,0}\frac{1}{r_{0}^{n+1}}-C_{n,1} \frac{(x_{1}-x_{2})}{r_{0}^{n+2}} \right. \\&\left. +C_{n,2}\frac{(x_{1}-x_{2})^{2}}{r_{0}^{n+3}}\right] , \end{aligned} \end{aligned}$$
(4)

where \(C_{n,k}=(-n-1)\)...\((-n-k)/k!\) is the binomial coefficient. The first term is constant. The second term represents a steady force that does not affect the interactional dynamics. The term proportional to \(x_{1}x_{2}\) represents the lowest-order coupling between the resonators’ motions. In the regime of \(\omega _{c},\omega _{j}\gg g_{j}\), the Hamiltonian of gravitational interaction can be obtained by quantizing mechanical oscillators in the rotating wave approximation [33],

$$\begin{aligned} H_{int}=C_{n,2}\frac{G_{4+n}m_{1}m_{2}}{r_{0}^{n+3}}2x_{1}x_{2}\cong \hbar \beta (a_{1}^{+}a_{2}+a_{1}a_{2}^{+}) \end{aligned}$$
(5)

and

$$\begin{aligned} \beta (n)=C_{n,2}\frac{G_{4+n}}{r_{0}^{n+3}}\frac{\sqrt{m_{1}m_{2}}}{\sqrt{ \omega _{1}\omega _{2}}}. \end{aligned}$$
(6)

This coefficient \(\beta \) can be defined as the extra dimensions induced coupling rate, which reveals the gravitational strength between two oscillators in 4 + n dimensions.

For small separations (\(\ll 10^{-4}\) m), Casimir forces provide the dominant background force, and we expect that the scheme can set the best limits in this regime. In the original point of view, the Casimir effect is derived from the change of the total energy of vacuum due to the presence of two materials. Over the past decade, in much research one has made efforts to predict Casimir interactions among different materials, geometries [34,35,36], including the Casimir force in multilayers [37], and nonlinear Casimir effects [38]. Considering the two adjacent levitated microdisks used here, we expect the fundamental Lifshitz theory can obtain an accurate estimation of the Casimir interaction. The Casimir potential between two extended dielectric flats can be expressed by [39]

$$\begin{aligned} V_{cas}=\frac{\hbar c\pi ^{2}}{720(r-d)^{3}}\left( \frac{\varepsilon -1}{ \varepsilon +1}\right) ^{2}\phi (\varepsilon ), \end{aligned}$$
(7)

where c is the vacuum speed of light, d is the thickness of the disk, \( \varepsilon \) is the electrostatic value of the dielectric polarization of the substance, and \(\phi (\varepsilon )\) is the dielectric function. We use the silica disk with the dielectric constant \(\varepsilon =2\). According to Ref. [39], for \(1/\varepsilon =0.5\), numerical values of the dielectric functions \(\phi (\varepsilon )=0.35\). Then we can manipulate Eq. (7) with the same means and obtain the Casimir coupling rate,

$$\begin{aligned} \beta _{Casimir}=\frac{0.04C_{2,2}\hbar c\pi ^{2}}{720(r_{0}-d)^{5}}\frac{1}{ \sqrt{m_{1}m_{2}}\sqrt{\omega _{1}\omega _{2}}}. \end{aligned}$$
(8)

Therefore the total interaction Hamiltonian, including the Casimir interaction, can be written as \(H_{int}^{\prime }=\hbar (\beta +\beta _{Casimir})(a_{1}^{+}a_{2}+a_{1}a_{2}^{+})\). If we compare Eq. (6) with Eq. (8), we find that increasing the disk’s mass leads to stronger gravitational coupling \(\beta \) and weaker Casimir coupling \(\beta _{casmir}\). Thus we can separate out the signals of the extra dimensions from a strong Casimir background by using the levitated microdisk with larger masses.

Based on the discussion above, the whole system can be considered as an optomechanical system where the left levitated microdisk of the optomechanical cavity not only couples to the cavity field by the radiation pressure, but also interacts with the right microdisk outside the cavity through the gravitational interaction and Casimir coupling. By applying the pump-probe field, we can obtain the Hamiltonian of the whole system:

$$\begin{aligned} \begin{aligned} H&=H_{c}+H_{\omega }+H_{g}+H_{int}^{\prime }-i\hbar \Omega _{pu}(c-c^{+}) \\&\quad -\,i\hbar \Omega _{pr}(ce^{i\delta t}-c^{+}e^{-i\delta t}). \end{aligned} \end{aligned}$$
(9)

Here \(\delta =\omega _{pu}-\omega _{pr}\) is the detuning of the probe field and pump field. The pump laser shows the driving amplitude \(\Omega _{pu}= \sqrt{2P_{pu}\kappa /\hbar \omega _{pu}}\). The probe beam has a driving amplitude \(\Omega _{pr}=\sqrt{2P_{pr}\kappa /\hbar \omega _{pr}}\), where \( P_{pu}(P_{pr})\) is the input power of the pump (probe) field and \(\kappa \) is the total decay rate of the cavity mode.

3 Forecasts

We use silica microdisks with the same size and density \(\rho =2.3\) g/cm\( ^{3}\). The mechanical frequency \(\omega _{j}\) depends on the intracavity intensity; it can be modulated by the power of trapping beam [32]. If we use the trapping laser wavelength \(\lambda =1.5\) \(\upmu \hbox {m}\) and power \( P_{1}=P_{2}=5.06\) W, we can get the axial trapping frequency \(\omega _{1}/2\pi =\omega _{2}/2\pi =10\) kHz.

The quality factor is solely determined by the air molecule impacts. The random collisions with residual air molecules provide the damping rate \( \gamma _{j}=\omega _{j}Q_{j}^{-1}\), and thus the quality factor due to the gas dissipation can be defined as \(Q_{j}=\pi \omega _{j}\rho \nu d/32p\) for the microdisks [23, 24] where \(\nu =\sqrt{k_{B}T/m_{gas}}\) is the thermal velocity of the gas molecules, p is the air pressure, and \(m_{gas}\) is the mass of a gas molecule in the chamber. Let us consider levitated microdisks with the same radius \(r_{1}=r_{2}=75\) \(\upmu \hbox {m}\) and thickness \(d=1\) \(\upmu \hbox {m}\). We get \(Q_{1}=Q_{2}=10^{8}\) for the ultralow pressure \(p=10^{-7}\) mbar at room temperature (\(T=300\) K).

The coupling strength \(\beta \) can be obtained from Eq. (6) by setting different n. In the following, we take the pump-cavity detuning \(\Delta _{pu}=0\). Here we use the Heisenberg equation of motion to solve the Hamiltonian of the levitated microdisk-cavity system. By solving the Heisenberg equation, we can obtain the transmission of the probe beam, \( \left| t\right| ^{2}\), defined as the ratio of the output and input field amplitudes at the probe frequency [40] (see the supplementary materials).

Fig. 2
figure 2

The \(n=2\) extra dimensions modulate the transmission spectrum of the probe field. A peak splitting caused by gravitational deviation and Casimir coupling can be well recognized in the spectrum

Full size image

Then we depict the transmission \(\left| t\right| ^{2}\) of the probe beam as a function of the probe-pump detuning \(\delta \) in Fig. 2. At first we assume \(\beta =\beta _{Casimir}=0\), then we get an enhanced peak which is located at \(\delta =\omega _{1}=10\) kHz; this just corresponds to the fundamental frequency of the levitated microdisk as shown by the black curve. Without the presence of extra dimensions \((n=0)\), we can only consider the Casimir coupling \(\beta _{Casimir}=2.5\times 10^{-4}\) Hz. Then we find that the resonance peak suffers a splitting in the spectrum characterized by the blue curve. Now, let us consider the large extra dimensions induced by the coupling between the two microdisks based on ADD theory. For 4 + 2 dimensions, \(n=2\), we have \(\beta =2\times 10^{-3}\) Hz. The result shows that the resonance frequency splitting can be amplified significantly in the spectrum as shown by the red curve. Here the transmitted spectrum of the probe laser can be effectively modulated by the number of extra dimensions. Without any interaction, one can obtain significant transmission of the probe laser at the resonant region. When gravity deviates from \(1/r^{2}\) in 4 + 2 extra dimensions and also the Casimir background force is taken into account, the enhanced peak splits and separates. Therefore we can adjust the resonance frequencies of the levitated microdisks to 10 kHz by modulating the trapping laser power; then the extra dimensions can be detected by the vibrational mode splitting of the microdisk resonators experimentally.

We define L as the separation between two peaks as shown in Fig. 2. The linear enhancement of L with \(\beta \) reminds us of the possibility to detect the gravity strength between the resonators by measuring the separation in the transmission spectrum. Their relationship can be expressed by \(L=2(\beta +\beta _{Casimir})\), which strongly reveals the deviation from gravitational inverse-square law, namely, a sign indicative of large extra dimensions. The resolution depends on the full width of half maximum (FWHM) of the peak, thus the minimal detectable coupling strength \(\beta _{\min }=L_{\min }/2=FWHM/2\). Considering the peak FWHM in Fig. 2 approximating \( 2\times 10^{-4}\)Hz, one can obtain \(\beta _{\min }\approx 0.1\) mHz.

The levitated resonators with larger thickness can set the better constraints, because the gravitational strength rapidly rises and the Casimir coupling decreases with increasing masses. We depict Fig. 3 to show the gravitational and Casimir coupling as a function of the disk thickness d according to Eqs. (6) and (8). For \(d=1\) \(\upmu \hbox {m}\), we find that \(\beta _{Casimir}\approx \beta /8\); thus the Casimir coupling is 8 times smaller than the gravitational coupling in this case. We expect the contribution of the large extra dimensions will be able to show itself clearly on the probe spectrum with the low Casimir background noise.

Fig. 3
figure 3

The coupling strength of extra dimensions and Casimir as a function of thickness of the microdisks. Under the condition of \(d=1\) \(\upmu \hbox {m}\), the Casimir coupling is about 8 times less than the gravitational coupling. The parameters are taken from Table 1

Full size image

In our scheme, the length of the cavity is 1 cm, while the separation between two microdisks is just 7 \(\upmu \hbox {m}\). If we trap two microdisks in the middle of the cavity, the distance between the microdisk and the mirror is much larger than the separation of two microdisks. Thus the Casimir and electrostatic force between the microdisk and the mirror can be safely neglected. In the Casimir force model we do not consider the frequency-dependent dielectric functions; there may be a few errors in the estimation of the Casimir force. But considering the gravity coupling in 4+2 dimensions is much larger than the Casimir induced coupling (about 8 times); those small errors will present no significant problems.

4 Electrostatic force background

If the two microdisks are electrically connected, electrons flow from the material with the smaller work function to the material with higher work function. This diffusion current builds up a double layer at the interface, resulting in an electrostatic potential (contact potential difference) \( \Delta \Phi \) given as \(\Delta \Phi =(\psi _{1}-\psi _{2})/e\) [41, 42], where \( \psi _{1}(\psi _{2})\) is the work function of the two samples. Since the two levitated microdisks are made of the same material (silica), they have the same work function and equal Fermi energies. Thus we have \(\psi _{1}=\psi _{2}\), and \(\Delta \Phi =0\). The surface potential difference is zero; thus it will not create electrostatic forces between the two levitated microdisks.

Variation of the crystallographic directions exposed at the surface of a clean polycrystalline metal results in a variation of the surface potential. This is referred to as the “patch effect”[43]. In order to avoid this effect, the two microdisks should be made by the same material in a cleanroom, and the crystallographic directions exposed at the two adjacent surfaces should be consistent.

Fig. 4
figure 4

The patch force as a function of the gap between two microdisks with thicknesses of \(d=1\) \(\upmu \hbox {m}\). The red and green dots show the gravity force of 4+2 dimensions and the sensitivity of measurement, respectively, in the separation of \(r_{0}=8\) \(\upmu \hbox {m}\)

Full size image

If the surface films, such as a contaminant layer, a natural oxide layer or lubricant, are removed purely tribochemically, no microfracture or plastic deformation takes place [42, 44]. For the effect of patch potentials, the force between the two parallel plates is

$$\begin{aligned} \frac{F_{patch}}{A}=-\frac{2\varepsilon _{0}\sigma ^{2}}{\left( k_{\max }^{2}-k_{\min }^{2}\right) }\int _{k_{\min }}^{k_{\max }}\frac{k^{3}}{\sinh ^{2}\left[ k(r_{0}-d)\right] }dk, \end{aligned}$$
(10)

which is an expression from Ref. [43] under the assumption that the surface patch potential correlations are constant in a certain wave number range \( k_{\min }<k<k_{\max }\). Here \(\varepsilon _{0}\) is the vacuum dielectric constant, \(A\approx 1.8\times 10^{4}\upmu \hbox {m}^{2}\) is the area of the microdisks, \(\sigma \) is the variance of the potential on one plate, and we apply the commonly used value \(\sigma =90\) mV. Based on AFM images of the surfaces, the minimum and maximum grain sizes of the samples were determined to be \(l_{patch}^{\min }=25\) nm and \(l_{patch}^{\max }=300\) nm [45, 46]. In reality, \(l_{patch}^{\max }\) will rather be of the order of a few \(\upmu \) m [47]. Here we take a conservative value in the calculation, \(l_{patch}^{\max }=3 \upmu \hbox {m}\). This results in \(k_{\min }=2\pi /l_{patch}^{\max }=2\upmu \hbox {m}^{-1}\) and \(k_{\max }=2\pi /l_{patch}^{\min }=251\upmu \hbox {m}^{-1}\). Then we depict the patch force as a function of the gap between two microdisks in Fig. 4. The gravity in 4+2 dimensions can be estimated by \(F_{G}=\partial V(r)/\partial r=3G_{6}m_{1}m_{2}/r_{0}^{4}\approx 3\times 10^{-15}\) N. The precision for the gravity measurement is at the level of \(F_{\min }\approx 3\times 10^{-16}\) N (see the discussion in Sect. 5). The result shows that the patch effect strongly depends on the separation between two microdisks. For \(r_{0}-d=1\) \(\upmu \hbox {m}\) (\(d=1\upmu \)m), we obtain \(F_{patch}=3\times 10^{-14}\) N \(\gg F_{\min },F_{G}\). In our scheme, the measurement can be achieved with the separation of \(r_{0}-d=7\upmu \hbox {m}\), corresponding \(F_{patch}=3\times 10^{-26}\) N \(\ll F_{\min },F_{G}\). Then the patch effect decreases quickly, as shown in Fig. 4; thus it does not play any significant role in our gravity measurement. Considering that it is a rough estimate, there might be practical problems we cannot consider at the moment.

In the past few years, new force measurement in the Casimir regime can be achieved by the isoelectronic technique [5, 10, 13] and torsion balance methods [4, 48]. Compared to the previous experiments, a hybrid microresonator-cavity system with optical pump-probe scheme is introduced to detect the large extra dimensions in this paper. In our optical scheme, the Casimir background noise can be reduced by using a specific geometry such as the enhancement of the thickness. The electrostatic force can be eliminated by using the sensors with the consistent material and surface crystallographic directions. We list all the main optomechanical parameters in Table 1.

Table 1 Optomechanical parameters of the levitated microdisks
Full size table

The mechanism underlying these effects can be explained as FWM in a three-level system. The simultaneous presence of a pump field and a probe field generates a radiation pressure force at the beat frequency, which drives the motion of the oscillator near its resonance frequency. In Fig. 1b, we let \(\left| N\right\rangle \), \(\left| n_{1}\right\rangle \) and \(\left| n_{2}\right\rangle \) denote the number states of the cavity photon, left microdisk phonons, and right microdisk phonons, respectively. The \(\left| N,n_{1},n_{2}\right\rangle \leftrightarrow \left| N+1,n_{1},n_{2}\right\rangle \) transition changes the cavity field. The initial energy level of the cavity photon \(\left| N,n_{1},n_{2}\right\rangle \) is dressed by the mechanical modes \(\left| N,n_{1}+1,n_{2}\right\rangle \) via the radiation pressure. Thus the \( \left| N+1,n_{1},n_{2}\right\rangle \leftrightarrow \left| N,n_{1}+1,n_{2}\right\rangle \) transition is caused by the radiation pressure coupling. The mechanical modes of the right levitated microdisk adds a fourth level \(\left| N,n_{1},n_{2}+1\right\rangle \). In the system, the energy level \(\left| N,n_{1}+1,n_{2}\right\rangle \) can be mainly modified by the gravitational coupling between two resonators. The coupling breaks down the symmetry of the OMIT interference, the single OMIT transparency window is split into two transparency windows, which yields the quantum coupling induced NMS as shown in Fig. 2.

5 Constraints and limits

The spectral resolution depends on the FWHM of the oscillation peak. The result shows that the smaller linewidth can be achieved by increasing the Q factor of the levitated resonators.

Fig. 5
figure 5

Limit on the compactification range \(R_{*}\) and the extra dimensions induced coupling \(\beta \) with the ADD formalism. The parameters take the same values as in Table 1

Full size image

Figure 5 presents the constraints on \(R_{*}\) for the number of extra dimensions, \(n=1,2,3\). The sloping lines represent the calculated coupling rate \(\beta \) for different n and \(R_{*}\). We depict the horizontal dash black line to indicate the limits of the detectable coupling strength \(\beta _{\min }\). \(R_{*}\) and \(\beta \) are constrained to be larger than the values of the intersections in the picture. The solid lines in the figure represent the detectable parameter space, the dot lines represent the undetectable region. The arrow indicates that the sensitivity can be improved through the optomechanical oscillators with higher Q factors. Considering the minimum measurable gravitational coupling rate \( \beta _{\min }=0.1\) mHz, we get the precision for the force measurement as \( F_{\min }=300\) aN. The Q factor of the optically trapped particles is limited only by collisions with residual air molecules, thus the sensitivity can be improved by decreasing the air pressure. The lower pressure limit of the sputter-ion pumps is in the range of \(10^{-11}\) mbar. Lower pressures in the range of \(10^{-12}\) mbar can only be achieved when the sputter-ion pump works in a combination with other pump methods [49, 50]. In our considerations, a conservative value is taken, \(p=10^{-7}\) mbar, which is usually required for achieving ultrahigh-Q mechanical oscillators and the ultrasensitive measurements in the levitated optomechanical system [12, 19, 23, 24, 51]. If we choose a lower air pressure (\(p=10^{-11}\) mbar), this scheme will obtain the FWHM in the spectrum with \(FWHM=10\) nHz, corresponding to the force sensitivity of \(F_{\min }=0.2\) aN. Our scheme yields 2–3 orders of magnitude improvement for the force sensing in the microscale [5].

The fundamental fluctuation processes impose the ultimate limits upon the sensitivity of the detection. The frequency stability \(\Delta \omega _{\min } \) is the key to performance of micro-resonators and their applications in the thermomechanical noise system. For the case of the high quality factor \( Q\gg 1\), the minimum detectable frequency shift limited by thermomechanical fluctuations of the levitated microdisks can be estimated via [52],

$$\begin{aligned} \Delta \omega _{\min }\approx \sqrt{\frac{k_{B}T\omega _{1}\Delta f}{ E_{c}Q_{1}}}, \end{aligned}$$
(11)

where \(\Delta f=1/2\pi \tau \) is the measurement bandwidth which is dependent upon the measurement averaging time \(\tau \). \(E_{c}=m_{1}\omega _{1}^{2}\langle x_{c}^{2}\rangle \) represents the maximum driving energy, \( \left\langle x_{c}\right\rangle \) is the maximum root mean square (rms) level. The resonator follows a predominantly linear response (Hooke’s law) at this level. For a Gaussian field distribution, the nonlinear coefficients are given by \(\xi =-2/W^{2}\) [53], here \(W\approx 75\) \(\upmu \hbox {m}\) is the trapping beam waist. For the displacements \(\left| x_{c}\right| \ll \left| \xi \right| ^{-1/2}=5\times 10^{-5}\) m the nonlinearity is negligible. In our considerations, \(x_{c}\) is taken to be 2 orders of magnitude smaller, and we choose \(x_{c}\approx 10^{-7}\) m. Considering the quality factor of the microdisk \(Q_{1}=1.7\times 10^{8}\) at room temperature, we obtain \(\Delta \omega _{\min }=0.8\) \(\upmu \hbox {Hz}\) \(<\beta _{\min }\). Here we suppose the measurement bandwidth \(\Delta f=10^{-4}\) Hz, corresponding to the measurement time \(\tau =1600\) s. The result shows that the thermomechanical noise can be controlled at a level lower than the claimed sensitivity. The phase noise presents a treatment of the problem of analyzing and measuring short-term frequency instabilities of the ultrastable oscillation. The Allen deviation is inversely proportional to the integration time. But a long integration time may increase the long-term instabilities due to the frequency drift from the environmental temperature changes and device aging and so on. An integration time of size of 1600 s is a good compromise between the two limit factors.

6 Conclusion

We study the dynamics of a driven optomechanical cavity coupled to a levitated resonator via the coupling induced by large extra dimensions, in which the splitting can be observed at the probe frequency. Our study reports a design for probing gravitational deviation in the range of 8 \(\upmu \) m with the pump-probe optical technology in cavity. Under the influence of non-Newtonian gravity, the transparency peak would show a distinct splitting in frequency space. We have shown that the coupling strength associated with such a hypothetical variation of gravity could be determined from a measurement of the splitting distance. The gravitational strength, characterized by the coupling strength \(\beta \), can also be determined by the splitting distance L. The Casimir coupling rate is about 8 times smaller than the gravitational strength in the system. The different surface potentials can be attenuated efficiently in our scheme, providing the precision measurement in the Casimir regime without the isoelectronic technique. We also hope that the precision can be significantly enhanced by experiments in ultrahigh vacuum.