Abstract
We consider the Jeans instability and the gravitational collapse of the rotating Bose–Einstein condensate dark matter halos, described by the zero temperature non-relativistic Gross–Pitaevskii equation, with repulsive interparticle interactions. In the Madelung representation of the wave function, the dynamical evolution of the galactic halos is described by the continuity and the hydrodynamic Euler equations, with the condensed dark matter satisfying a polytropic equation of state with index \(n=1\). By considering small perturbations of the quantum hydrodynamical equations we obtain the dispersion relation and the Jeans wave number, which includes the effects of the vortices (turbulence), of the quantum pressure and of the quantum potential, respectively. The critical scales above which condensate dark matter collapses (the Jeans radius and mass) are discussed in detail. We also investigate the collapse/expansion of rotating condensed dark matter halos, and we find a family of exact semi-analytical solutions of the hydrodynamic evolution equations, derived by using the method of separation of variables. An approximate first order solution of the fluid flow equations is also obtained. The radial coordinate dependent mass, density and velocity profiles of the collapsing/expanding condensate dark matter halos are obtained by using numerical methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
After almost one hundred years of intensive study and research the properties of dark matter remain elusive. The existence of dark matter is one of the fundamental assumptions of modern cosmology and astrophysics [1,2,3,4,5,6,7], and its nature is one of the most important open questions in physics. Presently, all available information on the dark sector is obtained from the study of its gravitational interactions with astrophysical systems.
Perhaps the strongest evidence for the existence of the dark matter in the Universe comes from the study of the galactic rotation curves [8]. For hydrogen clouds in stable circular orbits moving around the galactic center the rotational velocities first increase near the center of the galaxy, thus following the standard (Newtonian) gravitational theory, but then they remain approximately constant at an asymptotic value of the order of \(v_{tg\infty } \sim 200{-}300~\hbox {km/s}\). Hence the rotation curves implies the existence of a mass profile of the form \(M(r) = rv^2_{tg\infty } /G\), where G is the gravitational constant. This fundamental result implies that within a distance r from the center of the galaxy, even at large distances where very little baryonic (luminous) matter can be detected, the mass profile increases linearly with r. This type of behavior can be explained by assuming the presence of a new (and exotic) mass component, interacting only gravitationally with ordinary matter, and which most likely consists of new particle(s) not (yet) included in the standard model of particle physics. The behavior of the galactic rotation curves still provides the most convincing and compelling evidence for the existence of dark matter [9,10,11,12].
The second important astrophysical evidence for dark matter comes from the virial mass discrepancy in galaxy clusters [13]. Galaxy clusters are giant astrophysical systems formed of thousands of galaxies each, bounded together by their own gravitational interaction. The galaxies give around 1% of the mass of the clusters, while the high temperature intracluster gas represents around 9% of the cluster mass. But the total masses obtained by measuring the velocity dispersions of the galaxies exceed the total masses of all stars in the cluster by factors of the order of 200-400 [14]. Hence, in order to explain the cluster dynamics one needs to assume the presence of dark matter, representing around 90% of the mass of the cluster. Another strong evidence for the presence of dark matter follows from the measurement of the temperature of the intracluster medium, since a supplementary mass component is required to explain the determined depth of the gravitational potential of the clusters [14].
Several other astrophysical and cosmological observations have also provided compelling evidence for the presence of dark matter. From the cosmological perspective, the recent Planck satellite measurements of the Cosmic Microwave Background Radiation [15] led to the precise determination of the cosmological parameters. These results have indicated that baryonic matter only cannot explain the cosmological dynamics, and that the standard \(\Lambda \) Cold Dark Matter (\(\Lambda \hbox {CDM}\)) cosmological paradigm requiring the existence of dark matter is strongly favored by observations. For a consistent interpretation of the gravitational lensing data the existence of dark matter is also required [16,17,18].
Powerful observational evidences the existence of dark matter are yielded by the observations of a galactic cluster called the Bullet Cluster, consisting of two colliding clusters of galaxies. Due to collision of its two components that occurred in the past, in the Bullet Cluster cluster the baryonic and the dark matter components are separated [19]. Determinations of the cosmological parameters from the Planck data on the cosmic microwave background radiation did show convincingly that the Universe consists of 74% dark energy, 22% non-baryonic dark matter and only 4% baryonic matter [15].
Depending on the energy of the particles composing it, dark matter models can be classified generally into three major types, cold, warm and hot dark matter models, respectively, [20]. For the dark matter particle(s) the main candidates are the WIMPs (Weakly Interacting Massive Particles) and the axions, respectively [20]. WIMPs are hypothetical (and yet undetected) heavy particles, interacting through the weak force [21, 22]. Other popular dark matter candidates, the axions, are bosons that were first proposed as a solution of the strong CP (charge + parity) problem, which requires one to explain why quantum chromodynamics does not break the CP symmetry [23, 24].
There are also other approaches that attempt to interpret the observational data without resorting to dark matter. These explanations assume that on galactic or extragalactic scales the law of gravity (Newtonian or general relativistic) is modified. The earliest attempt to explain the rotation curves by modified gravity is MOND (Modified Newtonian Dynamics) theory, proposed initially in [25]. Other modified theories of gravity have also been used widely as alternative explanations to dark matter phenomenology [26,27,28,29,30,31,32,33,34,35,36]. For a recent review of the dark matter problem in some modified theories of gravity see [37].
An attractive possibility for the detection of the presence of dark matter may be provided by its possible annihilation into ordinary particles. If such physical processes really take place, then a large number of positrons and gamma-ray photons are produced, thus giving some clear observational signatures for the presence of dark matter. This possibility may be supported by the detection of excess positron emission in our galaxy [38,39,40,41,42,43,44,45]. Hence the excess gamma-ray and positron emissions in our galaxy could be interpreted as coming from the annihilation of dark matter with mass in the range of \(m \sim 10\)–100 GeV [38,39,40]. For an in depth discussion of this problem, as well as of the alternative possibilities for the interpretation of the observational data see [41,42,43,44,45].
Dark matter models can generally give good explanations of the phenomenological (and unexpected) behaviors of particle dynamics at the galactic and extragalactic level, including the constancy of the rotation curves, and the virial mass discrepancy. However, crucial conflicts do appear when one compares the results of the numerical simulations of the theoretical models with the observations. The observational data on nearly all observed galactic rotation curves indicate that in the presence of a single pressureless dark matter component they increase less sharply as compared to the predictions of the cosmological simulations of structure formation in the standard \(\Lambda \)CDM model. Moreover, the numerical simulations display dark matter density profiles that behave as \(\rho \sim 1/r\) (a cusp) at the galactic center [46]. On the other hand, observations of the galactic rotation curves show the existence of constant density cores [47, 48]. In dark matter physics this contradiction between theory and observations represents the so-called core-cusp problem. Dark matter models must also face the “too big to fail” question [49, 50]. The Aquarius simulations did show that in the dark matter halos predicted in the standard \(\Lambda \)CDM model the most massive subhalos are incompatible with the observations of the dynamics of the brightest dwarf spheroidal galaxies of the Milky Way [50]. For the dwarf spheroidal galaxies the best-fitting hosts have maximum velocities in the range \(12\; \mathrm{km/s}< V_{max} < 25~\hbox {km/s}\), while all the \(\Lambda \)CDM simulations give at least ten subhalos with velocities \(V_{max} > 25~~\hbox {km/s}\). In the framework of the \(\Lambda \)CDM-based models of the satellite population of the Milky Way these observational results cannot be interpreted. The main contradiction between theory and observations is related to the predictions of the densities of the satellites, with the predicted dwarf spheroidals having dark matter halos more massive by a factor of \(\sim \)5 than shown by the observations.
The problems mentioned above, related to the physical properties of the dark matter, may be explained if one extends the standard \(\Lambda \)CDM model by assuming that dark matter particles may have some kind of self-interaction. This model, called the self-interacting dark matter (SIDM) paradigm assumes the existence of supplementary interactions in the dark sector [51,52,53,54] that may allow momentum and energy exchange between particles that compose the dark matter halos. In these models the basic quantity describing the dark matter halo properties is the self-interaction cross section \(\sigma _{DM}\) divided by the dark matter particle mass m, \(\sigma _{DM}/m\). If the dark matter self-interactions have cross sections per mass of the same order of magnitude as the strong nuclear force, \(\sigma _{DM}/m\sim 1 \mathrm {g/cm}^{-2}\), this would thermalize the inner regions of dark matter halos where the baryonic matter is concentrated. On the other hand for \(\sigma _{DM}/m\ge 1 \mathrm {g/cm}^{-2}\) on galactic scales Self-Interacting Dark Matter models can explain the uniformity as well as the diversity of galaxy rotation curves [55,56,57]. Galaxy clusters also show the same diversity of properties of their Self-Interacting Dark Matter halos [58].
The possibility of a complex self-interaction of dark matter particles received some observational backing from the study of the data obtained from the study of 72 galaxy cluster collisions. The observations did include both ‘major’ and ‘minor’ mergers, and they were done by using the Hubble and Chandra Space Telescopes [59]. Important constraints on the non-gravitational forces acting on dark matter can be obtained from the study of the collisions between galaxy. The analysis presented in [59] gave an upper limit of \(\sigma _{DM}/m\) as \(\sigma _{DM}/m < 0.47~\hbox {cm}^{2} /\hbox {g}\) (at 95% Confidence Level). In [60] an upper limit on the self-interaction cross section of dark matter of \(\sigma _{DM}/m<1.28~\hbox {cm}^{2}/\hbox {g}\) (68% Confidence Level), was obtained. Different self-interacting dark matter models were investigated in [61,62,63,64]. In [65] the implications of the self-interaction of dark matter for the tidal stripping and evaporation of satellite galaxies in a Milky Way type galaxy were considered. The response of self-interacting dark matter halos to the growth of galaxy potentials using numerical simulations was investigated in [66], and a greater diversity of dark matter halo profiles was found. A self-interacting dark matter halo with \(\sigma _{DM}/m=0.1~\hbox {cm}^{2}/\hbox {g}\) gives a good fit to the measured dark matter density profile of A2667. The same halo simulated with \( \sigma _{DM}/m=0.5~\hbox {cm}^{2}/\hbox {g}\) does not produce a core profile dense enough to fit the observational data of A2667. Together with the previous findings in [59], these limits point towards the result that the constraint \(\sigma _{DM}/m\ge 0.1~\hbox {cm}^{2}/\hbox {g}\) is strongly disfavored for dark matter collision velocities greater than 1500 km/s.
Therefore, as suggested by the above observational results, we cannot reject a priori the possibility that dark matter is a self-interacting constituent of the Universe. Physical models of dark matter in which the fundamental particles are self-interacting may provide a better theoretical explanation of the observed phenomenology at galactic and extragalactic scales. But from both a phenomenological perspective, and from a fundamental theoretical and physical point of view, the best motivated self-interacting dark matter models can be constructed by assuming that presently dark matter is in the form of a Bose–Einstein condensate.
In the 1920s, by using statistical physics methods, Bose and Einstein [67,68,69] proposed that at temperatures smaller than a critical one, all integer spin particles will condense into the lowest quantum state. In this phase microscopic quantum phenomena become apparent at the macroscopic level. The Bose–Einstein condensation process occurs when the particles in the gas become correlated quantum mechanically, that is, when the de Broglie thermal wavelength turns to be greater than the mean interparticle distance. The transition to the condensate phase of the boson gas is initiated when the temperature T is smaller than the critical one, \(T_{cr}\), which is given by the expression [70,71,72,73]
where \(\rho _{cr}\) is the critical transition density, m is the mass of the particle in the boson gas, \(k_B\) is Boltzmann’s constant, and \(\zeta \) denotes the Riemann zeta function, respectively.
The experimental creation of Bose–Einstein condensates was first realized in dilute alkali gases in 1995 by cooling a dilute vapor of approximately two thousand rubidium-87 atoms to below 170 nK, using a combination of laser cooling and magnetic evaporative cooling [74,75,76]. The presence of a Bose–Einstein condensate in a bosonic system is indicated, from a physical and experimental point of view, by the appearance in both coordinate and momentum space distributions of the particles of sharp peaks.
Presently, the only evidence for the existence of Bose Einstein condensates on a microphysical scale appeared in laboratory experiments, which involve a very small scale. On the other hand, the possibility of the existence of some forms of bosonic condensates in the cosmic environment cannot be excluded a priori. Due to their superfluid properties, in high density general relativistic objects, like, for example, neutron or quark stars, the neutrons or the quarks could form Cooper pairs, which, once the temperature or density reach their critical values, would eventually condense. Bose–Einstein condensate stars may have maximum central densities of the order of \( 0.1-0.3\times 10^{16}~\hbox {g/cm}^3\), minimum radii in the range of 10-20 km, and maximum masses of the order of \(2M_{\odot }\), respectively. The study of their interesting physical and astrophysical properties is presently an active field of research [77,78,79,80,81,82,83,84,85,86,87].
Since dark matter is assumed to be a gas of bosonic particles, it naturally follows that it may have experienced a phase transition during its cosmological history, and presently it is in the form of a Bose–Einstein condensate. The possibility that dark matter may be in the form of a Bose–Einstein condensate was initially suggested in [88], and then rediscovered/reinvestigated, in [89,90,91,92,93,94,95,96,97,98,99]. The systematic investigation of the physical and astrophysical properties of the Bose–Einstein condensate dark matter halos, based on the non-relativistic Gross–Pitaevskii equation [100, 101] in the presence of an external confining gravitational potential, was started in [102]. A significant simplification of the mathematical and physical formalism required for the description of the gravitationally bounded Bose–Einstein condensates can be obtained by introducing the Madelung representation of the wave function. The Madelung representation provides an equivalent description of the Gross–Pitaevskii equation in a form similar to the hydrodynamic fluid flow equations in classical mechanics, that is, a continuity equation, and an Euler type equation, respectively. With the help of the Madelung hydrodynamical representation one obtains the fundamental result that Bose–Einstein condensed dark matter can be described as a non-relativistic, Newtonian gas, in a gravitational trapping potential, with the pressure and density obeying a polytropic equation of state, with polytropic index \(n=1\) [103]. From this result it follows that the radius R of the zero temperature Bose–Einstein condensate dark matter halo is given by \(R=\pi \sqrt{\hbar ^{2}a/Gm^{3}}\), where a is the scattering length [102]. The total mass M of the condensate dark matter halo is obtained: \(M=4\pi ^2\left( \hbar ^2a/Gm^3\right) ^{3/2}\rho _c=4R^3\rho _{c}/\pi \), where \( \rho _{c}\) is the central density of the galactic halo. The mass of the dark matter particle satisfies a particle mass-galactic radius relation given by [102]
The effectiveness of the Bose–Einstein condensate dark matter model was checked through the fitting of the Newtonian and general relativistic tangential velocity equation to a sample of observed rotation curves data of dwarf and low surface brightness galaxies, respectively.
The condensate dark matter halo may not necessarily be at zero temperature. In [104] the thermal correction to the dark matter density profile where obtained. An important result on the Bose–Einstein condensate dark matter halos is that their density profiles generally indicate the presence of an enlarged core, whose presence is due to the strong interaction between dark matter particles [105]. The investigations of the properties of the Bose–Einstein condensate dark matter on cosmological and astrophysical scales is a very interesting and active field of research [106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152]. Properties of the Fuzzy Dark Matter, a particular theoretical form of dark matter, assumed to be formed of an extremely light boson (\(m\sim 10^{-22}~\hbox {eV}\)), with a de Broglie wavelength of the order of \(\lambda \sim 1~\hbox {kpc}\), were investigated in [153].
While the static properties of the Bose–Einstein condensate dark matter halos have been extensively investigated, their rotational characteristics have received less attention. The presence of vortices in a self-gravitating Bose–Einstein condensate dark matter halo, consisting of ultra-low mass scalar bosons, was investigated in [96]. Rotation of the dark matter may induce a harmonic trap potential for vortices. In [109] a detailed study of the vortices in rotating Bose–Einstein condensate dark matter halos was performed, and strong bounds for the shape and quantity of vortices in the halo, for interaction strength, for the critical rotational velocity for the nucleation of vortices, and for the boson mass were found. In [110], by assuming that a vortex lattice forms, the effects of rotation on a superfluid Bose–Einstein condensate dark matter halo were investigated. On the rotation curves sub-structures similar to some observations in spiral galaxies may form. The equilibrium properties of self-gravitating, rotating Bose–Einstein condensate haloes, which satisfy the Gross–Pitaevskii–Poisson equations were studied in [121]. For a wide range of the Bose–Einstein condensate dark matter physical parameters vortices are generated. On the other hand, vortices cannot appear for a vanishing self-interaction, and they form when the self-interaction between dark matter particles is strong enough.
One of the fundamental concepts in modern astrophysics and cosmology is that of gravitational instability, initially discussed by Jeans [154]. Its importance is related to the prospect of estimating the scale of the condensations that may occur in an extended gaseous medium under the influence of small perturbations. The possibility of such an estimation will provide at least qualitative information regarding the formation of stars and of galaxies from an original cosmic medium. The main result of the original analysis by Jeans was that a self-gravitating infinite uniform gas at rest should be unstable against small perturbations proportional to \(\exp \left[ i\left( \vec {k}\cdot \vec {r} -\omega t\right) \right] \). The lineariazation of the equations of the ideal hydrodynamics and the Poisson equation results in the well-known dispersion relation \(\omega ^{2}=c_{s}^{2}k^{2}-4\pi G\rho \), where \( c_{s}=\left( \gamma k_{B}T/m\right) ^{1/2}\) is the adiabatic sound velocity, \(\rho \) is the density, T is the gas temperature, and \( \gamma =5/3\) is the ratio of specifics heats, respectively. When \(\omega ^{2}\) becomes negative, an instability arises once the perturbation wavelength \(\lambda =2\pi /k\) exceeds the critical value \(\lambda _{J}=c_{s} \sqrt{\pi /G\rho }\), \(\lambda >\lambda _{J}\). Thus, an originally uniform gas, due to the instability, should break into massive components with characteristic size of the order of \(\lambda _{J}\) [13]. The effects of the rotation and of other physical effects on the stability of a self-gravitating medium were considered in [155,156,157,158,159,160,161,162,163,164,165]. The kinetic theory of the Jeans instability was developed in [166,167,168,169,170], mainly using methods from plasma physics. For a detailed discussion of the Jeans instability and its role in astrophysics see [13].
An interesting property of the Bose–Einstein condensation processes is represented by the collapse and the ensuing explosion of the condensates [172]. Near a Feshbach resonance the atomic scattering length a can be changed, by adjusting an external magnetic field, over a large range. Once the sign of the scattering length is changed, a repulsive condensate of \(^{85}\) Rb atoms is transformed into an attractive one that subsequently reaches a collapsing and an exploding phase. The collapse of a Bose–Einstein condensate was investigated by using the semi-classical Fokker–Planck equation for a gas of free bosons in [114, 173, 174], and, for a \(1/r^b\) type potential, in [175].
The mechanisms of the gravitational collapse of the Bose–Einstein condensate dark matter halos was studied in [129], by using a variational approach, and by choosing an appropriate trial wave function. This approach allows the reformulation of the Gross–Pitaevskii equation with spherical symmetry as Newton’s equation of motion for a particle in an effective potential, which is determined by the zero point kinetic energy, the gravitational energy, and the particles interaction energy, respectively. The velocity of the condensate is proportional to the radial distance, with a time-dependent proportionality function. The collapse of the condensate ends with the formation of a stable configuration, corresponding to the minimum of the effective potential. The obtained results did show that the gravitational collapse of the condensed dark matter halos can lead to the formation of stable astrophysical systems with both galactic and stellar sizes.
It is the goal of the present paper to investigate the Jeans stability and the collapsing properties of the Bose–Einstein condensate dark matter halos in the presence of vortices, induced by the rotation of the halo. Rotation is a general feature of galactic dynamics, probably generated by some physical instability processes in the early Universe. To describe the Bose Einstein condensate galactic dark matter halos as a multi-particle bosonic system we adopt an effective approach based on the Gross–Pitaevskii equation [102]. The Gross–Pitaevskii equation gives an effective mean-field description of the gravitationally confined dark matter halo. The mathematical analysis of the condensed dark matter halos is greatly simplified by the introduction of the Madelung representation of the wave function, which allows the description of the dark matter in terms of the equations of the classical fluid dynamics, the continuity and the Euler equation, respectively. In this approach dark matter halos can de described as fluid structures obeying a polytropic equation of state, with polytropic index \(n=1\). The Euler evolution equation also contains the quantum force, derived from the quantum potential, and which represents a purely quantum effect. The assumptions of the rotation for the condensate dark matter halo leads to the necessity of taking into account the presence of quantized vortices. A vortex is an excitation of the bosonic system, and hence it is a state whose energy is higher than that of the ground state.
In order to investigate the Jeans stability of Bose–Einstein condensate dark matter halos we consider the perturbation of the hydrodynamic flow equations with respect to an appropriately chosen ground state, and we perform a local linear stability analysis, which includes the effects of the quantum pressure, of the quantum potential and of the rotation, as well as the self-gravity of the system. The dispersion relation for the propagation of the instabilities in the system is obtained, and the Jeans wave number for the rotating Bose–Einstein condensate dark matter halo is obtained. Once the Jeans wave number is known, we can immediately obtain the Jeans radius and mass, which give the critical length and mass scales above which condensate dark matter collapses. In the approximation when rotation and quantum force are ignored, the Jeans radius and mass coincide with the radius and mass of the static condensate. The effects of the rotation are also considered, and the Jeans radius and mass are also obtained for rotation dominated dark matter halos. Similar results can be obtained in the framework of the Thomas–Fermi approximation, by requiring that the total energy of the system is minimal.
Once the radius and mass of the Bose–Einstein condensate dark matter halo exceeds the Jeans limits for the critical stability, gravitational collapse or expansion follows. In order to study the collapse or the expansion of the condensate we derive first a semi-analytical solution to the spherical hydrodynamic equations governing the time and space evolution of a Bose–Einstein condensate dark matter halo. First we reduce the system of the coupled nonlinear partial equations describing the evolution of the galactic halo to a single, strongly nonlinear partial differential equation for the mass \(M=M(r,t)\) of the condensate. Then we factorize the mass function into products of a time-dependent factor and another factor depending only on the spatial variable r. This factorization means that both spatial and temporal profiles of the gravitational, mechanical and thermodynamic variables of the halo have a universal behavior, once they are factorized appropriately. To study the spatial profiles of the collapsing/expanding rotating dark matter halos we use approximate and numerical methods. A first order approximative solution of the mass function is explicitly obtained. The general mass, density and velocity spatial profiles are obtained by numerically integrating the mass equation. In relation with the general properties of the gravitational collapse we also show that homologous solutions to the hydrodynamic equations describing the time evolution of a Bose–Einstein condensate dark matter, wherein thermodynamic variables factorize into products of a time-dependent factor and another factor depending only on the scaled spatial variable \(\xi \equiv r/R(t)\), do not exist. This factorization means that spatial profiles of the thermodynamic variables remain time invariant. Since Bose–Einstein condensate dark matter halos do not have this property, it follows that the dynamics of the collapse of a condensed galactic halo is very different from other types of gravitational collapse, like, for example, the pre-supernova stellar core collapse.
The present paper is organized as follows. The basic properties of the Bose–Einstein condensate dark matter halos are presented in Sect. 2, where, with the use of the Madelung representation, the evolution equations of the condensed galactic halos are formulated in terms of the continuity and Euler equations of classical hydrodynamics. The Jeans instability of condensed dark matter halos confined by their own gravitational field is discussed in Sect. 3, by fully taking into account the effects of the rotation and the quantum effects. The limiting cases of the general dispersion relation are considered in detail. The time evolution of the Bose–Einstein condensate dark matter halos is investigated in Sect. 4, and it is shown that the hydrodynamic equations describing the dynamics of a rotating polytropic gas with polytropic index \(n=1\) do admit a separable solution, in which all physical quantities can be expressed as products of two functions, one depending on time only, and the second a function of the radial coordinate only. An approximate first order solution of the evolution equations is also obtained. The spatial dependence of the physical quantities is investigated by using numerical methods. We discuss and conclude our results in Sect. 5. In Appendix A we explicitly show that the hydrodynamic evolution equations describing a polytropic fluid with polytropic index \(n=1\) do not admit self-similar homologous solutions.
2 Gravitationally confined Bose–Einstein dark matter halos
Generally, Bose–Einstein condensation processes take place in a Bose gas with particle number density n when the thermal de Broglie wave length \(\lambda _{dB}=\sqrt{2\pi \hbar ^2/mk_BT}\), exceeds the mean interparticle distance \(n^{1/3}\). Then, as a result, the wave packets percolate in space. The critical condensation temperature can then be obtained qualitatively as \(T\le 2\pi \hbar ^2n^{2/3}/mk_B\) [102]. Under the assumption of an adiabatic cosmological expansion of the Universe, the temperature dependence of the number density of the particle is \(T\propto n^{2/3}\). Hence Bose–Einstein condensation occurs if the mass of the particle satisfies the condition \(m<1.87~\hbox {eV}\) [176], and therefore particles satisfying this mass limit could Bose–Einstein condense, and form large scale cosmological or astrophysical structures.
Due to the low temperature of the Bose–Einstein condensates, their physical properties can be understood within the so-called mean-field approximation. The success of the mean-field approach is determined by the dilute nature of the Bose gases. We can always write the Bose field operator as a sum of the condensate wave function and an operator describing the non-condensed bosons, so that \(\hat{\Psi }\left( \vec {r},t\right) =\Psi \left( \vec {r} ,t\right) +\hat{\Psi }^{\prime }\left( \vec {r},t\right) \), where \(\Psi \left( \vec {r},t\right) \equiv \left<\hat{\Psi }\left( \vec {r},t\right) \right>\) is the average value of \(\hat{\Psi }\left( \vec {r},t\right) \), and \(\hat{\Psi }^{\prime }\left( \vec {r},t\right) \) represents the fluctuations in the system. The single-particle density matrix \(\rho \) is given by \(\rho \left( \vec {r}, \vec {r}\;^{\prime }\right) =\left<\hat{\Psi }^{+}\left( \vec {r}\right) \hat{ \Psi }\left( \vec {r}\;^{\prime }\right) \right>\), where \(\hat{\Psi }^{+}\left( \vec {r}\right) \) is the field operator creating a particle at a point \(\vec {r} \), and \(\hat{\Psi }\left( \vec {r}\;^{\prime }\right) \) is the field operator annihilating a particle at \(\vec {r}\;^{\prime }\). In a dilute Bose gas close to \(T = 0\), one can neglect with a very good approximation the non-condensed bosons \(\hat{\Psi }^{\prime }\left( \vec {r},t\right) \). In this case the mean-field order parameter is given exactly by the quantum mechanical wave function \(\Psi \left( \vec {r},t\right) \), with well defined phase. Hence, the zero temperature dynamics of a Bose gas consisting of confined weakly interacting particles is described by a mean-field macroscopic wave function \(\Psi \). The wave function of the condensate behaves like a complex order parameter whose absolute value and phase contains all relevant information as regards the Bose–Einstein condensate system, and satisfies a nonlinear Schrödinger equation, called the Gross–Pitaevskii equation [100, 101].
Hence, gravitationally confined Bose–Einstein condensate dark matter halos are described by the coupled Gross–Pitaevskii and Poisson equations for the condensate wave function \(\Psi \), with a quartic nonlinear term, given by [70,71,72,73]
where \(U_{0}=4\pi \hbar ^{2}a/m\), a is the coherent scattering length (defined as the zero-energy limit of the scattering amplitude \(f_{scat}\)), m is the mass of the condensate particle, and \(V_{ext}\) is the external potential. In the following we assume that the exterior potential \(V_{ext}( \vec {r},t)\) is the gravitational potential \(V_{grav}\), \(V_{ext}(\vec {r} ,t)=V_{grav}\left( \vec {r},t\right) \equiv \phi \left( \vec {r},t\right) \). For a single component condensate dark matter halo \(\phi \left( \vec {r} ,t\right) \) satisfies the Poisson equation
where \(\rho =mn\left( \vec {r},t\right) =m\left| \Psi \left( \vec {r} ,t\right) \right| ^{2}\) is the mass density inside the Bose–Einstein condensate, \(n\left( \vec {r},t\right) =\left| \Psi \left( \vec {r} ,t\right) \right| ^{2}\) is the particle number density, and G is the gravitational constant, respectively. The probability density \(\left| \Psi \left( \vec {r},t\right) \right| ^{2}\) is normalized according to \( \int _{V}{n\left( \vec {r},t\right) d^{3}{\vec {r}}}=\int _{V}{\left| \Psi \left( \vec {r},t\right) \right| ^{2}d^{3}\vec {r}}=N\), where N is the total particle number in the dark matter halo, which can be obtained by integrating the norm of the wave function over the entire volume V of the Bose–Einstein condensate.
The time-dependent Gross–Pitaevski equation (3) can be derived from the action principle \(\delta \int _{t_{1}}^{t_{2}}L\mathrm{d}t=0\), where the Lagrangian L is given by [177]
where \(E=\int \varepsilon \mathrm{d}V\) is the total energy, with the energy density \( \varepsilon \) given by
If one multiplies Eq. (3) by \(\Psi ^{*}\) and subtracts the complex conjugate of the resulting equation, one arrives at the equation
Equation (7) has the form of a continuity equation for the particle density, and can be written as a continuity equation,
where the momentum \(\vec {j}\) of the condensate is defined by
where \(\vec {v}\) is the condensate velocity. By representing the wave function as [70,71,72,73]
where \(S \left( \vec {r},t\right) \) is the phase of the wave function, we obtain
which gives
and
respectively.
By substituting the wave function (10) into the Gross–Pitaevskii equation (3), it follows that it can be decomposed into two independent equations, the continuity equation (8), and the Hamilton–Jacobi equation
By taking the gradient of the above equation we obtain
where \(p=u_0\rho ^2\) is the quantum pressure, with \(u_0=2\pi \hbar ^2a/m^3\), while the last term in Eq. (15) is the quantum force, derived from the quantum potential \(V_Q=-\left( \hbar ^2/2m\right) \nabla ^2 \sqrt{\rho }/\sqrt{ \rho }\). By taking into account the mathematical identity
we can rewrite the Euler equation (15) as
The integration of Eq. (8) over the volume V of the condensate, using the Gauss theorem, leads immediately to the equation of the particle number conservation, which can be formulated as
From Eq. (18) it follows that the time variation of the particle number can be due only to the loss or gain of the dark matter particles moving in or out of the condensate through the surface S that encompasses the total volume V. For a static condensate, \(\vec {v}\equiv 0\), and \(\rho (R)\equiv 0 \), where R is the radius of the condensate, a condition which implies that the particle flux \(\vec {j}(R)=\rho (R)\vec {v}\equiv 0\). Hence, from Eq. (18), it follows that the total particle number in the Bose–Einstein condensate dark matter halo at zero temperature is a constant, \(N=\mathrm {constant}\).
For superfluid for which the phase of the wave function is nonsingular, the continuity and Euler Eqs. (8) and (17) represent a potential (irrotational) flow, since the condition \( \nabla \times \vec {v}=0\) is always satisfied, due to the definition (13) of the fluid velocity.
The vorticity can be present in a Bose–Einstein condensate due to the phase singularity lines [178,179,180]. Since the phase of the wave function is defined within a factor of \(2\pi \) only, Eq. (13), defining the condensate velocity, implies that the circulation of the velocity field along a closed contour must be quantized in units of \(\hbar /m\), according to the rule [178,179,180]
where n, called the topological charge of the flow, is an integer number. It also represents the winding number of the phase of the wave function along the contour. To obtain a non-zero circulation, the contour must winds around a line of zero density, along which the phase, as well as the velocity field, are no longer defined. The nucleation of the quantized vortices is a powerful experimental evidence for the existence of the macroscopic wave function describing the Bose–Einstein condensate. In laboratory experiments the observation of the quantized vortices is quite difficult due to the smallness of the size of the vortex core. This size is of the order of the so-called healing length [72]
where \(v_s\) is the velocity of the sound in the condensate (for \(\mathrm {He}^4\), the healing length is of the order of a few angstroms).
In the case of the presence in the condensate of a sufficiently large number of vortices we can write [178,179,180]
where \(\vec {\Omega }\) is the macroscopic angular velocity of the condensate, given by
where \(n_V\) is the areal vortex number density, defined as \(n_V = N_V /A_{\perp }\), and obtained by assuming that the singular velocity fields of the vortices are distributed uniformly in the plane of rotation with area \(A_{\perp }\). As we move away from the vortex, the velocity slowly decreases. If we move towards the vortices then the superfluid density tends to zero.
This approximation is called the approximation of the distributed vorticity, and it has been used very successfully to describe the dynamics of Bose–Einstein condensates containing vortex lattices. In the distributed vorticity approximation we introduce a rotational component in the velocity field of the condensate, so that we can write [178,179,180]
where \(\vec {v}_I\) represents the irrotational component, while \(\vec {v}_R = \vec {\Omega }\times \vec {r}\).
3 The Jeans instability for turbulent Bose–Einstein condensate dark matter halos
To study the astrophysical and cosmological implications of the presence of vortex turbulence in the condensate Bose–Einstein dark matter, and its impact on structure formation, we assume that as a result of an external/internal perturbation the Bose–Einstein condensate dark matter structure becomes unstable and evolves in time like a non-relativistic, dissipationless fluid. The dynamical evolution of the condensed dark matter halo is described by the continuity equation, the hydrodynamical Euler equation and the Poisson equation, respectively, which can be written as
where \(\vec {g}=-\nabla \phi \) is the gravitational acceleration. We take as the initial (unperturbed) state of the condensed dark matter the state characterized by the absence of the “real” gravitational interactions, \(\vec { g}=\vec {g}_{0}=0\), of the hydrodynamical flow, \(\vec {v}=\vec {v}_{0}=0\), and by constant values of the density and pressure, \(\rho =\rho _{0}\), \(p=p_{0}\) , respectively. Moreover, we assume an initial rotation of the dark matter cloud, so that \(\vec {\Omega }(0)=\vec {\Omega }_{0}\ne 0\). The instability in the dark matter halo results in the appearance of the gravitational interaction in the system, and of the small perturbations of the hydrodynamical quantities, which in the first order linear approximation can be represented as
where we assume \(-1 \ll \delta \rho /\rho _{0} \ll 1\), \(-1 \ll \delta p/p_{0} \ll 1\), \( \left| \delta \vec {g}\right| /\left| \vec {g}_{0}\right| \ll 1\), and \(\left| \delta \vec {\Omega }\right| /\left| \vec {\Omega }_{0}\right| \ll 1\), respectively. Therefore in the first order linear approximation Eqs. (25) and (26) take the form
where we have introduced the adiabatic speed of sound \(v_{s}\) in the unperturbed dark matter fluid, defined as
To obtain the first of the equations in (30) we have taken the variation of Eq. (28) as follows: \(\nabla \times \left( v_{0}+\delta \vec {v}\right) =\nabla \times \delta \vec {v}=2\delta \vec {\Omega }\), \(\delta \left| \vec {\Omega }\right| =\left( \pi \hbar /m\right) n_{V}\left( \delta n_{V}/n_{V}\right) =-\left| \vec {\Omega }\right| _{0}\delta \rho /\rho _{0}\), where we have assumed that \(\delta n_{V}/n_{V}=\delta \rho _{V}/\rho _{V}=-\delta \rho /\rho _{0}\), that is, the relative variation of the condensate areal density \(\rho _{V}=mn_{V}\) is inversely proportional to the variation of the density of the condensate normalized with respect to the initial density (the higher the mass density of the vortices, the lower the mass density of ordinary matter in the condensate).
After taking the partial derivative with respect to the time of the continuity equation (28), and applying the \(\nabla \) operator to Eq. ( 29), we obtain the propagation equation of the density perturbations in the Bose–Einstein condensate dark matter fluid as
To obtain Eq. (32) we have also used the mathematical identity \(\nabla \cdot \left( \delta \vec {v}\times \vec {\Omega }_0\right) =\vec {\Omega }_0\cdot \left( \nabla \times \delta \vec {v}\right) -\delta \vec {v}\cdot \left( \nabla \times \vec {\Omega }_0\right) =\vec {\Omega }_0\cdot \left( \nabla \times \delta \vec {v}\right) \).
We look now for a solution of Eq. (32) of the form \(\delta \rho =\sum A\left( \omega ,\left| \vec {k}\right| \right) \exp \left[ i\left( \omega t-\vec {k}\cdot \vec {r}\right) \right] \). Hence after substitution into the equation of this representation of the density variation we obtain for each component \(\omega \) the following dispersion relation:
The Jeans wave number \(\left| \vec {k}\right| _{J}\) corresponds to the vanishing of the eigenfrequency \(\omega \), and it is given as a solution of the algebraic equation
Hence for \(\vec {k}_{J}\) we find
where we have introduced the healing length of the condensate dark matter halo as defined by Eq. (20).
From the dispersion equation, rewritten as
it follows that, for \(\left| \vec {k}\right| <\left| \vec {k} \right| _{J}\), the angular frequency \(\omega \) becomes imaginary. This situation corresponds to an instability of the Bose–Einstein condensate dark matter fluid – \(\delta \rho \) can either exponentially increase or decrease, thus leading to a gravitational rarefaction (or condensation) in the dark matter halo. Hence, for \(\left| \vec {k}\right| <\left| \vec {k} \right| _{J}\), \(\omega \propto \pm v_{s}\sqrt{\vec {k}^{2}-\vec {k}_{J}^{2} }=i\mathrm {Im}\omega \), and therefore \(\delta \rho \propto \exp \left[ \pm \left| \mathrm {Im}\omega \right| t\right] \). When the mass of the Bose–Einstein condensate dark matter halo is greater than the mass of a sphere with radius \(R_{J}=2\pi /\left| \vec {k}\right| _{J}\), a gravitational instability occurs, and the dark matter cloud of particles would collapse. The critical mass delimitating the two phases is the Jeans mass \(M_{J}=\left( 4\pi /3\right) \left( 2\pi /\left| \vec {k}\right| _{J}\right) ^{3}\rho _{0}\). For the Bose Einstein condensate dark matter halos in the presence of rotation and vortices, the Jeans radius is given by
while for the Jeans mass we obtain
3.1 Jeans stability of the nonrotating Bose–Einstein condensate matter halos
We consider first the case of the collapse of the very slowly rotating condensate dark matter halos, having
Hence in this approximation the terms containing \(\left| \vec {\Omega } ^{2}\right| \) can be safely neglected in the expressions of the Jeans wave number, radius and mass. Therefore for the Jeans wave number of the slowly rotating/nonrotating Bose Einstein condensate dark matter halo we find the expression
If the condition
or, equivalently,
is satisfied, by power expanding the square root we obtain
In the opposite limit \(\left( 4\pi G\hbar ^2/m^2v_s^4\right) \rho _0 \gg 1\), or
we obtain
The effective radius \(R_{J}\) of the Bose–Einstein condensate dark matter configuration at the onset of the gravitational instability is given by
and it has the limiting values
and
respectively. The Jeans mass of the static Bose–Einstein condensate dark matter halo is given by
For \(\rho _{0} \gg \rho _{cr}\), for the Jeans mass we obtain the approximate expression
For \(\rho _0 \ll \rho _{cr}\) we find
The maximum mass of the high density astrophysical objects, like white dwarfs and neutron stars, described by polytropic equations of state, was derived by Landau and Chandrasekhar, and it can be approximated by the Chandrasekhar mass [181, 182],
where by \(m_{B}\) we have denoted the mass of the particles that give the most important contribution to the total stellar mass (protons and neutrons in the case of the white dwarfs and neutron stars, respectively) [181, 182]. Hence, the maximum mass of a degenerate star is fully determined by fundamental physical constants only, with the possible exception of some numerical factors that depend on the chemical composition of the star.
Interestingly enough, the Jeans mass for Bose–Einstein condensate dark matter halos given by Eq. (50) can also be written in a form similar to the Chandrasekhar maximum mass, if we associate to the dark matter particles an effective mass \(m_{eff}\) defined as
so that
For the adopted values of the physical parameters of the dark matter halos the numerical value of the effective mass is of the order of \(m_{eff}\approx 4.52\times 10^{-29}~\hbox {g}\).
On the other hand, one could also ask the question if Bose–Einstein condensate dark matter could form astrophysical objects and structures with the limiting mass given by the Chandrasekhar mass as given by Eq. (52). For the adopted mass of the dark matter particle \(m=1 \;\mathrm { meV}=1.78\times 10^{-36}~\hbox {g}\), the Chandrasekhar limit gives a mass of the order of \(M_{Ch}=1.62\times 10^{34}M_{\odot }=3.25\times 10^{57}~\hbox {g}\), which exceeds by three orders of magnitude the total mass of the ordinary matter in the Universe, \(4.5\times 10^{54}~\hbox {g}\) [?]. Therefore, it follows that the Chandrasekhar mass limit cannot lead to realistic descriptions of the physical properties of condensate dark matter clouds composed of particles having masses of the order of the mass values assumed for condensate dark matter particles.
3.2 The effects of the rotation
Generally, in the slow rotation limit when the factor \(\vec {\Omega } _{0}^{2}/\pi G\rho _{0}\) is still small, or of the order of unity, the rotation modifies the Jeans parameters (Jeans wavelength, radius and mass, respectively), by a factor of \(1+\chi \). Hence, if, for example, the condition
holds, then we immediately obtain
and
respectively. However, with the increase of the initial rotational velocity of the Bose–Einstein condensed dark matter halo, the effects of the rotation become more and more important. For a rotational angular velocity of \( \left| \vec {\Omega }_{0}\right| =10^{-14}\) s\(^{-1}\), we obtain \(\chi = \vec {\Omega }_{0}^{2}/\pi G\rho _{0}=477.47\), while for \(\left| \vec { \Omega }_{0}\right| =10^{-12}\) s\(^{-1}\) we have \(\chi =4.\,77\times 10^{6}\). Hence for the astrophysical and physical description of dark matter halos rotating with such initial angular velocities the effect of the rotation must be taken into account. Hence for rapidly rotating dark matter condensed clouds the Jeans wavelength becomes
or, equivalently,
For the adopted values of the physical and astrophysical quantities the parameter \(m^{4}\vec {\Omega }_{0}^{2}/4\pi ^{2}\hbar ^{2}a^{2}\rho _{0}^{2}\) has generally small values, much smaller than one. Therefore we can expand the square root into power series, and in the first approximation we obtain
Hence the Jeans radius and the Jeans mass of rapidly rotating Bose–Einstein condensate dark matter halos can be obtained:
and
respectively. Interestingly enough, in the case of the rotation dominated Bose–Einstein condensate dark matter halos, their physical and astrophysical properties are independent of the gravitational constant G, and they are fully determined by the fundamental quantum parameters m and a, characterizing the condensate, as well as by the angular velocity of the halo \(\left| \vec {\Omega }_{0}\right| \).
3.3 The Thomas–Fermi approximation
Finally, as a last step in our general analysis of the properties of the Bose–Einstein condensate dark matter halos we introduce the Thomas–Fermi approximation for the hydrodynamical description of the condensate. In order to perform our analysis, we decompose the total energy, \(E_{tot}\), into kinetic, interaction, quantum and gravitational contributions [70,71,72,73],
where
The kinetic energy is determined by the velocity field of the dark matter fluid. The interaction energy is related to the interaction of the particles in the condensate. The quantum energy is determined by square of the gradient of the square root of the density of the condensate, while the gravitational energy has its origin from the external potential of the field, acting as a trapping potential.
In the Thomas–Fermi approximation, we neglect in the total anergy balance the kinetic energy term \(-\left( \hbar ^{2}/2m\right) \Delta \) of the condensate particles. To obtain the conditions of the validity of the Thomas–Fermi approximation we consider a system composed of N bosons in a volume V, extended over a radius R, in the presence of a confining gravitational potential. The total mass of the system is denoted by M. Moreover, we assume that all bosons are in the same quantum state. The total energy \(E_{tot}\) of the system is given by \(E=E_{kin}+E_{int}+E_{grav}\). For a single particle the kinetic energy can be approximated as \(\hbar ^2/2mR^2\) [72], and hence the total kinetic energy of the system can be obtained: \(E_{kin}=N\hbar ^2/2mR^2\). The interaction energy is given by \( E_{int}=(1/2) \left( N^2/V\right) mg\) [72], while the gravitational potential energy can be approximated as \(E_{grav}=-\alpha GM^2/R\), where \(\alpha \) is a constant. For the \(n=1\) polytropic equation of state \(\alpha =3/4\) [103]. Therefore for the total energy of the bosonic system in a gravitational field we obtain the expression
If the condition
is satisfied, then the interaction energy is much larger than the kinetic energy, \(E_{int} \gg E_{kin}\). In order to check the validity of the condition in an astrophysical setting, we consider a galactic condensate of mass \( M=10^{10}M_{\odot }=2\times 10^{43}~\hbox {g}\). Then the number of the dark matter particles is of the order of \(N=M/m=1.12\times 10^{79}\) particles. If the radius of the condensate is \(R=10\) \(\hbox {kpc} = 3\times 10^{22}~\hbox {cm}\), then the quantity \(3Na/R=1.12\times 10^{41}\), a number that is obviously much greater than one, \(3Na/R \gg 1\). Hence in galactic Bose–Einstein condensate dark matter halos the contribution to the total energy of the kinetic energy of the particles can be safely neglected when compared to the interaction energy of the bosonic fluid. Therefore, in the case of bosonic systems consisting of a very large number of particles, the Thomas–Fermi approximation gives an excellent description of the physical and astrophysical properties of the condensate, corresponding to a precision level that can be recognized as exact.
On the other hand, the physical length scales of the order of \(R\approx \sqrt{m/4\pi \rho a}\), where \(\rho \) is the mean dark matter density, the Thomas–Fermi approximation is not valid anymore. For \(\rho =10^{-24}\; \mathrm {g/cm}^3\), we obtain \(R\approx 377.65~\hbox {cm}\), a length scale that is insignificant from the point of view of the galactic dark matter distribution. For the gravitational energy of the Bose–Einstein condensate dark matter halo we obtain the value \(E_{grav}=8.89\times 10^{56}\) ergs, why for the considered numerical values of the parameters of the dark matter halos the interaction energy has the value \(E_{int}=1.35\times 10^{56}\) ergs. Hence in gravitationally trapped galactic size condensates the interaction energy is of the same order of magnitude as the gravitational energy of the bosons. However, it is important to point out that \( E_{grav}>E_{int}\), a relation that shows that the dark matter halo is trapped by its gravitational energy.
Hence in the Thomas–Fermi approximation the total energy of the condensate dark matter halo is given by
The equilibrium radius corresponding to the minimum of the total energy is given by the solution of the algebraic equation
given by
which, except some numerical factors, coincides with Eq. (47), giving the Jeans radius of the condensate dark matter halo.
Therefore in our subsequent analysis of the gravitational collapse of Bose–Einstein condensate dark matter halos we will neglect, with a very good approximation, the kinetic energy term in the Gross–Pitaevskii equation (3), and, consequently, the quantum force, derived from the quantum potential, in the hydrodynamic description of the dynamics of the condensate. In the Thomas–Fermi approximation the chemical potential of the static condensate is given by
4 Time evolution of Bose–Einstein condensate dark matter halos
We consider now a Bose–Einstein condensate dark matter halo falling inward from an initial rest state. The halo is only under the effects of its own self-gravity. The basic equations describing the dynamical evolution of the condensate dark matter halo are then the continuity equation, the Euler equation, and the Poisson equation, which in spherical symmetry are given by
where in the Euler equation we have used the polytropic equation of state \( p=u_0\rho ^2\) of the condensate. The last term in Eq. (76) takes into account the effects of the rotation, and it has been obtained as follows. If \(\theta \) is the colatitude of a given point in the condensate with respect to the rotation axis, the centrifugal acceleration of the former is \(\Omega ^2 r\sin \theta \). Its radial component is \(\Omega ^2 r\sin ^2\theta \). In order to preserve the spherical symmetry of the dark matter halo we will neglect all the other components of the centrifugal acceleration, and take into account the mean value of \(\Omega ^2 r\sin ^2\theta \) on a sphere of radius r. Consequently we obtain for the centrifugal acceleration the expression \(2\Omega ^2r/3\) [183].
The Poisson equation (77) can be immediately integrated to give
where M(r, t), the total mass of the dark matter halo within radius r, is defined as
We multiply now the continuity equation (75) by \(4\pi r^2\). After using the relation \(4\pi r^2\rho =\partial M/\partial r\), and integrating with respect to r, we obtain
By using the expression of the gradient of the gravitational potential as given by Eq. (78), the Euler equation (76) becomes
Equations (80) and (81) represent a system of two coupled nonlinear partial differential equations whose solutions for v and M fully determine the dynamical evolution of the collapsing Bose–Einstein condensate dark matter halo. This system of equations can be reduced to a single equation describing the dynamical evolution of the collapse. From Eq. (80) we obtain
Substituting the above expression of the velocity into Eq. (81), and using the definition of the density in terms of the mass, we obtain the mass equation describing the time evolution of the Bose–Einstein condensate dark matter halo as
4.1 The stationary solution
We consider first the case of the rotating stationary (static) Bose–Einstein condensate dark matter halos. The stationary case corresponds to \(\vec {v} \equiv 0\), \(M=M_0(r)\), and \(\Omega =\mathrm {constant}\), respectively. In this situation the mass evolution equation (83) takes the form
where we have denoted
and
respectively. Eq. (84) has the general solution
where \(c_1\) and \(c_2\) are arbitrary constants of integration. The boundary condition
gives \(c_2\)=0, and therefore for the mass of the stationary Bose–Einstein condensate dark matter halo we obtain
For the density distribution of the rotating condensate we obtain
The condition
where \(\rho _c\) is the central density of the condensate, gives for the integration constant \(c_1\) the expression
Hence we finally obtain for the density and mass distribution of the rotating Bose–Einstein condensate dark matter halos the expressions
and
respectively. The radius \(R_0\) of the stationary condensate is determined from the condition \(\rho \left( R_0\right) =0\), and it can be obtained as a solution of the equation
where we have denoted
By taking into account that the left hand side of the above equation can be expanded in Taylor series as
we obtain for the determination of the radius of the rotating condensate dark matter halo the algebraic equation
In the first order of approximation we obtain for the stationary dark matter halo the approximate expression
In the case of the static condensate with \(\Omega \equiv 0\), the radius \(R_S\) of the dark matter halo is obtained exactly as
Then the radius of the rotating, stationary condensate dark matter halo can also be written in the form
The total mass of the rotating condensate dark matter halo is obtained:
In the case of the static condensate \(\sqrt{a_0}R_S=\pi \), and for the total mass \(M_S\) of the nonrotating dark matter halo we find
or
In the first order approximation the mass of the rotating condensate can be expressed in terms of the static radius as
4.2 Collapsing Bose–Einstein condensate dark matter halos
Obtaining some analytical or semi-analytical solutions of the equations describing the time evolution of Bose–Einstein condensate dark matter halos would allow one to construct a clearer picture of the relationship between the input physics and the behavior of the system, also making possible to understand astrophysical effects that are more difficult to understand with the extensive use of numerical methods for solving the hydrodynamical evolution equations. One of the powerful mathematical approaches for the study of the collapse processes in astrophysical phenomena is based on the idea of self-similarity, which consists in the rescaling of the radial coordinate r as \(r\rightarrow \xi =r/\alpha (t)\), where \(\alpha (t)\) is a function only dependent on time, and to assume that all the other physical parameters can be expressed as functions of \(\xi \) and of some function of time, so that an arbitrary physical quantity \(\Phi (r,t)\) can be written as \( \Phi (r,t)=\beta (t)\phi (\xi )\). An interesting consequence of the self-similar (homologous) evolution is that the initial density and mass profiles of the collapsing systems do not change. From a mathematical point of view after introducing the appropriately chosen self-similarity transformations, the system of nonlinear partial differential equations (80) and (81) can be reduced in many cases to a system of ordinary nonlinear differential equations. Some astrophysically relevant self-similar solutions describe the gravitational collapse of isothermal spheres or of polytropic spheres. It would then be interesting to consider self-similar solutions of the hydrodynamic equations describing the time evolution of Bose–Einstein condensate Dark matter halos. Unfortunately, the hydrodynamic equations describing the evolution of a polytropic gas with equation of state \(p\propto \rho ^2\) do not admit self-similar or homologous solutions (for a proof of this results see “Appendix A”. The main reason is that after introducing the self-similar variables in the standard way, the explicit time dependence of the equations cannot be eliminated for any choice of the time similarity functions.
4.2.1 The evolution equations
However, the dynamic evolution equation of the mass of the Bose–Einstein condensate dark matter halos, described by a polytropic equation of state with \(n=1\), and given by Eq. (83), does admit a separable, semi-analytical solution, which can be obtained under the assumption that the mass of the condensate can be represented as
where f(t) and m(r) are functions depending on the time and the radial coordinate r only. Then the velocity of the dark matter halo can be immediately obtained from Eq. (82) as
For the acceleration of the fluid we find
Then the mass equation (83) can be written as
The explicit time dependence in Eq. (109) can be removed, and the variables can be separated, if the function f(t) and the angular velocity \( \Omega (t)\) satisfy the conditions
where \(\alpha _{0}\), \(\beta _{0}\) and \(\omega _{0}\) are dimensional constants. Eq. (111) can be integrated immediately to give
where \(t_{0}\) is an arbitrary constant of integration. Then Eq. (110) reduces to
giving \(\alpha _{0}=-2/\beta _{0}^{2}\). Hence, the time dependence in the mass evolution equation cancels out, and for the radial mass distribution of the time evolving dark matter halo we obtain the equation
In the above equation \(\beta _{0}\) has the physical unit of second, while \( \omega _{0}\) has the units 1 / s. The function f(t) is dimensionless. Hence once the solution of Eq. (115) is known, the evolution of the physical parameters of the collapsing/expanding Bose–Einstein dark matter halos are given by
We rescale the radial coordinate r, the mass m(r), the density \(\rho (r,t)\) and the velocity v(r, t) according to the transformations
where \(R_{S}=\sqrt{\pi u_{0}/2G}\) and \(M_{S}=\left( 4/\pi \right) R_{S}^{3}\;\rho _{c}\) are the radius and the mass of the static condensate, while \(\eta \) and \(m_{0}(\eta )\) are the dimensionless radial coordinate and the dimensionless mass function, respectively. We denote \(\gamma _{0}^{2}=\omega _{0}^{2}/6\pi ^{2}G\rho _{c}\). Moreover, we fix in the following the constant \(\beta _{0}^{2}\) as
Hence for the physical parameters of the collapsing/expanding Bose–Einstein condensate dark matter halo we obtain the expressions
The dimensionless spatial density distribution of the density \(\theta \left( \eta \right) \) and velocity \(V(\eta )\) of the Bose–Einstein condensate dark matter halo can be obtained:
Then, in the new dimensionless variables, Eq. (115), describing the mass profile of the evolving dark matter halo, takes the form
or, equivalently,
For the central density of the condensate at the beginning of the contracting/expanding phase we obtain \(\rho (0,0)=\rho _c=\theta (0)/4\pi Gt_0^2\), which gives \(\theta (0)=\theta _0=4\pi G\rho _ct_0^2\).
4.3 The first order approximation
In the zeroth order approximation, we can neglect the right hand side in Eq. (120), which thus takes the form
and has the general solution
where \(C_1\) and \(C_2\) are arbitrary constants of integration. The boundary condition \(m_0^{(0)}(0)=0\) gives \(C_2=0\). For the dimensionless density we obtain
The boundary condition \(\theta ^{(0)}(0)=\theta _0\) gives \(C_1=\sqrt{\pi /2}\left( \theta _0-3\gamma _0^2\right) \). Hence we obtain the zeroth order solution of Eq. ( 120) as
The density is given by
To obtain the solution of Eq. (120) in the first order of approximation we substitute in its right hand side \(m(\eta )\) by \(m_0^{(0)}(\eta )\), thus obtaining
Hence in this approximation Eq. (120) becomes
with the general solution given by
where \(c_{3}\) and \(c_{4}\) are arbitrary constants of integration. The boundary condition \(m_{0}^{(1)}(0 )=0\) gives \(C_4=0\), while the density profile of the Bose–Einstein condensate dark matter halo is obtained:
By imposing the boundary condition \(\theta ^{(1)}(0)=1\) we obtain \(C_3= \sqrt{\pi /2} \left( 9576 \gamma _0^4-5139 \gamma _0^2+619\right) /45\). Hence for the spatial mass and density profiles of the dynamically evolving Bose–Einstein condensate dark matter halos we obtain, in the first order approximation, the expressions
and
respectively. In the first order approximation the spatial velocity profile of the evolving Bose–Einstein condensate dark matter halo can be obtained: \(V^{(1)}(\eta )=m_{0}^{(1)}(\eta )/\mathrm{d}m_{0}^{(1)}(\eta )/\mathrm{d}\eta \).
The above results simplify considerably in the case of the nonrotating condensate dark matter halos, with \(\gamma _0^2=0\). Hence, for a radially expanding/contracting Bose–Einstein condensate confined by its own gravitational field we obtain
In this approximation the mass and density are finite at the origin \(\eta =0\) , but the velocity diverges at the center of the contracting condensate dark matter halo.
4.4 Exact numerical profiles
Equation (121) can be reformulated mathematically as a first order dynamical system given by
The system of equations (136) and (137) must be integrated with the initial conditions \(m_0(0)=0\) and \(u(0)=0\), respectively. As for the dimensionless density \(\theta \) and velocity \(V(\eta )\) of the Bose–Einstein condensate dark matter they can be represented as
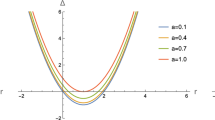
Variation of the dimensionless density profile \(\theta (\eta )\) as a function of the dimensional radial coordinate \(\eta \) of a collapsing rotating Bose–Einstein condensate dark matter halo for different values of the parameter \(\gamma _0\): static case with \(\gamma _0=0\), (solid curve), and dynamical evolution with \(\gamma _0=0\) (dotted curve), \(\gamma _0=0.25\) (short dashed curve), \(\gamma _0=0.50\) (dashed curve), \(\gamma _0=0.75\) (long dashed curve), and \(\gamma _0=0.90\) (long dashed curve), respectively. To numerically integrate the system of equations (136) and (137) we have used the initial conditions \(m_0\left( \eta _0\right) =\left( 4/\pi \right) \eta _0^3\) and \(u\left( \eta _0\right) =m_0'\left( \eta _0\right) =\left( 12/\pi \right) \eta _0^2\), with \(\eta _0=10^{-3}\)
Variation of the dimensionless mass profile \(m_0(\eta )\) as a function of the dimensional radial coordinate \(\eta \) of a collapsing rotating Bose–Einstein condensate dark matter halo for different values of the parameter \(\gamma _0\): static case with \(\gamma _0=0\), (solid curve), and dynamical evolution with \(\gamma _0=0\) (dotted curve), \(\gamma _0=0.25\) (short dashed curve), \(\gamma _0=0.50\) (dashed curve), \(\gamma _0=0.75\) (long dashed curve), and \(\gamma _0=0.90\) (long dashed curve), respectively. To numerically integrate the system of equations (136) and (137) we have used the initial conditions \(m_0\left( \eta _0\right) =\left( 4/\pi \right) \eta _0^3\) and \(u\left( \eta _0\right) =m_0'\left( \eta _0\right) =\left( 12/\pi \right) \eta _0^2\), with \(\eta _0=10^{-3}\)
Variation of the dimensionless velocity profile \(V(\eta )\) as a function of the dimensional radial coordinate \(\eta \) of a collapsing rotating Bose–Einstein condensate dark matter halo for different values of the parameter \(\gamma _0\) during its dynamical evolution for \(\gamma _0=0\) (solid curve), \(\gamma _0=0.25\) (dotted curve), \(\gamma _0=0.50\) (short dashed curve), \(\gamma _0=0.75\) (dashed curve), and \(\gamma _0=0.90\) (long dashed curve), respectively. To numerically integrate the system of equations (136) and (137) we have used the initial conditions \(m_0\left( \eta _0\right) =\left( 4/\pi \right) \eta _0^3\) and \(u\left( \eta _0\right) =m_0'\left( \eta _0\right) =\left( 12/\pi \right) \eta _0^2\), with \(\eta _0=10^{-3}\)
The variations of the dimensionless spatial density, mass and velocity profiles of the contracting/expanding Bose–Einstein condensate dark matter halos are represented in Figs. 1, 2 and 3, respectively. To numerically integrate the system of Eqs. (136) and (137) we have used the initial conditions \(m_0\left( \eta _0\right) =\left( 4/\pi \right) \eta _0^3\) and \(m_0'\left( \eta _0\right) =\left( 12/\pi \right) \eta _0^2\), with \(\eta _0=10^{-3}\). The spatial density profile of the dark matter halo during its dynamical evolution is represented in Fig. 1. The static solution in the absence of rotation is also represented, as the lower curve in the figure. In all cases the density profiles are described by monotonically decreasing functions of the dimensionless radius \(\eta \). The effects of the rotation of the halo can be clearly seen, and they lead to a significant impact on the density profiles. Near the origin, for \(\eta \) in the range \(0<\eta <0.25\), the density profiles are basically indistinguishable, but for larger values of \(\eta \) the effects of the rotation modify the overall density distribution. The impact of the rotation on the spatial mass distribution of the collapsing/expanding dark matter halos is presented in Fig. 2. The mass profiles are characterized by linearly increasing functions of \(\eta \). For \(\eta \) in the range \(0<\eta <1.1\), the mass distribution of the rotating collapsing/expanding condensate dark matter halo essentially coincides with the static mass distribution. The effects of the rotation become important for large values of the radius, once we are approaching the lower density regions at the outer boundary of the halo. The rotation can lead to a significant increase in the total mass of the halo, the increase being of the order of 20% for \(\gamma _0=0.9\).
The spatial velocity profiles of the dynamically evolving condensate dark matter halos are presented in Fig. 3. Similarly to the mass profile, the spatial distribution of the velocity is a monotonically increasing function of \(\eta \). For \(\eta \) in the range \(0<\eta <1.1\), the velocity profiles are (almost) identical, and the effects of rotation are extremely small. For small rotation velocities the velocity can be well approximated by a linear function of \(\eta \), so that \(V(\eta )\propto \eta \). However, for larger values of the dimensionless radial coordinate, the effects of the rotation become important at large distances from the halo center, and the velocity – radial coordinate relations is not linear anymore.
5 Discussions and final remarks
In the present paper we have investigated some of the possible physical and astrophysical consequences of the instabilities in a Bose–Einstein condensate dark matter halo. We have considered two distinct, but interrelated topics, the Jeans stability of condensate dark matter clouds, and the dynamics of the gravitational collapse that follows once the real size of the gravitationally confined system exceeds the Jeans scales.
The Bose–Einstein condensates are generally described by the Gross–Pitaevskii equation, which gives the ground state of a quantum system of identical bosons, and which is obtained by using the Hartree–Fock approximation and the pseudopotential interaction model. In the present approach we assume that dark matter is a Bose–Einstein condensate of a gas of bosons, which are in the same quantum state, and thus can be described by the same wavefunction. Hence, we interpret the galactic dark matter halos as huge quantum systems, whose properties can be described by a single wave function. To simplify our formalism we also adopt the assumption that dark matter is at zero temperature. Of course the presence of the excitations and of non-zero temperature effects may have important effects on the properties of condensate dark matter.
An important mathematical and physical property of the Gross–Pitaevskii equation is that, similarly to the standard Schrödinger equation, it admits a hydrodynamical representation, easily obtainable after representing the wave function in the Madelung variables. It turns out that in the hydrodynamic representation the Bose–Einstein condensates can be described as a perfect fluid, and its properties are characterized by the local density and local velocity only. The fluid satisfies a continuity and an Euler type equations, which contains the contributions of the quantum pressure \(p=u_0\rho ^2\), generated by the self-interaction of the field, and of the quantum potential \(V_Q\), both of these terms being essentially quantum mechanical in their origin. The velocity \(\vec {v}\) of the quantum fluid is related to the phase S of the wave function by the relation \(\vec { v}=\left( \hbar /m\right) \nabla S\), and the flow of the condensate fluid is rotationless, as long as S contains no singularities, as, for example, in a vortex. In the present approach we have also allowed the presence of vortices in the dark matter halo. The simplest method to create vortices in a condensate is through their rotation. Hence, under the natural assumption that Bose–Einstein condensate dark matter halos are rotating, one must also take into account the existence of vortices in the system. A Bose–Einstein condensate dark matter halo can rotate only due to the existence of quantized vortex lines. When the rotation frequency \(\Omega \) of the halo exceeds a critical value \(\Omega _c\), vortex nucleation occurs. In the present paper we have adopted the simple relation (22) between the angular velocity of the rotating condensate dark matter halos, and their vortex number density, which indicates that the quicker the dark matter halo rotates, the higher the number of vortices. On the other hand in rotating gravitationally trapped Bose–Einstein condensate dark matter halos the nucleation of vortices may also be a result of the instabilities of collective excitations.
In the present manuscript we have used the term turbulence in the sense that it is common in the physics of quantum fluids, meaning the presence in the fluid of quantized vortices [184, 185]. In this nomenclature turbulence is more related to the quantization of vortices than to the lack of viscosity of superfluids. On the other hand the term turbulence may also be interpreted as describing a phase of temporally and spatially disordered fluid motion, characterized by a large number of degrees of freedom interacting essentially nonlinearly [185]. The nonlinear interaction is usually a consequence of the presence of the term \(\left( \vec {v}\cdot \nabla \right) \vec {v}\) in the Euler equation.
The hydrodynamical description of the rotating condensate dark matter halos, confined by their own gravitational fields, opens the possibility of the study of the gravitational perturbations in galactic and extragalactic systems. By assuming some standard initial conditions, the linearization of the hydrodynamic equations describing the flow of the dark matter clouds leads to the dispersion relation (33), which is exact in the sense that it also includes both the effects of the rotation and of the quantum force. In the limit when the rotation and the quantum force effects are neglected, Eq. (33) reduces to the standard form of the Jeans frequency,
and to the Jeans radius \(R_J=\left( \sqrt{\pi /G\rho _0}\right) v_s\). The Jeans radius essentially depends on the speed of sound in the given astrophysical medium, and it is a measure of the linear dimensions of the condensations which will form in the medium on account of the gravitational instability. For matter obeying the ideal gas equation of state \(p=\left( k_B T/m\mu \right) \), where T is the temperature of the gas, \(\mu \) is the mean molecular weight, and \(k_B\) is the Boltzmann constant, we have \(v_s=\sqrt{ k_BT/m\mu }\), and \(R_J=\sqrt{\pi k_BT/G\rho _0m\mu }\). For an ideal gas the Jeans length is proportional to the temperature of the system, and inversely proportional to the density. On the other hand for a Bose–Einstein condensate in the same approximation we obtain \(R_J=\sqrt{4\pi ^2\hbar ^2a/Gm^3}\), and expression that depends only on the fundamental physical characteristics of the dark matter halo (particle mass and scattering length), and on the Planck constant. Hence, for a Bose–Einstein condensate at zero temperature the Jeans radius has an universal expression, independent on the macroscopic properties of the medium.
In the opposite limit of zero speed of sound (or negligible quantum pressure), the dispersion relation takes the form
giving a Jeans wave number given by
and a Jeans radius of the order of
In the absence of rotation, Eqs. (141) and (142) give the Jeans wave number and the Jeans radius corresponding to the Schrö dinger–Poisson model, described by the system of equations [24, 186,187,188,189]
where \(V_{g}\left( \vec {r},t\right) \) is the gravitational potential. The essential difference between the Schrödinger–Poisson and Gross–Pitaevskii–Poisson models of dark matter is that in the former the effect of the particle self-interaction is neglected, which implies that in the Schrödinger–Poisson model there is no quantum pressure term p, and the speed of sound in the dark matter halo is zero. By assuming a zero rotational velocity, for the Jeans radius and the Jeans mass of the dark matter halo in the Schrödinger–Poisson model we obtain the relations
and
respectively. In the Schrödinger–Poisson model all the physical and astrophysical properties of the dark matter halos are fixed by a single parameter, the mass of the dark matter particle. In order to obtain realistic astrophysical results applicable to the galactic or extragalactic scales very small particle masses are required, a problem the Bose–Einstein condensate dark matter model does not have.
We have also discussed the effects of the rotation on the condensate dark matter halos. In realistic astrophysical situations the condition \(\vec { \Omega }^{2}/\pi G\rho _{0}\gg 1\) may be satisfied. In this case the Jeans wave number is proportional to the angular velocity of the halo, while the Jeans radius and Jeans mass are inversely proportional to \(\left| \vec {\Omega } _{0}\right| \), and \(\left| \vec {\Omega }_{0}\right| ^{3}\), respectively. For large angular velocities the Jeans radius is very small, of the order of \(10^{-2}\) kpc, while the corresponding Jeans mass is of the order of \(90M_{\odot }\). These radius and mass values may correspond to stellar mass black holes, or other types of small compact objects (small in an astrophysical sense). In the case of ordinary baryonic matter the condition of instability for waves propagating perpendicularly to the axis of rotation is \(k_J^2v_s^2<4\pi G\rho _0-4\Omega ^2\) [156].
One constraint on the ratio and scattering length of the dark matter particle can be obtained from the condition \(2GM_{J}/c^{2}R_{J}<1\), requiring that dark matter halos cannot become black holes. This condition is essentially general relativistic, but we may assume that it is also valid in Newtonian mechanics. By adopting for the Jeans radius and mass the expressions (47) and (50), respectively, we obtain the constraint
Once the numerical values of the critical parameters of the condensate dark matter halos are reached, an instability develops in the system. One can interpret, from a simple physical point of view, the collapse of the Bose–Einstein condensate dark matter halos as follows. Once the number of particles N in the galactic halo becomes sufficiently high, so that \(N > N_c\), where \(N_c\) is a critical particle number, the attractive interparticle energy exceeds the quantum pressure, and the dark matter halo begins to collapse. During the collapsing stage, the density of dark matter particles increases in the vicinity of the galactic center.
To study the dynamical evolution of the halo one need to solve the full system of hydrodynamic equations describing the time and space evolution of the Bose–Einstein condensate. In the Thomas–Fermi approximation the basic equations describing the dynamics of the condensate coincide with the continuity and Euler equations of classical hydrodynamics. The effect of the rotation was also included by means of a term, averaged over the angle \(\theta \), proportional to the radial coordinate, and with a time-dependent angular frequency. In order to preserve spherical symmetry we assume that the rotation of the condensate is slow. The effect of the gravitational field is taken into account via the Poisson equation, which relates the gravitational potential of the confined condensate to its density, which is essentially quantum in its nature. After integrating the Poisson equation, the evolution equations can be reduced to a system of two coupled nonlinear partial differential equations, which can subsequently be reduced to a single nonlinear second order partial differential equations for the mass of the condensate M(r, t). For many hydrodynamic flow models in gravitational fields, with matter obeying a polytropic equation of state the equations of motion admit semi-analytical self-similar or homologously collapsing solutions [190,191,192,193,194].
When these solutions are valid scale radial profiles of thermodynamic variables remain time invariant. The homologous solutions are stable against linear nonspherical perturbations, a result which can explains the remarkable stability of the galactic dark matter halos. However, in the case of index \(n=1\) polytropes no self-similar solution does exist, and the solutions of the equations of motion cannot be written in the form \(\Phi (r,t)=f(t)g\left( r/t\right) \) [190,191,192,193,194]. This means that during their evolution the physical quantities describing Bose–Einstein condensate dark matter halos are not scale and time invariant. However, an exact semi-analytical solution of the evolution equations of the Bose–Einstein condensates self-confined by the gravitational field can be obtained by assuming the separability of the mass variable in the for \(M(r,t)=f(t)m(r)\). The function f(t) has the analytical form \(f(t)=\left( t_0\pm t\right) ^{-2}/4\pi ^2 G\rho _c\), where the minus sign corresponds to the collapse of the condensate, while the plus sign describes the expansion of the condensate dark matter halo. As for the mass function m(r), time evolution generates a universal condensate dark matter profile, which in the absence of rotation just slightly modifies the static mass and density profiles. However, once the rotation is taken into account, the mass and density profiles are significantly modified as functions of the angular velocity.
The obtained solution describes both an expanding and a collapsing phase. The expanding phase corresponds to the choice of plus sign in the function f(t), so that \(f(t)=\left( t_0+ t\right) ^{-2}/4\pi ^2 G\rho _c\). The Bose–Einstein condensate disperses in the space, with the local values of the physical parameters decreasing in time. In the large time limit the density as well as the radial and angular velocities tend to zero, and the Bose–Einstein condensate reaches a vacuum state. The minus sign in the function f(t) describes the collapse of the condensate. Both solutions are singular, for the expanding case the singularity occurs at the initial moment \(t=0\) (by a rescaling of the time variable one can remove the constant \(t_0\) from the results, \(t\rightarrow t+t_0\)), while in the case of the gravitational collapse the singularity is reached at the finite time \(t_0\). In order to obtain a rough estimate of \(t_0\), we assume that the mass distribution m(r) during the collapsing phase does not differ much from the stationary one. By series expanding Eq. (94) we obtain \(m(r)\approx M_0(r)\approx \left( 4\pi /3\right) \rho _c r^3\), an expression which allows us to estimate the velocity of the collapsing Bose–Einstein condensate dark matter halos as
At the beginning of the gravitational collapse at \(t=0\), the extension of the condensate cloud is given by its Jeans radius \(R_J\), which we approximate by Eq. (47). Moreover, we assume that the initial velocity of the collapsing boundary can be written as \(v\left( R_J,0\right) =\alpha c\), where \(\alpha \) is a constant. Then for the collapse time \(t_9\) of the condensate halo we obtain
An alternative estimate of the collapse time can be obtained by assuming that at the beginning of the collapse the total mass of the condensate dark matter halo \(M\left( R_J,0\right) =m\left( R_J\right) \) is given by the Jeans mass (50). Then we obtain for the collapse time the simple expression \(t_0\approx 1/2\pi \sqrt{G\rho _c}\).
It is interesting to note that, at least in the first order of approximation, the velocity of the condensate dark matter halo has the mathematical form of the cosmological Hubble law, \(v(t)=H(t)r\), with the Hubble function given by \(H(t)=2/\left( t_0\pm t\right) \). Moreover, as shown by the numerical simulations presented in Fig. 3, for small angular velocities the simple linear proportionality between the dimensionless velocity V and the radial dimensionless coordinate \(\eta \) is valid during the entire phase of the collapsing/expanding evolution.
A large number of cosmological and astrophysical observations, including the behavior of the galactic rotation curves, or the virial mass discrepancy in galaxy clusters points towards the possibility of the existence of dark matter in the Universe. If dark matter is present in the form of bosonic particles, then the possibility that it has the form of a Bose–Einstein condensate is strongly supported by the laws of quantum physics that show that a phase transition to a condensate state must occur, once the temperature reaches its critical value. A major adjustment in our interpretation of the basic principles of astrophysics and cosmology will be required if further observations would confirm this hypothesis. In the present papers we have introduced some basic theoretical tools that could help in the analysis and interpretation of the large scale structure formation in the presence of Bose–Einstein condensate dark matter.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Since this is a theoretical study, no data were generated.]
References
L.E. Strigari, Phys. Rep. 531, 1 (2013)
K.M. Zurek, Phys. Rep. 537, 91 (2014)
S. Courteau et al., Rev. Mod. Phys. 86, 47 (2014)
H. Baer, K.-Y. Choi, J.E. Kim, L. Roszkowski, Phys. Rep. 555, 1 (2015)
T. Aramaki et al., Phys. Rep. 618, 1 (2016)
M.R. Buckley, A.H.G. Peter, Phys. Rep. 761, 1 (2018)
S. Tulin, H.-B. Yu, Phys. Rep. 730, 1 (2018)
V. Rubin, W.K. Thonnard Jr., N. Ford, Astrophys. J. 238, 471 (1980)
M. Persic, P. Salucci, F. Stel, Mon. Not. R. Astron. Soc. 458, 4172 (1996)
J.I. Read, G. Iorio, O. Agertz, F. Fraternali, Mon. Not. R. Astron. Soc. 462, 3628 (2016)
E.V. Karukes, P. Salucci, (2016). arXiv:1609.06903 [astro-ph.GA]
H. Haghi, A.E. Bazkiaei, A. Hasani Zonoozi, P. Kroupa, Mon. Not. R. Astron. Soc. 458, 4172 (2016)
J. Binney, S. Tremaine, Galactic Dynamics (Princeton University Press, Woodstock, Princeton, 2008)
A.V. Kravtsov, S. Borgani, Ann. Rev. Astron. Astrophys. 50, 353 (2012)
P.A.R. Ade et al., Astron. Astrophys. 594, A13 (2016)
C. Wegg, O. Gerhard, M. Portail, Mon. Not. R. Astron. Soc. 463, 557 (2016)
J.B. Muñoz, E.D. Kovetz, L. Dai, M. Kamionkowski, Phys. Rev. Lett. 117, 091301 (2016)
A. Chudaykin, D. Gorbunov, I. Tkachev, Phys. Rev. D 94, 023528 (2016)
R. Massey et al., Nature 445, 286 (2007)
J.M. Overduin, P.S. Wesson, Phys. Rep. 402, 267 (2004)
Y. Cui, Mod. Phys. Lett. A 30, 1530028 (2015)
S. Matsumoto, S. Mukhopadhyay, Y.-L. Sming Tsai, Phys. Rev. D 94, 065034 (2016)
D. Castañeda Valle, E.W. Mielke, Phys. Lett. B 758, 93 (2016)
B. Schwabe, J.C. Niemeyer, J.F. Engels, Phys. Rev. D 94, 043513 (2016)
M. Milgrom, Astrophys. J. 270, 365 (1983)
M.K. Mak, T. Harko, Phys. Rev. D 70, 024010 (2004)
T. Harko, K.S. Cheng, Phys. Rev. D 76, 044013 (2007)
O. Bertolami, C.G. Boehmer, T. Harko, F.S.N. Lobo, Phys. Rev. D 75, 104016 (2007)
C.G. Boehmer, T. Harko, F.S.N. Lobo, JCAP 0803, 024 (2008)
H.R. Sepangi, S. Shahidi, Class. Quant. Grav. 38(26), 185010 (2009)
A.S. Sefiedgar, K. Atazadeh, H.R. Sepangi, Phys. Rev. D 80, 064010 (2009)
A.S. Sefiedgar, Z. Haghani, H.R. Sepangi, Phys. Rev. D 85, 064012 (2012)
O. Bertolami, P. Frazao, J. Paramos, Phys. Rev. D 86, 044034 (2012)
L. Lombriser, F. Schmidt, T. Baldauf, R. Mandelbaum, U. Seljak, R.E. Smith, Phys. Rev. D 85, 102001 (2012)
S. Capozziello, T. Harko, T.S. Koivisto, F.S.N. Lobo, G.J. Olmo, JCAP 07, 024 (2013)
T. Harko, F.S.N. Lobo, M.K. Mak, S.V. Sushkov, Mod. Phys. Lett. A 29, 1450049 (2014)
T. Harko, F.S.N. Lobo, Extensions of f(R) Gravity: Curvature-Matter Couplings and Hybrid Metric-Palatini Theory (Cambridge University Press, Cambridge, 2018)
M. Aguilar et al., Phys. Rev. Lett. 113, 221102 (2014)
F. Calore et al., JCAP 03, 38 (2015)
T. Daylan et al., Phys. Dark Universe 12, 1 (2016)
M.H. Chan, Phys. Rev. D 94, 023507 (2016)
M.H. Chan, Astrophys. J. 844, 9 (2017)
M.H. Chan, Phys. Rev. D 96, 043009 (2017)
M.H. Chan, C.H. Leung, Nat. Sci. Rep. 7, 14895 (2017)
M.H. Chan, Mon. Not. R. Astron. Soc. 474, 2576 (2018)
J.F. Navarro, C.S. Frenk, S.D.M. White, Astrophys. J. 462, 563 (1996)
A. Genina, A. Benitez-Llambay, C.S. Frenk, S. Cole, A. Fattahi, J.F. Navarro, K.A. Oman, T. Sawala, T. Theuns, Mon. Not. R. Astron. Soc. 474, 1398 (2018)
M. Arca-Sedda, R. Capuzzo-Dolcetta, Mon. Not. R. Astron. Soc. 464, 3060 (2017)
M. Boylan-Kolchin, J.S. Bullock, M. Kaplinghat, Mon. Not. R. Astron. Soc. 415, L40 (2011)
M. Boylan-Kolchin, J.S. Bullock, M. Kaplinghat, Mon. Not. R. Astron. Soc. 422, 1203 (2012)
E.D. Carlson, M.E. Machacek, L.J. Hall, Astrophys. J. 398, 43 (1992)
D.N. Spergel, P.J. Steinhardt, Phys. Rev. Lett. 84, 3760 (2000)
C. Firmani, E. D’Onghia, V. Avila-Reese, G. Chincarini, X. Hernández, MNRAS 315, L29 (2000)
R. Davé, D.N. Spergel, P.J. Steinhardt, B.D. Wandelt, Astrophys. J. 547, 574 (2001)
A. Kamada, M. Kaplinghat, A.B. Pace, H.-B. Yu, Phys. Rev. Lett. 119, 111102 (2017)
P. Creasey, O. Sameie, L.V. Sales et al., MNRAS 468, 2283 (2017)
T. Ren, A. Kwa, M. Kaplinghat, H.B. Yu, (2018). arXiv:1808.05695
A. Robertson, R. Massey, V. Eke et al., MNRAS 476, L20 (2018)
D. Harvey, R. Massey, T. Kitching, A. Taylor, E. Tittley, Science 347, 1462 (2015)
M. Jauzac et al., Mon. Not. R. Astron. Soc. 463, 3876 (2016)
E.D. Carlson, M.E. Machacek, J.L. Hall, Astrophys. J. 398, 43 (1992)
A.A. de Laix, R.J. Scherrer, R.K. Schaefer, Astrophys. J. 452, 495 (1995)
C.J. Saxton, I. Ferreras, Mon. Not. R. Astron. Soc. 405, 77 (2010)
C.J. Saxton, Mon. Not. R. Astron. Soc. 430, 1578 (2013)
G.A. Dooley, A.H.G. Peter, M. Vogelsberger, J. Zavala, A. Frebel, Mon. Not. R. Astron. Soc. 461, 710 (2016)
O.D. Elbert, J.S. Bullock, M. Kaplinghat, S. Garrison-Kimmel, A.S. Graus, M. Rocha, (2016). arXiv:1609.08626 [astro-ph.GA]
S.N. Bose, Z. Phys. 26, 178 (1924)
A. Einstein, Sitzungsberichte der Preussischen Akademie der Wissenschaften. Phys. Math. Klasse 1924, 261 (1924)
A. Einstein, Sitzungsberichte der Preussischen Akademie der Wissenschaften. Phys. Math. Klasse 1925, 3 (1925)
F. Dalfovo, S. Giorgini, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999)
L. Pitaevskii, S. Stringari, Bose-Einstein Condensation (Clarendon Press, Oxford, 2003)
C.J. Pethick, H. Smith, Bose-Einstein Condensation in Dilute Gases (Cambridge University Press, Cambridge, 2008)
A. Griffin, T. Nikuni, E. Zaremba, Bose-Condensed Gases at Finite Temperatures (Cambridge University Press, Cambridge, 2009)
M.H. Anderson, J.R. Ensher, M.R. Matthews, C.E. Wieman, E.A. Cornell, Science 269, 198 (1995)
C.C. Bradley, C.A. Sackett, J.J. Tollett, R.G. Hulet, Phys. Rev. Lett. 75, 1687 (1995)
K.B. Davis, M.O. Mewes, M.R. Andrews, N.J. van Drutten, D.S. Durfee, D.M. Kurn, W. Ketterle, Phys. Rev. Lett. 75, 3969 (1995)
M. Membrado, J. Abad, A.F. Pacheco, J. Sanudo, Phys. Rev. D 40, 2736 (1989)
X.Z. Wang, Phys. Rev. D 64, 124009 (2001)
P.H. Chavanis, T. Harko, Phys. Rev. D 86, 064011 (2012)
X.Y. Li, T. Harko, K.S. Cheng, JCAP 06, 001 (2012)
X.Y. Li, F. Wang, K.S. Cheng, JCAP 10, 031 (2012)
P.H. Chavanis, Eur. Phys. J. Plus 130, 181 (2015)
S. Latifah, A. Sulaksono, T. Mart, Phys. Rev. D 90, 127501 (2014)
A. Mukherjee, S. Shah, S. Bose, Phys. Rev. D 91, 084051 (2015)
B. Danila, T. Harko, Z. Kovacs, Eur. Phys. J. C 75, 203 (2015)
N. Kan, K. Shiraishi, Phys. Rev. D 94, 104042 (2016)
D. Croon, J.J. Fan, C. Sun, J. Cosmol. Astropart. Phys. 04, 008 (2019)
M. Membrado, A.F. Pacheco, J.S. Sanudo, Astron. Astrophys. 217, 92 (1989)
J. Sin, Phys. Rev. D 50, 3650 (1994)
S.U. Ji, S.J. Sin, Phys. Rev. D 50, 3655 (1994)
M. Membrado, J.A.L. Aguerri, Int. J. Mod. Phys. D 5, 257 (1996)
M. Membrado, Mon. Not. R. Astron. Soc. 296, 21 (1998)
W. Hu, R. Barkana, A. Gruzinov, Phys. Rev. Lett. 85, 1158 (2000)
J. Goodman, New Astron. 5, 103 (2000)
P.J.E. Peebles, Astrophys. J. 534, L127 (2000)
K.R.W. Jones, D. Bernstein, Class. Quantum Gravity 18, 1513 (2001)
R.P. Yu, M.J. Morgan, Class. Quantum Gravity 19, L157 (2002)
M.P. Silverman, R.L. Mallett, Gen. Relat. Gravity 34, 633 (2002)
A. Arbey, J. Lesgourgues, P. Salati, Phys. Rev. D 68, 023511 (2003)
E.P. Gross, Phys. Rev. 106, 161 (1957)
V.L. Ginzburg, L.P. Pitaevskii, Sov. Phys. JETP 7, 858 (1958)
C.G. Boehmer, T. Harko, JCAP 06, 025 (2007)
G.P. Horedt, Polytropes: Applications in Astrophysics and Related Fields (Kluwer Academic Publishes, New York, Boston, Dordrecht, 2004)
T. Harko, E.J.M. Madarassy, JCAP 01, 020 (2011)
T. Harko, JCAP 1105, 022 (2011)
P. Sikivie, Q. Yang, Phys. Rev. Lett. 103, 111301 (2009)
J.-W. Lee, Phys. Lett. B 681, 118 (2009)
J.-W. Lee, S. Lim, JCAP 1001, 007 (2010)
B. Kain, H.Y. Ling, Phys. Rev. D 82, 064042 (2010)
N.T. Zinner, Phys. Res. Int. 2011, 734543 (2011)
P.-H. Chavanis, Phys. Rev. D 84, 043531 (2011)
P.-H. Chavanis, L. Delfini, Phys. Rev. D 84, 043532 (2011)
P.-H. Chavanis, Phys. Rev. D 84, 063518 (2011)
P.-H. Chavanis, Phys. Rev. E 84, 031101 (2011)
T. Harko, Mon. Not. R. Astron. Soc. 413, 3095 (2011)
V.H. Robles, T. Matos, Mon. Mon. Not. R. Astron. Soc. 422, 282 (2012)
M.O.C. Pires, J.C.C. de Souza, JCAP 11, 024 (2012)
P.-H. Chavanis, Astron. Astrophys. 537, A127 (2012)
H. Velten, E. Wamba, Phys. Lett. B 709, 1 (2012)
T. Harko, G. Mocanu, Phys. Rev. D 85, 084012 (2012)
T. Rindler-Daller, P.R. Shapiro, Mon. Not. R. Astron. Soc. 422, 135 (2012)
F.S. Guzman, F.D. Lora-Clavijo, J.J. Gonzalez-Aviles, F.J. Rivera-Paleo, Phys. Rev. D 89, 063507 (2014)
T. Rindler-Daller, P.R. Shapiro, Mod. Phys. Lett. A 29, 1430002 (2014)
R.C. Freitas, S.V.B. Goncalves, JCAP 04, 049 (2013)
E.J.M. Madarassy, V.T. Toth, Comput. Phys. Commun. 184, 1339 (2013)
F.S. Guzman, F.D. Lora-Clavijo, J.J. Gonzalez-Aviles, F.J. Rivera-Paleo, JCAP 09, 034 (2013)
J.C.C. de Souza, M.O.C. Pires, JCAP 03, 010 (2014)
V.T. Toth, (2014). arXiv:1402.0600
T. Harko, Phys. Rev. D 89, 084040 (2014)
M. Dwornik, Z. Keresztes, L.A. Gergely, Chapter 6 of “Recent Development in Dark Matter Research”, ed. by N. Kinjo, A. Nakajima (Nova Science Publishers, 2014). arXiv:1312.3715
M.-H. Li, Z.-B. Li, Phys. Rev. D 89, 103512 (2014)
T. Harko, M.J. Lake, Phys. Rev. D 91, 045012 (2015)
E.J.M. Madarassy, V.T. Toth, Phys. Rev. D 91, 044041 (2015)
J.C.C. de Souza, M. Ujevic, Gen. Relat. Gravity 47, 100 (2015)
T. Harko, F.S.N. Lobo, Phys. Rev. D 92, 043011 (2015)
V.H. Robles, V. Lora, T. Matos, F.J. Sanchez-Salcedo, Astrophys. J. 810, 99 (2015)
T. Harko, P.-X. Liang, S.-D. Liang, G. Mocanu, JCAP 11, 027 (2015)
L.A. Martinez-Medina, H.L. Bray, T. Matos, JCAP 12, 025 (2015)
K. Schroven, M. List, C. Lämmerzahl, Phys. Rev. D 92, 124008 (2015)
H.-Y. Schive, T. Chiueh, T. Broadhurst, K.-W. Huang, Astrophys. J. 818, 89 (2016)
S.-R. Chen, H.-Y. Schive, T. Chiueh, Mon. Not. R. Astron. Soc. 468, 1338 (2017)
E. Calabrese, D.N. Spergel, Mon. Not. R. Astron. Soc. 460, 4397 (2016)
P.-H. Chavanis, Phys. Rev. D 94, 083007 (2016)
P.S. Bhupal Dev, M. Lindner, S. Ohmer, Phys. Lett. B 773, 219 (2017)
S. Sarkar, C. Vaz, L.C.R. Wijewardhana, Phys. Rev. D 97, 103022 (2018)
W.-J. Chung, L. Nelson, J. Cosmol. Astropart. Phys. 06, 010 (2018)
X. Zhang, M.H. Chan, T. Harko, S.-D. Liang, C.S. Leung, Eur. Phys. J. C 78, 346 (2018)
E. Kun, Z. Keresztes, S. Das, L.Á. Gergely, Symmetry 10, 520 (2018)
V. Sreenath, Phys. Rev. D 99, 043540 (2019)
J.-W. Lee, H.-C. Kim, J. Lee, (2019). arXiv:1901.00305
S. HajiSadeghi, S. Smolenski, J. Wudka, Phys. Rev. D 99, 023514 (2019)
M. Morikawa, S. Takahashi, (2019). arXiv:1903.02986
L. Hui, J.P. Ostriker, S. Tremaine, E. Witten, Phys. Rev. D 95, 043541 (2017)
J.H. Jeans, Philos. Trans. R. Soc. Lond. Ser. A 199, 1 (1902)
S. Chandrasekhar, Proc. R. Soc. Lond. A 210, 26 (1951)
S. Chandrasekhar, Astrophys. J. 119, 7 (1954)
W. Fricke, Astrophys. J. 120, 356 (1954)
S. Chandrasekhar, Vistas Astron. 1, 344 (1955)
N. Bel, E. Schatzman, Rev. Mod. Phys. 30, 1015 (1958)
I.L. Genkin, Sov. Astron. 12, 1004 (1969)
A.P. Boss, Astrophys. J. 244, 40 (1981)
V.M. Cadez, Astron. Astrophys. 235, 242 (1990)
B.G. Elmegreen, Astrophys. J. 433, 39 (1994)
T.A. Thompson, Astrophys. J. 684, 212 (2008)
G.-X. Li, Mon. Not. R. Astron. Soc. 465, 667 (2017)
D. Lynden-Bell, Mon. Not. R. Astron. Soc. 124, 279 (1962)
C. Simon, Bull. Acad. R. Belg. Soc. 97, 7 (1962)
P.A. Sweet, Mon. Not. R. Astron. Soc. 125, 285 (1963)
S.A. Trigger, A.I. Ershkovich, G.J.F. van Heist, P.P.J.M. Schram, Phys. Rev. E 69, 066403 (2004)
P.H. Chavaniss, Eur. Phys. J. B 85, 229 (2012)
A. Suárez, P.-H. Chavanis, Phys. Rev. D 98, 083529 (2018)
E.A. Donley, N.R. Claussen, S.L. Cornish, J.L. Roberts, E.A. Cornell, C.E. Wieman, Nature 412, 295 (2001)
J. Sopik, C. Sire, P.-H. Chavanis, Phys. Rev. E 74, 011112 (2006)
P.-H. Chavanis, C. Sire, Phys. Rev. E 83, 031131 (2011)
P.M. Lushnikov, Phys. Rev. A 82, 023615 (2010)
T. Fukuyama, M. Morikawa, T. Tatekawa, J. Cosmol. Astropart. Phys. 06, 033 (2008)
V.M. Perez-Garcia, H. Michinel, J.I. Cirac, M. Lewenstein, P. Zoller, Phys. Rev. A 56, 1424 (1997)
A. Fetter, J. Low Temp. Phys. 161, 445 (2010)
M. Caracanhas, A.L. Fetter, S.R. Muniz, K.M.F. Magalhaes, G. Roati, G. Bagnato, V.S. Bagnato, J. Low Temp. Phys. 166, 49 (2012)
M. Caracanhas, A.L. Fetter, G. Baym, S.R. Muniz, V.S. Bagnato, J. Low Temp. Phys. 170, 133 (2013)
S. Chandrasekhar, An Introduction to the Study of Stellar Structure (University of Chicago Press, Chicago, 1939)
S.L. Shapiro, S.A. Teukolsky, Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects (Wiley, New York, 1983)
R. Kippenhahn, A. Weigert, A. Weiss, Stellar Structure and Evolution (Springer, Berlin, Heidelberg, 2012)
R.J. Donnelly, C.E. Swanson, J. Fluid Mech. 173, 387429 (1986)
L. Madeira, M.A. Caracanhas, F.E.A. dos Santos, V.S. Bagnato, (2019). arXiv:1903.12215 [cond-mat.quant-gas]
L.M. Widrow, N. Kaiser, Astrophys. J. 416, L71 (1993)
H.Y. Schive, T. Chiueh, T. Broadhurst, Nat. Phys. 10, 496 (2014)
H.Y. Schive, M.H. Liao, T.P. Woo, S.K. Wong, T. Chiueh, T. Broadhurst, W.-Y.P. Hwang, Phys. Rev. Lett. 113, 261302 (2014)
M. Garny, T. Konstandin, J. Cosmol. Astropart. Phys. 01, 009 (2018)
P. Goldreich, S.V. Weber, Astrophys. J. 238, 991 (1980)
A. Yahil, Astrophys. J. 265, 1047 (1983)
P. Blottiau, J.P. Chieze, S. Bouquet, Astron. Astrophys. 207, 24 (1988)
Y.-Q. Lou, C.-H. Shi, Mon. Not. R. Astron. Soc. 445, 1186 (2014)
D.L. Li, Y.-Q. Lou, J. Esimbek, Mon. Not. R. Astron. Soc. 473, 2441 (2018)
Author information
Authors and Affiliations
Corresponding author
Appendix A: No self-similar contraction/expansion of Bose–Einstein condensate dark matter halos
Appendix A: No self-similar contraction/expansion of Bose–Einstein condensate dark matter halos
Equations (80) and (81) are invariant under the time reversal operations \(t\rightarrow -t\), \(v\rightarrow -v\), and \(\rho \rightarrow \rho \) , \(M\rightarrow M\), respectively. Hence, without any loss of generality, one can restrict the analysis to the range \(0 \le t < \infty \) of the time variable. In order to investigate the possibility of the existence of a self-similar solution that describes the collapse of Bose–Einstein condensate dark matter halos, we introduce first a similarity variable \(\xi \) , and assume that each physical quantity scales according to the following rules:
where \(\alpha (t)\), \(\beta (t)\), \(\gamma (t)\) and \(\eta (t)\) are continuous functions of the time variable t only.
Then we obtain first
In the self-similar variables the continuity equation (80) gives
while the Euler equation (81 takes the form
The existence of a similarity solution requires that the condition
must be satisfied by the functions \(\alpha (t)\) and \(\beta (t)\). The explicit time dependence in the evolution equations of the condensate dark matter halo could be removed if the conditions
are also satisfied, where \(c_i\), \(i=1,...,6\), are constants. The third relation in Eqs. (A6) determines the function \(\alpha (t)\) as a solution of the second order differential equation
with a particular solution given by
where \(C_1\) is an arbitrary constant of integration, and \(n=c_3/\left( c_3-1\right) \). The first two of the Eq. (A7) give
The substitution of the above relations into the first of Eqs. (A6) gives \(\alpha ^2(t)=\mathrm {constant}\), a result that obviously contradicts Eq. (A9). Hence the explicit time dependence in the hydrodynamic equations describing the dynamics of a polytropic fluid with equation of state \(p \sim \rho ^{\gamma }\), \(\gamma =2\), cannot be removed by means of the similarity transformations (A1), and therefore there are no self-similar solutions describing the evolution of Bose–Einstein condensate dark matter halos. However, for polytropic fluids with \(\gamma \ne 2\) the hydrodynamic type evolution equations always admit self-similar solutions.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Harko, T. Jeans instability and turbulent gravitational collapse of Bose–Einstein condensate dark matter halos. Eur. Phys. J. C 79, 787 (2019). https://doi.org/10.1140/epjc/s10052-019-7285-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7285-3