1 Introduction

A Higgs boson has been discovered in the first run of Large Hadron Collider (LHC) with 7 and 8 TeV energy in 2012 [1, 2] and some of its properties have been established. During the second run of LHC with 13 TeV center of mass energy, some measurements of the properties of the Higgs boson have improved [3,4,5,6,7] and new observations such as \(h \rightarrow b{\overline{b}}\) and \(pp\rightarrow t{\bar{t}} h\) have been reported [8,9,10].

The aforementioned Higgs boson properties established so far will be further improved by the High Luminosity program of the future LHC run (HL-LHC) [11,12,13,14]. At the HL-LHC, one can pin down the uncertainties on the Higgs boson couplings to a few percent level in some cases [15] and provide indirect hints to the awaited new physics. Moreover, in the clean environment of the \(e^+e^-\) collider such as ILC and CEPC, which can act like a Higgs factory, one can improve the Higgs boson measurements [18, 19].

Although all data collected by LHC seem to indicate that the Higgs boson particle is in perfect agreement with the SM predictions, there are many theoretical as well as experimental indications which point out that the SM is only an effective theory at low scale of a more fundamental one. One common feature of those Beyond SM (BSM) theories is an extended Higgs sector with an extra singlet, doublet, and/or triplet. Most of the higher Higgs representations with an extra doublet/singlet predict in their spectrum extra neutral and/or charged Higgs states. A discovery of another or several additional Higgs bosons would be considered as a clear evidence of an extended Higgs sector and a departure from the SM.

Following the discovery of a Higgs boson, there has been a large number of works dedicated to extending the SM Higgs sector by extra Higgs fields. Among the simplest one we mention:

A real singlet scalar that has a mixing with the SM Higgs boson [20], the popular two Higgs Doublet Model (2HDM) [21,22,23] with or without natural flavor conservation and the inert Higgs model that provides dark matter candidate [24,25,26,27]. Recently, there have been also phenomenological studies that extend the 2HDM with an additional real gauge-singlet scalar which acts like dark matter candidate [28, 29]. One can also extend the 2HDM by adding a real scalar singlet with non-vanishing expectation value that can mix with the doublets [30, 31]. These studies referred to this model as the next-to-minimal 2HDM (N2HDM).

In the two variants of the N2HDM, the scalar spectrum is richer than the traditional 2HDM, which implies an interesting phenomenology at colliders including but not restricted to scalar-to-scalar decays, exotic decays and fermiophobic scenarios which are precluded in the SM and occur hardly in the 2HDM. The model can easily accommodate a SM-like Higgs Boson that easily satisfies all the constraints from LHC measurements. Despite the existence of mixing among CP-even mass eigenstates, which would modify the SM-like Higgs couplings to fermions and gauge bosons, constraints from signal strength measurements can be easily satisfied (within the present range of systematic and statistical errors).

In the N2HDM, the scalar spectrum contains 3 CP-even states \(h_{1,2,3}\), one CP-odd A and a pair of charged Higgs \(H^\pm \). \(h_{1,2,3}\) are admixtures of the doublets and the singlet components while A and \(H^\pm \) are purely made of the doublets components.

A comprehensive analysis of the N2HDM has been carried by the authors of Ref. [31]. A general scan was performed over the parameter space to look for possible scenarios that allow any of the neutral Higgs bosons \(h_i\) to be identified with the discovered Higgs boson particle at the LHC. It is found that a large singlet-doublet admixture is still compatible with LEP and all LHC data, while satisfying all theoretical and experimental constraints [31]. In the present study, we would like to do a comprehensive study of N2HDM type-I for the case where \(h_2\) is the 125 GeV Higgs while \(h_1\) and A are lighter than \(h_2\). This scenario opens a new window for beyond Standard Model decays of \(h_2\) such as \(h_2\rightarrow h_1 h_1\) and probably \(h_2\rightarrow AA, AA^*, Z^*A\), \(W^*H^\pm \) which are still compatible with Higgs data.

Furthermore, we will study the possibility where the light Higgs \(h_1\) can be partially fermiophobic in N2HDM type-I as well as the consistency of the non-detected decay of \(h_2 \rightarrow h_1 h_1\) with LHC data followed by \(h_1 \rightarrow \gamma \gamma \) which leads to four photons final state at LHC [32].

We will also present some decays of the heavy Higgs \((h_3)\) into Standard Model particles and other decays to scalar-scalar and scalar-vector boson (\(h_3 \rightarrow h_1h_1,\ h_3 \rightarrow h_1 h_2,\ h_3 \rightarrow AZ,\ h_3 \rightarrow H^\pm W^\mp \))

The paper is organized as follow: Sect. 2 is devoted to the N2HDM and its parametrization, in Sect. 3 we review the theoretical and experimental constraints that the N2HDM is subject to. We present our numerical result in Sect. 4 and conclude in Sect. 5. Several technical details are given in the Appendix.

2 The 2HDM with a real singlet field: N2HDM

In this section, we present a review of the N2HDM. We discuss the scalar potential and derive the spectrum and the parametrization of the model. We also present the Yukawa textures and discuss the natural flavor conservation of the model. Couplings of the Higgs bosons to gauge bosons are also shown and their sum rules are discussed.

2.1 The Higgs potential

The scalar sector of N2HDM consists of two weak isospin doublets \(H_{i}\) (i = 1, 2), with hypercharge \(Y= 1\) and a real singlet field with hypercharge \(Y= 0\) which are given by

$$\begin{aligned} H_{i}&= \left( \begin{array}{c} \phi _i^\pm \\ \frac{1}{\sqrt{2}}(v_i + \phi _i + i \chi _i) \\ \end{array} \right) ~~\mathrm{and}~~S = \frac{1}{\sqrt{2}}(v_s + \phi _s) \end{aligned}$$
(1)

The most general renormalizable scalar potential for the model that respect \(SU(2)_L\otimes U(1)_Y\) gauge symmetry has the following form:

$$\begin{aligned} V(H_1,H_2,S)= & {} m^2_{11}\, H_1^\dagger H_1 +\, m^2_{22}\, H_2^\dagger H_2 \nonumber \\&-\, \mu ^2\, \left( H_1^\dagger H_2 + H_2^\dagger H_1\right) + \frac{1}{2}m^2_S S^2 \nonumber \\&+ \,\frac{\lambda _1}{2} \left( H_1^\dagger H_1 \right) ^2 + \frac{\lambda _2}{2} \left( H_2^\dagger H_2 \right) ^2 \nonumber \\&+ \,\lambda _3\, H_1^\dagger H_1\, H_2^\dagger H_2 + \lambda _4\, H_1^\dagger H_2\, H_2^\dagger H_1\nonumber \\&+\frac{\lambda _5}{2} \left[ \left( H_1^\dagger H_2 \right) ^2+ \left( H_2^\dagger H_1 \right) ^2 \right] \nonumber \\&+ \,\frac{\lambda _6}{8} S^4 +\frac{1}{2}[\lambda _7 H_1^\dagger H_1 +\lambda _8 H_2^\dagger H_2 ] S^2 \end{aligned}$$
(2)

where \(m_{11}^2, m_{22}^2\) and \(m_{S}^2\) are the mass parameters. By hermiticity of the scalar potential \(\lambda _{1,2,3,4,6,7,8}\) are dimensionless real parameters while \(\lambda _5\) and \(\mu ^2\) can be complex to allow CP violation in the scalar sector. In the present study, we assume that all scalar parameters are real. Therefore, the only source of CP violation is in the Cabbibo-Kobayashi-Maskawa matrix. We remind here that we allow a dimension 2 term \(\mu ^2\) which break softly \(Z_2\) symmetry. This discrete \(Z_2\) symmetry is usually imposed in order to avoid Flavor Changing Neutral Current (FCNC) at tree level in the Yukawa sector.

Assuming that spontaneous electroweak symmetry breaking (EWSB) is taking place at some electrically neutral point in the field space, and denoting the corresponding VEVs by

$$\begin{aligned} \langle H_{1} \rangle&=\frac{1}{\sqrt{2}}\left( \begin{array}{c} 0 \\ v_1 \\ \end{array} \right) ,\langle H_{2} \rangle =\frac{1}{\sqrt{2}}\left( \begin{array}{c} 0 \\ v_2\\ \end{array} \right) ~\mathrm{and}~\langle S \rangle =\frac{1}{\sqrt{2}}v_s \end{aligned}$$
(3)

The parameters \(m_{11}^2, m_{22}^2\) and \(m_{S}^2\) can be eliminated by the minimization conditions of the potential Eq. (2):

$$\begin{aligned} m_{11}^2= & {} \mu ^2 t_\beta - \frac{1}{2}\lambda _1v^2 c^2_{\beta } - \frac{1}{2}\lambda _{345}v^2 s^2_{\beta } - \frac{1}{4}\lambda _7 v_S^2 \end{aligned}$$
(4)
$$\begin{aligned} m_{22}^2= & {} \mu ^2 t_\beta ^{-1} - \frac{1}{2}\lambda _1v^2 s^2_{\beta }- \frac{1}{2}\lambda _{345}v^2 c^2_{\beta } - \frac{1}{4}\lambda _8 v_S^2 \end{aligned}$$
(5)
$$\begin{aligned} m_{S}^2= & {} - \frac{1}{2}\lambda _7 v^2 c^2_{\beta } - \frac{1}{2}\lambda _8 v^2 s^2_{\beta } - \frac{1}{4}\lambda _6 v_S^2 \end{aligned}$$
(6)

where \(s_x, c_x, t_x\) stand for \(\sin x\), \(\cos x\) and \(\tan x\) respectively, and \(\lambda _{345} = \lambda _3 + \lambda _4 + \lambda _5\) and \(t_\beta = v_2/v_1\).

After the EWSB of \(SU(2)_L\otimes U(1)_Y\) down to electromagnetic U(1), three of the nine Higgs degrees of freedom corresponding to the Goldstone bosons are absorbed by the longitudinal components of vector boson \(W^\pm \) and \(Z^0\). The remaining six degrees of freedom should manifest as physical Higgses: three CP-even scalars (\(h_1\), \(h_2\), \(h_3\) with \(m_{h_1}< m_{h_2}< m_{h_3}\)), one CP-odd A and a charged Higgs pair \(H^\pm \).

2.2 Higgs masses and mixing angles

The most general form of the squared mass matrix \(7\times 7\) of the Higgs sector can be recast, using Eqs. (4–6), into a block diagonal form of three submatrices: one \(3 \times 3\) matrix denoted in the following by \({\mathcal {M}}_{{\mathcal {CP}}_{even}}^2\) for CP-even sector, one \(2\times 2\) matrix \({\mathcal {M}}_{{\mathcal {CP}}_{odd}}^2\) for CP-odd sector and one \(2 \times 2\) matrix denoted by \({\mathcal {M}}_{\pm }^2\) for the charged sector.

The squared mass matrix for the charged fields \(\phi _{1,2}^{\pm }\) is:

$$\begin{aligned} {\mathcal {M}}_{\pm }^2= \left( \begin{array}{ll} \mu ^2 t_\beta - \frac{1}{2}\lambda _{45}^+v^2 s^2_{\beta }\,\,\,&{}\,\,\,-\mu ^2 + \frac{1}{2}\lambda _{45}^+v^2 s_\beta c_\beta \\ -\mu ^2 + \frac{1}{2}\lambda _{45}^+v^2 s_\beta c_\beta \,\,\,&{}\,\,\,\mu ^2 t_\beta ^{-1} - \frac{1}{2}\lambda _{45}^+v^2 c^2_{\beta }\\ \end{array} \right) \end{aligned}$$
(7)

with \(\lambda _{45}^+ = \lambda _{4}+\lambda _{5}\). This matrix is diagonalized by the following orthogonal matrix \(\mathcal {R}_{\beta }\), given by :

$$\begin{aligned} {\mathcal {R}}_{\beta }= & {} \left( \begin{array}{cc} c_\beta &{} -s_\beta \\ s_\beta &{} c_\beta \\ \end{array} \right) \end{aligned}$$
(8)

Among the two eigenvalues of \({\mathcal {M}}_{\pm }^2\), one is zero and corresponds to the charged Goldstone boson \(G^\pm \) while the other one corresponds to the charged Higgs boson \(H^\pm \) and is given by:

$$\begin{aligned} m_{H^\pm }^2= & {} \frac{1}{s_{2\beta }}\left[ 2\mu ^2 - \frac{1}{2}\lambda _{45}^+v^2 s_{2\beta } \right] \end{aligned}$$
(9)

The charged Higgs \(H^\pm \) and the charged goldstone \(G^\pm \) are orthogonal rotation of the weak eigenstates \(\phi _1^{\pm }\), \(\phi _2^{\pm }\),

$$\begin{aligned} G^\pm= & {} c_\beta \phi _1^{\pm }+ s_\beta \phi _2^{\pm }, \quad \quad H^\pm = - s_\beta \phi _1^{\pm }+ c_\beta \phi _2^{\pm } \end{aligned}$$
(10)

The neutral scalar and pseudo-scalar mass matrices are given by:

$$\begin{aligned} {\mathcal {M}}_{{\mathcal {CP}}_{even}}^2= \left( \begin{array}{lll} \mu ^2 t_\beta + \lambda _1v^2 c^2_{\beta } &{} -\mu ^2 + \lambda _{345} v^2 s_\beta c_\beta &{} \frac{\lambda _7vv_S c_\beta }{2\sqrt{2}} \\ -\mu ^2 + \lambda _{345} v^2 s_\beta c_\beta &{} \mu ^2 t_\beta ^{-1} + \lambda _2 v^2 s^2_{\beta } &{} \frac{\lambda _8vv_S s_\beta }{2\sqrt{2}} \\ \frac{\lambda _7vv_S c_\beta }{2\sqrt{2}} &{} \frac{\lambda _8vv_S s_\beta }{2\sqrt{2}} &{} \frac{\lambda _6v_S^2}{8} \end{array} \right) \nonumber \\ \end{aligned}$$
(11)

and

$$\begin{aligned} {\mathcal {M}}_{{\mathcal {CP}}_{odd}}^2= \left( \begin{array}{ll} \mu ^2 t_\beta - \lambda _5v^2 s^2_{\beta }\, &{} \, -\mu ^2 + \lambda _{5} v^2 s_\beta c_\beta \, \\ -\mu ^2 + \lambda _{5} v^2 s_\beta c_\beta \, &{} \, \mu ^2 t_\beta ^{-1} - \lambda _5 v^2 c^2_{\beta } \end{array} \right) \end{aligned}$$
(12)

The physical states \(h_i = \{h_1,\ h_2,\ h_3\}\) are obtained by an orthogonal transformation \(h_i = \mathcal {R}_{\alpha _{1,2,3}} \phi _i\), \((i=1,2,s)\) that diagonalizes the mass matrix \({\mathcal {M}}_{{\mathcal {CP}}_{even}}^2\),

$$\begin{aligned} \left( \begin{array}{ccc} h_1\\ h_2\\ h_3 \end{array} \right) = \mathcal {R}_{\alpha _{1,2,3}}\,\left( \begin{array}{ccc} \phi _1\\ \phi _2\\ \phi _s \end{array} \right) \end{aligned}$$
(13)

with:

$$\begin{aligned} \mathcal {R}_{\alpha _{1,2,3}} = \left( \begin{array}{lll} c_1 c_2 &{} s_1 c_2 &{} s_2 \\ -c_1 s_2 s_3 - s_1 c_3 &{} c_1 c_3 - s_1 s_2 s_3 &{} c_2 s_3 \\ -c_1 s_2 c_3 + s_1 s_3 &{} -c_1 s_3 - s_1 s_2 c_3 &{} c_2 c_3 \end{array} \right) \end{aligned}$$
(14)

with \(s_i=\sin \alpha _i \ \ c_i=\cos \alpha _i\).

Without loss of generality we assume that \(m_{h_1}< m_{h_2}<m_{h_3}\).

From Eq. (12), it is easy to get the two eigenvalues of \({\mathcal {M}}_{{\mathcal {CP}}_{odd}}^2\), one is vanishing and corresponds to the neutral Goldstone boson \(G^0\) while the other one corresponds to the pseudo-scalar A:

$$\begin{aligned} m_{A}^2= & {} \frac{1}{ s_\beta c_\beta }\left[ \mu ^2 - \lambda _{5}v^2 s_\beta c_\beta \right] \end{aligned}$$
(15)

The CP-odd state A and the neutral Goldstone \(G^0\) are obtained by an orthogonal rotation of the weak eigenstates \(\chi _1\), \(\chi _2\):

$$\begin{aligned} G^0= & {} c_\beta \chi _1+ s_\beta \chi _2,\quad \quad A= - s_\beta \chi _1+ c_\beta \chi _2. \end{aligned}$$
(16)

2.3 Yukawa texture

There are different types of Higgs couplings to fermions. The general structure of the Yukawa Lagrangian when both Higgs fields couple to all fermions is given by:

$$\begin{aligned} \mathcal {L}_Y= & {} {\overline{Q}}^0_L{\tilde{\varPhi }}_2\eta ^{U,0}_2U^0_R+{\overline{Q}}^0_L{\varPhi }_2\eta ^{D,0}_2D^0_R+{\overline{Q}}^0_L{\tilde{\varPhi }}_1\eta ^{U,0}_1U^0_R\nonumber \\&+\,{\overline{Q}}^0_L{\varPhi }_1\eta ^{D,0}_1D^0_R + \mathrm{h.c} \end{aligned}$$
(17)

where \(Q_L^0\) is the weak isospin quark doublet, \(U_R^0\) and \(D_R^0\) are the weak isospin quark singlets and \(\eta _{{1,2}}^{U,0}\), \(\eta _{{1,2}}^{D,0}\) are matrices in flavor space, then the above Lagrangian will generate Flavor Changing Neutral Currents (FCNC) at tree level which can invalidate some low energy observables in B, D and K physics. In order to avoid such FCNC, it is customary to invoke a \(Z_2\) symmetry that forbids FCNC couplings at tree level [33]. Depending on the \(Z_2\) assignment, we have four types of Yukawa interactions [34]. In the present study, we focus only on type-I where all fermions couple only to one of the two Higgs doublets. In this case:

$$\begin{aligned} \mathcal {L}_Y^I= & {} {\overline{Q}}^0_L{\tilde{\varPhi }}_2\eta ^{U,0}_2U^0_R+ {\overline{Q}}^0_L{\varPhi }_2\eta ^{D,0}_2D^0_R\nonumber \\&+\, {\overline{U}}^0_R \eta ^{U,0\dagger }_2{\tilde{\varPhi }}_2^\dagger Q^0_L+{\overline{D}}^0_R \eta ^{D,0\dagger }_2 \varPhi _2^+ Q^0_L \end{aligned}$$
(18)

Neutral Higgs couplings to a pair of fermions are:

$$\begin{aligned} {g_{h_1 f{\overline{f}}}}: \quad \frac{\mathcal {R}_{12}}{s_\beta }&= \frac{c_2 s_1}{s_\beta } \end{aligned}$$
(19)
$$\begin{aligned} {g_{h_2 f{\overline{f}}}} :\quad \frac{ \mathcal {R}_{22}}{s_\beta }&= \frac{(c_1c_3 -s_1s_2s_3)}{s_\beta } \end{aligned}$$
(20)
$$\begin{aligned} {g_{h_3 f{\overline{f}}}} :\quad \frac{ \mathcal {R}_{32}}{s_\beta }&= -\frac{(c_1s_3 +s_1s_2c_3)}{s_\beta } \end{aligned}$$
(21)

where f designate any type of fermions.

2.4 Higgs couplings to gauge bosons and sum rules

We present shortly here the Higgs couplings to gauge bosons and discuss the sum rules required by unitarity [35, 36] which could be derived either from the Lagrangian or using unitarity arguments by considering the processes \(ff\rightarrow VV\) and requiring that the term that increases with energy should cancel (see Ref. [37]). In Refs. [36] and [37], the sum rules are established for multi-Higgs doublet models using unitarity arguments for scattering amplitudes and also unitarity for the mixing matrix. In our case of N2HDM, as we will see below, these sum rules will apply as a consequence of the unitarity of the orthogonal matrix \(R_{ij}\). Just before presenting these sum rules, we also refer to the normalized couplings of neutral Higgs to a pair of gauge bosons \(V=Z, W\) that are given by:

$$\begin{aligned} g_{h_1 V V}: \quad c_\beta \mathcal {R}_{11}+s_\beta \mathcal {R}_{12}&= c_{\alpha _2} c_{\beta -\alpha _1}, \end{aligned}$$
(22)
$$\begin{aligned} g_{h_2 V V}: \quad c_\beta \mathcal {R}_{21}+s_\beta \mathcal {R}_{22}&= c_{\alpha _3} s_{\beta -\alpha _1} - s_{\alpha _2} s_{\alpha _3} c_{\beta -\alpha _1}, \end{aligned}$$
(23)
$$\begin{aligned} g_{h_3 V V}: \quad c_\beta \mathcal {R}_{31}+s_\beta \mathcal {R}_{32}&=- s_{\alpha _3} s_{\beta -\alpha _1}- s_{\alpha _2} c_{\alpha _3} c_{\beta -\alpha _1}, \end{aligned}$$
(24)

which satisfy the following sum rule:

$$\begin{aligned} \sum _{i=1}^3 g_{h_i V V}^2 =1 \end{aligned}$$
(25)

This sum rule imply that each coupling \(g_{h_iVV}\) is requested to satisfy: \(\mid g_{h_iVV}\mid \le 1\).

For the couplings between two Higgs bosons and one gauge boson, we can distinguish two cases, a neutral case which corresponds to \(h_i A Z \) vertex and charged case associated with \(h_i H^\mp W^\pm \) vertex. From the kinetic terms of the Higgs fields, one can derive the various trilinear couplings among neutral, charged Higgses and gauge bosons. In units of \(\lambda _{n}=\frac{\sqrt{g^2+{g^{'}}^2}}{2}(p_{h_i}-p_{A})_\mu \) for neutral Higgs, respectively in units of \(\lambda _{c}=\mp \frac{g}{2}(p_{h_i}-p_{H^\pm })_\mu \) for charged Higgs, we have:

$$\begin{aligned}&g_{h_1 V S}: -c_{\alpha _2} s_{\beta -\alpha _1}, \end{aligned}$$
(26)
$$\begin{aligned}&g_{h_2 V S}: c_{\alpha _3} c_{\beta -\alpha _1} + s_{\alpha _2} s_{\alpha _3} s_{\beta -\alpha _1}, \end{aligned}$$
(27)
$$\begin{aligned}&g_{h_3 V S}: -s_{\alpha _3} c_{\beta -\alpha _1} + s_{\alpha _2} c_{\alpha _3} s_{\beta -\alpha _1}, \end{aligned}$$
(28)

where V=Z and \(S=A\) for the neutral case and \(V=W^\pm \) and \(S=H^\mp \) for charged one.

In the N2HDM, one can easily derive the following sum rules:

$$\begin{aligned}&g_{h_i W^\pm W^\mp }^2 + g_{h_i W^\pm H^\mp }^2 + R_{i3}^2=1 , \quad i=1,2,3 \end{aligned}$$
(29)
$$\begin{aligned}&g_{h_i Z Z}^2 + g_{h_i Z A}^2 + R_{i3}^2=1, \quad i=1,2,3, \end{aligned}$$
(30)

where \(R_{i3}\) is the singlet component of the Higgs \(h_i\).

There exist an other relation, which relates \(h_if{\overline{f}}\) and \(h_iVV\) couplings and is given by:

$$\begin{aligned}&\sum _{i=1}^3 g_{h_iVV} g_{h_if{\overline{f}}}=1 \end{aligned}$$
(31)

where \(g_{h_iVV}\) and \(g_{h_if{\overline{f}}}\) are the normalized couplings of \(h_i\) to gauge bosons and fermions. The above relationship Eq. (31) can be derived from the Feynman rules and using the orthogonality of R matrix.

From above, it follows that:

  • if \(h_i\) is pure singlet (\(R_{i3}^2\approx 1\)), then from Eqs. (29, 30) one has \(g_{h_i WW}^2 + g_{h_i W^\pm H^\mp }^2\approx 0\) and \(g_{h_i ZZ}^2 + g_{h_i ZA}^2\approx 0\) which would imply that \(h_iVV\), \(h_iH^\pm W^\mp \) and \(h_iAZ\) must be very suppressed, and this will present a real challenge for the production and detection of such Higgs bosons.

  • if \(g_{h_iVV}=1\) which means that \(h_i VV\) is full strength, then both singlet component \(R_{i3}\) as well as \(g_{h_i SV}\) couplings must vanish. This scenario could happen only when \(h_i\) have no singlet component.

  • According to Eq. (25), if \(g_{h_iVV}=1\) then \(g_{h_jVV}=0\) for \(j\ne i\). This would imply from Eq. (31) that the reduced coupling to fermions must satisfy \(g_{h_if{\overline{f}}}=1\).

3 Theoretical and experimental constraints

The Two Higgs Doublets Model plus a Singlet possesses a large freedom in the scalar sector, coming from the large number of free parameters of the scalar potential. In order to obtain a viable model, many theoretical and experimental constraints have to be imposed on the scalar potential like perturbative unitarity, vacuum stability, electroweak precision observables and constraints from Higgs data. In what follows, we will briefly describe these constraints.

3.1 Boundedness from below (BFB) of the potential

In order to ensure a stable vacuum, the scalar potential has to be bounded from below in any directions in the field space as the field strength becomes extremely large. At large field values, the scalar potential is fully dominated by quartic couplings on which the BFB will depend only.

At large field strength, the potential defined by Eq. (2) is generically dominated by the quartic terms:

$$\begin{aligned}&V^{(4)}(H_1,H_2,S) \nonumber \\&\quad = \frac{\lambda _1}{2} \left( H_1^\dagger H_1 \right) ^2\nonumber \\&\qquad +\, \frac{\lambda _2}{2} \left( H_2^\dagger H_2 \right) ^2 + \lambda _3\, H_1^\dagger H_1\, H_2^\dagger H_2 + \lambda _4\, H_1^\dagger H_2\, H_2^\dagger H_1\nonumber \\&\qquad +\,\frac{\lambda _5}{2} \left[ \left( H_1^\dagger H_2 \right) ^2+ \left( H_2^\dagger H_1 \right) ^2 \right] \nonumber \\&\qquad +\,\frac{1}{8} \lambda _6 S^4 +\frac{1}{2} \lambda _7 \left( H_1^\dagger H_1 \right) S^2+\frac{1}{2}\lambda _8 \left( H_2^\dagger H_2 \right) S^2 \end{aligned}$$
(32)

The study of \(V^{(4)}(H_1,H_2,S) \) will thus be sufficient to obtain the main constraints. The full BFB constraints read as

$$\begin{aligned}&\lambda _1,\,\lambda _2\,,\,\lambda _6> 0 , \quad \lambda _3 + \sqrt{\lambda _1\lambda _2} > 0 \end{aligned}$$
(33)
$$\begin{aligned}&\lambda _3 + \lambda _4 - |\lambda _5| + \sqrt{\lambda _1\lambda _2} > 0 \end{aligned}$$
(34)
$$\begin{aligned}&\lambda _7> -\sqrt{\lambda _1\lambda _6}, \quad \quad \lambda _8 > -\sqrt{\lambda _2\lambda _6} \end{aligned}$$
(35)

for \(\lambda _7>0 \, \text {and}\, \lambda _8 > 0 \).

If \(\lambda _7\, \text {or}\, \lambda _8 < 0\), we have to satisfy two additional constraints:

$$\begin{aligned}&\lambda _3\,\lambda _6 - \lambda _7\lambda _8 + \sqrt{(\lambda _1\lambda _6 - \lambda _7^2)(\lambda _2\lambda _6 - \lambda _8^2)} > 0 \end{aligned}$$
(36)
$$\begin{aligned}&\lambda _6\,(\lambda _3+\lambda _4 +|\lambda _5|) - \lambda _7\lambda _8\nonumber \\&\qquad + \sqrt{(\lambda _1\lambda _6 - \lambda _7^2)(\lambda _2\lambda _6 - \lambda _8^2)} > 0 \end{aligned}$$
(37)

Full technical details on the proof of these constraints can be found in Appendix (A).

3.2 Perturbative unitarity

To constrain the scalar potential parameters of the N2HDM further one can ask that tree-level perturbative unitarity is preserved for a variety of scattering processes: gauge boson-gauge boson scattering, scalar-scalar scattering and also scalar-gauge boson scattering. Since the equivalence theorem states that at high energy limit \(\sqrt{s}\) the amplitudes of a scattering process involving longitudinally polarized gauge bosons V are asymptotically equal, up to correction of the order \(m_V/\sqrt{s}\), to the corresponding scalar amplitudes in which longitudinally polarized gauge bosons are replaced by their corresponding Goldstone bosons. We conclude that perturbative unitarity constraints can be implemented by considering pure scalar-scalar scattering only.

In order to derive the perturbative unitarity constraints on the scalar parameters of N2HDM we follow Refs. [38, 39]. According to [38, 39], one computes the scattering amplitude in the weak eigenstate basis where the quartic couplings have only \(\lambda _i\) dependence and no dependence on the mixing angles: \(\alpha _i\) and \(\beta \). The important point is that the amplitude expressed in the mass eigenstate fields can be transformed into the amplitude for the non-physical fields by making a unitary transformation. The eigenvalues for the scattering amplitude should be unchanged under such a unitary transformation.

In the Appendix (B) we present the technical details of the different \(2\rightarrow 2\) scattering amplitudes. The explicit forms of the eigenvalues at tree level are given by:

$$\begin{aligned} |\lambda _3+\lambda _4|\ ,\ |\lambda _3\pm \lambda _5|\ , \ |\lambda _3+2\lambda _4 \pm 3\lambda _5|< & {} 8\pi \\ \big |\frac{\lambda _7}{2}\big |\ , \ \big |\frac{\lambda _8}{2}\big |\ , \ |\frac{\lambda _6}{4}|< & {} 8\pi \\ \left| \frac{1}{2}(\lambda _1+\lambda _2\pm \sqrt{(\lambda _1-\lambda _2)^2+4\lambda _4^2})\right|< & {} 8\pi \\ \left| \frac{1}{2}(\lambda _1+\lambda _2\pm \sqrt{(\lambda _1-\lambda _2)^2+4\lambda _5^2})\right|< & {} 8\pi \end{aligned}$$

Other eigenvalues are coming from the cubic polynomial equation associated to the submatrix \({{\mathcal {M}}}_2\) corresponds to scattering with one of the following initial and final states: \((\phi _1^+\phi _1^-\), \(\phi _2^+\phi _2^-\), \(\frac{\phi _1\phi _1}{\sqrt{2}}\),\(\frac{\phi _2\phi _2}{\sqrt{2}}\),\(\frac{\phi _s\phi _s}{\sqrt{2}}\), \(\frac{\chi _1\chi _1}{\sqrt{2}}\),\(\frac{\chi _2\chi _2}{\sqrt{2}})\). For more details, see Appendix (B).

Moreover, we also force the potential to be perturbative by imposing that all quartic couplings of the scalar potential satisfy \(|\lambda _i| \le 8 \pi \) (\(i=1,\ldots ,8\)).

3.3 Electroweak precision test observables (EWPT)

The oblique parameters S, T, and U are known to provide an indirect probe of new physics BSM for theories that process \(SU(2) \times U(1)\) symmetry [41, 42]. These parameters quantify deviations from the SM in terms of radiative corrections to the W, Z and the photon self-energies. In the framework of N2HDM, the Higgs doublet couples to the W and Z gauge bosons via the covariant derivative. Due to singlet and doublet admixtures in the scalar sector, the singlet field will also couple to the gauge bosons W and Z. Therefore, both neutral Higgs \(h_i\), A and charged Higgs will contribute to S and T parameters which are very well constrained by electroweak precision test observables. These EWPT constraints will be converted to limits on the mixing angles and/or masses splitting among the N2HDM spectrum. The extra-contribution to S, T and U parameters for N2HDM are given in Appendix (C).

In order to study the correlation between S and T, we perform the \(\chi ^2\) test over the allowed parameter space of N2HDM. Our \(\chi ^2_{S, T}\) is defined as:

$$\begin{aligned} \chi ^2_{S,T}= & {} \frac{1}{\hat{\sigma }^2_{1}(1-\rho ^2)}(S - {\hat{S}})^2 + \frac{1}{\hat{\sigma }^2_{2}(1-\rho ^2)}(T - {\hat{T}})^2 \nonumber \\&- \,\frac{2\rho }{\hat{\sigma }_{1}\hat{\sigma }_{2}(1-\rho ^2)}(S - {\hat{S}})(T - {\hat{T}}), \end{aligned}$$
(38)

where S and T are the computed quantities within N2HDM framework [22, 43, 44]. \({\hat{S}}\) and \({\hat{T}}\) are the measured values of S and T, \(\hat{\sigma }_{1,2}\) are their one-sigma errors and \(\rho \) their correlation [45],

$$\begin{aligned} S = 0.04 \pm 0.11, \quad T = 0.09\pm 0.14, \quad \rho _{S,T} = 0.92 \end{aligned}$$
(39)

It is worth noting here that we have checked the limits on the oblique parameters with the 2HDM, in this sense, our results match exactly to those outlined in [46, 47].

In addition, we have indirect experimental constraints from B physics observables on the contribution of the N2HDM such as \(\tan \beta \) and \(m_{H^\pm }\). In the N2HDM, the charged Higgs coupling to fermions is not at all affected by the singlet component of the additional Higgs. Therefore, constraints from \(B\rightarrow X_s\gamma \) and \(B_q\) mixing will be the same as for the usual 2HDM model. We remind the reader that the recent experimental results presented by the Heavy Flavor Averaging Group (HFAG) [48] of \(B(B\rightarrow X_s \gamma )\) have changed in a significant way the bounds on the charged Higgs boson mass. For instance, in N2HDM Type-II, the measurement of the BR\((B \rightarrow X_s\gamma )\) constrains charged Higgs mass to be larger than about 570 GeV [45, 49], while in Type-I one can still obtain a charged Higgs boson with a mass as low as \(100-200\) GeV provided that \(\tan \beta \ge 2\). In addition, recent analysis [45] for the 2HDM shows that \(\varDelta m_s\) (resp \(B_d\rightarrow \mu \mu \)) constraint requests that \(\tan \beta >2.5\) (resp \(\tan \beta >3\)). In fact, \(\varDelta m_s\) is only sensitive to charged Higgs, then the limit \(\tan \beta >2.5\) would apply both for 2HDM and N2HDM. However, \(B_d\rightarrow \mu \mu \) is sensitive both to charged Higgs as well as to neutral higgses \(h_{1,2,3}\), therefore the limit on \(\tan \beta \) could be different in 2HDM and N2HDM. Therefore, in what follows we will require that \(\tan \beta >2.5\).

3.4 Constraints from Higgs data

Both ATLAS and CMS experiments of the LHC Run1 with 7 and 8 TeV and Run2 with 13 TeV confirmed the discovery of a Higgs boson with a mass around 125 GeV. Both groups performed several measurements on the Higgs boson couplings to the SM particles. Recently, both ATLAS and CMS Collaborations have announced the observation of Higgs bosons produced together with a top-quark pair [8, 9]. All these measurements seem to be in perfect agreement with SM predictions.

In the case of N2HDM, all tree-level Higgs couplings to fermions and gauge bosons are modified with the mixing parameters \(\alpha _i\) and \(\beta \). The loop-mediated processes such as \(gg\rightarrow h_i\), \(h_i\rightarrow \gamma \gamma \) and \(h_i\rightarrow \gamma Z\) will be affected both by the mixing angles as well as by the additional charged Higgs \(H^\pm \) loops which depend on the triple scalar coupling \(h_iH^\pm H^\mp \).

To study the effects of ATLAS and CMS measurements on N2HDM, we take into account experimental data from the observed cross section times branching ratio divided by the corresponding SM predictions for the various channels, i.e. the signal strengths of the Higgs boson defined by:

$$\begin{aligned} \mu _i^f = \frac{\sigma _i(h) Br(h \rightarrow f)}{\sigma _i^{SM}(h) Br^{SM}(h \rightarrow f)} \end{aligned}$$
(40)

where i stand for different modes of Higgs production. The dominant mechanisms of Higgs production are gluon fusion (ggF), followed by vector boson fusion (VBF), Higgs-strahlung (Vh) and associated production with top-quark pairs (\({\overline{t}}th\)).

All these various signal strength channels are included in our analysis through the public code HiggsBounds [50,51,52] and HiggsSignals [53] which also include previous LEP and Tevatron experimental searches.

As said previously, in our analysis, we will assume that \(h_2\) is the 125 GeV Higgs boson discovered while \(h_1\) would be lighter than \(h_2\). Therefore, once the decay channels \(h_2\rightarrow h_1h_1\) and/or \(h_2\rightarrow AA\) are open, the subsequent decays of \(h_1/A\) into fermions, photons or gluons, will lead either to invisible or undetected \(h_2\) decays that can be constrained by using global analysis to the present ATLAS and CMS data to Higgs couplings.

We stress here that there are also searches for non-detected decays of the SM Higgs boson both by ATLAS and CMS. CMS looks for the following SM Higgs production channels: gluon fusion, vector boson fusion, and Higgsstrahlung process \(pp\rightarrow VH\) (V=W or Z) with subsequent invisible Higgs decays. Upper limits are placed on \(Br(H\rightarrow invisible)\), as a function of the assumed production cross sections. The combination of all the above channels, assuming SM production, yields an upper limit of 0.24 on the \(BR(H\rightarrow invisible)\) at the 95\(\%\) confidence level [54]. ATLAS collaboration performs a search for an invisible decay of the Higgs through \(pp\rightarrow ZH\) process with a leptonic subsequent decay of the Z [55]. Their limit is slightly weaker than CMS results. In addition, it’s worth mentioning that a new observed (expected) upper limit of 0.19 (0.15) has been derived recently on the \(BR(H\rightarrow invisible)\) at the 95\(\%\) confidence level [56] from the combination of \(\sqrt{s}=~7,~8~\text {and}~13\) TeV searches data.

In our study, we will use the fact that the total branching fraction of the SM-like Higgs boson into undetected BSM decay modes is constrained, as mentioned, by \(BR(H\rightarrow invisible) \le 0.24\) where \(BR(H\rightarrow invisible)\) designate \(BR(h_2 \rightarrow h_1h_1)\) or the sum of \(BR(h_2 \rightarrow h_1h_1)\) and \(BR(h_2 \rightarrow AA)\), \(BR(h_2 \rightarrow Z^*A)\) and \(BR(h_2 \rightarrow W^* H^\pm )\) if the later is open.Footnote 1

4 Numerical results

Before discussing our results, we would like to comment on previous related works. In the previous studies on the N2HDM, several phenomenologically viable scenarios of N2HDM type-I and type-II were summarized in Ref. [31, 59, 60]. These studies discuss the allowed singlet-doublet admixture of Higgses \(h_i\) and also analyze the production and the decay rate of the non SM-like Higgs bosons into the most important SM final state channels, where one of the neutral scalar \(h_i\) is chosen as the discovered Higgs boson at 125 GeV, \(h_{125}\). The mass-degenerate case is suppressed by requiring a 5 GeV mass splitting between the \(h_{125}\) and the other neutral scalar.

In the above-mentioned studies, the branching ratios and decay widths of the Higgs bosons of the Next-to-Two-Higgs-Doublet Model (N2HDM) are computed with the N2HDECAYFootnote 2 code. The program is documented in [61].

We recall that another recent study on the extension of 2HDM by adding a singlet scalar is presented in Ref. [62], which discusses the implication of this extension on the decay rate of the heavy pseudo-scalar and the charged Higgs boson.

As mentioned previously, we concentrate here on the case where \(h_2\) is the SM-like Higgs, \(h_1\) is lighter than 125 GeV and investigate the phenomenology of the neutral Higgses \(h_{1,2,3}\).

4.1 Parameter scan

The scalar potential Eq. (2) has 15 independent parameters: four masses, 8 quartic couplings \(\lambda _{1,\ldots ,8}\) and 3 vacuum expectation values. Three masses can be eliminated by the use of the 3 minimization conditions Eq. (6). Moreover, after electroweak symmetry breaking, from the kinetic terms of the Higgs doublets, the W and Z gauge bosons acquire masses which are given by \(m_W^2 = \frac{1}{2}g^2 \left( v_1^2+v_2^2 \right) \) and \(m_Z^2 = \frac{1}{2}\left( g^2 +g'^2 \right) \left( v_1^2+v_2^2 \right) \), where g and \(g'\) are the \(SU_L(2)\) and \(U_Y(1)\) gauge couplings. The combination \(v_1^2 +v_2^2\) is thus fixed by the electroweak scale through the well known relation \(v^2=v_1^2 + v_2^2 =\left( 2\sqrt{2}G_F \right) ^{-1}\), and we are left with 11 free parameters. By simple algebraic calculations, from the mass matrix relations, one can express all the quartic couplings \(\lambda _i\) as a function of the physical masses, \(\mu ^2\), \(\tan \beta \) and the mixing angles \(\alpha _i\).Footnote 3 One can then take the following set of free independent parameters:

$$\begin{aligned} \alpha _{1,2,3},\, \tan \beta ,\, v_S,\, m_{h_{1,2,3}},\, m_{A},\, m_{H^\pm }\, \ \hbox {and}\ \ \mu ^2 \end{aligned}$$

with the convention \(m_{h_1}< m_{h_2} < m_{h_3}\).

Note that the usual 2HDM is recovered from N2HDM by taking the following limits:

$$\begin{aligned}&\alpha _1 \rightarrow \alpha +\frac{\pi }{2}, \ \ \alpha _2 \rightarrow 0 \ \ \hbox {and} \ \ \alpha _3 \rightarrow 0 \end{aligned}$$
(41)

In our analysis, we will study the consistency of having the second Higgs \(h_2\) as the 125 GeV SM-like Higgs. This scenario opens morebeyond Standard Model decay channels for \(h_2\) such as \(h_2\rightarrow h_1 h_1\) and probably \(h_2\rightarrow AA, AA^*, Z^*A, W^*H^\pm \). In order to calculate the decay widths and branching fractions of the Higgs bosons, we have implemented a private Fortran code, based on HDECAY [63]. The main program is linked to HiggsBounds and HiggsSignals libraries. We also implement the theoretical constraints (unitarity and boundedness from below), the oblique parameters (S, T, U). In the computation of the decay width of \(h_i\), we include the off-shell decays such as \(h_i\rightarrow \{Z^*A, W^{*\mp }H^\pm \} \) and \(h_i \rightarrow VV^*\) and also \(h_i\rightarrow V^*V^*\) if needed. We note also that in the case of \(h_i\rightarrow \gamma V\), with \(V=\gamma ,Z\), we include W, top, bottom and charged Higgs loops together with the high order QCD corrections to \(h_i\rightarrow \gamma V\).

In order to display the allowed regions for the parameters, we have considered both of the exclusions from both HiggsBounds-5.1beta and HiggsSignals-2.1.0beta to compute the value of \(\chi ^2_{min}\) considering the combination of 8 TeV and 13 TeV Higgs signal strength data from run-I and run-II. Thus, we show the best fit at \(95.5\%\) CL, which corresponds to \( \varDelta \chi ^2 \le 5.99\) where \(\varDelta \chi ^2 = \chi ^2-\chi ^{2}_{min}\).

Fig. 1
figure 1

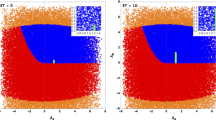
The left panel shows the parameter space allowed by the theoretical constraints (Unitarity, Perturbativity and BFB) for (\(\lambda _7,\lambda _8\)) for \(\lambda _6 =(1,4,12)\). Note the complete overlap between black, black and red for positive \(\lambda _{6,7}\). The right panel illustrates the correlation between oblique parameters S and T. The errors for \(\chi ^2_{ST}\)-square fit are 99.7\(\%\) CL (black), 95.5\(\%\) CL (green) and 68\(\%\) CL (red)

Full size image

In the left panel of Fig. 1, we show the allowed parameter for \(\lambda _{7,8}\) for various values of \(\lambda _6\) taking into account perturbative unitarity and BFB constraints. We note first that there is a complete overlap between the three colors for positive \(\lambda _{7,8}\). One can see that for negative \(\lambda _{7,8}\), the theoretical constraints restrict their strength for small \(\lambda _6\). The restriction is relaxed for large \(\lambda _6\approx 4\pi \).

In the right panel of Fig. 1, we present the correlation between S and T, after taking into account the theoretical constraints and the exclusion from Higgs Bounds at 95% CL. The red, green and black points represent the points with \(\varDelta \chi ^2_{ST}\) value within the \(1 \sigma \), \(2\sigma \) and \(3\sigma \) interval. Note that \( \varDelta \chi ^2_{ST}=\chi ^2_{ST}-\chi ^{2,min}_{ST}\) where \(\chi ^{2,min}_{ST}\) is the minimum value of \(\chi ^2_{ST}\) given by Eq. (38).

4.2 Results for N2HDM type I

In this section, we study the case of N2HDM type I, where both \(h_1\) and A could be rather light. We scan over the following range:

$$\begin{aligned}&m_{h_1}\in [10, 120]\ \text {GeV}, \ \ m_{h_3}\in [200, 700]\ \text {GeV}, \nonumber \\&\quad m_{H^\pm }\in [80, 700]\ \text {GeV}, \nonumber \\&m_{A}\in [62.5, 700]\ \text {GeV}, \ \ \mu ^2\in [0, 1.5\times 10^3]\ \text {GeV}, \nonumber \\&\quad v_{S} = 300\ \text {GeV}, \nonumber \\&\frac{-\pi }{2}<\alpha _{1}<\frac{\pi }{2}, \ \ \frac{-\pi }{6}<\alpha _{2,3}<\frac{\pi }{6}, \ \ \text {and} \ 2.5<\tan \beta <25, \nonumber \\ \end{aligned}$$
(42)

In our scan we allow \(h_1\) to be in the range [10, 124] GeV while \(m_A\ge 62.5\) GeV. In such configuration, only \(h_2\rightarrow h_1h_1\) and/or \(h_2\rightarrow AZ^*,H^\pm W^{\mp *}\) can be open. \(h_2\rightarrow AA^*\rightarrow Aff'\) is suppressed both by the phase space and the coupling of A to light fermions. The non detected decays of \(h_2\), which is identified here as the Higgs-SM-like, such as \(h_2\rightarrow h_1h_1, AA^*, AZ^*, H^\pm W^{\mp *}\) if open should not exceed 24% as we explain below.

To be consistent with the EW precision measurements, such light \(h_1\) and A are naturally also accompanied by a light charged Higgs. We recall that a light charged Higgs state is allowed by the constraint \(B\rightarrow X_s\gamma \) in N2HDM of type I.

4.3 \(h_1\) decays

We study first the decay of \(h_1\) into SM particles. As one can see from the couplings of \(h_1\) to fermions given by Eq. (19), \(h_1\) could be fermiophobic if \(R_{12}\propto \cos \alpha _2 \sin \alpha _1\) vanish. This scenario might happen if we take \(\alpha _1\approx 0\) and/or \(\alpha _2 \approx \pi /2\) which is possible since both \(\alpha _1\) and \(\alpha _2\) are free parameters in this model.

  • The case where \(\alpha _2=\pi /2\) corresponds to \(h_1\) being pure singlet and will not be discussed here.

  • The case where \(\alpha _1=0\) with \(\alpha _2\ne \pi /2\), \(h_1\) contains both doublet and singlet component.

Fig. 2
figure 2

\(Br(h_1\rightarrow W^+W^-)\) and \(Br(h_1\rightarrow \gamma \gamma )\) vs. \(Br(h_1\rightarrow b{\overline{b}}, \tau ^+\tau ^-)\) (left), and \(m_{h_1}\) (right) at 95% .CL

Full size image

In Fig. 2, we show the branching ratio of \(h_1\rightarrow W^+W^-\) as a function of \(h_1\rightarrow \gamma \gamma \) with \(Br(h_1\rightarrow b{\overline{b}}+\tau ^+\tau ^-)\) represented on the horizontal axis on the left panel, while on the right panel, we show \(m_{h_1}\). Since \(m_{h_1}\le 125\) GeV, \(h_1\rightarrow W^+W^-\) will proceed with one or both W being off-shell. We first mention that the singlet component of \(h_1\) does not exceed 50% in our case, which makes \(h_1\) dominated by doublet components. \(h_1\) has a large doublet component due to the large uncertainties on the LHC measurement, which does not constraint too much \(h_2VV\) and \(h_2ff\) couplings to be fully SM-like, and this leaves rather large room for \(h_1VV\) as well as \(h_3VV\). Fitting \(h_1VV\) within LHC uncertainties still allows \(h_1\) to have large doublet component.

As one can see, in most cases \(h_1\) would decay significantly into a bottom pair unless \(\alpha _1\) vanishes, which is the fermiophobic limit for \(h_1\). In this case, it is clear that \(h_1\rightarrow \gamma \gamma \) could reach its maximum value, when \(Br(h_1\rightarrow b{\overline{b}})\) and \(Br(h_1\rightarrow \tau ^+\tau ^-)\) are very suppressed. When \(h_1\) is fermiophobic, \(h_1\rightarrow VV^*\) or \(h_1\rightarrow V^*V^*\), \(V=Z,W\) can compete with \(h_1 \rightarrow \gamma \gamma \). In what follows, we only discuss \(h_1\rightarrow WW\) since \(h_1\rightarrow ZZ\) is smaller. In fact, \(h_1\rightarrow W^*W^*\) which is open for \(m_{h_1}<m_W\) is very suppressed due to phase space while for \(m_{h_1}\ge m_W\), \(h_1\rightarrow WW^*\) is open and could strongly compete with \(h_1 \rightarrow \gamma \gamma \). This is shown in the left and right panel of Fig. 2, where we can see \(Br(h_1\rightarrow WW^*)\) as a function of \(Br(h_1\rightarrow \gamma \gamma )\). Close to the fermiophobic limit where \(h_1\rightarrow b{\overline{b}}\) and \(h_1\rightarrow \tau ^+\tau ^-\) are suppressed, if the mass of \(h_1\) is larger than the W boson mass, then \(h_1\rightarrow WW^*\) can dominate \(h_1 \rightarrow \gamma \gamma \) in some cases.

Fig. 3
figure 3

\(Br(h_1\rightarrow \gamma \gamma )\) as a function of \(Br(h_1 \rightarrow \tau ^+ \tau ^- + b{\overline{b}})\) vs. \(Br(h_1 \rightarrow (H^{\pm }W^\mp + AZ)\) (left panel), \(Br(h_1 \rightarrow W^+W^-)\) (middle panel) and \(R_{11}^2\) (right panel) at 95%C.L

Full size image

One could have also the following scenario: both \(h_1\rightarrow f{\overline{f}}\), \(h_1\rightarrow VV^*\) and \(h_1\rightarrow \gamma \gamma , \gamma Z\) are rather small, while the branching ratio of \(Br(h_1\rightarrow A Z^*)+Br(h_1\rightarrow H^\pm W^{*\mp })\) becomes significant which can be understood from the sum rules Eq. (30). Due to the smallness of \(h_1VV\) coupling and \(R_{13}\) component, the sum rule given by Eq. (30) implies that \(h_1AZ\) and \(h_1W^\pm H^\mp \) could become significant. This is illustrated in the left panel of Fig. 2 with the black dots in the left-down corner where both \(Br(h_1\rightarrow W W^*) \approx Br(h_1\rightarrow \gamma \gamma )\approx 10^{-4}\) and also \(\sum Br(h_1\rightarrow \tau ^+ \tau ^- + b{\overline{b}})\) are rather small.

The above configuration is illustrated clearly in Fig. 3 (left and middle) where we show the correlation between \(\sum Br \left( h_1\rightarrow \tau ^+ \tau ^- + b{\overline{b}}\right) \) and \(Br(h_1\rightarrow \gamma \gamma )\) as a function of \(Br(h_1 \rightarrow H^{\pm }W^\mp + AZ)\) and \(Br(h_1 \rightarrow W^+W^-)\) on the horizontal axis. It can be seen that, when the fermionic (\(\tau ^+\tau ^-\), \(b{\overline{b}}\)) and bosonic (\(\gamma \gamma \), \(W^+W^-\), ZZ) decays of \(h_1\) are suppressed, the Higgs to Higgs decays \(h_1 \rightarrow H^{\pm }W^\mp \) and/or \(h_1 \rightarrow ZA\) become significant. As it can be seen, this happens only in a tiny region of the parameter space. In the right panel of Fig. 3, we can see that \(h_1\) has a large doublet component in most cases. The fact that \(Br(h_1 \rightarrow H^{\pm }W^\mp )\) and/or \(Br(h_1 \rightarrow ZA)\) are either maximal 100% or minimal close to 0% with no intermediate range is mainly due to HiggsSignal which requires that \(\chi ^2\) should have a correct value.

In Fig. 4 we illustrate \(\kappa _f^{h_1}\) as a function of \(\kappa _V^{h_1}\) with \(R_{1i} (i=1,2,3)\) component of \(h_1\) on the horizontal axis. Note that \(\kappa _V^{h_i}\) and \(\kappa _f^{h_i}\) are the normalized couplings of neutral Higgs to a pair of gauge bosons and to a pair of fermions respectively, discussed in Sects. (2.3) and (2.4); \(\kappa _V^{h_i} \equiv g_{h_i VV}\) and \(\kappa _f^{h_i} \equiv g_{h_i f f}\).

From this plot, one can read that the doublet component is rather large in most of the cases leaving only small singlet component which is less than 50% . One can also learn that when \(\kappa _f^{h_1}\) and \(\kappa _V^{h_1}\) are suppressed, the doublet component is very large. Which means that \(h_1\) is mainly coming from the doublet components. According to the sum rule Eq. (25), the strength of the SM Higgs interaction, at tree level, is shared by the three neutral Higgs bosons of the N2HDM, thus, the couplings of the neutral scalars to vector bosons cannot be enhanced over the SM value and for that we have \(\mid \kappa _V^{h_1}\mid \le 1\) which is consistent with Fig. 4. On the other hand, there is a large area of the parameter space where \(\mid \kappa _f(h_1)\mid \le 1\). On the right panel of Fig. 4, we show the sensitivity to \(\tan \beta \) where we can see a linear correlation between \(\kappa _f^{h_1}\) and \(\kappa _V^{h_1}\) at large \(\tan \beta \).

Fig. 4
figure 4

\(\kappa _f^{h_1}\) as a function of \(\kappa _V^{h_1}\) with \(R_{1i}^2\) (i=1,3) on the horizontal axis (left and middle panel), and with \(\tan \beta \) on the right panel

Full size image
Fig. 5
figure 5

\(\left( \kappa _V^{h_2},\kappa _f^{h_2}\right) \) in N2HDM type-I as a function of \(R_{22,23}\) (left and middle panel), and \(\tan \beta \) on the right panel. The black lozenge stands for the SM value

Full size image

Let us mention that in this scenario with suppressed \(h_1f{\overline{f}}\) and \(h_1VV\) couplings, \(h_1\) can not be produced in the usual channel such as gluon fusion, vector boson fusion or Higgsstrahlung. According to sum rules Eq. (30), if the singlet component of \(h_1\) is small and \(h_1VV\) coupling is suppressed, then \(h_1ZA\) and \(h_1W^\pm H^\mp \) are enhanced, therefore \(h_1\) can be produced in one of the following processes: \(pp\rightarrow Z^*\rightarrow h_1A\) or \(pp\rightarrow W^*\rightarrow h_1H^\pm \) which would lead respectively to the following final states ZAA or \(WH^\pm H^\mp \).

4.4 \(h_2\) decays

We now discuss the decay of the SM-like \(h_2\). We first show the consistency of \(h_2\rightarrow VV\) and \(h_2\rightarrow f{\overline{f}}\) with LHC data. For this purpose, we illustrate in Fig. 5 the correlation between \(\kappa _V^{h_2}\) and \(\kappa _f^{h_2}\) as a function of \(R_{2i}^2\). According to the sum rule Eq. (25), \(\kappa _V^{h_2}< 1\), and this is clearly illustrated in the plot. One can see from the plot that when \(\kappa _V^{h_2}\approx 1\) we have also \(\kappa _f^{h_2}\approx 1\), this is a consequence of the sum rule Eq. (31). However, the suppression of \(\kappa _V^{h_2}\) could be of the order of 12% and it could happen both for \(\kappa _f^{h_2}<1\) or \(\kappa _f^{h_2}>1\). Note that the suppression of both \(\kappa _f^{h_2}\) and \(\kappa _V^{h_2}\) takes place when the singlet component of \(h_2\) is rather large \(R_{23}^2>0.1\). One can see that \(\kappa _f^{h_2}\) could reach a value less than 0.8 for \(R_{23}^2\approx 0.25\). It is also clear from the plot that one can have an enhancement of \(\kappa _f^{h_2}\) in the range of \([1.05-1.15]\) for small singlet component of \(h_2\) (\(R_{23}^2\approx 0.1\)) and moderate \(\tan \beta \).

In Fig. 6, we show the correlation between \(\kappa _{gg}^{h_2}\) and \(\kappa _{\gamma \gamma }^{h_2}\) on the left panel and the correlation between \(\kappa _{\gamma \gamma }^{h_2}\) and \(\kappa _{\gamma Z}^{h_2}\) on the right panel, the SM value is indicated as a black box. \(\kappa _{gg}\), \(\kappa _{\gamma \gamma }\) and \(\kappa _{\gamma Z}\) are the scaling factors for loop-induced channels which are defined by:

$$\begin{aligned} \kappa _j^2 = \varGamma ^j/ \varGamma ^j_{SM}\,,~\quad j=gg,\ \gamma \gamma ,\ Z\gamma \end{aligned}$$
(43)

j stands for a given loop process decay and \(\varGamma ^j\) is the partial decay rate. Note that \({\kappa _{gg} \equiv \kappa _{gg}^{h_2}}\), \({\kappa _{\gamma \gamma } \equiv \kappa _{\gamma \gamma }^{h_2}}\), \({\kappa _{Z\gamma } \equiv \kappa _{Z\gamma }^{h_2}}\)

One can see that the deviations of \(\kappa _{gg}^{h_2}\), \(\kappa _{\gamma \gamma }^{h_2}\) and \(\kappa _{\gamma Z}^{h_2}\) from the SM value can reach 15%. Note that in both \(\kappa _{\gamma \gamma }^{h_2}\) and \(\kappa _{\gamma Z}^{h_2}\), we have, in most cases, a suppression of the rate compared to the value predicted by the SM. The figure also shows that we have suppression of \(\kappa _{gg}^{h_2}\), \(\kappa _{\gamma \gamma }^{h_2}\) and \(\kappa _{\gamma Z}^{h_2}\) rate for \(h_2\) with relatively large singlet component. We also stress that most of the cases \(\kappa _{\gamma Z}^{h_2}< \kappa _{\gamma \gamma }^{h_2}\).

Fig. 6
figure 6

Correlations: between \(\kappa _{gg}^{h_2}\) and \(\kappa _{\gamma \gamma }^{h_2}\) versus \(R_{23}^2\) and between \(\kappa _{\gamma \gamma }^{h_2}\) and \(\kappa _{Z \gamma }^{h_2}\) as a function of the singlet component \(R_{23}^2\) in N2HDM type-I at 95% C.L

Full size image
Fig. 7
figure 7

\(Br(h_2 \rightarrow h_1 h_1)\) and \(Br(h_2 \rightarrow AZ+ H^+W^-)\) versus \(\kappa _{h_2 AZ}\) (left) and \(\kappa _{h_2h_1h_1}\) (middle). On the right panel \(Br(h_2 \rightarrow AZ)\) versus \(\kappa _V^{h_2}\) as a function of \(\kappa _{h_2 AZ}\) at 95% C.L in N2HDM type-I

Full size image

As we have seen in Fig. 5, decays of \(h_2\) into SM particles such as WW, ZZ, \(b{\overline{b}}\) and \(\tau ^+\tau ^-\) are consistent with LHC measurements with deviations from SM predictions that could goes up to 10–15%. However, these deviations are mainly due to experimental uncertainties on all the LHC measurements which could be larger than 10% in some channels. Therefore, taking into account these uncertainties, there is still a room for the non-detected SM Higgs decays such as \(h_2\rightarrow h_1h_1, AA, AA^*, AZ^*, H^\pm W^*\). In our scan we assume that \(m_A>62.5\) GeV, therefore \(h_2\rightarrow AA\) will not be open and \(h_2\rightarrow AA^*\) is rather suppressed. We are only left with \(h_2\rightarrow h_1h_1, AZ^*, H^\pm W^*\) channels. As explained above, all these additional decays of the SM Higgs should not exceed 24%.

We show in Fig. 7 \(Br(h_2\rightarrow h_1h_1)\) as a function of \(Br(h_2\rightarrow Z^*A)+Br(h_2\rightarrow W^*H^\pm )\) with \(\kappa _{h_2h_1h_1}\) on the horizontal axis (left panel). While on the right panel we illustrate the singlet component of \(h_1\) on the horizontal axis. Note that the couplings \(h_1AZ\) and \(h_1W^\mp H^\pm \) are exactly the same (see Eq. (30)). Therefore, if \(m_A\approx m_{H\pm }\) then \(Br(h_2\rightarrow Z^*A)\) and \(Br(h_2\rightarrow W^*H^\pm )\) are of the same order. The total amount for \(Br(h_2\rightarrow h_1h_1)+Br(h_2\rightarrow Z^*A)+Br(h_2\rightarrow W^*H^\pm )\) should not exceed 24% as requested from the non-detected decay of the SM Higgs, and this is rather clear from Fig. 7. The plots also display the correlation between \(Br(h_2\rightarrow h_1h_1)\) and \(Br(h_2\rightarrow Z^*A)+Br(h_2\rightarrow W^{*\mp }H^\pm )\). When \(Br(h_2\rightarrow h_1h_1)\) is maximized, \(Br(h_2\rightarrow Z^*A)+Br(h_2\rightarrow W^{*\mp }H^\pm )\) is minimal and vice verse. One can have also a configuration where both \(Br(h_2\rightarrow h_1h_1)\) and \(Br(h_2\rightarrow Z^*A)+Br(h_2\rightarrow W^{*\mp }H^\pm )\) are of the same size. In the case where both A and \(H^\pm \) are heavier than 125 GeV, only \(h_2\rightarrow h_1h_1\) would contribute to the non-detected decay of \(h_2\).

On the middle panel of Fig. 7 it is clear that when the reduced coupling of \(h_2h_1h_1\) is large, the branching ratio \(Br(h_2\rightarrow h_1 h_1)\) is substantial which would provide an important production channel for \(h_1\) from \(h_2\) decay: \(gg\rightarrow h_2 \rightarrow h_1 h_1\) which could compete with the other production channels such as \(pp\rightarrow Wh_1\) and/or \(pp\rightarrow \{h_1A, h_1H^\pm \}\).

On the right panel of Fig. 7 we illustrate the correlation between \(Br(h_2\rightarrow Z^*A)\) and \(\kappa _V^{h_2}\) as a function of \(\kappa _{h_2AZ}\). As one can see from the plot, and according to the sum rule Eq. (30), when \(h_2VV\) is full strength, then \(Br(h_2\rightarrow Z^*A)\) is suppressed.

We have seen previously that \(Br(h_2\rightarrow h_1h_1)\) could be significant and can reach 20% in some case. In the case where \(h_1\) is dominated by the singlet component, it is well known that it is hard to produce it through the conventional channels such as ggF, VBF ect. Therefore, the process \(gg\rightarrow h_2\) followed by the decay \(h_2\rightarrow h_1h_1\) could be an important process for the production of \(h_1\). In the case where \(h_1\) is dominated by the singlet component, its decay to SM particle would be suppressed. In such case, it may be possible that \(h_1\) would decay to a pair of photons which could proceed through charged Higgs loops. Therefore, the process \(gg\rightarrow h_2 \rightarrow h_1h_1\) could lead to a spectacular 4 photons final states. In Fig. 8 (left) we illustrate the branching fraction \(Br(h_2\rightarrow h_1h_1)\times Br(h_1\rightarrow \gamma \gamma )^2\) as a function of \(m_{h_1}\). As can be seen, such branching fraction could reach 10% in some cases. On the right panel of Fig. 8, we show the production cross section for \(\sigma (gg\rightarrow h_2)\times Br(h_2\rightarrow h_1 h_1) \times Br(h_1\rightarrow \gamma \gamma )^2\).

Fig. 8
figure 8

\(Br(h_2 \rightarrow h_1 h_1)\times Br(h_1 \rightarrow \gamma \gamma )^2\) (left panel) and \( \sigma (gg \rightarrow h_2) \times Br(h_2 \rightarrow h_1 h_1)\times Br(h_1 \rightarrow \gamma \gamma )^2\) (middle and right panel) as a function of \(m_{h_1}\) versus \(Br(h_2 \rightarrow h_1 h_1)\) at 95% C.L in N2HDM type-I. Black triangles denote the excluded points from Fig. 9

Full size image

We note that for very small singlet component \(R_{13}\approx 0\) where \(h_1\) is fully dominated by the doublet components, one could have sizeable \(Br(h_2\rightarrow h_1h_1)\) as it has been noticed in the usual 2HDM [64, 65].

Recently, ATLAS published their results for the search of new phenomena in events with at least three photons [32] based on 8 TeV CM energy with 20.3 \(\hbox {fb}^{-1}\). This search was used to put constraint on an N-MSSM scenario which leads to four photons final states \(gg \rightarrow H \rightarrow a_1a_1\rightarrow 4 \gamma \) where a light pseudo-scalar, if dominated by singlet component, can decay fully into two photons with 100\(\%\) branching ratio. Following this work, it has been demonstrated in [65] that the kinematic distributions for \(qq\rightarrow H\rightarrow a_1a_1\rightarrow 4 \gamma \) and \(qq\rightarrow H\rightarrow h_1h_1\rightarrow 4 \gamma \) with \(h_1\) being CP-even are identical. Reference [65] also provide a projection for 14 TeV CM energy. Therefore results from [32] can be applied to our four photons final states. In Fig. 9, we present our predictions for \(pp\rightarrow h_2\rightarrow h_1h_1\rightarrow 4 \gamma \) for both 8 TeV and 14 TeV together with the 8 TeV exclusion from ATLAS analysis. ATLAS projection for 14 TeV is also shown in the lower band. It is clear that some benchmark points are already excluded by the 8 TeV data and the 14 TeV projection. However, several benchmarks are still alive.

Fig. 9
figure 9

Upper limit at 95% CL on \(\frac{\sigma (h_2)}{\sigma _{sm}}\times Br(h_2 \rightarrow h_1 h_1 \rightarrow 4 \gamma )\) as a function of \(m_{h_1}\) vs. \(Br(h_2 \rightarrow h_1 h_1)\) from ATLAS searches at 8 TeV (upper band) and the projection for 14 TeV (lower band) taken from [65]. The green and yellow color indicate the allowed regions at 68% and 95%, respectively

Full size image

4.5 \(h_3\) decays

We now discuss \(h_3\) decays. We show in Fig. 10 the branching fractions for \(h_3\rightarrow ff\), \(f=b, \tau , t\) and \(h_3\rightarrow VV\), \(V=\gamma , Z, W\) as a function of singlet component \(R_{33}\) and \(m_{h_3}\). It is clear that \(h_3\) is dominated by singlet component. One can see that before reaching the \(t\bar{t}\) threshold, \(h_3\rightarrow WW\) could be the dominant decay mode of \(h_3\) with a branching which can reach up to 80%, while \(h_3\rightarrow ZZ\) goes up to 20% and in such cases \(h_3\rightarrow h_1 h_1\) is suppressed. After reaching \(t\bar{t}\) threshold, \(h_3 \rightarrow t\bar{t}\) can be slightly larger than 10% for large \(m_{h_3}\) mass.

Fig. 10
figure 10

Correlation between \(Br(h_3 \rightarrow ff)\) and \(Br(h_3 \rightarrow VV)\) versus \(R_{33}^2\) (left) and \(m_{h_3}\) (right) (GeV) in N2HDM type-I

Full size image
Fig. 11
figure 11

Upper panels: (left) \(Br(h_3\rightarrow h_1 h_1)\) as a function of \(\kappa _{h_3 h_1 h_1}\) and (middle) \(Br(h_3\rightarrow h_2 h_2)\) as a function of \(\kappa _{h_3 h_2 h_2}\) with \(R_{33}^2\) displayed on the vertical and (right) the correlation between \(Br(h_3\rightarrow h_1 h_1)\) and \(Br(h_3\rightarrow h_2 h_2)\). Lower panels: correlation between \(Br(h_3\rightarrow h_1 h_1)\) and \(Br(h_3\rightarrow h_2 h_2)\) as a function of \(Br(h_3\rightarrow AA)\) (lower-left), as a function of \(Br(h_3\rightarrow WW)\) (lower-middle) and correlation between \(Br(h_3\rightarrow h_1 h_1)\) and \(Br(h_3\rightarrow h_1 h_2)\) as a function of \(m_{h_3}\)

Full size image
Fig. 12
figure 12

Correlation between \(Br(h_3 \rightarrow AZ)\) and \(Br(h_3 \rightarrow H^\pm W^\mp )\) versus \(R_{33}^2\) (left panel) and \(Br(h_3 \rightarrow AZ)\) as a function of \(\kappa _{h_3 AZ}\) and \(R_{33}^2\) (right panel)

Full size image
Fig. 13
figure 13

\(\sigma (pp \rightarrow h_3)\times Br(h_3 \rightarrow h_2h_2)\)(left panel), \(\sigma (pp \rightarrow h_3)\times Br(h_3 \rightarrow h_1h_1)\) (middle panel) and \(\sigma (pp \rightarrow h_3)\times Br(h_3 \rightarrow h_1h_2)\) (right panel) as a function of \(m_{h_3} (GeV)\) and \(R_{33}^2\) in N2HDM type-I. Solid line is the observed 95% CL exclusion limits on the production of a narrow width spin zero resonance decaying into a pair of Higgs bosons [68]

Full size image

We now discuss Higgs to Higgs decays, such as \(h_3\rightarrow h_1h_1,h_1h_2, h_2h_2\) and \(h_3\rightarrow ZA, W^\pm H^\mp \). In Fig. 11 (upper plot) we illustrate the branching ratio of \(h_3\rightarrow h_1h_1\) (left), \(h_3\rightarrow h_2h_2\) (middle) and their correlation (right). From the left panel, one can see that Br\((h_3\rightarrow h_1h_1)\) can be substantial and becomes the dominant decay mode, while from the middle panel it is clear that Br\((h_3\rightarrow h_2h_2)\) can reach 30% as a maximal value. In the case where \(Br(h_3\rightarrow h_1h_1)\) is the dominant decay, then one can have a new production mechanism for \(h_1\), namely: \(pp\rightarrow h_3\rightarrow h_1 h_1\). This production channel might be useful for the case where \(h_1\) has large singlet component in which case it will be challenging to produce it in the conventional channels.

In the lower panels of Fig. 11 we display the correlation between \(Br(h_3\rightarrow h_1 h_1)\), \(Br(h_3\rightarrow h_2 h_2)\) , \(Br(h_3\rightarrow AA)\), \(Br(h_3\rightarrow h_1h_2)\) as well as with \(Br(h_3\rightarrow WW)\).

It is clear that one can have a scenario where both \(Br(h_3\rightarrow h_2 h_2)\) and \(Br(h_3\rightarrow AA)\) are rather large with branching fractions of the order 40%. It is also clear that when \(Br(h_3\rightarrow h_1 h_1)\) and \(Br(h_3\rightarrow h_2 h_2)\) are suppressed then \(Br(h_3\rightarrow WW, ZZ)\) would become slightly large.

In Fig. 12 we show the branching fractions of \(h_3 \rightarrow AZ\) and \(h_3 \rightarrow H^\pm W^\mp \) versus \(R_{33}^2\). As one can see from the plots and according to the sum-rule Eq. (30), when \(h_3\) is dominated by the singlet component; \(R_{33}\approx 1\), then both \(h_3ZA\) and \(h_3W^\mp H^\pm \) couplings are suppressed resulting in a small branching ratio for both channels. For \(R_{33}\) away from 1, the branching fraction \(h_3 \rightarrow AZ\) and \(h_3 \rightarrow H^\pm W^\mp \) can be in the range of 10–40% in some cases.

Given that \(Br(h_3\rightarrow h_1h_1)\) can be sizeable, one can look to the amount of production cross section that one can get from \(h_3\) production followed by \(h_3\) decay into a pair of \(h_1\). We illustrate in Fig. 13 both \(pp\rightarrow h_3\rightarrow h_2h_2\) (left), \(pp\rightarrow h_3\rightarrow h_1h_1\) (middle) and \(pp\rightarrow h_3\rightarrow h_1h_2\) (right) where the production cross section of \(h_3\) is computed at \(\sqrt{s}=13\)TeV with Sushi [66, 67].

One can see that the production rate of \(h_1\) is large especially in the mass range \(200\ \text {GeV}\lesssim m_{h_3}\lesssim 250\ \text {GeV}\) when the decay channel \(h_3 \rightarrow h_1 h_1\) is kinematically allowed and both \(h_3 \rightarrow h_2 h_2\) and \(h_3 \rightarrow t {\overline{t}}\) are closed. The same behavior is observed in the middle panel, where the magnitude in the cross section is larger in the mass range \(250\ \text {GeV}\lesssim m_{h_3}\lesssim 350\ \text {GeV}\) when the decay channel \(h_3 \rightarrow h_2 h_2\) is opened and \(h_3 \rightarrow t {\overline{t}}\) mode is closed. However, one can see that after applying the constraints on the heavy scalar resonances decaying into two SM-like scalars with a mass of \(\sim 125\) GeV [68], some of the parameter space points are already excluded.

5 Conclusions

We have studied the two Higgs doublet model extended with a real singlet scalar. The spectrum contains 3 CP-even \(h_{1,2,3}\), one CP-odd and a pair of charged Higgs. We derive full set of perturbative unitarity constraints, boundedness from below constraints as well as the oblique parameters S, T and U.

In our analysis, we concentrate on the case where \(h_2\) is the SM Higgs boson observed at the LHC and assume that \(h_1\) is lighter than 125 GeV. We study the consistency of our scenario with both LHC data taken at 8 TeV and 13 TeV as well as with all the available LEP-II and Tevatron data. We have shown in the framework of N2HDM that:

  • \(h_1\) can be quasi-fermiophobic and would decay dominantly into two photons.

  • LHC data still allow a room for the non-detected decays of the SM-Higgs \(h_2\rightarrow h_1 h_1\) and others with a branching ratio of the order which can reach 24%. Such decay followed by two photons decay of \(h_1\) could lead to four photons signature, namely \(pp\rightarrow h_2\rightarrow h_1 h_1\rightarrow 4 \gamma \).

  • Comparison of ATLAS data with our four photons signal show that there is a large area of parameter space that still escapes ATLAS data

We have also shown that in N2HDM type I, \(h_2\) and \(h_3\) can decay to some exotic modes such as \(h_{2,3}\rightarrow h_1h_1\), \(h_{2,3}\rightarrow Z A\) and \(h_{2,3}\rightarrow W \pm H^\mp \) with substantial branching ratio. The production process \(gg\rightarrow h_{2,3}\) followed by the decays \(h_{2,3}\rightarrow h_1h_1, h_1h_2\) could be sizeable and could be an important source of production of \(h_1\) in the case where \(h_1\) have a large singlet component where it is rather difficult to produce it using the conventional channel.