1 Introduction

The most striking revelation of the modern cosmology is that the present universe is not only expanding yet in addition accelerating. This wonderful change in cosmic historical events has been demonstrated from a different set of high-accuracy observational data collected from different cosmic sources like Cosmic Microwave Background (CMB) [1,2,3], SuperNova type Ia (SNeIa) [4,5,6,7,8], large scale structure [9,10,11], weak lensing [12] and baryon acoustic oscillations [13]. In perspective on this it is currently believed that energy setting-up of universe has \(76 \%\) dark energy, \(20 \%\) dark matter and \(4 \%\) ordinary matter. The current accelerating expansion behavior of the universe is driven by an exotic type of force dubbed as dark energy having huge negative pressure with repulsive impacts. It is assumed that this dominant energy component repulsive by exotic gravity determines the eventual fate of the cosmos, but its enigmatic features are still not established. To investigate the perplexing nature of dark energy, various methodologies have been displayed. Modified theories of gravity are assumed to be one of the feasible decisions to reveal its mysterious nature. The modified theories are determined by replacing or adding curvature invariants as well as their matching generic functions in the geometric part of the Einstein–Hilbert action.

In the most recent years, modified theories of gravity at large scales have been proposed to observe the dark energy and dark matter in the dynamic and kinematic characteristics of stars. Although the dark energy and dark matter models are capable to solve problems effectively, nevertheless suffer from certain confinements that motivate the researchers to think about alternative theories of gravity. Moreover, the modified theories of gravity have played a significant role in attempts to explain or eliminate some of the shortcomings encountered when considering general relativity as the standard gravitational theory. Nowadays, some modifications in gravitational part of the general relativity action have been given the progression of time where the most smooth modification of general relativity is f(R) gravity [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32], which takes a general function of the Ricci scalar R in the Einstein–Hilbert action as its beginning stage. Along these lines, as a result of presenting an arbitrary function, there might be an opportunity to clarify the accelerated expansion and configuration formation of the Universe without including obscure types of dark energy or dark matter, modifying just the gravity part and not the matter one. Suitable f(R) gravity models have been assumed by some authors [30,31,32] which manifest the unification of late-time acceleration and early time inflation. Anyhow, some f(R) gravity defects in the solar system scale were announced, for example, in [33,34,35] and should exclude most of the f(R) models assumed so far. For the galactic scales, the f(R) theory additionally does not appear to be appropriate [36,37,38].

Another endeavor to expound on the issue of cosmic expanding conduct prompts to alternative theories. Specifically, Gauss–Bonnet theory is a notably strengthening modified theory in which Gauss–Bonnet invariant is \(G=R^2-4R_{\mu \nu }R^{\mu \nu }+R_{\mu \nu \lambda \sigma }R^{\mu \nu \lambda \sigma }\) where R, \(R_{\mu \nu }\) and \(R_{\mu \nu \lambda \sigma }\) signify the Ricci scalar, Ricci and Riemann tensors, respectively [39,40,41]. This 4-dimensional topological invariant completely avoids the instability of the spin-two phantom. Nojiri and Odintsov [42] presented modified Gauss–Bonnet gravity by embeddings nonexclusive function f(G) in the action of Einstein–Hilbert. Cognola and his colleagues [43] updated this impressive revelation to analyze the whole evolutionary worldview of the universe and suggested a few answers to deal with the problem of hierarchy. De Felice and Tsujikawa [44, 45] set up cosmologically suitable f(G) solutions which give reliable outcomes with close planetary system limitations. Bamba and his accomplices [46] investigated modified f(G) as well as f(G, R) models with some developing highlights of late-time cosmic acceleration and finite-time future singularities. They additionally introduced higher-order curvature and flow remedies to fix these singularities for comparing gravity models.

The curvature-matter coupling in modified theories is well-defined as a promising methodology may have the option to reveal the fascinating phenomenon of accelerated cosmic expansion. Harko and his accomplices [47] introduced curvature and flow matter coupling alluded as f(R, T) gravity for a better clarification of cosmic development. This modified theory generalized f(R) gravity by introducing an arbitrary function of the Ricci scalar R and the trace of the stress–energy tensor T. One can take note of that reliance of T might be presented by extraordinarily flawed fluids or quantum impacts. Due to the coupling among matter and geometry, the movement of test particles is non-geodesic and an additional acceleration is constantly present. The theory f(R, T) portrays the regime of the solar system very well [48]. New terms from this theory allow us to portray the galactic impacts of dark matter [49]. It was also indicated that f(R, T) gravity can give an extensive contribution to the deviation to the standard geodesic equation [50] and gravitational lensing [51]. This modified theory can be applied to investigate diverse issues of actual premium and may prompt some significant contrasts. Houndjo [52] constructed the cosmological reproduction of f(R, T) gravity for \(f(R, T)=f_{1}(R)+f_{2}(T)\) and talked about transition of matter-dominated stage to an acceleration stage. Moreover, several authors [53,54,55,56,57] have described that the cosmic acceleration of f(R, T) cosmology avoids the problem of dark energy because of the additional terms in T in field equations of the model, instead of being because of the presence of the cosmological constant. This new terms lead to the non-disappearance of the covariant derivative of the matter stress–energy tensor, i.e., \(\nabla ^{\mu }T_{\mu \nu }\ne 0\) [58,59,60,61]. The fact that the stress–energy tensor of this theory is not preserved can be connected, in a cosmological point of view, to the destruction of matter during the evolution of the universe. Many researchers [62,63,64,65,66,67,68,69,70,71,72] employed different techniques in astrophysical and cosmological phenomena within the scenario of f(R, T) theory, to discuss the consistency as well as stability of this theory.

Among the various situations proposed in the literature to contemplate gravitational phenomenology beyond general relativity, the one of astrophysical configuration models depicts both a strong probe for testing gravity on its strong field system [73] and a hopeful road to discover possible deviations from general relativity predictions. The main objective of this examination are compact spherical objects, for instance, white dwarfs and neutron stars, which depict the end-state of astrophysical progress of main-sequence stars, yet in addition other kinds of stars, for instance, brown and red dwarfs. Besides, along the decades other astrophysical objects have showed in the literature, for instance, hyperon stars [74], quark/hybrid stars [75, 76], strange stars [77,78,79,80,81,82,83,84,85,86,87,88,89,90], and significantly more exotic spheres such as boson stars [91].

The investigation of exact spherical solutions for relativistic objects is a troublesome issue due to the nearness of non-linear terms in the field equations. To determine this issue, we pursue the embedding class I method utilizing the Eisland condition to get obvious outcomes in finding new physically agreeable solutions for spherical compact structure. This is a direct, orderly and straightforward way to generate new anisotropic outcomes from a perfect distribution of fluid. The embedding class I method is a concept that shows countless intriguing constituents with regards to the construction of new spherical solutions, such as those presented in [92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117].

In this work, we have studied a new class of anisotropic general solutions to modified Einstein field equations for relativistic compact stellar structures by adopting the embedding class one method within the framework of f(R, T) gravity theory. We model an astrophysical compact configuration, namely an X-ray pulsar binary i.e., SMC X-4 and demonstrate that the new exact solution is physically suitable. The outside area is defined by the Schwarzschild vacuum geometry. The inside area is portrayed by a space–time that is acquired by embedding the manifold into a flat five-dimensional space–time. This paper is structured as follows. In Sect. 2, we have presented the basic formulation of class I space–time and the spherical symmetric metric. In Sect. 3, we give a general mathematical framework of our f(R, T) theory of gravity. In Sect. 4, we set up the relevant field equations for anisotropic matter distributions in f(R, T)-gravity, and their general solutions of anisotropic Karmarkar stars of class I space–time in Sect. 5. in Sect. 6, we have determined arbitrary constants by utilizing coordinating conditions. Some other physical salients of the anisotropic model have been described in Sects. 7 and 8 , which examines all the essential requirements that an anisotropic solution of the Einstein field equations in the system f(R, T) theory gravity must meet to be physically admissible. We finally summarize the outcomes in the last section.

2 Interior space–time and Karmarkar condition

The interior space–time for spherically symmetric space–time is chosen as,

$$\begin{aligned} ds_-^2=e^{\nu (r)}dt^2-e^{\lambda (r)}dr^2-r^2\left( d\theta ^2+\sin ^2\theta ~d\phi ^2\right) \end{aligned}$$
(1)

where \(\nu \) and \(\lambda \) are functions of the radial coordinate ‘r’ only.

It was proved by Eisenhart [118] that an embedding class one space (\(n+1\) dimensional space \(V^{n+1}\) can be embedded into a \(n + 2\) dimensional pseudo-Euclidean space \(E^{n+2}\)) can be described by a \(n+1\) dimensional space \(V^{n+1}\) if there exists a symmetric tensor \(a_{mn}\) which satisfies the following Gauss–Codazzi equations:

$$\begin{aligned} R_{mnpq}= & {} 2 e a_{m[_p} a_{q]_n} ~~\text{ and }~~ a_{m[n;p]}-\varGamma _{[n p]}^q a_{mq}+\varGamma ^q_{m[_n} a_{p]_q}\nonumber \\= & {} 0, \end{aligned}$$
(2)

where \(e = \pm 1\), \(R_{mnpq}\) denotes the curvature tensor and square brackets represent antisymmetrization. Here, \(a_{mn}\) are the coefficients of the second differential form. Moreover, A necessary and sufficient condition for the embedding class I of Eq. (2) in a suitable convenient form was given by Eiesland [119] as

$$\begin{aligned} R_{0101}R_{2323} = R_{0202}R_{1313}-R_{1202}R_{1303} \end{aligned}$$
(3)

The components of Riemannian tensor for the spherically symmetric interior space–time (1) are given as

$$\begin{aligned} R_{0101}= & {} -{1\over 4}e^\nu \left( -\nu ' \lambda ' +\nu '^{2} +2\nu ''\right) ,\nonumber \\ R_{2323}= & {} -r^2\sin ^2\theta \left( 1-e^{-\lambda }\right) ,~~~ R_{0202}= -{1\over 2}r \nu ' e^{\nu -\lambda }, \nonumber \\ R_{1313}= & {} -{1\over 2}\lambda ' r \sin ^2\theta , ~~~ R_{1202} = 0,~~~R_{1303}=0 \end{aligned}$$
(4)

By plugging the values of above Riemannian components into Eq. (3) we obtain a differential equation in \(\nu \) and \(\lambda \) of the form

$$\begin{aligned} (\lambda ' - \nu ')\nu 'e^\lambda + 2(1-e^\lambda )\nu '' + \nu '^{2} =0. \end{aligned}$$
(5)

The solutions of Eq. (5) are named as “embedding class one solution” and they can be embedded in five dimensional pseudo-Euclidean space.

On integration of Eq. (5) we get

$$\begin{aligned} e^\nu =\left( A+B\int \sqrt{e^\lambda -1}~dr\right) ^2 \end{aligned}$$
(6)

where A and B are constants of integration.

3 Mathematical formalism of f(R, T)-gravity

We devoted this section on how the f(R, T) was introduced. While deriving the Einstein’s field equations from Einstein–Hilbert action, the Ricci scalar is integrated over a four dimensional volume element \(d^4x\) as

$$\begin{aligned} S_{EH} = {1 \over 16\pi } \int R\sqrt{-g}~d^4x. \end{aligned}$$
(7)

Instead, if we choose f(R, T) in place of the Ricci scalar R, one can arrive at the f(R, T) field equations. Here, T being the trace of the stress–energy tensor, \(T_{\mu \nu }\) and the complete action in f(R, T) formalism is given by

$$\begin{aligned} S= & {} \frac{1}{16\pi }\int f(R,T)\sqrt{-g}~ d^{4}x+\int {\mathscr {L}}_{m}\sqrt{-g}~d^{4}x \end{aligned}$$
(8)

with g as the determinant of the metric tensor \(g_{\mu \nu }\). The second term is the source term for which the matter Lagrangian density \({\mathscr {L}}_m\) gives to stress tensor as

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\,\frac{\delta \big (\sqrt{-g}\,{\mathscr {L}}_m \big )}{\delta g^{\mu \nu }}. \end{aligned}$$
(9)

Adopting Harko et al. [47], we ansatz the Lagrangian density \({\mathscr {L}}_m\) is a function of \(g_{\mu \nu }\) only, then one can get from Eq. (9) as

$$\begin{aligned} T_{\mu \nu }=g_{\mu \nu } {\mathscr {L}}_m-2\frac{\partial {\mathscr {L}}_m}{\partial g^{\mu \nu }}. \end{aligned}$$
(10)

By the variation principle w.r.t \(g_{\mu \nu }\), (8) yields the field equations

$$\begin{aligned}&\left( R_{\mu \nu }- \nabla _{\mu } \nabla _{\nu } \right) f_R (R,T) \nonumber \\&\qquad +g_{\mu \nu } \Box f_R (R,T) - \frac{1}{2} f(R,T)g_{\mu \nu } \nonumber \\&\quad = 8\pi ~T_{\mu \nu } - f_T (R,T)~ \Big ( T_{\mu \nu }+\varTheta _{\mu \nu } \Big ), \end{aligned}$$
(11)

where \(f_R (R,T)={\partial f(R,T)}/{\partial R}\) and \(f_T (R,T)={\partial f(R,T)}/{\partial T}\). The \(\nabla _\mu \) denotes covariant derivative and box operator \(\Box \) is defined as

$$\begin{aligned} \Box \equiv {1 \over \sqrt{-g}} {\partial \over \partial x^\mu }\left( \sqrt{-g}~g^{\mu \nu } {\partial \over \partial x^\nu } \right) ~~ \text {with} ~~ \varTheta _{\mu \nu }=g^{\alpha \beta } {\delta T_{\alpha \beta } \over \delta g^{\mu \nu }}. \end{aligned}$$

The covariant derivative Eq. (11) [120] yields

$$\begin{aligned} \nabla ^{\mu }T_{\mu \nu }= & {} \frac{f_T(R, T)}{8\pi -f_T(R,T)}\bigg [(T_{\mu \nu }+\varTheta _{\mu \nu })\nabla ^{\mu }\ln f_T(R,T) \nonumber \\&+\nabla ^{\mu }\varTheta _{\mu \nu }-\frac{1}{2}g_{\mu \nu }\nabla ^{\mu }T\bigg ]. \end{aligned}$$
(12)

which implies that the stress-tensor in f(R, T) do not follow the conservation law as in general relativity. By using Eq. (10), the tensor \(\varTheta _{\mu \nu }\) is found to be

$$\begin{aligned} \varTheta _{\mu \nu }= - 2 T_{\mu \nu } +g_{\mu \nu }{\mathscr {L}}_m - 2g^{\alpha \beta }\,\frac{\partial ^2 {\mathscr {L}}_m}{\partial g^{\mu \nu }\,\partial g^{\alpha \beta }}.~~~ \end{aligned}$$
(13)

To find the field equations explicitly, we further assumed anisotropic fluid source with the energy–momentum tensor of the form

$$\begin{aligned} T_{\mu \nu }=(\rho +p_t) u_\mu u_\nu -p_t g_{\mu \nu }+(p_r-p_t)g_{\mu \nu }, \end{aligned}$$
(14)

provided, \({u_{\nu }}\) is the four velocity, satisfying \(u_{\mu }u^{\mu }= -1\) and \(u_{\nu }\nabla ^{\mu }u_{\mu }=0\), \(\rho \) is the matter density, \(p_r\) and \(p_t\) are the radial and transverse pressures. If we defined the isotropic pressure as \(-{\mathscr {P}}={\mathscr {L}}_m=(p_r+2p_t)/3\) [47], then (13) reduces to

$$\begin{aligned} \varTheta _{\mu \nu }=-2T_{\mu \nu }-{\mathscr {P}}g_{\mu \nu }. \end{aligned}$$
(15)

Further, we need to know the functional f(R, T) so that one can write the final form of the field equations. Therefore, we choose, \(f(R,T)= R+2\chi T\) [47], where \(\chi \) as the coupling constant. Now the field equations (12) takes the form

$$\begin{aligned} G_{\mu \nu }= 8\pi ~T_{\mu \nu }+\chi T~ g_{\mu \nu }+2\chi (T_{\mu \nu }+{\mathscr {P}}g_{\mu \nu }). \end{aligned}$$
(16)

Note that field equations (11) are reduced to Einstein field equations when f(R, T) \(\equiv R\). The assumed linear expression of f(R, T) has been accepted physically advantages while addressing cosmological and astrophysical problems. By substituting \(f(R,T)=R+2\chi T\) and (15) in Eq. (12), we obtain

$$\begin{aligned} \nabla ^{\mu }T_{\mu \nu }=-\frac{\chi }{2(4\pi +\chi )}\bigg [g_{\mu \nu }\nabla ^{\mu }T+2\,\nabla ^{\mu } \big ({\mathscr {P}} g_{\mu \nu } \big )\bigg ]. \end{aligned}$$
(17)

Therefore, the conservation equation in Einstein’s gravity can be recovered for \(\chi =0\).

4 Field equations in f(R, T)-gravity

For the spacetime given in (1), the field equation (16) becomes

$$\begin{aligned} 8\pi \rho _{eff}= & {} e^{-\lambda } \left( {\lambda ' \over r}-{1 \over r^2} \right) +{1 \over r^2} \end{aligned}$$
(18)
$$\begin{aligned} 8\pi p_{reff}= & {} e^{-\lambda } \left( {\nu ' \over r}+{1 \over r^2} \right) -{1 \over r^2} \end{aligned}$$
(19)
$$\begin{aligned} 8\pi p_{teff}= & {} {e^{-\lambda } \over 4}\left( 2\nu ''+\nu '^2+{2(\nu '-\lambda ') \over r}-\nu ' \lambda ' \right) \end{aligned}$$
(20)

where,

$$\begin{aligned} \rho _{eff}= & {} \rho +{\chi \over 24\pi } \Big (9\rho -p_r-2p_t\Big ) \nonumber \\ p_{reff}= & {} p_r-{\chi \over 24\pi } \Big (3\rho -7p_r-2p_t \Big ) \nonumber \\ p_{teff}= & {} p_t-{\chi \over 24\pi } \Big (3\rho -p_r-8p_t \Big ). \end{aligned}$$
(21)

On using the above definitions, the field equations (18)–(20) becomes

$$\begin{aligned} \rho= & {} \frac{e^{-\lambda }}{48 r^2 (\chi +2 \pi ) (\chi +4 \pi )} \Big [r \lambda ' \left\{ 16 (\chi +3 \pi )-r \chi \nu '\right\} \nonumber \\&+16 (\chi +3 \pi ) (e^{\lambda }-1)+r \chi \left\{ 2 r \nu ''+\nu ' \left( r \nu '+4\right) \right\} \Big ]\nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned} p_r= & {} \frac{e^{-\lambda }}{48 r^2 (\chi +2 \pi ) (\chi +4 \pi )} \Big [r \big \{\chi \lambda ' (r \nu '+8)-2 r \chi \nu '' \nonumber \\&+\nu ' \left( 20 \chi -r \chi \nu '+48 \pi \right) \big \}-16 (\chi +3 \pi )(e^{\lambda }-1) \Big ]\nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} p_t= & {} \frac{e^{-\lambda }}{48 r^2 (\chi +2 \pi ) (\chi +4 \pi )} \Big [r \Big \{-\lambda ' \big \{r (5 \chi +12 \pi ) \nu ' \nonumber \\&+4 (\chi +6 \pi )\big \}+2 r (5 \chi +12 \pi ) \nu ''+r (5 \chi +12 \pi ) \nu '~^2 \nonumber \\&+8 (\chi +3 \pi ) \nu '\Big \}+ 8 \chi \left( e^{\lambda }-1\right) \Big ] . \end{aligned}$$
(24)

Solving the above field equations exactly is a difficult task. Many authors have adopted several methods to obtained the solution. Recently, many authors have adopted the embedding class one approach to solve the field equations which often yields physically motivated solutions. Forwarding this technique, we are inspired to apply it in f(R, T)-gravity to solve exactly and its impact on the physical systems.

5 A class one solution in f(R, T)-theory

Since the field equations depend on metric functions \(\nu \) and \(\lambda \). To construct a viable anisotropic model, we have assumed \(g_{rr}\) as

$$\begin{aligned} e^\lambda =1+a r^2 \left( 1+b r^2+c r^4\right) \end{aligned}$$
(25)

where a,  b and c are non-zero positive constants.

By substituting the value of \(\lambda \) from Eqs. (25) into (6) we get

$$\begin{aligned} e^\nu =\left( A+\frac{2 a B\sqrt{c}~ r f_1(r) f_2(r) -f_5(r)}{16 c^{3/2} f_3(r)}\right) ^2 \end{aligned}$$
(26)

where

$$\begin{aligned} f_1(r)= & {} 1+ b r^2+c r^4,~~f_2(r) = b+2 c r^2 \\ f_3(r)= & {} r\sqrt{a f_1(r)},~~f_4(r) = 2 \sqrt{c} \sqrt{f_1(r)}+f_2(r) \\ f_5(r)= & {} a B \sqrt{f_1(r)}~ r (b^2-4 c) \log \left[ f_4(r)\right] \end{aligned}$$

By using the metric potentials \(\nu \) and \(\lambda \), we directly obtain the expression for thermodynamic variables like density, radial and transverse pressure and anisotropy as

$$\begin{aligned} \rho =\frac{\chi _1 f_5(r) \{a f_1(r)^2 r^2+f_9(r)\}-2 \sqrt{c} f_{17}(r)}{3 f_{11}(r) (\chi +2 \pi ) (\chi +4 \pi ) f_7(r)^2} \end{aligned}$$
(27)

where

$$\begin{aligned} f_6(r)= & {} \left[ a f_1(r)^2-f_2(r)\right] ,~~ f_7(r) = 1 + a r^2 f_1(r) \\ f_8(r)= & {} 8 A c f_3(r)+a B f_1(r) f_2(r) r \\ f_9(r)= & {} 3+ 5 b r^2+7 c r^4,~~\chi _1 = \chi +3 \pi \\ f_{10}(r)= & {} 9 \pi +5 \chi + 9 c r^4 \chi +21 \pi c r^4 \\ f_{11}(r)= & {} f_5(r) - 2 \sqrt{c} f_8(r)(r) \\ f_{12}(r)= & {} 4 A \chi _1 \left[ 1 +c r^4\right] f_3(r)+B r f_{10}(r) \\ f_{13}(r)= & {} \chi _1 + 7 c r^4 \chi +17 \pi c r^4 \\ f_{14}(r)= & {} 8 A c r^3 \chi _1 f_3(r)+3 B f_{13}(r) \\ f_{15}(r)= & {} 5 b^2 B r^2 \chi _1+b f_{14}(r)+2 c f_{12}(r) r \\ f_{16}(r)= & {} 4 A \chi _1 f_9(r)f_3(r)+ B r \chi \left[ 3+ 4 b r^2+5 c r^4\right] \\ f_{17}(r)= & {} a^2 B f_2(r) f_1(r)^3 r^3 \chi _1+a f_{15}(r) f_1(r) r+2 c f_{16}(r) \\ f_{18}(r)= & {} 9+ 8 b r^2+7 c r^4\\ \end{aligned}$$
$$\begin{aligned} p_r=\frac{a \left[ 2 \sqrt{c} g_7(r)-g_8(r)f_5(r)\right] }{3 g_{10} (\chi +2 \pi ) (\chi +4 \pi ) f_7(r)^2} \end{aligned}$$
(28)

where

$$\begin{aligned} g_1(r)= & {} 8 A c r^3 \chi _1 f_3(r)+3 B \left[ \pi -8 c r^4 \chi -13 \pi c r^4 \right] \nonumber \\ g_2(r)= & {} \chi f_{18}(r)+24 \pi f_1(r) \nonumber \\ g_3(r)= & {} B g_2(r) r-4 A f_3(r) \left[ 3 \pi f_1(r)-f_2(r) r^2 \chi \right] \nonumber \\ g_4(r)= & {} 2 \chi \left[ 5+ 6 c r^4\right] +21 \pi \left[ 1 + c r^4\right] \nonumber \\ g_5(r)= & {} B g_4(r) r-4 A \chi _1 \left[ 1+c r^4\right] f_3(r) \nonumber \\ g_6(r)= & {} b^2 B r^2 [3 \pi -\chi ]+b g_1(r)-2 c g_5(r) r \nonumber \\ g_7(r)= & {} a^2 B f_2(r) f_1(r)^3 r^3 \chi _1+a f_1(r) g_6(r) r-2 c g_3(r)\nonumber \\ g_8(r)= & {} r^2 \chi f_6(r) +3 \pi f_1(r)f_7(r)\nonumber \\ g_9(r)= & {} 8 A c f_3(r)+a B f_1(r) f_2(r) r \nonumber \\ g_{10}(r)= & {} f_5(r)-2 \sqrt{c} g_9(r)\nonumber \\ \varDelta= & {} \frac{a r^2 f_6(r) \left[ 2 \sqrt{c} \{h_2(r)-8 B c r\}-f_5(r)\right] }{2 (\chi +4 \pi ) f_7(r)^2 \left[ 2 \sqrt{c} h_2(r)-f_5(r)\right] }. \end{aligned}$$
(29)

where,

$$\begin{aligned}&h_1(r) = b^2 r^2+3 b c r^4+b+2 c r^2 \left( c r^4+1\right) \\&h_2(r) = 8 A c f_3(r)+a B r h_1(r) \end{aligned}$$

The variations of the above physical quantities are given in Figs. 2, 3 and 4. We should ensure that values of \(p_r /\rho \) and \(p_t/\rho \) at the interior must be less than unity for a physical system (Fig. 5).

The other physical parameters such as mass, compactness factor and red-shift can be determine as

$$\begin{aligned} m(r)= & {} {r\over 2}\left( 1- e^{-\lambda }\right) \nonumber \\= & {} {r\over 2}\left[ 1 - \frac{1}{1+ar^2\left( 1+b r^2 + c r^4\right) }\right] \end{aligned}$$
(30)

6 Boundary conditions and determination of constants

It is necessary that we should match our interior space–time to the exterior Schwarzschild [121] line element

$$\begin{aligned} ds^2= & {} \left( 1- {2 m\over r}\right) dt^2-\left( 1- {2 m\over r}\right) ^{-1}dr^2 \nonumber \\&-r^2\left( d\theta ^2+\sin ^2\theta ~d\phi \right) \end{aligned}$$
(31)

at the boundary \(r = R\).

Using the continuity of the metric coefficients \(e^\nu \) and \(e^\lambda \) across the boundary (\(r = R\)) and vanishing of radial pressure at the boundary (\(r = R\)) we get the following equations

$$\begin{aligned}&1-{2M\over r} = e^{\nu _s}=e^{-\lambda _s} \end{aligned}$$
(32)
$$\begin{aligned}&p_r(r=R)=0. \end{aligned}$$
(33)

On using the boundary conditions (32) and (33) we obtain the value of arbitrary constants as,

$$\begin{aligned} a= & {} -\frac{2 M}{R^2 [2 M-R] \left[ 1+b R^2+c R^4\right] } \\ A= & {} \sqrt{1-\frac{2 M}{R}} -\frac{2 a B \sqrt{c} R f_1(R) f_2(R) -f_5(R)}{16 c^{3/2} f_3(R)} \nonumber \\ B= & {} \frac{4 f_3(R) \sqrt{1-\frac{2 M}{R}}\left[ 3 \pi f_1(R)f_7(R)+\chi R^2 f_6(R)^2 \right] }{24 \pi R f_1(R) f_7(R) + R \left[ f_{18}(R) + 10 a R^2 f_1(R)^2 \right] \chi } \nonumber \end{aligned}$$
(34)

7 Energy conditions

In this section we are willing to verify the energy conditions namely null energy condition (NEC), dominant energy condition (DEC) and weak energy condition (WEC) at all points in the interior of a star which will be satisfied if the following inequalities hold simultaneously:

$$\begin{aligned} WEC&: T_{\mu \nu }t^\mu t^\nu \ge 0 ~~\textit{or} ~~ \rho \ge 0,~~~ \rho + p_i \ge 0 \end{aligned}$$
(35)
$$\begin{aligned} NEC&: T_{\mu \nu }l^\mu l^\nu \ge 0 ~~\textit{or}~~\rho + p_i \ge 0 \end{aligned}$$
(36)
$$\begin{aligned} DEC&: T_{\mu \nu }t^\mu t^\nu \ge 0 ~~\textit{or}~~ \rho \ge \mid p_i \mid \end{aligned}$$
(37)
$$\begin{aligned}&\quad \text{ where }~~ T_{\mu \nu }t_\mu \in ~~ \text{ nonspace-like } \text{ vector } \nonumber \\ SEC&: T_{\mu \nu }t^\mu t^\nu -{1\over 2} T^{\lambda }_{\lambda } t^\sigma t_\sigma \ge 0 ~~\textit{or}~~ \rho + \sum _i p_i \ge 0. \end{aligned}$$
(38)

where \(i \equiv (radial~ r,~~ transverse~ t)\), \(t^\mu \) and \(l^\mu \) are time-like vector and null vector respectively.

We will check the energy conditions with the help of graphical representation. In Fig. 7, we have plotted the L.H.S of the above inequalities which verifies that all the energy conditions are satisfied at the stellar interior.

8 Stability and equilibrium of the model

8.1 Equilibrium under various forces

Equilibrium state under three forces vi z gravitational, hydrostatics and anisotropic forces can be analyze whether they satisfy the generalized Tolman–Oppenheimer–Volkoff (TOV) equation or not and it is given by

$$\begin{aligned} -\frac{M_g(r)\left( \rho + p_r\right) }{r}e^{\frac{\nu - \lambda }{2}} - {dp_r\over dr} +{2\over r}\left( p_t - p_r\right) =0 , \end{aligned}$$
(39)

where \(M_g(r)\) represents the gravitational mass within the radius r , which can derived from the Tolman–Whittaker formula and the Einstein field equations and is defined by

$$\begin{aligned} M_g(r)=4\pi \int _0^r \left( T_t^t - T_r^r -T_\theta ^\theta -T_\phi ^\phi \right) r^2 e^{\frac{\nu +\lambda }{2}}dr . \end{aligned}$$
(40)

The above Eq. (40) reduced to

$$\begin{aligned} M_g(r) = \frac{1}{2} r\, e^{\frac{\left( \lambda -\nu \right) }{2}}\nu '. \end{aligned}$$
(41)

Plugging the value of \(M_g(r)\) in Eq. (39), we get

$$\begin{aligned}&-\frac{\nu '}{r}\left( \rho +p_r\right) -{dp_r\over dr}+{2\over r}\left( p_t-p_r\right) \nonumber \\&+ \frac{\chi }{3(8\pi +2\chi }{d\over dr}\left( 3\rho + p_r - 2 p_t\right) =0. \end{aligned}$$
(42)

The above expression may also be written as

$$\begin{aligned} F_g + F_h + F_a + F_{frt}= 0, \end{aligned}$$
(43)

where \(F_g\), \(F_h\), \(F_a\) and \(F_{frt}\) represents the gravitational, hydrostatics, anisotropic forces and extra term due to FRT modification respectively and can be written as,

$$\begin{aligned} F_g= & {} -\frac{\nu '}{r}\left( \rho +p_r\right) \end{aligned}$$
(44)
$$\begin{aligned} F_h= & {} -{dp_r\over dr} \end{aligned}$$
(45)
$$\begin{aligned} F_a= & {} \frac{2 \varDelta }{r} \end{aligned}$$
(46)
$$\begin{aligned} F_{frt}= & {} \frac{\chi }{3(8\pi +2\chi )}{d\over dr}\left( 3\rho - p_r-3 p_t\right) . \end{aligned}$$
(47)

The profile of three different forces are plotted in Fig. 8 and we can see that the system is in equilibrium state.

8.2 Causality and stability condition

In this section we are going to find the subliminal velocity of sound and stability condition. For a physically acceptable model of anisotropic fluid sphere the radial and transverse velocities of sound should be less than 1, which is known as the causality condition. The radial velocity (\(v_{sr}^2\)) and transverse velocity (\(v_{st}^2\)) of sound can be obtained as

$$\begin{aligned} v_r^2 = \frac{dp_r}{d\rho },~~~~v_t^2=\frac{dp_t}{d\rho } \end{aligned}$$
(48)

8.3 Adiabatic index and stability condition

For a relativistic anisotropic sphere the stability is related to the adiabatic index \(\varGamma \), the ratio of two specific heats, defined by [122],

$$\begin{aligned} \varGamma _r = \frac{\rho +p_r}{p_r}\frac{dp_r}{d\rho } \end{aligned}$$
(49)

Now \(\varGamma _r > 4/3\) gives the condition for the stability of a Newtonian sphere and \(\varGamma = 4/3\) being the condition for a neutral equilibrium proposed by [123]. This condition changes for a relativistic isotropic sphere due to the regenerative effect of pressure, which renders the sphere more unstable. For an anisotropic general relativistic sphere the situation becomes more complicated, because the stability will depend on the type of anisotropy.

8.4 Harrison–Zeldovich–Novikov static stability criterion

The stability analysis of Harrison et al. [124] and Zeldovich and Novikov [125] have shown that the adiabatic index of a pulsating star is same as in a slowly deformed matter. This leads to a stable configuration only if the mass of the star is increasing with central density i.e. \(\partial m/\partial \rho _c > 0\) and unstable if \(\partial m/\partial \rho _c < 0\). Figure 13 shows that the mass increases with increase in central density i.e. \(\partial m/\partial \rho _c > 0\), hence static stability criterion is fulfilled. It can also be noted that with the increase in \(\chi \)-parameter the range of perturbed density also increases. Therefore, during radial perturbations the change in density can be accommodate within the stable limit thus stabilizing the perturbed system.

8.5 Equation of state

In the investigation of compact stellar systems such as neutron stars, it is very important to know how the master thermodynamic factors are connected. This connection known as the EoS leads to a relationship between radial pressure \((p_r)\) and energy density \((\rho )\). The microphysics, as portrayed by the EoS, is connected to the macroscopic properties of the neutron star, specifically, their radii and masses, by means of the TOV equations, which give the immediate relation that is necessary to utilize astrophysical perceptions to restrict nuclear physics at very high densities. Nevertheless, the composition of a neutron star mainly relies upon the type of strong interactions, which are not well-understood in dense matter. Most models that have been studied can be advantageously gathered into three general classifications: non-relativistic potential models, relativistic field theoretical models, and relativistic Dirac–Brueckner–Hartree–Fock models. In addition, in every one of these methodologies, the presence of extra softening components, for instance, hyperons, Bose condensates, or quark matter can be incorporated. Subtleties of these methodologies have been additionally considered in Lattimer et al. [126] and Prakash et al. [127]. On the other hand, there are two general classes of EoS. First, normal EoS has a pressure which disappears when the density tends towards zero. Second, self-bound EoS have a pressure that disappears at an important finite density. Regard to the self-bound EoS the most popular model is the MIT bag model EoS. It was emphasized by Witten [128] that strange quark matter is the ultimate fundamental state of matter. This prompts the way that the inward and outside vacuum densities of the hadrons are totally different and that the vacuum pressure of the bag wall equilibrium the pressure of the quarks, stabilizing the ensemble system [129, 130]. In this way, the quark matter EoS then reads, \(p=1/3(\rho - 4B)\), where B is named bag constant and depicts the dissimilarity between the energy density of the perturbative and non-perturbative QCD vacuum. In this system, the interactions of quarks and gluons are sufficient small, neglecting quark masses and assuming that quarks are constricted to the bag volume. Regarding ordinary matter, the EoS portrays an interacting nucleon gas above a transition density \(1/3 \times \rho _{surface}\) to \(1/2 \times \rho _{surface}\), where \(\rho _{surface}\) is the surface density. Beneath this density, the fundamental state of matter comprises of dense nuclei in balance with a neutron-rich, low-density gas of nucleons. Regardless, the balance of the framework exists beneath the transition density [131, 132]. In this way, so as to clarify the auxiliary properties of compact stellar structures model at high densities, several authors have suggested the EoS \(p_r=p_r(\rho )\) ought to be very much approximated by a linear function of the energy density [133,134,135]. Moreover, a linear relationship between the radial pressure and the energy density guarantees the conservation of causality condition.

The EoS of the matter interior the stellar structure, \(p_r=p_r(\rho )\) for our stellar model is described in Fig. 12. Generally for these sort of models there is an approximately linear reliance of the pressure on the energy density of the matter. We can give an equation dependent on radial pressure and matter density i.e. likely EoS which has an major importance in the arena of astrophysics. So, in Fig. 12 we can graphically acknowledge the form of the EoS of the stellar model under investigation. Despite the complex relationship given between the radial pressure and energy density, the comportment that arises from the surface to the core of the object is approximately linear (the curves increases from regions of low to high densities). With this curve of the pressure-density relation, a simple polynomial linear interpolation of the standard equations of stellar structure can be described approximately by the following expression

$$\begin{aligned} p_r = \alpha (\rho -\rho _s), \end{aligned}$$
(50)

where \(\alpha \) is a non-negative constant. In this respect, it is clear from the above expression (Eq. 50) that when the radius coincides with the surface radius i.e \(r=R\) then the radial pressure vanishes i.e \(p_r=0\). This is so due to the energy density at zero pressure (surface energy density) i.e. \(\rho (R)=\rho _s\), which is generally a non-zero quantity. However, if the EoS obey polytropic form than the density vanishes at the boundary where \(p_r=0\).

9 Results and discussions

Modified gravity theories provide a significant possibility for resolving or avoiding certain problems encountered when regarding general relativity as the basic theory of gravity. One of the most formidable attributes of prolonged theories is the incorporation of coupling among gravitational and matter components that has prompted various scientists to uncover the shrouded mysteries of dark side (dark matter and dark energy). In this respect, we have worked with a specific modified gravity, so-called f(R, T) theory. Furthermore, we have taken simplified linear form of the arbitrary function f(R, T) given as \(f(R, T)=R+2\chi T\), where \(\chi \) is a dimensionless coupling constant, and the Lagrangian matter \({\mathscr {L}}_m=-{\mathscr {P}}=(p_r+2p_t)/3\) which has been provided by Harko et al. [47], to portray the complete solution of modified field equations for the distribution of anisotropic matter. The dependence on T of the theory can be due to the taking into account quantum effects (conformal anomaly), generating a potential path towards a quantum gravity theory, or to the conceivable presence of exotic imperfect fluids in the universe. This dependence on the coupling between terms of matter and curvature in alternative theories plays a fundamental role in the description of the attractive problem of cosmic accelerated expansion. The motivation of introducing trace of the stress–energy tensor may begin from the outcomes of some obscure gravitational co-operations or the effects of some fascinating fluid. It is anticipated that such coupling gives the non-vanishing conservation of stress–energy tensor as in other theories of gravity [59, 61]. Subsequently, an extra force emerges because of which huge test particles pursue the non-geodesic way while dust particles pursue the geodesic lines.

Our study is committed to a new class of generalized solutions for the anisotropic spherically symmetric relativistic stars. In our research, we adopted the embedding class one approach where a 4-dimensional inside space–time is embedded into the 5-dimensional flat Euclidean space within the framework of f(R, T) gravity theory, in order to obtain general solutions of the modified Einstein field equations. Significantly, it is demonstrated that for our system by considering the stress–energy tensor due to the complete matter distribution, we get the usual form of the energy conservation equation in Eq. (17). We have adopted the embedding class one approach to resolve the gravitational field equations which often yields physically motivated solutions. Forwarding this approach by considering the radius-radius component of the gravitational potential to be \(e^\lambda = 1+a r^2 (1+b r^2+c r^4)\) and we get the time-time component of the gravitational potential \(e^\nu \) in Eq. (26), in order to resolve exactly and its effect on the physical system in f(R, T) gravity.

Throughout our analysis and study of the physical discussions of the accomplished solutions, we have been taking into account a compact stellar configuration, namely an X-ray pulsar binary i.e., SMC X-4, having the observed mass as \(M = 1.29~M_\odot \) [136]. We present our outcomes for the diverse chosen parametric values of \(\chi \), viz., \(\chi =-1, -0.5, 0\), 0.5, 1, so as to derive unknown values of the different arbitrary constants of the astrophysical system in f(R, T) gravity. We presented the fundamental physical amounts that describe the stellar system. These amounts are the metric potentials, the density profile, the radial and transverse pressure profiles, anisotropy profile, equation of state parameter profiles, red-shift profile, energy conditions, TOV-equation profile, Velocity of sound profile, Stability factor profile and Adiabatic index profile. It is notable that in the investigation of anisotropic compact stellar configurations, all the amounts referenced above fulfill all the general prerequisites so as to portray a well behaved astrophysical inside. These general prerequisites are summarized as follows:

Fig. 1
figure 1

Variation of metric potentials w.r.t radial coordinate r for \(M =1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image
Fig. 2
figure 2

Density profile of SMC X-4 w.r.t radial coordinate r for \(M =1.29 M_\odot \), \(R = 8.831\) km and \(b = 0.0031 \,{\text {km}}^{-2}\)

Full size image
Fig. 3
figure 3

Radial and transverse pressure profile of SMC X-4 w.r.t radial coordinate r for \(M =1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image

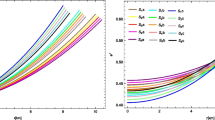
  • We have displayed the profile of physical amounts of both gravitational potentials, in particular, \(e^\lambda \) (in the upper panel) and \(e^\nu \) (in the lower panel) with respect to the radial coordinate r in Fig. 1, which show that these two physical amounts are finite at the origin and monotonically increasing towards the boundary at the surface. Figures 2 and 3 shown the density profile and the radial and transverse pressure profiles respectively. The three amounts have their greatest values at the core and decrease monotonically towards the limit with expanding radius. It is seen that the radial pressure is disappeared at the surface, this fact decides the anisotropic compact stellar structure size i.e. the radius of the spherical object. Besides, the value of \(\chi \) preponderantly affects the radial and transverse pressures, as should be obvious changing \(\chi \) from \(-1\) to 1, the upper value of radial pressure and transverse pressure increments with expanding \(\chi \), notwithstanding, the matter density is positive defined wherever inside the anisotropic compact stellar structure. All these physical amounts specifically appeared in Figs. 1, 2 and 3, viz., time-time component, radius–radius component, matter density, radial pressure and transverse pressure which mentioned above are free from mathematical singularities and with their most extreme values accomplished at the core of the anisotropic compact stellar configuration.

Fig. 4
figure 4

Anisotropy profile of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image
Fig. 5
figure 5

Equation of state parameter profiles of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image

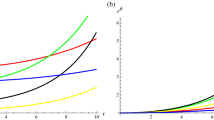
  • The plot corresponding to the anisotropy profile against radial coordinates r, which shows the behaviour of anisotropy factor wherever interior the astrophysical object is represented in Fig. 4. At the core of the spherical object \(\varDelta =0\), in effect at the core \(p_r=p_t\). In addition, as increment \(\varDelta \) grow up. Furthermore, the anisotropy factor is positive \(\varDelta >0\), it implies that \(p_t>p_r\) and in this manner one has a more compact and huge configurations. For this situation, the system encounters a repulsive force that balances the gravitational slope improving the equilibrium condition and steadiness. We note from Fig. 5 that the equation of state parameters corresponding to \(\omega _{r}={p_r}/{\rho }\) and \(\omega _{t}={p_t}/{\rho }\) with respect to the radial coordinate r are under 1, which proves that the physical system is well-respected wherever interior the compact stellar structure within the framework of f(R, T) gravity theory.

Fig. 6
figure 6

Red-shift profiles of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image

  • Regarding the surface redshift \(Z_s\), in the situation of isotropic matter distribution, the most extreme value that it can attain is \(Z_s=2\), which is in absolute concurrence with the Buchdahl’s limit \(u=M/R \le 4/9\). At that point from Eq. (30), we see that the gravitational red-shift of spherical object cannot be arbitrarily enormous due to Buchdahl’s limit. All things considered, when anisotropies are available into the matter content this limit can be surpassed. Toward this path Ivanov [137] indicated that for a achievable anisotropic spherical object models the upper bound of \(Z_s\) is 5.211, which corresponds to a model without cosmological constant and can not be surmounted. As Eq. (30) shows \(Z_s\) relies upon the \(e^{\lambda }\) gravitational potential. On the other hand in Fig. 6, we have shown graphically the surface red-shift with the compact star. From this figure, it is established that the gravitational red-shift inside standard value findings by Ivanov’s [137] which leads to the physical validity of the matter distribution of our astrophysical model.

Fig. 7
figure 7

Energy conditions of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image

  • From Fig. 7 it is seen that all inequalities mentioned above in (35)–(38) are fulfilled simultaneously at the stellar interior for various values of \(\chi \) coupling constant. Furthermore, the fact that the inequalities (35)–(38) known as the energy conditions are fulfilled averts non-physical domains, such as energy propagating quicker than the speed of light, negative matter density or void space willingly decomposing into remunerating districts of negative and positive energy.

Fig. 8
figure 8

TOV-equation profile of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image

  • Further, we have generated the four forces, namely, the hydrodynamic force (\(F_h\)), gravitational force (\(F_g\)), anisotropic force (\(F_a\)) and extra force (\(F_{frt}\)) arises due to f(R, T) gravity as mentioned in Eqs. (44)–(47) which gives the equilibrium of our stellar system. The profile of these four forces is emphatically connected to the values taken by the \(\chi \) coupling constant. From Fig. 8 we can perceive how the equilibrium of the stellar system is achieved under these various forces. In this way, we can feature certain points corresponding to the various values doled out to the parameter \(\chi \) in Fig. 8. In this plot, \(\chi \) parameter takes esteems \(-1, -0.5, 0, 0.5\) and 1, respectively. It is remarkable the impact of \(\chi \) parameter has on the conduct of hydrostatic force, extra force and gravitational force. As should be obvious, when \(\chi \) expands the hydrostatic and gravitational forces increment however the extra one diminishes. In spite of the fact that the extra force diminishes when \(\chi \) expands, the augmentation of the hydrostatic force toward this path keeps up the equilibrium of the system (the equivalent happens when \(\chi \) diminishes, for this situation the extra force increments and the hydrostatic force diminishes), this implies there is a supplement between the conduct of the two forces to counteract the gravitational gradient. Then again, the anisotropic force, although very weak compared to the other forces, is repulsive in nature from \(\varDelta >0\), which supports to counterbalance the gravitational force together with the hydrostatic and extra forces. According to the previous discussion, it is clear that the examination under four various forces that act on the spherical object gives an increasingly steady, compact and massive system.

Fig. 9
figure 9

Velocity of sound profiles of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image
Fig. 10
figure 10

Stability factor (\(v_t^2-v_r^2\)) profiles of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image
Fig. 11
figure 11

Adiabatic index profiles of SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image

  • With regard to the the steadiness of the astrophysical system, it was examined by analyzing the causality condition Abreu’s criterion, the adiabatic index \(\varGamma \) and the Harrison–Zeldovich–Novikov static stability criterion. The graphical portrayal of causality condition Abreu’s criterion is appeared in Figs. 9 and 10, for different values of \(\chi \) coupling constant. This indicates that our stellar model is totally steady, in light of the fact that the subliminal velocity of sound is under 1 wherever inside the spherical object. Furthermore there is no change in sign \(v^2_{t}-v^2_{r}\) and stability factor (\(v^2_{t}-v^2_{r}\)) lies somewhere in the range of \(-1\) and 0 for steady structure and 0 to 1 for unsteady structure. The graphical depiction of adiabatic index \(\varGamma \) is showed up in Fig. 11. This exhibits that our considered compact stellar systems show dynamical steady configuration for the picked values of coupling constant \(\chi \) as the value of \(\varGamma >4/3\). This shows that our considered anisotropic compact star models are inside the steadiness range even in the existence of curvature terms present in f(R, T) useful structure (Figs. 12, 13).

Fig. 12
figure 12

Behavior of equation of state for SMC X-4 for \(M = 1.29 M_\odot \), \(R = 8.831\) km and \(b =0.0031\,{\text {km}}^{-2}\)

Full size image
Fig. 13
figure 13

M–\(\rho _c\) curve and verification of static stability criterion

Full size image
Fig. 14
figure 14

M–R curve fitted with observed masses and estimation the radii for different values of \(\chi \)

Full size image
Table 1 Fitting of observed masses and radii with new predictions of radii w.r.t. \(\chi \)-parameter
Full size table

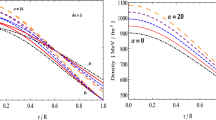
  • The beauty of this new solution is not only the embedding class one solution in f(R, T)-gravity but also in its \(M-R\) curve (Fig. 14). The \(M-R\) curve generated from this solution can accommodate a variety of compact stars from the less massive (Her X-1) to super massive (MSP J0740+6620). In Table 1 we have chosen 6 compact stars and their predicted radii for different values of \(\chi \)-coupling parameter. From this one can agree that the solution predicted the radii in good agreement with the observed values. Since the radius of MSP J0740+6620, the most massive neutron star observed yet is still unknown, we have predicted its radii for different values of \(\chi \).

As we have seen that the presented solution satisfy a variety of physically acceptable criteria and its M–R curve fitted quite well with observational values, one can immediately conclude that the solution might have astrophysical significance in future works.